- 1Department of Atmospheric, Oceanic, and Earth Sciences, George Mason University, Virginia, VA, United States
- 2Department of Geography and Geoinformation Science, George Mason University, Virginia, VA, United States
Episodes of extreme heat are increasing globally, and dry land surface states have been implicated as an amplifying factor in several recent heat waves. Metrics used to quantify land-heat coupling in the current climate, relating sensible heat fluxes to near-surface air temperature, are applied to multimodel simulations of the past, present, and future climate to investigate the evolving role of land–atmosphere feedbacks in cases of extreme heat. Two related metrics are used: one that describes the climatological state of land-heat coupling and one that gives an episodic estimate of land feedbacks, here defined as the metric’s value at the 90th percentile of monthly mean temperatures. To provide robust statistics, seasonal multimodel medians are calculated, with the significance of changes determined by the degree of model consensus on the sign of the change. The climatological land-heat coupling mirrors other metrics of land–atmosphere interaction, peaking in transition regions between arid and humid climates. Changes from preindustrial to recent historical conditions are dominated by decreased land surface controls on extreme heat, mainly over the broad areas that have experienced expanded or intensified agriculture over the last 150 years. Future projections for increased atmospheric CO2 concentrations show a waning of areas of weakened land-heat feedbacks, while areas of increasing feedbacks expand over monsoon regions and much of the midlatitudes. The episodic land-heat metric is based on anomalies, which creates a quandary: how should anomalies be defined in a nonstationary climate? When the episodic coupling is defined relative to the means and variances for each period, a broadly similar evolution to the climatological metric is found, with historically dominant decreases giving way to widespread moderate increases in future climate scenarios. Basing all statistics on preindustrial norms results in huge increases in the coupling metric, showing its sensitivity to the definition of anomalies. When the metric is reformulated to isolate the impact of changing land and temperature variability, the tropics and Western Europe emerge as regions with enhanced land feedbacks on heatwaves, while desert areas and much of the remainder of the midlatitudes show reduced land-heat coupling.
1 Introduction
Episodes of extreme heat are a growing concern as recent heat waves continue to display unusual intensity across more locations (Albergel et al., 2019; Petch et al., 2020; Yiou et al., 2020; Neal et al., 2022). There is growing evidence of the key role that land surface conditions play in exacerbating and prolonging heatwaves (Fischer et al., 2007; Hauser et al., 2016; Hirsch et al., 2019; Schumacher et al., 2019; Wehrli et al., 2020; Benson and Dirmeyer, 2021; Dirmeyer et al., 2021). Extreme heatwave periods with distinct soil moisture deficit signatures and climatological anomalies are often characterized by reductions in terrestrial evaporative cooling and increasing air temperature in parallel with elevated soil moisture deficits and atmospheric demand for water. Such perturbations in soil moisture contribute to dramatic variability in land–atmosphere interactions and seasonality disruption, thereby affecting surface heat and moisture fluxes and atmospheric conditions. Thus, they are also critically linked to hydrologic extremes (Zscheischler et al., 2018; Bevacqua et al., 2022; O et al., 2022). These relationships present an opportunity to interpret the mechanisms driving heatwave patterns in changing climate regimes (Seneviratne et al., 2010; Lau and Nath, 2014; Ukkola et al., 2018; Miralles et al., 2019).
Land–atmosphere interactions and their associated feedback sensitivities are acknowledged as vital components of the Earth system that affect extremes such as droughts and heatwaves (Santanello et al., 2018). Miralles et al. (2012) developed a relatively simple and straightforward pair of metrics to quantify the role of land surface anomalies in extreme heat, ostensibly in the form of soil moisture, but expressed through variations in surface heat fluxes between land and atmosphere. They put forward two metrics, one to quantify the climatology of land-heat feedbacks in any location and the other to identify whether specific heatwave episodes are augmented by land–atmosphere feedbacks. Their study applied the metrics to recent climate data from observationally based sources.
In this study, we adapt the metrics of Miralles et al. (2012) to apply to a host of climate model simulations of past, recent, and future climates. Given the constraints of those metrics, we ask several questions. What patterns exist for extreme heat anomalies under preindustrial conditions? How has heatwave intensity changed since the preindustrial period? How might heatwave susceptibility change with a doubling and/or quadrupling of anthropogenic-induced greenhouse gas emissions (CO2)? What conclusions may be drawn from the spatiotemporal variability of heatwave anomalies with the introduction of warming relative to preindustrial conditions? A major point that emerges from this study is the quandary of finding meaningful definitions of extreme heat in a warming climate and the role of the land surface therein. Section 2 describes the data sets, the metrics, and how they are applied to climate model output. Results are presented in Section 3, first for the climatological metric and then for the episodic one applied to the 90th percentile of extreme heat in climate model simulations. The conclusion is presented in Section 4.
2 Materials and methods
To quantify land surface feedback in the manner of Miralles et al. (2012), particularly their episodic coupling metric
The analysis is performed on three CMIP6 Diagnostic, Evaluation, and Characterization of Klima (DECK) simulations, which are the most numerous: 1) preindustrial control simulations (piControl), 2) historical simulations, and 3) emission-driven simulations, that is, 1% per year CO2 increase (1pctCO2). Table 1 lists the experiments and periods used. piControl simulations provide the baseline climatology for all comparisons. Historical simulations include multiple climate-forcing factors beyond CO2, including time-varying land cover and aerosols. 1pctCO2 runs are idealized simulations in which atmospheric CO2 is increased by 1% per year, beginning from piControl conditions, with no other changes. The 1pctCO2 runs were chosen for future simulations as they are available from many models and represent transience in the major climate forcing. The comparison between these historical and emission-forcing experiments to the piControl baseline provides an indication of how land surface feedbacks may have changed and contributed to extreme heatwave patterns since preindustrial conditions. For the 1pctCO2 simulation, two periods are considered from each model: 1) years 21–70, during which atmospheric CO2 concentrations double from ∼23% above preindustrial levels and 2) years 91–140 wherein atmospheric CO2 concentrations ultimately quadruple beyond preindustrial levels.
The strength of land surface coupling in relation to extreme heat is quantified using the soil moisture and near-surface temperature coupling metric described by Miralles et al. (2012):
where r is Pearson’s correlation coefficient,
where
whereby the sum of model sensible and latent heat represents net radiation, the P–T coefficient is
It should be noted that despite the title of the Miralles et al. (2012) article, the role of soil moisture is only inferred as a potential control on
In addition to the climatological metric
The overbars indicate a temporal mean (in this case, a climatological mean for each month of the year), while
While the climatological and land-heat metrics in Miralles et al. (2012) were derived using daily data, monthly means were extracted from CMIP6 climate model simulations in this study. The main impact of this approach is that a different timescale of extreme heat is sampled to compare temperature anomalies and associated land feedbacks over monthly periods; in this case, variations shorter than 1 month are not considered. Consequently, due to the highly nonlinear nature of moist thermodynamics, these calculations performed on monthly mean data will not be identical to computing monthly means based on daily observations. However, to investigate climate change, it is important to apply consistent formulation to all models in all cases, such that taking differences between experiments may ameliorate any systematic biases introduced by the application of these metrics to longer time scales.
The extreme heat coupling metrics are calculated separately for each month based on the respective experimental period wherein monthly values are seasonally averaged. For each model, metrics are calculated on its native grid, and then data from each model are regridded with nearest neighbor interpolation to a common, high-resolution global grid (2560 × 1280, roughly 0.14° × 0.14° grid cells) to preserve the spatial structure contribution from each model (Dirmeyer et al., 2013a; Dirmeyer et al., 2013b and several subsequent studies). Nearest neighbor interpolation, combined with the use of each model’s land–sea mask, removes the risk of introducing data from adjacent water-covered grid cells. Effectively, for the central latitude and longitude of each grid cell of the 2560 × 1280 grid, we find the value in each model’s unique grid cell that contains that coordinate, combine the data from all models for that location, and take the median. Only ice-free land grid cells common to at least 90% of the models on the high-resolution grid are populated with the data.
To compute the monthly mean metrics, surface sensible heat flux information is extracted directly from 30 CMIP6 models, whereas in Miralles et al. (2012), net radiation and surface latent heat flux were used to estimate surface sensible heat flux. However, most of these models do not provide net radiation or ground heat flux data; thus, surface potential sensible heat flux is estimated with the application of the P–T equation. Despite the integration of CMIP-derived monthly mean data as opposed to daily datasets, this approach does have a successful precedent for climate change investigations (e.g., Dirmeyer et al., 2013a; Dirmeyer et al., 2013b). Finally, monthly means are averaged to produce seasonal means. Field significance is tested using the approach outlined by Dirmeyer et al. (2013a) and Dirmeyer et al. (2013b).
We calculate for each model the 90th percentile value of
Defining the standard deviations of temperature and the two sensible heating variables also presents choices, and these choices depend directly on how the means are defined. For example, if
For comparisons, the 90th percentile value of
Finally, the significance of change is defined by the level of agreement among models, inasmuch as this can be considered an indicator of certainty (Pirtle et al., 2010; Parker, 2013; Brunner et al., 2020). Specifically, under the null hypothesis that each model will return a random sign of the difference between two cases with equal probability, the level of agreement among models is significant at the 99% confidence level if 22 or more models have the same sign of the change (p = 0.008). Such a stringent confidence level somewhat ameliorates the degree of agreement that may arise because we have included in our 30-model ensemble related models from within several modeling centers (see Supplementary Table S1). Furthermore, grid cells are masked white in difference plots when this confidence level is not met. As we are examining metrics related to extreme heat, we also do not consider grid cells at any location where the seasonal mean temperature in the warmest case is at or below 0°C.
3 Results
3.1 Climatological coupling
Figure 1 shows the multimodel median value of the climatological soil moisture–temperature coupling metric
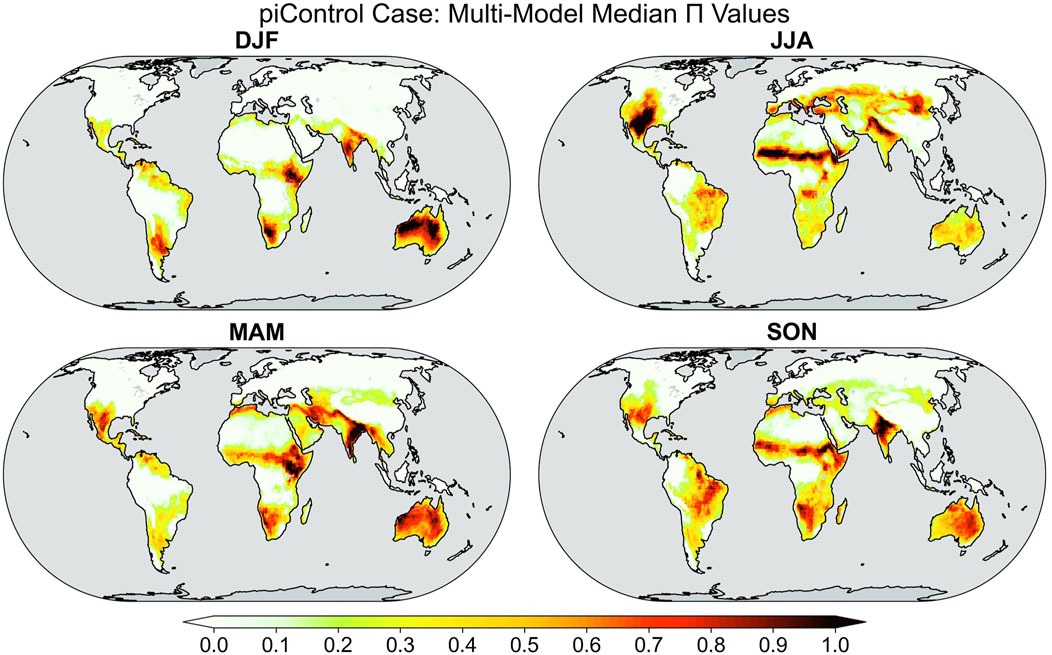
FIGURE 1. Multimodel median values of soil moisture–temperature coupling (
When comparing the coupling metric
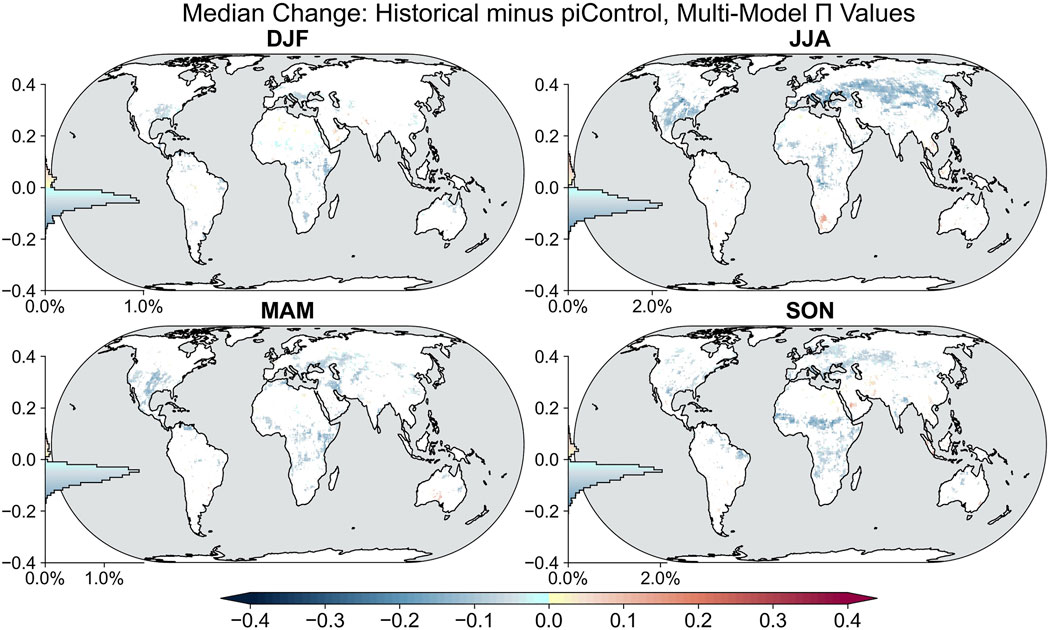
FIGURE 2. Multimodel median change in
As climate would be projected to approach the doubled CO2 level with no other changes from piControl conditions (Figure 3), decreases in
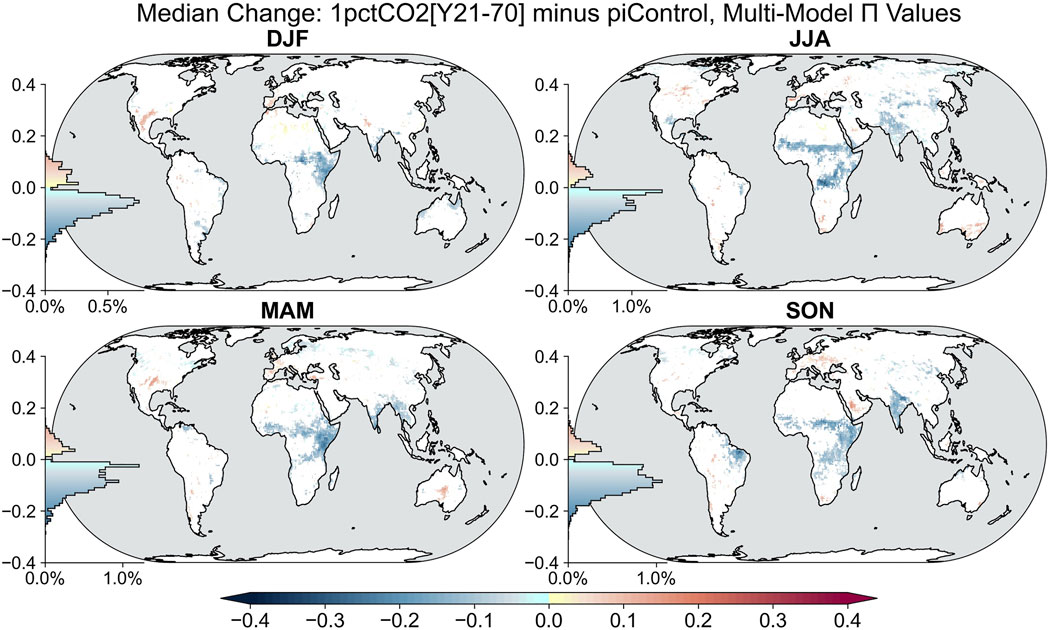
FIGURE 3. As in Figure 2 for the median change in
Shifting to the quadrupling CO2 scenario, the strongest and most widespread signals emerge. Areas of decreased soil moisture–temperature coupling in Africa and India persist and are joined by a large area of eastern South America during the JJA and SON seasons (Figure 4). However, there is a robust appearance of increased soil moisture control on extreme heat over many parts of the world across all seasons, matching or exceeding the area of decreased coupling. Beginning with boreal spring (MAM), a band of large consensus increases exists in
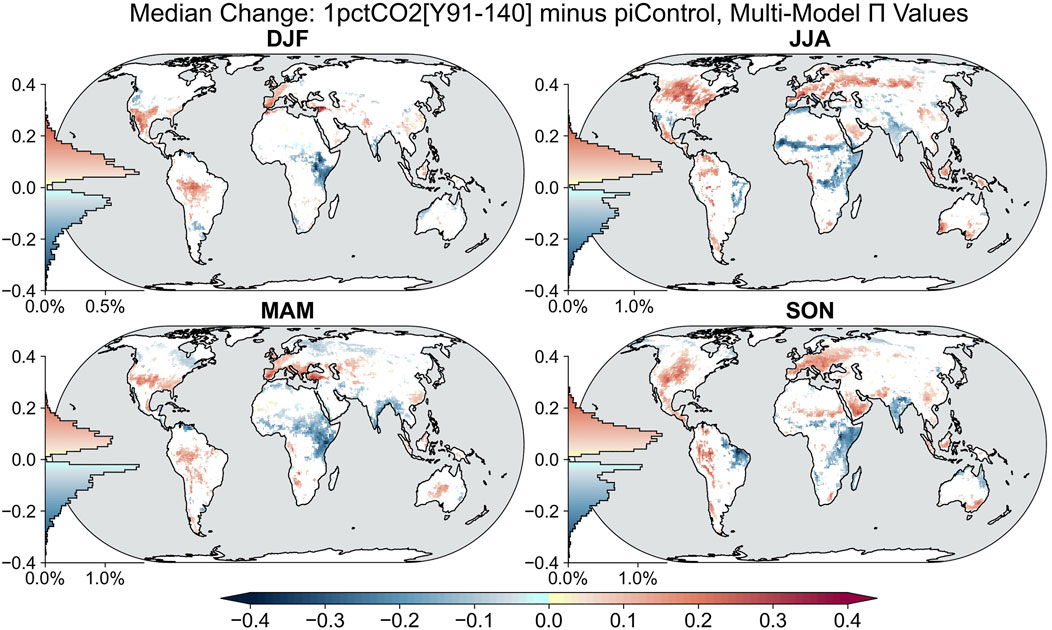
FIGURE 4. As in Figure 2 for the median change in
Moving into boreal summer and austral winter, widespread areas of strong increases in
In boreal fall and austral spring, broad areas of large increases persist in the Americas: over the central Rockies, Northern Great Plains, Northern Mexico, western Amazon, and Venezuela. Nearly all of Europe south of 55°N shows a consensus increase in
During boreal winter and austral summer (DJF), the most prominent feature is the broad area of a strong increase in
When compared to the median values of
3.2 Episodic coupling
Miralles et al. (2012) developed an instantaneous land–heat coupling metric
Conventionally, climate normals are defined using a trailing 30-year (or in common practice, a complete prior 3 decade) mean (Arguez and Vose, 2011), but it has been recognized that this practice is becoming inappropriate in a changing climate as the basis of defining anomalies for predicted events (e.g., Livezey et al., 2007; Milly et al., 2008). One alternative is to fit a regression, linear or otherwise, to data to create a time-varying normal. However, we should first ask the question of the purpose of a metric like
Figure 5 shows the result for the preindustrial simulations (piControl)—it is to be noted that the scale for
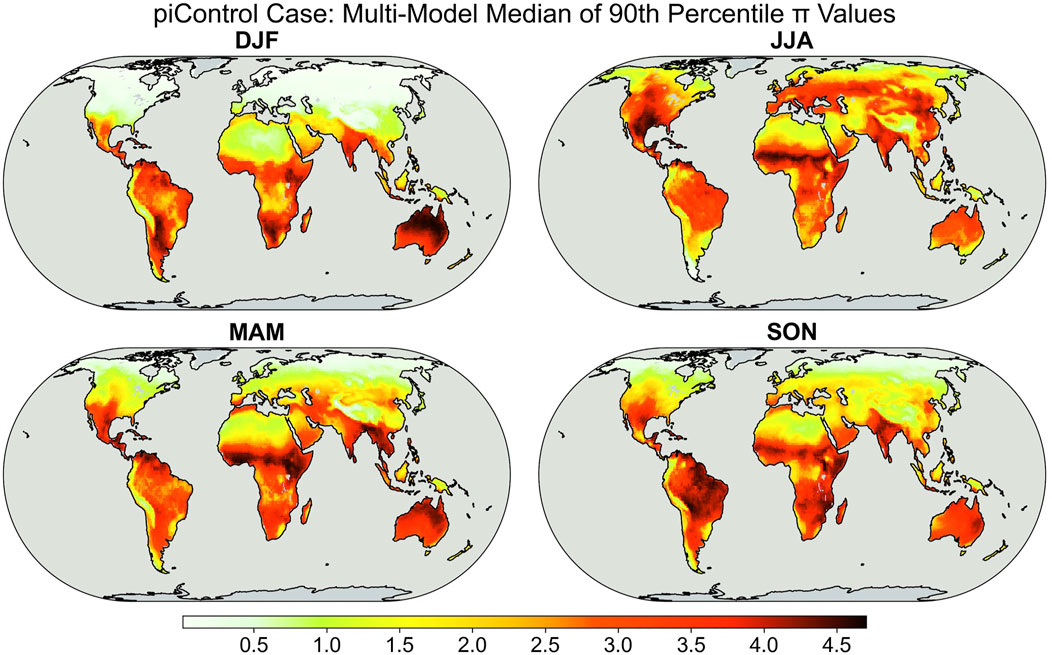
FIGURE 5. Multimodel median of the 90th percentile values of monthly scale soil moisture–temperature coupling (
Regionally, there are some clear patterns of seasonality. North America and much of midlatitude Eurasia show a clear oscillation between summer and winter. In East Asia, there is a South-to-North progression of high
High values of
We can see the impact of our choice of baseline for the definition of anomalies when we examine changes in the 90th percentile of
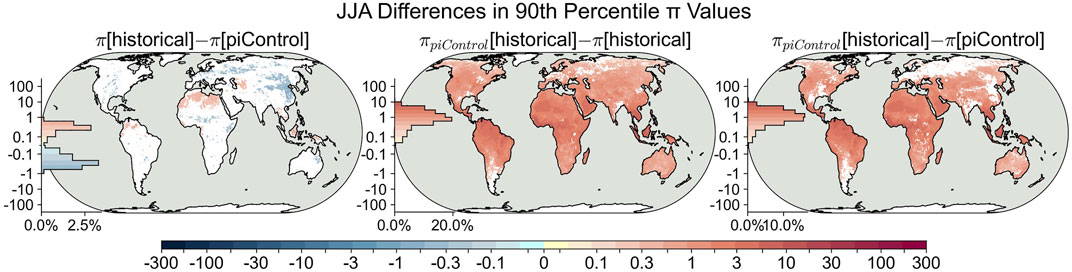
FIGURE 6. JJA multimodel median of differences in the 90th percentile values of
This pattern of change in the 90th percentile of
Returning to Figure 6, we see a very different picture when the baseline for anomalies during the historical period is kept at piControl levels and the piControl standard deviations for the terms used to calculate
Next, we examine the doubled and quadrupled CO2 periods compared with piControl. Using a trailing 30-year mean as the basis for climatology in the future projections, we see a pattern of changes for the quadrupled CO2 case (Figure 7) that is very similar to but skewed more strongly to positive differences and more significant areal coverage than the doubled CO2 case (Supplementary Figure S7). During all seasons, there are widespread consensus increases in the 90th percentile of
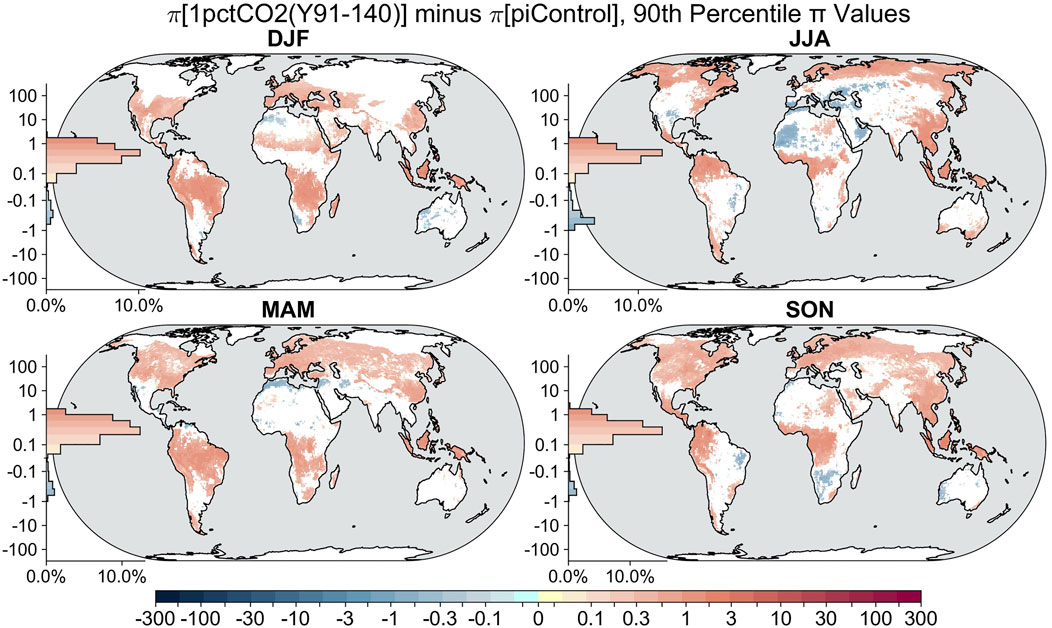
FIGURE 7. Multimodel median of differences in the 90th percentile values of
Unsurprisingly, if the preindustrial norms are used as the basis for calculating
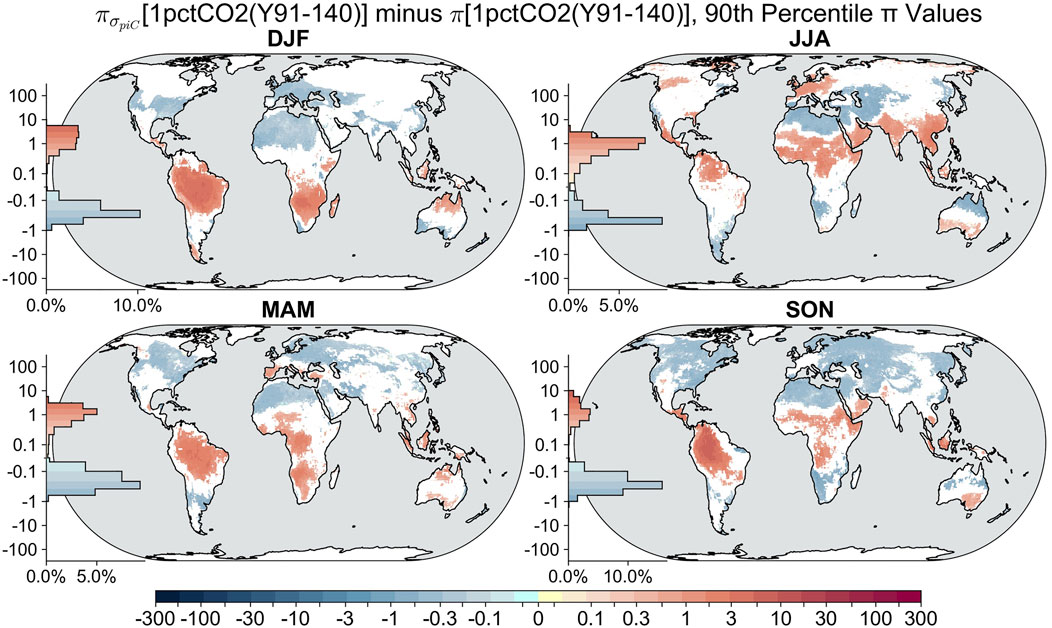
FIGURE 8. As in Figure 7 but with future values of
4 Discussion and conclusion
This study estimates past, present, and future heatwave susceptibility based on surface temperature, surface sensible heat flux, and surface latent heat flux as proposed by Miralles et al. (2012). The impact of climate change on climatological coupling via land–atmosphere temperature feedbacks has been examined with the climatological metric
Under preindustrial conditions (piControl), seasonally dependent hotspot regions of land–atmosphere coupling typically located in transitional zones between wet and dry climates in many other studies emerge once more during this analysis for
For the future climate scenarios (Figures 3, 4), coverage of increased soil moisture–heat flux–temperature coupling (i.e., positive values of
Consideration of the episodic land–atmosphere heat coupling metric of Miralles et al. (2012),
It is a much more nuanced problem to attribute the role of the land surface in the proliferation of extreme events within a changing climate as the very definition of “extreme” is by nature relative and potentially changing. This is particularly true when metrics are built with the assumption of a stationary climate as opposed to a changing one (Milly et al., 2008; Trenberth et al., 2014; Stevenson et al., 2022). The metric
Instead, two reasonable approaches are explored. When contemporaneous climate means and standard deviations (i.e., based on the trailing 30 years) are used to compare different periods (Figure 7 and Supplementary Figure S7), increased coupling from land to extreme heat cases becomes widespread over the moist tropics, much of the extratropics, and especially during summer in high-latitude regions. Decreased coupling appears over some of the more arid regions. However, one may assume that gradually increasing mean temperatures are not as much a factor for assessing land–atmosphere feedbacks as the changes in variability. When piControl standard deviations of temperature, sensible heat flux, and normalized sensible heat flux are used in all time periods, but anomalies are calculated based on recent climate norms, a different picture emerges (Figure 8 and Supplementary Figure S8). Increases in the 90th percentile of
These conclusions should be considered provisional and serve mainly as an indicator of the difficulty surrounding the construction of an interdisciplinary, widely applicable metric, that is, navigating through the uncertainty presented by a changing climate and the Earth system processes fostering these extreme events. For modeling studies, it is rather difficult to isolate and deduce a posteriori the role of land surface feedbacks on extremes (e.g., heatwaves and drought) from experiments that were not specifically designed to isolate the possible role of the land via specifically constructed sensitivity analyses. This discontinuity points to the merit and necessity of targeted multimodel climate change experiments (Seneviratne et al., 2013; Hurk et al., 2016; Lawrence et al., 2016). However, with an abundance of subfield-specific model intercomparison projects (MIPs; over 20 in CMIP6), such specialized sensitivity studies become undersubscribed and model uncertainty is amplified.
Projects like GSWP-2 (Dirmeyer et al., 2006), GLACE (Koster et al., 2004; Koster et al., 2006), GLACE-2 (Koster et al., 2011), and LUCID (Pitman et al., 2009) established a model count of about one dozen as an adequate minimum for global climate studies–a mark that has been difficult to match with recent specialized MIPs. However, these innovative strategies must progress beyond the monthly scale analyses presented here in addition to investigating changes in actual heatwave events that would require daily model output. Such data are available for a few CMIP6 models, but the sample distribution is not large enough to assuage concerns over model-dependent results. Furthermore, the relatively low resolution of climate change models may obscure processes and localized features that could alter these results. Perhaps for the next round of climate model intercomparisons, MIPs can be organized that target phenomena of looming societal concern such as heatwaves and droughts.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
PD conceived of the original research project and led the analysis and writing. RM and PD conducted data processing and computations. BG organized the discussion of the analysis and drafted the manuscript. DK, BG, RM, and PD contributed to the analysis of results and the manuscript.
Funding
PD’s participation was supported by National Oceanographic and Atmospheric Administration grant NA20OAR4310422. RM’s participation was supported by National Oceanographic and Atmospheric Administration grant NA20OAR4590316. BG’s participation was supported by the Department of Geography and Geoinformation Science at George Mason University. Data processing and preliminary analyses for this study were performed by the coauthors as part of a graduate class project in land–climate interactions in the Climate Dynamics Program of George Mason University, Fairfax, Virginia, United States. The lead author’s synthesis of the student material was supported by the Center for Ocean Land Atmosphere Studies (COLA).
Acknowledgments
The authors acknowledge Zahra Ghodsi Zadeh and Geoffrey Rath for their early participation in this work. Additionally, the authors thank Dr. René Orth and two reviewers for their constructive comments that have substantially improved the study and the effort of one reviewer to provide the collated list of specific atmosphere and land model component information in Supplementary Table S1, which saved us a great deal of effort.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.949250/full#supplementary-material
References
Abramowitz, G., Herger, N., Gutmann, E., Hammerling, D., Knutti, R., Leduc, M., et al. (2019). ESD reviews: Model dependence in multi-model climate ensembles: Weighting, sub-selection and out-of-sample testing. Earth Syst. Dyn. 10, 91–105. doi:10.5194/esd-10-91-2019
Albergel, C., Dutra, E., Bonan, B., Zheng, Y., Munier, S., Balsamo, G., et al. (2019). Monitoring and forecasting the impact of the 2018 summer heatwave on vegetation. Remote Sens. 11, 520. doi:10.3390/rs11050520
Arguez, A., and Vose, R. S. (2011). The definition of the standard WMO climate normal: The key to deriving alternative climate normals. Bull. Am. Meteorol. Soc. 92, 699–704. doi:10.1175/2010BAMS2955.1
Benson, D. O., and Dirmeyer, P. A. (2021). Characterizing the relationship between temperature and soil moisture extremes and their role in the exacerbation of heat waves over the contiguous United States. J. Clim. 34, 2175–2187. doi:10.1175/JCLI-D-20-0440.1
Berg, A., Lintner, B. R., Findell, K., Seneviratne, S. I., Hurk, B., Ducharne, A., et al. (2015). Interannual coupling between summertime surface temperature and precipitation over land: Processes and implications for climate change. J. Clim. 28, 1308–1328. doi:10.1175/JCLI-D-14-00324.1
Bevacqua, E., Zappa, G., Lehner, F., and Zscheischler, J. (2022). Precipitation trends determine future occurrences of compound hot–dry events. Nat. Clim. Chang. 12, 350–355. doi:10.1038/s41558-022-01309-5
Brunner, L., Pendergrass, A. G., Lehner, F., Merrifield, A. L., Lorenz, R., and Knutti, R. (2020). Reduced global warming from CMIP6 projections when weighting models by performance and independence. Earth Syst. Dyn. 11, 995–1012. doi:10.5194/esd-11-995-2020
Chen, L., and Dirmeyer, P. A. (2019). The relative importance among anthropogenic forcings of land use/land cover change in affecting temperature extremes. Clim. Dyn. 52, 2269–2285. doi:10.1007/s00382-018-4250-z
Chen, L., and Dirmeyer, P. A. (2020). Distinct impacts of land use and land management on summer temperatures. Front. Earth Sci. (Lausanne). 8, 245. doi:10.3389/feart.2020.00245
De Kauwe, M. G., Kala, J., Lin, Y.-S., Pitman, A. J., Medlyn, B. E., Duursma, R. A., et al. (2015). A test of an optimal stomatal conductance scheme within the CABLE land surface model. Geosci. Model Dev. 8, 431–452. doi:10.5194/gmd-8-431-2015
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., et al. (2011). The ERA-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 137, 553–597. doi:10.1002/qj.828
Dirmeyer, P. A., Balsamo, G., Blyth, E. M., Morrison, R., and Cooper, H. M. (2021). Land-atmosphere interactions exacerbated the drought and heatwave over northern Europe during summer 2018. AGU Adv. 2, e2020AV000283. doi:10.1029/2020AV000283
Dirmeyer, P. A., Gao, X., Zhao, M., Guo, Z., Oki, T., and Hanasaki, N. (2006). GSWP-2: Multimodel analysis and implications for our perception of the land surface. Bull. Am. Meteorol. Soc. 87, 1381–1398. doi:10.1175/BAMS-87-10-1381
Dirmeyer, P. A., Jin, Y., Singh, B., and Yan, X. (2013a). Evolving land–atmosphere interactions over north America from CMIP5 simulations. J. Clim. 26, 7313–7327. doi:10.1175/JCLI-D-12-00454.1
Dirmeyer, P. A., Jin, Y., Singh, B., and Yan, X. (2013b). Trends in land–atmosphere interactions from CMIP5 simulations. J. Hydrometeorol. 14, 829–849. doi:10.1175/JHM-D-12-0107.1
Dirmeyer, P. A., Schlosser, C. A., and Brubaker, K. L. (2009). Precipitation, recycling, and land memory: An integrated analysis. J. Hydrometeorol. 10, 278–288. doi:10.1175/2008JHM1016.1
Dirmeyer, P. A. (2011). The terrestrial segment of soil moisture-climate coupling. Geophys. Res. Lett. 38, L16702. doi:10.1029/2011GL048268
Dosio, A., Jury, M. W., Almazroui, M., Ashfaq, M., Diallo, I., Engelbrecht, F. A., et al. (2021). Projected future daily characteristics of African precipitation based on global (CMIP5, CMIP6) and regional (CORDEX, CORDEX-CORE) climate models. Clim. Dyn. 57, 3135–3158. doi:10.1007/s00382-021-05859-w
Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the coupled model intercomparison project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958. doi:10.5194/gmd-9-1937-2016
Fischer, E. M., Seneviratne, S. I., Lüthi, D., and Schär, C. (2007). Contribution of land-atmosphere coupling to recent European summer heat waves. Geophys. Res. Lett. 34, L06707. doi:10.1029/2006GL029068
Franks, P. J., Bonan, G. B., Berry, J. A., Lombardozzi, D. L., Holbrook, N. M., Herold, N., et al. (2018). Comparing optimal and empirical stomatal conductance models for application in Earth system models. Glob. Chang. Biol. 24, 5708–5723. doi:10.1111/gcb.14445
Hauser, M., Orth, R., and Seneviratne, S. I. (2016). Role of soil moisture versus recent climate change for the 2010 heat wave in Western Russia. Geophys. Res. Lett. 43, 2819–2826. doi:10.1002/2016GL068036
Hirsch, A. L., Evans, J. P., Virgilio, G. D., Perkins‐Kirkpatrick, S. E., Argüeso, D., Pitman, A. J., et al. (2019). Amplification of Australian heatwaves via local land-atmosphere coupling. J. Geophys. Res. Atmos. 124, 13625–13647. doi:10.1029/2019JD030665
Hu, T., and Sun, Y. (2022). Anthropogenic influence on extreme temperatures in China based on CMIP6 models. Int. J. Climatol. 42, 2981–2995. doi:10.1002/joc.7402
Hurk, B., Kim, H., Krinner, G., Seneviratne, S. I., Derksen, C., Oki, T., et al. (2016). LS3MIP (v1.0) contribution to CMIP6: The land surface, snow and soil moisture model intercomparison project – aims, setup and expected outcome. Geosci. Model Dev. 9, 2809–2832. doi:10.5194/gmd-9-2809-2016
Hurtt, G. C., Chini, L., Sahajpal, R., Frolking, S., Bodirsky, B. L., Calvin, K., et al. (2020). Harmonization of global land use change and management for the period 850–2100 (LUH2) for CMIP6. Geosci. Model Dev. 13, 5425–5464. doi:10.5194/gmd-13-5425-2020
Knutti, R., Furrer, R., Tebaldi, C., Cermak, J., and Meehl, G. A. (2010). Challenges in combining projections from multiple climate models. J. Clim. 23, 2739–2758. doi:10.1175/2009JCLI3361.1
Koster, R. D., Dirmeyer, P. A., Guo, Z., Bonan, G., Chan, E., Cox, P., et al. (2004). Regions of strong coupling between soil moisture and precipitation. Science 305, 1138–1140. doi:10.1126/science.1100217
Koster, R. D., Sud, Y. C., Guo, Z., Dirmeyer, P. A., Bonan, G., Oleson, K. W., et al. (2006). Glace: The global land–atmosphere coupling experiment. Part I: Overview. J. Hydrometeorol. 7, 590–610. doi:10.1175/JHM510.1
Koster, R. D., Guo, Z., Yang, R., Dirmeyer, P. A., Mitchell, K., and Puma, M. J. (2009). On the nature of soil moisture in land surface models. J. Clim. 22, 4322–4335. doi:10.1175/2009JCLI2832.1
Koster, R. D., Mahanama, S. P. P., Yamada, T. J., Balsamo, G., Berg, A. A., Boisserie, M., et al. (2011). The second Phase of the global land–atmosphere coupling experiment: Soil moisture contributions to subseasonal forecast skill. J. Hydrometeorol. 12, 805–822. doi:10.1175/2011JHM1365.1
Krishnamurti, T. N., Kishtawal, C. M., LaRow, T. E., Bachiochi, D. R., Zhang, Z., Williford, C. E., et al. (1999). Improved weather and seasonal climate forecasts from multimodel superensemble. Science 285, 1548–1550. doi:10.1126/science.285.5433.1548
Lau, N.-C., and Nath, M. J. (2014). Model simulation and projection of European heat waves in present-day and future climates. J. Clim. 27, 3713–3730. doi:10.1175/JCLI-D-13-00284.1
Lawrence, D. M., Hurtt, G. C., Arneth, A., Brovkin, V., Calvin, K. V., Jones, A. D., et al. (2016). The land use model intercomparison project (LUMIP) contribution to CMIP6: Rationale and experimental design. Geosci. Model Dev. 9, 2973–2998. doi:10.5194/gmd-9-2973-2016
Leduc, M., Laprise, R., Elía, R., and Šeparović, L. (2016). Is institutional democracy a good proxy for model independence? J. Clim. 29, 8301–8316. doi:10.1175/JCLI-D-15-0761.1
Livezey, R. E., Vinnikov, K. Y., Timofeyeva, M. M., Tinker, R., and Dool, H. M. (2007). Estimation and extrapolation of climate normals and climatic trends. J. Appl. Meteorol. Climatol. 46, 1759–1776. doi:10.1175/2007JAMC1666.1
Lorenz, R., Pitman, A. J., Hirsch, A. L., and Srbinovsky, J. (2015). Intraseasonal versus interannual measures of land–atmosphere coupling strength in a global climate model: GLACE-1 versus GLACE-CMIP5 experiments in ACCESS1.3b. J. Hydrometeorol. 16, 2276–2295. doi:10.1175/JHM-D-14-0206.1
Martens, B., Miralles, D. G., Lievens, H., van der Schalie, R., de Jeu, R. A. M., Fernández-Prieto, D., et al. (2017). GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 10, 1903–1925. doi:10.5194/gmd-10-1903-2017
Milly, P. C. D., Betancourt, J., Falkenmark, M., Hirsch, R. M., Kundzewicz, Z. W., Lettenmaier, D. P., et al. (2008). Stationarity is dead: Whither water management? Science 319, 573–574. doi:10.1126/science.1151915
Miralles, D. G., Gentine, P., Seneviratne, S. I., and Teuling, A. J. (2019). Land–atmospheric feedbacks during droughts and heatwaves: State of the science and current challenges. Ann. N. Y. Acad. Sci. 1436, 19–35. doi:10.1111/nyas.13912
Miralles, D. G., van den Berg, M. J., Teuling, A. J., and de Jeu, R. A. M. (2012). Soil moisture-temperature coupling: A multiscale observational analysis. Geophys. Res. Lett. 39, L21707. doi:10.1029/2012GL053703
Neal, E., Huang, C. S. Y., and Nakamura, N. (2022). The 2021 pacific northwest heat wave and associated blocking: Meteorology and the role of an upstream cyclone as a diabatic source of wave activity. Geophys. Res. Lett. 49, e2021GL097699. doi:10.1029/2021GL097699
Notaro, M. (2008). Statistical identification of global hot spots in soil moisture feedbacks among IPCC AR4 models. J. Geophys. Res. 113, D09101. doi:10.1029/2007JD009199
O, S., Bastos, A., Reichstein, M., Li, W., Denissen, J., Graefen, H., et al. (2022). The role of climate and vegetation in regulating drought-heat extremes. J. Clim. 1, 5677–5685. doi:10.1175/JCLI-D-21-0675.1
Palmer, T. N., Alessandri, A., Andersen, U., Cantelaube, P., Davey, M., Délécluse, P., et al. (2004). Development of a EUROPEAN multimodel ensemble system for seasonal-to-interannual prediction (demeter). Bull. Am. Meteorol. Soc. 85, 853–872. doi:10.1175/BAMS-85-6-853
Parker, W. S. (2013). Ensemble modeling, uncertainty and robust predictions. WIREs Clim. Change 4, 213–223. doi:10.1002/wcc.220
Perkins-Kirkpatrick, S. E., and Gibson, P. B. (2017). Changes in regional heatwave characteristics as a function of increasing global temperature. Sci. Rep. 7, 12256. doi:10.1038/s41598-017-12520-2
Petch, J. C., Short, C. J., Best, M. J., McCarthy, M., Lewis, H. W., Vosper, S. B., et al. (2020). Sensitivity of the 2018 UK summer heatwave to local sea temperatures and soil moisture. Atmos. Sci. Lett. 21, e948. doi:10.1002/asl.948
Pirtle, Z., Meyer, R., and Hamilton, A. (2010). What does it mean when climate models agree? A case for assessing independence among general circulation models. Environ. Sci. Policy 13, 351–361. doi:10.1016/j.envsci.2010.04.004
Pitman, A. J., de Noblet-Ducoudré, N., Cruz, F. T., Davin, E. L., Bonan, G. B., Brovkin, V., et al. (2009). Uncertainties in climate responses to past land cover change: First results from the LUCID intercomparison study. Geophys. Res. Lett. 36, L14814. doi:10.1029/2009GL039076
Priestley, C. H. B., and Taylor, R. J. (1972). On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Wea. Rev. 100, 81–92. doi:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2
Samaniego, L., Thober, S., Kumar, R., Wanders, N., Rakovec, O., Pan, M., et al. (2018). Anthropogenic warming exacerbates European soil moisture droughts. Nat. Clim. Chang. 8, 421–426. doi:10.1038/s41558-018-0138-5
Santanello, J. A., Dirmeyer, P. A., Ferguson, C. R., Findell, K. L., Tawfik, A. B., Berg, A., et al. (2018). Land-atmosphere interactions: The LoCo perspective. Bull. Am. Meteorol. Soc. 99, 1253–1272. doi:10.1175/BAMS-D-17-0001.1
Schumacher, D. L., Keune, J., Heerwaarden, C. C., Arellano, J. V.-G., Teuling, A. J., and Miralles, D. G. (2019). Amplification of mega-heatwaves through heat torrents fuelled by upwind drought. Nat. Geosci. 12, 712–717. doi:10.1038/s41561-019-0431-6
Schwingshackl, C., Hirschi, M., and Seneviratne, S. I. (2018). A theoretical approach to assess soil moisture–climate coupling across CMIP5 and GLACE-CMIP5 experiments. Earth Syst. Dyn. 9, 1217–1234. doi:10.5194/esd-9-1217-2018
Seneviratne, S. I., Corti, T., Davin, E. L., Hirschi, M., Jaeger, E. B., Lehner, I., et al. (2010). Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Science Rev. 99, 125–161. doi:10.1016/j.earscirev.2010.02.004
Seneviratne, S. I., Wilhelm, M., Stanelle, T., Hurk, B., Hagemann, S., Berg, A., et al. (2013). Impact of soil moisture-climate feedbacks on CMIP5 projections: First results from the GLACE-CMIP5 experiment. Geophys. Res. Lett. 40, 5212–5217. doi:10.1002/grl.50956
Shafiei Shiva, J., Chandler, D. G., and Kunkel, K. E. (2019). Localized changes in heat wave properties across the United States. Earth's. Future 7, 300–319. doi:10.1029/2018EF001085
Stevenson, S., Coats, S., Touma, D., Cole, J., Lehner, F., Fasullo, J., et al. (2022). Twenty-first century hydroclimate: A continually changing baseline, with more frequent extremes. Proc. Natl. Acad. Sci. U. S. A. 119, e2108124119. doi:10.1073/pnas.2108124119
Tebaldi, C., and Knutti, R. (2007). The use of the multi-model ensemble in probabilistic climate projections. Phil. Trans. R. Soc. A 365, 2053–2075. doi:10.1098/rsta.2007.2076
Teuling, A. J., Seneviratne, S. I., Stöckli, R., Reichstein, M., Moors, E., Ciais, P., et al. (2010). Contrasting response of European forest and grassland energy exchange to heatwaves. Nat. Geosci. 3, 722–727. doi:10.1038/ngeo950
Trenberth, K. E., Dai, A., van der Schrier, G., Jones, P. D., Barichivich, J., Briffa, K. R., et al. (2014). Global warming and changes in drought. Nat. Clim. Chang. 4, 17–22. doi:10.1038/nclimate2067
Ukkola, A. M., Pitman, A. J., Donat, M. G., Kauwe, M. G. D., and Angélil, O. (2018). Evaluating the contribution of land-atmosphere coupling to heat extremes in CMIP5 models. Geophys. Res. Lett. 0, 9003–9012. (early view). doi:10.1029/2018GL079102
Wang, B., Jin, C., and Liu, J. (2020). Understanding future change of global monsoons projected by CMIP6 models. J. Clim. 33, 6471–6489. doi:10.1175/JCLI-D-19-0993.1
Wehrli, K., Hauser, M., and Seneviratne, S. I. (2020). Storylines of the 2018 Northern Hemisphere heat wave at pre-industrial and higher global warming levels. Earth Syst. Dyn. 11, 855–873. doi:10.5194/esd-11-855-2020
Yiou, P., Cattiaux, J., Faranda, D., Kadygrov, N., Jézéquel, A., Naveau, P., et al. (2020). Analyses of the northern European summer heatwave of 2018. Bull. Am. Meteorol. Soc. 101, S35–S40. doi:10.1175/BAMS-D-19-0170.1
Zhao, T., and Dai, A. (2015). The magnitude and causes of global drought changes in the twenty-first century under a low–moderate emissions scenario. J. Clim. 28, 4490–4512. doi:10.1175/JCLI-D-14-00363.1
Zhao, T., and Dai, A. (2022). CMIP6 model-projected hydroclimatic and drought changes and their causes in the twenty-first century. J. Clim. 35, 897–921. doi:10.1175/JCLI-D-21-0442.1
Keywords: CMIP6, extreme heat, climate change, coupling metrics, near-surface air temperature, sensible heat, model consensus, land surface
Citation: Dirmeyer PA, Sridhar Mantripragada RS, Gay BA and Klein DKD (2022) Evolution of land surface feedbacks on extreme heat: Adapting existing coupling metrics to a changing climate. Front. Environ. Sci. 10:949250. doi: 10.3389/fenvs.2022.949250
Received: 20 May 2022; Accepted: 22 August 2022;
Published: 15 September 2022.
Edited by:
Merja H. Tölle, University of Kassel, GermanyReviewed by:
Patrick Laux, Karlsruhe Institute of Technology (KIT), GermanyRene Orth, Max Planck Institute for Biogeochemistry, Germany
Anna Merrifield, ETH Zürich, Switzerland
Copyright © 2022 Dirmeyer, Sridhar Mantripragada, Gay and Klein. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Paul A. Dirmeyer, cGRpcm1leWVAZ211LmVkdQ==
†ORCID: Paul A. Dirmeyer, 0000-0003-3158-1752; Rama Sesha Sridhar Mantripragada, 0000-0002-3334-0234; Bradley A. Gay, 0000-0003-2617-2559; David K. D. Klein, 0000-0003-3943-4570
 Paul A. Dirmeyer
Paul A. Dirmeyer Rama Sesha Sridhar Mantripragada
Rama Sesha Sridhar Mantripragada Bradley A. Gay
Bradley A. Gay David K. D. Klein
David K. D. Klein