Establishing log reduction values for wastewater treatment processes from ambient influent and effluent pathogen monitoring data

In developing wastewater treatment regulations and guidelines for potable reuse, the reduction of pathogens is of critical importance. In draft regulations, the state of California has proposed overall treatment process log reduction values (LRVs) of 20, 14, and 15 respectively for viruses, Giardia cysts, and Cryptosporidium oocysts, for direct potable reuse. In meeting the log reduction requirements, agencies have sought to obtain credit for LRVs achieved consistently through secondary biological and tertiary wastewater treatment, in addition to the LRVs achieved through advanced water treatment. The purpose of this paper is to illustrate how to determine pathogen LRVs, using ambient wastewater treatment pathogen monitoring data and the rank-paired covariant method of analysis.

Introduction

The purpose of this paper is to illustrate the use of the rank-paired covariant method of analysis to determine pathogen log reduction values (LRVs) for ambient wastewater pathogen monitoring data. Although not a research paper, the material presented has been organized in a research paper format under two general headings: 1) Materials and Methods and 2) Analysis and Discussion. Topics considered under the heading Materials and Methods include a discussion of how pathogen monitoring data are collected, the impact of sampling methods on the analysis of the resulting data used for the determination of LRVs, and the statistical analysis of Giardia cyst monitoring data. Under the heading Analysis and Discussion, the determination of the LRVs for secondary biological treatment, tertiary filtration treatment, and the overall treatment process are illustrated and discussed. Future approaches to the collection and analysis of pathogen monitoring data are also considered.

Collection of pathogen monitoring data

Wastewater unit treatment processes achieve variable levels of pathogen reduction. To meet the goals for pathogen reduction for potable reuse, the Division of Drinking Water (DDW) of the California State Water Resources Control Board has proposed granting LRV credits for secondary and tertiary treatment, based on a probability value of 5 percent (State Water Board - Division of Drinking Water, 2021). Thus, the key task in collecting and analyzing pathogen monitoring data is to establish the LRV value at the fifth percentile.

Use of ambient pathogens

Pathogen monitoring studies are typically conducted by measuring the concentration of ambient influent and effluent pathogen concentrations from a unit or combination of unit processes. A major challenge with ambient monitoring studies is the variability in the influent pathogen concentration, which leads to variability in the effluent concentrations, and makes it difficult to distinguish between effluent variability due to treatment versus influent variability. Pathogen monitoring studies with seeded pathogens, or pathogen surrogates, are usually not done, due to the prohibitive cost of such studies, especially for large wastewater treatment plants.

Impact of treatment process hydraulics

The flow regime through most wastewater treatment facilities, including those operated at a constant flowrate, can be characterized as non-ideal, also known as arbitrary flow, which results in both forward and backward mixing. The addition of return flows further complicates the flow regime. In ambient pathogen studies, in arbitrary flow systems, the effluent samples are impacted by a mixture of variable influent pathogen concentrations, which inhibits the pairing of influent and effluent samples. The effects of mixing caused by arbitrary flow persist even if the monitoring sample collection times are offset, based on the treatment process modal hydraulic retention time as determined by tracer studies.

Thus, the ambient pathogen monitoring data in systems with arbitrary flow conditions are unpaired. However, the calculation of unit process LRVs requires pairing of influent and effluent samples, unless independence is assumed. The data cannot be independent because if there were no Giardia cysts in the influent there would be no Giardia cysts in the effluent. Thus, the analysis of ambient pathogen data in a system with arbitrary flow conditions must include a manner of pairing the data. In addition, mixing also reduces the impact of influent variability on effluent concentrations. Thus, ideally, the degree of mixing should be characterized in ambient pathogen studies.

Giardia cyst monitoring data

The Giardia cyst monitoring data adapted for the purpose of illustration, summarized in Table 1 and Figure 1, are from a wastewater treatment facility (WWTF) with arbitrary flow conditions employing an activated sludge process, operated at constant flowrate, and with a fixed mean cell residence time. The plant influent monitoring samples were collected at the inlet to the primary sedimentation tanks. Following primary sedimentation, a portion of the primary effluent can be diverted to a flow equalization storage tank for later blending. The effluent samples for the secondary biological treatment process were collected from the discharge of the secondary sedimentation tanks. Tertiary effluent samples were collected from the effluent of an individual filter. The measured and log transformed Giardia cyst data for various locations in the treatment process, and a summary of the descriptive statistics for the data are also presented in Table 1. Details of the statistical analysis are considered in the following section.

TABLE 1

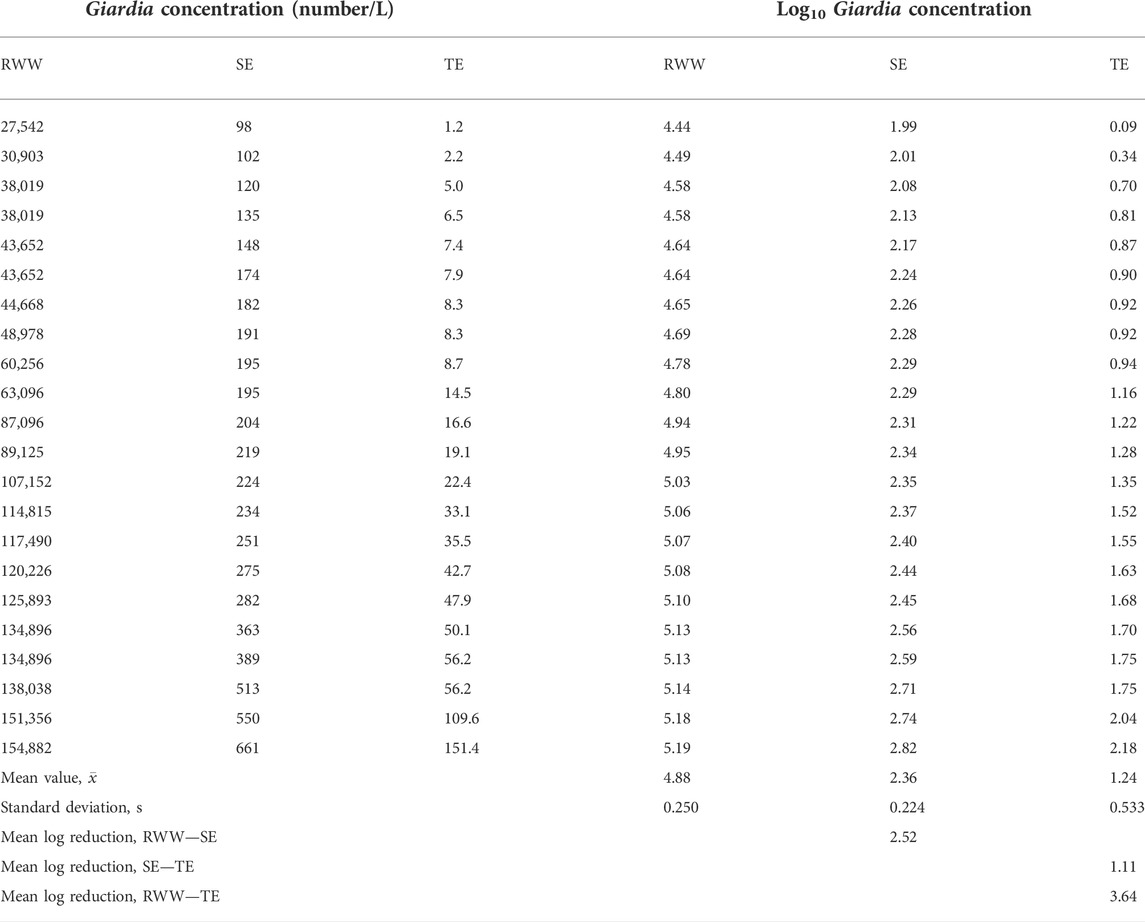
TABLE 1. Example of measured and log transformed Giardia cyst data for raw wastewater (RWW), secondary effluent (SE), and tertiary filtration effluent (TE). The monitoring data are listed in ascending order.

FIGURE 1

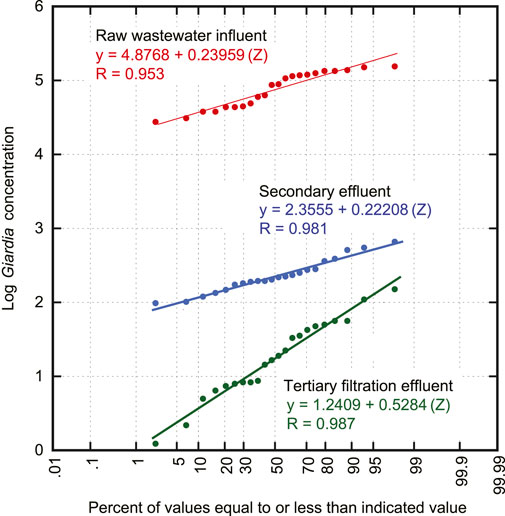
FIGURE 1. Typical data for Giardia for raw wastewater (RWW), secondary biological treatment effluent (SE), and tertiary filtration effluent (TE).

Preliminary data evaluation

The first step in the analysis of the data presented in Table 1 was to prepare probability plots for both the non-log transformed monitoring data and the corresponding log (base 10) transformed data on probability paper (Hazen, 1914) to determine the nature of the distributions. The Hazen probability plotting position equation was used in the preparation of the plots shown on Figure 1 (Yahaya et al., 2012). Because the log transformed data can be represented by straight lines with a high degree of correlation, the data are considered to be normally distributed. The finding that the logarithm of the measured values is normally distributed is consistent with what has been reported in the literature for the measurement of pathogens in wastewater and in the effluent from various treatment processes (Greenwood and Yule, 1917; Velz, 1951, 1952; Rose et al., 1996; Tchobanoglous et al., 2014). The normal statistics analyses for these data and the determination of variable independence are discussed below.

Review of probability distributions

In reviewing the probability distributions plotted on Figure 1, it will be noted that the plots for raw wastewater (RWW) and secondary biological treatment effluent (SE) diverge from each other, whereas the plots for SE and tertiary filtration effluent (TE) converge. Depending on the nature of the treatment processes, both diverging and converging probability distributions have been observed. For biological treatment processes, RWW and SE probability plots are typically divergent. For effluent filtration processes, the influent SE and effluent TE probability plots are typically convergent (see Supplementary Datasheet S1). Similarly, overall process probability plots of RWW and TE typically converge. Convergence or divergence is also of importance in the determination of whether the minimum process LRV will occur to the left or right of the mean value of the probability plots. Regardless of whether the probability plots are diverging or converging, a new distribution defining the LRV between two distributions is generated by combining the two separate dependent or independent probability distributions, as described below.

Rank pairing the monitoring data

A method of pairing the influent and effluent data must be assumed in the analysis of ambient pathogen monitoring studies with arbitrary flow conditions. Because the influent and effluent data are not independent, rank-pairing is proposed. In rank-pairing the effluent pathogen data are associated with influent pathogen data by rank. The rationale for rank-pairing is as follows. Low effluent pathogen concentrations are likely associated with low influent concentrations, and high effluent pathogen concentrations are likely associated with high influent concentrations.

Statistical analysis of Giardia cyst monitoring data

Because the log-transformed monitoring data were determined to be normally distributed, as described above, the resulting distributions can be quantified using normal statistical parameters such as the mean and standard deviation. The covariance, coefficient of correlation, and coefficient of determination can be used to further quantify the relationship between two correlated normal statistical distributions. The statistical analysis of pathogen monitoring data is discussed below. Determination of LRVs is described in the following three sections.

Normal statistics

The values for the mean and standard deviation for each of the sample distributions are presented in the respective columns below the data entries (see Table 1).

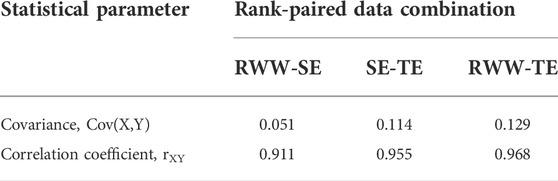
Covariance, coefficient of correlation, and coefficient of determination

Covariance is used to define the joint variability of the two variables or distributions. The covariance of the rank-paired distributions can be calculated using Eq. 1 (Whitlock and Schluter, 2012).

$\mathrm{Cov}\left(\text{X},\text{Y}\right)= \frac{{\displaystyle \sum \left({\mathrm{x}}_{\text{i}}-\overline{\text{x}}\right)\left({\text{y}}_{\text{i}}-\overline{\text{y}}\right)}}{\mathrm{n} - 1}(1)$

Where Cov(X,Y) = covariance between distributions X and Y.

${\text{x}}_{\text{i}}$ = value of x from the X distribution.

$\overline{\text{x}}$ = mean value of x from the X distribution.

${\text{y}}_{\text{i}}$ = value of y from the Y distribution.

$\overline{\text{y}}$ = mean value of y from the Y distribution.

N = number of data points.

Using the data given in Table 1, the computed covariance values for the rank-paired data, as given in Table 2, are 0.051, 0.114, and 0.129 for RWW-SE, SE-TE, and RWW-TE, respectively. A positive value means that the two distributions are covariant in that they both move in the same direction (upward). The covariance was also determined for the date-paired data, and found to be - 0.0062, essentially zero, suggesting that the data are independent, which cannot be true, as discussed above.

TABLE 2

TABLE 2. Rank-paired covariance and Pearson correlation coefficient values.

The Pearson coefficient of correlation, commonly defined as r_XY, is used to assess the degree to which the two distributions are correlated (Walpole et al., 2012; Whitlock and Schluter, 2012). The value of $r_{XY}$ is obtained by dividing the covariance by the product of the sample standard deviation of the two distributions. In equation form, $r_{XY}$ is computed as shown in Eq. (2).

${\mathrm{r}}_{\mathrm{X}\mathrm{Y}}= \frac{\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{X},\mathrm{Y}\right)}{{\mathrm{s}}_{\mathrm{X}}{\mathrm{s}}_{\mathrm{Y}}}(2)$

Where r_XY = Pearson correlation coefficient between variables X and Y.

Cov(X,Y) = covariance between distributions X and Y.

s_X = sample standard deviation for distribution X.

s_Y = sample standard deviation for distribution Y.

Using the numerical values given in Table 1, the r_XY value for the RWW-SE, SE-TE, and RWW-TE distributions is determined as follows.

The r_XY for RWW-SE is equal to 0.051/(0.250 × 0.224) = 0.911.

The r_XY for SE-TE is equal to 0.114/(0.224 × 0.533) = 0.955.

The r_XY for RWW-TE is equal to 0.129/(0.250 × 0.533) = 0.968.

A positive r_XY value in the range from 0.8 < r_XY <1, constitutes a strong positive correlation of the dependent variable Y with the independent variable X.

The corresponding coefficient of determination, defined as the square of the coefficient of correlation (r_XY)², for the three distributions is as follows.

For RWW-SE, (r_XY)² = (0.911)² = 0.830.

For SE-TE, (r_XY)² = (0.955)² = 0.912.

For RWW-TE, (r_XY)² = (0.968)² = 0.937.

Thus, for the RWW-SE, SE-TE, and RWW-TE distributions, about 83, 91, and 94 percent, respectively, of the variability in the measured effluent values (dependent variable) can be explained by the variability in the influent values (independent variable), using the rank-paired assumption. The remaining variability is assumed to be the variability in the log reduction performance for a given unit treatment process. For example, even if a biological wastewater treatment process is operated with a fixed MCRT of 10 d, in practice, it might fluctuate between 9 and 11 d. In tertiary filtration, the reduction efficiency is changing continually with the length of filter run.

Determination of Giardia cyst log reduction value for biological treatment

The LRV at 5 percent or any other percent probability for the biological treatment process can be determined by deriving a new probability distribution based on a covariant statistical analysis of the difference between the correlated influent (RWW) and effluent (SE) normal probability distributions. For the Giardia cyst data, given in Table 1, the following approach is used for estimating the LRV for biological treatment (RWW-SE).

For covariant distributions, the difference between two normal correlated probability distributions X and Y is given by the following relationship (Walpole et al., 2012).

$\mathrm{X}-\mathrm{Y} \sim \mathrm{N}\left[{\overline{\text{x}}}_{\text{X}}-{\overline{\text{x}}}_{\text{Y}}, {\mathrm{s}}_{\mathrm{X}}^2 + {\mathrm{s}}_{\mathrm{Y}}^2 – 2\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{X},\mathrm{Y}\right)\right](3)$

Where ${\overline{\text{x}}}_{\text{X}}$= sample mean value for distribution X.

${\overline{\text{x}}}_{\text{Y}}$ = sample mean value for distribution Y

s² = ${\text{s}}_{\text{X}}^2 + {\text{s}}_{\text{Y}}^2 – 2\mathrm{C}\mathrm{o}\mathrm{v}(\mathrm{X},\mathrm{Y})$ = variance of the new distribution.

For independent normal probability distributions, the covariance term in Eq. (3) is eliminated.

The value at a given probability for the new normal probability distribution can be estimated using the following expression.

$\text{Z}=\left[\text{x}-\left({\overline{\text{x}}}_{\text{X}}-{\overline{\text{x}}}_{\text{Y}}\right)\right]/\mathrm{s}(4)$

Where Z = number of normalized standard deviations greater than or smaller than the sample mean.

x = value of the new normal distribution at a specified probability value.

s = sample standard deviation for the new distribution.

At a probability value of 5 percent, which is used for estimating LRVs for pathogens, the corresponding Z value from standard statistical tables is ± 1.645. Substituting LRV_0.05 for x, the corresponding expression for LRV_0.05 is:

${\text{LRV}}_{0.05}=({\overline{\text{x}}}_{\text{X}}-{\overline{\text{x}}}_{\text{Y}})+\text{ s}\left(\text{Z at 0}\text{.}05\right)=\left({\overline{\text{x}}}_{\text{X}}-{\overline{\text{x}}}_{\text{Y}}\right)+\text{s}\left(-1\text{.}645\right)(5)$

Using the numerical values given in Table 1, the LRV_0.05 for the RWW-SE distribution is computed as follows.

(x̄_X - x̄_Y) = 4.88 – 2.36 = 2.52

s² = ${\mathrm{s}}_{\mathrm{X}}^2 + {\mathrm{s}}_{\mathrm{Y}}^2 – 2\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{X},\mathrm{Y}\right)$ = [(0.250)² + (0.224)² –2 (0.051)] = 0.0107.

$s = \sqrt{0.0107}$ = 0.1034.

LRV_0.05 = 2.52 + 0.103 (-1.645) = 2.52 - 0.17 = 2.35.

Alternatively, the LRV_0.05 can also be determined by analyzing the difference between the paired values as discussed in Supplementary Datasheet S1.

Determination of Giardia cyst log reduction value for tertiary treatment

The LRV_0.05 value for the tertiary filtration process, following secondary treatment (SE-TE), is computed as follows, using the data from Table 1 and Eq 5.

(x̄_X - x̄_Y) = 2.36–1.24 = 1.11

s² = ${\mathrm{s}}_{\mathrm{X} }^2+ {\mathrm{s}}_{\mathrm{Y}}^2 -$2Cov(X,Y) = [(0.224)² + (0.533)²–2 (0.114)] = 0.1063

s = $\sqrt{0.1063}$ = 0.326.

LRV_0.05 = 1.11 + 0.326 (-1.645) = 1.11 - 0.54 = 0.58.

In some cases, depending on the degree of convergence between the SE and TE distributions, it may not be possible to grant any LRV credit for tertiary filtration (see Supplementary Datasheet S1).

Combined log reduction value from raw wastewater influent to filter effluent

The minimum LRV_0.05 for the overall treatment process, based on the RWW-TE distributions is computed as follows, using the data from Table 1 and Eq 5.

(x̄_X–x̄_Y) = 4.88–1.24 = 3.64

s² = ${\text{s}}_{\text{X} }^2+ {\text{s}}_{\text{Y}}^2 –$2Cov(X,Y) = [(0.250)² + (0.533)²–2 (0.129)] = 0.0886

s = $\sqrt{0.0886}$ = 0.298.

LRV_0.05 = 3.64 + 0.298 (-1.645) = 3.64–0.49 = 3.15

Thus, for the overall treatment process data reported in Table 1, the minimum Giardia cyst LRV_0.05 derived from the difference between the RWW-TE distributions is 3.15. If the LRVs for the RWW-SE and SE-TF distributions were reported separately, the total LRV_0.05 for the entire treatment process would have been 2.93 (2.35 + 0.58).

The difference between the two LRVs (3.14 versus 2.93) is in part due to the TE distribution converging with respect to the RWW distribution whereas the SE distribution diverges. Combining converging and diverging distributions leads to larger rank-paired LRVs than combining converging or diverging distributions. The difference between the two LRVs is also due to differences in the covariance term that results from examining the correlation between different rank-paired distributions.

Because of the difference in LRV values, and the different pathogen removal mechanisms for the two processes, the conservative approach for granting regulatory LRV credits would be to focus on individual unit treatment processes and the development of unit process performance distributions. In addition, this approach is consistent with the US EPA drinking water regulations where the treatment process LRVs are additive, based on the assumption that every treatment process operates independently.

Estimating log reduction values subject to variable operating conditions

The data used in this paper were from a WWTF operated at constant flowrate, employing an activated sludge process including primary sedimentation, operated with a fixed MCRT. Determination of pathogen LRVs where the WWTF is operated under variable flow conditions is discussed below.

Log reduction values through secondary treatment processes

Where flow equalization is not possible, WWTFs must operate under varying flowrates, constituent concentrations, and constituent mass loading rates. For example, the quantity of solids removed by sedimentation during extreme peak flow events can be reduced by as much as 50 percent compared to the removal achieved at average flow. Variations in flowrate and constituent concentrations have been shown to deteriorate plant performance, especially in plants with limited (or excessive) volumetric capacity. Reduced WWTF performance is characterized by greater variability in the treated effluent constituent concentrations, including pathogenic microorganisms (Gujer and Erni, 1978; Niku et al., 1981a,b).

In WWTFs without flow equalization, the effectiveness of the operative pathogen reduction mechanisms is changing continually in response to these operational variations. Because it is difficult to know how the treatment process is operating when an effluent sample is collected, long-term randomly collected influent and effluent process data must be used to estimate the minimum LRVs that are achievable under non-steady-state conditions. Under these varying conditions, the covariant method of analysis, discussed and illustrated above, is recommended for determining the minimum LRV_0.05, which is of regulatory concern.

Log reduction values through tertiary filtration

The difficulty of estimating LRVs for pathogens through tertiary filtration is that the process is never at steady-state operation, regardless of whether the flowrate is constant or variable. For example, if a single dual-medium filter, operated under constant flow, is considered, it would be anticipated that, after the filter to waste ripening phase, the initial rate of constituent reduction will be greater than the corresponding rate at the end of a filter run when turbidity breakthrough occurs (Tchobanoglous et al., 2014). At the end of the run, when the pore spaces have been filled and the interstitial flow velocity through the filter has increased, there is less opportunity for pathogen reduction by chance contact or sorption and in many cases sorbed constituents can be stripped leading to increased effluent constituent concentrations. If filter to waste is not employed, higher pathogen counts could occur in the ripening phase. Pathogen reduction is complicated further if the flow is variable.

Because a filtration installation is comprised of multiple cells, it is difficult to know where in the filtration process each of the cells is operating. Thus, as discussed above, long-term randomly collected data from a blended effluent stream should be used, when possible, to estimate the minimum LRV that is achievable, based on the influent distribution. Further, while determination of the minimum LRV between RWW and TE effluent is possible, it is important to note that the reduction mechanisms in biological treatment and effluent filtration are different and the fact that the two processes operate under different modes (e.g., steady state versus dynamic continually changing).

Future verification of log reduction values

The field of pathogen monitoring and assessment is continually evolving. One promising approach to address the challenges with ambient pathogen studies under non-ideal flow conditions is to characterize the WWTP hydraulics with a tracer study. Information from the tracer study could be used to model the effects of mixing in the WWTP. The observed influent pathogen distribution would be used as input to the model, the tracer characterization would be used to model blending effects, and LRV distribution parameters would be adjusted until the observed effluent distribution is yielded by the model. From the LRV distribution, the fifth percentile LRV could be determined. Additionally, the covariance could be back calculated.

Another potential area of interest is in seeded studies. It may be practical to conduct seeded studies on small-scale facilities. In seeding studies, pathogens, or pathogen surrogates would be spiked into the WWTP influent at concentrations that are significantly higher than ambient concentrations. The seeded study design allows for the influent pathogen concentration to remain constant, which avoids the challenge of a variable influent pathogen concentration. Seeded studies conducted on systems that have been characterized with ambient pathogen studies could be used to validate ambient pathogen analysis approaches.

Summary

As water agencies seek to implement potable water reuse programs, obtaining credit for LRVs achieved through secondary and tertiary wastewater treatment processes will be an important consideration. The rank-paired covariant statistical approach, as discussed and illustrated in this paper, represents a rational method for estimating LRVs for wastewater unit treatment processes based on long-term monitoring data. In the future, as new and improved pathogen monitoring techniques are developed and tested, it may be necessary to revisit and update WWTP pathogen LRV crediting.

Data availability statement

The raw data supporting the conclusion of this article are presented in Table 1.

Author contributions

All the listed authors have made equal intellectual contribution to the work and approve it for publication.

Conflict of interest

JK was employed by Trussell Technologies, Inc. AO was employed by EOA.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.940014/full#supplementary-material

References

Greenwood, M., and Yule, G. (1917). On the statistical interpretation of some bacteriological methods employed in water analysis. J. Hyg. 16 (1), 36–54. doi:10.1017/S0022172400006501

PubMed Abstract | CrossRef Full Text | Google Scholar

Gujer, W., and Erni, P. (1978). The effect of diurnal ammonium load variation on the performance of nitrifying activated sludge processes. Prog. Wat. Tech. 10, 391–407.

Google Scholar

Hazen, A. (1914). Storage to be provided in impounding reservoirs for municipal water supply. New York, NY: Transactions of the American Society of Civil Engineers–1640. Paper No. 1308, 77, 12, 1539 (First known publication and introduction to the use of probability paper developed by Hazen).

Google Scholar

Niku, S., Schroeder, E. D., Tchobanoglous, G., and Samaniego, F. J. (1981a). Performance of activated sludge processes: Reliability, stability and variability. Washington, DC: U.S. Environmental Protection Agency, 8050977–R805101.

Google Scholar

Niku, S., Schroeder, E. D., Tchobanoglous, G., and Samaniego, F. J. (1981b). Performance of activated sludge processes: Reliability, stability and variability. Cincinnati, OH: U.S. Environmental Protection Agency. EPA-600/S2-81-227, Project Summary.

Google Scholar

Rose, J. B., Dickson, L. J., Farrah, S. R., and Carnahan, R. P. (1996). Removal of pathogenic and indicator microorganisms by a full-scale water reclamation facility. Water Res. 30 (11), 2785–2797. doi:10.1016/s0043-1354(96)00188-1

CrossRef Full Text | Google Scholar

State Water Board - Division of Drinking Water (2021). A proposed framework of regulating direct potable reuse in California addendum version 8-17-2021 DPR framework 2nd edition addendum – early draft of anticipated criteria for direct potable reuse," § 64669.45 pathogen Control and § 64669.115 alternatives, criteria to be added to the California code of regulations. Sacramento, CA: State Water Board - Division of Drinking Water. Title 22, Division 4, Chapter 17, Surface Water Treatment, as new Article 10, Direct Potable Reuse.

Google Scholar

Tchobanoglous, G., Stensel, H. D., Tsuchihashi, R., and Burton, F. L. (2014). “Wastewater engineering: Treatment and resource recovery,” in Metcalf and eddy/AECOM. 5th ed. (New York: McGraw-Hill Book Company).

Google Scholar

Velz, C. J. (1952). Graphical approach to statistics, water and sewage works. Reference Data, R106–R135.

Google Scholar

Velz, C. J. (1951). Graphical approach to statistics: Evaluation of bacterial density. Part IV, Water Sew. Works 98 (2), 262–265.

Google Scholar

Walpole, R. E., Myers, R. H., Myers, S. L., and Ye, K. E. (2012). Probability and statistics for engineers and scientists. 9th ed. Hoboken, NJ: Pearson Education Inc.

Google Scholar

Whitlock, M. C., and Schluter, D. (2012). The analysis of biological data. 2nd ed. New York: W.H. Freeman, Macmillan Learning.

Google Scholar

Yahaya, A. S., Yee, C. S., Ramli, N. A., and Ahmad, F. (2012). Determination of the best probability plotting position for predicting parameters of the weibull distribution. Int. J. Appl. Sci. Technol. 2 (3), 106–111.

Google Scholar