Sensitivity Analysis for Modeling of Cr(VI) Transfer From Soil to Surface Runoff

Heavy metal contamination in soil has become a serious environmental problem in China, and chromium is one of the major threats to human health. In order to better understand the transfer pattern of heavy metal hexavalent chromium from polluted sites into surface water, the influencing factors that affect solute transfer from soil into the surface runoff with linear and nonlinear adsorption equations based on a two-layer incomplete mixing model were analyzed in this study. The Quasi-Newton method was used to optimize model parameters by fitting with the experimental laboratory data of chromium (Cr(VI)) in surface runoff. The local sensitivity analysis and the Morris global sensitivity analysis approaches were used to assess the parameter importance of rainfall intensity p, the thickness of the mixing layer h_mix, incomplete mixing parameter α and γ, the soil adsorption parameters, and the initial soil water content θ₀. The study results showed that the optimized nonlinear models were better consistent with the experimental results than the linear adsorption equation model. The results of global sensitivity indicated that rainfall intensity p was the main factor influencing Cr(VI) transport from the soil into surface runoff. The h_mix and the α in the two-layer model were vital parameters that influenced such transport processes. Moreover, the soil adsorption properties and the θ₀ had the lowest effects on runoff Cr(VI) loss. The results indicate that for controlling pollution migration in surface runoff, it is essential to focus on the analysis of precipitation conditions and soil properties that control the thickness of the mixing layer and the degree of mixing.

Introduction

Due to the rapid development of industrialization and urbanization, heavy metal contamination in soil has become an essential aspect of global environmental pollution (Yang et al., 2018). Heavy metals (e.g., Cd, Cr, and Hg) in water bodies that originate either from contaminated soil or from the soil with natural heavy metal content may pose a threat to human health (Chen et al., 2021). Among them, hexavalent chromium (Cr⁶⁺) has received much attention due to its easy movement with stable and soluble properties (Sarkar et al., 2010) and its extensive sources from human activities, such as printing and dyeing, iron and steel manufacturing, leather tanning, chemical production, and fertilizers (Thangam et al., 2018). As a non-point pollution source, high content of chemicals in the soil migrate to the surface water and groundwater through the rainfall-runoff process, which is a crucial process of heavy metal pollution (Xiao et al., 2022). Therefore, it is of great significance to study the soil Cr(VI) loss and transfer into the rainfall-induced surface runoff.

The variations of Cr(VI) content in groundwater are usually characterized by convection, dispersion, adsorption, and reduction processes (Gorny et al., 2016). Various numerical methods depend on the lumped mixing layer approach (Donigian et al., 1977) and the diffusion approach (Wallach and van Genuchten 1990), and these approaches have been developed to analyze and illustrate experimental results. The mixing layer approach has gained more popularity than the diffusion approach by the ability to account for the influence of raindrops in the rainfall process (Li et al., 2017). It depends on the assumption that soil water mixes with surface runoff instantaneously and rainwater completely or incompletely in a thin layer below the soil surface without any contribution from the soil part under this mixing layer. Therefore, the thickness of the mixing layer determines the total amount of solutes transfer into the surface runoff (Ahuja and Lehman 1983; Tian et al., 2011a). Also, previous studies have found that the number of solutes in the soil entering surface runoff water when the subsurface drainage decreases exponentially with depth (Ahuja et al., 1981). However, the complete mixing method assumes that the soil water, surface water, and solute concentrations in rainwater within the mixed layer are the same during precipitation, which differs from the actual situation under subsurface drainage conditions. Hence, the complete mixing approach has been modified, and an incomplete mixing approach that considers the infiltration process has been developed (Wang et al., 1998). Both the complete mixing cell and incomplete uptake models were used to evaluate the transfer of soil-applied pesticide into the runoff in the field test (Young and Fry 2019). The result showed that the incomplete model provides more intuitive and reasonable results than the complete mixing model. Furthermore, it reported that the complete mixing cell model, as well as the refined equivalent model, facilitated the use of simplified parameters when describing the runoff process of solute transport to loess lands, while the incomplete mixed model was more suitable for practical situations (Yang et al., 2016). Tong et al. (2010) developed a two-layer incomplete mixing model to analyze the chemical components transported from soil to surface runoff water, which considers the surface runoff-ponding layer, soil mixing layer, and the lower layer below is regarded as the whole study system. This model is based on the assumption that the surface of the soil is (nearly) horizontal and the thickness of the mixing layer is considered constant, without considering lateral or return flows in the soil. The results of chemical components transfer from soil to the runoff in the unsaturated soil experiments were well explained by the simple two-layer incomplete mixing model, which verified model is reliable and reasonable (Wu et al., 2015; Tong et al., 2010).

Adsorption is an essential part of interpreting the transfer process, especially for heavy metal solutes, and solute transport models are usually combined with adsorption equations to analyze solute transport patterns. Laboratory test data was used to examine the modeling works with linear isotherm adsorption equation (Henry equation) by Wang (2012) and nonlinear isotherm adsorption equation (Langmuir and Temkin equation) by Wu et al. (2014, 2015). In addition, the selection impact of different adsorption models on the Cr(VI) loss simulation has been evaluated, and it suggested the Langmuir model is preferable (Xia et al., 2018). The model under each adsorption assumption is accompanied by a set of uncertain/unknown parameters. It is vital for model prediction accuracy to verify these uncertain parameters. Usually, we use the best-fit method to determine the parameters. Meanwhile, it is efficient to order the parameters’ priority in the prediction of solute concentration in the surface runoff before each parameter calibration (Song et al., 2015).

The sensitivity analysis (SA) aims to give intuitive and quantitative importance results for a specific parameter or a group of parameters that affect model performance (Saltelli et al., 2004), and it plays an important role in the model verification, parameterization, optimization, and uncertainty quantification (Song et al., 2015). Fundamental analysis of the parameter sensitivity in a model indicates how significant the simulation result relies on a single parameter, which is local sensitivity analysis (LSA). However, the parameters may relate to each other, which means one changing parameter may drive other parameters to change. Therefore, the result of local sensitivity is unreasonable. At this point, the global sensitivity analysis (GSA) is vital for investigating the effects of parameters systematically and the uncertainty of simulation results, thereby enhancing the interpretation of the system (Saltelli and Annoni 2010). A variety of GSA techniques have been applied to hydrogeological models, such as the screening method (Saltelli et al., 2008), regression analysis (Tiscareno-Lopez et al., 1993), meta-modeling method (Petropoulos et al., 2009), variance-based method (Xia et al., 2018), etc. Based on sensitivity analysis of fitting parameters in the two-layer incomplete mixing model (Tong et al., 2010) with different adsorption equations (such as α, γ, h_mix, k_d, K, S_max, and N). It suggested that the most important influencing factor is h_mix, and the sensitivity of adsorption parameters in the model gradually increases with time (Wu et al., 2015; Xia et al., 2018).

Many researchers have developed treatment processes to remediate Cr(VI) (Bansal et al., 2009; Lu et al., 2021). In contrast, few researchers devoted to the adsorptive solute of Cr(VI) transfer from soil into the surface runoff, especially, quantitative comparative analysis has not been carried out on the important influencing of multiple environmental factors, which is the main study in this article. As multi-factor analysis requires a large number of experiments, considering the toxicological damage of Cr(VI) to experimenters, this study was limited to the test results under a single environmental condition and relied on model simulation for analysis. In particular, some factors are interactive with each other, such as rainfall intensity and the thickness of the mixing layer (Tian et al., 2011a). Therefore, a comprehensive sensitivity analysis of various factors needs to be carried out. In this study, the model involves two sets of parameters, and in order to quantitatively examine the sensitivity of different models to their parameters, a series of sensitivity analyses were conducted. Among the GSA methods, the screening method is identifying the significance of input variables contributing to the output uncertainty in high-dimensionality models than exactly quantifying sensitivity (Saltelli et al., 2008), which reduces amounts of computation greatly. The Morris screening GSA method is widely used to solve the multi-parameter analysis due to its higher interpretability and practicability (Shin et al., 2013; Tian 2013). For analyzing the process of chemical transfer, the Henry and Langmuir adsorption equation was used in the modeling. The ODE45 method was applied to do the optimization of the parameters by using MATLAB. The LSA and Morris GSA were performed to evaluate the contribution and uncertainty of parameters to the variations in soil Cr(VI) released to surface runoff. These two sensitivity analysis methods performed well in the contaminant prediction and water science (Herman et al., 2013; Xu et al., 2018, 2019). In this study, the sensitivity of two adsorption models was compared to further understand the adsorption effect on heavy metal solute loss in the rainfall-runoff process.

Methods

Laboratory Experiment of Cr(VI) Loss

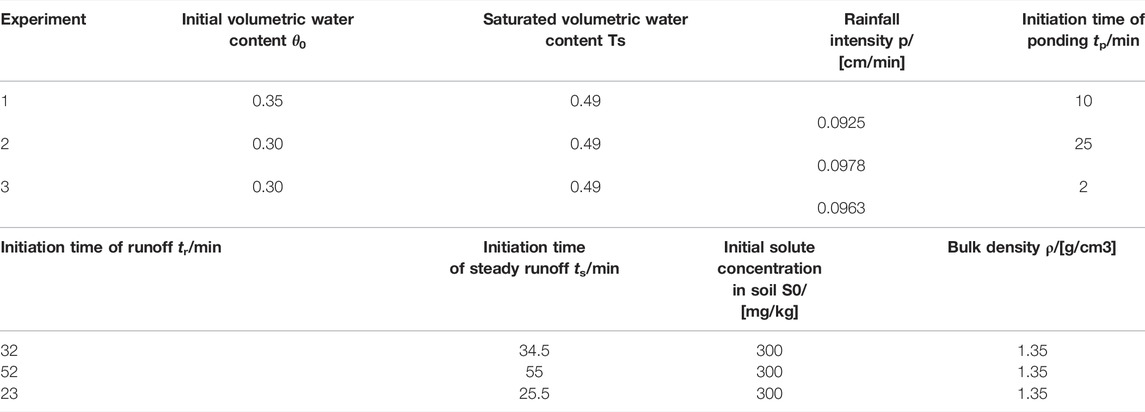
The experiment was implemented with a sandbox of 100 cm in length, 30 cm in width, and 40 cm in height in Figure 1 (Tong et al., 2010). A sand-gravel layer was laid at the bottom as a filter layer, and drainage holes were set in the middle of the bottom. The soil thickness is 23cm, and the maximum depth of ponding water h_p (t_r) is 1.1 cm. The chemical content of the water is nearly zero since distilled water was used in the rainfall. The drainage outlet was put 23 cm higher than the box bottom. The soil is collected from the background area, which can be regarded as soil without chromium. The initial soil concentration was set to 300 mg/kg, and it was ground, 2 mm screened dried silty sand. Then the calculated proportions of soil and potassium dichromate solution were well mixed. After standing for about 30 min, the sandbox was filled in layers. Surface runoff was collected approximately every 2 min, and the solute concentration of the water samples was determined using an Atomic Absorption Spectrometer (ContrAA-700, Analytic Jena AG). This experiment was conducted in 2012 and was duplicated twice in 2013. All of the experimental physical parameters are listed in Table 1.

FIGURE 1

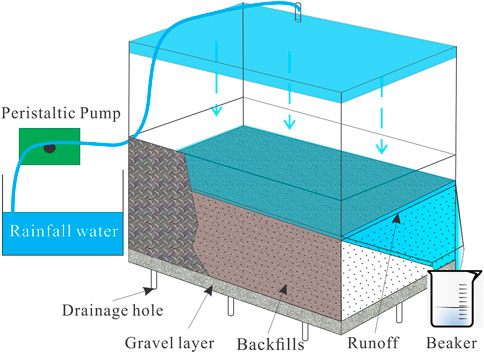
FIGURE 1. Schematic of the experimental apparatus (Tong et al., 2010).

TABLE 1

TABLE 1. Experimental and simulation parameters used in this test.

Mathematical Model

A brief description of the prediction model and laboratory experiments of solid solute transfer into the surface runoff is given in this paper, and more details were described in Tong et al. (2010). The two-layer system model (Figure 2) was applied to investigate the Cr(VI) transfer from soil into surface runoff under the Henry and Langmuir adsorption equations, where soil particles were ignored in the surface runoff process. There are two sections in the model. The upper section comprises the mixing layer and ponding-runoff layer, and the lower layer is the soil below the mixing layer. The equation of solute mass in the saturated mixing layer is

${\mathit{M}}_{\mathit{w}}={\mathit{C}}_{\mathit{w}}\left[\mathit{\alpha }\left({\mathit{h}}_{\mathit{w}}-{\mathit{h}}_{\mathit{m}\mathit{i}\mathit{x}}\cdot {\mathit{\theta }}_{\mathit{s}}\right)+{\mathit{h}}_{\mathit{m}\mathit{i}\mathit{x}}\cdot {\mathit{\theta }}_{\mathit{s}}\right],(1)$

where $M_w$ is the chemical mass dissolved in the water per unit area [μg/cm²]; $h_w$ is the depth of net water in the mixing layer and ponding-runoff layer [cm]; ${\theta }_s$ is saturated volumetric water content [cm³/cm³]; $h_{mix}$ is the thickness of the mixing layer, where the solute concentration is evenly distributed [cm]; $C_w$ is the concentration of the mixing layer and ponding-runoff layer [μg/cm³] = [μg/mL]; α (0<α ≤ 1) is the incomplete mixing parameter of solute between the soil water in the mixing layer and the ponding-runoff water.

FIGURE 2

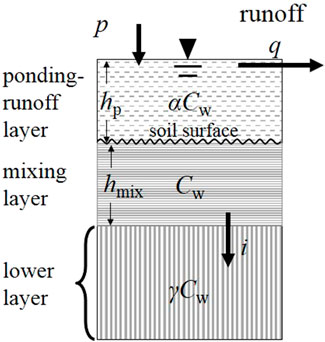
FIGURE 2. Simple two-layer incomplete mixing model (Non-actual size) (Tong et al., 2010).

The soluble chemical mass flows away via ponding-runoff and infiltration water. Hence, the following equation based on mass conservation is obtained:

$\frac{\mathit{d}{\mathit{M}}_{\mathit{w}}\left(\mathit{t}\right)}{\mathit{d}\mathit{t}}=-\mathit{\gamma }\cdot \mathit{i}\cdot {\mathit{C}}_{\mathit{w}}\left(\mathit{t}\right)-\mathit{\alpha }\cdot \mathit{q}\cdot {\mathit{C}}_{\mathit{w}}\left(\mathit{t}\right),(2)$

where γ (0<γ ≤ 1) is the incomplete mixing parameter of the solute between infiltration water and the soil water in the mixing layer; $q$ is the flow rate per unit area of surface runoff [cm/min]; $i$ is the infiltration flux [cm/min].

The increasing process of ponding water on the soil surface before runoff was considered, and the rainfall-induced runoff event can be divided into four stages, as shown in Figure 3.

FIGURE 3

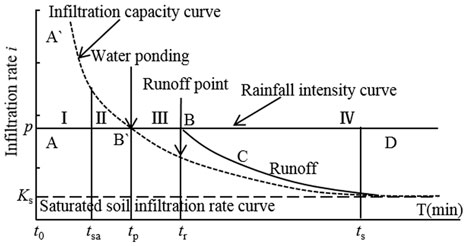
FIGURE 3. The curve of soil infiltration rate changes with time during a rainfall event (Mein and Larson 1973).

Period I: from the beginning of rainfall to the soil reaches saturation in the mixing layer and ponding-runoff layer, 0∼tsa; period II: from saturation state in mixing layer and ponding-runoff layer to surface ponding occurred, t_sa ∼ t_p; period III: from ponding to surface runoff occurred, tp ∼ t_r1; period IV: from surface runoff start to the end of rainfall; according to the different characteristics of soil infiltration rate, this period can be divided into two sub-periods:

o Sub-period I: soil infiltration linearly changes with time, t_r1∼t_r2

o Sub-period II: soil infiltration rate reaches a stable state, t_r2∼t_s

The solution variations in the experiment are divided into several different stages. Thus different equations were used for these stages in the mixing layer and ponding-runoff layer. α and γ are regarded as constants in the process of Cr(VI) loss from the soil into surface runoff and infiltration.

In this process, adsorption is a significant factor influencing the Cr(VI) loss. Two kinds of adsorption equations were used to describe this relationship.

Langmuir adsorption equation (Langmuir 1918):

$\frac{{\mathit{C}}_{\mathit{w}}}{\mathit{S}}=\frac{\mathbf{1}}{\mathit{K}{\mathit{S}}_{\mathit{m}\mathit{a}\mathit{x}}}+\frac{{\mathbf{C}}_{\mathit{w}}}{{\mathit{S}}_{\mathit{m}\mathit{a}\mathit{x}}},(3)$

where S is the capacity of equilibrium adsorption [mg/Kg], S_max is the single molecular layer adsorption saturated adsorption capacity [mg/Kg], K is a constant that describes the reaction energy, it links with the adsorption-desorption equilibrium constant for a reversible reaction [L/mg].

Henry Adsorption Equation

$\mathit{s}={\mathit{k}}_{\mathit{d}}{\mathit{C}}_{\mathit{w}},(4)$

where $k_d$ is the linear absorption coefficient [L/kg].

The Langmuir adsorption equation in the mixing model:

${\mathit{M}}_{\mathit{w}}={\mathit{C}}_{\mathit{w}}\left[\mathit{\alpha }\left({\mathit{h}}_{\mathit{w}}-{\mathit{h}}_{\mathit{m}\mathit{i}\mathit{x}}\cdot {\mathit{\theta }}_{\mathit{s}}\right)+{\mathit{h}}_{\mathit{m}\mathit{i}\mathit{x}}\cdot {\mathit{\theta }}_{\mathit{s}}\right]+{\mathit{h}}_{\mathit{m}\mathit{i}\mathit{x}}\cdot {\mathit{\rho }}_{\mathit{s}}\cdot \frac{{\mathit{C}}_{\mathit{w}}}{\mathit{B}{\mathit{C}}_{\mathit{w}}+\mathit{C}},(5)$

where $\mathit{B}=\frac{1}{{\mathit{S}}_{\mathit{max}} \frac{1}{\mathit{K}\cdot {\mathit{S}}_{\mathit{max}}}}$.

The Henry adsorption equation in the mixing model:

${\mathit{M}}_{\mathit{w}}={\mathit{C}}_{\mathit{w}}\left[\mathit{\alpha }\left({\mathit{h}}_{\mathit{w}}-{\mathit{h}}_{\mathit{m}\mathit{i}\mathit{x}}\cdot {\mathit{\theta }}_{\mathit{s}}\right)+{\mathit{h}}_{\mathit{m}\mathit{i}\mathit{x}}\cdot \left({\mathit{\theta }}_{\mathit{s}}+{\mathit{k}}_{\mathit{d}}{\mathit{\rho }}_{\mathit{s}}\right)\right].(6)$

The ODE equations used in the numerical calculation are shown in Supplementary Text S1.

Optimization

The experimental data were applied to calibrate the mathematical model with the Langmuir and Henry adsorption equations. Some parameters in the equations above were not obtained by the experiment test directly. The Quasi-Newton optimization method was used to calculate parameters of γ, α, h_mix, $k_d$ in the Henry equation and γ, α, h_mix, B, C in the Langmuir equation by fitting experimental results. The application of the Quasi-Newton method was shown in Supplementary Text S2.

Sensitivity Analysis

Local Sensitivity Analysis

In this work, the forward difference approximation was used to calculate the sensitivity of ith observation concerning jth parameter (Hill and Tiedeman 2007):

${\left(\frac{\mathit{\partial }{\mathit{y}}_{\mathit{i}}^{\prime }}{\partial {\mathit{b}}_{\mathit{j}}}\right)|}_{\mathit{b}}\approx \frac{{\mathit{y}}_{\mathit{i}}^{\prime }\left(\mathit{b}+\mathit{\Delta }\mathit{b}\right)-{\mathit{y}}_{\mathit{i}}^{\prime }\left(\mathit{b}\right)}{\mathit{\Delta }{\mathit{b}}_{\mathit{j}}},(7)$

where $y_i^{\prime }$ is the calculated result of ith observation; $b_j$ is the jth estimated parameter; $b$ is the vector of parameter values; $\mathit{\Delta }b$ is a vector of zero except that the jth parameter is $\mathit{\Delta }{b}_j$, $\mathit{\Delta }{b}_j$ should be 1–5% of $b_j$ (Saltelli et al., 2000).

Different parameters had different units, and for adequate comparing sensitivity of different parameters, approximations were converted to a dimensionless scaled form (Hill 1992; Hill. 1998):

$\mathit{d}\mathit{s}{\mathit{s}}_{\mathit{i}\mathit{j}}={\left(\frac{\partial {\mathit{y}}_{\mathit{i}}^{\prime }}{\partial {\mathit{b}}_{\mathit{j}}}\right)|}_{\mathit{b}}\left|{\mathit{b}}_j\right|{\mathit{\omega }}_{\mathit{ii}}^{\mathbf{1/2}},(8)$

where $ds{s}_{ij}$ is dimensionless scaled sensitivity of ith observation with respect to jth parameter; ${\omega }_{ii}$ is the weight in the ith simulation.

The total effect of different observations for one parameter is reflected in composite scaled sensitivity. It was calculated by the following equation (Hill 1992; Hill 1998):

$\mathit{c}\mathit{s}{\mathit{s}}_{\mathit{j}}={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\left(\frac{\mathit{d}\mathit{s}{\mathit{s}}_{\mathit{i}\mathit{j}}^{\mathbf{2}}}{\mathit{N}}\right)}^{\mathbf{1}/\mathbf{2}}},(9)$

where $cs{s}_j$ is composite scaled sensitivity (CSS) of jth parameter; N is the number of observations.

Global Sensitivity Analysis With the Morris Method

In the modeling, variations of some parameters may influence each other on the local estimation. GSA thoroughly considers the significance of one parameter under interactions with other parameters. In this study, the Morris method (Morris 1991; Saltelli et al., 2004) was implemented in calculating the global sensitivities of parameters. The Morris method is a one-at-a-time experiment. It is based on the element effect, which is the effect of changing one parameter at a time. The trajectory sampling was used in the Morris method to compute m parameters (m+1) simulations were calculated with a random start sampling point in one trajectory, the input space of each parameter is discretized into n levels, and the whole calculation contains r trajectories. The element effect of changing ith parameter in jth trajectory is

${\mathit{d}}_{\mathit{i}\mathit{j}}=\frac{\mathit{y}\left({\mathit{x}}_{\mathit{j}}+{\mathit{e}}_{\mathit{i}}\mathit{\Delta }\right)-\mathit{y}\left({\mathit{x}}_{\mathit{j}}\right)}{\mathit{\Delta }},(10)$

where $x_j=\left(x_1,x_2,\mathrm{...},x_m\right)$ of jth trajectory; $\mathit{\Delta }=1/\left(n-1\right)$; $e_i$ is a vector of zeros but with a unit at its ith component.

Once computations were completed, the average (μ) of one parameter in r trajectories reflects an estimation of the total-order effect, and the standard deviation (σ) described the variability of parameter space and the extent of parameter interactions (Herman et al., 2013).

${\mathit{\mu }}_{\mathit{i}}=\frac{\mathbf{1}}{\mathit{r}}{\displaystyle \sum _{\mathit{j}=1}^{\mathit{r}}{d}_{\mathit{i}\mathit{j}}},(11)$

${\mathit{\sigma }}_{\mathit{i}}=\sqrt{\frac{\mathbf{1}}{\mathit{r}}{\displaystyle \sum _{\mathit{j}=\mathbf{1}}^{\mathbf{r}}{\left({\mathit{d}}_{\mathit{i}\mathit{j}}-{\mathit{u}}_{\mathit{i}}\right)}^{\mathbf{2}}}}.(12)$

The specified value in local analysis and estimation ranges in the global analysis of seven parameters are listed in Table 2.

TABLE 2

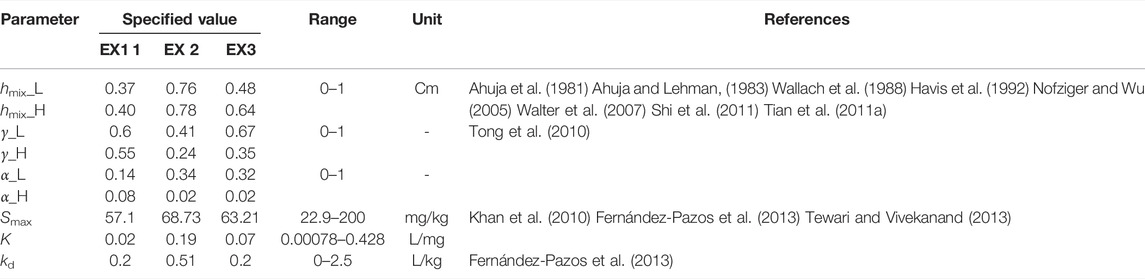
TABLE 2. The value ranges for local and global sensitivity analysis of all parameters. L and H represent Langmuir and Henry. EX1, EX1, and EX3 are short for the three experiments, 1, 2, and 3.

Results and Discussion

Experiment and Optimization Results

There are three categories of parameters in the optimization, including the two incomplete mixing parameters α and γ, the mixed layer thickness h_mix related to precipitation conditions (Ahuja et al., 1981), and the parameters of adsorption equations. Five and four parameters are involved in the modeling with corresponding Langmuir and Henry adsorption equations. The results of Quasi-Newton optimization are expressed in Figure 4, and the observed data (Experiment 1 is cited by Wang 2012; and Experiment 3 is cited by Wu et al., 2014) are presented as black squares. The simulations fit the experimental results quite well under both adsorption equations. The R-square of Langmuir adsorption and Henry adsorption ranged from 0.84 to 0.99. The results of the three experiments show that the initial concentration of Cr(VI) in the surface runoff was different between the three experiments, from 1.7 mg/L to 20 mg/L, and they reduced with time. In the early stage of the experiments, the concentration of soil heavy metal solutes was high, and the main factors affecting the solute concentration in runoff water were dissolution, mixing, and dilution. As the precipitation time extended, the density of surface soil pollutants decreased, and the concentration of solutes entering the surface runoff water also decreased rapidly. Surface pollutants precipitated from the soil, the influence of adsorption is strengthened, and deep pollutants contribute to the solute concentration in runoff water through convection, diffusion, and other effects.

FIGURE 4

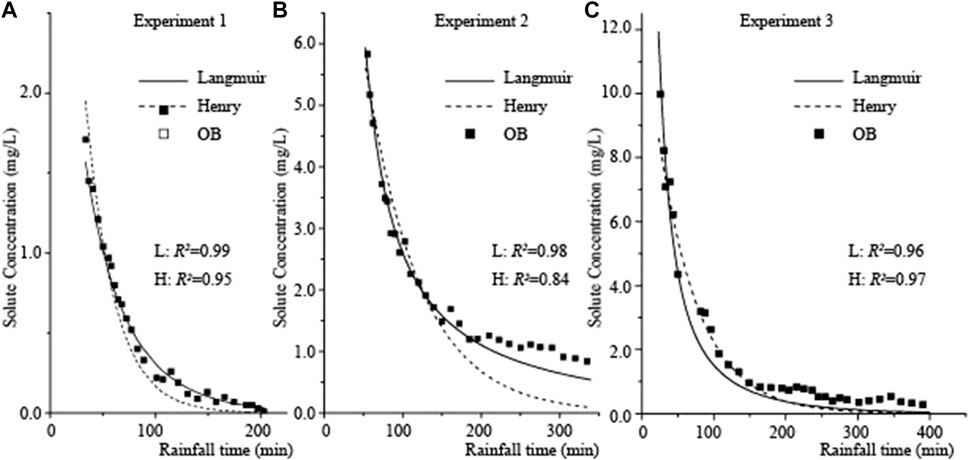
FIGURE 4. Comparison of experimental data and optimized models within Langmuir and Henry equation. Note: OB was for the Observation data.

The optimization results for all parameters are within a reasonable range which is from previous studies (Table 2). The γ is much larger than the α, which is consistent with the observations, and the solute concentration in surface runoff water (0.0 mg/L∼1.7 mg/L) is much smaller than that in subsurface drainage water (139.3 mg/L∼234.3 mg/L) in the experiment. Therefore, controlling subsurface drainage would be a practical approach to limit Cr(VI) migration from contaminated soils. In addition, this phenomenon is the same as in the case of fertilizer components loss in surface runoff from the soil with sandbox experiments (Tong et al., 2010). However, according to experiment and simulation results under the free subsurface drainage condition, the h_mix is one magnitude degree lower than the h_mix in this study (Tian et al., 2011a). Meanwhile, the soil was designed to be initially saturated without ponding depth, causing a much shorter runoff starting time than unsaturated soil (Tian et al., 2011b). Therefore, the deeper mixing layer is reasonable, considering the longer interaction time between soil and runoff water. The h_mix is close to the result of the experiment (0.356 cm), in which the water table was controlled to be 0 cm below the soil surface during the rainfall process (Tian et al., 2011b).

Local Sensitivity

For the LSA, the CSS of Cr(VI) concentration in surface runoff was calculated under each parameter’s Langmuir and Henry adsorption equations. Moreover, the value ranges of the parameters are listed in Table 2. In general, a larger CSS value represents more significance of such parameter to the simulated Cr(VI) concentration in surface runoff. The results of the LSA are shown in Figure 5.

FIGURE 5

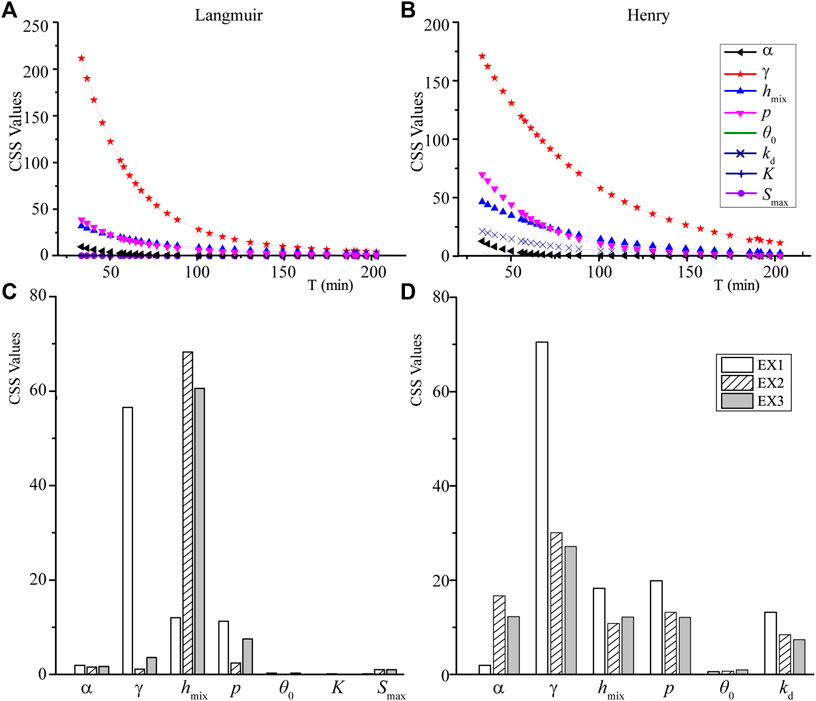
FIGURE 5. CSS values of Langmuir (A) and Henry (B) models along time during the rainfall-runoff process; (C) and (D) represent the mean values of CSS at different times for each parameter in the model with Langmuir and Henry equations, respectively.

As shown in Figures 5A,B, the model is more sensitive to the parameters in the early stage, and the sensitivity gradually decreases over time. Based on the results of the local sensitivity analysis of the three experimental results, it can be seen that the overall nonlinear adsorption model is more sensitive to parameters the mixing layer depth h_mix, the rainfall intense p and incomplete mixing parameter γ, and the remaining parameters including both parameters in the Langmuir adsorption equation are less sensitive (Figure 5C). However, the model with a linear adsorption equation is sensitive to all of the parameters except the initial water content (Figure 5D). The results illustrate that Cr(VI) transport and releasing are more influenced by the thickness of the mixing layer and ponding-runoff layer. These LSA results of the three experiments are not showing a similar trend but are not precisely consistent with each other, which indicates that the result of the LSA method varies with the calculated parameters and/or the experimental conditions.

Global Sensitivity

Unlike LSA, GSA considers the existence of correlations between parameters and gives a more comprehensive perspective of the sensitivity of different parameters. All parameters in LSA were examined in the GSA. The Morris trajectory method was applied for less computational cost than using the variance-based method. A simulation with level n = 4 and path r = 10 is good enough for most cases (Saltelli et al., 2004). Therefore, the Morris trajectory high-density sampling methods, where level n = 5 and path r = 10 in this study, were used to obtain more reliable results, and the results were plotted in Figure 6.

FIGURE 6

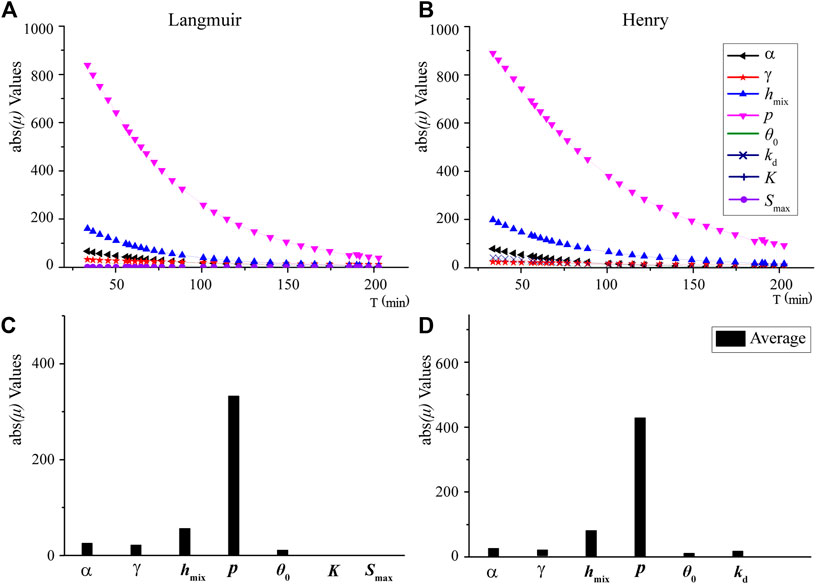
FIGURE 6. (A) and (B) represent that the absolute mean values of the element effect of each parameter abs(μ) are changing with time in the model with Langmuir and Henry equations; (C) and (D) is the average of elemental effects at different times for each parameter.

The model’s sensitivity to different parameters over time shows that the trend resembled the LSA, where the model is more sensitive to parameter changes in the early stage and gradually decreases with time (Figures 6 (a) and (b)). From the absolute mean values of element effect for each parameter abs(μ), the simulated results show that Cr(VI) concentration in surface runoff water is most sensitive to parameter p, followed by h_mix, α, γ, adsorption parameters, and θ₀, which are significantly different from the results of the LSA. This means that the model is most sensitive to p considering the interaction of the parameters, with which h_mix was also an essential parameter for the model. Overall, the model is fairly sensitive to the two incomplete parameters of α and γ in the simple two-layer model. The α has a more substantial effect on Cr(VI) loss in the surface runoff than γ, which is also different from the results of the LSA. Both from the LSA and GSA results, the parameters in the adsorption equations as well as θ₀ have relatively small effects on the results of Cr(VI) loss in surface runoff. The impact on the simulation results of adsorption parameters in the Henry linear equation is relatively more significant than that of the parameters in the Langmuir nonlinear adsorption equation. This is most likely due to the nonlinear adsorption equation having a more complex form and one more parameter, which decentralize the calculation, and when the parameters are compared individually, neither one has a significant effect on the simulation results.

The results of the LSA are significantly different from the results of the GSA. According to the GSA method, it is known that the result includes two parameters, one is the mean (μ) value of elemental effects, and the other is the standard deviation (σ) value of elemental effects. The value μ represents a general estimate of the sensitivity of a given input, and σ is a proxy for the input interaction and/or the non-linearity amount. The higher the value of σ represents less reliability of the sensitivity in the LSA (van Engelen et al., 2021). The absolute mean of the element effects and the standard deviation values are combined to analyze the model’s sensitivity to the parameters (Figure 7).

FIGURE 7

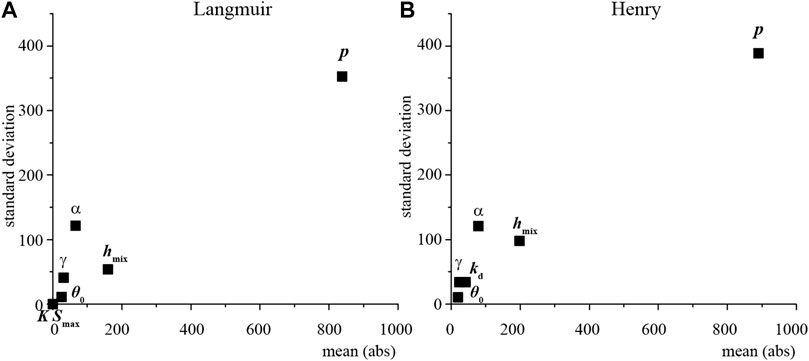
FIGURE 7. The absolute mean versus standard deviation of element effect for each parameter at the runoff start time.

As shown in Figure 7, p is the most critical factor controlling Cr(VI) loss in surface runoff. Meanwhile, both h_mix and α are essential to the model, but γ is less important. Under the linear adsorption equation condition, the adsorption coefficient k_d is more crucial to the model, while under the nonlinear adsorption assumption, all the parameters associated with the adsorption equation have little effect on the simulation results. The θ₀ has a minor effect on both models. According to experimental results the θ₀ is a vital parameter to the solutes concentrations in the surface runoff. It has been shown that the higher θ₀ is the greater runoff volume per unit time and higher solute concentration in the runoff, but less sediment mass in the runoff (Dong et al., 2018). The difference between the results of this study and the previous study is that the θ₀ was used only for the calculation of the ponding time but is less relevant to the subsequent calculation of the solute concentration in the surface runoff. The parameter h_mix gradually increases with p (Tian et al., 2011a), which enhances the impact of rainfall variability on the model. The γ is vital to the simulation result due to the high σ value resulting from the interaction of the strong parameters. Despite the parameter p, the GSA results are consistent with the previous study with the variance-based GSA (Xia et al., 2018). Therefore, it shows that the low computational effort of the Morris trajectory method is able to give reasonable results for the model in this study.

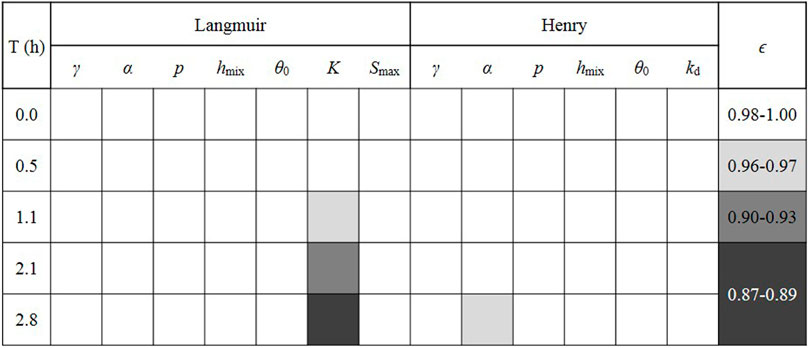
The mean of the absolute value of elementary effects (μ∗) is calculated to show non-monotonous effects (Campolongo et al., 2007). The two elementary effects parameters allow us to estimate a measure of non-monotonicity, ϵ, for each parameter:

$\epsilon =\frac{abs\left(\mu \right)}{{\mu }^{\ast }}.(14)$

An ϵ approaching one represents the elementary effect of the input is quite monotonous. The sign of the model’s response to changes in the input is always equal, regardless of the other input configurations. In contrast, close to zero means it is highly non-monotonous. As shown in Figure 8, only the nonlinear adsorptive parameter K variation showed a relatively high non-monotonicity for the simulation results with different model parameters. The rest of the parameter effects were monotonic. However, the sensitivity of the model to K was deficient in both the LSA and GSA and had little effect on the simulated results of Cr(VI) concentration in surface runoff.

FIGURE 8

FIGURE 8. The ϵ values of each parameter in the simulation during the rainfall process.

Conclusion

In order to better understand the Cr⁶⁺ transfer from contaminated fields under precipitation with subsurface drainage conditions, the main influencing factors of Cr(VI) loss in surface runoff under the two adsorption assumptions were explored on the basis of a previous experimental study. The numerical model was used in the calculation to solve the complex equations. The optimization with the Quasi-Newton method was applied to determine several vital parameters, such as γ, α, h_mix, k_d, K, and S_max. Then, the LSA and GSA were carried out on the significant parameters, such as p, γ, α, h_mix, θ₀, k_d, K, and S_max, in the model to investigate the effect of different parameters on the simulated Cr(VI) concentration in surface runoff. The main conclusions were obtained as follows:

• Quasi-Newton optimization performs very well in this study, and the optimization results well fit with the experimental data. In addition, the parameters determined from optimization were reasonable.

• The sensitivity of the model to all parameters gradually decreased as precipitation proceeded.

• The local sensitivity of the model to the parameters in descending order is γ, p, h_mix, and α. The sensitivity of the model to the parameters in the adsorption equations and the θ₀ was inferior.

• The GSA of the models shows that the models are also more sensitive to p, h_mix, and α, while not γ, θ₀, and parameters related to the adsorption equation.

In summary, this study supplemented the influence of environmental factors on runoff loss of adsorptive heavy metal chromium. The effects of rainfall intensity, the model mixing parameters, the thickness of the mixing layer, and adsorption conditions on the migration of hexavalent Chromium were quantitatively compared using a low computing cost GSA method. It turns out that the most important factors influencing the Cr(VI) transfer from soil into surface runoff during precipitation were the p, h_mix, α, and γ. θ₀ and the adsorption properties had a minor effect on the simulated Cr(VI) concentration in surface runoff. However, it should be mentioned that the θ₀ is a significant condition to the concentration variations in the surface runoff.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

XW was responsible for the main manuscript writing and data analysis; ZX completed the writing of the model program and analysis of the results; JT was responsible for providing the experimental data; and BH participated in the conclusion analysis.

Funding

This work was partly supported by the National Natural Science Foundation of China (Grant 42072271) and the Fundamental Research Funds for the Central Universities (Grant Nos. 2682022CX036 and 2652018179).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.917103/full#supplementary-material

Abbreviations

LSA, local sensitivity analysis; GSA, global sensitivity analysis.

References

Ahuja, L. R., and Lehman, O. R. (1983). The Extent and Nature of Rainfall‐soil Interaction in the Release of Soluble Chemicals to Runoff. J. Environ. Qual. 12 (1), 34–40. doi:10.2134/jeq1983.00472425001200010005x

CrossRef Full Text | Google Scholar

Ahuja, L. R., Sharpley, A. N., Yamamoto, M., and Menzel, R. G. (1981). The Depth of Rainfall-Runoff-Soil Interaction as Determined by 32 P. Water Resour. Res. 17 (4), 969–974. doi:10.1029/WR017i004p00969

CrossRef Full Text | Google Scholar

Bansal, M., Singh, D., and Garg, V. K. (2009). A Comparative Study for the Removal of Hexavalent Chromium from Aqueous Solution by Agriculture Wastes' Carbons. J. Hazard. Mater. 171, 83–92. doi:10.1016/j.jhazmat.2009.05.124

PubMed Abstract | CrossRef Full Text | Google Scholar

Campolongo, F., Cariboni, J., and Saltelli, A. (2007). An Effective Screening Design for Sensitivity Analysis of Large Models. Environ. Model. Softw. 22 (10), 1509–1518. doi:10.1016/j.envsoft.2006.10.004

CrossRef Full Text | Google Scholar

Chen, R., Zhang, Q., Chen, H., Yue, W., and Teng, Y. (2021). Source Apportionment of Heavy Metals in Sediments and Soils in an Interconnected River-Soil System Based on a Composite Fingerprint Screening Approach. J. Hazard. Mater. 411, 125125. doi:10.1016/j.jhazmat.2021.125125

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, W., Cao, C., Meng, X., Wang, Q., and Fu, Q. (2018). Experimental Studies on the Transfer of Dissolved Solutes from Soil into Surface Runoff on Loess Slopes in China. Appl. Water Sci. 8 (6). 10. doi:10.1007/s13201-018-0832-5

CrossRef Full Text | Google Scholar

Donigian, A. S., Beyerlein, D. C., Davis, H. H., and Crawford, N. H. (1977). Agricultural Runoff Management (ARM) Model, Version II; Refinement and Testing. Athens, Ga: Environ. Res. Lab. U.S. EPA.

Google Scholar

Fernández-Pazos, M. T., Garrido-Rodriguez, B., Nóvoa-Muñoz, J. C., Arias-Estévez, M., Fernández-Sanjurjo, M. J., Núñez-Delgado, A., et al. (2013). Cr(VI) Adsorption and Desorption on Soils and Biosorbents. Water Air Soil Pollut. 224 (1), 1–12. doi:10.1007/s11270-012-1366-3

CrossRef Full Text | Google Scholar

Gao, B., Todd Walter, M., Steenhuis, T. S., HogarthParlange, W. L. J. Y., and Parlange, J.-Y. (2004). Rainfall Induced Chemical Transport from Soil to Runoff: Theory and Experiments. J. Hydrology 295 (1-4), 291–304. doi:10.1016/j.jhydrol.2004.03.026

CrossRef Full Text | Google Scholar

Gorny, J., Billon, G., Noiriel, C., Dumoulin, D., Lesven, L., and Madé, B. (2016). Chromium Behavior in Aquatic Environments: a Review. Environ. Rev. 24 (4), 503–516. doi:10.1139/er-2016-0012

CrossRef Full Text | Google Scholar

Havis, R. N., Smith, R. E., and Adrian, D. D. (1992). Partitioning Solute Transport between Infiltration and Overland Flow under Rainfall. Water Resour. Res. 28, 2569–2580. doi:10.1029/92WR01366

CrossRef Full Text | Google Scholar

Heathman, G. C., Ahuja, L. R., and Lehman, O. R. (1985). The Transfer of Soil Surface-Applied Chemicals to Runoff. Trans. ASAE 28 (6), 1909–1915. doi:10.13031/2013.32540

CrossRef Full Text | Google Scholar

Herman, J. D., Kollat, J. B., Reed, P. M., and Wagener, T. (2013). Technical Note: Method of Morris Effectively Reduces the Computational Demands of Global Sensitivity Analysis for Distributed Watershed Models. Hydrol. Earth Syst. Sci. 17 (7), 2893–2903. doi:10.5194/hess-17-2893-2013

CrossRef Full Text | Google Scholar

Hill, M. C. (1992). A Computer Program (MODFLOWP) for Estimating Parameters of a Transient, Three-Dimensional Ground-Water Flow Model Using Nonlinear Regression. U.S. Geol. Surv. Open-File Rep. 91, 1–358. doi:10.3133/ofr91484

CrossRef Full Text | Google Scholar

Hill, M. C. (1998). Methods and Guidelines for Effective Model Calibration. U.S. Geological Survey Water-Resources Investigations Report 98 –4005 AvaliableAt: http://pubs.water. usgs.gov/wri984005/.

Google Scholar

Hill, M. C., and Tiedeman, C. R. (2007). Effective Groundwater Model Calibration: With Analysis of Data, Sensitivities, Predictions, and Uncertainty. Wiley-Interscience, 46–47.

Google Scholar

Khan, A. A., Muthukrishnan, M., and Guha, B. K. (2010). Sorption and Transport Modeling of Hexavalent Chromium on Soil Media. J. Hazard. Mater. 174 (1-3), 444–454. doi:10.1016/j.jhazmat.2009.09.073

PubMed Abstract | CrossRef Full Text | Google Scholar

Langmuir, I. (1918). The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 40, 1361–1403. doi:10.1021/ja02242a004

CrossRef Full Text | Google Scholar

Li, J., Tong, J., Xia, C., Hu, B. X., Zhu, H., Yang, R., et al. (2017). Numerical Simulation and Experimental Study on Farmland Nitrogen Loss to Surface Runoff in a Raindrop Driven Process. J. Hydrology 549, 754–768. doi:10.1016/j.jhydrol.2017.01.035

CrossRef Full Text | Google Scholar

Lu, S.-F., Wu, Y.-L., Chen, Z., Li, T., Shen, C., Xuan, L.-K., et al. (2021). Remediation of Contaminated Soil and Groundwater Using Chemical Reduction and Solidification/stabilization Method: a Case Study. Environ. Sci. Pollut. Res. 28 (10), 12766–12779. doi:10.1007/s11356-020-11337-3

CrossRef Full Text | Google Scholar

Mein, R. G., and Larson, C. L. (1973). Modeling Infiltration during a Steady Rain. Water Resour. Res. 9 (2), 384–394. doi:10.1029/WR009i002p00384

CrossRef Full Text | Google Scholar

Morris, M. D. (1991). Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 33 (2), 161–174. doi:10.2307/126904310.1080/00401706.1991.10484804

CrossRef Full Text | Google Scholar

Nofziger, D. L., and Wu, J. (2005). CHEMFLO™-2000 User's Manual: Interactive Software for Simulating Water and Chemical Movement in Unsaturated Soils Stillwater[Z]. OK: Oklahoma State University.

Google Scholar

Petropoulos, G., Wooster, M. J., Carlson, T. N., Kennedy, M. C., and Scholze, M. (2009). A Global Bayesian Sensitivity Analysis of the 1d SimSphere Soil-Vegetation-Atmospheric Transfer (SVAT) Model Using Gaussian Model Emulation. Ecol. Model. 220, 2427–2440. doi:10.1016/j.ecolmodel.2009.06.006

CrossRef Full Text | Google Scholar

Ren, A., Guo, B., Liu, S., and Zhou, B. (2000). Study on the Migration of Chromium in Soil. URBAN Environ. Urban Ecol. 13 (2), 54–56.

Google Scholar

Saltelli, A., and Annoni, P. (2010). How to Avoid a Perfunctory Sensitivity Analysis. Environ. Model. Softw. 25 (12), 1508–1517. doi:10.1016/j.envsoft.2010.04.012

CrossRef Full Text | Google Scholar

Saltelli, A., Chan, K., and Scott, E. M. (2000). Sensitivity Analysis. Hoboken, NJ: Wiley.

Google Scholar

Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D., et al. (2008). Global Sensitivity Analysis: The Primer. Chichester: John Wiley & Sons.

Google Scholar

Saltelli, A., Tarantola, S., Campolongo, F., and Ratto, M. (2002). “Sensitivity Analysis in Practice,” in Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models. Editor A. Saltelli. 1st ed. (Chichester, England: John Wiley & Sons). doi:10.1002/0470870958

CrossRef Full Text | Google Scholar

Sarkar, B., Xi, Y., Megharaj, M., Krishnamurti, G. S. R., Rajarathnam, D., and Naidu, R. (2010). Remediation of Hexavalent Chromium through Adsorption by Bentonite Based Arquad 2HT-75 Organoclays. J. Hazard. Mater. 183 (1-3), 87–97. doi:10.1016/j.jhazmat.2010.06.110

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, X., Wu, L., Chen, W., and Wang, Q. (2011). Solute Transfer from the Soil Surface to Overland Flow: A Review. Soil Sci. Soc. Am. J. 75 (4), 1214–1225. doi:10.2136/sssaj2010.0433

CrossRef Full Text | Google Scholar

Shin, M.-J., Guillaume, J. H. A., Croke, B. F. W., and Jakeman, A. J. (2013). Addressing Ten Questions about Conceptual Rainfall-Runoff Models with Global Sensitivity Analyses in R. J. Hydrology 503, 135–152. doi:10.1016/j.jhydrol.2013.08.047

CrossRef Full Text | Google Scholar

Song, X., Zhang, J., Zhan, C., Xuan, Y., Ye, M., and Xu, C. (2015). Global Sensitivity Analysis in Hydrological Modeling: Review of Concepts, Methods, Theoretical Framework, and Applications. J. Hydrology 523, 739–757. doi:10.1016/j.jhydrol.2015.02.013

CrossRef Full Text | Google Scholar

Tewari, H., and Vivekanand, (2013). Removal of Heavy Metals from Industrial Effluent Using Pinus Roxburghii Leaves as Biosorbent: Equilibrium Modelling. Water Sci. Technol. A J. Int. Assoc. Water Pollut. Res. 67 (9), 1894–1900. doi:10.2166/wst.2013.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Thangam, T. E. D., Kumar, V. N., and Vasline, Y. A. (2018). Decontamination of Hexavalent Chromium by Geo Chemical Fixation Method in a Hazardous Dump Site, Ranipet, Tamil Nadu, India. J. Eng. Appl. Sci. 13 (1), 208–212. doi:10.36478/jeasci.2018.208.212

CrossRef Full Text | Google Scholar

Tian, K., Huang, C. H., Tian, P., Wang, G. Q., Fu, X. D., and Guo, H. D. (2011b). Movement of Soil Solute under Simulated Rainfall Runoff. Trans. CSAE 27 (4), 81–87. doi:10.3969/j.issn.1002-6819.2011.04.014

CrossRef Full Text | Google Scholar

Tian, K., Huang, C. H., Tian, P., Wang, G. Q., and Fu, X. D. (2011a). Simulated Experiment of Mixing Zone Depth under Rainfall-Runoff Conditions. Trans. Chin. Soc. Agric. Eng. 27 (11), 188–192.

Google Scholar

Tian, W. (2013). A Review of Sensitivity Analysis Methods in Building Energy Analysis. Renew. Sustain. Energy Rev. 20, 411–419. doi:10.1016/j.rser.2012.12.014

CrossRef Full Text | Google Scholar

Tiscareno-Lopez, M., Lopes, V. L., Stone, J. J., and Lane, L. J. (1993). Sensitivity Analysis of the WEPP Watershed Model for Rangeland Applications I: Hillslope Processes. Trans. ASAE 36 (6), 1659–1672. doi:10.13031/2013.28509

CrossRef Full Text | Google Scholar

Tong, J.-X., Yang, J.-Z., Hu, B. X., and Bao, R.-c. (2010). Experimental Study and Mathematical Modelling of Soluble Chemical Transfer from Unsaturated/saturated Soil to Surface Runoff. Hydrol. Process. 24 (21), 3065–3073. doi:10.1002/hyp.7722

CrossRef Full Text | Google Scholar

van Engelen, J., Bierkens, M. F. P., Delsman, J. R., and Oude Essink, G. H. P. (2021). Factors Determining the Natural Fresh‐Salt Groundwater Distribution in Deltas. Water Res. 57 (1), e2020WR027290. doi:10.1029/2020WR027290

CrossRef Full Text | Google Scholar

Wallach, R., Jury, W. A., and Spencer, W. F. (1988). Transfer of Chemicals from Soil Solution to Surface Runoff: A Diffusion-Based Soil Model. Soil Sci. Soc. Am. J. 52 (3), 612–618. doi:10.2136/sssaj1988.03615995005200030002x

CrossRef Full Text | Google Scholar

Wallach, R., and van Genuchten, M. T. (1990). A Physically Based Model for Predicting Solute Transfer from Soil Solution to Rainfall-Induced Runoff Water. Water Resour. Res. 26 (9), 2119–2126. doi:10.1029/WR026i009p02119

CrossRef Full Text | Google Scholar

Walter, M. T., Gao, B., and Parlange, J.-Y. (2007). Modeling Soil Solute Release into Runoff with Infiltration. J. Hydrology 347 (3-4), 430–437. doi:10.1016/j.jhydrol.2007.09.033

CrossRef Full Text | Google Scholar

Wang, Q. J., Wang, W. Y., Shen, B., and Shao, M. A. (1998). Interacting Depth of Rainfall-Runoff-Soil Solute. J. Soil Eros. Soil Water Conservation 4 (2), 41–46.

Google Scholar

Wang, Y. (2012). Study on the Adsorptive Solute (Cr6+) Transfer from Soil to the Surface Runoff, Dissertation. Beijing: China University of Geosciences, 13–14. Thesis.

Google Scholar

Wu, J., Ran, Z. M., Liu, H. Q., and Du, J. (1997). Absorption Behavior of Chromium (VI) in Red Soils. Chongqing Environ. Sci. 19 (6), 22–26.

Google Scholar

Wu, X. J., Tong, J. X., and Tan, C. Q. (2015). Experiment and Simulation on Soil Cr(VI) Loss to Surface Runoff under Condition of Nonlinear Langmuir Adsorption. Trans. Chin. Soc. Agric. Eng. Trans. CSAE) 31 (1), 146–152.

Google Scholar

Wu, X. J., Tong, J. X., Tan, C. Q., Hu, B. X., and Yang, J. Z. (2014). Study on the Adsorptive Solute Cr(VI) Loss from Soil to Surface Runoff with Temkin Adsorption. AMM 641-642, 209–216. doi:10.4028/www.scientific.net/amm.641-642.209

CrossRef Full Text | Google Scholar

Xia, C.-A., Tong, J., Hu, B. X., Wu, X., and Guadagnini, A. (2018). Assessment of Alternative Adsorption Models and Global Sensitivity Analysis to Characterize Hexavalent Chromium Loss from Soil to Surface Runoff. Hydrol. Process. 32 (20), 3140–3157. doi:10.1002/hyp.13233

CrossRef Full Text | Google Scholar

Xiao, Y., Liu, K., Hao, Q., Xiao, D., Zhu, Y., Yin, S., et al. (2022). Hydrogeochemical Insights into the Signatures, Genesis and Sustainable Perspective of Nitrate Enriched Groundwater in the Piedmont of Hutuo Watershed, China. CATENA 212, 106020. doi:10.1016/j.catena.2022.106020

CrossRef Full Text | Google Scholar

Xu, Z., Hu, B. X., Xu, Z., and Wu, X. (2019). Simulating Seawater Intrusion in a Complex Coastal Karst Aquifer Using an Improved Variable-Density Flow and Solute Transport-Conduit Flow Process Model. Hydrogeol. J. 27, 1277–1289. doi:10.1007/s10040-018-1903-2

CrossRef Full Text | Google Scholar

Xu, Z., Hu, B. X., and Ye, M. (2018). Numerical Modeling and Sensitivity Analysis of Seawater Intrusion in a Dual-Permeability Coastal Karst Aquifer with Conduit Networks. Hydrol. Earth Syst. Sci. 22, 221–239. doi:10.5194/hess-22-221-2018

CrossRef Full Text | Google Scholar

Yang, Q., Li, Z., Lu, X., Duan, Q., Huang, L., and Bi, J. (2018). A Review of Soil Heavy Metal Pollution from Industrial and Agricultural Regions in China: Pollution and Risk Assessment. Sci. Total Environ. 642, 690–700. doi:10.1016/j.scitotenv.2018.06.068

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, T., Wang, Q., Liu, Y., Zhang, P., and Wu, L. (2016). A Comparison of Mathematical Models for Chemical Transfer from Soil to Surface Runoff with the Impact of Rain. CATENA 137, 191–202. doi:10.1016/j.catena.2015.09.014

CrossRef Full Text | Google Scholar

Young, D. F., and Fry, M. M. (2019). Field-scale Evaluation of Pesticide Uptake into Runoff Using a Mixing Cell and a Non-uniform Uptake Model. Environ. Model. Softw. 122, 104055. doi:10.1016/j.envsoft.2017.09.007

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, J., Feng, L., and Zou, W. (2011). A Prediction Model Based on Langmuir Theory for Equilibrium Adsorption Amount. J. Northeast. Univ. Nat. Sci. 32 (5), 749–751.

Google Scholar