A Hybrid Model of Ensemble Empirical Mode Decomposition and Sparrow Search Algorithm-Based Long Short-Term Memory Neural Networks for Monthly Runoff Forecasting

Monthly runoff forecasting plays a vital role in reservoir ecological operation, which can reduce the negative impact of dam construction and operation on the river ecosystem. Numerous studies have been conducted to improve monthly runoff forecast accuracy, of which machine learning methods have been paid much attention due to their unique advantages. In this study, a conjunction model, EEMD-SSA-LSTM for short, which comprises ensemble empirical mode decomposition (EEMD) and sparrow search algorithm (SSA)–based long short-term neural networks (LSTM), has been proposed to improve monthly runoff forecasting. The EEMD-SSA-LSTM model is mainly carried out in three steps. First, the original time series data is decomposed into several sub-sequences. Second, each sub-sequence is simulated by LSTM, of which the hyperparameters are optimized by SSA. Finally, the simulated results for each sub-sequence are summarized as the final results. The data obtained from two reservoirs located in China are used to validate the proposed model performance. Meanwhile, four commonly used statistical evaluation indexes are utilized to evaluate model performance. The results demonstrate that compared to several benchmark models, the proposed model can yield satisfactory forecast results and can be conducive to improving monthly runoff forecast accuracy.

Introduction

Water resource quantity is an extremely important restriction factor in ecological environmental protection and construction. As a fundamental work, monthly runoff forecasting plays a vital role in taking full advantage of water resources, including reservoir ecological operation. With characteristics of nonlinearity and randomness, the monthly runoff process is always affected by a variety of factors, such as precipitation, climate change, and human activities. Generally, it is a challenging task to forecast monthly runoff with reliable and applicable forecast accuracy. Hydrological models can be approximately divided into two categories: physical-driven (Liao et al., 2016; Solakian et al., 2020; Zhang et al., 2020; Dunkerley, 2021; Nonki et al., 2021; Xu et al., 2022) and data-driven models (Quilty et al., 2019; Feng et al., 2020; Liao et al., 2020; Darabi et al., 2021; Niu et al., 2021; Feng et al., 2022; Nguyen et al., 2022). Physical-driven models usually consider the physical genesis and mechanism of the runoff yield process and require a large amount of data for modeling. As a contrast, data-driven models only focus on the optimal functional relationship between input and output data, do not consider the physical mechanism of hydrological processes, and call for much less data. Due to the merit of ease of implementation, many studies have demonstrated the feasibility and reliability of data-driven models in monthly runoff forecasting (Huang et al., 2019; Feng et al., 2020; He et al., 2020; Feng et al., 2021).

With the development of machine learning, many kinds of data-driven models have been used in monthly runoff prediction, such as artificial neural networks (Jhong et al., 2018; Sibtain et al., 2021), support vector machine (Adnan et al., 2020), and random forest (Pandhiani et al., 2020). As a type of ANN, long short-term memory neural networks (LSTMs) have been successfully applied in monthly runoff forecasting (Chen et al., 2020; Mao et al., 2021; Wang et al., 2021). Although LSTM performs well, further improvement is still needed to enhance the forecast accuracy. In previous studies, there have been generally two strategies to improve the prediction accuracy. One is the data preprocessing technique that can reduce the nonstationary characteristics of the time series data and extract effective information hidden in data (Apaydin and Sibtain, 2021). The other is to adopt optimization algorithms to optimize the hyperparameters of the models (Feng et al., 2022).

As a data preprocessing technique, empirical mode decomposition (EMD) has been applied extensively in hydrological forecasting (Meng et al., 2019; Song et al., 2021). However, with the significant drawback of mode mixing of EMD, data with similar scales may appear in different intrinsic mode functions (IMFs) (Zhang and Hong, 2019). To overcome this defect, ensemble empirical mode decomposition (EEMD) is proposed by adapting the Gaussian white noise and widely used in many fields, such as hydrological forecasting and mechanical fault diagnosis (Zhang et al., 2018; Ali et al., 2020; Faysal et al., 2021; Wang et al., 2021). For example, Ali et al. (2020) investigated the EEMD combined with RF and kernel ridge regression model for monthly rainfall forecasts and verified that the hybrid model could attain better rainfall forecast accuracy. Yuan et al. (2021) used a combination of EEMD and LSTM to forecast daily runoff and significantly improved the forecast accuracy compared to the LSTM model. Many studies have reported optimized hyperparameters of LSTM in application, and several optimization algorithms were used. For instance, Yuan et al. (2018) investigated the accuracy of hybrid LSTM and ant lion optimizer model (LSTM-ALO) in monthly runoff forecasting and confirmed the effectiveness of the hybrid model. As an emerging optimization algorithm with the merits of robustness and strong global searching ability, the sparrow search algorithm (SSA) has become popular in solving optimization problems (Xue and Shen, 2020; Zhang and Ding, 2021; Li et al., 2022). At present, several studies have been conducted by utilizing both data preprocessing techniques and parameter optimization for models in hydrological forecasting. For example, Niu et al. (2019) utilized a combination of EEMD and an optimized extreme learning machine (ELM) to forecast reservoir monthly runoff, where the parameters of ELM were optimized by an improved gravitational search algorithm. Wang et al. (2021) used VMD-LSTM-PSO in daily runoff forecasting and verified its high forecast accuracy and stability. To the best of our knowledge, there are few studies that reported that EEMD and SSA-based LSTM (EEMD-SSA-LSTM) have been conducted in monthly runoff forecasting.

In this study, a hybrid of EEMD-SSA-LSTM is proposed for monthly runoff forecasting. The novel contribution can be conducted in three steps. First, EEMD is used to decompose the original sequence into several subsequences. Second, each subsequence is modeled and forecasted by LSTM, of which the hyperparameters are optimized by the SSA. Finally, the results for each subsequence are summarized as the final forecast result. The proposed model has been verified with monthly runoff data obtained from two reservoirs located in China, and the result shows that the proposed EEMD-SSA-LSTM model can afford satisfactory forecast accuracy and is reliable and applicable in practice.

Methodology

Ensemble Empirical Mode Decomposition

The conventional EMD is prone to mode aliasing when used to analyze time series data. To solve this problem, as an improvement, EEMD can effectively reduce mode aliasing by adding white noise. The specific EEMD steps can be stated as follows:

Step 1. Given a signal, the parameters of EEMD are set, including the maximum number of iterations, noise standard deviation, and number of realizations (NR).

Step 2. White noise $w_i\left(t\right)$ is added with standard normal distribution to generate a new signal:

$x_i\left(t\right)=x\left(t\right)+w_i\left(t\right).(1)$

Step 3. EMD is used to decompose the signal $x_i\left(t\right)$ into n IMFs and a trend item.

$x_i\left(t\right)={\displaystyle \sum _{j=1}^n{c}_{ij}\left(t\right)+r_i\left(t\right)}.(2)$

Step 4. Repeat steps 2 and 3 for NR times.

Step 5. Eq. 3 is used to calculate the IMFs and Eq. 4 is used to gain the final results.

$c_j\left(t\right)=\frac{1}{NR}{\displaystyle \sum _{i=1}^{NR}{c}_{ij}\left(t\right)},(3)$

$x\left(t\right)={\displaystyle \sum _{j=1}^n{c}_j\left(t\right)+r\left(t\right)},(4)$

where $c_j\left(t\right)$ represents the jth IMF and $r\left(t\right)$ denotes the trend item.

Sparrow Search Algorithm

The SSA, proposed by Xue and Shen (2020), is a novel swarm intelligent optimization algorithm, which has the advantages of less control parameters, strong local search ability, and fast convergence speed. In the SSA, sparrow swarms are divided into two categories: the producers and the scroungers. The producers can search for abundant food, while the scroungers follow the producers to find food. The main steps of the SSA are as follows:

1) The location of the producers is updated by using Eq. 5:

$X_{i,j}^{t+1}=\{\begin{array}{cc}{X}_{i,j}^t\cdot \exp \left(-\frac{i}{\alpha \cdot ite{r}_{\max }}\right)& if{R}_2<ST\\ X_{i,j}^t+Q\cdot L& if{R}_2\ge ST\end{array},(5)$

where t is the current iteration number; j = 1, 2,…,d; $ite{r}_{max}$ is the maximum number of iterations; $X_{i,j}$ is the position of the ith sparrow in the jth dimension; $\alpha \in \left(\mathrm{0,1}\right]$ is a random number. $R_2\in \left[\mathrm{0,1}\right]$ and $ST\in \left[0.5,1\right]$ denote the warning value and the safe value, respectively; $Q$ is a random number obeying normal distribution; and $L$ denotes a matrix of $1\times d$.

2) The location of the scroungers is updated by using Eq. 6:

$X_{i,j}^{t+1}=\{\begin{array}{cc}Q\cdot \exp \left(\frac{X_{worst}-X_{i,j}^t}{i^2}\right)& ifi>n/2\\ X_p^{t+1}+\left|X_{i,j}^t-X_p^{t+1}\right|\cdot A^{+}\cdot L& otherwise\end{array}.(6)$

When $i>n/2$, it indicates that the ith scrounger with worse fitness is most probable to fly to other places to find food and get more energy.

Supposing 10–20% of of sparrows are aware of danger, being aware of danger, a sparrow will quickly move to the safe area, which can be mathematically expressed as

$X_{i,j}^{t+1}=\{\begin{array}{l}{X}_{best}^t+\beta \cdot \left|X_{i,j}^t-X_{best}^t\right|if{f}_i>f_g\\ X_{i,j}^t+K\cdot \left(\frac{\left|X_{i,j}^t-X_{worst}^t\right|}{(f_i-f_w)+\epsilon }\right)if{f}_i=f_g\end{array},(7)$

where $X_{best}$ is the current global optimal position; $\beta$ is a random number of the step size control parameter, which obeys normal distribution with mean of 0 and variance of 1; $K\in \left[-\mathrm{1,1}\right]$ is a random number; $f_i$ is the fitness value of the current sparrow individual; $f_g$ is the current global optimal fitness value; $f_w$ is the current global worst fitness value; and $\epsilon$ is a constant.

Long Short-Term Neural Networks

LSTM is a type of recurrent neural network model (RNN) in essence and can solve the problem of gradient disappearance during backpropagation, which is faced by the conventional RNN. The LSTM model consists of an input layer, a hidden layer, and an output layer. In the hidden layer, three control units are established, which are input gate, forget gate, and output gate. The function of the input gate is to selectively record new information into the cell state; the forget gate is to selectively forget the information in the cell; and the output gate is to bring the stored information to the next neuron. The LSTM model is updated as follows:

$\text{Forget}\text{gate:}{f}_t=\sigma \left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right),(8)$

$\text{Input}\text{gate:}{i}_t=\sigma \left(W_{\text{i}}\cdot \left[h_{t-1},x_t\right]+b_i\right),(9)$

$\text{Output}\text{gate:}{o}_t=\sigma \left(W_o\cdot \left[h_{t-1},x_t\right]+b_o\right),(10)$

$\text{Input}\text{units:}{\tilde{c}}_t=\tanh \left(W_c\cdot \left[h_{t-1},x_t\right]+b_c\right),(11)$

$\text{Memory}\text{cells:}{c}_t=f_t\cdot c_{t-1}+i_t\cdot {\tilde{c}}_t,(12)$

$\text{Output}\text{units:}{h}_t=o_t\cdot \tanh \left(c_t\right),(13)$

where $f_t$, $i_t$, ${\tilde{c}}_t$, $c_t$, $o_t$, and $h_t$ denote forget gate, input gate, current cell state, final cell state, output gate, and the output of LSTM, respectively; $w_f$, $w_i$, $w_c$, and $w_o$ are the weights of forget gate, input gate, cell state, and output gate, respectively; $h_{t-1}$ is the output of the previous generation; $x_t$ is the input at time t; and $\sigma$ is the sigmoid function.

Hybrid Model for Monthly Runoff Forecasting

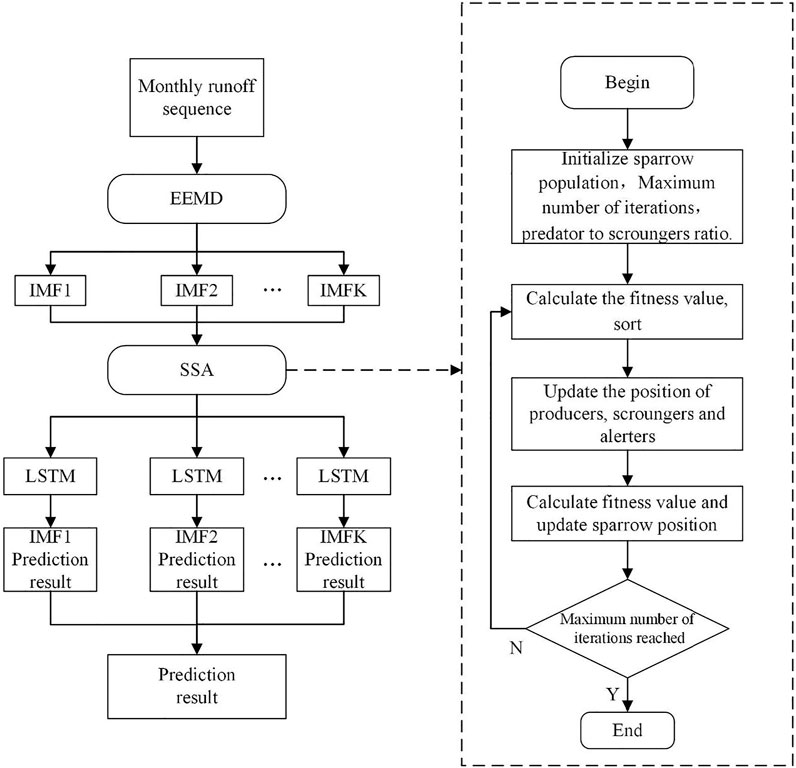
To forecast monthly runoff, a hybrid model of EEMD-SSA-LSTM was proposed. The specific flow chart of the proposed model is shown in Figure 1, and the main processes can be stated as follows:

FIGURE 1

FIGURE 1. Flowchart of EEMD-SSA-LSTM for monthly runoff forecasting.

Step 1Data processing. The original monthly runoff sequence is decomposed by the EEMD method, and several subsequences with different frequencies are obtained. The input variables for each subsequence are selected by partial autocorrelation function (PACF).

Step 2Parameter optimization. The SSA algorithm is used to optimize the hyperparameters of the LSTM model for each subsequence, including number of neurons, number of iterations, and learning rate.

Step 3Forecast and aggregation. Forecast results for each subsequence can be obtained by conducting the LSTM model for each subsequence, and the final forecast results can be obtained by simply aggregating the forecast results for each subsequence.

Evaluation Index

To evaluate the predictive ability of the proposed model, four frequently used evaluation indexes, that are root mean squared error (RMSE), mean absolute percentage error (MAPE), coefficient of correlation (R), and Nash coefficient (CE), are used to evaluate the model performance. For these four indexes, the closer the values of RMSE and MAPE are to 0 and the values of R and CE are to 1, the better the performance of the model. The specific formulas are as follows.

$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(Q_i-{\widehat{Q}}_i\right)}^2}},(14)$

$MAPE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|\frac{Q_i-{\widehat{Q}}_i}{Q_i}\right|}\times 100,(15)$

$R=\frac{{\displaystyle \sum _{i=1}^n\left(Q_i-{\overline{Q}}_i\right)\left({\widehat{Q}}_i-{\overline{\widehat{Q}}}_i\right)}}{\sqrt{{\displaystyle \sum _{i=1}^n{\left(Q_i-{\overline{Q}}_i\right)}^2{\displaystyle \sum _{i=1}^n{\left({\widehat{Q}}_i-\overline{\widehat{Q}}\right)}^2}}}},(16)$

$CE=1-\frac{{\displaystyle \sum _{i=1}^n{\left(Q_i-{\widehat{Q}}_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(Q_i-\overline{Q}\right)}^2}},(17)$

where $Q_i$ and ${\widehat{Q}}_i$ are the measured and forecasted values at the ith month, respectively; and ${\overline{Q}}_i$ and ${\overline{\widehat{Q}}}_i$ are the average of the measured and forecasted values, respectively.

Case Study

Study Area and Data

The Guangzhao and Xinfengjiang Reservoirs, located in southwestern and southern China, were selected as case studies, respectively. Located in Guizhou province, the Beipan River basin has a subtropical monsoon climate. The Guangzhao Reservoir is located in the middle reach of the Beipan River basin, in which the drainage area is 13548 km², the annual average rainfall is 1178 mm, and the annual average runoff is 257 m³/s. With 745 m of normal water level, 3.245 × 10⁹ m³ of storage volume as well as 1040 MW of installed capacity, the Guangzhao Reservoir is a leading reservoir with the main purpose of power generation and takes into account shipping, irrigation, and water supply. Located in Guangdong province, the Dongjiang River basin has a subtropical monsoon climate. The Xinfengjiang Reservoir is located in the Dongjiang River basin, of which the drainage area is 5740 km², the annual average rainfall is 1795 mm, and the annual average runoff is 192 m³/s. With 116 m of normal water level, 13.896 × 10⁹ m³ of storage volume as well as 336.1 MW of installed capacity, the Xinfengjiang Reservoir is a leading reservoir with the main purpose of power generation and takes into account irrigation, shipping, flood control, and water supply.

In this study, monthly runoff data covering from 1956 to 2017 were selected from the Guangzhao Reservoir, of which the data from 1956 to 2002 were chosen for calibration, and the remaining data were used for validation. Monthly runoff data covering from 1943 to 2015 were selected from the Xinfengjiang Reservoir, of which the data from 1943 to 1997 were chosen for calibration, and the remaining data were used for validation.

Data Decomposition

Via EEMD, monthly runoff data of the two reservoirs were decomposed into several subsequences. There are three important parameters of EEMD that affect the decomposition results, of which the white noise amplitude was set to 0.2 times the standard deviation of the sample data, NR was set to 100, and the maximum number of filtering iterations was set to 500. Once the parameters of EEMD are set, decomposition can be carried out.

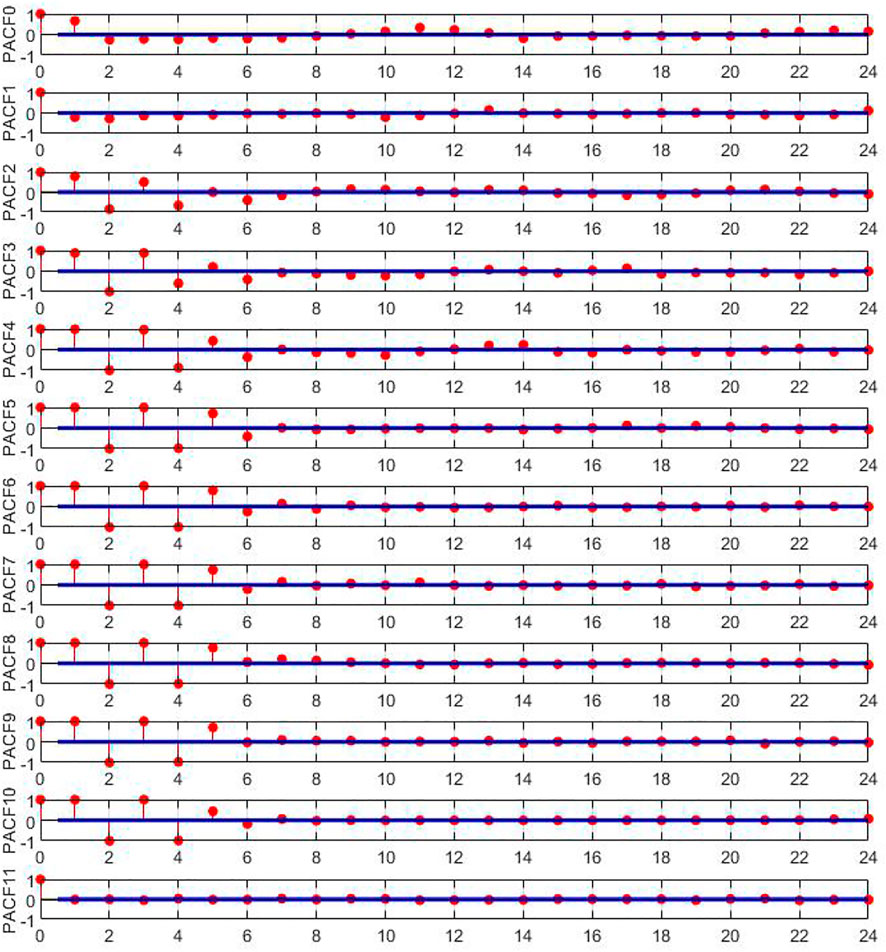
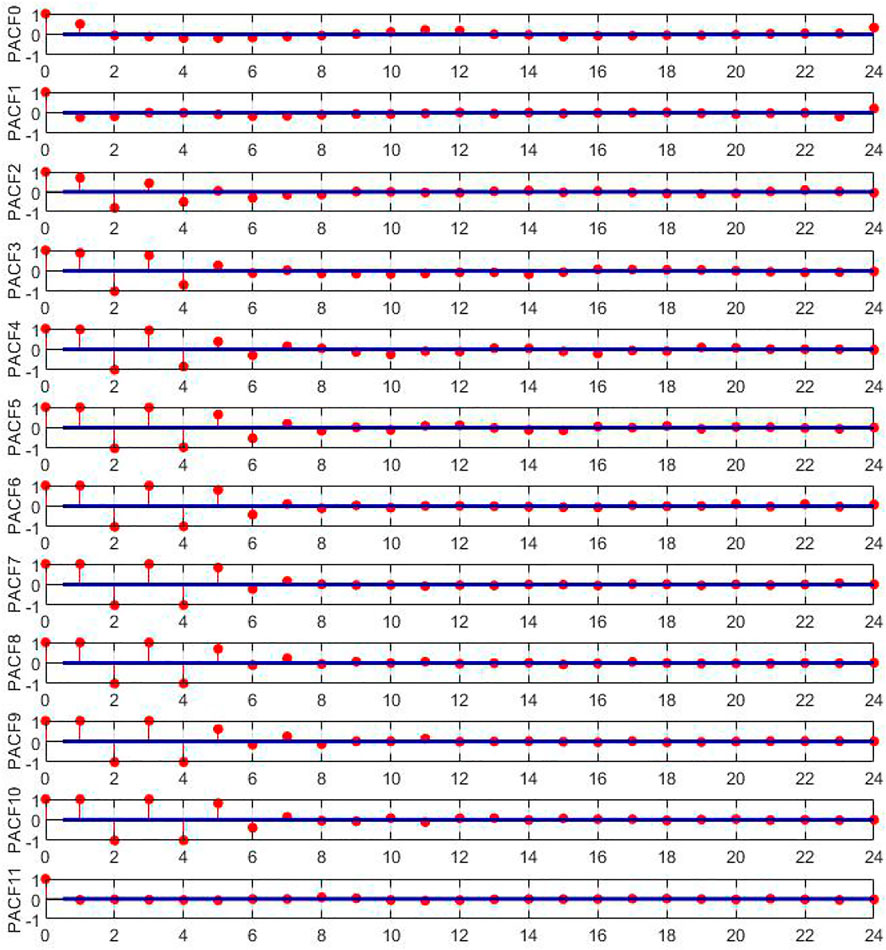
Input Determination

Selecting appropriate input variables has an important influence on the forecast result. In previous studies, several methods have been tried to determine input variables, and PACF has been frequently used as an efficient tool (Feng et al., 2020; Kumar et al., 2021). In PACF, input variables are determined when all PACF values fall within the confidence interval, and the previous values are selected as inputs. The PACF values of the original data and decomposed subsequences of the Guangzhao and Xinfengjiang reservoirs are shown in Figures 2, 3. According to Figures 2, 3, the input variables of the original data and subsequences are determined, and the selected input variables are shown in Tables 1, 2.

FIGURE 2

FIGURE 2. PACF values of each series for the Guangzhao Reservoir.

FIGURE 3

FIGURE 3. PACF values of each series for the Xinfengjiang Reservoir.

TABLE 1

TABLE 1. Selected input values of each series for the Guangzhao Reservoir.

TABLE 2

TABLE 2. Selected input values of each series for the Xinfengjiang Reservoir.

Model Development

In order to evaluate the performance of the proposed EEMD-SSA-LSTM model, five models are used for comparison, namely, backpropagation neural networks (BPNN), LSTM, EMD-BPNN, EMD-LSTM, and EMD-SSA-LSTM.

For the BPNN and LSTM models, input variables were determined by the PACF method, and the original monthly runoff data were inputted into the model for forecasting. For the EMD-BPNN and EMD-LSTM models, first, the original data were inputted into EMD and several subsequences were obtained; second, the PACF method was used to determine input variables of each subsequence, and thus the BPNN and LSTM models were built by simulating each subsequence; and finally forecasted values of each subsequence were summarized as the final forecast result. For the EMD-SSA-LSTM model, the decomposition of the original monthly runoff data, determination of input variables, and aggregation of forecast results of each subsequence were similar to those of the EMD-BPNN and EMD-LSTM models. The difference between them lies in that the hyperparameters of the LSTM for each subsequence are optimized by the SSA. For the EEMD-SSA-LSTM model, the procedures that need to be conducted are similar to the EMD-SSA-LSTM model, except for the decomposition method.

Results and Discussion

Forecast Results

The comparison results of different models for the Guangzhao and Xinfengjiang reservoirs are shown in Tables 3, 4, respectively.

TABLE 3

TABLE 3. Comparison of evaluation indexes of different models for the Guangzhao Reservoir.

TABLE 4

TABLE 4. Comparison of evaluation indexes of different models for the Xinfengjiang Reservoir.

For the Guangzhao Reservoir, it can be intuitively found that adopting data preprocessing methods can enhance model performance to some extent. For example, compared with the BP model in the validation, the LSTM model improves the forecast accuracy with decreases of 9.84% and 17.21% in the aspect of RMSE and MAPE and increases of 3.71% and 28.96% in the aspect of R and CE, respectively, and the EMD-BP model improves the forecast accuracy with decreases of 19.29% and 23.15% in the aspect of RMSE and MAPE and increases of 18.10% and 53.97% in the aspect of R and CE, respectively. Compared with the LSTM model, the EMD-LSTM model improves the forecast accuracy with decreases of 25.70% and 22.00% in the aspect of RMSE and MAPE and increases of 18.37% and 43.72% in the aspect of R and CE, respectively. Compared with the EMD-SSA-LSTM model, the EEMD-SSA-LSTM model improves the forecast accuracy with decreases of 31.70% and 39.62% in the aspect of RMSE and MAPE and increases of 5.71% and 14.96% in the aspect of R and CE, respectively.

For the Xinfengjiang Reservoir, the statistical results further confirm that different data preprocessing methods have different impacts on model forecast accuracy, and adopting optimization algorithms to optimize model parameters can effectively enhance model performance. For example, compared with the LSTM model in the validation, the EMD-LSTM model improves the forecast accuracy with decreases of 17.26% and 18.35% in the aspect of RMSE and MAPE and increases of 31.85% and 54.64% in the aspect of R and CE, respectively. Meanwhile, compared with the EMD-SSA-LSTM model, the EEMD-SSA-LSTM model improves the forecast accuracy with decreases of 23.17% and 13.83% in the aspect of RMSE and MAPE and increases of 6.99% and 16.41% in the aspect of R and CE, respectively.

To show the dynamic changes of runoff more intuitively, the runoff prediction diagrams of Guangzhao and Xinfengjiang reservoirs are depicted in Figures 4, 5, in which the trend of the predicted values by the EEMD-SSA-LSTM model is generally consistent with that of the observed values, and the fitting degree is better than others. The results show that the method of decomposing first and then assembling is feasible and proves that the EEMD-SSA-LSTM model can effectively improve the accuracy of monthly runoff prediction.

FIGURE 4

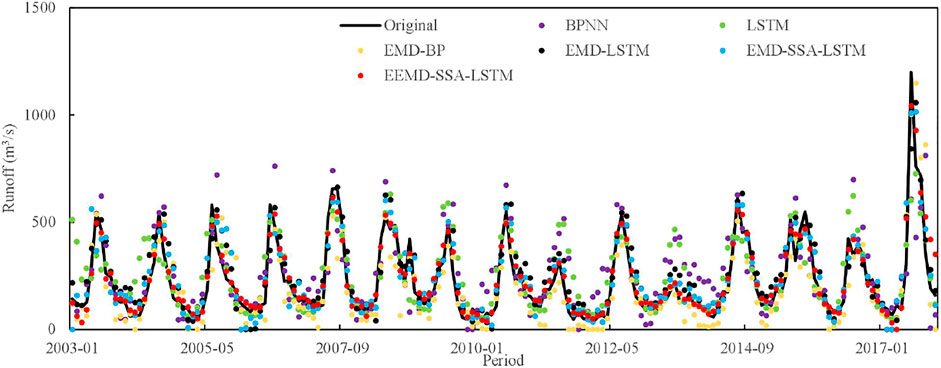
FIGURE 4. Comparison of the forecast results for the Guangzhao Reservoir during the validation period.

FIGURE 5

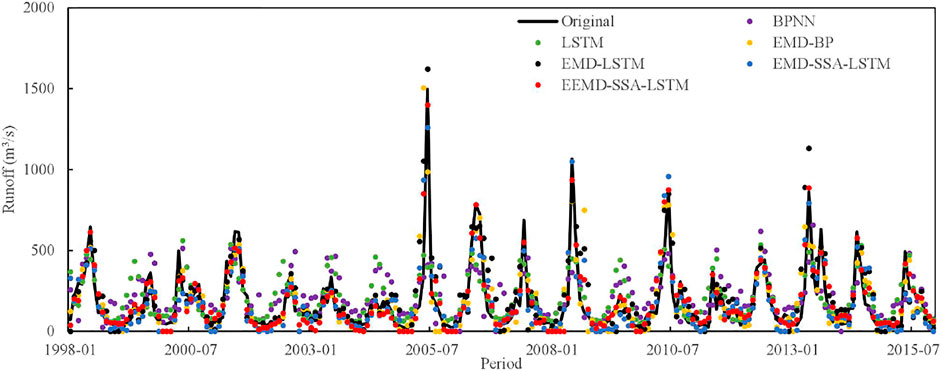
FIGURE 5. Comparison of the forecast results for the Xinfengjiang Reservoir during the validation period.

In order to further compare the performance of the six models, Figures 6, 7 are the scatter plots of different models for the Guangzhao and Xinfengjiang reservoirs. Compared with the other five models, the scatter points of the EEMD-SSA-LSTM model are mainly distributed on the 45° line, which shows that the decomposition method can extract the implicit complex and effective information, reduce the difficulty of model prediction, and improve the accuracy of runoff prediction.

FIGURE 6

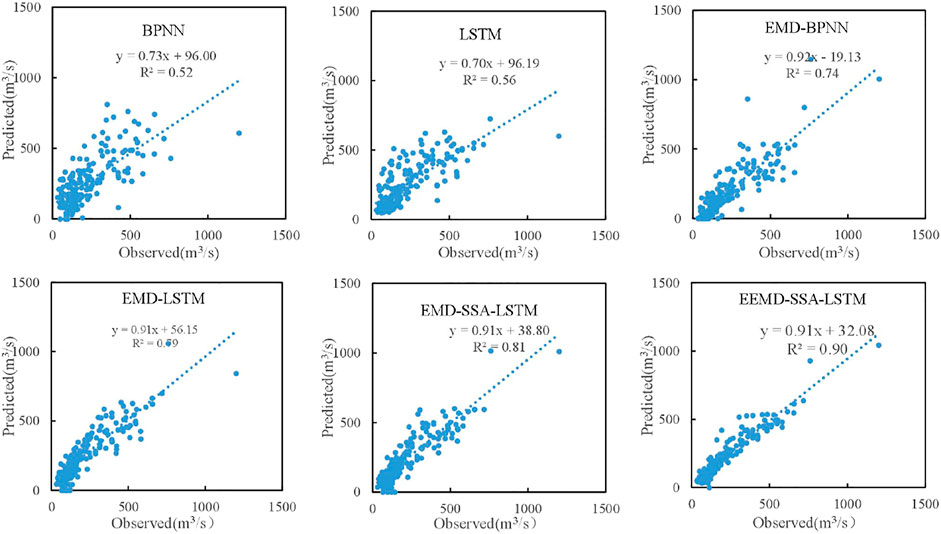
FIGURE 6. Comparison of scatter diagrams of forecast results for the Guangzhao Reservoir during the validation period.

FIGURE 7

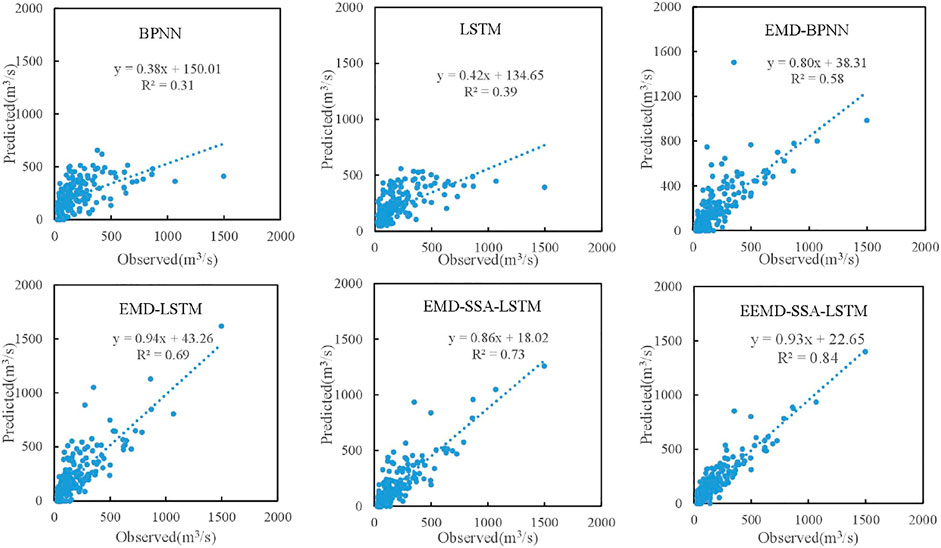
FIGURE 7. Comparison of scatter diagrams of forecast results for the Xinfengjiang Reservoir during the validation period.

To evaluate the performance of the EEMD-SSA-LSTM model for peak flow prediction, the peak flow estimation statistics for the six models are demonstrated in Tables 5, 6. For the Guangzhao Reservoir, the results are shown in Table 5, and the absolute mean values of the relative errors by using the BPNN, LSTM, EMD-BPNN, EMD-LSTM, EMD-SSA-LSTM, and EEMD-SSA-LSTM models are 24.87%, 32.49%, 23.33%, 15.74%, 11.83%, and 9.80%, respectively. For the Xinfengjiang Reservoir, it can be seen from Table 6 that the absolute average values of relative errors by BPNN, LSTM, EMD-BPNN, EMD-LSTM, EMD-SSA-LSTM, and EEMD-SSA-LSTM models are 44.87%, 44.71%, 26.01%, 22.50%, 24.25%, and 12.89%, respectively. The results demonstrate that, in terms of peak flow prediction, the EEMD-SSA-LSTM model has higher prediction accuracy than the other five models. Hence, the EEMD-SSA-LSTM model is more reliable in monthly runoff prediction.

TABLE 5

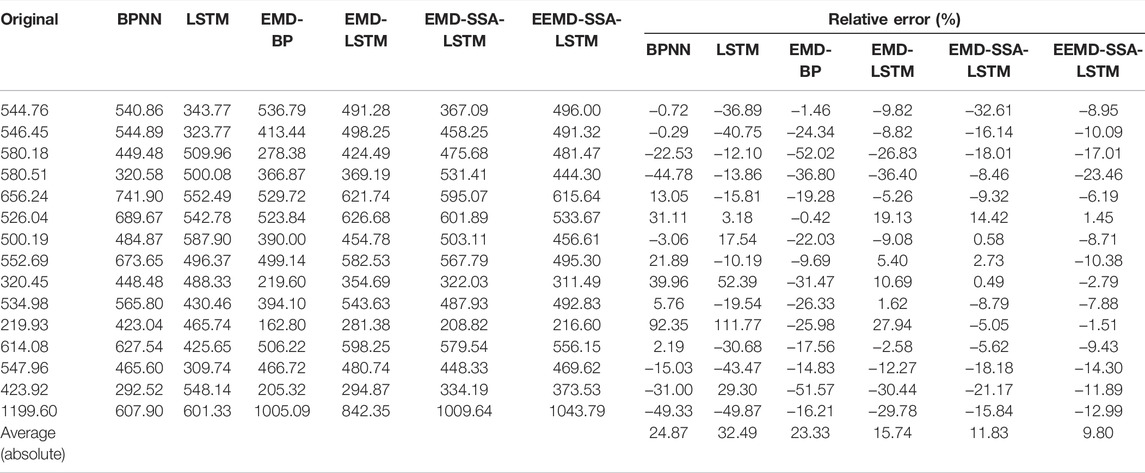
TABLE 5. Peak flow estimates of different models for the Guangzhao Reservoir during the validation period.

TABLE 6

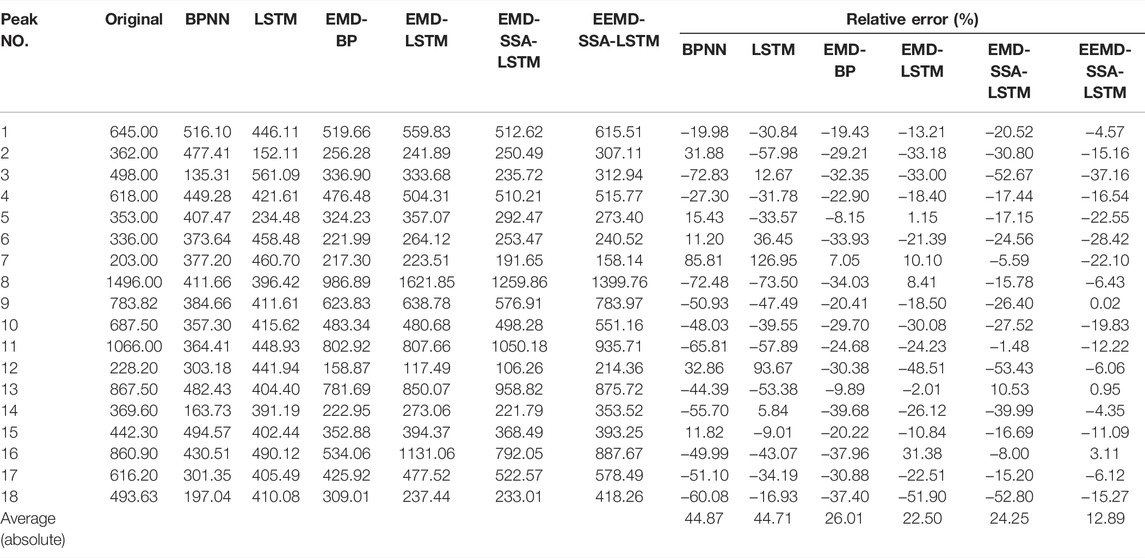
TABLE 6. Peak flow estimates of different models for the Xinfengjiang Reservoir during the validation period.

Discussion

According to the comparison results of the BPNN and LSTM models, the four statistical indexes of the LSTM model are better than those of the BPNN model, which indicates that the LSTM model has higher prediction accuracy than the BP model. The statistical results of BPNN, LSTM, EMD-BPNN, and EMD-LSTM indicate that adopting a data preprocessing technique can effectively improve the model performance. The comparison results of statistical indexes between the EMD-SSA-LSTM model and the EMD-LSTM model show that choosing the appropriate parameters has a great impact on the prediction accuracy of the model. The SSA optimization algorithm can select suitable parameters within a certain range, which improves the efficiency of model parameter selection and the accuracy of model prediction. The EEMD-SSA-LSTM model is better than the other five models in the four statistical indexes, which shows that the EEMD method can eliminate the data noise better than the EMD method to a certain extent. Via EEMD, the main features of the original sequence are further excavated, the complexity of the sequence is reduced, and the prediction accuracy is improved.

The reliability and feasibility of the proposed EEMD-SSA-LSTM model has been confirmed, but the model can be further studied in the future. It is still necessary to adopt a new decomposition algorithm to reduce the complexity of the sequence further. Although the SSA has stronger performance than traditional swarm optimization algorithms, the drawbacks of too fast convergence speed and easy to fall into local optimum should be overcome. Hence, it is necessary to optimize the SSA algorithm to improve the quality of model parameters.

Conclusion

In this study, a hybrid model, namely, EEMD-SSA-LSTM, for short, is proposed for monthly runoff forecasting. The innovation can be generally implemented in three steps. First, the EEMD method was used to decompose the original monthly runoff sequence into several subsequences. Then, the SSA algorithm was introduced to find the optimal hyperparameters of the LSTM model, and the models for each subsequence were built. Finally, the forecast results of each subsequence were summarized as the final forecast results. Monthly runoff data from China’s Guangzhao and Xinfengjiang reservoirs were adopted, and four standard statistical indexes were used to evaluate the model performance. The results demonstrate that, compared with the BP, LSTM, EMD-BP, EMD-LSTM, and EMD-SSA-LSTM models, the proposed EEMD-SSA-LSTM model has the highest forecast accuracy. Hence, the proposed hybrid model can yield satisfactory forecast precision and is an efficient tool for monthly runoff forecasting.

Data Availability Statement

The data analyzed in this study are subject to the following licenses/restrictions: Without the permission of reservoir management, we cannot make the dataset public. Requests to access these datasets should be directed to libaojian@ncwu.edu.cn.

Author Contributions

B-JL: Conceptualization, Methodology, and Writing—original draft; J-XY: Methodology, Data curation, and Writing—original draft; Q-YL: Writing—original draft and Formal analysis; W-CW: Writing—review and editing; T-HZ: Data collection and Investigation; LZ: Writing—review and editing; and G-LS: Editing.

Funding

This paper was supported by the National Natural Science Foundation of China (51709109).

Conflict of Interest

Author T-HZ was employed by Huadian Electric Power Research Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adnan, R. M., Liang, Z., Heddam, S., Zounemat-Kermani, M., Kisi, O., and Li, B. (2020). Least Square Support Vector Machine and Multivariate Adaptive Regression Splines for Streamflow Prediction in Mountainous Basin Using Hydro-Meteorological Data as Inputs. J. Hydrol. 586 (13), 124371. doi:10.1016/j.jhydrol.2019.124371

CrossRef Full Text | Google Scholar

Ali, M., Prasad, R., Xiang, Y., and Yaseen, Z. M. (2020). Complete Ensemble Empirical Mode Decomposition Hybridized with Random Forest and Kernel Ridge Regression Model for Monthly Rainfall Forecasts. J. Hydrol. 584 (15), 124647. doi:10.1016/j.jhydrol.2020.124647

CrossRef Full Text | Google Scholar

Apaydin, H., and Sibtain, M. (2021). A Multivariate Streamflow Forecasting Model by Integrating Improved Complete Ensemble Empirical Mode Decomposition with Additive Noise, Sample Entropy, Gini Index and Sequence-To-Sequence Approaches. J. Hydrol. 603 (22), 126831. doi:10.1016/j.jhydrol.2021.126831

CrossRef Full Text | Google Scholar

Chen, X., Huang, J., Han, Z., Gao, H., Liu, M., Li, Z., et al. (2020). The Importance of Short Lag-Time in the Runoff Forecasting Model Based on Long Short-Term Memory. J. Hydrol. 589, 125359. doi:10.1016/j.jhydrol.2020.125359

CrossRef Full Text | Google Scholar

Darabi, H., Torabi Haghighi, A., Rahmati, O., Jalali Shahrood, A., Rouzbeh, S., Pradhan, B., et al. (2021). A Hybridized Model Based on Neural Network and Swarm Intelligence-Grey Wolf Algorithm for Spatial Prediction of Urban Flood-Inundation. J. Hydrol. 603 (11), 126854. doi:10.1016/j.jhydrol.2021.126854

CrossRef Full Text | Google Scholar

Dunkerley, D. (2021). The Importance of Incorporating Rain Intensity Profiles in Rainfall Simulation Studies of Infiltration, Runoff Production, Soil Erosion, and Related Landsurface Processes. J. Hydrol. 603 (13), 126834. doi:10.1016/j.jhydrol.2021.126834

CrossRef Full Text | Google Scholar

Faysal, A., Ngui, W. K., Lim, M. H., and Leong, M. S. (2021). Noise Eliminated Ensemble Empirical Mode Decomposition Scalogram Analysis for Rotating Machinery Fault Diagnosis. Sensors 21 (23), 8114. doi:10.3390/s21238114

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, Z.-K., Niu, W.-J., Tang, Z.-Y., Jiang, Z.-Q., Xu, Y., Liu, Y., et al. (2020). Monthly Runoff Time Series Prediction by Variational Mode Decomposition and Support Vector Machine Based on Quantum-Behaved Particle Swarm Optimization. J. Hydrol. 583, 124627. doi:10.1016/j.jhydrol.2020.124627

CrossRef Full Text | Google Scholar

Feng, Z.-K., Niu, W.-J., Tang, Z.-Y., Xu, Y., and Zhang, H.-R. (2021). Evolutionary Artificial Intelligence Model via Cooperation Search Algorithm and Extreme Learning Machine for Multiple Scales Nonstationary Hydrological Time Series Prediction. J. Hydrol. 595 (14), 126062. doi:10.1016/j.jhydrol.2021.126062

CrossRef Full Text | Google Scholar

Feng, Z.-K., Shi, P.-F., Yang, T., Niu, W.-J., Zhou, J.-Z., and Cheng, C.-T. (2022). Parallel Cooperation Search Algorithm and Artificial Intelligence Method for Streamflow Time Series Forecasting. J. Hydrol. 606, 127434. doi:10.1016/j.jhydrol.2022.127434

CrossRef Full Text | Google Scholar

He, X., Luo, J., Li, P., Zuo, G., and Xie, J. (2020). A Hybrid Model Based on Variational Mode Decomposition and Gradient Boosting Regression Tree for Monthly Runoff Forecasting. Water Resour. Manag. 34 (2), 865–884. doi:10.1007/s11269-020-02483-x

CrossRef Full Text | Google Scholar

Huang, H., Liang, Z., Li, B., Wang, D., Hu, Y., and Li, Y. (2019). Combination of Multiple Data-Driven Models for Long-Term Monthly Runoff Predictions Based on Bayesian Model Averaging. Water Resour. Manag. 33 (9), 3321–3338. doi:10.1007/s11269-019-02305-9

CrossRef Full Text | Google Scholar

Jhong, Y.-D., Chen, C.-S., Lin, H.-P., and Chen, S.-T. (2018). Physical Hybrid Neural Network Model to Forecast Typhoon Floods. Water 10, 632. doi:10.3390/w10050632

CrossRef Full Text | Google Scholar

Kumar, R., Singh, M. P., Roy, B., and Shahid, A. H. (2021). A Comparative Assessment of Metaheuristic Optimized Extreme Learning Machine and Deep Neural Network in Multi-Step-Ahead Long-Term Rainfall Prediction for All-Indian Regions. Water Resour. Manage 35 (6), 1927–1960. doi:10.1007/s11269-021-02822-6

CrossRef Full Text | Google Scholar

Li, B.-J., Sun, G.-L., Li, Y.-P., Zhang, X.-L., and Huang, X.-D. (2022). A Hybrid Variational Mode Decomposition and Sparrow Search Algorithm-Based Least Square Support Vector Machine Model for Monthly Runoff Forecasting. Water Supply 22 (6), 5698–5715. doi:10.2166/ws.2022.136

CrossRef Full Text | Google Scholar

Liao, S.-L., Li, G., Sun, Q.-Y., and Li, Z.-F. (2016). Real-Time Correction of Antecedent Precipitation for the Xinanjiang Model Using the Genetic Algorithm. J. Hydroinformatics 18 (5), 803–815. doi:10.2166/hydro.2016.168

CrossRef Full Text | Google Scholar

Liao, S., Liu, Z., Liu, B., Cheng, C., Jin, X., and Zhao, Z. (2020). Multistep-Ahead Daily Inflow Forecasting Using the ERA-Interim Reanalysis Data Set Based on Gradient-Boosting Regression Trees. Hydrol. Earth Syst. Sci. 24 (5), 2343–2363. doi:10.5194/hess-24-2343-2020

CrossRef Full Text | Google Scholar

Mao, G., Wang, M., Liu, J., Wang, Z., Wang, K., Meng, Y., et al. (2021). Comprehensive Comparison of Artificial Neural Networks and Long Short-Term Memory Networks for Rainfall-Runoff Simulation. Phys. Chem. Earth Parts A/B/C 123, 103026. doi:10.1016/j.pce.2021.103026

CrossRef Full Text | Google Scholar

Meng, E., Huang, S., Huang, Q., Fang, W., Wu, L., and Wang, L. (2019). A Robust Method for Non-Stationary Streamflow Prediction Based on Improved EMD-SVM Model. J. Hydrol. 568, 462–478. doi:10.1016/j.jhydrol.2018.11.015

CrossRef Full Text | Google Scholar

Nguyen, D. H., Le, X. H., Anh, D. T., Kim, S.-H., and Bae, D.-H. (2022). Hourly Streamflow Forecasting Using a Bayesian Additive Regression Tree Model Hybridized with a Genetic Algorithm. J. Hydrol. 606 (16), 127445. doi:10.1016/j.jhydrol.2022.127445

CrossRef Full Text | Google Scholar

Niu, W.-J., Feng, Z.-K., Zeng, M., Feng, B.-F., Min, Y.-W., Cheng, C.-T., et al. (2019). Forecasting Reservoir Monthly Runoff via Ensemble Empirical Mode Decomposition and Extreme Learning Machine Optimized by an Improved Gravitational Search Algorithm. Appl. Soft Comput. 82, 105589. doi:10.1016/j.asoc.2019.105589

CrossRef Full Text | Google Scholar

Niu, W. J., Feng, Z. K., Xu, Y. S., Feng, B. F., and Min, Y. W. (2021). Improving Prediction Accuracy of Hydrologic Time Series by Least-Squares Support Vector Machine Using Decomposition Reconstruction and Swarm Intelligence. J. Hydrol. Eng. 26 (9), 1104021030. doi:10.1061/(asce)he.1943-5584.0002116

CrossRef Full Text | Google Scholar

Nonki, R. M., Lenouo, A., Tshimanga, R. M., Donfack, F. C., and Tchawoua, C. (2021). Performance Assessment and Uncertainty Prediction of a Daily Time-Step HBV-Light Rainfall-Runoff Model for the Upper Benue River Basin, Northern Cameroon. J. Hydrol. Regional Stud. 36 (18), 100849. doi:10.1016/j.ejrh.2021.100849

CrossRef Full Text | Google Scholar

Pandhiani, S. M., Sihag, P., Shabri, A. B., Singh, B., and Pham, Q. B. (2020). Time-Series Prediction of Streamflows of Malaysian Rivers Using Data-Driven Techniques. J. Irrigation Drainage Eng. 146, 04020013. doi:10.1061/(asce)ir.1943-4774.0001463

CrossRef Full Text | Google Scholar

Quilty, J., Adamowski, J., and Boucher, M. A. (2019). A Stochastic Data‐Driven Ensemble Forecasting Framework for Water Resources: A Case Study Using Ensemble Members Derived from a Database of Deterministic Wavelet‐Based Models. Water Resour. Res. 55 (1), 175–202. doi:10.1029/2018wr023205

CrossRef Full Text | Google Scholar

Sibtain, M., Li, X., Bashir, H., and Azam, M. I. (2021). A Hybrid Model for Runoff Prediction Using Variational Mode Decomposition and Artificial Neural Network. Water Resour. 48 (5), 701–712. doi:10.1134/s0097807821050171

CrossRef Full Text | Google Scholar

Solakian, J., Maggioni, V., and Godrej, A. N. (2020). On the Performance of Satellite-Based Precipitation Products in Simulating Streamflow and Water Quality during Hydrometeorological Extremes. Front. Environ. Sci. 8, 585451. doi:10.3389/fenvs.2020.585451

CrossRef Full Text | Google Scholar

Song, C., Chen, X., Wu, P., and Jin, H. (2021). Combining Time Varying Filtering Based Empirical Mode Decomposition and Machine Learning to Predict Precipitation from Nonlinear Series. J. Hydrol. 603, 126914. doi:10.1016/j.jhydrol.2021.126914

CrossRef Full Text | Google Scholar

Wang, X., Wang, Y., Yuan, P., Wang, L., and Cheng, D. (2021). An Adaptive Daily Runoff Forecast Model Using VMD-LSTM-PSO Hybrid Approach. Hydrol. Sci. J. 66 (9), 1488–1502. doi:10.1080/02626667.2021.1937631

CrossRef Full Text | Google Scholar

Xu, C., Han, Z., and Fu, H. (2022). Remote Sensing and Hydrologic-Hydrodynamic Modeling Integrated Approach for Rainfall-Runoff Simulation in Farm Dam Dominated Basin. Front. Environ. Sci. 9, 817684. doi:10.3389/fenvs.2021.817684

CrossRef Full Text | Google Scholar

Xue, J., and Shen, B. (2020). A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control Eng. 8 (1), 22–34. doi:10.1080/21642583.2019.1708830

CrossRef Full Text | Google Scholar

Yuan, R., Cai, S., Liao, W., Lei, X., Zhang, Y., Yin, Z., et al. (2021). Daily Runoff Forecasting Using Ensemble Empirical Mode Decomposition and Long Short-Term Memory. Front. Earth Sci. 9, 621780. doi:10.3389/feart.2021.621780

CrossRef Full Text | Google Scholar

Yuan, X., Chen, C., Lei, X., Yuan, Y., and Muhammad Adnan, R. (2018). Monthly Runoff Forecasting Based on LSTM-ALO Model. Stoch. Environ. Res. Risk Assess. 32 (8), 2199–2212. doi:10.1007/s00477-018-1560-y

CrossRef Full Text | Google Scholar

Zhang, C., and Ding, S. (2021). A Stochastic Configuration Network Based on Chaotic Sparrow Search Algorithm. Knowl.-Based Syst. 220, 106924. doi:10.1016/j.knosys.2021.106924

CrossRef Full Text | Google Scholar

Zhang, X., Bao, W., and Yuan, F. (2020). Spatial Runoff Updating Based on the Hydrologic System Differential Response for Flood Forecasting. J. Hydroinformatics 22 (6), 1573–1587. doi:10.2166/hydro.2020.045

CrossRef Full Text | Google Scholar

Zhang, X., Zhang, Q., Zhang, G., Nie, Z., and Gui, Z. (2018). A Hybrid Model for Annual Runoff Time Series Forecasting Using Elman Neural Network with Ensemble Empirical Mode Decomposition. Water 10, 416. doi:10.3390/w10040416

CrossRef Full Text | Google Scholar

Zhang, Z., and Hong, W.-C. (2019). Electric Load Forecasting by Complete Ensemble Empirical Mode Decomposition Adaptive Noise and Support Vector Regression with Quantum-Based Dragonfly Algorithm. Nonlinear Dyn. 98 (2), 1107–1136. doi:10.1007/s11071-019-05252-7

CrossRef Full Text | Google Scholar