- 1School of Environment, Key Laboratory of Water and Sediment Sciences of MOE, Beijing Normal University, Beijing, China
- 2School of Water Resources and Hydropower Engineering, North China Electric Power University, Beijing, China
- 3Power China ZhongNan Engineering Corporation Limited, Chang Sha, China
Because of landslides, seismic events, and/or unregulated human activities, a massive amount of loose solid materials are sometimes deposited at the confluence between the branch valley and stem stream, or blocked at the lateral channel contraction section in a river channel. Immersion of these granular materials in naturally-generated reservoirs tend to cause mass failure and even induce debris flow. However, the majority of previous studies primarily focused on post-event processes (i.e. flow hydraulics such as flood flow hydrographs, sediment transport or erosion, and river morphological changes) following dam failure. In this study, our attention is restricted to hydro-sediment dynamic processes that control unconsolidated dam failure as well as subsequent debris flow. This objective is achieved by conducting a series of experiments in a tilting flume and selecting the overtopping flows, vertical grading configurations, dam heights, and channel gradients as causative factors responsible for chain disaster in the form of dam failure and debris flow. We found that all experimental dams are either subject to partial failure through a gradual breach development or suddenly collapsed in en masse failure mode, debris flows induced by partial dam failures are likely to take place in the conditions of low overtopping flow and shallow channel slope. On the contrary, debris flows originated from en masse dam failures are shown to develop well in the opposite conditions. Also, the critical shear stresses for sediment entrainment under en masse dam failure cases are generally higher if compared with partial dam-failure equivalents. Moreover, the relative proportion of clear water to erodible solid materials is also related to dam failure mode, which will eventually determine debris-flow properties. These findings have strong implications for predicting and mitigating natural disasters of these kinds usually encountered in nature.
1 Introduction
Debris flows, as a typical water-driven as well as gravitational erosion process within which both liquid water and solid sediment are fully mixed and mobilised at an unexceptionally high velocity, have become more frequent and devastating in recent decades due to global climate change (i.e. extreme hydrological events) and extensive anthropogenic disturbances (He et al., 2017; Ruan et al., 2021). Over the past decades, a huge number of check dams were built in China to trap sediment and their effectiveness in soil as well as water conversation are well recognized. However, more and more dams in the gullies are gradually filled with sediment and fully exposed with low vegetation cover, these check dams are progressively collapsed at an accelerating scour rate and tend to increase the risk of erosional hazards (Kang et al., 2021; Li et al., 2021; Zhu et al., 2021) like dam failures and subsequent debris flows (Song and Choi 2021). For example, the debris flow event that took place on 8 August 2010 in Zhouqu county, Gansu province, China, caused 1765 fatalities and significant damages. It was found that the loose material trapped upslope of the dams was incorporated into the debris flow, the flow volume was amplified (Fang et al., 2019) and wreaked a terrible cost in human life and property.
Debris flow is well recognized as an important category of natural and destructive hazards. Following a landslide, earthquake, inappropriate human activities, or their coupled influence, a large volume of loose solid material could accumulate at the confluence between the branch valley and stem stream or the lateral channel contraction section. Both temporal and spatial concentration of these materials usually facilitate a sudden formation of unconsolidated granular dams to temporarily block the running flow course. As the time elapsed with these materials within a newly developed dam partially or fully immersed in a gradual rising flow stage forced by a continuous flow supply from upstream. Therefore, a naturally-formed dam of this kind could eventually become destabilized and breached as a result of overtopping, seepage, or piping, and the accompanying erosion of the dam body. According to the study of Takahashi and Nakagawa (1993), the majority of dam failures are caused by the water overtopping rather than by other forms of dam collapse due to either flow piping or seepage, and many dam failures at steep slopes could induce debris flows (Capart et al., 2001; Zech and Spinewine 2002; Zech et al., 2008; Xia et al., 2010).
In this context, an outburst of medium or large-scale dam-break induced debris flows can potentially turn out to be a catastrophic and pressing issue as the associated processes are highly transient and thus provide limited time for the rapid evacuation to operate downstream. As such, there have been continuing efforts to enhance our understanding of the consequences of dam break-type flows in the following three aspects over the past decades (Cao et al., 2004). That is, dam-break flows were viewed as an active agent of uncompacted sediment transfer in mountainous areas (Caine 1980; Cao et al., 2004; Godt and Coe 2007; Xia et al., 2010; Othman et al., 2019), as a transitory process involving hydraulic changes in conjunction with steep slopes in a channel (Chen and Simons 1979; Zech and Spinewine 2002; Cao et al., 2004; Carrivick 2010; Xia et al., 2010; Carrivick et al., 2011; Pu et al., 2012); and as a rapid reconstruction of landscape topography along the impacted downstream reach through erosion and deposition that is generally documented in the far field (Chen and Simons 1979; Brooks and Lawrence 1999; Capart et al., 2001; Zech and Spinewine 2002; Cao et al., 2004; Chen et al., 2004; Soares-Frazão et al., 2007; Zech et al., 2008). Obviously, many of these previous studies are comparatively more general and not specifically focused on the problem of dam-break debris flows, this might be due to the fact the formative mechanism and rheological proprieties of debris flows are more complex than a flood or even sediment-laden flow owing to high concentration of solid particles contained in the mixture and its intricate interactions with liquid flow. Also, these works are primarily devoted to flow changes (e.g. hydraulic jump and wave propagation), sediment transport, and/or morphological evolutions following the dam failures rather than those physical processes that intrinsically control the dam break and subsequent formation of debris flows; this is quite understandable because the flood or debris flows following the dam failure appear to constitute a direct and imminent threat to the infrastructures and human lives immediately downstream.
However, as dam-break debris flows usually occur in remote mountainous areas, it is prohibitively dangerous and difficult to implement the field observations due to their sudden occurrence, short lifespan, and powerful destruction (Cui 1992; Carrivick 2010). Although some field studies and interpretations of geological legacy mainly take place some time following the event (e.g. Brooks and Lawrence 1999; Chen et al., 2004), and this effort still cannot directly link outburst flood processes with products like sedimentary deposits (Carrivick et al., 2011). To overcome this, there are quite a few works particularly dedicated to studying the dam-break induced debris flows using experimental and numerical methods (Chen and Simons 1979; Takahashi and Nakagawa 1993; Visser 2000; Capart et al., 2001; Morris and Hassan 2002; Zech and Spinewine 2002; Spinewine et al., 2004; Sarno et al., 2013). Currently, there are still some major limitations associated with numerical treatments, such as 1) reliable data for model validation and calibration are still scarce and far from complete (Visser 2000; Morris and Hassan 2002; Shao and Lo 2003); 2) most available models are heavily dependent on crude assumptions, such as gradually varied shallow flow and constant sediment concentration (Zech and Spinewine 2002; Spinewine et al., 2004); and 3) most models are one-dimensional and cannot fully describe the dam failure triggered debris flows that significantly featured with two- and three-dimensional dynamic behaviours (Xia et al., 2010; Shi et al., 2018). In contrast, flume-based experiments offer the advantage to provide a detailed, mechanistic understanding of dam-break processes responsible for generating debris flows and producing satisfactory data sets that are of direct use to numerical code developments. Also, in the present study, some important causative factors, such as dam heights, channel slopes, water volume etc., can be controlled more precisely in a tilting flume to examine their relative influence on debris flows originating from various dam failure modes, and the dam breach and subsequent debris flow moving processes can be continuously observed over a short duration with the aid of an image tracking, acquisition, and analysis technique. Further, a general review of the state-of-the-art studies from the literature has shown that there are two representative experimental arrangements in the earlier research works. Because the typical study case with a gate positioned behind the dam body was carried out to study the post-dam-failure process by suddenly removing or lifting the gate, their results cannot be used to predict onset times of debris flow caused by the failure, which is critically indispensable for managing the disaster and reducing potential damage (Chen and Simons 1979; Takahashi and Nakagawa 1993). As for a complete, physical process from dam failure to debris flows, the latter case with water and dam body separated by a gate represents an ideal configuration to match well with natural analogue and will be adopted in the current experiments.
2 Experimental Set up
2.1 Experimental Facility
Our experiments were conducted in a flume consisting of an upstream header tank, a reservoir, a mid-stream channel, and a downstream sediment trap (see Figure 1A). Specifically, the header tank at the upstream end was close to a meter cube (i.e. 1.0 m long, 1.0 m wide, 1.1 m high) and used to store clear water. A specific volume of water was gradually supplied to the reservoir by means of carefully controlling a valve, and the reservoir was split into two lengthy segments: the rectangular section (i.e. 2.0 m long, 1.0 m wide, 0.5 m deep) and the laterally as well as vertically contracted section (i.e. 1.0 m in length, 1.0 m → 0.3 m in width, 0.5 m → 0.4 m in height), where an artificial dam was constructed and located in the lower contraction section. In the middle reach, the flume is geometrically rectangular and can be tilted within a wide range (i.e. 15° → 35°) to mobilize water-sediment mixture. At the downstream end, a trap was set up to mainly collect sediment particles. Also, two high-speed cameras (50 fps) were positioned in a forward and side-looking perspective respectively to record the dynamic behaviors that involved from dam break to debris flow motion, and three piezometer sensors were buried vertically within the dam body to measure the pore-fluid pressure.
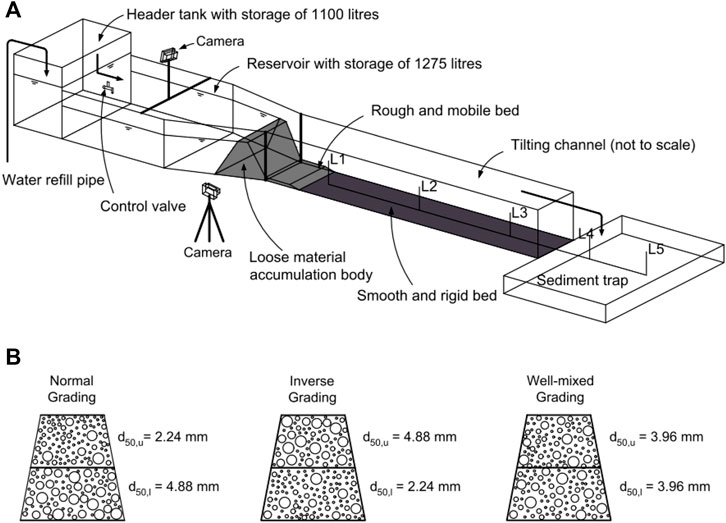
FIGURE 1. Schematics of experimental arrangement (A) and three vertical grading structures originated from corresponding configurations with lower layer medium grain size d50 being coarser, finer, or nearly equivalent to the upper layer d50 within artificial dam (B).
2.2 Experimental Conditions
In order to fully examine the impact of impounded flow on dam break and successive debris flow transport, our major experimental controls are considered to include steady flow condition, dam properties, and channel slope. According to previous studies regarding the effect of dam-related parameters on dam break (e.g. Cao et al., 2004; Carrivick 2010), both dam materials and dam height are highlighted to represent the main dam properties in the present study. As for the dam materials, we consider the vertical stratifications possibly developed from multiple discrete debris flows or distinct grading pattern resulting from a single event (e.g. Naylor 1980; Major 1997; Larcan et al., 2006; Starheim et al., 2013) as the basic guidance to generate three vertical structures for an artificial dam, namely, normal grading, inverse grading, and well-mixed grading that are illustrated in Figure 1B, these typical vertical grading configurations were produced by using three mixtures characterised by the same range of grain size considered (i.e. grain diameter d = 1.0 mm → 15.0 mm, see Figure 2) and different median grain size (i.e. d50 = 2.24, 3.96, and 4.88 mm). It is noted that the original sediment mixture with d50 = 3.96 mm were directly collected from the field loose materials legacy that contributes to frequent occurrence of debris flow in the mountainous region adjacent to Dongchuan Debris Flow Research Station, China, also widely known as the debris flow museum. The remaining two contrasting sediment mixtures with d50 = 2.24 mm, 4.88 mm were created by adding finer or coarser grains into the original mixture. Further, an artificial dam was constructed with one of these mixtures piled up within the bottom layer and another one within the top layer, which is clearly exemplified in Figure 1B. That is, for the vertical profile of the dam characterised by normal grading, the mixtures with d50 = 4.88 mm, 2.24 mm were placed in the bottom and top layer, respectively; the dam with inverse grading structure was in the opposite sediment setting; whereas the original mixture is adopted to create the well-mixed grading dam. In addition to the sediment materials, the second dam-related parameter is the dam height. Considering the minimum depth associated with the contracted section within the reservoir (i.e. 0.4 m), we have constructed the dams with 0.35 and 0.25 m in height, which corresponds to 157 and 90 kg in mass, respectively.
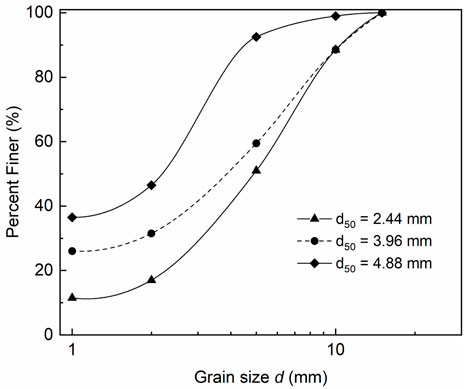
FIGURE 2. Grain size distributions of three loose sediment mixtures employed for producing artificial dams with varying vertical grading structures in the present experiment.
Regarding the flow condition, our attentions are primarily focused on the elapsed time for water flowing over the dam structure at a given flow rate to initiate the dam break and debris flow mobilization after the reservoir pre-filled with clear water from the header tank. The inflow rates of Q = 2.4 m3/h and 13.1 m3/h were achieved by controlling the valve with an accuracy of ±8%. Channel slope is also an important factor in affecting the dam break as well as debris flow transport (e.g. Chen et al., 2004). Herein, the tilting channel was inclined at S = 35° and 25°, respectively, where S = 35° represents the maximum slope that can be adjusted by the current flume facility.
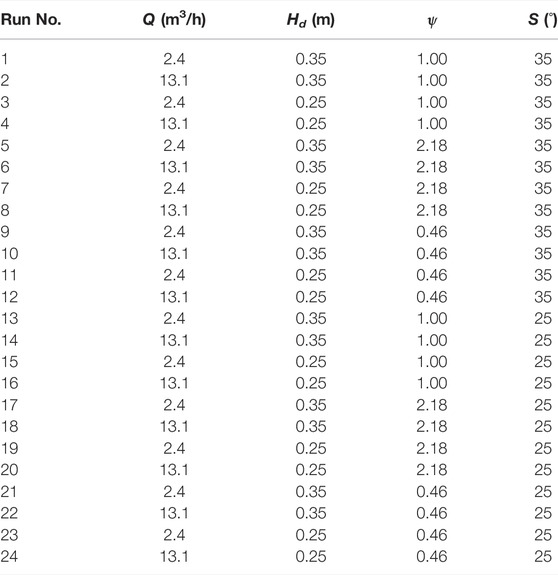
Summarising basic experimental conditions in this study that encompass normal, inverse, and well-mixed vertical grading structure within artificial dams; dam height Hd = 0.35 m, 0.25 m; flow rate Q = 2.4 m3/h, 13.1 m3/h; and channel slope S = 35°, 25° (see Table 1). According to the basic principle of factor combination, there are 24 runs in total which should be carried out according to orthogonal design principle (Cui et al., 2017).
2.3 Experimental Procedure
Prior to each test, the header tank was filled with clear water through a pump, and the sediment dam was manually built using the specific mixtures according to the prescribed criteria of vertical grading configuration and dam height. All the sediment materials are placed in the lower converging section within the reservoir and extended over a 0.4 m distance downstream in 5.0 mm thickness. Three piezometer sensors are buried vertically in the vertical locations of 0.3 m (Sensor V1), 0.2 m (Sensor V2), and 0.1 m (Sensor V3) from the dam base to measure the pore pressure. It is noted that 1) Sensor V1 is employed only for a high dam with Hd = 0.35 m; 2) Sensors labelled as V1 and V2 are always placed in the upper sediment sublayer; and 2) Sensor V3 is buried in the lower sediment sublayer within the high dam or coincides with the interface between upper and lower sediment sublayer within the low dam (see Figure 3). These sensors are positioned along the vertical centerline in order to successfully capture the hydrodynamic changes and internal erosions associated with the dam failing process. After dam construction was completed, two high-speed cameras were installed in a side-looking and downslope-looking position, respectively, and ensured with high definition to cover the spatial distance from the dam location to the downstream sediment trap.

FIGURE 3. Piezometer sensors positioned in equal spacing locations along the vertical centerline of high (left) and low (right) artificial dam before test. Note: all three sensors are used for high-elevation dam (A) and two sensors are employed for low-elevation dam (B).
The experiment was launched by opening the valve and delivering clear water to the reservoir at a flow rate of Q = 2.4 m3/s for each run. At the same time, the wire piezometer sensors and high-speed cameras were initiated to obtain a continuous record of tempo-spatial variabilities associated with dam failure and debris flow propagation, all measurements extracted from the cameras are interpreted with the aid of a regular grid with cell size (0.05 × 0.10 m) marked on the right side-wall glass. Following a gradual rise of water level in the reservoir, a large volume of white plastic beads was placed upstream of the dam and used as tracers to track the surface velocity in the dam-failure process and flow-sediment mixture displacement along the slope. It should be noted here that the opening of the valve was adjusted to generate the designated flow rate (i.e. Q = 2.4 m3/s or 13.1 m3/s) immediately after the reservoir was filled with water. Samples are taken in the successive points L1, L2, L3 once the debris flow formed and subsequently passed through the tilting channel (i.e. Measurement Points L1, L2, L3 located at 1.0, 3.0, 5.0 m downstream from the tilting channel inlet, see Figure 1A). It should be emphasized here that our experiment was terminated if no flow-sediment mixing materials rapidly developed into debris flow following either a partial or complete dam failure, the remaining flow in the reservoir was then released through the sediment trap. Additional samples collected from the points L4, L5 at the centerline were used to analyse the depositional behaviour of debris flows [i.e. these points L4, L5 are set at 0.5 m, 2.5 m downstream from the contacting interface between the channel outlet and sediment trap, see Figure 1A). After the experiment was completed, all sediment samples were subsequently dried in an oven, weighed, and sieved.
3 Theoretical Considerations
3.1 Quantification of Vertical Grading Structure
To quantitatively characterize vertical grading configurations in the dam structure, we have proposed a vertical grading coefficient that is expressed in the following form (e.g. Shu et al., 2017)
where d50-u and d50-l represent the median grain size of the non-uniform sediment mixture placed within the upper and lower layer in the entire sediment column, therefore, the vertical grading coefficient for the corresponding vertical structures in an artificial shown in Figure 1B can be specified as ψ = 0.46 for the normal grading, ψ = 2.18 for the inverse grading, and ψ = 1.00 for the well-mixed grading, respectively.
3.2 Impact of Flow Shear Stress on Sediment Transport
In an open channel flume, bed shear stress can be calculated using the depth-slope product,
where γ denotes the specific gravity for sediment and water, h is the flow depth. An accurate prediction of debris flows is always challenging due to the more complex processes involved. Also, the sediment entrainment has been considered as a fundamental issue. It has long been known that the incipient motion of loose sediment can be predicted by using Shields stress. Considering the non-uniform sediment mixture employed in the current experiment, a modified version of Shields’ relationship is given as
where τc is the dimensional Shields stress for initiating sediment motion (N/m2), γs is the specific gravity for sediment and water, respectively, d is grain size in diameter and replaced by d50 for performing the present calculations suggested by Wilcock (1988), Re* is the particle’s Reynolds number and written as
in which u* is the shear velocity (
Sediment entrainment is likely to take place once the shear stress of flow exceeds the particle’s critical Shields stress, namely, the ratio of τ/τc is larger than unity (Shu et al., 2017), reflecting the impact of flow intensity on sediment transport.
4 Experimental Results
4.1 Characteristics of Debris Flows Induced by Dam Failures
In our experiments, an instantaneous dam failure followed by the debris flow was observed to exclusively evolve in two dominant modes. The first mode of dam failure induced debris flow is characterized by the following features, that is, 1) Stage I: the overtopping flow inundated the dam and sediment on the dam crest was entrained by the overspill flow, small rills then formed through headcutting and progressively developed laterally and vertically into a significant breach through which the water was concentrated to flow; 2) Stage II: Following the continuous scouring of the dam body by the concentrated flow, erodable banks of the breach collapsed and then dammed the flow pathway; and 3) Stage III: As the static flow pressure from the blocked flow increased and built up to a critical level, all flow-sediment mixing materials in the breach were instantly and fully collapsed, this process eventually resulted in partial dam collapse and formation of (immature) debris flows (see Figure 4).

FIGURE 4. Post-experiment legacy to demonstrate partial (A) and en masse (B) dam failure mode observed in the present research.
In contrast, the second mode consisted of shared features that can be described as, 1) Stage I: A significant hydraulic jump formed through the flow overtopping of a steep granular slope under gravity effects, this resulted in massive sediment movement taking place at the toe of the downstream slope; 2) Stage II: As sediment transport occurred along the downstream slope, bed erosion was simultaneously found to migrate upstream and contributed to retrogressive slope failure; 3) Stage III: when retrogressive erosion was near the dam and coupled with bed erosion happened on the dam crest, then the dam height was reduced and its longitudinal profile became flattened with time, after a period of time along with dam becoming fully saturated as well as an increase of pore-fluid pressure, a macro instability occurred and contributed to en masse dam collapse that was closely followed by debris flow (see Figure 4).
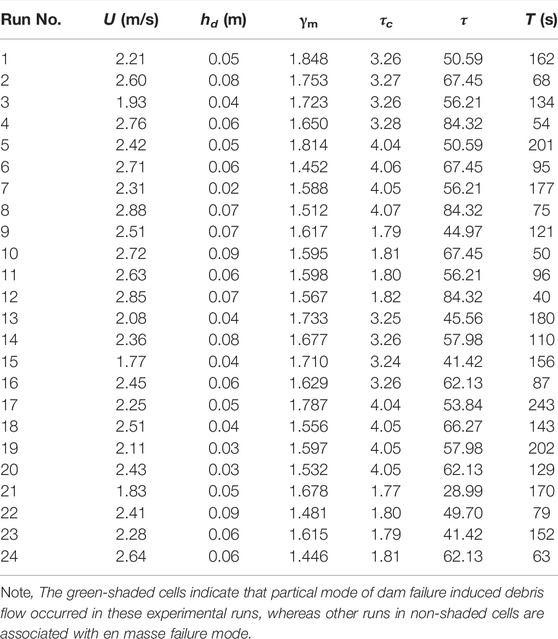
Such dynamic behaviours of dam failure induced debris flow are intrinsically linked to flow conditions, loose sediment materials, and channel slopes, which jointly determined the extent of flow infiltration, the tempo-spatial variations of pore-fluid pressure, the way in which the dam collapsed, a debris flow formed and move towards downstream. Herein, all flume-based runs are fully detailed and summarised in Table 2 in terms of experimental conditions and main results obtained.
It is shown that partial mode of dam failure induced debris flow occurred in 11 runs, whereas those in en masse mode were observed in the remaining 13 cases (see Table 1). In order to analyse the impact of four basic controls on dam failure generated debris flow in two dynamic modes. The response of dam failure generated debris flow in two process-based modes to different values associated with these experimental controls is plotted in Figure 5. Among these factors, the number of dam failure generated debris flows under high and low dam height configuration is almost identical regardless of their dynamic modes. In contrast, the dam failure triggered debris flows are more sensitive to fluctuations in flow conditions for both failure modes, namely, the partial dam failure induced debris flows are prone to take place in the low overspill flow process, while those in en masse mode, on the contrary, are more likely to occur in high flows. Also, both channel slope and vertical grading coefficient are shown to have significant effects on dam collapse followed by debris flow. Obviously, more partial dam failure and resultant debris flow events appear to preferentially occur in the inverse grading configuration and along lower channel slopes, while en masse dam collapse seems more likely to result in debris flows in the opposite conditions featured with normal grading pattern and higher slopes.
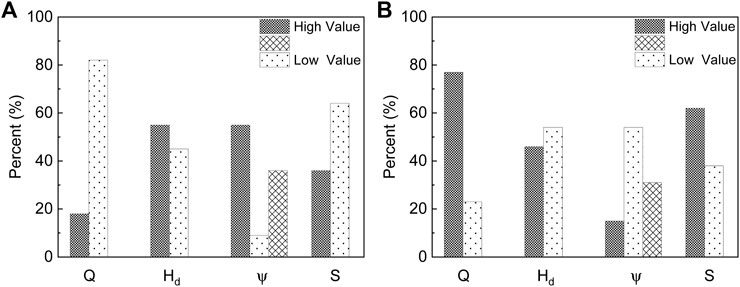
FIGURE 5. Percent of partial (A) and en masse (B) dam failure induced debris flows under high, moderate (only for ψ), and low controls in the preset tests.
4.2 Hydrodynamic Process of Dam Failures
A complete data set of temporal variations in pore water pressures measured within the dam could provide fundamental information for the interpretation of the failure mechanism (e.g. Gens and Alonso, 2006). As it has been found that the rates and styles of landslide are sensitive to pore-water pressure changes caused by changes in soil porosity accompanying shear deformation (Iverson et al., 2010), this equally holds true for the dam break induced debris flow, especially in partial and en masse failure mode. Also, the pore-fluid pressure, as an important indicator for internal dam stability assessment and significant triggering factor for the initiation of debris flow (e.g. Guo et al., 2018; Zhou et al., 2018), is highly sensitive to the hydraulic connectivity of loose sediment mixtures that we employed for constructing the model dams under different vertical grading configuration, which is found to have a significant impact on the dam failure mode in the present experiment. To better explain this, example plots of temporal variations in pore-fluid pressure measured in different dam failure mode with relative short and long duration are presented in Figure 6, respectively. In the partial dam failure, a noticeable temporal lag effect between measured peak pore pressure in three vertical locations are shown in Figure 6A. Specifically, the upper coarse sediment layer of the dam was observed to transiently reach a small peak piezometric head earlier, which is followed by the maximum piezometric head measured in the middle section of the dam, the peak piezometric head in the lower fine sediment layer of the dam were attained slightly later. It is important to understand that the unconsolidated materials within the dam body are brought to dilation because of the increase in pore water pressure caused by flow infiltration (Dai et al., 1999), thereby reducing the shear strength of dam materials (Chen et al., 2010) and consequently causing instability on dam structure (e.g. Iverson et al., 2010). This effect of pore pressure on vertical insatiability on the dam geotechnical structure is consistent with a rapid deepening (and enlargement) progress of breach from the dam head to the impervious, erosion-resistant bed in the partial dam failing process. As for the en masse dam failure illustrated through run No.4 (i.e. lower dam height, see Table 2), we observed a sudden and dramatic increase of pore water pressure in the upper bed layer, followed closely by the peak pore pressure attained for the lower sediment layer, this demonstrates a strong implication for the dam safety as internal dam instability originating from a significant increase of pore water pressure is mainly initiated by a higher upstream discharge.
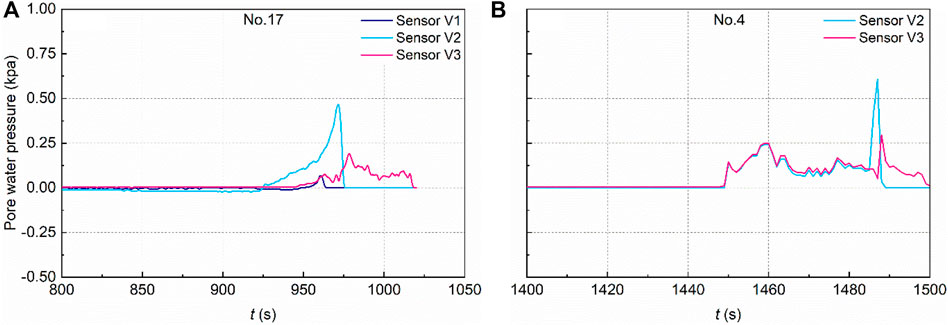
FIGURE 6. Example plots showing temporal variation in pore pressure measured from the partial (A) and en masse (B) collapsed dam, respectively.
Our analysis is further extended for comparing the pore water pressure that contributes to internal dam instability in partial and en masse dam failure mode. Figure 7 displays the magnitude of maximum pore water pressure measured for (low-Q) partial and (high-Q) en masse dam failure in comparative runs featured with the same vertical grading parameter (ψ) and dam height (H). In general, the maximum pore water pressure recorded for en masse dam failure is consistently greater than its partial failed counterpart, this well explains the critical role of flow rate upon inducing dam internal instability, because the high flow rate to penetrate into the dam body is responsible for generating high pore water pressure over a short duration, as a result, the resistant moment of a dam body is thus decreased by the increase of the water pressures and the resulting decrease of the intergranular pressures and the internal shearing resistance (Visser 2000), meanwhile, a high flow also leads to greater hydro-static and hydro-dynamic pressure for the upstream slope and dam crest, and a combination of pore water pressure, hydro-static, and hydro-dynamic pressure jointly causes external and internal dam instability and finally results in dam failure occurring in en masse mode. It is also noticeable that the pore water pressure seems to increase as vertical sediment grading (ψ) increases in a high-elevation dam (i.e. H = 35 cm), the main reason for this has been described earlier that a lower dam permeability is created by placing coarse sediment on the top of an artificial dam and lower bed layer therefore becoming more consolidated. Thus, an occurrence of dam collapse in an inverse grading configuration, regardless of partial or en masse dam failure mode, is basically initiated by a higher pore water pressure as presented in Figure 7.
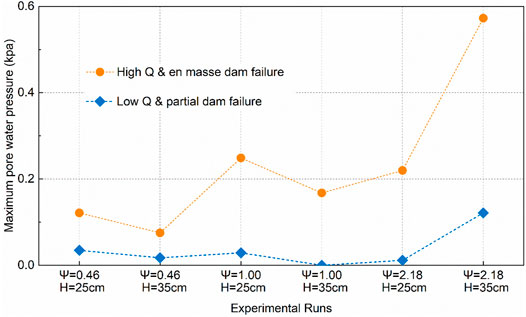
FIGURE 7. Maximum pore water pressure measured for partial and en masse failed dam in comparative runs characterised with the same vertical grading parameter and dam height.
4.3 Dynamic Process of Sediment Transport Associated With Dam Failures
It is statistically shown that the overtopping flow rate Q may have a critical role in determining whether debris flow formed in partial or en masse dam failure mode. This seems to be reasonable since a lower overtopping flow is more capable of entraining sediment and incising dam crest rather than forming a significant hydraulic jump on the downstream slope, this dam head cutting process continues to develop until outflow increases and finally equals to inflow, the flow depth in the reservoir therefore maintains a constant level below the dam crest and the overtopping flow is accordingly terminated. As the breach is incised to become wider and deeper, the flow depth tends to decrease with time, those bank geotechnical equilibrium characteristics are suddenly disrupted, such as the reduction in pore-fluid pressure (as discussed later) and weight of the ground, especially a rapid decline of the water level after a long lasting high water may endanger the dam stability (Visser 2000; Zech and Spinewine 2002), in such a way that micro-to-meso dam instability occurs along lower channel slopes. This consequently results in block-by-block bank failure and a rapid sediment accumulation within the breach. However, for en masse dam failure originated from high overtopping flows, retrogressive erosion dominantly occurs on the downstream slope and quickly proceeds from downstream toe to the upstream dam crest. In such a situation, the dam body was thoroughly inundated with an increased weight of the ground, especially when the channel slope is steeper. As a result, a macro-instability leads to an abrupt, complete dam failure, this is consistent with the effect of the high-intensity sprinkling on slope failure in Reid et al. (1997)’s work. Following the bulking of flow with eroded sediment, these partial or en masse dam failures somehow contribute to the formation of debris flows.
Also, we calculate the flow shear stress for both partial and en masse failure dam using Eq. 4 with average flow depth, as can be seen from Table 2, the stress ratio τ/τc is far above unity, indicating that the experimental overflow, either in low or high level, is capable of triggering dam failure and inducing debris flow in the present investigation. However, as the partial and en masse dam failure are prone to take place under low and high overtopping flow conditions, respectively, the corresponding stress ratio τ/τc for dam failure in both modes are in the respective range of 12.53–17.24 and 16.64–46.38. Evidently, the stress ratio corresponds approximately to τ/τc ≈ 17.0 could be used as a critical value to separate the distinct dam failures in partial and en masse behaviour. Again, due to the combined effect of high overflow rate (or shear stress) and severe erosion imposed upon a dam, the time elapsed from the beginning of flow overtopping to dam collapse is relatively shorter in en masse failure mode (Takahashi and Nakagawa 1993), that is, T = 40–152 s (see Table 2) if compared with those in partial failure mode (i.e. T = 129–243 s). This demonstrates that the overtopping flow not only determines the dam failure mode but also the timing of dam collapse, which is an important factor and must be accounted for in the dam failure predictions.
Compared to the effect of overflow rate Q on the dam failing behaviour, the vertical grading parameter ψ seems to have a secondary impact on the dam failure mode. It has been geotechnically identified that the coarser and finer sediment comprising loosely piled materials generally exhibit low and high initial porosity, respectively (e.g. Esselburn et al., 2011). If considering the dam in an inverse grading pattern with coarser and finer sediment placed in the top and bottom layer, this implies that low porosity in the upper layer could somehow facilitate flow infiltration even seepage initially, thereby depressing the development of a significant hydraulic jump along the downstream slope; while for the bottom layer filled with finer particles, their void ratio or porosity could be further reduced as a result of the packing effect that caused by the added weight of coarse particles laid in the upper layer. Once the dam was overtopped by the rising flow in the reservoir, those particles exposed on the dam crest are easily entrained and rills are gradually formed. At the same time, a low permeability in the lower layer composed of finer sediment also assists in preventing the occurrence of macro-instability, especially at a lower slope. In a normal grading configuration, a significant moving-towards-upstream hydraulic jump is evolved due to low porosity of finer sediment in the upper layer as well as the reduced porosity of packing coarser sediment placed in the bottom layer. In this case, the downstream slope is more susceptible to be eroded than the dam crest, a long-term immersion of the dam body in high overtopping flow could trigger the dam failure in en masse mode, especially under a steeper slope (Takahashi and Nakagawa 1993).
4.4 Implications of Hydro-Sediment Dynamics for Dam-failure-induced Debris Flows
Further analysis of transported samples in the flume channel indicates that the specific density of debris flow originated from partial dam failure is generally higher than those resulted from en masse dam failure, as shown in Table 2 and Figure 8. Similarly, a relevant analysis is also performed for the magnitude of dam-break-related mass as well as flow volume that collectively involved in debris-flow formation and transport. Figure 8 shows the mass loss due to contrasting dam failures in en masse and partial mode, the ensemble mean mass mobilised in partial dam failure is slightly lower but still varied within the same magnitude of order if compared with those displayed in en masse dam failure mode. Meanwhile, it is stated earlier that the total flow volume responsible for producing partial dam failures is usually significantly lower than en masse dam failure cases (e.g. see Figure 5). Such differential proportion of solid mass (due to dam collapse) and liquid water (released from the header tank) in debris-flow composition within two dam failure modes can explain this difference in the debris-flow specific gravity (γm, see Figure 8). For debris flow induced by partial dam failures, solid materials are proportionally sufficient relative to total water volume in debris flows, this leads to higher debris-flow specific gravity γm. By contrast, although a large amount of solid materials was derived from dam and involved in debris flows, a higher volume of liquid flow become dominantly in shaping debris flows to be low sediment concentration with low specific gravity γm.
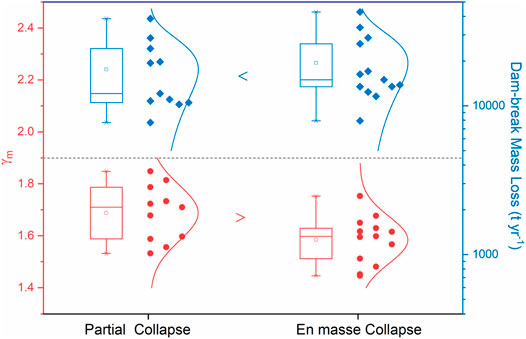
FIGURE 8. Magnitude of solid materials eroded from dam structure and specific gravity for debris flows developed in partial and en masse dam failure mode.
5 Conclusion
A flume-based study is conducted to determine the relative contribution of the overtopping flow rate (Q), dam height (Hd), vertical grading configuration (ψ), and channel slopes (S) to dam failure induced debris flows. After a series of tests by varying the values of these controls, the debris flows are shown to form under either partial or en masse dam failure mode. In the process of partial dam failure induced debris flows, small rills are initially formed through sediment transport on dam crest and subsequently resulted in a breach development through severe dam downcutting as well as lateral bank collapse, debris flow is thus formed by the bulking of flow and sediment in the breach evolved from partial dam failure. By contrast, a significant hydraulic jump formed on the downstream slope of a dam and migrated upstream as the time elapsed, thereby causing a retrogressive slope erosion and a reduction in dam height, with the dam relics fully saturated and pore pressure increased, macro dam stability was produced and contributed to a sudden, complete dam collapse.
We also found that the overtopping flow rate Q has a dominant control on the formation of debris flow in partial or en masse dam failure mode, the vertical grading parameter ψ appears to have a secondary impact; whereas the dam height Hd is shown to have a negligible influence. A detailed comparison clearly indicated that the partial dam failure induced debris flows are more likely to originate in the small overspill flow, inverse grading configuration, and lower channel slopes; while the en masse dam failure triggered debris flows are prone to occur in the opposite conditions. Under the effects of these controls considered, especially the overtopping flow, the following findings are drawn, 1) the characteristic time elapsed from the beginning of flow overtopping to en masse dam failure is relatively shorter than the time measured in partial failure process, and 2) the stress ratio τ/τc for dam failure induced debris flows in en masse dam failure is higher than in partial failure scenario, a critical stress ratio τ/τc ≈ 17.0 can be used to separate the debris flows resulting from these contrasting dam failing behaviours.
The effect of vertical grading configuration on dam failure induced debris flows is intrinsically correlated with the temporal evolution of pore-fluid pressure in dam structure. In the partial dam failure mode, as the breach gradually developed from the dam head to lower layer, a noticeable temporal lag effect between peak pore pressure measured at three vertical locations was thus obtained. By contrast, the temporal response of pore pressure in an en masse dam failure was relatively shorter between measured sections and the corresponding pore pressure was found to attain a higher peak value, this creates a macro and internal instability that imposed upon the dam structure. As a result, the propagation velocity and flow depth for debris flow originated from en masse dam failure is generally larger than those from partial dam failure. A combined behaviour of en masse dam failure induced debris flows that took place in a shorter period of time and loaded with higher velocity demonstrates a strong implication that a more destructive debris flow tends to be developed under a complete dam failure, this fundamental knowledge is essential to predict and alleviate the dam-failure-initiated debris flows.
Within this study, solid materials eroded from the dam structure are in the same magnitude of order in both dam failure modes. However, a total volume of liquid water contributed to partial dam failure (and formation of debris flow) is generally lower than en masse dam failure cases. As a result, debris flows following partial dam failure tend to have a higher specific gravity than originated from en masse dam failure.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author Contributions
AS the corresponding author, organized and revised the paper. LW organized the manuscript. FZ conducted the experiments and analysed the data. JZ, CP, ZZ and HC analysed the data.
Funding
This work was also supported financially by the CRSRI Open Research Program (Program SN: CKWV2015225/KY), the Key Project of National Natural Science Foundation (Grant No. 52039001), the Natural Science Foundation of China (Grant No. 52009041) and the Fundamental Research Funds for the Central Universities (Grant No. 2020MS024).
Conflict of Interest
FZ is employed by the company Power China ZhongNan Engineering Corporation Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Brooks, G. R., and Lawrence, D. E. (1999). The Drainage of the Lake Ha!Ha! Reservoir and Downstream Geomorphic Impacts along Ha!Ha! River, Saguenay Area, Quebec, canada. Geomorphology 28, 141–167. doi:10.1016/s0169-555x(98)00109-3
Caine, N. (1980). The Rainfall Intensity: Duration Control of Shallow Landslides and Debris Flows. Geogr. Ann. Ser. A, Phys. Geogr. 62, 23–27. doi:10.2307/520449
Cao, Z., Pender, G., Wallis, S., and Carling, P. (2004). Computational Dam-Break Hydraulics over Erodible Sediment Bed. J. Hydraul. Eng. 130, 689–703. doi:10.1061/(asce)0733-9429(2004)130:7(689)
Capart, H., Young, D. L., and Zech, Y. (2001). “Dam-break Induced Debris Flow,” in Particulate Gravity Currents, 149–156. doi:10.1002/9781444304275.ch11
Carrivick, J. L., Jones, R., and Keevil, G. (2011). Experimental Insights on Geomorphological Processes within Dam Break Outburst Floods. J. Hydrol. 408, 153–163. doi:10.1016/j.jhydrol.2011.07.037
Carrivick, J. L. (2010). Dam Break - Outburst Flood Propagation and Transient Hydraulics: A Geosciences Perspective. J. Hydrol. 380, 338–355. doi:10.1016/j.jhydrol.2009.11.009
Chen, Y. H., and Simons, D. B. (1979). An Experimental Study of Hydraulic and Geomorphic Changes in an Alluvial Channel Induced by Failure of a Dam. Water Resour. Res. 15, 1183–1188. doi:10.1029/wr015i005p01183
Chen, C.-Y., Chen, T.-C., Yu, F.-C., and Hung, F.-Y. (2004). A Landslide Dam Breach Induced Debris Flow ? a Case Study on Downstream Hazard Areas Delineation. Env. Geol. 47, 91–101. doi:10.1007/s00254-004-1137-6
Chen, N. S., Zhou, W., Yang, C. L., Hu, G. S., Gao, Y. C., and Han, D. (2010). The Processes and Mechanism of Failure and Debris Flow Initiation for Gravel Soil with Different Clay Content. Geomorphology 121, 222–230. doi:10.1016/j.geomorph.2010.04.017
Cui, Y.-f., Zhou, X.-j., and Guo, C.-x. (2017). Experimental Study on the Moving Characteristics of Fine Grains in Wide Grading Unconsolidated Soil under Heavy Rainfall. J. Mt. Sci. 14 (3), 417–431. doi:10.1007/s11629-016-4303-x
Cui, P. (1992). Study on Conditions and Mechanisms of Debris Flow Initiation by Means of Experiment. Chin. Sci. Bull. 12 (9), 759–763.
Dai, F., Lee, C. F., and Wang, S. (1999). Analysis of Rainstorm-Induced Slide-Debris Flows on Natural Terrain of Lantau Island, Hong Kong. Eng. Geol. 51, 279–290. doi:10.1016/S0013-7952(98)00047-7
Esselburn, J. D., Ritzi Jr, R. W., and Dominic, D. F. (2011). Porosity and Permeability in Ternary Sediment Mixtures. Groundwater 49 (3), 393–402.
Fang, Q., Tang, C., Chen, Z., Wang, S., and Yang, T. (2019). A Calculation Method for Predicting the Runout Volume of Dam-Break and Non-dam-break Debris Flows in the Wenchuan Earthquake Area. Geomorphology 327, 201–214. doi:10.1016/j.geomorph.2018.10.023
Gens, A., and Alonso, E. E. (2006). Aznalcóllar Dam Failure. Part 2: Stability Conditions and Failure Mechanism. Géotechnique 56 (3), 185–201.
Godt, J. W., and Coe, J. A. (2007). Alpine Debris Flows Triggered by a 28 July 1999 Thunderstorm in the Central Front Range, Colorado. Geomorphology 84, 80–97. doi:10.1016/j.geomorph.2006.07.009
Guo, X., Baroth, J., Dias, D., and Simon, A. (2018). An Analytical Model for the Monitoring of Pore Water Pressure inside Embankment Dams. Eng. Struct. 160, 356–365. doi:10.1016/j.engstruct.2018.01.054
He, S., Wang, D., Fang, Y., and Lan, H. (2017). Guidelines for Integrating Ecological and Biological Engineering Technologies for Control of Severe Erosion in Mountainous Areas - A Case Study of the Xiaojiang River Basin, China. Int. Soil Water Conservation Res. 5 (4), 335–344. doi:10.1016/j.iswcr.2017.05.001
Iverson, N. R., Mann, J. E., and Iverson, R. M. (2010). Effects of Soil Aggregates on Debris-Flow Mobilization: Results from Ring-Shear Experiments. Eng. Geol. 114, 84–92. doi:10.1016/j.enggeo.2010.04.006
Kang, C., Ren, D., Gao, X., Han, C., and Wang, Y. (2021). Study of Kinematic Characteristics of a Rock Avalanche and Subsequent Erosion Process Due to a Debris Flow in WenJia Gully, Sichuan, China. Nat. Hazards 106 (1), 937–964. doi:10.1007/s11069-021-04501-6
Larcan, E., Mambretti, S., and Pulecchi, M. (2006). A Procedure for the Evaluation of Debris Flow Stratification. WIT Trans. Ecol. Environ. 90, 81–88. doi:10.2495/deb060081
Li, Y., Hu, W., Wasowski, J., Zheng, Y., and McSaveney, M. (2021). Rapid Episodic Erosion of a Cohesionless Landslide Dam: Insights from Loss to Scour of Yangjia Gully Check Dams and from Flume Experiments. Eng. Geol. 280, 105971. doi:10.1016/j.enggeo.2020.105971
Major, J. J. (1997). Depositional Processes in Large‐Scale Debris‐Flow Experiments. J. Geol. 105, 345–366. doi:10.1086/515930
Morris, M., and Hassan, A. M. (2002). Breach Formation through Embankment Dams & Flood Defense Embankments: A State of the Art Review. Wallingford, United Kingdom: HR Wallingford. IMPACT-Project Workshop Paper.
Naylor, M. A. (1980). The Origin of Inverse Grading in Muddy Debris Flow Deposits: a Review. J. Sediment. Res. 50, 1111–1116. doi:10.1306/212f7b8f-2b24-11d7-8648000102c1865d
Othman, I. K., Jiang, Z., and Baldock, T. E. (2019). Influence of Grain Size on Sediment Transport during Initial Stages of Horizontal Dam Break-type Flows. J. Waterw. Port. Coast. Ocean. Eng. 145, 04019009. doi:10.1061/(asce)ww.1943-5460.0000510
Pu, J. H., Cheng, N.-S., Tan, S. K., and Shao, S. (2012). Source Term Treatment of SWEs Using Surface Gradient Upwind Method. J. hydraulic Res. 50 (2), 145–153. doi:10.1080/00221686.2011.649838
Reid, M. E., LaHusen, R. G., and Iverson, R. M. (1997). “Debris-flow Initiation Experiments Using Diverse Hydrologic Triggers,” in Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment, 1–11.
Ruan, H., Chen, H., Li, Y., Chen, J., and Li, H. (2021). Study on the Downcutting Rate of a Debris Flow Dam Based on Grain-Size Distribution. Geomorphology 391, 107891. doi:10.1016/j.geomorph.2021.107891
Sarno, L., Carravetta, A., Martino, R., and Tai, Y.-C. (2013). Pressure Coefficient in Dam-Break Flows of Dry Granular Matter. J. Hydraul. Eng. 139, 1126–1133. doi:10.1061/(asce)hy.1943-7900.0000772
Scotton, P., and Deganutti, A. M. (1997). Phreatic Line and Dynamic Impact in Laboratory Debris Flow Experiments. New York: ASCE, 777–786.
Shao, S., and Lo, E. Y. M. (2003). Incompressible SPH Method for Simulating Newtonian and Non-newtonian Flows with a Free Surface. Adv. water Resour. 26 (7), 787–800. doi:10.1016/S0309-1708(03)00030-7
Shi, Y., Li, S., Chen, H., He, M., and Shao, S. (2018). Improved SPH Simulation of Spilled Oil Contained by Flexible Floating Boom under Wave-Current Coupling Condition. J. Fluids Struct. 76, 272–300. doi:10.1016/j.jfluidstructs.2017.09.014
Shu, A., Wang, L., Zhang, X., Ou, G., and Wang, S. (2017). Study on the Formation and Initial Transport for Non-homogeneous Debris Flow. Water 9, 253. doi:10.3390/w9040253
Soares-Frazão, S., Le Grelle, N., Spinewine, B., and Zech, Y. (2007). Dam-break Induced Morphological Changes in a Channel with Uniform Sediments: Measurements by a Laser-Sheet Imaging Technique. J. Hydraulic Res. 45, 87–95. doi:10.1080/00221686.2007.9521835
Song, P., and Choi, C. E. (2021). Revealing the Importance of Capillary and Collisional Stresses on Soil Bed Erosion Induced by Debris Flows. J. Geophys. Res. Earth Surf. 126 (5), e2020JF005930. doi:10.1029/2020jf005930
Spinewine, B., Delobbe, A., Elslander, L., and Zech, Y. (2004). “Experimental Investigation of the Breach Growth Process in Sand Dikes,” in Second IAHR international conference on fluvial hydraulics, Napoli, Italy, 983–991. doi:10.1201/b16998-126
Starheim, C. C. A., Gomez, C., Harrison, J., Kain, C., Brewer, N. J., Owen, K., et al. (2013). Complex Internal Architecture of a Debris-Flow Deposit Revealed Using Ground-Penetrating Radar, Cass, New Zealand. N. Z. Geog 69, 26–38. doi:10.1111/nzg.12002
Takahashi, T., and Nakagawa, H. (1993). Flood and Debris Flow Hydrograph Due to Collapse of a Natural Dam by Overtopping. Proc. Hydraulic Eng. 37, 699–704. doi:10.2208/prohe.37.699
Wilcock, P. R. (1988). Methods for Estimating the Critical Shear Stress of Individual Fractions in Mixed-Size Sediment. Water Resour. Res. 24, 1127–1135. doi:10.1029/wr024i007p01127
Xia, J., Lin, B., Falconer, R. A., and Wang, G. (2010). Modelling Dam-Break Flows over Mobile Beds Using a 2D Coupled Approach. Adv. Water Resour. 33, 171–183. doi:10.1016/j.advwatres.2009.11.004
Zech, Y., and Spinewine, B. (2002). “Dam-break Induced Floods and Sediment Movement-State of the Art and Need for Research,” in First Workshop of the EU Project IMPACT (HR Wallingford).
Zech, Y., Soares-Frazão, S., Spinewine, B., and Le Grelle, N. (2008). Dam-break Induced Sediment Movement: Experimental Approaches and Numerical Modelling. J. Hydraulic Res. 46 (2), 176–190. doi:10.1080/00221686.2008.9521854
Zhou, Z.-H., Ren, Z., Wang, K., Yang, K., Tang, Y.-J., Tian, L., et al. (2018). Effect of Excess Pore Pressure on the Long Runout of Debris Flows over Low Gradient Channels: A Case Study of the DongYueGe Debris Flow in Nu River, China. Geomorphology 308, 40–53. doi:10.1016/j.geomorph.2018.01.012
Keywords: overtopping flow, hydro-sediment dynamic process, dam failure, debris flow, chain disaster
Citation: Shu A, Wang L, Zhu F, Zhu J, Pi C, Zhang Z and Christian H (2022) Hydrodynamic Process of Partial and en Masse Dam Failure Induced Debris Flows. Front. Environ. Sci. 10:905499. doi: 10.3389/fenvs.2022.905499
Received: 27 March 2022; Accepted: 06 April 2022;
Published: 11 May 2022.
Edited by:
Prashanth Reddy Hanmaiahgari, Indian Institute of Technology Kharagpur, IndiaReviewed by:
Huabin Shi, University of Macau, ChinaZhijing Li, Changjiang River Scientific Research Institute (CRSRI), China
Copyright © 2022 Shu, Wang, Zhu, Zhu, Pi, Zhang and Christian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anping Shu, c2h1YXBAYm51LmVkdS5jbg==
 Anping Shu
Anping Shu Le Wang
Le Wang Fuyang Zhu
Fuyang Zhu Jiapin Zhu
Jiapin Zhu Chengling Pi
Chengling Pi Ziru Zhang
Ziru Zhang Huarez Christian
Huarez Christian