Two-stage water resources allocation negotiation model for transboundary rivers under scarcity

In this article, the bankruptcy theory and bargaining games are used to construct a two-stage water resources allocation negotiation model (TSANM). A Nash-bargaining game model is used for the initial allocation, followed by an adjustment stage which considers factors such as water circumstances, water satisfaction, water risk, and water efficiency. The TSANM systematically considers the multi-dimensional attributes of water resources in the allocation process and may likely increase the participation of riparian countries. The proposed method is applied to allocate the contested water capital of the Tigris-Euphrates River. This gives initial allocation to Turkey, Syria, and Iraq of 30.00%, 22.00%, and 48.00%, respectively, and adjusted allocation of 24.98%, 21.30%, and 53.72%. Through collective bargaining and group negotiation, the stability and acceptability of allocation are effectively improved, absolute egalitarianism and utilitarianism are both avoided, and instead objectivity and fairness are emphasized in the water resources allocation process.

1 Introduction

Water is our most precious resource, not only because humans cannot survive without water, but also because water is indispensable in many other aspects of human life (Kong et al., 2021). However, population growth, industry development, accelerated urbanization, and global warming are producing a global water crisis (Vörösmarty et al., 2000; Elahi et al., 2021a; Elahi et al., 2022). More attention is placed upon the development and utilization of water resources in transboundary river basins by riparian countries predicated on their goals and interests (Degefu et al., 2018; Yuan et al., 2022b). When two or more countries share the limited water resources of a transboundary river basin, any competitive development and utilization between them can lead to water conflicts (Yuan et al., 2021a), which could threaten the efficiency usage of water resources and the security of those countries (Yuan et al., 2020).

Water allocation in transboundary rivers is a complex problem that includes resource decision-making centered on meeting regional needs (Wei et al., 2021), economic decision-making centered on social welfare (Kong et al., 2019; Xu et al., 2019), social decision-making centered on equity, and environmental decision-making centered on ecology (Sun et al., 2021). In order to maximize benefits, riparian countries should consider both the complex and systematic nature of the multi-dimensional attributes of water resources. Furthermore, if a water allocation scheme cannot be formulated in a timely and effective manner, water conflicts may intensify in the transboundary river basin, which will not only hinder the sustainable development of the riparian countries, but also threaten the security and stability of the river basin. Therefore, it is a major theoretical and practical challenge to design feasible mechanisms to optimize water allocation and support the resolution of conflicts over allocation. Currently, research in this area has mainly focused on three aspects: multi-objective optimization, game models, and bankruptcy theory.

Multi-objective optimization uses mathematical models to describe scenarios of limited water availability and develop algorithms to find the optimal allocation. Wang et al. (2008) developed an integrated hydrologic-economic river basin model that computed the optimal benefits of water resources for various coalitions of stakeholders. Li and Zhang, 2015 developed an inexact two-stage allocation model for water resources planning and management with uncertainty. Roozbahani et al. (2015) introduced a multi-objective model to identify sustainable water allocation in transboundary rivers. Avarideh et al. (2017) proposed a new conceptual model for quantification of the Convention provisions concerning equitable and reasonable water sharing. Yu and Lu (2018) integrated a Projection Pursuit Model and Grey Wolf Optimization producing a PPMGWO optimized model of water resources allocation in a transboundary river basin. Yuan et al. (2021b) combined a system dynamics model with multi-objective optimization in the study of optimal allocation of water resources. These studies focus on the construction of an optimal allocation model of water resources. However, the actions of stakeholders will directly affect the allocation of water resources in the transboundary river.

Game models are a mathematical method that can be used to describe the competitive relationship and strategic interaction among stakeholders that claim a shared scarce resource, simulate conflicts over water resources allocation, explore the rules of strategy choice, and identify feasible solutions (Madani 2010). For instance, Kucukmehmetoglu (2012) introduced a composite water resources allocation model integrating both game theory and Pareto Frontier concepts for the Tigris-Euphrates River System. Lee (2012) developed a multi-objective game-theory model that addressed economic and environmental concerns in water allocation decision-making scenarios. Degefu et al. (2016) proposed an asymmetric Nash bargaining solution concept for solving water sharing in transboundary river basins. Zeng et al. (2019) proposed a hybrid game theory and mathematical programming model for solving transboundary water conflicts, which considers both water quality and quantity. These researchers have constructed optimal allocation models through game theory. However, competition and cooperation of riparian countries coexist in the transboundary river, and these models do not represent very well this feature of water allocation.

Bankruptcy theory can be used to describe the problem of water resource allocation in the context of water scarcity (O’Neill 1982). Past research has produced the classical bankruptcy allocation rules—Proportion (p), Adjusted Proportion (AP), Constrained Equal Loss (CEL), Constrained Equal Award (CEA), and so on (Aumann and Maschler 1985; Thomson 2003; Thomson 2015; Moridi, 2019a; Moridi, 2019b). In addition, Mianabadi et al. (2015) proposed a weighted bankruptcy solution method to allocate the available water equitably and reasonably under homogeneous and heterogeneous group situations. Degefu et al. (2017) proposed by using coupling bankruptcy theory with the asymmetric Kalai-Smorodinsky bargaining solution concept, that a monotonic water allocation mechanism could be derived for transboundary river basins under water scarcity. Farjoudi et al. (2021) developed a probabilistic water quality management model for solving water conflicts based on the bankruptcy rules. These articles combined with multi-objective optimization or game theory in order to design a water allocation mechanism, however, these methods assume that water allocation can be completed once, and they do not take into account that water resources allocation may require multiple negotiations to arrive at a completed successful outcome.

All of this research represents a comprehensive and in-depth study of water allocation in transboundary river basins and provides an important reference for the design of allocation schemes. However, transboundary river water allocation involves heterogeneous water demand, with different goals and interests for riparian countries under different social-econo-environmental conditions (Yazdi and Moridi 2017). Forming satisfactory and mutually agreed upon agreements allocating limited water resources to multiple stakeholders with multiple optimization goals, riparian countries must use multi-stage negotiation (Yuan et al., 2016; Medeiros et al., 2017).

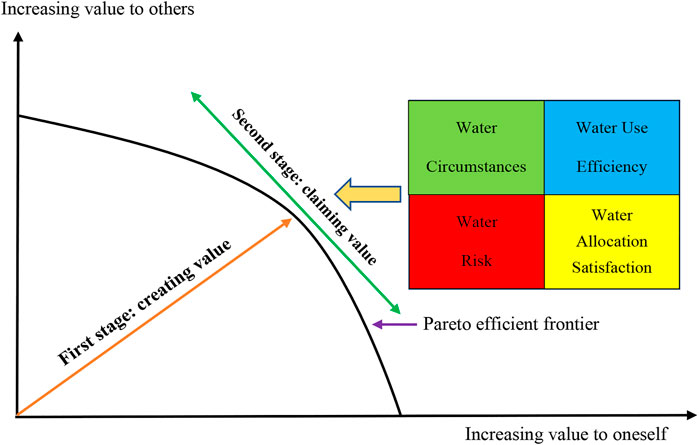
Since distributive negotiations will lead to a win-lose solution, riparian countries could construct a capable coordination institution to address the distributional conflicts associated with negotiation (Garrick et al., 2018), and follow participatory processes in the management of water resources in a transboundary river. This will provide better-informed and sustainable decisions and beneficial outcomes in a range of decision-making contexts where stakeholders are engaged in the management of water resources (Devente et al., 2016). Therefore, the riparian countries should cooperate in negotiations to equitably allocate water resources (Yuan et al., 2021a), where these negotiations will have two stages: creating value and claiming value (Brown 2012). In the first stage, the riparian countries create value through cooperation and improve the collective utility. In the second stage, they claim value to maximize their interests. Earlier studies have seldom considered these stages and their influences in water allocation schemes, so they cannot accurately simulate the decision-making behaviors and strategy-selection rules used in water allocation. Therefore, there is room for improvement in the applicability of allocation models.

This paper outlines the construction of a two-stage water resources allocation negotiation model. The model supports both individual rationality and group utility improvement to optimize the allocation of water resources. The rest of this research article is structured as follows. A two-stage allocation negotiation model (TSANM) for water allocation is constructed in Section 2. Section 3 presents the results obtained by applying the methods to the case study. Section 4 discusses the reason for the results. Section 5 summarizes and concludes the paper.

2 Modeling

In the first stage of negotiation, the countries will resolve any stalemate that might arise through collective negotiation over their initial offers and resistance points of water allocation, using an effective, widely accepted, and recognized cooperation mechanism to solve the “prisoner’s dilemma” in water conflicts and achieve Pareto Frontier efficiency to create value. The Nash bargaining game not only incorporates most of the characteristics of the problem of water allocation (Pande and McKee 2007), but also takes into account the resistance points of the riparian countries, where it conforms to the principles of individual and collective rationality (Dagan and Volij 1993). In this article, Bankruptcy theory is combined with the Nash bargaining game to yield a group allocation model.

In the second stage of the negotiation, the countries will claim value to achieve their goals and interests, they will ask to adjust the first-stage allocations based on their various requirements. On the one hand, a vertical comparison is about each country’s balancing its water allocation with its water circumstances (Xu et al., 2021). Countries differ in their external and internal circumstances with respect to water resources. These include geographic, hydrographic, hydrological, climatic, ecological, and other factors. Therefore, in the value-claiming stage, riparian countries will emphasize their circumstances of water resources, if water circumstances are greater in the river basin, the higher the water allocation, otherwise, the water allocation will be lower. On the other hand, they will also horizontally compare themselves against other countries with regard to satisfaction, risk and efficiency.

First, no country can achieve the absolute maximization of benefits under water scarcity, so they will be more inclined to take the principle of satisfaction. They will accept a water resource allocation mechanism if it is likely to provide some target level of satisfaction. Moreover, when the degree of satisfaction is compared, relatively unsatisfied countries will require larger allocations, and countries that are already relatively satisfied will need to make concessions.

Second, water resources allocation is related to a country’s industrial and agricultural development, the improvement of living standards, and the protection of the ecological environment. Thus, riparian countries will ask to adjust their water allocations according to the level of risk they face. Countries facing more risk will need larger allocations, while countries in a more secure situation will need to make concessions.

Finally, because scarcity endows water resources with higher value, the riparian countries will pay more attention to the efficiency of water resources used in the allocation adjustment. Higher water use efficiency produces more social welfare, therefore, a country with lower water use efficiency may be offered a lower allocation.

Taking into account all of these factors, we construct a multi-dimensional correction coefficient matrix to adjust the initial allocation and improve the efficiency as shown in Figure 1 (Elahi et al., 2021b). In the first stage, riparian countries negotiated to satisfy individual rationality and maximize the collective utility, and create value through cooperative negotiation to achieve Pareto optimality. In the second stage, riparian countries will require adjustment of water resources from four different dimensions and claim their value.

FIGURE 1

FIGURE 1. Sketch of the two-stage water resources allocation decision-making process.

Therefore, we assume that the countries in the transboundary river basin carry out negotiations on the allocation of water resources according to their interests and needs. There are $N=\left\{\mathrm{1,2},\cdots ,n\right\}$ countries in the basin. Riparian country $i\in N$ claims water demand $c_i$, and the water resources available for allocation are $E$. The sum of the demands of all the riparian countries exceeds the available water resources, $0\le E\le {\displaystyle \sum }_{i=1}^n{c}_i$, so it is necessary to design a resource allocation plan.

2.1 First stage allocation

In the first stage, the riparian countries make their initial offers and use cooperative negotiation to arrive at a preliminary allocation. After comparing the basic conditions, domestic water demand, process water demand, environmental water demand of each country, country $i$ proposes a proportionate allocation plan $E_i=\left\{e_{i1},e_{i2},\cdots ,e_{in}\right\}$. That is, $e_{ij}$ is the water allocation ratio for all countries proposed by country $i$ with $j=\left\{\mathrm{1,2},\cdots ,n\right\}$, ${\displaystyle \sum }_{j=1}^n{e}_{ij}=1$. Together, these plans determine a water resources allocation matrix $E$:

$E=\left|\begin{array}{cccc}{e}_{11}& e_{12}& \cdots & e_{1n}\\ e_{21}& e_{22}& \cdots & e_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ e_{n1}& e_{n2}& \cdots & e_{nn}\end{array}\right|(1)$

A positive ideal allocation plan $E^{+}=\left(e{\left(1\right)}^{+},e{\left(2\right)}^{+},\cdots ,e{\left(n\right)}^{+}\right)$ can be determined by comparing the water allocation plans proposed by various countries, where $e{\left(j\right)}^{+}=\underset{i=1\sim N}{\max }\left\{e_{ij}\right\}$. $E^{+}$ is an ideal plan that provides the largest allocation. However, under water resource bankruptcy, ${\displaystyle \sum }_{j=1}^{n}e{\left(j\right)}^{+}>1$, this plan exceeds the available water resources. Similarly, a negative ideal allocation plan can be determined: $E^{-}=\left(e{\left(1\right)}^{-},e{\left(2\right)}^{-},\cdots ,e{\left(n\right)}^{-}\right)$, where $e{\left(j\right)}^{-}=\underset{i=1\sim N}{\min }\left\{e_{ij}\right\}$. Here each country’s allocation is the minimum among all proposed schemes. This can be regarded as a threshold below which negotiations will be impossible to achieve. Therefore, the riparian countries should negotiate to form a plan that puts each country’s allocation between both the positive and negative ideal.

This problem can be described by a Nash bargaining game model, the optimal concession ratio satisfies the following maximization conditions as the equilibrium solution of the bargaining situation (Nash 1950; Degefu et al., 2016; Yuan et al., 2019):

$\begin{array}{l}\mathit{Max}\left\{{\left[e^{+}\left(1\right)-s_1-e^{-}\left(1\right)\right]}^{w_1}{\left[e^{+}\left(2\right)-s_2-e^{-}\left(2\right)\right]}^{w_2}\cdots {\left[e^{+}\left(n\right)-s_n-e^{-}\left(n\right)\right]}^{w_n}\right\}\\ s.t.\{\begin{array}{c}{\displaystyle \sum }_{i=1}^n\left(e^{+}\left(i\right)-s_i\right)=1\\ e^{+}\left(i\right)-s_i\ge e^{-}\left(i\right)\end{array}\end{array}(2)$

Where, $s_i$ is the concession ratio made by riparian country $i$, $w_i$ is the weight of the country in the basin, or its relative importance. Since the first stage is cooperation allocation, all the countries have the same weight. The initial allocation ratio of country $i$ is $\left(e^{+}\left(i\right)-s_i\right)$, where ${\displaystyle \sum }_{i=1}^n\left(e^{+}\left(i\right)-s_i\right)=1$, and the walkaway threshold is $e^{+}\left(i\right)-s_i\ge e^{-}\left(i\right)$.

To satisfy function (2), the optimal concession ratio needs to meet the following condition:

$s_i^{\ast }=e^{+}\left(i\right)-e^{-}\left(i\right)-w_i\left(1-{\displaystyle \sum }_{i=1}^n{e}^{-}\left(i\right)\right)(3)$

Therefore, the allocation to each country is:

$r_i=e^{+}\left(i\right)-s_i^{\ast }=e^{-}\left(i\right)-w_i\left(1-{\displaystyle \sum }_{i=1}^n{e}^{-}\left(i\right)\right)(4)$

And the initial allocation $R$ to all the riparian countries is:

$R=\left\{r_1,r_2,r_3,\cdots ,r_n\right\}(5)$

The first stage of allocation is integrative negotiation based on cooperation to maximize the group’s total utility. The goal is to create value and achieve individual rationality and collective optimality. However, after achieving Pareto improvement of their collective interests, the countries will claim value to obtain greater benefits for themselves.

2.2 Second stage allocation

In the second stage, the countries continue to negotiate on the allocation of water resources in view of their differences in water circumstances, satisfaction, risk, and efficiency (Yuan et al., 2016).

2.2.1 Adjustment for water circumstances

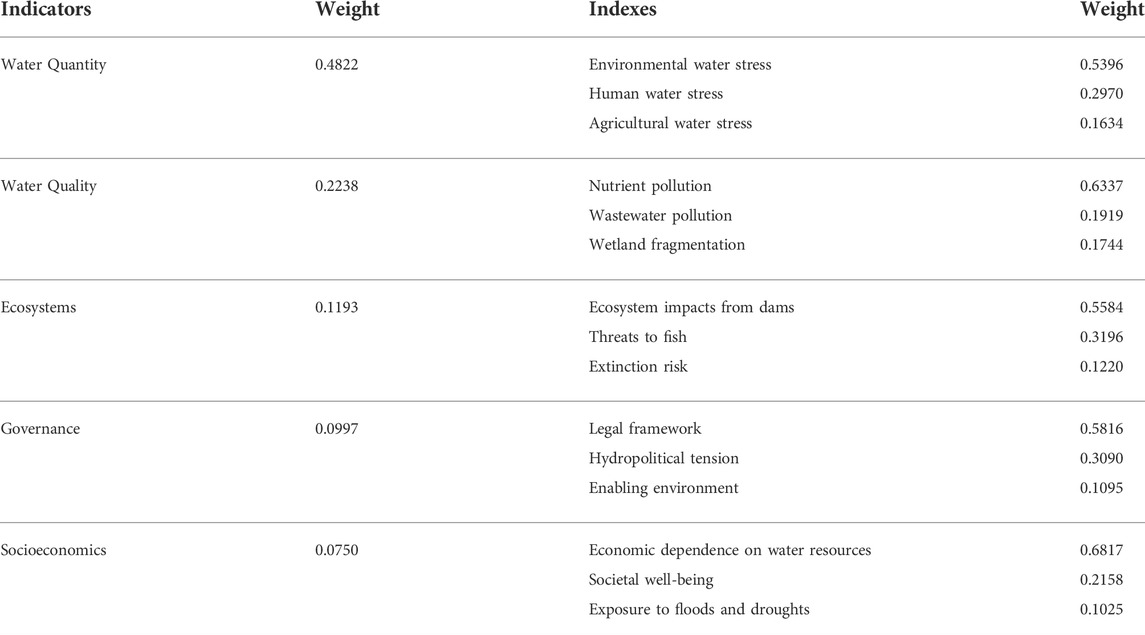
Helsinki Rules on the Uses of the Waters of International Rivers (International Law Association, 1965) and the Convention on the Law of Non-navigational Uses of International Watercourses (UN, 1997) could serve as guidelines for designing allocation mechanisms that are fair, efficient and sustainable. The indicators shown in Table 1 were used to build an index of the water circumstances of riparian countries in a transboundary river basin according to these international agreements.

TABLE 1

TABLE 1. Index for computing water circumstances of riparian countries.

The international rules propose that the weight of each factor is determined by its relative importance in relation to other relevant factors. Thus, we use a Projection Pursuit Model to determine the water circumstance coefficient $WCC$ (Yuan et al., 2019), $WCC=\left\{wc{c}_1,wc{c}_2,\cdots ,wc{c}_n\right\}$.

2.2.2 Adjustment for water satisfaction

As negotiators are restricted by their abilities, information, and other constraints in the decision-making process, they are inclined to make a decision with the satisfaction principle. However, satisfaction depends not only on their allocation per se, but also on their allocation compared to that of other countries (Tversky and Kahneman 1992). Where, $r_i$ is the allocation ratio of country $i$ in the first stage, and $e^{+}\left(i\right)$ is its positive ideal allocation ratio. The satisfaction with the initial allocation of country $i$ is $s_i=r_i/e^{+}\left(i\right)$. The satisfaction coefficient for the countries, $WSC=\left\{ws{c}_1,ws{c}_2,\cdots ,ws{c}_n\right\}$, is obtained by normalizing the satisfaction degree of the initial allocation:

$ws{c}_i=\frac{\left(s_i^{\prime }\right)}{{\displaystyle \sum }_{i=1}^n\left(s_i^{\prime }\right)}(6)$

The lower the satisfaction level, then additional water resources allocation is required, the higher the satisfaction level, the country is required to make concessions in order to reduce the allocation of water resources, therefore:

$s_i^{\prime }=\frac{1}{s_i}(7)$

2.2.3 Adjustment for water risk

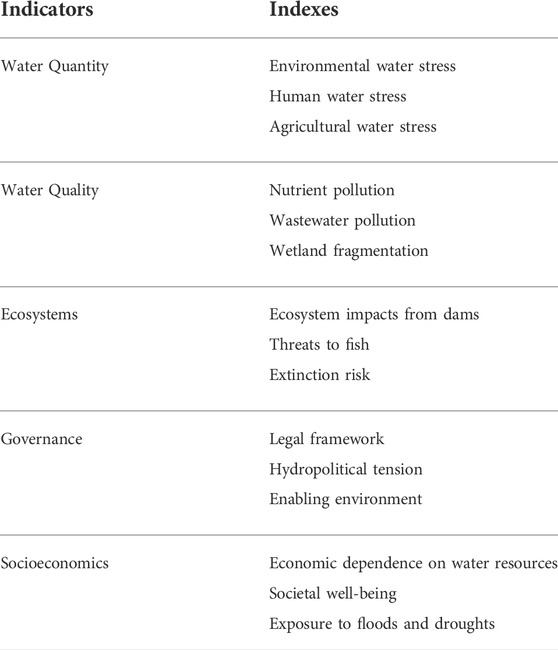
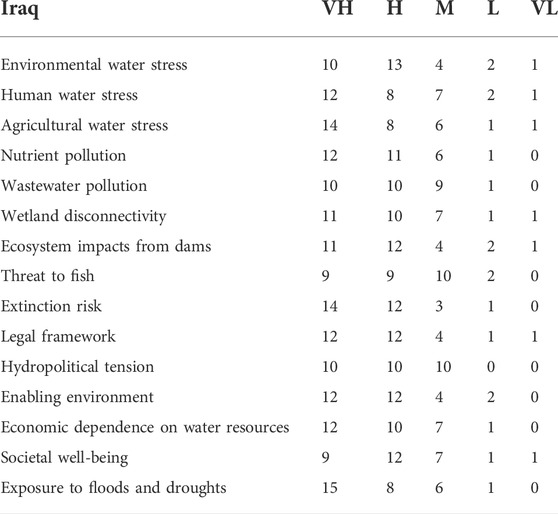
Given their different degrees of economic development and acceptance of water shortage, the risks faced by the riparian countries in the context of water shortage are also different (Gao et al., 2019). Countries facing greater risks must highlight their risks and ask for supplemental water. Since water resources are strongly related to domestic well-being, production capacity, and the ecology, the water risks related to water quantity, water quality, ecosystems, governance, and socioeconomics are shown in Table 2.

TABLE 2

TABLE 2. The indicators and indexes of water risk assessment.

Since some risk indicators are difficult to quantify, we combine the Analytic Hierarchy Process (Saaty 1994) and the Fuzzy Comprehensive Evaluation Method (Yang et al., 2018) to evaluate the water risk coefficient, $WRC=\left\{wr{c}_1,wr{c}_2,\cdots ,wr{c}_n\right\}$.

2.2.4 Adjustment for water use efficiency

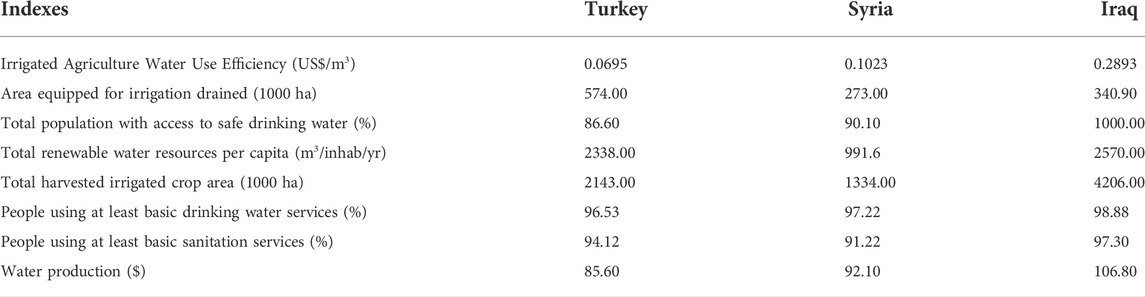
The water resources of the transboundary river are precious and scarce, so it is necessary to emphasize use efficiency to avoid opportunistic behaviors and inaction (An et al., 2018). In order to create an index of efficiency, we use the water use efficiency of irrigated agriculture, area equipped for irrigation, total population with access to safe drinking water, total renewable water resources per capita, total harvested irrigated crop area, people using at least basic drinking water services, people using at least basic sanitation services, and total water production. We then use the Entropy Method to calculate the water efficiency coefficient (Yuan et al., 2022a), $WEC=\left\{we{c}_1,we{c}_2,\cdots ,we{c}_n\right\}$, of riparian countries.

2.3 Final allocation

The final allocation ratio $X_i$ is decided by the Nash-bargaining allocation $r_i$ in the first stage allocation and the adjustment with water circumstances, satisfaction, risk, and efficiency in the second stage:

$X_i=\frac{\left(wc{c}_i+ws{c}_i+wr{c}_i+we{c}_i\right)r_i}{{\displaystyle \sum }_{i=1}^n\left(wc{c}_i+ws{c}_i+wr{c}_i+we{c}_i\right)r_i}(8)$

3 Case study and results

The Tigris-Euphrates is one of the most well-known transboundary river basins in the world. The basin consists of the Tigris and Euphrates Rivers where they roughly follow parallel courses through the heart of the Middle East (Figure 2). The two rivers have their sources within 80 km of each other in eastern Turkey and travel southeast through northern Syria and Iraq to the head of the Persian Gulf. As water conflicts have negatively impacted riparian countries’ water use and state relations, where cooperation can bring greater utility, riparian countries are willing to expand their benefits through cooperation based on their interests, or at least not harm their interests.

FIGURE 2

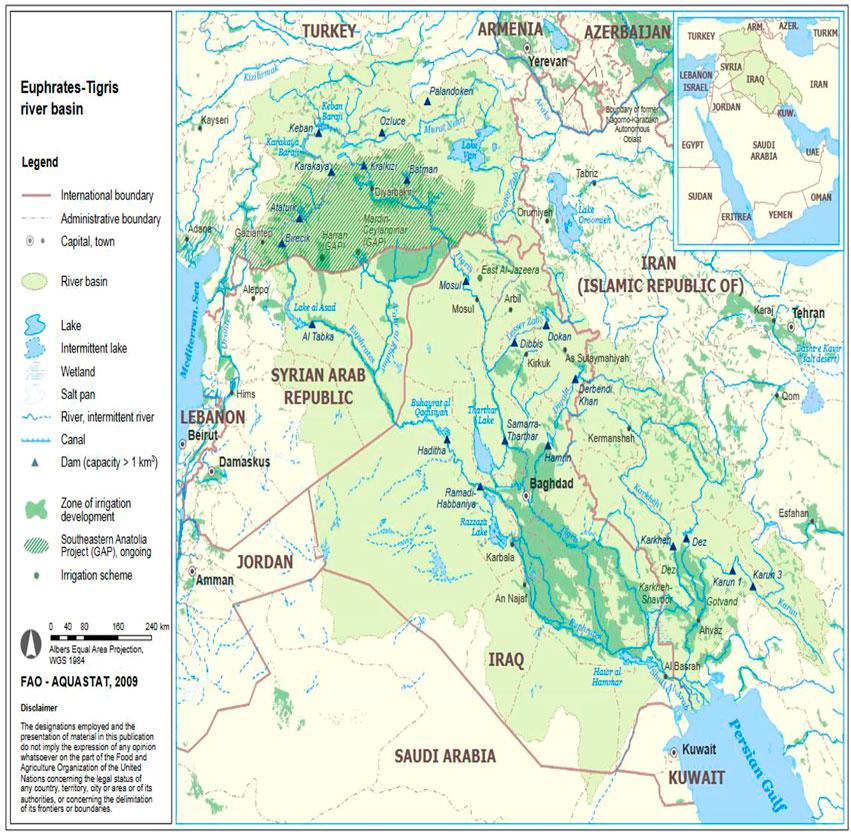
FIGURE 2. Tigris-euphrates river basin (TWAP, 2021).

3.1 First stage allocation

The available water resources in the river system totals 35,580 m³. However, the total water demand of the riparian countries is 54,700 m³, with Turkey, Syria, and Iraq claiming 14,000 m³, 12,600 m³, and 28,100 m³, respectively (Gurer 2004; Kucukmehmetoglu, 2009). The shortage of water resources with increasing water demand means that the three countries usually dispute water allocation schemes. These disputes threaten the safety of the river basin and jeopardize sustainable development. A reasonable water allocation model between these countries is urgently needed to prevent conflict.

We can postulate that the three countries are negotiating over the allocation of water resources and propose a plan for the ratio of water allocation based on its requirements and goals. Turkey’s allocation plan is $Q_{TUR}=\left\{\mathrm{0.40,0.27,0.33}\right\}$, Syria’s is $Q_{SYR}=\left\{\mathrm{0.25,0.35,0.40}\right\}$, and Iraq’s is $Q_{IRQ}=\left\{\mathrm{0.15,0.07,0.78}\right\}$. Then the positive ideal allocation plan is $E^{+}=\left\{\mathrm{0.40,0.35,0.78}\right\}$, and the negative ideal allocation plan is $E^{-}=\left\{\mathrm{0.15,0.07,0.33}\right\}$.

According to function (2), the concession ratio for each country needs to satisfy:

$\begin{array}{l}\mathit{Max}\left[\left(0.40-s_{TUR}-0.15\right)\left(0.35-s_{SYR}-0.07\right)\left(0.78-s_{IRQ}-0.33\right)\right]\\ s.t.\{\begin{array}{c}{s}_{TUR}+s_{SYR}+s_{IRQ}=0.53\\ 0.40-s_{TUR}\ge 0.15\\ 0.35-s_{SYR}\ge 0.07\\ 0.78-s_{IRQ}\ge 0.33\end{array}\end{array}(9)$

Using MATLAB software to solve function (9), we find that the optimal concession ratio is $s_{TUR}=0.10$, $s_{SYR}=0.13$, $s_{IRQ}=0.30$, so the initial allocation ratios are $R=\left\{r_{TUR},r_{SYR},r_{IRQ}\right\}=\left(\mathrm{0.30,0.22,0.48}\right)$ as shown in the Table 3.

TABLE 3

TABLE 3. First stage of water allocation results in the Tigris-Euphrates River.

3.2 Second stage allocation

3.2.1 Adjustment for water circumstances

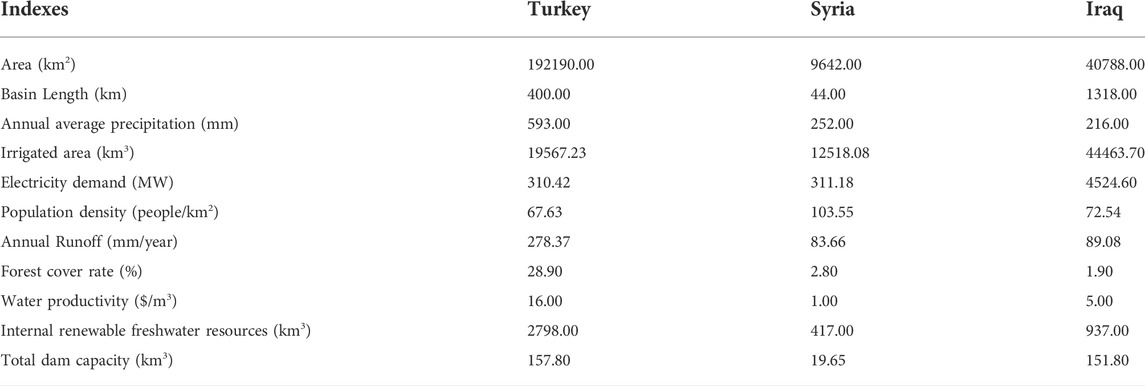
According to the indicators in Table 1, data was collected from the database of World Bank and the FAO’s AQUASTAT is shown in the Table 4.

TABLE 4

TABLE 4. The water circumstances data of the three countries.

We apply a real-coded accelerating genetic algorithm to optimize the projection and reduce the data dimension. The resulting water circumstances coefficients are obtained by applying the Projection Pursuit Model (Yuan et al., 2019):

$WC{C}_i=\left\{wc{c}_{TUR},wc{c}_{SYR},wc{c}_{IRQ},\right\}=\left(\mathrm{0.3694,0.5152,0.1154}\right)(10)$

3.2.2 Adjustment for water satisfaction

The three countries’ satisfaction levels with the initial allocation are:

$s_i=\left\{\frac{r_{TUR}}{q^{+}\left(TUR\right)},\frac{r_{SYR}}{q^{+}\left(SYR\right)},\frac{r_{IRQ}}{q^{+}\left(IRQ\right)}\right\}=\left(\mathrm{0.7500,0.6285,0.6153}\right)(11)$

According to function (7), $s_{TUR}^{\prime }=1.33$, $s_{SYR}^{\prime }=1.5911$, and $s_{IRQ}^{\prime }=1.6252$.

The water satisfaction coefficient $WSC$ calculated by function 6) is:

$WSC=\left\{ws{c}_{TUR},ws{c}_{SYR},ws{c}_{IRQ}\right\}=\left(\mathrm{0.2900,0.3517,0.3583}\right)(12)$

3.2.3 Adjustment for water risk

Eight experts were selected to score the importance of each index in Table 2, and the Analytic Hierarchy Process was applied to obtain the weight of each index as shown in Table 5.

TABLE 5

TABLE 5. Weights used in the water risk index.

The Fuzzy Comprehensive Evaluation Method is used to assess the water risk for Iraq. The risk levels are classified as very high (VH), high (H), moderate (M), low (L), or very low (VL) and they are scored as 100, 80, 60, 40, and 20, respectively, so the risk level $V=\left[\begin{array}{ccccc}100& 80& 60& 40& 20\end{array}\right]$. Thirty experienced managers and experts were selected to evaluate the degree of water risk. Summing the number of times each expert has scored each indicator, a single-factor fuzzy comprehensive evaluation matrix was constructed as shown in Table 6.

TABLE 6

TABLE 6. Fuzzy comprehensive evaluation matrix for Iraq.

Through the evaluation of the various indicators, the evaluation vector of Iraq from the five aspects of water quantity, water quality, ecosystems, governance, and socioeconomics are calculated and then normalized to obtain the membership vector $B$:

$\begin{array}{l}B=\left(\mathrm{0.4822,0.2238,0.1193,0.0997,0.075}\right)\circ \left[\begin{array}{ccccc}0.3749& 0.3566& 0.1739& 0.0612& 0.0333\\ 0.3813& 0.3544& 0.2250& 0.0333& 0.0058\\ 0.3575& 0.3680& 0.1931& 0.0626& 0.0186\\ 0.3794& 0.379& 0.1951& 0.0266& 0.0193\\ 0.3886& 0.3408& 0.2299& 0.0333& 0.0071\end{array}\right]\\ =\left(\mathrm{0.3757,0.3585,0.1939,0.0496,0.0220}\right)\end{array}(13)$

We can then obtain the overall risk evaluation score of Iraq through the comprehensive evaluation grade:

$Z_{Iraq}=V{B}^T=\left[\begin{array}{ccccc}100& 80& 60& 40& 20\end{array}\right]\left[\begin{array}{c}0.3757\\ 0.3585\\ 0.1939\\ 0.0496\\ 0.0220\end{array}\right]=80.3286(14)$

Using the same calculation procedure for Syria and Turkey, the risk evaluation scores for the three countries are $Z_{TUR}=53.9707$, $Z_{SYR}=72.1582$, and $Z_{IRQ}=80.3286$. After normalization, we obtain:

$WRC=\left\{wr{c}_{TUR},wr{c}_{SYR},wr{c}_{IRQ},\right\}=\left(\mathrm{0.2614,0.3495,0.3891}\right)(15)$

3.2.4 Adjustment for water use efficiency

According to the indicators in Table 2, we collected data from the database of AQUASTAT as shown in Table 7.

TABLE 7

TABLE 7. Water efficiency data for the three countries.

The water efficiency coefficients are calculated by the Entropy Method:

$WE{C}_i=\left\{we{c}_{TUR},we{c}_{SYR},we{c}_{IRQ}\right\}=\left(\mathrm{0.2196,0.1102,0.6702}\right)(16)$

Therefore, Table 8 shows the adjusted coefficient between the three countries.

TABLE 8

TABLE 8. The adjusted coefficient of three countries.

According to function (8), the final water resource allocation ratios are $X_i=\left\{x_{TUR},x_{SYR},x_{IRQ}\right\}=\left(\mathrm{0.2498,0.2131,0.5372}\right)$ as shown in the Table 9.

TABLE 9

TABLE 9. Second stage of water allocation result in the Tigris-Euphrates river.

4 Discussion

In the first stage of negotiation, the parties create value through the negotiation of baseline allocations. In the second stage, they claim value at the Frontier of Pareto efficiency to obtain greater benefits, adjusting the allocations using coefficients based on water circumstances, satisfaction, risk, and efficiency.

In the first-stage allocation, the countries’ concession ratio needs to satisfy the function $s_i^{\ast }=e^{+}\left(i\right)-e^{-}\left(i\right)-w_i\left(1-{\displaystyle \sum }_{i=1}^n{e}^{-}\left(i\right)\right)$. Iraq’s positive ideal allocation and negative ideal allocation are both relatively large. Syria has the lowest positive and negative ideal allocations, and the difference between Turkey’s positive ideal allocation and negative ideal allocation is the smallest. Iraq’s concession ratio is the largest, at 30.00%, since its positive ideal allocation is 78.00%, which becomes 48.00% and is still the highest after making the concession. Turkey’s concession ratio is the smallest, but its positive ideal allocation is higher than Syria’s, so the initial allocation ratio of Syria is 22.00%, with the remaining 30.00% allocated to Turkey.

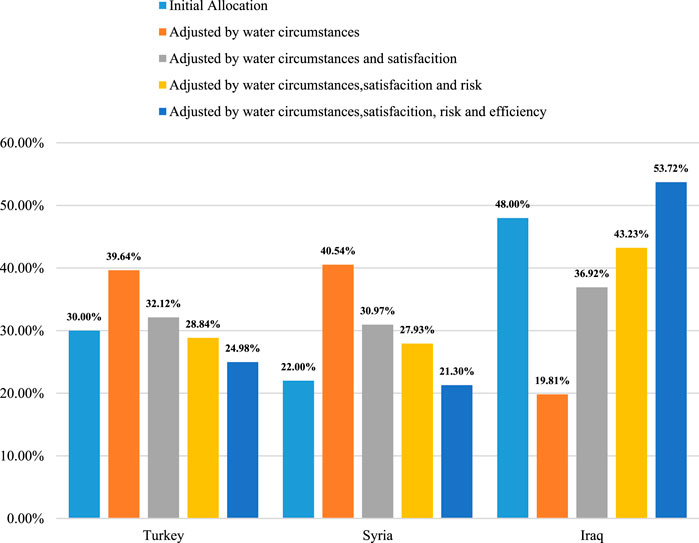
In the second-stage allocation, water allocations are adjusted in view of inter-country differences in water circumstances, satisfaction, risk, and efficiency as shown in Figure 3. Turkey’s allocation is reduced by 5.02%, Syria’s is reduced by 0.70%, and Iraq’s is increased by 5.72%.

FIGURE 3

FIGURE 3. Comparison of the allocation adjustments based on different coefficients.

The process of second-stage adjustment begins with the water circumstances coefficients, which are 0.3694 for Turkey, 0.5152 for Syria, and 0.1154 for Iraq. Among the riparian countries, Iraq has the largest positive indicators, such as area, length, and irrigation area, but also the worst negative indicators, such as renewable water resources, total dam capacity, and water productivity. Combined, these give Iraq the smallest water circumstances coefficient, and hence the largest water allocation adjustment. Its allocation ratio is decreased from 48.00% to 19.81%, while those of Turkey and Syria are increased.

For the water satisfaction adjustment, since Turkey’s initial allocation ratio (30.00%) is the closest to the positive ideal allocation (40.00%), its satisfaction is the highest; but the gap between the initial allocation and the positive ideal allocation is larger for Syria and Iraq. Therefore, the water satisfaction coefficient for Syria and Iraq is greater than for Turkey. This increases Iraq’s water resource allocation ratio to 36.92%, while the allocations for Turkey and Syria decline correspondingly.

Next is the water risk adjustment. According to the experts’ evaluation of 15 indexes, the risks related to water quantity, water quality, ecosystems, governance, and socioeconomics are higher in Syria and Iraq, although this differs from the water stress index estimated by the FAO (using the ratio of total freshwater withdrawal to the difference between total renewable water resources and environmental flow requirements—which does not consider the multi-dimensional properties of water resources). The cumulative adjustment results in a greater allocation for Iraq and smaller allocations for Turkey and Syria.

Finally, in the adjustment for water efficiency, Iraq’s agricultural water use efficiency, irrigation conditions, basic drinking water services, and water productivity are the highest, so its water efficiency adjustment coefficient is the largest, at 0.6702, while Syria, limited by domestic conditions, has the lowest indicators, giving an adjustment coefficient of only 0.1102. This raises Iraq’s water allocation ratio to 53.72%, while Turkey’s decreases to 24.98% and Syria’s to 21.30%.

Taking into account the four factors together, the magnitude of the adjustment is not large, which is conducive to the acceptance of the adjustment plan by the three countries. A large difference between the first and second stages would make acceptance less likely.

This paper has introduced the two-stage characteristics of cooperative negotiation and constructed a two-stage allocation negotiation model (TSANM) based on the Nash bargaining model. Previously proposed multi-stage water resource allocation models use other methods, such as AP rule. AP also allocates a common pool resource in two stages. In the initial allocation, the negotiators obtain $e_{1i}=\max \left\{0,E-{\displaystyle \sum }_{j\in N/\left\{i\right\}}{c}_j\right\}$, where ${\displaystyle \sum }_{j\in N/\left\{i\right\}}{c}_j$ is the sum of the claims of all the other agents. In the second stage, the remaining surplus water is allocated according to the proportional rule $e_{2i}=\left(E-{\displaystyle \sum }_{j\in N}{e}_{1j}\right)\frac{\left(c_i^E-e_{1i}\right)}{\left({\displaystyle \sum }_{j\in N}\left(c_j^E-e_j\right)\right)}$, where $c_i^E=\min \left\{c_i,E\right\}$. Therefore, the final allocation is:

$e_i=\max \left\{0,E-{\displaystyle \sum }_{j\in N/\left\{i\right\}}{c}_j\right\}+\left(E-{\displaystyle \sum }_{j\in N}{e}_{1j}\right)\frac{\left(c_i^E-e_{1i}\right)}{\left({\displaystyle \sum }_{j\in N}\left(c_j^E-e_j\right)\right)}(17)$

This result is shown in Table 10, the difference between the results of the two methods is not obvious. This shows that the TSANM constructed in this article has a certain reference in the allocation and can be accepted by the countries in the river basin. However, there is an essential difference between the TSANM and AP rule. If the riparian countries unanimously adopt the AP rule, the allocation will be carried out in the form of a contract. Next the riparian countries will claim more water based on the acquisition of larger water resources, because AP favors countries that have a greater water demand (Degefu and He 2016). In contrast, the TSANM described here is based on group decision-making among riparian countries. The countries form their respective positive and negative ideal allocations through group negotiation and bargaining, to reach an allocation result based on both individual rationality and group utility. In the second stage, the initial allocation of water resources is adjusted with reference to four water-related coefficients, and the relevant indicators and indexes are developed from relevant laws, rules, documents, and references. The countries could also negotiate to establish the adjustment coefficients and indexes to improve the acceptability of the allocation method and its results.

TABLE 10

TABLE 10. Allocation results from two methods.

5 Conclusion

5.1 Practical implication of the study

In this article, we have considered the challenges of a water resources allocation scheme in transboundary river basins. In view of the multi-dimensional attributes of water resources we constructed a two-stage allocation negotiation model. The Nash bargaining game model and bankruptcy theory are applied for the initial allocation, and for the second stage we proposed an adjustment model which considers factors such as water circumstances, water satisfaction, water risk, and water efficiency. The proposed framework strives to allocate water rationally and improve the acceptability of water resource allocation. The proposed method was applied to the Tigris-Euphrates River, producing initial allocation ratios of 30.00%, 22.00%, and 48.00% for Turkey, Syria, and Iraq, respectively, and adjusted allocation ratios of 24.98%, 21.30%, and 53.72%.

The TSANM described in this paper systematically considers the multi-dimensional attributes of water resources in the allocation process and may increase the participation of riparian countries. Through collective bargaining and negotiation, absolute egalitarianism and utilitarianism are both avoided, and instead objectivity and fairness are emphasized, including the acceptability of an improved allocation scheme. The two-stage allocation model proposed in this article has a strong basis and practical significance for water allocation in transboundary river basins.

5.2 Limitation of this research

This paper constructed a TSANM for water allocation in transboundary rivers. In the second stage for water resource allocation we addressed adjustment by water circumstances, satisfaction, risk, and efficiency. The adjustment of the four aspects is obtained through the calculation of indicators or in the form of questionnaires. The water risk of the riparian country is measured based on subjective evaluation in this article, which may not fully reflect the consideration of the riparian countries in the negotiation of water resources allocation. In addition, part of the data in the case study of this paper comes from a specific situational assumption, which leads to managerial insight implications that this study needs to be strengthened.

5.3 Future direction of study

Water resource allocation is a complex group decision-making problem in transboundary river basins under the changing climate (Lu et al., 2021; Akbari et al., 2022). Water allocation to different countries implies a trade-off between the benefits perceived by different sectors and environmental demands (KhazaiPoul et al., 2019), where they will bargain on the allocation of water resources and emphasize the asymmetry between them. Therefore, these are the directions and topics worthy of further research in the future. Firstly, how to account for the heterogeneity of riparian countries in a two-stage allocation model to more accurately describe the actual situation of water resources allocation. Secondly, using more reasonable methods and building a more systematic index system to adjust the initial allocation of water resources will help to improve the stability of water resource allocation (Avarideh et al., 2017). Finally, finding a real-world case study to simulate the model under the different scenarios and different weight will help to improve managerial insight implications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XW: Conceptualization, Methodology, Writing. WH: Supervision, Writing. LY: Conceptualization, Methodology, Software, Writing. YK: Methodology, Writing. DD: Visualization, Writing, Investigation. RL: Methodology, Writing. YQ: Methodology, Writing. DY: Methodology, Writing. TR: Writing- Reviewing and Editing.

Funding

This work was supported by the National Natural Science Foundation of China [No. 72104127], the Ministry of Education (MOE) of China, Project of Humanities and Social Sciences [No. 20YJCGJW009], the National Natural Science Foundation of China [No. 71874101 and 72004116], the Center for Reservoir Resettlement, China Three Gorges University [No. 2021KFJJ02].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akbari, F., Shourian, M., and Moridi, A. (2022). Assessment of the climate change impacts on the watershed-scale optimal crop pattern using a surface-groundwater interaction hydro-agronomic model. Agric. Water Manag. 265, 107508. doi:10.1016/j.agwat.2022.107508

CrossRef Full Text | Google Scholar

An, M., Butsic, V., He, W., Zhang, Z., Qin, T., Huang, Z., et al. (2018). Drag effect of water consumption on urbanization-A case study of the Yangtze River economic belt from 2000 to 2015. Water 10 (9), 1115. doi:10.3390/w10091115

CrossRef Full Text | Google Scholar

Aumann, R. J., and Maschler, M. (1985). Game theoretic analysis of a bankruptcy problem from the Talmud. J. Econ. Theory 36 (2), 195–213. doi:10.1016/0022-0531(85)90102-4

CrossRef Full Text | Google Scholar

Avarideh, F., Attari, J., and Moridi, A. (2017). Modelling equitable and reasonable water sharing in transboundary rivers: The case of sirwan-diyala river. Water Resour. manage. 31 (4), 1191–1207. doi:10.1007/s11269-017-1570-4

CrossRef Full Text | Google Scholar

Brown, J. G. (2012). Empowering students to create and claim value through the thomas-kilmann conflict mode instrument. Negot. J. 8 (1), 79–91. doi:10.1111/j.1571-9979.2011.00327.x

CrossRef Full Text | Google Scholar

Dagan, N., and Volij, O. (1993). The bankruptcy problem: a cooperative bargaining approach. Math. Soc. Sci. 26 (3), 287–297. doi:10.1016/0165-4896(93)90024-D

CrossRef Full Text | Google Scholar

Degefu, D. M., and He, W. (2016). Allocating water under bankruptcy scenario. Water Resour. manage. 30 (11), 3949–3964. doi:10.1007/s11269-016-1403-x

CrossRef Full Text | Google Scholar

Degefu, D. M., He, W., and Yuan, L. (2017). Monotonic bargaining solution for allocating critically scarce transboundary water. Water Resour. manage. 31 (9), 2627–2644. doi:10.1007/s11269-017-1648-z

CrossRef Full Text | Google Scholar

Degefu, D. M., He, W., Yuan, L., and Zhao, J. H. (2016). Water allocation in transboundary river basins under water scarcity: a cooperative bargaining approach. Water Resour. manage. 30 (12), 4451–4466. doi:10.1007/s11269-016-1431-6

CrossRef Full Text | Google Scholar

Degefu, D. M., Weijun, H., Zaiyi, L., Liang, Y., Zhengwei, H., and Min, A. (2018). Mapping monthly water scarcity in global transboundary basins at country-basin mesh based spatial resolution. Sci. Rep. 8 (1), 2144. doi:10.1038/s41598-018-20032-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Devente, J., Reed, M. S., Stringer, L. C., Valente, S., and Newig, J. (2016). How does the context and design of participatory decision making processes affect their outcomes? Evidence from sustainable land management in global drylands. Ecol. Soc. 21 (2), 24. doi:10.5751/ES-08053-210224

CrossRef Full Text | Google Scholar

Elahi, E., Khalid, Z., Tauni, M. Z., Zhang, H., and Lirong, X. (2021a)., 102255. Pakistan. doi:10.1016/j.technovation.2021.102255Extreme weather events risk to crop-production and the adaptation of innovative management strategies to mitigate the risk: A retrospective survey of rural Punjab, PakistanTechnovation

CrossRef Full Text | Google Scholar

Elahi, E., Khalid, Z., and Zhang, Z. (2022). Understanding farmers’ intention and willingness to install renewable energy technology: A solution to reduce the environmental emissions of agriculture. Appl. Energy 309, 118459. doi:10.1016/j.apenergy.2021.118459

CrossRef Full Text | Google Scholar

Elahi, E., Zhang, H., Lirong, X., Khalid, Z., and Xu, H. (2021b). Understanding cognitive and socio-psychological factors determining farmers’ intentions to use improved grassland: Implications of land use policy for sustainable pasture production. Land Use Policy 102, 105250. doi:10.1016/j.landusepol.2020.105250

CrossRef Full Text | Google Scholar

Farjoudi, S. Z., Moridi, A., Sarang, A., and Lence, B. J. (2021). Application of probabilistic bankruptcy method in river water quality management. Int. J. Environ. Sci. Technol. (Tehran). 18, 3043–3060. doi:10.1007/s13762-020-03046-8

CrossRef Full Text | Google Scholar

Gao, X., Shen, J., He, W., Sun, F., Zhang, Z., Zhang, X., et al. (2019). Changes in ecosystem services value and establishment of watershed ecological compensation standards. Int. J. Environ. Res. Public Health 16 (16), 2951. doi:10.3390/ijerph16162951

PubMed Abstract | CrossRef Full Text | Google Scholar

Garrick, D. E., Hernández-Mora, N., and O’Donnell, E. (2018). Water markets in federal countries: comparing coordination institutions in Australia, Spain and the western USA. Reg. Environ. Change 18 (6), 1593–1606. doi:10.1007/s10113-018-1320-z

CrossRef Full Text | Google Scholar

Gurer, I. (2004). “Water issue among the riparian states of Euphrates and Tigris transboundary rivers,” in Water in the Middle East and in north africa (Springer Berlin Heidelberg), 333–343. doi:10.1007/978-3-662-10866-6_28

CrossRef Full Text | Google Scholar

International Law Association (1965). Helsinki rules on the uses of the waters of international rivers. Available at: http://www.internationalwaterlaw.org/documents/intldocs/Helsinki_Rules_with_comments.pdf.

Google Scholar

KhazaiPoul, A., Moridi, A., and Yazdi, J. (2019). Multi-objective optimization for interactive reservoir-irrigation planning considering environmental issues by using parallel processes technique. Water Resour. manage. 33 (15), 5137–5151. doi:10.1007/s11269-019-02420-7

CrossRef Full Text | Google Scholar

Kong, Y., He, W., Yuan, L., Shen, J., An, M., Degefu, D. M., et al. (2019). Decoupling analysis of water footprint and economic growth: A case study of beijing–tianjin–hebei region from 2004 to 2017. Int. J. Environ. Res. Public Health 16 (23), 4873. doi:10.3390/ijerph16234873

CrossRef Full Text | Google Scholar

Kong, Y., He, W., Yuan, L., Zhang, Z., Gao, X., Zhao, Y., et al. (2021). Decoupling economic growth from water consumption in the yangtze river economic belt, China. Ecol. Indic. 123, 107344. doi:10.1016/j.ecolind.2021.107344

CrossRef Full Text | Google Scholar

Kucukmehmetoglu, M. (2009). A game theoretic approach to assess the impacts of major investments on transboundary water resources: The case of the Euphrates and Tigris. Water Resour. manage. 23 (15), 3069–3099. doi:10.1007/s11269-009-9424-3

CrossRef Full Text | Google Scholar

Kucukmehmetoglu, M. (2012). An integrative case study approach between game theory and Pareto frontier concepts for the transboundary water resources allocations. J. Hydrology 450 (45), 308–319. doi:10.1016/j.jhydrol.2012.04.036

CrossRef Full Text | Google Scholar

Lee, C. S. (2012). Multi-objective game-theory models for conflict analysis in reservoir watershed management. Chemosphere 87 (6), 608–613. doi:10.1016/j.chemosphere.2012.01.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, C. Y., and Zhang, L. (2015). An inexact two-stage allocation model for water resources management under uncertainty. Water Resour. manage. 29 (6), 1823–1841. doi:10.1007/s11269-015-0913-2

CrossRef Full Text | Google Scholar

Lu, S., Lian, Z., Sun, H., Wu, X., Bai, X., and Wang, C. (2021). Simulating trans-boundary watershed water resources conflict. Resour. Policy 73, 102139. doi:10.1016/j.resourpol.2021.102139

CrossRef Full Text | Google Scholar

Madani, K. (2010). Game theory and water resources. J. Hydrology 381 (3–4), 225–238. doi:10.1016/j.jhydrol.2009.11.045

CrossRef Full Text | Google Scholar

Medeiros, D. F. K. L., Urtiga, M. M., and Morais, D. C. (2017). Integrative negotiation model to support water resources management. J. Clean. Prod. 150, 148–163. doi:10.1016/j.jclepro.2017.02.160

CrossRef Full Text | Google Scholar

Mianabadi, H., Mostert, E., Pande, S., and van de Giesen, N. (2015). Weighted bankruptcy rules and transboundary water resources allocation. Water Resour. manage. 29 (7), 2303–2321. doi:10.1007/s11269-015-0942-x

CrossRef Full Text | Google Scholar

Moridi, A. (2019b). Dealing with reservoir eutrophication in a trans-boundary river. Int. J. Environ. Sci. Technol. (Tehran). 16, 2951–2960. doi:10.1007/s13762-018-1775-y

CrossRef Full Text | Google Scholar

Moridi, A. (2019a). A bankruptcy method for pollution load reallocation in river systems. J. Hydroinformatics 21, 45–55. doi:10.2166/hydro.2018.156

CrossRef Full Text | Google Scholar

Nash, J. (1950). The bargaining problem. Econometrica 2, 155–162. doi:10.2307/1907266

CrossRef Full Text | Google Scholar

O’Neill, B. (1982). A problem of rights arbitration from the Talmud. Math. Soc. Sci. 2 (4), 345–371. doi:10.1016/0165-4896(82)90029-4

CrossRef Full Text | Google Scholar

Pande, S., and McKee, M. (2007). Valuing certainty in a consensus-based water allocation mechanism. Water Resour. Res. 43 (2), W02427. doi:10.1029/2004WR003890

CrossRef Full Text | Google Scholar

Roozbahani, R., Schreider, S., and Abbasi, B. (2015). Optimal water allocation through a multi-objective compromise between environmental, social, and economic preferences. Environ. Model. Softw. 64, 18–30. doi:10.1016/j.envsoft.2014.11.001

CrossRef Full Text | Google Scholar

Saaty, T. L. (1994). How to make a decision: The analytic hierarchy process. Eur. J. Operational Res. 48 (1), 9–26. doi:10.1016/0377-2217(90)90057-I

CrossRef Full Text | Google Scholar

Sun, H., Edziah, B. K., Sun, C., and Kporsu, A. K. (2021). Institutional quality and its spatial spillover effects on energy efficiency. Socio-Economic Plan. Sci. 83, 101023. doi:10.1016/j.seps.2021.101023

CrossRef Full Text | Google Scholar

Thomson, W. (2003). Axiomatic and game-theoretic analysis of bankruptcy and taxation problems: A survey. Math. Soc. Sci. 45 (3), 249–297. doi:10.1016/S0165-4896(02)00070-7

CrossRef Full Text | Google Scholar

Thomson, W. (2015). Axiomatic and game-theoretic analysis of bankruptcy and taxation problems: An update. Math. Soc. Sci. 74, 41–59. doi:10.1016/j.mathsocsci.2014.09.002

CrossRef Full Text | Google Scholar

Tversky, A., and Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 5 (4), 297–323. doi:10.1007/BF00122574

CrossRef Full Text | Google Scholar

TWAP (2021). “The transboundary waters assessment programme (TWAP),” in The global transboundary river basins. Available at: http://twap-rivers.org/indicators/Report.ashx?type=BasinFactsheet&bcode=TIGR (accessed April 12, 2021).

Google Scholar

UN (1997). The convention on the law of the non-navigational uses of international Watercourses. Available at: http://legal.un.org/ilc/texts/instruments/english/conventions/8_3_1997.pdf.

Google Scholar

Vörösmarty, C. J., Green, P., Salisbury, J., and Lammers, R. B. (2000). Global water resources: Vulnerability from climate change and population growth. Science 289 (5477), 284–288. doi:10.1126/science.289.5477.284

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Fang, L., and Hipel, K. W. (2008). Integrated hydrologic-economic modeling of coalitions of stakeholders for water allocation in the south saskatchewan river basin. J. Hydrol. Eng. 13 (9), 781–792. doi:10.1061/(asce)1084-0699(2008)13:9(781)

CrossRef Full Text | Google Scholar

Wei, X., Wang, N., Luo, P., Yang, J., Zhang, J., and Lin, K. (2021). Spatiotemporal assessment of land marketization and its driving forces for sustainable urban–rural development in Shaanxi Province in China. Sustainability 13 (14), 7755. doi:10.3390/su13147755

CrossRef Full Text | Google Scholar

Xu, S., He, W., Shen, J., Degefu, D. M., Yuan, L., and Kong, Y. (2019). Coupling and coordination degrees of the core water–energy–food nexus in China. Int. J. Environ. Res. Public Health 16 (9), 1648. doi:10.3390/ijerph16091648

CrossRef Full Text | Google Scholar

Xu, S., He, W., Yuan, L., Degefu, D. M., Yang, Y., and Li, H. (2021). The relationship between coordination degree of the water–energy–food system and regional economic development. Sustainability 13 (3), 1305. doi:10.3390/su13031305

CrossRef Full Text | Google Scholar

Yang, W., Xu, K., Lian, J., Bin, L., and Ma, C. (2018). Multiple flood vulnerability assessment approach based on fuzzy comprehensive evaluation method and coordinated development degree model. J. Environ. Manag. 213, 440–450. doi:10.1016/j.jenvman.2018.02.085

PubMed Abstract | CrossRef Full Text | Google Scholar

Yazdi, J., and Moridi, A. (2017). Interactive reservoir-watershed modeling framework for integrated water quality management. Water Resour. manage. 31 (7), 2105–2125. doi:10.1007/s11269-017-1627-4

CrossRef Full Text | Google Scholar

Yu, S., and Lu, H. (2018). An integrated model of water resources optimization allocation based on projection pursuit model–Grey wolf optimization method in a transboundary river basin. J. Hydrology 559, 156–165. doi:10.1016/j.jhydrol.2018.02.033

CrossRef Full Text | Google Scholar

Yuan, L., He, W., Degefu, D. M., Kong, Y., Wu, X., Xu, S., et al. (2021a). Elucidating competing strategic behaviors using prospect theory, system dynamics, and evolutionary game: a case of transjurisdictional water pollution problem in China. Environ. Sci. Pollut. Res. 29, 20829–20843. doi:10.1007/s11356-021-17034-z

CrossRef Full Text | Google Scholar

Yuan, L., He, W., Degefu, D. M., Liao, Z., Wu, X., An, M., et al. (2020). Transboundary water sharing problem; a theoretical analysis using evolutionary game and system dynamics. J. Hydrology 582, 124521. doi:10.1016/j.jhydrol.2019.124521

CrossRef Full Text | Google Scholar

Yuan, L., He, W., Degefu, D. M., Soonja, K., Juqin, S., and Min, A. (2016). Two-stage concession game approach for analyzing greenhouse gases emission reduction schemes. Environ. Eng. Res. 21 (4), 420–426. doi:10.4491/eer.2016.071

CrossRef Full Text | Google Scholar

Yuan, L., He, W., Degefu, D. M., Wan, Z., Ramsey, T. S., and Wu, X. (2021b). A system dynamics simulation model for water conflicts in the Zhanghe River Basin, China. Int. J. Water Resour. Dev., 1–17. doi:10.1080/07900627.2021.1873107

CrossRef Full Text | Google Scholar

Yuan, L., He, W., Liao, Z., Degefu, D. M., An, M., Zhang, Z., et al. (2019). Allocating water in the Mekong River basin during the dry season. Water 11 (2), 400. doi:10.3390/w11020400

CrossRef Full Text | Google Scholar

Yuan, L., Li, R., He, W., Wu, X., Kong, Y., Degefu, D. M., et al. (2022a). Coordination of the industrial-ecological economy in the yangtze river economic belt, China. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.882221

CrossRef Full Text | Google Scholar

Yuan, L., Wu, X., He, W., Kong, Y., Degefu, D. M., and Ramsey, T. S. (2022b). A multi-weight fuzzy methodological framework for allocating coalition payoffs of joint water environment governance in transboundary river basins. Water Resour. manage. 36, 3367–3384. doi:10.1007/s11269-022-03206-0

CrossRef Full Text | Google Scholar

Zeng, Y., Li, J., Cai, Y., Tan, Q., and Dai, C. (2019). A hybrid game theory and mathematical programming model for solving trans-boundary water conflicts. J. Hydrology 570, 666–681. doi:10.1016/j.jhydrol.2018.12.053

CrossRef Full Text | Google Scholar