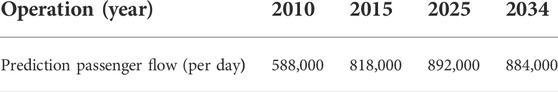Operational risk allocation in urban rail transit public–private partnership projects

Operation risk (OR) has affected sustainable development of urban rail transit (URT) public–private partnership (PPP) projects in China. Balanced distribution of operational risks among stakeholders (the public, government, and private companies) involved in URT PPP projects can maximize overall profit. Quantitative analysis of operational risk allocation of urban rail transit PPP project is the key to achieve balance. Few existing studies have quantitatively analyzed operation risk allocation (ORA) in URT PPP project. The objective of this research is to construct a quantitative risk allocation model among three participants by using cooperative game theory. The risk allocation model was modified based on the consideration of four factors affecting the allocation of operational risks: controllability, risk loss, affordability, and handling cost. A case was used as an empirical example, and possible problems were illustrated. The result shows it is necessary and feasible to let the public bear part of the operational risk of the project by raising ticket prices. The results reveal that the public will play an important role in balancing risk allocation. This study shows that an ORA model can suggest how to make the risk allocation process more reasonable, fair, and stable. Meanwhile, the quantitative approach proposed can also be used by stakeholders in achieving fairness and stability of the partnership.

1 Introduction

Over the last decade, urban rail transit systems (URT including subways, light rails, suburban railways, monorails, trams, and magnetic levitation systems) have played an increasingly important role in many large Chinese cities (Huang et al., 2018). Public–private partnerships (PPP) have been adopted to solve the financial problems and improve the operation efficiency of URT. But URT PPP projects are not more attractive for the private sector because of prominent operation risks (OR). This results from the contradiction between high construction costs and low ticket income (Siemiatycki and Jonathan, 2012), making it difficult to achieve reasonable returns in public concession duration (Hua, 2011). In order to increase profitability of URT PPP, and thus draw in private capital, the government often compensates losses to guarantee private sector absolute returns (Carpintero and Petersen, 2014). These financial subsidies can become a primary motivation for URT PPP projects (Neto et al., 2016; Zhang et al., 2016). Yet, in the long run, it can increase the financial burden of the government. In addition, when the government underwrites the whole operation risk, it could affect service quality. As such, it may not achieve sustainability of the PPP project. Research on the distribution of risks in PPP projects is typically quantitative and is based on fuzzy mathematics theory and game theory. Game theory, which emphasizes win–win cooperation, is better suited to solve the allocation problem of internal alliances than fuzzy mathematics theory.

Research suggests that cooperative game theory can be used to effectively solve the problem of allocation and help achieve fairness and stability of the partnership. This study contributes to the ORA of URT PPP using a perspective of cooperative game theory. As beneficiaries of ORA PPP projects, the government, private sector, and the public should take some ORs of the project. The main research objective of this study is to build an ORA cooperative game model, based on a revised Shapely approach, among the government, private investors, and the public. To demonstrate how the ORA cooperative game model may be applied, a case study using Beijing Metro Line 4 is presented.

2 Literature review

2.1 Risk allocation of public–private partnership projects

2.1.1 Risk allocation of participants

The majority of the existing literature on risk allocation of PPP projects focuses on a balance between public and private sectors (Valipour et al., 2019; Ma et al., 2018; Chou et al., 2012); the final arbitration framework is modeled to get the fairest risk-sharing agreement (Medda, 2007). A reasonable risk allocation mechanism may be the most critical factor for the success of a PPP project (Robert and Chan, 2015). Efficient risk allocation is understood as an instrument to apportion risks such that the party with the (superior) ability to manage risks assumes most of their responsibility (Aziz, 2011). However, risks in PPP are not always allocated to the party best able to manage them, but instead to the party least able to refuse them (Jin and Zhang, 2011). Misallocation often results from governments not taking their fair share of external risks (Shrestha et al., 2018), yet the majority of existing literature on PPPs has suggested that external risks need to be borne by the government (Bing et al., 2005; Jin and Zhang, 2011). This stems from the argument that government is in a stronger position to influence, adapt to, and manage large external political and economic forces, particularly over the long term. Governments are overly keen to attract private investment via PPP, but instead the private sector has greater influence during risk allocation negotiations. As a consequence, governments may have to pay considerable premiums in order to transfer those risks to the private sector, reducing the VFM in these projects (Witt and Liias, 2011).

2.1.2 Risk allocation methods of public–private partnership projects

For quantitative research on the PPP risk allocation method in recent years, there are mainly two types: one is based on the fuzzy mathematics theory, another is based on the game theory. For example, some scholars investigated practitioners with hands-on experience in PPP projects by three rounds of a Delphi questionnaire survey and established risk allocation criteria from this (Xu et al., 20102010; Ke et al., 2011; Mahdi nia et al., 2021). Risk allocation criteria and the fuzzy set approach were used to assess risk management capabilities of public and private parties and to predict risk allocation strategies. Based on expertise of 32 senior practitioners, extensive statistical analysis was used to examine how to maximize risk mitigation efficiency (Nguyen et al., 2018). A quantitative model was provided for risk allocation based on fuzzy theory and evaluated the control ability of project participants, and then identified the participant with the most influence on control of particular risks (Lam et al., 2007). Considering various influential factors, an artificial neural network (ANN) model was established for the whole decision-making process of PPP project risk allocation by fuzzy neural network technology (Jin and Zhang, 2011). Compared with fuzzy mathematics theory, game theory is more suitable for solving the distribution problem of internal alliance and emphasizes win–win cooperation (Li et al., 2017). Nash and Shapley put forward the Shapley value method to solve the distribution problem within the cooperative alliance based on the contribution value of participants, which provided a theoretical basis and methodology for the game players to seek win–win (Maschler et al., 1992). The construction principle and model solution of the Shapley value method are relatively simple, and the only optimal solution can be obtained, which is very suitable for solving the risk allocation problem of PPP project stakeholders (Xu and Li, 2010). Some scholars incorporates the influence of public equity and time value of money into the construction of model based on the Shapley value method to analyze optimal risk allocation between government departments and private companies (Zhang and Fang, 2017; Ke et al., 2019). In order to improve the rationality of risk allocation on PPP projects, the two-person game model with the participant’s risk preference considered was built. The application of the two-person game model indicated the probability, severity, and impact of risk factors were considered to prioritize risk allocation (Li et al., 2017).Game theory argues that there is a disagreement between the interests of concessionaire and government in determining the PPP project concession period (Shen et al., 2007). The game theory can effectively solve the conflict of interests and risks between the government and the concessionaires in the concession period (Ma et al., 2018).

2.2 Operation risk of urban rail transit public–private partnership projects

PPP could ease the government’s financial burden and improve operation efficiency by introducing the private sector into URT projects. PPPs, or other types of privatization, have improved efficiency of rail transit systems in a number of major cities, including Bangkok, Kuala Lumpur, Singapore, Hong Kong, and Seoul (Phang, 2007). The concept of public–private partnerships (PPPs) was officially embraced by the Chinese government in 2001, when the Chinese National Planning Committee issued the policy note entitled “Suggestions to Promote and Guide Private Investments.” This recommended the use of incentive mechanisms to attract private capital and extended the domains, in which private investment was permitted. But international experts have made it clear that China still has a long way to go to fully implement PPP. Compared to countries with more mature partnerships and more successful experiences (e.g., United Kingdom and Australia), and transient ones working on ‘effective governance’ (e.g., Spain, South Korea, and Japan), China is in a group of relative latecomers still working on long-term commitment to PPP, along with countries such as Thailand, Brazil, India, Germany, and the United States (Sophie, 2017). URT PPP project often suffer losses due to poor management and bad operation environment (Carpintero and Petersen, 2015). The sustainable operation of PPP project is the necessary guarantee for the success of the whole project (Ahmadabadi and Heravi, 2019).URT operation has long been a focus of industry and academia, with study relating to personnel, facilities, environment, management, and uncertain hazards (Hu et al., 2016). Operation safety (Xu et al., 2018), emergent effects (Ridgeway and MacDonald, 2017), plan arrangement (Ji et al., 2017), and operation efficiency (Gong et al., 2018) are current areas of focus. Operation risk is a collection of uncertain factors that affects the balance of revenue and expenditure of PPP projects in a long franchise period (Vecchi et al., 2018). Generally, the public sectors take the majority of responsibility for political and regulatory risks, and the private sectors take the majority of responsibility for macroeconomic and technical risks (Mandriperrott and Menzies, 2010; Zhao et al., 2016; Yuan et al., 2018). Providing efficient and high-quality public services is the main goal of URT PPP project (Yuan et al., 2018). Low fares at government-controlled prices increase the government’s risk. In fact, the public should also take the corresponding risks by paying for tickets. Paying attention to the importance of the public in the risk sharing of URT PPP projects is helpful to maintain the sustainability of urban rail PPP projects. As consumers of URT PPP projects, few researchers mentioned the risks taken by the public. Particularly in China, the lower ticket price set by the government increases the risk of the government. In fact, the public should also take the corresponding risks by paying for tickets.

By sorting out and analyzing the aforementioned literature, few studies have focused on the quantification of risk allocation of URT PPP project among the government, the private company, and the public. Existing studies focused on risk allocation between the public and private sectors in PPP projects, ignoring the importance of the public. The objective of this research is to construct a quantitative risk allocation model among three participants (the government, the private company, and the public), by using cooperative game theory. This research contains seven sections: Section 1: Introduction; Section 2: Literature review; Section 3: Methodology; Section 4: The ORA model of a URT PPP project; Section 5: Case study of Beijing Metro Line 4; Section 6: Discussion; and Section 7: Conclusions. In Sections 1–3, this article discussed the practical background, theoretical basis, and research framework. Section 4 proposed a quantitative model to explore the research gap in Sections 1, 2. In Sections 5, 6, the case study is conducted and the results of the case study are presented and discussed. Then, Section 7 gives the research conclusion.

3 Methodology

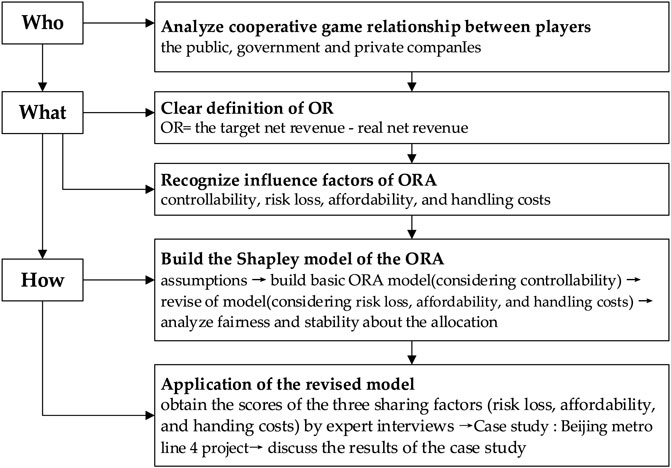
This study adopted a hybrid research method, as shown in Figure 1. First, the cooperative game relationship was analyzed to clarify the motivations and interests of participants. Second, the definition of OR for URT PPP projects and influence factors of ORA were outlined. Then, considering the controllable degree of each participant, the basic sharing model of URT PPP project management risk was built based on the Shapley model and basic cooperative game theory. The method can effectively solve the unique optimal solution in cooperative games without considering the influence of the influencing factors on the distribution results (Gately, 1974). The Shapley value considered the player’s contribution; it shows the fair principle of “more pay for more work.” The Shapley model was further modified by considering the degree of loss for government departments, social capital, and the public, and the ability to bear the management risk and management style for the rationality of the results. Finally, the revised model was used to analyze the risk allocation of Beijing Metro Line 4. In this case, scores for four influencing factors were obtained through expert interviews. The fair index, power index, and fission index of participants were used to analyze the allocation results.

FIGURE 1

FIGURE 1. Methodological steps.

4 The operation risk allocation model of an urban rail transit public–private partnership project

4.1 Cooperative game relationship and Operation risk of urban rail transit public–private partnership project

4.1.1 Cooperative game relationship and operation risk of urban rail transit public–private partnership project

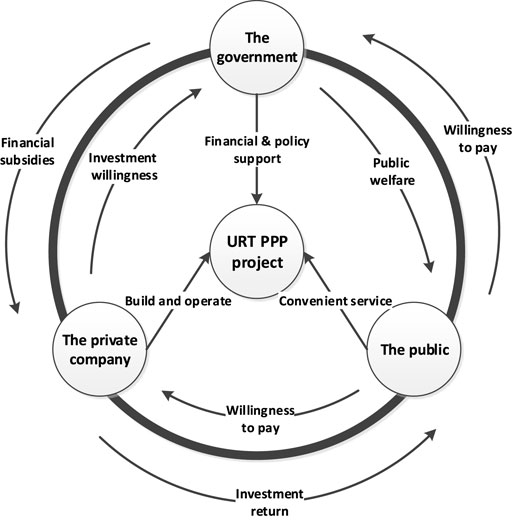
There are three direct stakeholders involved in URT PPP projects: the public, government, and private companies. Government hopes to reduce pressure on public funds by bringing in private capital, while maintaining public welfare (Aldrete et al., 2018). The introduction of private capital in URT projects is conducive to improving the efficiency of URT operation and promoting social equity. The primary goal of the private partners is maximizing profit (Trujillo et al., 2018) and achieving cost efficiency (Javed et al., 2014). At the same time, to expand market share and increase reputation gain is also the motivation for private partners to participate in PPP projects (Zhang et al., 2020). For the public, low ticket prices are key, which obviously affects profitability for private investors, requiring higher government subsidies. The public also hopes to enjoy high-quality services. There are trade-offs for all parties involved.

Ideally, government sets the stage, the private company carries out key roles, and the public benefits overall. More specifically, the government provides financial and policy support, private companies are responsible for construction and operation, and the public gets convenient, affordable, URT services, as shown in Figure 2. If parties are uncooperative, all lose out: financial burden, management difficulties, and political pressure for the government; private companies could face economic losses; and the public does not receive the URT services they desire (Zhang et al., 2019). A successful ORA scheme should promote the stability of the alliance to work toward long-term success.

FIGURE 2

FIGURE 2. Collaboration among the government, private investors, and public.

4.1.2 Operational risk

In the whole life cycle of the project, the operation risk of URT PPP project is manifested as the uncertainty of cash flow revenue and expenditure, which is the result of the combined effect of various risk factors, mainly including the risk of cost overrun and the risk of insufficient operating revenue. There are many factors that contribute to cost overruns, such as poor management, insufficient technical level, project change, construction delay, and interest rate fluctuations (Phang, 2007). Insufficient tickets revenue is the main reason for insufficient revenue. The operating revenue sources of URT PPP projects include tickets revenue and commercial revenue, while commercial income has little contribution (Hu et al., 2016). The risk of insufficient operating revenue hinders the sustainable development of urban rail transit PPP projects (World Bank, 2017). The traditional URT projects are completely operated by government investment. The construction and operation cost of the project comes from tax revenue contributed by the public. The public supports that the urban rail transit project is a social welfare provided by the government for the public, and its construction and operation risks should be entirely borne by the government (Lv et al., 2020). The public is highly sensitive to the ticket price of urban rail transit projects, especially in developing countries. Urban rail transit PPP projects need to achieve partial investment returns through fare income, which depends directly on the public willingness to pay. Compared with the government and private companies, the public is not directly involved in the pricing. However, the public’s acceptance of the ticket price is an important factor for pricing. It is acceptable for the public to increase the ticket price within a reasonable range to get better services. In order to better realize the rationality and efficiency of risk sharing, it is necessary to regard the public as a party of risk bearing.

The OR of an URT PPP project is best defined as the discrepancy between the target net revenue and real net revenue during the franchise period, expressed by Eq. 1:

$r=W-W_0-\theta ,(1)$

where $W$—target net revenue of the URT PPP project during the franchise period

$W_0$—real net revenue of the URT PPP project during the franchise period

$\theta$—operation risk from unforeseen obstacles, that is, economic losses, which follow a normal distribution $N(0,\sigma )$.

For target net revenue, the asset-weighted cost of an infrastructure investment project in a country with relatively stable macroeconomic policy is between 5 and 8%; in an unstable country, the asset-weighted cost is at least 12%–13% (Klein, 1997). Since the return on investment should be higher than weighted cost, and based on China’s economic environment, the reasonable return on investment of a URT PPP project should be 6%–8%. So, the target net real revenue return on investment (ROI) of 6%–8% is assumed in this article. The real net revenue depends on the project’s operational income and cost, with the operational income including ticket income, and other commercial revenue including advertisement, shops, and communication services.

4.1.3 Factors influencing operation risk allocation

A reasonable ORA mechanism could reduce the project risk probability and loss and management cost, which is beneficial for all parties. The ORA results could help promote all parties’ long-term stable cooperation and ensure the sustainable operation of the URT PPP project. Therefore, the participant’s sharing willingness should be taken into full consideration when design the ORA mechanism. Risk allocation should be consistent with controllability, risk loss, affordability, and handling costs (Xu et al., 2012). The more controllability, risk loss, and affordability a participant has, the more risk a participant should share; the more risk handling costs a participant takes on, the lower risk a participant should share. Therefore, the government’s, private companies’, and public’s controllability, risk loss, affordability, and handling costs are taken into account when building an URT PPP project’s ORA model.

Controllability refers to the reduction of project operation risk caused by participants’ joining the alliance. The controllability of the government is reflected in the significance of the construction and operation cost subsidy given by the government to reduce the operation risk of the project. The controllability of private company is reflected in the reduction of project losses due to the addition of social capital. The controllable degree of the public to the project operation risk is reflected in the reduction of the project operation loss due to the public fare payment. According to the “principle of symmetry between risk bearing and controllability,” the higher is the controllability of the sharing subject to the project operation risk, the more the risks it will bear (Phang, 2007; Chan et al., 2011).

Risk loss refers to the loss caused by the failure to implement the project if the participants do not bear the operation risk. According to the “principle of symmetry between risk bearing and loss,” the more obvious is the expected benefits brought by the project, the greater is the loss of participants without undertaking the project operation risk, and the stronger is their willingness to bear the risk (Phang, 2007; Chan et al., 2011).

Affordability refers to the ability to cope with the operational risks of urban rail transit PPP project. The government’s affordability reflects that it has sufficient financial strength to support financial subsidies. The affordability of the private company is reflected in the ability to deal with losses. The public’s affordability is reflected in the public’s ability to pay for ticket prices. According to the operating risk-sharing principle of “the principle of symmetry between risk bearing and bearing capacity,” the stronger the participants’ affordability, the more risks they will bear (Phang, 2007; Chan et al., 2011).

Handling costs refers to the cost of participants to deal with operational risks, including economic cost and time cost. For different risk factors, the response costs of each participant are different. This article only considers the results of the comprehensive response cost of operational risk. The higher the response cost, the lower the response efficiency, and the less operational risk should be borne.

4.2 Shapley model of operation risk allocation

4.2.1 Basic assumptions

To build the ORA model and determine its suitability, there are three assumptions:

1) No big changes in the political and legal environment, making $\theta =\text{0}$.

2) The public, government, and private company are reasonable game agents, and their game behavior follows individual and collective rationality guidelines.

3) Partners’ OR decision behavior is based on controllability, risk loss, affordability, and handling costs:

$\alpha$—controllability, the participants’ controllability and OR having a positive correlation

$\beta$— risk loss, the participants’ risk loss and OR having a positive correlation

$\gamma$—affordability, the participants’ affordability and OR having a positive correlation

$\chi$— handling costs, the participants’ handling costs and OR having a negative correlation

4.2.2 Basic model of operation risk allocation

The ORA model is designed to maximize fairness, as fairness is the driving force for participants’ cooperation and sustainable operation of a URT PPP project. This model should meet these constraints:

1) The project OR could be allocated among all participants and meet all participants’ willingness.

2) The allocation result is a function of individual and collective rationality, and all parties are cooperative.

Accordingly, the objective function and constraints are as follows:

$\min G(G>0)(2)$

$s.t{\displaystyle \sum _{i\in N}{R}_i}=r\left(N\right).(3)$

$R_i\le r_i,\mathrm{\&}r\left(N\right)<r\left(S\right),\forall S\subset N$

Eq. 2 indicates that the goal is to minimize the fair index $G$. Eq. 3 is not only a cooperative economic efficiency requirement but also the collective rationality condition known as Pareto-optimal conditions, that is, the total OR should be fully allocated among the participants, and the sum of distribution of all participants should be equal to the total OR.

The co-allocation of OR should be required to meet the individual rationality, also known as the individual rationality conditions, the participant-$i$, the final amount allocated to the participant ($R_i$) is less than the participant’s personal $i$ alone ($r_i$). The OR of alliance $N$ is less than the OR of alliance, where $S$ is all the subset that $N$ contains.

Based on the Shapley value, Eq 4 shows the risk share of the alliance ($N$) participants:

$R_i={\displaystyle \sum _{S\subseteq N}\frac{(n-k)!(k-1)!}{n!}}[r\left(S\right)-r(S/\left\{i\right\})],i=\left(\mathrm{1,2,3}\right).(4)$

Since the total number of $n$ individual-players is $n!$,the corresponding distribution of the program also has $n!$ species. $k$ is the number of elements in a subset of $S$. $r\left(S\right)$ reflects the OR of the small alliance-$S$. According to Eq. 1, $r\left(S\right)$ is the discrepancy between the target net revenue and real net revenue ($W_0$) of the alliance-$S$ during the franchise period, as shown in Eq. 5. $Q_S$ is total revenue of the alliance-$S$. $C_S$ is total cost of the alliance-$S$. $r(S/i)$ reflects when the participant-$i$ breaks the alliance, and thus the OR of the small alliance-$S$.

$r\left(S\right)=(Q_S-C_S)-W_0.(5)$

The Shapley value is based on the players’ expected contribution to OR. The higher a participant’s OR controllability, the more OR of that participants should take. Importantly, this model only reflects participants’ OR controllability, whereas participants’ ORA willingness was not taken into consideration. ORA willingness is also influenced by their controllability, risk loss, affordability, and handling costs, so it is necessary to further revise this model.

4.2.3 Further revision of the Shapley model

The revising factors are set as follows:

$H=\left\{\beta \gamma \chi \right\}.$

According to Table 1, the revising factors matrix $A$ of ORA is:

$A=\left[\begin{array}{ccc}{\beta }_1& {\gamma }_1& {\chi }_1\\ {\beta }_2& {\gamma }_2& {\chi }_2\\ {\beta }_3& {\gamma }_3& {\chi }_3\end{array}\right].(6)$

TABLE 1

TABLE 1. Measures used to revise the Shapley model.

Then, the normalization process is carried out for matrix $A$, resulting in matrix $B={\left(b_{ij}\right)}_{3\times 3}$.

Next, the integrated effects for the PPP project are set as:

$\lambda ={\left[\begin{array}{ccc}{\lambda }_1& {\lambda }_2& {\lambda }_3\end{array}\right]}^T,(7)$

$B\times \lambda ={\left[\begin{array}{ccc}{\psi }_1& {\psi }_2& {\psi }_3\end{array}\right]}^T,(8)$

where ${\lambda }_1$ is the integrated effect of risk loss on the ORA of PPP project;

${\lambda }_2$ is the integrated effect of affordability on the ORA of PPP project;

${\lambda }_3$ is the integrated effect of handling costs on the ORA of PPP project;

${\psi }_1$ is the integrated effect of all factors (risk loss, affordability, and handling costs) influencing the government’s ORA behavior;

${\psi }_2$ is the integrated effect of all factors (risk loss, affordability, and handling costs) influencing the private company’s ORA behavior;

${\psi }_3$ is the integrated effect of all factors (risk loss, affordability, and handling costs) influencing the public’s ORA behavior.

After fully considering participants’ risk loss, affordability, and handling costs, the Shapley value is revised as the following:

$R_i={R^{\prime }}_i+\left({\psi }_i-\frac{1}{n}\right)\times r\left(N\right).(9)$

4.3 Fairness and stability of the allocation

The allocation result undergoes further analysis regarding fairness and stability by the fair and fission indexes, respectively. First, to measure participant’s significance for the ORA, the Shapley–Shubik power index is used:

${\delta }_i=\frac{R_i-r_i}{{\displaystyle \sum _{i\in N}(R_i-r_i)}},{\displaystyle \sum _{i=1}^3{\delta }_i}=1.(10)$

The larger the Shapley–Shubik power index-${\delta }_i$is, the higher importance subject-$i$ has for ORA.

The fair index is calculated by the coefficient of variation of the Shapley–Shubik power index:

$G=\frac{\sigma }{\overline{\delta }},\overline{\delta }=\frac{1}{3}{\displaystyle \sum _{i=1}^3{\delta }_i},\sigma =\sqrt{\frac{1}{3}({\displaystyle \sum _1^3{({\delta }_i-\overline{\delta })}^2})}.(11)$

According to the objective function, when the fair index $G$ is closer to zero, which means the three participants’ Shapley–Shubik power values are more similar, allocation is fairer.

To analyze whether participants would break the agreement of the ORA scheme, the fission index was proposed to analyze the allocation stability (Mandriperrott and Menzies, 2010). The fission index $P{D}_i$ can be calculated by the follow formula:

$P{D}_i=\frac{{\displaystyle \sum _{j\ne i}{R}_j-r(S/i)}}{R_i-r_i}.(12)$

${\displaystyle \sum _{j\ne i}{R}_j}$ reflects when others cooperate and form alliance-$N$, and is the sum of all other participants’ OR except participant-$i$.

$r(S/i)$ reflects when the participant-$i$ breaks the alliance, and thus the OR of the small alliance-$S$.

If $P{D}_i>1$, participant-$i$ would drop out of alliance-$N$, and the cooperation alliance is not stable.

5 Case study of Beijing metro line 4

5.1 Introduction

The Beijing Metro Line 4 PPP project is the first URT PPP project in China and has attracted much attention. Most project operation data can be acquired by its Weibo and other sources, so data are more available than for other URT projects. Beijing Metro Line 4 is 28.6 km in length. The construction investment of this project was 153 billion yuan, 70% (107 billion yuan) funded by the government, and 30% (46 billion yuan) funded by Beijing MTR Corporation—a franchised company for 30 years. Beijing MTR Corporation is responsible for updating and maintaining project facilities. In the early stages of operation, to ensure public welfare and reasonable profit for the company, the government subsided project operation losses in full; this degree of risk allocation is unsustainable. This problem led to the “Beijing Metro Fares Reform” in 2014. It suggested the traditional model of government assuming all operation risk is an inherent problem, and OR is needed to be allocated more evenly.

5.2 Operation risk allocation scheme of the Beijing metro line 4 project

5.2.1 Calculating operation risk based on costs and revenue

Because Beijing Metro Line 4 is in the franchise period, the Beijing MTR Corporation has not released cost information. Therefore, costs are based on reference data of the “Urban Rail Transit Cost Analysis” from China’s transport price research center of Beijing Jiaotong University (Xu et al., 2010). The 30-years total cost including construction and operation is 35.55 billion yuan, thus an estimated annual cost of about 1.2 billion yuan.

Revenue includes the ticket and other operational revenue including advertising, communication, and metro store rent (these could be 10% of ticket revenue). The total revenue is calculated by:

$TR=AP\times F\times 1.1,$

where $TR$ is total revenue, $AP$ is average ticket price, and $F$ is metro passenger flow.

Before the 2014 reform, tickets cost the same as a bus ticket, that is, 2 yuan; this did not reflect the overall OR risk. Thus, we assumed the 2 yuan metro ticket as a no-risk ticket price $P\prime$, that is, $P\prime =2$ yuan. Since the metro is more convenient than the bus, a 3 yuan ticket is established as a “partial-risk” ticket price $P″$. These two prices are defaults for Shapley value calculation. The true risk ticket price is adjusted based on the partial-risk ticket price considering the participants’ controllability, risk loss, affordability, and handling costs.

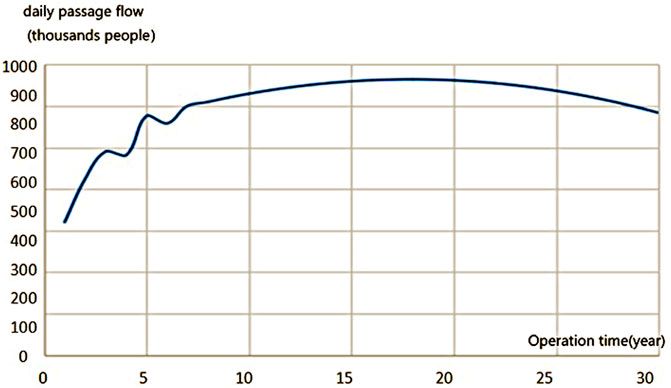
Metro passenger flow has characteristics of an S-shaped curve; as the metro passenger flow grows, it will not continue to increase because of congestion, mechanical failure, and new line shunts. Common S-shaped curve prediction models include the exponential, Gomperz curve, logistic growth, and multiplication curve. Model fitting was based on prediction data of the MVA company (Table2). Then, according to the “most relevant” principle, the multiplication curve model was selected (with a relative index 0.9023, higher than other three prediction models). The fitting model can be described as y = -0.1.105x²+39.587x+573.95, shown in Figure 3.

TABLE 2

TABLE 2. Prediction data for Beijing Metro Line 4.

FIGURE 3

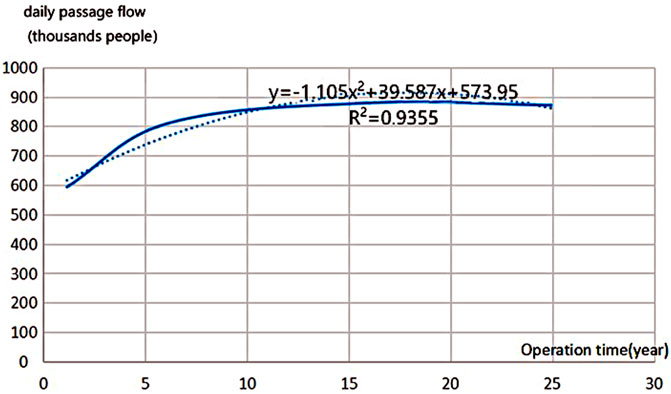
FIGURE 3. Prediction (solid line) and fitting (dotted line) curves of Beijing Metro Line 4 passenger flow.

Actual passenger flow exceeded the prediction passenger flow after 10 years of operation, so the fitting model needed to be adjusted according to the actual passenger flow (Figure 4). The actual passenger flow data is collected from the Beijing MTR Corporation official Weibo.

FIGURE 4

FIGURE 4. Passenger flow of Beijing Metro Line 4 project.

The passenger flow prediction model can be described as y = −1.768x² + 65.254x + 756.27 and its relative index 0.95. According to the forecasting model, the total passenger flow will be 13.254 billion passengers. Since this is a one ticket transfer and needs to be split with other lines, when the ticket is 2 yuan per person, the sharing revenue is 1.04 yuan, and total revenue of 30 years:

$Q\prime =1.04\times 13.254\times 1.1=15.158$ billion yuan.

When the ticket is 3 yuan per person, the sharing revenue is 1.56 yuan, so the total revenue and the real net revenue of 30 years are:

$Q″=1.56\times 13.254\times 1.1=22.744$ billion yuan.

$W=22.744-35.555=-12.822$ billion yuan.

Assuming the reasonable ROI of 6% (see the justification of this assumption previously), the target return of is about 47.79 billion yuan, and the actual ROI for the private company is 9%—thus meeting the private company’ expectations. According to the target ROI of 6%, the target net revenue is:

$W_0=47.79-35.55=12.24$ billion yuan.

Therefore, the operation risk value is:

$r=r\left(N\right)=(W-W_0)-\vartheta =(-12.822-12.24)-0=-25.042$ billion yuan.

5.2.2 Calculating project operation risk allocation

To calculate the ORA values of the government, private company, and public, we calculate the Shapley value of per participant operation risk based on controllability $\alpha$. Then, further considering factors of willingness of controllability $\alpha$, risk loss $\beta$, affordability $\gamma$, and handling costs $\vartheta$, the Shapley value is adjusted.

According to data from 5.2.1, the risk payoff function $r\left(S\right)$ under different cooperation levels can be:

If the government, the private company, and public do not cooperate, and there is no operation risk, so $r\left(0\right)=0$.

If the project is constructed and operated by the government alone, total cost may be 50 billion yuan. When the public do not take any operation risk, which means the public pays the no-risk ticket price $P\prime =2$ yuan, the government’s operation risk would be −47.06 billion yuan:

$r_1=r\left(\left\{1\right\}\right)=Q\prime -50{-\text{W}}_{\text{0}}=15.158-50-12.22=-47.062$ billion yuan.

If the project is constructed and operated by the private company alone, the total cost would be 40 billion yuan, with the no-risk ticket price $P\prime =2$ yuan, and the private company’s operation risk would be −37.06 billion yuan:

$r_2=r\left(\left\{2\right\}\right)=Q\prime -40-W_0=15.158-40-12.22=-37.062$ billion yuan.

If the project operation risk is taken by the public alone, the public’s operation risk would also be 47.79 billion yuan:

$r_3=r\left(\left\{3\right\}\right)=-47.79$ billion yuan.

If the government and private company cooperate, and the public do not take any operation risk (the ticket is $P_{\alpha }=2$ yuan):

$r\left(\mathrm{1,2}\right)=Q\prime -35.55-W_0=15.158-35.55-12.22=-32.612$ billion yuan.

If the government constructs and operates the project by itself, and the public is willing to take part of the operation risk (the ticket is $P″=3$ yuan):

$r\left(\mathrm{1,3}\right)=Q″-50-W_0=22.744-50-12.22=-39.476$ billion yuan.

If the project is constructed and operated by the private company, and the public is willing to take part of the operation risk:

$r\left(\mathrm{2,3}\right)=Q″-40{-\text{W}}_{\text{0}}=22.744-40-12.22=-29.476$ billion yuan.

When all participants (the government, private company, and public) cooperate, the project is a full PPP model, and the public pays the partial-risk ticket price $P″=3$ yuan, the operation risk payoff function is $r\left(\mathrm{1,2,3}\right)=r\left(N\right)=-25.042$ billion yuan.

According to the aforementioned OR payoff function and Eq. 4 in Section 4.2.2, the total OR for the government is:

$\begin{array}{l}R\left(1\right)=\frac{2!\times 0!}{3!}(r\left(1\right)-r\left(0\right))+\frac{1!\times 1!}{3!}(r\left(\mathrm{1,2}\right)-r\left(2\right))+\frac{1!\times 1!}{3!}(r\left(\mathrm{1,3}\right)-r\left(3\right))+\frac{0!\times 2!}{3!}(r\left(\mathrm{1,2,3}\right)-r\left(\mathrm{2,3}\right))\\ =\frac{2}{6}\times (-47.062-0)+\frac{1}{6}\times (-32.612+37.062)+\frac{1}{6}\times (-39.476+47.79)+\frac{2}{6}\times (-25.042+29.476)\\ =-12.102\text{billion yuan}\end{array}$

The total OR for the private company is:

$\begin{array}{l}R\left(2\right)=\frac{2!\times 0!}{3!}(r\left(2\right)-r\left(0\right))+\frac{1!\times 1!}{3!}(r\left(\mathrm{1,2}\right)-r\left(1\right))+\frac{1!\times 1!}{3!}(r\left(\mathrm{2,3}\right)-r\left(3\right))+\frac{0!\times 2!}{3!}(r\left(\mathrm{1,2,3}\right)-r\left(\mathrm{1,3}\right))\\ =\frac{2}{6}\times (-37.062-0)+\frac{1}{6}\times (-32.612+47.062)+\frac{1}{6}\times (-29.476+47.79)+\frac{2}{6}\times (-25.042+39.476)\\ =-2.083\text{billion}\text{yuan}\end{array}$

The total OR for the public is:

$\begin{array}{l}R\left(3\right)=\frac{2!\times 0!}{3!}(r\left(3\right)-r\left(0\right))+\frac{1!\times 1!}{3!}(r\left(\mathrm{1,3}\right)-r\left(1\right))+\frac{1!\times 1!}{3!}(r\left(\mathrm{2,3}\right)-r\left(2\right))+\frac{0!\times 2!}{3!}(r\left(\mathrm{1,2,3}\right)-r\left(\mathrm{1,2}\right))\\ =\frac{2}{6}\times (-47.79-0)+\frac{1}{6}\times (-39.476+47.062)+\frac{1}{6}\times (-29.476+37.062)+\frac{2}{6}\times (-25.042+32.612)\\ =-10.857\text{billion yuan}\end{array}$

The total operation risk for the government is −12.102 billion yuan, for the private company −2.083 billion yuan, and −10.857 billion yuan for the public. Compared with $r_i$, $R\left(i\right)$ is significantly higher, which indicates that cooperation can effectively reduce the risks of all parties.

According to 4.5 Eqs 10–12, the Shapley–Shubik power index ${\delta }_i$, fair index $G$, and fission index $P{D}_i$ are as follows:

${\delta }_1=\frac{R_1-r_1}{(R_1-r_1)+(R_2-r_2)+(R_3-r_3)}=0.327,{\delta }_2=0.327,{\delta }_3=0.346,$

$\overline{\delta }=0.33,\sigma \approx 0.0006,G=\frac{\sigma }{\overline{\delta }}\approx 0,$

$P{D}_1=\frac{(R_2+R_3)-r\left(\mathrm{2,3}\right)}{R_1-r_1}=0.47,P{D}_2=0.47,P{D}_3=\mathrm{0.50.}$

$G$ is closer to zero, which means allocation is fairer. All participants’ fission index values are $P{D}_i<1$, which means the cooperation alliance is stable.

5.2.3 Revising the operation risk allocation shapley value

According to the revision model described in Section 4.2.3, risk loss, affordability, and handing costs need to be considered, integrated as effect-${\psi }_i$. To measure the risk-sharing willingness of parties in Beijing Metro Line 4, the expert interview method was used to obtain the scores of the three sharing factors (risk loss, affordability, and handing costs) of the government, private company, and public. A total of 10 professionals experienced in the URT PPP project were interviewed. The 10 professionals consisted of two government officials, three contractors, two consultation managers, and three professors. Each expert’s interview lasted about 30 min. All the factors were measured by the Likert’s five point measurement method, that is, “1” to “5,” respectively, to indicate the importance of interest demands to the interviewees. Among them, 1 point means “very small,” 2 points means “small,” 3 points means “general,” 4 points means “large,” and 5 points means “very large.” Table 3 shows the ORA influence factor scores that is the weighted average value after the highest score and the lowest score are removed.

TABLE 3

TABLE 3. Sharing willingness score of the government, private company, and public.

Because participants’ risk loss is inversely proportional to operational risk-taking, the following is calculated:

$\chi \stackrel{\mathrm{ }}{\to }\frac{1}{\chi },\chi =\left[\begin{array}{ccc}3.0& 2.5& 3.5\end{array}\right]\stackrel{\frac{1}{\chi }}{\to }\left[\begin{array}{ccc}0.33& 0.40& 0.29\end{array}\right].$

When $\frac{1}{\chi }$ is directly proportional to the operation risk-taking, we then calculate: $u_{ij}=\frac{u_{ij}}{{\displaystyle \sum _{i=1}^3{u}_{ij}}}$ (i,j = 1,2,3) (see Table 3).

Table 4 is transformed to matrix $B$, which represents the influence value of risk loss, affordability, and handling costs:

$B=\left[\begin{array}{ccc}0.45& 0.43& 0.35\\ 0.31& 0.37& 0.43\\ 0.24& 0.20& 0.22\end{array}\right].$

The analytic hierarchy process (AHP) is used to measure the integrated effect, $\lambda$, by expert interviews (Table 5).

TABLE 4

TABLE 4. Sharing willingness score standardization of the government, private company, and public.

TABLE 5

TABLE 5. Judgment matrix based on expert interviews.

Which translates to:

$C=\left[\begin{array}{ccc}\beta & \gamma & \vartheta \end{array}\right]=\left[\begin{array}{ccc}1& 3& 4\\ 1/3& 1& 2\\ 1/4& 1/2& 1\end{array}\right],$

With the column normalization $u_{ij}=\frac{u_{ij}}{{\displaystyle \sum _{i=1}^3{u}_{ij}}}$ (i, j = 1,2,3), matrix $C\prime$ results in:

$C^{\prime }=\left[\begin{array}{ccc}0.632& 0.667& 0.571\\ 0.209& 0.222& 0.285\\ 0.159& 0.111& 0.144\end{array}\right].$

According to matrix $C\prime$, the weight vectors (eigenvalues) can be derived from line normalization processing $u_{ij}=\frac{u_{ij}}{{\displaystyle \sum _{j=1}^3{u}_{ij}}}$ (i, j = 1,2,3):

$\lambda =\left[\begin{array}{c}0.623\\ 0.239\\ 0.138\end{array}\right].$

The consistency check is based on the eigenvalues, using $\lambda \times W$, as follows:

$\lambda \times W=\left[\begin{array}{ccc}1& 3& 5\\ 1/3& 1& 3\\ 1/5& 1/3& 1\end{array}\right]\times \left[\begin{array}{c}0.623\\ 0.239\\ 0.138\end{array}\right]=\left[\begin{array}{c}1.892\\ 0.239\\ 0.138\end{array}\right].$

According the consistency check method of AHP:

${\zeta }_{\max }={\displaystyle \sum _{i=1}^3\frac{{\left(CW\right)}_i}{3W_i}}=3\text{.}018$

$CI=\frac{{\zeta }_{\max }-n}{n-1}=\frac{3.018-3}{3-1}=\mathrm{0.009.}$

The consistency check formula is $CR=\frac{CI}{RI}$, with $RI$ as the freedom index, shown in Table 6.

TABLE 6

TABLE 6. Freedom index.

In this study, n = 3, so $CI=0.015<0.1$, which means the index value through consistency check, and the eigenvalues $W$ is effective, and according to 4.4.3 Eq. 8:

$\left[\begin{array}{ccc}0.45& 0.43& 0.35\\ 0.31& 0.37& 0.43\\ 0.24& 0.20& 0.22\end{array}\right]\times \left[\begin{array}{c}0.623\\ 0.239\\ 0.138\end{array}\right]=\left[\begin{array}{c}0.431\\ 0.341\\ 0.228\end{array}\right].$

The aforementioned results show that the integrated effect of these three factors for the government is 0.431, for the private company 0.341, and 0.228 for the public.

According to the revised model (Eq. 8), when considering the three additional factors, the ORA Shapley value is revised as:

$R\prime \left(1\right)=-12.102+(0.34-\frac{1}{3})\times -25.042=-12.252$ billion yuan.

$R\prime \left(2\right)=-2.083+(0.289-\frac{1}{3})\times -25.042=-0.981$ billion yuan.

$R\prime \left(3\right)=10.857+(0.371-\frac{1}{3})\times -25.042=-11.809$ billion yuan.

After revising the ORA Shapley value and fully considering the participants’ willingness, the operation risk value of the government should be 12.252 billion yuan, the private company 0.981 billion yuan, and the public 11.809 billion yuan. Then the Shapley–Shubik power index ${\delta }_i$, fair index $G$, and fission index $P{D}_i$ are as follows:

$\delta {\prime }_1=\frac{R{\prime }_1-r_1}{(R{\prime }_1-r_1)+(R{\prime }_2-r_2)+(R{\prime }_3-r_3)}=0.326,\delta {\prime }_2=0.338,\delta {\prime }_3=0.336,$

$\overline{\delta }\prime =0.33,\sigma \prime \approx 0.0006,G\prime =\frac{\sigma \prime }{\overline{\delta \prime }}\approx 0,$

$PD{\prime }_1=\frac{(R{\prime }_2+R{\prime }_3)-r\left(\mathrm{2,3}\right)}{R{\prime }_1-r_1}=0.48,PD{\prime }_2=0.43,PD{\prime }_3=\mathrm{0.54.}$

After revising, $G\prime$ is closer to zero and $PD{\prime }_i<1$, which means allocation is fairer and the cooperation alliance is stable.

5.3 operation risk allocation analysis results

5.3.1 Analysis of revising Shapley values

The ORA results show that only when all participants cooperate the project’s operation can be reduced to the minimum, $\forall S\subseteq N$, $r\left(N\right)<r\left(S\right)$. Due to the high construction and operation costs, and low operation revenue, the projects are still at potential operation loss risk, which may be 25.042 billion yuan, $r\left(N\right)=r\left(\mathrm{1,2,3}\right)=-25.042$. If the government and public bear most of the operation risk, the government needs to give subsidies of 12.252 billion yuan, about 0.41 billion yuan per year; the public’ operation risk is about 11.809 billion yuan, so the per capital fares would increase to about 4.55 yuan, which basically agrees with the 4.4 yuan suggested in the 2014 reform plan. The private company will need to take operation risk of 0.981 billion yuan, an annual average operation risk of 32.7 million yuan, which could perhaps be reduced by improving operation and management approaches.

Allocation results consider participants’ controllability, risk loss, affordability, and handling costs. The three participants’ Shapley–Shubik power index values are similar, which suggests their contributions for controlling the project’s operation risk are equally important. The private company and public’s Shapley–Shubik power index values are slightly higher than the government, showing that URT PPP projects sustainable operation relies on the private company’s efficient operation and the public’s ticket revenue contribution, not only the government subsidy. The government’s financial subsidies are not the fundamental driving force for the sustainable operation of projects. The public obtained the lowest operation risk value and the highest fission index, and performed well in the controllability, risk loss and affordability, indicating that the public was capable and necessary in sharing operation risks.

5.3.2 Analysis of fairness and stability

Fair allocation results are critical for PPP stability. The fair index of $G\approx \text{0}$, suggests the allocation result is relatively fair. All participants’ fission index values are $P{D}_i<1$, suggesting stability. The public’s fission index is highest, and the private company’s the lowest, but high construction and operation cost may affect the government’s willingness further. Public expectations are to enjoy quality public services at low cost. In this ORA scheme, if ticket prices are raised, the public’s cooperation willingness would be affected, but cooperation would still be likely. The public fission index is far less than one, indicating that the increase in ticket prices within a certain range was acceptable. The metro makes public transit more convenient, particularly in a super city like Beijing. Therefore, an appropriate increase in ticket prices has little effect on public willingness to cooperate. Combined with the power index, the public’s power index is second only to the government, which means while raising ticket prices is more efficient for reducing overall OR, the public may reconsider full cooperation. With ROI 6%, the private company is willing to bear some operation risk, and their cooperation willingness is relatively high. Since the construction and operation of URT projects can not only improve the quality of public life but also conducive to the sustainable development of urban economy and society, the government has a strong willingness to cooperate.

6 Discussion

6.1 Shapley revision

The Shapley value can only reflect controllability—it is better if the controllability is more. But, using the risk allocation rule, there are three other factors influencing a participant’s allocation behavior, that is, risk loss, affordability, and handling costs. So, the Shapley value was revised considering these factors. Second, as for the revising results, other possibilities are listed in Table 7.

TABLE 7

TABLE 7. Contrast before and after Shapley revisions.

The government, private company and public’s risk loss, affordability, and handling costs were different, so OR shifts from the private company to the public (but the fairness index is close to zero, suggesting the revision still reflects fair allocation). After revision, the private company’s fission index decreased from 0.47 to 0.43, and the private company’s cooperation likelihood thus improved. Conversely, the public’s fission index increased from 0.5 to 0.54, and the cooperation stability had weakened. But all participants’ fission indexes were still less than one, reflecting that even after revision cooperation stability was possible.

6.2 Fair ticket prices

Metro fares are related to people’s livelihood and overall public well-being. According to “The Beijing national economic and social development statistical bulletin in 2014,” Beijing PCDI (per capita disposable income) in 2016 was 52,530 yuan, so monthly PCDI was about 4,377 yuan. If the ticket price is raised to 4.55 yuan, and an average communing cost is 9 yuan a day, a monthly cost of 270 yuan, this would account for 6.2% of their PCDI—this proportion is less than the international commuting cost standard of 11%. But a low-fare metro would require a public financing subsidy. Before the 2014 reform, the subsidy proportion for Beijing was much higher than other large cities like Shanghai, Guangzhou, and Shenzhen; the main reason was that in other cities fares are based on mileage (with a starting fare of 2 yuan). High subsidies, like that in Beijing, would affect other public subsidies, such as public service and health care. Relying too much on a transit subsidy could also lead to inefficiency and corruption, and thus influence social welfare more broadly.

6.3 The significance of research

In terms of theory, the public is included in the scope of risk sharing in urban rail transit PPP projects, breaking through the limitations of traditional research. The study emphasizes the importance of “cooperation,” risk sharing under the premise of cooperation, and advocates compromise and sharing in order to realize the synergy of society’s overall interests and promote the long-term operation of urban rail transit PPP projects. Risk allocation literature in PPP projects focuses on risk allocation between the public and private sectors without taking into account the actual. The public is a direct beneficiary of the operation of an urban rail transit PPP project, and according to the principle of “who benefits, who bears the risk,” the public should bear part of the operation risk of the project. It is a win–win decision for the public to bear some of the project’s operation risk in terms of the sustainable operation of urban rail transit PPP projects. This can not only help to increase the project’s operation efficiency, but it is also a necessity for the sustainable operation of urban rail transit PPP projects. With full consideration of the influencing factors affecting the sharing of operational risks of urban rail transit PPP projects, the Shapley value is improved based on the Shapley value method of the cooperation game to make the model more consistent with the sharing of operational risks of urban rail transit PPP projects. The fairness index and fission index are introduced to quantify and analyze the fairness and stability of the sharing results and improve the scientific and practicality of the model.

In terms of practice, the purpose of this study is to address the issue of sharing the operational risks of urban rail transit PPP projects, so that the results of the sharing can ensure relative fairness while fully mobilizing the cooperation of various stakeholders. It also rationalizes the collaborative relationship between the government, private company, and the public in order to promote the long-term development of PPP urban rail transit projects. The findings indicate that it is both necessary and feasible for the public to bear some operational risk. Low MTR fares do not improve the public’s overall social welfare. Instead, a reasonable increase in fares will not only have no significant impact on the general public’s daily life but will also contribute to the efficient use of government funds. It is unavoidable that an increase in metro fares will face public backlash. Urban rail transit is related to the immediate interests of the public and brings many conveniences to the public’s travel, so the public is also very supportive of the metro’s development (Gao and Lau, 2021). As a public policymaker, the government should give the public reasonable reasons for the fare increase and establish an open and transparent monitoring mechanism to promote the public’s understanding and support for the project’s sustainable operation.

6.4 Suggestions for sustainable development of urban rail transit public–private partnership projects

This study insists on using theory to direct practice and using practical problem-solving as the beginning and end points. Based on the findings of the research and the fundamentals of cooperative games, it aims to maximize total social benefits, stakeholder satisfaction, and sustainable project operation for PPP urban rail transit projects.

First, the government should create an efficient project operation information sharing platform and publish project operation information in real-time. The main content of the information sharing platform is that the rail transit project’s operating company (social capital) should publish actual passenger flow, operating income, and operating cost data such as labor wages and benefits, repair costs, electricity costs, operating costs, depreciation costs, operating costs, management costs, financial costs, business taxes, and surcharges online on a regular basis. Furthermore, the operating company should enter project implementation and the use of subsidy funds into this information platform, which will help government departments conduct audits, settlements, and project supervision and review during the concession period (Xiahou et al., 2022). The goal of developing an efficient information sharing platform for project operation is not only to provide the public with complete information on project cost and revenue but also to reduce information asymmetry between government agencies and operating companies.

Second, the government has to improve the oversight of PPP projects for urban rail transit. Establishing an effective administrative supervision body, defining the supervision boundary and responsibilities of government departments, ensuring the efficacy and uniformity of supervision of urban rail transit PPP projects, and creating a social supervision system for PPP projects are all things that should be carried out. In addition to reflecting the fairness of public participation in project supervision as a key stakeholder of the projects, social supervision is an important assurance to support the improvement of the operational efficiency of urban rail transit PPP projects. In order to broadly accept public opinion, strengthen communication with the public, and to some extent reduce social conflicts brought on by public opinion, it is necessary to establish a public complaint platform for urban rail transit PPP projects and to improve the hearing system for PPP projects.

Finally, novel profit models, to achieve stable target profits and provide reasonable profitability to social capital without profiteering. To reduce construction and operating costs, it is necessary to innovate financing models, reduce financing costs, and strengthen innovation in technology and management. Investigate actively the diversification of revenue sources and the property compensation mechanism of “raising roads with land” on the basis of financial investment and operational compensation. This will stimulate the management potential of social capital on the one hand, and promote the optimization of spatial development in urban areas on the other. The social capital should work to increase the quality of service and draw customers with excellent service as the project’s operator. In addition to assuring passenger flow, it should create businesses like retail and advertising facilities in the station to diversify its revenue streams.

7 Conclusion

The operation risk of URT projects has been a long-running, worldwide problem. This study emphasizes collective rationality and puts forward a fair value of cooperation, so as to realize a “win–win–win” of PPP. The Shapley model can help solve the problem of benefit distribution among partners; however, the Shapley model only reflects the degree of controllability of each contributor to the operation risk. It is necessary to further consider the degree of loss, bearing capacity, and response costs of each contributor to modify the model, so as to make the sharing model more reasonable. Fair and fission index were used to evaluate the results of risk allocation. The revised model was applied to the operational risk allocation of Beijing Metro Line 4. The fair index of $G\approx \text{0}$, suggested the allocation result was relatively fair. All participants’ fission index values were $P{D}_i<1$, suggesting stability. The allocation result indicated that the revised model was reasonable. Although less operational risks were allocated to the public, the public performed well in the controllability, risk loss, and affordability, which revealed that the public played an important role. The results proved that raising ticket prices had significant effect on risk reduction. However, exorbitant ticket prices increased the risk of public non-cooperation. Through game theory modeling of ORA of the PPP project, results show that: 1) it is reasonable to improve the Shapley model by fully considering the factors that affect risk sharing of all participants; 2) it is necessary and feasible to raise ticket prices and let the public bear part of the operational risk of the project; and 3) to control the operation risk of URT PPP project, first rely on efficient operation of private enterprises and, the contribution of public ticket revenue, and then rely on government subsidies. Under the condition of limited operating income and difficult cost control of urban rail transit project, reasonable allocation of operating risk is the key to sustainable operation of the project (Klein, 1997). The public contribution to operational risk allocation should be valued.

Real operation data are difficult to obtain. Therefore, this article is mainly based on the research results of previous studies: the feasibility study of Line 4, the ticket price cost review by Beijing rail transit published by Beijing Municipal Development and Reform Commission, and the passenger flow data published by Beijing Hong Kong Metro. Therefore, the project operation risk calculated based on these methods needs to be further verified according to additional empirical data. At the same time, there are information asymmetries in the practice process of PPP project among participants, which will affect the risk allocation. Further study is necessary on ORA under asymmetric information, which is of great significance for sustainable implementation of URT PPP projects. Apart from the government, private enterprises, and the public mentioned in the study, it also includes banks, financial institutions, consulting institutions, regulatory authorities, and so on for the PPP project of urban rail transit, but because the government, private enterprises, and the public are direct stakeholders, this article only considers risk allocation among them, without considering other stakeholders. This could be the next research topic, which is crucial to the risk allocation of PPP projects.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, PX and QJ; methodology, QZ; validation, QZ and ZL; formal analysis, QJ and QZ; investigation, ZL; data curation, QZ and QJ; writing—original draft preparation, QZ; writing—review and editing, QZ; supervision, PX. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Fundamental Research Funds for the Central Universities, Grant Number 2022CDJSKJC18.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadabadi, A. A., and Heravi, G. (2019). The effect of critical success factors on project success in public-private partnership projects: A case study of highway projects in Iran. Transp. policy 73 (JAN.), 152–161. doi:10.1016/j.tranpol.2018.07.004

CrossRef Full Text | Google Scholar

Aldrete, R., Bujanda, A., and Valdez, G. A. (2018). Valuing public-sector revenue risk exposure in transportation public–private partnerships. Transp. Res. Rec. J. Transp. Res. Board 2297 (1), 88. doi:10.3141/2297-11

CrossRef Full Text | Google Scholar

Aziz, A. M. A. (2011). Successful delivery of public-private partnerships for infrastructure development. J. Constr. Eng. Manag. 133 (12), 918–931. doi:10.1061/(ASCE)0733-9364(2007)133:12(918)

CrossRef Full Text | Google Scholar

Bing, L., Akintoye, A., Edwards, P. J., and Hardcastle, C. (2005). The allocation of risk in PPP/PFI construction projects in the UK. Int. J. Proj. Manag. 23 (1), 25–35. doi:10.1016/j.ijproman.2004.04.006

CrossRef Full Text | Google Scholar

Carpintero, S., and Petersen, O. H. (2015). Bundling and unbundling in public-private partnerships: Implications for risk sharing in urban transport projects. Proj. Manag. J. 46 (4), 35–46. doi:10.1002/pmj.21508

CrossRef Full Text | Google Scholar

Carpintero, S., and Petersen, O. H. (2014). PPP projects in transport: Evidence from light rail projects in Spain. Public Money & Manag. 34 (1), 43–50. doi:10.1080/09540962.2014.865935

CrossRef Full Text | Google Scholar

Chou, J.-S., Tserng, H. P., Lin, C., and Yeh, C.-P. (2012). Critical factors and risk allocation for PPP policy: Comparison between HSR and general infrastructure projects. Transp. Policy 22 (3), 36–48. doi:10.1016/j.tranpol.2012.05.009

CrossRef Full Text | Google Scholar

Chan, A., Yeung, J., Yu, C., Wang, S. Q., and Ke, Y. (2011). Empirical study of risk assessment and allocation of public-private partnership projects in China. J. Manage. Eng. 27 (3), 136–148. doi:10.1061/(asce)me.1943-5479.0000049

CrossRef Full Text | Google Scholar

Gao, Y., and Lau, C. K. (2021). Risk assessment of urban rail transit project using interpretative structural modelling: Evidence from China. Math. Problems Eng. 2021, 1–10. doi:10.1155/2021/5581686

CrossRef Full Text | Google Scholar

Gately, D. (1974). Sharing the gains from regional cooperation: A game theoretic application to planning investment in electric power. Int. Econ. Rev. 15 (1), 195. doi:10.2307/2526099

CrossRef Full Text | Google Scholar

Gong, X., Currie, G., Liu, Z., and Guo, X. (2018). A disaggregate study of urban rail transit feeder transfer penalties including weather effects. Transportation 45 (5), 1319–1349. doi:10.1007/s11116-017-9768-0

CrossRef Full Text | Google Scholar

Hu, X., Li, X., and Huang, Y. (2016). Urban rail transit risk evaluation with incomplete information. Procedia Eng. 137, 467–477. doi:10.1016/j.proeng.2016.01.282

CrossRef Full Text | Google Scholar

Hua, G (2011). “Study on PPP contract-models for urban rail transit(URT) projects in China,” in International Conference on Advances in Education & Management, Dalian, China, 6-7 August, 2011.

CrossRef Full Text | Google Scholar

Huang, W., Shuai, B., Sun, Y., Wang, Y., and Antwi, E. (2018). Using entropy-TOPSIS method to evaluate urban rail transit system operation performance: The China case. Transp. Res. Part A Policy Pract. 111 (MAY), 292–303. doi:10.1016/j.tra.2018.03.025

CrossRef Full Text | Google Scholar

Javed, A. A., Lam, P. T. I., and Chan, A. P. C. (2014). Change negotiation in public-private partnership projects through output specifications: An experimental approach based on game theory. Constr. Manag. Econ. 32 (4), 323–348. doi:10.1080/01446193.2014.895846

CrossRef Full Text | Google Scholar

Ji, Y., Fan, Y., Ermagun, A., Cao, X., Wang, W., Das, K., et al. (2017). Public bicycle as a feeder mode to rail transit in China: The role of gender, age, income, trip purpose, and bicycle theft experience. Int. J. Sustain. Transp. 11 (1-5), 308–317. doi:10.1080/15568318.2016.1253802

CrossRef Full Text | Google Scholar

Jin, X. H., and Zhang, G. (2011). Modelling optimal risk allocation in PPP projects using artificial neural networks. Int. J. Proj. Manag. 29 (5), 591–603. doi:10.1016/j.ijproman.2010.07.011

CrossRef Full Text | Google Scholar

Ke, F., Wang, S., Wu, C., Xia, G., and Hu, W. (2019). Optimization of concession period for public private partnership toll roads. Eng. Econ. 30 (1), 24–31. doi:10.5755/j01.ee.30.1.19215

CrossRef Full Text | Google Scholar

Ke, Y., Wang, S. Q., Chan, A., and Cheung, E. (2011). Understanding the risks in China's ppp projects: Ranking of their probability and consequence. Eng. Constr. Archit. Manag. 18 (5), 481–496. doi:10.1108/09699981111165176

CrossRef Full Text | Google Scholar

Klein, M. (1997). Managing guarantee programs in support of infrastructure investment. Washington, DC: World Bank Publications. Vol. 1812.

Google Scholar

Lam, K. C., Wang, D., Lee, P. T. K., and Tsang, Y. T. (2007). Modelling risk allocation decision in construction contracts. Int. J. Proj. Manag. 25 (5), 485–493. doi:10.1016/j.ijproman.2006.11.005

CrossRef Full Text | Google Scholar

Li, Y., Wang, X., and Wang, Y. (2017). Using bargaining game theory for risk allocation of public-private partnership projects: Insights from different alternating offer sequences of participants. J. Constr. Eng. Manag. 143 (3), 04016102. doi:10.1061/(asce)co.1943-7862.0001249

CrossRef Full Text | Google Scholar

Lv, J., Zhang, Y. Y., and Zhou, W. (2020). Alternative model to determine the optimal government subsidies in construction stage of PPP rail transit projects under dynamic uncertainties. Math. Problems Eng. 2020 (2), 1–12. doi:10.1155/2020/3928463

CrossRef Full Text | Google Scholar

Ma, G., Du, Q., and Wang, K. (2018). A concession period and price determination model for PPP projects: Based on real options and risk allocation. Sustainability 10 (3), 706. doi:10.3390/su10030706

CrossRef Full Text | Google Scholar

Mahdinia, M., Yarandi, M. S., Jafarinia, E., and Soltanzadeh, A. (2021). Development of a new technique for safety risk assessment in construction projects based on fuzzy analytic hierarchy process. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 7 (3), 04021037. doi:10.1061/ajrua6.0001157

CrossRef Full Text | Google Scholar

Mandriperrott, C., and Menzies, I. (2010). Private sector participation in light rail-light metro transit initiatives. Washington, DC: World Bank Publications.

Google Scholar

Maschler, M., and Owen, G. (1992). “The consistent shapley value for games without side payments,” in Rational interaction. Editor R. Selten (Berlin, Heidelberg: Springer). doi:10.1007/978-3-662-09664-2_2

CrossRef Full Text | Google Scholar

Medda, F. (2007). A game theory approach for the allocation of risks in transport public private partnerships. Int. J. Proj. Manag. 25 (3), 213–218. doi:10.1016/j.ijproman.2006.06.003

CrossRef Full Text | Google Scholar

Neto, D. d. C. e. S., Cruz, C. O., Rodrigues, F., and Silva, P. (2016). Bibliometric analysis of PPP and PFI literature: Overview of 25 Years of research. J. Constr. Eng. Manag. 142 (10), 06016002.1–06016002.8. doi:10.1061/(ASCE)CO.1943-7862.0001163

CrossRef Full Text | Google Scholar

Nguyen, D. A., Michael, G. J., and Gonzalez, E. E. (2018). Risk allocation in US public-private partnership highway project contracts. J. Constr. Eng. Manag. 144 (5), 4018017. doi:10.1061/(asce)co.1943-7862.0001465

CrossRef Full Text | Google Scholar

Phang, S. Y. (2007). Urban rail transit PPPs: Survey and risk assessment of recent strategies. Transp. Policy 14 (3), 214–231. doi:10.1016/j.tranpol.2007.02.001

CrossRef Full Text | Google Scholar

Ridgeway, G., and MacDonald, J. M. (2017). Effect of rail transit on crime: A study of los angeles from 1988 to 2014. J. Quant. Criminol. 33 (2), 277–291. doi:10.1007/s10940-016-9296-7

CrossRef Full Text | Google Scholar

Robert, O. K., and Chan, A. P. C. (2015). Review of studies on the critical success factors for public–private partnership (PPP) projects from 1990 to 2013. Int. J. Proj. Manag. 33 (6), 1335–1346. doi:10.1016/j.ijproman.2015.02.008

CrossRef Full Text | Google Scholar

Shen, L. Y., Bao, H. J., Wu, Y. Z., and Lu, W. S. (2007). Using bargaining-game theory for negotiating concession period for BOT-type contract. J. Constr. Eng. Manag. 133 (5), 385–392. doi:10.1061/(asce)0733-9364(2007)133:5(385)

CrossRef Full Text | Google Scholar

Shrestha, A., Chan, T. K., Aibinu, A. A., Chen, C., and Martek, I. (2018). Risk allocation inefficiencies in Chinese PPP water projects. J. Constr. Eng. Manag. 144 (4), 10. doi:10.1061/(asce)co.1943-7862.0001457

CrossRef Full Text | Google Scholar

Siemiatycki, M., and Friedman, J. (2012). The trade-offs of transferring demand risk on urban transit public–private partnerships. Public Works Manag. Policy 17 (3), 283–302. doi:10.1177/1087724x12436993

CrossRef Full Text | Google Scholar

Sophie, S. (2017). Swimming or drowning in the depths of partnership. Aust. J. Public Adm. 76 (3), 288–300. doi:10.1111/1467-8500.12241

CrossRef Full Text | Google Scholar

Trujillo, L., Inchausti-Sintes, F., Campos, J., and Manrique-de-Lara-Peate, C. (2018). Explaining success and failures in PPP transport projects: An econometric approach. Eur. J. Transp. Infrastructure Res. 18 (4), 569–583.

Google Scholar

Valipour, A., Yahaya, N., Noor, N. M., Valipour, I., and Tamošaitienė, J. (2019). A swara-copras approach to the allocation of risk in water and sewerage public–private partnership projects in Malaysia. Int. J. Strategic Prop. Manag. 23 (4), 269–283. doi:10.3846/ijspm.2019.8066

CrossRef Full Text | Google Scholar

Vecchi, V. (2018). “The key element of PPP: Risk,” in Public-private partnerships in health: Improving infrastructure and technology. Editors V. Vecchi, and M. Hellowell (Cham: Springer International Publishing), 43–64.

CrossRef Full Text | Google Scholar

Witt, E., and Liias, R. (2011). Comparing risk transfers under different procurement arrangements/rizikos perkėlimo, taikant skirtingas pirkimų tvarkas, palyginimas. Int. J. Strategic Prop. Manag. 15 (2), 173–188. doi:10.3846/1648715x.2011.582750

CrossRef Full Text | Google Scholar

World Bank (2017). Railway reform: Toolkit for improving rail sector performance. World Bank.

Google Scholar

Xiahou, X., Tang, L., Yuan, J., Zuo, J., and Li, Q. (2022). Exploring social impacts of urban rail transit ppp projects: Towards dynamic social change from the stakeholder perspective. Environ. Impact Assess. Rev. 93, 106700. doi:10.1016/j.eiar.2021.106700

CrossRef Full Text | Google Scholar

Xu, H., Jiao, L., Chen, S., Deng, M., and Shen, N. (2018). An innovative approach to determining high-risk nodes in a complex urban rail transit station: A perspective of promoting urban sustainability. Sustainability 10 (7), 2456. doi:10.3390/su10072456

CrossRef Full Text | Google Scholar

Xu, H., and Li, Q. (2010). “The game theory analysis of risk share for PPP project based on Shapley value,” in 2010 2nd IEEE International Conference on Information Management and Engineering, Chengdu, China, 16-18 April 2010.

Google Scholar

Xu, Y., Skibniewski, M. J., Zhang, Y., Chan, A. P. C., and Yeung, J. F. Y. (2012). Developing a concession pricing model for PPP highway projects. Int. J. Strategic Prop. Manag. 16 (2), 201–217. doi:10.3846/1648715x.2012.688071

CrossRef Full Text | Google Scholar

Xu, Y., Yeung, J., Chan, A., Chan, D., Shou, Q. W., Ke, Y., et al. (2010). Developing a risk assessment model for ppp projects in China — A fuzzy synthetic evaluation approach. Automation Constr. 19 (7), 929–943. doi:10.1016/j.autcon.2010.06.006

CrossRef Full Text | Google Scholar

Yuan, J., Li, W., Guo, J., Zhao, X., and Skibniewski, M. J. (2018). Social risk factors of transportation PPP projects in China: A sustainable development perspective. Int. J. Environ. Res. Public Health 15 (7), 1323. doi:10.3390/ijerph15071323

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., Albert, P. C., Feng, Y., Duan, H., and Ke, Y. (2016). Critical review on PPP research – a search from the Chinese and international journals. Int. J. Proj. Manag. 34 (4), 597–612. doi:10.1016/j.ijproman.2016.02.008

CrossRef Full Text | Google Scholar

Zhang, Q., Oo, B. L., and Lim, B. T. H. (2020). Corporate social responsibility practices by leading construction firms in China: A case study. Int. J. Constr. Manag. 22, 1420–1431. doi:10.1080/15623599.2020.1717107

CrossRef Full Text | Google Scholar

Zhang, Q., Oo, B. L., and Lim, B. T. H. (2019). Drivers, motivations, and barriers to the implementation of corporate social responsibility practices by construction enterprises: A review. J. Clean. Prod. 210, 563–584. doi:10.1016/j.jclepro.2018.11.050

CrossRef Full Text | Google Scholar

Zhang, X., and Fang, J. (2017). “Bargaining mechanism design of PPP project bidding,” in 5th Annual International Conference on Architecture and Civil Engineering (ACE 2017), Singapore, 8-9 May, 2017.

Google Scholar

Zhao, H., Jiang, H. J., and Li, X. (2016). “A decision model of risk allocation for urban rail transit projects under public-private-partnership model: A research framework,” in 2nd International Conference on Social Science and Development (ICSSD), 397–410.

CrossRef Full Text | Google Scholar