Selecting a Project Delivery System for Wastewater Treatment Plants With Related-Indicators Under a Pythagorean Fuzzy Environment

Identifying appropriate project delivery systems for wastewater treatment plants (PDSWTPs) plays an important role for wastewater industry decision makers. This study aims to develop a PDSWTP selection model to deal with the related-indicators case by combining the advantages of Pythagorean fuzzy sets and Bonferroni mean operators. The works of this study are as follows: 1) the case with related indicators is innovatively considered as specific to the water industry, and Bonferroni mean operator and Pythagorean fuzzy sets are introduced to PDSWTP selection, which can handle complexity and fuzziness for the actual application. 2) Pythagorean fuzzy weighted Bonferroni mean (PFWBM) and Pythagorean fuzzy weighted geometry Bonferroni mean (PFWGBM) operators are used to aggregate all related indicators in PDSWTP selection, and taking full advantage of PFWBM and PFWGBM operators, a selection framework for PDSWTPs is constructed. 3) To show the robustness, the PDSWTP selection results were given with different parameters in the proposed operators. Finally, a practice example is created, and the results shown are effective and applicable.

1 Introduction

With the continuous development of current environmental protection plans, the wastewater treatment plant has been widely used as an efficient treatment means in the whole wastewater treatment project. In recent years, wastewater treatment plants in the world have faced challenges due to standard upgrading and transformation since the new standards and requirements were introduced. From the American Society of Civil Engineers (ASCE) infrastructure report, many pipes older than 75 years need to be replaced or repaired, which will cost about $1 trillion. Additionally, there are more than 14,748 wastewater treatment plants that need to be upgraded to the current standard. This work will cost about $271 billion (ASCE, 2017; Shrestha and Batista, 2021). A recent ASCE report stated that the water infrastructure has large deficits (ASCE, 2020). Then, there is an important problem to face: how to carry out the project under such a huge funding gap. And how to execute the work to achieve sustainable development of the wastewater treatment plant project. Furthermore, this kind of project with repair, reconstruction, and expansion is a typically complex project, which requires a high-level team to make the project successful (Andary et al., 2020). And then, what kind of cooperation mode adopted in the process of cooperation can guarantee the sustainable development of the project, especially in the case of financial difficulties. The project delivery system (PDS) is a common cooperation model in the construction industry. With the progression of society, decision-makers now choose to use alternative PDSs to build projects, though the current design bid construction is the most widely used PDS in the construction industry.

Naturally, a critical problem is selecting an appropriate PDS, which can not only save time and money but can also reduce the quality of the project in times of economic hardship (Culp, 2011). The relationship among project participants has been defined in existing studies and determines how the project will be delivered by the contractor to the owner (ASCE, 1988; Chen et al., 2011). Commonly, the design-bid-build (DBB), design-build (DB), public-private partnership (PPP), and engineering procurement construction (EPC) systems are the main types of PDSs in the practical construction industry. And different PDSs have their own advantages and disadvantages. Obviously, selecting a more suitable PDS in the water industry is important for decision-makers, which may increase their chances of success for projects. This study will apply the PDSs DBB, DB, PPP, and EPC to the water industry.

Recently, there have been many research papers on selecting appropriate PDSs (Su et al., 2019; Ibrahim et al., 2020; Zhu et al., 2020; Ahmed and El-Sayegh, 2022), and the evaluation values information characterizing the indicators are mainly described by the fuzzy set theory (Jana et al., 2019a; Li et al., 2022). Liu and Liu (2019) used a fuzzy ordered weighted geometric averaging operator to aggregate decision-making information under a fuzzy environment, and then selected an appropriate PDS type. An et al. (2018) considered decision-making information based on an interval-valued intuitionistic fuzzy set, and then developed a group decision-making framework to select their favorite PDS for owners. For the complex decision-making information with many experts for PDS selection, Khanzadi et al. (2016) presented a decision-making approach through combining the advantages of the analytic hierarchy process method (AHP) and triangular fuzzy sets in characterizing decision-making information. Under a Pythagorean fuzzy environment, through extending TOPSIS, Su et al. (2019) established an improved TOPSIS PDS selection method, in which the evaluation values information was characterized by Pythagorean fuzzy numbers (PFNs). The existing research has given a broad theoretical foundation for PDS selection in the complex construction environment. However, the existing research has not considered certain internal relationships among decision information in decision-making problems. To summarize, few studies considering the existence of relevance among indicators when handling PDS selection have appeared in existing research, which is a study gap in the PDS selection problem. In other words, the existing methods for selecting PDSs will give a distorted result more or less.

The Bonferroni mean operator proposed by Bonferroni (1950) can comprehensively consider the internal relationship among criteria, indicators, and decision information. Subsequently, there are many theoretical research papers on Pythagorean fuzzy and Bonferroni mean operators. Liang et al. (2019) developed Pythagorean fuzzy Bonferroni mean and weighted Pythagorean fuzzy Bonferroni mean operators, and some special properties and cases were also discussed. For the multi-criteria group decision-making problem with Pythagorean fuzzy sets, Liang et al. (2018) proposed two new aggregation operators, which were Pythagorean fuzzy partitioned geometric Bonferroni mean and weighted Pythagorean fuzzy partitioned geometric Bonferroni mean operators. To capture the correlations among Pythagorean fuzzy input arguments, Yang et al. (2019) proposed Pythagorean fuzzy weighted Bonferroni mean and Pythagorean fuzzy weighted geometric Bonferroni mean operators based on the generalized operational laws of Pythagorean fuzzy sets, which also obtain the properties and special cases of the presented operators. Based on the interaction operational laws of PFNs, Wang and Li (2020) developed Pythagorean fuzzy interaction power Bonferroni mean and weighted Pythagorean fuzzy interaction power Bonferroni mean operators. Combining partitioned Bonferroni mean and power average, Zhu et al. (2019) given a family of Pythagorean fuzzy aggregation operators, were able to characterize the decision-making information with Pythagorean fuzzy numbers, which included Pythagorean fuzzy interaction power Bonferroni mean, Pythagorean fuzzy interaction power partitioned geometric Bonferroni mean, and weighted forms of them. A family of hesitant Pythagorean fuzzy operators and their properties were constructed and studied respectively, which included hesitant Pythagorean fuzzy interaction Bonferroni mean, hesitant Pythagorean fuzzy interaction weighted Bonferroni mean, hesitant Pythagorean fuzzy interaction geometric Bonferroni mean, and hesitant Pythagorean fuzzy interaction weight geometric Bonferroni mean operators. Considering Shapley fuzzy measure, Nie et al. (2019) explored a Pythagorean fuzzy partitioned normalized weighted Bonferroni mean operator through combining partitioned Bonferroni mean and its normalized weighted operator.

Though the existing research has provided an abundance of theory support, the selection of a PDS has not been determined for a specific industry, and how to apply the existing abundance theory to the practical problem of PDS is another gap in the practical research. How to select suitable project delivery systems for wastewater treatment plants (PDSWTPs) under the influence of several factors is a vital problem that needs to be settled urgently. From a theoretical perspective, it is a classical multiple criteria decision-making problem. That is, the PDSWTP selection process should rank all the alternative PDSWTPs under different factors affecting PDSWTP selection. Based on these, the purpose of this study is to establish a PDSWTP selection model with the existence of the relevance among indicators under a Pythagorean fuzzy environment, and to solve industry-specific problems. And to achieve it, this study comprehensively applies the Pythagorean fuzzy set (PFS) theory and Bonferroni mean operator to PDSWTP selection.

The main contributions of this study consist of four aspects: 1) This study innovatively investigated the correlation among indicators for PDS selection in a specific wastewater treatment industry, where the Bonferroni mean operator was introduced to handle this kind of PDSWTP selection problem. 2) The Pythagorean fuzzy weighted Bonferroni mean (PFWBM) and Pythagorean fuzzy weighted geometric Bonferroni mean (PFWGBM) operators were applied to characterize the indicator-related PDSWTP selection, in which the evaluation values information affecting PDSWTP selection are described by Pythagorean fuzzy numbers. 3) Taking full use of the advantages of PFSs and the PFWBM operator, a decision making model was developed for PDSWTP selection, and 4) a case study verifying the application and feasibility of the proposed method for PDSWTPs was given.

2 Preliminaries

This section presents the preliminaries including concepts and some corresponding operations for Pythagorean fuzzy sets, the Bonferroni mean operator, and weighted Bonferroni mean operator, which mainly consist of two parts: 1) the concept for the Pythagorean fuzzy number and its operations and 2) the definitions and the corresponding theorems on Bonferroni mean (BM), PFWBM, and PFWGBM operators. They are the preliminaries for establishing the PDSWTP selection method with related indicators.

2.1 Pythagorean Fuzzy Sets

This subsection gives some basic concepts, definitions, and operational laws of PFN, which are utilized in the following analysis.

Definition 1 (Yager and Abbasov, 2013) If $X$ be a fixed set, then

$P=\left\{\langle x,{\mu }_P\left(x\right),v_P\left(x\right)\rangle |x\in X\right\}$

is called a PFS on $X$ , where ${\mu }_P\left(x\right)$ and $v_P\left(x\right)$ are the membership degree and non-membership degree of $x\in X$, respectively, that is, ${\mu }_{\text{P}}$: $X\to \left[\mathrm{0,1}\right]$, $v_{\text{P}}$: $X\to \left[\mathrm{0,1}\right]$, and $0\le {\mu }_{\text{P}}^2+v_{\text{P}}^2\le 1$, $\forall x\in X$. Furthermore, ${\pi }_P\left(x\right)=\sqrt{1-{\mu }_P^2\left(x\right)-v_P^2\left(x\right)}$, $\forall x\in X$ , denotes the hesitation degree of the element $x\in X$ to $P$. In particular, if ${\pi }_P\left(x\right)=0$ for $\forall x\in X$, then $P$ is the typical fuzzy set. For brevity, $\alpha =\left({\mu }_{\alpha },v_{\alpha }\right)$ indicates the PFN (Wei, 2017), and ${\mu }_{\alpha }\in \left[\mathrm{0,1}\right]$ , $v_{\alpha }\in \left[\mathrm{0,1}\right]$, and $0\le {\mu }_{\alpha }^2+v_{\alpha }^2\le 1$.

Definition 2 (Ren et al., 2016) Let $\alpha$ be a PFN, then score function $S$ of the PFN $\alpha$ is defined as follows:

$\text{S}\left(\alpha \right)=\frac{1}{2}\left(1+{\mu }_{\alpha }^2-v_{\alpha }^2\right),\text{S}\left(\alpha \right)\in \left[\mathrm{0,1}\right].(1)$

Definition 3 (Wei, 2017; Jana et al., 2019b) Let $\alpha$ be a PFN, then accuracy function $H$ of the PFN $\alpha$ is defined as follows:

$\text{H}\left(\alpha \right)={\mu }_{\alpha }^2+v_{\alpha }^2,\text{H}\left(\alpha \right)\in \left[\mathrm{0,1}\right].(2)$

Generally, the larger the value of the score function, the larger the PFN. However, when the values of score functions between two PFNs are equal, the larger the value of the accuracy function and the larger the PFN. Therefore, we give the compared method for two PFNs.

Definition 4 (Ren et al., 2016) Let ${\alpha }_1=\langle {\mu }_{{\alpha }_1},v_{{\alpha }_1}\rangle$ and ${\alpha }_2=\langle {\mu }_{{\alpha }_2},v_{{\alpha }_2}\rangle$ be any two PFNs, then the comparison rules between the two ${\alpha }_1$ and ${\alpha }_2$ are:

1) If $\text{S}\left({\alpha }_1\right)<\text{S}\left({\alpha }_2\right)$, then ${\alpha }_1<{\alpha }_2$;

2) If $\text{S}\left({\alpha }_1\right)=\text{S}\left({\alpha }_2\right)$, then

If $\text{H}\left({\alpha }_1\right)<\text{H}\left({\alpha }_2\right)$, then ${\alpha }_1<{\alpha }_2$;

If $\text{H}\left({\alpha }_1\right)>\text{H}\left({\alpha }_2\right)$, then ${\alpha }_1>{\alpha }_2$.

Definition 5 (Reformat et al., 2014) Let $\alpha =\left({\mu }_{\alpha },v_{\alpha }\right)$, ${\alpha }_1=\left({\mu }_{{\alpha }_1},v_{{\alpha }_1}\right)$, and ${\alpha }_2=\left({\mu }_{{\alpha }_2},v_{{\alpha }_2}\right)$ be three PFNs, $\lambda >0$, and some basic operations of them are as follows:

(A1) ${\alpha }_1\oplus {\alpha }_2=\left(\sqrt{{\mu }_{{\alpha }_1}^2+{\mu }_{{\alpha }_2}^2-{\mu }_{{\alpha }_1}^2\cdot {\mu }_{{\alpha }_2}^2},v_{{\alpha }_1}\cdot v_{{\alpha }_2}\right);$

(A2) ${\alpha }_1\otimes {\alpha }_2=\left({\mu }_{{\alpha }_1}\cdot {\mu }_{{\alpha }_2},\sqrt{v_{{\alpha }_1}^2+v_{{\alpha }_2}^2-v_{{\alpha }_1}^2\cdot v_{{\alpha }_2}^2}\right)$

(A3) $\lambda \alpha =\left(\sqrt{1-{\left(1-{\mu }_{\alpha }^2\right)}^{\lambda }},v_{\alpha }^{\lambda }\right)$

(A4) ${\alpha }^{\lambda }=\left({\mu }_{\alpha }^{\lambda },\sqrt{1-{\left(1-v_{\alpha }^2\right)}^{\lambda }}\right)$;

(A5) ${\alpha }^c=\left(v_{\alpha },{\mu }_{\alpha }\right)$ is the complement of $\alpha$, with $c>0$.

And, Zhang and Xu (2014) also defined a Pythagorean fuzzy distance measure for PFNs.

Definition 6 (Zhang and Xu, 2014) Let ${\alpha }_1=\left({\mu }_{{\alpha }_1},v_{{\alpha }_1}\right)$ and ${\alpha }_2=\left({\mu }_{{\alpha }_2},v_{{\alpha }_2}\right)$ be two PFNs. Then, the distance between is defined as follows:

$d\left({\alpha }_1,{\alpha }_2\right)=\frac{1}{2}\left(\left|{\mu }_{{\alpha }_1}^2-{\mu }_{{\alpha }_2}^2\right|+\left|v_{{\alpha }_1}^2-v_{{\alpha }_2}^2\right|+\left|{\pi }_{{\alpha }_1}^2-{\pi }_{{\alpha }_2}^2\right|\right).(3)$

Definition 7 (Yager, 2014) Assume that ${\alpha }_i=\left({\mu }_i,v_i\right)$., $\left(i=\mathrm{1,2},\mathrm{...},n\right)$ is a PFN set and $w=\left(w_1,w_2,\mathrm{...},w_n\right)$ is the weight vector, where $w_i\in \left[\mathrm{0,1}\right]$ and ${\displaystyle \sum _{i=1}^n{w}_i}=1$, then a Pythagorean fuzzy weighted aggregate (PFWA) operator is expressed as:

$\text{P}\text{F}\text{W}\text{A}\left({\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_n\right)=\alpha \left({\displaystyle \sum _{i=1}^n{w}_i{\mu }_i},{\displaystyle \sum _{i=1}^n{w}_i{v}_i}\right).(4)$

2.2 Pythagorean Fuzzy Weighted Bonferroni Mean Operator

Definition 8 (Bonferroni, 1950) Let ${\alpha }_i$ $\left(i=\mathrm{1,2},\mathrm{...},n\right)$ be a collection of non-negative crisp numbers and $\text{p},q\ge 0$, then a Bonferroni mean operator of dimension $n$ is a mapping of BM: $R^n\to R$. Such that,

$\text{B}{\text{M}}^{\mathit{\text{p}},q}\left({\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_n\right)={\left(\frac{1}{n\left(n-1\right)}{\displaystyle \sum _{i,j=1,j\ne i}^n{\alpha }_i^{\mathit{\text{p}}}{\alpha }_j^q}\right)}^{\frac{1}{\mathit{\text{p}}+q}}.$

The BM operator only considers the interrelation of aggregated parameters and ignores the self-importance of them. So, Zhou and He (2012) introduced a weighted Bonferroni mean operator with reducibility to overcome this shortcoming.

Definition 9 (Zhou and He, 2012) Let ${\alpha }_i$ $\left(i=\mathrm{1,2},\mathrm{...},n\right)$ be a collection of non-negative crisp numbers and $\text{p},q\ge 0$ and the weight vector of $x_i$ be $W={\left(w_1,w_2,\mathrm{...},w_n\right)}^T$, satisfying $w_i\ge 0$ and ${\displaystyle {\sum }_{i=1}^n{w}_i}=1$, then a weighted Bonferroni mean (WBM) operator of dimension $n$ is a mapping of WBM: $R^n\to R$. Such that

$\mathrm{WB}{\text{M}}^{\mathit{\text{p}},q}\left({\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_n\right)={\left({\displaystyle \sum _{i,j=1,j\ne i}^n\frac{w_i{w}_j}{1-w_i}{\alpha }_i^{\mathit{\text{p}}}{\alpha }_j^q}\right)}^{\frac{1}{\mathit{\text{p}}+q}}.$

Definition 10 (Yang et al., 2019) Let $A_j$ $\left(j=\mathrm{1,2},\dots ,n\right)$ be a set of PFNs with the weighting vector $W={\left(w_1,w_2,\dots ,w_n\right)}^T$ and $w_j\ge 0$, ${\sum }_{j=1}^n{w}_j=1$, then the Pythagorean fuzzy weighted Bonferroni mean (PFWBM) operator of dimension $n$ is the mapping PFNWBM: ${\Omega }^n\to \Omega$, such that

$\mathrm{PFWB}{\text{M}}^{\mathit{\text{p}},q}\left({\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_n\right)={\left(\underset{l,j=1,l\ne j}{\overset{n}{\oplus }}\frac{w_l{w}_j}{1-w_l}{\alpha }_l^{\mathit{\text{p}}}\otimes {\alpha }_j^q\right)}^{1/\left(\mathit{\text{p}}+q\right)},$

where $\text{Ω}$ is the set of all PFNs.

Based on the operations in Definition 5 and the aggregation form for WBM in Definition 9, the following theorem will be deduced.

Theorem 2.1 Let ${\alpha }_j$ $\left(j=\mathrm{1,2},\mathrm{...},n\right)$ be a set of PFNs with the weighting vector $W={\left(w_1,w_2,\mathrm{...},w_n\right)}^T$ and $w_j\ge 0$, ${\sum }_{j=1}^n{w}_j=1$, and then the aggregated result by the PFWBM operator in Definition 7 can be expressed as:

$\mathrm{PFWB}{\text{M}}^{\mathit{\text{p}},q}={\left(\underset{l\ne j}{\underset{l,j=1}{\overset{n}{\oplus }}}\left(\frac{w_l{w}_j}{1-w_l}{\alpha }_i^{\mathit{\text{p}}}\otimes {\alpha }_j^q\right)\right)}^{\frac{1}{\mathit{\text{p}}+q}}=\left({\left(1+{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\mu }_j^{2\mathit{\text{p}}}{\mu }_j^{2q}\right)}^{\frac{w_l{w}_j}{1-w_l}}}\right)}^{\frac{1}{\mathit{\text{p}}+q}},1-{\left(1-{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\left(1-v_l^2\right)}^{\mathit{\text{p}}}{\left(1-v_j^2\right)}^q\right)}^{\frac{w_l{w}_j}{1-w_l}}}\right)}^{\frac{1}{\mathit{\text{p}}+q}}\right)$

Proof.

Since

${\alpha }_l^{\mathit{\text{p}}}=\left({\mu }_l^{\mathit{\text{p}}},\sqrt{1-{\left(1-{\nu }_l^2\right)}^{\mathit{\text{p}}}}\right),{\alpha }_j^q=\left({\mu }_j^q,\sqrt{1-{\left(1-{\nu }_j^2\right)}^q}\right)$

$\begin{array}{c}{\alpha }_l^{\mathit{\text{p}}}\otimes {\alpha }_j^q=\left({\mu }_l^{\mathit{\text{p}}}\cdot {\mu }_j^q,\sqrt{\left(1-{\left(1-{\nu }_l^2\right)}^{\mathit{\text{p}}}\right)+\left(1-{\left(1-{\nu }_j^2\right)}^q\right)-\left(1-{\left(1-{\nu }_l^2\right)}^{\mathit{\text{p}}}\right)\left(1-{\left(1-{\nu }_j^2\right)}^q\right)}\right)\\ =\left({\mu }_l^{\mathit{\text{p}}}\cdot {\mu }_j^q,\sqrt{1-{\left(1-{\nu }_l^2\right)}^{\mathit{\text{p}}}{\left(1-{\nu }_j^2\right)}^q}\right),\end{array}$

$\frac{w_l{w}_j}{1-w_l}{\alpha }_l^{\mathit{\text{p}}}\otimes {\alpha }_j^q=\left(\sqrt{1-{\left(1-{\mu }_l^{2\mathit{\text{p}}}\cdot {\mu }_j^{2q}\right)}^{\frac{w_l{w}_j}{1-w_l}}},{\left(\sqrt{1-{\left(1-{\nu }_l^2\right)}^{\mathit{\text{p}}}{\left(1-{\nu }_j^2\right)}^q}\right)}^{\frac{w_l{w}_j}{1-w_l}}\right),$

$\underset{l,j=1,l\ne j}{\overset{n}{\oplus }}\left(\frac{w_l{w}_j}{1-w_l}{\alpha }_l^{\mathit{\text{p}}}\otimes {\alpha }_j^q\right)=\left(1+{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\mu }_l^{2\mathit{\text{p}}}{\mu }_j^{2q}\right)}^{\frac{w_l{w}_j}{1-w_l}}},{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\left(1-{\nu }_l^2\right)}^{\mathit{\text{p}}}{\left(1-{\nu }_j^2\right)}^q\right)}^{\frac{w_l{w}_j}{2\left(1-w_l\right)}}}\right).$

So

$PFWB{M}^{\mathit{\text{p}},q}={\left(\underset{\begin{array}{l}l,j=1\\ l\ne j\end{array}}{\overset{n}{\oplus }}\left(\frac{w_l{w}_j}{1-w_l}{\alpha }_i^{\mathit{\text{p}}}\otimes {\alpha }_j^q\right)\right)}^{\frac{1}{\mathit{\text{p}}+q}}=\left({\left(1+{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\mu }_i^{2\mathit{\text{p}}}{\mu }_j^{2q}\right)}^{\frac{w_l{w}_j}{1-w_l}}}\right)}^{\frac{1}{\mathit{\text{p}}+q}},1-{\left(1-{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\left(1-{\nu }_l^2\right)}^{\mathit{\text{p}}}{\left(1-{\nu }_j^2\right)}^q\right)}^{\frac{w_l{w}_j}{1-w_l}}}\right)}^{\frac{1}{\mathit{\text{p}}+q}}\right)$

Definition 11 (Xia et al., 2013) Let ${\alpha }_i$ $\left(i=\mathrm{1,2},\mathrm{...},n\right)$ be a collection of non-negative crisp numbers and $\text{p},q\ge 0$, then a geometric Bonferroni mean operator of dimension $n$ is a mapping of GBM: $R^n\to R$. Such that,

$\text{G}\text{B}{\text{M}}^{\mathit{\text{p}},q}\left({\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_n\right)=\frac{1}{\mathit{\text{p}}+q}{\displaystyle \prod _{l,j=1,j\ne i}^n{\left(\mathit{\text{p}}{\alpha }_l+q{\alpha }_j\right)}^{\frac{1}{n\left(n-1\right)}}}.$

Similar to the BM operator, the GBM operator also ignored the weights of the aggregated arguments. Sun and Liu (2013) further improved the weighted geometric Bonferroni mean (WGBM) operator.

Definition 12 (Sun and Liu, 2013) Let ${\alpha }_i$ $\left(i=\mathrm{1,2},\mathrm{...},n\right)$ be a collection of non-negative crisp numbers, $\text{p},q\ge 0$, and the weight vector of ${\alpha }_i$ $\left(i=\mathrm{1,2},\mathrm{...},n\right)$ be $W={\left(w_1,w_2,\mathrm{...},w_n\right)}^T$ , with $w_i\ge 0$ and ${\sum }_{i=1}^n{w}_i=1$. Then a weighted geometric Bonferroni mean (WGBM) operator of dimension $n$ is a mapping of WGBM: $R^n\to R$. Such that

$\mathrm{WGB}{\text{M}}^{\mathit{\text{p}},q}\left({\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_n\right)=\frac{1}{\mathit{\text{p}}+q}{\displaystyle \prod _{l,j=1,j\ne l}^n{\left(\mathit{\text{p}}{\alpha }_l+q{\alpha }_j\right)}^{\frac{w_l{w}_j}{1-w_l}}},.$

Definition 13 (Yang et al., 2019) Let ${\alpha }_j$ $\left(j=\mathrm{1,2},\dots ,n\right)$ be a set of PFNs with the weighting vector $W={\left(w_1,w_2,\mathrm{...},w_n\right)}^T$ and $w_j\ge 0$, ${\sum }_{j=1}^n{w}_j=1$, then the Pythagorean fuzzy weighted geometric Bonferroni mean (PFWGBM) operator of dimension $n$ is the mapping PFNWBM: ${\Omega }^n\to \Omega$, such that

$\mathrm{PFWGB}{\text{M}}^{\mathit{\text{p}},q}\left({\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_n\right)=\frac{1}{\mathit{\text{p}}+q}\underset{l,j=1,l\ne j}{\overset{n}{\otimes }}{\left(\mathit{\text{p}}{\alpha }_l\oplus q{\alpha }_j\right)}^{\frac{w_l{w}_j}{1-w_l}},$

where $\text{Ω}$ is the set of all PFNs.

Based on the operations in Definition 5 and the aggregation form for WGBM in Definition 12, the following theorem will be deduced.

Theorem 2.2 Let ${\alpha }_j$ $\left(j=\mathrm{1,2},\mathrm{...},n\right)$ be a set of PFNs with the weighting vector $W={\left(w_1,w_2,\mathrm{...},w_n\right)}^T$ and $w_j\ge 0$, ${\sum }_{j=1}^n{w}_j=1$, and then the aggregated result by the PFWGBM operator in Definition 7 can be expressed as:

$\mathrm{PFWGB}{\mathrm{M}}^{\mathit{\text{p}},q}\left({\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_n\right)=\frac{1}{\mathit{\text{p}}+q}\underset{l,j=1,l\ne j}{\overset{n}{\otimes }}{\left(\mathit{\text{p}}{\alpha }_l\oplus q{\alpha }_j\right)}^{\frac{w_l{w}_j}{1-w_l}},$

Proof.

Since

$\mathit{\text{p}}{\alpha }_l=\left(\sqrt{1-{\left(1-{\mu }_l^2\right)}^{\mathit{\text{p}}}},{\nu }_l^{\mathit{\text{p}}}\right),q{\alpha }_j=\left(\sqrt{1-{\left(1-{\mu }_j^2\right)}^q},{\nu }_j^q\right),$

$\begin{array}{c}\mathit{\text{p}}{\alpha }_l\otimes q{\alpha }_j=\left(\sqrt{\left(1-{\left(1-{\mu }_l^2\right)}^{\mathit{\text{p}}}\right)+\left(1-{\left(1-{\mu }_j^2\right)}^q\right)-\left(1-{\left(1-{\mu }_l^2\right)}^{\mathit{\text{p}}}\right)\left(1-{\left(1-{\mu }_j^2\right)}^q\right)},{\nu }_l^{\mathit{\text{p}}}\cdot {\nu }_j^q\right)=\left(\sqrt{1-{\left(1-{\mu }_l^2\right)}^{\mathit{\text{p}}}{\left(1-{\mu }_j^2\right)}^q},{\nu }_l^{\mathit{\text{p}}}\cdot {\nu }_j^q\right),\end{array}$

${\left(\mathit{\text{p}}{\alpha }_l\otimes q{\alpha }_j\right)}^{\frac{w_l{w}_j}{1-w_l}}=\left({\left(1-{\left(1-{\mu }_l^2\right)}^{\mathit{\text{p}}}{\left(1-{\mu }_j^2\right)}^q\right)}^{\frac{w_l{w}_j}{2\left(1-w_l\right)}},\sqrt{1-{\left(1-{\nu }_l^{2\mathit{\text{p}}}\cdot {\nu }_j^{2q}\right)}^{\frac{w_l{w}_j}{1-w_l}}}\right),$

$\underset{l,j=1,l\ne j}{\overset{n}{\otimes }}{\left(\mathit{\text{p}}{\alpha }_l\oplus q{\alpha }_j\right)}^{\frac{w_l{w}_j}{1-w_l}}=\left({\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\left(1-{\nu }_l^2\right)}^{\mathit{\text{p}}}{\left(1-{\nu }_j^2\right)}^q\right)}^{\frac{w_l{w}_j}{2\left(1-w_l\right)}}},1+{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\mu }_l^{2\mathit{\text{p}}}{\mu }_j^{2q}\right)}^{\frac{w_l{w}_j}{1-w_l}}}\right).$

So

$\begin{array}{c}\mathrm{PFWGB}{\text{M}}^{\mathit{\text{p}},q}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\frac{1}{\mathit{\text{p}}+q}\underset{l,j=1,l\ne j}{\overset{n}{\otimes }}{\left(\mathit{\text{p}}{\alpha }_l\oplus q{\alpha }_j\right)}^{\frac{w_l{w}_j}{1-w_l}}\\ =\left(\sqrt{1-{\left(1-{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\left(1-{\mu }_l^2\right)}^{\mathit{\text{p}}}{\left(1-{\mu }_j^2\right)}^q\right)}^{\frac{w_l{w}_j}{1-w_l}}}\right)}^{\frac{1}{\mathit{\text{p}}+q}}},{\left(1+{\displaystyle \prod _{l,j=1,l\ne j}^n{\left(1-{\nu }_l^{2\mathit{\text{p}}}{\nu }_j^{2q}\right)}^{\frac{w_l{w}_j}{1-w_l}}}\right)}^{\frac{1}{\mathit{\text{p}}+q}}\right).\end{array}$

3 Project Delivery Systems for Wastewater Treatment Plants Selection Method Based on Pythagorean Fuzzy Weighted Bonferroni Mean and Pythagorean Fuzzy Weighted Geometry Bonferroni Mean

For a PDSWTP selection problem, the alternative PDSWTP selection set is $A=\left\{A_1,A_2,\mathrm{...},A_n\right\}$, and the indicators set affecting PDSWTP selection is $C=\left\{C_1,C_2,\mathrm{...},C_m\right\}$, where the weight vector of the indicator set is $W=\left\{w_1,w_2,\mathrm{...},w_m\right\}$, with $w_j\in \left[\mathrm{0,1}\right]$, and ${\sum }_{j=1}^n{w}_j=1$. Also, it is assumed that $t$ experts from the water industry, engineering industry, and other relevant industries give evaluation values information of each PDSWTP under different indicators, which are characterized by PFNs. If the PNF $e_{ij}^{\left(l\right)}=\langle {\mu }_{ij}^{\left(l\right)},{\nu }_{ij}^{\left(l\right)}\rangle$ denotes the evaluation value information of the $i\text{th}$ PDSWTP under the $j\text{th}$ indicator from the $l\text{th}$ expert, ${\mu }_{ij}^{\left(l\right)}$ and $v_{ij}^{\left(l\right)}$ denote membership and non-membership degrees, respectively. Thus, the evaluation values information matrix can be obtained as follows:

$E=\left(\begin{array}{ccc}{\text{e}}_{11}& \cdots & {\text{e}}_{1\text{m}}\\ ⋮& \ddots & ⋮\\ {\text{e}}_{\text{n}1}& \cdots & {\text{e}}_{\text{n}\text{m}}\end{array}\right),(5)$

where $e_{ij}=\langle {\mu }_{ij},v_{ij}\rangle$ is the aggregate information of the all evaluation values information $e_{ij}^{\left(l\right)}=\langle {\mu }_{ij}^{\left(l\right)},{\nu }_{ij}^{\left(l\right)}\rangle$ from $t$ experts.

3.1 Constructing the Decision-Making Indicator System for Project Delivery Systems for Wastewater Treatment Plants Selection

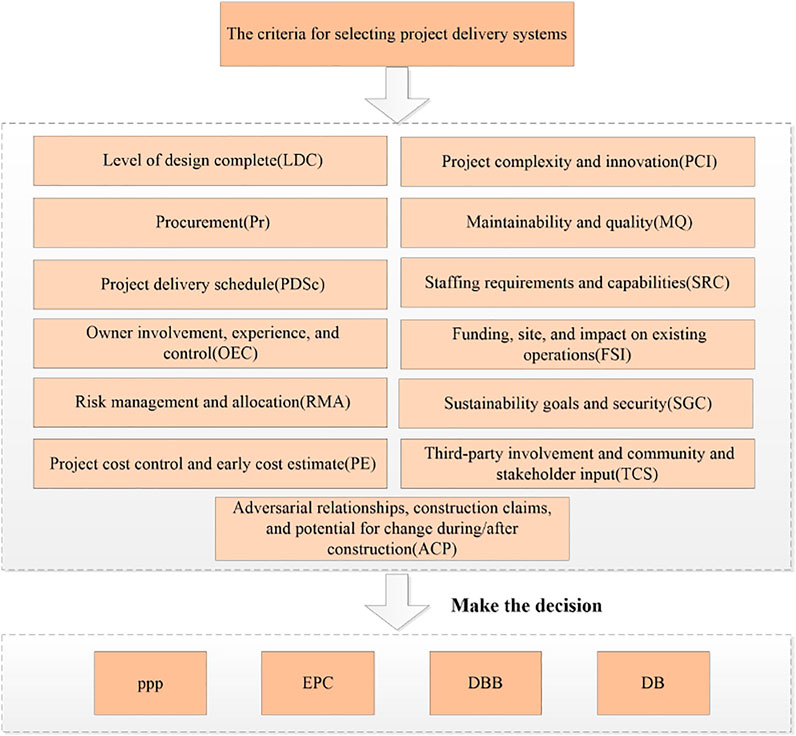
For a given PDS of the wastewater treatment plant project, the alternative PDSWTPs can be chosen from design-bid-build (DBB), design-build (DB), public-private partnership (PPP), and engineering procurement construction (EPC). Based on the existing research for the indictor system affecting PDSWTP selection, the indicators are shown in Figure 1 (Feghaly et al., 2020).

FIGURE 1

FIGURE 1. The criteria for selecting PDSs.

3.2 Aggregating the Evaluation Information From all Experts

From the PFWA operator in Definition 7, the evaluation information from all experts is aggregated and the comprehensive evaluation information for the PDSWTP selection is obtained. Therefore, the aggregate information of the $i\text{th}$ PDSWTP under the $j\text{th}$ indicator from $t$ experts obtained by Eq. 4 is $e_{ij}=e_{ij}\left(e_{ij}^{\left(1\right)},e_{ij}^{\left(2\right)},\dots ,e_{ij}^{\left(t\right)}\right)=e_{ij}\left({\displaystyle \sum _{l=1}^t{W}_l{\mu }_{ij}^{\left(l\right)}},{\displaystyle \sum _{l=1}^l{W}_l{v}_{ij}^{\left(l\right)}}\right)$, where $W_l$ is the weight of the $l\text{th}$ expert, $i=\mathrm{1,2},\dots ,n$, $j=\mathrm{1,2},\dots ,m$, and $l=\mathrm{1,2},\dots ,t$. And the $W_l$ can be obtained by different methods, such as, AHP, maximal deviation, etc. Moreover, the averaging weighting method is applied for convenience, that is, $W_1=W_2=\cdots =W_t=1/t$.

3.3 The Selection Procedure for the Alternative Project Delivery Systems for Wastewater Treatment Plants

For a given PDSWTP selection problem, various related industry experts are invited to evaluate PDSWTPs based on determined indicators affecting PDSWTP selection. As mentioned above, the alternative PDSWTP set is $A=\left(A_1,A_2,\dots ,A_n\right)$, the set of indicators is $C=\left(C_1,C_2,\dots ,C_m\right)$, and the weight vector of indicators is $W=\left(w_1,w_2,\dots ,w_m\right)$. There are $t$ experts who are invited to provide evaluation values information for the given PDSWTP selection problem, and the matrix $E^{\left(l\right)}$ denotes evaluation values information from the $l\text{th}$ expert. According to the above illustration, we provide a selection process for selecting a suitable PDSWTP from all alternative PDSWTPs, as shown in Figure 2.

FIGURE 2

FIGURE 2. The selection process for PDSWTPs.

Step 1: Aggregate the evaluation information from all experts.

If the evaluation information matrix from the $l\text{th}$ expert is $E^{\left(l\right)}={\left(e_{ij}^{\left(l\right)}\right)}_{n\times m}={\left({\mu }_{ij}^{\left(l\right)},v_{ij}^{\left(l\right)}\right)}_{n\times m}$, then the aggregated evaluation information matrix is $E={\left(e_{ij}\right)}_{n\times m}$ using Definition 7, where $e_{ij}=e_{ij}\left({\displaystyle \sum _{l=1}^t{W}_l{\mu }_{ij}^{\left(l\right)}},{\displaystyle \sum _{l=1}^t{W}_l{v}_{ij}^{\left(l\right)}}\right)$ and $W_1=W_2=\cdots =W_t=1/t$.

Step 2: Normalize the evaluation values information.

Normalizing all indicators affecting PDSWTP selection to the same magnitude scale and type is of great importance. The evaluation value information is normalized using the following Equation.

$e_{ij}=\{\begin{array}{c}{e}_{ij}=\left({\mu }_{\alpha },v_{\alpha }\right),\\ e_{ij}=\left(v_{\alpha },{\mu }_{\alpha }\right),\end{array}\begin{array}{c}{C}_j\mathrm{benifit}\mathrm{indicator}\\ C_j\mathrm{cost}\mathrm{indicator}\end{array}.(6)$

Step 3: Obtain the comprehensive evaluation values of all alternative PDSWTPs applying PFWBM and PFWGBM operators.

$\mathrm{PFWB}{\text{M}}^{\mathit{\text{p}},q}\left(e_{ij},\dots ,e_{im}\right)={\left(\underset{l,j=1,l\ne j}{\overset{m}{\oplus }}\frac{w_l{w}_j}{1-w_l}{e}_{il}^{\mathit{\text{p}}}\otimes e_{ij}^q\right)}^{1/\left(\mathit{\text{p}}+q\right)},(7)$

$\mathrm{PFWGB}{\text{M}}^{\mathit{\text{p}},q}\left(e_{i1},\dots ,e_{im}\right)=\frac{1}{\mathit{\text{p}}+q}\underset{l,j=1,l\ne j}{\overset{m}{\otimes }}{\left(\mathit{\text{p}}{\mathit{\text{e}}}_{i1}\oplus q{\mathit{\text{e}}}_{im}\right)}^{\frac{w_l{w}_j}{1-w_l}},(8)$

where $W=\left\{w_1,w_2,\dots ,w_m\right\}$ is the weight vector of indicators, and $w_j\ge 0$, ${\displaystyle {\sum }_{j=1}^m{w}_j}=1$.

Step 4: Calculate the score functions and accuracy degree functions of the comprehensive evaluation values for all alternative PDSWTPs.

To compare the comprehensive evaluation values for all alternative PDSWTPs, the score functions and accrue degree functions of them are calculated, and the calculation method and compared rules are shown in Definition 4.

Step 5: Rank all alternative PDSWTPs according to the values of score functions, and select the best suitable PDSWTP.

According to the outcome of comparison in Step 4, the larger the comprehensive evaluation value, the better the alternative PDSWTP. Therefore, the most suitable PDSWTP is selected.

4 Case Study

Due to the pressure of the current environment, the monitoring of river surface water is becoming more and more rigorous. And then, more wastewater treatment plants are facing upgrades, and more water environment treatment projects are also being carried out one after another. Now, in this case study, construction of a new concept wastewater treatment plant is planned in a county, which covers a total area of 150 Mu. The total investment of the project is 180 million Yuan. It is mainly responsible for the comprehensive treatment of domestic sewage within this area, sludge around the urban area, livestock manure, and other organic matter.

The project is expected to mainly include two parts: one is to build a new wastewater treatment plant with a wastewater treatment capacity of 40,000 tons per day, in which the treated water can meet the water quality requirements of a surface class IV water body; the other is to build a harmless and resource-based organic matter disposal center with a treatment capacity of 100 tons per day. The building area is a typical poverty-stricken county, and the annual financial revenue is less than 1 billion Yuan. In order to meet the relevant discharge standards of the river surface water and avoid being notified and fined by relevant departments, the county needs to seek financial and technical assistance.

Therefore, a suitable PDS achieving the sustainable development of this wastewater treatment plan project is required. Now, the owner needs to choose a satisfactory PDSWTP from four PDSWTPs, which include public-private partnership (PPP), engineering procurement construction (EPC), design build (DB), and design bid build (DBB). The PDSWTP selection is affected by several indicators, which are shown in Section 3.1. They are the level of design completed (LDC), procurement (Pr), project delivery schedule (PDSc), owner involvement, experience, and control (OEC), risk management, and allocation (RMA), project cost control and early cost estimate (PE), project complexity and innovation (PCI), maintainability and quality (MQ), staffing requirements and capabilities (SRC), funding, site, and impact on existing operations (FSI), sustainability goals and security (SGC), third-party involvement and community and stakeholder input (TCS), and adversarial relationships, construction claims, and potential for change during or after construction (ACP).

To ensure the reliability and availability of data, five experienced experts from the water and engineering industry, a scientific research institution, and a consulting firm are consulted. The work process generally includes the following procedure. 1) The owners introduces the content and goal of project, and the local capital situation. 2) The evaluation indicators and evaluation system are further explained for the whole project. 3) The collection and sort of all data are worked out, and experts discuss and provide their suggestions for this project.

4.1 An Illustration of the Proposed Methods

Using the selection procedure proposed in Section 3.3 to this given project, the four PDSWTPs (PPP, EPC, DBB, and DB) make up the alternative PDSWTP set $A=\left\{A_1,A_2,A_3,A_4\right\}$ of delivery options which is the set $C=\left\{C_1,C_2,C_3,C_4,C_5,C_6,C_7,C_8,C_9,C_{10},C_{11},C_{12},C_{13},\right\}$ that denotes the set of ten indicators (i.e., LDC, Pr, PDSc, OEC, RMA, PE, PCI, MQ, SRC, FSI, SGC, TCS, ACP). We assume that $\left(u_{ij}^{\left(l\right)},v_{ij}^{\left(l\right)}\right)\left(i=\mathrm{1,2,3,4};j=\mathrm{1,2},\dots ,13;l=\mathrm{1,2,3,4,5}\right)$ is the evaluation value from the $l\text{th}$ expert to delivery option $A_i$ with respect to criteria $C_j$, which is characterized by PFN (Ejegwa et al., 2021; Ejegwa et al., 2022); and $E_{4\times 10}^{\left(l\right)}={\left(E_{ij}^{\left(l\right)}\right)}_{4\times 13}={\left(u_{ij}^{\left(l\right)},v_{ij}^{\left(l\right)}\right)}_{4\times 13}\left(l=\mathrm{1,2,3,4,5}\right)$ denotes the PFN evaluation matrix (Ejegwa and Jana, 2021) from the $l\text{th}$ expert. They are as follows:

$E_{4\times 13}^{\left(1\right)}=\left(\begin{array}{cccccc}\mathit{\text{p}}\left(0.7,0.4\right)& \mathit{\text{p}}\left(0.7,0.3\right)& \mathit{\text{p}}\left(0.7,0.3\right)& \mathit{\text{p}}\left(0.7,0.2\right)& \mathit{\text{p}}\left(0.6,0.3\right)& \begin{array}{cc}\mathit{\text{p}}\left(0.8,0.2\right)& \mathit{\text{p}}\left(0.7,0.3\right)\end{array}\\ \mathit{\text{p}}\left(0.6,0.2\right)& \mathit{\text{p}}\left(0.7,0.2\right)& \mathit{\text{p}}\left(0.7,0.2\right)& \mathit{\text{p}}\left(0.6,0.4\right)& \mathit{\text{p}}\left(0.6,0.3\right)& \begin{array}{cc}\mathit{\text{p}}\left(0.6,0.3\right)& \mathit{\text{p}}\left(0.7,0.2\right)\end{array}\\ \mathit{\text{p}}\left(0.5,0.2\right)& \mathit{\text{p}}\left(0.8,0.3\right)& \mathit{\text{p}}\left(0.6,0.3\right)& \mathit{\text{p}}\left(0.5,0.4\right)& \mathit{\text{p}}\left(0.7,0.3\right)& \begin{array}{cc}\mathit{\text{p}}\left(0.5,0.4\right)& \text{p}\left(0.5,0.2\right)\end{array}\\ \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.4\right)& \text{p}\left(0.8,0.4\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.6,0.4\right)& \begin{array}{cc}\text{p}\left(0.7,0.3\right)& \text{p}\left(0.6,0.4\right)\end{array}\end{array}\begin{array}{cccccc}\text{p}\left(0.7,0.4\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.5,0.2\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.7,0.3\right)\\ \text{p}\left(0.7,0.2\right)& \text{p}\left(0.5,0.4\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.5,0.2\right)& \text{p}\left(0.5,0.4\right)\\ \text{p}\left(0.5,0.3\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.5,0.2\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.7,0.5\right)\\ \text{p}\left(0.6,0.4\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.5,0.3\right)& \text{p}\left(0.8,0.5\right)& \text{p}\left(0.5,0.3\right)& \text{p}\left(0.6,0.2\right)\end{array}\right)$

$E_{4\times 13}^{\left(2\right)}=\left(\begin{array}{cccccc}\text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.1\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.6,0.3\right)& \begin{array}{cc}\text{p}\left(0.8,0.2\right)& \text{p}\left(0.7,0.2\right)\end{array}\\ \text{p}\left(0.8,0.3\right)& \text{p}\left(0.5,0.2\right)& \text{p}\left(0.6,0.4\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.9,0.3\right)& \begin{array}{cc}\text{p}\left(0.7,0.4\right)& \text{p}\left(0.7,0.3\right)\end{array}\\ \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.4\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.7,0.3\right)& \text{p}\left(0.5,0.3\right)& \begin{array}{cc}\text{p}\left(0.5,0.4\right)& \text{p}\left(0.8,0.3\right)\end{array}\\ \text{p}\left(0.7,0.2\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.6,0.4\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.2\right)& \begin{array}{cc}\text{p}\left(0.6,0.3\right)& \text{p}\left(0.6,0.4\right)\end{array}\end{array}\begin{array}{cccccc}\text{p}\left(0.7,0.5\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.5,0.2\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.7,0.3\right)\\ \text{p}\left(0.5,0.4\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.7,0.3\right)& \text{p}\left(0.7,0.3\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.6,0.3\right)\\ \text{p}\left(0.5,0.3\right)& \text{p}\left(0.7,0.3\right)& \text{p}\left(0.6,0.4\right)& \text{p}\left(0.7,0.4\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.5,0.3\right)\\ \text{p}\left(0.6,0.2\right)& \text{p}\left(0.5,0.4\right)& \text{p}\left(0.4,0.2\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.7,0.4\right)\end{array}\right)$

$E_{4\times 13}^{\left(4\right)}=\left(\begin{array}{cccccc}\text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.7,0.1\right)& \text{p}\left(0.6,0.3\right)& \begin{array}{cc}\text{p}\left(0.8,0.2\right)& \text{p}\left(0.7,0.1\right)\end{array}\\ \text{p}\left(0.7,0.4\right)& \text{p}\left(0.7,0.3\right)& \text{p}\left(0.4,0.2\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.8,0.4\right)& \begin{array}{cc}\text{p}\left(0.7,0.4\right)& \text{p}\left(0.6,0.4\right)\end{array}\\ \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.5\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.7,0.2\right)& \begin{array}{cc}\text{p}\left(0.6,0.2\right)& \text{p}\left(0.6,0.3\right)\end{array}\\ \text{p}\left(0.8,0.4\right)& \text{p}\left(0.5,0.3\right)& \text{p}\left(0.7,0.4\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.7,0.4\right)& \begin{array}{cc}\text{p}\left(0.6,0.3\right)& \text{p}\left(0.6,0.3\right)\end{array}\end{array}\begin{array}{cccccc}\text{p}\left(0.7,0.5\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.5,0.2\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.7,0.3\right)\\ \text{p}\left(0.4,0.2\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.8,0.4\right)\\ \text{p}\left(0.5,0.3\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.6,0.4\right)& \text{p}\left(0.5,0.3\right)& \text{p}\left(0.5,0.3\right)\\ \text{p}\left(0.6,0.2\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.4\right)& \text{p}\left(0.6,0.4\right)& \text{p}\left(0.6,0.4\right)\end{array}\right)$

$E_{4\times 13}^{\left(5\right)}=\left(\begin{array}{cccccc}\text{p}\left(0.6,0.1\right)& \text{p}\left(0.7,0.3\right)& \text{p}\left(0.7,0.1\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.6,0.3\right)& \begin{array}{cc}\text{p}\left(0.8,0.2\right)& \text{p}\left(0.7,0.3\right)\end{array}\\ \text{p}\left(0.5,0.2\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.6,0.4\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.5,0.3\right)& \begin{array}{cc}\text{p}\left(0.6,0.3\right)& \text{p}\left(0.5,0.3\right)\end{array}\\ \text{p}\left(0.6,0.3\right)& \text{p}\left(0.8,0.5\right)& \text{p}\left(0.7,0.5\right)& \text{p}\left(0.4,0.2\right)& \text{p}\left(0.8,0.2\right)& \begin{array}{cc}\text{p}\left(0.5,0.3\right)& \text{p}\left(0.6,0.3\right)\end{array}\\ \text{p}\left(0.6,0.3\right)& \text{p}\left(0.5,0.4\right)& \text{p}\left(0.5,0.3\right)& \text{p}\left(0.5,0.3\right)& \text{p}\left(0.8,0.3\right)& \begin{array}{cc}\text{p}\left(0.4,0.2\right)& \text{p}\left(0.5,0.2\right)\end{array}\end{array}\begin{array}{cccccc}\text{p}\left(0.7,0.5\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.5,0.1\right)& \text{p}\left(0.8,0.2\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.7,0.3\right)\\ \text{p}\left(0.6,0.4\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.6,0.4\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.4\right)& \text{p}\left(0.7,0.3\right)\\ \text{p}\left(0.5,0.3\right)& \text{p}\left(0.8,0.3\right)& \text{p}\left(0.5,0.2\right)& \text{p}\left(0.6,0.3\right)& \text{p}\left(0.7,0.2\right)& \text{p}\left(0.4,0.2\right)\\ \text{p}\left(0.4,0.2\right)& \text{p}\left(0.6,0.2\right)& \text{p}\left(0.4,0.2\right)& \text{p}\left(0.7,0.4\right)& \text{p}\left(0.5,0.3\right)& \text{p}\left(0.5,0.3\right)\end{array}\right)$

According to the selection procedure for PDSWTPs, the steps are as follows:

Step 1: Construct Pythagorean fuzzy evaluation matrix through aggregating the evaluation information of five experts by Definition 5, and the weights of every expert are $W_1=W_2=\cdots =W_5=0.2$. The Pythagorean fuzzy evaluation matrix is determined as follows:

$E_{4\times 13}=\left(\begin{array}{cccccc}\text{p}\left(0.62,0.28\right)& \text{p}\left(0.70,0.24\right)& \text{p}\left(0.70,0.20\right)& \text{p}\left(0.72,0.18\right)& \text{p}\left(0.60,0.30\right)& \text{p}\left(0.80,0.20\right)\\ \text{p}\left(0.63,0.26\right)& \text{p}\left(0.63,0.26\right)& \text{p}\left(0.55,0.31\right)& \text{p}\left(0.70,0.29\right)& \text{p}\left(0.70,0.32\right)& \text{p}\left(0.61,0.32\right)\\ \text{p}\left(0.58,0.27\right)& \text{p}\left(0.74,0.40\right)& \text{p}\left(0.64,0.29\right)& \text{p}\left(0.55,0.29\right)& \text{p}\left(0.69,0.26\right)& \text{p}\left(0.57,0.33\right)\\ \text{p}\left(0.69,0.35\right)& \text{p}\left(0.60,0.33\right)& \text{p}\left(0.71,0.35\right)& \text{p}\left(0.66,0.30\right)& \text{p}\left(0.68,0.30\right)& \text{p}\left(0.57,0.32\right)\end{array}\begin{array}{cccccc}\text{p}\left(0.72,0.22\right)& \text{p}\left(0.70,0.48\right)& \text{p}\left(0.70,0.20\right)& \text{p}\left(0.50,0.18\right)& \text{p}\left(0.80,0.28\right)& \text{p}\left(0.64,0.20\right)\\ \text{p}\left(0.64,0.30\right)& \text{p}\left(0.54,0.32\right)& \text{p}\left(0.66,0.28\right)& \text{p}\left(0.61,0.30\right)& \text{p}\left(0.69,0.25\right)& \text{p}\left(0.67,0.26\right)\\ \text{p}\left(0.63,0.29\right)& \text{p}\left(0.52,0.30\right)& \text{p}\left(0.69,0.28\right)& \text{p}\left(0.54,0.28\right)& \text{p}\left(0.62,0.33\right)& \text{p}\left(0.65,0.27\right)\\ \text{p}\left(0.53,0.26\right)& \text{p}\left(0.55,0.25\right)& \text{p}\left(0.65,0.28\right)& \text{p}\left(0.48,0.28\right)& \text{p}\left(0.71,0.35\right)& \text{p}\left(0.56,0.32\right)\end{array}\begin{array}{c}\text{p}\left(0.70,0.30\right)\\ \text{p}\left(0.61,0.31\right)\\ \text{p}\left(0.54,0.34\right)\\ \text{p}\left(0.59,0.30\right)\end{array}\right)$

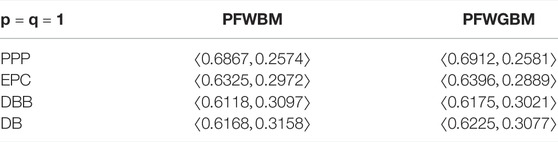
Step 2: From Eqs. 7, 8, the comprehensively evaluation results obtained by PFWBM and PFWGBM with $\text{p}=q=1$ are shown in Table 1.

TABLE 1

TABLE 1. The comprehensive evaluation results using the PFWBM and PFWGBM operators.

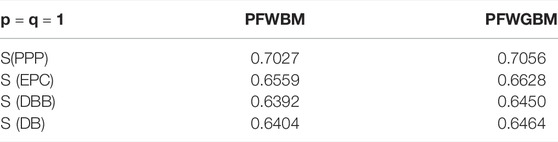
Step 3: Using Eqs. 1, 2, the score functions of the comprehensive evaluation values for all alternative PDSWTPs are calculated as shown in Table 2.

TABLE 2

TABLE 2. The comprehensive evaluation results using PFWBM and PFWGBM operators.

Step 4: From the results obtained in steps 3 and 4, the ranking order using the PFWBM operator is $PPP\succ EPC\succ DB\succ DBB$, when $\text{p}=q=1$, and the ranking order using the PFWGBM operator is $PPP\succ EPC\succ DB\succ DBB$. The ranking results using the two operators are the same. According to the ranking orders, the PPP is the best suitable PDSWTP.

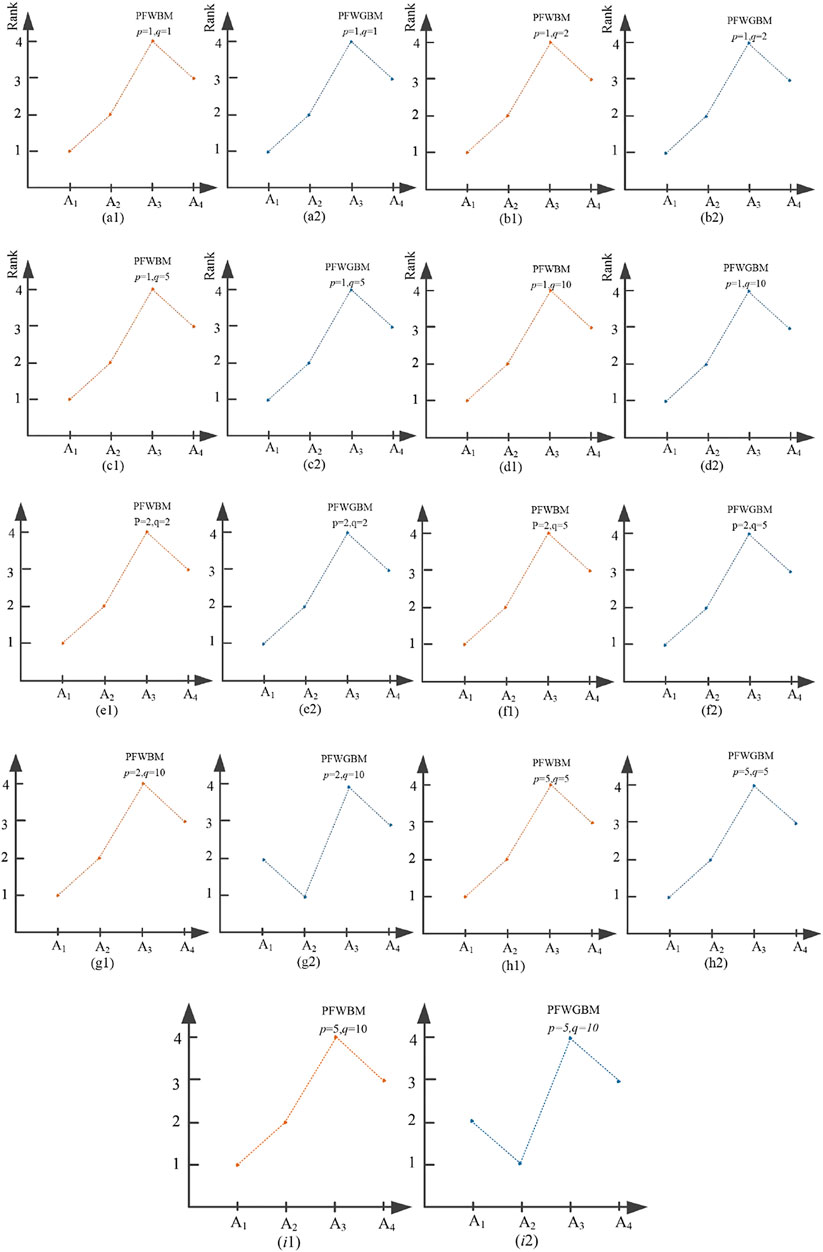
4.2 Sensitivity Analysis

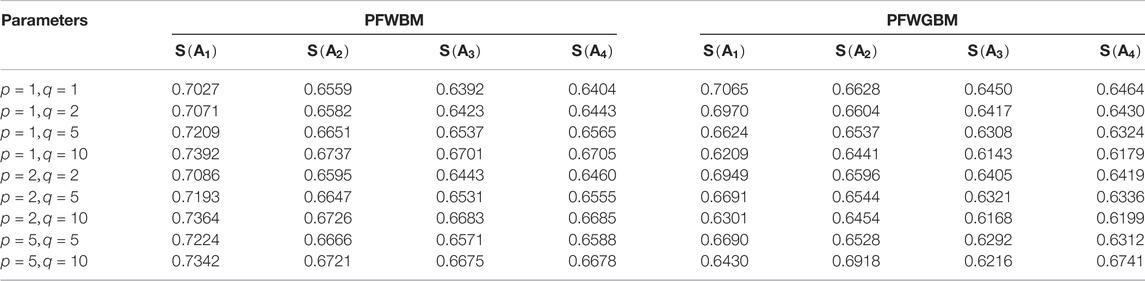
This subsection will give a sensitivity analysis for the result of the proposed method based on the abovementioned results, since the results using the PFWBM and PFWGBM vary with the change of the parameters $\text{p}$ and $q$. Firstly, the score function values of all alternatives obtained by the two operators can be calculated when the parameters $\text{p}$ and $q$ take different values. And the score function values of all alternatives are shown in Table 3.

TABLE 3

TABLE 3. The score function values with different parameters.

From the results in Table 3, the score function values of all alternatives increase with the increase of parameters. Therefore, the decision-maker can choose the appropriate values of parameters $\text{p}$ and $q$ according to their own risk preference. Subsequently, the ranking orders using PFWBM and PFWGBM operators can be obtained, as shown in Figure 3. It is obviously that the results using different methods are mostly the same. That is, the best suitable PDSWTP is PPP using PFWBM and also using PFWGBM. Other than that, only when the parameters take two cases: $\text{p}=2$, $q=10$ and $\text{p}=5$, $q=10$, the best system is EPC for the PFWGBM operator, which is shown as (g2) and (i2) in Figure 3. From Figure 3, the results obtained by PFWBM are all the same with different values of parameters $\text{p}$ and $q$, and PFWGBM operators are slightly different with the different values of $\text{p}$ and $q$. Based on this, the robustness of the proposed method is verified well.

FIGURE 3

FIGURE 3. The ranking orders with different parameters.

4.3 Comparative Analysis and Discussions

This section gives a comparative analysis between the proposed methods and the existing methods to state the advantage of the proposed methods.

In the method developed by Yager (2014), two aggregation operators, including a Pythagorean fuzzy weighted aggregate (PFWA) operator and Pythagorean fuzzy weighted geometric (PFWG) operator, were employed to aggregate the evaluation information, and then to rank the alternatives using the score and accuracy functions. Ma and Xu (2016) defined symmetric Pythagorean fuzzy weighted averaging (SPFWA) and symmetric Pythagorean fuzzy weighted geometric (SPFWG) operators, and also ranked the alternatives using the score and accuracy functions. The following gives the comparative analysis only discussing the case where parameters of the proposed methods are all equal to 1, since the robustness of them with different values for $\text{p}$ and $q$, as shown in Section 4.1, is very stable. The ranking orders using different methods are shown in Table 4.

TABLE 4

TABLE 4. The ranking orders of all alternatives with different operators.

As shown in Table 4, the ranking results using PFWA, PFWG, and SPFWG are the same, that is, $A_1\succ A_2\succ A_3\succ A_4$, while the results are all $A_1\succ A_2\succ A_4\succ A_3$ using SPFWA, PFWBM ($\text{p}=1$, $q=1$), and PFWGBM($\text{p}=1$, $q=1$). Therefore, the results obtained by the four methods are mostly the same, and the best PDSWTP is the same using each method, though there is a slightly difference between the existing methods and the proposed method. The main reason for the difference is that the proposed methods can capture the interrelationship among all indicators, which is more applicable to practical problems.

Compared with the existing method, the proposed method, in which the evaluation information is characterized by Pythagorean fuzzy numbers, showed more accurate results in the selection process and simultaneously considered the relationship among all factors affecting PDSWTP selection, so as to capture the authenticity of the practical problem. Moreover, from the result obtained in this case study, PPP is a best choice among all PDSs, which is a more suitable mode in practice compared to other modes. It can overcome the financial difficulties through giving full play to the advantage of capital and technology in the private sector.

From the perspective of engineering practice, the success of a project is often affected by many factors, and the relationships among them are complex. Specifically, the LDC is closely related to PDSc, the higher the level of LDC, the greater the impact on PDSc. And when the level of RMA is high, it can reasonably avoid the project risk and escort the project onto the right track, so as to ensure the timely delivery of the project. Additionally, when the accuracy of PE is higher, the potential of ACP may be reduced, which shows a strong relationship between PE and Pr. In fact, all criteria have a related correlation with SGC, since the change of each factor will lead to the difference of the sustainability and safety of the project. As such, the owner needs to invest more money to improve the project quality in order to promote the sustainability of the project, when MQ is extremely poor. And a high personnel demand and ability SRC, that is, a company that has high-tech talents, can greatly promote the success of the project, and so on. In short, the correlation between criteria should be considered in PDSWTP selection. Only considering the interrelation among all criteria can we highlight the accuracy of the selection result to the greatest extent, which avoids the occurrence of distortion or imprecision of the selection results.

5 Conclusion

PDSWTP selection plays an important role to effectively improve the construction management effect of wastewater treatment, and is affected by several factors such as the level of design completed, procurement, project delivery schedule, and so on. Commonly, the relationships among all indicators affecting PDSWTP selection are ignored in a practical situation. Based on this, this study aimed to investigate PDSWTP selection using existing theories.

To achieve this object, this study mainly focused on the characteristics and aggregation of fuzzy information in the actual PDSWTP selection process through combining the advantages of Pythagorean fuzzy sets and Bonferroni mean operators. Specifically, PFS can handle imprecise and ambiguous information and manage complex uncertainties in applications, and the Bonferroni mean operator can aggregate evaluation information of indicators with relevance in the selection process. Motivated by such considerations, in this line of the study, the Pythagorean fuzzy weighted Bonferroni mean operator and Pythagorean fuzzy weighted geometric Bonferroni mean operator were introduced, which could solve the PDSWTP selection problem.

The main contributions of this study are as follows: 1) Considering the existence of the relevance among all indicators affecting PDSWTP selection and the complexity and fuzziness of the actual selection process, this study innovatively introduced the Bonferroni mean operator and Pythagorean fuzzy to deal with PDSWTP selection problems. 2) To aggregate the evaluation information of all related indicators affecting PDSWTP selection, this study introduced the Pythagorean fuzzy weighted Bonferroni mean (PFWBM) and Pythagorean fuzzy geometry weighted Bonferroni mean (PFWGBM) operators using Pythagorean fuzzy sets theory and the Bonferroni mean operator. 3) A PDSWTP selection method based on the PFWBM and PFWGBM operators was established, which can deal with the related indicators for PDSWTP selection problem by taking advantage of PFSs and PFWMM operators. Finally, robust analysis of the PDSWTP selection was given through taking different the values of parameters $\text{p}$ and $q$, and by comparing the proposed method with PFWA, PFWG, SPFWA, and SPFWG operators, the best PDSWTP was the same from the ranking results. Moreover, a practice example of PDSWTP selection was given and showed the effectiveness and applicability of the proposed method.

Based on the above analysis, the advantages of the proposed methods are as follows: Firstly, the proposed methods, in which the evaluation values information was characterized by Pythagorean fuzzy sets, were more capable of representing evaluation values information with uncertainty, inconformity, and incompleteness. Second, the proposed method, which combined the Bonferroni mean operator and Pythagorean fuzzy sets theory, established a robust selection process to solve the PDSWTP selection problem. And the results obtained by the proposed method were more reliable. Compared with the existing methods, the proposed PDSWTP selection method considered the correlation among indicators, which extends the applied scope of the decision-making theory. Furthermore, the best suitable PDSWTP was PPP, which is more in line with the actual situation. Because the capital and technical resources were very scarce at the location of the project, the adoption of a PPP mode could give full play to the advantages of the capital and technical resources from the private sector, and promote the sustainability of the project, so as to better serve public and social services.

In future research, it is necessary to extend methods and theories to other MCDM problems, and more operator theories should be developed and extended to other fuzzy sets, such as supplier selection, risk assessment, and environment evaluation problems under an interval Pythagorean fuzzy set or triangle intuitionistic fuzzy set.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

HL and YC contributed to conception and design of the study. LS and FW organized the database. HL and YC wrote the first draft of the manuscript. LS and FW wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The authors acknowledge with gratitude the National Key RandD Program of China (No. 2018YFC0406905), MOE (Ministry of Education in China) Project of Humanities and Social Sciences (No. 19YJC630078), Youth Talents Teachers Scheme of Henan Province Universities (No. 2018GGJS080), the National Natural Science Foundation of China (No. 71302191), the Foundation for Distinguished Young Talents in Higher Education of Henan (Humanities and Social Sciences), China (No. 2017-cxrc-023), doctoral student Innovation Fund of North China University of Water Resources and Electric Power, Key Science and Technology Projects in Henan Province (212102310306) and the 2018 Henan Province Water Conservancy Science and Technology Project (GG201828). This study would not have been possible without their financial support.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, S., and El-Sayegh, S. (2022). The Challenges of Sustainable Construction Projects Delivery - Evidence from the UAE. Archit. Eng. Des. Manag. Early Access. doi:10.1080/17452007.2022.2027224

CrossRef Full Text | Google Scholar

An, X., Wang, Z., Li, H., and Ding, J. (2018). Project Delivery System Selection with Interval-Valued Intuitionistic Fuzzy Set Group Decision-Making Method. Group Decis. Negot. 27, 689–707. doi:10.1007/s10726-018-9581-y

CrossRef Full Text | Google Scholar

Andary, E. G., Abi Shdid, C., Chowdhury, A., and Ahmad, I. (2019). Integrated Project Delivery Implementation Framework for Water and Wastewater Treatment Plant Projects. Ecam 27 (3), 609–633. doi:10.1108/ECAM-02-2019-0075

CrossRef Full Text | Google Scholar

ASCE (2017). 2017 Infrastructure Report Card. Reston, VA: American Society of Civil Engineers. Available at: https://www.infrastructurereportcard.org/(accessed September 28, 2020).

Google Scholar

ASCE (1988). Quality in the Constructed Project: A Guideline for Owners, Designers, and Constructors. doi:10.1061/9780784411896

CrossRef Full Text | Google Scholar

ASCE (2020). The Economic Benefits of Investing in Water Infrastructure: How A Failure to Act Would Affect the Us Economic Recovery. Reston, VA: American Society of Civil Engineers. Available at: https://www.asce.org/uploadedFiles/Issues_and_Advocacy/Infrastructure/Content_Pieces/Failure%20to%20Act%20Water%20Wastewater%202020%20Final.pdf (Accessed September 28, 2020).

Google Scholar

Bonferroni, C. (1950). Sulle Medie Multiple Di Potenze. Boll. dell Union Mat. Ital. 5 (3-4), 267–270. available at: http://eudml.org/doc/196058.

Google Scholar

Chen, Y. Q., Liu, J. Y., Li, B., and Lin, B. (2011). Project Delivery System Selection of Construction Projects in China. Expert Syst. Appl. 38 (5), 5456–5462. doi:10.1016/j.eswa.2010.10.008

CrossRef Full Text | Google Scholar

Culp, G. (2011). Alternative Project Delivery Methods for Water and Wastewater Projects: Do They Save Time and Money? Leadersh. Manage. Eng. 11 (3), 231–240. doi:10.1061/(ASCE)LM.1943-5630.0000133

CrossRef Full Text | Google Scholar

Ejegwa, P. A., Adah, V., and Onyeke, I. C. (2022). Some Modified Pythagorean Fuzzy Correlation Measures with Application in Determining Some Selected Decision-Making Problems. Granul. Comput. 7, 381–391. doi:10.1007/s41066-021-00272-4

CrossRef Full Text | Google Scholar

Ejegwa, P. A., and Jana, C. (2021). “Some New Weighted Correlation Coefficients Between Pythagorean Fuzzy Sets and Their Applications,” in Pythagorean Fuzzy Sets. Editor H Garg (Singapore: Springer), 39–64. doi:10.1007/978-981-16-1989-2_2

CrossRef Full Text | Google Scholar

Ejegwa, P. A., Wen, S., Feng, Y., Zhang, W., and Chen, J. (2021). Some New Pythagorean Fuzzy Correlation Techniques via Statistical Viewpoint with Applications to Decision-Making Problems. Ifs 40 (5), 9873–9886. doi:10.3233/JIFS-202469

CrossRef Full Text | Google Scholar

Feghaly, J., El Asmar, M., Ariaratnam, S., Bearup, W., and Bearup, W. (2020). Selecting Project Delivery Methods for Water Treatment Plants. Ecam 27 (4), 936–951. doi:10.1108/ECAM-06-2019-0308

CrossRef Full Text | Google Scholar

Ibrahim, M. W., Hanna, A., and Kievet, D. (2020). Quantitative Comparison of Project Performance Between Project Delivery Systems. J. Manage. Eng. 36 (6), 04020082. doi:10.1061/(asce)me.1943-5479.0000837

CrossRef Full Text | Google Scholar

Jana, C., Muhiuddin, G., and Pal, M. (2019b). Some Dombi Aggregation of Q ‐Rng Orthopair Fuzzy Numbers in Multiple‐Attribute Decision Making. Int. J. Intell. Syst. 34 (12), 3220–3240. doi:10.1002/int.22191

CrossRef Full Text | Google Scholar

Jana, C., Senapati, T., and Pal, M. (2019a). Pythagorean Fuzzy Dombi Aggregation Operators and its Applications in Multiple Attribute Decision‐Making. Int. J. Intell. Syst. 34 (9), 2019–2038. doi:10.1002/int.22125

CrossRef Full Text | Google Scholar

Khanzadi, M., Nasirzadeh, F., Hassani, S. M. H., and Nejad Mohtashemi, N. (2016). An Integrated Fuzzy Multi-Criteria Group Decision Making Approach for Project Delivery System Selection. Sci. Iran. 23 (3), 802–814. doi:10.24200/sci.2016.2160

CrossRef Full Text | Google Scholar

Li, H., Cao, Y., and Su, L. (2022). Pythagorean Fuzzy Multi-Criteria Decision-Making Approach Based on Spearman Rank Correlation Coefficient. Soft Comput. 26 (2), 3001–3012. doi:10.1007/s00500-021-06615-2

CrossRef Full Text | Google Scholar

Liang, D., Darko, A. P., and Xu, Z. (2019). Pythagorean Fuzzy Partitioned Geometric Bonferroni Mean and its Application to Multi-Criteria Group Decision Making with Grey Relational Analysis. Int. J. Fuzzy Syst. 21, 115–128. doi:10.1007/s40815-018-0544-x

CrossRef Full Text | Google Scholar

Liang, D., Zhang, Y., Xu, Z., and Darko, A. P. (2018). Pythagorean Fuzzy Bonferroni Mean Aggregation Operator and its Accelerative Calculating Algorithm with the Multithreading. Int. J. Intell. Syst. 33 (3), 615–633. doi:10.1002/int.21960

CrossRef Full Text | Google Scholar

Liu, X., and Liu, H. (2019). Application of Fuzzy Ordered Weighted Geometric Averaging (FOWGA) Operator for Project Delivery System Decision-Making. Soft Comput. 23 (24), 13297–13307. doi:10.1007/s00500-019-03872-0

CrossRef Full Text | Google Scholar

Ma, Z., and Xu, Z. (2016). Symmetric Pythagorean Fuzzy Weighted Geometric/Averaging Operators and Their Application in Multicriteria Decision-Making Problems. Int. J. Intell. Syst. 31 (12), 1198–1219. doi:10.1002/int.21823

CrossRef Full Text | Google Scholar

Nie, R. X., Tian, Z. P., Wang, J. Q., and Hu, J. H. (2019). Pythagorean Fuzzy Multiple Criteria Decision Analysis Based on Shapley Fuzzy Measures and Partitioned Normalized Weighted Bonferroni Mean Operator. Int. J. Intell. Syst. 34, 297–324. doi:10.1002/int.22051

CrossRef Full Text | Google Scholar

Reformat, M. Z., and Yager, R. R. (2014). “Suggesting Recommendations Using Pythagorean Fuzzy Sets Illustrated Using Netflix Movie Data,” in Information Processing and Management of Uncertainty in Knowledge-Based Systems. Montpellier, France, 546–556. doi:10.1007/978-3-319-08795-5_56

CrossRef Full Text | Google Scholar

Ren, P., Xu, Z., and Gou, X. (2016). Pythagorean Fuzzy TODIM Approach to Multi-Criteria Decision Making. Appl. Soft Comput. 42, 246–259. doi:10.1016/j.asoc.2015.12.020

CrossRef Full Text | Google Scholar

Shrestha, P. P., and Batista, J. R. (2021). Transition from Traditional to Alternative Project Delivery Methods in Water and Wastewater Project: Executive Decision-Makers' Perspective. Ecam. doi:10.1108/ECAM-10-2020-0791

CrossRef Full Text | Google Scholar

Su, L., Li, H., Cao, Y., and Lv, L. (2019). Project Delivery System Decision Making Using Pythagorean Fuzzy TOPSIS. Ee 30 (4), 461–471. doi:10.5755/j01.ee.30.4.22041

CrossRef Full Text | Google Scholar

Sun, M., and Liu, J. (2013). Normalized Geometric Bonferroni Operators of Hesitant Fuzzy Sets and Their Application in Multiple Attribute Decision Making. J. Inf. Comput. Sci. 10 (9), 2815–2822. doi:10.12733/jics20101859

CrossRef Full Text | Google Scholar

Wang, L., and Li, N. (2020). Pythagorean Fuzzy Interaction Power Bonferroni Mean Aggregation Operators in Multiple Attribute Decision Making. Int. J. Intell. Syst. 35 (1), 150–183. doi:10.1002/int.22204

CrossRef Full Text | Google Scholar

Wei, G. (2017). Pythagorean Fuzzy Interaction Aggregation Operators and Their Application to Multiple Attribute Decision Making. Ifs 33 (4), 2119–2132. doi:10.3233/JIFS-162030

CrossRef Full Text | Google Scholar

Xia, M., Xu, Z., and Zhu, B. (2013). Geometric Bonferroni Means with Their Application in Multi-Criteria Decision Making. Knowledge-Based Syst. 40, 88–100. doi:10.1016/j.knosys.2012.11.013

CrossRef Full Text | Google Scholar

Yager, R. R., and Abbasov, A. M. (2013). Pythagorean Membership Grades, Complex Numbers, and Decision Making. Int. J. Intell. Syst. 28 (5), 436–452. doi:10.1002/int.21584

CrossRef Full Text | Google Scholar

Yager, R. R. (2014). Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Trans. Fuzzy Syst. 22 (4), 958–965. doi:10.1109/TFUZZ.2013.2278989

CrossRef Full Text | Google Scholar

Yang, Y., Chin, K. S., Ding, H., Lv, H. X., and Li, Y. L. (2019). Pythagorean Fuzzy Bonferroni Means Based on T‐Norm and its Dual T‐Conorm. Int. J. Intell. Syst. 34 (6), 1303–1336. doi:10.1002/int.22097

CrossRef Full Text | Google Scholar

Zhang, X., and Xu, Z. (2014). Extension of TOPSIS to Multiple Criteria Decision Making with Pythagorean Fuzzy Sets. Int. J. Intell. Syst. 29 (12), 1061–1078. doi:10.1002/int.21676

CrossRef Full Text | Google Scholar

Zhou, W., and He, J.-m. (2012). Intuitionistic Fuzzy Normalized Weighted Bonferroni Mean and its Application in Multicriteria Decision Making. J. Appl. Math. 2012, 1–22. doi:10.1155/2012/136254

CrossRef Full Text | Google Scholar

Zhu, X., Bai, K., Wang, J., Zhang, R., and Xing, Y. (2019). Pythagorean Fuzzy Interaction Power Partitioned Bonferroni Means with Applications to Multi-Attribute Group Decision Making. Ifs 36 (4), 3423–3438. doi:10.3233/JIFS-181171

CrossRef Full Text | Google Scholar

Zhu, X., Meng, X., and Chen, Y. (2020). A Novel Decision-Making Model for Selecting A Construction Project Delivery System. J. Civ. Eng. Manag. 26 (7), 635–650. doi:10.3846/jcem.2020.12915

CrossRef Full Text | Google Scholar