Pouyan Ahmadi1*
Hassan Elagami2,3
Franz Dichgans1
Christian Schmidt1,4
Benjamin S. Gilfedder2,3
Sven Frei3
Stefan Peiffer3
Jan H. Fleckenstein1,5*- 1Department of Hydrogeology, Helmholtz-Centre for Environmental Research, UFZ, Leipzig, Germany
- 2Limnological Research Station, Bayreuth Center of Ecology and Environmental Research, University of Bayreuth, Bayreuth, Germany
- 3Department of Hydrology, Bayreuth Center of Ecology and Environmental Research (BayCEER), University of Bayreuth, Bayreuth, Germany
- 4Department of Aquatic Systems Analysis and Management, Helmholtz-Centre for Environmental Research, UFZ, Leipzig, Germany
- 5Hydrologic Modelling Unit, Bayreuth Center of Ecology and Environmental Research (BayCEER), University of Bayreuth, Bayreuth, Germany
Microplastic (MP) particles are commonly found in freshwater environments such as rivers and lakes, negatively affecting aquatic organisms and potentially causing water quality issues. Understanding the transport and fate of MP particles in these environments is a key prerequisite to mitigate the problem. For standing water bodies (lakes, ponds) the terminal settling velocity (TSV) is a key parameter, which determines particle residence times and exposure times of organisms to MP in lakes. Here we systematically investigate the effects of the physical parameters density, volume, shape and roundness, surface roughness and hydrophobicity and lake water temperature on the TSV of a large number of particles with regular and irregular shapes (equivalent diameters: 0.5–2.5 mm) and different polymer densities using computational fluid dynamics (CFD) simulations. Simulation results are compared to laboratory settling experiments and used to evaluate existing, semi-empirical relationships to estimate TSV. The semi-empirical relationships were generally found to be in reasonable agreement with the CFD simulations (R2 > 0.92). Deviations were attributed to simplifications in their descriptions of particle shapes. Overall the CFD simulations also matched the TSVs from the experiments quite well, (R2 > 0.82), but experimental TSVs were generally slower than model TSVs with the largest differences for the irregular particles made from biodegradable polymers. The deviations of up to 58% were found to be related to the attachment of air bubbles on irregularities in the particle surfaces caused by the hydrophobicity of the MP particles. Overall, density was the most decisive parameter for TSV with increases in TSV of up to 400% followed by volume (200%), water temperature (47%) and particle roundness (45%). Our simulation results provide a frame of reference for an improved evaluation of the relative effects of different particle characteristics on their TSV in lakes. This will in turn allow a more robust estimation of particle residence times and potential exposure times of organism to MP in the different compartments of a lake.
1 Introduction
Plastic products have a broad range of applications in all fields of daily life due to their useful properties such as durability and ductility (Derraik, 2002; North and Halden, 2013). Their widespread use, in turn, has led to large amounts of plastic waste, which, if mismanaged, may pose a threat to the environment (Derraik, 2002; Barnes et al., 2009; Claessens et al., 2011). Plastic debris, in a wide variety of sizes, can be found in the oceans, as well as in terrestrial freshwater systems and the atmosphere (Barnes et al., 2009; de Souza Machado et al., 2018; Rochman, 2018; Frias and Nash, 2019; Liao and Chen, 2021). A significant share of the plastic found in the terrestrial and marine environments belongs to the microplastic (MP) fraction (<5 mm -(Barnes et al., 2009)). These MP particles may enter the environment as primary MP via the release from cosmetic products and cleaners, via losses from production plants and during transport (Gregory, 1983; Gregory, 1996; Fendall and Sewell, 2009; Doyle et al., 2011) or as secondary MP resulting from the break-down and erosion of larger plastic debris in the environment (Williams and Simmons, 1996; Browne et al., 2011; Wright et al., 2020). Although different size ranges have been used to define MP (Claessens et al., 2011; Van Cauwenberghe et al., 2013), an upper size limit of 5,000 µm has been introduced as the definition of MP by the National Oceanic and Atmospheric Administration (Lambert and Wagner, 2018; Sighicelli et al., 2018) and is commonly accepted as the upper size limit in the literature. The lower size limit is not as clearly defined and may vary between different studies depending on their scope and questions (Khatmullina and Isachenko, 2017; Kaiser et al., 2019; Waldschläger and Schüttrumpf, 2019).
Freshwater lakes are amongst the main receptors of MP in the terrestrial environment (Zbyszewski et al., 2014; Ballent et al., 2016; Fischer et al., 2016; Anderson et al., 2017; Vaughan et al., 2017; Hendrickson et al., 2018; Sighicelli et al., 2018). MP particles can be taken up by organisms in different compartments of a lake with detrimental effects on the organisms as well as other organisms at higher trophic levels (Cole et al., 2013; Wright et al., 2013; Cole et al., 2016; Coppock et al., 2019). Transport vectors of MP particles determine their horizontal and vertical distribution patterns in a lake (Khatmullina and Isachenko, 2017; Kaiser et al., 2019; Waldschläger and Schüttrumpf, 2019; Isachenko, 2020) and in turn control residence times in the lake compartments as well as exposure of organisms to MP particles. It is therefore of particular importance to understand the physical controls of particle settling in lakes (Elagami et al., 2022). Vertical transport vectors are strongly controlled by physical parameters that define the force balance between downward gravitational forces, drag forces and upward buoyant forces acting on the body of an individual MP particle. A terminal settling velocity (TSV) is reached at the point where the summation of drag and buoyant forces is approximately equal to the weight force (Chubarenko et al., 2016; Khatmullina and Isachenko, 2017; Zhang, 2017).
Several experimental studies have investigated the TSV of MP particles primarily in marine systems (Arora et al., 2010; Wright et al., 2013; Chubarenko et al., 2016; Kooi et al., 2016; Kowalski et al., 2016; Khatmullina and Isachenko, 2017; Zhang, 2017; Chubarenko et al., 2018; Akdogan and Guven, 2019; Kaiser et al., 2019), with studies explicitly addressing freshwater systems being rare (Khatmullina and Isachenko, 2017; Kaiser et al., 2019; Waldschläger and Schüttrumpf, 2019; Elagami et al., 2022). In some of these studies specific semi-empirical relationships have been developed to predict the TSV of MP particles in water considering particle size, density, and roundness as well as water density and kinematic viscosity (Dietrich, 1982; Khatmullina and Isachenko, 2017; Kaiser et al., 2019; Waldschläger and Schüttrumpf, 2019; Elagami et al., 2022). Comparisons with earlier, well established relationships developed for mineral particles (Dietrich, 1982) suggest that for certain MP characteristics adjustments to the known relationships are needed (Khatmullina and Isachenko, 2017; Waldschläger and Schüttrumpf, 2019). However, adjustments or new formulations on the basis of experiments only reflect the specific shapes of MP particles being used in the experiment and a more general, systematic assessment of the relative importance of different particle characteristics for TSV estimates would be useful. We take a first step in this direction.
Models are a useful tool for a systematic evaluation of particle transport in aquatic environments. Different types of models have been used to simulate the settling and transport of plastic debris, MP particles and individual MP particle in water bodies over a wide range of spatial scales. At global and regional scales studies have focused on MP transport in oceans using Eulerian circulation models for flow in combination with Lagrangian (Berlemont et al., 1990; Maximenko et al., 2012; Jalón-Rojas et al., 2019; Nooteboom et al., 2020; Guerrini et al., 2021) or Eulerian (advective dispersive) (Mountford and Morales Maqueda, 2019) transport formulations. These types of models rely on an adequate description of particle settling, which is typically obtained from semi-empirical relationships derived from experiments. At the smaller, process scale the direct forces acting on particles or sets of particles have been simulated using computational fluid dynamics (CFD) (Zhang, 2017; Jérémy et al., 2020) or Lattice Boltzmann methods (Trunk et al., 2021). While those approaches are computationally expensive they can account for arbitrary particle shapes and properties and provide valuable mechanistic insights into the dominant factors controlling particle settling. In turn they can also be used to validate and refine semi-empirical relationships from experiments. Following this argument, the main objective of this study is to systematically evaluate different factors, such as particle density, size (or volume) and shape, water temperature, and initial orientation of the particle, which control the settling behavior and in turn the TSV of MP particles. We further hypothesize that the hydrophobicity of the surfaces of pristine MP particles will significantly affect their settling behavior and TSV. Along those lines we quantify TSV of MP particle using CFD simulations of a large set of individual particles representing the following seven different polymers: Polystyrene (PS), Polyamide 66 (PA66), Polycaprolacton (PCL), Polylactic acid (PLA), Poly (L-lactic) acid (PLLA), Polybutylenadipate terephthalate (PBAT), Polyvinyl chloride (PVC), which are commonly found in the lake environment (Webb et al., 2013; Wright et al., 2013; Rocha-Santos and Duarte, 2015) over a range of shapes, densities and sizes. First we verify our simulation approach against a set of laboratory experiments using physical conditions and particle parameters in our simulations, which are identical to those from the laboratory experiments of (Elagami et al., 2022), We then compare our simulation results to existing semi-empirical relationships developed for estimating the TSV of mineral (Dietrich, 1982) and MP particles (Waldschläger and Schüttrumpf, 2019) before conducting a systematic, model-based evaluation of the key parameters controlling TSV and their relative importance.
2 Methods
Three methods were used to investigate the TSV of MP particles i) numerical simulations, ii) laboratory settling experiments, iii) semi-empirical settling relationships. For our analyses we used two general classes of particles in terms of their shapes: a) regular spherical particles and b) irregular particles with arbitrary shapes. Additionally we generated a set of virtual, axis-symmetrical (regular) particles derived from revolved polygons (see Section 2.4.1) for a systematic evaluation of the effects of particle roundness, which were only evaluated with the CFD model. The irregular MP particles were selected from larger sets of particles made from seven abundant polymers (PS, PA66, PCL, PLLA, PLA, PBAT, and PVC). These MP particles can be categorized into biodegradable (PCL, PLA and PLLA) versus non-biodegradable (PS, PA66, PBAT, PVC) polymers. Their size and density ranged from 500 to 2,200 μm and 1.03 to 1.38 kgm−3, respectively (cf. Supplementary Material S1, Supplementary TableS1). All biodegradable and non-biodegradable particles were provided by the Department of Macromolecular Chemistry at the University of Bayreuth, Germany. MP particles with sizes smaller than 500 µm were intentionally not considered as the simulation of their settling would require very fine numerical meshes in the simulations and excessive numerical costs, in particular if many particles are to be simulated. Furthermore the settling of very small particles will increasingly be affected by their electro-chemical surface properties and less by their physical shapes and properties (Zhang et al., 2017), so that other tools and methods would be required for an assessment of their settling. The same holds true for very specific shapes like fibers (Wei et al., 2021). Our study specifically focuses on particle settling in standing freshwater (e.g., freshwater lakes), which is in line with the experimental data available for verification. However, it is generally possible to also apply our methodology to other environments such as saltwater lakes, simply by changing the properties of the water in the model. Numerical simulations form the core of this work, while the experiments and semi-empirical relationships are used to provide a reference for the simulations. In the following the three different methods are described in more detail.
2.1 Model Setup and Boundary Conditions
To simulate the TSV of MP particles, we use the solver overInterDyMFoam out of the open source C++ toolbox OpenFOAM v1812 (Weller et al., 1998). The used solver is for two incompressible, immiscible fluids (water and air in this application), which employs the volume-of-fluid method to capture the water-air interface. It solves the Navier-Stokes equations and supports moving meshes using the overset method. In the present study, we employed the overset method (also known as Chimera framework (Houzeaux et al., 2014)), as it allows to simulate MP settling in a deep-water column without the need for any mesh deformation.
The general simulation setup consists of two mesh domains for i) the water column (background mesh) and ii) the particle and its close surroundings (overset mesh) as shown in Figure 1A. As the two mesh sets are disconnected, the approach allows for a large freedom in movement (6 DOF) of the simulated object, especially compared to traditional approaches which employ mesh morphing/deformation. While the background mesh remains stationary, the overset mesh can move according to the calculated forces on the enclosed object. During each time step, the cells covered by the overset mesh are removed from the background mesh (cell type “hole”). The results are exchanged/interpolated at the boundary between the background and overset mesh using specific patch types. As the overset mesh is moving, the holes and interfacial patch cells are re-defined for each time step based on the current position of the overset mesh.
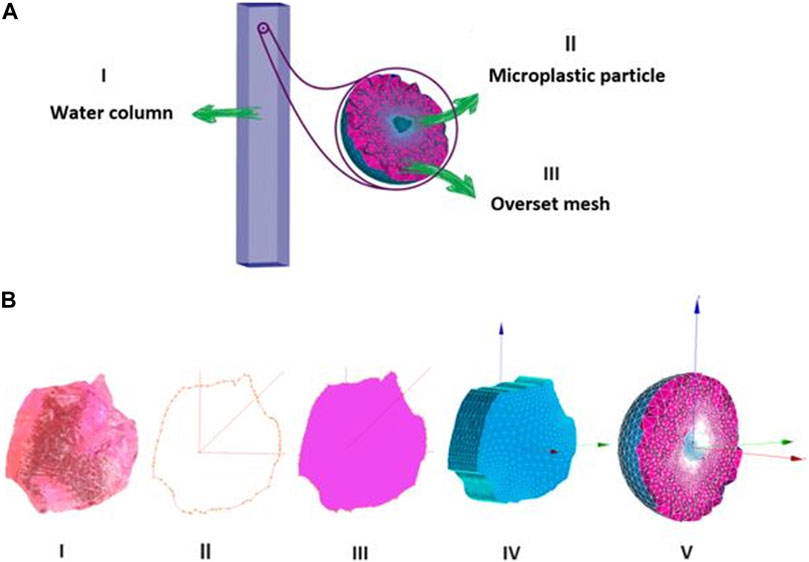
FIGURE 1. (A) Schematic of the used setup in all the simulations: I) Background mesh (water column-18 cm*18 cm*110 cm), II) body of a designed MP particle, III) Overset mesh around a MP particle, and (B) the steps in generating the particle and overset meshes: I) Image of a real MP particle II) Extracting boundary coordinates of the MP particle in a Cartesian coordinate system. III) Building surface plane of the MP particle IV) Extruding the built plane in the third dimension as much as its thickness V) Overset mesh around the 3D MP particle.
Figure 1B illustrates the design steps taken to mesh the arbitrarily shaped MP particle based on images taken from the particles in the laboratory experiments and how the overset mesh encloses the particle’s body. The SALOME 9.4 (Ribes and Caremoli, 2007) software was used to generate the numerical meshes for all simulation setups. The software ParaView (Ahrens et al., 2005) was used for visualization of the conducted simulations.
Figure 2A illustrates the general setup of the simulations representing the water column dimensions and the boundary conditions in the experiments (see Section 2.2 for more details). To implement the same condition as in the experiments, in all of the performed simulations 1 mm2s-1 and 0.9982 gcm−3 were considered as water kinematic viscosity and density at 20°C respectively. Moreover, the velocity boundary condition of “pressureInletOutletVelocity” was set to keep the upper side of the column open and in contact with air. In turn an air/water interfacial tension of “sigma: 0.007 kgs−2” was set for all simulations. The outer surface of the MP particle which is settling in the water (a viscous fluid), is surrounded by stationary walls of the column. Hence, to represent the velocity boundary conditions accordingly, the boundary types “movingWallVelocity” and “fixedValue” in OpenFOAM were used for the walls of the MP particle and water column, respectively. More details concerning the applied initial and boundary conditions for pressure, phase saturation and velocity have been provided in Supplementary Table S2. Quantities such as particle volume, mass, center of mass (COM), location, and moment of inertia (MOI) (cf. Supplementary Material S3), are important input parameters for the OpenFOAM solver and had to be accurately calculated beforehand.
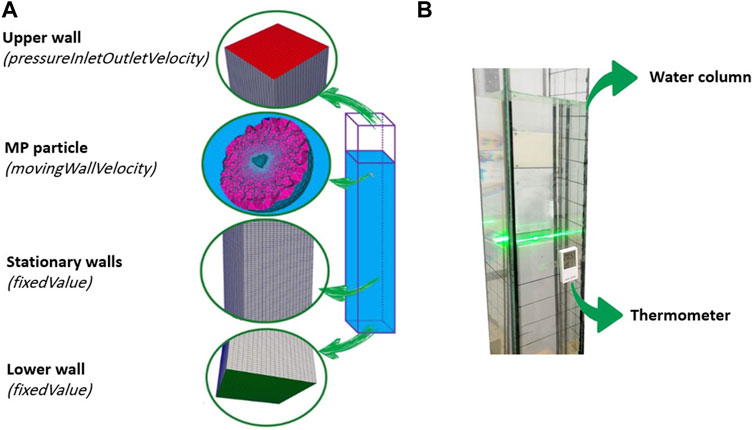
FIGURE 2. (A) Schematic of the whole simulation setup and the assigned velocity boundary conditions to each sub mesh set. (B) Water column used in the laboratory experiments including glass water container, and thermometer to check the temperature of water in the column.
2.2 Experiment Setup and Data
We used TSVs measured in the laboratory for a set of spherical and irregularly shaped MP particles (Elagami et al., 2022) for comparison with the CFD results. Besides that, we carried out an additional set of experiments to test our hypothesis, that the hydrophobicity of MP particles will affect their TSV. Settling experiments were first run for pristine, untreated PLA and PS particles in the size range from 1 to 2 mm and then repeated after the particles had been treated by immersion in a surfactant (Tween-20) for 2 hours. All the experiments were conducted using the same experimental setup as in (Elagami et al., 2022) consisting of a water column with the dimensions of 18 cm*18 cm*110 cm and a Particle Image Velocimetry (PIV) system to measure the settling velocity (Figure 2B). The 2D-PIV system (iLA 5,150) consists of a LED light sheet with 530 nm wave length as light source, a 40 fps high speed camera to track MP velocities during settlement, and also the hardware to synchronize the image acquisition frequency with the light source. The air conditioned laboratory and the water temperature were kept constant at 20°C and two thermometers were used to record the temperature of water during the experiments.
2.3 Comparison of Simulations to Semi-Empirical Relationships and Experimental Data
Comparison of the model with results from experiments and semi-empirical relationships was carried out in two steps: First, simulations of 120 irregular MP particles made of the polymers PS, PA66, PCL, PLLA, PLA, and PBAT from the experiments in (Elagami et al., 2022) were conducted to quantify their TSV and the findings were compared to the TSVs measured in the laboratory experiments. Images of some of these MP particles and the associated “model designed” particles for the numerical mesh in the simulations are illustrated in Supplementary Table S3 (cf. Supplementary Material S4) as an example. In the second step, simulated TSVs were compared to TSVs estimated based on two existing semi-empirical relationships between TSV and particle characteristics, namely i) the relationship originally proposed by Dietrich (1982), Dietrich, (1982) for mineral particles, which has been shown to return acceptable TSVs for regular MP particles (Khatmullina and Isachenko, 2017; Kaiser et al., 2019), and ii) the relationship formulated by Waldschläger et al. (2019) (Waldschläger and Schüttrumpf, 2019) for a broad size and shape range of MP particles. TSV of spherical particles with ten different sizes (0.5, 0.6, 0.75, 1, 1.25, 1.5, 1.75, 2, 2.25, and 2.5 mm) were simulated for each polymer with densities of 1.03 (PS), 1.12 (PA66), 1.14(PCL), 1.20(PLLA), and 1.38 gcm−3(PVC), and then the simulation results were compared to the TSV results of the same particles returned by the two semi-empirical relationships.
2.4 Evaluating the Influence of Physical Parameters on TSV of MP Particles
After confirming adequate performance of the model in the previous stage, the impact of particle roundness, size and density as well as water temperature on TSV were systematically evaluated to assess the sensitivity of the TSV of MP particles to the variation of each of the these physical parameters.
2.4.1 Effects of Shape Characteristics
To systematically investigate the effect of different levels of roundness on TSV we used regular polygons (Figure 3B). Increasing the number N of sides of a regular polygon, yields polygons with a growing number of sides of shorter length and more internal angles, which evolve towards a perfect circle when N approaches infinity. Revolving such regular polygons with identical areas around one of their symmetry axes, produces 3D shapes with equal volumes (Figure 3A). This procedure was followed to produce five series of regular polygons with the same areas of their 2D projections as circles with diameters of 0.5, 1, 1.5, 2, and 2.5 mm (cf. Supplementary Material S5, Supplementary Figure S2) to generate a set of “virtual particles” with increasing levels of roundness but the same volumes for a model-based assessment of the effects of roundness on TSV. To reduce the computational costs, simulations were only carried out for virtual particles with a density of 1.38 gcm−3 (PVC), to show the general trend of the impact of roundness on the TSV of MP particles.
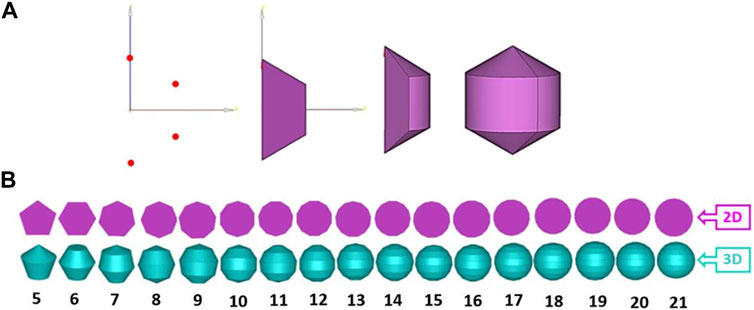
FIGURE 3. (A) The steps of generating a 3D regular hexagon. In the first step one half of a regular polygon is defined based on the coordinates of its vertices. This half-polygon is then rotated around one of its symmetry axes to form a 3D, regular, axis-symmetric particle; (B) 2D regular polygons and their corresponding 3D regular particles (for side numbers ranging from 5 to 21).
The level of roundness of the irregular MP particles used in our study was classified based on the Powers scale of roundness and the Corey Shape Factor (CSF), both of which are metrics having commonly been used in other studies (Dietrich, 1982; Khatmullina and Isachenko, 2017; Kaiser et al., 2019; Waldschläger and Schüttrumpf, 2019). The Powers scale of roundness is a measure, which defines particle roundness on a scale from 1 (very angular) to 6 (well rounded) based on the average of two assessments by independent observers using a graphical chart for comparison (Powers, 1953). The CSF is a measure of the flatness of a particle and is determined based on the lengths of its shortest, intermediate and longest perpendicular axes (Corey, 1949).
The surface area to volume ratio (SA:V) is also an important physical characteristic of MP particles, derived from their shape. It determines how drag forces are exerted on a MP particle and how these forces are distributed across its surface. The larger the SA:V, the more friction forces relative to gravitational forces will be exerted on the particle and consequently the less TSV the particle will have and vice versa. The SA:V was determined based on calculations of the particle surface area and volume from the numerical mesh for all regular and irregular MP particles.
2.4.2 Impact of Particle Density and Volume
First we selected a distinct set of polygon-shaped particles from the analysis of roundness and systematically increased their densities and sizes. These peculiar shapes of the particles were intentionally chosen to be able to simultaneously evaluate the relative influence of evolving particle roundness versus the effects of increasing particles size and density. To this end, the polygons with areas identical to a sphere with 1 mm diameter and the density of ρPVC = 1.1 gcm−3 were selected for the analysis. By choosing this initial size, the new set of virtual particles with increased sizes approximately stays within the size range of the MP definition. To examine the size effects, generated particles corresponding to the polygons with 5, 6, 7, 8, and 12 sides as well as a sphere were chosen and their volume enlarged by 10, 20, 50, and 100%. Similarly, the same percentages were used to increase the density of the original particles, which means that the initial density of ρPVC = 1.1 gcm−3 was increased by 10, 20, 50, and 100% to yield particle densities of 1.21, 1.32, 1.65, and 2.2 gcm−3 respectively. The highest density obtained using this procedure is only found in very heavy polymers (e.g., polytetrafluoroethylene (2.1–2.3 gcm−3) (Chubarenko et al., 2016)), which may be found less frequently in the environment. However, for the purpose of a systematic evaluation of density effects this was assumed to be acceptable.
In addition 10 irregular MP particles (from the particles used in Section 2.2) with an equivalent diameter range from 1 to 2 mm, a Powers scale of roundness (Powers, 1953) of 4 and a Corey Shape Factor (CSF), (Corey, 1949), ranging from 0.7 to 0.85, were selected as model particles to investigate the impact of an increase in size and density on TSVs. The initial density of the particles was assumed to be 1.1 gcm−3, and similar scenarios with respect to increasing volume and density as performed for regular particles were repeated for the irregular ones as well.
2.4.3 Temperature
Vertical temperature gradients and the associated changes in water density result in a thermal stratification of lakes during summer with the formation of an epilimnion, metalimnion, and hypolimnion (Herschy, 2012; Singh et al., 2019). The vertical temperature variations lead to changes in the kinematic viscosity of the water and the resulting TSV of the particles as the move from the relatively warm epilimnion, via the metalimnion to the colder hypolimnion (Gorham and Boyce, 1989; Singh et al., 2019). These changes in TSV will affect the residence times of MP particles in the different compartments of a stratified lake system. To quantify the effects of temperature changes on TSV in the different compartments, TSVs were simulated for the different temperature regimes. In temperate climates water temperatures in the three main compartments typically range from 18 to 24°C, 18–7.5°C, and 7.5–4°C in the epilimnion, metalimnion, and hypolimnion, respectively (Boehrer and Schultze, 2008). TSVs for 30 randomly selected irregular PVC particles (from the set of particles used in Section 2.3) were simulated for temperatures of 20, 10 and 4°C as characteristic temperatures for the epilimnion, metalimnion and hypolimnion respectively. The densities and kinematic viscosities of water at 10 and 4°C are 0.9997 gcm−3, 1.3063 mm2s-1 and 1 gcm−3, 1.5674 mm2s-1, respectively (Wagner and Kretzschmar, 2008).
3 Results
3.1 CFD Results for Irregular MP Particles Compared to Experimental Results and the Dietrich Relationship
The settling process for one of the 120 simulated irregular MP particles is illustrated in Figure 4A. In the initial phase of the settling the particle velocity dynamically changes as the particle shows secondary movements such as rotations and tumbling (Figure 4B at t = 1.2 s and Figure 4A, in-set A-F) before the particle reaches a stable orientation in the fluid with a constant settling velocity at t = 1.2 s. This initial, dynamic phase lasted around one second for all simulated particles. The second phase was characterized by a stable particle orientation (Figure 4A, G and H) and constant settling velocities for most particles. Some particles, however, showed small harmonic oscillations in their continuing downward movement, but with a constant average TSV.
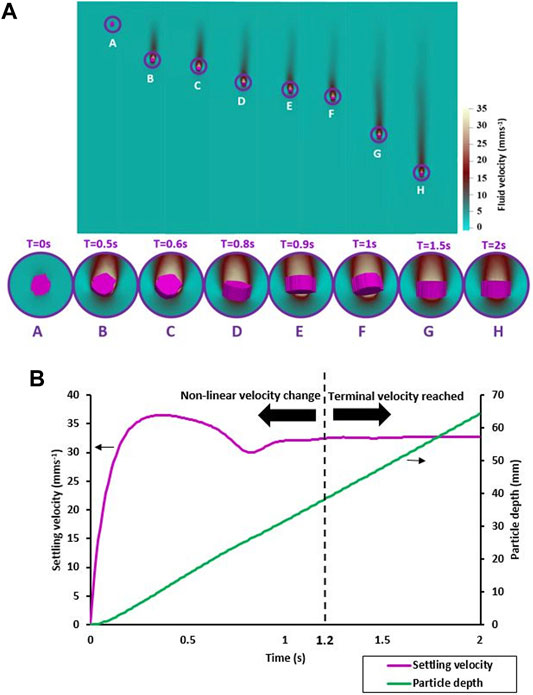
FIGURE 4. (A) The fluid velocity field around one of the 120 irregular MP particles at different point in time. Insets A to F show stages of the transient phase of settling, while insets G and H depict the phase after the TSV has been reached. Initial water velocity is zero and once the particle starts settling, the fluid velocity field around the particle shows changes in water velocity, while the velocity of the water in immediate contact with the particle reflects the settling velocity of the particle itself. (B) Velocity and particle location.
Simulated TSVs of 120 individual MP particles are plotted against the TSVs estimated by the Dietrich relationship in Figure 5A. CFD results are scattered along the 1:1 line with a slope of 0.95 and a coefficient of determination (R2) of 0.91. In Figure 5B TSVs simulated with CFD as well as TSVs from the Dietrich semi-empirical relationship are plotted against TSVs from the settling experiments. TSVs from CFD simulations as well as estimates based on the Dietrich relationship overestimate TSVs compared to the settling experiments. The coefficients of determination still showed relatively high values at 0.82 for both correlations and both trend lines have roughly the same slope of about 1.059. The strongest deviations were found for the biodegradable polymers (i.e., PCL, PLA and PLLA). However, a deviation was observed for PS, as a non-biodegradable polymer, as well. For PLA and PS particles an additional set of settling experiments were performed, initially with pristine untreated particles and subsequently with particles being treated with a surfactant to assess the effects of hydrophobicity on the TSV. Results of these additional experiments are plotted in Figure 5C. While the untreated particles show significantly slower experimental TSVs compared to the TSVs obtained from the CFD model, this deviation between simulated and experimental TSVs is practically removed for the treated particles. The R2 improved from R2 = 0.88 to R2 = 0.96 and from R2 = 0.086 to R2 = 0.82 between the untreated and treated particles for the PS- and PLA-particles respectively (Figure 5C).
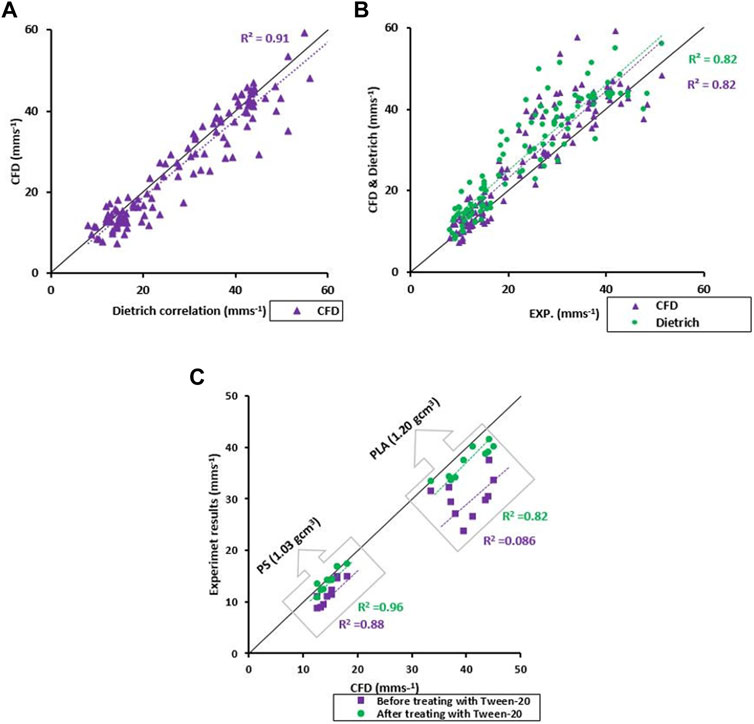
FIGURE 5. (A) CFD-simulated TSVs for 120 irregular MP particles plotted against TSVs estimated based on the Dietrich relationship. (B) CFD-based TSVs and TSVs estimated with the Dietrich relationship plotted against experimental results. (C) TSV changes due to particles’ surface treatment using Tween-20 for two sets of MP particles (PS and PLA both in the range from 1 to 2 mm), the purple squares illustrate the TSVs before treatment with Tween-20 and the green circles represent their TSVs from the re-run experiments after the treatmeant with Tween-20.
3.2 Evaluation of CFD Results for Spherical MP Particles Against the Semi-Empirical Relationships
In Figure 6 the CFD-simulated TSVs are plotted against particle size and density for a set of spherical particles. For comparision the TSVs estimated based on the (Waldschläger and Schüttrumpf, 2019) and (Dietrich, 1982) relationships are plotted for the same particles. For all polymers TSVs increased quasi-linearly with particle diameter. However, the slope of the quasi-linear relationship decreased with declining polymer density (densitiy declines from left to right in Figure 6).
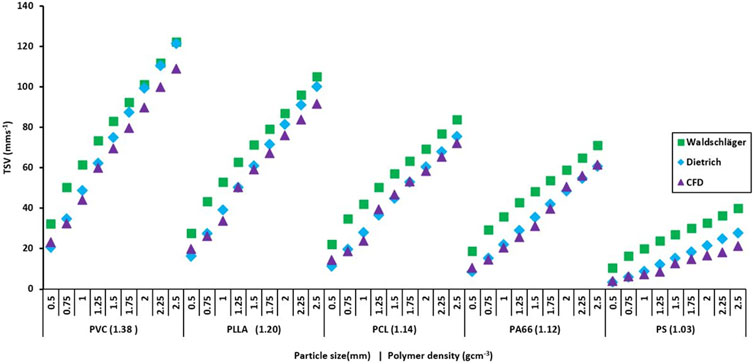
FIGURE 6. Comparison of the CFD-simulated TSVs and the TSVs estimated using the Dietrich and Walsdschläger empirical relationships. The diameters of the spheres and the polymer types (and their densities in brackets) are shown on the x-axis.
Overall the TSVs simulated with CFD are quite well matched by the values estimated from the Dietrich equation (R2 > 0.98). This is especially the case for the smallest diameters (0.5 and 0.75 mm), for which the simulated and estimated TSVs match very closely for all polymer types and densities. For larger diameters the match slightly deteriorates. In contrast, the TSVs predicted by the Walsdschläger relationship are systematically biased towards higher TSV values for all particle sizes and diameters. This bias gets slightly smaller with increasing particle size and density.
3.3 Systematic Investigation of the Relative Importance of Different Parameters on TSV
3.3.1 Roundness
Increasing the degree of roundness of the virtual particles from N = 5 to 9 causes a linear increase in TSVs for all the examined particle sizes (Figure 7A). Linear regressions between the degree of roundness (N) and the TSV yield coefficients of determination (R2) larger than 0.97 for all particles. The slope of the linear regressions steadily grows from the smallest (0.5 mm) to the largest (2.5 mm) particle diameter.
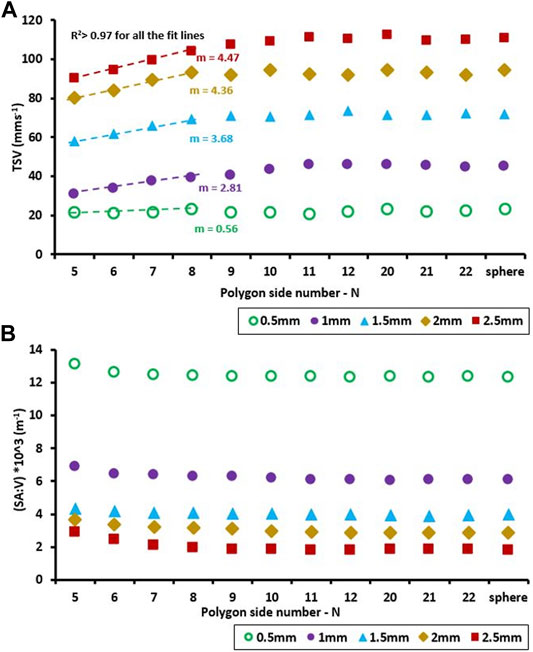
FIGURE 7. (A) Effects of increasing roundness on TSV of MP particles for five different particle sizes. The different symbols depict the different diameters of the equivalent perfect spheres, which have the same volumes as the respective virtual particles derived from the polygons. Particles in all simulations have a density of 1.38 gcm−3. (B) calculated SA:V for particles corresponding to the particles of panel A.
Comparing the changes in SA:V for increasing side numbers (Figure 7B) with the corresponding changes in TSVs (Figure 7A), shows that for a given particle diameter a decreasing SA:V is associated with an increase in TSV. However, for all the investigated particle diameters a threshold in N emerges at the value of 8, beyond which a further increase in N does not yield further increases in TSV. Beyond this threshold changes in SA:V with increasing N become minimal and in turn show little to no effect on the simulated TSVs. In this range TSV stays quasi-constant only showing minimal, non-systematic variations (Figure 7A, N > 8). Since the magnitudes of TSV and SA:V for N > 8 were very similar, we removed the data for 13 ≤ N ≤ 19 to improve the readability of the figure.
3.3.2 Surface Area to Volume Ratio–Particles With Irregular Shapes
The general relationship between SA:V and TSV, was also evaluated for all the 75 irregular MP particles used in the simulations in Section 3.1 (Figure 8). Sorting the TSVs in ascending order for each type of polymer depicted descending trends for SA:V ratios (dashed blue arrows in Figure 8). This inverse relationship indicates that lower SA:V generally facilitate faster TSVs. However, this trend shows significant scatter, in particular for the lighter polymers such as PS. Spearman rank correlations between the SA:V and TSV for each of the polymer classes yielded values ranging from 0.31 to 0.9, indicating only mild correlations between the two variables. In contrast spearman rank correlations between the particle volumes and TSV showed generally higher values ranging from 0.58 to 0.99, indicating that variability in TSV for the irregular particles investigated here is predominantly driven by variability in particle volume (i.e., weight), while the effect of variability in the SA:V is secondary.
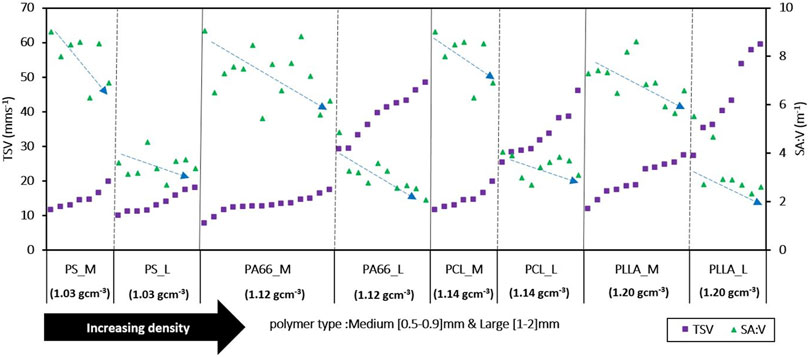
FIGURE 8. Simulated TSVs (left axis) and calculated SA:V (right axis) for the 75 irregular MP particles. The different polymers are arranged in the order of increasing density along the x-axis with their equivalent diameters being grouped into intervals of 0.5–0.9 mm (Medium, e.g., PS-M) and 1–2 mm (Large, PS-L). The TSVs in each subset of particles of a particular polymer (e.g., PS_M or PS_L) were arranged in increasing order from left to right. The blue dashed arrows indicate the general direction of the trend in SA:V over an increasing TSV.
3.3.3 Effects of Increasing Particle Size and Density on TSV
3.3.3.1 MP Particles With Regular Shapes
Effects of density and size (volume) on the TSV of the MP particles are depicted in Figure 9. For a 10% increase in density the TSV increases from 48% for the least rounded particle (N = 5) to 78% for a perfect sphere with a gradual increase with the degree of roundness. For density increases of 20, 50 and 100% the associated increases in TSV range between 107 and 139%, 206 and 275% and 401 and 483% respectively. The largest effects on TSV by increasing density can generally be seen for a perfect sphere, which has the smallest SA:V. Doubling the density of a sphere increases the associated TSV by approximately 50% compared to a respective particle derived from a polygon with five sides.
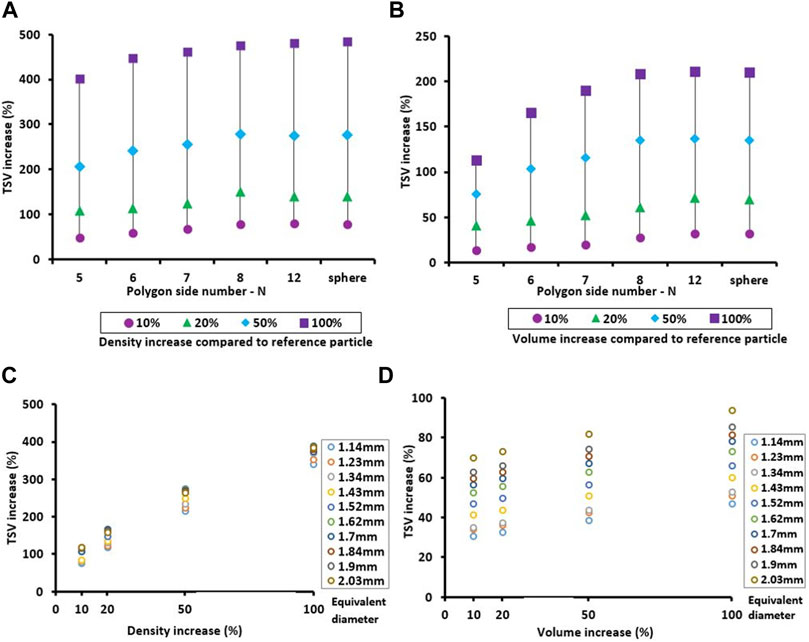
FIGURE 9. (A) Effects on TSV due to increasing the initial particle density (1.1 gcm3) by 10,20, 50, and 100% for particles with shapes derived from polygons with side numbers of 5,6,7,8,12 (see Figure 3) and a sphere with diameter of 1 mm (i.e., the level of roundness increases from left to right). (B) Effects on TSV due to increasing the initial particle volume (volume of a sphere with diameter of 1 mm) by 10, 20, 50, and 100% for the same particles as in A. (C) Effects of a density gain by 10, 20, 50, and 100% on TSVs for 10 randomly selected irregular particles (initial density = 1.1 gcm3). (D) Impact of volume increase by 10, 20, 50, and 100% for the same 10 irregular MP particles as in (C).
Plotting the increases in TSV for the same particles used in Figure 9A over the same percent increases in volume (Figure 9B) reveals similar patterns as for the increases in density, but at significantly lower magnitude. Increases in TSV for the least rounded particles (N = 5) ranged from 13 to 112% when and from 32 to 223% for a perfect sphere (N = ∞). Similar to the effects of increasing density the largest effect on TSV can be seen for particles approaching the shape of a sphere (N > 8).
3.3.3.2 MP Particles With Irregular Shapes
The effect of increasing the density of the irregular MP particles on their TSVs was generally quite similar to that observed for the regular particles (Figure 9C). For example, doubling the density of these particles led to an increase in TSV of up to five times, only slightly less than the maximum increase for the regular particles. However, the effect of increasing volume on TSV for the irregular MP particles deviated in magnitude from that of particles with regular shapes. While doubling the volume of the regular particles with a high level of roundness (e.g. N > 8) led to TSV increases of 200% (Figure 9B), the irregular particles only reached maximum TSV increases around 90% (Figure 9C). However, the regular particles with the least degree of roundness (N = 5) generally showed significantly smaller TSV increases (<120%), which are more in the range observed for the irregular particles. Interestingly, the clear sorting of the volume related TSV-increases for the irregular particles by their equivalent diameter (Figure 9D) was not seen for the effects of density-increases (Figure 9C). This indicates that changes in surface drag due to the increase in surface area resulting from the volume-increase is directly related to the particle’s equivalent diameter, while the equivalent diameter does not directly affect TSV changes due to an increase in density.
Calculating the coefficients of determination for the correlation between simulated TSVs, and the corresponding particles volumes and densities yielded values of R2 > 0.90, and R2 > 0.94, respectively. This implies that variations in particle TSV can be largely explained by variations in particle density and volume and that shape characteristics of the investigated particles play less of a role in determining the settling velocity.
3.3.4 Effects of Water Temperature on TSV
The TSVs in the epilimnion with an assumed reference temperature of 20°C are plotted against the TSVs in the metalimnion, with an assumed temperature of 10°C (light blue circles), and the hypolimnion with an assumed temperature of 4°C (dark blue triangles) for 30 MP particles (Figure 10). The average decrease in TSVs resulting from the temperature drop between the epilimnion and the hypolimnion is 32%. The largest temperature effects on TSVs can be seen for the smallest particles [equivalent diameter (cf. Supplementary Material S4, Eq. 5) from 0.57 to ∼1 mm], with a drop in TSVs from 32 to 46% compared to the reference temperature of 20°C.
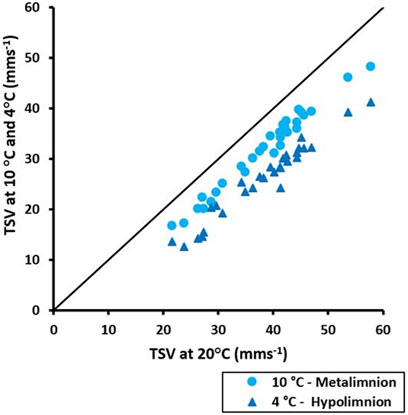
FIGURE 10. Effects of water temperature changes in a stratified lake assuming a temperature of 20°C in the epilimnion, 10°C in the metalimnion and 4°C in the hypolimnion on the settling velocity of 30 irregular MP particles with a density of 1.38 gcm−3.
4 Discussion
4.1 CFD-Based Assessment of the Initial Settling Process
Although the main purpose of our simulations was to quantify the TSVs of MP particles, which defines their overall settling times in lentic water bodies such as lakes (Lambert and Wagner, 2018), the transient CFD simulations also allow to evaluate the dynamic initial behavior during settling. The settling of all particles, with regular or irregular shape, showed two distinct phases during the initial settling period. The first phase represents the time period before the particle reaches the TSV. In this phase the irregular particles often show dynamic movements including rotations and tumbling with dynamical changes in settling velocities before they finally reach a stable settling position at the TSV. This marks the beginning of the second phase, in which the particles settle with a quasi-steady TSV. However, even after a steady TSV is reached, gentle secondary particle movements are possible depending on the particle’s shape. The specific time to reach the TSV needs to be considered in experimental setups (Khatmullina and Isachenko, 2017; Waldschläger and Schüttrumpf, 2019) to ensure that velocity measurements are done at a point where the forces exerted on the particle are balanced and the TSV has truly been reached. In our simulations, the initial phase of settling with transient velocities only lasted for a fraction of a second (usually t < 0.5 s) for symmetric particles such as spheres. In contrast for asymmetric particles with different roundness levels and stronger secondary movements, this phase could last up to one second (more details on the behavior of MP particles before reaching TSV, cf. Supplementary Material S6). The beginning of phase two is marked by the point when the particles reach their stable settling position at a steady TSV. However, some particles showed small oscillating secondary movements with very small harmonic velocity fluctuations around a steady average TSV during this phase. These oscillating, rotating, and tumbling secondary movements have also been reported from experimental work in the laboratory (Khatmullina and Isachenko, 2017; Waldschläger and Schüttrumpf, 2019). Given that the TSVs of the particles are reached very fast, the initial phase with transient velocities is negligible in terms of an assessment of the settling of particles in larger stagnant water bodies such as lakes.
4.2 Comparison of TSVs From CFD-Simulations, Semi-Empirical Relationships and Settling Experiments
The CFD model accounts for the exact particle shape and density and all the hydrodynamic forces that are exerted on the particle body. Therefore CFD simulations can be considered to reflect the true movement of a particle in water. As such CFD results can be used on the one hand to evaluate the accuracy of commonly used semi-empirical relationships, which make simplifications in the description of particles shapes, and on the other hand reveal additional non-hydrodynamic effects on particle TSVs by comparison with the results from settling experiments with the real MP particles of the same shapes and densities. In the following we will first briefly discuss the results from the spherical particles (Section 3.2) and then move to a more detailed discussion of the results from the irregular particles (Section 3.1).
4.2.1 Regular, Spherical Particles
For the spherical particles the CFD-simulated TSVs were generally better matched by estimates from the Dietrich relationship than by estimates obtained from the Waldschläger relationship (Waldschläger and Schüttrumpf, 2019) (Figure 6). The Dietrich relationship (Dietrich, 1982) had originally been developed for mineral particles of significantly higher densities (>2.2 gcm−3) than the polymers investigated in this study (<1.4 gcm−3). Surprisingly, however, it also yielded very reasonable TSV estimates for the much lower-density MP particles. This good agreement is likely due to the strong shape similarities between the mineral particles used to develop the Dietrich relationship (including smooth spheres, prolate ellipsoids, natural and crushed sediments (Dietrich, 1982)) and the MP particles we used in this study. In contrast the study by Waldschläger et al. (2019) (Waldschläger and Schüttrumpf, 2019) also included particles with significantly different shapes and also with lower densities and is in turn adapted to accommodate a broader range of particle characteristics. While we used very detailed descriptions of 3D particles shapes in our simulations, Waldschläger et al. (2019) only used the relatively coarse measures of the Powers scale of roundness and the CSF to describe particle shapes in their empirical relationships. These measures may not fully define all shape characteristics that affect the hydrodynamic forces acting on the particles during settling. This presumably explains the larger offset between the CFD-simulated TSVs and the TSV estimates based on the Waldschläger relationship.
4.2.2 Irregular Particles
Comparing the CFD-based TSVs with the TSVs obtained from the Dietrich semi-empirical relationship for the corresponding irregular MP particles yielded a strong correlation with an R2 of 0.91 and a deviation of the slope of the regression line to the 1:1 line of only 5% (Figure 5A). This indicates that the Dietrich relationship generally provides a good estimate of the TSVs of the particles with their respective shapes and densities. The scatter of the data points along the 1:1 line we attribute to the fact that the Dietrich relationship uses only three principal dimensions of a particle (i.e., longest, intermediate, shortest perpendicular axes) to calculate the particle equivalent diameter and its relative flatness (CSF) (Dietrich, 1982), which does not allow to account for individual details in differences in particle shapes. Furthermore, the Powers scale of roundness, a measure used in the Dietrich relationship to define the roundness of a particle is an observational measure, which for well-rounded elliptical and spherical particles with only small differences in their shapes will yield the same values.
Although the comparison between the CFD-simulated TSVs and the TSV estimates from the Dietrich semi-empirical relationship with the TSVs from the settling experiments overall showed a good agreement (R2 = 0.82), simulated (CFD) and estimated (Dietrich relationship) TSVs were generally biased towards faster TSVs compared to the experimentally determined values (Figure 5B). The strongest deviations we observed for the biodegradable polymers (PLLA, PCL, PLA), however, also MP particles of PS, a non-biodegradable light polymer, showed a noticeable deviation. We suspect that the hydrophobicity of the particle surfaces may have been the reason for this deviation between simulated and observed TSVs (Figure 5C). Hydrophobicity is a common characteristic of the surfaces of most polymers typically found in waste (Al Harraq and Bharti, 2021) and can enhance the sorption of hydrophobic contaminants to MP particles (Kwon et al., 2017) leading to bioaccumulation of these contaminants (Ziccardi et al., 2016). It can also potentially lead to the adhesive attachment of air (Al Harraq and Bharti, 2021). The latter process will change the net density of the particles by adding an additional upward force, which will affect their movement in water. This phenomenon is in fact a commonly used method to separate MP particles from water filled sediments (Renner et al., 2020).
The fact that the treatment with the surfactant Tween-20 shifted the experimental TSVs of PLA and PS particles to the CFDs-simulated TSV values (Figure 5C), strongly suggests that the observed TSVs deviations are related to effects of surface hydrophobicity. This general interpretation is further corroborated by the observation of discrete, large air bubbles at surface irregularities on some of the particles during settling in PIV images (Figure 11A-II). We attribute the generally stronger deviation of the experimentally determined TSVs from the respective CFD-simulated TSVs for the bio-degradable polymers to the fact that the surfaces of biodegradable polymers tend to have higher surface roughness to facilitate better degradation (Szewczyk et al., 2019; Moghadam and Tafreshi, 2020). Very small surface heterogeneities associated with those rougher surfaces (Al Harraq and Bharti, 2021) probably facilitate enhanced adhesive attachment of air at surface irregularities. Air-attachment, with potential effects on TSV, will also occur on the rough surface of non-biodegradable particles, but presumably to a lesser degree (Figure 11A-III). This could explain why we also observed a noticeable deviation of the experimental TSV from the respective CFD-estimate for the irregular particles made of PS (Figure 5C), a non-biodegradable polymer with a density (1.03 gcm−3) very close to that of water. The low density of the PS particles makes them more susceptible to changes in TSV due to attached air than the non-biodegradable particles made of denser polymers, for which no significant deviations between experiment and CFD had been observed.
FIGURE 11. Influence of polymer surface roughness on the TSV for PS polymer. (A) I- Irregular PS MP, the image was taken by microscope, II- the particle settling in water with an air bubble attached on it. This image was obtained from the PIV system, III- Particle roughness, image was taken by a Scanning Electron Microscope (SEM). (B) I- Regular PS MP (spherical shape - image by microscope, II- SEM image of the surface of the sphere.
The images of particles (taken by a light microscope, Zeiss Axioplan) and a high definition digital single lens reflex (DSLR) camera Cannon EOS 5D)) and their surfaces in Figure 11 generally illustrate the differences in the surface roughness of an irregular, non-biodegradable particle (Figure 11A-I) and a spherical non-biodegradable particle (Figure 11B-I) made from the same type of polymer (PS). The surface of the irregular particle shows larger irregularities and a generally rougher surface structure (Figure 11A-III) compared to the spherical particle with a relatively smooth surface (Figure 5B-II). The surface irregularities and the rougher surface of an irregular PS particle will better facilitate the attachment of larger air bubbles than the smoother surface of a respective spherical PS particle. This interpretation is further supported by earlier settling experiments using spherical particles with and without treatment with Tween-20, which had been conducted at the Limnological Research Station at Bayreuth University (personal communication, Hassan Elagami), which had practically shown no difference in the TSVs before and after treatment with Tween-20.
4.3 Roundness and SA:V Relationship and its Influence on TSVs of MP Particles
In previous studies the degree of roundness of a particle has commonly been considered as an important parameter for estimating the TSV of particles and it has usually been described by using the CSF and the Powers scale of roundness (Dietrich, 1982; Khatmullina and Isachenko, 2017; Waldschläger and Schüttrumpf, 2019). We examined the effect of roundness more systematically using exact 3D particle shapes obtained from revolving polygons with an increasing number of sides (see Section 2.4.1 for more details). Increasing the level of roundness leads to a decrease in SA:V (Figure 7B) and thus less drag forces being exerted on the particles body resulting in a faster TSV. This general inverse relationship between SA:V and TSV can be observed for the regular, spherical particles (Figure 7A) as well as the irregular particles (Figure 8). However, it is more evident for the virtual, regular particles investigated here as they all have the same volumes and densities, isolating roundness and the associated SA:V as the only variable parameters (Figure 7). However, even for the irregular MP particles shown in Figure 8, which have variable volumes, the general descending trend in SA:V for increasing TSVs is clearly discernable.
The gradual increase of the slopes of the regression lines for increasing particle diameters (Figure 7A) suggests that the magnitude of the effect of increasing roundness on a particle’s TSV increases with particle diameter. While the larger particles show significant increases in TSV over the initial increases in roundness, the smallest particles with a diameter of 0.5 mm practically do not show any significant change in TSV over the same increase in roundness. We attribute this to the drastic increase in SA:V when moving from particles with 1 mm diameter to the smallest particles with a diameter of 0.5 mm (Figure 7B). For these very small particles the SA:V is very high and in turn their TSV is driven more by the drag forces resulting from their large surface area relative to their volume than by additional hydrodynamic forces resulting from changes in their roundness.
4.4 Particle Density and Volume Effects on TSV
A comparison of the magnitudes of TSV increases associated with a density increase versus a volume increase for regular and irregular particles, respectively, showed a clear dominance of density over volume effects on TSV for the same percent increases in either parameter (Figure 9). By increasing the density of a MP particle, the only force that is amplified is weight, which will accelerate the downward movement of the particle. For the same percentage increase in volume in turn, the respective increase in weight and downward gravitational force is counteracted by additional upward forces resulting from an increase in drag due to the enlarged surface area and in the buoyancy of the particle, both attenuating the increase in TSV.
The relative increases in TSV in percent for the same percentage increases in density were very similar between the regular (Figure 9A) and irregular particles (Figure 9C) with values exceeding 400% for a doubling of the density. This was not the case for the same percentage increases in volume. While we observed TSV increases of up to 200% for the regular particles (Figure 9B) the irregular particles only showed TSV increases of less than 100% (Figure 9D). This illustrates the crucial role of shape irregularities in affecting the hydrodynamic forces (e.g., drag) acting on the irregular particles during settling and the resulting slow-down of their TSVs. Volume increases seem to amplify the effect of such irregularities causing a non-linear increase of the drag forces on the particles for increasing volumes. Interestingly for the irregular particles the ranking of their TSV increases relative to their equivalent particle diameter changed over the different increments in density gain (Figure 9C), while it stayed the same for volume increases. Likely the simultaneous increase in weight, drag and buoyancy associated with a volume increase maintains a certain balance in downward and upward forces acting on a particle of a specific shape. In contrast the more dramatic gains in weight due to the density increases seem to result in significant differences in the hydrodynamics forces (drag) that act on particles of different shapes and in turn counteract the gain in gravitational force.
4.5 Impact of Water Temperature on TSV
Our simulations on the effects of temperature on the TSV of MP particles (Figure 10) indicate that typical temperature differences between the compartments of a stratified lake in a temperate climate, will lead to significant differences in TSV (up to 46%). Differences in temperature and in turn density and kinematic viscosity of water in the different lake compartments have an influence on the drag forces exerted on the particles altering their TSVs. This temperature dependency of TSV can significantly affect the residence times of particles in the different lake compartments (Cole et al., 2016) and with that the exposure time of organisms to the MP particles (Elagami et al., 2022). This implies that the seasonal temperature evolution in the different lake compartments needs to be considered when evaluating exposure. In addition to the temparture effect, however, other parameters such as water oxygen content, salinity, water pH and changes in food quality and availability have to be taken into account to assess the complex patterns of interactions between organisms and MP particles in the different lake compartments (Migwi et al., 2020; Hiltunen et al., 2021; Hoffschroeer et al., 2021).
4.6 The Relative Importance of the Different Parameters Affecting Particle TSV
As highlighted by our analyses the TSV of MP particles in lakes and stagnant water bodies is affected by a range of different physical parameters such as density, volume, shape, surface roughness and hydrophobicity of the particles as well as the temperature and in turn density and viscosity of water. Evaluating the relative impact of these parameters on the TSV of MP particles quantitatively is challenging, as some of the parameters are coupled and their effects on TSV will overlap (Al Harraq and Bharti, 2021). Furthermore the settling of particles in the investigated size range (0.5–2.2 mm) is largely outside the true Stokes range of a laminar regime and hydrodynamic forces induced by turbulence will affect particle settling specifically for the larger particles. However, our rigorous, model-based evaluation of the hydrodynamic effects of the parameters listed above on particle TSVs, combined with respective laboratory settling experiments, including modifications to the particles’ hydrophobicity, allowed a more systematic, qualitative assessment of the relative importance of the different parameters. In the following we will compare the relative change of TSV in percent over the parameter ranges evaluated in our analyses, which reflect the ranges typically observed for MP particles found in the environment.
Our analyses demonstrate the importance of particle density for controlling TSV. While an increase in particle density directly affects the gravitational force driving settling, it has no impact on the particle’s volume and surface area, which would in turn change buoyancy and drag. A doubling of particle density led to TSV increases of up to 483 and 388% for regular and irregular particles respectively. In contrast, TSV increases of only 224% for the regular and 93% for the irregular particles could be realized for a doubling of particle volume. We attribute the significantly smaller TSV increase for the irregular particles to effects of the enlarged surface irregularities on drag and turbulence at the particle-water interface slowing down the settling velocity. The attachment of air on the surfaces of some of the biodegradable MP particles led to a reduction of the TSV by up to 58%, followed by relatively similar maximum changes in TSV of 47 and 45% due changes in water temperature and particle roundness respectively. Changes in particle roundness only significantly affected the TSVs of particles larger than 1 mm in diameter, while the smallest particles (0.5 mm diameter) were unaffected and their TSVs seemed to be controlled by their large SA:V. While the effects of water temperature and particle roundness similarly affected particles of all shapes and polymer types, effects of air attachment were most pronounced for particles with significant shape irregularities and rough surfaces (mainly the bio-degradable particles in our study), but also evident for irregular particles made of the lightest polymer PS with a density close to that of water (= 1.03 gcm−3). In contrast, regular, spherical particles with smooth surfaces did not show any significant effects of air attachment on TSV in our experiments.
5 Summary and Conclusion
In this study we systematically investigated the effects of different physical parameters on the TSV of MP particles in stagnant water bodies such as lakes. Parameters, which were varied over ranges typical for MP particles found in the environment, included particle density, volume, shape and roundness, surface hydrophobicity and water temperature. In total we conducted 683 individual CFD simulations of the settling behavior of MP particles of regular and irregular shapes and compared the simulation results to two semi-empirical equations to estimate particle TSVs as well as to laboratory settling experiments with the respective particles.
Our CFD simulations illustrated the peculiar, shape-dependent movement of irregular particles in the initial, transient phase of settling before reaching a quasi-steady TSV. This transient phase was found to be short, usually not exceeding one second, and is therefore negligible for estimating the time-scales of particle settling in larger stagnant water bodies such as lakes. The CFD-based calculations of TSV for MP particles of regular and irregular shapes were found to be in good agreement (R2 = 0.91) with TSV estimates obtained from the semi-empirical Dietrich equation (Dietrich, 1982), which is based on simple shape metrics and was originally developed for mineral (sediment) particles. Deviations from the CFD results can be attributed to the simplicity of the shape metrics used, which presumably play out more significantly for the lighter MP particles than for the heavier mineral particles, for which the relationship was originally developed. Surprisingly the comparison of our CFD-based TSVs with values obtained from another semi-empirical relationship, which was specifically developed for MP fragments, pellets and spheres (Waldschläger and Schüttrumpf, 2019) yielded a poorer agreement. We suspect that this deviation is related to differences between the shapes of the particles used to derive this relationship and the particle shapes in our study.
A comparison between the CFD-based TSV values and the experimentally determined values for the irregular particles also showed a good general agreement (R2 = 0.82), but with some more significant deviations for the particles made of biodegradable polymers and the very light non-biodegradable polymer PS (=1.03 gcm−3). Separating the data from the biodegradable particles form the other data revealed a significantly weaker correlation (R2 = 0.09), which we hypothesized to be related to the attachment of air on the particle surface due to its hydrophobicity. Our hypothesis was corroborated by the results of additional settling experiments, in which the MP particles were treated with a surfactant to reduce their surface hydrophobicity, which brought the experimental results into good agreement with the CFD results (R2 = 0.82). Maximum changes in TSV related to effects of hydrophobicity were on the order of 58%. Our results further indicated that the magnitude of air attachment on the hydrophobic particle surfaces seems to be related to the presence of larger surface irregularities as well as to the generally rougher surfaces of the bio-degradable polymers. The effects observed for the irregular, non-biodegradable PS particles are presumably related to their low density, which makes them more susceptible to TSV changes even at smaller magnitudes of air attachment. Regular, spherical particles with relatively smooth surfaces in contrast, did not show any measurable effects of air attachment on their TSVs.
For an evaluation of the relative importance of the different physical parameters investigated we conclude that density is the most decisive parameter for the TSV as it predominantly affects particle weight and in turn the gravitational force controlling TSV. Increases in TSV in excess of 400% could result from a doubling of density. In contrast, gains in weight due to a doubling of particle volume are counteracted by increases in buoyancy of the larger particle and drag on the enlarged particle surface leading to comparably smaller TSV increases on the order of 100–200%. Effects of air attachment follow with TSV changes of up to 58%, but they are restricted to particles with specific shape and surface characteristics. Effects of water temperature and particle roundness were responsible for maximum TSV changes of 47 and 45% respectively. Our systematic evaluation of the effects of key physical parameters on TSV provides a framework to evaluate their relative importance in future studies on the behavior of MP particles in lakes and can help to design future experiments on MP particle settling. It is clear, however, that the settling of MP particles in real lakes will also be affected by processes such as the formation of biofilms and/or mineral crusts on particle surfaces (Kaiser et al., 2017; Chen et al., 2019; Leiser et al., 2020; Elagami et al., 2022), the sorption of metals on particle surfaces (Leiser et al., 2021), particle interactions and aggregation (Leiser et al., 2021; Elagami et al., 2022; Wu et al., 2022), particle aging (Brandon et al., 2016) or the uptake and excretion by organisms (Koelmans et al., 2022), and turbulent flows (Kumar et al., 2021). How these processes interact with the basic physical processes investigated in this study and how that may change the settling behavior of MP particles remains to be investigated in future work.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
PA: Set up the CFD modeling framework, conducted the CFD simulations, designing the additional experiments, data interpretation and writing the manuscript. HE: Performed the laboratory experiments, assisted in data interpretation and writing the manuscript. FD: Contributed to the initial set-up of the CFD modeling framework, to data interpretation and writing of the manuscript. CS: Assisted in data interpretation and writing the manuscript. BG: Assisted in data interpretation and writing the manuscript. SF: Assisted in data interpretation and writing the manuscript. SP: Assisted in data interpretation and writing the manuscript. JF: Conceived the project, assisted in data interpretation and contributed to writing and editing of the manuscript.
Funding
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)–Project Number 391977956–SFB 1357.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to thank Ulrich Mansfeld and Martina Heider for taking the SEM images.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.875220/full#supplementary-material
References
Ahrens, J., Geveci, B., and Law, C. (2005). Paraview: An End-User Tool for Large Data Visualization. The visualization handbook, 717–731(8). doi:10.1016/b978-012387582-2/50038-1
Akdogan, Z., and Guven, B. (2019). Microplastics in the Environment: A Critical Review of Current Understanding and Identification of Future Research Needs. Environ. Pollut. 254, 113011. doi:10.1016/j.envpol.2019.113011
Al Harraq, A., and Bharti, B. (2021). Microplastics through the Lens of Colloid Science. ACS Environ. Au 2 (1), 3–10. doi:10.1021/acsenvironau.1c00016
Anderson, P. J., Warrack, S., Langen, V., Challis, J. K., Hanson, M. L., and Rennie, M. D. (2017). Microplastic Contamination in lake Winnipeg, Canada. Environ. Pollut. 225, 223–231. doi:10.1016/j.envpol.2017.02.072
Arora, C., Kumar, B. P., and Narayana, A. C. (2010). Influence of Particle Shape on Drag Coefficient for Commonly Occuring sandy Particles in Coastal Areas. Int. J. Ocean Clim. Syst. 1 (2), 99–112. doi:10.1260/1759-3131.1.2.99
Ballent, A., Corcoran, P. L., Madden, O., Helm, P. A., and Longstaffe, F. J. (2016). Sources and Sinks of Microplastics in Canadian Lake Ontario Nearshore, Tributary and beach Sediments. Mar. Pollut. Bull. 110 (1), 383–395. doi:10.1016/j.marpolbul.2016.06.037
Barnes, D. K. A., Galgani, F., Thompson, R. C., and Barlaz, M. (2009). Accumulation and Fragmentation of Plastic Debris in Global Environments. Phil. Trans. R. Soc. B 364 (1526), 1985–1998. doi:10.1098/rstb.2008.0205
Berlemont, A., Desjonqueres, P., and Gouesbet, G. (1990). Particle Lagrangian Simulation in Turbulent Flows. Int. J. Multiphase Flow 16 (1), 19–34. doi:10.1016/0301-9322(90)90034-g
Boehrer, B., and Schultze, M. (2008). Stratification of Lakes. Rev. Geophys. 46 (2), RG2005. doi:10.1029/2006rg000210
Brandon, J., Goldstein, M., and Ohman, M. D. (2016). Long-term Aging and Degradation of Microplastic Particles: Comparing In Situ Oceanic and Experimental Weathering Patterns. Mar. Pollut. Bull. 110 (1), 299–308. doi:10.1016/j.marpolbul.2016.06.048
Browne, M. A., Crump, P., Niven, S. J., Teuten, E., Tonkin, A., Galloway, T., et al. (2011). Accumulation of Microplastic on Shorelines Woldwide: Sources and Sinks. Environ. Sci. Technol. 45 (21), 9175–9179. doi:10.1021/es201811s
Chen, X., Xiong, X., Jiang, X., Shi, H., and Wu, C. (2019). Sinking of Floating Plastic Debris Caused by Biofilm Development in a Freshwater lake. Chemosphere. 222, 856–864. doi:10.1016/j.chemosphere.2019.02.015
Chubarenko, I., Bagaev, A., Zobkov, M., and Esiukova, E. (2016). On Some Physical and Dynamical Properties of Microplastic Particles in marine Environment. Mar. Pollut. Bull. 108 (1-2), 105–112. doi:10.1016/j.marpolbul.2016.04.048
Chubarenko, I., Esiukova, E., Bagaev, A., Isachenko, I., Demchenko, N., Zobkov, M., et al. (2018). “Behavior of Microplastics in Coastal Zones,” in Microplastic Contamination in Aquatic Environments. Editors E. Y. Zeng (Elsevier), 175–223. doi:10.1016/b978-0-12-813747-5.00006-0
Claessens, M., De Meester, S., Van Landuyt, L., De Clerck, K., and Janssen, C. R. (2011). Occurrence and Distribution of Microplastics in marine Sediments along the Belgian Coast. Mar. Pollut. Bull. 62 (10), 2199–2204. doi:10.1016/j.marpolbul.2011.06.030
Cole, M., Lindeque, P., Fileman, E., Halsband, C., Goodhead, R., Moger, J., et al. (2013). Microplastic Ingestion by Zooplankton. Environ. Sci. Technol. 47 (12), 6646–6655. doi:10.1021/es400663f
Cole, M., Lindeque, P. K., Fileman, E., Clark, J., Lewis, C., Halsband, C., et al. (2016). Microplastics Alter the Properties and Sinking Rates of Zooplankton Faecal Pellets. Environ. Sci. Technol. 50 (6), 3239–3246. doi:10.1021/acs.est.5b05905
Coppock, R. L., Galloway, T. S., Cole, M., Fileman, E. S., Queirós, A. M., and Lindeque, P. K. (2019). Microplastics Alter Feeding Selectivity and Faecal Density in the Copepod, Calanus helgolandicus. Sci. total Environ. 687, 780–789. doi:10.1016/j.scitotenv.2019.06.009
Corey, A. T. (1949). Influence of Shape on the Fall Velocity of Sand Grains. Fort Collins, CO: Colorado A & M College.
Derraik, J. G. B. (2002). The Pollution of the marine Environment by Plastic Debris: a Review. Mar. Pollut. Bull. 44 (9), 842–852. doi:10.1016/s0025-326x(02)00220-5
de Souza Machado, A. A., Kloas, W., Zarfl, C., Hempel, S., and Rillig, M. C. (2018). Microplastics as an Emerging Threat to Terrestrial Ecosystems. Glob. Change Biol. 24 (4), 1405–1416. doi:10.1111/gcb.14020
Dietrich, W. E. (1982). Settling Velocity of Natural Particles. Water Resour. Res. 18 (6), 1615–1626. doi:10.1029/wr018i006p01615
Doyle, M. J., Watson, W., Bowlin, N. M., and Sheavly, S. B. (2011). Plastic Particles in Coastal Pelagic Ecosystems of the Northeast Pacific Ocean. Mar. Environ. Res. 71 (1), 41–52. doi:10.1016/j.marenvres.2010.10.001
Elagami, H., Ahmadi, P., Fleckenstein, J. H., Frei, S., Obst, M., Agarwal, S., et al. (2022). Measurement of Microplastic Settling Velocities and Implications for Residence Times in Thermally Stratified Lakes. Limnology & Oceanography lno.12046, 1–12. doi:10.1002/lno.12046
Fendall, L. S., and Sewell, M. A. (2009). Contributing to marine Pollution by Washing Your Face: Microplastics in Facial Cleansers. Mar. Pollut. Bull. 58 (8), 1225–1228. doi:10.1016/j.marpolbul.2009.04.025
Fischer, E. K., Paglialonga, L., Czech, E., and Tamminga, M. (2016). Microplastic Pollution in Lakes and lake Shoreline Sediments - A Case Study on Lake Bolsena and Lake Chiusi (central Italy). Environ. Pollut. 213, 648–657. doi:10.1016/j.envpol.2016.03.012
Frias, J. P. G. L., and Nash, R. (2019). Microplastics: Finding a Consensus on the Definition. Mar. Pollut. Bull. 138, 145–147. doi:10.1016/j.marpolbul.2018.11.022
Gorham, E., and Boyce, F. M. (1989). Influence of lake Surface Area and Depth upon thermal Stratification and the Depth of the Summer Thermocline. J. Great Lakes Res. 15 (2), 233–245. doi:10.1016/s0380-1330(89)71479-9
Gregory, M. R. (1983). Virgin Plastic Granules on Some Beaches of Eastern Canada and Bermuda. Mar. Environ. Res. 10 (2), 73–92. doi:10.1016/0141-1136(83)90011-9
Gregory, M. R. (1996). Plastic 'scrubbers' in Hand Cleansers: a Further (And Minor) Source for marine Pollution Identified. Mar. Pollut. Bull. 32 (12), 867–871. doi:10.1016/s0025-326x(96)00047-1
Guerrini, F., Mari, L., and Casagrandi, R. (2021). The Dynamics of Microplastics and Associated Contaminants: Data-Driven Lagrangian and Eulerian Modelling Approaches in the Mediterranean Sea. Sci. Total Environ. 777, 145944. doi:10.1016/j.scitotenv.2021.145944
Hendrickson, E., Minor, E. C., and Schreiner, K. (2018). Microplastic Abundance and Composition in Western Lake Superior as Determined via Microscopy, Pyr-GC/MS, and FTIR. Environ. Sci. Technol. 52 (4), 1787–1796. doi:10.1021/acs.est.7b05829
Herschy, R. W., Herschy, R. W., Wolanski, E., Andutta, F., Delhez, E., Fairbridge, R. W., et al. (2012). Ecological Threat to Lakes and Reservoirs. Encyclopedia of Lakes and Reservoirs, 233–234. doi:10.1007/978-1-4020-4410-6_74
Hiltunen, M., Vehniäinen, E.-R., and Kukkonen, J. V. K. (2021). Interacting Effects of Simulated Eutrophication, Temperature Increase, and Microplastic Exposure on Daphnia. Environ. Res. 192, 110304. doi:10.1016/j.envres.2020.110304
Hoffschröer, N., Grassl, N., Steinmetz, A., Sziegoleit, L., Koch, M., and Zeis, B. (2021). Microplastic burden in Daphnia Is Aggravated by Elevated Temperatures. Zoology (Jena). 144, 125881. doi:10.1016/j.zool.2020.125881
Houzeaux, G., Eguzkitza, B., Aubry, R., Owen, H., and Vázquez, M. (2014). A Chimera Method for the Incompressible Navier-Stokes Equations. Int. J. Numer. Meth. Fluids. 75 (3), 155–183. doi:10.1002/fld.3886
Isachenko, I. (2020). Catching the Variety: Obtaining the Distribution of Terminal Velocities of Microplastics Particles in a Stagnant Fluid by a Stochastic Simulation. Mar. Pollut. Bull. 159, 111464. doi:10.1016/j.marpolbul.2020.111464
Jalón-Rojas, I., Wang, X. H., and Fredj, E. (2019). A 3D Numerical Model to Track marine Plastic Debris (TrackMPD): Sensitivity of Microplastic Trajectories and Fates to Particle Dynamical Properties and Physical Processes. Mar. Pollut. Bull. 141, 256–272. doi:10.1016/j.marpolbul.2019.02.052
Jérémy, R., Gaston, L. P., and Valyrakis, M. (2020). Coupled CFD-DEM Modelling to Assess Settlement Velocity and Drag Coefficient of Microplastics. EGU General Assembly 2020. doi:10.5194/egusphere-egu2020-10049
Kaiser, D., Estelmann, A., Kowalski, N., Glockzin, M., and Waniek, J. J. (2019). Sinking Velocity of Sub-millimeter Microplastic. Mar. Pollut. Bull. 139, 214–220. doi:10.1016/j.marpolbul.2018.12.035
Kaiser, D., Kowalski, N., and Waniek, J. J. (2017). Effects of Biofouling on the Sinking Behavior of Microplastics. Environ. Res. Lett. 12 (12), 124003. doi:10.1088/1748-9326/aa8e8b
Khatmullina, L., and Isachenko, I. (2017). Settling Velocity of Microplastic Particles of Regular Shapes. Mar. Pollut. Bull. 114 (2), 871–880. doi:10.1016/j.marpolbul.2016.11.024
Koelmans, A. A., Redondo-Hasselerharm, P. E., Nor, N. H. M., de Ruijter, V. N., Mintenig, S. M., and Kooi, M. (2022). Risk Assessment of Microplastic Particles. Nat. Rev. Mater., 1–15. doi:10.1038/s41578-021-00411-y
Kooi, M., Reisser, J., Slat, B., Ferrari, F. F., Schmid, M. S., Cunsolo, S., et al. (2016). The Effect of Particle Properties on the Depth Profile of Buoyant Plastics in the Ocean. Sci. Rep. 6 (1), 33882–33910. doi:10.1038/srep33882
Kowalski, N., Reichardt, A. M., and Waniek, J. J. (2016). Sinking Rates of Microplastics and Potential Implications of Their Alteration by Physical, Biological, and Chemical Factors. Mar. Pollut. Bull. 109 (1), 310–319. doi:10.1016/j.marpolbul.2016.05.064
Kumar, R., Sharma, P., Verma, A., Jha, P. K., Singh, P., Gupta, P. K., et al. (2021). Effect of Physical Characteristics and Hydrodynamic Conditions on Transport and Deposition of Microplastics in Riverine Ecosystem. Water 13 (19), 2710. doi:10.3390/w13192710
Kwon, J.-H., Chang, S., Hong, S. H., and Shim, W. J. (2017). Microplastics as a Vector of Hydrophobic Contaminants: Importance of Hydrophobic Additives. Integr. Environ. Assess. Manag. 13 (3), 494–499. doi:10.1002/ieam.1906
Lambert, S., and Wagner, M. (2018). Microplastics Are Contaminants of Emerging Concern in Freshwater Environments: An Overview. Freshw. microplastics, 1–23. doi:10.1007/978-3-319-61615-5_1
Leiser, R., Jongsma, R., Bakenhus, I., Möckel, R., Philipp, B., Neu, T. R., et al. (2021). Interaction of Cyanobacteria with Calcium Facilitates the Sedimentation of Microplastics in a Eutrophic Reservoir. Water Res. 189, 116582. doi:10.1016/j.watres.2020.116582
Leiser, R., Wu, G.-M., Neu, T. R., and Wendt-Potthoff, K. (2020). Biofouling, Metal Sorption and Aggregation Are Related to Sinking of Microplastics in a Stratified Reservoir. Water Res. 176, 115748. doi:10.1016/j.watres.2020.115748
Liao, J., and Chen, Q. (2021). Biodegradable Plastics in the Air and Soil Environment: Low Degradation Rate and High Microplastics Formation. J. Hazard. Mater. 418, 126329. doi:10.1016/j.jhazmat.2021.126329
Maximenko, N., Hafner, J., and Niiler, P. (2012). Pathways of marine Debris Derived from Trajectories of Lagrangian Drifters. Mar. Pollut. Bull. 65 (1-3), 51–62. doi:10.1016/j.marpolbul.2011.04.016
Migwi, F. K., Ogunah, J. A., and Kiratu, J. M. (2020). Occurrence and Spatial Distribution of Microplastics in the Surface Waters of Lake Naivasha, Kenya. Environ. Toxicol. Chem. 39 (4), 765–774. doi:10.1002/etc.4677
Moghadam, A., and Vahedi Tafreshi, H. (2020). On Liquid Bridge Adhesion to Fibrous Surfaces under normal and Shear Forces. Colloids Surf. A: Physicochemical Eng. Aspects. 589, 124473. doi:10.1016/j.colsurfa.2020.124473
Mountford, A. S., and Morales Maqueda, M. A. (2019). Eulerian Modeling of the Three‐Dimensional Distribution of Seven Popular Microplastic Types in the Global Ocean. J. Geophys. Res. Oceans. 124 (12), 8558–8573. doi:10.1029/2019jc015050
Nooteboom, P. D., Delandmeter, P., van Sebille, E., Bijl, P. K., Dijkstra, H. A., and von der Heydt, A. S. (2020). Resolution Dependency of Sinking Lagrangian Particles in Ocean General Circulation Models. PloS one. 15 (9), e0238650. doi:10.1371/journal.pone.0238650
North, E. J., and Halden, R. U. (2013). Plastics and Environmental Health: the Road Ahead. Rev. Environ. Health. 28 (1), 1–8. doi:10.1515/reveh-2012-0030
Powers, M. C. (1953). A New Roundness Scale for Sedimentary Particles. J. Sediment. Res. 23 (2), 117–119. doi:10.1306/d4269567-2b26-11d7-8648000102c1865d
Renner, G., Nellessen, A., Schwiers, A., Wenzel, M., Schmidt, T. C., and Schram, J. (2020). Hydrophobicity-water/air-based Enrichment Cell for Microplastics Analysis within Environmental Samples: A Proof of Concept. MethodsX. 7, 100732. doi:10.1016/j.mex.2019.11.006
Ribes, A., and Caremoli, C. (2007). “Salome Platform Component Model for Numerical Simulation,” in 31st annual international computer software and applications conference (COMPSAC 2007): IEEE), 553–564.
Rocha-Santos, T., and Duarte, A. C. (2015). A Critical Overview of the Analytical Approaches to the Occurrence, the Fate and the Behavior of Microplastics in the Environment. Trac Trends Analytical Chemistry. 65, 47–53. doi:10.1016/j.trac.2014.10.011
Rochman, C. M. (2018). Microplastics Research-From Sink to Source. Science. 360 (6384), 28–29. doi:10.1126/science.aar7734
Sighicelli, M., Pietrelli, L., Lecce, F., Iannilli, V., Falconieri, M., Coscia, L., et al. (2018). Microplastic Pollution in the Surface Waters of Italian Subalpine Lakes. Environ. Pollut. 236, 645–651. doi:10.1016/j.envpol.2018.02.008
Singh, P., Bagrania, J., and Haritash, A. (2019). Seasonal Behaviour of thermal Stratification and Trophic Status in a Sub-tropical Palustrine Water Body. Appl. Water Sci. 9 (5), 1–6. doi:10.1007/s13201-019-1011-z
Szewczyk, P. K., Ura, D. P., Metwally, S., Knapczyk-Korczak, J., Gajek, M., Marzec, M. M., et al. (2019). Roughness and Fiber Fraction Dominated Wetting of Electrospun Fiber-Based Porous Meshes. Polymers (Basel). 11 (1), 34. doi:10.3390/polym11010034
Trunk, R., Bretl, C., Thäter, G., Nirschl, H., Dorn, M., and Krause, M. J. (2021). A Study on Shape-dependent Settling of Single Particles with Equal Volume Using Surface Resolved Simulations. Computation. 9 (4), 40. doi:10.3390/computation9040040
Van Cauwenberghe, L., Claessens, M., Vandegehuchte, M. B., Mees, J., and Janssen, C. R. (2013). Assessment of marine Debris on the Belgian Continental Shelf. Mar. Pollut. Bull. 73 (1), 161–169. doi:10.1016/j.marpolbul.2013.05.026
Vaughan, R., Turner, S. D., and Rose, N. L. (2017). Microplastics in the Sediments of a UK Urban lake. Environ. Pollut. 229, 10–18. doi:10.1016/j.envpol.2017.05.057
Wagner, W., and Kretzschmar, H.-J. (2008). “IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam,” in International steam tables: properties of water and steam based on the industrial formulation IAPWS-IF97, 7–150.
Waldschläger, K., and Schüttrumpf, H. (2019). Effects of Particle Properties on the Settling and Rise Velocities of Microplastics in Freshwater under Laboratory Conditions. Environ. Sci. Technol. 53, 1958–1966. doi:10.1021/acs.est.8b06794
Webb, H., Arnott, J., Crawford, R., and Ivanova, E. (2013). Plastic Degradation and its Environmental Implications with Special Reference to Poly (Ethylene Terephthalate). Polymers 5, 1–18. doi:10.3390/polym5010001
Wei, X.-F., Bohlén, M., Lindblad, C., Hedenqvist, M., and Hakonen, A. (2021). Microplastics Generated from a Biodegradable Plastic in Freshwater and Seawater. Water Res. 198, 117123. doi:10.1016/j.watres.2021.117123
Weller, H. G., Tabor, G., Jasak, H., and Fureby, C. (1998). A Tensorial Approach to Computational Continuum Mechanics Using Object-Oriented Techniques. Comput. Phys. 12 (6), 620–631. doi:10.1063/1.168744
Williams, A. T., and Simmons, S. L. (1996). The Degradation of Plastic Litter in Rivers: Implications for Beaches. J. Coast Conserv. 2 (1), 63–72. doi:10.1007/bf02743038
Wright, S. L., Thompson, R. C., and Galloway, T. S. (2013). The Physical Impacts of Microplastics on marine Organisms: a Review. Environ. Pollut. 178, 483–492. doi:10.1016/j.envpol.2013.02.031
Wright, S. L., Ulke, J., Font, A., Chan, K. L. A., and Kelly, F. J. (2020). Atmospheric Microplastic Deposition in an Urban Environment and an Evaluation of Transport. Environ. Int. 136, 105411. doi:10.1016/j.envint.2019.105411
Wu, J., Ye, Q., Wu, P., Xu, S., Liu, Y., Ahmed, Z., et al. (2022). Heteroaggregation of Nanoplastics with Oppositely Charged Minerals in Aquatic Environment: Experimental and Theoretical Calculation Study. Chem. Eng. J. 428, 131191. doi:10.1016/j.cej.2021.131191
Zbyszewski, M., Corcoran, P. L., and Hockin, A. (2014). Comparison of the Distribution and Degradation of Plastic Debris along Shorelines of the Great Lakes, North America. J. Great Lakes Res. 40 (2), 288–299. doi:10.1016/j.jglr.2014.02.012
Zhang, H. (2017). Transport of Microplastics in Coastal Seas. Estuarine, Coastal Shelf Sci. 199, 74–86. doi:10.1016/j.ecss.2017.09.032
Zhang, Y., Xie, M., Adamaki, V., Khanbareh, H., and Bowen, C. R. (2017). Control of Electro-Chemical Processes Using Energy Harvesting Materials and Devices. Chem. Soc. Rev. 46 (24), 7757–7786. doi:10.1039/c7cs00387k
Keywords: CFD, Navier-Stokes equations, OpenFOAM, microplastic particles, terminal settling velocity
Citation: Ahmadi P, Elagami H, Dichgans F, Schmidt C, Gilfedder BS, Frei S, Peiffer S and Fleckenstein JH (2022) Systematic Evaluation of Physical Parameters Affecting the Terminal Settling Velocity of Microplastic Particles in Lakes Using CFD. Front. Environ. Sci. 10:875220. doi: 10.3389/fenvs.2022.875220
Received: 13 February 2022; Accepted: 24 March 2022;
Published: 13 April 2022.
Edited by:
Ping Wang, Beijing Forestry University, ChinaReviewed by:
Veerasingam S., Qatar University, QatarQiqing Chen, East China Normal University, China
Copyright © 2022 Ahmadi, Elagami, Dichgans, Schmidt, Gilfedder, Frei, Peiffer and Fleckenstein. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pouyan Ahmadi, cG91eWFuLmFobWFkaUB1ZnouZGU=; Jan H. Fleckenstein, amFuLmZsZWNrZW5zdGVpbkB1ZnouZGU=