Influence of multilayer cloud characteristics on cloud retrieval and estimation of surface downward shortwave radiation

Abstract: There are significant uncertainties in the retrieval accuracy of multilayer clouds with different phase states, leading to bias in the subsequent estimation of the surface downward shortwave radiation (DSR). Single-layer clouds are generally assumed for the retrieval of cloud optical and microphysical properties from satellite measurements, although multilayer clouds often occur in reality. In this article, the impact of multilayer clouds (thin ice clouds overlying lower-level water clouds) on the retrieval of cloud microphysical properties is simulated with the radiative transfer model RSTAR. The simulated results demonstrate the impact of double-layer clouds on the accuracy of retrieval of the cloud parameters and estimation of DSR. To understand the uncertainties of the input parameters, thorough sensitivity tests are simulated by RSTAR in the Results section. As compared with the retrieval results of single-layer clouds when the ice particle model of the upper-layer cloud is assumed to be ellipsoidal, the maximum relative bias in DSR is 0.63% when the COT for the ice cloud is 1.2 and for water cloud is 32.45. When the upper-layer ice cloud is assumed to be a hexagonal column, the maximum relative bias in DSR is 55.34% when the COT for the ice cloud is 2 and for the water cloud is 58.4. In addition, relative bias in DSR tends to increase both with radiance and ice cloud COT for a given radiance. This finding can provide a basis of reference for the estimation accuracy of radiative forcing in the IPCC report and the subsequent enhancement and improvement of retrieval algorithms.

1 Introduction

Clouds play an important role in the global energy budget and water cycle and are indispensable components of the Earth–atmosphere system (Liou, 2004). The distributions of clouds are diverse and complex. Owing to different macroscopic, microphysical, and optical properties, clouds have different radiation effects at shortwave and longwave regions and play different roles in radiative transfers of the Earth–atmosphere system (Charlson et al., 1987; Albrecht et al., 1988; Kiehl, 1994; Zhao and Garrett, 2015). The Intergovernmental Panel on Climate Change (IPCC) Sixth Assessment Report (AR-6) emphasized that the significance of clouds and lack of sufficient understanding of cloud characteristics are the main uncertainty factors for quantifying climate change caused by anthropogenic factors (Stocker et al., 2013; IPCC, 2021). Very small changes in the characteristics of clouds at the global scale could generate significant influences on the climate, and a growth of 4% in oceanic stratified clouds globally will counteract the predicted rise of the global surface temperature (approximately 2–3 K) caused by the doubling of atmospheric carbon dioxide (Randall et al., 1984). Therefore, an accurate understanding of cloud microphysical and optical properties is of extreme significance to us to deeply understand the complicated interactions among clouds, radiation, and climate and to further improve climate modeling and climate predictions (Zhao et al., 2012; Zhang et al., 2013; Wang and Zhao, 2017).

Satellite remote sensing has become an important approach for monitoring cloud microphysical and optical properties due to its well-calibrated instruments. Over the past several decades, researchers have made considerable progress in using satellite detection data to retrieve cloud optical thickness (COT) and effective particle radius (CER) (Arking and Childs, 1985; King, 1987; Twomey and Cocks, 1989; Nakajima et al., 1990; Nakajima et al., 1991; Zhao et al., 2002; Liu et al., 2003; Chen et al., 2009; Nauss and Kokhanovsky, 2011). The retrieval algorithm for COT and CER proposed by Nakajima et al. (1990) is among the most widely used algorithms currently available.

For the retrieval of COT and CER for water clouds, it is generally presumed that the clouds are uniformly distributed vertically and horizontally. Water cloud droplets are generally assumed to be spherical particles such that the Lorenz–Mie theory could accurately calculate the scattering properties of water clouds. By contrast, due to the inhomogeneous distribution and complexity of the particle shapes of ice clouds, their radiation characteristics no longer follow the Lorenz–Mie theory. Ice-cloud particle shape directly affects the computation of single scattering properties (e.g., phase function, scattering albedo, and asymmetry factor) and further affects calculations of ice cloud radiation values (Baum et al., 2005; Baum et al., 2011). Particularly, understanding ice crystal scattering properties is essential for retrieving ice cloud optical parameters. However, ice cloud particles have various habits and sizes, and their retrieval has significant uncertainties (Letu et al., 2016; Mei et al., 2018).

At present, the algorithms used for retrieval of cloud parameters are mostly based on single-layer assumption. This assumption ignores the presence of multilayer clouds and therefore causes uncertainties in retrieval. Satellite observations have been used for the detection and retrieval of ice cloud microphysical and optical properties with algorithms; a cloud property retrieval algorithm must be computationally efficient. For this reason, cloud retrieval algorithms usually assume a horizontally and vertically homogeneous single-layer plane parallel cloud, and radiative transfer calculations are performed in advance for specified values of input parameters and stored in a lookup table (LUT). The retrieved COT and CER values are obtained by interpolation in the LUT. However, actual water clouds have vertically inhomogeneous cloud structures due to the influence of cloud dynamical and microphysical processes (Saito et al., 2019). Alexandrov et al. (2020) evaluated the possibility of combining microphysical and macrophysical retrieval methods to retrieve vertical profiles of the microphysical characteristics of liquid clouds. Zhou et al. (2018) explored the impacts of single habit assumption (SHA), cloud inhomogeneity, and 3-D radiative effects on cloud optical thickness (COT) and on effective diameter (De) retrieval for midlatitude and tropical cirrus clouds done with MODIS.

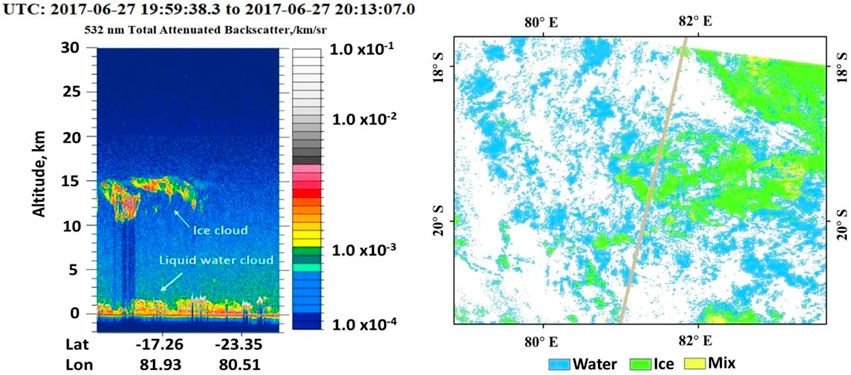
Accurate retrieval of COT and CER further affects the calculation accuracy of downward shortwave radiation (DSR). High-precision cloud microphysical parameters for different phases (ice and water clouds) are employed to derive the DSR product. The macro- and microphysical parameters of clouds with different phase states are adopted as input parameters to calculate DSR to improve its accuracy in regions covered by liquid or ice clouds (Letu et al., 2022). Due to the presence of multilayer clouds, inference of cloud microphysical properties from passive radiation measurements is compromised. Davis et al. (2009) illustrated an important limitation of the MODIS operational retrieval that overestimates the cirrus COT for scenes in which a cirrus layer overlaps a lower cloud layer. This limitation has been anticipated on the basis of the expected effect of multilayered cloud systems on the top of atmosphere radiance (Chang and Li, 2005). Figure 1 shows the vertical structure of a double-layered cloud observed by CALIPSO and the corresponding MODIS image, which shows that the upper layer is an ice cloud and the lower layer is a water cloud. Under the situation that an ice cloud overlaps a water cloud, the satellite measurements are the accumulation of information mostly from the cloud top, causing the estimated cloud properties to become biased by following the single-layer and homogeneous assumption.

FIGURE 1

FIGURE 1. CALIPSO double-layer clouds and MODIS cloud phase.

Multilayer clouds are nowadays recognized to have a major impact on the Earth–atmosphere radiation balance because of their high spatial and temporal coverage. However, these are still poorly understood due to the difficulties in describing the wide range of their microphysical and optical properties in remote sensing and global climate models. Multilayer clouds can be very complex in nature in terms of the total number of layers and the way of overlaying of varied cloud phase states. Generally speaking, when the upper layer is a thin cirrus cloud and the lower layer is a mid-low water cloud, the emitted radiation of the mid-low layer cloud can penetrate the translucent cirrus cloud to reach the satellite, resulting in an overestimation of the radiation emitted by the cirrus cloud (Liu, 2015). Sourdeval et al. (2013) proposed an algorithm to retrieve cirrus and multilayer clouds. Xiong et al. (2002) used AVHRR data to study the retrieval of cloud parameters in an Arctic area. When the effective particle radius is 30 µm and the thin cirrus cloud with COT of 0.2 overlapped on the lower-layer water cloud with variables CER and COT, the water cloud CER retrieved by the experiment was larger than the actual water cloud CER by 35%–50%, and the COT was less by 70%–80% (Xiong et al., 2002). Ye et al. (2009) used MODIS data to study a COT and effective particle radius retrieval algorithm under the conditions of multilayer clouds and found that the identification of multilayer clouds can reduce cloud parameter retrieval uncertainties.

In this article, to figure out the influence of vertical variations in cloud phases on cloud parameter retrieval and estimations of DSR, we use the RSTAR radiative transfer model to simulate the sensitivity of satellite-observed radiance and DSR for different cloud parameters, solar and satellite viewing geometries, and, on that basis, we estimate the retrieval bias of cloud parameters caused by the double-layer cloud structure. The quantitative analyses of the retrieval bias of cloud parameters can provide a reference basis for the accurate estimation of DSR and the improvement of subsequent cloud parameter retrieval algorithm.

2 Method and implementation

RSTAR is a comprehensive radiative transfer package designed for multiple purposes. It has been used in the development of sea color retrieval algorithm of satellite sensor ADEOS/OCTS and ADEOS-Ⅱ/GLI. It has also been used in evaluation of the relationship between aerosol and DSR, and retrieval of cloud microphysical properties and surface solar radiation (Letu et al., 2020; Ma et al., 2020). The RSTAR transfer model is used to understand the uncertainties of cloud and DSR retrievals over clouds those are assumed to be single layered while actually being double layered. The RSTAR model is a set of numerical models of atmospheric radiative transfer that are applicable to the plane parallel atmosphere (Nakajima and Tanaka, 1986; Nakajima and Tanaka, 1988), and the calculated wavelengths can cover 0.17–1,000 μm. The plane parallel atmosphere can be divided into 50 layers from the sea surface level to the highest altitude of 120 km, and six atmosphere models (Tropical, Mid-latitude summer, Mid-latitude winter, High-latitude summer, High-latitude winter, and US standard) can be selected. The cloud particle scattering model is composed of water and ice clouds. The ice cloud model further consists of various ice scattering kernels, such as spheroid and ellipsoidal shapes and hexagonal columns. Liou (1972) assumed that the ice crystal was a cylinder. The International Cirrus Experiment (ICE) project implemented in 1991 confirmed that the basic shape of ice crystals is approximately hexagonal (Letu et al., 2015; Key et al., 2002; C-Labonnote et al., 2000). So, we chose the ellipsoidal and hexagonal columns as typical shapes of ice cloud particles in our simulation. In the actual simulation, we input satellite geometric angle parameters (solar zenith angle, satellite zenith angle, and the difference between the solar and satellite azimuth angles) for any pixel point and defined the central wavelength and width of each waveband to be calculated, as well as the wind velocity at each point. The types of atmospheric models used were the U.S. standard atmosphere and standard aerosol models assumed to be of the rural type. The advantages of these models are flexible computation scheme, high computational accuracy, incorporation of many factors, and abundant output results. In this article, we have primarily used RSTAR to simulate satellite-observed radiance and estimate DSR (W/m²).

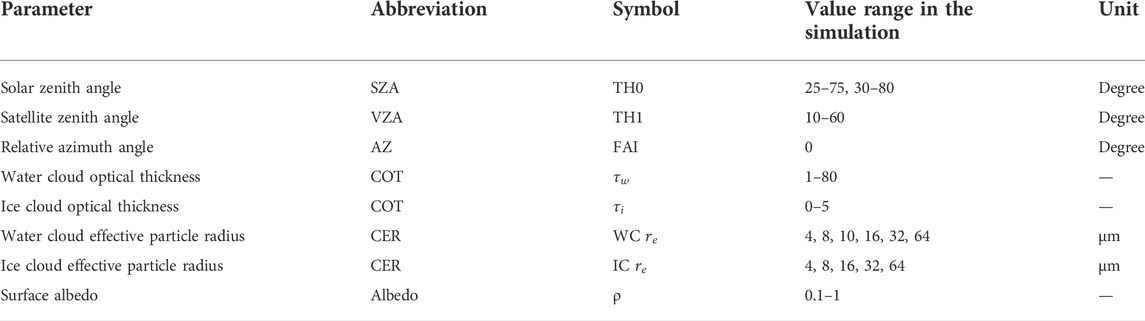
Theoretically, the radiance received by the satellite sensor not only depends on the solar irradiation and observation angle but also depends on the COT and effective particle radius of the cloud. Clouds are the important meteorological factors those affect the arrival of solar energy at the surface. Therefore, we first carried out an experiment on the sensitivity of the model’s simulated satellite-observed radiance and DSR to the relevant parameters and determined an appropriate selection of simulation parameters. The model sensitivity experiment was used to inspect the influence of different input parameters on the output results. In the simulation, we fixed other conditions and parameters and only changed one condition or parameter at a time to analyze the variation characteristics of satellite-observed radiance and DSR with the changes in the simulation conditions or single parameter; that is, the sensitivity to single factors was studied. The relevant model input parameters are listed in Table 1.

TABLE 1

TABLE 1. Input parameters used in the RSTAR.

3 Results and discussion

3.1 Sensitivity analysis of the simulated satellite-observed radiance to the input parameters

The sensitivity analysis was performed using the RSTAR model to understand the uncertainties of the most important input parameters, which included SZA, VZA, COT, CER, and surface albedo. This work is focused on double-layer cloud condition and does not involve the more complex multilayer cloud condition. In this study, we used a 0.64-μm (water and ice clouds at weakly absorbing channel) center wavelength to calculate the sensitivity of satellite-observed radiance to the input parameters. The radiance calculated for the different cloud phase states drastically decreases with increasing SZA range from 25° to 75° as shown in Figure 2A. The radiance of the hexagonal-column ice crystal is higher than that of the water cloud and ellipsoidal ice crystal models. The radiance increases with increasing VZA range from 10° to 60° as shown in Figure 2B. When the VZA is 50°, the difference among the three cases is small. The radiance of the water cloud, ellipsoidal ice crystal, and hexagonal-column ice crystal models are 196.9 W/m²/$\text{μm}$/sr, 194.3 W/m²/$\text{μm}$/sr, and 198 W/m²/$\text{μm}$/sr, respectively. The increasing trend of the radiance calculated by the hexagonal-column ice crystal model is relatively gentle, while the radiance calculated with the water cloud and ellipsoidal ice crystal models showed significant increases and was higher than that of the hexagonal-column ice crystal model when the angle was greater than 50°. The radiance increased with increasing COT in the three scattering models shown in Figure 2C. An increasing trend was obvious when COT was less than 10, but slowed down when COT was greater than 10. Figure 2D shows that when the CER is the same, the radiance calculated with the hexagonal-column ice crystal model is significantly higher than those of the ellipsoidal ice crystal and water cloud models. When the CER reaches 16 μm, the radiance shows a decreasing trend, while the decrease slows down as the CER exceeds 16 μm. When it reaches 64 μm, the difference between the calculated values of the water cloud and ellipsoidal ice crystal models is small. It can be seen from Figure 2 that the difference between the radiance calculated by the water cloud model and the ellipsoidal ice crystal model is small, and the variation trend is relatively consistent. The radiance calculated by the hexagonal-column ice crystal model is generally higher than that calculated by the water cloud model and the ellipsoidal ice crystal model.

FIGURE 2

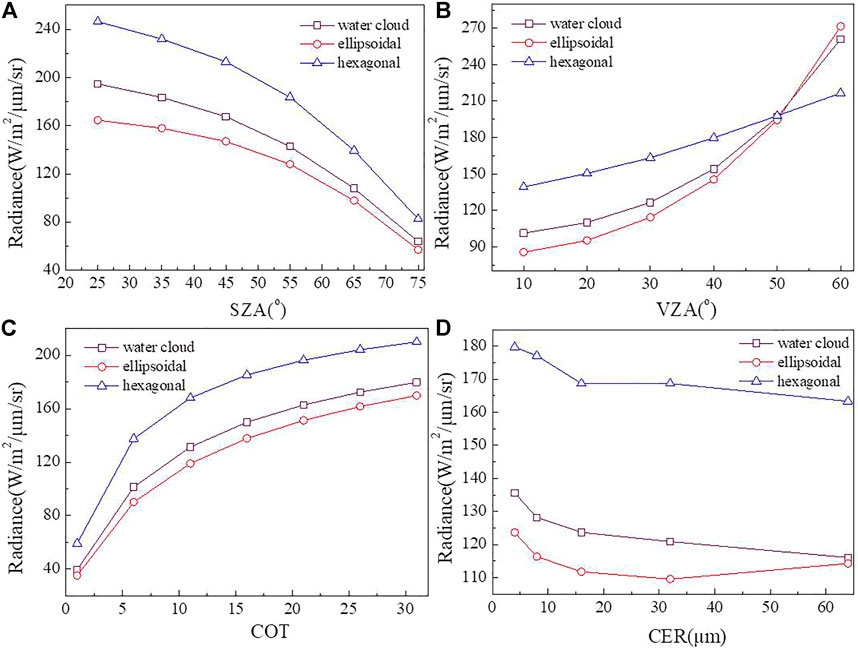
FIGURE 2. Sensitivity of satellite radiance to different parameters. (A) TH1 = 30^o, FAI = 0^o, $\text{ρ}\mathrm{=0}\mathrm{.1}$, IC $r_e\mathrm{=64}$ μm, WC $r_e\mathrm{=10}$ μm, $\text{τ }\mathrm{=10}$. (B) TH0 = 60^o, FAI = 0^o, $\text{ρ}\mathrm{=0}\mathrm{.1}$, IC $r_e\mathrm{=64}$ μm, WC $r_e\mathrm{=10}$ μm, $\text{τ }\mathrm{=10}$. (C) TH0 = 60^o, TH1 = 30^o, FAI = 0^o, $\text{ρ}\mathrm{=0}\mathrm{.1}$, IC $r_e\mathrm{=64}$ μm, WC $r_e\mathrm{=10}$ μm. (D) TH0 = 60^o, TH1 = 30^o, FAI = 0^o, $\text{ρ}\mathrm{=0}\mathrm{.1}$, $\text{τ }\mathrm{=10}$.

For clouds with different phases, the radiance values are obviously different. The different scattering characteristics of ice crystals lead to the different radiance characteristics of ice clouds. It has been proved that in the retrieval of ice cloud microphysical and optical parameters, the appropriate selection of an effective ice crystal model can avoid the retrieval bias caused by using different ice crystal models.

Then, the COTs of 1, 3, and 5 are used as the representative to analyze the variation trend and difference of radiance calculated with different cloud phase states and ice crystal scattering models. Figure 3A shows that when the SZA is 30°, the differences in calculated radiance for various cloud phase states under the same COT are relatively small. When COT is 1, the difference is 13.31 W/m²/$\text{μm}$/sr; when COT is 3, the difference is 39.6 W/m²/$\text{μm}$/sr; and when COT is 5, the difference is 53.2 W/m²/$\text{μm}$/sr. The radiance and variation trends for clouds composed of water and ellipsoidal ice crystals are relatively similar. Figure 3B shows that the radiance for the different cloud phase states increases with increase in VZA. The rising trend for the calculated values for a hexagonal column of ice crystals is relatively slow, and the variation trend for the calculated values for a water cloud is relatively consistent with the values for a hexagonal column of ice crystals and is smaller than the values for a hexagonal column of ice crystals for VZA below 30°. For VZA exceeding 30°, the upward trends increase and intersect at approximately 50°. Subsequently, the calculated values for the water cloud are higher than those for the hexagonal column of ice crystals. Figure 3C shows that the radiance calculated for the water cloud with different CERs increases as COT increases, and the increasing magnitude of enhancement is relatively obvious when COT is less than 11. When the CER is 4 μm and the water cloud optical thickness is 1, the calculated radiance is 43.38 W/m²/$\text{μm}$/sr, and when the water cloud optical thickness is 11, the calculated radiance is 140.4 W/m²/$\text{μm}$/sr. However, when the CER is smaller than 8 μm, the differences in the calculated values for 4 and 8 μm are relatively large. For example, when the water cloud optical thickness is 21 and the CER is 4 μm, the radiance is 170.7 W/m²/$\text{μm}$/sr; when the CER is 8 μm, the radiance is 164.4 W/m²/$\text{μm}$/sr; when the CER is 16 μm, the radiance is 160.2 W/m²/$\text{μm}$/sr; and when the CER is 32 μm, the radiance is 157.6 W/m²/$\text{μm}$/sr.

FIGURE 3

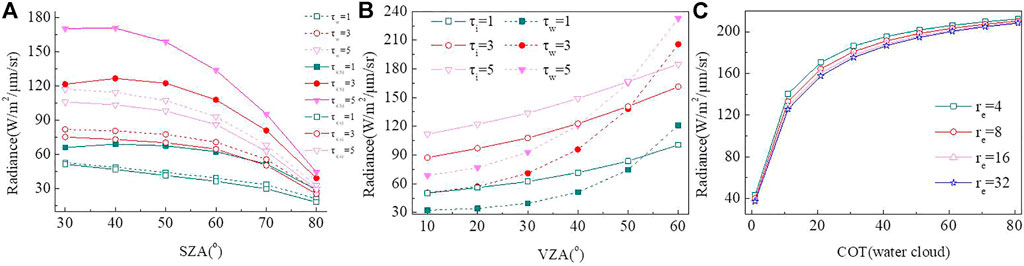
FIGURE 3. Sensitivity of radiance to clouds with different phase states and COT. (A) TH1 = 30°, FAI = 0°, IC $r_e\mathrm{=}32$ μm, WC $r_e\mathrm{=10}$ μm. (B) TH0 = 60°, FAI = 0°, IC $r_e\mathrm{=}32$ μm, WC $r_e\mathrm{=10}$ μm. (C) TH0 = 60°, TH1 = 30°, FAI = 0.

The results show that the radiance for water and ice cloud models is significantly different as a function of SZA, VZA, COT, and CER because of the different single-scattering and microphysical properties between water and ice cloud particles. Therefore, it is important to differentiate the water and ice cloud properties respectively to ensure accurate calculation of the DSR.

3.2 Sensitivity analysis of the simulated downward shortwave radiation to input parameters

The accuracy of the calculated DSR depends largely on the reliability of the cloud parameters (Letu et al., 2022). In cloudy conditions, the simulation using the RSTAR model on the downward shortwave radiation at the surface contains several important input parameters: solar zenith angle, COT, and effective particle radius for different phase states. The values of the simulated waveband were in the range of 0.295–3 µm, which is the interval wherein solar energy is concentrated, and we selected 30 representative wavebands (0.295, 0.30, 035, 0.38, 0.40, 0.412, 0.443, 0.45, 0.46, 0.49, 0.52, 0.545, 0.565, 0.625, 0.67, 0.71, 0.749, 0.763, 0.865, 1.05, 1.13, 1.24, 1.38, 1.5, 1.63, 1.70, 1.80, 2.21, 2.50, and 3.00) to calculate DSR. In the actual calculation process, in order to balance the calculation speed and accuracy, 30 typical wavelengths are selected as integration nodes. The 30 typical solar spectrum nodes can reach 99% of the dense (262 integration nodes) downward shortwave radiation spectrum integration value and meet the requirements of calculation speed and accuracy (Ma et al., 2019).

The DSR of the three cloud types with different input parameters was analyzed. The DSR decreases rapidly with increasing the SZA range from 25° to 75° as shown in Figure 4A. The DSR calculated by the hexagonal-column ice crystal model is significantly lower than that calculated using the water cloud and ellipsoidal ice crystal models, and the difference between these decreases gradually. The DSR increases with increasing surface albedo as shown in Figure 4B. The difference between the DSR calculated by water cloud and that calculated by the ellipsoidal ice crystal model is very small when the surface albedo is 0.7. The calculated value of water cloud is 341.42 W/m², the calculated value of the ellipsoidal ice crystal model is 340.85 W/m², and the calculated value of water cloud is higher than that of the ellipsoidal ice crystal model. When the surface albedo is 1, the difference between the three reaches the minimum. The multiple scattering effect between the atmospheric medium and the surface can be seen in Figure 4B, and the single scattering albedo of the water cloud also contributes to the results. The DSR decreases gradually with the increase of COT as shown in Figure 4C. When COT is less than 10, the DSR decreases obviously, and the decreasing trend is slow when COT is greater than 10, and the trend of the three changes seems consistent. Figure 4D shows that the DSR calculated by the hexagonal-column ice crystal model is significantly lower than that of the water cloud and ellipsoidal ice crystal models. The results of the water cloud and ellipsoidal ice crystal models are very close.

FIGURE 4

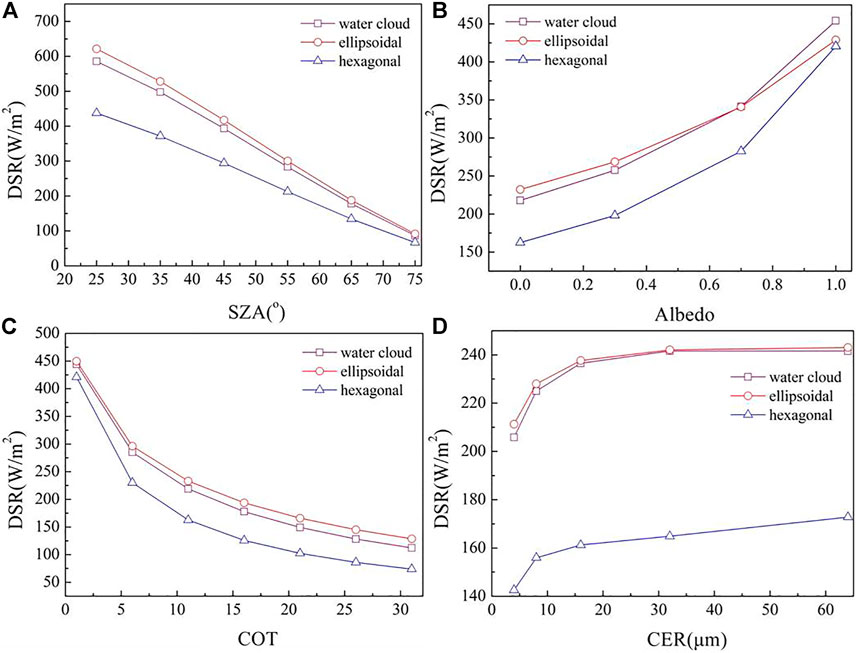
FIGURE 4. Sensitivity of DSR to different parameters. (A) $\text{ρ}\mathrm{=0}\mathrm{.1}$, IC $r_e\mathrm{=64}$ μm, WC $r_e\mathrm{=10}$ μm, $\text{τ}\mathrm{=10}$. (B) TH0 = 60^o, IC $r_e\mathrm{=64}$ μm, WC $r_e\mathrm{=10}$ μm, $\text{τ}\mathrm{=10}$. (C) TH0 = 60^o, $\text{ρ}\mathrm{=0}\mathrm{.1}$, IC $r_e\mathrm{=64}$ μm, WC $r_e\mathrm{=10}$ μm. (D) TH0 = 60^o, $\text{ρ}\mathrm{=0}\mathrm{.1}$, $\text{τ}\mathrm{=10}$.

Taking the COTs of 1, 3, and 5 as the representative, we analyzed the variation trend and difference of DSR calculated by assuming different phases and ice crystal models. Figure 5A shows that the DSR calculated for different cloud phase states exhibited rapidly declining trends with increasing SZA and the differences between the calculated values for water clouds and the hexagonal-column ice crystal gradually decreased. The calculated value for a hexagonal-column ice crystal is smaller than that for a water cloud. When the SZA is 30° and COT is 5, the difference is the largest and reaches 140.45 W/m². At the same time, the calculated value for a hexagonal-column ice crystal is smaller than that for ellipsoidal ice crystals. When the SZA is 30° and COT is 5, the difference is the largest and reached 165.93 W/m². Figure 5B shows that the DSR calculated for different cloud phase states exhibited upward trends with increasing surface albedo, and the differences gradually decreased. Under the same COT, the calculated values for the water cloud model were higher than the calculated value for the hexagonal column ice cloud model. The asymmetry parameter might be the reason for the values to be almost equal in Figure 5B. Yang et al. (2013) compared and analyzed more than six shapes to describe ice crystal particles in ice clouds, and the new data library presented in this article provides the basic and consistent single-scattering data for a selection of ice crystal sizes and shapes observed in the atmosphere. RSTAR uses the phase functions indirectly. Chen and Zhang, 2018 analyzed the effects of ice crystal habit weight on ice cloud optical properties and radiation by referring to Yang’s method and simulated the shortwave band–averaged bulk extinction coefficient and shortwave band–averaged asymmetry factor. The shortwave band–averaged bulk extinction coefficient calculated by each assumption is almost the same, and the difference is mainly caused by the difference of asymmetry factor. Ice crystal particles have higher backscattering, the calculated values were almost equal when the water cloud optical thickness is 5 and the ice cloud optical thickness is 3. Figure 5C shows that in the case of double-layer cloud, when COT of the lower-layer water cloud is small, the COT of the upper-layer ice cloud has a great influence on the calculation of the DSR, and the difference decreases with increase in the water cloud optical thickness. By comparing the ellipsoidal ice crystals with hexagonal ice crystals, the hexagonal ice crystals have a greater influence on the calculation of DSR. As the COT of the upper ice cloud increases, the DSR gradually decreases.

FIGURE 5

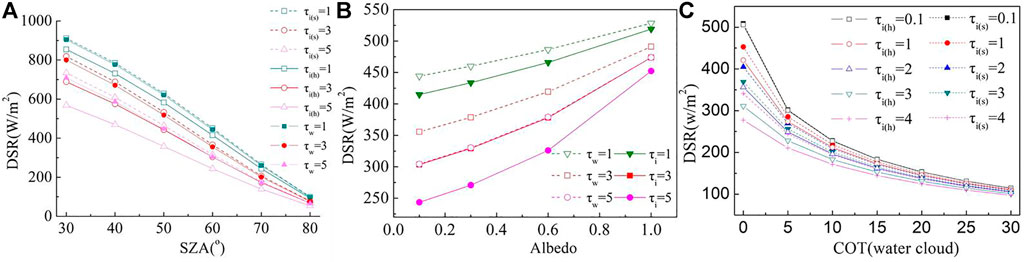
FIGURE 5. Sensitivity of DSR to clouds with different phase states and COTs. (A) $\text{ρ}$ = 0.1, IC $r_e$ = 32 μm, WC $r_e$ = 10 μm. (B) TH0 = 60° (C) TH0 = 60°, $\text{ρ}$ = 0.1.

The simulation of ice cloud radiative transfer composed of different ice crystal models is not only for the radiance values observed by satellites but also of great significance for the accurate calculation of DSR. There is a significant difference between the DSRs calculated by the ice crystal models with different shapes. The reason for these differences is that the asymmetry factors of ice crystals with different shapes are different. It shows that choosing the shape of ice particles correctly is very important to accurately calculate the DSR. According to the above sensitivity analysis, we constructed reasonable LUTs those help in calculating relative bias and improving the accuracy of DSR. The relative bias calculated in this article refers to the ratio between the DSR calculated by simulation in the single-layer cloud model and the differences between the DSRs calculated by single-layer and double-layer cloud models.

3.3 Statistical analysis of the retrieval bias of downward shortwave radiation in the case of double-layer clouds

The accurate retrieval of cloud microphysical parameters such as COT and CER is the premise for accurate simulations of DSR. Regarding multilayer clouds, the radiance values of the same pixel observed by satellite contain integrated information on upper-layer ice clouds and lower-layer water clouds. According to the results of the sensitivity analysis presented in section 3.1, when the SZA is 30°, the differences in calculated radiance for COT under different cloud phase states were relatively small. When the VZA is approximately 50°, the calculated radiance values for different cloud phase states intersect. Therefore, when we used RSTAR to analyze the retrieval bias of cloud parameters caused by double-layer clouds, we selected SZA of 30°, VZA of 50°, and AZ of 0° as representative for the simulation. When the CER exceeded 8 μm, the differences in calculated radiance were relatively small. In the mid-latitude region, water cloud particle radius of 10 μm and ice cloud particle radius of 65 μm are typical, so we selected a water cloud particle radius of 10 μm and an ellipsoidal ice crystal particle radius of 65 μm as the input values in the simulation.

As shown in Figure 6, when the solar elevation angle is fixed, we selected ice cloud optical thicknesses of 0–3, CER of 64 μm, water cloud optical thicknesses of 1–80, and CER of 10 μm as representative. We used the LUTs to determine the combinations of water cloud and ice cloud optical thicknesses that produce the same radiance values observed by the satellite.

FIGURE 6

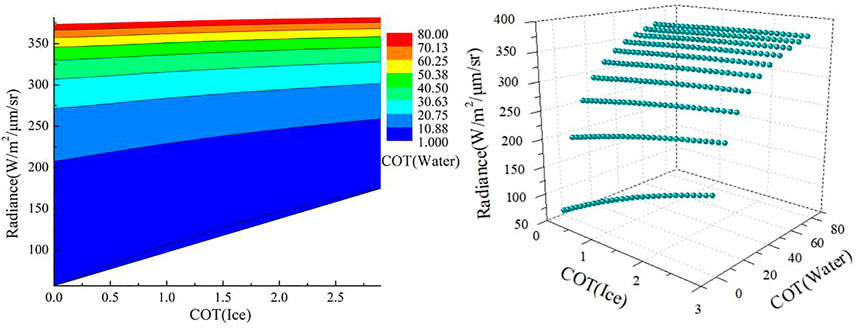
FIGURE 6. Equal radiance values for different cloud phase states. TH0 = 30°, TH1 = 50°, FAI = 0°, ${\tau }_w$ = 1–80, ${\tau }_i$ = 0–3, IC $r_e$ = 64 μm, WC $r_e$ = 10 μm.

For the double-layer cloud, the upper-layer ice cloud is composed of ellipsoidal ice crystals; COTs are 0, 0.4, 0.8, 1.2, and 2; the CER is 65 μm; and the representative CER of the lower-layer water cloud is 10 μm. We used the lookup table method to retrieve the corresponding overlap values in ice cloud and water cloud optical thicknesses that could yield the same radiance value observed by the satellite sensor, and we calculated the DSR under the combined situation (Table 2). The simulation results indicate that under the same radiance value observed by the satellite, the ice cloud and water cloud optical thicknesses could be combined in multiple ways. When the modeled ice crystals were ellipsoidal, the differences between the retrieved water cloud and ice cloud optical thicknesses were relatively small. Therefore, the differences of DSR were also relatively small, and the maximum relative bias reached 0.63%. The results were consistent with the conclusions obtained in the sensitivity analysis.

TABLE 2

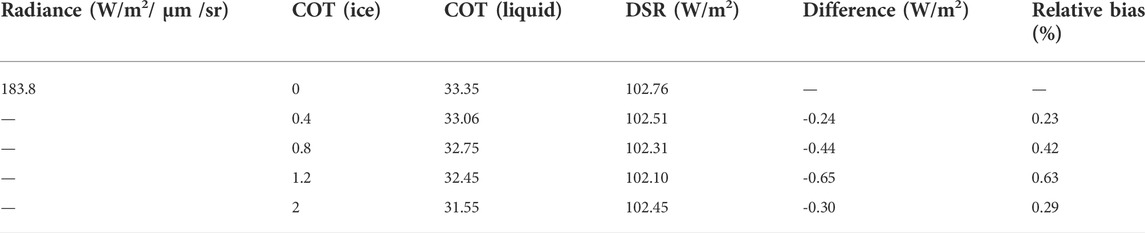
TABLE 2. Differences in DSR for double-layer clouds (the upper ice cloud is composed of ellipsoidal ice crystals) with different optical thicknesses.

For the double-layer clouds, when the upper-layer ice cloud is a hexagonal-column ice crystal, the COTs are 0, 0.4, 0.8, 1.2, and 2; the CER is 65 μm; and the representative CER of the particles composing the lower-layer water cloud is 10 μm. We calculated the DSR corresponding to each combined situation (Table 3) under the same satellite observation radiance. The simulation results indicate that in comparison with ellipsoidal ice crystals, the differences in the water cloud and ice cloud optical thicknesses obtained from the retrieval of the cloud, presuming the hexagonal-column ice crystal under the same radiance value were very large, and the relative bias exhibited an upward trend as radiance increased. When the radiance value is 186.2 W/m²/$\text{μm}$/sr, the largest relative bias is 23%; when the radiance value is 198.1 W/m²/$\text{μm}$/sr, the largest relative bias is 32.7%; and when the radiance value is 214.1 W/m²/$\text{μm}$/sr, the largest relative bias is 55.34%. In comparison to the single-layer water cloud, larger ice cloud optical thicknesses correspond to the increased influence on the calculation accuracy of DSR, and the increasing difference trend became relatively slow.

TABLE 3

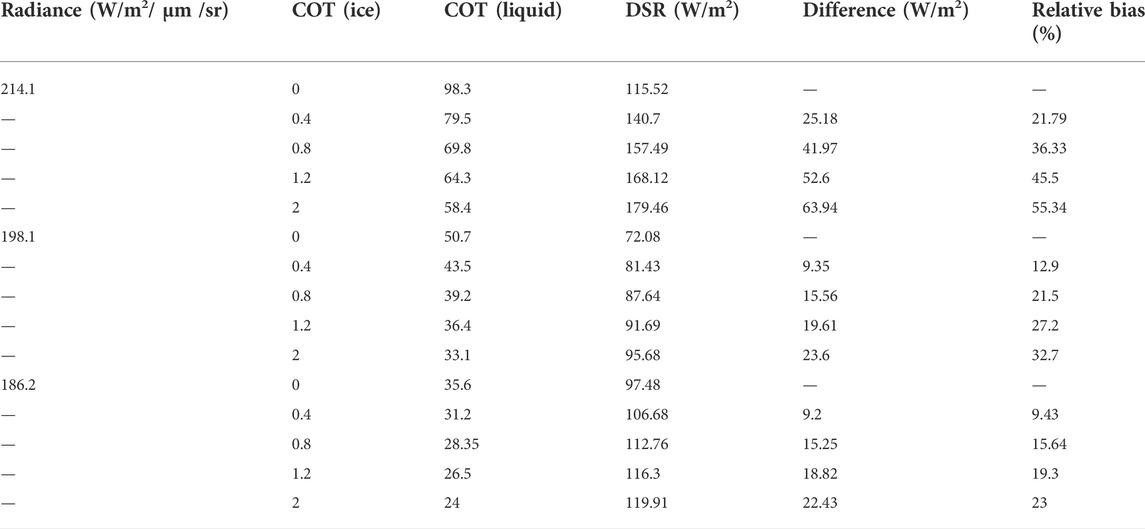
TABLE 3. Differences in DSR for multilayer clouds (the upper ice cloud is composed of hexagonal ice crystals) with different optical thicknesses.

4 Conclusion

In this study, we used the RSTAR radiative transfer model to analyze the sensitivity of satellite-observed radiance and DSR to various cloud parameters, solar zenith angle, and satellite observation angle. We quantitatively estimated the bias on the retrieval of cloud parameters and estimation of surface solar radiation caused by different cloud phase states and an assumption of a double-layer cloud in the ice crystal model, and the following conclusions drawn:

(1) Different cloud parameters (cloud phase, COT, CER, and ice crystal model), SZA, and surface albedo can affect the satellite-observed radiance and DSR. Moreover, it is shown that the variation trends for the calculated values of water clouds and ellipsoidal ice crystals are relatively consistent, and the calculated values for hexagonal-column ice crystals are considerably different from the first two.

(2) For the same pixel level radiance, we can use different combinations of ice and water clouds to retrieve different optical and microphysical parameters, which, as a consequence, will impact uncertainties in estimates of surface solar radiation. The analyses indicate that relative to the retrieval results of single-layer clouds, when the particle shapes of an upper-layer ice cloud are ellipsoidal, the estimation bias in surface solar radiation caused by retrieval bias is relatively small, and the highest relative bias reaches 0.63%. When the particle shapes for the upper-layer ice cloud column were hexagonal, the ice cloud optical thickness is 2 and the water cloud optical thickness is 58.4. The highest relative bias for the estimation of surface solar radiation caused by the retrieval bias of cloud optical thickness reached 55.34%, and the relative bias exhibited an increasing trend as radiance increased. A thick upper layer tends to hide a lower layer and precludes accurate estimation of its properties. Therefore, when we retrieve cloud parameters from satellite measurements, we cannot neglect the influences caused by double-layer clouds. At the same time, it is also important to choose the appropriate ice crystal model.

As compared to water clouds, ice crystals have complex nonspherical properties, which can result in large uncertainties in the cloud radiative impacts, and the accuracy of calculated DSR depends largely on the reliability of cloud parameters. Future work should focus on the case of the triple layers or more complex overlay. For an extensive validation, more measurements will be taken into account. The bias analysis method presented in this article can provide reference for the evaluation of remote sensing cloud products at present and the evaluation of radiative forcing by cloud products in future IPCC reports (Yang et al., 2013; Chen and Zhang, 2018).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author contributions

AR: methodology data analysis and writing—original draft preparation. RM, GT: Simulations of the result in the manuscript using RSTAR radiative transfer model, and writing—original draft preparation. HL, HS: validations and editing original draft. JX, CS: conceptualization and data acquisition. JH, YB, and LC: validations, investigation, review ing and editing. All authors read the manuscript, contributed to the discussion, and gave valuable suggestions to improve the manuscript.

Funding

This work was supplied by National Key Research and Development Program of China (Grant No. 2017YFA0603502), National Natural Science Foundation of China (Grant Nos. 91837204, 41905023, 42175152), and Youth Innovation Promotion Association CAS (No. 2021122).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer CZ declares a shared affiliation, with one of the authors and GT to the handling editor at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albrecht, B. A., Randall, D. A., and Nicholls, S. (1988). Observations of marine stratocumulus clouds during FIRE. Bull. Am. Meteorol. Soc. 69 (6), 618–626. doi:10.1175/1520-0477(1988)069<0618:oomscd>2.0.co;2

CrossRef Full Text | Google Scholar

Alexandrov, M. D., Miller, D. J., Rajapakshe, C., Fridlind, A. M., Diedenhoven, B., Cairns, B., et al. (2020). Vertical profiles of droplet size distributions derived from cloud-side observations by the research scanning polarimeter: Tests on simulated data. Atmos. Res. 239, 104924. doi:10.1016/j.atmosres.2020.104924

PubMed Abstract | CrossRef Full Text | Google Scholar

Arking, A., and Childs, J. D. (1985). Retrieval of cloud cover parameters from multispectral satellite images. J. Clim. Appl. Meteor. 24 (4), 322–333. doi:10.1175/1520-0450(1985)024<0322:roccpf>2.0.co;2

CrossRef Full Text | Google Scholar

Baum, B. A., Heymsfield, A. J., Yang, P., and Bedka, S. T. (2005). Bulk scattering properties for the remote sensing of ice clouds. Part I: Microphysical data and models. J. Appl. Meteorology 44 (12), 1885–1895. doi:10.1175/jam2308.1

CrossRef Full Text | Google Scholar

Baum, B. A., Yang, P., Heymsfield, A. J., Schmitt, C. G., Xie, Y., Bansemer, A., et al. (2011). Improvements in shortwave bulk scattering and absorption models for the remote sensing of ice clouds. J. Appl. Meteorol. Climatol. 50 (5), 1037–1056. doi:10.1175/2010jamc2608.1

CrossRef Full Text | Google Scholar

C-Labonnote, L., Brogniez, G., Doutriaux-Boucher, M., Buriez, J. C., Gayet, J. F., and Chepfer, H. (2000). Modeling of light scattering in cirrus clouds with inhomogeneous hexagonal monocrystals. comparison with in-situ and adeos-polder measurements. Geophys. Res. Lett. 27 (1), 113–116. doi:10.1029/1999gl010839

CrossRef Full Text | Google Scholar

Chang, F. L., and Li, Z. (2005). A near-global climatology of single-layer and overlapped clouds and their optical properties retrieved from terra/MODIS data using a new algorithm. J. Clim. 18 (22), 4752–4771. doi:10.1175/jcli3553.1

CrossRef Full Text | Google Scholar

Charlson, R. J., Lovelock, J. E., Andreae, M. O., and Warren, S. G. (1987). Oceanic phytoplankton, atmospheric sulphur, cloud albedo and climate. Nature 326 (6114), 655–661. doi:10.1038/326655a0

CrossRef Full Text | Google Scholar

Chen, Q., and Zhang, H. (2018). Effects of ice crystal habit weight on ice cloud optical properties and radiation. Acta Meteorol. Sin. 76 (2), 279–288. doi:10.11676/qxxb2017.088

CrossRef Full Text | Google Scholar

Chen, Y., Tang, R., Zhou, Y., and Mao, J. (2009). Microphysical characteristic parameters product retrieved by FY-2C/D satellite and its application in the precipitation analysis. Meteorol. Mon. 35 (2), 15–18. doi:10.1016/S10036326(09)600844

CrossRef Full Text | Google Scholar

Davis, S. M., Avallone, L. M., Kahn, B. H., Meyer, K. G., and Baumgardner, D. (2009). Comparison of airborne in situ measurements and moderate resolution imaging spectroradiometer (MODIS) retrievals of cirrus cloud optical and microphysical properties during the midlatitude cirrus experiment (MidCiX). J. Geophys. Res. 114 (D2), D02203. doi:10.1029/2008jd010284

CrossRef Full Text | Google Scholar

IPCC (2021). Climate change 2021: The physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental Panel on climate change. Cambridge: Cambridge University Press.

Google Scholar

Key, J. R., Yang, P., Baum, B. A., and Nasiri, S. L. (2002). Parameterization of shortwave ice cloud optical properties for various particle habits. J. Geophys. Res. 107 (D13), 4181. doi:10.1029/2001jd000742

CrossRef Full Text | Google Scholar

Kiehl, J. T. (1994). Sensitivity of a GCM climate simulation to differences in continental versus maritime cloud drop size. J. Geophys. Res. 99 (D11), 23107–23115. doi:10.1029/94jd01117

CrossRef Full Text | Google Scholar

King, M. D. (1987). Determination of the scaled optical thickness of clouds from reflected solar radiation measurements. J. Atmos. Sci. 44 (13), 1734–1751. doi:10.1175/1520-0469(1987)044<1734:dotsot>2.0.co;2

CrossRef Full Text | Google Scholar

Letu, H., Yuhai, B., Xu, J., Qing, S., and Bao, G. (2015). Radiative properties of cirrus clouds based on hexagonal and spherical ice crystals models. Spectrosc. Spectr. Analysis 35 (5), 1165–1168.

Google Scholar

Letu, H., Ishimoto, H., Riedi, J., Nakajima, T. Y., C -Labonnote, L., Baran, A. J., et al. (2016). Investigation of ice particle habits to be used for ice cloud remote sensing for the GCOM-C satellite mission. Atmos. Chem. Phys. 16 (18), 12287–12303. doi:10.5194/acp-16-12287-2016

CrossRef Full Text | Google Scholar

Letu, H., Yang, K., Nakajima, T. Y., Ishimoto, H., Nagao, T. M., Riedi, J., et al. (2020). High-resolution retrieval of cloud microphysical properties and surface solar radiation using himawari-8/ahi next-generation geostationary satellite. Remote Sens. Environ. 239 (111583). doi:10.1016/j.rse.2019.111583

CrossRef Full Text | Google Scholar

Letu, H., Nakajima, T. Y., Wang, T., Shang, H., Ma, R., Yang, K., et al. (2022). A new benchmark for surface radiation products over the East Asia-Pacific region retrieved from the Himawari-8/AHI next-generation geostationary satellite. Bull. Am. Meteorological Soc. 103 (5), E873–E888. doi:10.1175/BAMSD200148.1

CrossRef Full Text | Google Scholar

Liou, K. N. (1972). Electromagnetic scattering by arbitrarily oriented ice cylinders. Appl. Opt. 11 (3), 667–674. doi:10.1364/ao.11.000667

PubMed Abstract | CrossRef Full Text | Google Scholar

Liou, K. N. (2004). An introduction to atmospheric radiation. BeiJing: China Meteorological Press.

Google Scholar

Liu, J., Dong, C. H., and Zhang, W. J. (2003). Determination of the optical thickness and effective radius of water clouds by FY-1C data. J. Infrared Millim. Waves 22 (6), 436–440. doi:10.3321/j.issn:1001-9014.2003.06.009

CrossRef Full Text | Google Scholar

Liu, J. (2015). Retrieval bias analysis of ice cloud optical thickness based on the FY-2 satellite. Acta Meteorol. Sin. 73 (6), 1121–1130. doi:10.11676/qxxb2015.076

CrossRef Full Text | Google Scholar

Ma, R., Letu, H., Shang, H., Ana, R., He, J., Han, X., et al. (2019). Estimation of downward surface shortwave radiation from Himawari-8 atmospheric products. J. Remote Sens. 23 (5), 924–934. doi:10.11834/jrs.20198033

CrossRef Full Text | Google Scholar

Ma, R., Letu, H., Yang, K., Wang, T., Shi, C., Xu, J., et al. (2020). Estimation of surface shortwave radiation from himawari-8 satellite data based on a combination of radiative transfer and deep neural network. IEEE Trans. Geosci. Remote Sens. 58, 5304–5316. doi:10.1109/tgrs.2019.2963262

CrossRef Full Text | Google Scholar

Mei, L., Rozanov, V., Vountas, M., and Burrows, J. P. (2018). The retrieval of ice cloud parameters from multi-spectral satellite observations of reflectance using a modified XBAER algorithm. Remote Sens. Environ. 215, 128–144. doi:10.1016/j.rse.2018.06.007

CrossRef Full Text | Google Scholar

Nakajima, T., and King, M. D. (1990). Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part I: Theory. J. Atmos. Sci. 47 (15), 1878–1893. doi:10.1175/15200469(1990)047<1878:DOTOTA>2.0.CO;2

CrossRef Full Text | Google Scholar

Nakajima, T., King, M. D., Spinhirne, J. D., and Radke, L. F. (1991). Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part II: Marine stratocumulus observations. J. Atmos. Sci. 48 (5), 728–751. doi:10.1175/1520-0469(1991)048<0728:dotota>2.0.co;2

CrossRef Full Text | Google Scholar

Nakajima, T., and Tanaka, M. (1986). Matrix formulations for the transfer of solar radiation in a plane-parallel scattering atmosphere. J. Quantitative Spectrosc. Radiat. Transf. 35 (1), 13–21. doi:10.1016/0022-4073(86)90088-9

CrossRef Full Text | Google Scholar

Nakajima, T., and Tanaka, M. (1988). Algorithms for radiative intensity calculations in moderately thick atmospheres using a truncation approximation. J. Quant. Spectrosc. Radiat. Transf. 40 (1), 51–69. doi:10.1016/0022-4073(88)90031-3

CrossRef Full Text | Google Scholar

Nauss, T., and Kokhanovsky, A. A. (2011). Retrieval of warm cloud optical properties using simple approximations. Remote Sens. Environ. 115 (6), 1317–1325. doi:10.1016/j.rse.2011.01.010

CrossRef Full Text | Google Scholar

Randall, D. A., Coakley, J. A., Fairall, C. W., Kropfli, R. A., and Lenschow, D. H. (1984). Outlook for research on subtropical marine stratification clouds. Bull. Amer. Meteor. Soc. 65 (12), 1290–1301. doi:10.1175/1520-0477(1984)065<1290:ofrosm>2.0.co;2

CrossRef Full Text | Google Scholar

Saito, M., Yang, P., Hu, Y., Liu, X., Loeb, N., Smith, W. L., et al. (2019). An efficient method for microphysical property retrievals invertically inhomogeneous marine waterclouds using MODIS‐Cloud Satmeasurements. JGR. Atmos. 124, 2174–2193. doi:10.1029/2018jd029659

CrossRef Full Text | Google Scholar

Sourdeval, O., C.-Labonnote L, , Brogniez, G., and Baran, A. J. (2013). Simultaneous multi-layer retrievals of ice and liquid water cloud properties using passive measurements. Am. Inst. Phys. 1531 (1), 252–255. doi:10.1063/1.4804754

CrossRef Full Text | Google Scholar

Stocker, T. F., Qin, D., Plattner, G. K., Tignor, M., Allen, S. K., Boschung, J., et al. (2013). IPCC, 2013: Climate change 2013: The physical science basis. Contribution of working group I to fifth assessment report of the intergovernmental Panel on climate change. Comput. Geom. 18 (2), 95–123. doi:10.1017/CBO9781107415324

CrossRef Full Text | Google Scholar

Twomey, S., and Cocks, T. (1989). Remote sensing of cloud parameters from spectral reflectance in the near-infrared. Beiträge zur Phys. Atmosphäre 62 (3), 172–179.

Google Scholar

Wang, Y., and Zhao, C. (2017). Can MODIS cloud fraction fully represent the diurnal and seasonal variations at DOE ARM SGP and Manus sites? J. Geophys. Res. Atmos. 122 (1), 329–343. doi:10.1002/2016jd025954

CrossRef Full Text | Google Scholar

Xiong, X., Lubin, D., Li, W., and Stamnes, K. (2002). A critical examination of satellite cloud retrieval from AVHRR in the Arctic using SHEBA data. J. Appl. Meteor. 41 (12), 1195–1209. doi:10.1175/1520-0450(2002)041<1195:aceosc>2.0.co;2

CrossRef Full Text | Google Scholar

Yang, P., Bi, L., Baum, B. A., Liou, K. N., Kattawar, G. W., Mishchenko, M. I., et al. (2013). Spectrally consistent scattering, absorption, and polarization properties of atmospheric ice crystals at wavelengths from 0.2 to 100 μm. J. Atmos. Sci. 70 (1), 330–347. doi:10.1175/jas-d-12-039.1

CrossRef Full Text | Google Scholar

Ye, J., Li, W. B., and Yan, W. (2009). Retrieval of the optical thickness and effective radius of multilayered cloud using MODIS data. Acta Meteorol. Sin. 67 (4), 613–622. doi:10.1142/9789814261210_0051

CrossRef Full Text | Google Scholar

Zhang, H., Peng, J., Jing, X. W., and Li, J. N. (2013). The features of cloud overlapping in Eastern Asia and their effect on cloud radiative forcing. Sci. China Earth Sci. 56 (5), 737–747. doi:10.1007/s11430-012-4489-x

CrossRef Full Text | Google Scholar

Zhao, C., and Garrett, T. J. (2015). Effects of Arctic haze on surface cloud radiative forcing. Geophys. Res. Lett. 42 (2), 557–564. doi:10.1002/2014gl062015

CrossRef Full Text | Google Scholar

Zhao, F., Sun, T., Ding, Q., Kong, Q., Hu, W., Xun, S., et al. (2002). An iterative algorithm for the retrieval of cloud properties from NOAA-AVHRR imagery. Acta Meteorol. Sin. 60 (5), 594–601. doi:10.1002/mop.10502

CrossRef Full Text | Google Scholar

Zhao, C., Xie, S., Klein, S. A., Protat, A., Shupe, M. D., McFarlane, S. A., et al. (2012). Toward understanding of differences in current cloud retrievals of ARM ground-based measurements. J. Geophys. Res. 117 (D10), 63–74. doi:10.1029/2011jd016792

CrossRef Full Text | Google Scholar

Zhou, Y., Sun, X., Mielonen, T., Li, H., Zhang, R., Li, Y., et al. (2018). Cirrus cloud optical thickness and effective diameter retrieved by MODIS: Impacts of single habit assumption, 3-D radiative effects, and cloud inhomogeneity. J. Geophys. Res. Atmos. 123, 1195–1210. doi:10.1002/2017jd027232

CrossRef Full Text | Google Scholar