Applicability of Flow Resistance Formulae for Sand-Bed Channels: An Assessment Using a Very Large Data Set

Among numerous flow resistance formulae for sand-bed channels, this study selected five for evaluation and in order to cover flow conditions in sand-bed river channels as widely as possible, a total of 1,636 sets of field measures were collected from the hydrological stations of two large river systems of China—the Yellow and Yangtze Rivers, in addition to the data compiled by Brownlie. The performance of the selected formulae in yielding the values of Manning resistance coefficient n was evaluated against the total of 6,805 datasets. In many cases, the formula of Ma et al. yielded unreasonable n values of <0, while that of Deng et al. and formulae 1 and 2 of Zhang et al. yielded n values with large errors. The formula of Wu and Wang yielded n values varying within the scope only in the case of n < 0.04. By dividing the absolute relative errors (AREs) from the selected formulae into six groups of 0–0.05, 0.05–1, 0.1–0.2, 0.2–0.5, 0.5–1, and >1, it can be found that, for all five selected formulae, ARE occurred in the group 0.2–0.5 occupied the largest percentage, while in each of the adjacent groups of 0.5–1 and 0.1–0.2 it also occupied a very large percentage. Hence, all five formulae still need to improve their predicting ability.

Introduction

There are a plethora of flow resistance formulae available for sand-bed river channels, but river scientists and engineers have been facing the very difficult problem of selecting a convincing one in practical problem solving (Zhang et al., 2020). Although the following Manning resistance formula (Manning, 1890; Herschel, 1897) was developed a long time ago to calculate the resistance to flow in fixed-bed open channels, it still is widely applied to determine the flow resistance of sand-bed river channels:

$V=\frac{1}{n}{R}^{2/3}{J}^{1/2}(1)$

where V is the average velocity of channel flow, R is the hydraulic radius of the channel, J is the energy slope of flow, and n is the Manning roughness coefficient.

Because the roughness of a riverbed can be reflected by the size of the sediments composing the bed, the Manning roughness coefficient n in Eq. 1 has frequently been determined using the following relationship:

$n=D^{1/6}/A(2)$

where D and A are a representative bed sediment size and a roughness parameter, respectively.

The sediments composing a riverbed, however, are hardly uniform, and there has been no consensus of opinions on what size of the non-uniform sediments can represent the role of D in Eq. 2. While the study by Chang (1939) granted support to the use of D₅₀, nevertheless, Meyer-Peter and Muller (1948) argued that it is more appropriate to use D₉₀ to represent D and consequently found A = 26. However, Maynord (1991) used a large number of flume data collected from various sources and identified that the use of particle size D₉₀ gave slightly better results than the use of D₅₀, with A taking 21.6 and 22.8 respectively for D₅₀ and D₉₀. In the reformulation of the Meyer-Peter and Muller (1948) equation, Huang (2010) also discovered that utilizing D₅₀ or D₉₀ had no effect on the accuracy of flow resistance calculations.

The roughness of a channel can be divided into grain roughness and form roughness for a riverbed with bedforms (Einstein, 1952; Engelund, 1961). While it has been assumed that a representative size of riverbed sediments, such as D₉₀ or D₆₅, may accurately reflect the grain roughness of a flat riverbed (Engelund and Hansen, 1967; van Rijn, 1982; Kamphuis, 1974; Zhang et al.,2012a; Zhang et al., 2012b; Niazkar et al., 2019), form roughness is closely related to the strength of flow acting on a channel bed, usually reflected with the Shields parameter (Yalin, 1963; van Rijn, 1984). Using data from the Compendium of Solids Transport Data compiled by Brownlie (1981), nevertheless, Peterson and Peterson (1988) made a comparison of the bed roughness values between observational data and the results calculated from different flow resistance formulae and commented that the commonly applied formulae with the Shields parameter as the sole factor were insufficient. Importantly, they demonstrated that the roughness of a mobile bed is also a function of the Froude number (Fr) and a dimensionless settling velocity (Zhang et al., 1998). On the basis of both physical reasoning and dimensional analysis, Wu and Wang (1999) proposed a relationship to determine the roughness of a mobile bed by relating the roughness parameter A in Eq. 2 to a non-dimensional shear stress parameter and Fr. Importantly, they tested the relationship with a large number of data observed in experimental flumes and fields collected from different sources and demonstrated that the values of n computed using their relationship yielded results consistent with the measured data at a much higher level than when using the other methods. Table 1 presents the selection of a representative sediment size D and the corresponding value of roughness parameter A by different investigators.

TABLE 1

TABLE 1. Comparisons of A and D for different investigators.

In contrast to the approach of selecting a representative sediment size D in Eq. 2, many studies determined the value of the Manning roughness coefficient n in Eq. 1 directly from a statistical analysis of field observations. Using field observations from the lower Yellow River, Chien and Wan (1983) analyzed the variation of n at various flow and sediment conditions and consequently recognized that n is closely related to both of the relative strength of tractive force and sediment size D₆₅. Zhao and Zhang (1997) presented a detailed physical analysis of the effects of the rough thickness of channel bed on flow velocity, and a relationship expressing n as a complex function of flow depth, sediment size D₅₀, and Fr received a high level of validation with a larger number of field observations obtained from the lower reach of the Yellow River. By reanalyzing the flume experimental data provided by Guy et al. (1966) and field observations at stations located in the middle and lower reaches of the Yellow River, however, Deng et al. (2007) identified that $n$ had a poor relationship with flow discharge and depth, but increased initially and then decreased with an increase in sediment concentration. Importantly, they found that n had a good relationship with Fr and that a power function was shown to be fitting the collected data well.

Using 64 sets of data observed in experimental flumes and more than 1,000 sets of data measured during 1958–1959 at six hydrological stations located in the lower reach of the Yellow River, Ma et al. (2017) evaluated the performance of three roughness formulae proposed respectively by van Rijn (1984), Zhao and Zhang (1997), and Qin et al. (1995). They identified that the formula of Zhao and Zhang fitted best the observations from natural rivers, while the van Rijn formula performed well in laboratory flumes. In addition, Ma et al. (2017) reanalyzed the collected data, and their statistical regression results demonstrated that n showed a very close relationship with Fr. Recently, Zhang et al. (2020) presented a systematic review of the progress on the determination of the roughness of a moving bed channel and highlighted the need to treat Fr as a primary parameter in the establishment of a practically useful flow resistance formula. Consequently, they proposed two formulae to determine n. The first formula is in a relatively simple form considering the effect of Fr only, while the second formula is in a comprehensive form taking into account the effects of Fr, sediment size D₅₀, roughness parameter A, and the von Kármán constant that reflects the effect of sediment concentration on flow energy consumption. While complex in form, the second formula had a much higher level of accuracy. The validation of the two roughness formulae clearly showed that the results generated by both were in a good agreement with a large number of data measured from natural rivers, although deviating slightly from observations in experimental flumes.

It is apparent that most flow resistance formulae were derived with reference to the data observed from experimental flumes and/or from natural rivers collected or conducted by original author(s), supplemented with some data obtained by one or several other researchers. Furthermore, the performance of a formula has often been assessed tentatively based on its agreement with a limited amount of data collected. In addition, there is considerable overlap of the data employed in the development of many formulae, with data incorporated in the subsequent evaluations of their performance. All of these contributed to the proliferation rather than the consolidation of flow resistance formulae for mobile-bed channels (Mark Powell, 2014; Ferro, 2018a; Ferro, 2018b; Di Stefano et al., 2020; Carollo and Ferro, 2021; Nicosia et al., 2021; Yadav et al., 2022). So far, none of the previously developed formulae has been either universally accepted or recognized as being especially appropriate for practical application. Although the performance of many formulae had been evaluated under a relatively wide range of hydraulic conditions, either from laboratory and/or from the field (e.g., Huang et al., 2004; Zhang, 2012a; Zhang, 2012b; Zhang et al., 2020), a collection of more observational datasets has become possible recently, and it is necessary to evaluate which flow resistance formula can give better predictions. For this purpose, this study selected flow resistance formulae for mobile-bed channels that have been most quoted in the literature and collected observational data wide in varying ranges and large in number from various sources. A set of statistical indicators was then used to evaluate the performance of the selected formulae against a large observational dataset collected in this study.

Selection of Formulae

The selection of formulae for evaluation in this study was mainly in terms of popularity and the number and range of data used for developing them. From a detailed literature review of the progress on the development of the formulae, those developed by Wu and Wang (1999), Deng et al. (2007), Ma et al. (2017), and Zhang et al. (2020) satisfied these criteria and so were selected.

The flow resistance formula developed by Wu and Wang (1999) takes a form of:

$\begin{array}{c}\mathrm{l}\mathrm{g}\frac{A}{g^{1/2}{F}^{1/3}}=0.911-0.273\mathrm{l}\mathrm{g}T-0.051{\left(\mathrm{l}\mathrm{g}T\right)}^2+0.135{\left(\mathrm{l}\mathrm{g}T\right)}^3\end{array}(3)$

where g is the acceleration due to gravity, Fr is the Froude number ($=V/\sqrt{gh}$, where h is the flow depth), and $T$ is the non-dimensional shear stress of flow acting on the riverbed sediments.

To obtain the value of T in Eq. 3, the following relationships need to be applied:

$T={\tau }^{\prime }/{\tau }_{c50};{\tau }^{\prime }={\left(\frac{n^{\prime }}{n}\right)}^{3/2}\tau ;n^{\prime }=\frac{D_{50}^{1/6}}{20};\tau = gRJ(4)$

where ${\tau }^{\prime }$, ${\tau }_{c50}$, $n^{\text{'}}$, and $\tau$ are respectively the shear stress of flow acting on the riverbed sediments, the critical shear stress with D₅₀ representing the size of bed sediments, the grain roughness coefficient, and the shear stress of flow acting on the channel boundary, in which the critical shear stress ${\tau }_{c50}$ was determined from the following relationships given by Chien and Wan (1983) after their modification of the Shields curve:

$\frac{{\tau }_{c50}}{\left({\gamma }_s-\gamma \right)D_{50}}=0.126D_{\ast }^{-0.44};D\ast =D_{50}{\left(\frac{{\gamma }_s-\gamma }{\gamma }\frac{g}{{\nu }^2}\right)}^{1/3}(5)$

where $\nu$ is the kinematic viscosity coefficient in square centimeters per second cm²/s.

By reanalyzing the flume experimental data provided by Guy et al. (1966) and field observations at stations located in the middle and lower reaches of the Yellow River, Deng et al. (2007) obtained the following power–function relationship between n and Fr by using a statistical regression method:

$\begin{array}{c}n=0.005F{r}^{-0.7336}\end{array}(6)$

Using 64 sets of data observed in experimental flumes and more than 1,000 sets of data measured during 1958–1959 at six hydrological stations located in the lower reach of the Yellow River, based on data from both experimental flumes and field measurements in the Lower Yellow River, Ma et al. (2017) developed the following regression formula:

$\begin{array}{c}n=-0.0124\mathrm{l}\mathrm{n}Fr+0.0009\end{array}(7)$

Zhang et al. (2020) proposed two flow resistance relationships: the simple one, referred to as formula 1 of Zhang et al. in this study, takes the form

$\begin{array}{c}n=\frac{0.01}{0.1+1.85Fr}\end{array}(8)$

When the influences of bed materials and sediment concentration on flow energy expenditure were taken into account, Zhang et al. (2020) presented a more comprehensive formula, referred to as formula 2 of Zhang et al. in this study, taking the form

$\begin{array}{c}n=\frac{0.9D_{50}^{1/6}{\left(\kappa /{\kappa }_0\right)}^{1/5}}{A_{50}\left(0.1+1.85Fr\right)}\end{array}(9)$

where $\kappa$ is the Karman coefficient of flow, ${\kappa }_0=0.4$. $\kappa$ has a relationship with sediment concentration $S_V$ in the form

$\kappa ={\kappa }_0\left(1-4.2\sqrt{S_V}\left(0.365-S_V\right)\right)(10)$

The sources and other details pertaining to the development of the five formulae selected above are summarized in Table 2.

TABLE 2

TABLE 2. The flow resistance formulae investigated in this study.

Data Sources

Laboratory and Field Data Compiled by Brownlie (1981)

The datasets compiled by Brownlie (1981) contained 7,027 records (5,263 laboratory records and 1,764 field records) in 77 data files. All of the records were collected from various studies conducted during the 20th century and provide a historically complete set of alluvial channel observations. This data collection was inspired by the data compendium of Peterson and Howells (1973), and in comparison with previous data compendiums, this compendium corrected early errors, completed omissions, and added about 2,500 new records consisting of 10 basic hydraulic parameters. If no data were available, it was recorded as −1.

Data From the Yellow and Yangtze Rivers

In the drainage basins of the Yellow and Yangtze Rivers, numerous hydrological stations have been set up by the state government of China since the 1950s, and the measured data have been made available in hydrological almanacs, including flow discharge, slope, sediment concentration, average velocity, channel width, flow depth, median size of bed material, and the Manning resistance coefficient (Ma and Huang, 2016; Yellow River hydrological almanac, 2019). This study collected the measured data from the hydrological stations at Huayuankou, Jiahetan, Gaocun, Sunkou, Luokou, Tuchengzi, and Lijin in the Lower Yellow River, at Shizuishan (II), Bayan Gaole, and Toudaoguai in the upper reach of the Yellow River, and at Xianyang (II), Lintong, and Huaxian in the main tributary of the Weihe River. In the Yangtze River basin, the data collected were from the hydrological stations at Yichang, Luoshan, Datong, Jianli, Chenjiawan, and Xinchang in the trunk river and at Buhe, Hanjiang, Xincheng, and Guchen in the main tributaries.

In the following evaluation of the performance of the five selected formulae, datasets that lacked any of D₅₀, gradient, water temperature, and sediment concentration and had a value of <6 for the width/depth ratio were removed from the original data in order to maintain consistency with the studies by van Rijn (1984) and Peterson and Peterson (1988). As a result, 3,327 datasets (3,623 from experimental flumes and 1,546 from the field) compiled by Brownlie (1981) and 958 field datasets from the Yellow and Yangtze Rivers were selected. The sources and varying ranges of the parameters used in this study are provided in Table 3. All datasets are presented in Supplementary Data Sheet S1.

TABLE 3

TABLE 3. Datasets used in this study.

In a comparison of the information presented in Tables 2 and 3, it is clearly seen in Table 2 that the datasets used in this study are larger than those used in the development and validation of each of the five flow resistance formulae selected. In the following analysis, each of the five formulae was examined in light of all datasets collected. Except for minor amendments, which have been discussed in the computational procedure of the Ma et al. (2017) formula, each formula was applied in a precise manner specified by the original author(s).

Method of Evaluation

To evaluate the performance of the five formulae against the large datasets collected in this study, several statistical parameters were adopted in this study. Table 4 shows the expressions of these parameters. RMSE is the root mean square error between the observed data and computed results, CD is the square of Pearson’s correlation coefficient that reflects the proportion of the total variance in the observed data, and NA is the Nash coefficient that evaluates the agreement between the computed and observed values, with NA = 1 indicating perfect agreement between the computed and observed values. Furthermore, ARE (absolute relative error), computed as the ratio of the absolute error between the prediction and observation results to the observed value, was used to depict whether the predicted value was overestimated or underestimated. RE (relative error) was also used, and an MSE = 0 means that the computed value agreed perfectly with the observed value on the whole, while RE > 0 or RE < 0 indicate respectively that an overestimation or an underestimation occurred. Moreover, the percentages of data with relative errors of ≤50% and 25% (P₅₀ and P₂₅, respectively) and the percentages of the data with an overestimated error (POE) were also deployed (Nash and Sutcliffe, 1970; Bjerklie et al., 2005; López et al., 2007).

TABLE 4

TABLE 4. Statistical parameters and expressions.

Performance of the Selected Formulae in Different Datasets

Laboratory Data of Brownlie

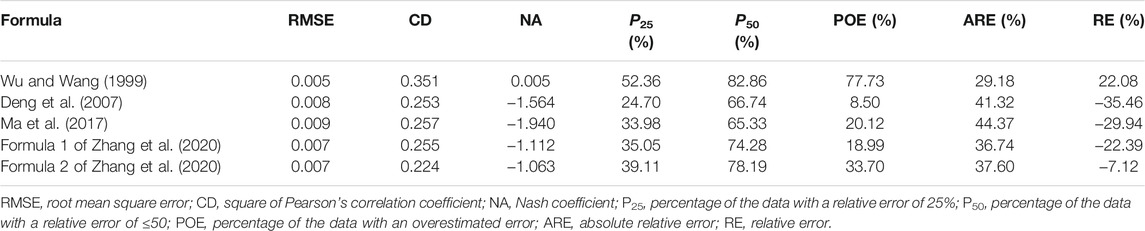
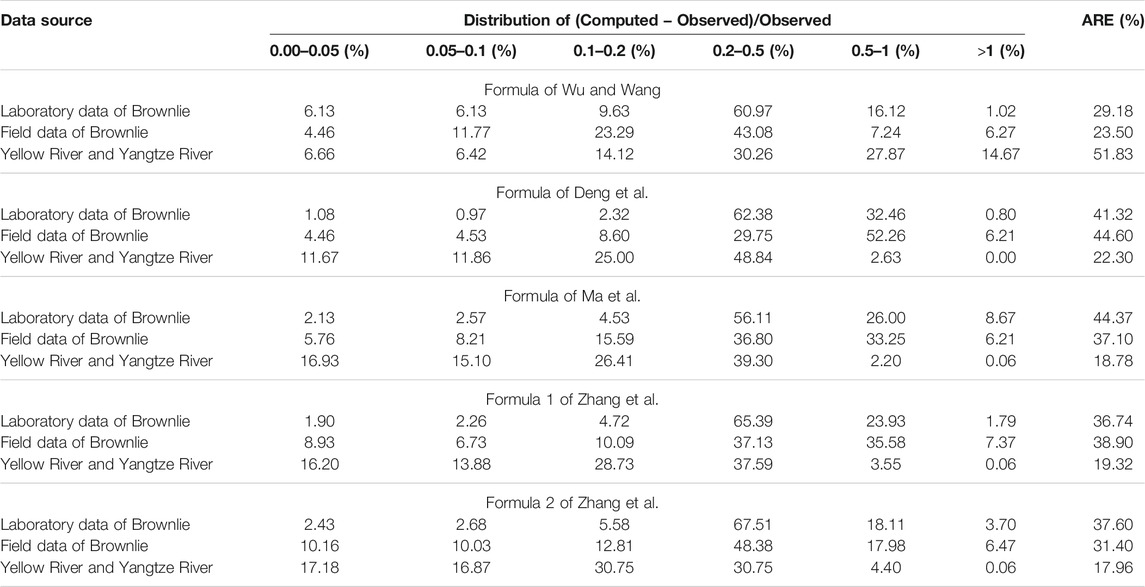
In terms of the laboratory data compiled by Brownlie (1981), the values of n computed from the five selected formulae against the observed counterparts are presented in Figure 1. It can be seen from Figures 1A–E that the differences between the computed and the observed values of n varied beyond the range of 2:1–1:2 (ratio of the computed to the observed). In many cases, the Ma et al. formula even yielded unreasonable results of <0, as shown in Figure 1C. Relatively speaking, nevertheless, the values of n computed using the formula of Wu and Wang were closer to the observed counterparts, typically when n was <0.04.

FIGURE 1

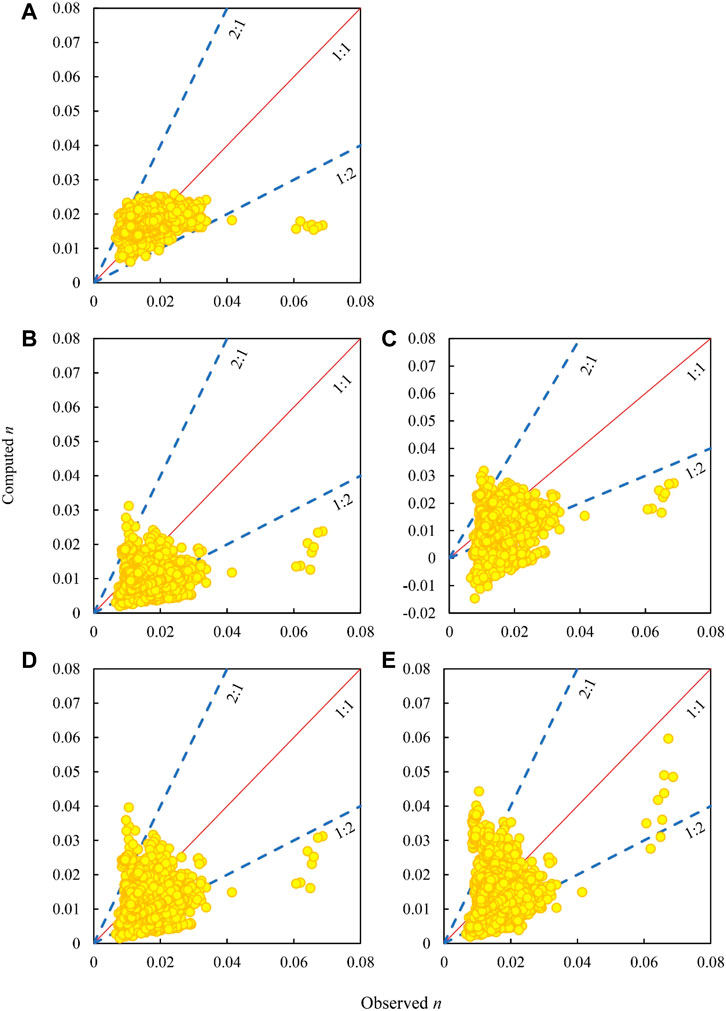
FIGURE 1. Computed n values against the observed n valued for the laboratory data of Brownlie. (A) Wu and Wang formula. (B) Deng et al. formula. (C) Ma et al. formula. (D) Formula 1 of Zhang et al. (E) Formula 2 of Zhang et al.

The statistical results on the correlation of the values of n computed from the five formulae against the observed counterparts in terms of the laboratory data of Brownlie are provided in Table 5. The correlation coefficient (CD) of the results computed using the formula of Wu and Wang was 0.351, the highest among the five formulae, while the other four yielded correlation coefficient results of generally <0.3. Among the NA values of the five formulae, only that by Wu and Wang yielded results with NA > 0, manifesting that the results were generally closer to the average level of the observations; that is, the points in Figure 1A are much more evenly distributed on both sides of the 1:1 line. All of these indicated that the formula of Wu and Wang outperformed the other four equations in Brownlie’s laboratory data.

TABLE 5

TABLE 5. Statistical results for the laboratory data of Brownlie.

Field Data of Brownlie

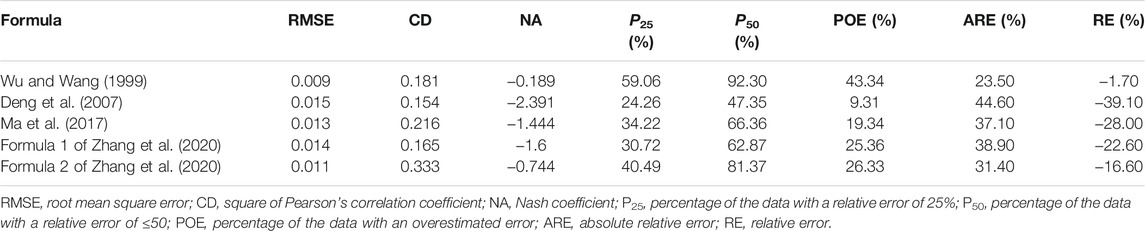
Using the field data compiled by Brownlie (1981), the values of n computed from each formula against the observed n values are presented in Figures 2A–E. It can be noticed from Figure 2 that the differences between the computed and the observed values of n varied beyond the range of 2:1–1:2 (ratio of the computed to the observed). Relatively speaking, nevertheless, the distribution of the n values computed using the Wu and Wang formula against the observed n values was much less scattered than those computed using the other four formulae.

FIGURE 2

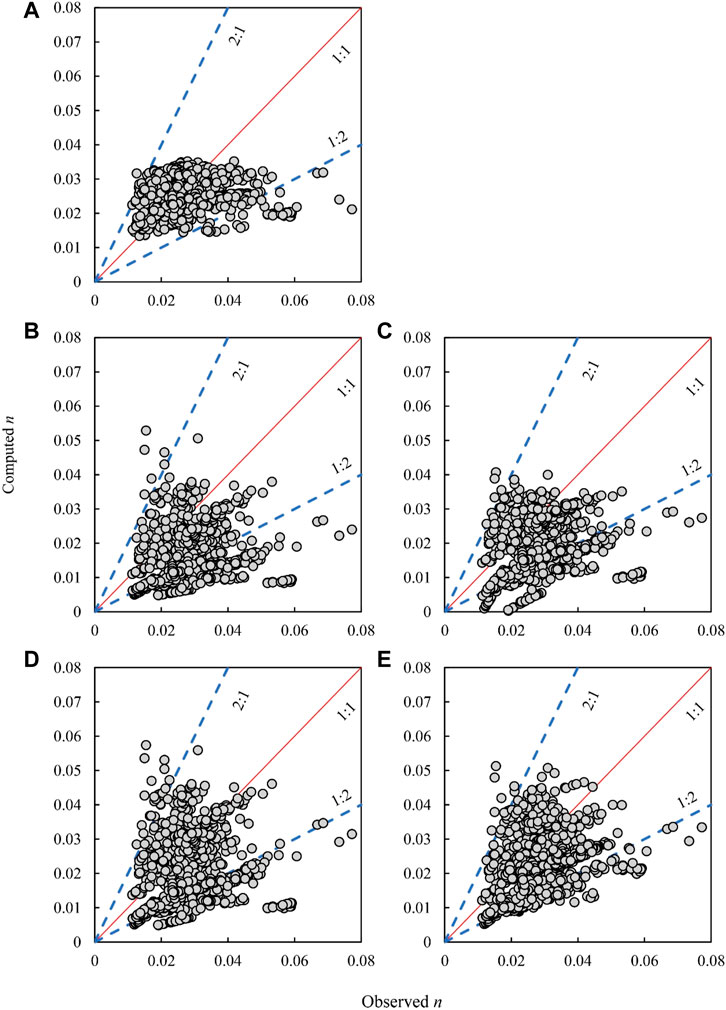
FIGURE 2. Computed n values against the observed n values for the field data of Brownlie. (A) Wu and Wang formula. (B) Deng et al. formula. (C) Ma et al. formula. (D) Formula 1 of Zhang et al. (E) Formula 2 of Zhang et al.

The performance of the five selected formulae in the field data of Brownlie is summarized in Table 6. The CD computed using formula 2 of Zhang et al. was 0.333, which is the highest among the five formulae, while the CD values of the other four formulae were <0.3. Although the AREs of the results computed using formula 2 of Zhang et al. and the formula of Wu and Wang took smaller values of 31.4% and 23.5%, respectively, their P₅₀ values were respectively 92.3% and 81.37%, indicating that the results computed using the Wu and Wang formula and formula 2 of Zhang et al. fitted the observed values at respective degrees of 92.3% and 81.37% within an error of 50%. Hence, the Wu and Wang formula yielded results best fitting the observed values among the five selected formulae.

TABLE 6

TABLE 6. Statistical results for the field data of Brownlie.

Data From the Yellow and Yangtze Rivers

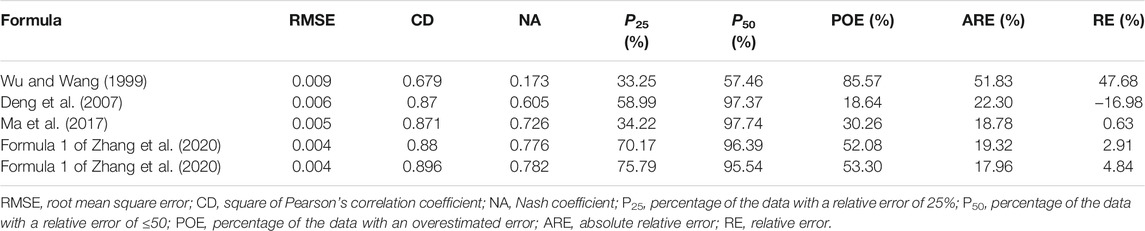
Using data collected from the hydrological stations in the main tributaries and the trunk reach of the Yellow and Yangtze Rivers, the values of n computed from the five selected formulae against the observed values of n are presented in Figures 3A–E. It can be seen that, except for the results computed using the Wu and Wang formula, the differences between the values of n computed from the other four formulae and the observed n varied within the range of 2:1–1:2 (ratio of the computed to the observed). Relatively speaking, nevertheless, the values of n computed using formula 1 of Zhang et al. were distributed more uniformly on both sides of the 1:1 line and so fitted the observations to the highest level among the five selected formulae.

FIGURE 3

FIGURE 3. Computed n values against the observed $n$ values for the data from the Yellow and Yangtze Rivers. (A) Wu and Wang formula. (B) Deng et al. formula. (C) Ma et al. formula. (D) Formula 1 of Zhang et al. (E) Formula 2 of Zhang et al.

The statistical results of the performance of the five formulae in the data collected from the drainage basins of the Yellow and Yangtze Rivers are shown in Table 7. The CD values of the results computed using the Deng et al. formula, Ma et al. formula, and formulae 1 and 2 of Zhang et al. were all very high, respectively 0.87, 0.871, 0.88, and 0.896, and the AREs of the results computed using the four formulae were no larger than 22.3%. In addition, the NA and P₅₀ of the results computed using the four formulae were all larger than 0.6% and 95%, respectively. On the contrary, the results computed using the Wu and Wang formula only had values of 0.679 for CD, 51.83% for ARE, 0.173 for NA, and 57.46% for P₅₀. Except for the Wu and Wang formula, hence, the other four selected formulae were all able to yield results best fitting the observed values.

TABLE 7

TABLE 7. Statistical results for data from the Yellow and Yangtze Rivers.

All Datasets

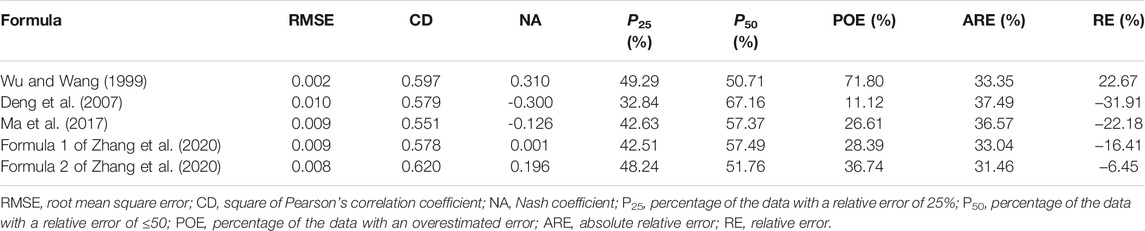
In terms of the laboratory and field data compiled by Brownlie (1981) and the data collected from the hydrological stations in the main tributaries and the trunk reach of the Yellow and Yangtze Rivers in this study, the values of n computed from each selected formula against the observed n values are presented in Figures 4A–E. It can be seen that the formula of Ma et al. yielded an unreasonable result of n < 0 in many cases (Figure 4C). While the formula of Deng et al. and formulae 1 and 2 of Zhang et al. yielded results varying significantly beyond the range of 2:1–1:2 (ratio of the computed to the observed), the formula of Wu and Wang yielded results varying mostly within the scope, typically in cases of n < 0.04.

FIGURE 4

FIGURE 4. Computed n values against observed n values for all datasets. (A) Wu and Wang formula. (B) Deng et al. formula. (C) Ma et al. formula. (D) Formula 1 of Zhang et al. (E) Formula 2 of Zhang et al.

Statistical results of the performance of the five selected formulae in all datasets used in this study are shown in Table 8. The CD values of the results computed using all five formulae were not very high and varied within the small range of 0.551–0.62. The AREs of the results computed using the five formulae were considerably small and also varied within the small range of 31.46%–37.49%. However, the NA values of the results computed using the Deng et al. formula, the Ma et al. formula, and formula 1 of Zhang et al. were negative or very close to 0, while the NA values of the results computed using the formula of Wu and Wang and formula 2 of Zhang et al. were positive, with the Wu and Wang formula yielding a much larger NA of 0.31. All of these demonstrated that formula 2 of Zhang et al. and the formula of Wu and Wang were the most appropriate in all datasets, despite their low calculation accuracy.

TABLE 8

TABLE 8. Statistical results for all datasets.

Distribution of Relative Errors and Performance Ranking

The AREs of n (computed n − Observed n)/Observed n) by all five selected formulae were computed for the three datasets, i.e., the laboratory data and field data compiled by Brownlie (1981) and the data from the drainage basins of the Yellow and Yangtze Rivers collected in this study. The distribution of AREs in the six groups of 0–0.05, 0.05–1, 0.1–0.2, 0.2–0.5, 0.5–1, and >1 is presented in Table 9 and shown in Figure 5. In the laboratory data of Brownlie, the AREs in the group 0.2–0.5 by all five selected formulae occupied around 60%, and there was a very small difference among the percentages in the group for the five formulae. The AREs in the group 0.5–1 occupied around 20%, while the AREs of each of the other groups occupied a very small percentage (Figure 5A).

TABLE 9

TABLE 9. Distribution of the prediction ratios

FIGURE 5

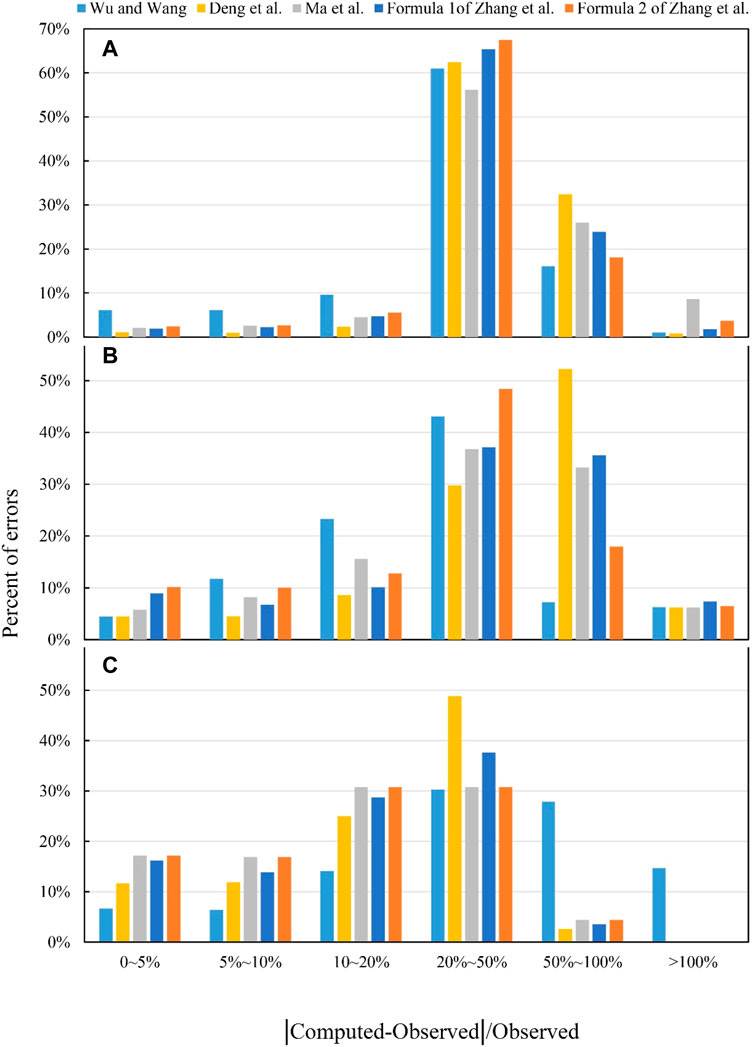
FIGURE 5. Distribution of the IC₅₀ values by the five selected formulae. (A) Laboratory data of Brownlie. (B) Field data of Brownlie. (C) Data from the Yellow and Yangtze Rivers.

In the field data of Brownlie, however, the AREs in the groups of 0.2–0.5 and 0.5–1 by all five formulae occupied large and nearly equal percentages of around 35%, while those in each of the other groups occupied only a very small percentage (Figure 5B). In the data from the Yellow and Yangtze Rivers, the AREs in the two groups of 0.1–0.2 and 0.2–0.5 by all five formulae occupied large and nearly equal percentages of slightly larger than 30%, while the AREs in the two groups of 0.05–0.1 and <0.05 occupied nearly equal percentages of about 18% (Figure 5C). Overall, it was obvious that the relative errors in the range of 0.2–0.5 accounted for the biggest percentage, with each of the nearby groups of 0.5–1 and 0.1–0.2 accounting for a sizable portion as well. This clearly manifests that the AREs by all five flow resistance formulae occupied a very large percentage almost in the same range of 0.1–1; hence, the five formulae needed to improve their predicting ability. Importantly, it is noticeable from Table 9 and Figure 5 that the AREs by each of the five selected flow resistance formulae were considerably large among the three datasets used.

The formula of Wu and Wang performed better in the laboratory and field data of Brownie, with ARE <30%. In the data from the Yellow and Yangtze Rivers, nevertheless, ARE >50% and the group of ARE >100% still accounted for 14.67% of the total. The formula of Deng et al. considerably yielded large values of 41.3% and 44.6% for ARE in the laboratory data and field data of Brownlie, respectively. In the data from the Yellow and Yangtze Rivers, nevertheless, the formula allowed ARE to take a relatively small value of 22.3%, and the group of ARE <0.5 occupied a very large percentage of 97.37% of the total. The formula of Ma et al. also yielded considerably large values of 44.37% and 33.1% for ARE in the laboratory data and field data of Brownlie, respectively. In the data from the Yellow and Yangtze Rivers, the formula allowed ARE to take a considerably small value of 18.78%, and the group of ARE <0.5 occupied 97.74% of the total. Hence, the formulae of Deng et al. and Ma et al. performed best in the data from the Yellow and Yangtze Rivers among the three datasets used. Formulae 1 and 2 of Zhang et al. yielded relatively small values of <40% for ARE in the laboratory data and field data of Brownlie, respectively. In the data from the Yellow and Yangtze Rivers, meanwhile, the formulae allowed ARE to take considerably small values of 19.32% and 17.96%, and the group of ARE <0.5 occupied 96.39% and 95.54% of the total. Hence, formulae 1 and 2 of Zhang et al. both performed well in the data from the Yellow and Yangtze Rivers among the three datasets used.

Because different formulae performed at considerably different levels in the different datasets used, ARE appears a suitable index to evaluate the performance of the five selected flow resistance formulae in the three datasets. Assuming that the performance of a formula can be ranked to the highest level “I” when 0 < ARE < 20%, to the relatively high level “II” when 20% < ARE < 30%, to the moderate level “III” when 30% < ARE < 40%, to the relatively low level “IV” when 40% < ARE < 50%, and to the lowest level “V” when ARE > 50%, the detailed ranks of the performance of the five selected flow resistance formulae in the three datasets are provided in Table 10.

TABLE 10

TABLE 10. Rating standards of data fitting.

It can be clearly seen from Table 10 that the formula of Ma et al. and formulae 1 and 2 of Zhang et al. gained the highest rank I in the data from the Yellow and Yangtze Rivers, while they gained the moderate rank III or the relatively low rank IV in the laboratory and field data of Brownlie. In contrast, the formula of Wu and Wang gained the relatively high rank II in the laboratory and field data of Brownlie, yet the lowest rank V in the data from the Yellow and Yangtze Rivers. Within the two relatively extremal cases, the formula of Deng et al. gained a relatively low rank IV in the laboratory and field data of Brownlie and also a relatively high rank II in the data from the Yellow and Yangtze Rivers.

Conclusion

Among the numerous flow resistance formulae for sand-bed channels, this study selected five for evaluation in terms of theoretical advances and the scope and quantity of the data used in the development, including those developed by Wu and Wang (1999), Deng et al. (2007), Ma et al. (2017), and Zhang et al. (2020). In order to cover flow conditions in sand-bed river channels as widely as possible, this study collected 1,636 sets of field measures from the hydrological stations in two large river systems of China (the Yellow and Yangtze Rivers), in addition to the data compiled by Brownlie (1981) that, in complete form, included 3,623 sets of laboratory data and 1,546 sets of field data from different nations and areas. The conclusion of this paper is generally used in alluvial rivers. A detailed statistical analysis of the performance of the five selected flow resistance formulae in yielding the values of the Manning resistance coefficient n using the very large number of datasets, 6,805 sets in total, led to the following important findings:

1) The formula of Wu and Wang yielded n values best fitting the laboratory and field data of Brownie, yet fitting the data from the Yellow and Yangtze Rivers at a relatively low degree. In contrast, the formula of Ma et al. and formulae 1 and 2 of Zhang et al. yielded n values fitting the data from the Yellow and Yangtze Rivers at a very high degree, yet fitting the laboratory and field data of Brownie at a moderate degree. The formula of Deng et al. yielded n values fitting the laboratory and field data of Brownlie and the data from the Yellow and Yangtze Rivers both at a relatively low degree.

2) In all datasets, the Ma et al. formula yielded unreasonable n values of <0 in many cases, while the formula of Deng et al. and formulae 1 and 2 of Zhang et al. yielded n values varying considerably beyond the range of 2:1–1:2. Nevertheless, the Wu and Wang formula yielded n values varying mostly within the scope, typically in cases of n < 0.04.

3) By dividing the AREs from the five selected formulae into six groups of 0–0.05, 0.05–1, 0.1–0.2, 0.2–0.5, 0.5–1, and >1, it can be found that, for all five selected formulae, the AREs in the group 0.2–0.5 occupied the largest percentage, while each of the adjacent groups of 0.5–1 and 0.1–0.2 occupied a very large percentage. This means that all five formulae needed to enhance the accuracy of their predicting capability.

4) The formula of Ma et al. and formulae 1 and 2 of Zhang et al. gained the highest rank for fitting the data from the Yellow and Yangtze Rivers, yet gained a moderate rank or a relatively low rank for the laboratory and field data of Brownlie. In contrast, the Wu and Wang formula gained a relatively high rank for the laboratory and field data of Brownlie, yet gained the lowest rank for the data from the Yellow and Yangtze Rivers. Within the two relatively extremal cases, the formula of Deng et al. gained a relatively low rank for the laboratory and field data of Brownlie, yet gained a relatively high rank for the data from the Yellow and Yangtze Rivers.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

HP, HH, GY, and HZ contributed to the conception and design of the study. HP organized the database, performed the statistical analysis, and wrote the first draft of themanuscript. HH wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported financially by the National Natural Science Foundation of China (grant nos. 41971010 and 41561144012) and the National Key Research and Development Program of China (grant no. 2016YFC0402502).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the Yellow River Water Conservancy Commission and Yangtze River Water Conservancy Commission of China for permission to access the measured hydrological and river channel data.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.840653/full#supplementary-material

References

Bjerklie, D. M., Dingman, S. L., and Bolster, C. H. (2005). Comparison of Constitutive Flow Resistance Equations Based on the Manning and Chezy Equations Applied to Natural Rivers. Water Resour. Res. 41, W11502. doi:10.1029/2004WR003776

CrossRef Full Text | Google Scholar

Brownlie, W. R. (1981). Compilation of Alluvial Channel Data: Laboratory and Field. Report No. KH-R-43B. Pasadena, California: W. M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology.

Google Scholar

Carollo, F. G., and Ferro, V. (2021). Experimental Study of Boulder Concentration Effect on Flow Resistance in Gravel Bed Channels. Catena 205, 105458. doi:10.1016/j.catena.2021.105458

CrossRef Full Text | Google Scholar

Chang, Y. L. (1939). Laboratory Investigation of Flume Traction and Transportation. T. Am. Soc. Civ. Eng. 104, 1246–1284. doi:10.1061/taceat.0005049

CrossRef Full Text | Google Scholar

Chien, N., and Wan, Z. H. (1983). Mechanics of Sediment Movement. Beijing: Science Publications. (in Chinese).

Google Scholar

Deng, A., Guo, Q., and Chen, J. (2007). Study on the Roughness in Sediment-Laden Flows. J. Sediment Res. 2007 (05), 24–29. (in Chinese). doi:10.16239/j.cnki.0468-155x.2007.05.005

CrossRef Full Text | Google Scholar

Di Stefano, C., Nicosia, A., Palmeri, V., Pampalone, V., and Ferro, V. (2020). Flow Resistance Law under Suspended Sediment Laden Conditions. Flow Meas. Instrumentation 74, 101771. doi:10.1016/j.flowmeasinst.2020.101771

CrossRef Full Text | Google Scholar

East Parkistan Water and Power Development Authority (1967). Flume Studies of Roughness and Sediment Transport of Movable Bed of Sand. Dahka, Bangladesh: Annu. Rep. of Hydr. Res. Lab.

Google Scholar

Einstein, H. A., and Barbarossa, N. L. (1952). River Channel Roughness. T. Am. Soc. Civ. Eng. 117, 1121–1132. doi:10.1061/taceat.0006666

CrossRef Full Text | Google Scholar

Engelund, F., and Hansen, E. A. (1967). Monograph on Sediment Transport in Alluvial Streams. Copenhagen K: Technical University of Denmark Østervoldgade 10.

Google Scholar

Engelund, F. (1961). Hydraulic Resistance of Alluvial Streams. J. Hydraulics Division, ASCE 92 (2), 315–327.

Google Scholar

Ferro, V. (2018a). Assessing Flow Resistance in Gravel Bed Channels by Dimensional Analysis and Self-Similarity. Catena 169, 119–127. doi:10.1016/j.catena.2018.05.034

CrossRef Full Text | Google Scholar

Ferro, V. (2018b). Flow Resistance Law under Equilibrium Bed-Load Transport Conditions. Flow Meas. Instrumentation 64, 1–8. doi:10.1016/j.flowmeasinst.2018.10.008

CrossRef Full Text | Google Scholar

Gilbert, G. K. (1914). The Transportation of Débris by Running Water. U.S. Geol. Surv. Prof. Pap. 86.

Google Scholar

Guy, H. P., Simons, D. B., and Richardson, E. V. (1966). Summary of Alluvial Channel Data from Flume Experiments, 1956-1961. Washington: UNITED STATES GOVERNMENT PRINTING OFFICE.

Google Scholar

Herschel, C. (1897). On the Origin of the Chezy Formula. J. Assoc. Eng. Societies 18, 363–369.

Google Scholar

Huang, H. Q. (2010). Reformulation Of The Bed Load Equation Of Meyer-Peter And Müller in Light of The Linearity Theory For Alluvial Channel Flow[J]. Water Resources Res. 46 (9), 161–170.

CrossRef Full Text | Google Scholar

Huang, C., Zhao, X., and Gong, M. (2004). Comparisons Of Flow Resistance Equations In Movable Bed. J. Sediment Res. 2004 (5), 1–7. (in Chinese). doi:10.16239/j.cnki.0468-155x.2004.05.001

CrossRef Full Text | Google Scholar

Jaeger, C. (1961). Engineering Fluid Mechanics London: Blackie.

Google Scholar

Kamphuis, J. W. (1974). Determination of Sand Roughness for Fixed Beds. J. Hydraulic Res. 12 (2), 193–203. doi:10.1080/00221687409499737

CrossRef Full Text | Google Scholar

Kuhnle, R. A. (1993). Fluvial Transport of Sand and Gravel Mixtures with Bimodal Size Distributions. Sediment. Geology. 85, 17–24. doi:10.1016/0037-0738(93)90072-d

CrossRef Full Text | Google Scholar

Liu, X. L. (1986). Nonuniform Bed Load Transport Rate and Coarsening Stabilization. Master's Thesis. China: Chengdu University of Technology.

Google Scholar

López, R., Barragán, J., and Colomer, M. Á. (2007). Flow Resistance Equations without Explicit Estimation of the Resistance Coefficient for Coarse-Grained Rivers. J. Hydraulic 338, 113–121. doi:10.1016/j.jhydrol.2007.02.027

CrossRef Full Text | Google Scholar

Ma, Y., and Huang, H. Q. (2016). Controls of Channel Morphology and Sediment Concentration on Flow Resistance in a Large Sand-Bed River: A Case Study of the Lower Yellow River. Geomorphology 264, 132–146. doi:10.1016/j.geomorph.2016.03.035

CrossRef Full Text | Google Scholar

Ma, Y., Xia, J., and Zhang, X. (2017). Verification and Comparison of Flow Resistance Formulae over Movable Beds. Eng. J. Wuhan Univ. 50 (4), 481–486. (in Chinese). doi:10.14188/j.1671-8844.2017-04-001

CrossRef Full Text | Google Scholar

Manning, R. (1890). On the Flow of Water in Open Channels and Pipes. Proc. Inst. Civil Eng. Ireland 20, 161–206.

Google Scholar

Mark Powell, D. (2014). Flow Resistance in Gravel-Bed Rivers: Progress in Research. Earth-Science Rev. 136, 301–338. doi:10.1016/j.earscirev.2014.06.001

CrossRef Full Text | Google Scholar

Maynord, S. T. (1991). Flow Resistance of Riprap. J. Hydraulic Eng. 117 (6), 687–696. doi:10.1061/(asce)0733-9429(1991)117:6(687)

CrossRef Full Text | Google Scholar

Meyer-Peter, E., and Müller, R. (1948). “Formulas for Bed Load Transport, Paper Presented at 2nd Meeting,” in Int. Assoc. for Hydroaul. Environ.Eng. and Res. (Madrid).

Google Scholar

Nash, J. E., and Sutcliffe, J. V. (1970). River Flow Forecasting through Conceptual Models Part I - A Discussion of Principles. J. Hydrol. 10, 282–290. doi:10.1016/0022-1694(70)90255-6

CrossRef Full Text | Google Scholar

Niazkar, M., Talebbeydokhti, N., and Afzali, S. H. (2019). Development of a New Flow-Dependent Scheme for Calculating Grain and Form Roughness Coefficients. KSCE J. Civil Eng. 23, 2108–2116. doi:10.1007/s12205-019-0988-z

CrossRef Full Text | Google Scholar

Nicosia, A., Di Stefano, C., Pampalone, V., Palmeri, V., and Ferro, V. (2021). Assessing an Overland Flow Resistance Approach under Equilibrium Sediment Transport Conditions. CATENA 207, 105578. doi:10.1016/j.catena.2021.105578

CrossRef Full Text | Google Scholar

Peterson, A. W., and Peterson, A. E. (1988). Mobile Boundary Flow: An Assessment of Velocity and Sediment Discharge Relationships. Can. J. Civ. Eng. 15 (4), 539–546. doi:10.1139/l88-074

CrossRef Full Text | Google Scholar

Peterson, A. W., and Howells, R. F. (1973). A Compendium of Solids Transport Data for Mobile Boundary Channels. Canada: Department of Civil Engineering, University of Alberta. Report No. HY-1973-ST3.

Qin, R., Liu, S., and Wang, C. (1995). Characteristics Of Channel Resistance And Sediment Transport In The Lower Yellow River. J. Sediment Res. (4), 10–18. (in Chinese).

Google Scholar

Samaga, B. R., Raju, K. G. R., and Garde, R. J. (1986). Bed Load Transport of Sediment Mixtures. J. Hydraulic Eng. 112 (11), 1003–1017. doi:10.1061/(asce)0733-9429(1986)112:11(1003)

CrossRef Full Text | Google Scholar

Taylor, B. D. (1971). Temperature Effects In Alluvial Streams[J]. California Institute of Technology.

van Rijn, L. C. (1982). Equivalent Roughness of Alluvial Bed. J. Hydraulics Division, ASCE 108, HY10. doi:10.1061/jyceaj.0005917

CrossRef Full Text | Google Scholar

van Rijn, L. C. (1984). Sediment Transport, Part III: Bed Forms and Alluvial Roughness. J. Hydraul. Eng. 110 (12), 1733–1754. doi:10.1061/(asce)0733-9429(1984)110:12(1733)

CrossRef Full Text | Google Scholar

Wang, S. (1990). Experimental Study on Hydraulic Resistance of Alluvial Streams. J. Hydraulic Eng. 1990 (12), 18–29. (in Chinese).

Google Scholar

Wilcock, P. R., and McArdell, B. W. (1993). Surface-based Fractional Transport Rate: Mobilization Thresholds and Partial Transport of a Sand-Gravel Sediment. Water Resour. Res. 29 (24), 1297–1312. doi:10.1029/92wr02748

CrossRef Full Text | Google Scholar

Wu, W., and Wang, S. S. Y. (1999). Movable Bed Roughness in Alluvial Rivers. J. Hydraulic Eng. 125 (12), 1309–1312. doi:10.1061/(asce)0733-9429(1999)125:12(1309)

CrossRef Full Text | Google Scholar

Yadav, A., Sen, S., Mao, L., and Schwanghart, W. (2022). Evaluation of Flow Resistance Equations for High Gradient Rivers Using Geometric Standard Deviation of Bed Material. J. Hydrol. 605, 127292. doi:10.1016/j.jhydrol.2021.127292

CrossRef Full Text | Google Scholar

Yalin, M. S. (1963). An Expression for Bed-Load Transportation[J]. J. Hydraul. Div. Asce 89, 221–250.

CrossRef Full Text | Google Scholar

Yellow River hydrological almanac (2019). The Yellow River Water Resources Commission. China: Zhengzhou.

Google Scholar

Zhang, H., Zhang, L., Peng, H., Cai, R., and Zhang, L. (2020). Research on Cognition and Calculation Method of Alluvial River Roughness. J. Hydraulic Eng. 51 (07), 774–787. (in Chinese). doi:10.13243/j.cnki.slxb.20200130

CrossRef Full Text | Google Scholar

Zhang, L. (2012a). Analysis of the Present Situation of Open Channels Roughness. J. Hydraulic Eng. 43 (10), 1154–1162. (in Chinese). doi:10.13243/j.cnki.slxb.2012.10.007

CrossRef Full Text | Google Scholar

Zhang, L. (2012b). Reasons for the Abnormal Channel Roughness of the Yellow River and the Solution to its Problems. J. Hydraulic Eng. 43 (10), 1154–1162. (in Chinese). doi:10.13243/j.cnki.slxb.2012.11.004

CrossRef Full Text | Google Scholar

Zhang, R., Xie, J., Wang, M., and Huang, J. (1998). Dynamics of River Sedimentation. Beijing: Water Resources and Electric Power Publication. (in Chinese).

Google Scholar

Zhao, L., and Zhang, H. (1997). Study of Flow Frictional Characteristics in the Lower Yellow River Channel. Yellow River 9, 17–20+62. (in Chinese).

Google Scholar