Trait-Based Model Reproduces Patterns of Population Structure and Diversity of Methane Oxidizing Bacteria in a Stratified Lake

In stratified lakes, methane oxidizing bacteria are critical methane converters that significantly reduce emissions of this greenhouse gas to the atmosphere. Efforts to better understand their ecology uncovered a surprising diversity, vertical structure, and seasonal succession. It is an open question how this diversity has to be considered in models of microbial methane oxidation. Likewise, it is unclear to what extent simple microbial traits related to the kinetics of the oxidation process and temperature optimum, suggested by previous studies, suffice to understand the observed ecology of methane oxidizing bacteria. Here we incorporate niche partitioning in a mechanistic model of seasonal lake mixing and microbial methane oxidation in a stratified lake. Can we model MOB diversity and niche partitioning based on differences in methane oxidation kinetics and temperature adaptation? We found that our model approach can closely reproduce diversity and niche preference patterns of methanotrophs that were observed in seasonally stratified lakes. We show that the combination of trait values resulting in coexisting methanotroph communities is limited to very confined regions within the parameter space of potential trait combinations. However, our model also indicates that the sequence of community assembly, and variations in the stratification and mixing behavior of the lake result in different stable combinations. A scenario analysis introducing variable mixing conditions showed that annual weather conditions and the pre-existing species also affect the developing stable methanotrophic species composition of the lake. Both, effect of pre-existing species and the environmental impact suggest that the MOB community in lakes may differ from year to year, and a stable community may never truly occur. The model further shows that there are always better-adapted species in the trait parameter space that would destabilize and replace an existing stable community. Thus, natural selection may drive trait values into the specific configurations observed in nature based on physiological limits and tradeoffs between traits.

Introduction

In recent years, considerable efforts have been made to better understand the ecology of methane oxidizing bacteria (MOB) in lakes. MOB are a diverse group of mainly Alpha- and Gammaproteobacteria that have the unique ability to use methane as their sole carbon and energy source (Hanson and Hanson, 1996). In lakes, these bacteria are an important sink for methane and significantly reduce methane emissions to the atmosphere (Kankaala et al., 2006; Conrad, 2009; Schubert et al., 2012; Zimmermann et al., 2021). This is a crucial process, as lake sediments are an important source of methane. Despite the activity of MOB, methane emission from lakes is responsible for about 75% of the emission of greenhouse gases from lacustrine systems (DelSontro et al., 2018) and its total emission might even offset the continental carbon sink (Bastviken et al., 2011). In seasonally or permanently stratified lakes with an anoxic hypolimnion MOB are found within the entire water column (Kojima et al., 2009; Tsutsumi et al., 2011; Mayr et al., 2020c). During stratification, methane oxidation strongly limits diffusive methane losses from such lakes. However, ebullition presents a shortcut to the atmosphere that allows significant amounts of methane to escape and often represents the dominant emission pathway, accounting for between 60% and 70% of total global emissions from lakes and reservoirs (DelSontro et al., 2018). The losses of stored methane during lake turnover appear to be again strongly limited by methane oxidation (Zimmermann et al., 2021).

Recent studies have brought to light the intriguing diversity, vertical structure and seasonal succession of MOB in stratified lakes (Mayr et al., 2020a, Mayr et al., 2020c; Reis et al., 2020; Rissanen et al., 2020; Martin et al., 2021). The fact that all MOB rely on methane and oxygen as primary resources, raises the question of how diversity within this functional group is maintained despite Hardin’s competitive exclusion principle (Hardin, 1960). This is analogous to the situation of phytoplankton, which has been the inspiration of much research and the subject of much debate among ecologists as the “paradox of the plankton” (Hutchinson, 1961). For plankton, many explanations have been proposed, ranging from niche partitioning (Salcher, 2013), selective grazing and chaotic fluid motion to a dominance of stochastic processes (i.e., neutral theory) and many more (Roy and Chattopadhyay, 2007; Record et al., 2014). While we thus have a comprehensive general understanding of the ecological mechanisms that limit the competitive exclusion principle (Chesson, 2000; Maynard et al., 2020), the case of MOB diversity has not been thoroughly studied, and we propose that they can be an interesting test case for ecological theory. The potential for using trait-based approaches in prokaryotic microbial ecology has been highlighted (Martiny et al., 2015), noting in particular that many traits appear to be phylogenetically conserved, so that traits can frequently be related to taxonomic identities.

In our recent publications we have suggested that niche partitioning (species sorting) can at least partly explain the vertical (spatial) structuring of MOB in lakes (Mayr et al., 2020c) and that environmental drivers also partly explain temporal variability (Guggenheim et al., 2020). MOB niches may derive from various adaptations in MOB to temperature regimes and nutrient conditions, but also to the availability of the main substrate, i.e., through enzymes with variable substrate affinity or complementary metabolic costs. In MOB, there is a considerable body of evidence that adaptations to substrate availability plays a role for their ecology. MOB isolates are known to have a range of different affinities to methane (Knief and Dunfield, 2005; Dam et al., 2012) with high-affinity variants being able to oxidize methane at very low (e.g., atmospheric) levels. The particulate and soluble forms of methane monooxygenase (pMMO and sMMO) also differ in their kinetic properties, with sMMO exhibiting a lower methane affinity. Our previous research showed that both the observed vertical structures and seasonal succession of MOB community composition in a stratified lake were accompanied by differences in the methane oxidation kinetics (Mayr et al., 2020b) and potentially also temperature adaptation (Mayr et al., 2020a). Among the patterns observed in MOB populations were discrete population maxima above, within and below the oxycline under stable stratification (Mayr et al., 2020a), as well as in the epilimnion and anoxic hypolimnion (Guggenheim et al., 2020); on the temporal scale, succession and blooming of previously rare MOB taxa was observed during the autumn lake mixing (Mayr et al., 2020a). Statistical analyses of driving factors consistently pointed to the importance of the methane gradient and temperature, although other environmental factors as well as ecological interactions may play a role as well (Guggenheim et al., 2020).

In Zimmerman et al. (2021), we built a model to evaluate how MOB limited outgassing in seasonally stratified lakes during fall turnover. The approach was based on a mechanistic model to assess the dynamical development of the MOB biomass. Here, we build on this work to develop a trait-based model for MOB in a stratified lake. Trait-based models have a rich, yet recent, history in phytoplankton ecology (Litchman and Klausmeier, 2008) and were originally developed primarily to understand patterns of niche differentiation and diversity. The potential of such models to also improve our mechanistic understanding of biogeochemical processes has also been highlighted (Litchman et al., 2015; Zakharova et al., 2019). Traits that regulate both responses and effects are an interesting target for modeling. As a response trait, methane oxidation provides a growth advantage where methane is an abundant or perhaps the only available source of energy and carbon; and as an effect trait it may alter the availability of methane and oxygen in the system. On the other hand, pure response traits like temperature growth optima may still be related to biogeochemical effects if they are correlated with response traits. A key element of trait-based models is the concept of trade-offs between traits, i.e., limitations in the ability of organisms to optimize trait combinations arbitrarily. In lakes, trait-based models of MOB mostly followed a statistical approach to explain environmental drivers affecting MOB (Thottathil et al., 2019; Reis et al., 2020). Our approach instead follows an equation-based approach to study the diversity of MOB in a stratified lake.

Our previous work suggested that methane affinity and temperature growth optimum might be among the most important traits of MOB in stratified freshwater lakes. We here explored with the first trait-based mechanistic model of microbial methane oxidation, to what extent a model based on a minimal set of traits, i.e., just the two main parameters of methane oxidation kinetics and temperature optima, can reproduce observed patterns of MOB diversity. The microbial growth model specifically considers Monod-type methane oxidation kinetics associated with MOB “species” with three independent traits as suggested in Mayr et al. (2020a), Mayr et al. (2020c): maximum growth rates, methane half-saturation constants of the Monod-type kinetics and temperature dependence of methane oxidation. In order to limit complexity in this first attempt, we neglect further potential traits (such as kinetic or inhibitory effects of oxygen) as well as environmental drivers such as (micro) nutrient concentrations.

We further combine a 1D physical lake model with a simplified biogeochemical model for oxygen and methane to provide a realistic simulated lake environment. This model was developed with data available for Rotsee, a small, shallow, seasonally stratified eutrophic lake near the city of Lucerne, Switzerland. Our data and the modeled dynamics include the seasonal mixing of the lake as previously described (Schubert et al., 2012; Mayr et al., 2020a; Zimmermann et al., 2021). The model thus couples the trait-based approach directly with a physical and biogeochemical model of the lake’s temperature and methane dynamics.

We then explored whether simulated MOB communities with species based on the three kinetic traits can qualitatively reproduce stable niche differentiation over the simulated vertical and temporal gradients of temperature, methane and oxygen of Rotsee simulated over several years. We assembled communities of 2, 3, and 4 species starting from trait combinations actually observed in the MOB populations of Rotsee. We explore the stability of such communities against new species with different trait combinations and changes in the simulated lake environment. Finally, we explore the spatiotemporal abundance patterns of the simulated species and compare them with observed population patterns.

Methods

Basic Structure of the Physical and Biogeochemical Model

Our first objective was to reproduce the temporal evolution of the thermal structure in the water column of Lake Rotsee to derive physical parameters such as time and space varying temperature and vertical diffusion as well as dissipation coefficient. For this purpose, we calibrated the physical lake model Simstrat version 2.1.2 (Gaudard et al., 2019) to temperature observations in Lake Rotsee, Switzerland, that were available for multiple years. Assuming that we can neglect feedback of chemical and biological processes in the lake on the physical processes, we used this calibrated physical model to pre-calculate the physical framework of our biogeochemical model and thereby improved its computational efficiency.

Our second objective was to build a simple biogeochemical model that would on the one hand reproduce the concentrations of methane and oxygen, i.e., reproduce the observed seasonal dynamics of the biogeochemical boundary conditions for methane oxidation. On the other hand, we use this model of the lake to explore the population dynamics of different “species” (trait combinations) of methane oxidizing bacteria, and the conditions for stable coexistence of multiple species.

The model that we used for this second objective is based on the classical reaction-diffusion equation:

${\partial }_{t}u=D{\mathit{\nabla }}^{2}u+R\left(u\right)(1)$

where $u$ is the vector of concentrations, $R\left(u\right)$ describes the local reaction kinetics and $D$ is the diagonal turbulent diffusion coefficient matrix. For numerical integration, we used a finite volume discretisation method that takes into account the lake bathymetry with a Crank-Nicolson integration scheme with Neumann boundary conditions (Moukalled et al., 2015). Areas A and volumes V for each grid cell of the finite volume discretization were derived from the lake bathymetry (Zimmermann et al., 2021). Numerical discretization and integration was implemented in Julia 1.2 (Bezanson et al., 2017) and is available on GitHub (see Data Availability Statement).

Using this diffusion-reaction system, we modelled methane, oxygen, and MOB species concentrations in the water column. The diffusion-coefficients were pre-calculated with the above mentioned physical model. Simulations were performed with a spatial resolution of 10 cm and time steps of 15 min. We used the same diffusion-reaction equation to model concentrations of organic matter, methane and oxygen in the sediment. For the sediment, the diffusion-coefficient was taken from available literature as described below (see section “Methane Production in the Sediment”). The complete set of additional processes that are part of the term $R\left(u\right)$ as well as the needed parameters (Tables 1, 2) are discussed below. For a full set of equations, see Supplementary Methods S1.

TABLE 1

TABLE 1. Set of the parameters used in the physical model.

TABLE 2

TABLE 2. Set of the parameters used in the biogeochemical model.

Gas Exchange With the Atmosphere

We modelled the exchange of methane and oxygen with the atmosphere with the boundary layer model of Liss and Slater (1974).

$F_{atm}=k\left(C-C_{eq}\right)(2)$

where $F_{atm}$ is the flux into the atmosphere, $C$ is the surface water concentration, $C_{eq}$ is the equilibrium concentration and $k$ is the transfer velocity. The temperature dependence of solubility of O₂ and CH₄ were considered. We used the surface-renewal model to calculate the transfer velocity based on the dissipation of turbulent kinetic energy (Zappa et al., 2007; MacIntyre et al., 2010; Read et al., 2012):

$k=\eta {\left(\mathit{ϵ}\nu \right)}^{1/4}S{c}^{-n}(3)$

where $\mathit{ϵ}$ is the rate of dissipation of turbulent kinetic energy near the air-water interface, $\nu$ is the kinematic viscosity, and $\eta$ is an empirically derived, depth-dependent scaling coefficient. For this conceptual model, $\eta$ was set to $1/\left(2\pi \right)$ based on theoretical considerations (Soloviev et al., 2007). The rate of dissipation $\mathit{ϵ}$ was pre-calculated for each time step by the physical model. We determined the Schmidt number $Sc$ for methane and oxygen with an exponent of $n=-1/2$ (Wanninkhof, 2014).

The exchange of methane and oxygen with the atmosphere was implemented as a reaction term in the topmost cell of the spatially discrete diffusion-reaction system. Primary production was not considered, which is a deliberate simplification.

Water Column Oxygen Depletion

For eutrophic lakes in Switzerland, an average areal oxygen depletion rate in the water column of 0.9 g O₂ m⁻² d⁻¹ has been estimated (Müller et al., 2012). With an estimated sediment surface area of 0.49 km² and a total volume of 0.0044 km³, we assumed a water column biochemical oxygen demand (WBOD) of 3,190 μmol O₂ m⁻³ d⁻¹. The water column biochemical oxygen demand was modelled as a constant reaction term in the diffusion-reaction system throughout the water column.

Methane Production in the Sediment

The methane production and flux from the sediment was parameterized with a simplified sediment model using a constant sedimentation velocity $F_{OM,sed}$ of organic material, a methane production velocity $V_{max,sed}$ that is oxygen inhibited ($K_{I,O_2}$) and limited by the availability of organic material and an apparent constant exchange velocity with the water column (Supplementary Method S1). The input of organic matter to the sediment was implemented as reaction terms in the top-most cell of the sediment. Likewise, the exchange of methane and oxygen with the water column was added as a reaction term in the top-most cell of the sediment as well as the deepest cell of the water column. Temperature effects were not considered for this term as temperature fluctuations in the sediment are rather small and the effect of oxygen was assumed to be more important.

Growth Model for MOB

We assumed that methane oxidation rates were limited by methane, oxygen and temperature (Mayr et al., 2020a, Mayr et al., 2020c; Zimmermann et al., 2021). We used a Monod kinetics to describe limitation by methane. For oxygen, we assumed that MOB were able to grow at nanomolar oxygen concentrations (Milucka et al., 2015; Oswald et al., 2015) according to a Monod kinetics but were inhibited at higher oxygen concentrations (Thottathil et al., 2019). The sensitivity of pMMO to oxygen has been shown on isolated and purified enzymes and is most likely related to copper oxidation (Nguyen et al., 1998). We used a Ratkowski 2 model to formulate the temperature dependence of the methane oxidation rate (Ratkowsky et al., 1983). To our knowledge, there is no evidence on the exact shape of the temperature dependence of MOB growth rates but Ratkowski’s growth rate model provides a common approach that has been successfully applied to describe the temperature dependence of a variety of bacterial species (Longhi et al., 2017). The combination of the three limiting factors leads to the following set of equations:

$r_{MOX}=V_{max}\left(T\right)\frac{\left[C{H}_4\right]}{\left[C{H}_4\right]+K_{M,C{H}_4}}\frac{\left[O_2\right]}{\left[O_2\right]+K_{M,O_2}}\frac{K_{I,O_2}}{\left[O_2\right]+K_{I,O_2}}(4)$

$V_{max}\left(T\right)={\left(b\left(T-T_{min}\right)\left(1-exp\left[c\left(T-T_{max}\right)\right]\right)\right)}^2(5)$

where $K_{M,C{H}_4}$ is the half-saturation constant for methane, $T_{min}$ and $T_{max}$ are the minimum and maximum temperature at which the methane oxidation rate is zero. By solving the first derivative of Eq. 5 at $T_{opt}$, i.e., where $V_{max}\left(T\right)$ has its maximum and the derivative is zero, we can calculate the coefficients $b$ and $c$ from the four parameters $T_{min}$, $T_{max}$, $T_{opt}$ and $V_{max}\left(T_{opt}\right)$:

$c=\left[T_{min}LambertW\left(\gamma \right)-T_{opt}LambertW\left(\gamma \right)+T_{opt}-T_{max}\right]/\left[\left(T_{min}-T_{opt}\right)\left(T_{opt}-T_{max}\right)\right](6)$

$\gamma =-exp\left(\frac{T_{max}-T_{opt}}{T_{min}-T_{opt}}\right)\left(T_{max}-T_{opt}\right)/\left(T_{opt}-T_{min}\right)(7)$

$b=\sqrt{V_{max}/({(T_{min}-T_{opt})}^2\cdot {(exp(c\cdot (T_{opt}-T_{max}))-1)}^2)}(8)$

where $LambertW$ is the inverse function of $f\left(x\right)=x{e}^x$.

Furthermore, we assumed that growth rates are directly proportional to methane oxidation rates, and we used typical values for the carbon use efficiency $y_{CCE}$ (Leak and Dalton, 1986) as the fraction of oxidized methane that is incorporated into biomass. The growth rate $r_{MOB}$ is therefore only a fraction of the methane oxidation rate:

${\mu }_{MOB}=y_{CCE}\cdot r_{MOX}-m(9)$

Mortality $m$ was estimated from published laboratory experiments (Roslev and King, 1995) and was divided into a base mortality $m_{anox}$ and an additional oxygen-dependent component:

$m=m_{anox}+m_{ox}\frac{\left[O_2\right]}{\left[O_2\right]+K_{mo,O_2}}(10)$

Model Calibration

To calibrate the physical and biogeochemical model, we used PEST version 1.4 (Doherty, 2015). Meteorological data for the physical model were obtained from MeteoSwiss (see Data Availability). The primary calibration target was to reproduce available temperature profiles from 2014 to 2017. To calibrate the sediment model, we used seasonal methane profiles from 2016 (Mayr et al., 2020a; Zimmermann et al., 2021).

Mapping and Analysis of the Trait Space and Coexistence Patterns

Based on our hypothesis that methane oxidation kinetics and temperature adaptation are the main driver for niche partitioning of MOB in stratified lakes, we described each MOB species by three traits that form a three-dimensional trait space $T$ (Figure 1A): its optimal temperature range, its affinity for methane and its maximum growth rate. Each point in this trait space $T$ corresponds to a unique trait combination that describes a potential MOB species in the lake.

FIGURE 1

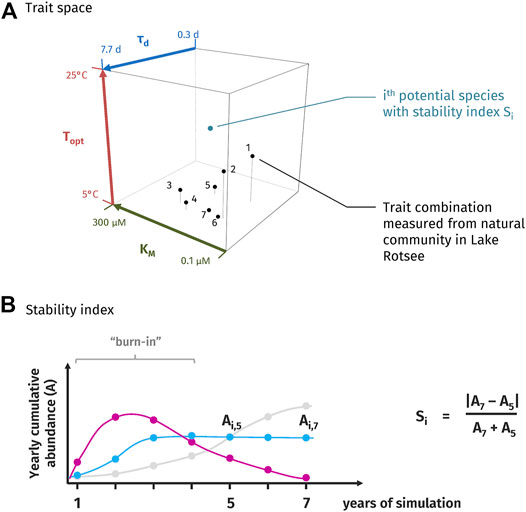
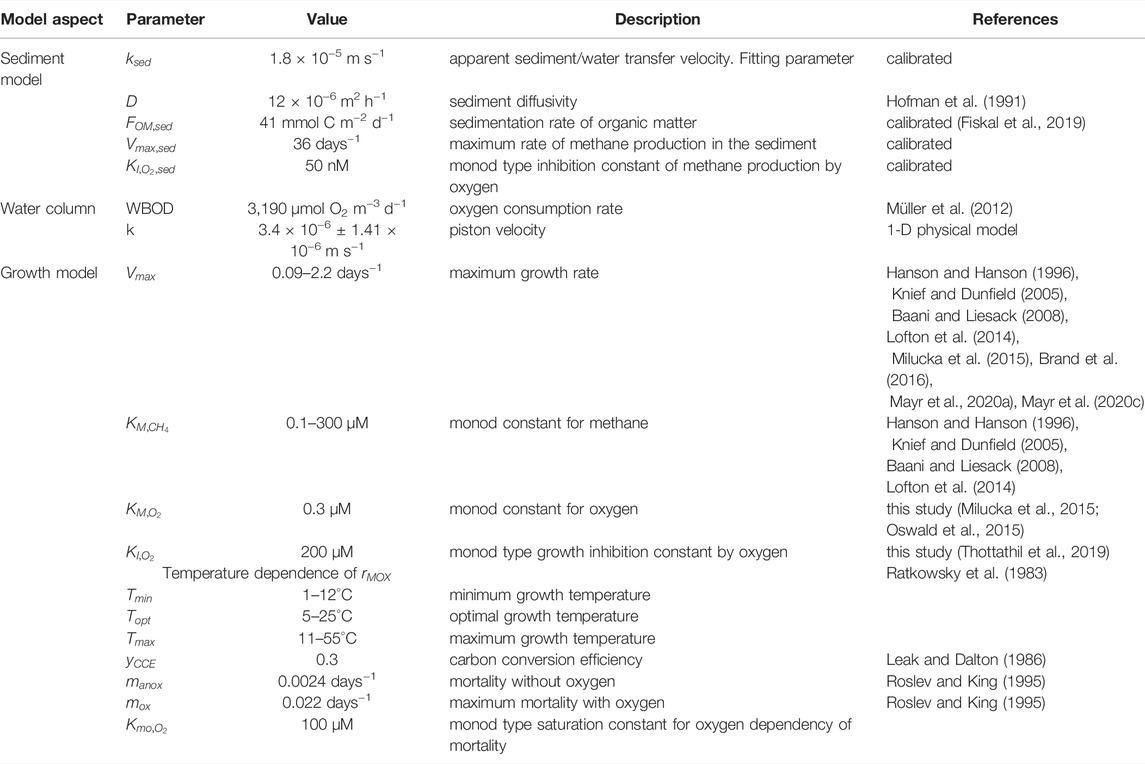
FIGURE 1. Visualization of the methodological approach to analyze coexistence patterns in the model. (A) The 3-dimensional space of potential trait values for MOB is depicted as a cube. The range of trait values was derived to include trait values measured in Lake Rotsee (Mayr et al., 2020b). The affinity for methane is shown as the half-saturation constant for methane (high affinity = low K_M). The maximum growth rate is shown as doubling time. Most of the measured MOB assemblages in Lake Rotsee (shown in black) showed adaptation to low temperatures of 5–8°C and had slow methane oxidation rates of about 60 pmol cell⁻¹ d⁻¹ (full list of trait values in Supplementary Table S1). A single assemblage was abundant at higher temperatures of 16°C. However, we only have trait measurements of MOB assemblages from October to December, and we expect that there could be more trait combinations with adaptation to higher temperature earlier in the year and the range was accordingly set from 5 to 25°C. Similarly, other trait ranges were set somewhat in excess of measured trait combinations of assemblages, taking into account that traits of individual species can be averaged out in the assemblages (B) The stability index of a single species was calculated based on the difference between the yearly cumulative abundance in the fifth and seventh year of simulation. Lines illustrate the abundance of different MOB species in the model. The species in blue illustrates a species with a stable abundance after the initial “burn-in” phase. The species in pink illustrates an unstable species with decreasing concentrations. Another unstable species with increasing concentration is shown in grey.

We used the above described biogeochemical model to explore the abundance and coexistence of single MOB species from the trait space $T$ or whole communities of MOB species (multiple points in $T$). Based on preliminary explorations of the burn-in time of the model, we ran simulations for 7 years to allow the MOB species to establish their niches. For our simulation, we chose the meteorological forcing of a specific year and repeated these conditions in every year of the simulation. We thus simplified the problem by removing interannual variability and thereby focus on the development of population structure under realistic, but defined seasonal variations. For each species, we computed the annual cumulative abundance by simply adding up over depth and time.

To track survival or disappearance of species and long-term stability of the community, we defined a set of criteria. A species was considered a reoccurring member of the community if its annual cumulative abundance reached at least 10³ cells in the last year of the simulation. For recurring members, we defined a stability index $S_i$ where the stability $S_i$ of a species $i$ was calculated as the relative change of the cumulative abundance from year 5 to year 7 (Figure 1B):

$S_i=\frac{\left|A_7-A_5\right|}{A_7+A_5}(11)$

This index was chosen as a simple proxy for stability that meets the following criteria: 1) the values range from 0 to 1, where 0 means stable (no change in abundance from year 5 to year 7) and 1 means unstable (extinction or infinitely many cells), and 2) the index is computationally efficient. If the simulation contained more than one species, we used the maximum value of all individual stabilities as the stability of the whole community. For a community, an overall stability index close to 0 indicates stable coexistence, whereas an overall stability index close to 1 indicates unstable coexistence.

To find and analyze trait combinations in multi-species communities that result in a stable coexistence, we generated maps of the stability index. To do so, we normalized each trait dimension (i.e., temperature optimum $T_{Topt}$ , affinity for methane $T_{KM}$ and maximum growth rate $T_{Vmax}$) and analyzed coexistence patterns in this normalized 3-dimensional trait space $T$ (Figure 1A). The transformation from the normalized space $T$ into actual trait values was performed as follows:

$T_{opt}=15+10\cdot \{\begin{array}{c}\left(T_{Topt}-0.5\right).2T_{Topt}\ge 0.5\\ \left(T_{Topt}\cdot 2-1\right)T_{Topt}<0.5\end{array}\left[\text{°C}\right](\mathrm{12a})$

$T_{min}=7+\{\begin{array}{c}5\cdot \left(T_{Topt}-0.5\right).2T_{Topt}\ge 0.5\\ 6\cdot \left(T_{Topt}\cdot 2-1\right)T_{Topt}<0.5\end{array}\left[\text{°C}\right](\mathrm{12b})$

$T_{max}=33+22\cdot \{\begin{array}{c}\left(T_{Topt}-0.5\right)\cdot 2T_{Topt}\ge 0.5\\ \left(T_{Topt}\cdot 2-1\right)T_{Topt}<0.5\end{array}\left[\text{°C}\right](\mathrm{12c})$

$K_M={10}^{\left(2.5-3.5\cdot T_{KM}\right)}\cdot 1000\left[\mathrm{\mu }\text{mol}{\text{m}}^{-3}\right](13)$

$V_{max}=\left(0.1+1.9\cdot T_{Vmax}\right)\cdot {10}^{-5}\left[{\text{s}}^{-3}\right](14)$

Note, that $K_M$ is normalized logarithmically while $T_{opt}$ and $V_{max}$ were normalized linearly. Equations 12b, 12c describe our assumption on how temperature minimum and temperature maximum are situated around the temperature optimum. To our knowledge, there is no comprehensive dataset to derive this dependency and the two equations remain pragmatic assumptions.

We subdivided the normalized trait space into a grid with a resolution of 0.05 normalized trait units in every dimension. Each grid point in this trait space denotes a potential trait combination. The stability of a given point (a species) in T can be determined in isolation (single species) or tested in the presence of a community of $n$ other species with different trait combinations.

In a first set of numerical experiments, we explored the stability of trait combinations and community compositions in an iterative way. For this purpose, we introduce the following nomenclature: $T_n$ denotes the stability pattern of a whole community with n species that are known to be in a stable configuration and one additional species (n + 1). This allowed us to determine if the addition of a new species destabilizes a community that is otherwise stable, or if the new species can coexist with the previously stable community. For example, in $T_0$ every grid point denotes the stability of a single species with the trait combination at that specific grid point. In $T_1$, every grid point denotes the stability of the coexistence of the species at the grid point with a previously chosen, stable species from $T_0$. This allowed us to start out with a single stable species and iteratively explore which other species we can add to compose more and more complex stable communities.

In a second set of numerical experiments, the focus was on the effect of an additional species on a community that is known to be stable. According to the same principle, we define $P_n$ as the stability pattern of only the already known, stable community with n species, when an additional species (n + 1) from the grid is added (i.e., without taking the stability of the added species into account). For example, in P₃ every grid point denotes the stability of the previously stable community of three species after addition of a fourth species with the trait combination at the grid point. The resulting stabilities associated with every grid-point in the trait spaces $T_n$ and $P_n$ were visualized using Wolfram Mathematica version 12.0.

Classification of Abundance Patterns

Based on the exploration of stability patterns (see Results), we determined a surface within the three dimensional trait space that covers trait combinations that are all coexisting with each other. The specific coexistence surface used for this exercise was selected to be close to the measured values of MOB assemblages in Rotsee. From this surface, we selected 1,564 species and ran a 7-year simulation. Because many of the 1,564 species will behave very similarly, our goal was to categorize the dominant abundance patterns. Due to the large number of observations and data points, classical statistical classification techniques are not suitable for this task. Instead, we used a technique that originates from the domain of unsupervised machine learning: self-organizing maps (SOM, Kohonen, 1982; Asan and Ercan, 2012). We used the implementation of the Julia package SOM.jl (see Code Availability) and trained eight neurons with all resulting abundance patterns to classify the dominant abundance patterns.

Results and Discussion

Modelling Lake Stratification, Overturn and Methane Dynamics

The modelled development of stratification, mixing and methane concentrations qualitatively agreed well with field observations (Figure 2). The physical model overestimated surface water temperatures and underestimated water temperatures at the bottom of the lake (Figure 2A; Supplementary Figure S1). However, the mixed layer depths were in good agreement with the field observations, meaning that the stratification and mixing process was generally well reproduced. The modelled methane profiles qualitatively fitted well with measured methane profiles, which indicates that our biogeochemical model captured the most essential processes (Figure 2A; Supplementary Figure S1). Note that the aim of the model was not to reproduce the observations perfectly. For the purpose of this study, it was sufficient that the model was able to reproduce the general dynamics of the system (i.e., seasonal dynamics of stratification, accumulation of methane in the hypolimnion and subsequent lake overturn, which transports accumulated methane to the mixed layer) and to yield concentration values that are comparable to the observations (Figure 2B).

FIGURE 2

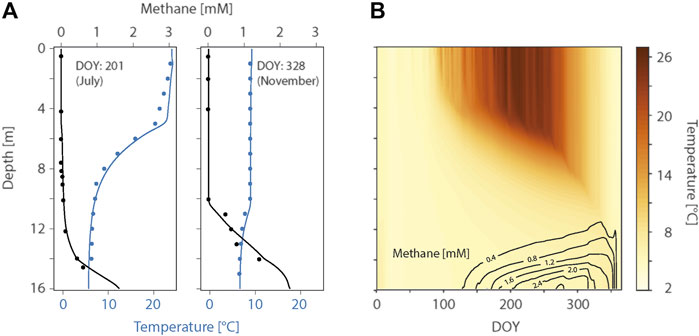
FIGURE 2. Seasonal evolution of stratification, mixing and methane profiles in Lake Rotsee in 2016. (A) Typical profiles of measured (dots) and modelled (solid lines) temperatures and methane concentrations in 2016. Additional profiles are shown in Supplementary Figure S1. Log-scaled methane profiles are provided in Supplementary Figure S4. Methane profiles were computed without considering microbial methane oxidation, suggesting that the methane gradient is largely controlled by the physical stratification and mixing process rather than microbial activity. In July (left panel) the lake is stratified, and methane starts to accumulate in the hypolimnion. In November, lake cooling has deepened the mixed layer to about 10 m and transports methane from the hypolimnion into the mixed layer. (B) The seasonal evolution of lake temperatures simulated by the physical model is shown as a filled contour plot. The accumulation of methane predicted by the biogeochemical model is indicated by black contour lines that are labelled with methane concentrations in mM.

The modelled methane profiles within the water-column fitted well with observations even when we modelled methane profiles without considering microbial methane oxidation (Figure 2A; Supplementary Figure S1). This suggests that the shape of the methane gradient in the water-column (i.e., especially the position of the methane interface) is not a direct indication for microbial activity. In particular, the depth where methane concentrations started to increase matched well with the field observations suggesting that the position of the methane-oxygen counter gradient is largely controlled by the physical stratification and mixing process rather than microbial activity. Even though this indicates that microbial methane oxidation does not alter methane concentrations substantially, growth of methanotrophs is still supported by the flux of methane. The decreasing methane concentrations towards the mixed layer results in a flux of methane into the epilimnion. During stable stratification, this methane flux supports growth of methanotrophic bacteria right at the oxycline (Zimmermann et al., 2021). Without considering microbial methane oxidation, the model overestimated methane concentrations in the epilimnion during the late overturn in autumn (Supplementary Figure S1). Increased concentrations result from the progressing thermocline deepening, which substantially increases the methane flux to the epilimnion. As shown in (Zimmermann et al., 2021), a rapidly growing assemblage of MOB in the epilimnion is able to oxidize almost all of this methane and keep methane concentrations low.

When the lake was completely mixed at the beginning of the year, the model predicted higher methane concentrations at the bottom of the lake than observed (Supplementary Figure S1). Even though water temperatures are low at this time, psychrophilic methanotrophs might be able to oxidize this methane (Trotsenko and Khmelenina, 2005). To our knowledge, however, there are no systematic measurements of MOB abundance and activity in stratified lakes during winter. Growth of MOB during this early, well-mixed phase might be an alternative explanation or might at least partially contribute to the methanotroph biomass observed in the anoxic hypolimnion during stable stratification (Oswald et al., 2016; Mayr et al., 2020a, 2020c; Zimmermann et al., 2021). At temperatures of about 5—6°C and without oxygen, this biomass might be well preserved for a considerable amount of time even when oxygen is no longer available in the hypolimnion (Roslev and King, 1995).

The sediment model is very simplified and needed substantial calibration. Our objective was to close our model with realistic sediment fluxes. In our model, the sediment water fluxes were on average 23 μmol m⁻² d⁻¹ (0.4 mg m⁻² d⁻¹) with a peak in fall at about 55 μmol m⁻² d⁻¹ (0.9 mg m⁻² d⁻¹). This flux was actually fitted to reproduce observed methane concentration in the hypolimnion. When compared to the literature, our model flux is in the lower range of the reported sediment-water methane fluxes. Huttunen et al. (2006) reported fluxes for eutrophic boreal lakes range over a wide range 0.44—76 mg m⁻² d⁻¹. Similarly, the flux at temperature close to 4°C in Mindelsee ranged from 0.1 to 0.15 mmol m⁻² d⁻¹ (1.6–2.4 mg m⁻² d⁻¹) while Bastkiven et al. (2008) indicated higher methane fluxes in the hypolimnion of three lakes in the United States (3–13 mmol m⁻² d⁻¹ (48–209 mg m⁻² d⁻¹) for the hypolimnion). Steinsberger et al. (2017) also reported similar fluxes ranging from 0.08 to 4.24 mg m⁻² d⁻¹ for 5 Swiss lakes.

Configurations of Coexisting Species

We were interested in whether we can establish diversity and niche differentiation of MOB in our model, based on measured methane oxidation kinetics and temperature adaptation. We ran model simulations, which considered seven individual model species with trait value combinations derived from values determined for natural MOB assemblages in Rotsee water samples (Mayr et al., 2020b, Supplementary Table S1). While the measurements were obtained from mixed communities (Supplementary Table S2) and temperature optima were not determined experimentally, it appeared reasonable that average trait values of the community would approximate those of dominant species in each sample, and that these organisms would be adapted to the in-situ temperature, which was therefore used as the temperature optimum. Simulations with this set of species, however, did not result in a stable coexistence and niche differentiation in the model (Supplementary Figure S2). After the 7-year simulation period, only two of the seven simulated species were stable and dominated the MOB abundance whereas the other five species showed decreasing abundances or fell below the survival threshold (10³ cells cumulative annual abundance). Therefore, we decided to systematically explore conditions for stable coexistence of MOB species in our model.

To search for combinations of MOB species that form a stable community in the model, we first examined each potential trait combination of a single species and determined which of these trait combinations resulted in a stable abundance in the lake (Figure 3). The resulting stability map for single species $T_0$ was monotonous in the sense that $T_0$ was split into two homogeneous regions: an unstable region towards low growth rates and low methane affinities and a stable region towards fast growth and high methane affinity. Interestingly, the transition between stability and instability was not gradual but limited to a thin, curved zone (red color in Figure 3).

FIGURE 3

FIGURE 3. Mapping coexisting communities of MOB in Lake Rotsee. The 3-dimensional space of potential trait values for MOB is depicted as a cube. Each point in the three-dimensional trait space is shaded according to the long-term recurrence of the respective trait-combination by itself or together with the pre-defined species of a stable assemblage. Here, we show the stability of single species in the simulated Rotsee. The arrows next to the axes label indicate increasing methane affinity, increasing adaptation to warm temperatures and increasing maximum methane oxidation rates, respectively. Regions of trait combinations with stable recurrence after 7 years are shaded in blue, regions of instable trait combinations in yellow. The transition between stable and unstable recurrence $\left(0.25<S_i>0.55\right)$ is shaded in red. Seven trait combinations determined for MOB assemblages during a field campaign in Rotsee (Mayr et al., 2020b, Supplementary Table S1) are indicated as dots. In model simulations with all these seven species as a community, only two species remained stable and above the abundance threshold over the 7-year simulation (blue dots).

The trait combinations determined from lake water samples (Figure 3, black dots) were all located within the stable region, which means that each individual species in this set would establish a stable abundance in the model. However, in combination with each other, some of the modelled species were not competitive under the model conditions. In the model, only two of the measured trait combinations were able to coexist (Figure 3, blue dots).

To explore which combinations of species would be able to coexist in the model, we assembled custom communities with the following procedure (illustrated in Figure 4A): We started by selecting a species with a custom trait combination close to the trait combinations measured for Lake Rotsee communities. Subsequently, we tested this trait combination against all other trait combinations for stable coexistence (Figure 4A, $T_1$). The resulting coexistence space $T_1$ consisted of confined regions (blue, Figure 4A) containing all possible stable partners. Interestingly, the stable regions were at some distance from the selected starting species, whereas the space in the immediate vicinity was largely unstable. This is in good agreement with Hardin’s competitive exclusion principle (Hardin, 1960). Within the confines of the limited number of traits in our model, a competing species whose trait values differ only slightly will most likely either replace the original species, or is not competitive unless changes in several trait values compensate each other exactly. Species with more distant trait values are more likely to coexist because they can occupy a different niche.

FIGURE 4

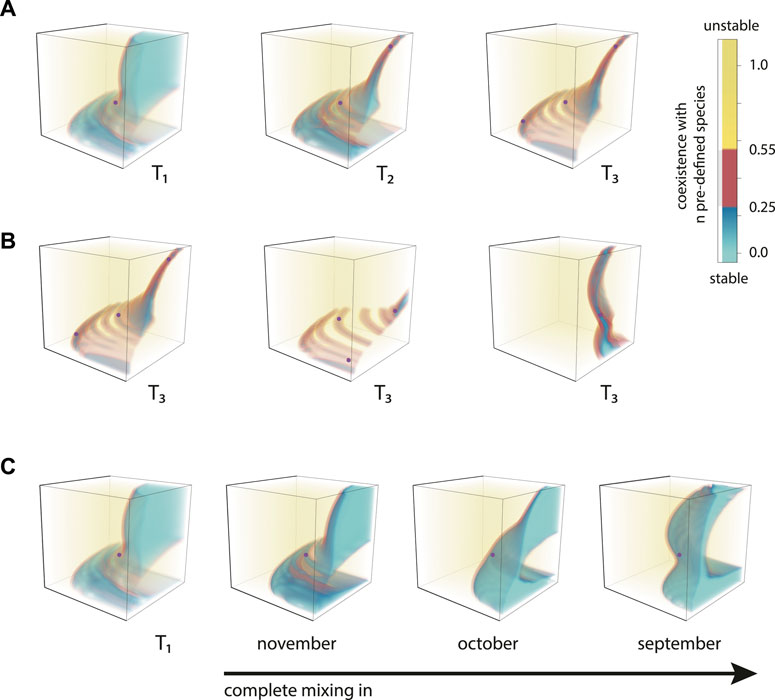
FIGURE 4. (A) Regions of stable trait configurations with an increasing number of pre-defined species. The trait combination of the pre-defined species is indicated with purple dots. In $T_1$, a single species that was stable in $T_0$ is pre-defined, and the shading corresponds to the long-term coexistence of the pre-defined species with any second species in the trait space. In $T_2$, two coexisting species are pre-defined, and the shading corresponds to the long-term coexistence of the two pre-defined species with any third species in the trait space. The same principle applies to $T_3$. The banded pattern of emerging regions with stable coexistence is an artefact of the map resolution. (B) Depending on the selection process of species from $T_1$ to $T_3$, different configurations of stable communities emerge in $T_3$ (each point in the three-dimensional trait space is shaded according to the stability of the original community together with the species with the trait combination at that point). (C) Stability depends on the environmental conditions. We artificially introduced a strong wind-event into our simulations that completely mixed the water column in either September, October or November in each of the repeated 7 years of the simulation. Depending on the mixing behavior, the region of partners forming a stable community with a single pre-defined species (dark purple dot) has a different shape. To reduce distraction, axes labeling was omitted. The view and scaling is the same for all cubes and is equivalent to the cube in Figure 3.

Based on this analysis, we again selected one new species with a trait combination that formed a stable coexistence with the first trait combination. We then repeated the procedure of combining this pre-defined pair with all other trait combinations and determined the regions in the trait space that lead to a stably coexisting three-species assemblage (Figure 4A, $T_2$). This procedure can be repeated to combine several coexisting species from different regions of the trait space. We observed that the parameter space containing further partners which can coexist with the pre-defined assemblage shrinks as the number of coexisting species in the model increases (Figure 4A). The shrinking parameter space remains confined to a thin surface, indicating that the available niche space for additional partners is limited.

Within the trait space an unlimited number of configurations of coexisting species exists, which raises the question which trait distribution is effectively realized in nature. In our model, the shape of the region where coexisting trait combinations are located depended on the selection of pre-defined species (Figure 4B). This implies that there could be an exclusion mechanism, where the abundances of a few “founder” species in the beginning of the season already define which additional species are able to coexist with those already present.

To allow setting up reasonable criteria for stable coexistence, our lake model repeats the same meteorological conditions each simulated year, thus also the environmental conditions and the same mixing patterns unrealistically re-occur over the seven modelled years. We explored the potential impact of variable mixing conditions by artificially introducing mixing events at different times of the repeated annual cycle and evaluating the effect on the coexistence space with a single pre-existing species (T₁). This scenario analysis showed that the shape of regions of coexistence depended on the seasonal dynamics of lake stratification and mixing (Figure 4C). Different annual weather conditions will influence the stable species composition.

Both the effect of the pre-existing species and the environmental impact discussed above would suggest that under real-world conditions, the MOB community in lakes may differ from year to year, and a perennial stable community may never truly occur—instead changing conditions and species assemblies would continually open new niche spaces while other niches become obsolete. Multi-year Datasets on MOB communities in stratified lakes that would allow us to test if this prediction of our model is true in nature are currently not available. Longer-lasting modeling runs could include variable dynamics of annual warming, mixing and cooling. Such an extended approach could further explore the effects of the chaotic part in the annual oscillations on the long-term stability of the MOB community.

Abundance Patterns of Simulated Species in Space and Time

We analyzed abundance patterns of a large number of species (Figure 5) whose trait combinations were located on a coexistence surface that was selected to fall close to the measured trait combinations. Based on self-organizing map classification, we found at least 4 distinct abundance patterns (Figure 5, blue, orange, yellow, pink). One pattern was associated with species that were mainly abundant in the hypolimnion (Figure 5, pink), a pattern observed for example in the Methylococcales species ASV_4 in Rotsee (Mayr et al., 2020a). Two patterns showed an abundance maximum at the interface of the mixed layer and the hypolimnion during stratified conditions or in the mixed layer (Figure 5, blue, orange). Overall, these modelled patterns approximate the three main spatial niches quite well, which we proposed under stratified conditions (Epilimnion, Interface, Hypolimnion) previously (Mayr et al., 2020c). This indicates that the simple kinetic trait combinations used in our model suffice to reproduce this fundamental niche partitioning pattern of MOB in stratified lakes. Three patterns were further associated with species that became abundant in the mixed layer during different stages and different durations of the mixing period (Figure 5, blue, orange, pink). This matches observations from our previous study where we reported temporal succession of species dominating in the mixed layer during lake overturn (Mayr et al., 2020a). A pattern observed in nature, in Rotsee, e.g., for Methylocytis (Guggenheim et al., 2020), but not in our model was that of an abundance increase towards the lake surface during summer stratification. This indicates that certain traits or processes that determine the distribution of this taxon are not represented in our model. Overall, our custom assembled communities showed spatiotemporal abundance patterns remarkably similar to previously observed depth profiles and temporal dynamics of methanotroph species in Lake Rotsee (Mayr et al., 2020a). Considering the simple trait space used in the model, this finding is noteworthy and provides considerable support to the hypothesis that kinetic traits of the methane oxidation are a central adaptive strategy, and thus a basis for niche differentiation in freshwater methanotrophs.

FIGURE 5

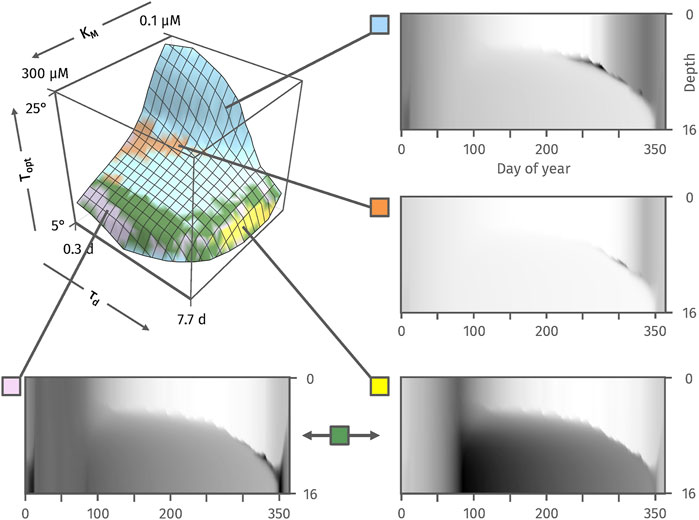
FIGURE 5. Classification of normalized (0 = least abundant/white, 1 = most abundant/black) spatiotemporal abundance patterns using a self-organizing maps approach (Asan and Ercan, 2012). We ran a 7-year simulation with an initial set of 1,564 species whose trait combinations were sampled from a regular grid on the shown coexistence surface within the trait space. The coexistence surface approximates the regions of coexistence in Figure 4A, T₃. A self-organizing map with eight neurons was trained on all 1,564 normalized abundance patterns. We colored the surface of trait combinations to indicate the associated neuron that shows highest activation for the specific abundance pattern. Only five of the eight neurons specialized to a specific region on the surface. Each of the five neurons can reproduce the input/pattern to which it has specialized. The four clearly distinct abundance patterns are shown as heat maps (dark colors indicate high abundance, light colors indicate low abundance, i.e., white = 0, black = 1) representing abundance over depth and time in year 7 of the simulation. The neuron associated with the abundance pattern in green showed a combination of the two neighboring patterns.

Destabilizing a MOB Community

Moving from the stability pattern $T_1$ to $T_3$ reduces the stable trait space significantly (Figure 4A). Therefore, we hypothesize that with increasing number of community members, the region of stable trait configurations ultimately narrows down to a thin layer or surface. This would indicate that “stable” communities are actually easily disturbed if a new species invade them or if one of the members of the community acquires new trait values through adaptive evolution. In order to explore this idea further, we iteratively assembled a stable community $C_1$ of three species (Figure 6A, red dots) and determined its stability when added additional species. The region of additional species that would destabilize the original community covered the entire space on one side of the narrow layer of coexistence: the side towards higher growth rates, high affinity and adaptation to low temperatures. Members of the original community $C_1$ will be replaced by additional species with such trait combinations and therefore, the shape of the region with stable partners would change accordingly. We iteratively assembled a new stable community $C_2$ with species from the region that would destabilize the original community $C_1$ (Figure 6B). When we again determined the stability of this community $C_2$ after the addition of a new species, we observed the same distribution of stability and instability. Within our simplified model, unrestricted evolution towards optimized trait combinations would cause the surface of coexistence to shift gradually towards an increasingly optimized community and ultimately a “superorganism” that would outperform all other species. The observed diversity of the methanotrophic assemblage in real lakes points to a clear limitation of our model and to barriers precluding the evolution of such a superorganism, i.e., physiological limits or tradeoffs between and with additional traits. This further suggests that, if methane oxidation kinetics and adaptation to temperature are the dominant traits that explain coexistence and niche differentiation, the observed trait combinations should be aligned on a specific surface within the trait space $T$ where physiological restrictions and tradeoffs prevent further optimization of the trait values.

FIGURE 6

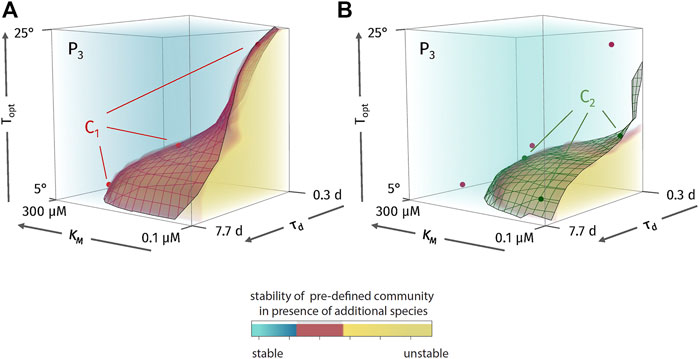
FIGURE 6. (A) Stability space ($P_3$) of a stable community $C_1$ of three species (red dots) when an additional species is added. In $P_3$, each point in the three-dimensional trait space is shaded according to the stability of only the original community, when the species with the trait combination at that point is added to the community. The thin layer of coexistence in the stability space $T_3$ (Figure 4B, first cube on the left) is shown as an approximated smooth surface (red wire frame). Regions where the additional species would destabilize the original community are shaded in yellow. The stable community is destabilized and replaced by the addition of any “better adapted” species in this yellow region. (B) A stable community $C_2$ with three species (green dots) from the yellow region in panel (A). The three species of community $C_1$ are shown as red dots. The thin layer of coexistence in the stability space $T_3$ (Figure 4B, second cube from the left) is shown as an approximated smooth surface (green wire frame). The stability space ($P_3$) of this community shows the same property of destabilization. Thus invasion or evolution of better adapted species would invariably lead to a contraction of the stable community (red arrows in panel (A)) towards a highly optimized community or ultimately even to a “superorganism.” Compared to Figure 4, the trait-spaces are shown from a slightly tilted angle.

As noted earlier, trait values observed for MOB communities in Lake Rotsee did not result in a stable community in our model. Assuming that the three traits we modelled are the main explanatory variables for the observed niche differentiation, we would expect that observed trait values should be positioned at least approximately near one of the thin layers of potential coexistence. We approximated such a layer of coexistence that runs close to observed values (Figure 4B, first cube from the left) shown also as the smooth surface of community $C_1$ in Figure 6A (red wire frame). Even though the curvature of this surface roughly approximates the trait combinations actually observed in Lake Rotsee, several values diverged considerably, e.g., towards adaptation to lower temperature than allowed for stable coexistence (Supplementary Figure S3). As temperature optima were not measured but simply assumed to correspond to in-situ temperatures, it may not be surprising that we see such a divergence. The limited number of observations and the uncertainty associated with the measured values do not allow assessing how well kinetics and temperature adaptation can explain the observed trait distribution. Other traits not considered in our model may be important and may allow coexistence despite incompatible methane oxidation kinetics or temperature adaptation. Such additional traits could include oxygen tolerance (Nguyen et al., 1998), syntrophic strategies (Milucka et al., 2015; Skennerton et al., 2017), starvation metabolisms (Kalyuzhnaya et al., 2013) or acquisition strategies for other nutrients, such as nitrogen or copper (Auman et al., 2001; Semrau et al., 2013). Clearly, our physical and biogeochemical model is likewise a highly simplified representation of reality, that does not account for stochastic variability in the environment.

Conclusion and Outlook

With the observation of a fascinating diversity, vertical structure and seasonal succession of methane oxidizing bacteria in stratified lakes, the question arose how this diversity is maintained. Here we investigated with our trait-based mechanistic model of microbial methane oxidation if and how well we can reproduce and explain the observed patterns of lacustrine MOB diversity in a seasonally stratified lake.

With our model, we successfully recreate diversity and niche differentiation patterns of methanotrophs very similar to observed patterns in seasonally stratified lakes. This finding provides support to the hypothesis that the traits used in our model—kinetic traits of the methane oxidation and different temperature optima—are indeed central adaptive strategies, and thus a basis for niche differentiation in freshwater methanotrophs. However, in the model, the combination of trait values that allowed coexistence was rapidly confined to narrow regions in the parameter space as we increased the number of species, raising the question how these exact combinations would be realized in nature or whether there are mechanisms that widen these narrow regions. We argue that evolutionary convergence to the physiological limit that is inherent in the underlying biochemical and cellular systems is one mechanism that pushes trait values to these narrow regions on evolutionary time scales. In addition, the sequence of colonization or the annual variability of the stratification and mixing behavior of the lake may allow different stable configurations from year to year or on even shorter timescales, which may provide another way to maintain a higher diversity than expected from the competitive exclusion principle. Additional physiological traits (e.g., oxygen tolerance, symbiotic strategies or starvation tolerance) not considered here might be important for niche differentiation and may widen the space for coexistence.

The modeled environment was necessarily simplified; the data used to build our model of the Rotsee water column focused on the turnover period, and we have only a coarse representation of the methane-oxygen interface in the model. Specifically, we excluded the possible effects of nutrients (nitrogen, phosphorus), micronutrients such as copper (Guggenheim et al., 2019), and we neglected lateral exchange in our 1-D model (Thalasso et al., 2020). In particular, the parameterization of the sediment model can be questioned and improved as well. Adding more detail and expanding the kinetic parameter space will add more niches and more potential for a stable diversity of the MOB community. Nevertheless, our approach is the first attempt to combine a fundamentally realistic lake physical and biogeochemical model with a trait-based population model and thus provides the first opportunity to test the validity of a trait-based approach for MOB ecology against environmental data. Further, our model approach provides ample opportunity for future expansion, e.g., to test the importance of further traits, and for application in other lakes.

In this study, we have not yet analysed whether the trait-based approach for modelling methane oxidation affects the accuracy of the biogeochemical model. The question whether MOB diversity has to be taken into account when modelling methane emissions and microbial methane oxidation in lakes remains to be investigated. We found that the rough shape of the methane gradient in the studied lake is largely controlled by the physical stratification and mixing process, but, e.g., methane concentrations in the mixed layer during overturn would be overestimated without considering methane oxidation - and thus methane emissions would be overestimated. There may thus be a number of situations and research questions where knowledge of changes in methane oxidation kinetics, which our trait-based approach could provide, may be of importance. For example, the amount of outgassing of methane will depend on whether the most abundant MOB in the epilimnion in summer or in the mixed layer during lake overturn is a high affinity MOB or not. The improvement of incorporating trait diversity in a biogeochemical model may also become important when conditions change rapidly. Under such conditions, a trait-based model may predict how oxidation kinetics change and may provide a better system description. Finally, it would be interesting to explore if a high trait diversity results in more efficient methane oxidation in a system, especially if this diversity is independently controlled by other factors, such as, e.g., temperature, micronutrient availability or pollution.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: Physico-chemical data is available at the ETH Research Collection (https://doi.org/10.3929/ethz-b-000350091).

The source code of the physical model is available on GitHub (http://doi.org/10.5281/zenodo.3274379). The source code of the numerical discretization of the reaction-diffusion equation used for the biogeochemical model is available as a Julia package (https://github.com/zimmermm/FiniteVolumeRDS.jl). The actual implementation of the biogeochemical model as well as the microbial growth model for Lake Rotsee is available on GitHub (https://github.com/zimmermm/MOBDiversityModel).

Author Contributions

MZ, MM, HB, and BW conceptualized the study. MZ and DB conceptualized the model. MZ developed the model under supervision of DB and with inputs by HB, MM, and BW. MM and MZ acquired the data. MZ wrote the first draft of the manuscript and created the figures. All authors contributed text during revisions of the manuscript and were involved in commenting and editing the paper. HB and BW acquired the funding.

Funding

The Swiss National Science Foundation (grant CR23I3_156759), ETH Zurich and Eawag funded this research. Open access funding provided by Swiss Federal Institute of Aquatic Science and Technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Karin Beck, Andreas Brand, Jason Day, Patrick Kathriner, Miro Meyer, Michael Plüss and Serge Robert for their help and advice in the field and the lab. We acknowledge the helpful discussions and feedback by Carsten Schubert, Blake Matthews and Anita Narwani. We thank Andreas Brand for his advice and support during the first phase of the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.833511/full#supplementary-material

References

Asan, U., and Ercan, S. (2012). “An Introduction to Self-Organizing Maps,” in Computational Intelligence Systems in Industrial Engineering. Atlantis Computational Intelligence Systems. Editor C. Kahraman (Paris: Atlantis Press), 6, 295–315. doi:10.2991/978-94-91216-77-0_14

CrossRef Full Text | Google Scholar

Auman, A. J., Speake, C. C., and Lidstrom, M. E. (2001). nifH Sequences and Nitrogen Fixation in Type I and Type II Methanotrophs. Appl. Environ. Microbiol. 67, 4009–4016. doi:10.1128/AEM.67.9.4009-4016.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Baani, M., and Liesack, W. (2008). Two Isozymes of Particulate Methane Monooxygenase with Different Methane Oxidation Kinetics Are Found in Methylocystis Sp. Strain SC2. Proc. Natl. Acad. Sci. U.S.A. 105, 10203–10208. doi:10.1073/pnas.0702643105

PubMed Abstract | CrossRef Full Text | Google Scholar

Bastviken, D., Cole, J. J., Pace, M. L., and Van de Bogert, M. C. (2008). Fates of Methane from Different Lake Habitats: Connecting Whole-Lake Budgets and CH4emissions. J. Geophys. Res. 113, a–n. doi:10.1029/2007JG000608

CrossRef Full Text | Google Scholar

Bastviken, D., Tranvik, L. J., Downing, J. A., Crill, P. M., and Enrich-Prast, A. (2011). Freshwater Methane Emissions Offset the Continental Carbon Sink. Science 331, 50. doi:10.1126/science.1196808

PubMed Abstract | CrossRef Full Text | Google Scholar

Bezanson, J., Edelman, A., Karpinski, S., and Shah, V. B. (2017). Julia: A Fresh Approach to Numerical Computing. SIAM Rev. 59, 65–98. doi:10.1137/141000671

CrossRef Full Text | Google Scholar

Brand, A., Bruderer, H., Oswald, K., Guggenheim, C., Schubert, C. J., and Wehrli, B. (2016). Oxygenic Primary Production below the Oxycline and its Importance for Redox Dynamics. Aquat. Sci. 78, 727–741. doi:10.1007/s00027-016-0465-4

CrossRef Full Text | Google Scholar

Chesson, P. (2000). Mechanisms of Maintenance of Species Diversity. Annu. Rev. Ecol. Syst. 31, 343–366. doi:10.1146/annurev.ecolsys.31.1.343

CrossRef Full Text | Google Scholar

Conrad, R. (2009). The Global Methane Cycle: Recent Advances in Understanding the Microbial Processes Involved. Environ. Microbiol. Rep. 1, 285–292. doi:10.1111/j.1758-2229.2009.00038.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Dam, B., Dam, S., Kube, M., Reinhardt, R., and Liesack, W. (2012). Complete Genome Sequence of Methylocystis Sp. Strain SC2, an Aerobic Methanotroph with High-Affinity Methane Oxidation Potential. J. Bacteriol. 194, 6008–6009. doi:10.1128/JB.01446-12

PubMed Abstract | CrossRef Full Text | Google Scholar

DelSontro, T., Beaulieu, J. J., and Downing, J. A. (2018). Greenhouse Gas Emissions from Lakes and Impoundments: Upscaling in the Face of Global Change. Limnol. Oceanogr. Lett. 3, 64–75. doi:10.1002/lol2.10073

PubMed Abstract | CrossRef Full Text | Google Scholar

Doherty, J. (2015). Calibration and Uncertainty Analysis for Complex Environmental Models. Australia: Watermark Numerical Computing Brisbane. Available at: https://doi.org/10.1111/gwat.12360.

Google Scholar

Fiskal, A., Deng, L., Michel, A., Eickenbusch, P., Han, X., and Lagostina, L. (2019). Effects of Eutrophication on Sedimentary Organic Carbon Cycling in Five Temperate Lakes. Biogeosciences 16, 3725–3746. doi:10.5194/bg-16-3725-2019

CrossRef Full Text | Google Scholar

Gaudard, A., Råman Vinnå, L., Bärenbold, F., Schmid, M., and Bouffard, D. (2019). Toward an Open Access to High-Frequency Lake Modeling and Statistics Data for Scientists and Practitioners – the Case of Swiss Lakes Using Simstrat v2.1. Geosci. Model Dev. 12, 3955–3974. doi:10.5194/gmd-12-3955-2019

CrossRef Full Text | Google Scholar

Guggenheim, C., Brand, A., Bürgmann, H., Sigg, L., and Wehrli, B. (2019). Aerobic Methane Oxidation under Copper Scarcity in a Stratified Lake. Sci. Rep. 9, 4817. doi:10.1038/s41598-019-40642-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Guggenheim, C., Freimann, R., Mayr, M. J., Beck, K., Wehrli, B., and Bürgmann, H. (2020). Environmental and Microbial Interactions Shape Methane-Oxidizing Bacterial Communities in a Stratified Lake. Front. Microbiol. 11, 579427. doi:10.3389/fmicb.2020.579427

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanson, R. S., and Hanson, T. E. (1996). Methanotrophic Bacteria. Microbiol. Rev. 60, 439–471. doi:10.1128/mr.60.2.439-471.1996

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardin, G. (1960). The Competitive Exclusion Principle. Science 131, 1292–1297. doi:10.1126/science.131.3409.1292

PubMed Abstract | CrossRef Full Text | Google Scholar

Hofman, P., de Jong, S., Wagenvoort, E., and Sandee, A. (1991). Apparent Sediment Diffusion Coefficients for Oxygen and Oxygen Consumption Rates Measured with Microelectrodes and Bell Jars: Applications to Oxygen Budgets in Estuarine Intertidal Sediments (Oosterschelde, SW Netherlands). Mar. Ecol. Prog. Ser. 69, 261–272. doi:10.3354/meps069261

CrossRef Full Text | Google Scholar

Hutchinson, G. E. (1961). The Paradox of the Plankton. Am. Nat. 95, 137–145. doi:10.1086/282171

CrossRef Full Text | Google Scholar

Huttunen, J. T., Väisänen, T. S., Hellsten, S. K., and Martikainen, P. J. (2006). Methane Fluxes at the Sediment-Water Interface in Some Boreal Lakes and Reservoirs. Boreal Environ. Res. 11 (1), 27–34.

Google Scholar

Kalyuzhnaya, M. G., Yang, S., Rozova, O. N., Smalley, N. E., Clubb, J., Lamb, A., et al. (2013). Highly Efficient Methane Biocatalysis Revealed in a Methanotrophic Bacterium. Nat. Commun. 4, 2785. doi:10.1038/ncomms3785

PubMed Abstract | CrossRef Full Text | Google Scholar

Kankaala, P., Huotari, J., Peltomaa, E., Saloranta, T., and Ojala, A. (2006). Methanotrophic Activity in Relation to Methane Efflux and Total Heterotrophic Bacterial Production in a Stratified, Humic, Boreal Lake. Limnol. Oceanogr. 51, 1195–1204. doi:10.4319/lo.2006.51.2.1195

CrossRef Full Text | Google Scholar

Knief, C., and Dunfield, P. F. (2005). Response and Adaptation of Different Methanotrophic Bacteria to Low Methane Mixing Ratios. Environ. Microbiol. 7, 1307–1317. doi:10.1111/j.1462-2920.2005.00814.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohonen, T. (1982). Self-organized Formation of Topologically Correct Feature Maps. Biol. Cybern. 43, 59–69. doi:10.1007/BF00337288

CrossRef Full Text | Google Scholar

Kojima, H., Iwata, T., and Fukui, M. (2009). DNA-based Analysis of Planktonic Methanotrophs in a Stratified Lake. Freshw. Biol. 54, 1501–1509. doi:10.1111/j.1365-2427.2009.02199.x

CrossRef Full Text | Google Scholar

Leak, D. J., and Dalton, H. (1986). Growth Yields of Methanotrophs. Appl. Microbiol. Biotechnol. 23, 470–476. doi:10.1007/BF02346062

CrossRef Full Text | Google Scholar

Liss, P. S., and Slater, P. G. (1974). Flux of Gases across the Air-Sea Nterface. Nature 247, 181–184. doi:10.1038/247181a0

CrossRef Full Text | Google Scholar

Litchman, E., and Klausmeier, C. A. (2008). Trait-Based Community Ecology of Phytoplankton. Annu. Rev. Ecol. Evol. Syst. 39, 615–639. doi:10.1146/annurev.ecolsys.39.110707.173549

CrossRef Full Text | Google Scholar

Litchman, E., Pinto, P. de. T., Edwards, K. F., Klausmeier, C. A., Kremer, C. T., and Thomas, M. K. (2015). Global Biogeochemical Impacts of Phytoplankton: a Trait-Based Perspective. J. Ecol. 103, 1384–1396. doi:10.1111/1365-2745.12438

CrossRef Full Text | Google Scholar

Lofton, D. D., Whalen, S. C., and Hershey, A. E. (2014). Effect of Temperature on Methane Dynamics and Evaluation of Methane Oxidation Kinetics in Shallow Arctic Alaskan Lakes. Hydrobiologia 721, 209–222. doi:10.1007/s10750-013-1663-x

CrossRef Full Text | Google Scholar

Longhi, D. A., Dalcanton, F., de Aragão, G. M. F., Carciofi, B. A. M., and Laurindo, J. B. (2017). Microbial Growth Models: A General Mathematical Approach to Obtain μ Max and λ Parameters from Sigmoidal Empirical Primary Models. Braz. J. Chem. Eng. 34, 369–375. doi:10.1590/0104-6632.20170342s20150533

CrossRef Full Text | Google Scholar

MacIntyre, S., Jonsson, A., Jansson, M., Aberg, J., Turney, D. E., and Miller, S. D. (2010). Buoyancy Flux, Turbulence, and the Gas Transfer Coefficient in a Stratified Lake. Geophys. Res. Lett. 37, L24604 1–5. doi:10.1029/2010GL044164

CrossRef Full Text | Google Scholar

Martin, G., Rissanen, A. J., Garcia, S. L., Mehrshad, M., Buck, M., and Peura, S. (2021). Candidatus Methylumidiphilus Drives Peaks in Methanotrophic Relative Abundance in Stratified Lakes and Ponds across Northern Landscapes. Front. Microbiol. 12, 669937. doi:10.3389/fmicb.2021.669937

PubMed Abstract | CrossRef Full Text | Google Scholar

Martiny, J. B. H., Jones, S. E., Lennon, J. T., and Martiny, A. C. (2015). Microbiomes in Light of Traits: A Phylogenetic Perspective. Science 350, aac9323. doi:10.1126/science.aac9323

PubMed Abstract | CrossRef Full Text | Google Scholar

Maynard, D. S., Miller, Z. R., and Allesina, S. (2020). Predicting Coexistence in Experimental Ecological Communities. Nat. Ecol. Evol. 4, 91–100. doi:10.1038/s41559-019-1059-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Mayr, M. J., Zimmermann, M., Dey, J., Brand, A., Wehrli, B., and Bürgmann, H. (2020a). Growth and Rapid Succession of Methanotrophs Effectively Limit Methane Release during Lake Overturn. Commun. Biol. 3, 108. doi:10.1038/s42003-020-0838-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Mayr, M. J., Zimmermann, M., Dey, J., Wehrli, B., and Bürgmann, H. (2020b). Lake Mixing Regime Selects Apparent Methane Oxidation Kinetics of the Methanotroph Assemblage. Biogeosciences 17, 4247–4259. doi:10.5194/bg-17-4247-2020

CrossRef Full Text | Google Scholar

Mayr, M. J., Zimmermann, M., Guggenheim, C., Brand, A., and Bürgmann, H. (2020c). Niche Partitioning of Methane-Oxidizing Bacteria along the Oxygen–Methane Counter Gradient of Stratified Lakes. ISME J. 14, 274–287. doi:10.1038/s41396-019-0515-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Milucka, J., Kirf, M., Lu, L., Krupke, A., Lam, P., Littmann, S., et al. (2015). Methane Oxidation Coupled to Oxygenic Photosynthesis in Anoxic Waters. ISME J. 9, 1991–2002. doi:10.1038/ismej.2015.12

PubMed Abstract | CrossRef Full Text | Google Scholar

Moukalled, F., Darwish, M., and Mangani, L. (2015). The Finite Volume Method in Computational Fluid Dynamics : An Advanced Introduction with OpenFOAM and Matlab. Berlin: Springer.

Google Scholar

Müller, B., Bryant, L. D., Matzinger, A., and Wüest, A. (2012). Hypolimnetic Oxygen Depletion in Eutrophic Lakes. Environ. Sci. Technol. 46, 9964–9971. doi:10.1021/es301422r

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, H.-H. T., Elliott, S. J., Yip, J. H.-K., and Chan, S. I. (1998). The Particulate Methane Monooxygenase from Methylococcus Capsulatus (Bath) Is a Novel Copper-Containing Three-Subunit Enzyme. J. Biol. Chem. 273, 7957–7966. doi:10.1074/jbc.273.14.7957

PubMed Abstract | CrossRef Full Text | Google Scholar

Oswald, K., Milucka, J., Brand, A., Hach, P., Littmann, S., Wehrli, B., et al. (2016). Aerobic Gammaproteobacterial Methanotrophs Mitigate Methane Emissions from Oxic and Anoxic Lake Waters. Limnol. Oceanogr. 61, S101–S118. doi:10.1002/lno.10312

CrossRef Full Text | Google Scholar

Oswald, K., Milucka, J., Brand, A., Littmann, S., Wehrli, B., Kuypers, M. M. M., et al. (2015). Light-dependent Aerobic Methane Oxidation Reduces Methane Emissions from Seasonally Stratified Lakes. PLoS ONE 10, e0132574. doi:10.1371/journal.pone.0132574

PubMed Abstract | CrossRef Full Text | Google Scholar

Ratkowsky, D. A., Lowry, R. K., McMeekin, T. A., Stokes, A. N., and Chandler, R. E. (1983). Model for Bacterial Culture Growth Rate throughout the Entire Biokinetic Temperature Range. J. Bacteriol. 154, 1222–1226. doi:10.1128/jb.154.3.1222-1226.1983

PubMed Abstract | CrossRef Full Text | Google Scholar

Read, J. S., Hamilton, D. P., Desai, A. R., Rose, K. C., MacIntyre, S., Lenters, J. D., et al. (2012). Lake-size Dependency of Wind Shear and Convection as Controls on Gas Exchange. Geophys. Res. Lett. 39, L094055 1–5. doi:10.1029/2012GL051886

CrossRef Full Text | Google Scholar

Record, N. R., Pershing, A. J., and Maps, F. (2014). The Paradox of the “Paradox of the Plankton. ICES J. Mar. Sci. 71, 236–240. doi:10.1093/icesjms/fst049

CrossRef Full Text | Google Scholar

Reis, P. C. J., Thottathil, S. D., Ruiz-González, C., and Prairie, Y. T. (2020). Niche Separation within Aerobic Methanotrophic Bacteria across Lakes and its Link to Methane Oxidation Rates. Environ. Microbiol. 22, 738–751. doi:10.1111/1462-2920.14877

PubMed Abstract | CrossRef Full Text | Google Scholar

Rissanen, A. J., Saarela, T., Jäntti, H., Buck, M., Peura, S., Aalto, S. L., et al. (2020). Vertical Stratification Patterns of Methanotrophs and Their Genetic Controllers in Water Columns of Oxygen-Stratified Boreal Lakes. FEMS Microbiol. Ecol. 97, fiaa252 1–16. doi:10.1093/femsec/fiaa252

CrossRef Full Text | Google Scholar

Roslev, P., and King, G. M. (1995). Aerobic and Anaerobic Starvation Metabolism in Methanotrophic Bacteria. Appl. Environ. Microbiol. 61, 1563–1570. doi:10.1128/aem.61.4.1563-1570.1995

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy, S., and Chattopadhyay, J. (2007). Towards a Resolution of ‘the Paradox of the Plankton’: A Brief Overview of the Proposed Mechanisms. Ecol. Complex. 4, 26–33. doi:10.1016/j.ecocom.2007.02.016

CrossRef Full Text | Google Scholar

Salcher, M. M. (2013). Same Same but Different: Ecological Niche Partitioning of Planktonic Freshwater Prokaryotes. J. Limnol. 73, 74-87. doi:10.4081/jlimnol.2014.813

CrossRef Full Text | Google Scholar

Schubert, C. J., Diem, T., and Eugster, W. (2012). Methane Emissions from a Small Wind Shielded Lake Determined by Eddy Covariance, Flux Chambers, Anchored Funnels, and Boundary Model Calculations: a Comparison. Environ. Sci. Technol. 46, 4515–4522. doi:10.1021/es203465x

PubMed Abstract | CrossRef Full Text | Google Scholar

Semrau, J. D., Jagadevan, S., DiSpirito, A. A., Khalifa, A., Scanlan, J., Bergman, B. H., et al. (2013). Methanobactin and MmoD Work in Concert to Act as the ‘copper-Switch’ in Methanotrophs. Environ. Microbiol. 15, 3077–3086. doi:10.1111/1462-2920.12150

PubMed Abstract | CrossRef Full Text | Google Scholar

Skennerton, C. T., Chourey, K., Iyer, R., Hettich, R. L., Tyson, G. W., and Orphan, V. J. (2017). Methane-fueled Syntrophy through Extracellular Electron Transfer: Uncovering the Genomic Traits Conserved within Diverse Bacterial Partners of Anaerobic Methanotrophic Archaea. mBio 8, e00530-17. doi:10.1128/mBio.00530-17

PubMed Abstract | CrossRef Full Text | Google Scholar

Soloviev, A., Donelan, M., Graber, H., Haus, B., and Schlüssel, P. (2007). An Approach to Estimation of Near-Surface Turbulence and CO2 Transfer Velocity from Remote Sensing Data. J. Mar. Syst. 66, 182–194. doi:10.1016/j.jmarsys.2006.03.023

CrossRef Full Text | Google Scholar

Steinsberger, T., Schmid, M., Wüest, A., Schwefel, R., Wehrli, B., and Müller, B. (2017). Organic Carbon Mass Accumulation Rate Regulates the Flux of Reduced Substances from the Sediments of Deep Lakes. Biogeosciences 14 (13), 3275–3285. doi:10.5194/bg-14-3275-2017

CrossRef Full Text | Google Scholar

Thalasso, F., Sepulveda-Jauregui, A., Gandois, L., Martinez-Cruz, K., and Gerardo-Nieto, O., Astorga-España, M. S., et al. (2020). Sub-oxycline Methane Oxidation Can Fully Uptake CH₄ Produced in Sediments: Case Study of a Lake in Siberia. Sci. Rep. 10, 3423. doi:10.1038/s41598-020-60394-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Thottathil, S. D., Reis, P. C. J., and Prairie, Y. T. (2019). Methane Oxidation Kinetics in Northern Freshwater Lakes. Biogeochemistry 143, 105–116. doi:10.1007/s10533-019-00552-x

CrossRef Full Text | Google Scholar

Trotsenko, Y. A., and Khmelenina, V. N. (2005). Aerobic Methanotrophic Bacteria of Cold Ecosystems. FEMS Microbiol. Ecol. 53, 15–26. doi:10.1016/j.femsec.2005.02.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsutsumi, M., Iwata, T., Kojima, H., and Fukui, M. (2011). Spatiotemporal Variations in an Assemblage of Closely Related Planktonic Aerobic Methanotrophs. Freshw. Biol. 56, 342–351. doi:10.1111/j.1365-2427.2010.02502.x

CrossRef Full Text | Google Scholar

Wanninkhof, R. (2014). Relationship between Wind Speed and Gas Exchange over the Ocean Revisited. Limnol. Oceanogr. Methods 12, 351–362. doi:10.4319/lom.2014.12.351

CrossRef Full Text | Google Scholar

Wüest, A., and Lorke, A. (2003). Small-Scale Hydrodynamics in Lakes. Annual Review of Fluid Mechanics 35, 373–412. doi:10.1146/annurev.fluid.35.101101.161220

CrossRef Full Text | Google Scholar

Zakharova, L., Meyer, K. M., and Seifan, M. (2019). Trait-based Modelling in Ecology: A Review of Two Decades of Research. Ecol. Model. 407, 108703. doi:10.1016/j.ecolmodel.2019.05.008

CrossRef Full Text | Google Scholar

Zappa, C. J., McGillis, W. R., Raymond, P. A., Edson, J. B., Hintsa, E. J., Zemmelink, H. J., et al. (2007). Environmental Turbulent Mixing Controls on Air-Water Gas Exchange in Marine and Aquatic Systems. Geophys. Res. Lett. 34, L10601 1–6. doi:10.1029/2006GL028790

CrossRef Full Text | Google Scholar

Zimmermann, M., Mayr, M. J., Bürgmann, H., Eugster, W., Steinsberger, T., Wehrli, B., et al. (2021). Microbial Methane Oxidation Efficiency and Robustness during Lake Overturn. Limnol. Oceanogr. Lett. 6, 320–328. doi:10.1002/lol2.10209

CrossRef Full Text | Google Scholar