- School of Economics and Management, East China Jiaotong University, Nanchang, China
Using provincial panel data spanning from 1995 to 2020, this paper examines the nonlinear interrelationship between logistics carbon dioxide emissions and output growth. For this purpose, we conduct a nonlinear co-integration test in heterogeneous panels; our results suggests a long-run relationship between these two variables. In contrast, adjustment to the equilibrium is inherently nonlinear. Furthermore, we estimate a panel smooth transition vector error correction model. Our major contributions, as we know, are the first study confirming the existence of a dynamic mechanism between logistics carbon dioxide emissions and regional output growth and the Environmental Kuznets Curve in China. Last, the interaction between logistics carbon dioxide emissions and regional output growth varies over the output growth in Chinese provinces and autonomous regions. Our results highlight the importance of considering possible nonlinearities in analyzing output-carbon dioxide emissions causality nexus and designing energy policies.
Introduction
In recent years, global warming and environmental pollution have renewed interest in the low-carbon economy, which has primarily been discussed by the Chinese government and academic communities. China is responsible for 15% of global greenhouse gas emissions, of which CO2 emissions make up 80%.
In the past decade, the average annual growth rate of CO2 emissions has been 17.8% in China, which is at the forefront of the world (Zhao and Hu, 2013). The Chinese government pledged at the Paris Conference on Climate Changes in November 2015 that carbon dioxide emissions would peak around 2030. In April 2016, China formally ratified the Paris Agreement, and in September 2020, the 75th United Nations General Assembly vowed to take stronger action and work toward becoming carbon neutral before 2060.
However, China is still under intense pressure to reduce emissions in order to meet this target.
Logistics is a high-energy-consuming industry that also generates a significant amount of CO2 emissions. In China, the logistics sector has emerged as one of the biggest consumers of energy resources, according to Xu and Yu’s calculation of the CO2 emissions of the industry in 2020.
According to the International Energy Agency’s 2009 report “Transport, Energy, and Carbon Emissions: Towards Sustainability,” the transportation sector accounts for approximately 25% of global CO2 emissions. In light of this, all counties are working toward creating a cleaner logistics sector. To address these worries. Alinaghian and Goli (2017) proposed an uncertain integrated model for locating temporary depots in affected areas, allocating affected areas to these centres, and routing required goods through such centres.
The proposed model pursued to reduce the time required to reach the last relief centre. Goli et al. (2021) specifically address the prediction of dairy product demand to improve logistics systems for dairy product transportation, allowing for a brief consumption period, as a result of their insights into green logistics. Furthermore, Tirkolaee et al. (2022) developed a novel mathematical model based on Pareto-based algorithms to design a sustainable mask Closed-Loop Supply Chain Network during the COVID-19 outbreak for the first time. Their efforts contribute to the reduction of environmental degradation through green transportation.
Our research here is primarily connected to two strands of the literature. The first strand concerns to the existence of the Environmental Kuznets Curve, which has piqued the interest of academics, practitioners, and regulators since Kyoto Protocol was signed.
Understanding the link between CO2 emissions and economic growth helps economies in developing energy policies and sustainable energy resources. Pao and Tsai (2010) studied the relationship between pollutant emissions, energy consumption and output growth in BRIC countries. This study shows that energy consumption has a positive long-term effect on CO2 emissions, being statistically significant. In contrast, the relationship between actual output and CO2 emissions shows an inverted U-shaped relationship with a threshold income effect. Wang et al. (2011) used a data set of 28 provinces in China. They found that there is an inverted U-shaped relationship between CO2 emissions in energy consumption and output growth by a panel co-integration test. They ascribed higher per capita CO2 emissions in China to the overuse of energy resources. Using a data set from 12 countries in the Middle East and North Africa, Arouri et al. (2012) showed that energy consumption influences CO2 emissions positively in the long run. A quadratic relationship exists between actual GDP and CO2 emissions, confirming the EKC hypothesis. Based on the autoregressive distributed lag model, Baek and Kim (2013) confirmed that the EKC relationship held in South Korea over the past 40 years. Recently, Khan and Eggoh (2021) re-assessed the relationship between economic growth and pollution emissions using a large panel of 146 economies from 1990 to 2016. Their empirical findings support the existence of the Environmental Kuznets Curve hypothesis for the global sample as well as for income-specific sub-samples. Rahman et al. (2020) investigates the impact of CO2 emissions, population density, and trade openness on the economic growth of five South Asian countries from 1990 to 2017. The obtained results reveal that CO2 emissions and population density positively, and trade openness negatively affect the economic growth in South Asia. Further, Anwar et al. (2022) investigated the major determinants of CO2 emissions in Far East countries in the period of 1980–2017, finding that urbanization, economic growth and trade openness significantly determine CO2 emission in the selected countries.
Although in recent years, numerous studies have thoroughly investigated the nexus between economic growth and CO2 emissions, and concluded a positive relationship between CO2 emissions and economic growth in various degrees, many studies conclude quite different from the conventional view. Lu (2000) specified a state-space model between per capita carbon emissions and per capita GDP and found that the relationship between the two is not simply inverted U-shaped but tells a more complicated story. Choi et al. (2010) explored the EKC relationship between China, a newly industrialized country, South Korea, and Japan, a developed economy, using data from 1971 to 2006. Their findings suggest that the EKC relationship exhibits different temporal patterns across different countries, which vary according to the countries level of economic development.
The results show that China has an N-shaped curve, Japan has a U-shaped curve, and Korea has an inverted U-shaped curve. Wang (2012) conducted the most comprehensive study (98 countries involved), examining the non-linear relationship between CO2 emissions from oil and GDP while accounting for population growth. This study found that a threshold effect exists in the relationship between emissions and growth and it was concluded that the impact of CO2 emissions varies from low-income to wealthy countries. Similarly, Li and Ya (2012) investigated the long-term equilibrium relationship between the carbon emissions from China’s manufacturing, construction, and transportation industries and output growth from the standpoint of harmoniously industrial development. CO2 emissions stimulate economic growth in the short term, but their influence gradually fades and finally becomes stationary in the long term. The contribution of CO2 emissions from the transportation and construction industries to economic growth decreases initially before increasing as a result of the industrial adjustment. Muhammad (2019) examined the link between economic growth, energy consumption and CO2 emissions for the panel of 68 countries between 2001–2017, that included developed, emerging and Middle East and North Africa (MENA) countries. Economic growth in developed and emerging countries increased energy consumption, while declining in MENA countries; due to an increase in energy consumption CO2 emissions increased in all countries.
Adebayo et al. (2021) re-examine the relationship between urbanization, CO2 emissions, gross capital formation, energy use, and economic growth in South Korea using data from 1965 to 2019, finding that CO2 emissions trigger economic growth and that the energy-induced growth hypothesis is validated, but the EKC relationship collapses. Sun et al. (2021) examined the dynamic relationship between carbon emissions, trade, energy consumption, urbanization, and output growth from 1992 to 2015. The Environmental Kuznets Curve (EKC) assumption is confirmed only in three panels, and output growth has a significant positive effect on environmental pollution in all panels.
The second strand is associated with the nexus between CO2 emissions and output growth in the logistics industry. Abbes and Bulteau (2018) investigates the dynamic effects of GDP growth, motorization rate, transport pollution coefficient, and energy intensity on CO2 emissions from the transport sector in Tunisia. In the long run, the statistically insignificant effects of per capita GDP on transport carbon emissions in the long run suggest that these emissions can be controlled without disrupting economic growth.This can be accomplished by developing short-sea shipping between major cities in order to reduce traffic congestion and carbon emissions.
Liu et al. (2019) examine the impact of income and region on environmental logistics performance index scores and discuss the potential for reduction in oil consumption intensity and carbon intensity in those countries. The main finding is that the environmental logistics performance index generally perform well in the environmental logistics performance index.
The environmental logistics performance index, like the logistics performance index, is closely related to income and region. Similar to the characteristics of the logistics performance index, the environmental logistics performance index is also closely related to income and region. Liu et al. (2021) employ a Global Malmquist-Luenberger Index approach to evaluate the green productivity growth of road transportation in China at the provincial level based on the Data Envelopment Analysis and Directional Distance Function, finding that, at the regional level, the road transportation industries in Western and Central China achieved green productivity growth because of the catch-up effect and the economies of scale, respectively. Wang (2021) confirms that, with the growth of GDP per capita, the degree of coupling and coordination between the logistics and financial industries has promoted the increase of carbon emissions in various regions. Still, the promotion effect is an inverted U-shaped trend that first increases and then decreases. Recently, Awan et al. (2022) investigate the nexus between transport sector-based carbon dioxide emissions, economic growth, innovation, and urbanization. Furthermore, the study analyzes the Environmental Kuznets Curve (EKC) hypothesis for the transport sector in balanced panel data of 33 high-income countries from 1996 to 2014 using a robust and novel quantile methodology. Findings reveal the validity of an N-shape EKC curve for the transport sector. The study recommends shifting to public transportation systems to help curb environmental degradation through green transportation. Aydin et al. (2022) investigate the impact of energy intensity on the relationship between logistic growth and environmental pollution in 45 countries that support the One Belt One Road project proposed to revitalize the historical Silk Road between 2007 and 2018. According to the findings of the study, the relationship between logistics growth and environmental pollution is not linear, and energy intensity level plays an important role in this relationship (Tirkolaee et al., 2022). Hassan et al. (2022) examine the dynamic linkage among nuclear energy, public service transportation, real income, and innovative technology with CO2 emissions in China. Results show that innovative technology mitigates environmental pollution. As a result, different perspectives from previous studies lead to different theoretical insights into the relationship between output growth and CO2 emissions, and no definitive policy framework exists to address the escalating problem of greenhouse gas emissions. Furthermore, in the logistics sector, the existing literature focuses primarily on different aspects of logistics such as transportation (Fleisher and Chen, 1997; Lu et al., 2019), and telecommunication (Jing and Ab-Rahim, 2020).
However, the literature lacks a deeper examination of the logistics sector’s output using a large panel dataset. Most of relevant studies focus on the relationship between energy consumption and output growth at a national level. Yuan et al. (2008) discovered a co-integration relationship between energy consumption and output growth between 1978 and 2004. Other studies concentrate on a large number of countries at the same time. Li et al. (2021) investigate the economic and environmental impacts of green logistics performance for One Belt and Road Initiative (OBRI) countries from 2007 to 2019. According to the findings, green logistics performance improves OBRI economic growth while enhancing environmental pollution in these countries. Their studies, however, assume that model parameters do not change over time and, as a result, ignore China’s heterogeneity across regions, which is one of the main causes of estimation bias. To overcome the limitations of their studies, we use the panel smooth transition regression model (PSTR) proposed by Gonzalez et al. (2005). This model is lent to analyze the relationship between CO2 emissions and output growth of the logistics sector in different regions to investigate the heterogeneity and time-varying parameters of the PSTR model across regions. It is of great significance to clarify the debate on whether an EKC relationship exists between CO2 emissions of the logistics sector and output growth based on our econometric framework.
Econometric framework
Nonlinear panel co-integration test
Consider the following panel regression model:
where
If the error term
Where
Furthermore, assume that
Imposing a constraint on Eq. 4 that
The test of co-integration is based on the parameter
Under null hypothesis, the first-order Taylor approximation yields the following auxiliary regression equation:
where
In practice, an appropriate lag order should be selected for the auxiliary regression model Eq. 6. Following Uçar and Omay (2009), the average of the co-integration test statistics is first taken over the entire panel data, and then the nonlinear panel co-integration test statistics can be computed. The standardized
where
According to Pesaran (2007), we use the t statistic in Eq. 7 to compute the panel unit root test statistic, and
A common obstacle encountered in panel regression is the presence of cross-section interdependence, which invalidate traditional unit root and co-integration tests. This paper follows the methodology proposed by Pesaran (2004), whose test statistic is represented as:
where
Nonlinear panel smooth transition vector error correction model
According to Gonzalez et al. (2005), we specify the panel smooth transition vector error correction model (PSTRVEC) as follows:
for
To model regime-shifts in the short-run and long-run, Gonzalez et al. (2005) and Omay and Kan (2010) consider the employment of the following logistic transition function:
where
For
Firstly, specify an appropriate linear panel model which fits the selected data excellently; Secondly, test null hypothesis of a linear panel model. If linearity is rejected, select an appropriate transition variable
In the second step above, the complexity of testing null of linearity results from unidentified ‘notorious’ parameters under null hypothesis. To overcome this problem, the transition function may be replaced with the appropriate Taylor approximation (Luukkonen et al., 1988). For example, the
where
where
When the transition variable
The methodology to estimate the panel smooth transition vector error correction model
The PSTRVEC model can be estimated using nonlinear least square methodology once the transition variable and the appropriate function form is selected, and the optimization algorithm requires that the initial values of the model parameters be chosen accurately. And then a two-dimensional grid search technique is adopted to search for the initial values of parameters
Empirical results
In this section, we use the annual dataset of 30 provinces and autonomous regions in Mainland China except for Tibet during the sample period from 1995 to 2020, and apply empirical techniques specified in the previous section to examine the dynamic interrelationship between logistics CO2 emissions and output growth. Using the gross national product data of provinces and autonomous regions to measure the output (
The panel unit root test and panel co-integration test
We first test the stationarity of output (
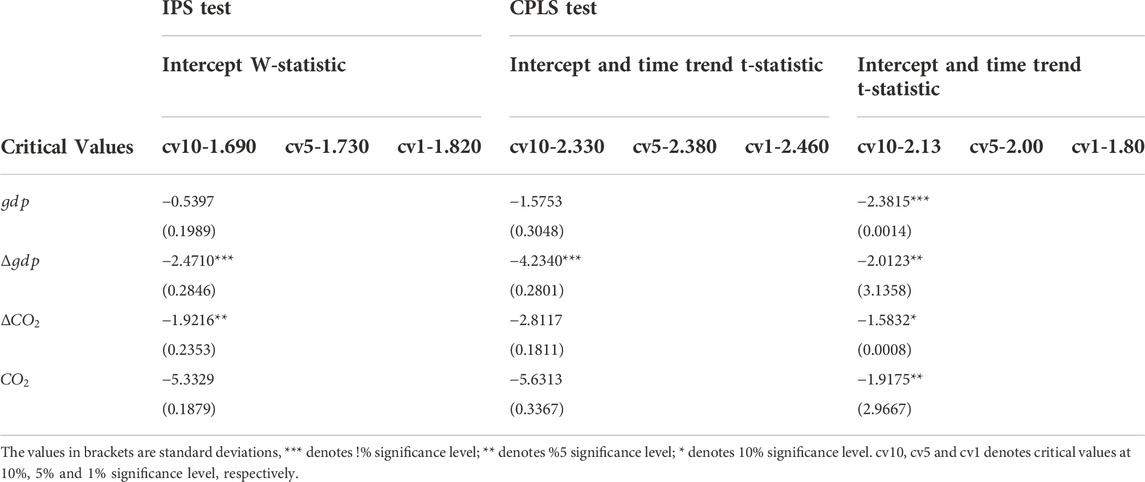
Closed in parentheses beneath estimated coefficients in Table 2 are their companion t-statistics. We collect the residuals obtained from panel regression equations and implement a nonlinear co-integration test based on Eq. 8 and the linear co-integration test proposed by Pedroni (1999). These tests indicate a statistically significant cross-section dependence [measured by the CD statistic, (Pesaran, 2004)]. Indeed, the CD statistic of the CO2 emissions (after being taken logarithm) is 90.286 (the companion p-value is 0.000); The CD statistic for the logarithm of output is 94.252 (the companion p-value is 0.000). In the presence of cross-section dependence, the bootstrap algorithm should be used to obtain the p values associated with the two test statistics, which are shown in Table 3.
Although the IPS test shows that there is no co-integration relationship between CO2 emissions and output of the logistics industry, the CPLS test shows the presence of co-integration between these two series. We estimate the nonlinear panel error correction model expressed by Eq. 10 allowing for nonlinear co-integration. Before estimating the PSTRVEC model, we estimate an appropriate linear model and perform linearity diagnosis first. The optimal lag orders of linear models are selected according to the AIC criterion, and parameter estimates are shown as follows:
*** denotes significance at 1% level, ** denotes significant level at 5%, * denotes significance at 10% level. The values in brackets are standard deviations.
The coefficients associated with error correction terms have correct signs in both equations and are statistically significant. Their negative coefficients indicate that a reverse adjustment dynamics exits between output growth and CO2 emissions growth in the logistics sector. when they converge to the long-term equilibrium. Furthermore, other coefficients are statistically significant and have the expected signs.
Results of linearity tests
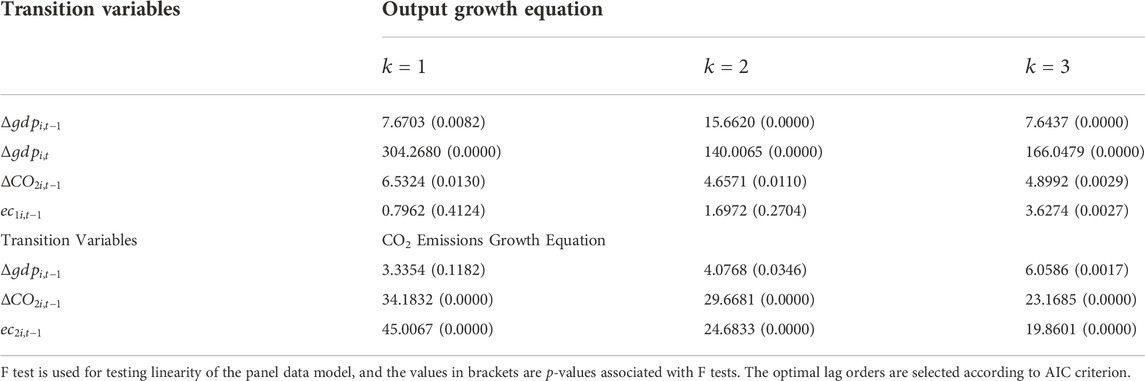
Although the linear models can achieve expected estimates to a certain extent, we test the linearity underlying the regression models in Eq. 12 yet on the safe side. For
As Table 4 shows, the null hypothesis of linearity can be rejected at the traditional significance level for both the output growth equation and the CO2 emissions growth equation. As many studies show, there may be many reasons for the nonlinearity between output growth and CO2 emissions growth. Specifically, identified nonlinearity arises mainly from output growth (i.e. different phases of the economic cycle). However, in CO2 emissions growth equation, the nonlinear relationship is mainly caused by CO2 emissions growth. Considering that the nonlinear relationship in different equations attributes to different transition variables, we choose output growth and CO2 emissions growth as the transition variables in two equations respectively, and implement a series of
The estimates of the panel smooth transition vector error correction model
Table 5 shows that among all F tests, the companion p-value of
As analyzed by the previous subsection, the relationship between output growth and CO2 emissions growth varies over different phases of business cycle. Hence, it is reasonable to apply the estimated logistic transition function below,
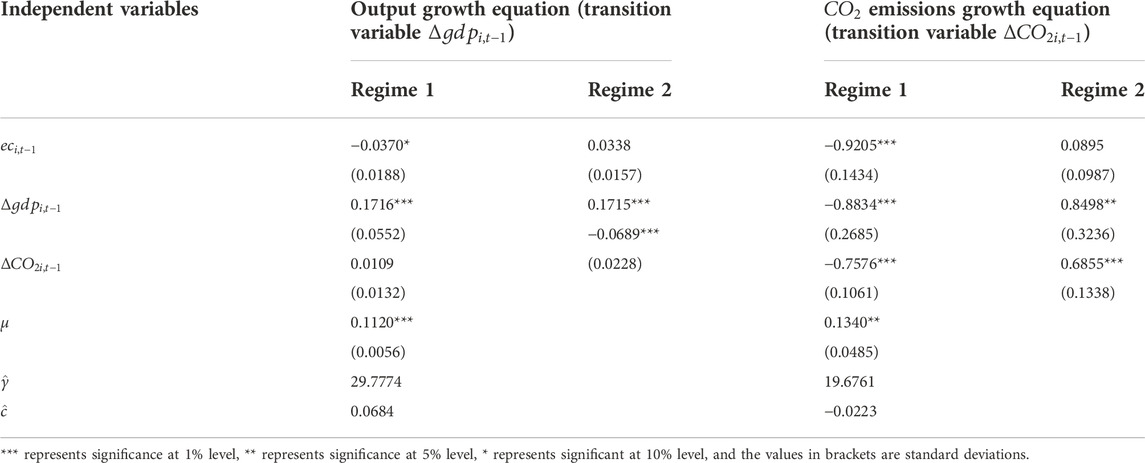
to two PSTRVEC equations, and estimated results are shown in Table 7.
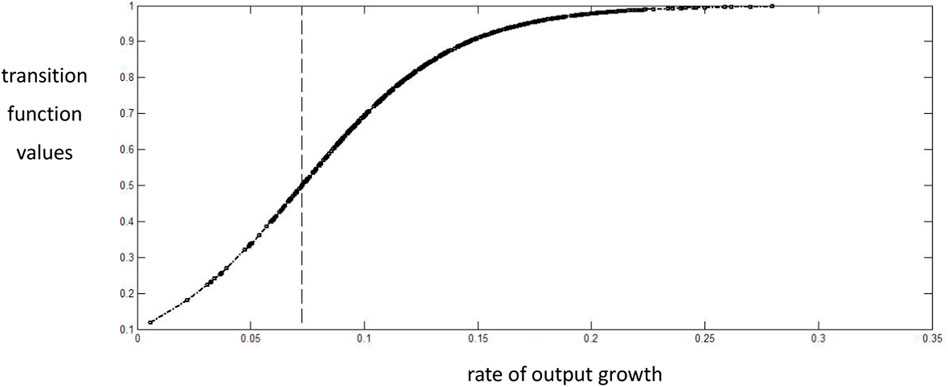
As discussed above, the regime shifts of the PSTRVEC model are captured by transition function
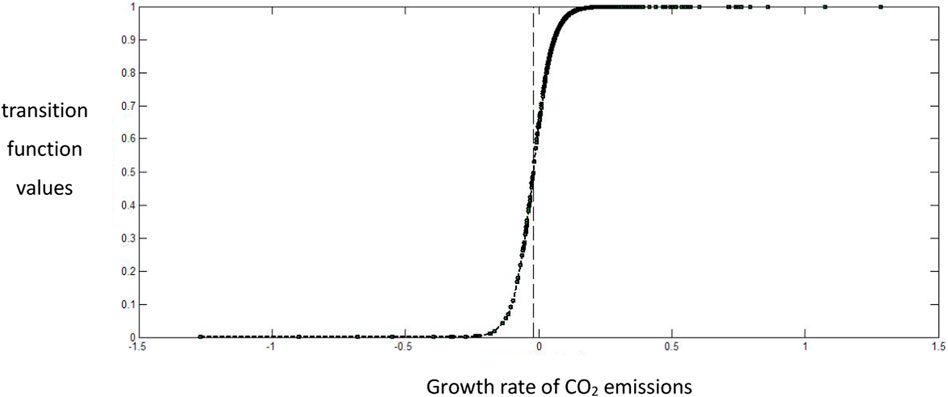
FIGURE 1. The scatter graph of the estimated transition function in the CO2 emissions growth equation of the logistics sector.
We discuss the estimated coefficients of the PSTRVEC model Eq. 10. First, consider the output growth equation. When the economy is in a low output growth phase (i.e. when the output growth rate is lower than the mid-point value of the transition function,
The mechanism of automatic stability is essential for the economy to escape from the low output growth phase. The estimated coefficient for CO2 emissions growth in the logistics sector is 0.0109, which is statistically insignificant, implying that output growth increases as CO2 emissions growth soars in the phase of the lower regime of output growth, although the evidence is (statistically) weak. When the economy is in the expansionary phase (i.e. when the output growth rate is higher than the midpoint value of regime transition function,
Now consider the CO2 emissions growth equation. When CO2 emissions growth is at a low level, the estimated coefficient of the error correction term is equal to −0.9205, which is expected and statistically significant, indicating that the relationship between output growth and CO2 emissions growth can be adjusted to a long-term equilibrium in the opposite direction. When CO2 emissions growth is in a higher regime, the estimated coefficient of the error correction term is −0.831 (= −0.9205 + 0.0895), and its sign is as still expected. There exists a automatic stability mechanism between economic growth and CO2 emissions growth such that the economy approaches to a long-term equilibrium, but at slower speed than in the lower regime of CO2 emissions growth. This finding is very informative, implying the necessity of macroeconomic intervention once CO2 emissions of the logistics industry are at a higher growth level. In the lower regime of CO2 emissions growth, the estimated coefficient of output growth is −0.8834, which is statistically significant. In comparison, in the higher regime of CO2 emissions growth, the estimated coefficient of output growth becomes −0.0336 (= −0.8834 + 0.8498). This finding indicates that, when CO2 emissions growth is low, an increase in output growth might lead to a decrease in CO2 emissions growth in the logistics sector, because output growth benefits CO2 emissions reduction in the long term. However, if the CO2 emissions growth is in a higher regime, the effect of output growth on CO2 emissions reduction will be substantially reduced (shown by the fact that, when CO2 emissions growth is in higher regime, the estimated coefficient is −0.0336).
When taking output growth
Conclusion and implications
We use a panel dataset from 30 provinces and autonomous regions examining the dynamic relationship between CO2 emissions growth and output growth in the logistics sector over the period 1995–2020. The panel co-integration test is implemented using a nonlinear smooth transition regression model. In the presence of nonlinear co-integration between two variables considered, the PSTRVEC model is specified and estimated. The PSTRVEC model can explore the nonlinear and asymmetric dynamic relationship between CO2 emissions growth and output growth in the logistics sector. Several findings can be drawn from previous empirical analyses:
Firstly, only when the possible asymmetric relationship between CO2 emissions growth and output growth of the logistics sector is considered, can we identify a nonlinear co-integration underlying the dynamic path approaching to their long-term equilibrium state. This empirical finding suggests that an emissions reduction policy will have an asymmetric impact on China’s output growth of the logistics industry.
The green logistics performance significantly impacts on output growth, but when output growth rounds the critical point, the impacts become positive. In the logistics sector, CO2 emissions growth and output growth react differently to the deviation from the equilibrium path approaching their stable state in a different way. Hence, such an automatic stability process is very complex. This adjustment mechanism depends on which phases output growth and CO2 emissions growth situate, respectively. In the higher regime of output growth, the automatic stability mechanism is weaker than in the lower phase of output growth. When CO2 emissions growth in the logistics industry is at a higher level, the speed of adjustment to the equilibrium path is much slower. In addition, from a cross-sectional perspective, the relationship between CO2 emissions growth and output growth in the logistics sector varies over geographical regions, depending on different levels of output growth. In developed regions, the adjustment speed of the equilibrium between CO2 emissions growth and output growth is slower, and the response of the output growth rate to the equilibrium deviation from the equilibrium sate is lower than in less developed regions.
Secondly, as the nonlinear panel unit root test shows, the dynamic relationship between CO2 emissions growth and output growth in the logistics industry is nonlinear. We are able to reject null hypothesis of a linear relationship when using three alternative transition variables. This finding suggests that researchers and policy makers must take into account the possible non-linear relationship between CO2 emissions growth and output growth in the logistics industry. In the output growth equation, the null hypothesis of linearity is more convincingly rejected when the lagged output growth is used as a transition variable. In the CO2 emissions growth equation, when the lagged CO2 emissions growth is used as a transition variable, the null hypothesis of a linear relationship is more convincingly rejected. These findings suggest that the EKC hypothesis holds in China. In the lower phase of output growth, the CO2 emissions growth of the logistics industry is pro-cyclical, while when the output growth rounds a critical point, the CO2 emissions growth might become counter-cyclical.
Empirical results can appeal to policymakers to a more integrated and sustainable perspective, which gives higher priority to economic growth by reducing CO2 emissions in the logistics sector. When exploring the relationship between CO2 emissions growth and output growth in logistics sector, we find that the traditional linear relationship is not suitable. Our conclusions are important for policy authorities to consider potential asymmetries. The automatic stability mechanism of the dynamic relationship between CO2 emissions and output growth in logistics industry is weaker during periods of higher output growth (or developed regions), indicating that China can conduct energy conservation policies to reduce CO2 emissions in the logistics industry without worrying about damaging the long-term output growth. Energy conservation policies for CO2 emissions reduction should not only limit the adverse effect on output growth in the short run, but also not harm output growth in long-term. In addition, we find that, when the initial output growth is relatively low, the output growth does not increase the CO2 emissions of the logistics industry in the short term at all. However, in the long run, this is another story. In different output growth stages and different regions, the relationship between CO2 emissions growth and output growth in the logistics industry reveals different patterns, which requires the government to consider regional gaps when designing energy saving and emission reduction policies. The Chinese government should focus on reducing CO2 emissions of the logistics industry in economically developed areas, and formulate measures in favor of those developed areas and green logistics performance.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
In this article JW proposed the research ideas, formed the overall research goal, and completed the writing. Review and revision of the manuscript. He is the first to study the Nonlinear Dynamic Interrelationship between CO2 Emissions and Output Growth in the Logistics Sector.
Funding
We acknowledge financial support from the research project “Research on Parameter dentification and Application of DSGE Models: Allowing for Indeterminacy” (Approval Number: 71863008) sponsored by National Natural Science Foundation of China, and from the research project “A Research on Bias Correction of Long Memory Semiparametric Estimators and Application of ARFIMA Models under High-Frequency Cantagion” (Approval Number: 72263010) sponsored by National Natural Science Foundation of China.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1In Eq. 1,
References
Abbes, S., and Bulteau, J. (2018). Growth in transport sector CO2 emissions in Tunisia: An analysis using a bounds testing approach. Int. J. Glob. Energy Issues 41 (1-4), 176–197. doi:10.1504/ijgei.2018.092334
Adebayo, T. S., Awosusi, A. A., Kirikkaleli, D., Akinsola, G. D., and Mwamba, M. N. (2021). Can CO2 emissions and energy consumption determine the economic performance of South Korea? A time series analysis. Environ. Sci. Pollut. Res. 28 (29), 38969–38984. doi:10.1007/s11356-021-13498-1
Alinaghian, M., and Goli, A. (2017). Location, allocation and routing of temporary health centers in rural areas in crisis, solved by improved harmony search algorithm. Int. J. Comput. Intell. Syst. 10, 894–913. doi:10.2991/ijcis.2017.10.1.60
Arouri, M. E., Youssef, A., M’henni, H., and Rault, C. (2012). Energy consumption, economic growth and CO2 emissions in Middle East and North african countries. Energy Policy 45, 342–349. doi:10.1016/j.enpol.2012.02.042
Awan, A., Alnour, M., Jahanger, A., and Onwe, J. C. (2022). Do technological innovation and urbanization mitigate carbon dioxide emissions from the transport sector? Technol. Soc. 71, 102128. doi:10.1016/j.techsoc.2022.102128
Aydin, C., Aydin, H., and Altinok, H. (2022). Does the level of energy intensity matter in the effect of logistic performance on the environmental pollution of OBOR countries? Evidence from PSTR analysis. J. Environ. Plan. Manag., 1–19. doi:10.1080/09640568.2022.2030685
Baek, J., and Kim, H. S. (2013). Is economic growth good or bad for the environment? Empirical evidence from Korea. Energy Econ. 36, 744–749. doi:10.1016/j.eneco.2012.11.020
Cerrato, M., de Peretti, C., Larsson, R., and Sarantis, N. (2009). A nonlinear panel unit root test under cross section dependence, working papers 2009_28. Glasgow, United Kingdom: Department of Economics, University of Glasgow.
Choi, E., Heshmati, A., and Yongsung, C. (2010). An empirical study of the relationships between CO2 emissions, economic growth and openness. IZA Discussion Paper No. 5304 SSRN Available at: https://ssrn.com/abstract=1708750. doi:10.2139/ssrn.1708750
Fleisher, B. M., and Chen, J. (1997). The coast-noncoast income gap, productivity and regional economic policy in China. J. Comp. Econ. 25 (2), 220–236. doi:10.1006/jcec.1997.1462
Goli, A., Khademi-Zare, H., Tavakkoli-Moghaddam, R., Sadeghieh, A., Sasanian, M., and Kordestanizadeh, R. M. (2021). An integrated approach based on artificial intelligence and novel meta-heuristic algorithms to predict demand for dairy products: A case study. Netw. Comput. neural Syst. 32 (1), 1–35. doi:10.1080/0954898x.2020.1849841
Gonzalez, A., Teräsvirta, T., and Dijk, D. (2005). Panel smooth transition regression model. Sydney, NSW: Quantitative Finance Research Centre, University of Technology.
Hansen, B. (1999). Threshold effects in non-dynamic panels: Estimation, testing and inference. J. Econ. 93 (2), 345–368. doi:10.1016/s0304-4076(99)00025-1
Hassan, S. T., Khan, D., Zhu, B., and Batool, B. (2022). Is public service transportation increase environmental contamination in China? The role of nuclear energy consumption and technological change. Energy 238, 121890. doi:10.1016/j.energy.2021.121890
IPCC (2006). “Summary for policymakers,” in Climate change: The physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change [stocker, T.F., D. Qin, G.-K. Plattner, M.
Jing, A. H. Y., and Ab-Rahim, R. (2020). Information and communication technology (ICT) and economic growth in ASEAN-5 countries. J. Public Adm. Governance 10 (2), 2033. doi:10.5296/jpag.v10i2.16589
Kapetanios, G., Shin, Y., and Snell, A. (2003). Testing for a unit root in the nonlinear STAR framework. J. Econ. 112, 359–379. doi:10.1016/s0304-4076(02)00202-6
Kapetanios, G., Shin, Y., and Snell, A. (2006). Testing for cointegration in nonlinear smooth transition error correction models. Econom. Theory 22 (2), 279–303.
Khan, M., and Eggoh, J. (2021). Investigating the direct and indirect linkages between economic development and CO2 emissions: A PSTR analysis. Environ. Sci. Pollut. Res. 28 (8), 10039–10052. doi:10.1007/s11356-020-11468-7
Kim, T.-H., Pfaffenzeller, N. E. S., Rayner, T., and Newbold, P. (2003). Testing for linear trend with application to relative primary commodity prices. J. Time Ser. Anal. 24, 539–551.
Li, H., and Ya, K. (2012). Research on the relationship between Industrial carbon emission and economic development in China. Macroeconomics (11), 46–52.
Li, X., Sohail, S., Majeed, M. T., and Ahmad, W. (2021). Green logistics, economic growth, and environmental quality: Evidence from one belt and road initiative economies. Environ. Sci. Pollut. Res. 28 (24), 30664–30674. doi:10.1007/s11356-021-12839-4
Liu, C., Ji, W., AbouRizk, S. M., and Siu, M. F. (2019). Equipment logistics performance measurement using data-driven social network analysis. J. Constr. Eng. Manag. 145 (5), 04019033. doi:10.1061/(asce)co.1943-7862.0001659
Liu, H., Yang, R., Wu, D., and Zhou, Z. (2021). Green productivity growth and competition analysis of road transportation at the provincial level employing Global Malmquist-Luenberger Index approach. J. Clean. Prod. 279, 123677. doi:10.1016/j.jclepro.2020.123677
Lu, H. (2000). An analysis on China’s economy development and on state space model of environment —take air pollution as an example. J. Finance Econ. (10), 53–59.
Lu, Q., Liu, H., Yang, D., and Liu, H. (2019). Effects of urbanization on freight transport carbon emissions in China: Common characteristics and regional disparity. J. Clean. Prod. 211, 481–489. doi:10.1016/j.jclepro.2018.11.182
Luukkonen, R., Saikkonen, P., and Teräsvirta, T. (1988). Testing linearity against smooth transition autoregressive models. Biometrika 75, 491–499. doi:10.1093/biomet/75.3.491
Maki, D. (2010). An alternative procedure to test for cointegration in STAR models. Math. Comput. Simul. 80, 999–1006. doi:10.1016/j.matcom.2009.12.003
Muhammad, B. (2019). Energy consumption, CO2 emissions and economic growth in developed, emerging and Middle East and North Africa countries. Energy 179, 232–245. doi:10.1016/j.energy.2019.03.126
Omay, T., and Kan, E. Ö. (2010). Re-examining the threshold effects in the inflation–growth nexus with cross-sectionally dependent non-linear panel: Evidence from six industrialized economies. Econ. Model. 27 (5), 996–1005. doi:10.1016/j.econmod.2010.04.011
Pao, H-T., and Tsai, C-M. (2010). CO2 emissions, energy consumption and economic growth in BRIC countries. Energy Policy 38, 7850–7860. doi:10.1016/j.enpol.2010.08.045
Pedroni, P. (1999). Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxf. Bull. Econ. Stat. 61, 653–670. doi:10.1111/1468-0084.61.s1.14
Pesaran, M. H. (2007). A simple panel unit root test in the presence of cross-section dependence. J. Appl. Econ. Chichester. Engl. 22 (2), 265–312. doi:10.1002/jae.951
Pesaran, M. H. (2004). “General diagnostic tests for cross-section dependence in panels,” in Cam-bridge working papers in economics 0435 (UK: University of Cambridge).
Rahman, M. M., Saidi, K., and Mbarek, M. B. (2020). Economic growth in South Asia: The role of CO2 emissions, population density and trade openness. Heliyon 6 (5), e03903. doi:10.1016/j.heliyon.2020.e03903
Sun, Y., Li, M., Zhang, M., Khan, H. S. U. D., Li, J., Sun H., Z., et al. (2021). A study on China’s economic growth, green energy technology, and carbon emissions based on the Kuznets curve (EKC). Environ. Sci. Pollut. Res. 28 (6), 7200–7211. doi:10.1007/s11356-020-11019-0
Teräsvirta, T. (1994). Specification, estimation, and evaluation of smooth transition autoregressive models. J. Am. Stat. Assoc. 89, 208–218. doi:10.2307/2291217
Tirkolaee, E. B., Goli, A., Ghasemi, P., and Goodarzian, F. (2022). Designing a sustainable closed-loop supply chain network of face masks during the COVID-19 pandemic: Pareto-based algorithms. J. Clean. Prod. 333, 130056. doi:10.1016/j.jclepro.2021.130056
Uçar, N., and Omay, T. (2009). Testing for unit root in nonlinear heterogeneous panels. Econ. Lett. 104 (1), 5–8. doi:10.1016/j.econlet.2009.03.018
Wang, K. M. (2012). Modelling the nonlinear relationship between CO2 emissions from oil and economic growthEmissions from Oil and Economic Growth. Econ. Model. 29, 1537–1547. doi:10.1016/j.econmod.2012.05.001
Wang, L. (2021). Research on logistics carbon emissions under the coupling and coordination scenario of logistics industry and financial industry. Plos one 16 (12), e0261556. doi:10.1371/journal.pone.0261556
Wang, S. S., Zhou, D. Q., Zhou, P., and Wang, Q. W. (2011). CO2Emissions, energy consumption and economic growth in China: A panel data analysis. Energy Policy 39, 4870–4875. doi:10.1016/j.enpol.2011.06.032
Yuan, J. H., Kang, J. G., Zhao, C. H., and Hu, Z. G. (2008). Energy consumption and economic growth: Evidence from China at both aggregated and disaggregated levels. Energy Econ. 30 (6), 3077–3094. doi:10.1016/j.eneco.2008.03.007
Keywords: logistics carbon dioxide, emissions, economic growth, environmental kuznets curve, nonlinear co-integration
Citation: Wu J (2022) A study of the nonlinear dynamic interrelationship between CO2 emissions and logistics sector output growth. Front. Environ. Sci. 10:1066960. doi: 10.3389/fenvs.2022.1066960
Received: 11 October 2022; Accepted: 15 November 2022;
Published: 09 December 2022.
Edited by:
Reza Lotfi, Yazd University, IranReviewed by:
Gerhard-Wilhelm Weber, Poznań University of Technology, PolandAlireza Goli, University of Isfahan, Iran
Copyright © 2022 Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jinshun Wu, d3VqaW5zaHVuNjcxN0AxNjMuY29t
 Jinshun Wu
Jinshun Wu