q-Rung orthopair fuzzy hypersoft ordered aggregation operators and their application towards green supplier

Green Supply Chain Management (GSCM) is essential to ensure environmental compliance and commercial growth in the current climate. Businesses constantly look for fresh concepts and techniques for ensuring environmental sustainability. To keep up with the new trends in environmental concerns related to company management and procedures, Green Supplier Selection (GSS) criteria are added to the traditional supplier selection processes. This study aims to identify general and environmental supplier selection criteria to provide a framework that can assist decision-makers in choosing and prioritizing appropriate green supplier selection. The development and implementation of decision support systems aimed to solve these difficulties at a rapid rate. In order to manage inaccurate data and simulate decision-making problems. Fuzzy sets introduced by Zadeh, are a useful technique to handle the imperfectness and uncertainty in different problems. Although fuzzy sets can handle incomplete information in different real worlds problems, but its cannot handle all type of uncertainty such as incomplete and indeterminate data. Therefore different extensions of fuzzy sets such as intuitionistic fuzzy, pythagorean fuzzy and q-rung orthopair fuzzy sets introduced to address the problems of uncertainty by considering the membership and non-membership grade. However, these concepts have some shortcomings in the handling uncertainty with sub-attributes. To overcome this difficulties Khan et al. developed the structure of q-rung orthopair fuzzy hypersoft sets by combining q-rung orthopair fuzzy sets with hypersoft sets. A remarkable and beneficial research work is done in the field of q-rung orthopair fuzzy hypersoft sets, and then we think about the application. In this paper, we use the structure of q-rung orthopair fuzzy hypersoft in multi-criteria supplier selection problems. For this, we present aggregation operator to solve multi-criteria decision-making (MCDM) problems with q-rung orthopair fuzzy hypersoft (q-ROFH) information, known as ordered weighted geometric aggregation operator. Since the uncertainty and vagueness is an unavoidable feature of multi-criteria decision-making problems, the proposed structure can be a useful tool for decision making in an uncertain environment. Further, the expert opinions were investigated using the multi-criteria decision-making (MCDM) technique, which helped identify interrelationship and causal preference of green supplier evaluation aspects that used aggregation operators. Finally, a numerical example of the proposed method for the task of Green Supplier Selection is presented.

1 Introduction

Green innovation is an environmental management concept that aims to reduce the deterioration of the environment caused by urban sprawl, industrial waste, and unsustainable use of resources. Nowadays, the government and the public are more concerned about the environment. Several government regulations and GI systems have been implemented to protect the environment. As a result, the study of “green supply chain networks”, also known as environmentally friendly supply chains, has gained popularity. It raises specific research questions regarding decisions regarding the product life cycle, inventory, refund procedures, channel conflicts, and coordination information (Hall and Vredenburg, 2003). There are enough products that are well-suited for green innovation. A supply chain network can also enhance green innovation in several ways. Instead of using polyester and polyurethane to make different products such as the textile industry, cold drink companies, and shoe companies can produce them with friendly environmental materials that are easier to recycle or dispose of after use. The objective of the present study is to determine the ideal green innovation level of the product in order to maximize the income of players and minimize the damage caused to consumers. In real life situations, it is impossible to find out the production of environmentally friendly and less harmful green innovative products under uncertain environment and to overcome such glitches. Many researchers used the parameters. Recently, environmental pollution and resource shortages have become global concerns of great importance. In order to meet the urgent needs of resource conservation and environmental friendliness, modern enterprise production management must focus on finding a balance between economic benefits and ecologically sustainable development (Gegovska et al., 2020; Qu et al., 2020). In 2018, Banaeian et al, (2018) discussed green supplier selection by using different techniques of fuzzy group decision. Mabrouk (Mabrouk, 2021) used the determinants of supplier selection process with green consideration. Also analyzed the collection of factors from existing literature of green supplier. In addition there are some studies that use the green supplier’s company as the standard for selecting supplier (Badi and Pamucar, 2020; Zhang et al., 2022). Further, some researchers (Erceg and Mularifović, 2019; Pamucar, 2020) used different techniques to select supplier by social, economic and environmental practices.Decision-making technique is used to choose the best option from a range of viable possibilities, each of which contains several criteria. Owing to time restrictions and the lack of understanding of the problem domain, decision makers usually describe their choices using verbal descriptions and ranges rather than specific facts or numbers. Many researchers propose employing fuzzy logic in MCDM scenarios in order to overcome this issue. Zadeh introduced the theme of fuzzy logic to create human logic from incomplete and imprecise information by defining ambiguous statements (Zadeh, 1965; 1973). Moreover, fuzzy logic may also incorporate information from human experience and provide it with an engineering perspective so that it can govern and create ambiguous systems with uncertainty (Siddique and Adeli, 2013). Therefore, the amount of uncertainty in the decision-making process increases when fuzzy logic is added to MCDM tools. As a result, the decision-making outcomes become more accurate and practical (Yang et al., 2017). The earliest use of fuzzy numbers in MCDM was the fuzzy sets theory, which Bellman and Zadeh (Bellman and Zadeh, 1970) proposed. Due to the ambiguity of decision -makers’ preferences, this notion was created to solve MCDM challenges. Zadeh’s fuzzy sets theory deals only with membership grade.Later, Atanassov, 1986) introduced the notion of the intuitionistic fuzzy set (IFS) in 1986. Since then, real-world MCDM issues and challenges have frequently been addressed using the IFS concept. As IFS deals with both positive and negative membership grade, but only if the sum is less than or equal to 1. In 2002 De et al, (2000) developed some operations on intuitionistic fuzzy sets. In 2011, Wang and Liu, 2011) proposed different operations on IFS and developed some aggregation operators by using the basic operational laws. Also developed multi-attribute decision making (MADM) problem. Many researchers (Li, 2005; Liu and Wang, 2007; Xu, 2011) used intuitionistic fuzzy sets in decision making problems.It is important to keep in mind that the sum of membership and non-membership grades when exceeds 1, then IFS does not fulfill the condition. Alternatively, the Pythagorean fuzzy set (PFS) concept, which is a generalization of IFS, introduced by Yager and Abbasov, (2013). Here, the alternative’s membership grade and non-membership grade must fulfill the condition that the square sum of both the membership and non-membership grades are equal to or less than 1. Peng and Yang, (2015) developed some results on pythagorean fuzzy sets. In 2018 Li and Zeng, (2018) proposed a variety of distance measures for pythagorean fuzzy sets and pythagorean fuzzy numbers. Many researchers developed different aggregation operators under pythagorean fuzzy environment, Peng and Yuan, (2016) Pythagorean fuzzy point aggregation operators, Akram et al, (2019) Pythagorean Dombi fuzzy aggregation operators, Wei and Lu, (2018) Pythagorean fuzzy power aggregation operators.Yager, (2016) introduced the theme of generalized orthopair fuzzy sets which is also known as q-rung orthopair fuzzy set.Molodtsov, (1999) suggested the idea of soft set theory, which was completely a new technique for describing uncertainty which traditional mathematical tools cannot handle. Later, Maji et al, (2001) created the fuzzy structure of the soft set by merging the fuzzy set and the soft set. In order to solve decision-making problems, Kong et al, (2008) Kong et al, (2009) used the soft set theoretic technique. Majumdar and Samanta, (2011), have investigated the problem of soft and fuzzy soft sets in terms of similarity measure. Since then, the structures of fuzzy soft sets have been actively used by many researchers, and many studies have also been added to the literature (Feng et al., 2008; Ahmad and Kharal, 2009; Yang et al., 2009; Jiang et al., 2010).Progressively, Smarandache, (2018) developed a novel method for dealing with uncertainties. The soft set was converted into a hypersoft set (HSS) by generalising functionality into a multi-decision function. Subsequently, the HSS theory garnered considerable interest from researchers (Saqlain et al., 2020a; Saqlain et al., 2020b; Gayen et al., 2020; Martin and Smarandache, 2020; Saeed et al., 2020). Furthermore Rahman et al, (2022a) proposed the decision-making methods for possibility intuitionistic fuzzy hypersoft sets (IFHSS) based on the similarity measure. Zulqarnain et al, (2020); (2021a) proposed decision making technique under IFHS environment based on correlation coefficient and aggregation operators. Rahman et al, (2022b) proposed innovative MCDM method employing a well-established method for suppler selection in the construction sector with a rough approximation of the fuzzy hypersoft set (FHS). Zulqarnain et al, (2021b) extended the impression of the IFHSS to Pythagorean fuzzy hypersoft sets (PFHSSs). The decision support model for the diagnosis of COVID-19 patients was reported by Saeed et al, (2022) using a complex fuzzy hypersoft set (CFHS). The interval-valued complex fuzzy hypersoft set (IVCFHS) was first introduced by Rahman et al, (2021), with a few basic operations. Zulqarnain et al, (2021b) developed the correlation-based technique for order performance by similarity to ideal solution (TOPSIS) strategy for PFHS and used their proven method to choose the best face mask. Siddique et al, (2021) provided aggregation operators (AOs) for PFHSS and developed an MCDM technique with their suggested operators.In the decision-making problem with a complex and vague statement, Yager has provided a q-ROF-set for the decision-making process. It offers a universal platform for handling vagueness and uncertainty. For more appropriate decision analysis, some researchers have used fuzzy hpersoft sets in the decision-making problem. To get a more powerful tool, fuzzy hypersoft set combined with q rung orthopair fuzzy set. It is more effective in decision-making.

Objective: One of the toughest challenge in green supplier selection is handling uncertainty. The detection of green supplier is a challenging problem for decision maker. In this case the decision maker find out the best green supplier selection process by using aggregation operators. Consequently, we observe uncertainty in determining the aggregation operators, and therefore in the green supplier selection. In this study, we take a MADM approach towards green supplier selection by using some attributes to examine their capabilities in encountering uncertainty in green supplier selection.The reminder of this paper is arranged as follows.Section 2, presents literature review about the previous study. In Section 3, we conduct research limitations and motivation. Section 4, presents some basic materials related to our proposed structure. Then we introduce some operational laws and aggregation operators in Section 5, which helpful for the decision making problem. In Section 6, an algorithm for MCDM technique is present to show the uses of anticipated aggregation operators in decision making problems. In addition, in order to show the applicability of the proposed technique, this study present a numerical example to analyze the technique and the final results are similar to q-ROFHSNs. Section 7, presents the comparative study of the existing structures with the proposed structure. Finally, the paper summarizes and present future research direction in Section 8.

2 Literature review

The selection of green suppliers using economic and environmental criteria in the medical industry has shown us the flexibility and importance that are not harmful to the environment (Puška et al., 2022). A critical review of the green supply chain management for a more sustainable manufacturing industry in China (Sheng et al., 2022). The authors found that the existing relevant legal system needs to be improved, especially in terms of tax subsidies, incentive mechanisms, environmental information disclosure, and the range of industries involved. Corresponding suggestions are proposed in response to these identified problems. A new group decision-making model based on the plan-do-check-act (PDCA) to evaluate the green supply chain management performance of manufacturing organizations, and uses an integrated fuzzy multicriteria decision-making approach (MCDM) in which the fuzzy analytical hierarchy process method (FAHP) determines the weights of the criteria and the fuzzy technique for order preference by similarity with the ideal solution method (FTOPSIS) classifies organizations (Ghosh et al., 2022). Finding a selection of green suppliers (ESG) in the best way will help agricultural producers to apply green agricultural production using uncertainty in decision-making. And to avoid the possibility of uncertainty in the decision-making of experts, the Z numbers were used in conjunction with the fuzzy LMAW method (Logarithmic Methodology of Additive Weights) and the Fuzzy CRADIS method (Compromise Classification of Alternatives from the Distance to the Ideal Solution) (Puška et al., 2022). The criteria for choosing suppliers for each company are constant (Sénquiz-Díaz, 2021). In order to determine the supplier that best meets the objective defined by the company, a given number of suppliers that correspond to a specific number of criteria must be taken into account (Stević et al., 2019). A company can save operating expenses and increase its competitiveness by strategically choosing its suppliers (Yazdani et al., 2017). Different criteria are used by companies using the green supplier selecion technique, the most common are related to environmental and economic factors. Multi-criteria decision-making techniques (MCDM) are frequently in the environment of green supplier selection.Practical applications of q-rung orthopair fuzzy hypersoft set include problems for which the complete mathematical description is unavailable, or where the usage of precise model is highly inconvenient. The structure of q-rung orthopair fuzzy hypersoft set have the ability to overcome this difficulties.Research gap: Khan et al, (2022b) introduced the theme of q-rung orthopair fuzzy hypersoft sets with certain fundamental operational laws and aggregation operators, which can handle the various interactions between input arguments. Khan et al, (2022a) then suggested aggregation operators based on operational laws, such as weighted average and weighted geometric. To our knowledge, there are no studies on ordered aggregation operators in the literature. However, in spite of the existing works on q-rung orthopair fuzzy and hypersoft sets. Therefore, in this study, we propose the ideas of the ordered weighted average and ordered weighted geometric aggregation operators to fill this gap in the literature. Finally, we develop applications using these aggregation operators in decision-making processes. The ordered aggregation operators are used in a suitable application that is based on a green supplier selection.

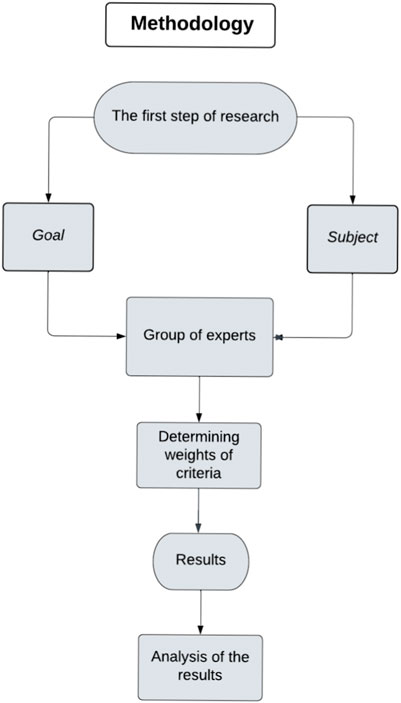
Methodology: The methodology used in this study consists of the following steps. Step 1: The first step of research. A) Goal and subject. Step 2: Group of experts. Step 3: Determining weights of criteria. Step 4: Results. Step 5: Analysis of the result and evaluation with the help of experts. Figure 1 show the methodology used in this research work.

FIGURE 1

FIGURE 1. Flow chart.

3 Research limitations and motivation

The q-ROFHSS is a hybrid of hypersoft and q-rung orthopair fuzzy set, which is a widely used mathematical technique for handling coherence, uncertainty, and incomplete information. Since aggregation operators have been determined to be essential in decision making. To our knowledge, the literature does not use the ordered aggregation operators under q-rung orthopair fuzzy hypersoft environment. However, neither the above techniques nor their deliberate association with membership grade and non-membership grade of many sub-attributes of the studied parameters has a relevant quantitative study of the q-ROFHSN. More precisely, the process is not disturbed by the effects of other membership or non-membership grades on the average geometric operator. Therefore, when certain aggregation operators are taken into account, the results are not favorable and the appropriate preference for alternatives is not found. As a result, it is interesting to consider how to incorporate these q-ROFHSNs into ordered operator. To address these issues, we’ll push some ordered aggregation operator under q-ROFHS environment, including the q-ROFHSOWA and q-ROFHSOWG operators.

4 Materials and methods

In this section some basic concepts related to the our proposed structure are collected.

Definition 4.1. (Zadeh, 1965) In a fuzzy set, A is the Universe of information and M can be defined as a set of ordered pairs and can be represented mathematically as: $A=\left\{⟨y,{\mu }_A(y)⟩:y\in M\right\}$. Here, μ_A(y) represents the degrees of membership of y in A, where μ_A(y) ∈ [0, 1].

Definition 4.2. (Smarandache, 2018) Let M be a universal set and A₁ × A₂ ×⋯ × A_n = H ⊆ E(E represents the set of attributes). The pair (T, H) is said to be a hypersoft set over M, where T is a function T: A → P(M), which is defined as

$T_{e_{ij}}\left(m_{ij}\right)=\left\{⟨m_{ij},T_{e_{i}j}\left(m_{ij}\right)⟩\in P\left(M\right),e_{ij}\in H\right\}$

Definition 4.3. (Zulqarnain et al., 2021b) Let M be a universal set and A₁ × A₂ ×⋯ × A_n = H ⊆ E(E represents the set of attributes). The pair (T, H) is said to be a Pythagorean fuzzy hypersoft set over M, here T is a function T: A → P(M), which is defined as

$T_{e_{ij}}\left(m_{ij}\right)=\left\{⟨m_{ij},{\phi }_{e_{ij}}\left(m_{ij}\right),{\psi }_{e_{ij}}\left(m_{ij}\right)⟩:m_{ij}\in P\left(M\right),e_{ij}\in H\right\}$

where φ represents the membership grade and ψ represents non-membership grade of an object m_ij ∈ M to a set $T_{e_{ij}}$ respectively, with the condition that

$0\le {\left({\phi }_{e_{ij}}\left(m_{ij}\right)\right)}^2+{\left({\psi }_{e_{ij}}\left(m_{ij}\right)\right)}^2\le 1$

Definition 4.4. (Khan et al., 2022b) Let M be a universal set and A₁ × A₂ ×⋯ × A_n = H ⊆ E(E represent the sets of attributes). The pair (T, H) is said to be a q-ROFHS over M, where T is a function T: H → q−ROFH(M), which is defined as

$T_{e_{ij}}\left(m_{ij}\right)=\left\{⟨m_{ij},{\phi }_{e_{ij}}\left(m_{ij}\right),{\psi }_{e_{ij}}\left(m_{ij}\right)⟩:m_{ij}\in M,e_{ij}\in H\mathrm{\hspace{0.17em}and\hspace{0.17em}}q\ge 1\right\}$

where q−ROFH(M) denotes the collection of all possible sub sets of q-ROF of M. Here φ_ij and ψ_ij represent membership and non-membership of an object m_ij ∈ M to a set $T_{e_{ij}}$ respectively, with the condition that

$0\le {\left({\phi }_{e_{ij}}\left(m_{ij}\right)\right)}^q+{\left({\psi }_{e_{ij}}\left(m_{ij}\right)\right)}^q\le 1,\left(q\ge 1\right)$

For simplicity, $T_{e_{ij}}(m_{ij})=⟨m_{ij},{\phi }_{e_{ij}}(m_{ij}),and{\psi }_{e_{ij}}(m_{ij})⟩$ are denoted as $T_{e_{ij}}(m_{ij})=⟨{\phi }_{e_{ij}},{\psi }_{e_{ij}}⟩$ is represents a q-ROFHN.

Definition 4.5. (Khan et al., 2022a) An average weighted q-rung orthopair fuzzy hypersoft (q-ROFHWA) operator is defined as:

$q-ROFHWA\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)={\oplus }_{j=1}^n{v}_j\left({\oplus }_{i=1}^m{w}_i{E}_{a_{ij}}\right)$(4.1)

where $w_i=\left\{\mathrm{1,2},\dots ,n\right\}$ and $v_j=\left\{\mathrm{1,2},\dots ,m\right\}$ are the weight vectors for the experts and sub-attributes of the selected parameters with the condition that, $w_i>0,{\sum }_{i=1}^m{w}_i=1,$and $v_j>0,{\sum }_{j=1}^n{v}_j=1$.Then the mapping of the q-ROFHWA operator is defined as qROFHWA: Δⁿ → Δ is the collection of all q-ROFHNs.

Definition 4.6. (Khan et al., 2022a) A weighted geometric q-rung orthopair fuzzy hypersoft (q-ROFHWG) operator is defined as:

$q-ROFHWG\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)={\otimes }_{j=1}^n{v}_j\left({\otimes }_{i=1}^m{w}_i{E}_{a_{ij}}\right)$(4.2)

where $w_i=\left\{\mathrm{1,2},\dots ,n\right\}$ and $v_j=\left\{\mathrm{1,2},\dots ,m\right\}$ are the weight vectors for experts and sub-attributes of the selected parameters with the condition that, $w_i>0,{\sum }_{i=1}^m{w}_i=1,$and $v_j>0,{\sum }_{j=1}^n{v}_j=1$.Then the mapping for the q-ROFHWG operator is defined as qROFHWG: Δⁿ → Δ is the collection of all q-ROFHNs.

Definition 4.7. (Khan et al., 2022a) The score function of the q-ROFHNs is defined as $S_{e_{ij}}={\phi }_{e_{ij}}{(m_{ij})}^q-{\psi }_{e_{ij}}{(m_{ij})}^q$

5 Operational laws and ordered weighted geometric aggregation operator for q-ROFH set

In this section the algebraic operational laws, q-ROFHOWA and q-ROFHOWG aggregation operators with properties are proposed.

Definition 5.1. An ordered weighted averaging q-rung orthopair fuzzy hypersoft (q-ROFHOWA) operator is defined as:

$\begin{array}{ll}\hfill q-ROFHOWA\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)& ={\oplus }_{j=1}^n{v}_j\left({\oplus }_{i=1}^m{w}_i{E}_{\sigma a_{ij}}\right)\hfill \\ \hfill & =\left(\sqrt[q]{1-\prod _{j=1}^n{\left(\prod _{1=1}^m{\left(1-{\phi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j},}\prod _{j=1}^n{\left(\prod _{1=1}^m{\left({\psi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j}\right)\hfill \end{array}$(5.1)

where $w_i=\left\{\mathrm{1,2},\dots ,n\right\}$ and $v_j=\left\{\mathrm{1,2},\dots ,m\right\}$ are the weight vectors for experts and sub-attributes of the selected parameters with the condition that, $w_i>0,{\sum }_{i=1}^m{w}_i=1,$and $v_j>0,{\sum }_{j=1}^n{v}_j=1$.Then the mapping for q-ROFHOWA operator is defined as q−ROFHOWA: Δⁿ → Δ is the collection of all q-ROFHNs.

Definition 5.2. Let $T_{e_{ij}}(m_{ij})=({\phi }_{e_{ij}},{\psi }_{e_{ij}})$, $T_{e_{11}}(m_{11})=({\phi }_{e_{11}},{\psi }_{e_{11}})$ and $T_{e_{12}}(m_{12})=({\phi }_{e_{12}},{\psi }_{e_{12}})$ be two q-ROFHNs. Then algebraic operational laws are define as:1. $T_{e_{11}}\oplus T_{e_{12}}=(\sqrt[q]{{\phi }_{e_{11}}^q+{\phi }_{e_{12}}^q-{\phi }_{e_{11}}^q{\phi }_{e_{12}}^q},{\psi }_{e_{11}}{\psi }_{e_{12}})$2. $T_{e_{11}}\otimes T_{e_{12}}=({\phi }_{e_{11}}{\phi }_{e_{12}},\sqrt[q]{{\psi }_{e_{11}}^q+{\psi }_{e_{12}}^q-{\psi }_{e_{11}}^q{\psi }_{e_{12}}^q})$3. $\lambda T_{e_{ij}}=(\sqrt[q]{1-{\left(1-{\phi }_{e_{ij}}^q\right)}^{\lambda }},{\left({\psi }_{e_{11}}\right)}^{\lambda })$4. $T_{e_{ij}}^{\lambda }=({\left({\phi }_{e_{ij}}\right)}^{\lambda }.\sqrt[q]{1-{\left(1-{\psi }_{e_{ij}}^q\right)}^{\lambda }})$The following aggregation operators for q-ROFHNs are based on algebraic operational laws.

Definition 5.3. Ordered weighted geometric q-rung orthopair fuzzy hypersoft (q-ROFHOWG) operator is defined as:

$q-ROFHOWG\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)={\otimes }_{j=1}^n{v}_j\left({\otimes }_{i=1}^m{w}_i{E}_{\sigma a_{ij}}\right)$(5.2)

where $w_i=\left\{\mathrm{1,2},\dots ,n\right\}$ and $v_j=\left\{\mathrm{1,2},\dots ,m\right\}$ are weight vectors for the experts and sub-attributes of the selected parameters with the condition that, $w_i>0,{\sum }_{i=1}^m{w}_i=1,$and $v_j>0,{\sum }_{j=1}^n{v}_j=1$.Then the mapping for the q-ROFHOWG operator is defined as q−ROFHOWG: Δⁿ → Δ is the collection of all q-ROFHNs.

Theorem 5.4. Let $E_{a_{ij}},(i=\mathrm{1,2},\dots ,n)(j=\mathrm{1,2},\dots ,m)$ be the collection of q-ROFHNs, then their aggregated value by using the q-ROFHOWG operator is also q-rung orthopair fuzzy hypersoft values, and $q-ROFHOWG\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)=({\prod }_{j=1}^n{\left({\prod }_{1=1}^m{\left({\phi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j},\sqrt[q]{1-{\prod }_{j=1}^n{\left({\prod }_{1=1}^m{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}})$ where $w_i=\left\{\mathrm{1,2},\dots ,n\right\}$ and $v_j=\left\{\mathrm{1,2},\dots ,m\right\}$ are the weight vectors for the experts and sub-attributes of the selected parameters respectively, having the condition that, $w_i>0,{\sum }_{i=1}^m{w}_i=1,$ and $v_j>0,{\sum }_{j=1}^n{v}_j=1$, and σ_ij are permutations of (i = 1,2,…m) and (j = 1,2,…,n) such that $E_{{\sigma }_{(i-1)j}}\ge E_{{\sigma }_{(i)j}}$ and $E_{{\sigma }_{i(j-1)}}\ge E_{{\sigma }_{i(j)}}\forall i,j$.

Proof. The q-ROFHOWG operator can be proven using the principle of mathematical induction as follows:For m = 1, we get w_i = 1. Then,

$\begin{array}{ll}\hfill & q-ROFHOWG\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)\hfill \\ \hfill & ={\otimes }_{j=1}^n{v}_j{E}_{\sigma a_{1j}}\hfill \\ \hfill & =\left(\prod _{j=1}^n{\left({\phi }_{\sigma a_{ij}}\right)}^{v_j},\sqrt[q]{1-\prod _{j=1}^n{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{v_j}}\right)\hfill \\ \hfill & =\left(\prod _{j=1}^n{\left({\prod }_{i=1}^1{\left({\phi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j},\sqrt[q]{1-\prod _{j=1}^n{\left(\prod _{i=1}^1{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\right)\hfill \end{array}$(5.3)

For n = 1, v_j = 1 is obtained.

$\begin{array}{ll}\hfill & q-ROFHOWA\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)\hfill \\ \hfill & ={\otimes }_{i=1}^m{w}_i{E}_{\sigma a_{i1}}\hfill \\ \hfill & =\left(\prod _{i=1}^m{\left({\phi }_{\sigma a_{ij}}\right)}^{w_i},\sqrt[q]{1-\prod _{i=1}^m{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i},}\right)\hfill \\ \hfill & =\left(\prod _{j=1}^1{\left(\prod _{i=1}^m{\left({\phi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j},\sqrt[q]{1-\prod _{j=1}^1{\left(\prod _{i=1}^m{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j},}\right)\hfill \end{array}$(5.4)

Therefore, Eq. 3.3 holds for m = 1 and n = 1. Suppose the equation holds for m = k₂, n = k₁+1, and m = k₂+1, n = k₁. Then,

$\begin{array}{c}={\otimes }_{j=1}^{k_1+1}{v}_j\left({\otimes }_{i=1}^{k_2}{w}_i{E}_{\sigma a_{ij}}\right)\end{array}$(5.5)

$\begin{array}{c}=\left(\prod _{j=1}^{k_1+1}{\left(\prod _{1=1}^{k_2}{\left({\phi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j}\sqrt[q]{1-\prod _{j=1}^{k_1+1}{\left(\prod _{i=1}^{k_2}{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\right)\hfill \end{array}$

$\begin{array}{ccc}\hfill & =\hfill & {\otimes }_{j=1}^{k_1}{v}_j\left({\otimes }_{i=1}^{k_2+1}{w}_i{E}_{\sigma a_{ij}}\right)\hfill \end{array}$(5.6)

$\begin{array}{ccc}\hfill & =\hfill & \left(\prod _{j=1}^{k_1}{\left(\prod _{1=1}^{k_2+1}{\left({\phi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j},\sqrt[q]{1-\prod _{j=1}^{k_1}{\left(\prod _{i=1}^{k_2+1}{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\right)\hfill \end{array}$

Now the equation for n = k₁+1 and m = k₂+1 is proven.

${\otimes }_{j=1}^{k_1+1}{v}_j\left({\otimes }_{i=1}^{k_2+1}{w}_i{E}_{\sigma a_{ij}}\right)$(5.7)

$\begin{array}{ccc}\hfill & =\hfill & {\otimes }_{j=1}^{k_1+1}{E}_{\sigma a_j}\left({\otimes }_{i=1}^{k_2}{w}_i{E}_{\sigma a_{ij}}\otimes w_{i+1}{E}_{\sigma a_{\left(k_2+1\right)j}}\right)\hfill \\ \hfill & =\hfill & \left({\otimes }_{j=1}^{k_1+1}{\otimes }_{i=1}^{k_2}{w}_i{v}_j{E}_{\sigma a_j}\right)\left({\otimes }_{j=1}^{k_1+1}{v}_j{w}_{i+1}{E}_{\sigma a_{\left(k_2+1\right)\left(j\right)}}\right)\hfill \end{array}$(5.8)

$=2\prod _{j=1}^{k_1+1}{\left(\prod _{1=1}^{k_2+1}{\left({\psi }_{\sigma a_{\left(i\right)\left(j\right)}}\right)}^{w_i}\right)}^{v_j}\otimes 2\prod _{j=1}^{k_1+1}{\left(\prod _{1=1}^{k_2+1}{\left({\psi }_{\sigma a_{\left(k_2+1\right)\left(j\right)}}\right)}^{w_{k_2+1}}\right)}^{v_j}$

$\begin{array}{cc}\hfill & =2\prod _{j=1}^{k_1+1}{\left(\prod _{i=1}^{k_2+1}{\left({\phi }_{\sigma a_{\left(i\right)\left(j\right)}}\right)}^{w_i}\right)}^{v_j},\sqrt[q]{1-\prod _{j=1}^{k_1+1}{\left(\prod _{i=1}^{k_2+1}{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\hfill \end{array}$(5.9)

$\begin{array}{cc}\hfill & ={\otimes }_{j=1}^{k_1+1}{v}_j\left({\otimes }_{i=1}^{k_2+1}{w}_i{E}_{\sigma a_{ij}}\right)\hfill \end{array}$

Therefore, this is valid for n = k₁+1 and m = k₂+1.

Example 5.5. Let X = {X₁, X₂, X₃, X₄} be set as decision makers with w_i = (0.3,0.4,0.1,0.2)^T. The group of experts will choose a business location under the set of attributes $A=\left\{a_1\right.=$ skill base in the area, a₂ = potential growth for business} with their corresponding sub-attributes $a_1=\left\{a_{11}\right.=$communication and negotiation, a₁₂ = networking}, $a_2=\left\{a_{21}\right.=$strong sales growth, a₂₂ = strong leadership}. Let A = a₁ × a₂ be a set of sub-attributes where,$A=\{a_{11},a_{12}\}\times \{a_{21},a_{22}\}=\{(a_{11},a_{21}),(a_{11},a_{22}),(a_{12},a_{21}),(a_{12},a_{22})\}=A=\{{\mathring{a}}_1,{\mathring{a}}_2,{\mathring{a}}_3,{\mathring{a}}_4\}$ denotes the set of sub-attributes with: weight v_j = (0.3,0.3,0.4,0.1)^T. The hypothetical score values for all attributes in q-ROFHSNs with q = 5, is given as:

$\left(H,A\right)=\left[\begin{array}{c}\hfill \left(0.88,0.99\right)\left(0.77,0.99\right)\left(0.99,0.33\right)\left(0.77,0.66\right)\hfill \\ \hfill \left(0.55,0.99\right)\left(0.99,0.44\right)\left(0.77,0.99\right)\left(0.66,0.99\right)\hfill \\ \hfill \left(0.77,0.88\right)\left(0.77,0.99\right)\left(0.55,0.66\right)\left(0.99,0.44\right)\hfill \\ \hfill \left(0.55,0.88\right)\left(0.88,0.55\right)\left(0.66,0.88\right)\left(0.77,0.88\right)\hfill \end{array}\right]$

To obtain the order position of a matrix:

$\left(H,A\right)=\left[\begin{array}{c}\hfill \left(0.99,0.33\right)\left(0.88,0.99\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.77,0.99\right)\left(0.66,0.99\right)\left(0.55,0.99\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.77,0.99\right)\left(0.77,0.88\right)\left(0.55,0.66\right)\hfill \\ \hfill \left(0.88,0.55\right)\left(0.77,0.88\right)\left(0.66,0.88\right)\left(0.55,0.88\right)\hfill \end{array}\right]$

It is known

$q-ROFHOWG\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)=\left({\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left({\phi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j},\sqrt[q]{1-{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\right)=\left({\prod }_{j=1}^4{\left({\prod }_{i=1}^4{\left({\phi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j},\sqrt[q]{1-{\prod }_{j=1}^4{\left({\prod }_{i=1}^4{\left(1-{\psi }_{\sigma a_{ij}}^5\right)}^{w_i}\right)}^{v_j}}\right)$

$\begin{array}{ccc}\hfill & =\hfill & \begin{array}{c}\hfill {\left\{{\left(0.99\right)}^{0.3}{\left(0.99\right)}^{0.4}{\left(0.99\right)}^{0.1}{\left(0.88\right)}^{0.2}\right\}}^{0.3}\hfill \\ \hfill {\left\{{\left(0.88\right)}^{0.3}{\left(0.77\right)}^{0.4}{\left(0.77\right)}^{0.1}{\left(0.77\right)}^{0.2}\right\}}^{0.3}\hfill \\ \hfill {\left\{{\left(0.77\right)}^{0.3}{\left(0.66\right)}^{0.4}{\left(0.77\right)}^{0.1}{\left(0.66\right)}^{0.2}\right\}}^{0.4}\hfill \\ \hfill {\left\{{\left(0.77\right)}^{0.3}{\left(0.55\right)}^{0.4}{\left(0.55\right)}^{0.1}{\left(0.55\right)}^{0.2}\right\}}^{0.1},\hfill \\ \hfill \left\{\begin{array}{c}\hfill \sqrt[5]{1-{\left({\left(1-0.33^5\right)}^{0.3}{\left(1-0.44^5\right)}^{0.4}{\left(1-0.44^5\right)}^{0.1}{\left(1-0.55^5\right)}^{0.2}\right)}^{0.3}}\hfill \\ \hfill \sqrt[5]{1-{\left({\left(10.905-0.99^5\right)}^{0.3}{\left(1-0.99^5\right)}^{0.4}{\left(1-0.99^5\right)}^{0.1}{\left(1-0.88^5\right)}^{0.2}\right)}^{0.3}}\hfill \\ \hfill \sqrt[5]{1-{\left({\left(1-0.99^5\right)}^{0.3}{\left(1-0.99^5\right)}^{0.4}{\left(1-0.88^5\right)}^{0.1}{\left(1-0.88^5\right)}^{0.2}\right)}^{0.4}}\hfill \\ \hfill \sqrt[5]{1-{\left({\left(1-0.66^5\right)}^{0.3}{\left(1-0.99^5\right)}^{0.4}{\left(1-0.66^5\right)}^{0.1}{\left(1-0.88^5\right)}^{0.2}\right)}^{0.1}}\hfill \end{array}\right\}\hfill \end{array}\hfill \\ \hfill & =\hfill & \left(0.769,0.1997\right)\hfill \end{array}$

Remark 5.6. If the value of q is fixed, that is q = 1, then the proposed q-ROFHOWG operator reduces to intuitionistic fuzzy hypersoft ordered weighted geometric (IFHOWG) operator.

Remark 5.7. If the value of q is fixed, that is q = 2, then the proposed q-ROFHOWG operator reduces to Pythagorean fuzzy hypersoft ordered weighted geometric (PFHOWG) operator.

Remark 5.8. If there are single parameters, that is e₁, e₂, … , e_n, the proposed q-ROFHOWG operator reduces to q-rung orthopair fuzzy soft ordered weighted geometric (q-ROFSOWG) operator.

Remark 5.9. From these remarks it is clear that the IFHOWG, PFHOWG and q-ROFSOWG operators are the specials cases of the proposed q-ROFHOWG operator.

5.1 Properties of q-ROFHOWG operator

The following section proposes the properties of the q-ROFHOWG operator, such as idempotent, bounded, and monotonic. These properties can be proved by the following theorems.

(Idempotency) Let $E_{a_{ij}}=({\phi }_{a_{ij}},{\psi }_{a_{ij}})$ be a collection of q-ROFHNs, for all i = 1, 2, … , n and j = 1, 2, … , m. If $E_{\sigma a_{ij}}=E_{11}$ is mathematically identical, then $q-ROFHOWG\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)=E$.

Proof. As it is known,

$q-ROFHOWG\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)=\left(2\prod _{j=1}^{k_1+1}{\left(\prod _{i=1}^{k_2+1}{\left({\phi }_{\sigma a_{\left(i\right)\left(j\right)}}\right)}^{w_i}\right)}^{v_j},\sqrt[q]{1-\prod _{j=1}^{k_1+1}{\left(\prod _{i=1}^{k_2+1}{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\right)$(5.10)

As $E_{\sigma a_{(i)(j)}}=E_{ij}$, so;

$\begin{array}{ccc}\hfill & =\hfill & \left(2{\left({\left({\phi }_{\sigma a_{\left(i\right)\left(j\right)}}\right)}^{\sum _{i=1}^m{w}_i}\right)}^{\sum _{j=1}^n{v}_j},\sqrt[q]{1-{\left({\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{\sum _{i=1}^m{w}_i}\right)}^{\sum _{j=1}^n{v}_j}}\right)\hfill \\ \hfill & =\hfill & \left(2\left({\phi }_{\sigma a_{\left(i\right)\left(j\right)}}\right),\sqrt[q]{1-\left(1-{\psi }_{\sigma a_{ij}}^q\right)}\right)\hfill \\ \hfill & =\hfill & \left({\phi }_{a_{ij}},{\psi }_{a_{ij}}\right)=E\hfill \end{array}$(5.11)

(Boundedness) Let $E_{a_{ij}}=({\phi }_{a_{ij}},{\psi }_{a_{ij}})$ be a collection of q-ROFHNs, for all i = 1, 2, ..m, and j = 1, 2, … , n. If $E_{\min \min }=\min \min E_{a_{(i)(j)}}$ and $E_{\max \max }=\max \max E_{a_{(i)(j)}}$, then $E_{\min \min }\le q-ROFHOWG\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)\le E_{\max \max }$, where w_i and v_j are weight vectors for expert’s and sub-attributes of the selected parameters, such that $w_i>0,{\sum }_{i=1}^m{w}_i=1$, and $w_i>0,{\sum }_{i=1}^n{v}_j=1$.

Proof. Let $f(x)=\sqrt[q]{1-(1-x^q),}x\in [\mathrm{0,1}]$ then

$\frac{d}{dx}\left(f\left(x\right)\right)=-q{x}^{q-1}\left(\sqrt[q]{\left(\frac{1-x^q}{q}\right)-1}\right)<0,$

So f(x) is decreasing function on [0,1]. As ${\psi }_{\min \min }\le {\psi }_{a_{ij}}\le {\psi }_{\max \max }$, hence $f\left({\psi }_{{\min }_j{\min }_i}\right)\le f\left({\psi }_{a_{ij}}\right)\le f\left({\psi }_{{\max }_j{\max }_i}\right)$. $\iff \sqrt[q]{1-{\max }_j{\max }_i^q\psi }\le \sqrt[q]{1-{\psi }_{\sigma a_{ij}}^q}\le \sqrt[q]{1-{\min }_j{\min }_i^q\psi }$$\iff \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left(1-{\max }_j{\max }_i^q\psi \right)}^{w_i}\right)}^{v_j}}\le \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\le \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left(1-{\min }_j{\min }_i^q\psi \right)}^{w_i}\right)}^{v_j}}$ $\iff \sqrt[q]{{\left({\left(1-{\max }_j{\max }_i^q\psi \right)}^{{\sum }_{i=1}^m{w}_i}\right)}^{{\sum }_{j=1}^n{v}_j}}\le \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left(1-{\psi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\le \sqrt[q]{{\left({\left(1-{\min }_j{\min }_i^q\psi \right)}^{{\sum }_{i=1}^m{w}_i}\right)}^{{\sum }_{j=1}^n{v}_j}}$$\iff \sqrt[q]{-1+{\min }_j{\min }_i{\phi }^q}\le \sqrt[q]{-{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left(1-{\phi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\le \sqrt[q]{-1+{\max }_j{\max }_i{\phi }^q}$ $\iff {\min }_j{\min }_i\left(\phi \right)\le \sqrt[q]{1-{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left(1-{\phi }_{\sigma a_{ij}}^q\right)}^{w_i}\right)}^{v_j}}\le {\max }_j{\max }_i\left(\phi \right)$ (3.12)As ${\psi }_{\min \min }\le {\psi }_{a_{ij}}\le {\psi }_{\max \max }$, hence $f\left({\psi }_{{\min }_j{\min }_i}\right)\le f\left({\psi }_{a_{ij}}\right)\le f\left({\psi }_{{\max }_j{\max }_i}\right)$. $\iff \sqrt[q]{{\min }_j{\min }_i\psi }\le \sqrt[q]{{\psi }_{\sigma a_{ij}}}\le \sqrt[q]{{\max }_j{\max }_i\psi }$ $\iff \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left({\min }_j{\min }_i\psi \right)}^{w_i}\right)}^{v_j}}\le \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left({\psi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j}}\le \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left({\max }_j{\max }_i\psi \right)}^{w_i}\right)}^{v_j}}$ $\iff \sqrt[q]{{\left({\left({\min }_j{\min }_i\psi \right)}^{{\sum }_{i=1}^m{w}_i}\right)}^{{\sum }_{j=1}^n{v}_j}}\le \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left({\psi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j}}\le \sqrt[q]{{\left({\left({\max }_j{\max }_i\psi \right)}^{{\sum }_{i=1}^m{w}_i}\right)}^{{\sum }_{j=1}^n{v}_j}}$$\iff \sqrt[q]{{\min }_j{\min }_i\psi }\le \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left({\psi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j}}\le \sqrt[q]{{\max }_j{\max }_i\psi }\iff {\min }_j{\min }_i\left(\psi \right)\le \sqrt[q]{{\prod }_{j=1}^n{\left({\prod }_{i=1}^m{\left({\psi }_{\sigma a_{ij}}\right)}^{w_i}\right)}^{v_j}}\le {\max }_j{\max }_i\left(\psi \right)$(3.13) Let $q-ROFHOWA\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)=E$. Then equation (3.12)–(3.13) can be written as ${\min }_j{\min }_i\left({\psi }^q\right)\le {\psi }_{\sigma a_{ij}}^q\le {\max }_j{\max }_i\left({\psi }^q\right)$ and ${\min }_j{\min }_i\left(\phi \right)\le {\phi }_{\sigma a_{ij}}\le {\max }_j{\max }_i\left(\phi \right)$. Thus,

$S\left(H\right)={\psi }^q-{\phi }^q\le {\psi }_{{\max }_j{\max }_i}^q-{\psi }_{{\min }_j{\min }_i}^q=S\left(H_{\max }\right)$

$S\left(H\right)={\psi }^q-{\phi }^q\ge {\psi }_{{\min }_j{\min }_i}^q-{\psi }_{{\max }_j{\max }_i}^q=S\left(H_{\min }\right)$

If S(H) < S(H_max) and S(H) > S(H_min), then we have

$H_{\min }<q-ROFHOWA\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)<H_{\max }$

If S(H) = S(H_max), then we have ${\psi }^q={\psi }_{{\max }_j{\max }_i}^q$ and ${\phi }^q={\phi }_{{\max }_j{\max }_i}^q$. Thus A(H) = ψ^q+φ. Therefore,

$q-ROFHOWA\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)<H_{\max }$

If S(H) = S(H_min), then we have ${\psi }^q-\phi ={\psi }_{{\min }_j{\min }_i}^q$ and ${\psi }^q={\psi }_{{\min }_j{\min }_i}^q$ and $\phi ={\phi }_{{\min }_j{\min }_i}$ Thus $A(H)={\psi }^q+\phi ={\phi }_{{\min }_j{\min }_i}^q+{\psi }_{{\min }_j{\min }_i}$. Therefore,

$q-ROFHOWA\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)<H_{\min }$

So, we get

$H_{\min }\le q-ROFHOWA\left(E_{a_{11}},E_{a_{12}},\dots ,E_{a_{nm}}\right)\le H_{\max }$

6 Multi criteria decision making technique

In this section, we will develop the methodology to apply the proposed operators in MCDM problems using q-ROFHNs and solve a numerical example. In addition, we also develop the decision-making technique (DM) to reduce MCDM restrictions and to validate the effects of proposed AOs. And also, a quantifiable data are provide to support the practical aspect of the planned approach.Assume that S = {S₁, S₂, … S_s} is a set alternative and O = {O₁, O₂, … O_r} is a group of experts. Let $w={(w_1,w_2,\dots w_n)}^T$ is a weight vector for experts with w_i > 0, and ${\sum }_{i=1}^n{w}_i=1$. Let T = {T₁, T₂, … T_m} be a set of parameters with sub-attributes $\acute{Q}=\{q_{1p}\times q_{2p}\times \cdots \times q_{mp}\}$ with weight vector $v_j>0,{\sum }_{j=1}^n{v}_j=1$. The group of experts examined the alternatives in the form of q-ROFHNs as ${\left(S_{a_{ij}}\right)}_{n\times m}={({\phi }_{a_{ij}},{\psi }_{a_{ij}})}_{n\times m}$.Then, we apply he proposed approach to MCDM problem by applying q-ROFHOWA/q-ROFHOWG operators. Figure 2 shows the graphical representation of MCDM method's steps. The following algorithm can be used to make a decision. Step 1: Construct a decision matrix based on the experts’ evaluations of each alternative in the form of q-ROFHNs.$\left(O,\acute{Q}\right)={\left[T_{e_{ij}}^q\right]}_{n\times m}=\left(\begin{array}{c}\hfill T_{e_{11}}^q{T}_{e_{12}}^q\dots T_{e_{1m}}^q\hfill \\ \hfill T_{e_{21}}^q{T}_{e_{22}}^q\dots T_{e_{2m}}^q\hfill \\ \hfill ..\dots .\hfill \\ \hfill ..\dots .\hfill \\ \hfill ..\dots .\hfill \\ \hfill T_{e_{n1}}^q{T}_{e_{n2}}^q\dots T_{e_{nm}}^q\hfill \end{array}\right)$Step 2: If all criteria are of the same type, there is no need for normalisation; however, there are two types of criteria, which are known as benefit type attribute B_b and cost type attribute B_c in MCDM. In this case, using the normalisation formula, the matrix $S_{a_{ij}}$ is changed into a normalising matrix ${\left(D_{a_{ij}}\right)}_{m\times n}$ = $\left\{\begin{array}{c}{E}_{a_{ij}}^c=({\phi }_{a_{ij}},{\psi }_{a_{ij}})\text{\hspace{0.17em}Cost\hspace{0.17em}type\hspace{0.17em}attributes}\hfill \\ E_{a_{ij}}=({\psi }_{a_{ij}},{\phi }_{a_{ij}})\text{\hspace{0.17em}Benefit\hspace{0.17em}type\hspace{0.17em}attributes}\hfill \end{array}\right.$Step 3: To obtain the order position of the proposed decision matrix.Step 4: Use the developed ordered weighted aggregation operator to accumulate all the alternative in a decision matrix.Step 5: Calculate the score values for each alternatives.Step 6: Select the appropriate alternative as the best option.

FIGURE 2

FIGURE 2. Flow chart.

6.1 Example

In order to choose appropriate green suppliers, manufacturers invite a group of experts to evaluate the three potential green suppliers using a system of criteria, including product performance (A1), supplier development potential (A2), and pollution control (A3). They find specialists who can confirm links between influential elements of success affecting the performance of green suppliers. The experts are tasked with organizing sets of pairwise comparisons in terms of impacts and orientation between the performance factors of green suppliers, consisting of sub-attributes such as product lines (AS1), increasing efficiency and effectiveness (AS2), lowering supplier developmental potential (AP1), increasing supplier developmental potential (AP2), and reducing or eliminating fireplaces (AC1) which avoid burning leaves (AC2). Let A = a₁ × a₂ × a₃ be a set of sub-attributes $A=\{a_{11},a_{12}\}\times \{a_{21},a_{22}\}\times \{a_{31},a_{32}\}=\left\{(a_{11},a_{21},a_{31})\right.,(a_{11},a_{22},a_{32}),(a_{11},a_{22},a_{31}),(a_{11},a_{21},a_{32}),(a_{12},a_{21},a_{31}),(a_{12},a_{22},a_{32}),(a_{12},a_{22},a_{31}),$$\left.(a_{12},a_{21},a_{32})\right\}=A=\{{\mathring{a}}_1,{\mathring{a}}_2,{\mathring{a}}_3,{\mathring{a}}_4,{\mathring{a}}_5,{\mathring{a}}_6,{\mathring{a}}_7,{\mathring{a}}_8\}$ denotes the set of sub-attributes with weight.v_j = (0.15,0.14,0.16,0.12,0.13,0.11,0.10,0.09)^T. Let {O₁,O₂,O ₃} be a set of experts with weight w_i = (0.2,0.3,0.4,0.1)^T.

$\begin{array}{ccc}\hfill & \hfill & {\text{Decision\hspace{0.17em}matrix\hspace{0.17em}for\hspace{0.17em}Alternative\hspace{0.17em}S}}_1\hfill \\ \hfill & \hfill & \left[\begin{array}{c}\hfill \left(0.66,0.99\right)\left(0.77,0.99\right)\left(0.99,0.33\right)\left(0.77,0.66\right)\left(0.88,0.99\right)\left(0.77,0.99\right)\left(0.99,0.33\right)\left(0.77,0.99\right)\hfill \\ \hfill \left(0.55,0.66\right)\left(0.99,0.44\right)\left(0.55,0.99\right)\left(0.66,0.99\right)\left(0.66,0.99\right)\left(0.66,0.88\right)\left(0.77,0.66\right)\left(0.88,0.66\right)\hfill \\ \hfill \left(0.44,0.88\right)\left(0.77,0.99\right)\left(0.44,0.66\right)\left(0.99,0.44\right)\left(0.77,0.88\right)\left(0.77,0.55\right)\left(0.88,0.33\right)\left(0.77,0.44\right)\hfill \\ \hfill \left(0.55,0.44\right)\left(0.88,0.55\right)\left(0.66,0.88\right)\left(0.77,0.88\right)\left(0.88,0.66\right)\left(0.77,0.66\right)\left(0.99,0.55\right)\left(0.55,0.66\right)\hfill \end{array}\right]\hfill \end{array}$

$\begin{array}{ccc}\hfill & \hfill & {\text{Decision\hspace{0.17em}matrix\hspace{0.17em}for\hspace{0.17em}Alternative\hspace{0.17em}S}}_2\hfill \\ \hfill & \hfill & \left[\begin{array}{c}\hfill \left(0.55,0.66\right)\left(0.44,0.99\right)\left(0.88,0.33\right)\left(0.77,0.66\right)\left(0.44,0.99\right)\left(0.77,0.55\right)\left(0.99,0.66\right)\left(0.77,0.99\right)\hfill \\ \hfill \left(0.77,0.88\right)\left(0.77,0.99\right)\left(0.44,0.66\right)\left(0.99,0.44\right)\left(0.77,0.44\right)\left(0.77,0.55\right)\left(0.88,0.33\right)\left(0.88,0.44\right)\hfill \\ \hfill \left(0.88,0.99\right)\left(0.77,0.99\right)\left(0.99,0.44\right)\left(0.77,0.66\right)\left(0.88,0.66\right)\left(0.77,0.99\right)\left(0.99,0.44\right)\left(0.77,0.99\right)\hfill \\ \hfill \left(0.55,0.66\right)\left(0.99,0.44\right)\left(0.33,0.99\right)\left(0.66,0.99\right)\left(0.44,0.99\right)\left(0.33,0.88\right)\left(0.77,0.66\right)\left(0.88,0.66\right)\hfill \end{array}\right]\hfill \end{array}$

$\begin{array}{ccc}\hfill & \hfill & {\text{Decision\hspace{0.17em}matrix\hspace{0.17em}for\hspace{0.17em}Alternative\hspace{0.17em}S}}_3\hfill \\ \hfill & \hfill & \left[\begin{array}{c}\hfill \left(0.99,0.66\right)\left(0.44,0.99\right)\left(0.88,0.33\right)\left(0.77,0.66\right)\left(0.44,0.99\right)\left(0.77,0.55\right)\left(0.99,0.66\right)\left(0.77,0.99\right)\hfill \\ \hfill \left(0.44,0.88\right)\left(0.77,0.66\right)\left(0.55,0.88\right)\left(0.99,0.33\right)\left(0.66,0.44\right)\left(0.77,0.66\right)\left(0.55,0.33\right)\left(0.88,0.77\right)\hfill \\ \hfill \left(0.66,0.99\right)\left(0.77,0.99\right)\left(0.99,0.44\right)\left(0.77,0.66\right)\left(0.88,0.66\right)\left(0.77,0.99\right)\left(0.99,0.44\right)\left(0.77,0.99\right)\hfill \\ \hfill \left(0.33,0.88\right)\left(0.77,0.99\right)\left(0.44,0.66\right)\left(0.99,0.44\right)\left(0.77,0.44\right)\left(0.77,0.55\right)\left(0.88,0.33\right)\left(0.88,0.44\right)\hfill \end{array}\right]\hfill \end{array}$

$\begin{array}{ccc}\hfill & \hfill & {\text{Decision\hspace{0.17em}matrix\hspace{0.17em}for\hspace{0.17em}Alternative\hspace{0.17em}S}}_4\hfill \\ \hfill & \hfill & \left[\begin{array}{c}\hfill \left(0.99,0.44\right)\left(0.99,0.44\right)\left(0.99,0.33\right)\left(0.77,0.99\right)\left(0.77,0.55\right)\left(0.77,0.44\right)\left(0.44,0.66\right)\left(0.33,0.88\right)\hfill \\ \hfill \left(0.88,0.33\right)\left(0.88,0.77\right)\left(0.77,0.66\right)\left(0.77,0.66\right)\left(0.66,0.44\right)\left(0.55,0.88\right)\left(0.55,0.33\right)\left(0.44,0.88\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.99,0.44\right)\left(0.88,0.66\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\left(0.66,0.99\right)\hfill \\ \hfill \left(0.99,0.66\right)\left(0.99,0.66\right)\left(0.88,0.33\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\left(0.77,0.55\right)\left(0.44,0.99\right)\left(0.44,0.99\right)\hfill \end{array}\right]\hfill \end{array}$

The decision matrices with ordered position as follows:

$\begin{array}{ccc}\hfill & \hfill & {\text{Decision\hspace{0.17em}matrix\hspace{0.17em}for\hspace{0.17em}Alternative\hspace{0.17em}S}}_1\hfill \\ \hfill & \hfill & \left[\begin{array}{c}\hfill \left(0.99,0.33\right)\left(0.99,0.33\right)\left(0.88,0.99\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\left(0.66,0.99\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.88,0.66\right)\left(0.77,0.66\right)\left(0.66,0.99\right)\left(0.66,0.99\right)\left(0.66,0.88\right)\left(0.55,0.99\right)\left(0.55,0.66\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.88,0.33\right)\left(0.77,0.99\right)\left(0.77,0.88\right)\left(0.77,0.55\right)\left(0.77,0.44\right)\left(0.44,0.88\right)\left(0.44,0.66\right)\hfill \\ \hfill \left(0.99,0.55\right)\left(0.88,0.66\right)\left(0.88,0.55\right)\left(0.77,0.88\right)\left(0.77,0.66\right)\left(0.66,0.88\right)\left(0.55,0.66\right)\left(0.55,0.44\right)\hfill \end{array}\right]\hfill \end{array}$

$\begin{array}{ccc}\hfill & \hfill & {\text{Decision\hspace{0.17em}matrix\hspace{0.17em}for\hspace{0.17em}Alternative\hspace{0.17em}S}}_2\hfill \\ \hfill & \hfill & \left[\begin{array}{c}\hfill \left(0.99,0.66\right)\left(0.88,0.33\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\left(0.77,0.55\right)\left(0.55,0.66\right)\left(0.44,0.99\right)\left(0.44,0.99\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.88,0.44\right)\left(0.88,0.33\right)\left(0.77,0.99\right)\left(0.77,0.88\right)\left(0.77,0.55\right)\left(0.77,0.33\right)\left(0.44,0.66\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.99,0.44\right)\left(0.88,0.99\right)\left(0.88,0.66\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.88,0.66\right)\left(0.77,0.66\right)\left(0.66,0.99\right)\left(0.55,0.66\right)\left(0.44,0.99\right)\left(0.33,0.99\right)\left(0.33,0.88\right)\hfill \end{array}\right]\hfill \end{array}$

$\begin{array}{ccc}\hfill & \hfill & {\text{Decision\hspace{0.17em}matrix\hspace{0.17em}for\hspace{0.17em}Alternative\hspace{0.17em}S}}_3\hfill \\ \hfill & \hfill & \left[\begin{array}{c}\hfill \left(0.99,0.66\right)\left(0.99,0.66\right)\left(0.88,0.33\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\left(0.77,0.55\right)\left(0.44,0.99\right)\left(0.44,0.99\right)\hfill \\ \hfill \left(0.99,0.33\right)\left(0.88,0.77\right)\left(0.77,0.66\right)\left(0.77,0.66\right)\left(0.66,0.44\right)\left(0.55,0.88\right)\left(0.55,0.33\right)\left(0.44,0.88\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.99,0.44\right)\left(0.88,0.66\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\left(0.66,0.99\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.88,0.44\right)\left(0.88,0.33\right)\left(0.77,0.99\right)\left(0.77,0.55\right)\left(0.77,0.44\right)\left(0.44,0.66\right)\left(0.33,0.88\right)\hfill \end{array}\right]\hfill \end{array}$

$\begin{array}{ccc}\hfill & \hfill & {\text{Decision\hspace{0.17em}matrix\hspace{0.17em}for\hspace{0.17em}Alternative\hspace{0.17em}S}}_4\hfill \\ \hfill & \hfill & \left[\begin{array}{c}\hfill \left(0.99,0.44\right)\left(0.99,0.44\right)\left(0.99,0.33\right)\left(0.77,0.99\right)\left(0.77,0.55\right)\left(0.77,0.44\right)\left(0.44,0.66\right)\left(0.33,0.88\right)\hfill \\ \hfill \left(0.88,0.33\right)\left(0.88,0.77\right)\left(0.77,0.66\right)\left(0.77,0.66\right)\left(0.66,0.44\right)\left(0.55,0.88\right)\left(0.55,0.33\right)\left(0.44,0.88\right)\hfill \\ \hfill \left(0.99,0.44\right)\left(0.99,0.44\right)\left(0.88,0.66\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\left(0.66,0.99\right)\hfill \\ \hfill \left(0.99,0.66\right)\left(0.99,0.66\right)\left(0.88,0.33\right)\left(0.77,0.99\right)\left(0.77,0.66\right)\left(0.77,0.55\right)\left(0.44,0.99\right)\left(0.44,0.99\right)\hfill \end{array}\right]\hfill \end{array}$

The aggregated values using the q-ROFHOWG operator of the alternatives are given as follows.S₁ = (0.5649, 0.2988), S₂ = (0.7798, 0.1896), S₃ = (0.7654, 0.3877), S₄ = (0.6685, 0.1679).The score values are given as follows.S₁ = 0.05514, S₂ = 0.28810, S₃ = 0.25392, S₁ = 0.13337, S₄ = 0.1337. The order of alternative is S₂ > S₃ > S₄ > S₁, hence S₂ is the best alternative.

7 Comparative analysis and discussion

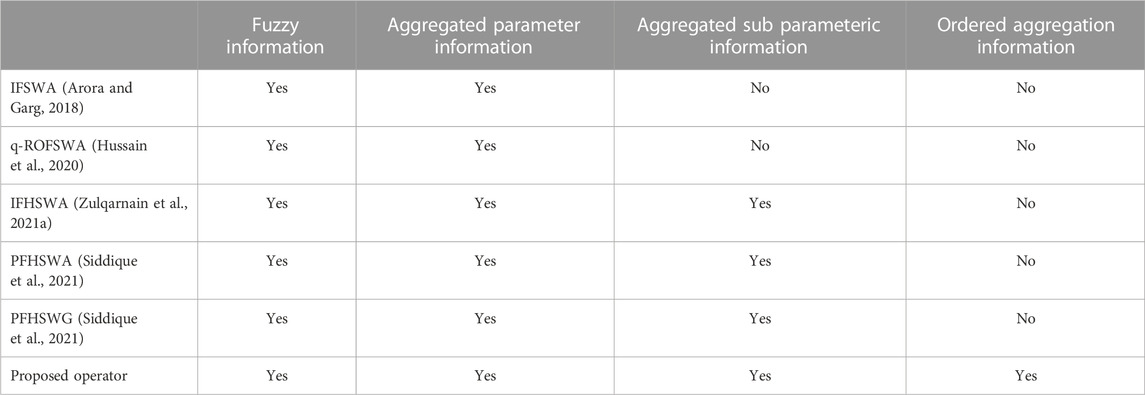
In this section, an evaluation of the proposed model is planned to demonstrate its effectiveness of the proposed method. For this purpose, we compare our proposed method with some existing methods. Zulqarnain et al. (Arora and Garg, 2018) developed intuitionistic fuzzy soft weighted average aggregation operator. If we assign the membership and non-membership i. e 0.88 and 0.99, then their sum exceeds 1. Hussain et al, (2020) developed q-ROFSWA operators, which cannot handle the parameterized values of alternatives. So in this case the method failed to cope the situation. Similarly, if we take IFHSWA aggregation operator, so thus method also fail and did not full the condition that the sum of membership and non-membership may not exceeds 1. On the other side the PFHSWA and PFHSWG aggregation operators also failed to tackle the situation. So the proposed approach full all these situations. The aggregation operators created by Khan et al, (2022a) can expertly compress with the multiple sub-attributes of the alternatives. However, these aggregation operators may sometimes not produce certain undesirable results. We, therefore, opted for the ordered aggregation operators in the q-ROFHS environment, which is achieved by managing several sub-attributes equivalents to existing aggregation operators, in order to manage these complexity in uncertain environment. q-ROFHSS is therefore the greatest interpretation of PFHSS. The advantage of the proposed technique is that they have the ability to solve real worlds problems by using their parameterizations properties with q > 2. The planned approach is effective and realistic, using the q-ROFHOWA and q-ROFHOWG operators. A creative MCDM model in the q-ROFH environment is built. The planned model is more capable than common approaches and can generate the most appropriate results in MCDM problems. The proposed approach will therefore be more effective, significant, and improved compared to the other models in different versions of the fuzzy sets. Table 1 show the study of comparative analysis.

TABLE 1

TABLE 1. Comparison of q-ROFHSs operators with some existing operators.

8 Conclusion

The circumstances of group decision -making usually involve complex criteria that are influenced by a number of other factors. The selection of appropriate criteria and the choice of green suppliers are essential for the operations of every business. Their prosperity depends directly on how this situation is resolved. An organized approach would divide the examination of the green supplier selection problem into two sections: criteria and methodology. The assessment of decision-makers is expressed in the form of q-ROFHNs. In this study, the ambiguity and incompleteness of the information were resolved using the proposed structure. In addition, q-ROFHOWG aggregation operators were developed. Based on these operators, a novel MCDM strategy for green supplier management was created. Additionally, a real-world example of selecting green suppliers was provided to demonstrate the viability of the suggested operators. The suggested approach could successfully solve various challenges in the selection of green suppliers, including giving decision-makers, a pleasant environment for assessment and encouraging a relatively high degree of consensus among decision-makers, while properly examining the weights of decision-makers. Therefore, this study offers a more useful and effective method for selecting green-suppliers for the actual businesses. In future the proposed structure can be applied in different decision making techniques such as Complex Proportional Assessment (COPRAS) method, TOPSIS method, Analytic Hierarchy Process (AHP) method, VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method and (an acronym in Portuguese for Interative Multi-criteria Decision Making (TODIM) method. And we would consider the impact of the psychological factors of experts on the results of the decision in the problem of selecting green suppliers. In addition, the new method can also be applied in the selection of investment projects and in various other fields.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

Thanks to American University of the Middle East for their support in this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.1048019/full#supplementary-material

References

Ahmad, B., and Kharal, A. (2009). Research article on fuzzy soft sets

Google Scholar

Akram, M., Dudek, W. A., and Dar, J. M. (2019). Pythagorean dombi fuzzy aggregation operators with application in multicriteria decision-making. Int. J. Intelligent Syst. 34, 3000–3019. doi:10.1002/int.22183

CrossRef Full Text | Google Scholar

Arora, R., and Garg, H. (2018). A robust aggregation operators for multi-criteria decision-making with intuitionistic fuzzy soft set environment. Sci. Iran. 25, 931–942.

Google Scholar

Atanassov, K. (1986). Intuitionistic fuzzy sets. fuzzy sets Syst. 20 (1), 87–96.

CrossRef Full Text | Google Scholar

Badi, I., and Pamucar, D.University of Defence in Belgrade, Department of Logistics, Belgrade, Serbia (2020). Supplier selection for steelmaking company by using combined grey-marcos methods. Decis. Mak. Appl. Manag. Eng. 3, 37–48. doi:10.31181/dmame2003037b

CrossRef Full Text | Google Scholar

Banaeian, N., Mobli, H., Fahimnia, B., Nielsen, I. E., and Omid, M. (2018). Green supplier selection using fuzzy group decision making methods: A case study from the agri-food industry. Comput. Operations Res. 89, 337–347. doi:10.1016/j.cor.2016.02.015

CrossRef Full Text | Google Scholar

Bellman, R. E., and Zadeh, L. A. (1970). Decision-making in a fuzzy environment. Manag. Sci. 17, B-141–B-164. B–141. doi:10.1287/mnsc.17.4.b141

CrossRef Full Text | Google Scholar

De, S. K., Biswas, R., and Roy, A. R. (2000). Some operations on intuitionistic fuzzy sets. Fuzzy sets Syst. 114, 477–484. doi:10.1016/s0165-0114(98)00191-2

CrossRef Full Text | Google Scholar

Erceg, Ž., and Mularifović, F. (2019). Integrated mcdm model for processes optimization in supply chain management in wood company. Operational Res. Eng. Sci. Theory Appl. 2, 37–50.

CrossRef Full Text | Google Scholar

Feng, F., Jun, Y. B., and Zhao, X. (2008). Soft semirings. Comput. Math. Appl. 56, 2621–2628. doi:10.1016/j.camwa.2008.05.011

CrossRef Full Text | Google Scholar

Gayen, S., Smarandache, F., Jha, S., Singh, M. K., Broumi, S., and Kumar, R. (2020). Introduction to plithogenic hypersoft subgroup (Infinite Study).

Google Scholar

Gegovska, T., Koker, R., and Cakar, T. (2020). Green supplier selection using fuzzy multiple-criteria decision-making methods and artificial neural networks. Comput. Intell. Neurosci. 2020, 1–26. doi:10.1155/2020/8811834

CrossRef Full Text | Google Scholar

Ghosh, S., Mandal, M. C., and Ray, A. (2022). A pdca based approach to evaluate green supply chain management performance under fuzzy environment. Int. J. Manag. Sci. Eng. Manag., 1–15. doi:10.1080/17509653.2022.2027292

CrossRef Full Text | Google Scholar

Hall, J., and Vredenburg, H. (2003). The challenge of innovating for sustainable development. MIT Sloan Manag. Rev. 45, 61.

Google Scholar

Hussain, A., Ali, M. I., Mahmood, T., and Munir, M. (2020). q-rung orthopair fuzzy soft average aggregation operators and their application in multicriteria decision-making. Int. J. Intelligent Syst. 35, 571–599. doi:10.1002/int.22217

CrossRef Full Text | Google Scholar

Jiang, Y., Tang, Y., Chen, Q., Wang, J., and Tang, S. (2010). Extending soft sets with description logics. Comput. Math. Appl. 59, 2087–2096. doi:10.1016/j.camwa.2009.12.014

CrossRef Full Text | Google Scholar

Khan, S., Gulistan, M., Kausar, N., Kousar, S., Pamucar, D., and Addis, G. M. (2022a). Analysis of cryptocurrency market by using q-rung orthopair fuzzy hypersoft set algorithm based on aggregation operators. Complexity 2022, 1–16. doi:10.1155/2022/7257449

CrossRef Full Text | Google Scholar

Khan, S., Gulistan, M., and Wahab, H. A. (2022b). Development of the structure of q-rung orthopair fuzzy hypersoft set with basic operations. Punjab Univ. J. Math. 53, 881–892. doi:10.52280/pujm.2021.531204

CrossRef Full Text | Google Scholar

Kong, Z., Gao, L., and Wang, L. (2009). Comment on “a fuzzy soft set theoretic approach to decision making problems”. J. Comput. Appl. Math. 223, 540–542. doi:10.1016/j.cam.2008.01.011

CrossRef Full Text | Google Scholar

Kong, Z., Gao, L., Wang, L., and Li, S. (2008). The normal parameter reduction of soft sets and its algorithm. Comput. Math. Appl. 56, 3029–3037. doi:10.1016/j.camwa.2008.07.013

CrossRef Full Text | Google Scholar

Li, D.-F. (2005). Multiattribute decision making models and methods using intuitionistic fuzzy sets. J. Comput. Syst. Sci. 70, 73–85. doi:10.1016/j.jcss.2004.06.002

CrossRef Full Text | Google Scholar

Li, D., and Zeng, W. (2018). Distance measure of pythagorean fuzzy sets. Int. J. Intelligent Syst. 33, 348–361. doi:10.1002/int.21934

CrossRef Full Text | Google Scholar

Liu, H.-W., and Wang, G.-J. (2007). Multi-criteria decision-making methods based on intuitionistic fuzzy sets. Eur. J. Operational Res. 179, 220–233. doi:10.1016/j.ejor.2006.04.009

CrossRef Full Text | Google Scholar

Mabrouk, N. (2021). Green supplier selection using fuzzy delphi method for developing sustainable supply chain. Decis. Sci. Lett. 10, 63–70. doi:10.5267/j.dsl.2020.10.003

CrossRef Full Text | Google Scholar

Maji, P. K., Biswas, R., and Roy, A. (2001). Fuzzy soft sets.

Google Scholar

Majumdar, P., and Samanta, S. (2011). On similarity measures of fuzzy soft sets. Int. J. Adv. Soft Comput. Appl. 3, 1–8.

Google Scholar

Martin, N., and Smarandache, F. (2020). Concentric plithogenic hypergraph based on plithogenic hypersoft sets–A novel outlook (Infinite Study).

Google Scholar

Molodtsov, D. (1999). Soft set theory—First results. Comput. Math. Appl. 37, 19–31. doi:10.1016/s0898-1221(99)00056-5

CrossRef Full Text | Google Scholar

Pamucar, D.University of Defence, Military academy, Department of logistics, Belgrade, Serbia (2020). Normalized weighted Geometric Dombi Bonferoni Mean Operator with interval grey numbers: Application in multicriteria decision making. Rep. Mech. Eng. 1, 44–52. doi:10.31181/rme200101044p

CrossRef Full Text | Google Scholar

Peng, X., and Yang, Y. (2015). Some results for pythagorean fuzzy sets. Int. J. Intelligent Syst. 30, 1133–1160. doi:10.1002/int.21738

CrossRef Full Text | Google Scholar

Peng, X., and Yuan, H. (2016). Fundamental properties of pythagorean fuzzy aggregation operators. Fundam. Inf. 147, 415–446. doi:10.3233/fi-2016-1415

CrossRef Full Text | Google Scholar

Puška, A., Beganović, A., Stojanović, I., and Murtič, S. (2022). Green supplier’s selection using economic and environmental criteria in medical industry. Environ. Dev. Sustain., 1–22.

Google Scholar

Qu, G., Zhang, Z., Qu, W., and Xu, Z. (2020). Green supplier selection based on green practices evaluated using fuzzy approaches of topsis and electre with a case study in a Chinese internet company. Int. J. Environ. Res. public health 17, 3268. doi:10.3390/ijerph17093268

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahman, A. U., Saeed, M., Khalid, A., Ahmad, M. R., and Ayaz, S. (2021). Decision-making application based on aggregations of complex fuzzy hypersoft set and development of interval-valued complex fuzzy hypersoft set. Neutrosophic Sets Syst. 46, 22.

Google Scholar

Rahman, A. U., Saeed, M., Khalifa, H. A., Afifi, W. A., et al. (2022a). Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets. AIMS Math. 7(3), 3866–3895. doi:10.3934/math.2022214

CrossRef Full Text | Google Scholar

Rahman, A. U., Saeed, M., Mohammed, M. A., Majumdar, A., and Thinnukool, O. (2022b). Supplier selection through multicriteria decision-making algorithmic approach based on rough approximation of fuzzy hypersoft sets for construction project. Buildings 12, 940. doi:10.3390/buildings12070940

CrossRef Full Text | Google Scholar

Saeed, M., Ahsan, M., Saeed, M. H., Rahman, A. U., Mehmood, A., Mohammed, M. A., et al. (2022). An optimized decision support model for Covid-19 diagnostics based on complex fuzzy hypersoft mapping. Mathematics 10, 2472. doi:10.3390/math10142472

CrossRef Full Text | Google Scholar

Saeed, M., Ahsan, M., Siddique, M. K., and Ahmad, M. R. (2020). A study of the fundamentals of hypersoft set theory (Infinite Study).

Google Scholar

Saqlain, M., Jafar, N., Moin, S., Saeed, M., and Broumi, S. (2020a). Single and multi-valued neutrosophic hypersoft set and tangent similarity measure of single valued neutrosophic hypersoft sets. Neutrosophic Sets Syst. 32, 317–329.

Google Scholar

Saqlain, M., Moin, S., Jafar, M. N., Saeed, M., and Smarandache, F. (2020b). Aggregate operators of neutrosophic hypersoft set (Infinite Study).

Google Scholar

Sénquiz-Díaz, C. (2021). Transport infrastructure quality and logistics performance in exports. ECONOMICS-Innovative Econ. Res. 9, 107–124. doi:10.2478/eoik-2021-0008

CrossRef Full Text | Google Scholar

Sheng, X., Chen, L., Yuan, X., Tang, Y., Yuan, Q., Chen, R., et al. (2022). Green supply chain management for a more sustainable manufacturing industry in china: a critical review, 1–33.Environ. Dev. Sustain.

Siddique, I., Zulqarnain, R. M., Ali, R., Jarad, F., and Iampan, A. (2021). Multicriteria decision-making approach for aggregation operators of pythagorean fuzzy hypersoft sets. Comput. Intell. Neurosci. 2021, 1–19. doi:10.1155/2021/2036506

CrossRef Full Text | Google Scholar

Siddique, N., and Adeli, H. (2013). Computational intelligence: Synergies of fuzzy logic, neural networks and evolutionary computing. John Wiley and Sons.

Google Scholar

Smarandache, F. (2018). Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets Syst. 22, 168–170.

Google Scholar

Stević, Ž., Vasiljević, M., Puška, A., Tanackov, I., Junevičius, R., and Vesković, S. (2019). Evaluation of suppliers under uncertainty: A multiphase approach based on fuzzy ahp and fuzzy edas. Transport 34, 52–66. doi:10.3846/transport.2019.7275

CrossRef Full Text | Google Scholar

Wang, W., and Liu, X. (2011). Intuitionistic fuzzy geometric aggregation operators based on einstein operations. Int. J. Intelligent Syst. 26, 1049–1075. doi:10.1002/int.20498

CrossRef Full Text | Google Scholar

Wei, G., and Lu, M. (2018). Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int. J. Intelligent Syst. 33, 169–186. doi:10.1002/int.21946

CrossRef Full Text | Google Scholar

Xu, Z. (2011). Intuitionistic fuzzy multiattribute decision making: An interactive method. IEEE Trans. Fuzzy Syst. 20, 514–525.

Google Scholar

Yager, R. R., and Abbasov, A. M. (2013). Pythagorean membership grades, complex numbers, and decision making. Int. J. Intelligent Syst. 28, 436–452. doi:10.1002/int.21584

CrossRef Full Text | Google Scholar

Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 25, 1222–1230. doi:10.1109/tfuzz.2016.2604005

CrossRef Full Text | Google Scholar

Yang, S., Nasr, N., Ong, S., and Nee, A. (2017). Designing automotive products for remanufacturing from material selection perspective. J. Clean. Prod. 153, 570–579. doi:10.1016/j.jclepro.2015.08.121

CrossRef Full Text | Google Scholar

Yang, X., Lin, T. Y., Yang, J., Li, Y., and Yu, D. (2009). Combination of interval-valued fuzzy set and soft set. Comput. Math. Appl. 58, 521–527. doi:10.1016/j.camwa.2009.04.019

CrossRef Full Text | Google Scholar

Yazdani, M., Chatterjee, P., Zavadskas, E. K., and Zolfani, S. H. (2017). Integrated qfd-mcdm framework for green supplier selection. J. Clean. Prod. 142, 3728–3740. doi:10.1016/j.jclepro.2016.10.095

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. control 8, 338–353. doi:10.1016/s0019-9958(65)90241-x

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1973). Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man, Cybern., 28–44. doi:10.1109/tsmc.1973.5408575

CrossRef Full Text | Google Scholar

Zhang, N., Zhou, Q., and Wei, G. (2022). Research on green supplier selection based on hesitant fuzzy set and extended linmap method. Int. J. Fuzzy Syst. 24, 3057–3066. doi:10.1007/s40815-022-01250-x

CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Siddique, I., Ali, R., Pamucar, D., Marinkovic, D., and Bozanic, D. (2021a). Robust aggregation operators for intuitionistic fuzzy hypersoft set with their application to solve mcdm problem. Entropy 23, 688. doi:10.3390/e23060688

PubMed Abstract | CrossRef Full Text | Google Scholar

Zulqarnain, R. M., Xin, X. L., and Saeed, M. (2021b). A development of pythagorean fuzzy hypersoft set with basic operations and decision-making approach based on the correlation coefficient. Theory Appl. Hypersoft Set 6.

Google Scholar

Zulqarnain, R. M., Xin, X. L., and Saeed, M.School of Science, Xi'an Polytechnic University, Xi'an 710048, ChinaDepartment of Mathematics, School of Science, University of Management and Technology, Lahore, Pakistan (2020). Extension of topsis method under intuitionistic fuzzy hypersoft environment based on correlation coefficient and aggregation operators to solve decision making problem. AIMS Math. 6, 2732–2755. doi:10.3934/math.2021167

CrossRef Full Text | Google Scholar