Exploring the driving forces of CO2 emission changes in Chinese cities: A production-theoretical decomposition analysis

Analyzing the forces driving CO₂ emissions in cities could provide valuable information for carbon reduction policies in China. This study uses an improved production-theoretical decomposition analysis to evaluate the CO₂ emissions of 282 cities in China during 2003–2017. The empirical results show that the scale, energy intensity, and desirable output productivity effects contributed to about 15.03%, 3.64%, and 2.3% growths in CO₂ emissions on average, respectively, while the potential CO₂ emission and undesirable output productivity effects were responsible for 5.81% and 5.72% reductions in CO₂ emissions. By classifying the sample cities and analyzing them further, it was found that the potential CO₂ emission effect has a stronger inhibitory impact in resource-based cities. However, the promoting effects of the scale effect is more obvious in non-resource-based cities. From a spatial distribution perspective, the potential CO₂ emission effect has a more obvious inhibitory role, and the energy intensity effect is a strong measure for controlling the growth of CO₂ emissions in the eastern region. However, the contribution of the scale effect to CO₂ emissions is more pronounced in the western region. In addition, we found that the desirable output productivity effects had a suppressive effect in the eastern region and facilitating effects in the central and western regions. The undesirable output productivity effect had a suppressive effect on the growth of CO₂ emissions in all three regions, but the suppressive effects were more pronounced in the eastern region.

1 Introduction

In recent years, global climate change has become an important issue that has sustained attention from many countries around the world (Liu et al., 2019; Awodumi and Adewuyi, 2020; Beltrami et al., 2021; Rehman et al., 2021). The massive emissions of carbon dioxide (CO₂), one of the greenhouse gases, cause serious global warming. The International Energy Agency (IEA) reported that CO₂ emissions would increase by nearly 5% to 33 billion tons in 2021 and that its main driver is coal demand, which is expected to grow by 4.5%, exceeding the 2019 levels and nearing its historical peak since 2014 (IEA, 2021b). Notably, cities consume two-thirds of the energy while generating over 70% of the global annual CO₂ emissions (IEA, 2021a). Therefore, the urban CO₂ emissions need more attention.

Consequently, it is an effective measure to mitigate global climate change via research on the forces driving CO₂ emission changes and by formulating targeted policies. Therefore, many scholars have studied the driving factors of CO₂ emissions (Li Y. et al., 2018; Wang and Zhang, 2021). Over the past few decades, China has become the largest developing country in the world. Rapid economic growth usually results in consumption of large amounts of fossil-based energy, with extremely high CO₂ emissions. Nowadays, as the country with the highest CO₂ emissions in the world, the Chinese government is formulating and implementing relevant policies to achieve “dual carbon” and “sustainable development” plans in response to global energy conservation and emission reduction targets. Chinese cities are responsible for about 85% of the overall CO₂ emissions in China (Mi et al., 2016). As a result, the issue of CO₂ emissions from Chinese cities deserves widespread attention (Shan et al., 2022).

To explore the causes of changes in the CO₂ emissions, the index decomposition analysis (IDA) and structural decomposition analysis (SDA) are two basic methodologies used to analyze the factors driving CO₂ emissions; these were first proposed by Ang et al. (1998) and Chang and Lin (1998) to quantify the potential factors driving changes in terms of different indicators and to provide valuable information for decision makers. Essentially, the IDA as an accounting method can easily capture the impacts of various factors on energy consumption or changes in CO₂ emissions given a dataset. Moreover, the IDA affords the advantages of low data requirements while facilitating calculation and data analysis (Ang and Zhang, 2000; Yang et al., 2021). The IDA generally considers factors such as CO₂ and energy intensities while ignoring the effects of other factors such as scale and technical efficiency, and ignoring these factors may skew the results so as to impact policy-making (Lin and Du, 2014).

SDA is a widely used analytical tool for modeling the relationship between supply and demand in an economy built upon the input–output theory (Chang and Lin, 1998; Wang and Han, 2021). Thus, the research scope of SDA involves the study of a single economy or multiple economies. De Araújo et al. (2020) used the SDA to explore changes in the structure and CO₂ emissions of the European Union (EU) after accession of new member states. The SDA has high data requirements and relatively complex calculations, which are generally applicable to the analysis of CO₂ emissions generated in trade between countries (Wang Q. et al., 2022).

Zhou and Ang (2008) proposed a new approach of decomposition analysis based on production theory called the PDA, which combines a distance function and data envelopment analysis (DEA) to decompose the changes in the total CO₂ emissions. Given a set of input and output data, the production theory starts with the theoretical definition of general production technology using the best practice boundary based on the distance function. Then, the distance between the entity and best boundary indicates the degree of production inefficiency, through which the production efficiency and technology level of the entity can be assessed (Wang H. et al., 2018).

Based on literature, the PDA shows that low economic development, energy structure, and energy efficiency are the factors that contribute to China’s CO₂ emissions (Wang et al., 2015); moreover, high technical efficiency contributes to the promotion of energy intensity, while capital–energy substitution has counterproductive effects (Zhou et al., 2022). From the point of view of production efficiency, improving the efficiency of energy use and emission technology will contribute to the emission reduction targets of the Chinese provinces (Wang H. et al., 2018). Wang et al. (2019) proposed an improved PDA method based on the non-radial directional distance function (DDF) and global Malmquist–Luenberger productivity index called the DDF-PDA; the researchers applied DDF-PDA to examine CO₂ emissions from China’s energy industry and found that the methodology evaluates the decomposition efficiency more accurately and alleviates the infeasibility of linear programming compared to the traditional SDF-PDA. Tian et al. (2022) demonstrated the effects of efficiency and technology on the changes in sulfur dioxide (SO₂) emissions from China’s industries during cleaner production and terminal treatment via the decomposition analysis method of the two-stage production theory. Nevertheless, using any one method alone to explore the factors driving CO₂ emissions would not solve some of the complicated problems, so some scholars have integrated the IDA and PDA to formulate a new combined decomposition method (Ding et al., 2021; Wang Q. et al., 2022).

Numerous scholars have investigated the sources of urban CO₂ emissions from production, consumption, or income perspectives (Zhang et al., 2016; Shao et al., 2020) and found that the emissions from fixed capital formation are dominant in most cities (Mi et al., 2019); to achieve the goal of reducing CO₂ emissions, policy formulation should therefore focus on aspects such as encouraging low carbon consumption for residents and controlling capital investments in high-income CO₂-emitting enterprises (Li J. S. et al., 2018). There are some studies on urban CO₂ emissions that have focused mainly on national, regional, and provincial spatial scales, and many of these studies are analyzed from sectoral perspective (Li C. et al., 2022). In the research works on CO₂ emissions using city unit data, possible scenarios for urban emission reductions applicable to individual cities have been proposed; for example, a scenario for Kyoto City found that Japan could achieve the national challenge goal of 80% CO₂ reduction by 2050 (Shigeto et al., 2012). Sun et al. (2020) proposed an urban-industrial symbiosis system strategy and conducted feasibility studies on applying this strategy in the industrial city of Shenyang; they discovered that implementation of the system allowed the city to recover a certain amount of energy while reducing CO₂ emissions.

Given the circumstances discussed above, the previously reported studies still have some drawbacks. First, among the studies on the factors driving urban CO₂ emissions, very few have conducted global and systematic analyses of all cities in China. Second, the PDA methods have rarely been applied to existing studies on urban CO₂ emissions. However, low carbon emission reduction targets cannot be achieved without studying the CO₂ emissions from cities as they are the basic units of environmental policy implementations and priority areas for emission reductions (Fang et al., 2022).

In this study, we examine the specific factors driving the growth of CO₂ emissions in 282 Chinese cities from 2003 to 2017 from an improved production-theoretical decomposition perspective. Moreover, this study aims to fill the existing research gaps in the following areas: first, we consider useful insights and holistic analysis to reveal the specific driving effects behind urban CO₂ emissions that can be used for implementation of CO₂ emission mitigation target policies in China. Second, we overcome the drawbacks of the Shephard production function in the traditional PDA model and use the improved PDA model proposed by Wang et al. (2019) to explore the drivers of urban CO₂ emissions. This improved PDA model uses a non-radical and non-angular production function, which improves the accuracy of the estimation results and obtains more accurate drivers of the urban CO₂ emission changes, thereby helping the achievement of urban CO₂ emission reduction targets. Third, in addition to the systematic analysis of the drivers of urban CO₂ emission changes as a whole, detailed and rigorous analyses from two heterogeneous perspectives, namely resource-based and non-resource-based cities as well as regional spatial heterogeneity, are considered.

The remainder of this work is organized as follows. Section 2 discusses the methodology and data that support the results and discussion in Section 3. Section 4 presents the conclusions and policy implications of this study.

2 Methodology and data

2.1 Non-radial directional distance function

To describe a production process, we suppose that there are $n\left(n=\mathrm{1,2},...,N\right)$ decision-making units (DMU_S), the input matrix is $\mathrm{x}=\left(x_1^t,x_2^t,x_3^t,...,x_N^t\right),x\in R_{+}^N$, the desirable output matrix is $\mathrm{y}=\left(y_1^t,y_2^t,y_3^t,...,y_M^t\right),\mathit{y}\in R_{+}^M$, and the undesirable output matrix is $\mathrm{b}=\left(b_1^t,b_2^t,b_3^t,...,b_l^t\right),\mathit{b}\in R_{+}^I$, where $\mathrm{t}\left(t=\mathrm{1,2},...\mathit{T}\right)$. Therefore, the production technology (T) can be expressed as in Eq. 1:

$\mathit{T}=\left\{\left(x,y,b\right):x\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{e}\left(y,b\right)\right\}.(1)$

Based on Eq. 1, T is defined as environmental production technology, and each input can generate desirable and undesirable outputs. As described by Fare et al. (1989), if the outputs satisfy the assumption of strong disposability, then the undesirable outputs are identical to the desirable outputs and can be treated freely. In the production process, along with the desirable output growth, we need to control the increase in undesirable outputs. Therefore, this study assumes that the undesirable outputs are weakly disposable, as shown in (a). In addition, T must satisfy the null-jointness expressed by (b).

(a) If $\left(x,y,b\right)ϵT$ and $0\le \theta \le 1$, then $\left(x,\theta y,\theta b\right)ϵT$;

(b) If $\left(x,y,b\right)ϵT$ and$b=0$, then$y=0$.

As shown above, hypothesis (a) implies that the reduction in undesirable outputs must be accompanied by a proportional reduction in the desirable outputs, and hypothesis (b) implies that the generation of undesirable outputs is inevitable in the production process.

From the limitations of the Shephard distance function, traditional PDA measures the efficiency of breakdown of the elements relatively independently, which causes each decomposition efficiency using the distance function orientation to have an obvious difference. Under this circumstance, the measured efficiency is underestimated, leading to misunderstanding by the policymakers and the inability to create scientific and effective carbon reduction policies. The non-radial DDF can adjust the input and output non-proportional changes to allow an increase in the desirable outputs while ensuring reduction of the undesirable outputs, thereby overcoming the defects of the DEA method in the traditional PDA decomposition process. According to Zhou et al. (2012), the non-radial distance function is defined as follows:

$\overrightarrow{\mathrm{D}}\left(x,y,b;g\right)=\mathrm{s}\mathrm{u}\mathrm{p}\left\{{\omega }^T\beta :\left(\left(x,y,b\right)+g\times \mathit{d}\mathit{i}\mathit{a}\mathit{g}\left(\beta \right)\right)ϵT\right\},(2)$

where g is a clear direction vector given as $g=\left(-g_x,g_y,-g_b\right)$, indicating that the desirable outputs increase and undesirable outputs decrease. $\omega ={\left({\omega }_m^x,{\omega }_i^y,{\omega }_j^b\right)}^T$is the standardized weight matrix related to the number of input–output indicators, and $\beta ={\left({\beta }_m^x,{\beta }_i^y,{\beta }_j^b\right)}^T\ge 0$ represents the vector scale factor. We obtain $\overrightarrow{D}\left(x,y,b;g\right)$ from the linear programming approach in Eq. 3, whose specific programming method is as follows:

$\begin{array}{c}\overrightarrow{D}\left(x,y,b;g\right)=\max {\omega }_m^x{\beta }_m^{x,t}+{\omega }_i^y{\beta }_i^{y,t}+{\omega }_j^b{\beta }_j^{b,t},\\ s.t.{\displaystyle \sum }_{n=1}^N{z}_n^t{x}_{mn}^t\le x_m^t+{\beta }_m^{x,t}{g}_{xm},m=1,...,M,\\ {\displaystyle \sum }_{n=1}^N{z}_n^t{y}_{in}^t\ge y_i^t+{\beta }_i^{y,t}{g}_{yi},i=1,...,I,\\ {\displaystyle \sum }_{n=1}^N{z}_n^t{b}_{jn}^t=b_j^t+{\beta }_j^{b,t}{g}_{bj},j=1,...,J,\\ z_n\ge 0,n=1,...,N,t=1,...,T,\\ {\beta }_m^x,{\beta }_i^y,{\beta }_j^b\ge 0.\end{array}(3)$

Although the non-radial DDF overcomes the limitations of the traditional Shephard distance function, it may cause potential infeasibilities in the linear programming when measuring the cross-period DDF (Oh, 2010). Therefore, this study adopts the global non-radial DDF to overcome this defect, and the linear programming approach is as shown in Eq. 4:

$\begin{array}{c}{\overrightarrow{D}}^G\left(x,y,b;g\right)=\max {\omega }_m^x{\beta }_m^{x,G}+{\omega }_i^y{\beta }_i^{y,G}+{\omega }_j^b{\beta }_j^{b,G},\\ s.t.{\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{n=1}^N{z}_n^t{x}_{mn}^t\le x_m^t+{\beta }_m^{x,G}{g}_{xm},m=1,...,M,\\ {\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{n=1}^N{z}_n^t{y}_{in}^t\ge y_i^t+{\beta }_i^{y,G}{g}_{yi},i=1,...,I,\\ {\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{n=1}^N{z}_n^t{b}_{jn}^t=b_j^t+{\beta }_j^{b,G}{g}_{bj},j=1,...,J,\\ z_n\ge 0,n=1,...,N,t=1,...,T,\\ {\beta }_m^x,{\beta }_i^y,{\beta }_j^b\ge 0.\end{array}(4)$

In the research process, we can adjust the direction vector g based on the objective. If $\overrightarrow{D}\left(x,y,b;g\right)=0$ or ${\overrightarrow{D}}^G\left(x,y,b;g\right)=0$, then the DMU measured is in the efficient frontier g best-practice direction and there is no efficiency loss. On the contrary, if $\overrightarrow{D}\left(x,y,b;g\right)>0$ or ${\overrightarrow{D}}^G\left(x,y,b;g\right)>0$, then the DMU is considered to have an efficiency loss along the direction vector g. According to Zhou et al. (2012), the standardized weight matrix is set as $\omega =\left(\mathrm{0,1}/\mathrm{6,1}/\mathrm{6,1}/\mathrm{3,1}/3\right)$.

2.2 Decomposition of CO₂ emissions

The traditional PDA method has drawbacks such as underestimating the classification efficiency and infeasibility of linear programming, which lead to potential bias or incomplete decomposition results. In contrast, the DDF-PDA presented herein alleviates the two problems associated with the traditional PDA, in addition to identifying the potential factors driving changes in CO₂ emissions more precisely (Wang et al., 2019).

Here, the input factors are set as the capital input (K), labor input (L), and energy input (E); the desirable output is the gross regional product (Y) and the undesirable output is the CO₂ emission (C). According to Kim and Kim (2012) and Wang et al. (2019), we decompose the CO₂ emissions in Chinese cities into an extended Kaya identity, as shown in Eq. 5.

$\begin{array}{cc}{C}_n^s=\left[\frac{C_n^s}{E_n^s}\right]\left[\frac{E_n^s}{Y_n^s}\right]\left[Y_n^s\right]& s\in \left\{T,T+1\right\}\end{array}.(5)$

Combining the non-radial DDF, we rewrite the extended Kaya identity in Eq. 5 as Eq. 6 to decompose the CO₂ emission changes.

$\begin{array}{c}{C}_n^s=\left[\frac{C_n^s\left(1-{\overrightarrow{D}}_{n,C}^G\left(·s\right)\right)}{E_n^s\left(1-{\overrightarrow{D}}_{n,E}^G\left(·s\right)\right)}\right]\times \left[\frac{E_n^s\left(1-{\overrightarrow{D}}_{n,E}^G\left(·s\right)\right)}{Y_n^s\left(1+{\overrightarrow{D}}_{n,Y}^G\left(·s\right)\right)}\right]\times \left[Y_n^s\right]\times \left[\frac{1}{\left(1-{\overrightarrow{D}}_{n,C}^G\left(·s\right)\right)}\right]\times \left[\left(1+{\overrightarrow{D}}_{n,Y}^G\left(·s\right)\right)\right]\end{array}.(6)$

In Eq. 6, we replace the elements ${\overrightarrow{D}}_{n,C}^G\left(K^s,L^s,E^s,Y^s,C^s;{\overrightarrow{g}}^s\right)$, ${\overrightarrow{D}}_{n,Y}^G\left(K^s,L^s,E^s,Y^s,C^s;{\overrightarrow{g}}^s\right)$, and ${\overrightarrow{D}}_{n,E}^G\left(K^s,L^s,E^s,Y^s,C^s;{\overrightarrow{g}}^s\right)$ with ${\overrightarrow{D}}_{n,C}^G\left(·s\right)$, ${\overrightarrow{D}}_{n,E}^G\left(·s\right)$, and ${\overrightarrow{D}}_{n,Y}^G\left(·s\right)$, respectively. The same replacement is used in the following decomposition. Specifically, we decompose the CO₂ emissions between time periods T and T+1 in Eq. 7.

$\begin{array}{c}\begin{array}{c}{R}_{tot}^{T,T+1}=\frac{C_n^{T+1}}{C_n^T}\\ =\left[\frac{C_n^{T+1}\left(1-{\overrightarrow{D}}_{n,C}^G\left({·}^{T+1}\right)\right)/E_n^{T+1}\left(1-{\overrightarrow{D}}_{n,E}^G\left({·}^{T+1}\right)\right)}{C_n^T\left(1-{\overrightarrow{D}}_{n,C}^G\left({·}^T\right)\right)/E_n^T\left(1-{\overrightarrow{D}}_{n,E}^G\left({·}^T\right)\right)}\right]\\ \times \left[\frac{E_n^{T+1}\left(1-{\overrightarrow{D}}_{n,E}^G\left({·}^{T+1}\right)\right)/Y_n^{T+1}\left(1+{\overrightarrow{D}}_{n,Y}^G\left({·}^{T+1}\right)\right)}{E_n^T\left(1-{\overrightarrow{D}}_{n,E}^G\left({·}^T\right)\right)/Y_n^T\left(1+{\overrightarrow{D}}_{n,Y}^G\left({·}^{T+1}\right)\right)}\right]\\ \times \left[\frac{Y_n^{T+1}}{Y_n^T}\right]\times \left[\frac{\left(1-{\overrightarrow{D}}_{n,C}^G\left({·}^T\right)\right)}{\left(1-{\overrightarrow{D}}_{n,C}^G\left({·}^{T+1}\right)\right)}\right]\times \left[\frac{\left(1+{\overrightarrow{D}}_{n,Y}^G\left({·}^{T+1}\right)\right)}{\left(1+{\overrightarrow{D}}_{n,Y}^G\left({·}^T\right)\right)}\right]\\ =R_{PCFC}^{T,T+1}\times R_{PEIC}^{T,T+1}\times R_{SCA}^{T,T+1}\times R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}\times R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}.\end{array}\end{array}(7)$

According to Eq. 7, the CO₂ emission changes in Chinese cities can be decomposed into five effects. On the right-hand side of Eq. 7, the first component is the CO₂ emission effect ($R_{PCFC}^{T,T+1}$), which accounts for the potential CO₂ emission changes in the Chinese cities. The second component represents the effects of potential energy intensity changes and is defined as the energy intensity effect ($R_{PEIC}^{T,T+1}$). The third component represents the scale effect ($R_{SCA}^{T,T+1}$), which reflects the contributions of economic activities to CO₂ emission changes in the Chinese cities. The fourth component ($R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$) and fifth component ($R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$) are defined as the undesirable and desirable output productivity effects, respectively, based on the global Malmquist–Luenberger (GML) productivity index. Specifically, the values of $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ and $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ are the reciprocals of the undesirable and desirable output productivity indexes based on the GML productivity index, respectively. For all the values of each effect in Eq. 7, the effect plays a negative role in decreasing CO₂ emissions in the Chinese cities if its value is greater than unity. On the contrary, if the value of each effect is less than unity, it will contribute to a decrease in the CO₂ emissions.

Based on Oh (2010), we can further decompose the desirable and undesirable output productivity effects in Eq. 7 into Eq. 8 and Eq. 9, respectively.

$\begin{array}{l}{R}_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}=\frac{\left(1-{\overrightarrow{D}}_{n,C}^G\left({·}^T\right)\right)}{\left(1-{\overrightarrow{D}}_{n,C}^G\left({·}^{T+1}\right)\right)}\\ =\left[\frac{\left(1-{\overrightarrow{D}}_{n,C}^T\left({·}^T\right)\right)}{\left(1-{\overrightarrow{D}}_{n,C}^{T+1}\left({·}^{T+1}\right)\right)}\right]\times \left[\frac{\left(1-{\overrightarrow{D}}_{n,C}^G\left({·}^T\right)\right)/\left(1-{\overrightarrow{D}}_{n,C}^T\left({·}^T\right)\right)}{\left(1-{\overrightarrow{D}}_{n,C}^G\left({·}^{T+1}\right)\right)/\left(1-{\overrightarrow{D}}_{n,C}^{T+1}\left({·}^{T+1}\right)\right)}\right]\\ =\left[\frac{T{E}_{n,C}^T}{T{E}_{n,C}^{T+1}}\right]\times \left[\frac{BP{G}_{n,C}^T}{BP{G}_{n,C}^{T+1}}\right]\\ =R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}\times R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}\end{array}(8)$

$\begin{array}{l}{R}_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}=\frac{\left(1+{\overrightarrow{D}}_{n,Y}^G\left({·}^T\right)\right)}{\left(1+{\overrightarrow{D}}_{n,Y}^G\left({·}^{T+1}\right)\right)}\\ =\left[\frac{\left(1+{\overrightarrow{D}}_{n,Y}^T\left({·}^T\right)\right)}{\left(1+{\overrightarrow{D}}_{n,Y}^{T+1}\left({·}^{T+1}\right)\right)}\right]\times \left[\frac{\left(1+{\overrightarrow{D}}_{n,Y}^G\left({·}^T\right)\right)/\left(1+{\overrightarrow{D}}_{n,Y}^T\left({·}^T\right)\right)}{\left(1+{\overrightarrow{D}}_{n,Y}^G\left({·}^{T+1}\right)\right)/\left(1+{\overrightarrow{D}}_{n,Y}^{T+1}\left({·}^{T+1}\right)\right)}\right]\\ =\left[\frac{T{E}_{n,Y}^T}{T{E}_{n,Y}^{T+1}}\right]\times \left[\frac{BP{G}_{n,Y}^T}{BP{G}_{n,Y}^{T+1}}\right]\\ =R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}\times R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}\end{array}(9)$

In Eqs. 8, 9, the respective desirable and undesirable output productivity effects are decomposed into two components each. On the right-hand sides of Eqs. 8, 9, the first components represent the technical efficiency change effects ($R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}$ and $R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}$), which account for the reciprocals of the efficiency changes. The range of technical efficiency values is from 0 to 1. The higher the value, the higher is the technical efficiency. Specifically, if $R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}>1$ or $R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}>1$, it means that the technical efficiency is negative for controlling the CO₂ emissions. On the contrary, if $R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}<1$ or $R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}<1$, it reflects that the technical efficiency is better for reducing CO₂ emissions.

The second components of the right-hand sides of Eqs. 8, 9 capture the effects of the best-practice gap changes on CO₂ emissions ($R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}$ and $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}$). Meanwhile, $R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}$ and $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}$ also represent the reciprocals of these best-practice gap changes, whose values range from 0 to 1. The best-practice gap is a proxy of the distance that shows how close the contemporary and global technology frontiers are under the direction vectors (Oh, 2010). Under this consideration, $R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}>1$ or $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}>1$ indicates a technical regress, which negatively controls CO₂ emissions. On the contrary, $R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}<1$ or $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}<1$ reflects technical progress that is better for reducing CO₂ emissions.

Combing Eqs. 8, 9, the final decomposition of the CO₂ emissions in Chinese cities is expressed as in Eq. 10.

$\begin{array}{c}\begin{array}{c}{R}_{tot}^{T,T+1}=\frac{C_n^{T+1}}{C_n^T}\\ =R_{PCFC}^{T,T+1}\times R_{PEIC}^{T,T+1}\times R_{SCA}^{T,T+1}\times \underset{R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}}{\underbrace{R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}\times R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}}}\times \underset{R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}}{\underbrace{R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}\times R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}}}\end{array}\end{array}.(10)$

2.3 Data

In this study, 282 prefecture-level cities in China from 2003 to 2017 were selected as the research samples. The data on capital input is measured using the total investment in fixed assets. Labor input is measured by the number of employees at the end of a year. Energy input is represented by the electricity consumption data of urban districts (Yuan et al., 2020). The GDP and CO₂ emissions of the cities are selected as the desirable and undesirable outputs, respectively. The CO₂ emission data were retrieved from Chen et al. (2020). Specifically, the Defense Meteorological Satellite Program/Operational Linescan System (DMSP/OLS) and National Polar-Orbiting Partnership/Visible Infrared Imaging Radiometer Suite (NPP/VIIRS) were used together to calculate the energy-related CO₂ emissions from 282 cities in China for 2003 to 2017. They are included in the model as the undesirable outputs in this work (Chen et al., 2020). The socioeconomic and environmental data were mainly retrieved from the China City Statistical Yearbook. The indicators and descriptive statistics of the input and output variables are shown in Table 1.

TABLE 1

TABLE 1. Indicators and descriptive statistics of the input and output variables.

3 Results and discussion

3.1 Results of CO₂ emission decomposition

To better understand how the factors shape the changes in CO₂ emissions in Chinese cities, Figure 1 shows the results of the decomposed components from 2003 to 2017. According to our estimations, the $R_{SCA}^{T,T+1}$ represented the most significant component of CO₂ emission change at the city level, with an average value of 1.1503, indicating that the $R_{SCA}^{T,T+1}$ accounts for 15.03% of the CO₂ emission growth rate. Specifically, $R_{SCA}^{T,T+1}$ boosted CO₂ emissions across the entire study period, especially from 2003 to 2011. This indicated that the economic activities in Chinese cities led to increased CO₂ emissions, which echoed previous research (Zhao et al., 2020a; Zhao et al., 2020b).

FIGURE 1

FIGURE 1. Changes in the CO₂ emission decomposition components.

Meanwhile, $R_{PEIC}^{T,T+1}$ measures the potential energy intensity changes on CO₂ emission changes, and it was the second most important component of CO₂ emission changes in Chinese cities, with an average value of 1.0364. As shown in Figure 1, the impact of $R_{PEIC}^{T,T+1}$ on the decrease in CO₂ emissions was negative for most of the study period. Furthermore, $R_{PEIC}^{T,T+1}$ fluctuated around unity for most of the study period except 2006–2007. This suggests that the economic development of the Chinese cities still relies on fossil-based energy and that the energy structure needs to be optimized to reduce CO₂ emissions (Wang et al., 2021).

Conversely, $R_{PCFC}^{T,T+1}$ is the force that drives the reduction in CO₂ emissions in Chinese cities, with an average value of 0.9419. However, the value of $R_{PCFC}^{T,T+1}$ was greater than unity during 2007–2009 and 2011–2012. In the other periods, the value of $R_{PCFC}^{T,T+1}$ was lower than unity, especially in 2016–2017. A possible reason for this is the improvement in the energy mix of the Chinese cities and relatively high energy consumption efficiency during the production process. Moreover, to meet the global climate goals, cities in China need to realize successful transition to low-carbon energy systems, which indicates that the proportion of non-fossil fuels will increase in the energy systems (Li K. et al., 2022).

$R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ is an important component of the CO₂ emission change in Chinese cities, with an average value of 0.9428. In other words, $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ curbed the growth of CO₂ emissions by approximately 5.72% in Chinese cities. From a time-series perspective, $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ values in four study periods played positive roles in the CO₂ emissions shown in Figure 1. Among the $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ values that led to decreased CO₂ emissions, $R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}$ and $R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}$ contributed to the growth of CO₂ emissions in the cities by 5.72% and −6.82%, respectively. Therefore, technological progress has contributed to the reduction of CO₂ emissions, but technical efficiency should still be improved so as to promote the realization of China’s emission reduction targets more effectively (Pan et al., 2022).

The impact of $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ on the reduced growth of CO₂ emissions was negative, with an average value of 1.0230. In other words, $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ accounted for a CO₂ emission growth of about 2.3% in Chinese cities. The results in Figure 1 show that $R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}$ accounts for the CO₂ emissions of approximately −0.48% from Chinese cities, which indicates improvement in the technical efficiency during the process. In addition, $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}$ was a positive factor for $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$, with an average value of 1.0911, and the values of $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}$ that were greater than unity corresponded to technical regression.

As presented in Figure 2, the observation period can be divided into five stages, including the beginning years (2003–2005), the 11th five-year period (2006–2010), the 12th five-year period (2011–2015), the recent years (2016–2017), and the entire study period (2003–2017). We note that the differences in the contributions of the components to CO₂ emissions change among these five stages. The changing trends with respect to $R_{PCFC}^{T,T+1}$ negatively contributed to a decrease in CO₂ emission growth for all the study stages, with only slight gaps between the beginning years, 11th five-year period, and 12th five-year period. Moreover, there was a significant decrease in $R_{PCFC}^{T,T+1}$, which indicated that $R_{PCFC}^{T,T+1}$ was the dominant contributor to reductions in CO₂ emissions in recent years (2016–2017). Simultaneously, the $R_{PEIC}^{T,T+1}$ continued to promote CO₂ emission growths in all study stages, except for the recent years. Moreover, this promotion effect showed an upward trend, and the contribution peaked to 39.92% in the 11th five-year period.

FIGURE 2

FIGURE 2. Contributions of different components to CO₂ emissions in five stages.

Compared with the other decomposition components, $R_{SCA}^{T,T+1}$ contributed to CO₂ emission growths in all five study periods shown in Figure 2. From the beginning to the 12th five-year period, $R_{SCA}^{T,T+1}$ experienced a decreasing trend from an average value of 1.1983 to 1.0936. On the contrary, there was an upward trend from the 12th five-year period to the entire study period, increasing from an average value of 1.0936 to 1.1449. The growth caused by $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ in these five stages was negative for the last four stages after being positive from 2003 to 2005. During the last four stages, there were significant fluctuations, especially in the 12th five-year period, which positively contributed to decreased growth of CO₂ emissions in Chinese cities. Among $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$, $R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}$ and $R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}$ showed their own fluctuation characteristics, as shown in Figure 2. Meanwhile, $R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}$was the main obstacle preventing a decrease in the growth of CO₂ emissions from the average value.

During the first two stages, the values of $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ were consistently less than unity, which indicated that $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ suppressed CO₂ growth in Chinese cities. However, these inhibitory effects were converted to facilitatory effects in the later stages of study due to the values of $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ being consistently greater than unity. Meanwhile, among $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$, $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}$was the main obstacle preventing a decrease in the growth of CO₂ emissions from the average value, which was inconsistent with the effect of $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ on the change in CO₂ emissions in Chinese cities.

Compared with other research periods, some decomposition effects played better roles in controlling the urban CO₂ emissions in China during the 11th and 12th five-year periods, as shown in Figure 2, e.g., $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ and $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$. Furthermore, this phenomenon is closely related to China’s policies and measures. The Chinese government attaches great importance to energy conservation and emission reduction. In the 11th five-year plan period, the Chinese government proposed binding targets of 20% reduction in energy consumption per unit of GDP and 10% decrease in the total emissions of major pollutants. To achieve these goals, China has made efforts to adjust its industrial structure, promote technological progress, and strengthen regulation. In the 12th Five Year Plan period, the Chinese government added some new binding targets and called for the comprehensive use of adjusting its industrial and energy structures, saving energy and improving energy efficiency, as well as other means of promoting energy conservation and emission reduction.

3.2 City classification based on different criteria

3.2.1 Heterogeneity analysis in resource-based and non-resource-based cities

In 2013, the Chinese government issued China’s Sustainable Development Plan for Resource-Based Cities (2013–2020), which indicates that the development of resource-based cities is dependent on resource-intensive industries. In this condition, low carbon and energy transition are challenges for the resource-based cities. Owing to the heterogeneity of economic development and landscape in Chinese cities, we classified the cities as resource-based and non-resource-based cities to compare the decomposition components of the CO₂ emission changes and find specifically targeted policy suggestions for these two types of cities. Figure 3 shows the classification results for the resource-based and non-resource-based cities; Figure 4 shows the classification results of the two types of cities for the different study periods according to the average values of the decomposed components.

FIGURE 3

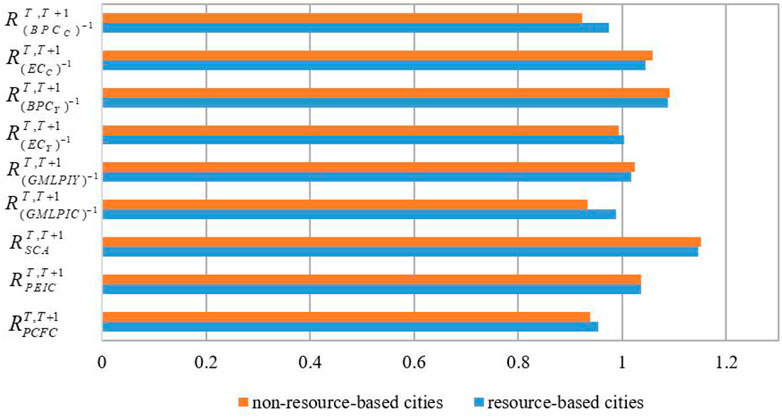
FIGURE 3. Decomposed components of the CO₂ emission changes in resource-based and non-resource-based cities.

FIGURE 4

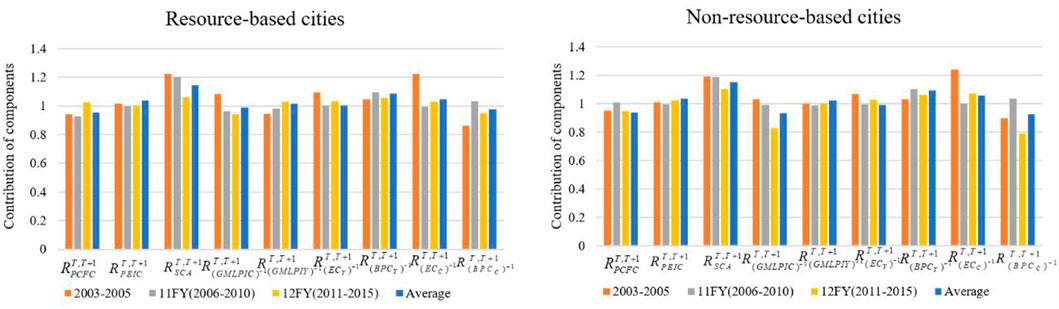
FIGURE 4. Decomposition effects of CO₂ emissions in resource-based and non-resource-based cities for different periods.

Comparing the decomposition components of CO₂ emission changes between the resource-based and non-resource-based cities, we found that the driving forces of the differences were generally in the same direction for both types of cities in China (Figure 3). In particular, $R_{PEIC}^{T,T+1}$, $R_{SCA}^{T,T+1}$, and $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ contributed to increase in CO₂ emissions in both the resource- and non-resource-based cities as a whole. Moreover, as further decomposition terms of $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ and $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$, $R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}$ and $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}$ showed trends of promoting increase in CO₂ emissions in both city types because their calculated average values were greater than unity. On the contrary, the other decomposition components generally accounted for reductions in CO₂ emissions, representing the inhibitory effects on the growth of CO₂ emissions.

Further, although the directions of action are roughly similar, different decomposition effects have different impacts on the types of cities. As shown in Figure 3, $R_{PCFC}^{T,T+1}$ inhibited CO₂ emissions, and this inhibition effect is more significant in the resource-based cities although the difference is not very large. Potential carbon emission reductions in the non-resource-based cities are higher. In terms of changes in $R_{PEIC}^{T,T+1}$, there is little difference between the two city types, although the value for the resource-based cities is slightly larger than that of the non-resource-based cities. This is closely related to the country’s emphasis on low-carbon development of resource-based cities.

Given the heterogeneity between the resource-based and non-resource-based cities, $R_{SCA}^{T,T+1}$ promoted CO₂ emissions in both types of cities but was more pronounced in the non-resource-based cities. $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ suppressed CO₂ emissions in both types of cities. Moreover, this inhibitory effect was more obvious in the non-resource-based cities. Through the calculated results, it was found that the strong inhibitory effects of $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ on CO₂ emissions in non-resource-based cities was due to technological progress. Meanwhile, the promotion effects of $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ on CO₂ emission increase was higher in the non-resource-based cities than in the resource-based cities. The value of $R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}$ was greater than unity in the non-resource-based cities, indicating that the technical efficiency reduced. However, in resource-based cities, the value of $R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}$ was less than unity, which indicated that the technical efficiency improved. The value of $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}$ was greater than unity in both types of cities, implying that there is technological regression in both city types.

To facilitate presentation, Figure 4 shows the decomposition effects of the CO₂ emissions in resource-based and non-resource-based cities for the different periods. As seen in Figure 4, during 2003–2005, $R_{PCFC}^{T,T+1}$ showed a restraining effect on CO₂ emissions in both types of cities. On the contrary, during the 11th five-year period, the restraining effects of non-resource-based cities turned to a small promoting effect. However, during the 12th five-year period, resource-based cities showed promotion effects and non-resource-based cities exhibited inhibitory effects, with the degree of change being not very significant. The change directions of $R_{PEIC}^{T,T+1}$ in the resource-based and non-resource-based cities are the same for each period, and the impact on CO₂ emissions is greater in resource-based cities, which shows that the resource-based cities need more measures such as industrial transfer and technology updates to realize sustainable development of the city. The promoting effects of $R_{SCA}^{T,T+1}$ were more obvious in the resource-based cities during 2003–2005 and was significantly flat during the 11th five-year period; it became more obvious in the 12th five-year period for the average level in the non-resource-based cities.

During 2003–2005, $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ played a promoting role in both types of cities, and the effects were more obvious in the resource-based cities. In the other time periods, it played a suppressive role. Specifically, during the 12th five-year period, the inhibitory effects of the non-resource-based cities were more significant. The value of $R_{{\left(E{C}_C\right)}^{-1}}^{T,T+1}$ was greater than unity in the non-resource-based cities in all study periods. On the contrary, during the 11th five-year period, technical efficiency improved in the resource-based cities, and no obvious improvements in technical efficiency were observed in the other periods. Furthermore, except for technological regression during the 11th five-year period, $R_{{\left(BP{C}_C\right)}^{-1}}^{T,T+1}$ has showed technological progress in both resource-based and non-resource-based cities for the other time periods. $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ presented an inhibitory effect on CO₂ emissions during 2003–2005 and 2006–2010 but showed a promoting effect during the 12th five-year plan period, with the promotion of resource-based cities being more obvious. The value of $R_{{\left(E{C}_Y\right)}^{-1}}^{T,T+1}$ was greater than unity in the resource-based cities, reducing technical efficiency and promoting CO₂ emissions. On the contrary, in the non-resource-based cities, there is room for CO₂ emission reduction. However, the value of $R_{{\left(BP{C}_Y\right)}^{-1}}^{T,T+1}$ was greater than unity in both types of cities at different periods, indicating technological regression and promotion of CO₂ emissions.

3.2.2 Heterogeneity analysis of regional differences in the driving effects of CO₂ emission changes

From a spatial distribution perspective, we can compare the regional differences in the driving effects of CO₂ emission changes. Figure 5 illustrates the driving effects of CO₂ emission changes and provides insights into the decomposition trends in the study periods in the eastern, central, and western regions. In general, the volatility of $R_{PCFC}^{T,T+1}$ is relatively large. This trend in the three regions revealed a diversification of the decomposition components driving reductions in CO₂ emissions, with inhibition at the beginning, then promotion, and finally inhibition again. Specifically, this fluctuation is the largest in the eastern region, and the inhibition effect is more obvious. In the eastern region, $R_{PCFC}^{T,T+1}$ has been shown to suppress CO₂ emissions for most of the years compared to the other two regions. Specifically, in 2016–2017, $R_{PCFC}^{T,T+1}$ inhibited growth in CO₂ emissions in eastern cities, accounting for 0.5140 of the decline in CO₂ emissions on average. Cities in the eastern region are dominated by developed cities such as Beijing and Shanghai. The development of the digital economy and high-tech industries reduces the possibility of potential increase in the CO₂ emissions in the future (Wang et al., 2020a). This implies that the effect of $R_{PCFC}^{T,T+1}$ on suppressing the increase in CO₂ emission is stronger than those in other regions.

FIGURE 5

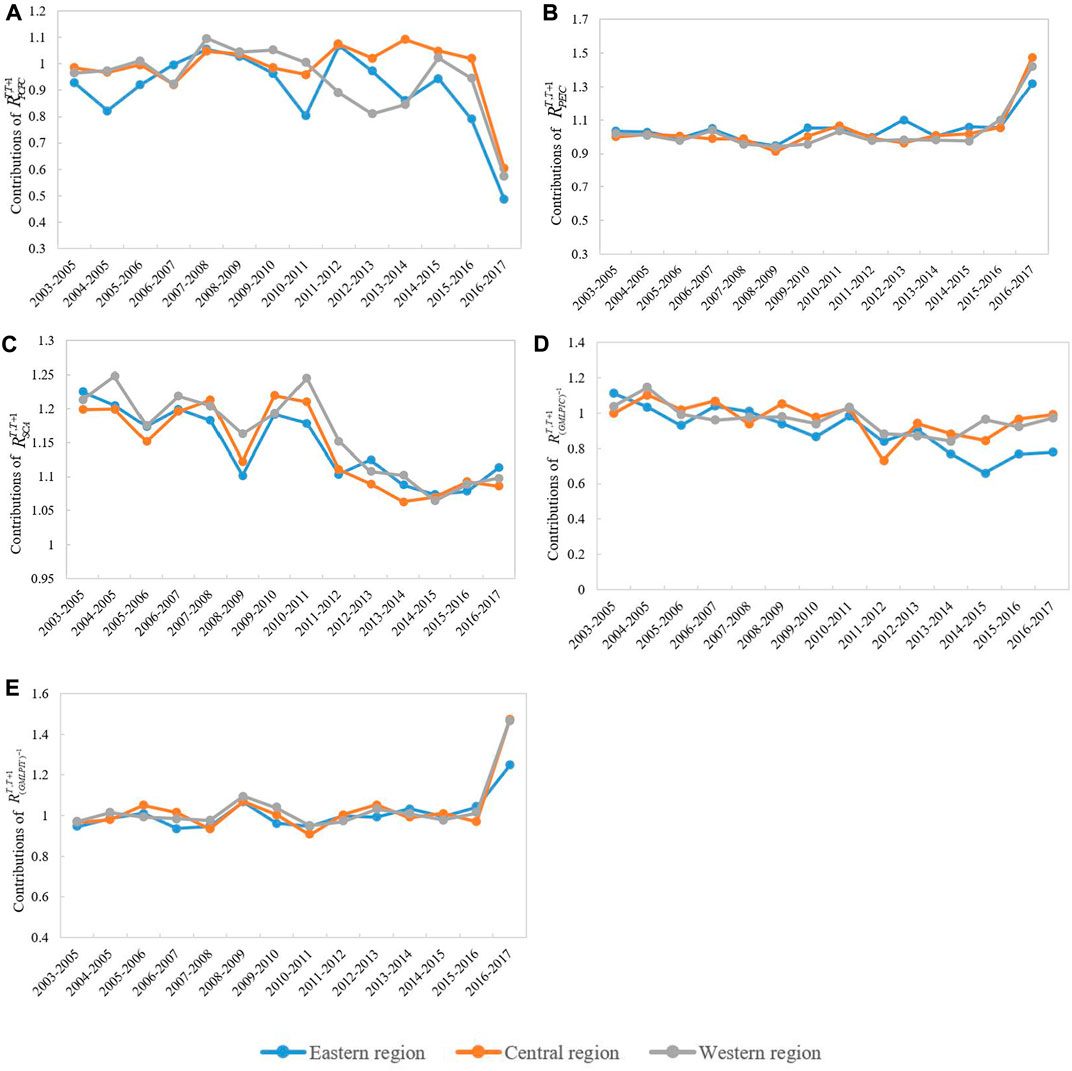
FIGURE 5. Driving effects of CO₂ emission changes in three regions during the period of 2003–2017: (A) $R_{PCFC}^{T,T+1}$; (B) $R_{PEIC}^{T,T+1}$; (C) $R_{SCA}^{T,T+1}$; (D) $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$; (E) $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$.

Overall, $R_{PEIC}^{T,T+1}$ at the regional level showed a stable and upward trend from 2003 to 2017. In the process, changes in the eastern region are larger than those in the other regions, and $R_{PEIC}^{T,T+1}$ is the core force driving the changes in CO₂ emissions; it is greater than unity for most years, showing a promotional effect during 2011–2012. In contrast, the central and western regions showed more years with inhibitory effects. Moreover, $R_{PEIC}^{T,T+1}$ showed a trend of promoting growth of CO₂ emissions in the central and western regions, indicating that $R_{PEIC}^{T,T+1}$ should be a powerful factor controlling the increase in CO₂ emissions from each region. Although China has always advocated achieving carbon peak and carbon neutralization through energy transformation, it is difficult to control CO₂ emissions by improving the energy structure because of the large energy consumption. This implies that reducing the energy intensity by improving the energy structure and energy efficiency can achieve CO₂ emission reductions in the long term, which confirms the findings of Wang et al. (2020b).

It is worth mentioning that $R_{SCA}^{T,T+1}$ plays a role in promoting growth of CO₂ emissions in all years, but this role fluctuates greatly for different regions. The $R_{SCA}^{T,T+1}$ mainly measures the impact of local economic activities on the growth of CO₂ emissions. According to Figure 5C, the fluctuation of $R_{SCA}^{T,T+1}$ is largest in the western region, followed by the central region, and finally the eastern region. This is closely related to the differences in the speed of economic development in the three regions. Although the development of eastern China is better than that of the central and western regions, owing to China’s recent advocacy of a regional integration strategy through coordinated regional development, the development of the central and western regions is faster than that of the eastern region, which makes the $R_{SCA}^{T,T+1}$ promotion of CO₂ emissions more obvious. However, from this, we also note that in the early stages of economic development, we should implement a high-quality development strategy to control the increase in CO₂ emissions effectively.

Furthermore, $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ shows a decreasing trend in fluctuation, which means that the growth of CO₂ emissions is inhibited by $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ in all three regions. Thus, the increase in CO₂ emissions can be effectively controlled by promoting the increase of total factor productivity of the CO₂ emissions through technological progress and efficiency improvements. In short, $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ decreased significantly in the eastern region. This tells us that although the eastern region has higher CO₂ emissions, it also has the greatest potential to control these emissions. In contrast, although the CO₂ emission productivity indexes of cities in the central and western regions show growing trends, these are not obvious. According to the decomposition of CO₂ emission growth, the inhibitory effect of $R_{{\left(GMLPIC\right)}^{-1}}^{T,T+1}$ in the central and western regions is around the average value of unity, so it is possible to promote growth of CO₂ emissions at any time. This indicates that the existing total factor productivity of CO₂ emissions cannot effectively restrain the growth of CO₂ emissions, while placing higher requirements for the improvements in CO₂ emission technology and efficiency in the central and western regions (Wang S. et al., 2018; Wang S. et al., 2022).

Moreover, $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ shows a slow upward trend in volatility. Specifically, $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ is expressed as the inverse of the desirable output productivity, showing a trend of promoting growth of CO₂ emissions, which means that the desirable output productivity showed a decreasing trend. The trend of lower desirable output productivity among the three regions is more pronounced in the central and western regions, as shown in Figure 5E. Fortunately, the impact of $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ on CO₂ emissions has more years of suppression, which means that the increase in CO₂ emissions can be effectively restrained through improvement of the desirable output productivity. From the perspective of the differences between the eastern, central, and western regions, $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ showed more years of inhibiting CO₂ emissions in the eastern region, followed by the central and western regions. $R_{{\left(GMLPIY\right)}^{-1}}^{T,T+1}$ in the central and western regions tends to increase the CO₂ emissions. Therefore, the desirable output productivities of the central and western regions still need to be improved to avoid higher CO₂ emission increases from economic growth.

4 Conclusion and policy implications

This study applied an improved PDA method that combines the non-radial DDF and GML productivity index with the traditional PDA framework to decompose the CO₂ emissions of 282 Chinese cities from 2003 to 2017. Moreover, this study also classified these 282 cities into groups based on different criteria to analyze and decompose the results in greater depth. Based on the empirical results, the conclusions are drawn as follows:

First, the decomposition results of CO₂ emission growth show that the scale effect was the most significant contributor in Chinese cities. Simultaneously, the energy intensity and desirable output productivity effects played important roles in increasing CO₂ emissions. With respect to the internal factors of the desirable output productivity effect, the desirable output technical efficiency change effect reduced CO₂ emissions significantly, while the desirable output best practice gap change increased CO₂ emissions with significant fluctuations. On the contrary, potential CO₂ emission changes and undesirable output productivity effects were the dominant contributors to CO₂ emission reductions in Chinese cities. Among the undesirable output productivity effects, the undesirable output technical efficiency change effect negatively affected CO₂ emission reduction, while the undesirable output best practice gap change reduced CO₂ emissions in Chinese cities.

Second, this study classified 282 Chinese cities based on two criteria as resource-based and non-resource-based cities as well as the differences in the urban spatial location distribution. Based on the resource-based and non-resource-based cities, we found that although the different CO₂ emission decomposition effects in the two types of cities were consistent with the overall direction of action, the degrees of action were different. Specifically, the potential CO₂ emission effects could greatly restrain the growth of CO₂ emissions in resource-based cities. However, the promotional scale effect was more obvious in the non-resource-based cities. The progress of CO₂ emission technology in the non-resource-based cities caused the undesirable output productivity effect to greatly inhibit the increase in CO₂ emissions. Although the desirable output efficiency of the resource-based cities improved, the desirable output production efficiency had negative effects on reducing CO₂ emissions owing to the outdated technologies.

Third, given the difference in the urban spatial location distribution, this study divided the cities into eastern, central, and western regions. The potential CO₂ emission effects was more obvious in the eastern region. The energy intensity effect was a powerful measure to control the increase in CO₂ emissions in all regions, especially the eastern region. The promotional scale effect on CO₂ emissions showed significant fluctuations for each region. Compared with the other two regions, the promotional effect of the western region was more obvious. Undesirable output productivity had the effect of inhibiting the increase in CO₂ emissions in the three regions, but this was more obvious in the eastern region. The desirable output productivity had a restraining effect in the eastern region but had promotional effects in the central and western regions.

Based on the above conclusions, we offer the following policy recommendations. First, economic development leads to emergence of the scale effect, which is the main factor for the increase in CO₂ emissions. To control the increase in CO₂ emissions in Chinese cities, the government could further strengthen technological innovations, focus on energy structure optimization, promote clean energy production, and reduce the dependence of economic growth on traditional fossil-based energy sources, thereby reducing CO₂ emissions. In addition, the Chinese government could significantly control the use of fossil fuels and widely promote electrification to improve energy efficiency. Second, to control the increase in CO₂ emissions effectively, resource-based cities could pay more attention to improvements in technology. For instance, accelerate the transition from a single-energy-led economy to a diversified and integrated economy as well as promote urban repair and ecological restoration. Moreover, the Chinese government can control CO₂ emissions by upgrading the industries, such as integration of manufacturing with information technology, service industry, culture, and tourism. Third, we note that the development of China’s eastern, central, and western regions is uneven; hence, the government could appropriately implement a differential system when formulating emission reduction policies, e.g., assigning the provinces with low total CO₂ emissions and low intensities the task of reducing CO₂ emission intensities at the lowest level, while turning to the western region when approving carbon market quotas.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author contributions

RC: data curation, formal analysis, writing—original draft; ZZ: investigation, visualization, writing—original draft, conceptualization, supervision.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Ang, B. W., and Zhang, F. Q. (2000). A survey of index decomposition analysis in energy and environmental studies. Energy 25, 1149–1176. doi:10.1016/s0360-5442(00)00039-6

CrossRef Full Text | Google Scholar

Ang, B. W., Zhang, F. Q., and Choi, K.-H. (1998). Factorizing changes in energy and environmental indicators through decomposition. Energy 23, 489–495. doi:10.1016/s0360-5442(98)00016-4

CrossRef Full Text | Google Scholar

Awodumi, O. B., and Adewuyi, A. O. (2020). The role of non-renewable energy consumption in economic growth and carbon emission: Evidence from oil producing economies in africa. Energy Strategy Rev. 27, 100434. doi:10.1016/j.esr.2019.100434

CrossRef Full Text | Google Scholar

Beltrami, F., Fontini, F., and Grossi, L. (2021). The value of carbon emission reduction induced by renewable energy sources in the Italian power market. Ecol. Econ. 189, 107149. doi:10.1016/j.ecolecon.2021.107149

CrossRef Full Text | Google Scholar

Chang, Y. F., and Lin, S. J. (1998). Structural decomposition of industrial CO₂ emission in taiwan: An input-output approach. Energy Policy 26, 5–12. doi:10.1016/s0301-4215(97)00089-x

CrossRef Full Text | Google Scholar

Chen, J., Gao, M., Cheng, S., Hou, W., Song, M., Liu, X., et al. (2020). County-level CO₂ emissions and sequestration in china during 1997–2017. Sci. Data 7, 391–412. doi:10.1038/s41597-020-00736-3

PubMed Abstract | CrossRef Full Text | Google Scholar

de Araújo, I. F., Jackson, R. W., Neto, A. B. F., and Perobelli, F. S. (2020). European Union membership and CO₂ emissions: A structural decomposition analysis. Struct. Chang. Econ. Dyn. 55, 190–203. doi:10.1016/j.strueco.2020.06.006

CrossRef Full Text | Google Scholar

Ding, T., Huang, Y., He, W., and Zhuang, D. (2021). Spatial–temporal heterogeneity and driving factors of carbon emissions in China. Environ. Sci. Pollut. Res. 28, 35830–35843. doi:10.1007/s11356-021-13056-9

CrossRef Full Text | Google Scholar

Fang, G., Gao, Z., Tian, L., and Fu, M. (2022). What drives urban carbon emission efficiency?–Spatial analysis based on nighttime light data. Appl. Energy 312, 118772. doi:10.1016/j.apenergy.2022.118772

CrossRef Full Text | Google Scholar

Färe, R., Grosskopf, S., Lovell, C. K., and Pasurka, C. (1989). Multilateral productivity comparisons when some outputs are undesirable: A nonparametric approach. Rev. Econ. Stat. 71, 90–98. doi:10.2307/1928055

CrossRef Full Text | Google Scholar

IEA, (2021a). Empowering cities for a net zero future. Available at: https://www.iea.org/reports/empowering-cities-for-a-net-zero-future, Paris.

Google Scholar

IEA, , (2021b). Global energy review 2021. Available at: https://www.iea.org/reports/global-energy-review-2021, Paris.

Google Scholar

Kim, K., and Kim, Y. (2012). International comparison of industrial CO₂ emission trends and the energy efficiency paradox utilizing production-based decomposition. Energy Econ. 34, 1724–1741. doi:10.1016/j.eneco.2012.02.009

CrossRef Full Text | Google Scholar

Li, C., Li, H., and Qin, X. (2022a). Spatial heterogeneity of carbon emissions and its influencing factors in china: Evidence from 286 prefecture-level cities. Int. J. Environ. Res. Public Health 19, 1226. doi:10.3390/ijerph19031226

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J. S., Zhou, H., Meng, J., Yang, Q., Chen, B., and Zhang, Y. (2018a). Carbon emissions and their drivers for a typical urban economy from multiple perspectives: A case analysis for beijing city. Appl. Energy 226, 1076–1086. doi:10.1016/j.apenergy.2018.06.004

CrossRef Full Text | Google Scholar

Li, K., Qi, S., and Shi, X. (2022b). The COVID-19 pandemic and energy transitions: Evidence from low-carbon power generation in China. J. Clean. Prod. 368, 132994. doi:10.1016/j.jclepro.2022.132994

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Su, B., and Dasgupta, S. (2018b). Structural path analysis of India's carbon emissions using input-output and social accounting matrix frameworks. Energy Econ. 76, 457–469. doi:10.1016/j.eneco.2018.10.029

CrossRef Full Text | Google Scholar

Lin, B., and Du, K. (2014). Decomposing energy intensity change: A combination of index decomposition analysis and production-theoretical decomposition analysis. Appl. Energy 129, 158–165. doi:10.1016/j.apenergy.2014.04.101

CrossRef Full Text | Google Scholar

Liu, C., Jiang, Y., and Xie, R. (2019). Does income inequality facilitate carbon emission reduction in the US? J. Clean. Prod. 217, 380–387. doi:10.1016/j.jclepro.2019.01.242

CrossRef Full Text | Google Scholar

Mi, Z., Zhang, Y., Guan, D., Shan, Y., Liu, Z., Cong, R., et al. (2016). Consumption-based emission accounting for Chinese cities. Appl. energy 184, 1073–1081. doi:10.1016/j.apenergy.2016.06.094

CrossRef Full Text | Google Scholar

Mi, Z., Zheng, J., Meng, J., Zheng, H., Li, X., Coffman, D. M., et al. (2019). Carbon emissions of cities from a consumption-based perspective. Appl. Energy 235, 509–518. doi:10.1016/j.apenergy.2018.10.137

CrossRef Full Text | Google Scholar

Oh, D. H. (2010). A global Malmquist-Luenberger productivity index. J. Product. Anal. 34, 183–197. doi:10.1007/s11123-010-0178-y

CrossRef Full Text | Google Scholar

Pan, A., Zhang, W., Shi, X., and Dai, L. (2022). Climate policy and low-carbon innovation: Evidence from low-carbon city pilots in China. Energy Econ. 112, 106129. doi:10.1016/j.eneco.2022.106129

CrossRef Full Text | Google Scholar

Rehman, A., Ma, H., and Ozturk, I. (2021). Do industrialization, energy importations, and economic progress influence carbon emission in Pakistan. Environ. Sci. Pollut. Res. 28, 45840–45852. doi:10.1007/s11356-021-13916-4

CrossRef Full Text | Google Scholar

Shan, Y., Guan, Y., Hang, Y., Zheng, H., Li, Y., Guan, D., et al. (2022). City-level emission peak and drivers in China. Sci. Bull. doi:10.1016/j.scib.2022.08.024

CrossRef Full Text | Google Scholar

Shao, L., Geng, Z., Wu, X., Xu, P., Pan, T., Yu, H., et al. (2020). Changes and driving forces of urban consumption-based carbon emissions: A case study of shanghai. J. Clean. Prod. 245, 118774. doi:10.1016/j.jclepro.2019.118774

CrossRef Full Text | Google Scholar

Shigeto, S., Yamagata, Y., Ii, R., Hidaka, M., and Horio, M. (2012). An easily traceable scenario for 80% CO2 emission reduction in Japan through the final consumption-based CO₂ emission approach: A case study of kyoto-city. Appl. Energy 90, 201–205. doi:10.1016/j.apenergy.2011.03.049

CrossRef Full Text | Google Scholar

Sun, L., Fujii, M., Li, Z., Dong, H., Geng, Y., Liu, Z., et al. (2020). Energy-saving and carbon emission reduction effect of urban-industrial symbiosis implementation with feasibility analysis in the city. Technol. Forecast. Soc. Change 151, 119853. doi:10.1016/j.techfore.2019.119853

CrossRef Full Text | Google Scholar

Tian, Y., Wang, Y., Hang, Y., and Wang, Q. (2022). The two-stage factors driving changes in China's industrial SO₂ emission intensity: A production-theoretical decomposition analysis. Sci. Total Environ. 814, 152426. doi:10.1016/j.scitotenv.2021.152426

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Ang, B., and Zhou, P. (2018a). Decomposing aggregate CO₂ emission changes with heterogeneity: An extended production-theoretical approach. Energy J. 39, 39. doi:10.5547/01956574.39.1.hwan

CrossRef Full Text | Google Scholar

Wang, Q., Chiu, Y.-H., and Chiu, C.-R. (2015). Driving factors behind carbon dioxide emissions in China: A modified production-theoretical decomposition analysis. Energy Econ. 51, 252–260. doi:10.1016/j.eneco.2015.07.009

CrossRef Full Text | Google Scholar

Wang, Q., and Han, X. (2021). Is decoupling embodied carbon emissions from economic output in Sino-US trade possible? Technol. Forecast. Soc. Change 169, 120805. doi:10.1016/j.techfore.2021.120805

CrossRef Full Text | Google Scholar

Wang, Q., Han, X., and Li, R. (2022a). Does technical progress curb India's carbon emissions? A novel approach of combining extended index decomposition analysis and production-theoretical decomposition analysis. J. Environ. Manag. 310, 114720. doi:10.1016/j.jenvman.2022.114720

CrossRef Full Text | Google Scholar

Wang, Q., Wang, Y., Hang, Y., and Zhou, P. (2019). An improved production-theoretical approach to decomposing carbon dioxide emissions. J. Environ. Manag. 252, 109577. doi:10.1016/j.jenvman.2019.109577

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., and Zhang, F. (2021). The effects of trade openness on decoupling carbon emissions from economic growth–evidence from 182 countries. J. Clean. Prod. 279, 123838. doi:10.1016/j.jclepro.2020.123838

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Chen, M., and Song, M. (2018b). Energy constraints, green technological progress and business profit ratios: Evidence from big data of Chinese enterprises. Int. J. Prod. Res. 56, 2963–2974. doi:10.1080/00207543.2018.1454613

CrossRef Full Text | Google Scholar

Wang, S., Sun, X., and Song, M. (2021). Environmental regulation, resource misallocation, and ecological efficiency. Emerg. Mark. Finance Trade 57, 410–429. doi:10.1080/1540496x.2018.1529560

CrossRef Full Text | Google Scholar

Wang, S., Tang, Y., Du, Z., and Song, M. (2020a). Export trade, embodied carbon emissions, and environmental pollution: An empirical analysis of China's high-and new-technology industries. J. Environ. Manag. 276, 111371. doi:10.1016/j.jenvman.2020.111371

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Wang, X., and Chen, S. (2022b). Global value chains and carbon emission reduction in developing countries: Does industrial upgrading matter? Environ. Impact Assess. Rev. 97, 106895. doi:10.1016/j.eiar.2022.106895

CrossRef Full Text | Google Scholar

Wang, S., Wang, X., and Tang, Y. (2020b). Drivers of carbon emission transfer in China—An analysis of international trade from 2004 to 2011. Sci. Total Environ. 709, 135924. doi:10.1016/j.scitotenv.2019.135924

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Hao, Y., and Feng, C. (2021). A race between economic growth and carbon emissions: What play important roles towards global low-carbon development? Energy Econ. 100, 105327. doi:10.1016/j.eneco.2021.105327

CrossRef Full Text | Google Scholar

Yuan, H., Feng, Y., Lee, C.-C., and Cen, Y. (2020). How does manufacturing agglomeration affect green economic efficiency? Energy Econ. 92, 104944. doi:10.1016/j.eneco.2020.104944

CrossRef Full Text | Google Scholar

Zhang, B., Qiao, H., Chen, Z., and Chen, B. (2016). Growth in embodied energy transfers via China’s domestic trade: Evidence from multi-regional input–output analysis. Appl. energy 184, 1093–1105. doi:10.1016/j.apenergy.2015.09.076

CrossRef Full Text | Google Scholar

Zhao, Z., Shi, X., Zhao, L., and Zhang, J. (2020a). Extending production-theoretical decomposition analysis to environmentally sensitive growth: Case study of Belt and Road Initiative countries. Technol. Forecast. Soc. Change 161, 120289. doi:10.1016/j.techfore.2020.120289

CrossRef Full Text | Google Scholar

Zhao, Z., Yuan, T., Shi, X., and Zhao, L. (2020b). Heterogeneity in the relationship between carbon emission performance and urbanization: Evidence from China. Mitig. Adapt. Strateg. Glob. Chang. 25, 1363–1380. doi:10.1007/s11027-020-09924-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, P., Ang, B., and Wang, H. (2012). Energy and CO₂ emission performance in electricity generation: A non-radial directional distance function approach. Eur. J. operational Res. 221, 625–635. doi:10.1016/j.ejor.2012.04.022

CrossRef Full Text | Google Scholar

Zhou, P., and Ang, B. W. (2008). Decomposition of aggregate CO₂ emissions: A production-theoretical approach. Energy Econ. 30, 1054–1067. doi:10.1016/j.eneco.2007.10.005

CrossRef Full Text | Google Scholar

Zhou, P., Zhang, H., and Zhang, L. (2022). The drivers of energy intensity changes in Chinese cities: A production-theoretical decomposition analysis. Appl. Energy 307, 118230. doi:10.1016/j.apenergy.2021.118230

CrossRef Full Text | Google Scholar