An assessment of future tidal marsh resilience in the San Francisco Estuary through modeling and quantifiable metrics of sustainability

Introduction

Tidal marshes form along coastlines at the dynamic interface between land and sea. There is great societal interest in preserving and restoring tidal marshes due to the many ecosystem services they provide including critical habitat for fish, birds, and mammals, shoreline protection, carbon sequestration, sediment trapping, and water quality improvement (Costanza et al., 2008; Roman and Burdick, 2012; Kroeger et al., 2017; Powell et al., 2019). The persistence of tidal marshes on the landscape relies on their ability to bounce back or be “resilient” in the face of disturbance. Ecological resilience is the ability of an ecosystem to withstand change and maintain similar structure, function, and services (Holling, 1973; Gunderson, 2000). Inherent in this definition is an assumption that disturbed ecosystems will return to a particular reference state or dynamic (Grimm and Wissel, 1997). The type of disturbance considered under the rubric of resilience has changed since originally defined. Disturbance can no longer simply be considered as recovery from a single discrete event because, under climate change, the resilience of tidal marshes is increasingly being challenged by chronic, concurrent disturbances such as sea-level rise (SLR), heightened wave-induced flooding, invasive species, and changes in sediment availability (Khanna et al., 2018; Masselink and Lazarus, 2019).

A clear understanding of what promotes ecological resilience under climate change is needed for the effective long-term management of coastal wetlands (Raposa et al., 2016; Stagg et al., 2016; Cahoon et al., 2020). Natural resource agencies, non-governmental organizations, and restoration practitioners require guidance on which management actions can increase the resiliency of degraded wetlands and how to restore coastal wetlands with a keen eye toward sustainability (Raposa et al., 2016). In addition, ensuring future wetland resilience is critical for many nations that have incorporated blue carbon strategies into their carbon inventories and nationally determined contributions to the United Nations Framework Convention on Climate Change (Crooks et al., 2018; Herr et al., 2019).

The demonstrated need for quantifying marsh resilience under SLR has prompted new research on potential metrics. A suite of resilience measures has been proposed in the past 5 years, with some encompassing basic marsh properties and others representing new approaches for characterizing marsh function (Table 1). Some were developed to be applied at a national scale, (e.g.,Holmquist et al., 2021) and others at local scales (e.g.,van Belzen et al., 2017; Neijnens et al., 2021). All of the metrics in Table 1 have been developed using field experiments, field-derived data, and/or remotely-sensed data. Due to the range of geomorphological conditions under which tidal wetlands form, the number of environmental drivers and stressors, and the variability of such drivers across spatial and temporal scales, it has been challenging to identify a universal metric(s) that can gauge any situation. An evaluation by Wasson et al. (2019) found that metrics quantifying how vegetation is distributed across the tidal frame were the best at predicting tidal marsh trajectories (Table 1), yet the non-vegetated to vegetated marsh ratio and flood-ebb sediment differential were also found to be valuable measures of resilience. Others have also stressed the flood-ebb sediment differential as well as a net-positive sediment budget as important resilience metrics (Ganju et al., 2017; Nowacki and Ganju, 2019). Although sediment is critical for the formation of many types of tidal marshes (Ganju et al., 2015; Ganju, 2019; Masselink and Lazarus, 2019), these sediment metrics cannot be considered universal as inorganic sediment is not an essential component of all tidal marshes (Cahoon et al., 2020). Therefore, metrics are needed that can be applied across all tidal marshes. Along this line, metrics that provide a means for determining a tipping point or temporal threshold for marshes in decline would be especially advantageous for improved coastal management under SLR.

TABLE 1

TABLE 1. Compendium of individual metrics used to assess tidal marsh resilience to date.

Marsh sustainability models, which have been used for quite some time to determine the threshold for drowning (Fagherazzi et al., 2020 and references therein), can also be used to explore the formation and future resilience of marshes. In so doing, various tipping points can be determined for particular scenarios of SLR. For this purpose, we introduce a new version of the 2D cohort Marsh Equilibrium Model (Morris et al., 2002; Morris et al., 2021) called the Coastal Wetland Equilibrium Model (CWEM), which uses measured depth profiles of organic matter concentration, hereafter referred to as loss on ignition (LOI), and calculated bulk density values from cores to initialize sediment cohorts. We acknowledge that a comprehensive treatment of marsh sustainability requires a lateral migration component. An assessment of potential lateral migration corridors is being conducted separately.

We applied CWEM to the Sacramento-San Joaquin Delta of California (hereafter the Delta). The Delta presents an excellent testing ground for CWEM because it contains a range of tidal freshwater marshes from minerotrophic to organogenic, which have been resilient for the past ∼6800 years (Drexler et al., 2009a; Drexler et al., 2009b; Drexler, 2011). The main objectives of our study were to 1) interpret the history of the Delta from numerous peat core profiles of bulk density and LOI and 2) project the future of the Delta for different sea-level rise scenarios using CWEM.

In projecting the future resilience of Delta marshes under different SLR scenarios, we gave special attention to three quantitative temporal metrics of marsh resilience. The first is the time remaining before marsh drowning or survival time. This is a function of current relative marsh elevation, tide range, the projected centenary SLR (CSLR), and the vertical distribution of marsh vegetation. The vertical distribution is described as a dimension of the range of tolerance by Shelford (1931) or as a dimension of a species’ realized niche by Hutchinson (1957). The second metric of resilience is the time to the marsh tipping point at which the vertical accretion rate begins to decrease with further increases in the rate of SLR (RSLR). The last temporal resilience measure we explore is the conditional probability of a centenary regime change from one state to another, where the states are drowned marsh, suboptimal marsh elevation (below the tipping point), and super-optimal marsh elevation (above the tipping point). We chose these temporal metrics because they can be applied to all kinds of tidal marshes and provide a means for identifying marshes in decline.

Several marsh sustainability models have been developed for the San Francisco Estuary (Stralberg et al., 2011; Deverel et al., 2014; Schile et al., 2014; Swanson et al., 2014; Buffington et al., 2021; Delta Stewardship Council, 2021). Of these only two were applied across the Delta region (Swanson et al., 2015; Delta Stewardship Council, 2021). In Swanson et al. (2015), the application of the Wetland Accretion Rate Model of Ecosystem Resilience (WARMER I) showed that Delta marshes are generally resilient to sea-level rise of up to 88 cm by 2100, but at an SLR of 179 cm over 90% of the marshes were projected to drown (Swanson et al., 2015). Marshes in high-energy environments such as major channels and the confluence of rivers were more sustainable than marshes in backwater areas. The application of WARMER II by the Delta Stewardship Council (2021) showed that by 2085, mid-and high tidal freshwater marshes (those with elevations above MSL) remain sustainable under an SLR of 61 cm, but that conversion from high marsh to low marsh (MHHW to MSL) occurs with 107 cm of SLR. Above 183 cm, all Delta marshes were projected to drown, which is similar to the result from Swanson et al. (2015). Unlike this study, neither Swanson et al. (2015) nor the Delta Stewardship Council (2021) had a large soil core dataset from sites across the Delta to inform their projections, and neither assessed temporal metrics of resilience, particularly the tipping points along which marshes begin their decline toward drowning.

CWEM further improves upon previous modeling efforts through its improved parameterizations, particularly of belowground organic matter distribution, accumulation, and decomposition, its incorporation of new data on vertical plant distribution, and its ability to include episodic sediment pulses from major storms, which in California consist mainly of atmospheric rivers (Dettinger et al., 2011). These improvements allow for more realistic projections of marsh resilience under potential future scenarios in the Delta region.

Methods and data

Study site description

The Delta is part of a 163,000 km² watershed bounded by the Sierra Nevada and Cascade Range of California (Cloern et al., 2011). It is situated at the landward end of the San Francisco Estuary where the Sacramento and San Joaquin Rivers meet (Figure 1). The climate of the region is characterized as Mediterranean with cool winters and hot, dry summers (Atwater, 1980). Tides in the Delta are semi-diurnal and micro-tidal with a normal tidal range of approximately 1 m (Shlemon and Begg, 1975; Atwater, 1980). Mean annual precipitation across the Delta region ranges from 32.9 to 44.9 cm with high interannual variability (He, 2022). More than 80% of precipitation occurs from November to March and most freshwater inflow to the Delta occurs from January to June because of storage in the snowpack and releases from reservoirs (Knowles and Cayan, 2002). The water flowing through the Delta is a key component in the highly engineered, water delivery system in the state of California (California Department of Water Resources, 2021a; USDA National Agricultural Statistics Service, 2021).

FIGURE 1

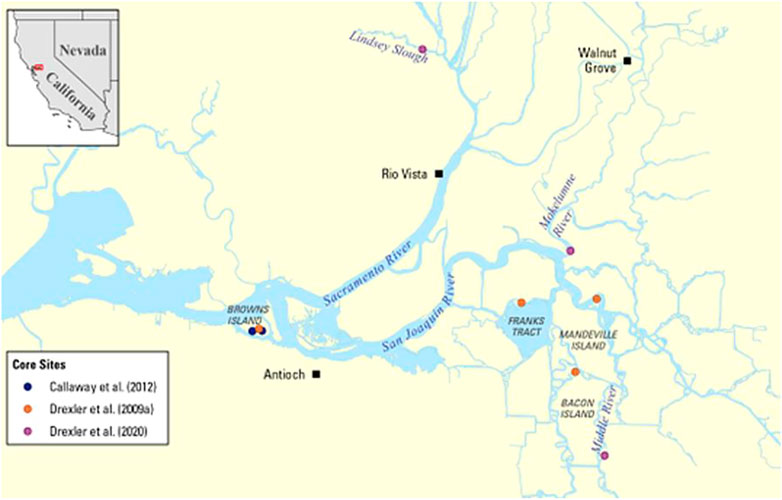
FIGURE 1. Location of the Sacramento-San Joaquin Delta in California and the peat cores that were collected across the region.

Historically, the Delta was a 2,300 km² region containing hundreds of channels and extensive tracts of tidal wetlands (Drexler et al., 2009a; Whipple et al., 2012). Highly organic “peat” soils ranging up to ∼15 m thick formed predominantly in the central and western Delta (Dachnowski-Stokes, 1936; Weir, 1937; Atwater and Belknap, 1980). Throughout its history, the Delta has largely been a tidal freshwater region, however, the western periphery has long been an ecotone between fresh and slightly brackish conditions (Drexler et al., 2014). A historical ecology study showed that before the mid-1800s, the Delta consisted of a broad expanse of tidal freshwater emergent wetlands in the central Delta, flooded basins adjacent to riparian forests along the Sacramento River and its tributaries in the north, and a broad floodplain of the San Joaquin River and its tributaries in the south (Whipple et al., 2012).

Studies of plant fossils including Schoenoplectus spp. (bulrush) achenes and rhizomes have shown those plant communities in the Delta have not changed much from the past (Weir, 1937; Goman and Wells, 2000; Drexler et al., 2009a; Drexler et al., 2009b; Drexler, 2011). Emergent tidal freshwater marshes dominated by bulrushes (Schoenoplectus californicus, S. acutus, S. americanus, and hybrids) and also containing cattails (Typha angustifolia, T. latifolia, T. domingensis, and hybrids), common reed (Phragmites australis) and western lady fern (Athyrium filix-femina) historically covered ∼70% of the Delta with riparian forest and shrub-scrub wetlands, seasonal floodplains, open water, and non-tidal wetlands covering the remainder of the region (Whipple et al., 2012; Cloern et al., 2021).

From the mid-1800s to the 1930 s, 98% of the Delta was drained and converted to agriculture (Thompson, 1957; Atwater, 1980). This massive conversion of the Delta resulted in a precipitous decline in pelagic fishes such as the endemic Delta smelt Hypomesus transpacificus (Sommer et al., 2007; Newman and Brandes, 2010; Durand, 2015) and land-surface subsidence of up to 9 m due mainly to microbial oxidation of the highly organic peat soils (Deverel and Leighton, 2010; Deverel et al., 2016). The Delta has also been strongly impacted by the hydraulic mining era (1849–1884) during the California Gold Rush when ∼300 million metric tons of sediment were liberated into the Sacramento River Valley, resulting in Hg and Pb contamination throughout the entire Estuary (Bouse et al., 2010; Drexler et al., 2016), and increasing suspended sediment loads for well over 100 years (Drexler, 2011; Drexler et al., 2016). The impacts on the Delta following drainage have prompted large-scale restoration efforts, including an effort to restore and protect 12,141 ha of Delta habitat in a program called EcoRestore (California Department of Water Resources, 2021b).

Peat core data

The data from 14 peat cores used in this analysis were previously collected in historical (non-farmed) tidal marshes as part of three separate studies in the Delta (Figure 1). Wetland sites were all freshwater except for Browns Island, which is oligohaline (Drexler, 2011). Deep cores ranging from 4–9 m in depth were collected from Browns Island, Franks Wetland, Mandeville Tip, and Bacon Channel Island in 2005 and 2007 (Drexler et al., 2009a). The cores collected by Callaway et al. (2012) on Browns Island were 50 cm long and collected in 2010. Finally, peat cores of 50 cm in length were collected from Lindsey Slough, Mokelumne River, and Middle River in 2018 (Drexler et al., 2020). All cores were collected with a piston corer to avoid compaction. Cores were sectioned to 2 cm, analyzed for % LOI and bulk density, and dated using ¹⁴C, ¹³⁷Cs, and ²¹⁰Pb following methods in (Drexler et al., 2009a; Callaway et al., 2012; Drexler et al., 2020). Core data consisting of age and LOI were normalized to NAVD88 elevations and binned into 5 cm slices, and the depth of each section was computed relative to the local surface elevation.

For this study, we have composited the data from the peat cores and assume that they represent a fair sample of the Delta. We posit that during their ∼6700-year history, Delta wetlands as a whole have responded in a consistent way to major environmental drivers including SLR, floods and droughts, the Gold Rush in the mid-late 1800s, and the massive transformation to agriculture in the late 1800s and early 1900s (Drexler et al., 2009a; Drexler et al., 2016).

The Coastal Wetland Equilibrium Model

The Coastal Wetland Equilibrium Model (CWEM), formerly the Marsh Equilibrium Model (MEM), has been modified for this application with the addition of a revised front end and an episodic disturbance option. MEM has been described elsewhere in detail (Morris and Callaway, 2018; Morris et al., 2021). CWEM incorporates a revised model of sediment diagenesis referred to as a cohort model (Morris and Bowden, 1986). Episodic disturbance can be due to extratidal floods that deposit a defined layer of mineral sediment at a specified frequency. The front end of the model refers to how the sediment cohorts are initialized.

The relative elevation of the marsh surface within the vegetation growth range (Figure 2A) determines the biomass (Figure 2B). Marsh elevation increases by total net accretion (Figure 2C), which is determined by mineral inputs to the surface (Figure 2D) and organic inputs into cohorts from roots and rhizomes (Figure 2F), hereafter referred to simply as roots. Conceptually, a wetland pedon can be considered to be a stack of annual laminations or cohorts that are buried by successive generations of cohorts (Morris and Bowden, 1986). Cohorts are generated from the annual lamination of mineral sediment onto the surface, which is determined by the concentration of suspended sediment, and depth and duration of flooding (Figure 2E). Over time, the surface lamination or cohort is buried by a succession of new annual cohorts and, as the surface cohort is buried, it passes through the root zone and inherits a succession of organic inputs (Figure 2F) from root turnover, some of which is labile and some refractory. The labile fraction will decay (Figure 2G). The cohorts also will contain live roots. Organic inputs and losses change the volumes of the cohorts. In general, the cohorts first swell as they move deeper through the root profile, and then they shrink as the root turnover at depth decreases and the decay of labile material increases. Eventually, cohort volumes and composition stabilize as they pass below the root zone. The final cohort volume consists of the original sediment deposit plus the total production of refractory organic matter in the layers above. Cohort composition generates the depth profile of LOI (Figure 2H).

FIGURE 2

FIGURE 2. Schematic diagram of the dependencies and outputs of CWEM.

The model must be initialized with a stack of cohorts filled by some means. Previously this was done by assuming the wetland was in equilibrium with a constant RSLR. With these assumptions, the model computed the theoretical profiles of LOI and bulk density of a marsh at equilibrium. This is referred to as the Cohort Theory Model (CTM). We used an alternative method in CWEM to initialize the time-zero cohorts using the averaged Delta depth profiles of LOI. With known LOI, we populated the cohorts at time-zero using the ideal mixing model (Morris et al., 2016). This was accomplished by equating the annual rate of vertical accretion (dZ/dt) (cm) to cohort volume V_T (cm³) and solving for the inorganic and organic weights from a known, dry LOI (g/g) as follows:

$dZ/dt={\mathrm{V}}_{\mathrm{T}}={\mathrm{V}}_{\mathrm{o}}+{\mathrm{V}}_{\mathrm{i}}(1)$

where V_o and V_i are the volumes of organic and mineral matter. Eq. 1 can be rewritten as

${\mathrm{V}}_{\mathrm{T}}={\mathrm{W}}_{\mathrm{o}}/k_{\mathit{1}}+{\mathrm{W}}_{\mathrm{i}}/k_{\mathit{2}}(2)$

where W_o and W_i are the organic and inorganic weights and k₁ and k₂ are their constant and known self-packing densities (Morris et al., 2016). The cohort’s LOI is:

$\mathrm{L}\mathrm{O}\mathrm{I}={\mathrm{W}}_{\mathrm{o}}/\left({\mathrm{W}}_{\mathrm{o}}+{\mathrm{W}}_{\mathrm{i}}\right)(3)$

We substitute W_i from Eq. 3 for W_i in Eq. 2, and can then calculate W_o and, subsequently, W_i. Thus, every cohort can be populated with organic and mineral weights from the profile of LOI (Supplementary Figure S1). However, the fractionation of organic matter between labile and refractory parts is unknown, except below the root zone where all or a majority of W_o is refractory. The live root fraction is estimated from literature values for belowground biomass and the vertical distribution of roots for the specific species of interest. After subtracting the live fraction from W_o, the remainder was assumed to be refractory. Next, the model was run for 10 iterations to generate stable distributions of refractory, labile organic matter, and volume, i.e., the root mass in each cohort is allowed to turnover for 10 annual cycles at constant sea level to generate labile and refractory decay products and stable volumes. This completed the initialization step.

The full model inputs are included in Supplementary Table S1. Uncertainties in key model parameters, namely starting elevation and centenary sea-level rise, were dealt with by solving the model for the ranges of possibilities. For example, the spatial distribution of elevations of Delta marshes can be assumed to span the full vertical range of the marsh vegetation between about −98 and 60 cm relative to MSL. Another uncertainty is the future sea level, which could be 40–200 cm higher than today in 100 years. Hereafter, the estimates of centenary sea-level rise will be referred to as CSLR. Simulated starting or initial elevations (MSL) will be referred to as IREs. Model simulations of 100 years each were run for permutations consisting of CSLR between 40 and 200 in 10 cm increments and IRE between −97 and 68 in 5 cm increments.

Because vertical accretion in the San Francisco Estuary is also influenced by major storms/atmospheric rivers (Thorne et al., 2022), additional model runs were added to incorporate such episodic disturbance. Inputs for episodic disturbance were determined as follows. The median frequency of large atmospheric rivers in the Delta region (categories 3–5), which increase sediment availability, was found to be approximately 3 years, based on data between 1953–2017 from Gershunov et al. (2017). Next, a range of surficial deposits was chosen to be 2 mm, 3 mm, and a maximum of 6 mm, which was close to the mean surficial deposit (6.5 mm) measured at Browns Island in the Delta after a Category five atmospheric river (Thorne et al., 2022). The permutations resulted in 3D response surfaces where the response variables were the metric of interest, and the independent variables were the IRE and CSLR. Outputs were also grouped into a 2 × 3 matrix consisting of two starting conditions of relative elevation and three final conditions, also of relative elevation.

Hindcasts

The performance of CWEM was evaluated by hindcasting started in CE 1905 and run forward for 100 years. The starting relative elevation and sediment LOI profile were taken from the 14 dated peat cores described above. The data were binned into 5 cm intervals and averaged to give a synoptic view of the Delta’s marsh history, including LOI and age-depth profiles. From the average age-depth profile it was determined that the 19th-century accretion rate, hence cohort volume, was linear and 3 mm/yr. The volumes of organic and mineral matter were computed from the depth distribution of LOI. It was assumed that the modern LOI fraction at the depth of the 1905 section represented the marsh surface at that time and that the distribution of LOI below that depth was as it is today. However, the modern organic matter concentration at the 1905 depth is devoid of live roots and labile organic matter. Moreover, the fraction of modern refractory organic matter at that depth and greater is inflated by the additions of refractory root production that would have been added as the 1905 cohort was buried by successive cohorts. To approximate the initial 1905 distribution of organic matter and its composition, the simplifying assumption was made to add to this refractory organic pool the live-root volume and labile organic matter calculated from the distribution and turnover of live roots. This approximated what the surface profile of LOI should have looked like in 1905. After this initialization procedure was complete, the model was run forward for 100 years to 2005 (the hindcast) and then for another century (the forecast) after that. The rate of sea-level rise was held constant at 2 mm/yr, which was the prevailing rate during the 20th century in San Francisco (NOAA, 2022).

Results

Delta marsh formation

The LOI of Delta peats varied with core depth (Figure 3B and Supplementary Figure S2). Binning and averaging deep cores show that there has been an overall rise in LOI from about 23% at −740 cm to a high of 74% at −72 cm below the modern land surface (Supplementary Figure S2). Then between 1849 and 1884 hydraulic mining during the California Gold Rush transported a sufficient quantity of mineral sediment into the Delta to drop the LOI from approximately 70%–20% (Figure 3B). This dramatic change reflects the ∼300 million tons of sediment liberated into the Sacramento River watershed during the hydraulic mining period (Bouse et al., 2010) and the fact that a majority of cores used in this study are located in or near the Sacramento River watershed. Subsequently, the LOI is rebounding and surface peats now have an organic matter concentration of about 35% (Figure 3B).

FIGURE 3

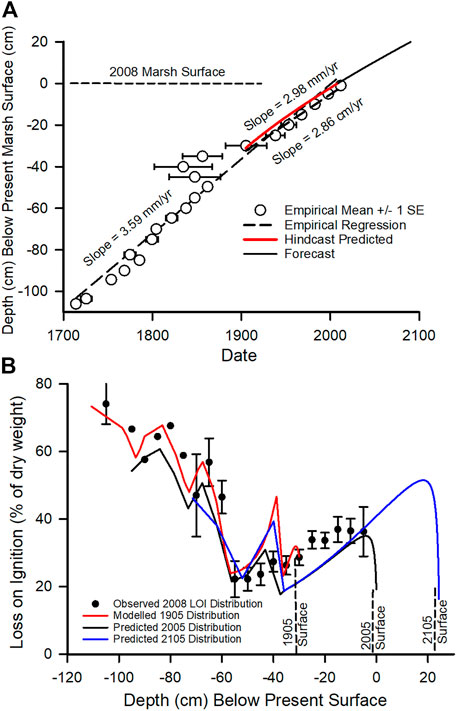
FIGURE 3. (A) Observed depths (unfilled circles) of dated core sections grouped into 5-cm depth bins (mean ± 1 SE) with hindcasted (red line) and forecasted (black line) depths versus date. (B) Depth distributions of loss on ignition (LOI) values at the start of the hindcast (1905), at present (2005) and 100 years into the future. Note: the ground surface of the 1905 profile, which is the start of the hindcast, was about 30 cm below the current surface as shown in (A). The simulations assumed a constant SLR of 2 mm/yr.

Hindcasts of marsh age and accretion rate starting in the year 1905 (Figure 3A) and average LOI in sediment (Figure 3B) were consistent with the observed data and were approximately linear. Observed and predicted accretion rates between 1905 and 2005 were 2.86 and 2.98 mm/yr, respectively, and a regression of predicted vs. actual depth of sediment returned an R² of 0.96 (p < 0.0003, n = 7). The root mean squared error (RMSE) was 2.5 cm. An analysis of age-depth profiles extending back to the calendar year 1713 at 106 cm below the present surface (Figure 3A) also showed an overall linear trend with a higher accretion rate, 3.59 mm/yr, than the 20th-century average (Figure 3A).

Hydraulic mining during the Gold Rush period resulted in a rapid decline in LOI, which was followed by a recovery (rising LOI) (Figure 3B and Supplementary Figure S2). There has been a rise in mean LOI in core data from 21.5% at −54 cm depth to 36.8% at −15 cm depth (Figure 3B). The hindcast of the evolving depth profile of sediment LOI (Figure 3B) correctly captured this recovery. A regression of predicted LOI against the observed data for the top 30 cm core segment (100-year) covered by the hindcast returned an R-square of 0.76 (n = 6, p < 0.02).

Resilience projections

Three temporal metrics were used to gauge marsh resilience. For the first, time remaining before marsh drowning, we included permutations of IRE from −100 to 60 cm and CSLR from 40–200 cm. This resulted in a 3-dimensional surface (Figure 4) with the lowest point near IRE −100 cm and CSLR 200. A marsh surface near the lower limit of its vegetation will not survive a rapid RSLR. Survival time was about 100 years at the highest CSLR when initial marsh elevation was close to the upper limit, 60 cm. The greatest survival times, more than 200 years, occurred at low CSLR across a range of IREs between −60 and 68 cm. Sea level would need to rise as much as 1.65 m, the vertical range of the vegetation, when the marsh elevation is at the upper limit before the marsh would drown, even in the absence of any vertical accretion. Assuming that the mean surface elevation of the cores, 29 cm relative to mean sea level, is representative of the average elevation of remaining Delta marshes, then the survival time of the typical Delta marsh is 100 years or more even at a CSLR of 200 cm (Figure 5).

FIGURE 4

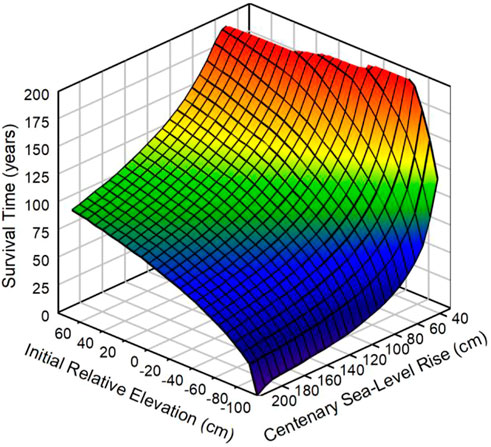
FIGURE 4. Predicted survival time of the vegetated marsh surface for different combinations of initial relative elevation (IRE) and centenary sea-level rise (CSLR). The range of IRE spans the vertical growth range of the vegetation. The range of CSLR sea-level rise spans the possible scenarios.

FIGURE 5

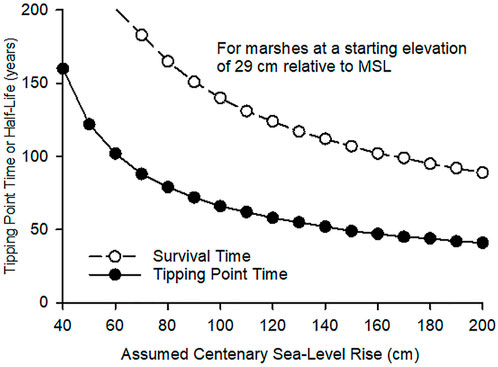
FIGURE 5. Survival and tipping point times (TPTs) for a Delta marsh at the average elevation (29 ± 23 cm rel. MSL) of the ground surface of the cores collected throughout the region.

The next resilience metric evaluated was time to the marsh tipping point, which is the relative elevation at which vertical accretion begins to decrease with further increases in the RSLR. The tipping point time (TPT) is equal approximately to the marsh half-life (Figure 5). For the average Delta marsh, assuming that the cores are representative, the TPT is 50 years or more at CSLR rates of as much as 200 cm. The TPT is also the optimal elevation for the vegetation, which was specified here as 10 cm relative to MSL. Consequently, only initial elevations greater than 10 cm have TPTs. Like survival time, TPT depended on the initial marsh elevation and the CSLR (Table 2 and Supplementary Figure S3). TPT was zero at 10 cm, the optimum elevation, and increased at higher IRE. The highest TPT occurred at the combination of the highest IRE and lowest CSLR.

TABLE 2

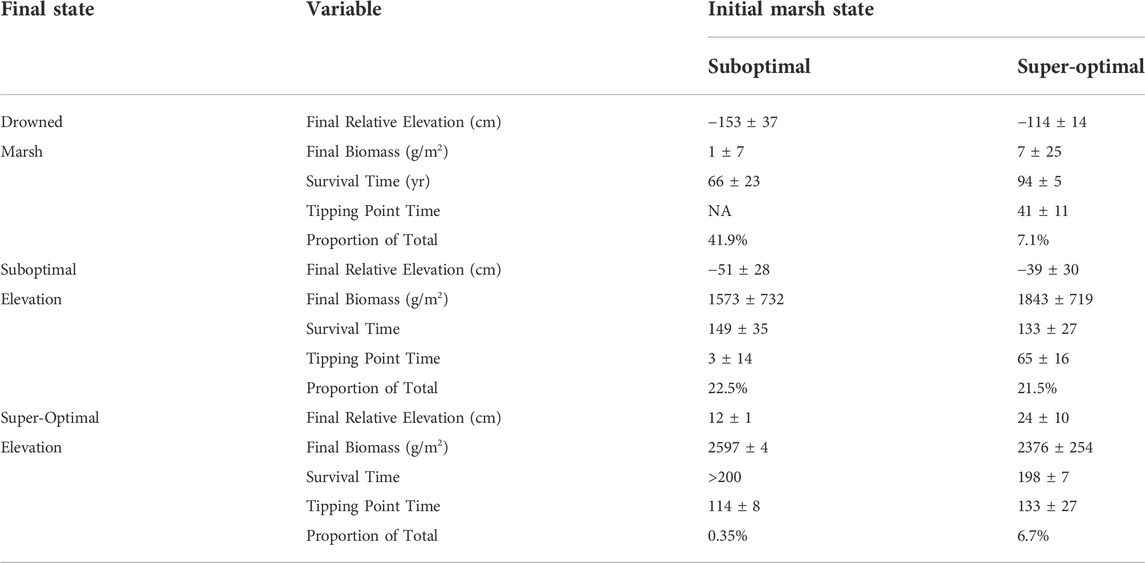
TABLE 2. Conditional probabilities of centenary regime change computed from permutations of starting relative elevation from -98 to 68 cm in 5 cm increments and centenary sea-level rise of 40–200 cm in 10 cm increments. Outcomes were organized into three groups (drowned marsh, suboptimal, and super-optimal elevations) by class of starting elevation (suboptimal and super-optimal).

The third metric of resilience is the conditional probability of regime change. Very broadly, the initial marsh state can be classified in terms of relative elevation—it will be either above the tipping point or below. The outcome of a CWEM permutation of CSLR and IRE also will be marsh elevation above or below the tipping point and, additionally, drowned marsh (Table 2). For this exploratory metric, it is assumed that any centenary sea-level rise between 40 and 200 cm is equally possible and that the elevation of today’s marsh surface can lie with equal probability anywhere between the upper and lower elevation range of the vegetation. The results demonstrate that the odds are high that Delta marshes will drown in the next 100 years, assuming that the IRE and CSLR are equally probable and independent. Even when starting at a super-optimal elevation, the probability of ending at a super-optimal elevation is only 6.7%. The highest probability is an outcome below the growth zone when starting at a suboptimal elevation.

Atmospheric rivers

Major storms known as atmospheric rivers increase discharge rates and suspended sediment concentrations in rivers, resulting in episodic increases in mineral sediment deposition on marshes (Thorne et al., 2022). This was simulated by assuming triennial surface deposits of 2, 3, or 6 mm (Table 3 and Table 4). When sediment inputs were raised from 0 to 6 mm, the final proportion of wetlands started suboptimally and ended super-optimally increased from 0.35% to 5.4% (Table 3). The proportions ending as drowned marsh decreased from 41.9% to 26.8%. In the class of simulations that started at super-optimal elevations, increasing triennial sediment deposits to 6 mm decreased the proportion of drowned marsh from 7.1% to 1.04% and more than doubled the proportion of marshes ending 100 years at super-optimal elevations. Among simulations that started at suboptimal elevations, the most probable outcome changed from a drowned state to a suboptimal state when the triennial deposit was raised to 6 mm (Table 3). The most probable outcome of marshes starting at suboptimal elevations was either that of a drowned or suboptimal state, irrespective of the disturbance regime (0–6 mm; Table 3).

TABLE 3

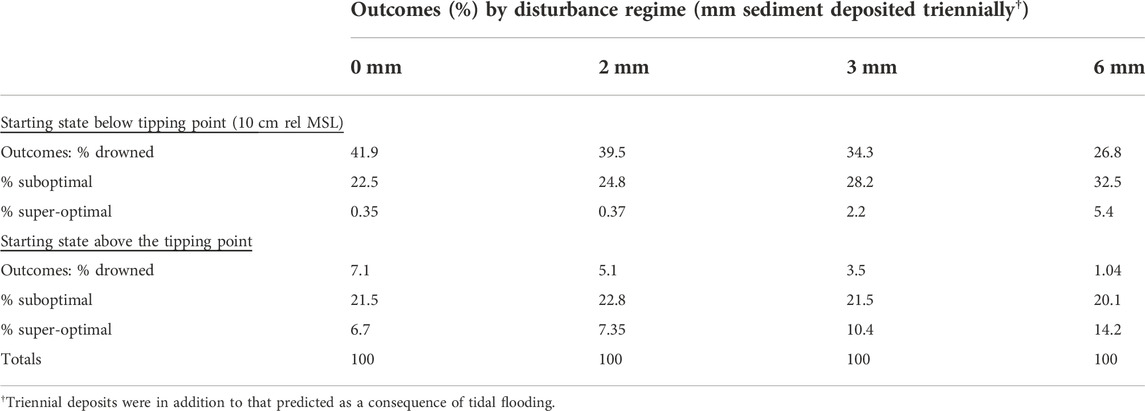
TABLE 3. Percentages of simulation results culminating in states of drowned, suboptimal, and super-optimal elevations following 100-year simulations as functions of episodic disturbance regime and starting state. The percentage outcomes are grouped according to simulated amounts of sediment deposited triennially and generated from model permutations of starting elevation in 5 cm increments and CSLR (from 40 to 200 cm per 100 years) in 10 cm increments.

TABLE 4

TABLE 4. Mean survival times (±1 SD) as functions of episodic disturbance regime and starting elevation. Outcomes were classified into three categories—drowned, suboptimal, and super-optimal elevation. Starting elevations were classified as either suboptimal (-97 to 10 cm) or super-optimal (10–60 cm). The survival times are shown as functions of amounts of episodic sediment deposits occurring triennially and were generated from model permutations of starting elevation in 5 cm increments and CSLR (from 40 to 200 cm per 100 years) in 10 cm increments.

Survival times were relatively insensitive to simulated triennial deposits of 0–6 mm. The mean survival time of marshes that started suboptimally below the tipping point ranged from 66 to 77 years, depending on the magnitude of the simulated mineral deposit, and for those starting above the tipping point, the mean survival time varied between 94 and 98 years (Table 4). Irrespective of the disturbance regime and original state, the subgroup of wetlands in simulations ending 100-year at a super-optimal elevation had survival times about 200 years or more (Table 4). Drowned marshes had survival times of less than 100 years, and simulations ending at suboptimal elevations all had mean survival times exceeding 100 years.

General principles

The change in absolute marsh elevation (cumulative accretion) varied with IRE, and CSLR (Figure 6), and demonstrates an important principle: Accretion is not uniform across a topographic gradient and will vary across space and time depending on the initial relative elevation and CSLR. There were parameter combinations that resulted in both deceleration and acceleration in the accretion rate. For example, at the highest extremes of IRE (40 cm) and CSLR (200 cm), accretion decelerated through time, but at the extreme low IRE (−100 cm) and high CSLR, there was an acceleration in accretion. The greatest acceleration in accretion rate occurred at a combination of low IRE and high CSLR which produced the greatest quarterly elevation gain, 20.7 cm between years 75–100 of the simulation, and the greatest total accretion, 59.9 cm, probably due to the increasing importance of mineral sedimentation (Figure 6). This also corresponded to the lowest survival time (Figure 4). The greatest deceleration occurred at the combination of high CSLR (200 cm) and high IRE (60 cm).

FIGURE 6

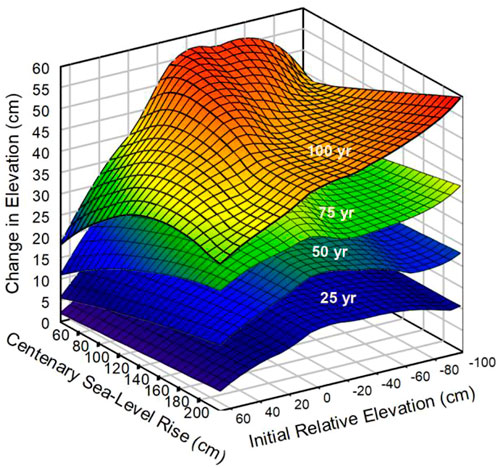
FIGURE 6. The total change in marsh surface elevation at 25-year intervals from the start for different combinations of initial relative elevation and centenary sea-level rise. See Supplementary Figure S3 for details.

Sediment LOI is a useful indicator of marsh condition, but it varies with sediment depth (Figure 3B) and is challenging to characterize with model simulations that generate outputs that evolve over time and with starting conditions. We used the LOI at 15 cm depth as an index of sediment organic matter content because it is well within the root zone and is responsive to current conditions. Results from 100-year simulations showed that the final LOI-15 was greatest when final relative (to MSL) elevation was high (Figure 7). High final relative elevation occurred when CSLR was less than 120 cm and IRE greater than 10 cm, i.e., when marsh elevation was relatively high at the start and CSLR was not greater than the limits of accretion. However, note that the variability in the final LOI-15 was highest at relative elevations of 10 cm (the tipping point) to −20 cm. The LOI-15 at 10 cm relative elevation was 62% ± 23%, then at 20 cm the LOI increased to 78% and the standard deviation of outputs declined to 6.7%. An LOI >60% is a signal that the marsh has been in its most stable state, but the high variability in LOI at lower relative elevations shows that there were exceptions (Figure 7). Depending on the CSLR and IRE, unstable wetlands with high LOI are possible.

FIGURE 7

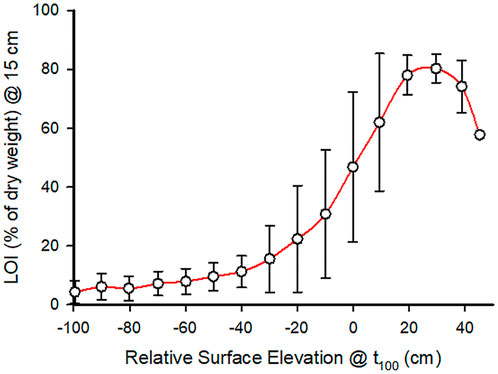
FIGURE 7. Mean (±1 SD) % LOI determined by CWEM for peat 15 cm depth below the marsh surface versus relative marsh surface elevation (relative to MSL at time = 100 years) from permutations of centenary SLR between 40 and 200 cm and IRE between −97 and 68 cm.

Discussion

Delta marsh formation

The mean LOI profile determined from the Delta cores can be used to infer its history through the millennia. There was a general increase in the mean LOI of binned peat sections from approximately −900 cm to −70 cm below the land surface (Supplementary Figure S2), which corresponds to steady peat accretion over the past ∼6700 years in Delta wetlands and represents a peat column that, depending on location, originally ranged from 2 to 15 m thick (Dachnowski-Stokes, 1936; Weir, 1950; Atwater and Belknap, 1980; Drexler et al., 2009a). With a rise in relative elevation and depth of flooding and duration, the importance of mineral sedimentation in tidal wetlands ultimately decreases (Morris et al., 2021). Mean LOI decreased back to about 20% during the Gold Rush era, and this has been followed by a recovery in mean LOI from approximately 22.5% at −54 cm depth to 37% at −15 cm below the land surface (Figure 3B). The model predicts continued increases in relative elevation and LOI provided that SLR continues on a low trajectory. Another prediction is that the vertical accretion will decelerate as marsh relative elevation approaches its highest possible relative elevation, and evidence for this is the decrease in the slope of the depth-age profile of 3.6 mm/yr over the last three centuries to 2.9 mm/yr during the last century.

The 20th-century accretion rate of approximately 3 mm/yr (Figure 3A) exceeded the long-term trend of sea-level rise in San Francisco of 1.97 mm/yr (NOAA, 2022). Consequently, LOI and relative elevation have been rising following the Gold Rush era. There were anomalies in the age-depth profile around 1850 that likely resulted from hydraulic mining, but this did not set the marshes on a permanently new trajectory. Relative marsh elevations returned to the course they were on before the Gold Rush due to the eventual exhaustion of the plume from the hydraulic mining period that took over 100 years to move through the entire estuary (Schoellhamer, 2011; Schoellhamer et al., 2013). One of the predictions of Marsh Equilibrium Theory (Morris et al., 2021) is that marsh relative elevation and accretion rate will equilibrate to the local RSLR. Perturbations such as the Gold Rush will disturb the equilibrium trajectory, but following the perturbation, the marsh will return to its equilibrium trajectory. This is a consequence of the feedback that determines the equilibrium—the interactions among flooding duration and depth, sedimentation rate, and primary production. This demonstrates that the system is inherently resilient up to a point.

Resilience projections

The large vertical range of the vegetation combined with high relative marsh elevation provides Delta marshes with resilience and elevation capital sufficiently great to tolerate centenary sea-level rise (CSLR) as high as 200 cm (Figure 4). For a Delta marsh of average elevation (29 cm MSL), the TPT at which vertical accretion no longer keeps up with the rate of sea-level rise is 50 years or more for CSLR up to 200 cm (Figure 4). Previous marsh sustainability modeling of the Delta capped the ability of marshes to remain sustainable only to ∼180 cm by 2100 (Swanson et al., 2015; Delta Stewardship Council, 2021). There are many differences in model parameterizations and assumptions between our study and those of Swanson et al. (2015) and Delta Stewardship Council (2021). Of particular importance are our new parameterizations of belowground organic matter distribution, accumulation, and decomposition, which incorporate root dynamics, and our use of a much broader vegetation growth range. The growth range is a function of the physiology of the wetland vegetation and the tide range. Species that have a high tolerance of hypoxia will have a lower vertical limit than a species intolerant of hypoxia, and at the upper extreme, a species with a high tolerance of osmotic stress will have a higher vertical limit. Our analysis shows that the ability of one important Delta marsh species, Schoenoplectus californicus, to grow very low in the tidal frame (Hester et al., 2016), has profound consequences for marsh sustainability at high rates of sea-level rise. Salinity change is a factor we did not consider, but an analysis by Buffington et al. (2021) suggests that changes in plant community composition and salinity should have minor effects on wetland elevation through 2100.

Despite the relatively favorable outlook for Delta marsh sustainability, our analysis of temporal resilience metrics shows that all tidal wetlands in the Delta have a limited lifetime and TPT. Currently, the RSLR may be only 4 mm/yr, but if it accelerates to raise the sea level by 2 m in the next 100 years (starting from the average surface elevation of the cores), the survival time will be 89 years, and the TPT will be reached in 41 years (Figure 5). Even if the CSLR is just 1 m, the TPT will still be just 66 years. Furthermore, the productivity of a wetland should be maximal at or near its tipping point at which further acceleration in SLR will reduce the relative elevation and productivity. The relative elevation of a tidal wetland is useful for identifying the areas at greatest risk. The greatest risk of drowning will be for an area at the lower limit of the vegetation unless it is on a prograding delta lobe. But with the exception that, the risk of drowning is greater for any area below the tipping point elevation.

Because the variability of marsh elevation is high in the Delta (SD of elevation of the cores = 23 cm), we also considered an additional metric, the conditional probability of regime change. The probability of marshes drowning in 100 years among those starting in a stable state (the upper half of the growth curve) was 7.1% (Table 2). The probability of marshes ending in a stable state also was only about 7%. Among those starting at suboptimal elevations, the probability of drowning was 41.9%. The most probable outcome was an unstable state (in the suboptimal range of elevations) at which 44% of all simulations ended after 100 years (Table 2). The suboptimal range is not a stable place, because increases in sea level for a marsh in the suboptimal range will decrease primary production and organic accretion.

Atmospheric rivers

The baseline simulations did not allow for episodic inputs of sediment such as those generated by atmospheric rivers (Thorne et al., 2022), so we added episodic inputs ranging up to 6 mm of sediment triennially (Table 3 and Table 4). Episodic inputs of sediment increased the proportion of simulations ending in a stable state. Triennial sediment additions of 6 mm increased the proportion of marshes surviving (the total of suboptimal and super-optimal percentages) from 51% to 72% and decreased the proportion drowning from 49% to 28%. If converted to a yearly supplement of 2 mm, this sediment boost represents ∼7.6% of the ∼1.67 million metric tons of sediment (Supplementary Table S2) delivered to the Delta each year (Wright and Schoellhamer, 2005). Thus, atmospheric rivers, which liberate large amounts of sediment into Delta waterways, are potentially important for marsh sustainability. This is especially relevant because atmospheric rivers are projected to become stronger, more frequent, and represent a greater proportion of total precipitation along the west coast of the United States in the future (Rhoades et al., 2020; Stern et al., 2020).

The total amount of suspended sediment a particular marsh receives, however, depends on several factors. These include the hydrodynamics and hydrogeomorphic zone of the marsh, the temporal variability of suspended sediment concentration in contributing rivers, the amount of wind-related resuspension in channels and flooded islands, and the ability of the vegetation to effectively trap large amounts of sediment (Drexler, 2011; Marineau and Wright, 2015; Schoellhamer et al., 2018; Cahoon et al., 2020). Therefore, episodic sediment boosts from atmospheric rivers may have substantial geographic variability, resulting in very high accretion in some marshes and only minor increases in others. Further, episodic delivery of sediment may not ultimately provide a boost if overall sediment availability does not continue at current levels. Future projections indicate that sediment loads and suspended sediment concentrations may increase by the end of the century in the Delta region (Stern et al., 2020); however, recent trends in suspended sediment concentrations in Delta waterways show a small but consistent decline (Work et al., 2021). For these reasons, sediment availability and its relationship to marsh vertical accretion in the San Francisco Estuary warrant further study.

Implications for wetland management

The temporal metrics in this paper, time to marsh drowning, time to marsh tipping point, and the probability of a regime shift, can provide managers with critical actionable information on the resilience of tidal marshes on the landscape. Armed with this information, managers can better plan management actions for tidal marshes losing elevation, prioritize wetland restoration projects that have the best chance of long-term survival, and establish marsh migration corridors. In many places including the San Francisco Estuary, future sediment availability is uncertain, so a “sooner than later” approach for restoration or enhancement may be preferable to waiting until marshes near their tipping points (San Francisco Estuary Institute, A.S.C., 2015). In the Delta region specifically, due to the configuration of levees, roadways, and land ownership, finding migration corridors can be challenging (Delta Stewardship Council, 2021). For these reasons, the most cost-effective restoration approach in the Delta and other areas with limited sediment availability and migration space is seizing opportunities where elevations and sediment supply are still favorable and migration corridors already exist. For marshes nearing their tipping points, thin-layer placement (TLP) of sediment midway between the tipping point elevation and the upper vertical vegetation limit can be highly effective in boosting marsh surface elevations (Myszewski and Alber, 2017). To regain marsh resilience, marsh elevation targets for TLP should be midway between the tipping point elevation and the upper vertical limit. Although TLP can be expensive, managers can determine the optimal schedule for sediment application by balancing costs with the valuable ecosystem services regained by a functional marsh. Overall, whichever management actions are chosen to mitigate sea-level rise impacts on tidal marshes, their ultimate success relies strongly on a clear understanding of marsh resilience and intervening well before they are projected to drown.

Data availability statement

All of the model inputs and any related citations are provided in Supplementary Table S1. The peat core data can be found in the literature cited in the Peat Core Data section under Methods and Data. Further inquiries can be directed to the corresponding author.

Author contributions

JM was responsible for model development. JD and LV provided data and contributed to data interpretation. JM and JD wrote the first draft and all authors contributed to the final version of the manuscript.

Funding

This project was supported with funding from the California Department of Fish and Wildlife Grant #3600BQ1996039 and a grant from the United States National Science Foundation (DEB 1654853 to JM).

Acknowledgments

We thank Kevin Buffington (USGS) and the anonymous journal reviewers for their helpful reviews of the manuscript and the SFEI advisors for their thoughtful comments throughout the project. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the United States Government.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.1039143/full#supplementary-material

References

Atwater, B. F. (1980). Attempts to correlate late quaternary climatic records between san Francisco Bay, the sacramento-san Joaquin delta, and the Mokelumne River, California. Newark: University of Delaware. PhD.

Google Scholar

Atwater, B. F., and Belknap, D. F. (1980). “Tidal-wetland deposits of the Sacramento-San Joaquin Delta, California,” in Quaternary Depositional Environments of the Pacific Coast. Proceedings of the Pacific Coast Paleogeography, Symposium 4. Editors M. E. Field, A. H. Bouma, I. P. Colburn, R. G. Douglas, and J. C. Ingle (Los Angeles: Society of Economic Paleontologists and Mineralogists, Pacific Section), 89–103.

Google Scholar

Bouse, R. M., Fuller, C. C., Luoma, S. N., Hornberger, M. I., Jaffe, B. E., and Smith, R. E. (2010). Mercury-contaminated hydraulic mining debris in san Francisco Bay. San Franc. Estuary Watershed Sci. 8 (1), 1–28. doi:10.15447/sfews.2010v8iss1art3

CrossRef Full Text | Google Scholar

Buffington, K. J., Janousek, C. N., Dugger, B. D., Callaway, J. C., Schile-Beers, L. M., Borgnis Sloane, E., et al. (2021). Incorporation of uncertainty to improve projections of tidal wetland elevation and carbon accumulation with sea-level rise. PLOS ONE 16 (10), e0256707. doi:10.1371/journal.pone.0256707

PubMed Abstract | CrossRef Full Text | Google Scholar

Cahoon, D. R., McKee, K. L., and Morris, J. T. (2020). How plants influence resilience of salt marsh and mangrove wetlands to sea-level rise. Estuaries Coasts 44, 883–898. doi:10.1007/s12237-020-00834-w

CrossRef Full Text | Google Scholar

California Department of Water Resources (2021b). California EcoRestore [online]. Available: https://water.ca.gov/Programs/All-Programs/EcoRestore (Accessed July 11, 2022).

Google Scholar

California Department of Water Resources (2021a). Delta conveyance [online]. Available: https://water.ca.gov/deltaconveyance (Accessed July 11, 2022).

Google Scholar

Callaway, J. C., Borgnis, E. L., Turner, R. E., and Milan, C. S. (2012). Carbon sequestration and sediment accretion in san Francisco Bay tidal wetlands. Estuaries Coasts 35 (5), 1163–1181. doi:10.1007/s12237-012-9508-9

CrossRef Full Text | Google Scholar

Cloern, J. E., Knowles, N., Brown, L. R., Cayan, D., Dettinger, M. D., Morgan, T. L., et al. (2011). Projected evolution of California's San Francisco Bay-Delta-River system in a century of climate change. PLOS ONE 6 (9), e24465. doi:10.1371/journal.pone.0024465

PubMed Abstract | CrossRef Full Text | Google Scholar

Cloern, J. E., Safran, S. M., Vaughn, L. S., Robinson, A., Whipple, A. A., Boyer, K. E., et al. (2021). On the human appropriation of wetland primary production. Sci. Total Environ. 785, 147097. doi:10.1016/j.scitotenv.2021.147097

CrossRef Full Text | Google Scholar

Costanza, R., Perez-Maqueo, O., Martinez, M. L., Sutton, P., Anderson, S., and Mulder, K. (2008). The value of coastal wetlands for hurricane protection. Ambio 37, 241–248. doi:10.1579/0044-7447(2008)37[241:TVOCWF]2.0.CO;2

PubMed Abstract | CrossRef Full Text | Google Scholar

Couvillion, B. R., and Beck, H. (2013). Marsh collapse thresholds for coastal Louisiana estimated using elevation and vegetation index data. J. Coast. Res. 58, 58–67. doi:10.2112/SI63-006.1

CrossRef Full Text | Google Scholar

Crooks, S., Sutton-Grier, A. E., Troxler, T. G., Herold, N., Bernal, B., Schile-Beers, L., et al. (2018). Coastal wetland management as a contribution to the US national greenhouse gas inventory. Nat. Clim. Chang. 8 (12), 1109–1112. doi:10.1038/s41558-018-0345-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Dachnowski-Stokes, A. P. (1936). Peat land in the Pacific Coast states in relation to land and water resources. Washington, DC, USA: U.S.D.O. Agriculture.

Google Scholar

Delta Stewardship Council (2021). Building resilience amid rapid change. Sacramento, CA: Delta Stewardship Council Annual Report. https://deltacouncil.ca.gov/pdf/2021-annual-report.pdf.

Google Scholar

Dettinger, M. D., Ralph, F. M., Das, T., Neiman, P. J., and Cayan, D. R. (2011). Atmospheric rivers, floods and the water resources of California. Water 3 (2), 445–478. doi:10.3390/w3020445

CrossRef Full Text | Google Scholar

Deverel, S., Ingram, T., Lucero, C., and Drexler, J. (2014). Impounded marshes on subsided islands: Simulated vertical accretion, processes, and effects, Sacramento-San Joaquin Delta, CA USA. San Franc. Estuary Watershed Sci. 12, 1–23. doi:10.15447/sfews.2014v12iss2art5

CrossRef Full Text | Google Scholar

Deverel, S. J., Ingrum, T., and Leighton, D. (2016). Present-day oxidative subsidence of organic soils and mitigation in the Sacramento-San Joaquin Delta, California, USA. Hydrogeol. J. 24, 569–586. doi:10.1007/s10040-016-1391-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Deverel, S. J., and Leighton, D. A. (2010). Historic, recent, and future subsidence, Sacramento-San Joaquin Delta, California, USA. San Franc. Estuary Watershed Sci. 8, 1–23. doi:10.15447/sfews.2010v8iss2art1

CrossRef Full Text | Google Scholar

Drexler, J. Z. (2011). Peat formation processes through the millennia in tidal marshes of the Sacramento–San Joaquin Delta, California, USA. Estuaries Coasts 34 (5), 900–911. doi:10.1007/s12237-011-9393-7

CrossRef Full Text | Google Scholar

Drexler, J. Z., de Fontaine, C. S., and Deverel, S. J. (2009a). The legacy of wetland drainage on the remaining peat in the Sacramento — San Joaquin Delta, California, USA. Wetlands 29 (1), 372–386. doi:10.1672/08-97.1

CrossRef Full Text | Google Scholar

Drexler, J., Fontaine, C., and Brown, T. (2009b). Peat accretion histories during the past 6, 000 Years in marshes of the sacramento–san Joaquin delta, CA, USA. Estuaries Coasts 32, 871–892. doi:10.1007/s12237-009-9202-8

CrossRef Full Text | Google Scholar

Drexler, J. Z., Alpers, C. N., Neymark, L. A., Paces, J. B., Taylor, H. E., and Fuller, C. C. (2016). A millennial-scale record of Pb and Hg contamination in peatlands of the Sacramento–San Joaquin Delta of California, USA. Sci. Total Environ. 551-552, 738–751. doi:10.1016/j.scitotenv.2016.01.201

PubMed Abstract | CrossRef Full Text | Google Scholar

Drexler, J. Z., Davis, M. J., Woo, I., and De La Cruz, S. (2020). Carbon sources in the sediments of a restoring vs. historically unaltered salt marsh. Estuaries Coasts 43 (6), 1345–1360. doi:10.1007/s12237-020-00748-7

CrossRef Full Text | Google Scholar

Drexler, J. Z., Paces, J. B., Alpers, C. N., Windham-Myers, L., Neymark, L. A., Bullen, T. D., et al. (2014). ²³⁴U/²³⁸U and δ⁸⁷Sr in peat as tracers of paleosalinity in the Sacramento-San Joaquin Delta of California, USA. Appl. Geochem. 40, 164–179. doi:10.1016/j.apgeochem.2013.10.011

CrossRef Full Text | Google Scholar

Durand, J. (2015). A conceptual model of the aquatic food web of the upper San Francisco Estuary. San Franc. Estuary Watershed Sci. 13, 1–37. doi:10.15447/sfews.v13iss3art5

CrossRef Full Text | Google Scholar

Fagherazzi, S., Mariotti, G., Leonardi, N., Canestrelli, A., Nardin, W., and Kearney, W. S. (2020). Salt marsh dynamics in a period of accelerated sea level rise. JGR. Earth Surf. 125 (8), e2019JF005200. doi:10.1029/2019JF005200

CrossRef Full Text | Google Scholar

Ganju, N. K., Defne, Z., Kirwan, M. L., Fagherazzi, S., D’Alpaos, A., and Carniello, L. (2017). Spatially integrative metrics reveal hidden vulnerability of microtidal salt marshes. Nat. Commun. 8 (1), 14156. doi:10.1038/ncomms14156

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganju, N. K., Kirwan, M. L., Dickhudt, P. J., Guntenspergen, G. R., Cahoon, D. R., and Kroeger, K. D. (2015). Sediment transport-based metrics of wetland stability. Geophys. Res. Lett. 42 (19), 7992–8000. doi:10.1002/2015GL065980

CrossRef Full Text | Google Scholar

Ganju, N. K. (2019). Marshes are the new beaches: Integrating sediment transport into restoration planning. Estuaries Coasts 42 (4), 917–926. doi:10.1007/s12237-019-00531-3

CrossRef Full Text | Google Scholar

Gershunov, A., Shulgina, T., Ralph, F. M., Lavers, D. A., and Rutz, J. J. (2017). Assessing the climate-scale variability of atmospheric rivers affecting Western North America. Geophys. Res. Lett. 44 (15), 7900–7908. doi:10.1002/2017GL074175

CrossRef Full Text | Google Scholar

Goman, M., and Wells, L. (2000). Trends in river flow affecting the northeastern reach of the San Francisco Bay estuary over the past 7000 years. Quat. Res. 54 (2), 206–217. doi:10.1006/qres.2000.2165

CrossRef Full Text | Google Scholar

Grimm, V., and Wissel, C. (1997). Babel, or the ecological stability discussions: An inventory and analysis of terminology and a guide for avoiding confusion. Oecologia 109 (3), 323–334. doi:10.1007/s004420050090

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunderson, L. H. (2000). Ecological resilience-in theory and application. Annu. Rev. Ecol. Syst. 31, 425–439. doi:10.1146/annurev.ecolsys.31.1.425

CrossRef Full Text | Google Scholar

He, M. (2022). Assessing changes in 21st century mean and extreme climate of the sacramento–san Joaquin delta in California. Climate 10 (2), 16. doi:10.3390/cli10020016

CrossRef Full Text | Google Scholar

Herr, D., Vegh, T., and Von Under, M. (2019). “State of international policy for blue carbon actions,” in A blue carbon primer: The state of coastal wetland carbon science, practice, and policy (Boca Raton, FL: CRC Press).

Google Scholar

Hester, M. W., Willis, J. M., and Sloey, T. M. (2016). Field assessment of environmental factors constraining the development and expansion of Schoenoplectus californicus marsh at a California tidal freshwater restoration site. Wetl. Ecol. Manag. 24 (1), 33–44. doi:10.1007/s11273-015-9448-9

CrossRef Full Text | Google Scholar

Holling, C. S. (1973). Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 4, 1–23. doi:10.1146/annurev.es.04.110173.000245

CrossRef Full Text | Google Scholar

Holmquist, J. R., Schile-Beers, L., Buffington, K., Lu, M., Mozdzer, T. J., Riera, J., et al. (2021). Scalability and performance tradeoffs in quantifying relationships between elevation and tidal wetland plant communities. Mar. Ecol. Prog. Ser. 666, 57–72. doi:10.3354/meps13683

CrossRef Full Text | Google Scholar

Hutchinson, G. E. (1957). Concluding remarks. Cold Spring Harb. Symposia Quantitative Biol. 22, 415–427. doi:10.1101/SQB.1957.022.01.039

CrossRef Full Text | Google Scholar

Khanna, S., Santos, M. J., Boyer, J. D., Shapiro, K. D., Bellvert, J., and Ustin, S. L. (2018). Water primrose invasion changes successional pathways in an estuarine ecosystem. Ecosphere 9 (9), e02418. doi:10.1002/ecs2.2418

CrossRef Full Text | Google Scholar

Knowles, N., and Cayan, D. R. (2002). Potential effects of global warming on the Sacramento/San Joaquin watershed and the San Francisco estuary. Geophys. Res. Lett. 29 (18), 38-1–38-4. doi:10.1029/2001GL014339

CrossRef Full Text | Google Scholar

Kroeger, K. D., Crooks, S., Moseman-Valtierra, S., and Tang, J. (2017). Restoring tides to reduce methane emissions in impounded wetlands: A new and potent blue carbon climate change intervention. Sci. Rep. 7 (1), 11914. doi:10.1038/s41598-017-12138-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Marineau, M. D., and Wright, S. A. (2015). “Effects of human alterations on the hydrodynamics and sediment transport in the Sacramento-San Joaquin Delta, California,” in Proceedings International Association of Hydrological Sciences (New Orleans, LA: Copernicus Publications), 399–406.

CrossRef Full Text | Google Scholar

Masselink, G., and Lazarus, E. (2019). Defining coastal resilience. Water 11, 2587. doi:10.3390/w11122587

CrossRef Full Text | Google Scholar

Morris, J. T., Barber, D. C., Callaway, J. C., Chambers, R., Hagen, S. C., Hopkinson, C. S., et al. (2016). Contributions of organic and inorganic matter to sediment volume and accretion in tidal wetlands at steady state. Earth's. Future 4 (4), 110–121. doi:10.1002/2015EF000334

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, J. T., and Bowden, W. B. (1986). A mechanistic, numerical model of sedimentation, mineralization, and decomposition for marsh sediments. Soil Sci. Soc. Am. J. 50, 96–105. doi:10.2136/sssaj1986.03615995005000010019x

CrossRef Full Text | Google Scholar

Morris, J. T., Cahoon, D. R., Callaway, J. C., Craft, C., Neubauer, S. C., and Weston, N. B. (2021). “Marsh equilibrium theory: Implications for responses to rising sea level,” in Salt marshes: Function, dynamics, and stresses. Editors D. M. FitzGerald, and Z. J. Hughes (Cambridge: Cambridge University Press), 157–177.

CrossRef Full Text | Google Scholar

Morris, J. T., and Callaway, J. C. (2018). “Physical and biological regulation of carbon sequestration in salt marshes,” in A blue carbon primer: The state of coastal wetland carbon science, practice, and policy. Editors L. Windam-Meyers, S. Crooks, and T. Troxler (Boca Raton: CRC Press), 67–79.

CrossRef Full Text | Google Scholar

Morris, J. T., Sundareshwar, P. V., Nietch, C. T., Kjerfve, B., and Cahoon, D. R. (2002). Responses of coastal wetlands to rising sea level. Ecology 83, 2869–2877. doi:10.1890/0012-9658(2002)083[2869:rocwtr]2.0.co;2

CrossRef Full Text | Google Scholar

Myszewski, M. A., and Alber, M. (2017). in Use of thin layer placement of dredged material for salt marsh restoration. Editor G.D.O.N. Resources (Athens, GA: Georgia Coastal Research Council).

Google Scholar

Neijnens, F. K., Siteur, K., van de Koppel, J., and Rietkerk, M. (2021). Early warning signals for rate-induced critical transitions in salt marsh ecosystems. Ecosystems 24 (8), 1825–1836. doi:10.1007/s10021-021-00610-2

CrossRef Full Text | Google Scholar

Newman, K. B., and Brandes, P. L. (2010). Hierarchical modeling of juvenile chinook salmon survival as a function of sacramento–san Joaquin delta water exports. North Am. J. Fish. Manag. 30 (1), 157–169. doi:10.1577/M07-188.1

CrossRef Full Text | Google Scholar

NOAA (2022). Relative Sea level trend 9414290 san Francisco. California: NOAA.

Google Scholar

Nowacki, D. J., and Ganju, N. K. (2019). Simple metrics predict salt-marsh sediment fluxes. Geophys. Res. Lett. 46 (21), 12250–12257. doi:10.1029/2019GL083819

CrossRef Full Text | Google Scholar

Powell, E. J., Tyrrell, M. C., Milliken, A., Tirpak, J. M., and Staudinger, M. D. (2019). A review of coastal management approaches to support the integration of ecological and human community planning for climate change. J. Coast. Conserv. 23 (1), 1–18. doi:10.1007/s11852-018-0632-y

CrossRef Full Text | Google Scholar

Raposa, K. B., Wasson, K., Smith, E., Crooks, J. A., Delgado, P., Fernald, S. H., et al. (2016). Assessing tidal marsh resilience to sea-level rise at broad geographic scales with multi-metric indices. Biol. Conserv. 204, 263–275. doi:10.1016/j.biocon.2016.10.015

CrossRef Full Text | Google Scholar

Rhoades, A. M., Jones, A. D., Srivastava, A., Huang, H., O'Brien, T. A., Patricola, C. M., et al. (2020). The shifting scales of Western U.S. landfalling atmospheric rivers under climate change. Geophys. Res. Lett. 47 (17), e2020GL089096. doi:10.1029/2020GL089096

CrossRef Full Text | Google Scholar

Roman, C. T., and Burdick, D. M. (2012). “A synthesis of research and practice on restoring tides to salt marshes,” in Tidal marsh restoration: A synthesis of science and management. Editors C. T. Roman, and D. M. Burdick (Washington D.C. Island Press), 3–10.

CrossRef Full Text | Google Scholar

San Francisco Estuary Institute, A.S.C. (2015). Baylands ecosystem habitat goals project [online]. Available: https://www.sfei.org/projects/baylandsgoals (Accessed July 21, 2022).

Google Scholar

Schepers, L., Kirwan, M., Guntenspergen, G. R., and Temmerman, S. (2020). Evaluating indicators of marsh vulnerability to sea level rise along a historical marsh loss gradient. Earth Surf. Process. Landf. 45 (9), 2107–2117. doi:10.1002/esp.4869

CrossRef Full Text | Google Scholar

Schile, L. M., Callaway, J. C., Morris, J. T., Stralberg, D., Parker, V. T., and Kelly, M. (2014). Modeling tidal marsh distribution with Sea-Level rise: Evaluating the role of vegetation, sediment, and upland habitat in marsh resiliency. PLOS ONE 9 (2), e88760. doi:10.1371/journal.pone.0088760

PubMed Abstract | CrossRef Full Text | Google Scholar

Schoellhamer, D. H. (2011). Sudden clearing of estuarine waters upon crossing the threshold from transport to supply regulation of sediment transport as an erodible sediment pool is depleted: San Francisco Bay, 1999. Estuaries Coasts 34 (5), 885–899. doi:10.1007/s12237-011-9382-x

CrossRef Full Text | Google Scholar

Schoellhamer, D., McKee, L., Pearce, S., Kauhanen, P., Salomon, M., Dusterhoff, S., et al. (2018). Sediment Supply to San Francisco Bay, Water Years 1995 through 2016: Data, trends, and monitoring recommendations to support decisions about water quality, tidal wetlands, and resilience to sea level rise. Richmond, CA: San Francisco Estuary Institute.

Google Scholar

Schoellhamer, D., Wright, S., and Drexler, J. (2013). Adjustment of the San Francisco estuary and watershed to decreasing sediment supply in the 20th century. Mar. Geol. 345, 63–71. doi:10.1016/j.margeo.2013.04.007

CrossRef Full Text | Google Scholar

Shelford, V. E. (1931). Some concepts of bioecology. Ecology 12 (3), 455–467. doi:10.2307/1928991

CrossRef Full Text | Google Scholar

Shlemon, R. J., and Begg, E. L. (1975). Late quaternary evolution of the sacramento-san Joaquin delta, California. Quat. Stud. 13, 259–266.

Google Scholar

Sommer, T., Armor, C., Baxter, R., Breuer, R., Brown, L., Chotkowski, M., et al. (2007). The collapse of pelagic fishes in the upper San Francisco Estuary: El colapso de los peces pelagicos en la cabecera del estuario San Francisco. Fisheries 32 (6), 270–277. doi:10.1577/1548-8446(2007)32[270:TCOPFI]2.0.CO;2

CrossRef Full Text | Google Scholar

Stagg, C. L., Krauss, K. W., Cahoon, D. R., Cormier, N., Conner, W. H., and Swarzenski, C. M. (2016). Processes contributing to resilience of coastal wetlands to sea-level rise. Ecosystems 19 (8), 1445–1459. doi:10.1007/s10021-016-0015-x

CrossRef Full Text | Google Scholar

Stern, M. A., Flint, L. E., Flint, A. L., Knowles, N., and Wright, S. A. (2020). The future of sediment transport and streamflow under a changing climate and the implications for long-term resilience of the San Francisco Bay-Delta. Water Resour. Res. 56 (9), e2019WR026245. doi:10.1029/2019WR026245

CrossRef Full Text | Google Scholar

Stralberg, D., Brennan, M., Callaway, J. C., Wood, J. K., Schile, L. M., Jongsomjit, D., et al. (2011). Evaluating tidal marsh sustainability in the face of Sea-Level rise: A hybrid modeling approach applied to san Francisco Bay. PLoS ONE 6 (11), e27388. doi:10.1371/journal.pone.0027388

PubMed Abstract | CrossRef Full Text | Google Scholar

Swanson, K. M., Drexler, J. Z., Fuller, C. C., and Schoellhamer, D. H. (2015). Modeling tidal freshwater marsh sustainability in the Sacramento-San Joaquin Delta under a broad suite of potential future scenarios. San Franc. Estuary Watershed Sci. 13, 1–21. doi:10.15447/sfews.2015v13iss1art3

CrossRef Full Text | Google Scholar

Swanson, K. M., Drexler, J. Z., Schoellhamer, D. H., Thorne, K. M., Casazza, M. L., Overton, C. T., et al. (2014). Wetland accretion rate model of ecosystem resilience (WARMER) and its application to habitat sustainability for endangered Species in the San Francisco estuary. Estuaries Coasts 37 (2), 476–492. doi:10.1007/s12237-013-9694-0

CrossRef Full Text | Google Scholar

Thompson, J. D. (1957). The settlement geography of the sacramento-san Joaquin delta, California. Stanford, CA, USA: Stanford University.

Google Scholar

Thorne, K., Jones, S., Freeman, C., Buffington, K., Janousek, C., and Guntenspergen, G. (2022). Atmospheric river storm flooding influences tidal marsh elevation building processes. JGR. Biogeosciences 127 (3), e2021JG006592. doi:10.1029/2021JG006592

CrossRef Full Text | Google Scholar

USDA National Agricultural Statistics Service (2021). Census of agriculture, 2017 ranking of market value of Ag products sold in California. Available at: https://www.nass.usda.gov/Publications/AgCensus/2017/Online_Resources/Rankings_of_Market_Value/California/#skipnav (Accessed July 28, 2022).

Google Scholar

van Belzen, J., van de Koppel, J., Kirwan, M., Wal, D., Herman, P., Dakos, V., et al. (2017). Vegetation recovery in tidal marshes reveals critical slowing down under increased inundation. Nat. Commun. 8, 15811. doi:10.1038/ncomms15811

PubMed Abstract | CrossRef Full Text | Google Scholar

Wasson, K., Ganju, N. K., Defne, Z., Endris, C., Elsey-Quirk, T., Thorne, K. M., et al. (2019). Understanding tidal marsh trajectories: Evaluation of multiple indicators of marsh persistence. Environ. Res. Lett. 14 (12), 124073. doi:10.1088/1748-9326/ab5a94

CrossRef Full Text | Google Scholar

Weir, W. (1950). Subsidence of peat lands of the Sacramento-San Joaquin Delta, California. Hilg. 20, 37–56. doi:10.3733/hilg.v20n03p037

CrossRef Full Text | Google Scholar

Weir, W. W. (1937). Subsidence of peat land on the Sacramento-San Joaquin Delta of California. Madison, WI: Trans. 6th Commission International Society Soil Science.

Google Scholar

Whipple, A. A., Grossinger, R. M., Rankin, D., Stanford, B., and Askevold, R. A. (2012). Sacramento-san Joaquin delta historical ecological investigation: Exploring pattern and process. Richmond, CA: San Francisco Estuary Institute-Aquatic Science Center. https://www.sfei.org/DeltaHEStudy.

Google Scholar

Work, P. A., Downing-Kunz, M., and Drexler, J. Z. (2021). Trapping of suspended sediment by submerged aquatic vegetation in a tidal freshwater region: Field observations and long-term trends. Estuaries Coasts 44 (3), 734–749. doi:10.1007/s12237-020-00799-w

CrossRef Full Text | Google Scholar

Wright, S. A., and Schoellhamer, D. H. (2005). Estimating sediment budgets at the interface between rivers and estuaries with application to the Sacramento-San Joaquin River Delta. Water Resour. Res. 41 (9). doi:10.1029/2004WR003753

CrossRef Full Text | Google Scholar