Analyzing the effect of different types of pollution with bipolar complex fuzzy power Bonferroni mean operators

When any amount of harmful materials (any substance or any type of energy) is introduced into the climate at a rate quicker than it very well may be scattered or securely put away, then pollution occurs. These harmful materials are known as pollutants which can be natural and can also be manmade such as trash generated by factories. These harmful materials harm the quality of land, air, and water and cause various types of pollution, which affects the environment. In this article, we analyze the effect of various types of pollution on the environment and evaluate the most harmful type of pollution through an illustrative example by employing power Bonferroni mean (BM) operators in the setting of the bipolar complex fuzzy set (BCFS), like bipolar complex fuzzy (BCF) power BM (BCFPBM), BCF weighted power BM (BCFWPBM), BCF power geometric BM (BCFPGBM), and BCF weighted power geometric BM (BCFWPGBM) operators and a decision-making (DM) procedure created on these operators in the environment of the BCFS which are introduced in this article. Furthermore, we illustrate that the introduced operators and a DM procedure in the environment of the BCFS are more effective and have a wide model and advantages than certain prevailing works.

Introduction

According to Pure Earth (an environmental organization), over 200 million people from all over the world are affected by toxic pollution. In certain parts of the world where pollution is high, women give birth to babies with defects, children have lost $30$ to $40$ IQ points, and the average life might be around 45 years due to various kinds of diseases. Various things beneficial to people cause pollution, such as generating electricity from burning coal, cars discharging through exhaust pipes, sewage and garbage produced by homes and industries, and utilizing pesticides and herbicides. Finding out which pollutants have greater effects on the environment is a genuine life DM issue.

Zadeh (1965) introduced the model of the fuzzy set (FS) for addressing abstruse and ambiguous information in genuine life issues. Before the model of the FS, there was a model of a crisp set in which every element has a satisfying grade (SG), either $0$ or $1$. In the FS, every element has a satisfying grade either $0$ or $1$ or any value between them. Thus, the FS is a generalization of the crisp set, enlarging the range from the set of $0$ and $1$ to the interval $\left[0,1\right]$. Scholars have employed the FS in various fields, such as DM (De, 2020), economy (Rytova and Gutman, 2019), and medicine (Choudhury et al., 2021). Kwon et al. (2022) combined the AHP and FS theory. Gulistan et al. (2022) described a new fuzzy decision support system. Jiang (2022) presented an improved algorithm for the FS. Chen and Tian (2022) developed the FS QCA approach. Scholars have often modified the FS and defined additional models because of the lack of the ability of the FS to address more complicated information such as the complex interval-valued Pythagorean fuzzy set (Ali et al., 2021), distance measures based on picture FS (PFS), rough set (Sahu et al., 2021), interval-valued PFS (Ashraf et al., 2022), and DM approach based on the integration of the fuzzy CoCoSO method (Narang et al., 2022).

Zhang (1994) introduced one of the modifications of the FS called the bipolar FS (BFS). In the BFS, every element has a positive satisfying grade (PSG) between $0$ and $1$ and a negative satisfying grade between $-1$ and $0$. Singh (2022) interpreted bipolar fuzzy (BF) concept reduction by granular-based weighted entropy. Pandey et al. (2022) described BF centrality measures. The graphs in the environment of the BF set were studied by various authors, including Poulik and Ghorai (2020), Wan et al. (2022), and Bharathi and Felixia (2022). Gong and Hua (2022) initiated fuzzy edge connectivity in BF networks. The DM technique for BF sets was developed by Yamini et al. (2022). The multi-criteria DM (MCDM) technique for BF was created by Rajalakshmi and Mary (2022) and Garai et al. (2022). Riaz et al. (2022) defined sine trigonometric (ST) aggregation operators (AOs) for BF sets. Jana et al. (2019) introduced BF Dombi AOs (DAOs), and Wei et al. (2018) introduced BF Hamacher AOs (HAOs).

Ramot et al. (2002) developed another modification of the FS called the complex FS (CFS) because the FS cannot handle data involving a second dimension or extra fuzzy information. In the CFS, every element has a satisfying grade in $\left\{z\in \mathbb{C}\mathbb{|}z\le 1\right\},$ i.e., a unit disc of a complex plane with SG in the polar form, i.e., $r{e}^{\mathfrak{i}\theta }$. Tamir et al. (2011) have provided another version of the CFS by considering the range of the satisfying grade as a unit square in a complex plane instead of a unit circle, i.e., every element of the CFS has a satisfying grade in a unit square and is in the structure of the Cartesian form, i.e., $\alpha +\mathfrak{i}\beta$. Akram et al. (2021) presented a competition graph in the environment of the CFS. Zeeshan and Khan (2022) developed a DM technique based on the CFS. Akram and Bashir (2021) described ordered, weighted, quadratic, and averaging operators based on the CFS. Hu et al. (2019) proposed CF power AOs. Mahmood and Ur Rehman (2022a) provided one of the most modified models of the FS because the FS lacks the ability to tackle negative aspects of human beings, as well as information involving the second dimension, and called it a bipolar complex fuzzy set (BCFS). The BCFS also modified the model of the BFS and CFS as the BFS lacks the ability to tackle the data containing the second dimension, and the CFS lacks the ability to tackle the negative aspects of human beings. In the BCFS, every element has the PSG in the first quadrant and NSG in the third quadrant of a unit square in a complex plane. Ur Rehman and Mahmood (2022) defined generalized dice similarity measures (SM) for the bipolar complex fuzzy (BCF) set.

To get a more accurate alternative method, we have to consider the given assessment information and the relationship between them. The power average (PA) and power-ordered weighted average operators were first established by Yager (2001), which incorporate variable weights. Xu and Yager (2009) used power geometric operators, and Garg et al. (2021) established PA operators in the setting of the T-spherical FS. There is another apparatus called the BM operator defined by Bonferroni (1950), which considers the interrelationship of inputs. It has been utilized in numerous fields: the geometric BM (GBM) was used by Zhu et al. (2012), the BM operator was utilized in the intuitionistic FS (IFS) by Xu and Yager (2010), and picture fuzzy BM operators were investigated by Ateş and Akay (2020). Liu and Li (2017) developed PBM operators for the interval-valued IFS (IVFS). Furthermore, PA has the ability to ignore the effect of the smallest or largest information by taking various weights, and the BM operator has the ability to consider the interrelationship of each input argument. However, in DM issues and circumstances, the PA and DM operators lack the ability to tackle the data in the model of the BCFS.

The BCFS can easily portray fuzzy data or information containing positive and negative aspects, as well as extra fuzzy information (second dimension), and is very handy in dealing with complicated DM issues and genuine life issues. The model of the BCFS is wider and richer than certain prevailing conceptions like FS, BFS, and CFS, and numerous scholars have defined various AOs in the setting of the BCFS. Mahmood et al. (2021) have defined BCF HAOs, and Mahmood and Ur Rehman (2022b) have defined DAOs for the BCF set. Mahmood et al. (2022a) initiated AOs, and Rehman et al. (2022) presented Frank AOs in the environment of the BCF set. The BM operators based on BCFS were defined by Mahmood et al. (2022b). However, these defined AOs have their drawbacks, and these operations have one common drawback; it is that these operators cannot provide a fair and unbiased weight vector to the attributes because in these operators, the decision expert provides weight vectors to each attribute on his/her own choice. In the literature, there is no such structure or operator which can overcome this dilemma. Thus, this research gap created various questions such as

• How do we get fair and unbiased decisions if the data are in the structure of the BCFS?

• How do we make decisions if the weight vector is not given and the information is in the setting of the BCFS?

• How do we get the advantages of the combination of PA and BM operators in the environment of the BCFS?

Up until now, no one has answered these questions; thus, in this study, we answer these questions by combining PA, geometric BM, and BM operators in the environment of the BCFS to introduce BCFPBM, BCFWPBM, BCFPGBM, and BCFWPGBM operators. Furthermore, we describe what we are achieving from this study.

• The structure of the BCFS is one of the most advanced and widely used structures, and up until now, no one has defined these operators in the environment of the BCFS.

• Over time, the information became more complicated and tricky and almost impossible to handle with ordinary mathematical models and operators. This study will help handle complicated and tricky data and provide a fair decision. This study is the requirement of time.

• PA, GBM, and BM operators have their advantages; this study provides us with all these advantages together.

• To show the practical advantage of this study, we investigate a genuine-life numerical example related to the environment in this study.

• By taking the arbitrary weight vector, the introduced operators would be reduced to the BM operators, as defined by Mahmood et al. (2022b). Thus, the defined operators are the modification of BM operators, as defined by Mahmood et al. (2022b).

In the Background section, we review the basic concept of pollution and its types, as well as the idea of the BCFS and its properties. In the BCF power Bonferroni mean operators section, we introduce power BM operators in the setting of BCF sets to define BCFPBM, BCFWPBM, BCFPGBM, and BCFWPGBM operators. In the Application section, we introduce a DM procedure for solving genuine life issues and then present a numerical example related to pollution and its types. In the Comparison section, we show that the introduced PBM operators (BCFPBM, BCFWPBM, BCFPGBM, and BCFWPGBM) and a DM procedure in the environment of BCFS are more effective than other prevailing operators. The Conclusion section contains the concluding remarks of this article.

Background

The word pollution originates from the Latin word polluere, which essentially implies contamination. Thus, in a simple way, pollution is something that pollutes the climate. According to Pure Earth (an environmental organization), over 200 million people from all over the world are affected by toxic pollution. Various beneficial things can cause pollution, such as generating electricity from burning coal causes pollution in the air, cars discharging pollutants through exhaust pipes, the sewage and garbage produced by homes and industries cause water and land pollution, and the use of pesticides to kill insects and weeds causes water pollution , which is harmful to wildlife. These pollutants harm the quality of land, air, and water. Various kinds of pollution can be caused by natural events and also by artificial activities. The four major types of pollution are

1) Air pollution,

2) Water pollution,

3) Soil pollution, and

4) Noise pollution.

Figure 1 portrays the types of pollution.

FIGURE 1

FIGURE 1. Major types of pollution.

1) Air pollution: There is an exact synthetic structure of the air that we breathe. Its vast majority comprises oxygen, dormant gases, nitrogen, and water fume. When the pollutants or things are introduced in the air, which are not normally there, they cause air pollution. A usual kind of air pollution takes place when people emit particles of burning fuels into the air. This sort of pollution seems to be excess, having a large number of minuscule particles, drifting in the air. One more typical sort of air pollution is caused by harmful gases, like nitrogen oxides, sulfur dioxide, chemical fumes, and carbon monoxide. When these gases are introduced in the air, they can be a part of the chemical reactions and produce smog and acid rain. Over two million people die every year because of air pollution. The impact of air pollution on human well-being can fluctuate generally contingent upon the contamination. Assuming the poison is exceptionally harmful, the consequences for well-being can be far and wide extreme. For instance, the leakage of methyl isocyanate gas in Bhopal, India, in 1984, killed more than two thousand people, and in north, two hundred thousand people experienced respiratory issues.

2) Water pollution: When chemicals or other harmful substances such as sewage, fertilizers, metals, mercury, and pesticides are introduced into the water, then water pollution occurs. All over the world, 44 percent of streams, $64$ percent of lakes, and 30 percent of the bay are not hygienic for fishing and swimming as per the Environmental Protection Agency (EPA). According to the EPA, the usual pollutants in the USA are mercury, nitrogen, bacteria, and phosphorus.

3) Soil pollution: Household and industrial garbage and waste cause soil pollution. According to the EPA, USA generated over 258 million tons of waste and garbage in 2014. More than half, i.e., 136 million tons, of the waste was assembled in landfills, and merely 34% was composted. The effects of land pollution are not that noticeable, but its implication can easily be observed. Oil spills, industrial accidents, acid rain, improper waste disposal, mining activities, etc., are a few usual reasons for soil pollution.

4) Noise pollution: despite the fact that people cannot smell or see noise pollution, it influences the climate. When various sounds reach the harmful level, for example, sound coming from industries, jets, etc., it causes noise pollution. It is obvious that there are immediate connections between well-being and noise, causing hearing loss, increase in the blood pressure, speech interference, and pressure-related ailments. For instance, according to the WHO, thousands of people die every year because of noise pollution. Ships cause underwater noise pollution. Similarly Noise pollution influence wild species to impart stronger, which can reduce their life expectancy.

Definition 1. (Mahmood and Ur Rehman, 2022b) The theory is modeled as follows.

${\mathcal{M}}_{BCFS}=\left\{\left(\xi ,\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P\left(\xi \right),{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\left(\xi \right)\right)\right)|\xi \in {{\rm E}}_{\xi }\right\}=\left\{\left(\xi ,\left(\begin{array}{c}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}\left(\xi \right)+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP}\left(\xi \right),\\ {{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}\left(\xi \right)+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\left(\xi \right)\end{array}\right)\right)|\xi \in {{\rm E}}_{\xi }\right\}(1)$

is known as the BCFS, where ${{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P\left(\xi \right)$ is known as a positive satisfying grade and ${{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\left(\xi \right)$ is known as a negative satisfying grade and ${{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}\left(\xi \right),{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP}\left(\xi \right)\in \left[0,1\right]$ and ${{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}\left(\xi \right),{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\left(\xi \right)\in \left[-1,0\right].$ A set ${\mathcal{M}}_{BCFS}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right)$ is identified as the BCF number (BCFN).

Definition 2. (Mahmood and Ur Rehman, 2022b) For a BCFN ${\mathcal{M}}_{BCFS}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right)$, the score value (SV) and accuracy value (AV) would be obtained as follows:

$\mathcal{S}\left({\mathcal{M}}_{BCFS}\right)=\frac{1}{4}\left(2+{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP}+{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right),\mathcal{S}\left({\mathcal{M}}_{BCFS}\right)\in \left[0,1\right],(2)$

$\mathcal{H}\left({\mathcal{M}}_{BCFS}\right)=\frac{{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP}+{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}}{4},\mathcal{H}\left({\mathcal{M}}_{BCFS}\right)\in \left[0,1\right].(3)$

Definition 3. (Mahmood and Ur Rehman, 2022b) If we have two BCFNs ${\mathcal{M}}_{BCFS-1}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-1}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IN}\right)$ and ${\mathcal{M}}_{BCFS-2}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{IN}\right)$, with $\sigma \ge 0$, then

1) ${\mathcal{M}}_{BCFS-1}\oplus {\mathcal{M}}_{BCFS-2}=\left(\begin{array}{c}{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RP}+{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{RP}-{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RP}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{RP}\\ +\mathfrak{i}\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IP}+{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{IP}-{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IP}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{IP}\right),\\ -\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RN}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{RN}\right)+\mathfrak{i}\left(-\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IN}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{IN}\right)\right)\end{array}\right)$,

2) ${\mathcal{M}}_{BCFS-1}\otimes {\mathcal{M}}_{BCFS-2}=\left(\begin{array}{c}{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RP}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IP}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{IP},\\ {{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RN}+{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{RN}+{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RN}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{RN}\\ \mathfrak{i}\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IN}+{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{IN}+{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IN}{{\rm Y}}_{{\mathcal{M}}_{BCFS-2}}^{IN}\right)\end{array}\right),$

3) $\sigma {\mathcal{M}}_{BCFS-1}=\left(\begin{array}{c}1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RP}\right)}^{\sigma }+\mathfrak{i}\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IP}\right)}^{\sigma }\right),\\ -{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RN}\right|}^{\sigma }+\mathfrak{i}\left(-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IN}\right|}^{\sigma }\right)\end{array}\right),$

4) ${\mathcal{M}}_{BCFS-1}^{\sigma }=\left(\begin{array}{c}{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RP}\right)}^{\sigma }+\mathfrak{i}{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IP}\right)}^{\sigma },\\ -1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{RN}\right)}^{\sigma }+\mathfrak{i}\left(-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-1}}^{IN}\right)}^{\sigma }\right)\end{array}\right)$.

Definition 4. (He et al., 2014) Take a group of real numbers ${\mathcal{M}}_{R-ƥ}=\left({\mathcal{M}}_{R-1},{\mathcal{M}}_{R-2},{\mathcal{M}}_{R-3},\dots ,{\mathcal{M}}_{R-\text{ŋ}}\right),$ with $\mathcal{u},\mathcal{v}>0$, then the power BM operator is inspected as

$PB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{R-1},{\mathcal{M}}_{R-2},{\mathcal{M}}_{R-3},\dots ,{\mathcal{M}}_{R-\text{ŋ}}\right)={\left(\frac{1}{{\text{ŋ}}^2-\text{ŋ}}{\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}{\left(\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{R-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{R-l}\right)+1\right)}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\\ \otimes {\left(\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{R-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{R-l}\right)+1\right)}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}\end{array}\right)\right)}^{1/\mathcal{u}+\mathcal{v}}.(4)$

Definition 5. (He et al., 2014) Take a group of real numbers ${\mathcal{M}}_{R-ƥ}=\left({\mathcal{M}}_{R-1},{\mathcal{M}}_{R-2},{\mathcal{M}}_{R-3},\dots ,{\mathcal{M}}_{R-\text{ŋ}}\right),$ with $\mathcal{u},\mathcal{v}>0$, then the power GBM operator is inspected as

$PGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{R-1},{\mathcal{M}}_{R-2},\dots ,{\mathcal{M}}_{R-\text{ŋ}}\right)=\frac{1}{\mathcal{u}+\mathcal{v}}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}\mathcal{u}{\left({\mathcal{M}}_{R-ƥ}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{R-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{R-l}\right)+1\right)}}\\ \oplus \mathcal{v}{\left({\mathcal{M}}_{R-ɋ}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{R-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{R-l}\right)+1\right)}}\end{array}\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}.(5)$

In Def (4) and (5), $Ⱦ\left({\mathcal{M}}_{R-ƥ}\right)={\displaystyle \sum }_{\begin{array}{c}ɋ=1\\ ɋ\ne ƥ\end{array}}^{\text{ŋ}}Sup\left({\mathcal{M}}_{R-ƥ},{\mathcal{M}}_{R-ɋ}\right)$ is the support to ${\mathcal{M}}_{R-ƥ}$ from ${\mathcal{M}}_{R-ɋ}$ with these axioms

1) $\mathit{Sup}\left({\mathcal{M}}_{R-ƥ},{\mathcal{M}}_{R-ɋ}\right)\in \left[0,1\right],$

2) $\mathit{Sup}\left({\mathcal{M}}_{R-ƥ},{\mathcal{M}}_{R-ɋ}\right)=Sup\left({\mathcal{M}}_{R-ɋ},{\mathcal{M}}_{R-ƥ}\right),$

3) $\mathit{Sup}\left({\mathcal{M}}_{R-ƥ},{\mathcal{M}}_{R-ɋ}\right)\ge Sup\left({\mathcal{M}}_{R-r},{\mathcal{M}}_{R-s}\right)$ if $\mathfrak{D}\left({\mathcal{M}}_{R-ƥ},{\mathcal{M}}_{R-ƥ}\right)<\mathfrak{D}\left({\mathcal{M}}_{R-r},{\mathcal{M}}_{R-s}\right)$, where $\mathfrak{D}$ is any distance measured.

BCF power Bonferroni mean operators

In this section of this article, we introduce power BM operators in the setting of BCF sets to define BCFPBM, BCFWPBM, BCFPGBM, and BCFWPGBM operators.

Definition 6. Take a group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$, then the BCFPBM operator is inspected as

$BCFPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)={\left(\frac{1}{{\text{ŋ}}^2-\text{ŋ}}{\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}{\left(\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\\ \otimes {\left(\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}\end{array}\right)\right)}^{1/\mathcal{u}+\mathcal{v}},(6)$

where $\mathcal{u},\mathcal{v}>0$ and $Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)={\displaystyle \sum }_{\begin{array}{c}ɋ=1\\ ɋ\ne ƥ\end{array}}^{\text{ŋ}}\mathit{Sup}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)$ are the support to ${\mathcal{M}}_{BCFS-ƥ}$ from ${\mathcal{M}}_{BCFS-ɋ}$ with the following axioms

1) $\mathit{S}\mathit{u}\mathit{p}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)\in \left[0,1\right]$,

2) $\mathit{S}\mathit{u}\mathit{p}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)=\mathit{S}\mathit{u}\mathit{p}\left({\mathcal{M}}_{BCFS-ɋ},{\mathcal{M}}_{BCFS-ƥ}\right),$

3) $\mathit{S}\mathit{u}\mathit{p}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)\ge \mathit{S}\mathit{u}\mathit{p}\left({\mathcal{M}}_{BCFS-r},{\mathcal{M}}_{BCFS-s}\right)$ if $\mathfrak{D}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ƥ}\right)<\mathfrak{D}\left({\mathcal{M}}_{BCFS-r},{\mathcal{M}}_{BCFS-s}\right)$, where $\mathfrak{D}$ is the distance measured among BCFSs.

Theorem 1. The aggregated outcome from Eq. 6 based on the group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ is a BCFN and inspected as

$BCFPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\\ +\mathfrak{i}{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\end{array}\\ -1+{\left(1-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\end{array},\\ +\mathfrak{i}\left(-1+{\left(1-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\right)\end{array}\right).(7)$

Proof. Suppose that ${\mathfrak{F}}_{ƥ}=\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}\left(ƥ=1,2,\dots ,\text{ŋ}\right)$, then Eq. 7 becomes

$BCFPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)={\left(\frac{1}{{\text{ŋ}}^2-\text{ŋ}}{\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}{\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\\ \otimes {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}\end{array}\right)\right)}^{1/\mathcal{u}+\mathcal{v}}.(8)$

First, determine ${\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}$ and ${\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}$ as follows:

$\begin{array}{c}{\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}=\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}+\mathfrak{i}\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right),-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}+\mathfrak{i}\left(-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)\right),\\ {\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}=\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}+\mathfrak{i}\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right),-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}+\mathfrak{i}\left(-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)\right).\end{array}$

Now,

$\begin{array}{c}{\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}=\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}+\mathfrak{i}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}},\\ -1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}+\mathfrak{i}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\end{array}\right),\\ {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}=\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}+\mathfrak{i}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}},\\ -1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}+\mathfrak{i}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\end{array}\right).\end{array}$

Now, determine ${\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\otimes {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}$ and get:

$\begin{array}{c}{\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\otimes {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}=\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}+\mathfrak{i}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}},\\ -1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}+\mathfrak{i}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\end{array}\right)\otimes \left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}+\mathfrak{i}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}},\\ -1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}+\mathfrak{i}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\end{array}\right)\\ =\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\\ +\mathfrak{i}\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right),\end{array}\\ \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)+\end{array}\\ \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\times \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\end{array}\\ +\mathfrak{i}\left(\begin{array}{c}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)+\\ \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\times \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\end{array}\right)\end{array}\right)\\ =\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\\ +\mathfrak{i}\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right),\end{array}\\ -1+\left(\begin{array}{c}1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\\ \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\times \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\end{array}\right)\end{array}\\ +\mathfrak{i}\left(-1+\left(\begin{array}{c}1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\\ \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\times \left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\end{array}\right)\right)\end{array}\right)\\ =\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\\ +\mathfrak{i}\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right),\end{array}\\ -1+\left(\begin{array}{c}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\left(1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)+\\ 1\left(1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\end{array}\right)\end{array}\\ +\mathfrak{i}\left(-1+\left(\begin{array}{c}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\left(1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)+\\ 1\left(1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\end{array}\right)\right)\end{array}\right)\\ =\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\\ +\mathfrak{i}\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right),\end{array}\\ -1+\left(1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\times \left(1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)\end{array}\\ +\mathfrak{i}\left(-1+\left(1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\times \left(1+\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)\right)\end{array}\right)\\ =\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\\ +\mathfrak{i}\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right),\end{array}\\ -1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\end{array}\\ +\mathfrak{i}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\end{array}\right).\end{array}$

Next, determine ${\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}{\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\otimes {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}$

${\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}{\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\otimes {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}1-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\\ +\mathfrak{i}\left(1-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)\end{array}\\ -{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\end{array},\\ +\mathfrak{i}\left(-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\end{array}\right).$

Now,

$\frac{1}{{\text{ŋ}}^2-\text{ŋ}}{\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}{\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\otimes {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\\ +\mathfrak{i}\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)\end{array}\\ -{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\end{array},\\ +\mathfrak{i}\left(-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)\end{array}\right).$

Finally, determine ${\left(\frac{1}{{\text{ŋ}}^2-\text{ŋ}}{\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}{\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\otimes {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}\right)}^{1/\mathcal{u}+\mathcal{v}}$ as

${\left(\frac{1}{{\text{ŋ}}^2-\text{ŋ}}{\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}{\left({\mathfrak{F}}_{ƥ}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\otimes {\left({\mathfrak{F}}_{ɋ}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}\right)}^{1/\mathcal{u}+\mathcal{v}}=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\\ +\mathfrak{i}{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\end{array}\\ -1+{\left(1-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\end{array},\\ +\mathfrak{i}\left(-1+{\left(1-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\right)\end{array}\right).(9)$

Now, replace ${\mathfrak{F}}_{ƥ}=\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}$ in Eq. 9, then

${\left(\frac{1}{{\text{ŋ}}^2-\text{ŋ}}{\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}{\left(\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\\ \otimes {\left(\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}\end{array}\right)\right)}^{1/\mathcal{u}+\mathcal{v}}=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\\ +\mathfrak{i}{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\end{array}\\ -1+{\left(1-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\end{array},\\ +\mathfrak{i}\left(-1+{\left(1-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\right)\end{array}\right)$

$=BCFPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right).$

The BCFPBM operator holds the following axioms.

1) Idempotency: Let ${\mathcal{M}}_{BCFS-ƥ}={\mathcal{M}}_{BCFS}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right),ƥ=\mathrm{1,2},..,\text{ŋ}.$ Then,

$BCFPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)={\mathcal{M}}_{BCFS}.$

2) Commutativity: Let ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ have the permutation ${\mathcal{M}}_{BCFS-ƥ}^{\prime }=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime P},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime N}\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{\prime IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$. Then,

$BCFPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=BCFPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1}^{\prime },{\mathcal{M}}_{BCFS-2}^{\prime },\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}^{\prime }\right).$

3) Boundedness: Let a group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ and let ${\mathcal{M}}_{BCFS}^{-}=\left(\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right\}+\mathfrak{i}\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right\},\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right\}+\mathfrak{i}\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right\}\right)$ and ${\mathcal{M}}_{BCFS}^{+}=\left(\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right\}+\mathfrak{i}\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right\},\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right\}+\mathfrak{i}\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right\}\right)$. Then,

${\mathcal{M}}_{BCFS}^{-}\le BCFPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)\le {\mathcal{M}}_{BCFS}^{+}.$

Definition 7. Take a group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$, then the BCFWPBM operator is inspected as

$BCFWPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)={\left(\frac{1}{{\text{ŋ}}^2-\text{ŋ}}{\displaystyle \sum }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}{\left(\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathrm{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}{\mathcal{M}}_{BCFS-ƥ}\right)}^{\mathcal{u}}\\ \otimes {\left(\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathrm{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}{\mathcal{M}}_{BCFS-ɋ}\right)}^{\mathcal{v}}\end{array}\right)\right)}^{1/\mathcal{u}+\mathcal{v}},(10)$

where $\mathcal{u},\mathcal{v}>0$ and $Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)={\displaystyle \sum }_{\begin{array}{c}ɋ=1\\ ɋ\ne ƥ\end{array}}^{\text{ŋ}}Sup\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)$, and ${\mathcal{w}}_{\mathfrak{v}}=\left({\mathcal{w}}_{\mathfrak{v}-1},{\mathcal{w}}_{\mathfrak{v}-2},\dots ,{\mathcal{w}}_{\mathfrak{v}-\mathrm{ŋ}}\right)$ is the weight vector (WV) with the property that ${\mathcal{w}}_{\mathfrak{v}-\mathrm{ƥ}}\in \left[0,1\right]$ and ${\displaystyle \sum }_{ƥ=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-\mathrm{ƥ}}=1$.

Theorem 2. The aggregated outcome from Eq. 10 based on the group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ is a BCFN and inspected as

$BCFWPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\\ +\mathfrak{i}{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\end{array}\\ -1+{\left(1-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right|}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right|}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\end{array},\\ +\mathfrak{i}\left(-1+{\left(1-{\left|-{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}-1+{\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right|}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left|{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right|}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right|}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\right)\end{array}\right).(11)$

The BCFWPBM operator holds the following axioms.

1) Idempotency: Let ${\mathcal{M}}_{BCFS-ƥ}={\mathcal{M}}_{BCFS}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right),ƥ=\mathrm{1,2},..,\text{ŋ}.$ Then,

$BCFWPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)={\mathcal{M}}_{BCFS}.$

2) Commutativity: Let ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ have the permutation ${\mathcal{M}}_{BCFS-ƥ}^{\prime }=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime P},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime N}\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{\prime IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$. Then,

$BCFWPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=BCFWPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1}^{\prime },{\mathcal{M}}_{BCFS-2}^{\prime },\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}^{\prime }\right).$

3) Boundedness: Let a group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ and let ${\mathcal{M}}_{BCFS}^{-}=\left(\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right\}+\mathfrak{i}\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right\},\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right\}+\mathfrak{i}\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right\}\right)$ and ${\mathcal{M}}_{BCFS}^{+}=\left(\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right\}+\mathfrak{i}\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right\},\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right\}+\mathfrak{i}\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right\}\right)$. Then,

${\mathcal{M}}_{BCFS}^{-}\le BCFWPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)\le {\mathcal{M}}_{BCFS}^{+}$

Definition 8. Take a group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$, then the BCFPGBM operator is inspected as

$BCFPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=\frac{1}{\mathcal{u}+\mathcal{v}}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}\mathcal{u}{\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\\ \oplus \mathcal{v}{\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\end{array}\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}},(12)$

where $\mathcal{u},\mathcal{v}>0$ and $Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)={\displaystyle \sum }_{\begin{array}{c}ɋ=1\\ ɋ\ne ƥ\end{array}}^{\text{ŋ}}Sup\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)$ is the support to ${\mathcal{M}}_{BCFS-ƥ}$ from ${\mathcal{M}}_{BCFS-ɋ}$ with these axioms:

1) $\mathit{Sup}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)\in \left[0,1\right],$

2) $\mathit{Sup}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)=Sup\left({\mathcal{M}}_{BCFS-ɋ},{\mathcal{M}}_{BCFS-ƥ}\right),$

3) $\mathit{Sup}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)\ge Sup\left({\mathcal{M}}_{BCFS-r},{\mathcal{M}}_{BCFS-s}\right)$ if $\mathfrak{D}\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ƥ}\right)<\mathfrak{D}\left({\mathcal{M}}_{BCFS-r},{\mathcal{M}}_{BCFS-s}\right)$, where $\mathfrak{D}$ is the distance measured among BCFSs.

Theorem 3. The aggregated outcome from Eq. 12 based on the group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ is a BCFN and inspected as

$BCFPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}1-{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\\ +\mathfrak{i}\left(1-{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\right),\end{array}\\ -{\left|-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(\begin{array}{c}-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{u}}\\ \times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{v}}\right)\end{array}\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right|}^{1/\mathcal{u}+\mathcal{v}}\end{array}\\ +\mathfrak{i}\left(-{\left|-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(\begin{array}{c}-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{u}}\\ \times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{v}}\right)\end{array}\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right|}^{1/\mathcal{u}+\mathcal{v}}\right)\end{array}\right).(13)$

Proof. Suppose that ${\mathfrak{F}}_{ƥ}=\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}\left(ƥ=1,2,\dots ,\text{ŋ}\right)$, then Eq. 13 becomes

$BCFGPB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=\frac{1}{\mathcal{u}+\mathcal{v}}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}\mathcal{u}{\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\\ \oplus \mathcal{v}{\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}\end{array}\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}.(14)$

First, determine ${\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}$ and ${\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}$ as follows:

${\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}=\left({\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}+\mathfrak{i}{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}},-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{{\mathfrak{F}}_{ƥ}}+\mathfrak{i}\left(-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{{\mathfrak{F}}_{ƥ}}\right)\right),$

${\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}=\left({\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}+\mathfrak{i}{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}},-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{{\mathfrak{F}}_{ɋ}}+\mathfrak{i}\left(-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{{\mathfrak{F}}_{ɋ}}\right)\right).$

Now,

${\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}=\left(\begin{array}{c}1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}+\mathfrak{i}\left(1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right),\\ -{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}+\mathfrak{i}\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\right)\end{array}\right),$

${\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}=\left(\begin{array}{c}1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}+\mathfrak{i}\left(1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right),\\ -{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}+\mathfrak{i}\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\end{array}\right).$

Now, determine ${\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\oplus {\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}$ and get

${\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\oplus {\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}=\left(\begin{array}{c}1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}+\mathfrak{i}\left(1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right),\\ -{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}+\mathfrak{i}\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\right)\end{array}\right)\otimes \left(\begin{array}{c}1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}+\mathfrak{i}\left(1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right),\\ -{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}+\mathfrak{i}\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\end{array}\right)$

$=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}+1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\\ -\left(\left(1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\times \left(1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\end{array}\\ +\mathfrak{i}\left(\begin{array}{c}1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}+1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\\ -\left(\left(1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\right)\times \left(1-{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\end{array}\right),\end{array}\\ -\left(\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\right)\right)\end{array}\\ +\mathfrak{i}\left(-\left(\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\right)\right)\right)\end{array}\right)$

$=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}1-\left({\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\\ +\mathfrak{i}\left(1-\left({\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right),\end{array}\\ -\left(\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\right)\right)\end{array}\\ +\mathfrak{i}\left(-\left(\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\right)\right)\right)\end{array}\right).$

Next, determine ${\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left({\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\oplus {\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}\right).$

${\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left({\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\oplus {\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}\right)=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\\ +\mathfrak{i}{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right),\end{array}\\ -1+{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\right)\right)\right)\end{array}\\ -1+{\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\right)\right)\right)\end{array}\right).$

Now,

${\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left({\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\oplus {\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\\ +\mathfrak{i}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left({\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}},\end{array}\\ -1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\end{array}\\ +\mathfrak{i}\left(-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)\end{array}\right).$

Finally, determine $\frac{1}{\mathcal{u}+\mathcal{v}}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left({\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\oplus {\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}$ as follows:

$\frac{1}{\mathcal{u}+\mathcal{v}}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left({\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\oplus {\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}$

$=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}1-{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\\ +\mathfrak{i}\left(1-{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{{\mathfrak{F}}_{ƥ}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{{\mathfrak{F}}_{ɋ}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\right),\end{array}\\ -{\left|-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(\begin{array}{c}-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\\ \times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\end{array}\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right|}^{1/\mathcal{u}+\mathcal{v}}\end{array}\\ +\mathfrak{i}\left(-{\left|-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(\begin{array}{c}-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{{\mathfrak{F}}_{ƥ}}\right|}^{\mathcal{u}}\\ \times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{{\mathfrak{F}}_{ɋ}}\right|}^{\mathcal{v}}\right)\end{array}\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right|}^{1/\mathcal{u}+\mathcal{v}}\right)\end{array}\right).(15)$

Now, replace ${\mathfrak{F}}_{ƥ}=\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}$ in Eq. 15, then

$\frac{1}{\mathcal{u}+\mathcal{v}}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left({\mathcal{u}\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{{\mathfrak{F}}_{ƥ}}\oplus {\mathcal{v}\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{{\mathfrak{F}}_{ɋ}}\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}1-{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\\ +\mathfrak{i}\left(1-{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\right),\end{array}\\ -{\left|-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(\begin{array}{c}-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{u}}\\ \times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{v}}\right)\end{array}\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right|}^{1/\mathcal{u}+\mathcal{v}}\end{array}\\ +\mathfrak{i}\left(-{\left|-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(\begin{array}{c}-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{u}}\\ \times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{\frac{\text{ŋ}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{v}}\right)\end{array}\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right|}^{1/\mathcal{u}+\mathcal{v}}\right)\end{array}\right)$

$=BCFPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right).$

The BCFPGBM operator holds the following axioms.

1) Idempotency: Let ${\mathcal{M}}_{BCFS-ƥ}={\mathcal{M}}_{BCFS}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right),ƥ=\mathrm{1,2},..,\text{ŋ}.$ Then,

$BCFPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)={\mathcal{M}}_{BCFS}.$

2) Commutativity: Let ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ have the permutation ${\mathcal{M}}_{BCFS-ƥ}^{\prime }=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime P},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime N}\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{\prime IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$. Then,

$BCFPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=BCFPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1}^{\prime },{\mathcal{M}}_{BCFS-2}^{\prime },\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}^{\prime }\right).$

3) Boundedness: Let a group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ and let ${\mathcal{M}}_{BCFS}^{-}=\left(\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right\}+\mathfrak{i}\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right\},\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right\}+\mathfrak{i}\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right\}\right)$ and ${\mathcal{M}}_{BCFS}^{+}=\left(\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right\}+\mathfrak{i}\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right\},\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right\}+\mathfrak{i}\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right\}\right)$. Then,

${\mathcal{M}}_{BCFS}^{-}\le BCFPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)\le {\mathcal{M}}_{BCFS}^{+}.$

Definition 9. Take a group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$, then the BCFWPGBM operator is inspected as

$BCFWPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=\frac{1}{\mathcal{u}+\mathcal{v}}{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(\begin{array}{c}\mathcal{u}{\left({\mathcal{M}}_{BCFS-ƥ}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\\ \oplus \mathcal{v}{\left({\mathcal{M}}_{BCFS-ɋ}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\end{array}\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}},(16)$

where $\mathcal{u},\mathcal{v}>0$ and $Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)={\displaystyle \sum }_{\begin{array}{c}ɋ=1\\ ɋ\ne ƥ\end{array}}^{\text{ŋ}}Sup\left({\mathcal{M}}_{BCFS-ƥ},{\mathcal{M}}_{BCFS-ɋ}\right)$, and ${\mathcal{w}}_{\mathfrak{v}}=\left({\mathcal{w}}_{\mathfrak{v}-1},{\mathcal{w}}_{\mathfrak{v}-2},\dots ,{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ŋ}}\right)$ is the weight vector (WV) with the property that ${\mathcal{w}}_{\mathfrak{v}-\mathrm{ƥ}}\in \left[0,1\right]$ and ${\displaystyle \sum }_{ƥ=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-\mathrm{ƥ}}=1$.

Theorem 4. The aggregated outcome from Eq. 16 based on the group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ is a BCFN and is inspected as

$BCFWPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}1-{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RP}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\\ +\mathfrak{i}\left(1-{\left(1-{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\begin{array}{c}{\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{u}}\\ \times {\left(1-{\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IP}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right)}^{\mathcal{v}}\end{array}\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right)}^{1/\mathcal{u}+\mathcal{v}}\right),\end{array}\\ -{\left|-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(\begin{array}{c}-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{u}}\\ \times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{RN}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{v}}\right)\end{array}\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right|}^{1/\mathcal{u}+\mathcal{v}}\end{array}\\ +\mathfrak{i}\left(-{\left|-1+{\left({\displaystyle \prod }_{\begin{array}{c}ƥ=1,ɋ=1\\ ƥ\ne ɋ\end{array}}^{\text{ŋ}}\left(1-\left(\left(\begin{array}{c}-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ƥ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ƥ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{u}}\\ \times \left(-{\left|-1+{\left(1+{{\rm Y}}_{{\mathcal{M}}_{BCFS-ɋ}}^{IN}\right)}^{\frac{\text{ŋ}{\mathcal{w}}_{\mathfrak{v}-\mathfrak{ɋ}}\left(Ⱦ\left({\mathcal{M}}_{BCFS-ɋ}\right)+1\right)}{{\displaystyle \sum }_{l=1}^{\text{ŋ}}{\mathcal{w}}_{\mathfrak{v}-l}\left(Ⱦ\left({\mathcal{M}}_{BCFS-l}\right)+1\right)}}\right|}^{\mathcal{v}}\right)\end{array}\right)\right)\right)\right)}^{1/{\text{ŋ}}^2-\text{ŋ}}\right|}^{1/\mathcal{u}+\mathcal{v}}\right)\end{array}\right).(17)$

The BCFWPGBM operator holds these axioms:

1) Idempotency: Let ${\mathcal{M}}_{BCFS-ƥ}={\mathcal{M}}_{BCFS}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right),ƥ=\mathrm{1,2},..,\text{ŋ}.$ Then,

$BCFWPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)={\mathcal{M}}_{BCFS}.$

2) Commutativity: Let ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ have the permutation ${\mathcal{M}}_{BCFS-ƥ}^{\prime }=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime P},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime N}\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{\prime IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{\prime IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$. Then,

$BCFWPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)=BCFPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1}^{\prime },{\mathcal{M}}_{BCFS-2}^{\prime },\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}^{\prime }\right).$

3) Boundedness: Let a group of BCFNs ${\mathcal{M}}_{BCFS-ƥ}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}-ƥ}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right),ƥ=ƥ,2,\dots ,\text{ŋ}$ and let ${\mathcal{M}}_{BCFS}^{-}=\left(\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right\}+\mathfrak{i}\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right\},\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right\}+\mathfrak{i}\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right\}\right)$ and ${\mathcal{M}}_{BCFS}^{+}=\left(\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RP}\right\}+\mathfrak{i}\underset{ƥ}{\max }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IP}\right\},\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{RN}\right\}+\mathfrak{i}\underset{ƥ}{\min }\left\{{{\rm Y}}_{{\mathcal{M}}_{BCFS-ƥ}}^{IN}\right\}\right)$. Then,

${\mathcal{M}}_{BCFS}^{-}\le BCFWPGB{M}^{\mathcal{u},\mathcal{v}}\left({\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}\right)\le {\mathcal{M}}_{BCFS}^{+}.$

Application

In the aforementioned sections, we reviewed pollution and its types and introduced PBM operators based on the BCFS. Thus, here, we would study pollution and its types through introduced operators. As we know that pollution is a worldwide issue, big cities generally have more pollution than small cities or towns. Pollution can easily expand to those areas where no one lives. For instance, some chemicals and pesticides are observed in the Antarctic ice sheet. In the northern Pacific Ocean, a tremendous assortment of tiny plastic particle structures is called the Great Pacific Garbage Patch. Winds can carry radioactive material, inadvertently let out of an atomic reactor, and spread it over the planet. Water and air convey pollutants. Sea flows and migrating fish convey marine toxins all over. Pollution is of four major types, i.e., 1. air pollution, 2. water pollution, 3. soil pollution, and 4. noise pollution, and the causes of every type are different. Every type of pollution has a different effect on the environment. To find out the most harmful type of pollution for the environment is a DM issue. Thus, we would display how we can employ the introduced operators for the BCFS to solve this DM issue.

To employ the introduced operators for the BCFS to solve the DM issue, we define a DM procedure as follows based on the introduced operators in the environment of the BCFS.

Taking $\text{ŋ}$ alternatives, i.e., ${\mathcal{M}}_{BCFS-1},{\mathcal{M}}_{BCFS-2},\dots ,{\mathcal{M}}_{BCFS-\text{ŋ}}$ and $m$ attributes ${\mathcal{A}}_{b-1},{\mathcal{A}}_{b-2},\dots ,{\mathcal{A}}_{b-m}$ with WV ${\mathcal{w}}_{\mathfrak{v}}=\left({\mathcal{w}}_{\mathfrak{v}-1},{\mathcal{w}}_{\mathfrak{v}-2},\dots ,{\mathcal{w}}_{\mathfrak{v}-m}\right)$ with a property that ${\mathcal{w}}_{\mathfrak{v}-\mathrm{ɋ}}\in \left[0,1\right]$ and ${\displaystyle \sum }_{ɋ=1}^m{\mathcal{w}}_{\mathfrak{v}-\mathrm{ɋ}}=1$, assume that the decision analyst or expert described his/her opinion in the model of BCFS and structured a decision matrix involving BCFNs that is ${\mathcal{M}}_{BCFS}=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)=\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right)$, where ${{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP}\in \left[0,1\right]$ and ${{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\in \left[-1,0\right]$. The steps for DM are as follows:

Step 1: In genuine life issues, the information or data can be cost or benefit. Benefits do not require normalization, but costs do:

${\mathcal{N}}_{BCFS}=\{\begin{array}{cc}\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)& forbenefit,\\ {\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)}^c& forcost,\end{array}(18)$

where ${\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^P,{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^N\right)}^c={\left({{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP},{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right)}^c$$=\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RP}+\mathfrak{i}\left(1-{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IP}\right),-1-{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{RN}+\mathfrak{i}\left(-1-{{\rm Y}}_{{\mathcal{M}}_{BCFS}}^{IN}\right)\right).$

Step 2: After completing step 1, the aggregated values of given information or data are determined by employing any introduced operator (BCFPBM, BCFWPBM, BCFPGBM, and BCFWPGBM).

Step 3: After finding out the aggregated values, the SV of these aggregated values would be determined by employing Eq. 2, and if any two SVs are equal, then accuracy values (AVs) are determined by employing Eq. 3. Furthermore, the ranking would be made based on these SVs and AVs and would reach the best alternative.

In the following section, we solve a numerical example by employing the introduced operators and DM procedure based on the BCFS to address genuine life issues.

Numerical example

Suppose $\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{r}$ types of pollution, i.e., ${\mathcal{M}}_{BCFS-1}=\mathrm{A}\mathrm{i}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{ŋ}$, ${\mathcal{M}}_{BCFS-2}=\mathrm{S}\mathrm{o}\mathrm{i}\mathrm{l}\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{ŋ}$, ${\mathcal{M}}_{BCFS-3}=\mathrm{N}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{ŋ}$, and ${\mathcal{M}}_{BCFS-4}=\mathrm{W}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{ŋ},$ are under consideration and four attributes of the environment, i.e., ${\mathcal{A}}_{b-1}=\mathrm{L}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{s}\mathrm{p}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}$, ${\mathcal{A}}_{b-2}=\mathrm{h}\mathrm{y}\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{h}\mathrm{p}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}$, ${\mathcal{A}}_{b-3}=\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}\mathrm{s}\mathrm{p}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}$, and ${\mathcal{A}}_{b-4}=\mathrm{b}\mathrm{i}\mathrm{o}\mathrm{s}\mathrm{p}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e},\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{o}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}$. The decision analyst or expert provides the values of the effects of these types of pollution on the environment (Table 1). Now, we determine the most harmful type of pollution. For this, we would follow the steps of the DM procedure.

TABLE 1

TABLE 1. Decision matrix containing BCFNs is provided by an expert.

Step 1: In this example, we do not need to perform the first step.

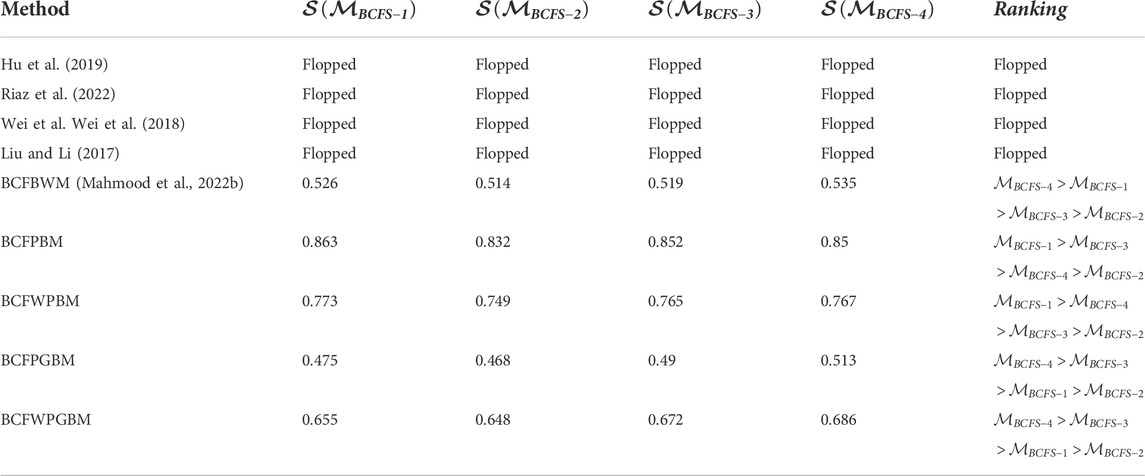
Step 2: The aggregated values of data in Table 1 are determined by employing introduced BCFPBM, BCFWPBM, BCFPGBM, and BCFWPGBM operators, which are explored in Table 2.

TABLE 2

TABLE 2. Aggregated values of information are described in Table 1.

Step 3: SVs of these aggregated values determined by employing Eq. 2 are presented in Table 3.

TABLE 3

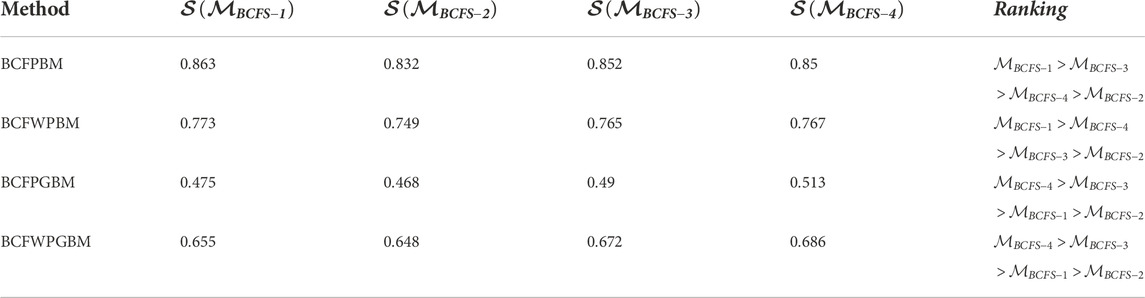
TABLE 3. SVs of the aggregated values of Table 2 and their ranking.

The rankings in Table 3 show that according to the introduced BCFPBM and BCFWPBM, ${\mathcal{M}}_{BCFS-1}=Airpollutio\text{ŋ}$ has more effect on the environment than the others, and according to the introduced BCFPGBM and BCFWPGBM, ${\mathcal{M}}_{BCFS-4}=Waterpollutio\text{ŋ}$ has more effect on the environment than the others.

Comparison

The introduced PBM operators (BCFPBM, BCFWPBM, BCFPGBM, and BCFWPGBM) and a DM procedure in the environment of the BCFS are more effective than other prevailing operators. We now take prevailing theories, including the CF power and DM procedure defined by Hu et al. (2019), sin trigonometric AOs and the DM procedure in the environment of the BF set defined by Riaz et al. (2022), Hamacher AOs and the DM procedure in the environment of the BF set established by Wei et al. (2018), PBM AOs and the DM procedure in the setting of the interval-valued intuitionistic FS (IVIFS) introduced by Liu and Li (2017), and BM AOs and the DM procedure for the BCFS introduced by Mahmood et al. (2022b). We consider the data provided in Table 1 and aggregate it with the assistance of these prevailing theories and the operators and the DM procedure introduced in this article. The results are shown in Table 4.

TABLE 4

TABLE 4. SVs were determined by the method proposed in this study and from previous studies.

The results indicate that existing theories, for example, Hu et al. (2019), Riaz et al. (2022), Wei et al. (2018), and Liu and Li (2017), cannot solve the DM issue because the data form the structure of the BCFS. Hu et al. (2019) can merely solve the data in the model of CFS and cannot tackle the negative aspects, while Riaz et al. (2022) and Wei et al. (2018) merely resolve the information in the setting of the BFS and cannot overcome the second dimension, and Liu and Li (2017) merely resolve the information in the model of IVIFS and cannot address the second dimension and negative aspects. Furthermore, the results show that BM AO (BCF Bonferroni mean AO) (Mahmood et al., 2022b) for the BCFS and the DM approach handle the data and give us the result that ${\mathcal{M}}_{BCFS-4}$ is the finest choice, but anyone can say that this decision or selection is biased and not fair because of the weight vector that the decision analyst provides to each attribute on his own choice, for example, in this case, we take the weight vector $\left(0.08,0.06,0.06,0.8\right)$ and $\mathcal{u}=\mathcal{v}=2$. However, in the case of the proposed PBM AOs for BCFS and the DM approach, we can see that the corresponding BCFPBWM gives us that ${\mathcal{M}}_{BCFS-1}$ is the finest alternative. In the proposed work, the decision analyst cannot provide the weight vector by his/her own choice and has to find it out through the proper formula, and in this example, we used the distance formula presented by Mahmood and Ur Rehman (2022b) in the formula of finding out the weight vector. This shows the investigated AOs get better and fair outcomes than the old ones. The results also show that the introduced operators and the DM procedure are appropriate tools for addressing uncertain and vague information in the environment of the BCFS. Also, the introduced operators can reduce the setting of the FS (by overlooking the NSG and unreal parts in the PSG), BFS (by making the unreal parts in both the PSG and NSG equal to zero), and CFS (by overlooking the NSG). Thus, the introduced operators and the procedure are more robust than other prevailing operators and DM procedures.

Conclusion

In this article, we studied the effect of pollution and its types on the environment by employing the introduced PBM operators and the DM procedure in the setting of the BCFS. The procedure by which the water, land, air, or other components of the natural environment are made unsafe or dirty to use is known as pollution. Pollution occurs by introducing any sort of pollutant into the environment, but the pollutant need not be visible, for example, temperature, light, and sound can be taken as pollutants if introduced into the environment artificially. For this study, we introduced the PBM operator in the setting of the BCFS, which are BCFPBM, BCFWPBM, BCFPGBM, and BCFWPGBM operators. Furthermore, we defined a DM procedure based on these PBM operators in the setting of the BCF set. After that, we described a numerical example in which we took four types of pollution and determined which type of pollution is more harmful and dangerous to the environment. We found that air pollution is more harmful than others by utilizing BCFPBM and BCFWPBM operators, and water pollution is more harmful than others by utilizing BCFPGBM and BCFWPGBM operators. Moreover, we illustrated that the introduced PBM operators and a DM procedure in the environment of the BCFS are more effective and have a wide model and advantages than certain prevailing works. We also showed that the investigated PBM AOs and the DM procedure for the BCFS gave us better and fair results than the prevailing similar AOs and DM procedures. The investigated operators and the DM procedure for the BCFS have certain limitations as well like they cannot tackle the data in the structure of BCF soft sets, complex bipolar intuitionistic fuzzy sets, BCF linguistic sets, etc.

In the future, our goal would be to review various notions like the bipolar complex fuzzy soft set (SS) (Mahmood et al., 2022c), Pythagorean FS (Li et al., 2022), picture FS (Ullah, 2021), picture fuzzy SSs (Khan et al., 2019), T-spherical FS (Javed et al., 2022), complex bipolar intuitionistic FS (Jan et al., 2022), enhancing digital innovation for the sustainable transformation of manufacturing industry (Yin et al., 2022) and try to employ the introduced work in these notions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, XY, TM, and UU; methodology, XY, TM, and UU; software, XY, TM, and UU; formal analysis, XY, TM, and UU; investigation, XY, TM, and UU; writing—original draft, XY, TM, and UU; writing—review and editing, XY, TM, and UU.

Funding

This work is supported by the National Natural Science Foundation of China (61877014, 12271132) and the funds provided by the Department of Education of Guangdong Province (2022A1515011460, 2021ZDJS044, PNB2103, 2021B1212040015).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akram, M., and Bashir, A. (2021). Complex fuzzy ordered weighted quadratic averaging operators. Granul. Comput. 6 (3), 523–538. doi:10.1007/s41066-020-00213-7

CrossRef Full Text | Google Scholar

Akram, M., Sattar, A., Karaaslan, F., and Samanta, S. (2021). Extension of competition graphs under complex fuzzy environment. Complex Intell. Syst. 7 (1), 539–558. doi:10.1007/s40747-020-00217-5

CrossRef Full Text | Google Scholar

Ali, Z., Mahmood, T., Ullah, K., and Khan, Q. (2021). Einstein geometric aggregation operators using a novel complex interval-valued pythagorean fuzzy setting with application in green supplier chain management. Rep. Mech. Eng. 2 (1), 105–134. doi:10.31181/rme2001020105t

CrossRef Full Text | Google Scholar

Ashraf, A., Ullah, K., Hussain, A., and Bari, M. (2022). Interval-valued picture fuzzy maclaurin symmetric mean operator with application in multiple attribute decision-making. Rep. Mech. Eng. 3 (1), 301–317. doi:10.31181/rme20020042022a

CrossRef Full Text | Google Scholar

Ateş, F., and Akay, D. (2020). Some picture fuzzy Bonferroni mean operators with their application to multicriteria decision making. Int. J. Intell. Syst. 35 (4), 625–649. doi:10.1002/int.22220

CrossRef Full Text | Google Scholar

Bharathi, T., and Felixia, S. (2022).Bipolar felicitous fuzzy graphs. AIP Conf. Proc. AIP Publishing LLC 2385, 130031. doi:10.1063/5.0071535

CrossRef Full Text | Google Scholar

Bonferroni, C. (1950). Sulle medie multiple di potenze. Boll. dell'Unione Mat. Ital. 5 (3-4), 267–270.

Google Scholar

Chen, H., and Tian, Z. (2022). Environmental uncertainty, resource orchestration and digital transformation: A fuzzy-set QCA approach. J. Bus. Res. 139, 184–193. doi:10.1016/j.jbusres.2021.09.048

CrossRef Full Text | Google Scholar

Choudhury, B. S., Dhara, P. S., and Saha, P. (2021). An application of fuzzy logic on importing medicines. Int. J. Healthc. Manag. 14 (2), 456–461. doi:10.1080/20479700.2019.1658160

CrossRef Full Text | Google Scholar

De, S. K. (2020). On degree of fuzziness and fuzzy decision making. Cybern. Syst. 51 (5), 600–614. doi:10.1080/01969722.2020.1723872

CrossRef Full Text | Google Scholar

Garai, T., Biswas, G., and Santra, U. (2022). “A novel MCDM method based on possibility mean and its application to water resource management problem under bipolar fuzzy environment,” in International conference on intelligent and fuzzy systems (Cham: Springer), 405–412.

CrossRef Full Text | Google Scholar

Garg, H., Ullah, K., Mahmood, T., Hassan, N., and Jan, N. (2021). T-spherical fuzzy power aggregation operators and their applications in multi-attribute decision making. J. Ambient. Intell. Humaniz. Comput. 12 (10), 9067–9080. doi:10.1007/s12652-020-02600-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, S., and Hua, G. (2022). Fuzzy edge connectivity in bipolar fuzzy networks and the applications in topology design. Int. J. Intell. Syst. 37, 5425–5442. doi:10.1002/int.22797

CrossRef Full Text | Google Scholar

Gulistan, M., Khan, Z., Al-Shamiri, M. M., Azhar, M., Ali, A., Madasi, J. D., et al. (2022). A new fuzzy decision support system approach; analysis and applications. AIMS Math. 7 (8), 14785–14825. doi:10.3934/math.2022812

CrossRef Full Text | Google Scholar

He, Y., He, Z., Wang, G., and Chen, H. (2014). Hesitant fuzzy power Bonferroni means and their application to multiple attribute decision making. IEEE Trans. Fuzzy Syst. 23 (5), 1655–1668. doi:10.1109/tfuzz.2014.2372074

CrossRef Full Text | Google Scholar

Hu, B., Bi, L., and Dai, S. (2019). Complex fuzzy power aggregation operators. London: Mathematical Problems in Engineering. doi:10.1155/2019/9064385

CrossRef Full Text | Google Scholar

Jan, N., Maqsood, R., Nasir, A., Alhilal, M. S., Alabrah, A., and Al-Aidroos, N. (2022). A new approach to model machine learning by using complex bipolar intuitionistic fuzzy information. J. Funct. Spaces 2022, 1–17. doi:10.1155/2022/3147321

CrossRef Full Text | Google Scholar

Jana, C., Pal, M., and Wang, J. Q. (2019). Bipolar fuzzy Dombi aggregation operators and its application in multiple-attribute decision-making process. J. Ambient. Intell. Humaniz. Comput. 10 (9), 3533–3549. doi:10.1007/s12652-018-1076-9

CrossRef Full Text | Google Scholar

Javed, M., Javeed, S., Ahmad, J., Ullah, K., and Zedam, L. (2022). Approach to multiattribute decision-making problems based on neutrality aggregation operators of picture fuzzy information. J. Funct. Spaces 2022, 1–16. doi:10.1155/2022/2762067

CrossRef Full Text | Google Scholar

Jiang, Z. (2022). Improved algorithm of fuzzy set gravity centre in track system teaching field. London: Mathematical Problems in Engineering. doi:10.1155/2019/9064385

CrossRef Full Text | Google Scholar

Khan, M. J., Kumam, P., Ashraf, S., and Kumam, W. (2019). Generalized picture fuzzy soft sets and their application in decision support systems. Symmetry 11 (3), 415. doi:10.3390/sym11030415

CrossRef Full Text | Google Scholar

Kwon, K., Kang, M., Kim, D., and Choi, H. (2022). New tunnel risk assessment model combining ahp and fuzzy set theory. Available at SSRN 4156575.

Google Scholar

Li, H., Cao, Y., Su, L., and Wang, F. (2022). Selecting a project delivery system for wastewater treatment plants with related-indicators under a pythagorean fuzzy environment. Front. Environ. Sci. 560. doi:10.3389/fenvs.2022.883630

CrossRef Full Text | Google Scholar

Liu, P., and Li, H. (2017). Interval-valued intuitionistic fuzzy power Bonferroni aggregation operators and their application to group decision making. Cogn. Comput. 9 (4), 494–512. doi:10.1007/s12559-017-9453-9

CrossRef Full Text | Google Scholar

Mahmood, T., Rehman, U. U., Ahmmad, J., and Santos-García, G. (2021). Bipolar complex fuzzy Hamacher aggregation operators and their applications in multi-attribute decision making. Mathematics 10 (1), 23. doi:10.3390/math10010023

CrossRef Full Text | Google Scholar

Mahmood, T., Rehman, U. U., Ali, Z., Aslam, M., and Chinram, R. (2022). Identification and classification of aggregation operators using bipolar complex fuzzy settings and their application in decision support systems. Mathematics 10 (10), 1726. doi:10.3390/math10101726

CrossRef Full Text | Google Scholar

Mahmood, T., ur Rehman, U., Ali, Z., and Aslam, M. (2022). Bonferroni mean operators based on bipolar complex fuzzy setting and their applications in multi-attribute decision making. AIMS Math. 7 (9), 17166–17197. doi:10.3934/math.2022945

CrossRef Full Text | Google Scholar

Mahmood, T., Rehman, U. U., Jaleel, A., Ahmmad, J., and Chinram, R. (2022). Bipolar complex fuzzy soft sets and their applications in decision-making. Mathematics 10 (7), 1048. doi:10.3390/math10071048

CrossRef Full Text | Google Scholar

Mahmood, T., and Ur Rehman, U. (2022a). A novel approach towards bipolar complex fuzzy sets and their applications in generalized similarity measures. Int. J. Intell. Syst. 37 (1), 535–567. doi:10.1002/int.22639

CrossRef Full Text | Google Scholar

Mahmood, T., and Ur Rehman., U. (2022b). A method to multi-attribute decision making technique based on Dombi aggregation operators under bipolar complex fuzzy information. Comp. Appl. Math. 41 (1), 47–23. doi:10.1007/s40314-021-01735-9

CrossRef Full Text | Google Scholar

Narang, M., Joshi, M. C., Bisht, K., and Pal, A. (2022). Stock portfolio selection using a new decision-making approach based on the integration of fuzzy CoCoSo with Heronian mean operator. Decis. Mak. Appl. Manag. Eng. 5 (1), 90–112. doi:10.31181/dmame0310022022n

CrossRef Full Text | Google Scholar

Pandey, S. D., Ranadive, A. S., Samanta, S., and Sarkar, B. (2022). Bipolar-valued fuzzy social network and centrality measures. Discrete Dyn. Nat. Soc. 2022, 1–13. doi:10.1155/2022/9713575

CrossRef Full Text | Google Scholar

Poulik, S., and Ghorai, G. (2020). Note on “Bipolar fuzzy graphs with applications”. Knowledge-Based Syst. 192, 105315. doi:10.1016/j.knosys.2019.105315

CrossRef Full Text | Google Scholar

Rajalakshmi, R., and Mary, K. J. R. (2022). Assessment for choosing the best alternative fuel under bipolar-valued fuzzy multi criteria decision making. AIP Conference Proceedings. AIP Publ. LLC 2385, 080001.

CrossRef Full Text | Google Scholar

Ramot, D., Milo, R., Friedman, M., and Kandel, A. (2002). Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 10 (2), 171–186. doi:10.1109/91.995119

CrossRef Full Text | Google Scholar

Rehman, U. U., Mahmood, T., Albaity, M., Hayat, K., and Ali, Z. (2022). Identification and prioritization of DevOps success factors using bipolar complex fuzzy setting with Frank aggregation operators and analytical hierarchy process. IEEE Access 10, 74702–74721. doi:10.1109/access.2022.3190611

CrossRef Full Text | Google Scholar

Riaz, M., Pamucar, D., Habib, A., and Jamil, N. (2022). Innovative bipolar fuzzy sine trigonometric aggregation operators and SIR method for medical tourism supply chain. London: Mathematical Problems in Engineering. doi:10.1155/2019/9064385

CrossRef Full Text | Google Scholar

Rytova, E., and Gutman, S. (2019). Assessment of regional development strategy in the context of economy digitization on the basis of fuzzy set method IOP conference series: Mater. IOP Conf. Ser. Mat. Sci. Eng.IOP Publ. 497 (No. 1), 012060. doi:10.1088/1757-899x/497/1/012060

CrossRef Full Text | Google Scholar

Sahu, R., Dash, S. R., and Das, S. (2021). Career selection of students using hybridized distance measure based on picture fuzzy set and rough set theory. Decis. Mak. Appl. Manag. Eng. 4 (1), 104–126. doi:10.31181/dmame2104104s

CrossRef Full Text | Google Scholar

Singh, P. K. (2022). Bipolar fuzzy concepts reduction using granular-based weighted entropy. Soft Comput. 26, 9859–9871. doi:10.1007/s00500-022-07336-w

CrossRef Full Text | Google Scholar

Tamir, D. E., Jin, L., and Kandel, A. (2011). A new interpretation of complex membership grade. Int. J. Intell. Syst. 26 (4), 285–312. doi:10.1002/int.20454

CrossRef Full Text | Google Scholar

Ullah, K. (2021). Picture fuzzy Maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Mathematical problems in engineering 2021, 1098631. doi:10.1155/2021/1098631

CrossRef Full Text | Google Scholar

Ur Rehman., U., and Mahmood, T. (2022). The generalized dice similarity measures for bipolar complex fuzzy set and its applications to pattern recognition and medical diagnosis. Comp. Appl. Math. 41 (6), 265–330. doi:10.1007/s40314-022-01948-6

CrossRef Full Text | Google Scholar

Wan, C., Deng, F., Li, S., Omidbakhsh Amiri, S., Talebi, A. A., and Rashmanlou, H. (2022). Novel concepts in bipolar fuzzy graphs with applications. J. Math. 2022, 1–9. doi:10.1155/2022/8162474

CrossRef Full Text | Google Scholar

Wei, G., Alsaadi, F. E., Hayat, T., and Alsaedi, A. (2018). Bipolar fuzzy Hamacher aggregation operators in multiple attribute decision making. Int. J. Fuzzy Syst. 20 (1), 1–12. doi:10.1007/s40815-017-0338-6

CrossRef Full Text | Google Scholar

Xu, Z., and Yager, R. R. (2010). Intuitionistic fuzzy Bonferroni means. IEEE Trans. Syst. Man. Cybern. B Cybern. 41 (2), 568–578. doi:10.1109/TSMCB.2010.2072918

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Z., and Yager, R. R. (2009). Power-geometric operators and their use in group decision making. IEEE Trans. Fuzzy Syst. 18 (1), 94–105.

Google Scholar

Yager, R. R. (2001). The power average operator. IEEE Trans. Syst. Man. Cybern. A 31 (6), 724–731. doi:10.1109/3468.983429

CrossRef Full Text | Google Scholar

Yamini, C., Saravanamoorthi, P., and Kailasavalli, S. (2022). A decision-making method for selecting TMT rod based on bipolar valued fuzzy sets. J. Algebraic Statistics 13 (2), 126–133. doi:10.52783/jas.v13i2.146

CrossRef Full Text | Google Scholar

Yin, S., Zhang, N., Ullah, K., and Gao, S. (2022). Enhancing digital innovation for the sustainable transformation of manufacturing industry: A pressure-state-response system framework to perceptions of digital green innovation and its performance for green and intelligent manufacturing. Systems 10 (3), 72. doi:10.3390/systems10030072

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. control 8 (3), 338–353. doi:10.1016/s0019-9958(65)90241-x

CrossRef Full Text | Google Scholar

Zeeshan, M., and Khan, M. (2022). 2103-6568 Complex fuzzy sets with applications in decision-making. Iran. J. Fuzzy Syst. 19 (4), 147–163. doi:10.22111/ijfs.2022.7093

CrossRef Full Text | Google Scholar

Zhang, W. R. (1994). “Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis,” in NAFIPS/IFIS/NASA'94. Proceedings of the first international joint conference of the north American fuzzy information processing society biannual conference. The industrial fuzzy Control and intellige (IEEE), 305–309.

Google Scholar

Zhu, B., Xu, Z., and Xia, M. (2012). Hesitant fuzzy geometric Bonferroni means. Inf. Sci. 205, 72–85. doi:10.1016/j.ins.2012.01.048

CrossRef Full Text | Google Scholar