Side Tributary Distribution of Quasi-Uniform Iterative Binary Tree Networks for River Networks

Self-similarity and plane-filling are intrinsic structure properties of natural river networks. Statistical data indicates that most natural river networks are Tokunaga trees. Researchers have explored to use iterative binary tree networks (IBTNs) to simulate natural river networks. However, the characteristics of natural rivers such as Tokunaga self-similarity and plane-filling cannot be easily guaranteed by the configuration of the IBTN. In this paper, the generator series and a quasi-uniform iteration rule are specified for the generation of nonstochastic quasi-uniform iterative binary tree networks (QU-IBTNs). First, we demonstrate that QU-IBTNs definitely satisfy self-similarity. Second, we show that the constraint for a QU-IBTN to be a Tokunaga tree is that the exterior links must be replaced in the generator series with a neighboring generator that is larger than the interior links during the iterative process. Moreover, two natural river networks are examined to reveal the inherent consistency with QU-IBTN at low Horton-Strahler orders.

Introduction

River networks are typically considered to be dendritic, self-similar, and plane-filling in plane shape (Horton, 1945; Tokunaga, 1966; Mandelbrot, 1982; Peckham, 1995b). With this in mind, their scalings have been comprehensively studied. The first method for quantifying the scale of streams in a river network was given by Horton (1945), and then modified by Strahler (1952) to create what is now known as the Horton-Strahler (H-S) ordering method. This method gives every stream an H-S order according to its position in the confluencing structure of a river network. It has become one of the most basic concepts in river network topology. Furthermore, the Horton ratios, which are the bifurcation ratio R_B, the length ratio R_L, and the area ratio R_A, have been well established and verified (Horton, 1945; Strahler, 1952). These ratios reflect the self-similarity of a river network by approximately formed geometric sequences.

Tokunaga (1966), Tokunaga (1978) introduced a bivariate stream ordering method based on the H-S method. The Tokunaga ordering method quantifies different confluences by using the H-S order in pairs to describe the flow of a tributary into its main stem. The mean ratio of the number of streams with H-S order ω to the number of streams with H-S order ω+k, which are the streams that H-S order ω streams flow into, is defined as the side-branching ratio T_k. Furthermore, Tokunaga (1978, 1984) recognized that the side-branching ratio characterizes the self-similar structure of a binary tree river network. Therefore, a strict constraint for a binary tree network to be a Tokunaga tree is that T_k varies geometrically with k but independently with ω. By using this constraint of side-branching ratios, large natural river networks have been proved to be Tokunaga trees (Tokunaga, 1978; Peckham, 1995a; Mantilla et al., 2010; Zanardo et al., 2013; Gupta and Mesa, 2014).

Additionally, studies on similarity and fractals have made the synthetic generation of iterative networks an efficient tool for simulating real systems with self-similarity. Some of these synthetic iterative networks have been used for hydrological simulations of their analogous natural river networks (Claps et al., 1996; Menabde et al., 2001; Veitzer and Gupta, 2001; Wang and Wang, 2002; Hung and Wang, 2005). Furthermore, recursive replacement networks have been introduced to show that the Horton laws are well predicted (Peckham, 1995a; Veitzer and Gupta, 2000; Mcconnell and Gupta, 2008). Synthetic trees generated by the Tokunaga model have been used to statistically evaluate the Tokunaga self-similarity, and have been compared with natural river networks (Zanardo et al., 2013). Besides the iterative replacement networks, the diffusion-limited aggregation (DLA) model using random walk as synthetic mechanism can also be used for river network generation, and is similar to natural river networks (Masek and Turcotte, 1993). However, none of these synthetic networks have been proved to be self-similar or Tokunaga trees, either mathematically or theoretically. Therefore, it is unreasonable to use them to capture the properties of natural river networks.

Using synthetic iterative networks to simulate natural river networks has limitations that need to be overcome, mainly in two aspects. First, a commonly accepted and rigorous mathematical definition of generators for river networks is needed. The lack of a rigorous definition of generators (Wang and Wang, 2002; Troutman, 2005) results in an inability to guarantee the basicness and completeness of the generator population. A basic and complete binary generator series has been specially and explicitly defined and graphed by Zhang et al. (2009), and has been proved to be effective and fundamental by means of comparison with data from China and the United States (Zhang et al., 2009). Second, the constraints of Tokunaga trees should be strictly added during the generation of synthetic iterative networks.

The main objectives of this paper involve specifying a common mathematical framework so as to 1) reemphasize the standard generator series for iterative networks; 2) generate an iterative binary tree network using the generator series and iteration rules; and 3) find the appropriate constraint that guarantees a synthetic iterative network to be a Tokunaga tree.

This paper is organized as follows. Materials and Method briefly reviews the rules and definitions of the H-S method, Tokunaga ordering method, Tokunaga tree, Generators and rules for the iterative binary tree networks (IBTNs). In Results, the mathematical derivations of side tributary distribution are shown recursively and graphically for quasi-uniform iterative binary tree networks (QU-IBTNs). The sufficient and necessary conditions for a QU-IBTN to be a Tokunaga tree are discussed in Discussion. Two natural river networks are given as examples to verify the feasibility of QU-IBTNs.

Materials and Method

Tokunaga Tree

Horton (1945) and Strahler (1952) defined the classification method for the hierarchical structure of a river network by means of stream order as follows:

1) every source channel has an H-S order 1;

2) two streams with the same order, $\omega$, confluence to a stream ordered $\omega +1$; and

3) two streams with different orders, $u,v(u<v)$, confluence to a stream with ordered $v$.

The H-S order of the whole network, $\text{Ω}$, is defined as the highest order of all streams. The H-S ordering method is shown in Figure 1.

FIGURE 1

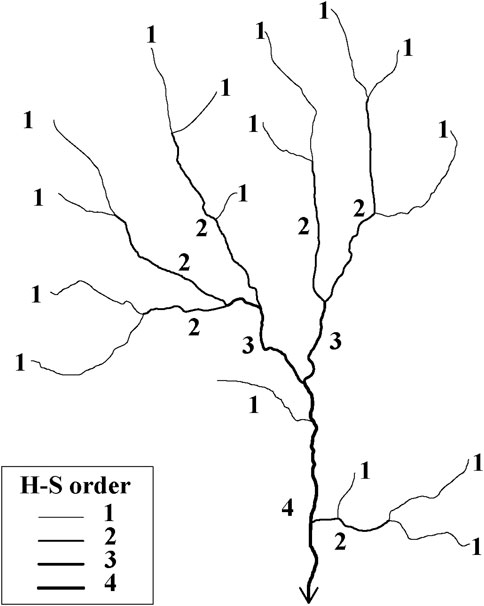
FIGURE 1. H-S ordering method schematic diagram for the illustrated river network with H-S order 4. There are 16 streams with H-S order 1, 6 streams with H-S order 2, 2 streams with H-S order 3, and 1 stream with H-S order 4. The arrow at the bottom is the outlet of this river network.

Tokunaga (1966) proposed an extended ordering method based on the H-S order. The Tokunaga ordering method reflects the topological relation of a side-branching tributary flowing into another stream with a higher order. His work plays an important role in analyzing the topology of river networks because it represents the inherent self-similarity of a river network.

A stream with H-S order $\omega$ as a side-branching tributary flowing into a stream ordered ${\omega }^{\prime }$ is assigned a Tokunaga order $\left(\omega ,{\omega }^{\prime }\right)$, for which $\omega <{\omega }^{\prime }$. A pair of streams as sources of a stream ordered $\omega +1$ is assigned a Tokunaga order $\left(\omega ,\omega \right)$. Figure 2 shows the Tokunaga ordering method applied to an example binary tree.

FIGURE 2

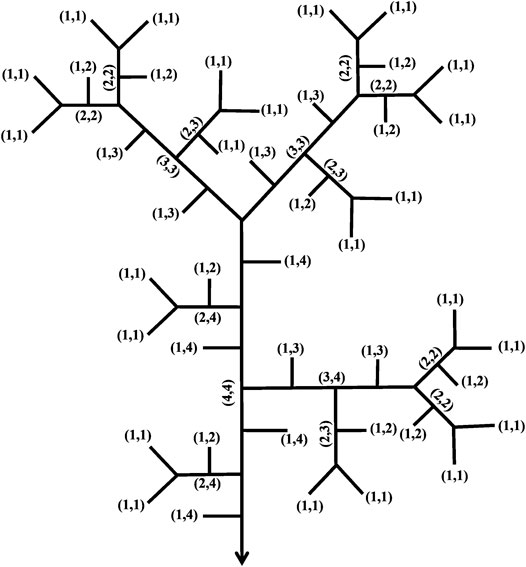
FIGURE 2. Schematic diagram for the Tokunaga ordering method for a binary tree (from Zhang et al., 2009).

For a binary tree network, the Tokunaga stream number matrix N specifies the number of streams with Tokunaga order $\left(\omega ,{\omega }^{\prime }\right)$, $N_{\omega ,{\omega }^{\prime }}$, as:

$\mathit{N}=\left(\begin{array}{cccccc}{N}_{\mathrm{1,1}}& N_{\mathrm{1,2}}& N_{\mathrm{1,3}}& \dots & N_{1,(\text{Ω}-1)}& N_{1,\text{Ω}}\\ & N_{\mathrm{2,2}}& N_{\mathrm{2,3}}& \dots & \dots & N_{2,\text{Ω}}\\ & & & \dots & \dots & \dots \\ & & & & N_{\left(\text{Ω}-1\right),(\text{Ω}-1)}& N_{\left(\text{Ω}-1\right),\text{Ω}}\\ & & & & & N_{\text{Ω},\text{Ω}}\end{array}\right)(1)$

For example, the Tokunaga stream number matrix of the binary tree in Figure 2 is:

$\mathit{N}=\left(\begin{array}{cccc}22& 11& 6& 4\\ & 6& 3& 2\\ & & 2& 1\\ & & & 1\end{array}\right)(2)$

Eq. 2 defines the ordering method in Figure 2, which shows 22 streams with Tokunaga order (1,1), 11 streams with Tokunaga order (1,2), and so on.

The Tokunaga side-branching ratio $T_{\omega ,\omega +k} \left(1\le k\le \text{Ω}-\omega \right)$, which is determined in terms of the ratio of the number of streams with the H-S order $\omega$ flowing into streams with the H-S order $\omega +k$ to the number of streams with the H-S order $\omega +k$, is defined as:

$T_{\omega ,\omega +k}=\frac{N_{\omega ,\omega +k}}{N_{\omega +k}}=\frac{N_{\omega ,\omega +k}}{{{\displaystyle \sum }}_{i=\omega +k}^{\text{Ω}}{N}_{\omega +k,i}},1\le k\le \text{Ω}-\omega (3)$

An upper triangular matrix T, which is calculated in terms of the Tokunaga stream number matrix N by Eq. 3, is defined as the side-branching ratio matrix with a dimension of $\text{Ω}-1$. The side-branching ratio matrix of the binary tree in Figure 2 is:

$\mathit{T}=\left(\begin{array}{ccc}1& 2& 4\\ & 1& 2\\ & & 1\end{array}\right)(4)$

The necessary condition for a network to be self-similar is that the side-branching ratio $T_k$ is independent of $\omega$ (Peckham, 1995a), that is:

$T_{\omega ,\omega +k}=T_k(5)$

For a network to be a Tokunaga tree in a statistical sense, the side-branching ratio must satisfy the constraint (Peckham, 1995a):

$T_k=a{c}^{k-1}(6)$

Here, $a$ is the average number of streams of H-S order $\omega$ flowing into streams of order $\omega$ + 1, and c is the average rate of increase of the side-branching ratios of side tributaries with different order.

In Figure 2, $T_1=1,T_2=2,T_3=4$, and consequently $T_k=2^{k-1}$, which means that the binary tree in Figure 2 is a Tokunaga tree with $a=1$ and $c=2$.

Iterative Binary Tree Networks

The basic elements of a synthetic iterative network are 1) the generators, which are the smallest units of an iterative network, and 2) the iteration rules, which specify the growth pattern of the network using the generators. Different combinations of generators and iteration rules result in different networks. Iterative network models must be based on a series of generators. Each generator should be unique, and the generator series should be complete (Zhang et al., 2009; Mantilla et al., 2010).

Generator Series

Self-similarity has been considered to be an inherent characteristic of river networks since Mandelbrot first described their fractal nature (Mandelbrot, 1982; Peckham, 1995b). Since then, various methods to create synthetic networks have been proposed based on generator iteration (Veitzer and Gupta, 2000; Wang and Wang, 2002; Hung and Wang, 2005; Zhang et al., 2009; Mantilla et al., 2010). However, generators are not sequential and complete until they are cataloged by their topological structure (Zhang et al., 2009; Mantilla et al., 2010). Figure 3 shows the first four generators in a generator series. Each generator in the series can be denoted by an index λ, which is a positive integer in sequential order. The generator series in Figure 3 is the basis of the iterative networks discussed in this paper.

FIGURE 3

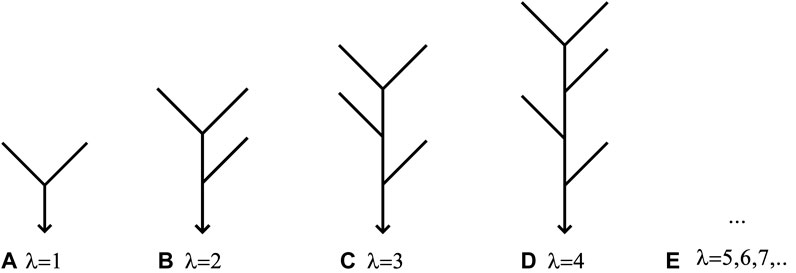
FIGURE 3. Diagrammatic infinite generator series for the topological structure of iterative binary tree networks. Here, λ is the index of each generator [revised from Zhang et al. (2009)].

Iteration Rule

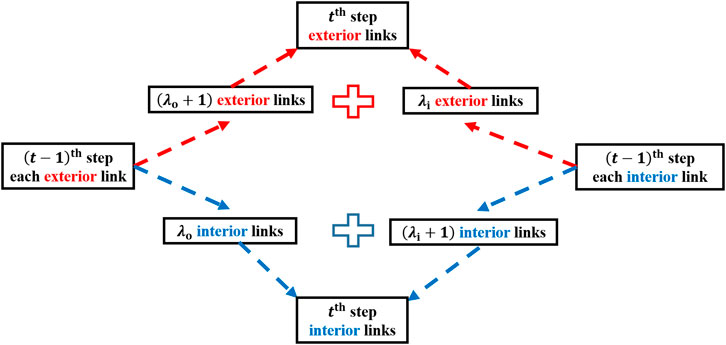
The generation of a synthetic iterative network, specifically an ITBN, is based on iteration definitions and rules. First, we give some basic definitions for an iterative network. An exterior link is an unbroken section of stream that extends from a source to the first junction, and corresponds to a stream with H-S order 1, whereas an interior link connects two successive junctions or the last junction with the outlet (Shreve, 1966). The generators for the replacement of interior and exterior links are chosen from the series in Figure 3 and are denoted by λ_i and λ_o, respectively. Both interior and exterior links are replaced by the interior generator λ_i and exterior generator λ_o, respectively, in each step of the iterative process. The length of each link is assumed to be 1 in this paper. We use one link as the initial case (t = 0), and then the exterior generator λ_o as the first iterative step (t = 1).

The iteration rule discussed in this paper is taking λ_i as the constant interior generator and λ_o as the constant exterior generator in each step of the iterative process. This iteration rule is quasi-uniform because of the consistent generators in every iterative step. Therefore, the iterative network generated by this rule is defined as a QU-IBTN. Figure 4 shows two examples of how to generate QU-IBTNs using λ_i = 1, λ_o = 2 (Figures 4A–D) and λ_i = 2, λ_o = 3 (Figures 4E–H), respectively.

FIGURE 4

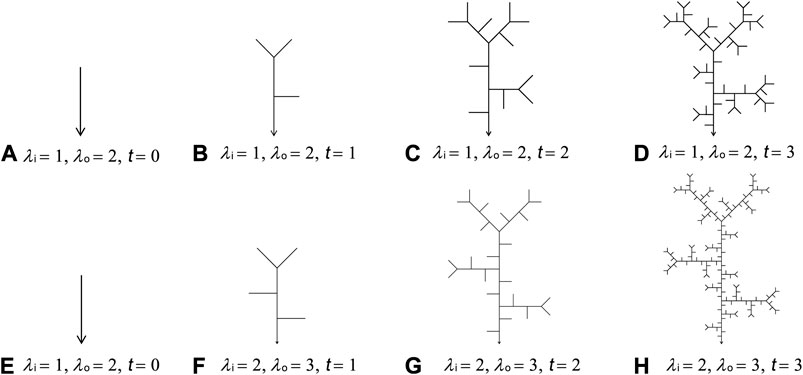
FIGURE 4. QU-IBTNs (A) and (E): initial cases (t = 0); (B–D): generator λ_i = 1 and λ_o = 2 after 1, 2, and 3 iteration steps; (F–H): generator λ_i = 2 and λ_o = 3 after 1, 2, and 3 iteration steps.

The invariance of generators in each iterative step for QU-IBTNs is strictly consistent with the definition of self-similarity. However, although the relevant iterative processes must not only have the sequentially and mathematically expressible generator series, but must also agree with the explicit given iteration rule, whether the QU-IBTN is a Tokunaga tree has never been examined graphically and recursively using a mathematical method.

Side Tributary Distribution of QU-IBTNs

The generation of a QU-IBTN begins with one link, the interior generator λ_i, and the exterior generator λ_o (i.e. the QU-IBTN is λ_o itself when t = 1). According to the iteration rule and Tokunaga ordering method, there are five stream number generating laws that must be obeyed during the iterative process.

The components of the generating law equations are defined as follows:

$N_{t,\omega }$ is the number of streams with H-S order $\omega$ at the $t$th iterative step;

$N_{t,(\omega ,{\omega }^{\prime })}$ is the number of streams $(\omega ,{\omega }^{\prime })$ at the $t$th iterative step;

$M_t^{\text{o}}$ is the number of exterior links at the $t$th iterative step; and

$M_t^{\text{i}}$ is the number of interior links at the $t$th iterative step.

Law 1: H-S Order Law

The H-S order of the QU-IBTN is $\Omega =t+1$ after the $t$th iterative step, that is:

$N_{t,\omega }={\displaystyle \sum _{{\omega }^{\prime }=\omega }^{\Omega }{N}_{t,(\omega ,{\omega }^{\prime })}}={\displaystyle \sum _{{\omega }^{\prime }=\omega }^{t+1}{N}_{t,(\omega ,{\omega }^{\prime })}}(7)$

Law 1 serves to replace the upper bound of the H-S order with the iterative step number in the calculations.

Law 2: Iteration Unchanging Law

The H-S orders of every stream and the entire network increase by 1 from the $\left(t-1\right)$th iterative step to the $t$th iterative step. Therefore, the number of streams $(\omega ,{\omega }^{\prime })$ in the $t$th iterative step (i.e., $N_{t,(\omega ,{\omega }^{\prime })}$) equals the number of streams $(\omega -1,{\omega }^{\prime }-1)$ in the $\left(t-1\right)$^th iterative step, that is:

$N_{t,\left(\omega ,{\omega }^{\text{′}}\right)}=N_{t-1,\left(\omega -1,{\omega }^{\text{′}}-1\right)}(8)$

By recursion from the $\left(t-k\right)$th iterative step to the $t$th iterative step, the relationship between the numbers of streams is found to be:

$N_{t,(\omega ,{\omega }^{\text{′}})}=N_{t-k,(\omega -k,{\omega }^{\text{′}}-k)}(9)$

Law 2 ensures that the corresponding equality relationship between the number of streams in the different iterative steps is satisfied.

Law 3: The Source Stream Law

Every pair of source streams with order $\left(\mathrm{1,1}\right)$ at the $t$th iterative step comes from one exterior link at the $(t-1)$th iterative step, which is shown as an example of QU-IBTNs by the choices λ_i = 1, and λ_o = 2 in Figure 5.

FIGURE 5

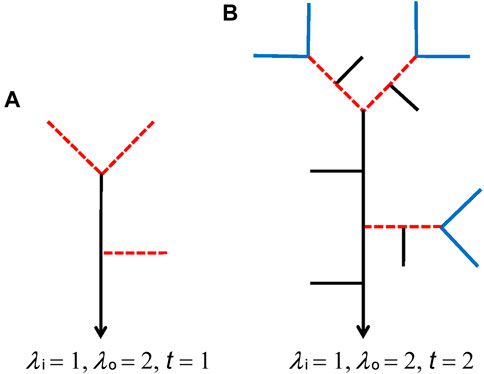
FIGURE 5. Generation of sources in the iterative process. The sources at the second step are generated by the exterior links at the first step. The red dotted lines in both (A) and (B) are the exterior links of QU-IBTNs at the first step in (A). The blue lines in (B) are the sources at the second step that are generated by the red dotted lines.

Figure 5 shows the generation of sources in Figure 5B from exterior links in Figure 5A. Consequently, the relationship between the sources at the $t$th step and the exterior links in the $(t-1)$th step is found to be:

$N_{t,\left(\mathrm{1,1}\right)}=2N_{t-\mathrm{1,1}}^{ }=2{\displaystyle \sum _{{\omega }^{\text{′}}=1}^t{N}_{t-1,(1,{\omega }^{\text{′}})}}(10)$

According to Eq. 9 in Law 2 and Eq. 10, the number of streams with order $(k,k)$ in the $t$th step can be determined by the number of exterior links at the ($t-k+1$)th step:

$N_{t,(k,k)}=N_{t-k+1,\left(\mathrm{1,1}\right)}(11)$

Law 4: The Neighbor-Ordered Side-branch Law

In every iterative step, the relationship between the number of streams with Tokunaga order (1,1) and order (1,2) that depend on the exterior generator ${\lambda }_{\text{o}}$ is:

$N_{t,\left(\mathrm{1,2}\right)}=\frac{{\lambda }_{\text{o}}-1}{2}{N}_{t,\left(\mathrm{1,1}\right)}(12)$

Figure 6 shows a ratio of 3/6 for the number of streams with the order (1,2) and the number of streams with the order (1,1) in the QU-IBTN generated by the choices λ_i = 1, λ_o = 2 at the second iterative step.

FIGURE 6

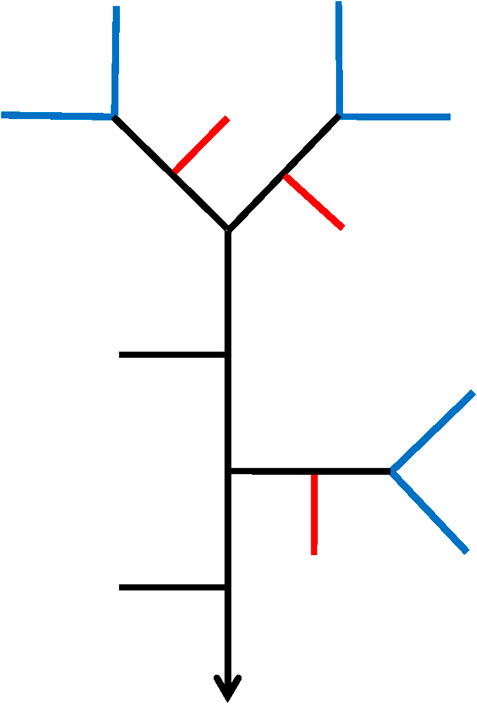
FIGURE 6. The QU-IBTN generated by λ_i = 1, λ_o = 2, t = 2 at the second step. The red lines are the streams with Tokunaga order (1,2) and the blue lines are the sources, which are the streams with Tokunaga order (1,1).

According to Eq. 9 in Law 2 and Eq. 12, the number of side branches that flow into streams that are 1 order greater (i.e., $(k,k+1)$) is:

$N_{t,(k,k+1)}=N_{t-k+1,\left(\mathrm{1,2}\right)}=\frac{{\lambda }_{\text{o}}-1}{2}{N}_{t-k+1,\left(\mathrm{1,1}\right)}(13)$

Law 5: The Greater-Ordered Side-branch Law

1) The streams with Tokunaga order (1,3) at the $t$th iterative step are generated by the $\frac{{\lambda }_{\text{o}}}{{\lambda }_{\text{o}}-1}{N}_{t-1,\left(\mathrm{1,2}\right)}$ interior links between the streams with Tokunaga order (1,2) at the $(t-1)$th iterative step. Additionally, each interior link produces ${\lambda }_{\text{i}}$ streams with Tokunaga order (1,3). Therefore, the number of streams with Tokunaga order (1,3) is:

$N_{t,\left(\mathrm{1,3}\right)}=\left(\frac{{\lambda }_{\text{o}}}{{\lambda }_{\text{o}}-1}{N}_{t-1,\left(\mathrm{1,2}\right)}\right){\lambda }_{\text{i}}=\frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{{\lambda }_{\text{o}}-1}{N}_{t-1,\left(\mathrm{1,2}\right)}(14)$

According to Equation 9 and 14, the number of side branches that flow into streams that are 2 orders greater [i.e., $(k,k+2)$] is:

$N_{t,(k,k+2)}=N_{t-k+1,\left(\mathrm{1,3}\right)}=\frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{{\lambda }_{\text{o}}-1}{N}_{t-k,\left(\mathrm{1,2}\right)}(15)$

Figure 7 shows the generation of streams with Tokunaga order (1,3) in the QU-IBTN with λ_i = 1, λ_o = 2, from the second to third iterative step.

2) The streams with Tokunaga order $\left(1,{\omega }^{\text{′}}+1\right),{\omega }^{\text{′}}\ge 3$ at the $t$th iterative step are generated by the $\left(\frac{{\lambda }_{\text{i}}+1}{{\lambda }_{\text{i}}}{N}_{t-1,(1,{\omega }^{\text{'}})}\right)$ interior links between streams with Tokunaga order $(1,{\omega }^{\text{′}})$ at the $(t-1)$th iterative step. Each interior link produces ${\lambda }_{\text{i}}$ streams with Tokunaga order $(1,{\omega }^{\text{′}}+1)$. Therefore, the number of streams with Tokunaga order $(1,{\omega }^{\text{′}}+1)$ is:

$N_{t,(1,{\omega }^{\text{′}}+1)}=\left(\frac{{\lambda }_{\text{i}}+1}{{\lambda }_{\text{i}}}{N}_{t-1,(1,{\omega }^{\text{′}})}\right){\lambda }_{\text{i}}=\left({\lambda }_{\text{i}}+1\right)N_{t-1,(1,{\omega }^{\text{′}})},{\omega }^{\text{′}}\ge 3(16)$

FIGURE 7

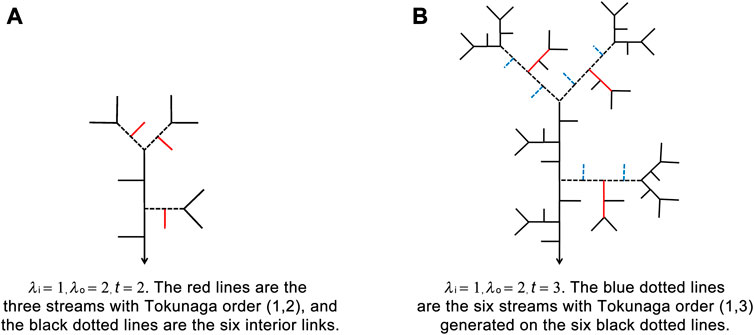
FIGURE 7. Streams with Tokunaga order (1,3) in QU-IBTNs are generated using λ_i = 1, λ_o = 2 from the second step in (A) to third iterative step in (B).

Figure 8 shows the generation of streams with Tokunaga order (1,4) in the QU-IBTN with λ_i = 1, λ_o = 2 from the second to third iterative step.

FIGURE 8

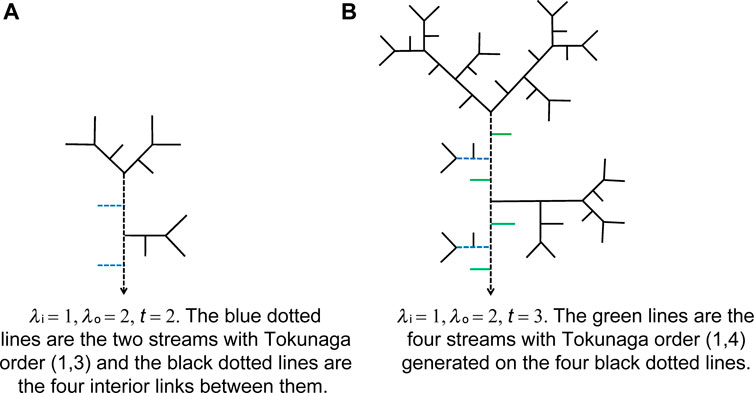
FIGURE 8. Streams with Tokunaga order (1,4) in QU-IBTNs are generated using λ_i = 1, λ_o = 2 from the second step in (A) to third iterative step in (B).

According to Equation 9 and 16, the number of side branches that flow into streams that are ${\omega }^{\text{'}}$ orders greater (i.e. $(k,k+{\omega }^{\prime }))$ is:

$N_{t,(k,k+{\omega }^{\text{′}})}=N_{t-k+1,(1,{\omega }^{\text{′}}+1)}=\left({\lambda }_{\text{i}}+1\right)N_{t-k,(1,{\omega }^{\text{′}})},{\omega }^{\text{′}}\ge 3(17)$

Tokunaga Matrix ${\mathit{N}}_{\mathit{t}}$ of IBTNs

During the $t$th iterative step, $\left({\lambda }_{\text{o}}+1\right)$ exterior links grow from the $M_{t-1}^{\text{o}}$ exterior links and ${\lambda }_{\text{i}}$ exterior links grow from the $M_{t-1}^{\text{i}}$ interior links. Additionally, ${\lambda }_{\text{o}}$ interior links grow from the $M_{t-1}^{\text{o}}$ exterior links and $\left({\lambda }_{\text{i}}+1\right)$ interior links grow from the $M_{t-1}^{\text{i}}$ interior links. Figure 9 shows the numerical relationship of the exterior and interior links between the $(t-1)$th step and $t$th step.

FIGURE 9

FIGURE 9. The generation of each interior and exterior link from the $(t-1)$th to the $t$th iterative step.

Eq. 18 describes the relationship for increase of exterior and interior links between the $(t-1)$th and $t$th iterative step, illustrated in Figure 9, as:

$\{\begin{array}{c}{M}_t^{\text{o}}=\left({\lambda }_{\text{o}}+1\right)M_{t-1}^{\text{o}}+{\lambda }_{\text{i}}{M}_{t-1}^{\text{i}}\\ M_t^{\text{i}}={\lambda }_{\text{o}}{M}_{t-1}^{\text{o}}+\left({\lambda }_{\text{i}}+1\right)M_{t-1}^{\text{i}}\\ M_t^{\text{o}}=M_t^{\text{i}}+1\end{array},t\ge 2(18)$

For the initial condition $t=1$, we have $M_1^{\text{o}}={\lambda }_{\text{o}}+1$, and $M_1^{\text{i}}={\lambda }_{\text{o}}$.

From Eqs 10, Eqs 18, it is clear that the number of exterior links at the $(t-1)$th step $M_{t-1}^{\text{o}}$ and the number of streams with order (1,1) at the $t$th step $N_{t,\left(\mathrm{1,1}\right)}$ are:

$N_{t,\left(\mathrm{1,1}\right)}=2M_{t-1}^{\text{o}}=\left(2{\lambda }_{\text{o}}+1+\frac{{\lambda }_{\text{o}}-{\lambda }_{\text{i}}}{{\lambda }_{\text{o}}+{\lambda }_{\text{i}}}\right){\left({\lambda }_{\text{o}}+{\lambda }_{\text{i}}+1\right)}^{t-1}+\frac{2{\lambda }_{\text{i}}}{{\lambda }_{\text{o}}+{\lambda }_{\text{i}}}(19)$

The Tokunaga matrix ${\mathit{N}}_{\mathit{t}}$ of the QU-IBTN, which is generated by the interior generator ${\lambda }_{\text{i}}$ and the exterior generator ${\text{λ}}_{\text{o}}$ at the $t$th step, follows Law 1 through Law 5. Its diagonal elements, ${\mathit{N}}_{\mathit{t}}(k,k)$, are calculated using Eqs 11, 18 in Law 3. The elements ${\mathit{N}}_{\mathit{t}}(k,k+1)$ next to the diagonal elements come from Eq. 13 in Law 4. The farther elements ${\mathit{N}}_{\mathit{t}}\left(k,k+2\right)$ and ${\mathit{N}}_{\mathit{t}}\left(k,k+{\omega }^{\text{'}}\right)$, in which ${\omega }^{\text{'}}\ge 3$, are from Eqs 15, 17 in Law 5. The initial conditions are $N_{1,\left(\mathrm{1,1}\right)}=2$, $N_{1,\left(\mathrm{1,2}\right)}={\text{λ}}_{\text{o}}-1$, and $N_{1,\left(\mathrm{2,2}\right)}=1$. The dimension of the matrix ${\mathit{N}}_{\mathit{t}}$is $\Omega \times \Omega$ (i.e., $\left(t+1\right)\times \left(t+1\right))$.

Using the first row of ${\mathit{N}}_{\mathit{t}}$ as an example, we find that:

$\begin{array}{l}\left(\begin{array}{cccc}{N}_{t,\left(\mathrm{1,1}\right)}& N_{t,\left(\mathrm{1,2}\right)}& N_{t,\left(\mathrm{1,3}\right)}& N_{t,\left(\mathrm{1,4}\right)}\end{array} N_{t,\left(\mathrm{1,5}\right)}\cdots \right)=\left(\begin{array}{cccc}{N}_{t,\left(\mathrm{1,1}\right)}& \frac{{\lambda }_{\text{o}}-1}{2}{N}_{t,\left(\mathrm{1,1}\right)}& \frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{{\lambda }_{\text{o}}-1}{N}_{t-1,\left(\mathrm{1,2}\right)}& \left({\lambda }_{\text{i}}+1\right)N_{t-1,\left(\mathrm{1,3}\right)} \left({\lambda }_{\text{i}}+1\right)N_{t-1,\left(\mathrm{1,4}\right)} \cdots \end{array}\right)\\ =\left(\begin{array}{cccc}{N}_{t,\left(\mathrm{1,1}\right)}& \frac{{\lambda }_{\text{o}}-1}{2}{N}_{t,\left(\mathrm{1,1}\right)}& \frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{2}{N}_{t-1,\left(\mathrm{1,1}\right)}& \left({\lambda }_{\text{i}}+1\right)\frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{{\lambda }_{\text{o}}-1}{N}_{t-2,\left(\mathrm{1,2}\right)}{\left({\lambda }_{\text{i}}+1\right)}^2{N}_{t-2,\left(\mathrm{1,3}\right)} \cdots \end{array}\right)\\ =\left(\begin{array}{cccc}{N}_{t,\left(\mathrm{1,1}\right)}& \frac{{\lambda }_{\text{o}}-1}{2}{N}_{t,\left(\mathrm{1,1}\right)}& \frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{2}{N}_{t-1,\left(\mathrm{1,1}\right)}& \left({\lambda }_{\text{i}}+1\right)\frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{2}{N}_{t-2,\left(\mathrm{1,1}\right)}{\left({\lambda }_{\text{i}}+1\right)}^2\frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{2}{N}_{t-3,\left(\mathrm{1,1}\right)}\cdots \end{array}\right)\end{array}(20)$

In the following equations, $\widehat{a}=\frac{{\lambda }_{\text{o}}-1}{2}$, $\widehat{b}=\frac{{\lambda }_{\text{i}}{\lambda }_{\text{o}}}{{\lambda }_{\text{o}}-1}$, and $\widehat{c}={\lambda }_{\text{i}}+1$. The matrix ${\mathit{N}}_{\mathit{t}}$ is in the form of the general terms $m_{i,j} (1\le i,j\le t+1=\Omega )$ as follows:

In the first column of ${\mathit{N}}_{\mathit{t}}$:

$m_{\mathrm{1,1}}=N_{t,\left(\mathrm{1,1}\right)}(21)$

In the second column of ${\mathit{N}}_{\mathit{t}}$:

$m_{\mathrm{1,2}}=\widehat{a}{m}_{\mathrm{1,1}},m_{\mathrm{2,2}}=N_{t-1,\left(\mathrm{1,1}\right)}(22)$

In the third column of ${\mathit{N}}_{\mathit{t}}$:

$m_{\mathrm{1,3}}=\widehat{b}\widehat{a}{m}_{\mathrm{2,2}},m_{\mathrm{2,3}}=\widehat{a}{m}_{\mathrm{2,2}},m_{\mathrm{3,3}}=N_{t-2,\left(\mathrm{1,1}\right)}(23)$

In the $j^{\text{th}}$ column $\left(4\le j\le t\right)$, the parameter $\widehat{c}$ appears in the terms shown below:

$m_{j,j}=N_{t-j+1,\left(\mathrm{1,1}\right)},m_{j-1,j}=\widehat{a}{m}_{j-1,j-1},m_{i,j}={\widehat{c}}^{j-i-2}\widehat{b}\widehat{a}{m}_{j-1,j-1},1\le i\le j-2(24)$

In the ${\left(t+1\right)}^{\text{th}}$ column, the exterior generator ${\text{λ}}_{\text{o}}$ affects the elements as follows:

$m_{t+1,t+1}=1,m_{t,t+1}=\widehat{a}{m}_{t,t}={\text{λ}}_{\text{o}}-1,m_{i,t+1}={\widehat{c}}^{t-1-i}\widehat{b}\widehat{a}{m}_{t,t}={\text{λ}}_{\text{o}}{\lambda }_{\text{i}}{\widehat{c}}^{t-1-i},1\le i\le t-1(25)$

The recursion of elements in Eqs 21–25 form the matrix ${\mathit{N}}_{\mathit{t}}$as:

${\mathit{N}}_{\mathit{t}}=\left(\begin{array}{cccccccc}{m}_{\mathrm{1,1}}& \widehat{a}{m}_{\mathrm{1,1}}& \widehat{b}\widehat{a}{m}_{\mathrm{2,2}}& {\widehat{c}}^{ }\widehat{b}\widehat{a}{m}_{\mathrm{3,3}}& \dots & \dots & {\widehat{c}}^{t-3}\widehat{b}\widehat{a}{m}_{t-1,t-1}& {\widehat{c}}^{t-2}\widehat{b}\widehat{a}{m}_{t,t}\\ & m_{\mathrm{2,2}}& \widehat{a}{m}_{\mathrm{2,2}} & \widehat{b}\widehat{a}{m}_{\mathrm{3,3}}& \dots & \dots & {\widehat{c}}^{t-4}\widehat{b}\widehat{a}{m}_{t-1,t-1}& {\widehat{c}}^{t-3}\widehat{b}\widehat{a}{m}_{t,t}\\ & & m_{\mathrm{3,3}} & \widehat{a}{m}_{\mathrm{3,3}} & \dots & \dots & \dots & \dots \\ & & & \dots & \dots & \dots & \dots & \dots \\ & & & & m_{t-2,t-2}& \widehat{a}{m}_{t-2,t-2}& \widehat{b}\widehat{a}{m}_{t-1,t-1}& \widehat{c}\widehat{b}\widehat{a}{m}_{t,t}\\ & & & & & m_{t-1,t-1}& \widehat{a}{m}_{t-1,t-1}& \widehat{b}\widehat{a}{m}_{t,t}\\ & & & & & & m_{t,t}& \widehat{a}{m}_{t,t}\\ & & & & & & & 1\end{array}\right)(26)$

The sum of the ${\left(k+1\right)}^{\text{th}}$ row in the matrix ${\mathit{N}}_{\mathit{t}}$ is the number of streams with H-S order 1at the ${\left(t-k\right)}^{\text{th}}$ iterative step, which is also essentially the number of the exterior links. The number of exterior links at the ${\left(t-k\right)}^{\text{th}}$ iterative step is:

$M_{t-k}^{\text{o}}={\displaystyle \sum }_{\mathit{j}=\mathit{k}+1}^{\mathit{t}+1}{\mathit{N}}_{\mathit{t}}\left(k+1,j\right)(27)$

Furthermore, the number of streams (1,1) at the ${\left(t-k+1\right)}^{\text{th}}$ iterative step (i.e., $N_{t-k+1,\left(\mathrm{1,1}\right)}$) is twice the number of the exterior links at the ${\left(t-k\right)}^{\text{th}}$ iterative step (i.e., $M_{t-k}^{\text{o}}$) for any $1\le k\le t-1$ according to Eq. 10 in Law 3. Therefore:

$\frac{N_{t-k+1,\left(\mathrm{1,1}\right)}}{M_{t-k}^{\text{o}}}=\frac{m_{k,k}}{M_{t-k}^{\text{o}}}=\frac{m_{k,k}}{{{\displaystyle \sum }}_{\mathit{j}=\mathit{k}+1}^{\mathit{t}+1}{\mathit{N}}_{\mathit{t}}\left(k+1,j\right)}=2,1\le k\le t-1(28)$

Side-Branching Ratio Matrix ${\mathit{T}}_{\mathit{t}}$ of IBTNs

The side-branching ratio matrix ${\mathit{T}}_{\mathit{t}}$ is composed of the side-branching ratio $T_{i,k+1}$ as its element ${\mathit{T}}_{\mathit{t}}\left(i,k\right)$. According to the definition of $T_{i,k+1}$ in Eq. 3, the expression for $T_{i,k+1}$ is:

${\mathit{T}}_{\mathit{t}}\left(i,k\right)=T_{i,k+1}=\frac{{\mathit{N}}_{\mathit{t}}\left(i,k+1\right)}{{{\displaystyle \sum }}_{\mathit{j}=\mathit{k}+1}^{\mathit{t}+1}{\mathit{N}}_{\mathit{t}}\left(k+1,j\right)}=\frac{{\mathit{N}}_{\mathit{t}}\left(i,k+1\right)}{m_{k,k}/2}(29)$

We can get the expression for ${\mathit{N}}_{\mathit{t}}\left(i,k+1\right)$ in ${\mathit{N}}_{\mathit{t}}$ as:

${\mathit{N}}_{\mathit{t}}\left(i,k+1\right)=\{\begin{array}{c}\widehat{a}{m}_{k,k}, i=k\\ {\widehat{c}}^{k-i-1}\widehat{b}\widehat{a}{m}_{k,k}, i\le k-1\end{array}(30)$

We modify the form of ${\mathit{N}}_{\mathit{t}}\left(i,k+1\right)$ in Eq. 29 using Eq. 30; therefore, the final form for ${\mathit{T}}_{\mathit{t}}\left(i,k\right)$ is:

${\mathit{T}}_{\mathit{t}}\left(i,k\right)=\{\begin{array}{c}2\widehat{a}, i=k\\ 2{\widehat{c}}^{k-i-1}\widehat{b}\widehat{a}, i\le k-1\end{array}(31)$

By combining Eq. 3 and the condition ${\mathit{N}}_{\mathit{t}}\left(t+1,t+1\right)=1$ in the $t^{\text{th}}$ column of the matrix ${\mathit{T}}_{\mathit{t}}$, we get:

${\mathit{T}}_{\mathit{t}}\left(i,t\right)=T_{i,t+1}=\frac{{\mathit{N}}_{\mathit{t}}\left(i,t+1\right)}{{\mathit{N}}_{\mathit{t}}\left(t+1,t+1\right)}={\mathit{N}}_{\mathit{t}}\left(i,t+1\right)(32)$

Using Eqs 31, 32, we get the matrix ${\mathit{T}}_{\mathit{t}}$ as follows:

${\mathit{T}}_{\mathit{t}}=\left(\begin{array}{cccccc}{\lambda }_{\text{o}}-1& {\lambda }_{\text{i}}{\lambda }_{\text{o}}& {\lambda }_{\text{i}}{\lambda }_{\text{o}}\left({\lambda }_{\text{i}}+1\right)& \dots & {\lambda }_{\text{i}}{\lambda }_{\text{o}}{\left({\lambda }_{\text{i}}+1\right)}^{t-3}& {\text{λ}}_{\text{o}}{\lambda }_{\text{i}}{\left({\lambda }_{\text{i}}+1\right)}^{t-2}\\ & {\lambda }_{\text{o}}-1& {\lambda }_{\text{i}}{\lambda }_{\text{o}}& \dots & {\lambda }_{\text{i}}{\lambda }_{\text{o}}{\left({\lambda }_{\text{i}}+1\right)}^{t-4}& {\text{λ}}_{\text{o}}{\lambda }_{\text{i}}{\left({\lambda }_{\text{i}}+1\right)}^{t-3}\\ & & \dots & \dots & \dots & \dots \\ & & & {\lambda }_{\text{o}}-1& {\lambda }_{\text{i}}{\lambda }_{\text{o}}& {\text{λ}}_{\text{o}}{\lambda }_{\text{i}}\left({\lambda }_{\text{i}}+1\right)\\ & & & \cdot & {\lambda }_{\text{o}}-1& {\text{λ}}_{\text{o}}{\lambda }_{\text{i}}\\ & & & .& & {\text{λ}}_{\text{o}}-1\\ & & & .& & \end{array}\right)(33)$

The efficient and necessary condition to be a self-similar network is that ${\mathit{T}}_{\mathit{t}}$ must to be a Toeplitz matrix according to Eq. 5. The QU-IBTNs with the interior generator ${\text{λ}}_{\text{i}}$ and exterior generator ${\text{λ}}_{\text{o}}$ are definitely self-similar because the elements on the diagonal are equal in Eq. 33, which is a Toeplitz matrix. This is also shown in terms of the results for side-branching ratios:

$T_1={\lambda }_{\text{o}}-1,T_k={\lambda }_{\text{i}}{\lambda }_{\text{o}}{\left({\lambda }_{\text{i}}+1\right)}^{k-2},2\le k\le t(34)$

For strict Tokunaga self-similarity, the elements in ${\mathit{T}}_{\mathit{t}}$ must satisfy Eq. 6. Therefore, the necessary condition for a QU-IBTN to be a Tokunaga tree is:

${\lambda }_{\text{o}}={\lambda }_{\text{i}}+1(35)$

No matter which values of ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$ are selected to generate a QU-IBTN, this QU-IBTN must be self-similar. However, a QU-IBTN is a Tokunaga tree only when ${\lambda }_{\text{o}}={\lambda }_{\text{i}}+1$. This means that when we use QU-IBTNs to simulate natural river networks, which are Tokunaga trees, we need to generate a QU-IBTN with the special condition that ${\lambda }_{\text{o}}={\lambda }_{\text{i}}+1$.

To demonstrate the constraints on self-similarity versus Tokunaga self-similarity, we provide the following two examples.

Example 1: ${\lambda }_o={\lambda }_i$

When the generators ${\lambda }_{\text{o}}={\lambda }_{\text{i}}$, the side-branching ratios given by Eq. 34 are:

$T_1={\lambda }_{\text{o}}-1,T_k={\lambda }_{\text{o}}^2{\left({\lambda }_{\text{o}}+1\right)}^{k-2},2\le k\le t(36)$

The side-branching ratio $T_k (1\le k)$ contains different constants, but does not define a geometric series. Therefore, the QU-IBTN with ${\lambda }_{\text{o}}={\lambda }_{\text{i}}$ is self-similar but not a Tokunaga tree, as pointed out by Peckham (1995a).

Example 2: ${\lambda }_o={\lambda }_i+1$

When the exterior link generator and the interior link generator satisfy the condition ${\lambda }_{\text{i}}={\lambda }_{\text{o}}-1$, the side-branching ratios given by Eq. 34 are:

$T_k=\left({\lambda }_{\text{o}}-1\right){\lambda }_{\text{o}}^{k-1},k\ge 1(37)$

According to Eq. 37, this QU-IBTN is a Tokunaga tree with $a={\lambda }_{\text{o}}-1$ and $c={\lambda }_{\text{o}}$. Based on statistics, the necessary condition for a QU-IBTN to be a Tokunaga tree in Eq. 37 is consistent with the result presented by Veitzer and Gupta (2000).

Results

Natural River Networks

In the following, we use the Yellow River in China (H-S order 11) and the Amazon River in South America (H-S order 12) as examples to verify whether or not they follow the rules of QU-IBTNs and the constraint of a Tokunaga tree. Figure 10 shows the river networks extracted from digital elevation model (DEM) data with a 30 m resolution (Li et al., 2018; Li et al., 2020).

FIGURE 10

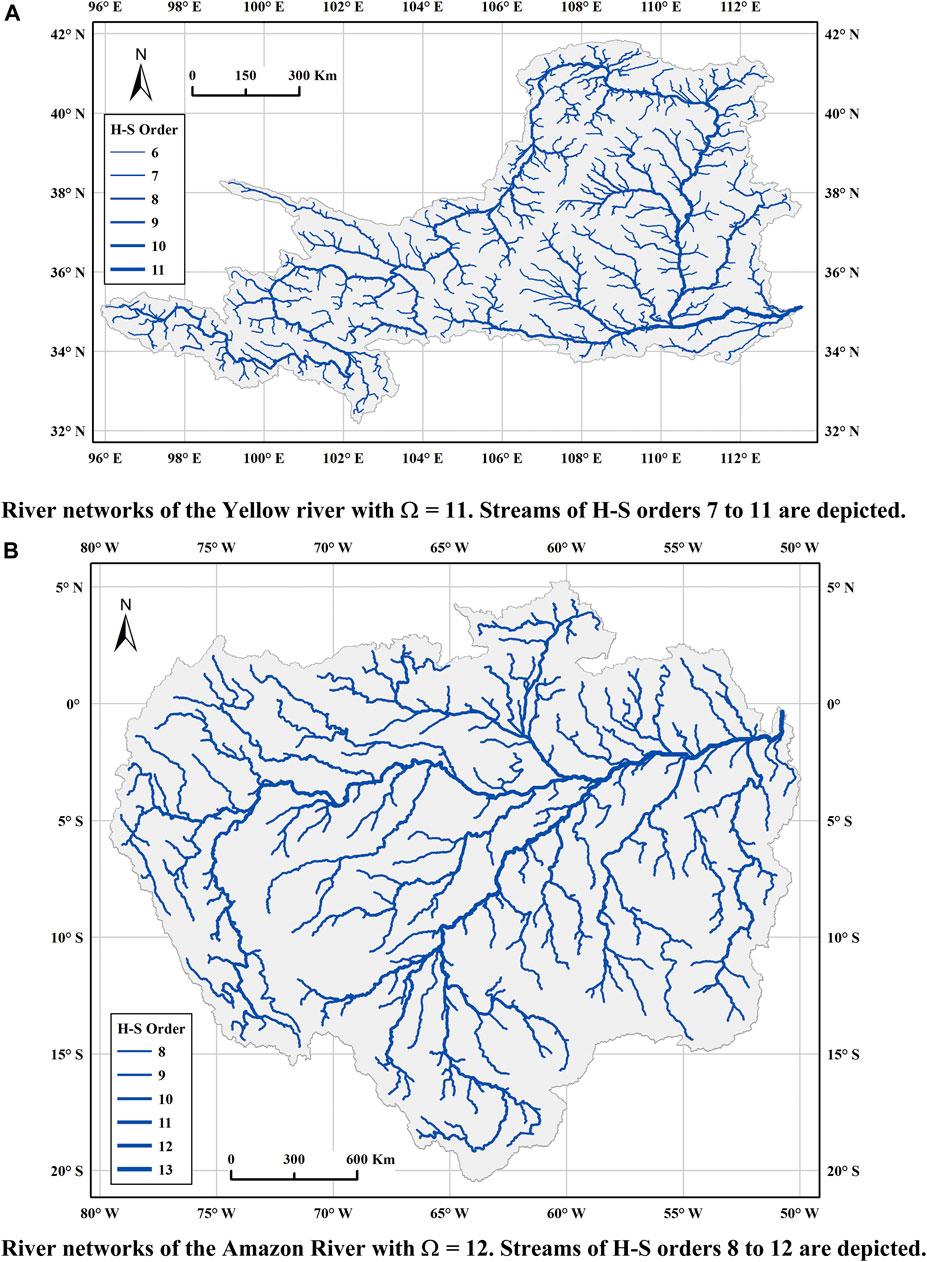
FIGURE 10. River networks of the Yellow River and the Amazon River with streams of no less than an H-S order 7 are shown in the figure.

Supplementary Table S1 (shown in Supplementary Material) shows the Tokunaga matrices of the stream numbers $N_{\omega ,{\omega }^{\prime }}$ for both the Yellow River and the Amazon River.

The similarities Between Natural River Networks and Tokunaga Trees

Supplementary Table S2 (shown in Supplementary Material) shows the side-branching ratio matrices for the side-branching ratios $T_{i,j}$ based on Eq. 3 for the two rivers.

Supplementary Table S2 also shows that the branching ratio values have large fluctuations for main stems with large H-S orders, as shown in Figure 11.

FIGURE 11

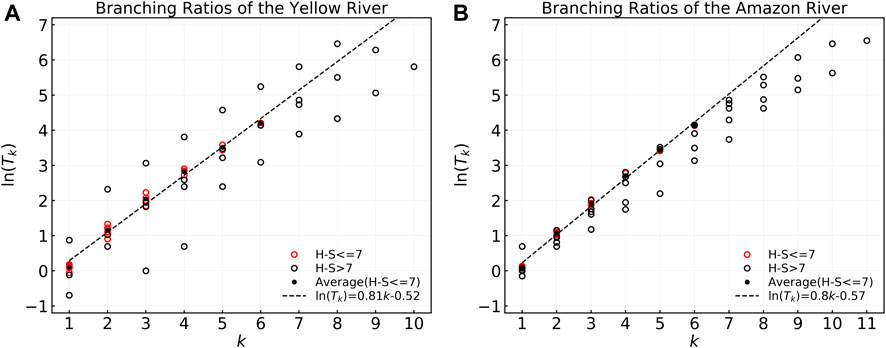
FIGURE 11. Branching ratios, $T_k$, of the Yellow River and theAmazon River for every $k$. The black circles are the branching ratios shown in the shaded sections of the matrices of Supplementary Table S2. The red circles are the remaining data in the matrices. The black points are the average values of the black circles. The dotted black line is the fit of the black points using the least squares regression method.

The statistical side-branching ratio matrices of the two rivers in Supplementary Table S2 and Figure 11 show that the statistical results of $T_k$ vary greatly compared with the theoretic self-similarity derivation, which is uniform for a fixed k. The black circles in Figure 11 denote the $T_k$ data in the shaded sections of Supplementary Table S2 that are less affected by local geomorphology and terrain, and therefore are more concentrated in their distribution. The red circles in Figure 11 are the $T_k$ data excluding the shaded sections of Supplementary Table S2; these are seen to scatter far away from each other. We now use streams with H-S orders 1 to 7 (i.e., the shaded sections of Supplementary Table S2 and the black circles in Figure 11) to analyze the Tokunaga self-similarity of the two natural river networks. The values of the black points in Figure 11, which are the statistical average values, $\overline{T_k}$, of $T_k$ for each k (1 ≤ k ≤ 6), are (1.11, 3.19, 7.76, 16.91, 33.53, 67.09) for the Yellow River and (1.11, 2.93, 6.90, 14.97, 30.86, 62.41) for the Amazon River.

The side-branching ratio series in Figure 11 were verified to satisfy as 1.34 × 2.25^k−1 and 1.26 × 2.23^k−1 using the least squares method, as shown in Figure 11 in terms of the dotted black lines with coefficients of determination R² > 0.99.

Therefore, the Tokunaga parameters can be evaluated using $a_{\text{Yellow}}\cong 1.34,c_{\text{Yellow}}\cong 2.25$ and $a_{\text{Amazon}}\cong 1.26,c_{\text{Amazon}}\cong 2.23$.

The Similarities Between Natural River Networks and QU-IBTNs

We construct $\mathit{N}\_{\mathit{R}}_{\mathit{t}}$ matrices with the same dimension of ${\mathit{N}}_{\mathit{t}}$ in Supplementary Table S1 in terms of:

$\mathit{N}\_{\mathit{R}}_{\mathit{t}}\left(k,k+1\right)=\frac{{\mathit{N}}_{\mathit{t}}\left(k,k+1\right)}{{\mathit{N}}_{\mathit{t}}\left(k,k\right)},1\le k\le \Omega -1(38)$

$\mathit{N}\_{\mathit{R}}_{\mathit{t}}\left(k,k+2\right)=\frac{{\mathit{N}}_{\mathit{t}}\left(k,k+2\right)}{{\mathit{N}}_{\mathit{t}}\left(k+1,k+2\right)},1\le k\le \Omega -2(39)$

and

$\mathit{N}\_{\mathit{R}}_{\mathit{t}}(i,k)=\frac{{\mathit{N}}_{\mathit{t}}\left(i,k\right)}{{\mathit{N}}_{\mathit{t}}\left(i+1,k\right)},1\le i\le k-3,4\le k\le \Omega (40)$

The $\mathit{N}\_{\mathit{R}}_{\mathit{t}}$ matrices for the Yellow River and the Amazon River using Eqs 38–40 are listed in Supplementary Table S3 (shown in Supplementary Material).

According to the standard form of the Tokunaga matrix ${\mathit{N}}_{\mathit{t}}$ in Eq. 26, $\widehat{a}$ values are expressed in Eq. 38 by the ratios of ${\mathit{N}}_{\mathit{t}}(k,k+1)$ to ${\mathit{N}}_{\mathit{t}}(k,k)$ ($1\le k\le \Omega -1$); $\widehat{b}$ values are expressed in Eq. 39 by the ratios of ${\mathit{N}}_{\mathit{t}}(k,k+2)$ to ${\mathit{N}}_{\mathit{t}}(k+1,k+2)$ ($1\le k\le \Omega -2$); and $\widehat{c}$ values are expressed in Eq. 40 by the ratios of ${\mathit{N}}_{\mathit{t}}(i,k)$ to ${\mathit{N}}_{\mathit{t}}(i+1,k)$ ($1\le i\le k-3,4\le k\le \Omega$).

We calculate ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$ for each iterative step from every row of the matrix $\mathit{N}\_{\mathit{R}}_{\mathit{t}}$ in Supplementary Table S3, as shown in the Methods section. The matrices of the ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$ values are defined as $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}$ in Supplementary Table S4 (shown in Supplementary Material).

In the $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}$ matrices in Supplementary Table S4, the first element in each row is the value of the exterior generator ${\lambda }_{\text{o}}$ for each iterative step, and the following elements in the row are the interior generators ${\lambda }_{\text{i}}$ for each corresponding iterative step. Figure 12 shows the values of the generators ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$ for each iterative step in Supplementary Table S4 for both the Yellow River and the Amazon River.

1) The exterior generators ${\lambda }_{\text{o}}$ (i.e., the gray solid points) vary slightly for the higher iterative steps (greater than 6) in Supplementary Table S4 and Figure 12. At the higher iterative steps, the streams are closer to the source streams, which allows them to evolve freely according to the same formative mechanism because they have enough space to grow. Freedom and space allows streams between different iterative steps in a river network, and even for different river networks, to be uniform and similar, which can be seen in terms of the uniformity of the generators ${\lambda }_{\text{o}}$.

2) The interior generators ${\lambda }_{\text{i}}$ (i.e., the black circles) are concentrated and approaching uniform for the higher iterative steps in Supplementary Table S4 and Figure 12. The last column in the Yellow River $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}$ matrix in Supplementary Table S4 shows the interior generators for the main stem of the Yellow River basin. The changes in this column are results from the geomorphology and terrain, which constrain the generators on the main stems. The Amazon River $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}$ matrix also shows the same changes in this column. For the lower iterative steps, the generators shown in Supplementary Table S4 are generators for streams with high H-S orders, which are also influenced by the geomorphology and terrain. To satisfy the conditions of uniformity of generators and similarity of the river networks, we need to exclude the streams that are heavily constrained by the geomorphology and terrain.

3) The interior generators ${\lambda }_{\text{i}}$ (i.e., the black circles) vary slightly at iterative steps 7 to 11 for the Yellow River, and steps 8 to 12 for the Amazon River, as shown in Supplementary Table S4 and Figure 12. The average values for each iterative step (i.e., the dotted black line) are almost stable between iterative steps 7 and 11 for the Yellow River and steps 8 and 12 for the Amazon River. The exterior generators ${\lambda }_{\text{o}}$ are consistent at these iterative steps. The stability and consistency of the generators ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$ at high iterative steps confirms that the two natural river networks follow the rules of QU-IBTNs in a statistical sense. We use the average values of ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$ in the shaded section in Supplementary Table S4 from iterative steps 7–11 and 8–12 separately to evaluate the generator of the Yellow River and the Amazon River. The calculations for the generators are provided in the Methods section. The statistical averages for the exterior generator and the interior generator are evaluated using ${\lambda }_{\text{o}-\text{Yellow}}\cong 2.11, {\lambda }_{\text{i}-\text{Yellow}}\cong 1.34$ for the Yellow River and ${\lambda }_{\text{o}-\text{Amazon}}\cong 2.1$0, ${\lambda }_{\text{i}-\text{Amazon}}\cong 1.26$ for the Amazon River.

FIGURE 12

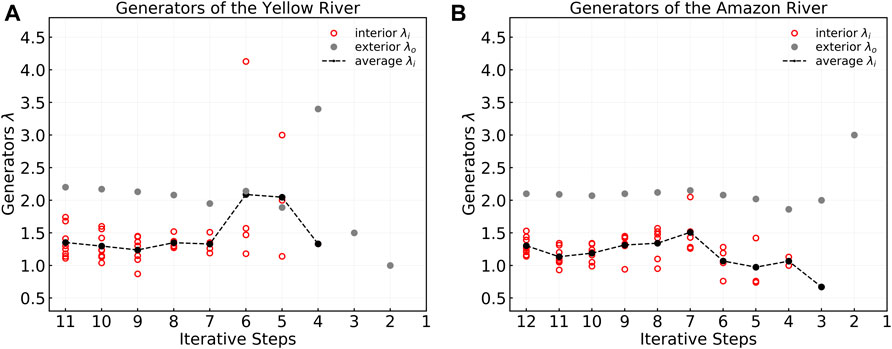
FIGURE 12. Generators of the Yellow River and the Amazon River for each iterative step. The gray solid points are the exterior generators ${\lambda }_{\text{o}}$. The black circles are the interior generators ${\lambda }_{\text{i}}$. The dotted black line corresponds to the average value of the interior generators ${\lambda }_{\text{i}}$ for each row, excluding those in the last column of Supplementary Table S4. Analysis and Conclusions for Supplementary Table S4 and Figure 12.

Table 1 lists the generators and Tokunaga parameters for the Yellow River and the Amazon River.

TABLE 1

TABLE 1. The generators (${\lambda }_{\text{i}},{\lambda }_{\text{o}}$) and Tokunaga parameters (a,c) for the Yellow River and the Amazon River.

Analysis and conclusions for Table 1:

1) In our analysis, we have removed the main stems with high H-S orders at the low iterative steps, as these are controlled by the local geomorphology and terrain. The QU-IBTN rules and Tokunaga self-similarity are well demonstrated using the Yellow River and the Amazon River in terms of the uniformity and equality of the generators and branching ratios for streams with low H-S orders at high iterative steps.

2) According to the sufficient and necessary condition for a QU-IBTN to be a Tokunaga tree in Eq. 35, we should have $a={\lambda }_{\text{i}}, c={\lambda }_{\text{o}}$ and ${\lambda }_{\text{o}}-{\lambda }_{\text{i}}= c-a=1$. However, from Table 1, there is a difference between $c$ and ${\lambda }_{\text{o}}$ because of the different data and methods used for calculation.

Discussion

The QU-IBTNs proposed above illustrate how to generate iterative binary tree networks simulating natural river networks. The complete mathematic iterative steps with graphic deduction are demonstrated in iterative orders. The iterative process is sustained by the self-similarity theory. The synthetic QU-IBTNs are close to the natural river networks in similarity characteristics parameters by two examples.

When generated by exterior generator ${\lambda }_{\text{o}}=2$ and interior generator ${\lambda }_{\text{i}}=1$, the QU-IBTN is equivalent to the Shreve model (Shreve, 1966), for which the bifurcation ratio is $R_{\text{B}}=4$ and the Tokunaga parameters are $a=1, c=2$(Peckham, 1995a). This is the only case of a plane-filling IBTN (Zhang et al., 2009). Therefore, only the Shreve model can generate a plane-filling Tokunaga tree, and only the IBTN plane-filling Tokunaga tree fits the Shreve model.

Although in theory the Shreve model should be the most ideal topology network that approaches natural river networks because it is a Tokunaga tree and plane-filling, there is an obvious contradiction that topological parameters such as $R_B=4$, $a=1$, and $c=2$ of the Shreve model are far from those of natural river networks [Average values of $R_B$, $a$ and $c$ are around 4.4, 1.1 and 2.5 (Peckham, 1995a; Dodds and Rothman, 1999; Dodds, 2000; Pelletier and Turcotte, 2000; Mantilla et al., 2010; Zanardo et al., 2013; Wang et al., 2016)]. Furthermore, the entire natural river network is determined not only by topological characteristics (such as stream number, $R_B$ and Tokunaga parameters), but also geometrical characteristics (such as stream length and confluence angle) that depend on the energy conservation and the relation between sediment and water discharge. Consequently, the Shreve model is an ideal model to simulate the topology of river networks, but it is an unsatisfactory model for simulating the geometrical properties of natural river networks. Furthermore, a layout for an ideal plane-filling Tokunaga tree is still needed.

We have supposed that the hypothesis of the uniformity of link length in the IBTN may lead to differences in the bifurcation ratio as compared with natural river networks under the condition of plane-filling. The link length and confluence angles of IBTNs should be redefined according to the values of the stream length ratios of natural river networks when considering plane-filling.

Some aspects of the linkages between the structure of river networks and the processes that shape them remain somewhat unclear and difficult to understand (Abrahams, 1984; Montgomery and Dietrich, 1992; Perron et al., 2012; Seybold et al., 2017). A considerable body of research is available on the topologic structure associated with stream numbers and self-similarity of river networks (Peckham, 1995a; Dodds, 2000; Pelletier and Turcotte, 2000; Veitzer and Gupta, 2000; Mcconnell and Gupta, 2008; Mantilla et al., 2010; Zanardo et al., 2013). Recently, confluence angles (also referred to as junction angles) of a number of natural river networks, which represent a geometric component of river network structure, have been statistically evaluated and shown to depend on the climatic setting (Devauchelle et al., 2012; Seybold et al., 2017). These treatments of confluence angles may provide important clues in further studies to explore the following two questions: 1) where does a stream emerge from an unchannelized region? and 2) how far downstream does this stream extend until it merges into another stream?

Conclusion

In this paper we provide a complete mathematical and graphical deduction of QU-IBTNs with specified generator series and iteration rule. Our conclusions are as follows:

1) For the QU-IBTN generated by the generator series and iteration rule in this paper, five intrinsic stream number laws—which determine the distribution of source streams and side-branches following into streams of greater orders—are graphically and recursively analyzed and satisfied.

2) As defined in this paper, the QU-IBTN are demonstrated to be self-similar.

3) The sufficient and necessary constraint for a QU-IBTN to be a Tokunaga tree is that the exterior links must be replaced with a neighboring generator in the generator series that is larger than the interior links during the iterative process. This defines a generation method for a simulated network that is identical to a natural river network in topology.

4) Two natural river networks, i.e. the Yellow River, China and the Amazon River, South America, are shown to be Tokunaga trees and QU-IBTNs within specified H-S order scales.

The self-similarity of river networks is a classical topic, and there are many researchers working on this topic using varied methods, including mathematicians who are good at fractal theory (Kovchegov and Zaliapin, 2020). Other researchers might use random and mathematical foundations in their own research. Our manuscript here is an intuitive, accessible and understandable initial tool to measure the self-similarity of river networks. The advance of generator series, the integer iterative rules showing directly by graphs, and the corresponding mathematical derivations are new and different from others’ methods. The QU-IBTNs are built just in a few finite iterative steps as shown in the figures. QU-IBTNs in random scales will be generated by coding in the future. However, to some extent we are doing the same thing as other researchers-just find a way to demonstrate the self-similarity and Tokunaga property of river networks. This is what we think we can share with other researchers, and help make progress in river network simulations in the future.

Methods

The Method for Calculating ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$ From the Matrix $\mathit{N}\_{\mathit{R}}_{\mathit{t}}$

For the $k^{\text{th}}$ row in matrix $\mathit{N}\_{\mathit{R}}_{\mathit{t}}$, $\Omega -k+1$ is the corresponding iterative step. The matrix $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}$ expresses the generators ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$. The exterior generator at the ${\left(\Omega -k+1\right)}^{\text{th}}$ iterative step is:

${\lambda }_{\text{o}}\left(\Omega -k+1\right)=\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}\left(k,k+1\right)=2\times \mathit{N}\_{\mathit{R}}_{\mathit{t}}\left(k,k+1\right)+1, 1\le k\le \Omega -1(\mathrm{M1})$

The interior generators in the $k^{\text{th}}$ row (i.e., the ${\left(\Omega -k+1\right)}^{\text{th}}$ iterative step) are:

${\lambda }_{\text{i}\_1}\left(\Omega -k+1\right)=\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}\left(k,k+2\right)=\frac{{\lambda }_{\text{o}}\left(k\right)-1}{{\lambda }_{\text{o}}\left(k\right)}\times \mathit{N}\_{\mathit{R}}_{\mathit{t}}(k,k+2), 1\le k\le \Omega -2(\mathrm{M2})$

and

$\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}\left(k,i\right)=\frac{{\lambda }_{\text{i}\_1}\left(\Omega -k+1\right)}{{\lambda }_{\text{i}\_1}\left(\Omega -k\right)}\times \mathit{N}\_{\mathit{R}}_{\mathit{t}}(k,i), 1\le k\le i-3,4\le i\le \Omega (\mathrm{M3})$

In the matrix $\mathit{N}\_{\mathit{R}}_{\mathit{t}}$, the elements $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}\left(k,k+1\right)$ ($1\le k\le \Omega -1$) in Equation (M1) correspond to the exterior generator at the $\left(\Omega -k+1\right)\text{th}$ iterative step. The elements $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}\left(k,k+2\right)$ and $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}\left(k,i\right)$ ($k+3\le i\le \Omega$) are the interior generators at the $\left(\Omega -k+1\right)\text{th}$ iterative step.

For the Yellow River and the Amazon River, the statistically averaged values for ${\lambda }_{\text{o}-\text{Yellow}}$ and ${\lambda }_{\text{o}-\text{Amazon}}$ are:

${\lambda }_{\text{o}-\text{Yellow}}=\frac{{{\displaystyle \sum }}_{k=1}^5{\lambda }_{\text{o}}\left(12-k\right)}{5}=\frac{{{\displaystyle \sum }}_{k=1}^5{\mathit{N}}_{\lambda \mathit{t}}\left(k,k+1\right)}{5}=2.11(\mathrm{M4})$

and

${\lambda }_{\text{o}-\text{Amazon}}=\frac{{{\displaystyle \sum }}_{k=1}^5{\lambda }_{\text{o}}\left(13-k\right)}{5}=\frac{{{\displaystyle \sum }}_{k=1}^5{\mathit{N}}_{\lambda \mathit{t}}\left(k,k+1\right)}{5}=1.34(\mathrm{M5})$

For the Yellow River and the Amazon River, the statistically averaged values for ${\lambda }_{\text{i}-\text{Yellow}}$ and ${\lambda }_{\text{i}-\text{Amazon}}$ are:

${\lambda }_{\text{i}-\text{Yellow}}=\frac{{\displaystyle {\sum }_{k=1}^5{\displaystyle {\sum }_{i=k+2}^{10}{\mathit{N}}_{\lambda \mathit{t}}\left(k,i\right)}}}{5}=2.10(\mathrm{M6})$

and

${\lambda }_{\text{i}-\text{Amazon}}=\frac{{\displaystyle {\sum }_{k=1}^5{\displaystyle {\sum }_{i=k+2}^{11}{\mathit{N}}_{\lambda \mathit{t}}\left(k,i\right)}}}{5}=1.26(\mathrm{M7})$

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LZ, the corresponding author, did all the mathematics derivations. KYW organized the manuscript. TJL did the derivations and provided the data. XL, BYG, and GXC collected the data and plot figures. JHW and YFH processed the data and revised the manuscript.

Funding

This paper is supported by the State Key laboratory of Plateau Ecology and Agriculture, Qinghai Univerisity (2021-KF-10), National Natural Science Foundation of China (52109092), and Huazhong University of Science and Technology (3004242101).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Data supporting Figure 10 and Supplementary Table S1 in this study were obtained from a digital elevation model (DEM) data with a 30 m resolution. I would like to thank Rina Schumer and Gary Parker for their useful comments and revisions of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2021.792289/full#supplementary-material

Supplementary Table S1 | The Tokunaga matrices ${\mathit{N}}_{\mathit{t}}$ for the Yellow River and the Amazon River.

Supplementary Table S2 | The side-branching ratio matrices ${\mathit{T}}_{\mathit{t}}$ for the Yellow River and the Amazon River.

Supplementary Table S3 | The $\mathit{N}\_{\mathit{R}}_{\mathit{t}}$ matrices for the Yellow River and the Amazon River.

Supplementary Table S4 | The $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}$ matrices of generators ${\lambda }_{\text{o}}$ and ${\lambda }_{\text{i}}$ for the Yellow River and the Amazon River.

References

Abrahams, A. D. (1984). The Development of Tributaries of Different Sizes along Winding Streams and Valleys. Water Resour. Res. 20, 1791–1796. doi:10.1029/wr020i012p01791

CrossRef Full Text | Google Scholar

Claps, P., Fiorentino, M., and Oliveto, G. (1996). Informational Entropy of Fractal River Networks. J. Hydrol. 187, 145–156. doi:10.1016/s0022-1694(96)03092-2

CrossRef Full Text | Google Scholar

Devauchelle, O., Petroff, A. P., Seybold, H. F., and Rothman, D. H. (2012). Ramification of Stream Networks. Proc. Natl. Acad. Sci. 109, 20832–20836. doi:10.1073/pnas.1215218109

PubMed Abstract | CrossRef Full Text | Google Scholar

Dodds, P. S. (2000). Geometry of River Networks. Ph.D. Thesis. Massachusetts Institute of Technology.

Google Scholar

Dodds, P. S., and Rothman, D. H. (1999). Unified View of Scaling Laws for River Networks. Phys. Rev. E 59, 4865–4877. doi:10.1103/PhysRevE.59.4865

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, V. K., and Mesa, O. J. (2014). Horton Laws for Hydraulic-Geometric Variables and Their Scaling Exponents in Self-Similar Tokunaga River Networks. Nonlin. Process. Geophys. 21, 1007–1025. doi:10.5194/npg-21-1007-2014

CrossRef Full Text | Google Scholar

Horton, R. E. (1945). Erosional Development of Streams and Their Drainage Basins; Hydrophysical Approach to Quantitative Morphology. Geol. Soc. Am. Bull. 56 (3), 275–370. doi:10.1130/0016-7606(1945)56[275:edosat]2.0.co;2

CrossRef Full Text | Google Scholar

Hung, C.-P., and Wang, R.-Y. (2005). Coding and Distance Calculating of Separately Random Fractals and Application to Generating River Networks. Fractals 13 (1), 57–71. doi:10.1142/S0218348X05002738

CrossRef Full Text | Google Scholar

Kovchegov, Y., and Zaliapin, I. (2020). Random Self-Similar Trees: A Mathematical Theory of Horton Laws. Probab. Surv. 17, 1–213. doi:10.1214/19-PS331

CrossRef Full Text | Google Scholar

Li, J., Li, T., Liu, S., Shi, H., and Shi, H. Y. (2018). An Efficient Method for Mapping High-Resolution Global River Discharge Based on the Algorithms of Drainage Network Extraction. Water 10 (4), 533. doi:10.3390/w10040533

CrossRef Full Text | Google Scholar

Li, J. Y., Li, T. J., Zhang, L., Bellie, S., Fu, X. D., Huang, Y. F., et al. (2020). A D8-Compatible High-Efficient Channel Head Recognition Method. Environ. Model. Softw. 125, 104624. doi:10.1016/j.envsoft.2020.104624

CrossRef Full Text | Google Scholar

Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. New York: W. H. Freeman.

Google Scholar

Mantilla, R., Troutman, B. M., and Gupta, V. K. (2010). Testing Statistical Self-Similarity in the Topology of River Networks. J. Geophys. Res. 115, 1–12. doi:10.1029/2009JF001609

CrossRef Full Text | Google Scholar

Masek, J. G., and Turcotte, D. L. (1993). A Diffusion-Limited Aggregation Model for the Evolution of Drainage Networks. Earth Planet. Sci. Lett. 119, 379–386. doi:10.1016/0012-821x(93)90145-y

CrossRef Full Text | Google Scholar

Mcconnell, M., and Gupta, V. K. (2008). A Proof of the Horton Law of Stream Numbers for the Tokunaga Model of River Networks. Fractals 16 (3), 227–233. doi:10.1142/S0218348X08003958

CrossRef Full Text | Google Scholar

Menabde, M., Veitzer, S., Gupta, V., and Sivapalan, M. (2001). Tests of Peak Flow Scaling in Simulated Self-Similar River Networks. Adv. Water Resour. 24, 991–999. doi:10.1016/S0309-1708(01)00043-4

CrossRef Full Text | Google Scholar

Montgomery, D. R., and Dietrich, W. E. (1992). Channel Initiation and the Problem of Landscape Scale. Science 255, 826–830. doi:10.1126/science.255.5046.826

PubMed Abstract | CrossRef Full Text | Google Scholar

Peckham, S. D. (1995b). Self-similarity in the Three-Dimensional Geometry and Dynamics of Large River Basins. Ph.D.Thesis. USA: University of Colorado.

Google Scholar

Peckham, S. D. (1995a). New Results for Self-Similar Trees with Applications to River Networks. Water Resour. Res. 31 (4), 1023–1029. doi:10.1029/94WR03155

CrossRef Full Text | Google Scholar

Pelletier, J. D., and Turcotte, D. L. (2000). Shapes of River Networks and Leaves: Are They Statistically Similar? Phil. Trans. R. Soc. Lond. B 355, 307–311. doi:10.1098/rstb.2000.0566

CrossRef Full Text | Google Scholar

Perron, J. T., Richardson, P. W., Ferrier, K. L., and Lapôtre, M. (2012). The Root of Branching River Networks. Nature 492, 100–103. doi:10.1038/nature11672

PubMed Abstract | CrossRef Full Text | Google Scholar

Seybold, H., Rothman, D. H., and Kirchner, J. W. (2017). Climate's Watermark in the Geometry of Stream Networks. Geophys. Res. Lett. 44 (5), 2272–2280. doi:10.1002/2016gl072089

CrossRef Full Text | Google Scholar

Shreve, R. L. (1966). Statistical Law of Stream Numbers. J. Geol. 74 (1), 17–37. doi:10.1086/627137

CrossRef Full Text | Google Scholar

Strahler, A. N. (1952). Hypsometric (Area-altitude) Analysis of Erosional Topography. Geol. Soc. Am. Bull. 63, 1117–1142. doi:10.1130/0016-7606(1952)63[1117:haaoet]2.0.co;2

CrossRef Full Text | Google Scholar

Tokunaga, E. (1978). Consideration on the Composition of Drainage Networks and Their Evolution, Geograph. Rep 13, 1–27.

Google Scholar

Tokunaga, E. (1984). Ordering of divide Segments and Law of divide Segment Numbers. Trans. Jpn. Geomorphol. Union 5 (2), 71–77.

Google Scholar

Tokunaga, E. (1966). The Composition of Drainage Network in Toyohira River basin and Valuation of Horton’s First Law (In Japanese with English Summary). Geophys. Bull. Hokkaido Univ. 15, 1–19.

Google Scholar

Troutman, B. M. (2005). Scaling of Flow Distance in Random Self-Similar Channel Networks. Fractals 13, 265–282. doi:10.1142/S0218348X05002945

CrossRef Full Text | Google Scholar

Veitzer, S. A., and Gupta, V. K. (2000). Random Self-Similar River Networks and Derivations of Generalized Horton Laws in Terms of Statistical Simple Scaling. Water Resour. Res. 36 (4), 1033–1048. doi:10.1029/1999WR900327

CrossRef Full Text | Google Scholar

Veitzer, S. A., and Gupta, V. K. (2001). Statistical Self-Similarity of Width Function Maxima with Implications to Floods. Adv. Water Resour. 24, 955–965. doi:10.1016/S0309-1708(01)00030-6

CrossRef Full Text | Google Scholar

Wang, G. Q., Li, T. J., Zhang, L., et al. (2016). River basin Geometry. Beijing, China: Science Press, 133–138. (in Chinese).

Google Scholar

Wang, P.-J., and Wang, R.-Y. (2002). A Generalized Width Function of Fractal River Network for the Calculation of Hydrologic Responses. Fractals 10 (2), 157–171. doi:10.1142/S0218348X02001038

CrossRef Full Text | Google Scholar

Zanardo, S., Zaliapin, I., and Foufoula-Georgiou, E. (2013). Are American Rivers Tokunaga Self-Similar? New Results on Fluvial Network Topology and its Climatic Dependence. J. Geophys. Res. Earth Surf. 118, 1–18. doi:10.1002/jgrf.2002910.1029/2012jf002392

CrossRef Full Text | Google Scholar

Zhang, L., Dai, B., Wang, G., Li, T., and Wang, H. (2009). The Quantization of River Network Morphology Based on the Tokunaga Network. Sci. China Ser. D-Earth Sci. 52 (11), 1724–1731. doi:10.1007/s11430-009-0176-y

CrossRef Full Text | Google Scholar

Glossary

$\omega$ H-S order [-]

$N_{\omega }$ the number of streams with H-S order $\omega$ [-]

$R_{\text{B}}$ bifurcation ratio (i.e. the ratio of the number of streams [-])

$\left(\omega ,{\omega }^{\prime }\right)$ a stream as a side-branching tributary with H-S order $\omega$ that flows into a stream ordered ${\omega }^{\prime },$ assigned by a Tokunaga order $\left(\omega ,{\omega }^{\prime }\right)$ [-]

$N_{\omega ,{\omega }^{\prime }}$ the number of streams with Tokunaga order $\left(\omega ,{\omega }^{\prime }\right)$ [-]

N Tokunaga stream number matrix composed by $N_{\omega ,{\omega }^{\prime }}$ [-]

$T_{\omega ,\omega +k}$ the ratio of the number of streams with the H-S order $\omega$ that flow into streams with the order $(\omega +k)$ to the number of streams with the H-S order $(\omega +k$) [-]

T Tokunaga side-branching ratio matrix composed by $T_{\omega ,\omega +k}$ [-]

$T_k$ the side-branching ratio [-]

$a$ the average number of streams with the H-S order $\omega$ that flow into streams $\mathrm{ordered}\omega +1$[-]

$c$ the average increasing rate of the side-branching ratio of side tributaries $\mathrm{with\; a\; different\; order}$ [-]

$\lambda , {\lambda }_{\text{o}},{\lambda }_{\text{i}}$ generator, exterior generator, interior generator [-]

$t$ iterative steps [-]

$M_t^{\text{o}},M_t^{\text{i}}$ the number of exterior links and interior links at the $t$th iteration step [-]

$N_{t,(\omega ,{\omega }^{\prime })},N_{t,\omega }$ the number of streams with Tokunaga order $(\omega ,{\omega }^{\text{′}})$ and H-S order $\omega$ at the $t$th $\mathrm{iterative\; step}$ [-]

${\mathit{N}}_{\mathit{t}}$ , ${\mathit{T}}_{\mathit{t}}$ Tokunaga matrix and side-branching ratio matrix of the QU-IBTN, which is $\mathrm{generated\; by\; the\; interior\; generator}{\lambda }_{\text{i}}$ and the exterior generator ${\text{λ}}_{\text{o}}$ at the $t$th step [-]

$\mathit{N}\_{\mathit{R}}_{\mathit{t}}$, $\mathit{N}\_{\mathit{\lambda }}_{\mathit{t}}$ a transformation of ${\mathit{N}}_{\mathit{t}}$; a transformation of $\mathit{N}\_{\mathit{R}}_{\mathit{t}}$ and represents the ${\mathit{\lambda }}_{\mathit{o}}$ $\mathrm{and}{\mathit{\lambda }}_{\mathit{i}}$ values [-]