Inclusive Multiple Model Using Hybrid Artificial Neural Networks for Predicting Evaporation

Predicting evaporation is essential for managing water resources in basins. Improvement of the prediction accuracy is essential to identify adequate inputs on evaporation. In this study, artificial neural network (ANN) is coupled with several evolutionary algorithms, i.e., capuchin search algorithm (CSA), firefly algorithm (FFA), sine cosine algorithm (SCA), and genetic algorithm (GA) for robust training to predict daily evaporation of seven synoptic stations with different climates. The inclusive multiple model (IMM) is then used to predict evaporation based on established hybrid ANN models. The adjusting model parameters of the current study is a major challenge. Also, another challenge is the selection of the best inputs to the models. The IMM model had significantly improved the root mean square error (RMSE) and Nash Sutcliffe efficiency (NSE) values of all the proposed models. The results for all stations indicated that the IMM model and ANN-CSA could outperform other models. The RMSE of the IMM was 18, 21, 22, 30, and 43% lower than those of the ANN-CSA, ANN-SCA, ANN-FFA, ANN-GA, and ANN models in the Sharekord station. The MAE of the IMM was 0.112 mm/day, while it was 0.189 mm/day, 0.267 mm/day, 0.267 mm/day, 0.389 mm/day, 0.456 mm/day, and 0.512 mm/day for the ANN-CSA, ANN-SCA, and ANN-FFA, ANN-GA, and ANN models, respectively, in the Tehran station. The current study proved that the inclusive multiple models based on improved ANN models considering the fuzzy reasoning had the high ability to predict evaporation.

1 Introduction

Evaporation is a crucial parameter in hydrology and water resource management (Adnan et al., 2019). Predicting evaporation is an essential issue for monitoring water resources. In arid regions, evaporation prediction is vital for decision-makers because of water shortage (Malik et al., 2020a; Seifi and Riahi, 2020). Direct and indirect methods are used for predicting evaporation. The stochastic, statistical, and empirical models are considered as indirect methods for predicting evaporation. However, the utilization of instruments for predicting evaporation has some limitations when there is heavy rain or wind speed. The indirect methods use the various climate data so as not to be accessible for modelers (Seifi and Soroush, 2020). The inherent evaporation process is complex and nonlinear. The soft computing models have the high ability for predicting different target variables such as streamflow (Adnan et al., 2021a; Adnan et al., 2021b), rainfall (Adnan et al., 2021c), and evapotranspiration (Alizamir et al., 2020; Malik et al., 2020b).

Machine learning algorithms are recently widely used to predict evaporation. Abghari et al. (2012) used wavelet artificial neural networks (ANN) to predict evaporation in one station in Iran. It was observed that the wavelet as a preprocessing data could improve the standalone ANN model. The main advantage of their study was the hybridization of the ANN model using a wavelet. Their new hybrid ANN (ANN-wavelet) can be used for predicting time series of other hydrological variables.

Tabari et al. (2012) applied an adaptive neuro-fuzzy interface system (ANFIS) and ANN model for predicting evaporation for a semi-region of Iran. It was observed that the ANN model had better accuracy than the ANFIS model. Also, the main contribution of their study was to investigate the effect of different training algorithms on the outputs. The results indicated that the momentum learning algorithm was the best algorithm. The RMSE and MAE of the ANN model were 0.81 mm/day and 0.63 mm/day.

Guven and Kisi (2013) used an ANN, ANFIS, and linear genetic programming for predicting evaporation. The wind speed, relative humidity, solar radiation, and air temperature were used as the models’ inputs. It was observed that linear genetic programming outperformed the ANN and ANFIS model. Also, the main contribution of this study was to investigate the effect of different inputs on the outputs.

Kisi (2013) investigated the accuracy of the evolutionary neural networks (ENN) for predicting evaporation. The accuracy of the ENN was benchmarked against the ANN, fuzzy logic, and ANFIS models. It was observed that the ENN had better accuracy than the other models. The main advantage of this study was developing the ANN models using classical and optimization methods. This study had a comprehensive between the classical training algorithms and optimization algorithms. The mean absolute error of ENN for two stations was 0.749 and 0.759 mm.

Kim et al. (2015) investigated the accuracy of the ANN, genetic programming, and the self-organizing feature maps-neural networks for predicting evaporation. They found that the genetic programming, ANN, and self-organizing feature maps-neural networks outperformed the multiple linear regression models. This study guided the modelers to use genetic programming for predicting time series of different hydrological variables.

Kisi et al. (2016) applied classification and regression tree (CART), ANN, and chi-squared automatic interaction detector (CSIAD) for predicting evaporation. The relative humidity, minimum temperature, maximum temperature, and wind speed were used as the models’ inputs. This study guided the modelers in predicting evaporation in a station using data of neighborhood stations.

Regarding the comparison of the accuracy of the models, the ANN outperformed the regression tree (CART) and chi-squared automatic interaction detector models. Keshtegar et al. (2016) applied a conjugate line search method for predicting evaporation. The results demonstrated that the conjugate line search method performed better than the ANFIS and decision tree model. They developed a conjugate line search method based on mathematical functions with nonlinear forms.

Arunkumar et al. (2017) used ANN, genetic programming, and decision tree models for predicting daily evaporation. The sunshine hours, dew point temperature, relative humidity, maximum temperature, and minimum temperature were used as the inputs to the models. It was observed that the genetic programming outperformed the other models. Wang et al. (2017) evaluated the capability of the least square support vector machine, decision tree model, and fuzzy genetics for predicting evaporation. It was found that the fuzzy genetics and the least square support vector machine outperformed the decision tree model. Ghorbani et al. (2018) coupled the firefly algorithm with the ANN model for predicting evaporation. It was concluded that the ANN- firefly algorithm (FFA) outperformed the standalone MLP and support vector machine models. Their study developed the MLP model using the FFA. The MLP-FFA model converged earlier than the standalone MLP model. The new MLP-FFA was suitable for different simulation problems such as classification problems. The NSE and RMSE of MLP-FFA were 0.92 and 1.406 mm/day.

Sebbar et al. (2019) used an online sequential extreme learning machine (OSELM) and an optimally pruned extreme learning machine (OPELM) for predicting evaporation. They stated that both models had a high ability for predicting evaporation. Keshtegar et al. (2019) coupled the response surface method and the support vector machine (RSM-SVM) for predicting evaporation. It was found that the RSM-SVM outperformed the SVM, ANN, and RSM models for predicting evaporation. Guan et al. (2020) coupled the SVM model with the krill algorithm for predicting evaporation. The results demonstrated that the SVM-krill algorithm improved the accuracy of the standalone SVM models for predicting evaporation. Their study developed the SVM models using a krill optimization algorithm. Their new SVM model was helpful in predicting other hydrological variables.

Although significant improvements and capabilities were found in using machine learning, several challenges are yet to be addressed in future research (Yuan et al., 2018). First, the selection of the best inputs to the models has major complexity. Second, the utilization of preprocessing methods is necessary for finding the best input combination. Furthermore, decreasing computational time and fast convergence are the other challenges of the utilization of machine learning models. The previous studies only determine the best and worst models. Consequently, this paper aims to predict daily evaporation in seven synoptic stations of Iran. To address the above-mentioned challenges in this study, these strategies are suggested by the current paper. First, a new version of the GT is utilized to select the best input for predicting daily evaporation. A robust optimization algorithm, namely, the capuchin search algorithm (CSA), is used to enhance the Gamma test performance based on decreasing time-consuming. Second, as observed in previous articles, the ANN models can predict evaporation, but the powerful optimization algorithms obtain the model parameters. In this study, the CSA as a new optimization algorithm is used to train the ANN models for finding value parameters. The CSA was introduced by Braik et al. (2021). Braik et al. (2021) tested the CSA on complex engineering problems and mathematical functions. The results indicated that the CSA outperformed particle swarm, multiverse optimization algorithm (MVOA), and moth flame optimization algorithm (MFO). Furthermore, in this article, to decrease the computational costs, fuzzy reasoning conception is used to correct the obtained structure of the ANN. Thus, the current study uses this conception for removing redundant weight connections to decrease the computational cost. In this article, an IMM provides synergy among the models to increase the outputs’ accuracy. The novelty of the current research includes introducing a new version of ANN-CSA for predicting evaporation. The new model is benchmarked against the ANN-sine cosine algorithm (ANN-SCA), ANN-firefly algorithm (ANN-FFA), ANN-GA, and ANN models. The aim of the study is to predict daily evaporation in different climates in Iran based on daily data. The new model, ANN-CSA-fuzzy reasoning, is used in no articles, and thus, this new conception can help modelers in the simulation and modeling fields. This study simultaneously improved the accuracy of the ANN models based on powerful optimization algorithms and decreased the computational time based on fuzzy reasoning. Introducing inclusive multiple models is another innovation of the current study. The IMM is used to improve the accuracy of the hybrid ANN-CSA, ANN-SCA, ANN-GA, ANN-FFA, and ANN models. The rest of the paper is arranged as follows. The second section describes the methods and materials. The third section presents the case study. The discussion and results are presented in the fourth section. Finally, the conclusions are presented in the fifth section.

2 Materials and Methods

2.1 Artificial Neural Network

The ANN model acts based on biological neural networks. Easy implementation, generalizability, and nonlinear computation are the advantages of the MLP model (Banadkooki et al., 2020; Seifi et al., 2020). The input, hidden, and output layers are the computational layers of the ANN model (Figure 1). The connection weights connect each layer to the next layer. The nonlinear nature of activation functions of the ANN models helps to train the complex neural networks. The ANN model acts based on the following equation. Eq. 1 uses the bias, weight connections, and inputs to give the final outputs.

$Y=B_0+{\displaystyle {\sum }_{j=1}^{noh}{B}_{j}f\left(w_{oj}+{\displaystyle {\sum }_{i=1}^{nin}{w}_{ij}{x}_i}\right)},(1)$

where $Y$: output, $B_0$: a bias for output layer, $B_j$: a bias for the hidden layer, $w_{ij}$: the weight of i input to j hidden layer neuron, $w_{oj}$: the weight in the output layer connecting the jth neuron in the hidden layer, x_i: input, noh: number of hidden neurons, n (in): number of inputs, and f: activation function. Regarding the successful application of the sigmoid function in the previous articles (Banadkooki et al., 2020; Seifi et al., 2020), the sigmoid function is used as an activation function in this study:

$f\left(y\right)=\frac{1}{1+e^{-y}},(2)$

where f(y): activation function, y: the input to the activation function $\left(w_{oj}+{\displaystyle \sum _{i=1}^{nin}{w}_{ij}{x}_i}\right)$. The backpropagation algorithm is commonly used for training ANN, although it may trap in the local optimums and does not have the fast convergence. At the forward level, the random values of ANN parameters are initialized randomly. Then, the input signal propagated from the input layer to the output layer. Then, the backward level is implemented. In the backward level, the bias and weight are changed so that the error values are minimized. However, the current study uses the new optimization algorithms instead of traditional training algorithms based on their fast convergence. In addition, it uses advanced operators to avoid traps in local optimums and their high accuracy.

FIGURE 1

FIGURE 1. The location of synoptic stations.

2.2 Capuchin Search Algorithm

CSA was inspired by the live capuchins. The alpha male is the leader of capuchins. In some species, the male and female guide other capuchins for finding a food source (Braik et al., 2021). In the first level, the location of capuchins is initialized randomly. The CSA had better performance than the other optimization algorithms in terms of accuracy, convergence, and CPU time. The leaders share their information with followers. It is one of the advantages of CSA. Thus, the quality of solutions can be increased in each iteration.

The initial location of the capuchins is initialized using Eq. 3 (Braik et al., 2021). Eq. 3 is used to determine the initial location of capuchins based on the upper and lower bound of decision variables.

$z_i=u{p}_j+r\times \left(u{p}_j-l{o}_j\right).(3)$

$z_i$: the position of the ith capuchin, $u{p}_j$: the upper bound of the ith capuchin in the jth dimension, $l{o}_j$: the lower bound of the ith capuchin in the jth dimension, and r: a random number. The location of the alpha capuchins in the group is defined as follows (Braik et al., 2021):

$z_j^i=foo{d}_j+\frac{P_{bf}{\left(v{e}_j^i\right)}^2\sin \left(2\theta \right)}{g},0.10\le \epsilon \le 0.20,(4)$

where $z_j^i$: the location of the alpha capuchins in the jth dimension, food _j: the position of food in the jth dimension, $P_{bf}$: the probability of the balance generated by the tail of the capuchins, $g$: the gravitational force, $\epsilon$: a random number $\theta$: the jumping angle: the velocity of the alpha capuchins in the jth dimension. In fact, Eq. 4 updates the location of the alpha capuchins based on the jumping angle and the location of the food source. The parameters of $v{e}_j^i$ and velocity are defined as follows:

$v{e}_j^i=\sigma v_j^i+\kappa a_1\left(z_{bestj}^i-z_j^i\right)r_1+\kappa a_2\left(foo{d}_j-z_j^i\right),(5)$

$\theta =\frac{3}{2}r.(6)$

$v_j^i$: the velocity of the ith alpha capuchin in the jth dimension, $z_{bestj}^i$: the best location of the ith alpha capuchin, r: random number, $a_1$ and $a_2$: constant, $\sigma$ : the inertia coefficient, and $\kappa$ a: lifetime exponential function (Braik et al., 2021).

$\kappa \text{a}=\eta e^{-{\eta }_1\left(\frac{I}{I_{max}}{\left(\right)}^{{\eta }_2}\right)},(7)$

where $I$: iteration number, I_max: maximum number of iterations, $\eta$: constant-coefficient ($\eta$:2), ${\eta }_1$: constant-coefficient (${\eta }_1$:21), and ${\eta }_2$: constant coefficient. Each alpha capuchin uses the leap, climbing, walking, and movement in different directions to update their positions. $\kappa \text{a}$ is an important parameter for balancing between exploitation and exploration.

• Leap and waking mechanism.

A leader capuchin uses leap and walking mechanisms when they cannot find food on the trees. In this condition, they can leap on the ground from one place to another. The location of an alpha capuchin as a leader based on the leap mechanism is updated as follows (Braik et al., 2021).

$z_j^i=F_j+\frac{P_{ef}{P}_{bf}{\left(v_j^i\right)}^2\sin \left(2\theta \right)}{g},0.20\le \epsilon \le 0.30,(8)$

where $P_{ef}$: the elasticity probability of the capuchin movement for jumping from a side of a river to the other side. The elasticity probability helps the CSA to carry out a global search on the ground. Eq. 8 uses the elasticity probability to increase the leaping distance on the ground. When alpha capuchins cannot find food on the tress, their locations are updated as follows:

$z_j^i=z_j^i+v_j^i,\leftarrow 0.30\le \epsilon \le \mathrm{0.50.}(9)$

The advantage of the CSA is to consider the different strategies for updating the location of an alpha male as the best solution in the search space. Thus, the best solution can guide the other followers well based on updating its location using different strategies.

• Swing operation

The swing operation is another ability of alpha capuchins for finding food. Thus, the location of alpha capuchins is updated based on the swing motion as follows, as stated by (Braik et al., 2021):

$x_j^i=F_j+\kappa P_{bf}\times \sin \left(2\theta \right),0.5<\epsilon \le 0.75,(10)$

where $x_j^i$: new location of alpha capuchin.

The alpha capuchins may climb the other trees to find food. Thus, the location of the alpha capuchins can be updated based on the climbing operator (Braik et al., 2021).

$z_j^i=foo{d}_j+\kappa P_{bf}\left(v_j^i-v_j^{i-1}\right),0.75\le \epsilon \le 1.0,(11)$

where $v_j^i$: the current velocity of the ith capuchin, and $v_j^{i-1}$: the previous.

• Movement in the different directions

The last effort of alpha capuchins for finding food is movement in several new directions in order to find a better food source. Thus, this potential allows the alpha capuchin to search the problem space accurately (Braik et al., 2021).

$x_j^i=\kappa \text{a}\times \left(l{o}_j+\epsilon \times \left(u{p}_j-l{o}_j\right)\right).(12)$

Eq. 12 is useful to search the search space for finding better solutions entirely.

Finally, the followers update their position as follows:

$x_j^i=\frac{1}{2}\left(x_{\alpha j}^i+x_j^{i-1}\right),(13)$

where $x_j^i$: the current position of followers in the jth dimension, $x_j^{i-1}$: the previous location of the followers in the jth dimension, and $x_{\alpha j}^i$: the location of the alpha leader. Figure A1 in the Supplementary Appendix shows the CSA flowchart.

2.3 Sine Cosine Algorithm

The SCA is one of the powerful algorithms that is used for solving various optimization problems such as feature selection (Neggaz et al., 2020), global optimization (Gupta et al., 2020), optimal operation of hydropower systems (Feng et al., 2020), image segmentation (Ewees et al., 2020), and engineering design problems (Rizk-Allah, 2018). The excellent balance between exploration and exploitation and easy implementation are the advantages of the SCA. Mirjalili (2016) introduced the SCA based on the characteristics of the trigonometric functions sine and cosine. First, the initial solutions are randomly initialized. In the SCA, the location of each solution is changed based on the sine and cosine functions. The location of solutions is changed as follows (Mirjalili et al., 2020).

$S_{i,j}^{t+1}=S_{i,j}^t+r_1\times \sin \left(r_2\right)\times \left|r_3{S}_{bes{t}_j}^t-S_{ij}^t\right|\leftarrow if\left(r_4\right)<0.5,(14)$

$S_{i,j}^{t+1}=S_{i,j}^t+r_1\times \cos \left(r_2\right)\times \left|r_3{S}_{bes{t}_j}^t-S_{ij}^t\right|\leftarrow if\left(r_4\right)\ge 0.5,(15)$

where $S_{i,j}^{t+1}$: the ith solution in the jth dimension at iteration t, $S_{bes{t}_j}^t$: the best solution, r₁, r₂, r₃, and r₄: random parameters. The r₁ is updated as follows:

$r_1=2-2\times \frac{t}{T},(16)$

where t: number of iterations, and T: maximum number of iterations. The r₁ parameter is an important parameter for determining the area of the nest solution. The direction of the movement of the solution is determined based on parameter r₂. The parameter r₃ is an important parameter for emphasizing or deemphasizing the influence of the target in the determining distance. The r₄ parameter is used for switching between the sine and cosine functions to update the location of solutions. Figure A2 in the Supplementary Appendix shows the SCA flowchart.

2.4 Firefly Algorithm

The FFA is a robust optimization algorithm for solving various problems such as global optimization problems (Wu J. et al. (2020)), training ANN (Bui et al., 2020), matching biomedical (Xue, 2020), fuzzy clustering (Langari et al., 2020), and the vehicle routing problem (Trachanatzi et al., 2020). The FFA acts based on different assumptions. The brighter firefly can attract other fireflies. The objective function of the firefly shows the brightness of the firefly. A firefly with a better objective function has more brightness. Each firefly has a special attractiveness, so that the attractiveness should be determined in each iteration. The increasing distance of fireflies from other fireflies can decrease their attractiveness for other fireflies. To update the location of fireflies, the previous location of fireflies, the attractiveness, and the distance. First, the random parameters of FFA are initialized. Then, the initial location of fireflies is initialized. The location of the firefly is changed as follows:

$l{o}_i^{\prime }=l{o}_i+{\beta }_o{e}^{-\gamma m}\left(l{o}_i-l{o}_j\right)+\alpha \zeta ,(17)$

$r_{ij}=\sqrt{{{\displaystyle {\sum }_{k=1}^D\left(l{o}_{ik}-l{o}_{jk}\right)}}^2},(18)$

where $l{o}^{\prime }$: the new location of the ith firefly, $l{o}_i$: the location of the ith firefly, ${\beta }_o$: initial attractiveness, $\zeta$: random parameter, $\alpha$: scaling factor, $l{o}_{ik}$: the k element in the location of firefly i, $l{o}_{jk}$: the k element in the location of firefly j, D: number of dimensions, $l{o}_j$: the location of the jth firefly, $r_{ij}$: the distance between firefly i and j. To move a firefly toward another firefly, it is essential to compute the light intensity:

$I=I_0.e^{\gamma r^2},(19)$

where $I$: light intensity, $I_0$: initial light intensity, and $\gamma$: absorption coefficient. Figure A3 in in the Supplementary Appendix shows the FFA flowchart.

2.5 Genetic Algorithm

The GA is one of the optimization algorithms that is widely used for optimizing different problems such as training machine learning algorithms (Park et al., 2020), optimal design of the building environment (Zhang T. et al., 2020), optimization of the culture condition (Zhang Q. et al., 2020), optimizing bank lending decisions (Metawa et al., 2017), and face recognition (Zhi and Liu, 2019). The GA has consisted of the population of chromosomes that gradually mature during the optimization process to converge to an optimal solution. Three operators, namely, reproduction, crossover, and mutation, are used in the GA. The GA uses a reproduction operator for choosing the best chromosome regarding its fitness value. The crossover operator combines the particular parts of the individuals (parent) to provide new solutions. To provide a random change in the elements (allele) of a chromosome, a mutation operator is used to increase the population’s diversity.

2.6 Fuzzy Reasoning

To decrease the computational time, fuzzy reasoning is used to correct the structure of the obtained hybrid and standalone ANN models. When the structure of the ANN is too big, the computational time increases. An excessive number of weights with low values is considered redundant connections. The fuzzy reasoning tries to identify the hidden units with no activity based on finding weak weight conception (Melo and Watada, 2016). The current study uses a fuzzy IF-THEN rule to decrease the number of weak weights in the ANN model’s structures. A fuzzy IF-THEN rule is used to reduce redundant weights. If the number of hidden neurons is too big, the generalization is weak. If the number of hidden neurons in the hidden layer is small, learning is consequently poor (Melo and Watada, 2016). Structural learning is a strategy to decrease the computational time and improve the difficulty of specifying the ANN structure. The aim of this strategy is to remove hidden neurons with no activity. The hidden neurons with no activity do not affect decreasing error function in the structure of the ANN model. Three rules were used for the fuzzy reasoning. The learning cycle, RMSE rule, and weight rule are three rules for fuzzy reasoning. In structural learning, the unnecessary weights with low values were eliminated based on the goodness factor. The summation of all the forward propagated signals to the last layer is known as the goodness factor. The goodness factor is computed based on the following equation. The units with the least activity or the weights with the low values in the hidden layers are identified using the goodness factor.

$g_i^k={\displaystyle \sum _j{\left(w_{i,j}^k,o_i^k\right)}^2},(20)$

where $g_i^k$: goodness factor, $o_i^k$ is the i output from the k layer, and $w_{i,j}^k$ is the weighted link. The choice of redundant weights is carried out after the learning in all patterns is performed. For better performance, the fuzzy interface that targets the weight that leads to the defective unit is utilized. A threshold is defined in the next level for the RMSE rule as the second rule. If the RMSE has slight changes after removing weights, these weights are considered redundant. Thus, if the goodness factor identifies to remove some weights, the RMSE should be checked as the second conditional rule. If these two rules are satisfied, the values of weights also should be checked so that the weights with the low values are removable. The learning cycle is used as a rule because the weights are initialized with the low values in the initial stages, and thus, they are susceptible to elimination. The learning cycle rule prevents removing weight with low values in the initial levels of the simulations. The RMSE criterion is used as the second rule. If there is not a decrease in RMSE, it is regarded that the weight has no effect on the prediction error, and thus this weight is redundant. In fact, the weights with no effectiveness do not change the RMSE value, and they are considered redundant weights. However, the learning cycle and RMSE membership functions (MFs) are not sensitive to data complexity and noise in training ANN. Thus, the weight-rule as the third rule is used to decrease redundant weights. The number of learning means the number of epochs. One epoch means that each sample in the training data has had an opportunity to change the internal model parameters. The goodness factor is used to assess the effect of each hidden unit in the hidden layer. The high value of goodness factor provides a large effect on the whole units of level k + 1 from the unit. The unit with the lowest goodness factor is considered the most inactive unit in the layer. The unit is defective if the goodness factor <0.99. Thus, the goodness factor <0.99 is a threshold for removing weight. This goodness factor is helpful to identify the weak weight in inactive units. The modelers use membership functions of three rules for removing weak weight. The minimum operator is used by the fuzzy interface system to choose the minimum value for each of the 3 MFs. The obtained membership function values for the learning cycle should be subtracted from 1. The minimum value from the MFs is chosen in the next level, and it is multiplied by the value of the weight to be removed. If the outcome is 0, the weight is removed. When the weak weight is disregarded in the ANN model, the connection weights associated with the weak weight (connections between two nodes) also are removed.

The monotonically decreasing sigmoid for the weight and RMSE is used as follows:

$S\left(x,\alpha ,\beta ,\gamma \right)=\left[\begin{array}{l}0\leftarrow x<\alpha \\ 2^{\frac{{\left(x-\alpha \right)}^2}{{\left(\gamma -\alpha \right)}^2}}\leftarrow \alpha \le x<\beta \\ 1-2^{\frac{{\left(x-\alpha \right)}^2}{{\left(\gamma -\alpha \right)}^2}}\leftarrow \beta \le x<\gamma \\ 1\leftarrow x>\omega \end{array}\right].(21)$

The monotonically increasing sigmoid for the learning cycle is used as follows.

$S\left(x,\alpha ,\beta ,\gamma \right)=\left[\begin{array}{cc}0\leftarrow x<\alpha & 337\\ \begin{array}{l}{2}^{\frac{{\left(x-\alpha \right)}^2}{{\left(\gamma -\alpha \right)}^2}}\leftarrow \alpha \le x<\beta \\ 1-2^{\frac{{\left(x-\alpha \right)}^2}{{\left(\gamma -\alpha \right)}^2}}\leftarrow \beta \le x<\gamma \\ 0\leftarrow x>\gamma \end{array}& \begin{array}{l}338\\ 339\end{array}\end{array}\right],(22)$

where $\gamma$, $\alpha$, $\beta$, and $\omega$:the parameters of membership functions.

2.7 Hybridizing ANN Based on Optimization Algorithms and Fuzzy Reasoning

The weight and bias of the ANN models are the unknown values that are obtained by the training process. To find the ANN parameters (weight and bias) using optimization algorithms based on fuzzy reasoning, the following levels are performed. 1) To prepare input data and divide data into the training and testing data. 2) Run the ANN model based on training data at the training level. The initial guess for the weight and bias is used. 3) The training accuracy is estimated. In this study, the root mean square error (RMSE) as a common criterion is used to assess the models’ accuracy at the training level. 4) If the value of RMSE is low, the weak weight can be removed by fuzzy reasoning. 5) When the low weights are removed in Section 4, the RMSE is rechecked. If its value is decreased, the performance of fuzzy reasoning is stopped. The elimination of weights was stopped because the weak weights were removed in the previous levels, and the elimination of the remaining weight connections changed the RMSE. In fact, the remaining weights were the effective weights in the structure of the ANN model. 6) If the convergence is met, the testing level is performed; otherwise, the optimization algorithms link to the ANN. 7) The weight and bias are considered as the decision variables in the optimization algorithms. The location of agents in the algorithms is encoded to represent the value of weight and bias. 8) The fitness of each agent is calculated for each solution to obtain the quality of solutions. 9) The operators of the algorithms are used to change the location of agents. It means that the value of weight and bias is updated. 10) If the convergence creation is satisfied, the weight and bias values are inserted into the ANN to rerun it; otherwise, go to Step 6.

3 Case Study

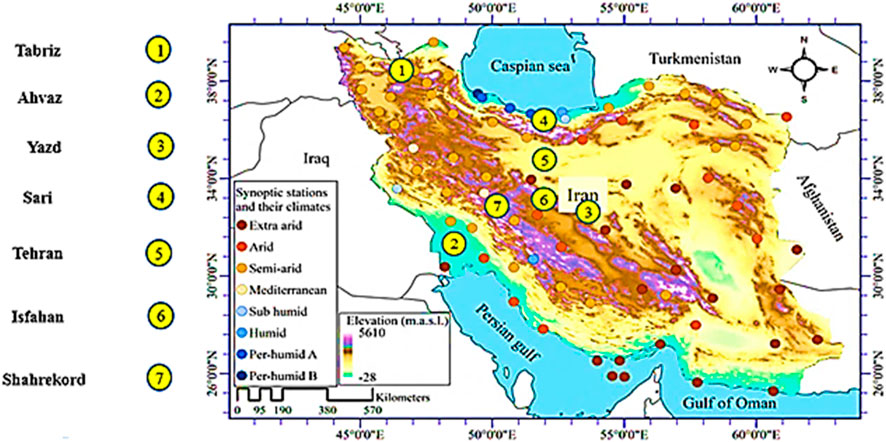
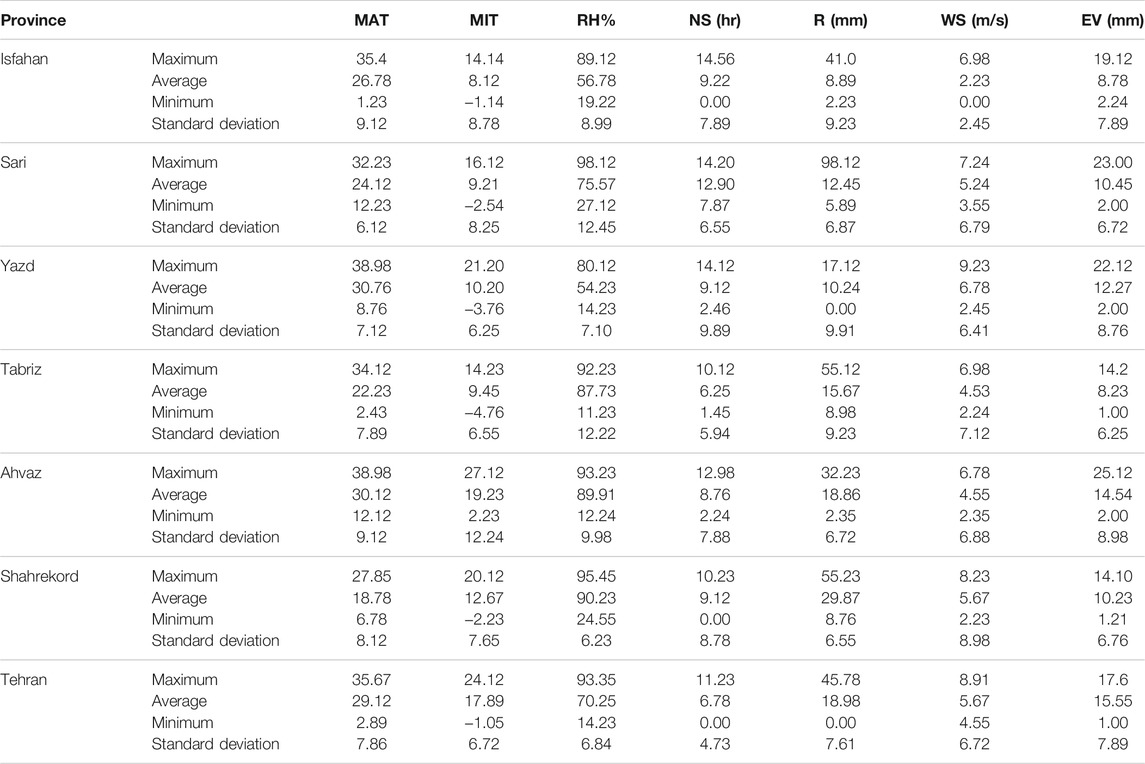
Iran is in an arid and semi-arid climate. Significant climate anomalies are observed in Iran. Many drought events are observed in the different cities of Iran. Also, water shortage is a primary challenge in Iran. Figure 1 shows the location of the stations. In this study, the standalone and hybrid ANN models were used to predict seven provinces of Iran’s daily evaporation with different climates. As observed in Table 1, the relative humidity (RH), wind speed (WS), number of sunny hours (NS), maximum temperature (MAT), minimum temperature (MIT), and rainfall (R) were used as the inputs to the models. Thus, it is necessary to use a preprocessing method for selecting the best input scenario. In this study, an improved Gamma method is applied to select the best input combination. The data were collected from seven synoptic stations (Tabriz, Tehran, Sari, Yazd, Ahvaz, Sharekord, and Isfahan) of Iran from 2011 to 2014 (1,080 days). Figure 1 shows the evaporation time series. Since Iran faces a drought period, evaporation prediction is an important duty for decision-makers. However, the modelers can test the models of the current study in the different regions of the world.

TABLE 1

TABLE 1. The characteristics of data.

3.1 Improved Gamma Test

The GT is a powerful tool for identifying the best input scenarios that are applied in various fields, such as determining the inputs for predicting groundwater (Azadi et al., 2020), determining the inputs for modeling evaporation (Malik et al., 2020a), input selection for predicting solar radiation (Biazar et al., 2020), and selection of the best inputs for evapotranspiration (Seifi and Riahi, 2020). Assume a set of data based on the following equation:

$\left\{\left(b_i,c_i\right),1\le i\le M\right\},(23)$

where $b_i\in R^m$: the input vectors are confined to some closed bounded, $c_i$: the output vectors are confined to some closed bounded, M: the total number of observations. The only hypothesis made is that the underlying relationship of the system is as follows:

$c=f\left(b_1,\dots ,b_m\right)+r.(24)$

where f: smooth function, and r: random variable. The smooth data model cannot calculate the Gamma statistic ($\Gamma$). The gamma test acts based on the $V\left[i,k\right]$ that is the kth nearest neighbors $b_N\left[i,k\right]$. The delta function is used to derive the gamma test as follows:

${\delta }_M\left(k\right)=\frac{1}{M}{\displaystyle {\sum }_{i=1}^M\left|b_{N\left(i,k\right)}-b_i\right|},(25)$

where $\left|\mathrm{...}\right|$: Euclidean distance. The gamma function of the outputs is computed as follows:

${\gamma }_M\left(k\right)=\frac{1}{M}{{\displaystyle \sum }}_{i=1}^M\left|c_{N\left(i,k\right)}-c_i\right|,(26)$

where ${\gamma }_M\left(k\right)$: corresponding c value of the kth nearest neighbor of bi. The unvaried linear regression was used to compute the Gamma statistic $\left(\tau \right)$ as follows:

$\gamma =A\delta +\Gamma ,(27)$

where A and $\Gamma$: the gradient and intercept of the regression line ($\delta$ = 0). The lowest value $\Gamma$ shows the best input combination. Another index in the gamma test is the $V_{ratio}$ that is computed as follows:

$V_{ratio}=\frac{\Gamma }{{\sigma }^2\left(y\right)},(28)$

where ${\sigma }^2\left(y\right)$: the variance of output. The lowest value $V_{ratio}$ shows the best input combination. Regarding six inputs, 2⁶–1 input combinations can be provided, and thus, it is challenging to compute the $V_{ratio}$ and $\Gamma$ for each input combination. The new hybrid gamma test was utilized in the current study to decrease the time-consuming and challenging. In this study, CSA was hybridized with the gamma test to improve the gamma test’s ability. First, the name of input variables is regarded as the decision variables. The CSA provided a random input combination as the candidate solutions. Then, the $\Gamma$ is calculated for each input scenario. The computations finish when the stop criterion is satisfied. If the hybrid gamma test was not used, it is difficult to compute $V_{ratio}$ and $\Gamma$ for each input combination. Also, the hybrid gamma test can be useful for the next studies when the modelers encounter more input data. The hybrid gamma test can automatically give the best input combination. Also, Table A1 of the Supplementary Appendix shows the correlation values of inputs with evaporation.

3.2 Avoid Overfitting in ANN Models

Liu et al. (2008) proposed a method that was different from other modes for preventing overfitting. Their method was named the optimization approximation algorithm (OAA). The method can prevent overfitting without the use of a validation set or any disturbance to the observed data. The value of easily computable relation coefficient called signal-to-noise-ratio-figure (SNRF) and threshold signal-to-noise-ratio-figure was used to reach the stop criterion. The SNRF was computed based on modeling errors at each iteration and the sample size was used to obtain the threshold SNRF (SNRF_N). Liu et al. (2008) assumed that the data included the noise (NO_i) and signal (SI_i) components. Thus, the energy error in Eq. 29 was computed based on the noise and signal components. The error signal was computed based on summing NO_i with SI_i. The energy error was computed as follows (Liu et al., 2008).

$E\left(SI+NO\right)=C\left(e_i,e_i\right){\displaystyle {\sum }_{i=1}^n{e}_i^2},(29)$

where $e_i$: the error signal for ith case and $C\left(e_i,e_i\right)$: the auto correlations function.

It should be considered that there is a high correlation between the signal in the neighboring samples while there is not a high correlation between the noise in the neighboring cases so one may write [40]:

$C\left(S{I}_i,S{I}_i\right)\simeq C\left(S{I}_i,S{I}_{i-1}\right),(30)$

$C\left(N{O}_i,N{O}_i\right)=0,(31)$

where C: correlation, NO_i: ith noise, S_i: ith signal, and S_i-1: i-1 th signal.

Each sample has two neighbors. Afterward, the signal energy is computed as follows.

${\displaystyle {\sum }_{i=1}^n{e}_i{e}_{i-1}}=C\left(e_i,e_{i-1}\right)=C\left(S_i,S_{i-1}\right)=E\left(S\right).(32)$

Then, the noise energy is computed as follows:

$E\left(n\right)=E\left(n+s\right)-E\left(s\right).(33)$

Finally, the SNRF is computed as follows:

$\text{SNRF}=\frac{\text{E}\left(\text{S}\right)}{\text{E}\left(\text{NO}\right)}=\frac{{\displaystyle {\sum }_{\text{i}=1}^{\text{N}}{\text{e}}_{\text{i}}{\text{e}}_{\text{i}-1}}}{{\displaystyle {\sum }_{\text{i}=1}^{\text{N}}{\text{e}}_{\text{i}}^2}-{\displaystyle {\sum }_{\text{i}=1}^{\text{N}}{\text{e}}_{\text{i}}{\text{e}}_{\text{i}-1}}}.(34)$

Liu et al. (2008) stated that the training terminated when the SNRF reached SNRF_N. The SNRF_N was computed as follows:

${\text{SNRF}}_{\text{N}}\simeq \frac{1.7}{\text{N}}.(35)$

Hence, the process should be continued until SNRF < SNRF_N or the maximum number of function calls is reached.

3.3 Choice of Data Set for Training and Testing Level

One of the effective methods for choosing a representative subset with size P from the original database of size N is the subset selection of maximum dissimilarity. The reliable data set for training level and testing level were obtained based on SSMD (Riahi-Madvar et al., 2021). The main benefit of the SSMD is the chosen data not to focus on a specified area. Assume that Z is the data set as Z= (z₁, z₂,…,z_n), a set of v = 1, 2, … , P points regarded as the applications for training. If DIS_ij² is regarded as the distance between the ith and jth point and k points have been chosen (k < n), the minimum distance from the applicant point P to k points is defined as follows:

${\text{Dis}}_{\text{ij}}^2={\Vert {\text{x}}_{\text{j}}-{\text{x}}_{\text{i}}\Vert }^2={\displaystyle {\sum }_{\text{k}=1}^{\text{n}}{\left({\text{z}}_{\text{ki}}-{\text{z}}_{\text{kj}}\right)}^2}.(36)$

${\text{Δ}}_{\text{i}}^2\left(\text{k}\right)=\min \left({\text{Dis}}_{1\text{i}}^2,{\text{Dis}}_{2\text{i}}^2,\mathrm{..},{\text{Dis}}_{\text{ki}}^2\right).(37)$

The (k+1)th candidate point in the training data was chosen from the remaining (P-k).

${\text{Δ}}_{\text{k}+1}^2=\max \left({\text{Δ}}_{\text{i}}^2\left(\text{k}\right)\right),\text{i}\ne \text{m}\text{.}(38)$

The SSMD is performed based on the following levels (Memarzadeh et al., 2020). 1) The datasets are normalized. 2) The first point of data from the Z dataset is chosen near the mean of the data set. 3) The second point of the data set with the large distance with the first data set is chosen. 4) The third point is chosen at the farthest distance from the previous two points. 5) The selected points are regarded as the training data set. The remaining ones are regarded as the testing data set. A total of 70% of data and 30% of data were chosen for training and testing levels.

3.4 Inclusive Multiple Model

The previous articles use individual models for predicting evaporation. The worst and the best models for predicting hydrological variables were determined. In this article, an IMM model was used to provide synergy among hybrid and standalone ANN models. The inclusive multiple model (IMM) uses the outputs of the ANN-CSA, ANN-FFA, ANN-SCA, ANN-GA, and ANN models to increase the outputs’ precision based on utilizing the benefits of different models. The outputs were obtained in the first level by the ANN-CSA, ANN-FFA, ANN-SCA, ANN-GA, and ANN models. Then, the outputs of the hybrid and standalone ANN models were used as the input to another ANN model. In fact, the models’ outputs in the first level are considered lower-order modeling results. In this study, the following indexes were used to compare the models:

• Root mean square error (ideal values are close to zero)

$\text{RMSE}=\sqrt{\frac{1}{\text{m}}{\displaystyle {\sum }_{\text{i}=1}^{\text{m}}{\left({\text{EV}}_{\text{es}}-{\text{EV}}_{\text{ob}}\right)}^2}}.(39)$

The scatter index (SI < 0.10: good performance, SI:0.10 < SI < 0.20: fair performance, and SI > 0.30: poor performance) (Li et al., 2013).

$\text{SI}=\frac{\text{RMSE}}{\text{E}{\overline{\text{V}}}_{\text{ob}}}.(40)$

Mean absolute error (MAE):

$\text{MAE}=\frac{1}{\text{m}}{{\displaystyle \sum }}_{\text{i}=1}^{\text{m}}\left|{\text{EV}}_{\text{es}}-{\text{EV}}_{\text{ob}}\right|.(41)$

Nash Sutcliffe efficiency (NSE) (The closest values to 1 are ideal).

$\text{NSE}=1-\frac{{{\displaystyle \sum }}_{\text{i}=1}^{\text{m}}{\left({\text{EV}}_{\text{es}}-{\text{EV}}_{\text{ob}}\right)}^2}{{{\displaystyle \sum }}_{\text{i}=1}^{\text{m}}{\left({\text{EV}}_{\text{OB}}-\text{E}{\overline{\text{V}}}_{\text{ob}}\right)}^2}.(42)$

• R² (coefficient of determination)

${\text{R}}^2=\left(\frac{{{\displaystyle \sum }}_{\text{i}=1}^{\text{m}}\left({\text{EV}}_{\text{ob}}-\text{E}{\overline{\text{V}}}_{\text{ob}}\right)\left({\text{EV}}_{\text{es}}-\text{E}{\overline{\text{V}}}_{\text{es}}\right)}{\sqrt{\left[{{\displaystyle \sum }}_{\text{i}=1}^{\text{m}}{\left({\text{EV}}_{\text{ob}}-\text{E}{\overline{\text{V}}}_{\text{ob}}\right)}^2\right]}\left[{{\displaystyle \sum }}_{\text{i}=1}^{\text{m}}{\left({\text{EV}}_{\text{es}}-\text{E}{\overline{\text{V}}}_{\text{es}}\right)}^2\right]}\right),(43)$

where SD: Standard deviation, m: number of data, ${\text{EV}}_{\text{ob}}$: observed CO₂, $\text{E}\overline{\text{V}}$: average observed data, and ${\text{EV}}_{\text{es}}$: estimated data.

Centered root mean square error (CRMSE):

$CRMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^N\left(E{V}_{iobs}-E{\overline{\mathit{V}}}_{iobs}\right)-\left(E{V}_{ies}-E{\overline{\mathit{V}}}_{ies}\right)}}{N}},(44)$

where $E{\overline{V}}_{iobs}$: avenge observed data, and $E{\overline{\mathit{V}}}_{ies}$: avenge estimated data.

4 Discussion

4.1 Finding Random Parameters of the Algorithms

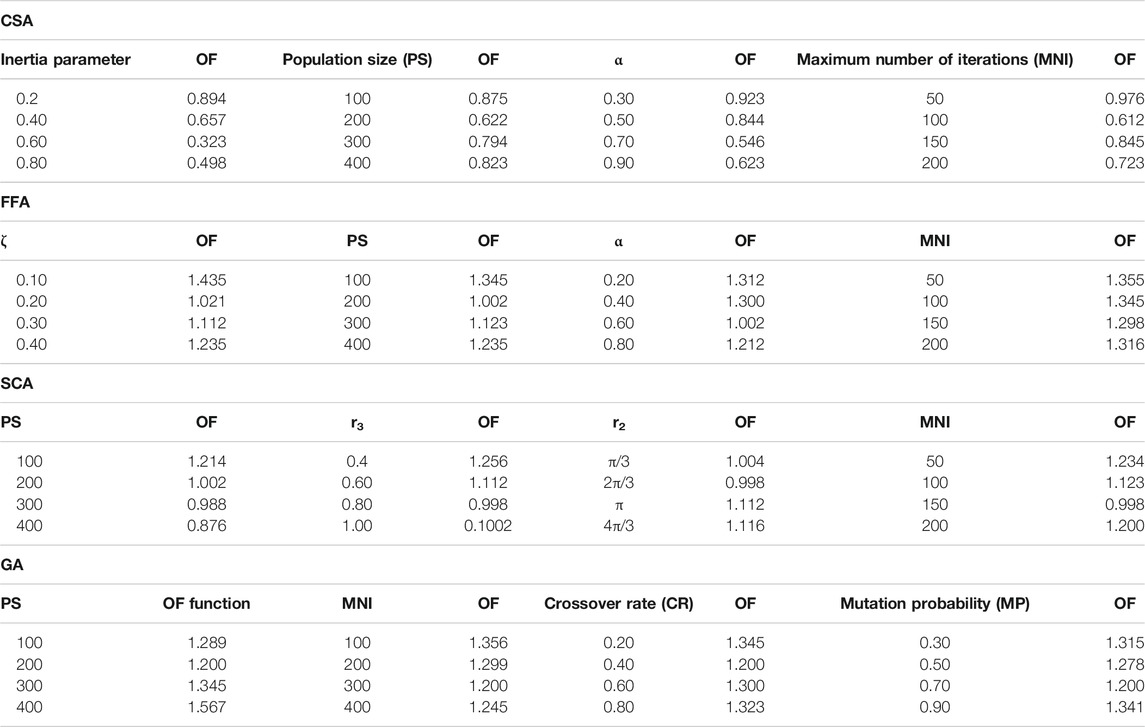
The random parameters affect the accuracy of the algorithms. A sensitivity analysis (SA) helps modelers find the optimal values of random parameters. An SA can be used to compute the objective function’s variation by changing the value of random parameters. In fact, SA shows how the variations of the value of random parameters affect the objective function (OF) value. As the RMSE is an OF in this study, random parameters’ best values minimize RMSE. To find the best value of random parameters, the Ahvaz station is chosen as a sample. The population size (PS) of CSA varied from 100 to 400 in Table 2, and the OF varied from 0.875 to 0.823. The least value of OF occurred at the population size = 200. Thus, the best size of the population was 200. The inertia parameter varied from 0.20 to 0.80, and the least value of the OF occurred at inertia parameter = 0.60. As observed in Table 2, the best value of the mutation probability and the maximum number of iterations (MNO) were 0.70 and 300, respectively.

TABLE 2

TABLE 2. Sensitivity analysis for random parameters of optimization algorithms in Ahvaz station.

As observed in Table 2, parameters of optimization algorithms were obtained based on the sensitivity analysis of Table 2. The number of hidden layers in the ANN models was obtained based on Eq. 45:

$N_h=\sqrt{N_{in}+N_{out}}+\alpha ,(45)$

where $N_h$: number of hidden layers, $N_{in}$: number of inputs, and $\alpha$: a value between 0 and 10. To obtain the optimal value of the number of hidden layers and hidden neurons, the OF variation vs. the number of hidden layers and neurons was computed. The learning coefficient and momentum coefficient were 0.01 and 0.001. The values of momentum and learning coefficient were changed to achieve the least value of an OF. Table A2 in the Supplementary Appendix shows the details of the computations.

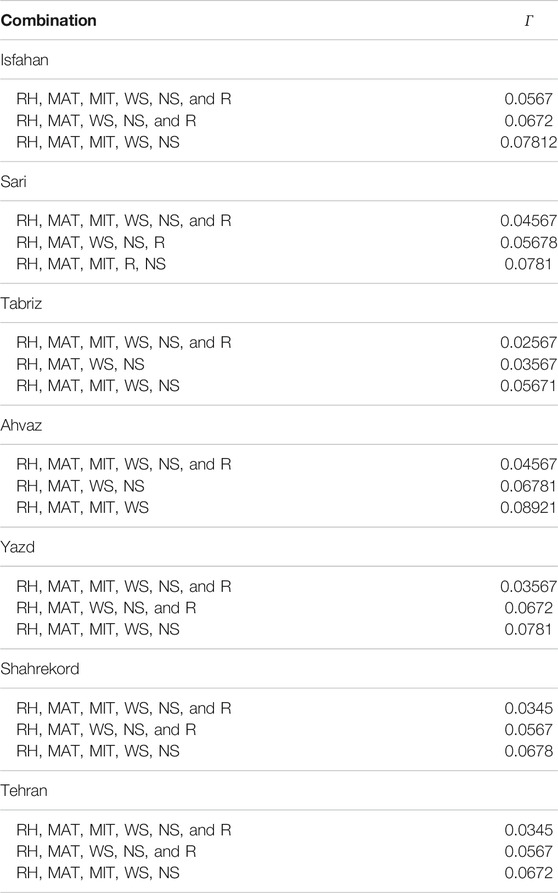
4.2 Choice of the Best Input Combinations

Table 3 indicates the first-best input scenario to the third-best input scenario for all stations. As observed in Table 4, MAT, MIT, RH, WS, NS, R, and RH were the best input scenarios for all stations because they had the least values of $\mathit{\Gamma }$. For example, the $\Gamma$ of MAT, MIT, RH, WS, NS, R, and RH as the best input combination in Isfahan was 0.0567 while it was 0.0672 and 0.07812 for the (RH, MAT, WS, NS, and R) and (RH, MAT, MIT, WS, and NS) as the second best and the third best input combination. Thus, the combination of MAT, MIT, RH, WS, NS, and R was used as the best input combination to the models for all stations.

TABLE 3

TABLE 3. The optimum input variations for various scenarios.

TABLE 4

TABLE 4. Statistical results for different models based on error indexes.

This study used the hybrid gamma test to choose the best input combination because the authors face 2⁶–1 input combinations. The results indicated that using all input variables provided the best performance. However, it does not mean that the modelers need six input variables to predict evaporation in the next case studies or other research. This study only encourages the modelers to use advanced methods such as the hybrid gamma test for selecting the best input combination. The utilization of the hybrid gamma test is not limited to the number of input variables. The researchers of the current study accessed six input variables, but the other researchers can predict the evaporation with any number of inputs. The reasons for the use of the hybrid gamma test are as follows: 1) Before the modelers used the hybrid gamma test, it was unclear that using all input variables provided the highest accuracy. However, the previous researchers also proved that using all input variables cannot always give the highest accuracy. Qasem et al. (2019) accessed four input variables for predicting evaporation, but the best input combination included three input variables. They indicated that it is not obvious having all input variables to make better predictions. This issue should be checked. The increasing number of inputs cannot always increase the accuracy. When the modelers did not use the advanced methods for choosing the best input combination, the different input scenarios should be defined for predicting evaporation. This issue leads to increasing time. As Qasem et al. (2019) did not choose the best input combination using an advanced test, they represented seven input scenarios. When the modelers define input scenarios, these scenarios may not cover the best input scenario. For these reasons, the authors need to use the advanced gamma test. 2) the researchers can use a hybrid gamma test with any number of input variables. The aim of the method is not to say that the modelers always need all inputs for predicting evaporation. The study aims to encourage the modelers to use advanced methods for choosing the best input combination. For example, suppose the modelers access three input variables. In that case, the modelers can investigate the effect of each input on the outputs based on removing each variable input from the initial input combination one by one. However, this method is not suitable when the modelers face a large number of input data. If the modelers use the hybrid gamma test, the gamma test automatically gives the best input combination without requiring additional efforts to compute $\Gamma$ and $V_{ratio}$ for 2³–1 input scenario. 3) If the correlation coefficient between the inputs and outputs is used, the researchers only can identify the most effective inputs. Afterward, they must manually provide the different input scenarios. Thus, the gamma test can be a good alternative to correlation because the hybrid method automatically gives the best input combination without requiring defining 2⁶–1 input combinations.

4.3 Analysis of Results for Different Stations

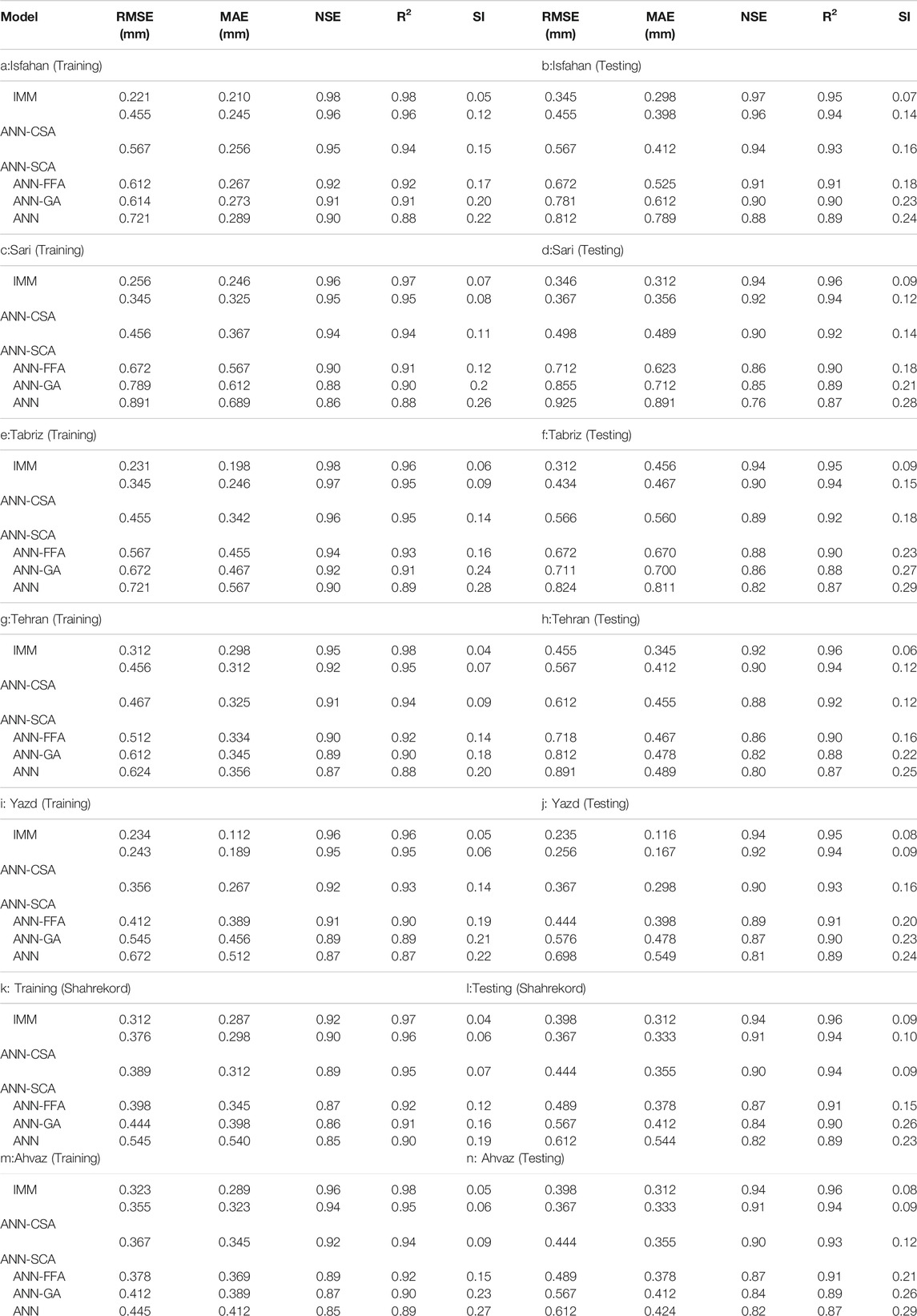
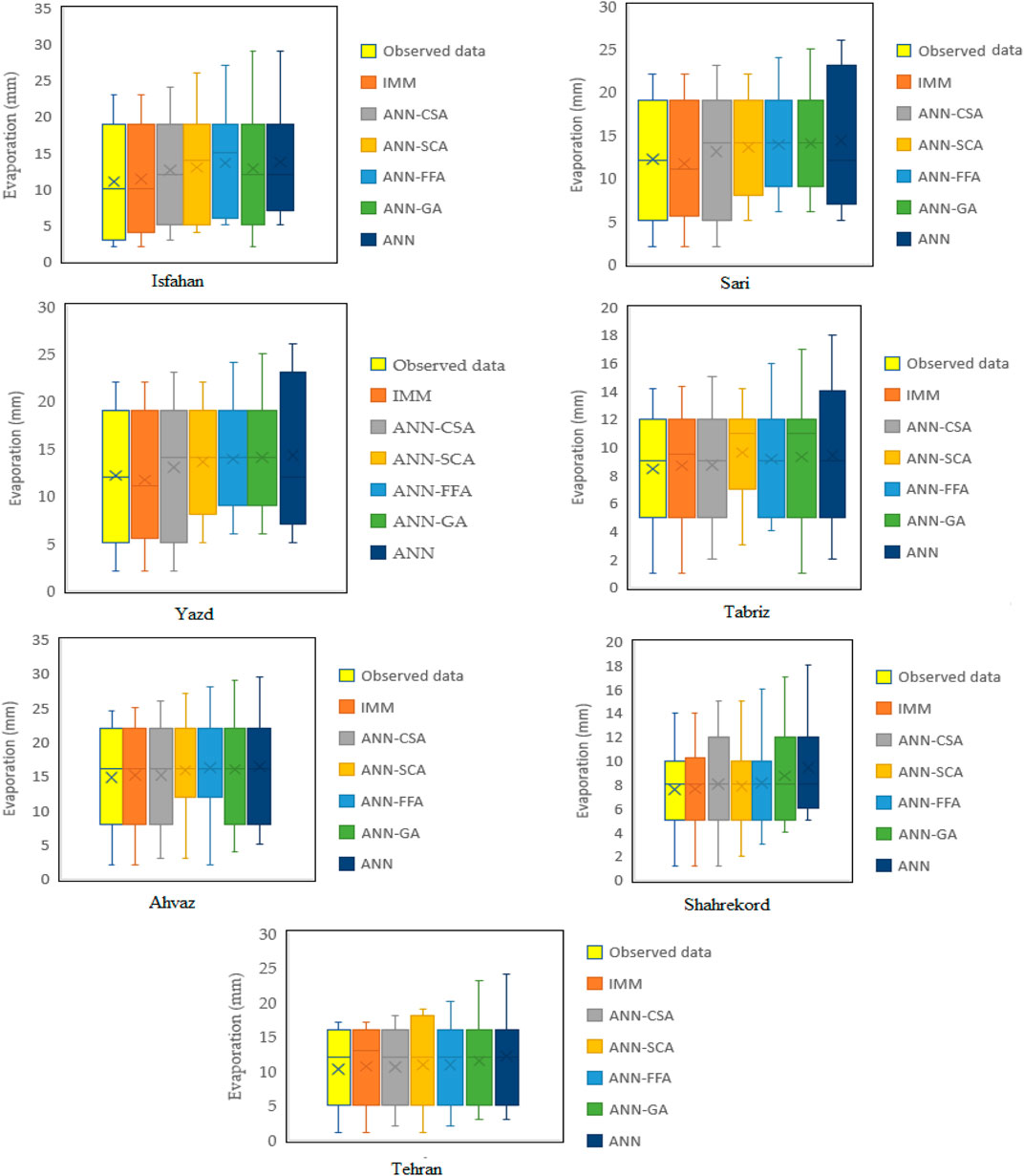
Table 4 shows the performance of different models in the different stations. Table 4A shows the results in the training level in the Isfahan station. The R² of the ANN-CSA was 0.92 in the Isfahan station, but it was 0.90, 0.88, 0.85, and 0.82 for the ANN-SCA, ANN-FFA, ANN-GA, and ANN models. The IMM decreased the MAE of the ANN-CSA, ANN-SCA, and ANN-FFA, ANN-GA, and ANN model by 14, 18, 22, 24, and 28%, respectively. The ANN model obtained the lowest NSE and R². The results also indicated that the ANN-CSA had higher NSE and R² compared to the ANN-SCA, ANN-GA, ANN-FFA, and ANN models. Table 4B shows the performance of models in the testing level for the Isfahan station. The IMM improved the RMSE values of the ANN-CSA, ANN-SCA, ANN-FFA, ANN-GA, and ANN model by 25, 40, 48, 56, and 57%, respectively. Table 4C shows the results for the Sari station at the training level. The RMSE of the ANN-CSA was 0.345 mm/day, while it was 0.456, 0.672, 0.789, and 0.891 for the ANN-SCA, ANN-FFA, ANN-GA, and ANN models. The ANN-CSA’s performance was better than the ANN-SCA, ANN-FFA, ANN-GA, and ANN models but the IMM model decreased MAE and RMSE of the ANN-CSA model. The MAE of the IMM in Table 4C was 0.246 mm/day, while the MAE of the ANN-CSA, ANN-SCA, and ANN-FFA, ANN-GA, and ANN models was 0.325 mm/day, 0.367 mm/day, 0.567 mm/day, 0.612 mm/day, and 0.689 mm/day, respectively. However, the IMM model’s accuracy was based on using the outputs of all models as the inputs improved the accuracy of all models. The testing results of models in the Sari station were observed in Table 4D. Leta et al. (2018) evaluated the performance of the hydrological models based on NSE, and four classes were defined for the NSE values: (NSE > 0.80: very good), (0.70 < NSE ≤ 0.8: good), (0.5 < NSE ≤ 0.7: satisfactory), and (NSE ≤ 0.50: unsatisfactory). Regarding this classification, the IMM performance, ANN-CSA, ANN-SCA, ANN-FFA, and ANN models were very good, and the performance of the ANN model was good. Table 4E presents the accuracy of the models for the Tabriz station at the training level. The RMSE of the ANN-CSA was 0.345 mm/day, while it was 0.455 mm/day, 0.567 mm/day, 0.672, and 0.721 for the ANN-SCA, ANN-FFA, ANN-GA, and ANN models. It means that the CSA was a reliable training algorithm for training ANN but providing a synergy among different models increased the CSA’s accuracy. The performance of models indicated that the IMM had the best accuracy among other models. Regarding the highest RMSE and MAE and the lowest NSE and R², the ANN model had the lowest performance. Table 4 shows the accuracy of models in the testing level of the Tabriz station. Regarding the classification of Leta et al. (2018) for the R² value, (R² > 0.85: very good), (0.75 < R² ≤ 0.85: good), (0.60 < R² ≤ 0.75: satisfactory), and (R² ≤ 0.60: unsatisfactory), the performance of the IMM, ANN-CSA, and ANN-SCA, were very good and the performance of the ANN-FFA, ANN-GA, and ANN models were good, respectively. Table 4G shows the accuracy of the models for the Tehran station at the training level. The ANN-CSA MAE was 0.312 mm/day, while it was 0.325 mm/day, 0.334 mm/day, 0.345 mm/day, and 0.356 mm/day for the ANN-SCA ANN-FFA, ANN-GA, and ANN models. As observed in Table 4G, the IMM decreased RMSE of the ANN-CSA, ANN-SCA, ANN-FFA, ANN-GA, and ANN models by 32, 34, 40, 50, and 51%, respectively. Regarding the classification of R² and NSE based on the study of Leta et al. (2018), the accuracy of the ANN model was perfect and good. Table 4H presents the accuracy of the models in the Tehran station at the testing level. The MAE of the IMM was 0.112 mm/day, while it was 0.189 mm/day, 0.267 mm/day, 0.267 mm/day, 0.389 mm/day, 0.456 mm/day, and 0.512 mm/day for the ANN-CSA, ANN-SCA, and ANN-FFA, ANN-GA, and ANN models, respectively. Table 4I shows the training results for the Yazd station. The hybrid ANN models had higher NSE and R² than the standalone ANN models. Table 4J shows the testing results for the Yazd station. Regarding the classification of R² and NSE based on the study of Leta et al. (2018), the ANN model had a good performance at the testing level. The ANN-CSA decreased MAE of the ANN-SCA, ANN-FFA, ANN-GA, and ANN models by 57, 61, 70, 76, and 79%, respectively. Table 4K shows the training results for the Shahrekord station. The RMSE of the IMM in Table 4K was 18, 21, 22, 30, and 43% lower than those of the ANN-CSA, ANN-SCA, ANN-FFA, ANN-GA, and ANN Models. Table 4L shows the testing results for the Shahrekord station. As observed in Table 4L, regarding the classification of R² and NSE values of the study (Li et al., 2013), the ANN model’s performance was satisfactory and good based on the R and NSE values. Table 4M shows the training results for the Ahvaz station. The performance of the ANN model was worse than the other models. Table 4N shows the testing results for the models in the Ahvaz station. This section’s analysis results were the same as with the study of Seifi and Soroush (2020). They reported that ANN model’s performance coupled with the optimization algorithms was better than the ANN model. The current study results agreed with those studies of Malik et al. (2020b), Mohamadi et al. (2020). Malik et al. (2020b) used the multiple model-ANN for predicting evaporation. The multiple ANN model’s abilities were benchmarked against the SVM, multi-gene genetic programming (MGGP), and decision tree models. It was reported that the RMSE of the multiple model-ANN was lower than those of the other models. Mohamadi et al. (2020) coupled the ANN models with FFA and shark algorithm for predicting evaporation. It was observed that the hybrid ANN models performed better than the ANN models. Wu L. et al. (2020) reported the high capability of the optimization algorithms to improve the MLA’s accuracy. Moayedi et al. (2021) coupled ANN with an electromagnetic optimization algorithm. They reported that the hybrid new ANN model was an accurate model for predicting evaporation. Figure 1B in Supplementary Appendix shows the scatterplots of models. The results indicated that the IMM had the highest accuracy. All data sets were used to draw scatter plots. The results of Table 4 indicated that the IMM model had the highest accuracy in all stations. As observed in Figure 2B, the box plots of the MAE values indicated that the IMM had the best accuracy among other models. However, the value of the MAE other models in the different stations is variable. If the values of errors such as MAE and RMSE of models in one station are more than other stations, the following reasons can be considered: 1) The climate of regions affects the accuracy of models. The data should be selected in a way that covers the entire climate of the region. For example, air pressure is an important parameter that can be used as another input variable. This parameter can play an important role in predicting evaporation in some stations. 2) Measurement of data may be associated with more errors at some stations. This issue may lead to an increase in errors. The mentioned reasons can be modified in the next studies although the IMM model had the lowest accuracy in all stations.

FIGURE 2

FIGURE 2. The box plots for the models.

The IMM model in this study had better results than the other models. Since this model used the advantages of multiple hybrid ANN models, the results of IMM were better than the other model. Each of the individual ANN models has advantages and disadvantages. Thus, the use of the advantages of all models in an ensemble structure could improve the accuracy of hybrid and standalone ANN models. Among different optimization algorithms, CSA has better results than the other optimization algorithms. The agents of CSA shared their information together. Also, the leader as the best solution guided the other solutions to update their status. Thus, CSA has robust abilities for global and local searches. The mentioned advantages of CSA caused it to have better results than the other algorithms. It should be considered that the leap and waking mechanism are the important operators because these operators help the CSA to escape from the local optimums. The solutions with low quality using these mechanisms increase their quality. The SCA has better performance than the FFA and GA, but the CSA outperformed the SCA. Although the SCA has good accuracy, its performance highly relies on random parameters. The SCA in this study outperformed the FFA and GA because the users used the sensitivity analysis. If the users only want to use the suggested values of random parameters in the original paper, it may lead to high errors. The modelers should adopt the random parameters based on their modeling process and data points. However, the ability of CSA to escape from local optimums was higher than the SCA because the CSA used leap and wake operators. The FFA had better accuracy than the GA. While a leader (global solution) guided the other solutions in the CSA and SCA to improve their quality, the FFA provides a new solution based on the ith and jth solutions. The ANN models did not use optimization algorithms. They used classical training algorithms. The results of the used ANN models of the current study were worse than the optimized ANN models because the classical training algorithms had a lower ability than the optimization algorithms in finding optimal solutions.

Table 4 also shows the SI values. The performance of models in the Isfahan station indicated that the IMM performance was excellent in the testing and training level, while the performance of the ANN model was fair in the training and testing level. It was observed that the IMM had excellent performance in the Tehran station in the testing and training levels. The performance of the ANN-CSA was excellent in the Tehran station. Among hybrid ANN models, the ANN-GA had the weakest performance based on the adequate performance in the testing and training level of the Sari station. The IMM and ANN-CSA had excellent performance in the Tabriz station in the training level, while the ANN-SCA and ANN-FFA performance was good at the training level.

The IMM and ANN model’s performance in the Ahvaz station was excellent and lacking in the training and testing levels. Finally, the performance of the IMM, ANN-CSA, and the ANN-SCA was excellent in the Shahrekord stations. Figure 2 shows the boxplots of the observed and predicted data. As observed in this figure, the IMM model provided more accurate results than the other models in the different stations. The ANN-SCA among different hybrid models provided the most accurate results. The ANN model as the standalone model provided the worst results among different models. To understand the difference in the models’ performance with and without fuzzy reasoning, the CPU time of the models is reported in Figure 3. As observed in Figure 3, the hybrid ANN model predicted evaporation over a shorter time than the standalone ANN model. The models with fuzzy reasoning had a shorter time than the models without reasoning fuzzy. For example, the time of ANN-CSA based on fuzzy reasoning in Sari, Isfahan, Tabriz, Yazd, Ahvaz, Tehran, and Shahrekord stations were 210, 220, 200, 190, 197, 200, and 190 s, while the CPU time of the ANN-CSA without reasoning fuzzy in Sari, Isfahan, Tabriz, Yazd, Ahvaz, Tehran, and Shahrekord stations was 245, 260, 256, 220, 206, 340, and 370 s, respectively. The IMM was the best model for predicting evaporation. The current study results agreed with those studies of Norouzi et al. (2020) and Shabani et al. (2021). These studies indicated that the IMM model could improve the MLA models’ accuracy based on receiving outputs of different models as inputs. Thus, they can provide a robust synergy among different models.

FIGURE 3

FIGURE 3. The CPU time of models with and without fuzzy reasoning.

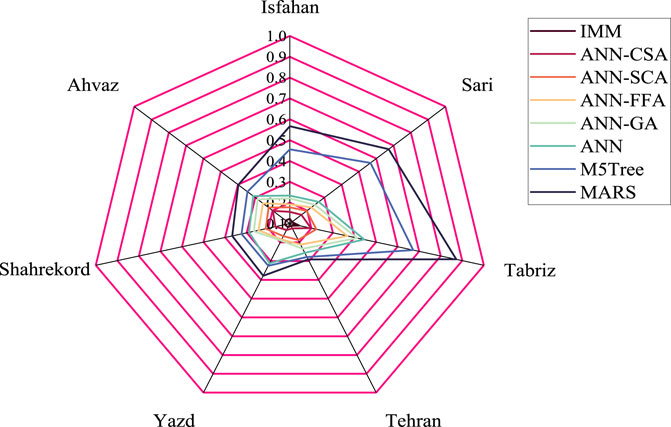
Although the current study models had a high efficiency for predicting evaporation, a comparison with classical methods such as the M5Tree model and multivariate adaptive regression spline (MARS) is required. M5Tree models use the input and output data to provide a decision tree. The MARS constructs several splines and a number of knots between these splines to predict target variables. The MARS uses the basis function for allocating data in each spline. Figure 4 shows the radar chart for the models based on CRMSE. As observed in this figure, the CRMSR of the IMM, ANN-CSA, ANN-SCA, ANN-FA, ANN-GA, ANN, M5Tree, and MARS was 0.123, 0.156, 0.198, 0.178, 0.192, 0.221, 0.234, 0.456, and 0.567 in the Isfahan station, respectively. The CRMSR of the IMM, ANN-CSA, ANN-SCA, ANN-FA, ANN-GA, ANN, M5Tree, and MARS at the testing level was 0.119, 0.134, 0.167, 0.185, 0.191, 0.312, 0.325, and 0.378 in the Yazd station, respectively.

FIGURE 4

FIGURE 4. Radar charts for comparing the models using CRMSE.

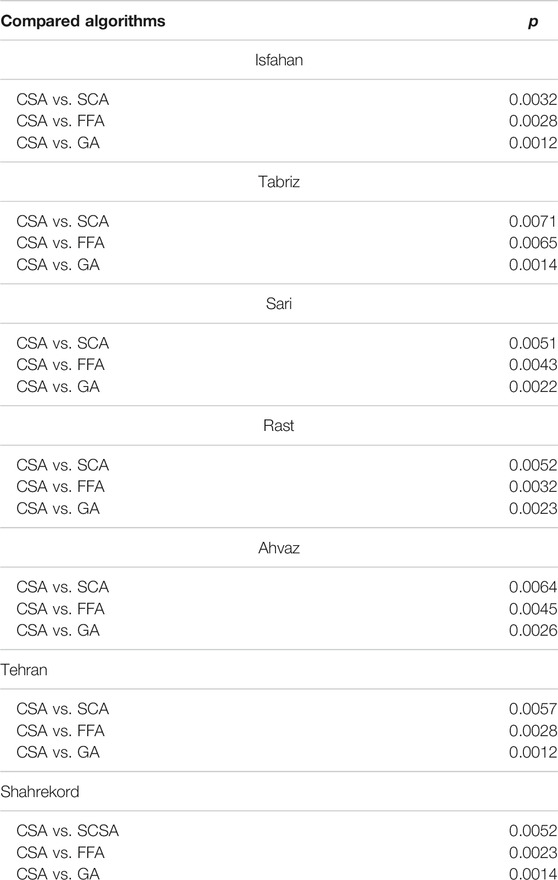
In this study, the Wilcoxon test was used to show the superiority of the CSA to the other algorithms. It is a nonparametric statistical test to show the significance of the results. The significance of the superiority of the CSA to the other algorithms is observed in Table 5 based on p values, which are lower than 0.05. In all stations, the CSA outperformed other algorithms. The p values determine the significance level of the two methods. A model is statistically significant in this study if the model results in a p-value less than 0.050.

TABLE 5

TABLE 5. The obtained results from the Wilcoxon test over different stations.

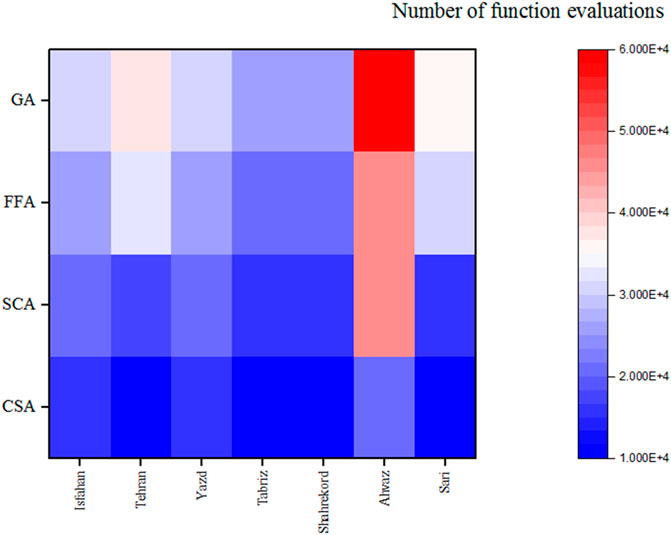
Figure 5 compares algorithms based on a number of function evaluations (NOFE) (population size*number of iterations). As observed in this figure, the CSA with lower NOFE outperformed the other algorithms in different stations. For example, the NOFE of CSA, SCA, FFA, and GA was 15,000, 20,000, 25,000, and 30,000, respectively, in the Isfahan station. The GA had the highest NFOE and the worst performance in all stations.

FIGURE 5

FIGURE 5. The heat map of NOFE.

4.4 Further Discussion

Regarding the obtained results in this study, the following points should be considered: As evaporation relies on the various climate parameters, a robust preprocessing method is required to determine the best input combination for predicting evaporation. The collection of data and preparing the structure of models are the challenges of this paper. However, the current paper’s soft computing models need enough data points to achieve the best accuracy.

The performance of an MLA can be global when the model can predict evaporation under different climate conditions. The IMM model was the best model for different synoptic stations in different climate conditions in this study. The used IMM model of the current study is suitable for predicting other hydrological variables such as rainfall, temperature, and streamflow. It can be used in different fields such as drought and flood control. The IMM models are better than the Bayesian average model because these models do not require statistical computations such as prior and posterior distributions. The models of the current study can be used for predicting evaporation under climate change. The information and data of the climate scenarios can be used as the inputs to the used soft computing models of the current paper for predicting evaporation. The models of the current study can be used for predicting evaporation in different regions of the world.

The optimization algorithms improve the accuracy of the models based on statistical error indexes and CPU time. The fuzzy reasoning based on identifying and removing the weak weights decreases the computational time. The subsequent studies can focus on the input uncertainties and uncertainties of model parameters. In this study, an improved GT could identify the best input combination accurately. Another approach for identifying the best input combination is using a multi-objective optimization algorithm. It is enough to define two objective functions where the first objective function is used to determine the ANN parameters, while the second objective function is utilized to determine the best input combination. The multi-objective algorithms use the Pareto front and the conception of the nondominated solutions for finding the best solution. The other MLAs such as ANFIS, SVM, and decision tree models can be coupled with the current study’s optimization algorithms to improve the model’s accuracy. The application of the introduced models in the current study is not limited to predicting evaporation. The new models can be used for predicting other variables such as temperature, rainfall, streamflow, and other variables. The new models can be used as effective tools for predicting evaporation when there is not enough data. The climate data may not be accessible for all modelers, and thus, the latitude, longitude, and the number of days can be used as the inputs to the models for predicting evaporation. All error indexes showed the superiority of the IMM models. The successive researchers can use a multi-criteria decision model to assign a rank to each model. The results of the current study improved the accuracy of the previous research. Qasem et al. (2019) used the support vector machine (SVM), ANN, wavelet ANN, and wavelet SVM (WSVM) for predicting evaporation. They predicted monthly evaporation using 288 data sets based on the different input combinations. Their best model used temperature and solar radiation as the input. The results indicated that the RMSE and MAE of the best model was 0.701 and 0.525 in the test stage for the Tabriz station of Iran, while the current study based on the IMM model gave the RMSE of 0.312 and MAE of 0.256, respectively. Also, the RMSE and MAE of the ANN-SCA indicated that the used ANN-SCA provided better results than that of the study of Qasem et al. (2019). Mohamadi et al. (2020) used the hybrid ANN and ANFIS models to predict evaporation based on 156 data sets. The relative humidity, temperature, and sunny hours were the best input scenario. The best hybrid model was the ANFIS-shark algorithm. The MAE of the ANFIS-shark algorithm was 1.165 and 1.269 in the training and testing level, while the current study models based on 1,000 data points provided lower MAE in the compassion of Mohamadi et al. (2020). Malik et al. (2020b) used multi-genetic programming, SVM, multivariate adaptive regression spline, and multiple ANN models to predict evaporation in two India stations. They used the 324 monthly data points for the Pantnagar station and 156 monthly data sets for the Ranichauri station. The study results confirmed that the multiple ANN models similar to the IMM model of the current study had the best results. While the multiple ANN models of the current study used the different hybrid ANN models, the multiple ANN model of Malik et al. (2020b) used the outputs of the multigenetic programming, SVM, multivariate adaptive regression spline, and decision tree model. The results indicated that the RMSE of the multiple ANN model of the study of Malik et al. (2020b) in the testing level 0.536 and 0.638 for the Pantnagar and Ranichauri stations while the IMM model used in the current study for more data points provided lower RMSE in comparison of the study of Malik et al. (2020). Ghorbni et al. (2018) predicted daily evaporation for 1,080 data sets. The ANN-firefly algorithm for predicting two stations in Iran, namely, Talesh and Manjil, was used. The maximum temperature, minimum temperature, relative humidity, wind speed, and sunshine hours were used as the inputs to the models. The RMSE and MAE for the 1,090 data sets of ANN-FFA were 0.887 and 0.62 in the training and 1.007 and 0.709 in the testing level of the Talesh station. The comparison of results with the current study indicated that the current study models, especially the IMM, provided better results than the study of Ghorbni et al. (2018).

The results of the current study are useful for water resource management and agriculture management. The current study models can be useful for the optimal operation of dam reservoirs when the decision-makers need to estimate the evaporation accurately in the continuity equation (Ehteram et al., 2020; Seifi et al., 2020; Sammen et al., 2021; Seifi et al., 2021). Additionally, the IMM model and other introduced models of the current study can be useful for predicting other hydrological variables such as runoff, rainfall, temperature, and streamflow. Thus, the application of models is not limited to the current study. Also, these models had a high potential for predicting evaporation for future periods based on climate scenarios. First, the modelers can predict the climate input data based on climate scenarios and models. Afterward, the inputs of the future period are inserted into the models to predict evaporation for future periods. Using all input data cannot always give the best accuracy. Qasem et al. (2019) used different input combinations for predicting evaporation. The best input combination used temperature and solar radiation. They used ANN models, and the results indicate that the ANN models based on temperature and solar radiation gave better results than the ANN models based on input combinations of temperature, solar radiation, relative humidity, and wind speed. The importance of the used GT in this study is related to the same issue. In this study, using all input data gave the best accuracy, but regarding the results of other studies such as Qasem et al. (2019), the determination of the best inputs based on GT is an important issue because the input combinations with fewer inputs may give better results. In this condition, if the modelers use the coupled GT, they may not test different input scenarios. When the modelers have different input data, they can use the GT for decreasing computational costs. It should be considered the modelers in the original version of GT have to compute the $\Gamma$ and $V_{ratio}$ for different scansions. When the GT was coupled with the optimization algorithms, the coupled GT could be the best input combination because the name of the input variables is inserted into the optimization algorithms. Afterward, the algorithm provides the random population-based on introduced decision variables to give the best input combinations among the entire probable forms.

The model parameters and inputs to the models are the sources of uncertainty. The robust optimization algorithms can be used for estimating model parameters. Thus, the uncertainty of model parameters may decrease using robust optimization algorithms. The subsequent studies can quantify uncertainty in the modeling process.

5 Conclusion

Predicting evaporation is an important issue for water resource management. Predicting evaporation is a complex process because it depends on the different climate parameters. Thus, identifying effective parameters on evaporation and developing robust models for predicting evaporation is an important issue. In this study, a new hybrid model, the ANN-CSA, based on fuzzy reasoning conception, was used to predict Iran’s seven synoptic stations’ daily evaporation. Then, the ANN-CSA’s ability was benchmarked against the ANN-FFA, ANN-SCA, ANN-GA, and ANN models. Then, the models’ outputs were utilized as the ANN model to predict the daily evaporation based on the inclusive multiple models. The fuzzy reasoning was used to remove the redundant weights of the ANN model. To identify the best input scenario, the CSA was coupled with the Gamma test. The hybrid Gamma test decreased time for selecting the best input scenario. The RMSE of the IMM in the Isfahan station was 0.221 mm/day while the RMSE of the ANN-CSA, ANN-SCA, ANN-FFA, ANN-GA, and ANN model was 0.455 mm/day, 0.567 mm/day, 0.612 mm/day, 0.614 mm/day, and 0.721 mm/day, respectively. The NSE of the IMM mode in the testing level was 0.94, while it was 0.92, 0.90, 0.86, 0.85, and 0.82 for the ANN-SCA, ANN-FFA, ANN-GA, and ANN models, respectively, in the Sari station. The results for the other stations indicated that the IMM performed better than the other models. The models’ relative error indicated that the ANN-CAS performed better than the ANN-FFA, ANN-SCA, ANN-GA, and ANN models. The current study’s general results indicated that the IMM and reasoning conception are two critical tools for predicting hydrological variables. One of the limitations of the current study is gathering input data. Also, the use of ANN-CSA has challenges because the CSA has many computational levels. It needs to the high ability of modelers. Additionally, the adjusting of CSA parameters is an important issue. If the modelers do not accurately set the CSA parameters, it may lead to error computations.

The next studies also can investigate the effect of other inputs such as number of days and air pressure for predicting evaporation. The results of the current study are useful for optimal operation of reservoir dam, water resource management, agriculture, and irrigation management.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, methodology, software, and formal analysis, ME and FP, AM; writing—original draft preparation, AA and AE-S; writing—review and editing, AM and AA; visualization, MV; supervision, AE-S, data collection and preprocessing, ME and FP All authors have read and agreed to the published version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abghari, H., Ahmadi, H., Besharat, S., and Rezaverdinejad, V. (2012). Prediction of Daily Pan Evaporation Using Wavelet Neural Networks. Water Resour. Manage. 26, 3639–3652. doi:10.1007/s11269-012-0096-z

CrossRef Full Text | Google Scholar

Adnan, R. M., Jaafari, A., Mohanavelu, A., Kisi, O., and Elbeltagi, A. (2021a). Novel Ensemble Forecasting of Streamflow Using Locally Weighted Learning Algorithm. Sustainability 13, 5877. doi:10.3390/su13115877

CrossRef Full Text | Google Scholar

Adnan, R. M., Malik, A., Kumar, A., Parmar, K. S., and Kisi, O. (2019). Pan Evaporation Modeling by Three Different Neuro-Fuzzy Intelligent Systems Using Climatic Inputs. Arab J. Geosci. 12. doi:10.1007/s12517-019-4781-6

CrossRef Full Text | Google Scholar

Adnan, R. M., Mostafa, R., Yaseen, Z. M., Shahid, S., Zounemat-Kermani, M., and Zounemat-Kermani, M. (2021b). Improving Streamflow Prediction Using a New Hybrid ELM Model Combined with Hybrid Particle Swarm Optimization and Grey Wolf Optimization. Knowledge-Based Syst. 230, 107379. doi:10.1016/j.knosys.2021.107379

CrossRef Full Text | Google Scholar

Adnan, R. M., Petroselli, A., Heddam, S., Santos, C. A. G., and Kisi, O. (2021c). Comparison of Different Methodologies for Rainfall-Runoff Modeling: Machine Learning vs Conceptual Approach. Nat. Hazards 105, 2987–3011. doi:10.1007/s11069-020-04438-2

CrossRef Full Text | Google Scholar

Alizamir, M., Kisi, O., Muhammad Adnan, R., and Kuriqi, A. (2020). Modelling Reference Evapotranspiration by Combining Neuro-Fuzzy and Evolutionary Strategies. Acta Geophys. 68, 1113–1126. doi:10.1007/s11600-020-00446-9

CrossRef Full Text | Google Scholar

Arunkumar, R., Jothiprakash, V., and Sharma, K. (2017). Artificial Intelligence Techniques for Predicting and Mapping Daily Pan Evaporation. J. Inst. Eng. India Ser. A. 98, 219–231. doi:10.1007/s40030-017-0215-1

CrossRef Full Text | Google Scholar

Azadi, S., Amiri, H., Ataei, P., and Javadpour, S. (2020). Optimal Design of Groundwater Monitoring Networks Using Gamma Test Theory. Hydrogeol J. 28, 1389–1402. doi:10.1007/s10040-020-02115-z

CrossRef Full Text | Google Scholar

Banadkooki, F. B., Ehteram, M., Panahi, F., Sh. Sammen, S. S., Othman, F. B., and El-Shafie, A. (2020). Estimation of Total Dissolved Solids (TDS) Using New Hybrid Machine Learning Models. J. Hydrol. 587, 124989. doi:10.1016/j.jhydrol.2020.124989

CrossRef Full Text | Google Scholar

Biazar, S. M., Rahmani, V., Isazadeh, M., Kisi, O., and Dinpashoh, Y. (2020). New Input Selection Procedure for Machine Learning Methods in Estimating Daily Global Solar Radiation. Arab J. Geosci. 13. doi:10.1007/s12517-020-05437-0

CrossRef Full Text | Google Scholar

Braik, M., Sheta, A., and Al-Hiary, H. (2021). A Novel Meta-Heuristic Search Algorithm for Solving Optimization Problems: Capuchin Search Algorithm. Neural Comput. Applic 33, 2515–2547. doi:10.1007/s00521-020-05145-6

CrossRef Full Text | Google Scholar

Bui, D.-K., Nguyen, T. N., Ngo, T. D., and Nguyen-Xuan, H. (2020). An Artificial Neural Network (ANN) Expert System Enhanced with the Electromagnetism-Based Firefly Algorithm (EFA) for Predicting the Energy Consumption in Buildings. Energy 190, 116370. doi:10.1016/j.energy.2019.116370

CrossRef Full Text | Google Scholar

Ehteram, M., Salih, S. Q., and Yaseen, Z. M. (2020). Efficiency Evaluation of Reverse Osmosis Desalination Plant Using Hybridized Multilayer Perceptron with Particle Swarm Optimization. Environ. Sci. Pollut. Res. 27, 15278–15291. doi:10.1007/s11356-020-08023-9

CrossRef Full Text | Google Scholar

Ewees, A. A., Abd Elaziz, M., Al-Qaness, M. A. A., Khalil, H. A., and Kim, S. (2020). Improved Artificial Bee Colony Using Sine-Cosine Algorithm for Multi-Level Thresholding Image Segmentation. IEEE Access 8, 26304–26315. doi:10.1109/ACCESS.2020.2971249

CrossRef Full Text | Google Scholar

Feng, Z.-k., Liu, S., Niu, W.-j., Li, B.-j., Wang, W.-c., Luo, B., et al. (2020). A Modified Sine Cosine Algorithm for Accurate Global Optimization of Numerical Functions and Multiple Hydropower Reservoirs Operation. Knowledge-Based Syst. 208, 106461. doi:10.1016/j.knosys.2020.106461

CrossRef Full Text | Google Scholar

Ghorbani, M. A., Deo, R. C., Yaseen, Z. M., H. Kashani, M. M., and Mohammadi, B. (2018). Pan Evaporation Prediction Using a Hybrid Multilayer Perceptron-Firefly Algorithm (MLP-FFA) Model: Case Study in North Iran. Theor. Appl. Climatol 133, 1119–1131. doi:10.1007/s00704-017-2244-0

CrossRef Full Text | Google Scholar

Guan, Y., Mohammadi, B., Pham, Q. B., Adarsh, S., Balkhair, K. S., Rahman, K. U., et al. (2020). A Novel Approach for Predicting Daily pan Evaporation in the Coastal Regions of Iran Using Support Vector Regression Coupled with Krill Herd Algorithm Model. Theor. Appl. Climatol 142, 349–367. doi:10.1007/s00704-020-03283-4

CrossRef Full Text | Google Scholar

Gupta, S., Deep, K., Mirjalili, S., and Kim, J. H. (2020). A Modified Sine Cosine Algorithm with Novel Transition Parameter and Mutation Operator for Global Optimization. Expert Syst. Appl. 154, 113395. doi:10.1016/j.eswa.2020.113395

CrossRef Full Text | Google Scholar

Guven, A., and Kisi, O. (2013). Monthly pan Evaporation Modeling Using Linear Genetic Programming. J. Hydrol. 503, 178–185. doi:10.1016/j.jhydrol.2013.08.043

CrossRef Full Text | Google Scholar

Keshtegar, B., Heddam, S., Sebbar, A., Zhu, S.-P., and Trung, N.-T. (2019). SVR-RSM: a Hybrid Heuristic Method for Modeling Monthly pan Evaporation. Environ. Sci. Pollut. Res. 26, 35807–35826. doi:10.1007/s11356-019-06596-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Keshtegar, B., Piri, J., and Kisi, O. (2016). A Nonlinear Mathematical Modeling of Daily pan Evaporation Based on Conjugate Gradient Method. Comput. Elect. Agric. 127, 120–130. doi:10.1016/j.compag.2016.05.018

CrossRef Full Text | Google Scholar

Kim, S., Shiri, J., Singh, V. P., Kisi, O., and Landeras, G. (2015). Predicting Daily pan Evaporation by Soft Computing Models with Limited Climatic Data. Hydrological Sci. J. 60, 1120–1136. doi:10.1080/02626667.2014.945937

CrossRef Full Text | Google Scholar

Kişi, Ö. (2013). Evolutionary Neural Networks for Monthly pan Evaporation Modeling. J. Hydrol. 498, 36–45. doi:10.1016/j.jhydrol.2013.06.011

CrossRef Full Text | Google Scholar

Kisi, O., Genc, O., Dinc, S., and Zounemat-Kermani, M. (2016). Daily pan Evaporation Modeling Using Chi-Squared Automatic Interaction Detector, Neural Networks, Classification and Regression Tree. Comput. Elect. Agric. 122, 112–117. doi:10.1016/j.compag.2016.01.026

CrossRef Full Text | Google Scholar

Langari, R. K., Sardar, S., Amin Mousavi, S. A., and Radfar, R. (2020). Combined Fuzzy Clustering and Firefly Algorithm for Privacy Preserving in Social Networks. Expert Syst. Appl. 141, 112968. doi:10.1016/j.eswa.2019.112968

CrossRef Full Text | Google Scholar

Leta, O., El-Kadi, A., Dulai, H., and Ghazal, K. (2018). Assessment of SWAT Model Performance in Simulating Daily Streamflow under Rainfall Data Scarcity in Pacific Island Watersheds. Water 10, 1533. doi:10.3390/w10111533

CrossRef Full Text | Google Scholar

Li, M.-F., Tang, X.-P., Wu, W., and Liu, H.-B. (2013). General Models for Estimating Daily Global Solar Radiation for Different Solar Radiation Zones in mainland China. Energ. Convers. Manag. 70, 139–148. doi:10.1016/j.enconman.2013.03.004

CrossRef Full Text | Google Scholar

Liu, Y., Starzyk, J. A., and Zhu, Z. (2008). Optimized Approximation Algorithm in Neural Networks Without Overfitting. IEEE Trans. Neural Netw. 19 (6), 983–995. doi:10.1109/TNN.2007.915114

PubMed Abstract | CrossRef Full Text | Google Scholar

Malik, A., Kumar, A., Kim, S., Kashani, M. H., Karimi, V., Sharafati, A., et al. (2020b). Modeling Monthly pan Evaporation Process over the Indian central Himalayas: Application of Multiple Learning Artificial Intelligence Model. Eng. Appl. Comput. Fluid Mech. 14, 323–338. doi:10.1080/19942060.2020.1715845

CrossRef Full Text | Google Scholar

Malik, A., Rai, P., Heddam, S., Kisi, O., Sharafati, A., Salih, S. Q., et al. (2020a). Pan Evaporation Estimation in Uttarakhand and Uttar Pradesh States, India: Validity of an Integrative Data Intelligence Model. Atmosphere 11, 553. doi:10.3390/ATMOS11060553

CrossRef Full Text | Google Scholar

Melo, H., and Watada, J. (2016). Gaussian-PSO with Fuzzy Reasoning Based on Structural Learning for Training a Neural Network. Neurocomputing 172, 405–412. doi:10.1016/j.neucom.2015.03.104

CrossRef Full Text | Google Scholar

Memarzadeh, R., Zadeh, H. G., Dehghani, M., Riahi-Madvar, H., Seifi, A., and Mortazavi, S. M. (2020). A Novel Equation for Longitudinal Dispersion Coefficient Prediction Based on the Hybrid of SSMD and Whale Optimization Algorithm. Sci. Total Environ. 716, 137007.

PubMed Abstract | CrossRef Full Text | Google Scholar

Metawa, N., Hassan, M. K., and Elhoseny, M. (2017). Genetic Algorithm Based Model for Optimizing Bank Lending Decisions. Expert Syst. Appl. 80, 75–82. doi:10.1016/j.eswa.2017.03.021

CrossRef Full Text | Google Scholar

Mirjalili, S. M., Mirjalili, S. Z., Saremi, S., and Mirjalili, S. (2020). “Sine Cosine Algorithm: Theory, Literature Review, and Application in Designing bend Photonic crystal Waveguides,” in Studies in Computational Intelligence (Springer), 201–217. doi:10.1007/978-3-030-12127-3_12

CrossRef Full Text | Google Scholar

Mirjalili, S. (2016). SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowledge-Based Syst. 96, 120–133. doi:10.1016/j.knosys.2015.12.022

CrossRef Full Text | Google Scholar

Moayedi, H., Ghareh, S., and Foong, L. K. (2021). Quick Integrative Optimizers for Minimizing the Error of Neural Computing in pan Evaporation Modeling. Eng. Comput. 11 (5), 32–55. doi:10.1007/s00366-020-01277-4

CrossRef Full Text | Google Scholar

Mohamadi, S., Ehteram, M., and El-Shafie, A. (2020). Accuracy Enhancement for Monthly Evaporation Predicting Model Utilizing Evolutionary Machine Learning Methods. Int. J. Environ. Sci. Technol. 17, 3373–3396. doi:10.1007/s13762-019-02619-6

CrossRef Full Text | Google Scholar

Neggaz, N., Ewees, A. A., Elaziz, M. A., and Mafarja, M. (2020). Boosting Salp Swarm Algorithm by Sine Cosine Algorithm and Disrupt Operator for Feature Selection. Expert Syst. Appl. 145, 113103. doi:10.1016/j.eswa.2019.113103

CrossRef Full Text | Google Scholar

Norouzi, R., Arvanaghi, H., Salmasi, F., Farsadizadeh, D., and Ghorbani, M. A. (2020). A New Approach for Oblique Weir Discharge Coefficient Prediction Based on Hybrid Inclusive Multiple Model. Flow Meas. Instrumentation 76, 101810. doi:10.1016/j.flowmeasinst.2020.101810

CrossRef Full Text | Google Scholar

Park, D., Cha, J., Kim, M., and Go, J. S. (2020). Multi-objective Optimization and Comparison of Surrogate Models for Separation Performances of Cyclone Separator Based on CFD, RSM, GMDH-Neural Network, Back Propagation-ANN and Genetic Algorithm. Eng. Appl. Comput. Fluid Mech. 14, 180–201. doi:10.1080/19942060.2019.1691054

CrossRef Full Text | Google Scholar

Qasem, S. N., Samadianfard, S., Kheshtgar, S., Jarhan, S., Kisi, O., Shamshirband, S., et al. (2019). Modeling Monthly pan Evaporation Using Wavelet Support Vector Regression and Wavelet Artificial Neural Networks in Arid and Humid Climates. Eng. Appl. Comput. Fluid Mech. 13, 177–187. doi:10.1080/19942060.2018.1564702

CrossRef Full Text | Google Scholar

Riahi-Madvar, H., Gholami, M., Gharabaghi, B., and Morteza Seyedian, S. (2021). A Predictive Equation for Residual Strength Using a Hybrid of Subset Selection of Maximum Dissimilarity Method with Pareto Optimal Multi-Gene Genetic Programming. Geosci. Front. 12, 101222. doi:10.1016/j.gsf.2021.101222

CrossRef Full Text | Google Scholar

Rizk-Allah, R. M. (2018). Hybridizing Sine Cosine Algorithm with Multi-Orthogonal Search Strategy for Engineering Design Problems. J. Comput. Des. Eng. 5, 249–273. doi:10.1016/j.jcde.2017.08.002

CrossRef Full Text | Google Scholar

Sammen, S. S., Ehteram, M., Abba, S. I., Abdulkadir, R. A., Ahmed, A. N., and El-Shafie, A. (2021). A New Soft Computing Model for Daily Streamflow Forecasting. Stoch Environ. Res. Risk Assess. 35, 2479–2491. doi:10.1007/s00477-021-02012-1

CrossRef Full Text | Google Scholar

Sebbar, A., Heddam, S., and Djemili, L. (2019). Predicting Daily Pan Evaporation (Epan) from Dam Reservoirs in the Mediterranean Regions of Algeria: OPELM vs OSELM. Environ. Process. 6, 309–319. doi:10.1007/s40710-019-00353-2

CrossRef Full Text | Google Scholar

Seifi, A., Ehteram, M., and Dehghani, M. (2021). A Robust Integrated Bayesian Multi-Model Uncertainty Estimation Framework (IBMUEF) for Quantifying the Uncertainty of Hybrid Meta-Heuristic in Global Horizontal Irradiation Predictions. Energ. Convers. Manag. 241, 114292. doi:10.1016/j.enconman.2021.114292

CrossRef Full Text | Google Scholar

Seifi, A., Ehteram, M., Singh, V. P., and Mosavi, A. (2020). Modeling and Uncertainty Analysis of Groundwater Level Using Six Evolutionary Optimization Algorithms Hybridized with ANFIS, SVM, and ANN. Sustainability 12, 4023. doi:10.3390/SU12104023

CrossRef Full Text | Google Scholar

Seifi, A., and Riahi, H. (2020). Estimating Daily Reference Evapotranspiration Using Hybrid Gamma Test-Least Square Support Vector Machine, Gamma Test-Ann, and Gamma Test-Anfis Models in an Arid Area of iran. J. Water Clim. Change 11, 217–240. doi:10.2166/wcc.2018.003

CrossRef Full Text | Google Scholar

Seifi, A., and Soroush, F. (2020). Pan Evaporation Estimation and Derivation of Explicit Optimized Equations by Novel Hybrid Meta-Heuristic ANN Based Methods in Different Climates of Iran. Comput. Elect. Agric. 173, 105418. doi:10.1016/j.compag.2020.105418

CrossRef Full Text | Google Scholar

Shabani, E., Hayati, B., Pishbahar, E., Ghorbani, M. A., and Ghahremanzadeh, M. (2021). A Novel Approach to Predict CO2 Emission in the Agriculture Sector of Iran Based on Inclusive Multiple Model. J. Clean. Prod. 279, 123708. doi:10.1016/j.jclepro.2020.123708

CrossRef Full Text | Google Scholar

Tabari, H., Hosseinzadeh Talaee, P., and Abghari, H. (2012). Utility of Coactive Neuro-Fuzzy Inference System for pan Evaporation Modeling in Comparison with Multilayer Perceptron. Meteorol. Atmos. Phys. 116, 147–154. doi:10.1007/s00703-012-0184-x

CrossRef Full Text | Google Scholar

Trachanatzi, D., Rigakis, M., Marinaki, M., and Marinakis, Y. (2020). A Firefly Algorithm for the Environmental Prize-Collecting Vehicle Routing Problem. Swarm Evol. Comput. 57, 100712. doi:10.1016/j.swevo.2020.100712

CrossRef Full Text | Google Scholar

Wang, L., Niu, Z., Kisi, O., Li, C. a., and Yu, D. (2017). Pan Evaporation Modeling Using Four Different Heuristic Approaches. Comput. Elect. Agric. 140, 203–213. doi:10.1016/j.compag.2017.05.036

CrossRef Full Text | Google Scholar

Wu, J., Wang, Y.-G., Burrage, K., Tian, Y.-C., Lawson, B., and Ding, Z. (2020). An Improved Firefly Algorithm for Global Continuous Optimization Problems. Expert Syst. Appl. 149, 113340. doi:10.1016/j.eswa.2020.113340

CrossRef Full Text | Google Scholar

Wu, L., Huang, G., Fan, J., Ma, X., Zhou, H., and Zeng, W. (2020). Hybrid Extreme Learning Machine with Meta-Heuristic Algorithms for Monthly pan Evaporation Prediction. Comput. Elect. Agric. 168, 105115. doi:10.1016/j.compag.2019.105115

CrossRef Full Text | Google Scholar

Xue, X. (2020). A Compact Firefly Algorithm for Matching Biomedical Ontologies. Knowl Inf. Syst. 62, 2855–2871. doi:10.1007/s10115-020-01443-6

CrossRef Full Text | Google Scholar

Yuan, X., Chen, C., Lei, X., Yuan, Y., and Muhammad Adnan, R. (2018). Monthly Runoff Forecasting Based on LSTM-ALO Model. Stoch Environ. Res. Risk Assess. 32, 2199–2212. doi:10.1007/s00477-018-1560-y

CrossRef Full Text | Google Scholar

Zhang, Q., Deng, D., Dai, W., Li, J., and Jin, X. (2020). Optimization of Culture Conditions for Differentiation of Melon Based on Artificial Neural Network and Genetic Algorithm. Sci. Rep. 10, 1. doi:10.1038/s41598-020-60278-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, T., Liu, Y., Rao, Y., Li, X., and Zhao, Q. (2020). Optimal Design of Building Environment with Hybrid Genetic Algorithm, Artificial Neural Network, Multivariate Regression Analysis and Fuzzy Logic Controller. Building Environ. 175, 106810. doi:10.1016/j.buildenv.2020.106810

CrossRef Full Text | Google Scholar

Zhi, H., and Liu, S. (2019). Face Recognition Based on Genetic Algorithm. J. Vis. Commun. Image Representation 58, 495–502. doi:10.1016/j.jvcir.2018.12.012

CrossRef Full Text | Google Scholar