Pan Xiong1
Cheng Long2
Huiyu Zhou3Roberto Battiston4,5
Angelo De Santis6
Dimitar Ouzounov7Xuemin Zhang1Xuhui Shen8*- 1Institute of Earthquake Forecasting, China Earthquake Administration, Beijing, China
- 2School of Computer Science and Engineering, Nanyang Technological University, Singapore, Singapore
- 3School of Computing and Mathematical Sciences, University of Leicester, Leicester, United Kingdom
- 4Department of Physics, University of Trento, Trento, Italy
- 5National Institute for Nuclear Physics, The Trento Institute for Fundamental Physics and Applications, Trento, Italy
- 6Istituto Nazionale di Geofisica e Vulcanologia, Rome, Italy
- 7Center of Excellence in Earth Systems Modeling & Observations, Chapman University, Orange, CA, United States
- 8National Institute of Natural Hazards, Ministry of Emergency Management of China, Beijing, China
During the lithospheric buildup to an earthquake, complex physical changes occur within the earthquake hypocenter. Data pertaining to the changes in the ionosphere may be obtained by satellites, and the analysis of data anomalies can help identify earthquake precursors. In this paper, we present a deep-learning model, SeqNetQuake, that uses data from the first China Seismo-Electromagnetic Satellite (CSES) to identify ionospheric perturbations prior to earthquakes. SeqNetQuake achieves the best performance [F-measure (F1) = 0.6792 and Matthews correlation coefficient (MCC) = 0.427] when directly trained on the CSES dataset with a spatial window centered on the earthquake epicenter with the Dobrovolsky radius and an input sequence length of 20 consecutive observations during night time. We further explore a transferring learning approach, which initially trains the model with the larger Electro-Magnetic Emissions Transmitted from the Earthquake Regions (DEMETER) dataset, and then tunes the model with the CSES dataset. The transfer-learning performance is substantially higher than that of direct learning, yielding a 12% improvement in the F1 score and a 29% improvement in the MCC value. Moreover, we compare the proposed model SeqNetQuake with other five benchmarking classifiers on an independent test set, which shows that SeqNetQuake demonstrates a 64.2% improvement in MCC and approximately a 24.5% improvement in the F1 score over the second-best convolutional neural network model. SeqNetSquake achieves significant improvement in identifying pre-earthquake ionospheric perturbation and improves the performance of earthquake prediction using the CSES data.
Introduction
Earth observation by satellites offers several advantages such as wide coverage, short repeat observation period, fast data update, and non-restriction by ground conditions, which makes up for the shortcomings of conventional ground-based observations that cannot attain large-area, dynamic, and continuous earthquake precursor information (Shen et al., 2013). Among such observation satellites, the China Seismo-Electromagnetic Satellite (CSES) (Shen et al., 2018) [as known as ZhangHeng-1 (ZH-1)] and DEMETER (Detection of Electromagnetic Emissions Transmitted from Earthquake Regions) (Parrot, 2006) were launched in February 2018 and June 2004, respectively, which have been designed to detect variations in the electromagnetic environment in space to support earthquake monitoring and research. These satellites have accumulated a wealth of scientific data and enabled many research achievements over the years of their continuous operation.
Ionospheric anomalies related to earthquakes are typically investigated via case studies and statistical analyses. Two magnitude 6.9 and 7.4 earthquakes struck the area of Kii-Peninsula (Lat = 33.05°N, Long = 136.78°E) on September 5, 2004 at 10.07.07 and 14.57.18 UT, respectively, were the first for which many ionospheric perturbations were identified as earthquake precursors using the DEMETER data (Parrot et al., 2006a). It was discovered by Zhang et al. (2009) that the ion density dropped suddenly 3 days before the Wenchuan earthquake struck on May 12, 2008, and that the ion density dropped to its lowest level 3 days before the earthquake. About a month before the earthquake, the equatorial ionosphere started to exhibit anomalies, and it peaked 8 days before the mainshock (Ryu et al., 2014b). Píša et al. (2011) showed that the plasma density increased remarkably before an earthquake in Chile. Many studies have confirmed that ionospheric perturbations recorded by DEMETER can detect anomalies related to earthquakes with good sensitivity, including the 2007 Pu’er earthquake (Mofiz and Battiston, 2009; He et al., 2011), and earthquakes in L’Aquila (Bertello et al., 2018) and Haiti (Athanasiou et al., 2011). The CSES data have also recorded perturbations in ionospheric plasma parameters before large earthquakes. The first earthquake with Ms > 7.0 recorded by CSES was the Ms 7.1 earthquake in Mexico on February 17, 2018; disturbances in low-frequency electromagnetic waves and ionospheric plasma were found 1 day before the earthquake (Shen et al., 2020). Yan et al. (2018b) analyzed the electron density observed by the Langmuir probe (LAP) on the CSES before the Ile Hunter M7.1 earthquake on August 29, 2018, and found that the electron density (Ne) near the epicenter suddenly increased 12 and 9 days before the event. The 6.9-magnitude 2018 Bayan earthquake has also been studied in detail for co-seismic and precursor phenomena (Piersanti et al., 2020b) using CSES, ERA-5, and ground data. Vertical Total Electron Content (VTEC) precursor anomalies were detected starting 5.3 h before the earthquake, accompanied by a sharp, temporary decrease of the Frequency Resonance Line (FLR) 6 h before the earthquake and followed by a similar co-seismic FLR decrease. Marchetti et al. (2020) investigated ionosphere disturbances associated with the Ms 7.5 earthquake in Indonesia on September 28, 2018, by analyzing the electron density and magnetic data from the CSES during a quiet geomagnetic period and found that anomalies were concentrated around 2.7 months before the quake. In addition, there are many techniques used to detect pre-earthquake ionospheric anomalies, such as Global Navigation Satellite System (GNSS), Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC), etc. Shi et al. (2021) investigated ionospheric anomalies in the F2 region (Nmf2), vertical structure (GNSS radio occultation profile) and multi-height (electron density) pre-earthquake anomalies for the Concepcion, Chile, earthquake (February 27, 2010, Mw 8.8). The findings indicate that there were evident local Nmf2 disturbances in the epicenter region for up to 5 h on the 21st and 25th of February. The perturbations of the radio occultation profiles, as well as the interaction of other layers of the ionosphere, indicated the presence of fluctuation signals with significant long-wavelength fluctuations >50 km in the F layer. Total electron content (TEC) and oblique electron content (STEC) data from GNSS sites near the April 25, 2015 Mw7.8 earthquake in Nepal (Shi et al., 2020) and the January 23, 2018 Mw7.9 earthquake in Alaska (Zhang et al., 2021), after processing and analysis by the singular spectrum analysis (SSA) method, revealed a large-scale TEC anomaly in the epicenter and conjugate region.
Statistical research is a way for studying pre-earthquake ionospheric anomalies. Němec et al. (2008,2009) conducted statistical research using electric-field data up to 10 kHz, and the statistics show a significant reduction in wave intensity of 4–6 dB in several hours before the earthquake. Similar but less prominent (only two sigmas) results were also found by Píša et al. (2012,2013). The correlation between the equatorial anomalies observed by DEMETER and seismic activities have been analyzed based on electric-field measurements (Hobara et al., 2013) and equatorial plasma density (Ryu et al., 2014a). Further, other statistical analyses using the complete DEMETER dataset have shown that the number of disturbances first increases and then gradually decreases during earthquakes (Li and Parrot, 2013; Yan et al., 2017; Parrot and Li, 2018; Xiong et al., 2020). De Santis et al. (2019c) used 2.5 years of data from the Swarm satellite to analyze magnetic field and electron density data for months before and after the 12 strong earthquakes. They discovered significant concentrations of electron density and magnetic anomalies that occurred 2 months to a few days before the earthquakes and magnetic anomalies that occurred after the earthquakes. De Santis et al. (2019b) then used more Swarm three-satellite data (4.7 years) to confirm the findings. The CSES team has examined strong earthquakes with Ms > 6.0 in China and earthquakes of Ms > 7.0 worldwide since the CSES launch and explored the characteristics and mechanisms of ionospheric disturbances characteristics before and after earthquakes (Shen et al., 2020).
However, most existing studies have only examined pre-earthquake ionospheric anomalies in the context of specific earthquakes; the lack of consistent analysis methods and anomaly evaluation metrics may lead to inconsistent analysis results for the same earthquakes. Therefore, suitable and generalizable research methods must be developed. In this study, we proposed and tested an efficient analysis method for pre-earthquake ionospheric perturbations discrimination using electromagnetic satellite data accumulated over many years by utilizing deep-learning techniques widely used in recent earthquake studies (Rouet-Leduc et al., 2018; Bergen et al., 2019; Gulia and Wiemer, 2019; Ross et al., 2019; Xiong et al., 2020).
Pre-earthquake perturbation identification using LAP data (Lebreton et al., 2006; Yan et al., 2018a) with electron temperature and electron density data from the CSES and DEMETER datasets was explored using a sequence-to-sequence architecture based on deep transfer learning; these data covered earthquakes worldwide. As CSES has only accumulated a few years of data since its launch, and thus, has covered relatively less earthquakes, the analysis of these data may not be robust. An extensive database containing more than 6 years of data from DEMETER and the transfer-learning technique (Pan and Yang, 2010) was used to overcome this limitation. First, we employed the DEMETER data to train an ensemble model combined with a convolutional neural network (CNN) and a bidirectional long short-term memory (Bi-LSTM) network. We then further trained the model with a small set of CSES data. The proposed method, known as SeqNetQuake, is a deep-learning method based on a sequence-based classification neural network for pre-earthquake perturbation identification, and its performance is compared to that of other state-of-the-art techniques. Finally, the method’s results allowed us to perform a test of hypothesis regarding the physical mechanisms of earthquake-induced ionospheric perturbations.
Data and Processing
Dataset
CSES and DEMETER satellites were both launched specifically with the purpose of monitoring earthquakes. The DEMETER satellite was launched in 2004 by France and ceased data collection at the end of 2010, with an operating time of 6.5 years (Parrot, 2006). Data along more than 30,000 orbits were obtained, which provided a solid data foundation for the research in earthquake monitoring and ionospheric physics. During the operation of the DEMETER satellite, preliminary preparations for the CSES program were initiated and successfully launched on February 2, 2018 (Shen et al., 2020). However, compared to DEMETER, CSES is designed for a lower orbit altitude of 507 km, which is closer to the ionospheric peak region; the lifting and lowering nodes are at 14:00 and 02:00 local time, also known as day-side or night-side orbits, and the day-side observation time is when the peak ionospheric electron density occurs; the satellite revisiting time is set to 5 days, which is denser than the 16 days revisiting time of the DEMETER satellite.
Of the scientific payloads on CSES, the LAP is the in situ space plasma detection device (Liu et al., 2018). LAP can measure electron density (Ne) in the range of 5 × 102–1×107 cm−3, and electron temperature (Te) in the range of 500–10,000 K, with a relative accuracy of 10%, allowing the analysis of Ne and Te to study space plasma physical phenomena and ionospheric changes caused by earthquakes, magnetic storms, and other events. CSES data, including LAP electron density and electron temperature from August 1, 2018 to June 22, 2020, were utilized in this study. During this period, 6004 EQs with magnitudes ≥4.8 were recorded (USGS: http://www.usgs.gov). Due to the impact of the magnetic storm and the Sumatra earthquake from November to December 2004, we excluded the data from the DEMETER satellite in 2004 and started our study using the data from 2005 onwards. The DEMETER data used in this study included LAP electron density and electron temperature from 2005 to the end of 2010. During this period (about 6 years), 20,727 EQs with magnitudes ≥4.8 were recorded. The Kp index was referenced to avoid the effect of solar and magnetic activities (Kp > 3) in this paper.
Data Processing
To avoid mixing pre-and post-seismic effects, we deleted the aftershocks from the list of earthquakes in this study (Yan et al., 2017). In our study, all the seismic events in the area of 2° × 2° centered on the epicenter and within 15 days after the given earthquake were considered aftershocks. The choice of 15 days as the largest anticipation time of the pre-earthquake anomaly was made for convenience; otherwise, we could not exclude dependence on the impending earthquake magnitude (De Santis et al., 2019b). We first sorted the list of seismic events by time, selecting and removing the aftershocks for an earthquake (given earthquake) in the list in turn. After these operations, we dropped 3013 and 11,815 aftershocks for CSES and DEMETER data analysis. Finally, 2991 (CSES) and 8912 (DEMETER) independent earthquakes remained on the list, respectively. Additionally, we also deleted the data corresponding to the aftershocks.
To validate the dependability of machine learning technologies and to enhance their robustness, we generated the same number of artificial non-seismic events as real earthquakes, randomizing and shifting times and locations to avoid overlapping with the real earthquakes. We randomly sampled time, latitude, and longitude within the selected spatio-temporal range, following the given constraints: 1) the longitude or latitude is not within 10° before and after the longitude or latitude of a real earthquake, and 2) the time is not within 15 days before and after a real earthquake.
The operational modes of the Langmuir Probe onboard CSES include survey mode and burst mode (Yan et al., 2018a). As the sweeping period of the two modes is different, we used simple linear interpolation to interpolate the data in the survey mode so that the time resolution of the two modes was 1.5 s.
Methods
The continuously observed satellite data is susceptible to errors caused by satellite payload interference, space environment, and other factors. To avoid such errors, we used fixed-length sliding windows (also called “sequences”) to partition continuous observation data and used them as inputs to our proposed model. Moreover, because time series data is a strongly auto-correlated series of values, we segmented the data as continuous, but not overlapping, sliding windows. To ensure that the data in each time window were continuous, we carefully checked the time difference between the first and the last data points sorted by time in each time window and deleted time series windows with unreasonable time differences (i.e., gaps). Then, we formulated the pre-earthquake ionospheric perturbation discrimination task as a multiclass multivariate time series classification problem, where the non-seismic-related data were labeled as 0, seismic-related data were labeled as 1, and the data with a Kp index greater than 3 (regardless of whether the data were related to an earthquake) were labeled as 2, which indicated density perturbations due to solar and magnetic activity (Parrot et al., 2006b), as depicted in Figure 1. The labeled sequence data are well illustrated in Supplementary Figure S1, which show real cases of different labels. The red dashed boxes in Supplementary Figure S1 indicate non-seismic data with labeled 0. The green dashed boxes indicate seismic-related data with labeled 1 before the Chile Ms 8.8 earthquake on February 27, 2010. The blue dashed boxes are synchronous perturbations (labeled as 2) with large fluctuations in the data during the large magnetic storm on May 15, 2005.
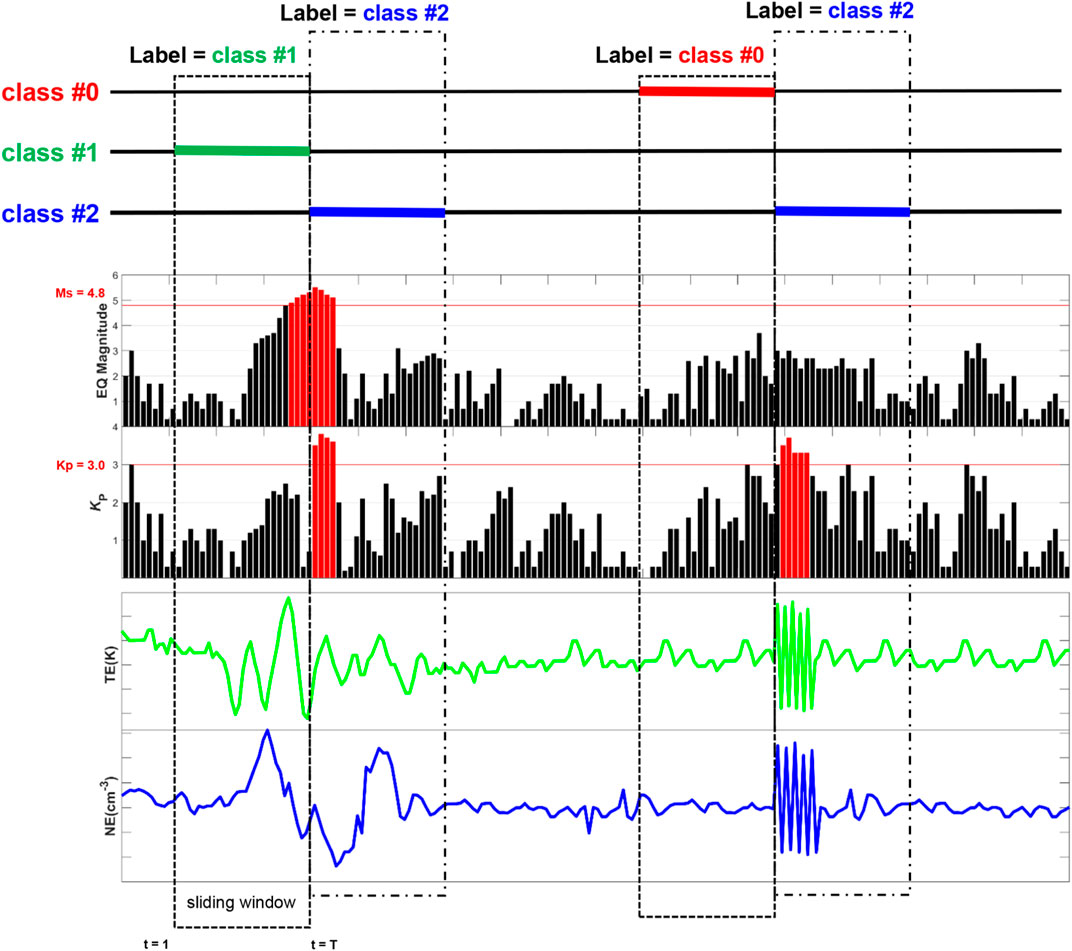
FIGURE 1. Sequence labeling after segmenting the data with a sliding window. Consecutive observations of Ne and Te are segmented by non-overlapping sliding windows. T is the length of the window. Non-seismic data are labeled as 0 (class #0), seismic-related data are labeled as 1 (class #1), and data with a Kp index >3 are labeled as 2 (class #2), regardless of whether or not they are related to an earthquake.
The Earth’s magnetic field experiences temporal fluctuations and displays known trends associated with the movement of the poles, and time series data have strong autocorrelation properties. Each dataset was rigorously divided into two contiguous parts: the first 80% (chronologically) of the data were used for model training, and the last 20% for testing and final evaluation. Specifically, the DEMETER dataset was divided into TR0 (training set) and TS0 (test set), and the CSES dataset was divided into TR1 (training set) and TS1 (test set). We first trained the deep-learning models with the DEMETER dataset; its architecture is shown in Figure 2. Then, we further tuned the models with the CSES dataset for transfer learning.
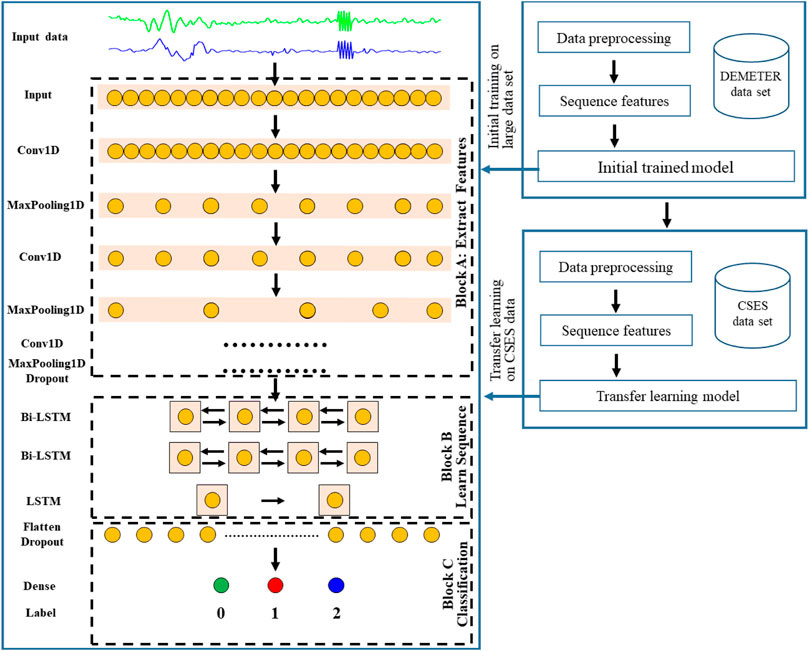
FIGURE 2. Generalized model architecture of SeqNetQuake and the transfer learning process. Conv1D: 1-D convolutional neural network; MaxPooling1D: 1-D max-pooling layer; Dropout: drop-out layer; Bi-LSTM: bidirectional long short-term memory layer. “Flatten” and “Dense” are the names of the functional layers.
Deep Neural Networks
In our study, we combined a CNN and Bi-LSTM to train our proposed model SeqNetQuake (Figure 2). The model’s architecture is composed of one-dimensional convolutional layers, a one-dimensional Bi-LSTM structural layer, and a fully connected (FC) block. The SeqNetQuake model employs CNN layers to extract features from the input data and Bi-LSTMs for sequence prediction. SeqNetQuake reads subsequences of the main sequence as blocks, extracts features from each block, and then allows the LSTM layer to interpret the extract features. To enable the same CNN model to read each subsequence in the window, the whole CNN model is wrapped in a TimeDistributed layer. After flattening the retrieved features, they are forwarded to the Bi-LSTM layer for reading, and further features are extracted. Conceptually, the 1D convolutional layers are used to extract the data features, after which the Bi-LSTM structures optimize the feature extraction in the sequential data. Finally, an FC layer is employed to generate a classification probability. The loss function was categorical cross-entropy, and the optimization was performed using the Adam method (Kingma and Ba, 2014).
The suggested model was developed using the Keras (v 2.3.0) interface with TensorFlow 2.0 (Abadi et al., 2016). To facilitate fast training, all models were built on a server equipped with two Intel Xeon E5-2650 v4 CPU processors, 128 GB of RAM, and an NVIDIA GeForce RTX 2080 Ti graphics processing unit (GPU) (Oh and Jung, 2004). As the proposed method is sensitive to the selected parameters, Bayesian hyperparameter tuning (Snoek et al., 2012) was utilized to determine the parameters that provide the best performance, and the Hyperopt Python package (Bergstra et al., 2013) was used to implement it. In this process, the negative of the F-measure (F1) was used as the return value (loss) of the objective function. The process selects the most promising hyperparameters based on their ability to minimize an objective function by building a probability model based on the past evaluation results. Thus, this study can better perform with fewer iterations than the required efforts to conduct random and grid searches. Supplementary Table S2 provides the information on the search space for the significant parameters of SeqNetQuake. The maximum number of iterations for each model was set to 100. Supplemental Dataset S1 provides the hyperparametric optimization trial results for all the datasets passed through SeqNetQuake and other benchmarking classifiers when we train the model.
Transfer Learning
Transfer learning describes when a complex model that has been trained using a large dataset for a specific task is further trained for a related task with limited data (Pan and Yang, 2010). We used the training data from the large DEMETER dataset (TR0) for initial training, the test data of the large DEMETER dataset (TS0) was used for testing the initial model, and then transfer learning was employed using the small CSES training dataset (TR1) (Figure 2). All the weights/parameters that were learned using TR0 were retrained for TR1. We trained all the model weights without freezing any layer during transfer learning, as this approach provides better results (Hanson et al., 2020). The small CSES test dataset (TS1) was used as an independent test set during transfer learning, and the hyperparameters used were the same as those employed when we train the models on the TS0 dataset.
Performance Evaluation
The DEMETER and CSES datasets are often class imbalanced where the number of the samples representing non-seismic class is much higher than the number of the samples in the other classes (Japkowicz and Stephen, 2002). In this case, a trivial classifier that predicts each sample as the majority class can obtain very high accuracy, and therefore, the overall classification accuracy is not accurate to evaluate the performance. Therefore, we use the F-measure (F1) evaluation model, which considers the correct classification of each class to be equally important. The F1-score is a metric that combines precision and recall. It is usually described as the harmonic mean of both. Thus, the class imbalance is countered by weighting different classes according to their sample proportions.
Beyond the metric mentioned above, which emphasize the positives, the Matthews correlation coefficient (MCC) (Matthews, 1975) is also adopted.
Further, receiver operating characteristic (ROC) curves, plots of the true positive rate (TPR) against the false-positive rate (FPR), were used to evaluate the classifier’s output quality in this study. ROC curves are typically used in binary classification contexts to evaluate the output of a classifier. To extend the ROC curve and ROC area for multiclass classification, the output is binarized, and one ROC curve can be drawn and used to evaluate classifier quality per class. In addition, we calculated the area under the ROC curve, termed as AUC, which is used to distinguish different models. Higher AUC values were considered to be indicative of superior methods for the identification of pre-earthquake ionospheric perturbations.
Finally, to visually demonstrate the classification performance of each class, ternary probability diagrams and confusion matrixes were used to show the probability distributions for each input class of the test data and the distribution of the predictions and actual values.
Comparison of the Methods
Five state-of-the-art methods were benchmarked for the study task: the gradient boosting machine (GBM) (Friedman, 2001), deep neural network (DNN) (LeCun et al., 2015), random forest (RF) (Geurts et al., 2006), CNN (Krizhevsky et al., 2012), and LSTM (Hochreiter and Schmidhuber, 1997) models. These methods were implemented in Python (v 3.6) with scikit-learn (v 0.20.0) and Keras (v 2.3.0). As the investigated models are sensitive to parameter selection, we chose parameters that yielded the best performance using Bayesian hyperparameter tuning, as described above. After optimal parameters were determined for each method, the performances of the different methods were compared.
Results
Direct Training Using CSES Data
We first directly trained the proposed SeqNetQuake model using the CSES dataset, which was further contiguously divided into a training set (TR1) and a test set (TS1). Given that there is no universal standard for the lengths of the input sequence and the spatial window, we initially configured the data with 10 consecutive observations as the input sequence length, a spatial window centered at the epicenter, a deviation of 3°, and nighttime data in the initial configuration (DataSet 01 in Supplementary Table S1).
As shown in Supplementary Figure S2, ROC curves are adopted as a performance metric, as they depict relative trade-offs between true positives (benefits) and false positives (costs) for each class; the model’s performance using nighttime data is displayed for three classes. Supplementary Figures S2A–C demonstrates that the AUC values of classes 0 and 1 are higher than 0.7, indicating that the model can roughly identify the time series related to earthquakes and non-seismic events, but the AUC of class 2 is only 0.6128, indicating that the model’s accuracy in identifying space weather such as magnetic storms is not high. This may be attributed to the smaller number of samples used to train class 2, which could have led the model to fail to extract the features of this class. Supplementary Figure S2D shows the bar plot curves of MCC, F1 score, and accuracy, which reflect the model’s overall performance. The results are similar to those implied by the ROC curves, indicating that the model can distinguish, to some extent, earthquakes, non-seismic, and space events. In general, the performance of the model based on the initial configuration was reasonable but relatively weak. Therefore, we explored whether combining datasets with different temporal and spatial features or different models may offer better performance.
Nighttime vs. Daytime Data
Data acquisition time may impact pre-earthquake electromagnetic perturbation identification. A daytime dataset (DataSet 02 in Supplementary Table S1) was generated to demonstrate the influence of data acquisition time. As shown in Figure 3 and Table 1, benchmarking datasets collected during the daytime and nighttime were used to compare SeqNetQuake’s results with different data acquisition times. We employed AUC, MCC, F1, and accuracy metrics to evaluate the model’s performance.
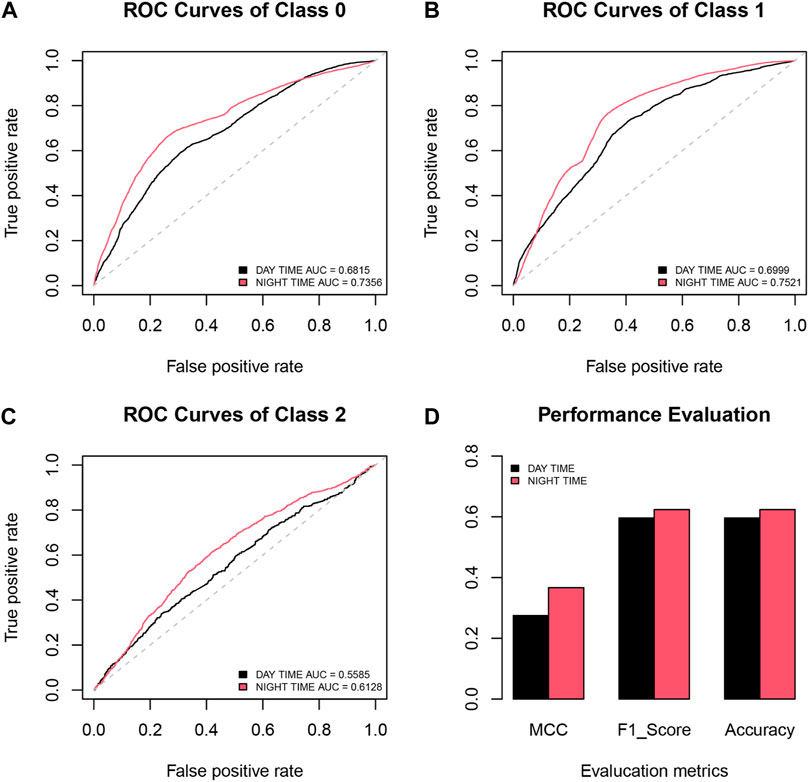
FIGURE 3. Receiver operating characteristic (ROC) curves displaying the performance comparison between model use in the nighttime and daytime data for (A) class 0, (B) class 1 and (C) class 2. (D) Bar plot curves of Matthews correlation coefficient (MCC), F1 score, and accuracy comparing model performance for nighttime and daytime data use.
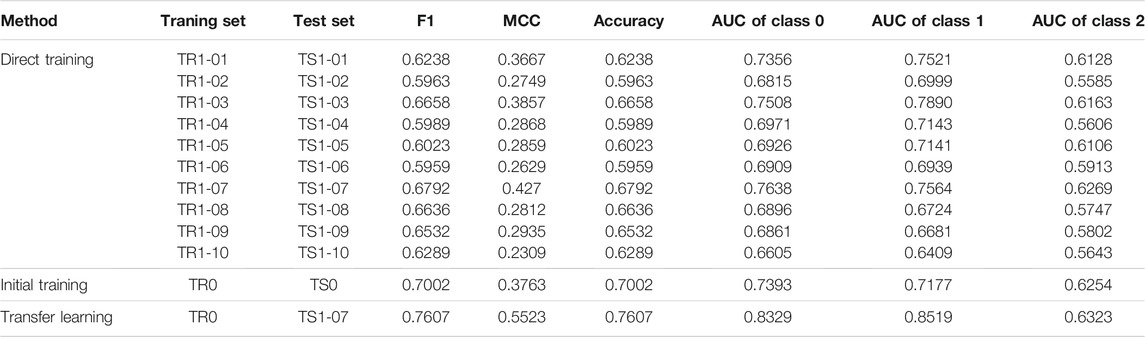
TABLE 1. Performance of SeqNetQuake on the test set after direct training, initial training, and transfer learning. Data from DEMETER were divided into a training set (TR0) and test set (TS0), and data from CSES were divided into TR1 (training set) and TS1 (test set).
In general, we discovered that the use of the nighttime datasets (DataSet 01 in Supplementary Table S1) leads to better classification performance than the daytime dataset for the same spatial and temporal features (Table 1). The ROC curves of SeqNetQuake for both datasets are shown in Figures 3A–C, and we can see that the AUC curve of SeqNetQuake with the nighttime data is a little higher than that with the daytime data, with about 8, 8, and 10% improvements in AUC for the three classes. When all the classes are considered, the F1 score of SeqNetQuake increases from 0.5963 to 0.6238 when the nighttime data are used, compared to those when the daytime data are used, and MCC improves by 33% (Table 1). Figure 3D compares the daytime and nighttime MCC, F1 score, and accuracy values, all of which show better performance with the nighttime data. These findings may represent a small number of significant changes in daytime data, since ionospheric conditions are often more disrupted during the day, making identification of seismic electromagnetic impacts more challenging. This conclusion is consistent with statistical findings on electromagnetic disturbances associated with earthquake activity (De Santis et al., 2019b; Němec et al., 2008,2009; Píša et al., 2012,2013).
Effect of Input Sequence Length
We observed that using the dataset with 10 consecutive observations (DataSet 01) per sliding window as the input sequence length yields good classification performance. To further study whether the SeqNetQuake method can identify pre-earthquake perturbations using different input sequence lengths, datasets with an input sequence length of 20 consecutive observations (DataSet 03), 30 consecutive observations (DataSet 04), 40 consecutive observations (DataSet 05), and 50 consecutive observations (DataSet 06) were generated (Supplementary Table S1).
Figure 4 shows the ROC curves and MCC, F1 score, and accuracy bar plot curves for the datasets with different input sequence lengths. Table 1 shows the classification performance measures using SeqNetQuake. As shown in Table 1, the overall F1 scores range from 0.5959 to 0.6658, and the MCC ranges from 0.2629 to 0.3875 for different datasets; these values are also demonstrated in performance comparison in Figure 4D. When the input sequence length increases, the model’s performance fluctuates; the best performance is achieved using the dataset with the input sequence length of 20 consecutive observations (DataSet 03). The ROC curves shown in Figures 4A–C also suggest that SeqNetQuake provides satisfactory performance for each class using DataSet 03. However, SeqNetQuake’s performance becomes worse if the input sequence length increases by more than 20. We infer from these findings that the length of the input sequence has an impact on the results of the SeqNetQuake model and that the best performance is achieved with an input sequence of 20 consecutive observations.
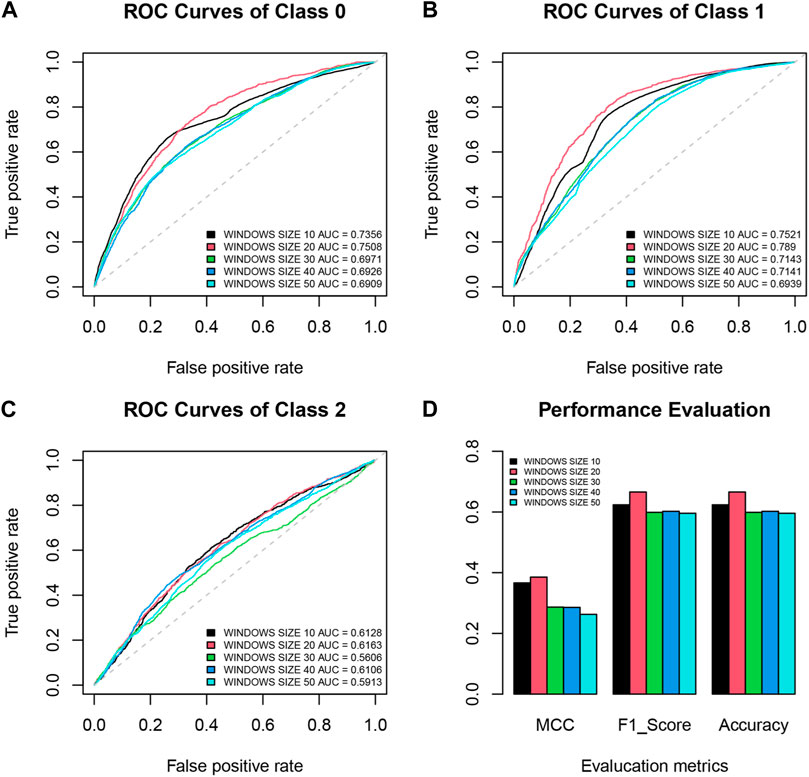
FIGURE 4. Receiver operating characteristic (ROC) curves comparing model performance with window sizes of 10, 20, 30, 40, and 50 for (A) class 0, (B) class 1 and (C) class 2. (D) Bar plot curves of Matthews correlation coefficient (MCC), F1 score, and accuracy with window sizes of 10, 20, 30, 40, and 50.
Effect of Different Spatial Windows
SeqNetQuake performed well for a circular region centered at the epicenter with a deviation of 3° (DataSet 03). To further explore the influence of different spatial windows on the model’s performance, satellite datasets using spatial windows with Dobrovolsky radius (DataSet 07), a deviation of 5° (DataSet 08), 7° (DataSet 09), and 12° (DataSet 10) were generated (Supplementary Table S1).
Rows 6 to 10 in Table 1 show the SeqNetQuake’s performance using the five datasets, and Figure 5 shows the ROC curves and MCC, F1 score, and accuracy bar plot curves. SeqNetQuake attains the best performance using the dataset with the spatial window radius given by the Dobrovolsky’s formula (DataSet 07), achieving an F1 score of 0.6792 and an MCC of 0.427. Comparing the results from Figure 5D and Table 1 reveals a slight increase in the overall performance achieved when the spatial windows are larger. This trend is also shown in the ROC curves in Figures 5A–C, and the AUC value of DataSet 07 is the best among the datasets. Though the explanation for these results is unclear, it might concern the fact that, geometrically, a disturbance traveling upward from the earth surface may alter the ionosphere’s characteristics, and the radius of the affected region matches the radius estimated using Dobrovolsky’s formula.
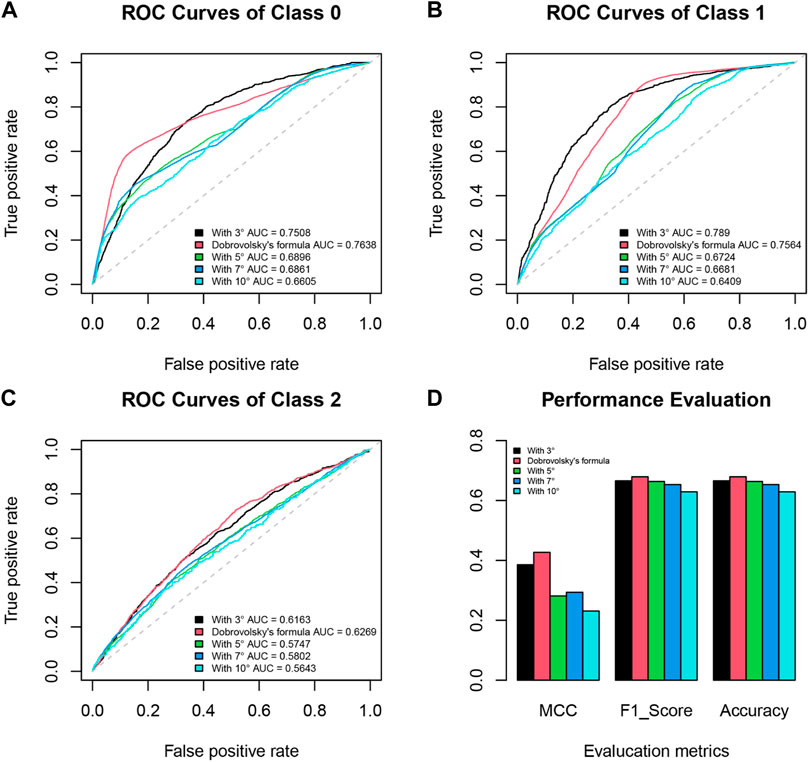
FIGURE 5. Receiver operating characteristic (ROC) curves comparing model performance with different spatial window radii (3°, Dobrovolsky’s formula, 5°, 7°, and 10° for (A) class 0, (B) class 1, and (C) class 2. (D) Bar plot curves of Matthews correlation coefficient (MCC), F1 score, and accuracy.
Initial Training on DEMETER Data and Transfer Learning on CSES Data
A DEMETER dataset was generated based on the optimal spatio-temporal feature configuration for the CSES data (DataSet 11 in Supplementary Table S1). In this study, deep transfer learning, although it is first applied to DEMETER to be transferred to CSES, considers the properties and features of CSES data. In other words, it is shaped/adapted to CSES data features.
We first trained the SeqNetQuake model using the full DEMETER dataset, which was contiguously divided into a training set (TR0) and test set (TS0). Using TR0 for training, TS0 for testing, and the sliding sequences as model input, we trained deep-learning models with its architecture shown in the left panel of Figure 2. The performance of the best model using TS0 is shown in Table 1. The F1 score of 0.7002 and MCC of 0.3763 for TS0 suggest the robustness of the trained model.
The model obtained using the DEMETER data was further trained using the CSES data employing TR1 (training set) and TS1 (test set), which corresponds to a transfer-learning process. The TS1 set was independent of the training data (TR0 and TR1). Table 1 and Figure 6D further illustrate the performance of the initial training and transfer training. The F1 score improved by 8% from 0.7002 to 0.7607, and MCC increased from 0.3763 to 0.5523 using TR0 for training, confirming the robustness of the model trained using the larger DEMETER dataset. The ROC curves in Figures 6A–C provide a visual performance comparison of each class and further demonstrate the result.
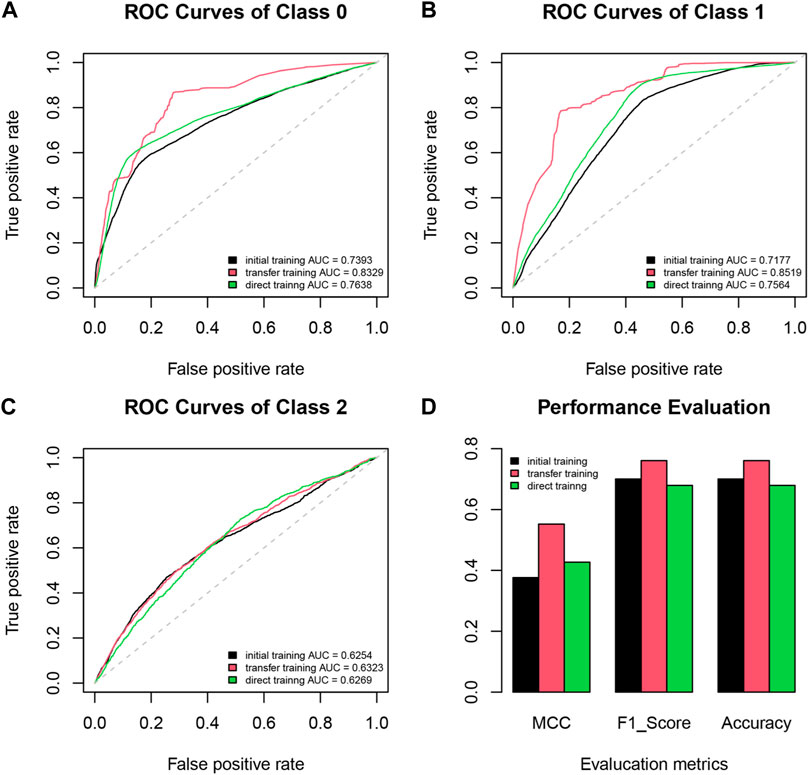
FIGURE 6. Receiver operating characteristic (ROC) curves comparing the performance of initial training, transfer training, and direct training for (A) class 0, (B) class 1 and (C) class 2. (D) Bar plot curves of Matthews correlation coefficient (MCC), F1 score, and accuracy.
Comparison Between Transfer Learning and Direct Learning
We selected the model with the best performance in direct learning, the SeqNetQuake model trained on Dataset 07 (called SeqNetQuake-DT), and compared it with the model trained using transfer learning (called SeqNetQuake-TL). Table 2 compares the performance of the two approaches, and Figure 6D shows the bar plot of the performance metrics. Figures 6A–C compares the ROC curves yielded by direct training and transfer learning for the independent test set TS1.
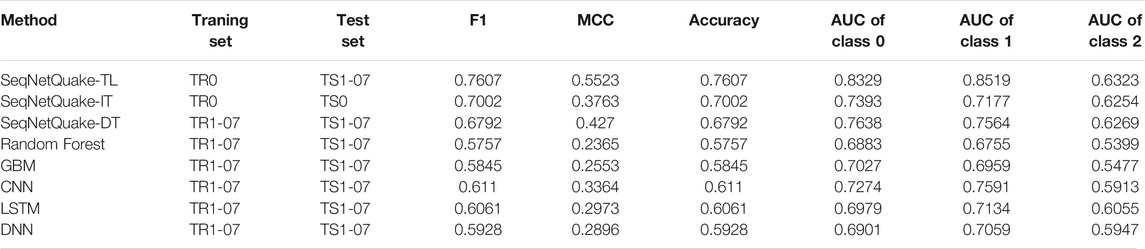
TABLE 2. Performance of all classifiers on the test set TS1. Data from DEMETER were divided into a training set (TR0) and test set (TS0), and data from CSES were divided into TR1 (training set) and TS1 (test set). SeqNetQuake-TL, SeqNetQuake-IT, and SeqNetQuake-DT indicate the SeqNetQuake model trained via transfer learning, initial training, and direct training.
The performance of direct learning was significantly lower than that of transfer learning, yielding a 10% reduction in the F1 score and a 23% reduction of the MCC value. These results confirm the difficulty of using small training data sets (TR1) for direct learning and the need to use large data sets that can effectively exploit the capabilities of the deep-learning networks.
To further confirm the performance of transfer learning, ternary probability diagrams and a confusion matrix were used to indicate the distribution of the predicted and true values and allow more profound insight into the classification performance of the models. Supplementary Figure S3 and Figure 7 show the ternary probability diagrams and the confusion matrix for the three classes obtained from SeqNetQuake-DT and SeqNetQuake-TL, respectively.
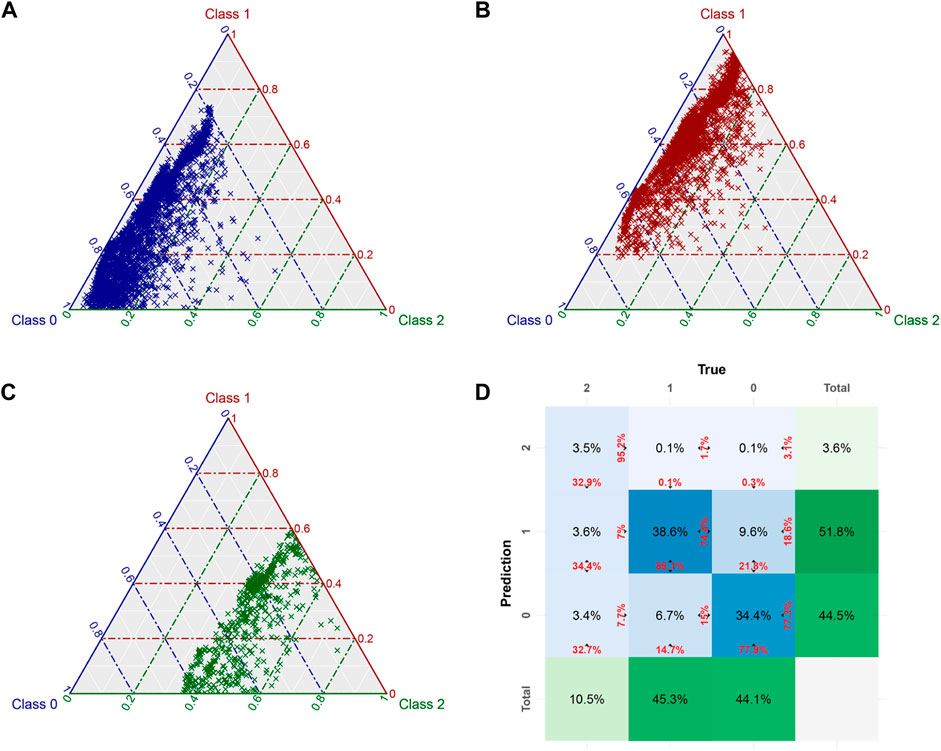
FIGURE 7. Ternary probability diagrams showing transfer learning results for (A) class 0, (B) class 1, and (C) class 2 using the test data. Class 0, class 1, and class 2 are shown in blue, red, and green, respectively; the color of the dot itself represents the real class, and the distance projected from each dot to each class axis represents the probability of that class in the model prediction. (D) Confusion matrix indicating the distribution of the predicted and true values. The normalized count (overall percentage) is shown in the center of each tile. The column percentage is shown at the bottom of each tile, and the row percentage is shown on the right. Sum tiles to the right and bottom of the plot show the overall distribution of predictions and targets. Note that the color intensity is based on the counts.
The ternary probability diagrams allow a qualitative evaluation of the classification results. The number of the correctly classified samples in class 0 increases significantly, as evidenced from Supplementary Figure S3A and Figure 7A; the same trend also appears in the qualitative comparison of class 1 in Supplementary Figure S3B and Figure 7B. For class 2, the direct training results (Supplementary Figure S3B) show that the probability that the model would discriminate the true class is generally only around 0.4. With transfer learning, the probability is significantly improved and is typically higher than 0.5 (Figure 7C). As class 2 only represents 10.5% of samples, far less than the proportions of the other two classes (which are 45.3 and 44.1%, respectively), the model likely fails to fully learn the features of this class, causing a higher error rate.
The confusion matrixes shown in Supplementary Figure S3D and Figure 7D show significant improvements in precision regarding class 2, from 75.3% before transfer learning to 95.2% after. Further, transfer learning achieves 9 and 13.06% improvements in precision for classes 0 and 1, respectively. Therefore the misclassification rate of each class drops significantly after transfer learning. Transfer learning achieves satisfactory results in the classification of classes 0 and 1, and the probability distributions for each class of the test data (Figure 7D) show that 77.9 and 85.1% of the input samples, respectively, are correctly classified (recall).
Comparison With Other Classifiers
Table 2 and Figure 8D report the performance of our transfer-learning model (SeqNetQuake-TL) with five other benchmarking classifiers for the independent test set TS1-07. The performance of the existing methods ranges from F1 = 0.5757 to 0.7607 and MCC = 0.2365 to 0.552. However, SeqNetQuake-TL offers the best performance, improving MCC by 64.2% MCC and F1 by about 24.5% over those for the next-best CNN model. Figures 8A–C compares the ROC curves obtained for the SeqNetQuake-TL model with those of the five other classifiers, and SeqNetQuake-TL again demonstrates the best performance with a 14.5% improvement in AUC for class 0 and a 12.2% improvement for class 1 over the second-best CNN model and a 4.4% improvement in AUC for class 2 over the second-best LSTM model.
FIGURE 8. Receiver operating characteristic (ROC) curves displaying the performance comparison of SeqNetQuake-TL, gradient boosting machine (GBM), deep neural network (DNN), random forest (RF), convolutional neural network (CNN), and long short-term memory (LSTM) models for (A) class 0, (B) class 1 and (C) class 2. (D) Bar plot curves of Matthews correlation coefficient (MCC), F1 score, and accuracy.
Excellent neural network architecture may explain why SeqNetQuake outperforms all the other predictors. First, SeqNetQuake’s CNN network layers allows us to extract local parallel features. Then, the Bi-LSTM layer (composed of multiple memory modules with a two-cell topological structure) extracts long-distance dependent features and performs sequence learning, thereby mitigating the influence of the front and back features of each attribute feature point. Finally, the model obtains the classification results through the FC layer and the Softmax classifier, improving SeqNetQuake’s accuracy and reducing false positives. Notably, the DNN, CNN, and LSTM models performed better than the RF and GBM models, suggesting that the deeper neural network models are much more efficient in computation and the number of the parameters.
Possible Physical Mechanisms of Earthquake-Induced Ionospheric Perturbations
Lithospheric-ionospheric coupling is a topic that has been qualitatively discussed in several papers. Several studies have investigated the physical mechanisms of ionospheric pre-earthquake perturbations (Hayakawa et al., 2010; Pulinets and Ouzounov, 2011; Wu et al., 2012; Ouzounov et al., 2018; De Santis et al., 2019a; De Santis et al., 2020; Freund et al., 2021). Hypotheses regarding these mechanisms were presented by Pulinets et al. (2015) and Kuo et al. (2014), who proposed complex lithosphere–atmosphere–ionosphere coupling as the physical basis of the generation of short-term earthquake precursors. Recently, a detailed mathematical model providing a quantitative description of the Magnetospheric-Ionospheric-Lithospheric-Coupling (MILC) was introduced and successfully tested with data from individual earthquakes (Piersanti et al., 2020a). A key feature of the MILC model is based on the development of an Acoustic Gravity Wave (AGW) (Carbone et al., 2021) interacting mechanically with the ionosphere and then electromagnetically with the magnetosphere. The AGW coupling mechanism is quite general and can provide for both co-seismic and precursor lithospheric-ionospheric coupling. In the case of co-seismic coupling, the AGW is generated by ground surface motion (solid, liquid). In contrast, in the case of precursor coupling, the AGW can be generated by phenomena which modifying the temperature or the electrical properties of the atmospheric column above the EQ preparation zone.
One example of such mechanisms is radon release following by its radioactive decay, emitting alpha particles of 5.2 MeV, a large value used in comparison to the ionization energy required for the dissociation of an atmospheric molecule (32 eV). One alpha particle is sufficient to generate 150,000 pairs of positive and negative ions, thereby creating an excess of positive airborne ions near the Earth’s surface, which can influence the ionosphere. Radon gas accumulates with time in the lower crust and upper mantle and can exhibit large-scale distribution in the rocks. During the preparation phase of an earthquake, these gas domains can become hydrostatically unstable and force their way upward through the lithosphere. The rapid lithospheric degassing followed by radon atoms radioactive decays would trigger several atmospheric processes near Earth’s surface, leading to changes in air conductivity and temperature and therefore changes to the near-ground atmospheric electric field (Ouzounov et al., 2018; Pulinets and Ouzounov, 2018).
Crustal strain measurements typically fail to detect any unusual changes before earthquakes (Soter, 1999), while radon outgassing has been observed before the earthquake (Gold and Soter, 1985; Riggio and Santulin, 2015; Fu et al., 2019), and they are considered as a possible EQ precursor.
Discussion and Conclusion
Previous studies have applied machine learning with the DEMETER data for earthquake prediction and pre-earthquake perturbation analysis. Li et al. (2020) statistically investigated seismo-ionospheric influencing factors; however, the FPR of the statistical results reached 50.2%. The relationship between earthquakes and ultralow frequency (ULF) wave activity in the nighttime ionosphere was investigated by Ouyang et al. (2020). According to their research, the accuracy of detecting electromagnetic pre-earthquake disturbances was 34%. Xu et al. (2010) used a back-propagation neural network to predict seismic events in 2008 with DEMETER data and achieved an accuracy of 69.96%. Finally, Wang et al. (2014) adopted the frequent itemset algorithm to predict earthquakes of Ms > 5.0 in Taiwan, China, and achieved a maximum sensitivity of 70.01%.
When the performance of these models was compared, the SeqNetQuake method outperformed the others. SeqNetQuake offers three main advantages over those existing methods. First, hyperparametric optimization is applied for all the engaged methods, allowing researchers to identify the most suitable parameters at each step. Therefore, technology can be selected with high confidence, and the selection of a robust method is assured. Second, a more advanced deep-learning architecture is used than that in traditional statistical and data-mining methods. Finally, the majority of existing techniques are verified using a limited sample size; this includes the method proposed by Wang et al. (2014), which may exhibit a significant bias toward results covering a wider geographic region or a longer time period. However, in the present study, SeqNetQuake was trained with all the DEMETER data and nearly 2 years of the CSES data worldwide, and global features were learned during the training process. Hence, SeqNetQuake has strong generalizability. One limitation of SeqNetQuake, however, is its significant computational complexity owing to its complex network architecture. This issue may be resolved by increasing the number of processing resources available, such as additional CPUs or GPUs.
Recent research (Ikuta et al., 2020; Eisenbeis and Occhipinti, 2021) showed that claimed TEC anomalies were actually artifacts. However, their negative response is mainly based on the criticisms to some previous papers (Heki, 2011; Heki and Enomoto, 2015; He and Heki, 2017). In this paper, we do not define anomalies in the same way the criticized papers define the TEC anomalies. On the other hand, most seismologists will say that tectonic plates are always in a state of stress, and the stress is always present because the tectonic system constantly adjusts to a state of self-organized criticality, which theoretically would indicate that when and where the earthquake occurred are inherently unpredictable (Bak et al., 1987). Nevertheless, Ramos et al. (2009) proved that earthquakes are preceded by continuous and detectable changes in the interior of the earth’s crust, and these changes can be monitored and have been achieved for prediction purposes: this argument was also confirmed by De Santis et al. (2019b) and Varotsos et al. (2020), with statistical and theoretical arguments, respectively.
In our paper, we proposed the use of deep learning for pre-earthquake ionospheric perturbations identification using the SeqNetQuake model and identifying optimal training regimes and parameter settings. The proposed model offers better performance than five state-of-the-art models. Finally, our analysis results verify the hypothesis regarding the physical mechanisms of earthquake-induced ionospheric perturbations. These results also support that the use of big satellite data analytics and transfer learning can successfully improve the pre-earthquake ionospheric perturbation identification performance. The SeqNetQuake algorithm is useful in the analysis of precursor effects in electromagnetic satellite data.
Data Availability Statement
The CSES data can be acquired from the website (www.leos.ac.cn), and DEMETER data can be accessed through the website https://cdpp-archive.cnes.fr/. The used Kp indices were provided from the World Data Center for Geomagnetism, Kyoto (http://wdc.kugi.kyoto-u.ac.jp/wdc/Sec3.html).
Author Contributions
PX, HZ, RB, AS, DO, and XS: Conceptualization, Methodology, Software. PX and XZ: Data curation, Writing-Original draft preparation. HZ, RB, and AS: Visualization, Investigation. RB and XS: Supervision. PX, CL, and HZ: Software, Validation: PX, CL, HZ, RB, AS, and DO: Writing- Reviewing and Editing.
Funding
This work is funded by the National Key Research and Development of China under Grant No. 2018YFC1503505. This work is also supported by the LIMADOU-Science under Grant No. 2020-31-HH.0, a project funded by the Italian Space Agency (ASI), and INGV Further and MiUR Pianeta Dinamico-Working Earth Project.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2021.779255/full#supplementary-material
Supplementary Figure S1 | Electron density (Ne) and electron temperature (Te) sequence labels from real cases.
Supplementary Figure S2 | Receiver operating characteristic (ROC) curves demonstrating the performance of SeqNetQuake using nighttime data.
Supplementary Figure S3 | Ternary probability diagrams showing the results of SeqNetQuake-DT.
Supplementary Table S1 | Datasets with different features generated using DEMETER and CSES data.
Supplementary Table S2 | Search space of parameters for the SeqNetQuake model.
References
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., et al. (2016). Tensorflow: A System for Large-Scale Machine Learning. Paper presented at the 12th {USENIX} symposium on operating systems design and implementation ({OSDI} 16)
Athanasiou, M. A., Anagnostopoulos, G. C., Iliopoulos, A. C., Pavlos, G. P., and David, C. N. (2011). Enhanced ULF Radiation Observed by DEMETER Two Months Around the strong 2010 Haiti Earthquake. Nat. Hazards Earth Syst. Sci. 11 (4), 1091–1098. doi:10.5194/nhess-11-1091-2011
Bak, P., Tang, C., and Wiesenfeld, K. (1987). Self-organized Criticality: An Explanation of the 1/fnoise. Phys. Rev. Lett. 59 (4), 381–384. doi:10.1103/physrevlett.59.381
Bergen, K. J., Johnson, P. A., de Hoop, M. V., and Beroza, G. C. (2019). Machine Learning for Data-Driven Discovery in Solid Earth Geoscience. Science 363 (6433). Available at: https://www.ncbi.nlm.nih.gov/pubmed/30898903. doi:10.1126/science.aau0323
Bergstra, J., Yamins, D., and Cox, D. D. (2013). “Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures,” in Paper presented at the Proceedings of the 30th International Conference on International Conference on Machine Learning, ICML 2013, Atlanta, GA, USA, 16–21 June 2013, 28, 115–123.
Bertello, I., Piersanti, M., Candidi, M., Diego, P., and Ubertini, P. (2018). Electromagnetic Field Observations by the DEMETER Satellite in Connection with the 2009 L'Aquila Earthquake. Ann. Geophys. 36 (5), 1483–1493. doi:10.5194/angeo-36-1483-2018
Carbone, V., Piersanti, M., Materassi, M., Battiston, R., Lepreti, F., and Ubertini, P. (2021). A Mathematical Model of Lithosphere-Atmosphere Coupling for Seismic Events. Sci. Rep. 11 (1), 8682. Available at: https://www.ncbi.nlm.nih.gov/pubmed/33883652. doi:10.1038/s41598-021-88125-7
De Santis, A., Abbattista, C., Alfonsi, L., Amoruso, L., Campuzano, S. A., Carbone, M., et al. (2019a). Geosystemics View of Earthquakes. Entropy (Basel) 21 (4). Available at: https://www.ncbi.nlm.nih.gov/pubmed/33267126. doi:10.3390/e21040412
De Santis, A., Marchetti, D., Pavón-Carrasco, F. J., Cianchini, G., Perrone, L., Abbattista, C., et al. (2019b). Precursory Worldwide Signatures of Earthquake Occurrences on Swarm Satellite Data. Sci. Rep. 9 (1), 20287. Available at: https://www.ncbi.nlm.nih.gov/pubmed/31889060. doi:10.1038/s41598-019-56599-1
De Santis, A., Marchetti, D., Spogli, L., Cianchini, G., Pavón-Carrasco, F. J., Franceschi, G. D., et al. (2019c). Magnetic Field and Electron Density Data Analysis from Swarm Satellites Searching for Ionospheric Effects by Great Earthquakes: 12 Case Studies from 2014 to 2016. Atmosphere 10 (7), 371. doi:10.3390/atmos10070371
De Santis, A., Cianchini, G., Marchetti, D., Piscini, A., Sabbagh, D., Perrone, L., et al. (2020). A Multiparametric Approach to Study the Preparation Phase of the 2019 M7.1 Ridgecrest (California, United States) Earthquake. Front. Earth Sci. 8, 540398. doi:10.3389/feart.2020.540398
Eisenbeis, J., and Occhipinti, G. (2021). The TEC Enhancement before Seismic Events Is an Artifact. J. Geophys. Res. Space Phys. 126 (4), e2020JA028733. doi:10.1029/2020ja028733
Freund, F. T., Heraud, J. A., Centa, V. A., and Scoville, J. (2021). Mechanism of Unipolar Electromagnetic Pulses Emitted from the Hypocenters of Impending Earthquakes. Eur. Phys. J. Spec. Top. 230 (1), 47–65. doi:10.1140/epjst/e2020-000244-4
Friedman, J. H. (2001). Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 29 (5), 1189–1232. Available at: http://www.jstor.org/stable/2699986. doi:10.1214/aos/1013203451
Fu, C.-C., Lee, L.-C., Yang, T. F., Lin, C.-H., Chen, C.-H., Walia, V., et al. (2019). Gamma Ray and Radon Anomalies in Northern Taiwan as a Possible Preearthquake Indicator Around the Plate Boundary. Geofluids 2019, 1–14. doi:10.1155/2019/4734513
Geurts, P., Ernst, D., and Wehenkel, L. (2006). Extremely Randomized Trees. Mach Learn. 63 (1), 3–42. journal article. doi:10.1007/s10994-006-6226-1
Gold, T., and Soter, S. (1985). Fluid Ascent through the Solid Lithosphere and its Relation to Earthquakes. Pure Appl. Geophys. PAGEOPH 122 (2-4), 492–530. doi:10.1007/BF00874614
Gulia, L., and Wiemer, S. (2019). Real-time Discrimination of Earthquake Foreshocks and Aftershocks. Nature 574 (7777), 193–199. Available at: https://www.ncbi.nlm.nih.gov/pubmed/31597971. doi:10.1038/s41586-019-1606-4
Hanson, J., Litfin, T., Paliwal, K., and Zhou, Y. (2020). Identifying Molecular Recognition Features in Intrinsically Disordered Regions of Proteins by Transfer Learning. Bioinformatics 36 (4), 1107–1113. Available at: https://www.ncbi.nlm.nih.gov/pubmed/31504193. doi:10.1093/bioinformatics/btz691
Hayakawa, M., Kasahara, Y., Nakamura, T., Muto, F., Horie, T., Maekawa, S., et al. (2010). A Statistical Study on the Correlation between Lower Ionospheric Perturbations as Seen by Subionospheric VLF/LF Propagation and Earthquakes. J. Geophys. Res. Space Phys. 115 (A9), n/a. doi:10.1029/2009ja015143
He, L., and Heki, K. (2017). Ionospheric Anomalies Immediately before M W 7.0-8.0 Earthquakes. J. Geophys. Res. Space Phys. 122 (8), 8659–8678. doi:10.1002/2017ja024012
He, Y., Yang, D., Qian, J., and Parrot, M. (2011). Anomaly of the Ionospheric Electron Density Close to Earthquakes: Case Studies of Pu'er and Wenchuan Earthquakes. Earthq Sci. 24 (6), 549–555. doi:10.1007/s11589-011-0816-0
Heki, K., and Enomoto, Y. (2015). M W Dependence of the Preseismic Ionospheric Electron Enhancements. J. Geophys. Res. Space Phys. 120 (8), 7006–7020. doi:10.1002/2015ja021353
Heki, K. (2011). Ionospheric Electron Enhancement Preceding the 2011 Tohoku-Oki Earthquake. Geophys. Res. Lett. 38 (17), n/a. doi:10.1029/2011gl047908
Hobara, Y., Nakamura, R., Suzuki, M., Hayakawa, M., and Parrot, M. (2013). Ionospheric Perturbations Observed by the Low Altitude Satellite DEMETER and Possible Relation with Seismicity. J. Atmos. Electr. 33 (1), 21–29. doi:10.1541/jae.33.21
Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9 (8), 1735–1780. Available at: https://www.ncbi.nlm.nih.gov/pubmed/9377276. doi:10.1162/neco.1997.9.8.1735
Ikuta, R., Hisada, T., Karakama, G., and Kuwano, O. (2020). Stochastic Evaluation of Pre‐Earthquake TEC Enhancements. J. Geophys. Res. Space Phys. 125 (11), e2020JA027899. doi:10.1029/2020ja027899
Japkowicz, N., and Stephen, S. (2002). The Class Imbalance Problem: A Systematic Study1. Intell. Data Anal. 6 (5), 429–449. doi:10.3233/ida-2002-6504
Kingma, D. P., and Ba, J. (2014). Adam: A Method for Stochastic Optimization. arXiv preprint arXiv:1412.6980
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “Imagenet Classification with Deep Convolutional Neural Networks,” in Paper Presented at the Advances in Neural Information Processing Systems 25 (NIPS 2012): 26th Annual Conference on Neural Information Processing Systems (United States: Morgan Kaufmann Publishers, Inc).
Kuo, C. L., Lee, L. C., and Huba, J. D. (2014). An Improved Coupling Model for the Lithosphere-Atmosphere-Ionosphere System. J. Geophys. Res. Space Phys. 119 (4), 3189–3205. doi:10.1002/2013ja019392
Lebreton, J.-P., Stverak, S., Travnicek, P., Maksimovic, M., Klinge, D., Merikallio, S., et al. (2006). The ISL Langmuir Probe experiment Processing Onboard DEMETER: Scientific Objectives, Description and First Results. Planet. Space Sci. 54 (5), 472–486. doi:10.1016/j.pss.2005.10.017
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521 (7553), 436–444. Available at: https://www.ncbi.nlm.nih.gov/pubmed/26017442. doi:10.1038/nature14539
Li, M., and Parrot, M. (2013). Statistical Analysis of an Ionospheric Parameter as a Base for Earthquake Prediction. J. Geophys. Res. Space Phys. 118 (6), 3731–3739. doi:10.1002/jgra.50313
Li, M., Shen, X., Parrot, M., Zhang, X., Zhang, Y., Yu, C., et al. (2020). Primary Joint Statistical Seismic Influence on Ionospheric Parameters Recorded by the CSES and DEMETER Satellites. J. Geophys. Res. Space Phys. 125 (12), e2020JA028116. doi:10.1029/2020ja028116
Liu, C., Guan, Y., Zheng, X., Zhang, A., Piero, D., and Sun, Y. (2018). The Technology of Space Plasma Iin-Ssitu Measurement on the China Seismo-Electromagnetic Satellite. Sci. China Technol. Sci. 62 (5), 829–838. doi:10.1007/s11431-018-9345-8
Marchetti, D., De Santis, A., Shen, X., Campuzano, S. A., Perrone, L., Piscini, A., et al. (2020). Possible Lithosphere-Atmosphere-Ionosphere Coupling Effects Prior to the 2018 Mw = 7.5 Indonesia Earthquake from Seismic, Atmospheric and Ionospheric Data. J. Asian Earth Sci. 188, 104097. doi:10.1016/j.jseaes.2019.104097
Matthews, B. W. (1975). Comparison of the Predicted and Observed Secondary Structure of T4 Phage Lysozyme. Biochim. Biophys. Acta (Bba) - Protein Struct. 405 (2), 442–451. . Available at: https://www.ncbi.nlm.nih.gov/pubmed/1180967. doi:10.1016/0005-2795(75)90109-9
Mofiz, U. A., and Battiston, R. (2009). Possible Ion-Acoustic Soliton Formation in the Ionospheric Perturbations Observed on DEMETER before the 2007 Pu'er Earthquake. Earthq Sci. 22 (3), 257–262. journal article. doi:10.1007/s11589-009-0257-1
Němec, F., Santolík, O., Parrot, M., and Berthelier, J. J. (2008). Spacecraft Observations of Electromagnetic Perturbations Connected with Seismic Activity. Geophys. Res. Lett. 35 (5), L05109. doi:10.1029/2007GL032517
Němec, F., Santolík, O., and Parrot, M. (2009). Decrease of Intensity of ELF/VLF Waves Observed in the Upper Ionosphere Close to Earthquakes: A Statistical Study. J. Geophys. Res. Space Phys. 114 (A4), n/a. doi:10.1029/2008JA013972
Oh, K.-S., and Jung, K. (2004). GPU Implementation of Neural Networks. Pattern Recognition 37 (6), 1311–1314. Available at: http://www.sciencedirect.com/science/article/pii/S0031320304000524. doi:10.1016/j.patcog.2004.01.013
Ouyang, X. Y., Parrot, M., and Bortnik, J. (2020). ULF Wave Activity Observed in the Nighttime Ionosphere above and Some Hours before Strong Earthquakes. J. Geophys. Res. Space Phys. 125 (9), e2020JA028396. doi:10.1029/2020ja028396
Ouzounov, D., Pulinets, S., Tiger Liu, J.-Y., Hattori, K., and Han, P. (2018). “Multiparameter Assessment of Pre-Earthquake Atmospheric Signals,” in Pre‐Earthquake Processes (Hoboken, NJ, USA; Washington, D.C.: John Wiley & Sons, Inc.; American Geophysical Union), 339–359. doi:10.1002/9781119156949.ch20
Pan, S. J., and Yang, Q. (2010). A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 22 (10), 1345–1359. doi:10.1109/tkde.2009.191
Parrot, M., and Li, M. (2018). “Statistical Analysis of the Ionospheric Density Recorded by the DEMETER Satellite during Seismic Activity,” in Pre‐Earthquake Processes (Hoboken, NJ, USA; Washington, D.C.: John Wiley & Sons, Inc.; American Geophysical Union), 319–328. doi:10.1002/9781119156949.ch18
Parrot, M., Berthelier, J. J., Lebreton, J. P., Sauvaud, J. A., Santolik, O., and Blecki, J. (2006a). Examples of Unusual Ionospheric Observations Made by the DEMETER Satellite over Seismic Regions. Phys. Chem. Earth, Parts A/B/C 31 (4-9), 486–495. doi:10.1016/j.pce.2006.02.011
Parrot, M., Buzzi, A., Santolík, O., Berthelier, J. J., Sauvaud, J. A., and Lebreton, J. P. (2006b). New Observations of Electromagnetic Harmonic ELF Emissions in the Ionosphere by the DEMETER Satellite during Large Magnetic Storms. J. Geophys. Res. 111, A08301. doi:10.1029/2005ja011583
Parrot, M. (2006). Special Issue of Planetary and Space Science 'DEMETER'. Planet. Space Sci. 54 (5), 411–412. doi:10.1016/j.pss.2005.10.012
Piersanti, M., Materassi, M., Battiston, R., Carbone, V., Cicone, A., D’Angelo, G., et al. (2020a). Magnetospheric–Ionospheric–Lithospheric Coupling Model. 1: Observations during the 5 August 2018 Bayan Earthquake. Remote Sensing 12 (20), 3299. doi:10.3390/rs12203299
Piersanti, M., Pezzopane, M., Zhima, Z., Diego, P., Xiong, C., Tozzi, R., et al. (2020b). Can an Impulsive Variation of the Solar Wind Plasma Pressure Trigger a Plasma Bubble? A Case Study Based on CSES, SWARM and THEMIS Data. Adv. Space Res. 67 (1), 35–45. doi:10.1016/j.asr.2020.07.046
Píša, D., Parrot, M., and Santolík, O. (2011). Ionospheric Density Variations Recorded before the 2010 Mw 8.8 Earthquake in Chile. J. Geophys. Res. Space Phys. 116, A08309. doi:10.1029/2011JA016611
Píša, D., Němec, F., Parrot, M., and Santolík, O. (2012). Attenuation of Electromagnetic Waves at the Frequency ∼1.7 kHz in the Upper Ionosphere Observed by the DEMETER Satellite in the Vicinity of Earthquakes. Ann. Geophys. 55 (1), 157–163. doi:10.4401/ag-5276
Píša, D., Němec, F., Santolík, O., Parrot, M., and Rycroft, M. (2013). Additional Attenuation of Natural VLF Electromagnetic Waves Observed by the DEMETER Spacecraft Resulting from Preseismic Activity. J. Geophys. Res. Space Phys. 118 (8), 5286–5295. doi:10.1002/jgra.50469
Pulinets, S., and Ouzounov, D. (2011). Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) Model – an Unified Concept for Earthquake Precursors Validation. J. Asian Earth Sci. 41 (4-5), 371–382. doi:10.1016/j.jseaes.2010.03.005
Pulinets, S., and Ouzounov, D. (2018). “The Possibility of Earthquake Forecasting: Learning from Nature,” in Learning from Nature (Bristol, UK: IOP Publishing). doi:10.1088/978-0-7503-1248-6
Pulinets, S. A., Ouzounov, D. P., Karelin, A. V., and Davidenko, D. V. (2015). Physical Bases of the Generation of Short-Term Earthquake Precursors: A Complex Model of Ionization-Induced Geophysical Processes in the Lithosphere-Atmosphere-Ionosphere-Magnetosphere System. Geomagn. Aeron. 55 (4), 521–538. doi:10.1134/S0016793215040131
Ramos, O., Altshuler, E., and Måløy, K. J. (2009). Avalanche Prediction in a Self-Organized Pile of Beads. Phys. Rev. Lett. 102 (7), 078701. Available at: https://www.ncbi.nlm.nih.gov/pubmed/19257719. doi:10.1103/PhysRevLett.102.078701
Riggio, A., and Santulin, M. (2015). Earthquake Forecasting: a Review of Radon as Seismic Precursor. Bollettino di Geofisica Teorica Ed. Applicata 56 (2), 95–114. doi:10.4430/bgta0148
Ross, Z. E., Trugman, D. T., Hauksson, E., and Shearer, P. M. (2019). Searching for Hidden Earthquakes in Southern California. Science 364 (6442), 767–771. Available at: https://www.ncbi.nlm.nih.gov/pubmed/31000593. doi:10.1126/science.aaw6888
Rouet-Leduc, B., Hulbert, C., and Johnson, P. A. (2018). Continuous Chatter of the Cascadia Subduction Zone Revealed by Machine Learning. Nat. Geosci 12 (1), 75–79. doi:10.1038/s41561-018-0274-6
Ryu, K., Lee, E., Chae, J. S., Parrot, M., and Pulinets, S. (2014a). Seismo-ionospheric Coupling Appearing as Equatorial Electron Density Enhancements Observed via DEMETER Electron Density Measurements. J. Geophys. Res. Space Phys. 119 (10), 8524–8542. doi:10.1002/2014ja020284
Ryu, K., Parrot, M., Kim, S. G., Jeong, K. S., Chae, J. S., Pulinets, S., et al. (2014b). Suspected Seismo-Ionospheric Coupling Observed by Satellite Measurements and GPS TEC Related to the M7.9 Wenchuan Earthquake of 12 May 2008. J. Geophys. Res. Space Phys. 119 (12), 10,305–310,323. doi:10.1002/2014ja020613
Shen, X., Zhang, X., Hong, S., Jing, F., and Zhao, S. (2013). Progress and Development on Multi-Parameters Remote Sensing Application in Earthquake Monitoring in China. Earthq Sci. 26 (6), 427–437. doi:10.1007/s11589-013-0053-9
Shen, X., Zong, Q.-G., Zong, Q.-G., and Zhang, X. (2018). Introduction to Special Section on the China Seismo-Electromagnetic Satellite and Initial Results. Earth Planet. Phys. 2 (6), 439–443. doi:10.26464/epp2018041
Shen, X., Zhima, Z., Shigeng, Y., Jianping, D., Jianping, H., Xinghong, Z., et al. (2020). The CSES Mission and its Preliminary Results. Aerospace China 21 (1), 5–18. doi:10.3969/j.issn.1671-0940.2020.01.001
Shi, K., Guo, J., Liu, X., Liu, L., You, X., and Wang, F. (2020). Seismo-ionospheric Anomalies Associated with Mw 7.8 Nepal Earthquake on 2015 April 25 from CMONOC GPS Data. Geosci. J. 24 (4), 391–406. doi:10.1007/s12303-019-0038-3
Shi, K., Guo, J., Zhang, Y., Li, W., Kong, Q., and Yu, T. (2021). Multi-Dimension and Multi-Channel Seismic-Ionospheric Coupling: Case Study of Mw 8.8 Concepcion Quake on 27 February 2010. Remote Sensing 13 (14)–2724. doi:10.3390/rs13142724
Snoek, J., Larochelle, H., and Adams, R. P. (2012). Practical Bayesian Optimization of Machine Learning Algorithms. Paper presented at the Advances in neural information processing systems
Soter, S. (1999). Macroscopic Seismic Anomalies and Submarine Pockmarks in the Corinth–Patras Rift, Greece. Tectonophysics 308 (1-2), 275–290. doi:10.1016/s0040-1951(99)00090-6
Varotsos, P. A., Sarlis, N. V., and Skordas, E. S. (2020). Self-organized Criticality and Earthquake Predictability: A Long-Standing Question in the Light of Natural Time Analysis. EPL (Europhysics Letters) 132 (2), 29001. doi:10.1209/0295-5075/132/29001
Wang, Y. D., Pi, D. C., Zhang, X. M., and Shen, X. H. (2014). Seismo-ionospheric Precursory Anomalies Detection from DEMETER Satellite Data Based on Data Mining. Nat. Hazards 76 (2), 823–837. doi:10.1007/s11069-014-1519-3
Wu, L.-x., Qin, K., and Liu, S.-j. (2012). GEOSS-based Thermal Parameters Analysis for Earthquake Anomaly Recognition. Proc. IEEE 100 (10), 2891–2907. doi:10.1109/jproc.2012.2184789
Xiong, P., Long, C., Zhou, H., Battiston, R., Zhang, X., and Shen, X. (2020). Identification of Electromagnetic Pre-Earthquake Perturbations from the DEMETER Data by Machine Learning. Remote Sensing 12 (21), 3643. doi:10.3390/rs12213643
Xu, F., Song, X., Wang, X., and Su, J. (2010). “Neural Network Model for Earthquake Prediction Using DMETER Data and Seismic Belt Information,” in Paper presented at the 2010 Second WRI Global Congress on Intelligent Systems.
Yan, R., Parrot, M., and Pinçon, J.-L. (2017). Statistical Study on Variations of the Ionospheric Ion Density Observed by DEMETER and Related to Seismic Activities. J. Geophys. Res. Space Phys. 122, 12,421–12,429. doi:10.1002/2017ja024623
Yan, R., Guan, Y., Guan, Y., Shen, X., Huang, J., Zhang, X., et al. (2018a). The Langmuir Probe Onboard CSES: Data Inversion Analysis Method and First Results. Earth Planet. Phys. 2 (6), 1–10. doi:10.26464/epp2018046
Yan, R., Shen, X., Shen, X., Huang, J., Wang, Q., Chu, W., et al. (2018b). Examples of Unusual Ionospheric Observations by the CSES Prior to Earthquakes. Earth Planet. Phys. 2 (6), 515–526. doi:10.26464/epp2018050
Zhang, X., Shen, X., Liu, J., Ouyang, X., Qian, J., and Zhao, S. (2009). Analysis of Ionospheric Plasma Perturbations before Wenchuan Earthquake. Nat. Hazards Earth Syst. Sci. 9 (4), 1259–1266. Available at: https://www.nat-hazards-earth-syst-sci.net/9/1259/2009/. doi:10.5194/nhess-9-1259-2009
Keywords: earthquake, pre-earthquake anomalies, CSES and DEMETER satellites, ionospheric plasma, transfer deep learning, physical mechanisms
Citation: Xiong P, Long C, Zhou H, Battiston R, De Santis A, Ouzounov D, Zhang X and Shen X (2021) Pre-Earthquake Ionospheric Perturbation Identification Using CSES Data via Transfer Learning. Front. Environ. Sci. 9:779255. doi: 10.3389/fenvs.2021.779255
Received: 18 September 2021; Accepted: 21 October 2021;
Published: 04 November 2021.
Edited by:
Giovanni Martinelli, National Institute of Geophysics and Volcanology, ItalyReviewed by:
Mukesh Gupta, Catholic University of Louvain, BelgiumJinyun Guo, Shandong University of Science and Technology, China
Copyright © 2021 Xiong, Long, Zhou, Battiston, De Santis, Ouzounov, Zhang and Shen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xuhui Shen, shenxh@seis.ac.cn