The Broadband Albedo of Snow

The asymptotic radiative transfer theory is used to derive the analytical approximation for the broadband albedo of pure and polluted snow surfaces. The technique for the determination of the effective snow grain size and also the snow specific surface area from the shortwave broadband albedo measurements is proposed.

Introduction

The surface broadband albedo (BBA) α is defined as the ratio of the surface upward radiation flux to the downward radiation flux within a certain wavelength range. If the wavelength region $\lambda \in \left[{\lambda }_1,{\lambda }_2\right]$ is set in the range 0.25–5.0 μm, α is the shortwave (SW) albedo, while the ranges 0.25–0.4, 0.4–0.7 μm and 0.7–5.0 μm correspond to the ultraviolet (UV), visible (VIS) and near-infrared (NIR) albedo, respectively. The shortwave broadband albedo can be measured using a pyranometer. A thermopile pyranometer is a sensor based on thermopiles designed to measure the broad band of the solar radiation flux density (and also surface—reflected light flux density) from a 180° field of view for given illumination conditions. It usually measures in the spectral range 0.3–2.8 μm with a largely flat spectral sensitivity. The pyranometers operate in various networks including World Meteorological Organization Baseline Surface Radiation Network (BSRN) (McArthur, 2005) and Programme for Monitoring of the Greenland Ice Sheet (PROMICE) (Fausto et al., 2021). Various cut off filters installed on pyranometers are used to monitor the ultraviolet, visible and near-infrared broadband albedo (Aoki et al., 2003; Meinander et al., 2008; Aoki et al., 2011). The snow albedo depends on the snow grain size (Nolin and Dozier, 1993), snow wetness (Green et al., 2006), presence of various impurities (Di Mauro et al., 2015; Dumont et al., 2017; Skiles et al., 2018; Skiles and Painter, 2019), solar elevation and several other parameters (Pirazzini, 2004; Pirazzini, 2009).

The main task of this work is to propose simple parametrizations of pure and polluted snow broadband albedo in terms of snow microstructure. The derived equations can be used both for the estimation of clean snow microstructure and also in the Global Circulation Models (GCMs), which require simple functions to compute band averaged albedo (Marshall and Oglesby, 1994). There are numerous parameterizations of broadband albedo of pure snow and snow containing various impurities (Marshall and Warren, 1987; Marshall, 1989; Brun et al., 1992; Pirazzini, 2009; Gardner and Sharp, 2010; Dang et al., 2015; Kokhanovsky et al., 2020). A comprehensive review of various snow albedo parameterizations is given by Dang et al. (2015). The difference of our work from other parametrizations is that it is based on the new update on the ice refractive index in the visible (Picard et al., 2016). Also we used the asymptotic radiative transfer theory (Kokhanovsky and Zege, 2004), which makes it possible to propose highly accurate exponential approximation for the broadband pure snow albedo in terms of a single parameter—the effective attenuation scale (EAS). The parametrization of polluted snow albedo in terms of EAS and pollution load/type is also proposed.

Theory

Pure Snow

The snow broadband albedo is defined as (Aoki et al., 2011)

$\alpha =\frac{{{\displaystyle \int }}_{{\lambda }_1}^{{\lambda }_2}r\left(\lambda \right)F\left(\lambda \right)d\lambda }{{{\displaystyle \int }}_{{\lambda }_1}^{{\lambda }_2}F\left(\lambda \right)d\lambda }(1)$

where $r\left(\lambda \right)$ is the spectral snow albedo, $F\left(\lambda \right)$ is the incident spectral solar flux at the snow surface. This work is aimed at the parametrization of snow albedo in relatively clean regions such as Arctic and Antarctica. The function $F\left(\lambda \right)$ is determined by the solar spectral irradiance at the top of atmosphere, atmospheric transmittance and solar elevation. In this work we assume that the solar zenith angle is 60° in the calculation of the spectral dependence $F\left(\lambda \right)$. The function $F\left(\lambda \right)$ depends on the solar zenith angle. However, this dependence only weakly influences the BBA calculations (Grenfell and Perovich, 2008) because this function appears both in the dominator and nominator of Eq. 1. Also we use the parameterization of the smoothed function $F\left(\lambda \right)$ proposed by Kokhanovsky et al. (2020):

$F\left(\lambda \right)=f_0+f_1\exp \left(-\psi \lambda \right)+f_2\text{exp}\left(-\gamma \lambda \right)(2)$

where the corersponding parameters are given in Table 1. The multiplication of the function $F\left(\lambda \right)$ by the spectrally independent parameter does not influence the calculations of BBA (Eq. 1).

TABLE 1

TABLE 1. The coefficients of approximation given by Eq. (2) (Kokhanovsky et al., 2020, with corrections for misprints).

The spectral albedo of clean plane-parallel snow surfaces is given by (Kokhanovsky et al., 2020):

$r\left(\lambda \right)=\text{exp}(-\sqrt{k\left(\lambda \right)s})(3)$

where $k(\lambda$) = 4π$\chi /\lambda$ is the bulk ice absorption coefficient, $\chi \text{is the imaginary part of ice refractive index},$

$s=u^2\left({\mu }_0\right)l(4)$

is the effective attenuation scale (EAS), $u\left({\mu }_0\right)$ is the photon escape function, ${\mu }_0$ is the cosine of the incidence angle. The parameter $l$ is related to the effective grain diameter (EGD) d (Kokhanovsky et al., 2019):

$l=\zeta d(5)$

where the shape factor $\zeta =16B/9(1-g)$ depends on the shape of ice grains. Here, g is the asymmetry parameter and $B$ is the absorption enhancement factor (Kokhanovsky, 2006; Libois et al., 2014). Kokhanovsky (2006) has found that the shape factor is in the range 13–20 with the largest value corresponding to the case of spherical ice grains. We assume that $\zeta$ = 16 in this study. The value of $\zeta$ can be considered as an additional parameter of the parameterization in terms of EGD, which accounts for the shape of particles.

The following expression for the escape function proposed by Kokhanovsky et al. (2021) is used:

$u\left({\mu }_0\right)=\frac{3}{5}{\mu }_0+\frac{1+\sqrt{{\mu }_0}}{3}(6)$

Let us substitute Eqs. 2, 3 into Eq. 1 and account for the fact that $k\left(\lambda \right)s\ll 1$ in the UV and the visible. Then it follows for the UV and visible albedo:

$\alpha =1-\sqrt{ps},(7)$

where

$p={\left[\frac{{{\displaystyle \int }}_{{\lambda }_1}^{{\lambda }_2}\sqrt{k\left(\lambda \right)}F\left(\lambda \right)d\lambda }{{{\displaystyle \int }}_{{\lambda }_1}^{{\lambda }_2}F\left(\lambda \right)d\lambda }\right]}^2(8)$

and $\left[{\lambda }_1,{\lambda }_2\right]$ depend on the spectral region studied. The f$\text{unction} y\left(\lambda \right)=\sqrt{k\left(\lambda \right)}$ can be approximated by the polynomial of the second order in the UV and the visible:

$y\left(\lambda \right)=a+b\lambda +c{\lambda }^2(9)$

where the coefficients for various spectral intervals are given in Table 2. We have used the data for the imaginary part of ice refractive index obtained by Picard et al. (2016) (http://pp.ige-grenoble.fr/pageperso/picardgh/ice_absorption/). The substitution of Eqs. 2 and (9) in Eq. 8 makes it possible to derive the analytical expression for the parameter p. Namely, it follows:

$p={(a+b\langle \lambda \rangle +c\langle {\lambda }^2\rangle )}^2(10)$

where

$\langle {\lambda }^n\rangle =\frac{{{\displaystyle \int }}_{{\lambda }_1}^{{\lambda }_2}{\lambda }^{n}F\left(\lambda \right)d\lambda }{{{\displaystyle \int }}_{{\lambda }_1}^{{\lambda }_2}F\left(\lambda \right)d\lambda }(11)$

This integral can be evaluated analytically. In particular, one derives:

$\langle \lambda \rangle =\frac{{\displaystyle \sum _{n=0}^2{f}_n{X}_n}}{{\displaystyle \sum _{n=0}^2{f}_n{A}_n}},\langle {\lambda }^2\rangle =\frac{{\displaystyle \sum _{n=0}^2{f}_n{Y}_n}}{{\displaystyle \sum _{n=0}^2{f}_n{A}_n}}(12)$

where

$A_0={\lambda }_2-{\lambda }_1,A_1=Q\left({\lambda }_1,\psi \right)-Q\left({\lambda }_2,\psi \right),A_2=Q\left({\lambda }_1,\gamma \right)-Q\left({\lambda }_2,\gamma \right)(13)$

$X_0=({\lambda }_2^2-{\lambda }_1^2)/2,X_1=M\left({\lambda }_1,\psi \right)-M\left({\lambda }_2,\psi \right),X_2=M\left({\lambda }_1,\gamma \right)-M\left({\lambda }_2,\gamma \right)(14)$

$Y_0=({\lambda }_2^3-{\lambda }_1^3)/3,Y_1=N\left({\lambda }_1,\psi \right)-N\left({\lambda }_2,\psi \right),Y_2=N\left({\lambda }_1,\gamma \right)-N\left({\lambda }_2,\gamma \right)(15)$

$Q(\lambda ,v)=\exp (-v\lambda )/v,M(\lambda ,v)=(1+v\lambda )\exp (-v\lambda )/v^2,N(\lambda ,v)=(1+{(1+v\lambda )}^2)\exp (-v\lambda )/v^3.(16)$

The values $\langle \lambda \rangle$, $\langle {\lambda }^2\rangle$, and p calculated using equations given above for several spectral intervals $\left[{\lambda }_1,{\lambda }_2\right]$ are given in Table 2.

TABLE 2

TABLE 2. The coefficients of approximation given by Eqs. 9, 10, 12.

Eq. 7 is valid at small values of the product η = ps. To extend the applicability of Eq. 7 with respect to the value of the parameter η, we propose to use the following parameterization of the UV and visible albedo:

${\alpha }_{UV,VIS}=\exp (-\sqrt{ps})(17)$

where the value of p is given by Eq. 10. Eq. 7 follows from Eq. 17 at η$\to 0.$ One can state that the UV and visible broadband albedos depend on just one parameter–the effective attenuation scale s. It appears that the same is true for the NIR and SW albedo of pure snow. In particular, we have found that the NIR and shortwave albedo can be parameterized as follows:

$\alpha ={\alpha }_0+{\alpha }_1\exp \left(-\sqrt{ps}\right).(18)$

Eq. 17 follows from Eq. 18 at ${\alpha }_0=0 \text{and} {\alpha }_1=1.$The values of ${\alpha }_0,$ ${\alpha }_1$and p in Eq. 18 for various bands $\left[{\lambda }_1,{\lambda }_2\right]$ were derived from the numerical evaluation of integrals present in Eq. 1 with account for Eqs. 2, 3. The numerical fitting of the derived dependence of the broadband albedo on the parameter s to the function shown in Eq. 18 using the software package ORIGIN has been used. We have used the data for the imaginary part of ice refractive index given by Picard et al. (2016) (in the visible and UV) and data of Warren and Brandt (2008) at longer wavelengths. The values of the derived parameters ${\alpha }_0,$ ${\alpha }_1$and p are given in Table 3. In Table 3 and also in the text below we consider three spectral ranges: 0.3–0.7, 0.7–2.5 and 0.3–2.5 μm. The first interval incorporates UV and visible wavelengths and the second interval incorporates NIR wavelengths.

TABLE 3

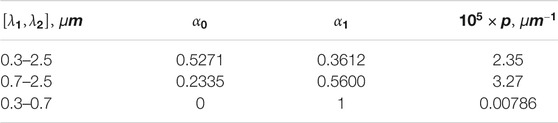
TABLE 3. The coefficients of approximation given by Eq. (18).

The dependence of the visible (0.3–0.7 $\mu m,$ which also includes UV part), NIR (0.7–2.5 μm) and shortwave (0.3–2.5 μm) albedo on the effective grain diameter calculated using analytical Eq. 18 with account for data in Table 3 and the numerical calculation using Eq. 1 at ${\mu }_0=0.65$are given in Figure 1. The results derived using the parametrizations proposed by Dang et al. (2015) are shown in Figure 1 as well. It follows approximately that BBA(SW)=(BBA(VIS)+BBA(NIR))/2.

FIGURE 1

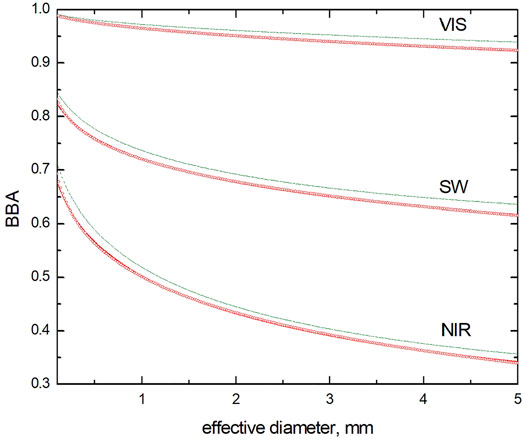
FIGURE 1. The dependence of the VIS (0.3–0.7 μm), SW (0.3–2.5 μm) and NIR (0.7–2.5 μm) broadband albedo of pure snow on the effective snow grain diameter calculated using Eq. 18 (red solid lines), the parametrization by Dang et al. (2015) (upper green lines) and results of numerical calculations using Eq. 1 (red circles).

We have found that the difference between numerical calculations using Eq. 1 and analytical Eq. 18 with account for data given in Table 3 is smaller than 1% for the shortwave and visible albedo and it is smaller than 2% for the NIR albedo at the diameters d > 0.1 mm characteristic for terrestrial snow covers. This difference is smaller that the respective error of the BBA measurement. The difference between the parameterization given by Eq. 18 and former parametrization given by Dang et al. (2015) is below 2% in the visible, 3% in the shortwave, and 6% in the NIR regions with our parametrization providing smaller albedos for a given size of ice grains. This is mostly due to the fact that the new compilation of the ice refractive index (Picard et al., 2016) gives larger values of the imaginary part of ice refractive index in the VIS/NIR part of the electromagnetic spectrum as compared to the corresponding values given by Warren and Brandt (2008). Also our model is based on the assumption that ice grains are irregularly shaped as compared to the parameterization for snow BBA based on the model of ice spheres proposed by Dang et al. (2015). The effective ice grain diameter used by us is defined as $d=\frac{3v}{2\sigma }$, where $v$ is the average volume of grains and $\sigma$ is there average area of the ice grain projection on the surface perpendicular to the incoming light (Zege and Kokhanovsky, 2004). It follows for the spherical particles that $\sigma$ = $\pi d^2/4$ and the effective diameter used by ice coincides with that used by Dang et al. (2015) in the case of spherical ice grains.

Eq. 18 can be used in the simplifaction of the corresponding blocks in Global Circulation Models (GCMs). It follows from Eq. 18 that the values of BBA of snowpacks with various microstructure coinside, if the effective attenuation scale s is the same. Also our new snow BBA albedo parametrization can be used for the determination of the snow BBA for given sizes of ice grains and illumination conditions and also for the solution of inverse problems of snow optics. In particular, it follows for the effective pure snow grain diameter from Eq. 18:

$d=\frac{l{n}^{2}z}{\zeta p{u}^2\left({\mu }_0\right)}(19)$

where $z=(\alpha -{\alpha }_0)/{\alpha }_1$. Also the snow specific surface area (SSA) can be derived from the BBA measurements. It is defined as $SSA=K/{\rho }_{i}d$, where ${\rho }_i$ is the density of ice, $K=\frac{3\Sigma }{2\sigma },\Sigma \text{is the average surface area of ice grains}.$The parameter K is equal to 6 for the spherical ice grains (and also for randomly oriented ice convex particles of the same shape) because it follows in this case: $\Sigma =4\sigma$. As a matter of fact, the value of K can be derived from independent measurements of the effective diameter and SSA for a given snowpack.

The dependence of the effective ice grain diameter on the SW BBA derived using Eq. 19 at u = 1 corresponding to the case of overcast sky (spherical or white sky BBA (Kokhanovsky et al., 2019)) is given in Figure 2, where the correspondence between SW BBA values and international snow classification (Fierz et al., 2009) is also presented.

FIGURE 2

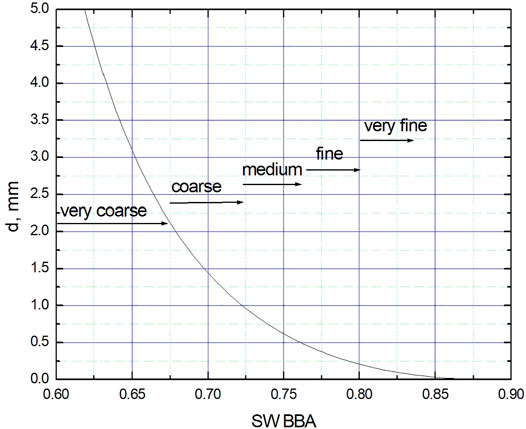
FIGURE 2. The correspondence between values of the effective ice grain diameter and SW BBA of pure snow. The ranges of SW BBA corresponding to the international classification (Fierz et al., 2009) for the snow grain sizes are given as well.

We show the temporal behaviour of the SW BBA as measured by the Programme for Monitoring of the Greenland Ice Sheet (PROMICE) network of pyranometers (Fausto et al., 2021) at the East GRIP (EGP) location (75.6N, 36 W) in Greenland and also temporal variation of the ice grain diameter derived from Eq. 19 in Figure 3. Also in situ ground measurements of the grain diameter as reported by Kokhanovsky et al. (2019) for July 8, 9, and 13 (2018) are given. One can see that the SW broadband albedo at EGP does not change considerably for the time interval studied. It is close to 0.8. The grain diameter is in the range 0.1–0.4 mm for most of cases. The diameters of grains derived from in situ measurements are close to those derived from Eq. 19.

FIGURE 3

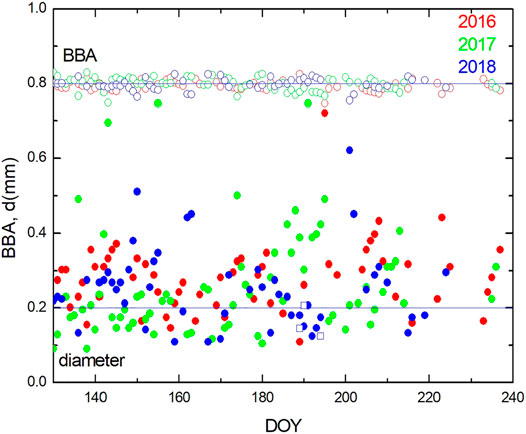
FIGURE 3. The daily-averaged shortwave broadband albedo measured at the EGP PROMICE station (open circles) and ice grain diamaters derived using Eq. 19 for years 2016–2018 (filled circles) as the function of the Day Of Year (DOY). Boxes show the effective ice grain diameters measured in situ at the site on July 8, 9 and 13 (2018).

The snow specific surface area derived from shortwave BBA measurements is given in Figure 4. It is mostly in the range 15–45 kg/$m^2$, which is consistent with the values of the SSA for the wind packed snow (Domine et al., 2008) to be expected at the EGP site located at 2.66 km above the sea level far from the ocean.

FIGURE 4

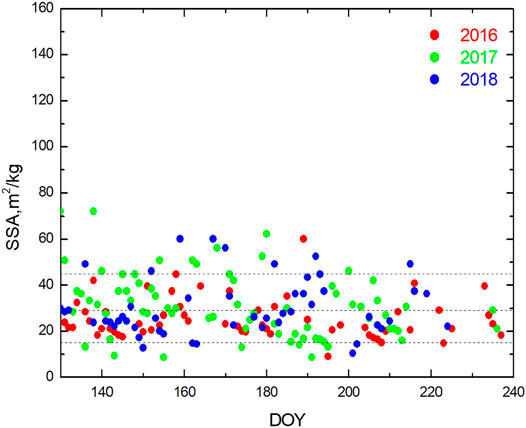
FIGURE 4. The snow specific surface area at the EGP site derived from the daily shortwave albedo measurements for years 2016–2018.

The intercomparison of the SSA determined from the SW BBA observations and those performed in the vicinity of the EGP station using NIR hemispherical snow reflectance observations under artificial light illumination conditions (Gallet et al., 2009) is given in Figure 5. Further details on the measurements of the SSA at the EGP station using NIR observations are given by Kokhanovsky et al. (2019). It follows that SW BBA and NIR measurements provide similar values of the SSA. This is due to the fact that both BBA and spectral snow reflectance measurements provide the same quantity–the effective snow grain diameter, which is used to derive the snow specific surface area. The difference in the measurements is due to the local variation of the SSA as shown in Figure 5 and also due to different average light penetration depths for the NIR (at 1.31 μm) hemispherical reflectance and SW BBA measurements.

FIGURE 5

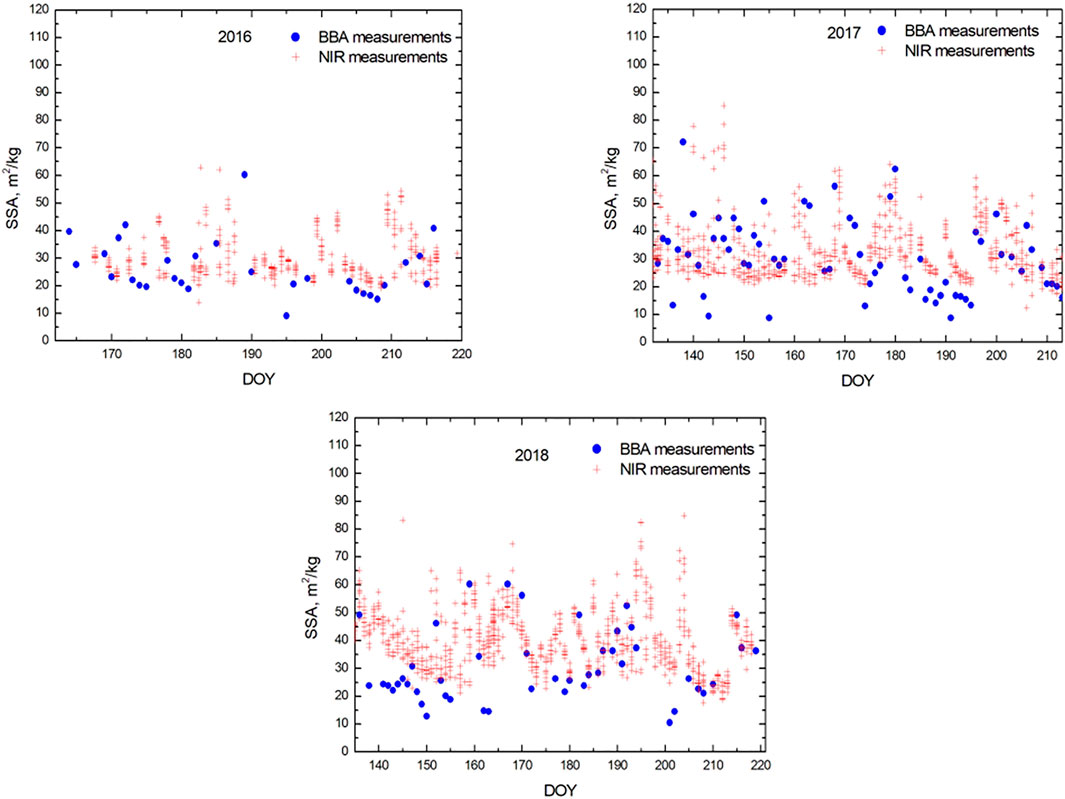
FIGURE 5. The temporal behaviour of SSA derived from NIR reflectance and SW BBA measurements at the EGP site in Greenland for years 2016–2018. The BBA and NIR observations are not absolutely collocated in space and time domains. The NIR measurements are performed in the vicinity of the BBA observations on a 100 m transect (10 stations for every day at a given time). The average daily BBA values are presented.

The aveage values of shortwave broadband albedo measured at EGP site for 2016–2018 and average values of the ice grain diameter and snow specific surface area (derived using daily SW BBA measurements) are given in Table 4. It appears that the interannual variations are quite small at the site.

TABLE 4

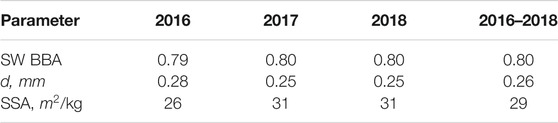
TABLE 4. The average values of the measured shortwave broadband albedo and derived ice grain diameter d and SSA at the EGP location in Greenland for several years. The average values for 2016–2018 time period are given as well.

We compare the average values of the SSA for the 2 months (June, July) derived at the EGP site from BBA measurements for several years and also similar results from NIR measurements in Table 5. One can see that both datasets produce similar results for the average values of BBA. Clearly, the determination of the SSA from routine BBA measurements requires a fraction of time as compared to the hemispherical snow reflectance measurements under the artificial light (a laser diode) illumination conditions.

TABLE 5

TABLE 5. The average values of the SSA at the EGP location in Greenland derived using SW BBA and NIR hemispherical reflectance measurements in June–July (2016–2018). The number of days, when BBA and NIR hemispherical measurements have been performed do not coincide. The values of SSA above 60 $m^2$/kg have been removed from the calculation of averages because the determination of SSA from the NIR measurements is not reliable in this case (Gallet et al., 2009).

Polluted Snow

Let us consider the polluted snow now. Then it follows for the spectral albedo (Kokhanovsky et al., 2021):

$r(\lambda )=\text{exp}(-\sqrt{\left(k\left(\lambda \right)+G{\left(\frac{\lambda }{{\lambda }_0}\right)}^{-x}\right)s})(20)$

where

$G=\frac{k_p\left({\lambda }_0\right)}{B}c(21)$

$c=\frac{c_p}{c_i}$ is the relative concentration of pollutants in a snow layer, $c_p \left(c_i\right)$ $\text{is the volumetric concentration of pollutants }\left(\text{ice grains}\right),$ $k_p\left({\lambda }_0\right)$is the volumetic pollutant absorption coefficient at the wavelength${\lambda }_0$, x is the absorption Angstrom exponent, B is the snow absorption enhancement coefficient (Kokhanovsky and Zege, 2004; Libois et al., 2014). It has been assumed that the impurity volumetric absorption coefficient $k_p\left(\lambda \right)$ can be presented as (Kokhanovsky et al., 2021):

$k_p\left(\lambda \right)=k_p\left({\lambda }_0\right){(\lambda /{\lambda }_0)}^{-x}(22)$

and light scattering effects by pollutants are ignored as compared to light scattering by ice grains. Eq. 3 follows from Eq. 20 at c = 0 as it should be.

One can derive using Eqs. 1, 20 for the shortwave BBA in the spectral range 0.3–2.5 μm:

$\alpha =\frac{{\alpha }_{vis}^{pol}+Q{\alpha }_{nir}}{1+Q}(23)$

where ${\alpha }_{vis}^{pol}$ is the visible BBA (0.3–0.7 μm) for the polluted snow, ${\alpha }_{nir}$ is the NIR BBA (0.7–2.5 μm) of the pure snow and

$Q=\frac{{{\displaystyle \int }}_{0.7\mu m}^{2.5\mu m}F\left(\lambda \right)d\lambda }{{{\displaystyle \int }}_{0.3\mu m}^{0.7\mu m}F\left(\lambda \right)d\lambda } (24)$

The parameter Q gives the ratio of incident light flux in the band 0.3–0.7 μm to that at the NIR band 0.7–2.5 μm. It appears that Q = 1.08 and, therefore, one can assume that the SW albedo is approximately equal to the average of VIS and NIR albedos (similar to the case of pure snow SW BBA discussed above). The NIR BBA ${\alpha }_{nir}$ in Eq. 23 is given by Eq. 18 under assumption that NIR BBA is not influenced by the pollutants. This is often the case (Kokhanovsky et al., 2020). Therefore, the problem is reduced to the parameterization of ${\alpha }_{vis}^{pol}$ (Eq. 23).

It follows from Eq. 20 for the UV and visible albedo of polluted snow:

$r=1-\sqrt{(k\left(\lambda \right)+G{(\lambda /{\lambda }_0)}^{-x})s}(25)$

assuming that $b=(k\left(\lambda \right)+G{\lambda }^{-x})s\to 0$, which is a reasonable assumption in the visible and UV. Therefore, one derives for the visible BBA of polluted snow using Eqs. 1, 25:

${\alpha }_{vis}^{pol}=1-\sqrt{Ws},(26)$

where

$W={\left[\frac{{{\displaystyle \int }}_{{\lambda }_1}^{{\lambda }_2}\sqrt{k\left(\lambda \right)+G{(\lambda /{\lambda }_0)}^{-x}}F\left(\lambda \right)d\lambda }{{{\displaystyle \int }}_{{\lambda }_1}^{{\lambda }_2}F\left(\lambda \right)d\lambda }\right]}^2(27)$

The numerical simulations show that the parameter $W$ can be parametried as follows in the spectral range 0.3–0.7 μm:

$W=p_{vis}+mG\text{exp}\left(\gamma x\right)(28)$

where the corresponding constants m and are γ given in Table 6. The constant$p_{vis}$ coinsides with constant p for the visible range given in Table 3. This ensures that Eq. 26 coincides with Eq. 7 at c = 0 (pure snow case).

TABLE 6

TABLE 6. The coefficients of approximation given by Eq. (28).

To extend the area of applicability of Eq. 26 we shall use an exponential approximation:

${\alpha }_{p_{vis}}^{pol}=\text{exp}\left(-\sqrt{(p+q)s}\right)(29)$

where

$q=mGexp\left(\gamma x\right).(30)$

Eq. 29 is the final parametrization of the polluted snow visible broadband albedo. One can see that the visible BBA depends on the effective absorption scale s (d, ${\mu }_0$), absorption Angström parameter $x$ and also on the pollution impact parameter G (dependent on the relative concentration of pollutants c, the volumetric absorption coefficient of pollutants at the selected wavelength $k_0\equiv k_p\left(1\text{μm}\right)$) and the solar light absorption enhancement factor B$)$. Eq. 17 follows from Eq. 29 at c = 0 (pure snow).

The shortwave snow albedo of polluted snow can be derived using analytical Eqs. 18, 23, 29. Namely, it follows:

$\alpha =\frac{\exp (-\sqrt{(p_{vis}+mG{e}^{\gamma x})s})+Q({\alpha }_0^{nir}+{\alpha }_1^{nir}\exp (-\sqrt{p_{nir}s}))}{1+Q},(31)$

where ${\alpha }_0^{nir}=0.2335,{\alpha }_1^{nir}=0.56$, $p_{nir}$ = 32.7$m^{-1}$ (Table 3).

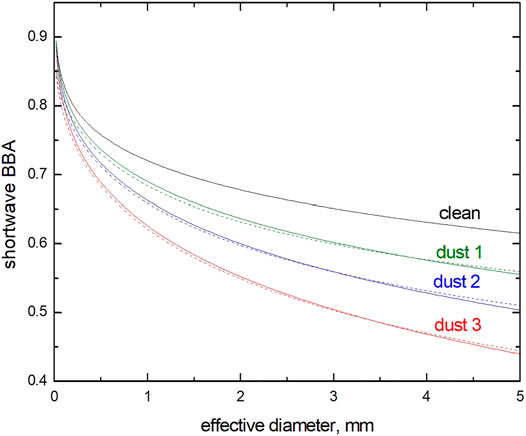
The accuracy of this approximation as compared to the numerical integration using Eq. 1 is shown in Figure 6 for snow contaminated by soot aerosol and the same solar zenith angle as in Figure 1. It has been assumed in calculations that (Kokhanovsky and Zege, 2004): B = 1.8, x = 1, and $k_0=10\mu m^{-1}$. The results similar to those reported in Figure 6 except for the dust–loaded snow are given in Figure 7. It has been assumed that B = 1.8, the solar zenith angle equal to 27°, and values of the pair (x, G) coincide with those derived by Kokhanovsky et al. (2021) for the alpine snow polluted by the Saharan dust. They are given in Table 7 together with the derived value of the effective ice grain diameter for each case. It follows from Figure 7 that the proposed parameterizations can be used to derive shortwave snow broadband albedo with a high accuracy.

FIGURE 6

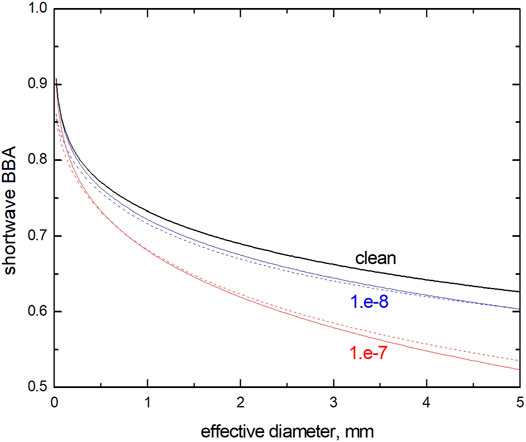
FIGURE 6. The dependence of the shortwave BBA on the efefctive diameter of grains at the relative volumetric concentration of pollutants c equal to ${10}^{-7}$ and ${10}^{-8}$ and also for clean snow. The dashed lines show results derived using the analytical approximation. The solid line corresponds to the numerical calcualtion uisng Eq. 1.

TABLE 7

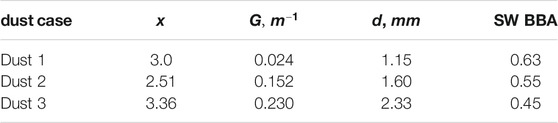
TABLE 7. The parameters of dust-loaded snow (Kokhanovsky et al., 2021).

FIGURE 7

FIGURE 7. The same as in Figure 6 except for the dust–loaded (see Table 7) and clean snow.

The spectral albedo measurements in the range 400–900 nm as reported by Kokhanovsky et al. (2021) can be used to estimate the shortwave snow albedo. This is possible because the parameters q and s (Eq. 29) can be assessed from spectral measurements. The SW BBA for the polluted snow cases investigated by Kokhanovsky et al. (2021) is presented in Table 7. The corresponding values were derived using Eq. 31 and data presented in Table 7.

Conclusion

In this work new simple approximations for the snow broadband albedo are proposed. The derivations are based on the asymptotic radiative transfer for plane - parallel homogeneous semi—infinite snow surfaces. The effects of underlying surfaces and snow vertical inhomogeneity are not accounted for. The derived equations can be corrected for slope and sensor tilts as discussed by Weiser et al. (2016).

The standard pyranometers with a glass dome measure in the spectral range 0.3–2.8 μm. Both the snow reflectivity and solar incident flux are small in the spectral range 2.5–5.0 μm. Therefore, our parametrizations can be used in the spectral ranges 0.3–2.8 and 0.3–5.0 μm as well. The accuracy of asymptotic radiative transfer theory decreases with increase of light absorption in snow. Therefore, the accuracy of the visible and shortwave albedo parametrization is higher as compared to that of NIR albedo parameterization, especially for aged polluted snow with large ice grains (Figure 6). The developed exponential parametrizations of pure and polluted snow albedo can be used in the Golobal Circulation Models and also for the estimation of the snow grain size/snow specific surface area from pure snow broadband albedo measurements. Also we demonstrate a possibility for the determination of the shortwave broadband albedo from spectral albedo measurements in narrow spectral intervals (say, 400–900 nm).

The parameterizations refer to the plane of the blue sky albedo. The results for the spherical (white sky) albedo can be derived from equations given above assuming that the escape function u = 1 (Kokhanovsky et al., 2019).

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared past collaborations with the author.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, orclaim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Data from the Programme for Monitoring of the Greenland Ice Sheet (PROMICE) were provided by the Geological Survey of Denmark and Greenland (GEUS) at http://www.promice.dk (Fausto et al., 2021). The author is grateful to two reviewers for useful suggestions.

References

Aoki, T., Hachikubo, A., and Hori, M. (2003). Effects of snow physical parameters on shortwave broadband albedos. J. Geophys. Res. 108, 4616. doi:10.1029/2003JD003506

CrossRef Full Text | Google Scholar

Aoki, T., Kuchiki, K., Niwano, M., Kodama, Y., Hosaka, M., and Tanaka, T. (2011). Physically based snow albedo model for calculating broadband albedos and the solar heating profile in snowpack for general circulation models. J. Geophys. Res. 116, D11114. doi:10.1029/2010JD015507

CrossRef Full Text | Google Scholar

Brun, E., David, P., Sudul, M., and Brunot, G. (1992). A numerical model to simulate snow-cover stratigraphy for operational avalanche forecasting. J. Glaciol. 38, 13–22. doi:10.1017/s0022143000009552

CrossRef Full Text | Google Scholar

Dang, C., Brandt, R. E., and Warren, S. G. (2015). Parameterizations for narrowband and broadband albedo of pure snow and snow containing mineral dust and black carbon. J. Geophys. Res. Atmos. 120, 5446–5468. doi:10.1002/2014JD022646

CrossRef Full Text | Google Scholar

Di Mauro, B., Fava, F., Ferrero, L., Garzonio, R., Baccolo, G., Delmonte, B., et al. (2015). Mineral dust impact on snow radiative properties in the European Alps combining ground, UAV, and satellite observations. J. Geophys. Res. Atmos. 120, 6080–6097. doi:10.1002/2015JD023287

CrossRef Full Text | Google Scholar

Domine, F., Albert, M., Huthwelker, T., Jacobi, H.-W., Kokhanovsky, A. A., Lehning, M., et al. (2008). Snow physics as relevant to snow photochemistry. Atmos. Chem. Phys. 8, 171–208. doi:10.5194/acp-8-171-2008

CrossRef Full Text | Google Scholar

Dumont, M., Arnaud, L., Picard, G., Libois, Q., Lejeune, Y., Nabat, P., et al. (2017). In situ continuous visible and near-infrared spectroscopy of an alpine snowpack. The Cryosphere 11, 1091–1110. doi:10.5194/tc-11-1091-2017

CrossRef Full Text | Google Scholar

Fausto, R. S., van As, D., Mankoff, K. D., Vandecrux, B., Citterio, M., Ahlstrøm, A. P., et al. (2021). PROMICE automatic weather station data. Earth Syst. Sci. Data Discuss. [preprint]in review https://doi.org/10.5194/essd-2021-80

Google Scholar

Fierz, C., Armstrong, R. L., Durand, Y., Etchevers, P., Greene, E., McClung, D. M., et al. (2009). The International Classification for Seasonal Snow on the Ground. IHP-VII Technical Documents in Hydrology N°83, IACS Contribution N°1. Paris: UNESCO-IHP.

Google Scholar

Gallet, J.-C., Domine, F., Zender, C. S., and Picard, G. (2009). Measurement of the specific surface area of snow using infrared reflectance in an integrating sphere at 1310 and 1550 nm. The Cryosphere 3, 167–182. doi:10.5194/tc-3-167-2009

CrossRef Full Text | Google Scholar

Gardner, A. S., and Sharp, M. J. (2010). A review of snow and ice albedo and the development of a new physically based broadband albedo parameterization. J. Geophys. Res. 115, F01009. doi:10.1029/2009JF001444

CrossRef Full Text | Google Scholar

Green, R. O., Painter, T. H., Roberts, D. A., and Dozier, J. (2006). Measuring the expressed abundance of the three phases of water with an imaging spectrometer over melting snow. Water Resour. Res. 42, W10402. doi:10.1029/2005WR004509

CrossRef Full Text | Google Scholar

Grenfell, T. C., and Perovich, D. K. (2008). Incident spectral irradiance in the Arctic Basin during the summer and fall. J. Geophys. Res. 113, D12117. doi:10.1029/2007JD009418

CrossRef Full Text | Google Scholar

Kokhanovsky, A. A. (2006). Scaling constant and its determination from simultaneous measurements of light reflection and methane adsorption by snow samples. Opt. Lett. 31, 3282–3284. doi:10.1364/ol.31.003282

PubMed Abstract | CrossRef Full Text | Google Scholar

Kokhanovsky, A. A., and Zege, E. P. (2004). Scattering optics of snow. Appl. Opt. 43, 1589–1602. doi:10.1364/ao.43.001589

PubMed Abstract | CrossRef Full Text | Google Scholar

Kokhanovsky, A., Box, J. E., Vandecrux, B., Mankoff, K. D., Lamare, M., Smirnov, A., et al. (2020). The determination of snow albedo from satellite measurements using fast atmospheric correction technique. Remote Sensing 12, 234. doi:10.3390/rs12020234

CrossRef Full Text | Google Scholar

Kokhanovsky, A., Di Mauro, B., Garzonio, R., and Colombo, R. (2021). Retrieval of dust properties from spectral snow reflectance measurements. Front. Environ. Sci. 9, 42. doi:10.3389/fenvs.2021.644551

CrossRef Full Text | Google Scholar

Kokhanovsky, A., Lamare, M., Danne, O., Brockmann, C., Dumont, M., Picard, G., et al. (2019). Retrieval of snow properties from the Sentinel-3 Ocean and Land Colour Instrument. Remote Sensing 11, 2280. doi:10.3390/rs11192280

CrossRef Full Text | Google Scholar

Libois, Q., Picard, G., Dumont, M., Arnaud, L., Sergent, C., Pougatch, E., et al. (2014). Experimental determination of the absorption enhancement parameter of snow. J. Glaciol. 60, 714–724. doi:10.3189/2014j0g14j015

CrossRef Full Text | Google Scholar

Marshall, S. E. (1989). A physical parameterization of snow albedo for use in climate models, NCAR cooperative thesis 123. Medium Ævum 58, 175. Natl. Cent. for Atmos. Res., Boulder, Colo. doi:10.2307/43632553

CrossRef Full Text | Google Scholar

Marshall, S. E., and Warren, S. G. (1987). Parameterization of snow albedo for climate models, in Large scale effects of seasonal snow cover, IAHS Publ., vol. 166, edited by B. E. Goodison, R. G. Barry, and J. Dozier, pp. 43–50, International Association of Hydrological Sciences, Washington, D. C.

Google Scholar

Marshall, S., and Oglesby, R. J. (1994). An improved snow hydrology for GCMs. part 1: Snow cover fraction, albedo, grain size, and age. Clim. Dyn. 10, 21–37. doi:10.1007/bf00210334

CrossRef Full Text | Google Scholar

McArthur, L. J. B. (2005). “Baseline Surface Radiation Network (BSRN),” in Operations Manual Version 2.1, WCRP-121. WMO/TD-No. 1274, Geneva.

Google Scholar

Meinander, O., Kontu, A., Lakkala, K., Heikkilä, A., Ylianttila, L., and Toikka, M. (2008). Diurnal variations in the UV albedo of arctic snow. Atmos. Chem. Phys. 8, 6551–6563. doi:10.5194/acp-8-6551-2008

CrossRef Full Text | Google Scholar

Nolin, A. W., and Dozier, J. (1993). Estimating snow grain size using AVIRIS data. Remote sensing Environ. 44 (2-3), 231–238. doi:10.1016/0034-4257(93)90018-s

CrossRef Full Text | Google Scholar

Picard, G., Libois, Q., and Arnaud, L. (2016). Refinement of the ice absorption spectrum in the visible using radiance profile measurements in Antarctic snow. The Cryosphere 10, 2655–2672. doi:10.5194/tc-10-2655-2016

CrossRef Full Text | Google Scholar

Pirazzini, R. (2009). Challenges in snow and ice albedo parameterizations. Geophysica 45 (1-2), 41–62.

Google Scholar

Pirazzini, R. (2004). Surface albedo measurements over Antarctic sites in summer. J. Geophys. Res. 109, D20118. doi:10.1029/2004JD004617

CrossRef Full Text | Google Scholar

Skiles, S. M., Flanner, M., Cook, J. M., Dumont, M., and Painter, T. H. (2018). Radiative forcing by light-absorbing particles in snow. Nat. Clim Change 8 (11), 964–971. doi:10.1038/s41558-018-0296-5

CrossRef Full Text | Google Scholar

Skiles, S. M., and Painter, T. H. (2019). Toward understanding direct absorption and grain size feedbacks by dust radiative forcing in snow with coupled snow physical and radiative transfer modeling. Water Resour. Res. 55, 7362–7378. doi:10.1029/2018WR024573

CrossRef Full Text | Google Scholar

Warren, S. G., and Brandt, R. E. (2008). Optical constants of ice from the ultraviolet to the microwave: A revised compilation. J. Geophys. Res. 113, D14220. doi:10.1029/2007JD009744

CrossRef Full Text | Google Scholar