- School of Resource and Environment and Safety Engineering, University of South China, Hengyang, China
The soil–water characteristic curve (SWCC) is an essential parameter for studying the mechanical properties of unsaturated tailings, and it plays an important role in stability assessment and prediction of unsaturated tailings dams. In this paper, the matrix suction was measured indirectly by a filter paper-based method to investigate the effects of key factors (gradation, temperature, and initial dry density) on the soil–water characteristic curves of fine-grained tailings, and the Van Genuchten model was adopted to obtain the empirical equation of SWCC and to verify the accuracy of experimental results. The results showed the following: 1) the Van Genuchten model fits well the relationship between matric suction and volumetric moisture content of fine-grained tailings, indicating that experimental data determined by filter paper-based method is accurate and appropriate; 2) at the same volumetric moisture content, the matrix suction increased with decreasing average particle size, and the decrease in temperature will increase the matrix suction and water-holding capacity of fine-grained tailings, and the matrix suction of the tailings in summer is 38.3% lower than that in winter under the natural volumetric moisture content (14.0%); 3) when the saturation degree of fine-grained tailings is less than 60%, the greater the initial dry density, the better the water-holding capacity and matrix suction.
Introduction
As the hydraulic structure for tailings storage, tailings reservoir is one of the major hazardous sources for the mining enterprises. The operational status of a tailings reservoir is directly related to the operation of mining enterprises and the safety of the lives and properties of people living downstream. In recent years, fine-grained tailings have become the primary dam-building materials of tailings reservoirs due to the pervasiveness of fine-grained mineral processing technology in China. The physical and mechanical properties of these fine-grained tailings with small average particle sizes and poor permeability are more vulnerable to environmental factors than coarse-grained tailings. The changes in rainfall intensity, temperature, and the dry–wet cycle will affect the matric suction and cohesion of unsaturated fine-grained tailings, resulting in instability of the tailings dam (Lersow, 2010; Ma et al., 2021).
The soil–water characteristic curve (SWCC), as an important parameter of unsaturated soil, shows the relationship curve between moisture content and suction. The changing trend of the curve reflects the water holding capacity and porosity characteristics of the soil, and many engineering properties such as hydraulic conductivity, shear strength, coefficient of diffusion, etc. can be estimated from it (Fredlund and Rahardjo, 1993). The previous research results show that gradation, temperature, and initial dry density are the key factors affecting the SWCC of tailings, so it is necessary to quantitatively evaluate the effect of key factors on the SWCC to analyze the stability of the unsaturated part of the tailings dam. There are many instruments available for measuring the matric suction, such as the Tensiometer Method (Marinho et al., 2008), Pressure apparatus (Bechtold et al., 2018; Jiang et al., 2020), Electrical resistance blocks (Zeitoun et al., 2021), etc., and indirect methods, such as the Filter paper-based method (Mahler and Mendes, 2005; Fattah et al., 2021), Empirical method (Kern, 1995), etc. During the past few decades, many empirical models have been developed to predict SWCC, such as the Van-Genuechten (1980), Brooks-Corey (1964), Fredlund and Xing (1994), Gardner (1958), etc., and researchers also compared and evaluated the applicability and consistency of various empirical models (Matlan et al., 2015; Fattah et al., 2021). Based on this, the scholars investigated the SWCC of clay (Tripathy et al., 2014; Li et al., 2017), sand (Yan and Zhang, 2015), and expansive soil (Tamer et al., 2017; Ahmed et al., 2018), and they analyzed the effect of dry density (Birle et al., 2008; Gallage and Uchimura, 2010), void ratio (Heshmati and Motahari, 2015), grain size distribution (Chen et al., 2018; Zhai et al., 2020), and temperature (ElKeshky, 2011; Qiao et al., 2019) on the SWCC.
Although many studies have been conducted to analyze the SWCC of various soils, none of these investigations have highlighted a comprehensive evaluation of the effect of key factors on SWCC of fine-grained tailings from the microscopic mechanism. And fine-grained tailings are significantly different in physical properties and mechanical behavior from the general soil due to the complex mineral composition, high content of fine particles. The results of previous studies show that gradation, temperature, and initial dry density have the most significant influence on the physical and mechanical properties of unsaturated tailings. Therefore, in this paper, the matrix suction was determined by filter paper-based method to investigate the effect of gradation, temperature, and initial dry density on the SWCC of fine-grained tailings. In addition, the Van Genuchten model, as the most widely used mathematical model for fitting SWCC, was adopted to verify the accuracy of the experimental results in this paper. The fitting parameters and empirical equations for the SWCC were also obtained to provide a basis for mechanical properties, seepage calculations, and stability evaluation of fine-grained tailings dam.
Materials and Experiments
Experimental Principle
The filter paper-based method is a widely used method to indirectly measure the matric suction of soil, which has the advantages of low price, ease of operation, and large measurement range, but it must, however, be measured under an environment of a certain humidity and temperature. When a dry filter paper is placed on or in a soil sample for a few days, the filter paper will absorb the moisture from soil by evaporation and capillary action, and the moisture can be balanced between the soil and the filter paper at last. After moisture equilibration, the matrix suction of the soil was determined by a recommended rate formula according to the volumetric moisture content of the filter paper.
“Whatman No.203” quantitative filter paper of 70 mm diameters and hardened low ash was used to determine the matrix suction of tailings. The matrix suction was rated based on the rate formula recommended by ASTM D5298-10 (2010) with the following Eq. 1 (Fredlund and Rahardjo, 1993):
where
The Van Genuchten model was used to obtain the empirical equation of the SWCC. The mathematical expression of Van Genuchten models is shown in Eq. 2 (Van-Genuechten, 1980):
where
Experimental Materials and Specimen Preparation
The raw tailings were chosen came from the discharge outlet of the Gao Wanqiu tailings reservoir in Hunan province, China. The physical properties of the raw tailings were determined according to ASTM recommended test methods (ASTM D2216-19, 2019; ASTM D854-14, 2014; ASTM D7263-21, 2021), as shown in Table 1.
The particle size distribution of tailings samples was determined by a Screening Test (ASTM D6913-04, 2017), and the particle sizes smaller than 0.074 mm were determined by the Winner 2,000 Laser Particle Size Analyzer (Zhang et al., 2015). The experimental results showed that the mass of tailings with particle diameters lower than 200 mesh (0.074 mm) accounts for more than 30% of the total mass.
A physical model of fine-grained tailings sedimentation was established by an acrylic tube with an inner diameter of 20 cm and a height of 100 cm to obtain the tailings with different gradations. The raw tailings and water were put into the physical model in a mass ratio of 1:2 and stirred evenly with a wooden stick for 10 min. After the fine-grained tailings were deposited, the water was discharged out of the tube. Along the direction of gravity sedimentation, the tailings were divided equally into three layers (top tailings, middle tailings, and bottom tailings) from top to bottom of the model, as shown in Figure 1. The volumetric water content of the saturated tailings at the top, middle, and bottom of the physical model were in-situ measured by RS-485 Soil Moisture Sensor before the water was drained out, which was 44, 41, and 38%, respectively.
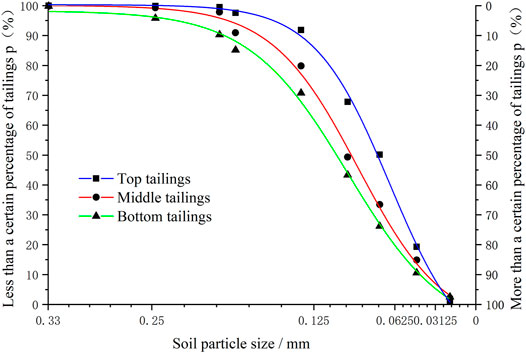
The sedimentary tailings were sampled in the middle of each layer, and the particle characteristics of each tailings sample were analyzed by screening test and laser particle size analysis. Additionally, the particle size distribution curve of different sedimentary tailings was plotted according to experimental results, as shown in Figure 2.
The particle characteristics of different sedimentary tailings were calculated according to Figure 2, and the results are shown in Table 2.
Raw tailings with different burial depths have different porosity and dry density under the confining pressure. To determine the effect of different initial dry densities on the matrix suction of fine-grained tailings, the raw tailings with a volumetric moisture content of 14% were compacted under the vertical pressure of 0, 150, and 300 kPa, which are roughly consistent with gravity stress of tailings at burial depths of 0, 10, and 20 m, respectively. In addition, the initial dry densities of tailings under the vertical pressure of 0, 150, and 300 kPa were calculated as 1.27, 1.41, and 1.55 g/cm3, respectively.
Experimental Procedures
First, dry the tailings samples with a thermostatic drying chamber (105∼110°C) for no less than 10 h.
Second, wet the dry tailings samples to different volumetric moisture content (3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, and 36% up to saturation moisture content), respectively. Tailings samples with different moisture content are made into cylindrical specimens, and the specimens are placed into sealed jars for 2 days to allow for the tailings and water homogenization.
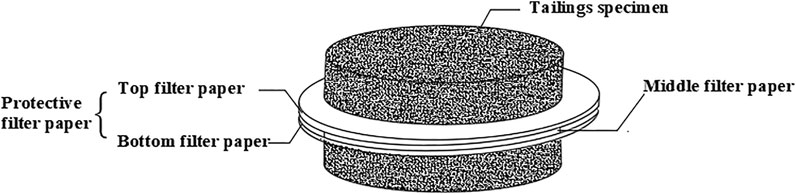
Third, put three sheets of filter paper baked over 2 h into the tailings specimens, the top and bottom filter paper are designed to protect the middle filter paper from damage, as shown in Figure 3. Weigh the mass of middle filter paper with a High-precision Electronic Scale before placing it into the tailings specimens.
Fourth, place the tailings specimen with the filter paper into the sealed jar, and place the sealed jar into a constant temperature and humidity box for 7 days to balance the moisture content between the filter paper and fine-grained tailings. Then keep the box with constant humidity, and change the temperature of the box to investigate the effect of temperature on the soil–water characteristic curve. Tailings specimens in the sealed jar are shown in Figure 4.
Fifth, take the middle filter paper out of the tailings specimen, and measure its mass within 30 s, as the filter paper is sensitive to moisture, and calculate the volumetric moisture content of filter paper.
Sixth, calculate the matrix suction
Last, use the Van Genuchten model to obtain the empirical equation of SWCC and to verify the accuracy of experimental results.
Results and Discussion
Effect of Particle Gradation on the SWCC of Fine-Grained Tailings
The fitting parameters and correlation coefficients of the Van Genuchten model at different gradations were obtained as shown in Table 3.
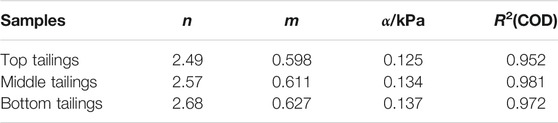
TABLE 3. Fitting parameters of the Van Genuchten model for the SWCC of tailings at different gradations.
As can be seen from Table 3, the correlation coefficient R2 values were 0.952, 0.981, and 0.972, respectively, indicating that the Van Genuchten model fits the experimental data determined by filter paper-based method at different gradations. Additionally, the top tailings have maximum fitting parameters of
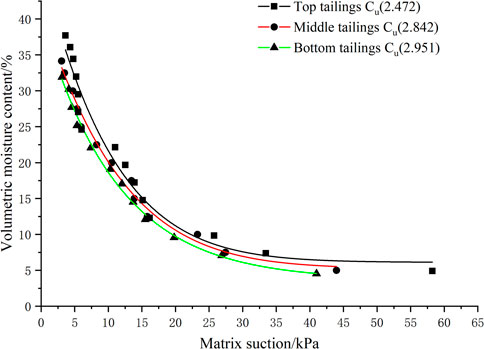
The experimental data and best-fit SWCC of fine-grained tailings at different gradations as shown in Figure 5. The matrix suction of fine-grained tailings increased with decreasing volumetric moisture content, and the increasing trend of matrix suction at different gradations is consistent and can be divided into three stages: the slow growth stage (volumetric moisture content more than 20%), stable growth stage (volume moisture content between 10 and 20%), and sharp growth stage (volumetric moisture content less than 10%).
The average particle size and non-uniformity coefficient of each tailings sample are different due to the gravity sedimentation, which affects the water-holding capacity and matrix suction of the fine-grained tailings. From table 2, we can see that the top tailings have a minimum average particle size (d60 = 0.089 mm) and non-uniformity coefficient (Cu = 2.472), while the bottom tailings have a maximum average particle size (d60 = 0.121 mm) and non-uniformity coefficient (Cu = 2.951). At the same volumetric moisture content, the matrix suction of top tailings is greater than that of bottom tailings, the matrix suction of top tailings is 18.6% higher than that of bottom tailings under natural volumetric moisture content (14.0%). According to the experimental results of the previous studies (Chen et al., 2018; Zhai et al., 2020), the matrix suction increased with decreasing soil particle size (Negative correlation) and with increasing non-uniformity coefficient (Positive correlation). However, as can be seen from Figure 5, experimental results show that tailings (Top tailings) with minor uniformity coefficients have larger matrix suction, indicating that the particle size plays a more important role than the non-uniformity coefficient to affect the matrix suction of fine-grained tailings.
For the unsaturated soil, according to the Young–Laplace equation (Young, 1805; Laplace, 1806), there is the following relationship among the additional pore pressure, the curvature radius of the meniscus, and the surface tension of fluids, as shown in Eq. (3):
where
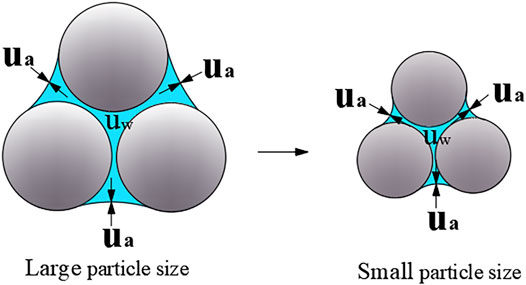
At the same volumetric moisture content, the change of particle size will change the curvature radius of the meniscus. The smaller the particle size of fine-grained tailings, the larger the curvature radius of the meniscus. So, the fine-grained tailings with smaller particle sizes have greater matrix suction (
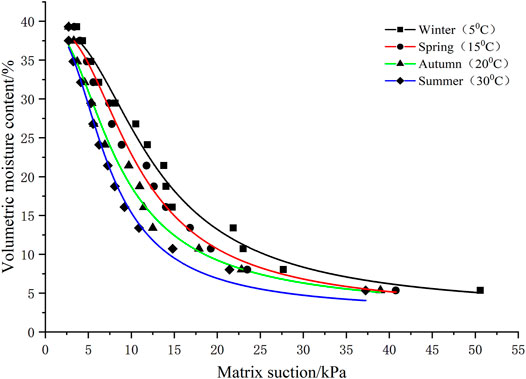
Effect of Ambient Temperature on the SWCC of Fine-Grained Tailings
Temperature theoretically affects the matrix suction of soil in direct and indirect aspects, especially in the case of large temperature differences. The local average temperature in Spring (15°C), Summer (30°C), Autumn (20°C), and Winter (5°C) are chosen in this experimental program to analyze the effect of seasonal temperature changes on the SWCC of fine-grained tailings.
The fitting parameters and correlation coefficients of the Van Genuchten model at different ambient temperatures were obtained, as shown in Table 4.
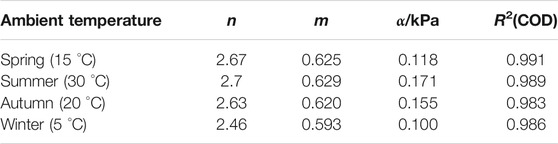
TABLE 4. Fitting parameters of the Van Genuchten model for the SWCC of tailings at different ambient temperature.
As can be seen in Table 4, the correlation coefficient R2 values were 0.991, 0.989, 0.983, and 0.986, indicating that the Van Genuchten model fits the experimental data determined by filter paper-based method at different ambient temperatures. The fitting parameter
As can be seen from Figure 7, the ambient temperature has a significant effect on the matrix suction of fine-grained tailings. At the same volumetric moisture content, the lower the ambient temperature, the greater the matrix suction. The matrix suction of the tailings in summer is 38.3% lower than that in winter under the natural volumetric moisture content (14.0%). Therefore, it should be considering the effect of reduced matrix suction of fine-grained tailings on the stability of tailings dams in hot summer.
The influence mechanism of temperature on matrix suction is different from that of particle size. At the same volumetric moisture content, the kinetic energy of liquid molecules increases (v1 < v2), and the intermolecular interaction force (F1 > F2) weakens with the increase of temperature, reducing the surface tension of fluids and resulting in a decrease in the matrix suction of fine-grained tailings, as shown in Figure 8.
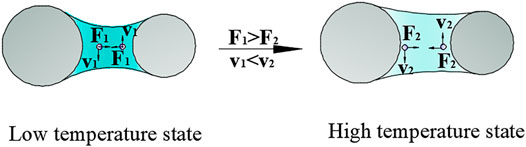
FIGURE 8. Molecules velocity and intermolecular interaction forces between tailings particles at different temperatures.
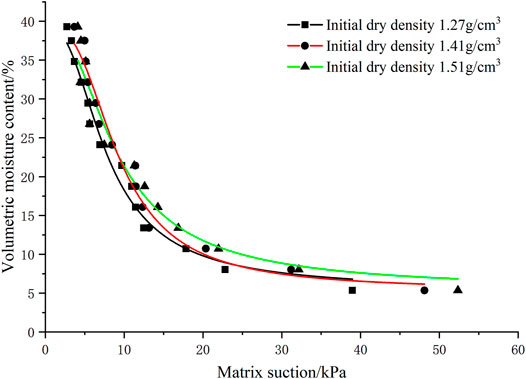
Effect of Initial Dry Density on SWCC of Fine-Grained Tailings
The fitting parameters and correlation coefficients of the Van Genuchten model at different initial dry densities were obtained as shown in Table 5.
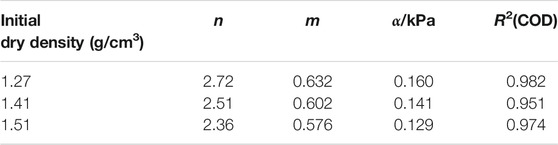
TABLE 5. Fitting parameters of the Van Genuchten model for the SWCC of tailings at different initial dry densities.
As can be seen from Table 5, the correlation coefficient R2 values were 0.982, 0.951, and 0.974, indicating that the Van Genuchten model can well-fit the experimental data determined by filter paper-based method at different initial dry densities. The fitting parameter
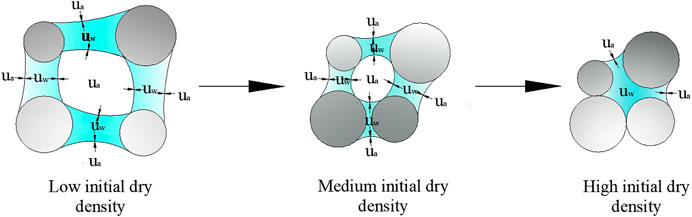
As can be seen from Figure 9, when the degree of saturation is less than 60%, the matrix suction of the fine-grained tailings increased by increasing the initial dry density: the greater the compaction of the tailings, the greater the matrix suction. When the degree of saturation is greater than 60%, the matrix suction of fine-grained tailings does not vary significantly.
As can be seen from Figure 10, when the initial dry density of fine-grained tailings increases, the air between pores and water is compressed, and the spacing distance between particles decreases, resulting in a decrease in the curvature radius of the meniscus and increase in matrix suction. When the tailings are over compacted, the gravitational water in the pores is extruded, which reduces the contact surface area between the gravitational water and the tailings particles. Instead, the matric suction of the tailings decreases when the saturation degree is greater than 60%.
Conclusion
This paper investigated the effects of gradation, temperature, and initial dry density on the SWCC of fine-grained tailings by the laboratory tests and theoretical analysis, and the following conclusions were obtained.
First, the correlation coefficient R2 value of Van Genuchten model is more than 0.95, and the physical significance of the fitting parameters α, m, and n are also consistent with the experimental results, indicating that the matrix suction is determined by the filter paper-based method was accurate and appropriate.
Second, the top tailings have better water-holding capacity, more uniform particle size distribution, and smaller porosity than the bottom tailings. At the same volumetric moisture content, the matrix suction of top tailings is greater than that of bottom tailings, and the particle size plays a more important role than the non-uniformity coefficient to affect the matrix suction of fine-grained tailings.
Third, at the same volumetric moisture content, the lower the ambient temperature, the greater the matrix suction and water-holding capacity of fine-grained tailings. The matrix suction of the tailings in summer was 38.3% lower than that in winter under the natural volumetric moisture content (14%) because an increase in temperature reduces the surface tension and viscosity of the water.
Finally, when the saturation degree of fine-grained tailings is less than 60%, the greater the initial dry density, the better the water-holding capacity and matrix suction.
The research results provide a reference to quantify the effect of gradation, temperature, and initial dry density on the engineering properties of fine-grained tailings. However, there are inevitable differences in the weighing process of the filter paper due to the light weight and high moisture sensitivity of the filter paper. The calibration curve of the filter-paper method has certain limitations for different types of filter paper, which easily leads to certain errors between the measured value and the actual value of the matrix suction. Therefore the focus in subsequent research should be on how to reduce and eliminate the errors caused by these factors.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This study was supported by the National Natural Science Foundation of China (11875164), Natural Science Foundation of Hunan Province (2019JJ50496, 2021JJ30571), Science and Technology Department Key R and D Plan Project of Hunan Province (2019SK 2011), Scientific Research Project of Education Department of Hunan Province (20B496), and Uranium Tailings Depot Resiliency Engineering Technology Research Center of Hunan Province.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmed, M. A., Tamer, Y. E., and Mosleh, A. A. (2018). Hysteresis Soil–Water Characteristic Curves of Highly Expansive clay. Eur. J. Environ. Civil Eng. 22 (9), 1041–1059. doi:10.1080/19648189.2016.1229232
ASTM D2216-19 (2019). Standard Test Methods for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass. West Conshohocken, PA: ASTM.
ASTM D5298-10 (2010). Standard Test Method for Measurement of Soil Potential (Suction) Using Filter Paper. West Conshohocken, PA: ASTM.
ASTM D6913-04 (2017). Standard Test Methods for Particle-Size Distribution (Gradation) of Soils Using Sieve Analysis. West Conshohocken, PA: American Society for Testing Materials.
ASTM D7263-21 (2021). Standard Test Methods for Laboratory Determination of Density (Unit Weight) of Soil Specimens. West Conshohocken, PA: ASTM.
ASTM D854-14 (2014). Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. West Conshohocken, PA: ASTM.
Bechtold, M., Dettmann, U., Wöhl, L., Durner, W., Piayda, A., and Tiemeyer, B. (2018). Comparing Methods for Measuring Water Retention of Peat Near Permanent Wilting point. Soil Sci. Soc. America J. 82 (3), 601–605. doi:10.2136/sssaj2017.10.0372
Birle, E., Heyer, D., and Vogt, N. (2008). Influence of the Initial Water Content and Dry Density on the Soil-Water Retention Curve and the Shrinkage Behavior of a Compacted clay. Acta Geotech. 3 (3), 191–200. doi:10.1007/s11440-008-0059-y
Brooks, R., and Corey, A. (1964). Hydraulic Properties of Porous media. Hydrology Paper. Fort Collins, Colorado: Colorado State University.
Chen, X., Hu, K., Chen, J., and Zhao, W. (2018). Laboratory Investigation of the Effect of Initial Dry Density and Grain Size Distribution on Soil-Water Characteristic Curves of Wide-Grading Gravelly Soil. Geotech Geol. Eng. 36 (2), 885–896. doi:10.1007/s10706-017-0362-1
ElKeshky, M. M. (2011). Temperature Effect on the Soil Water Retention Characteristic. Phoenix, Arizona: Arizona State University.
Fattah, M. Y., Majeed, Q. G., and Joni, H. H. (2021). Comparison between Methods of Soil Saturation on Determination of the Soil Water Characteristic Curve of Cohesive Soils. Arab J. Geosci. 14 (2), 1–10. doi:10.1007/s12517-020-06362-y
Fredlund, D. G., and Rahardjo, H. (1993). Soil Mechanics for Unsaturated Soils. New York: John Wiley & Sons.
Fredlund, D. G., and Xing, A. (1994). Equations for the Soil-Water Characteristic Curve. Can. Geotech. J. 31 (4), 521–532. doi:10.1139/t94-061
Gallage, C. P. K., and Uchimura, T. (2010). Effects of Dry Density and Grain Size Distribution on Soil-Water Characteristic Curves of Sandy Soils. Soils and Foundations 50 (1), 161–172. doi:10.3208/sandf.50.161
Gardner, W. R. (1958). Mathematics of Isothermal Water Conduction in Unsaturated Soil. Highway Research Board Special Report, Washington, 78–87.
Heshmati, A. A., and Motahari, M. R. (2015). Modeling the Dependency of Suction Stress Characteristic Curve on Void Ratio in Unsaturated Soils. KSCE J. Civ Eng. 19 (1), 91–97. doi:10.1007/s12205-013-1185-0
Jiang, X., Wu, L., and Wei, Y. (2020). Influence of Fine Content on the Soil-Water Characteristic Curve of Unsaturated Soils. Geotech Geol. Eng. 38 (2), 1371–1378. doi:10.1007/s10706-019-01096-5
Kern, J. S. (1995). Evaluation of Soil Water Retention Models Based on Basic Soil Physical Properties. Soil Sci. Soc. America J. 59 (4), 1134–1141. doi:10.2136/sssaj1995.03615995005900040027x
Lersow, M. (2010). “Safe closure of uranium mill tailings ponds-on basis of long-term stability-proofs linked with an extensive environmental monitoring,” in 6th International Congress on Environmental Geotechnics, New Delhi, India, November 2010. doi:10.13140/RG.2.1.4805.7364
Li, J. H., Lu, Z., Guo, L. B., and Zhang, L. M. (2017). Experimental Study on Soil-Water Characteristic Curve for Silty clay with Desiccation Cracks. Eng. Geology. 218, 70–76. doi:10.1016/j.enggeo.2017.01.004
Ma, D., Kong, S., Li, Z., Zhang, Q., Wang, Z., and Zhou, Z. (2021). Effect of wetting-drying cycle on hydraulic and mechanical properties of cemented paste backfill of the recycled solid wastes. Chemosphere 282 (10), 131163. doi:10.1016/j.chemosphere.2021.131163
Mahler, C., and Mendes, C. (2005). Measurement of Suction of Thick Textured Soil Using Filter Paper Method and Equivalent Tensiometer—EQT. Berlin Heidelberg: Springer.
Marinho, F. A. M., Take, W. A., and Tarantino, A. (2008). Measurement of Matric Suction Using Tensiometric and axis Translation Techniques. Geotech Geol. Eng. 26 (6), 615–631. doi:10.1007/s10706-008-9201-8
Matlan, S. J., Taha, M. R., and Mukhlisin, M. (2015). Assessment of Model Consistency for Determination of Soil-Water Characteristic Curves. Arab J. Sci. Eng. 41 (4), 1233–1240. doi:10.1007/s13369-015-1888-2
Qiao, X., Ma, S., Pan, G., and Liu, G. (2019). Effects of Temperature Change on the Soil Water Characteristic Curve and a Prediction Model for the Mu Us Bottomland, Northern China. Water 11 (6), 1235. doi:10.3390/w11061235
Tamer, Y. E., Ahmed, M. A., Muawia, D., and Mosleh, A. A. (2017). Effect of Compaction State on the Soil Water Characteristic Curves of Sand–Natural Expansive clay Mixtures. Eur. J. Environ. Civil Eng. 21 (3), 289–302. doi:10.1080/19648189.2015.1112844
Tripathy, S., Tadza, M. Y. M., and Thomas, H. R. (2014). Soil-Water Characteristic Curves of Clays. Can. Geotech. J. 51 (8), 869–883. doi:10.1139/cgj-2013-0089
Van Genuchten, M. T. (1980). A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. America J. 44 (6), 892–898. doi:10.2136/sssaj1980.03615995004400050002x
Yan, W. M., and Zhang, G. (2015). Soil-Water Characteristics of Compacted sandy and Cemented Soils with and without Vegetation. Can. Geotech. J. 52 (9), 1331–1344. doi:10.1139/cgj-2014-0334
Zeitoun, R., Vandergeest, M., Vasava, H. B., Machado, P. V. F., Jordan, S., Parkin, G., et al. (2021). In-situ Estimation of Soil Water Retention Curve in silt Loam and Loamy Sand Soils at Different Soil Depths. Sensors 21 (2), 447–461. doi:10.3390/s21020447
Zhai, Q., Rahardjo, H., Satyanaga, A., and Dai, G. (2020). Estimation of the Soil-Water Characteristic Curve from the Grain Size Distribution of Coarse-Grained Soils. Eng. Geology. 267, 105502. doi:10.1016/j.enggeo.2020.105502
Zhang, K., Chanpura, R. A., Mondal, S., Wu, C.-H., Sharma, M. M., Ayoub, J. A., et al. (2015). Particle-Size-Distribution Measurement Techniques and Their Relevance or Irrelevance to Wire-Wrap-Standalone-Screen Selection for Gradual-Formation-Failure Conditions. SPE Drilling & Completion 30 (2), 164–174. doi:10.2118/168152-PA
Keywords: fine-grained tailings, filter paper-based method, unsaturated tailings, Van Genuchten model, soil water characteristic curve (SWCC)
Citation: Cao B, Tian Y, Gui R and Liu Y (2021) Experimental Study on the Effect of Key Factors on the Soil–Water Characteristic Curves of Fine-Grained Tailings. Front. Environ. Sci. 9:710986. doi: 10.3389/fenvs.2021.710986
Received: 19 May 2021; Accepted: 08 July 2021;
Published: 30 August 2021.
Edited by:
Qingsheng Bai, Freiberg University of Mining and Technology, GermanyReviewed by:
Dan Ma, China University of Mining and Technology, ChinaHao Wu, China University of Mining and Technology, China
Copyright © 2021 Cao, Tian, Gui and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rong Gui, MjAwOTAwMDUwN0B1c2MuZWR1LmNu; Yong Liu, bGl1eW9uZzgxNjY4QDE2My5jb20=
†These authors have contributed equally to this work
 Baofeng Cao
Baofeng Cao Yakun Tian†
Yakun Tian† Rong Gui
Rong Gui