Comparing Multi-Criteria Decision-Making Methods for the Assessment of Flow Release Scenarios From Small Hydropower Plants in the Alpine Area

Growing energy demand and targets for reducing greenhouse gas emissions are driving a significant hydropower (HP) generation expansion in the Alpine area. However, despite its advantages, HP implementation causes several impacts on the ecological status of river systems and the preservation of characteristic landscapes. The use of decision-making tools, like multi-criteria decision-making (MCDM) methods, can provide helpful support to achieve more sustainable solutions for complex water management problems. In Aosta Valley (NW Italy), an MCDM experimental approach is being applied to define the optimal environmental flow scenario to be released by HP plants, in an attempt to balance energy production needs, economic profitability and environmental safeguard. Four criteria are considered (energy, environment and fishing, landscape, economy) and key stakeholders are involved in the entire decision-making process. However, there is a need to test also other MCDM methodologies in order to understand if an alternative approach could be more suitable for future, more complex, HP management decisions. Therefore, in this paper, seven different MCDM methods are applied to an existing small run-of-the-river HP plant for the selection of the optimal flow release scenario, i.e., SAW, WPM, AHP, TOPSIS, VIKOR, ELECTRE III, and the initially adopted method, SHARE MCA. The results obtained with the application of the different MCDM methods are investigated and statistically compared. The strengths and weaknesses of the different methodological approaches are also discussed. Based on the comparative results and the consequent evaluations, SHARE MCA, WPM, and VIKOR appear to have the most interesting characteristics in terms of overall feasibility.

Introduction

Hydropower (HP) generation is a key topic for Alpine water resources management. Indeed, within the goals for renewable energy growth to reduce greenhouse gases (GHG) emissions (European Commission [EC], 2009), the contribution of HP production is considered particularly important for serving the energy demand of the Alpine states (Alpine Convention–Platform Water Management in the Alps, 2011) and helping the stabilization of the European energy grid (Alpine Convention, 2009). For these reasons, during the twentieth century, hydropower capacity has further increased in the Alps, providing more than 90% of electricity production (Gingrich et al., 2009), and applications for new, particularly small and micro, HP stations, are still increasing (Ferrario and Castiglioni, 2017).

However, despite its clear benefits, HP generation can also have significant negative impacts on the aquatic ecology (e.g., interruption of the river continuity, changes in river morphology, hydro-peaking, leading to a considerable loss of biodiversity) and on the natural sceneries (Brunke, 2002; Truffer et al., 2003; Stähly et al., 2019). These pressures are not only caused by large dams and reservoirs: the wide distribution of small HP plants in the Alps, for example, has a cumulative effect, deeply altering natural habitats in a considerable number of watercourses, especially in mountainous areas (Vezza et al., 2014).

Moreover, river stretches that are in or near natural conditions are becoming increasingly rare, leading to conflicts over water use and management, e.g., agriculture, hydropower, drinking water, ecological needs (Bratrich et al., 2004; Schneider et al., 2014). These conflicts could even intensify in the future due to the expected changes in water availability caused by climate change (Scheurer et al., 2018). Therefore, achieving sustainable solutions concerning HP generation, ensuring the compatibility with environmental protection requirements, is extremely important to avoid irreversible impacts (Alpine Convention–Platform Water Management in the Alps, 2018). Furthermore, improving the dialogue among all stakeholders is strongly recommended to prevent/overcome conflicts among water uses (Alpine Convention, 2009). Thus, common guidelines and support for decision-making are increasingly required to tackle this challenging issue (Alpine Convention–Platform Water Management in the Alps, 2011).

A methodological approach for conflict management providing helpful support to complex decision-making problems is the multi-criteria decision-making (MCDM, Soncini-Sessa et al., 2000; Opricović and Tzeng, 2008). MCDM represents a collection of techniques with the overall goal to determine a preference ordering among alternative decision options, whose performance is scored against multiple criteria (Steele et al., 2009). The MCDM process can support decision-making by helping to structure the problem and providing all involved actors with a common language for discussing and learning about the problem (Köhler et al., 2019). It has also the potential to improve transparency, auditability, and analytic rigor of decisions (Šantl and Steinman, 2015). MCDM is widely applied in the field of water management (e.g., Joubert et al., 2003; Alamanos et al., 2018; Manikkuwahandi et al., 2019), usually characterized by many decisional actors with multiple, conflicting objectives (Hajkowicz and Collins, 2007).

Since the use of MCDM in real decision-making processes can lead to relevant actions (e.g., construction of a dam, allocation of water resources to a specific use, etc.), a thorough evaluation on if and how the choice of the different MCDM methods might affect the preference ordering among alternative options (and therefore, the final decision) is highly relevant and could also provide specific guidance on selecting the most appropriate approach to be used when dealing with hydropower management decisions. However, only few studies in the field of HP planning and management (e.g., Adhikary et al., 2013; Carriço et al., 2014) have applied different MCDM techniques to the same problem comparing their results and briefly discussing, mainly in qualitative terms, the obtained rankings.

For this purpose, in this study, different MCDM methods are considered and tested in a real case study of HP management in Aosta Valley, a small Alpine region in the North-West of Italy. In this region, an experimental approach based on multi-criteria analysis is being used to define environmental flows to be released by HP plants. The decision-making approach, implemented by the Regional River Strategic Plan (Regione Autonoma Valle d’Aosta [RAVA], 2006), involves key institutional stakeholders to assess the compatibility of water diversions with environmental conditions. Four criteria are usually considered, i.e., Energy, Environment and fishing, Landscape, and Economy, each quantified by indicators based on the watercourse discharge.

The main aim of this paper consists of testing, in a real case study (Vassoney et al., 2020), the applicability and effectiveness of different MCDM methods for the selection of the optimal flow release scenario to be implemented downstream of a small run-of-the-river HP plant. In addition to the model initially adopted in the region, named SHARE MCA, six other MCDM methods were selected among the most used in literature (Zanakis et al., 1998; Zamani-Sabzi et al., 2016), i.e., SAW (Simple additive Weighting), WPM (Weighted Product Method), AHP (Analytic Hierarchy Process), TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution), VIKOR (Vlšekriterijumsko KOmpromisno Rangiranje, i.e., multicriteria optimization and compromise ranking), and ELECTRE III (ELimination Et Choix Tradusiant la REalité, i.e., Elimination and Choice Translating Reality), in order to evaluate whether an alternative methodology could be more suitable for future official decision-making processes.

In the following sections, after a short overview of the differentMCDM techniques used in literature (section “Short Overview of theMulti-Criteria Decision-Making Use in the Field of Hydropower”), the MCDM framework (section “Definition of the Decision Matrix”) and the methods considered in this study (section “Multi-Criteria Decision-Making Methods”) are described. Their comparative analyses (sections from “Comparative Analyses of Different MCDM Methods’ Results” to “Evaluation of the Overall Methodological Approach for the Different MCDM Techniques”) and the case study (section “Case Study”) are also presented. The rankings obtained from the different methods are compared to each other and statistically analyzed through Kendall’s tau and Spearman’s rho correlation tests (section “Comparison of the Rankings Obtained Through the Different MCDM Methods”). A sensitivity analysis is also performed by varying the weights of criteria (section “Results of the Sensitivity Analysis”). Finally, the different methodological approaches are investigated in terms of suitability for the considered decision-making problem and according to some significant characteristics, like the necessary datasets, ease of use, reliability, and degree of stakeholders’ involvement and training (sections “Evaluation of the Different Methodological Approaches”). The obtained results and the consequent evaluations are discussed in section “Discussion”: on this basis, the most appropriate methods for future, more complex HP management decisions (e.g., involving a system of withdrawals at watershed level) are identified.

Materials and Methods

Short Overview of the Multi-Criteria Decision-Making Use in the Field of Hydropower

Over the last decades, different MCDM techniques have been employed in studies concerning the planning, management, or policy assessment of renewable energy projects, including hydropower (Vassoney et al., 2017). One of the most frequently applied MCDM methods is AHP. This method was used, for example, by Supriyasilp et al. (2009) to study the potential to develop HP projects in the Ping River Basin (Thailand), considering 64 potential sites. Fuentes-Bargues and Ferrer-Gisbert (2015) also proposed an application of AHP to select the best small run-of-the-river HP plant among three alternative projects in the Miño-Sil river basin (Spain), while Kumar and Katoch (2015) used AHP to establish a ranking of the most sustainable installed capacity range (i.e., mini, small, and large) of run-of-the-river HP projects for the Himalayan region (India). On the contrary, Jiménez Capilla et al. (2016) used a spatial MCDM, based on AHP and geographical information systems (GIS), to determine the optimal location for an upper reservoir of a pumped-storage system in the Guadalfeo river basin (Spain).

However, other MCDM methods have also been adopted for decision problems concerning HP planning and management. For example, Multi-Attribute Value Theory (MAVT) was applied by Karjalainen et al. (2013) to assess restoration options for the regulated Iijoki River (Finland) and by Barton et al. (2020), in a Bayesian Network, to select the optimal scenario combining weir removal and discharge regimes downstream of an HP plant in the Mandal River (Norway). TOPSIS was selected by Wang et al. (2014) to analyze the overall efficiency of HP generation in Canada, comparing five provinces, and by Chien et al. (2020) to select the optimal location for the installation of HP plants in Vietnam. Also, Opricović and Tzeng (2008) proposed VIKOR for HP system planning on the Drina River (former Yugoslavia), while Vučijak et al. (2013) suggested the same method to aid decision-makers during the design process of HP plants. As concerns the outranking methods, ELECTRE was used, for example, by Stevović et al. (2014) to select the most sustainable system of small HP plants in the Prokletije region (Montenegro) and by Saracoglu (2015) to rank five alternative small HP plant investments in Turkey, while PROMETHEE (Preference Ranking Organization METHod for the Enrichment of Evaluations) was applied by Singh and Nachtnebel (2016) to evaluate and rank six small HP schemes in Nepal.

Furthermore, applications of MCDM in a fuzzy environment are increasingly used (e.g., Tzimopoulos et al., 2013; Dong et al., 2015; Wibowo et al., 2015; Majumder et al., 2020), since the fuzzy sets theory allows including qualitative criteria, for which measuring the exact value is difficult, or criteria affected by imprecision due to the lack of available information (Khanzadi et al., 2016). Some authors have also presented and tested new MCDM techniques. For example, Marttunen and Suomalainen (2005) developed a new value-tree-based Excel spreadsheet model (REGAIM) for the definition of more sustainable regulation strategies for four large connected regulated lakes in the Pirkanmaa region (Finland). Ji et al. (2015) developed an integrated fuzzy entropy-weight MCDM (IFEMCDM) method and applied it to risk assessment for 10 HP stations along the Xiangxi River, in China. More recently, Yang et al. (2020) proposed a novel stochastic multicriteria acceptability analysis (SMAA) model coupling with TOPSIS and gray correlation analysis (SMAA-TOPSIS&GCA model) to solve stochastic decision-making for short-term HP generation operation under uncertain environment.

Finally, some studies have also applied different MCDM techniques to the same problem and compared the obtained rankings. For example, Özelkan and Duckstein (1996) used PROMETHEE I and II, geometrical analysis for interactive assistance (GAIA), multi criterion Q-analysis (MCQA I, II, III), compromise programming (CP), and cooperative game theory (CGT) to rank different water resources projects designed at the Austrian part of the Danube river, demonstrating that there are not substantial ranking differences between the methods. Adhikary et al. (2013) applied Simple Additive Weighting (SAW), Weighted Product Method (WPM), and AHP-TOPSIS for the selection of a hydro turbine manufacturer for small HP generation, showing that the rankings are not significantly affected by the choice of the MCDM method. Also, Carriço et al. (2014) compared SAW and ELECTRE III for the selection of the best energy-efficient option for a water supply system in the Algarve region (Portugal) and discussed the advantages and drawbacks of the two methods. Moreover, Ehteram et al. (2018) used complex proportional assessment (COPRAS), TOPSIS, modified TOPSIS, and Weighted Aggregated Sum Product Assessment (WASPAS) to evaluate different algorithms for the optimization of a reservoir operation for HP generation. They assessed the results of the different MCDM models by comparing each ranking with the ranking calculated using the Borda aggregation method.

This short overview demonstrates that several MCDM methods, even theoretically very different, have been considered in the literature and have been applied in various management contexts, to solve different kinds of decision-making problems concerning hydropower. No method can be considered better than the others in any situation. Decision-makers should select among the several existing techniques the ones more fitting to their decisional context (e.g., considering the set of laws, river environmental features, local knowledge, etc.) and to stakeholders’ technical background and level of participation. For this reason, investigating different MCDM methods is important and can help improving the quality of decision-making.

Definition of the Decision Matrix

An MCDM problem is characterized by a finite set of m alternatives, denoted as A = {A_i | i = 1, …, m}, that are evaluated according to n criteria, represented as C = {C_j | j = 1, …, n}. The criteria can represent a benefit or a cost. A benefit criterion is desirable to be maximized, i.e., the higher an alternative scores in terms of this criterion, the better the alternative is; on the contrary, for cost criteria lower values are preferable (Ceballos et al., 2016). Moreover, each criterion is assigned a weight, expressing its relative importance. These weights can be denoted as W = {w_j | j = 1, 2, …, n} and they are usually normalized, so that their sum is equal to one: ${\sum }_{\mathrm{j}=1}^n{w}_j=1$ (Triantaphyllou and Baig, 2005).

Therefore, the MCDM problem can be concisely expressed in a matrix form, where rows and columns indicate the alternatives and the criteria, respectively, as shown in Table 1. Each element x_ij of the decision matrix represents the score of the alternative A_i with respect to the criterion C_j.

TABLE 1

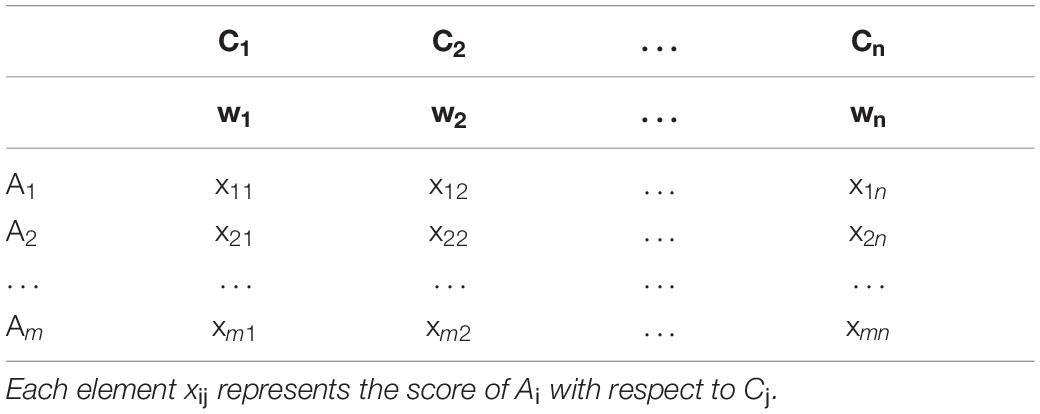
Table 1. Decision matrix of an MCDM problem characterized by m alternatives (A_i) and n criteria (C_j), associated with a weight w_j.

Multi-Criteria Decision-Making Methods

The objective of the problem is to rank the alternatives according to their overall performance value, obtained by combining their scores with the weights (Altunok et al., 2010). A wide range of algorithms can be used in this task, corresponding to the various existing MCDM methods (Hajkowicz and Collins, 2007).

Different classifications have been proposed in the literature. For example, a distinction can be based on the level of compensation allowed by the method. Compensatory techniques (e.g., SAW, AHP), which allow the compensation of poor performances of some criteria by high performances of other criteria, and non-compensatory techniques (e.g., ELECTRE III) can be identified (Banihabib et al., 2017). Triantaphyllou and Baig (2005) also proposed different categories based on the theoretical approach used to evaluate the alternatives. They identified methods that use aggregation techniques considering two separate sets of criteria, i.e., benefit and cost criteria (e.g., AHP, SAW, WPM); outranking methods, based on a pairwise comparison of the alternatives (e.g., ELECTRE group of methods, TOPSIS, PROMETHEE); methods that use an explicit tradeoffs approach based on the “value functions” (e.g., multi-attribute utility theory—MAUT); and methods that use the notion of a reference set of alternatives (preference disaggregation approaches).

In the present study, the following seven MCDM methods are considered and applied to the same decision problem (release scenario from a small HP plant) to compare their ranking performance:

• SAW—Simple additive weighting (Fishburn, 1967), which ranks the alternatives based on their weighted sum performance;

• WPM—Weighted product method (Bridgman, 1922), in which the alternatives are compared by multiplying different ratios, one for each criterion, raised to the power of the corresponding weight;

• AHP—Analytic hierarchy process (Saaty, 1980), which relies on pairwise comparisons of the alternatives on each criterion and an additive aggregation to calculate the overall performances;

• TOPSIS—Technique for order preference by similarity to ideal solution (Hwang and Yoon, 1981), in which the alternatives are ranked based on their distance from defined ideal and negative-ideal solutions;

• VIKOR—Multi-criteria optimization and compromise ranking (Opricović, 1998), which seeks the compromise solution based on the closeness to a defined ideal solution;

• ELECTRE III—Elimination and choice translating reality (Roy, 1978), which is based on an outranking relation between the alternatives (i.e., considering two alternatives A_1 and A_2, A_1 outranks A_2 if there are strong enough reasons to state that A_1 is “at least as good as” A_2 and no enough reasons to state the contrary) and on the use of pseudo-criteria;

• SHARE MCA (SHARE project, 2012), which is the method initially used in the Aosta Valley region, based on a hierarchical framework, the use of normalization functions, and an additive aggregation to calculate the final performances.

The reason for the selection of the first six methods (to be compared with the method adopted in the region) is that they are among the most popular and widely used in the literature and each of them corresponds to a different approach to solve MCDM problems. Different techniques are also used for the normalization of the decision matrix, which is necessary to handle different types of variables (e.g., criteria characterized by different units of measure, benefit and cost criteria). Only ELECTRE III does not require normalization and it can also handle ordinal or descriptive (imprecise) criteria (Zanakis et al., 1998). Moreover, the output of ELECTRE III and VIKOR differs from the other methods and a global ranking of the alternatives is not always achieved (Zamani-Sabzi et al., 2016).

The computational details of the selected MCDM methods are described in Supplementary Section 1.

Comparative Analyses of Different MCDM Methods’ Results

Different MCDM methods can produce different ranking results. Therefore, in order to measure the degree of agreement of different methods, non-parametric correlation tests, like Kendall’s tau and Spearman’s rho, can be used. These two statistical tests analyze the obtained rankings by measuring their pairwise correlations (Zamani-Sabzi et al., 2016). In this study, Kendall’s tau and Spearman’s rho correlation tests were performed to analyze the correlation among the rankings obtained with the different MCDM methods applied to the same case study. Only VIKOR and ELECTRE III were excluded from these statistical comparisons since they produce a different type of ranking of the alternatives (Zamani-Sabzi et al., 2016). The correlation tests were implemented in Matlab©, 2019b.

In addition to the non-parametric correlation tests, the Borda method (de Borda, 1781) was also used to aggregate the rankings obtained with the different MCDM methods. The similarity of each ranking with the aggregated order achieved through the Borda technique was investigated to compare the performance of the considered MCDM models (excluding again VIKOR and ELECTRE III).

The key features of Kendall’s tau and Spearman’s rho correlation tests and the Borda method are described in Supplementary Section 2.

Furthermore, for all the seven considered MCDM methods, two additional tests were performed to measure their degree of agreement (Zanakis et al., 1998; Athawale and Chakraborty, 2012), i.e.:

• agreement between the top three ranked alternatives and

• number of ranks matched, expressed as the percentage of the number of considered alternatives.

Sensitivity Analysis

Sensitivity analysis is an important procedure that allows testing the degree of change in the overall ranking of the alternatives when input data are slightly modified (Steele et al., 2009). Indeed, some stakeholders’ subjective preferences are introduced in each MCDM method, like the evaluation of criteria, the allocation of weights, the choice of preference functions, etc. Therefore, sensitivity analysis can be used to assess the stability and the robustness of the ranking obtained taking into account stakeholders’ preferences (Singh and Nachtnebel, 2016).

In this study, a sensitivity analysis was performed to investigate the robustness of each considered MCDM method when affected by weight uncertainty. Two different schemes of weights were defined. The first scheme (Table 3) is represented by the set of weights actually adopted in the case study described in subsection “Case Study.” In the second scheme (Table 6), equal importance is assigned to the main criteria of the hierarchical structure. This is a typical situation, adopted by several authors to test the sensitivity of the results (Kokaraki et al., 2019).

Evaluation of the Overall Methodological Approach for the Different MCDM Techniques

Based on previous studies comparing different MCDM techniques (e.g., Mahmoud and Garcia, 2000; Hodgett, 2016; Dotoli et al., 2020), the following features were taken into account to compare the considered MCDM methods:

• Need for additional parameters: it assesses the amount of information (both technical and non-technical) required to the user (i.e., the decision-maker or involved stakeholders), thus increasing the subjectivity and the time necessary for the implementation of the method;

• Ease of understanding and transparency: it evaluates whether the method is easily understandable by all the stakeholders (including administrators and stakeholders without a technical background). The evaluation is based on an estimation of the time required to the user to understand and accept the procedures of the method;

• Characteristics of the input data: it evaluates the possibility to use both quantitative and qualitative scores. It also assesses the possibility to consider a large number of alternatives and/or criteria without compromising the feasibility of the procedure;

• Level of transformation of the original data: it takes into account the presence of one or more phases in the procedure that transform the initial data of the decision matrix (e.g., the normalization) and the risk to lose some information during their processing;

• Visualization of the results: it considers the typology of results obtained by the method, e.g., complete or partial ranking, availability of a performance score associated with each alternative, etc.;

• Consistency of the results: it evaluates the robustness of the ranking produced by the method, based on the results of the sensitivity analysis. The consistency is low if the ranking of the alternatives is completely modified after a slight variation of the weights;

• Discrimination of the results: it evaluates the percentage difference between the alternatives within the ranking generated by the method and/or the identification of some alternatives as indifferent;

• Overall feasibility and replicability: it assesses the global applicability of the method, not only in the considered case study, which is relatively simple, but also in more complex HP management decision-making processes, for example involving a system of withdrawals at watershed level.

The assessment was carried out based on the results obtained from the application of the different MCDM methods to the case study and on the remarks made by the authors after testing the different methods together with specific feedback collected from some stakeholders involved in the case study and a representative of the Regional Water Authority.

Case Study

The analyzed case study is a small run-of-the-river HP plant located in Aosta Valley (NW Italy), in the municipality of Brusson, on the Graines torrent (Figure 1), 4th order tributary of the Po river (mean annual discharge < 1 m³/s, watershed area = about 20 km²). The HP plant is characterized by a total head of 125 m, with the water intake located at 1,479 m a.s.l., and an average annual nominal power of 566 kW (a mean annual discharge of 462 l/s is withdrawn).

FIGURE 1

Figure 1. Location of the Graines torrent and HP plant (black dot symbol) in the Aosta Valley region (NW Italy).

The HP plant license, issued in 2010, was subject to revision in order to define a new flow release scheme ensuring a compatible balance between production needs and the safeguard of the watercourse environmental conditions. The MCDM technique initially adopted in the case study was the SHARE MCA method (described in Supplementary Subsection 1.7). The decision-making process, coordinated by the Regional Water Authority, officially involved key stakeholders, i.e., members of the HP company and representatives of the different concerned Regional technical bodies (Regional Agency for the Protection of the Environment, Regional Fisheries Consortium, Regional Landscape Protection Service, Regional environmental assessment and air quality protection Service, Regional flora, fauna, hunting and fishing Service). The HP company was required to implement a hydrological monitoring program, in order to provide a reliable and updated flow data series. Based on these measured data, nine different flow release alternatives (from ALT 0 to ALT 8) were defined, in addition to the initial scenario (“reference alternative”—ALT 0). Some “real-time” alternatives, based, for each month, on a minimum flow value to be released in the streambed, incremented by an additional release, varying on an hourly basis, calculated as a percentage (from 12.5 to 30%) of the watercourse discharge measured upstream of the dam, were also included. The considered alternatives are presented in Table 2.

TABLE 2

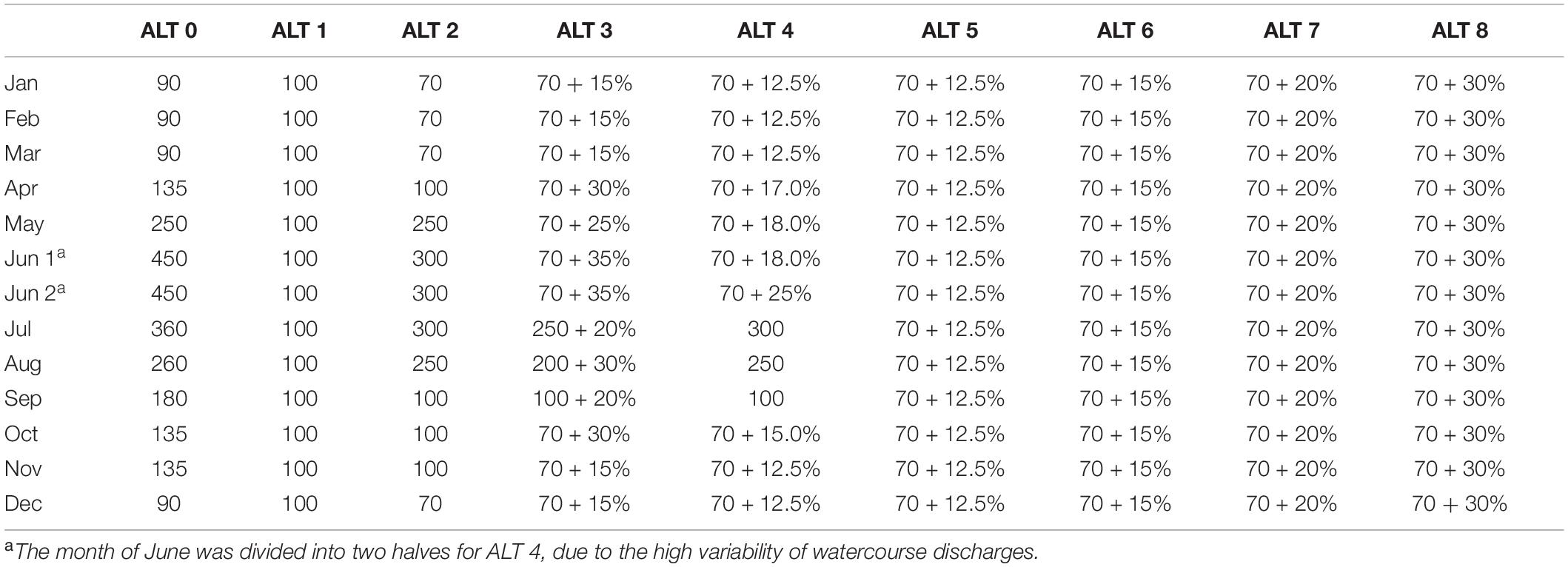
Table 2. Monthly values of the environmental flow releases (l/s) defined for the nine considered alternatives: the percentage values represent a percentage of the watercourse discharge measured upstream of the withdrawal point, while the other numerical values are the fixed flow rates in l/s defined by the involved stakeholders.

The decision tree (i.e., the hierarchical framework of the decision problem) defined for the case study (Figure 2) has four main criteria, i.e., Energy, Environment and fishing, Landscape, and Economy, representing the main concerned stakes, each quantified by one or more indicators, defined by the corresponding stakeholders. All indicators are desirable to be maximized.

FIGURE 2

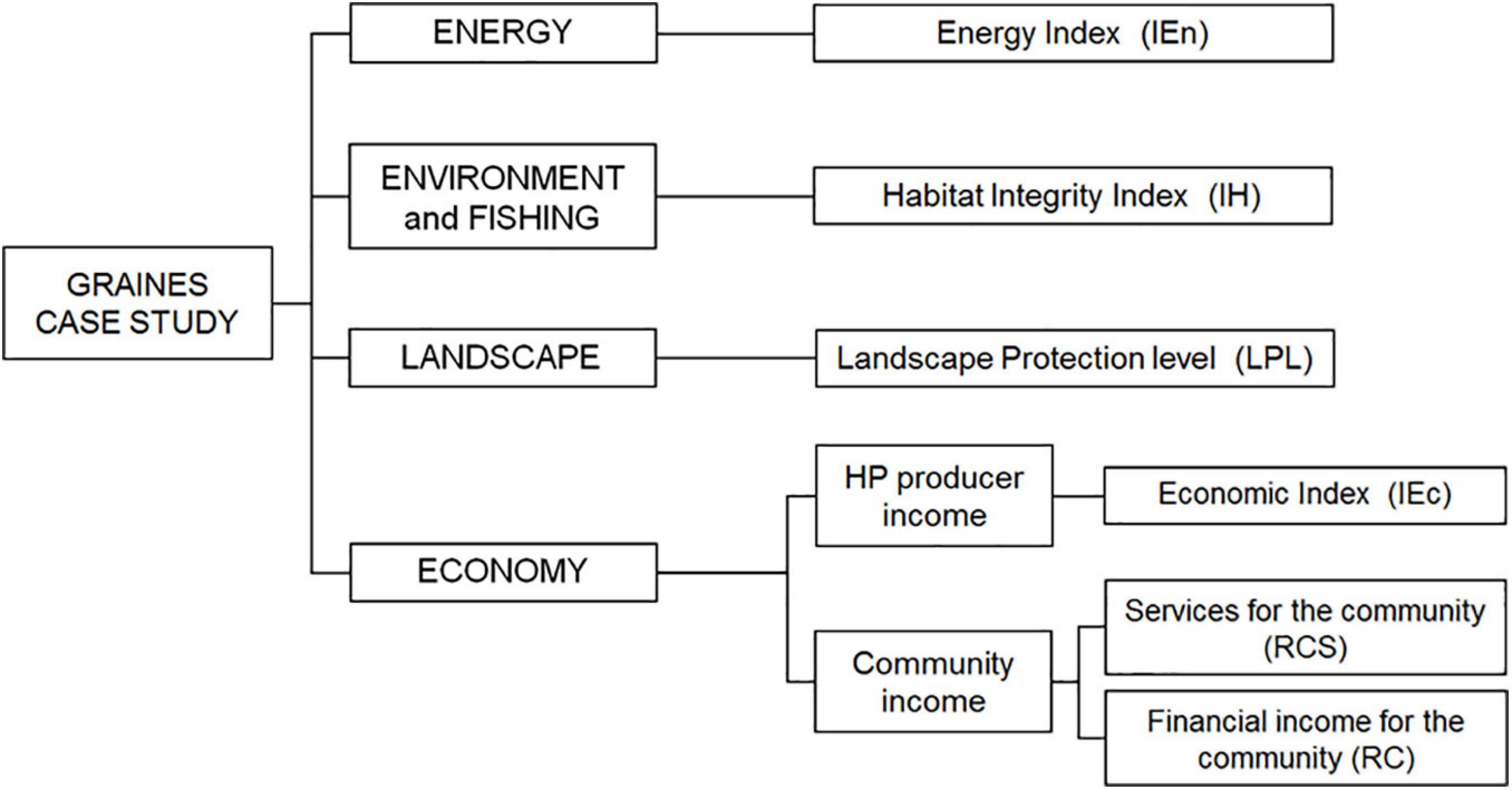
Figure 2. Decision tree of the case study: one or more indicators (on the right) are associated with each of the four considered criteria (in capital letters). Criteria and indicators represent the “branches” and the “leaves,” respectively, of the decision tree.

The Energy Index (IEn) was defined to represent the stake of hydropower production, which contributes to reducing GHG emissions. It quantifies the energy production losses due to flow releases. Its score ranges between 0 and 1. It is calculated through Eq. (1):

$IEn=E_i/E_0(1)$

where E_i is the energy produced by applying the i-th alternative (kWh) and E_0 is the theoretic energy production calculated according to the average annual nominal power of the HP plant (kWh).

The Habitat Integrity Index (IH) was adopted to assess the effects of HP withdrawals on fish population and river environment (Vassoney et al., 2019). It quantifies the available habitat for fish in the bypassed stretch through the MesoHABSIM approach, for different flow scenarios (Parasiewicz, 2007). Its score ranges between 0 and 1. Eq. (2) is used:

$IH=\min (ISH,ITH)(2)$

where ISH is the index of stream habitat spatial availability, assessing the alteration of the spatial amount of habitat availability for fish when the HP withdrawal is present compared to reference conditions and ITH is the index of stream habitat temporal availability, assessing the temporal change of stress periods duration for fish (Vezza et al., 2017).

The Landscape Protection Level (LPL) was defined to assess how the landscape perception changes according to the flow releases. Its score varies between 0 and 165. It is calculated according to Eq. (3):

$LPL=CF+RF+VEF(3)$

where CF is the Constraint Factor, calculated on the basis of national and regional landscape protection constraints and of the watercourse visibility, RF is the Release Factor, based on water flow releases in the bypassed stretch, and VEF is the Visual Elements Factor, assessed by landscape experts analyzing the alteration of the downstream stretch based on a set of photos.

While the other criteria are quantified by a single indicator, the economic criterion was further divided into two sub-criteria, representing the HP producer economic income and the community income (linked to services and fees paid by the HP company according to national and regional rules), respectively, and quantified by different indicators. The Economic Index (IEc) evaluates the economic losses of the HP company due to water flow releases, based on Eq. (4):

$IEc=\frac{E_i\cdot {\text{€}}_{\text{en}}-C_i}{E_0\cdot {\text{€}}_{\text{en}}-C_0}(4)$

where E_i is the energy produced by applying the i-th alternative (kWh), E_0 is the energy production according to the average annual nominal power of the HP plant (kWh), €_en is the energy sale price (€/kWh), while C_i and C_0 represent the HP plant management and maintenance costs related to the i-th alternative and to E_0, respectively (€). The indicator ranges between 0 and 1.

The other two economic indicators, representing the community income, vary between 0 and 1. Services for the community (RCS) estimates the quality and amount of services offered by the HP company to the community living in the area affected by the withdrawal. It is an indicator based on an ordinal scale of five classes (corresponding to the following scores: 0.2, 0.4, 0.6, 0.8, and 1), based on the fact that a higher income for the HP company is generally associated with a larger amount of services for the community living in the area. Finally, Financial income for the community (RC) quantifies the economic income for the community living in the area, due to different fees and royalties paid by the HP producer. Since some of these fees represent a percentage of HP energy production and trade, the indicator score is calculated on the basis of the Economic Index, according to Eq. (5):

$RC=IE{c}^2(5)$

More information about the alternatives and the indicators considered in the case study, as well as the complete decision-making process, is available in Vassoney et al. (2020).

Application of the Different MCDM Methods to the Case Study

The same alternatives and indicators described above were considered in all the MCDM methods. In addition, the same set of weights, agreed upon by the stakeholders involved in the decision-making process concerning the Graines torrent, was adopted. For the sensitivity analysis, the second scheme of weights (assigning equal importance to the main criteria) was also applied to all the methods.

Furthermore, most of the MCDM methods considered in this study (SAW, WPM, TOPSIS, and VIKOR) are based on simple algorithms and thus their computation procedure was implemented in Microsoft Excel^®. For the AHP method, all the mathematical calculations, including the pairwise comparison process, consistency analysis and normalization of results, were performed using the SuperDecisions^® software, version 3.2.0 (Creative Decision Foundation, 2019). On the contrary, J-ELECTRE software, version 2.0 (Pereira et al., 2019) was used to implement the mathematical procedures of ELECTRE III, including the calculation of the concordance, discordance and credibility matrices, the ascending and descending rankings, and the final pre-order of the alternatives. Finally, the calculations of the SHARE MCA method were performed by means of the SESAMO SHARE software (SHARE project, 2012), which directly computes the normalized indicator scores, the weighted values, and the final performance value of each alternative.

As concerns the additional parameters required by some MCDM methods (see Supplementary Section 3, for more information), the following procedures were carried out for their definition:

• AHP: pairwise comparisons for the criteria and sub-criteria/indicators were simulated by the authors, based on the set of weights agreed upon by the different stakeholders involved in the case study during its initial implementation. Comparisons of alternatives with respect to each indicator, on the contrary, were performed through direct input, i.e., by introducing in the designated “direct input area” of the software the scores x_ij of the decision matrix. The reasons for this choice were partly linked to the difficulty to directly involve the decision-maker or all the initially involved stakeholders in real pairwise comparisons (due to time constraints). However, this procedure allowed considering input data (scores and weights) analogous to the values also processed by all the other MCDM methods. Therefore, the final AHP results were comparable with the rankings obtained with the other techniques since they were not affected by different input data.

• VIKOR: the coefficient υ was defined by the authors. It was set equal to 0.5 in order to compromise the two strategies of “majority of criteria” and “individual regret.”

• ELECTRE III: the definition of indifference, preference, and veto thresholds (q_j, p_j, and v_j) for each indicator was based on evaluations made by the authors with the support of some experts and stakeholders involved in the decision-making process. In particular, the indifference threshold was assessed, for each indicator, by evaluating the level of uncertainty associated with the procedure of quantification of the indicator. It was assumed that, for a difference of scores below this level of uncertainty, the discrimination between the two corresponding alternatives was difficult and therefore this value could be used as an indifference threshold. The preference and veto thresholds, on the contrary, were established for each indicator by taking into account the level of satisfaction of the corresponding stakeholder. More information about the definition of the three thresholds for each indicator is available in Supplementary Section 3.

• SHARE MCA: the normalization functions were elaborated, together with the elaboration of each indicator, by the group of stakeholders involved in the decision-making process.

Results

The seven considered MCDM methods (SAW, WPM, AHP, TOPSIS, VIKOR, ELECTRE III, SHARE MCA) were applied to the same case study on the Graines torrent, to identify the optimal flow release scenario to be implemented downstream of a small run-of-the-river HP plant.

Table 3 represents the decision matrix of the considered case study, with the score of each indicator for the nine flow release alternatives. These scores of each indicator were obtained by applying the corresponding procedures described in subsection “Case Study.” In the table, the set of weights actually adopted in the case study and the type of indicator (i.e., benefit or cost) are also shown. As already mentioned, all these data were used for the implementation of all the considered MCDM methods, in order to obtain comparable results.

TABLE 3

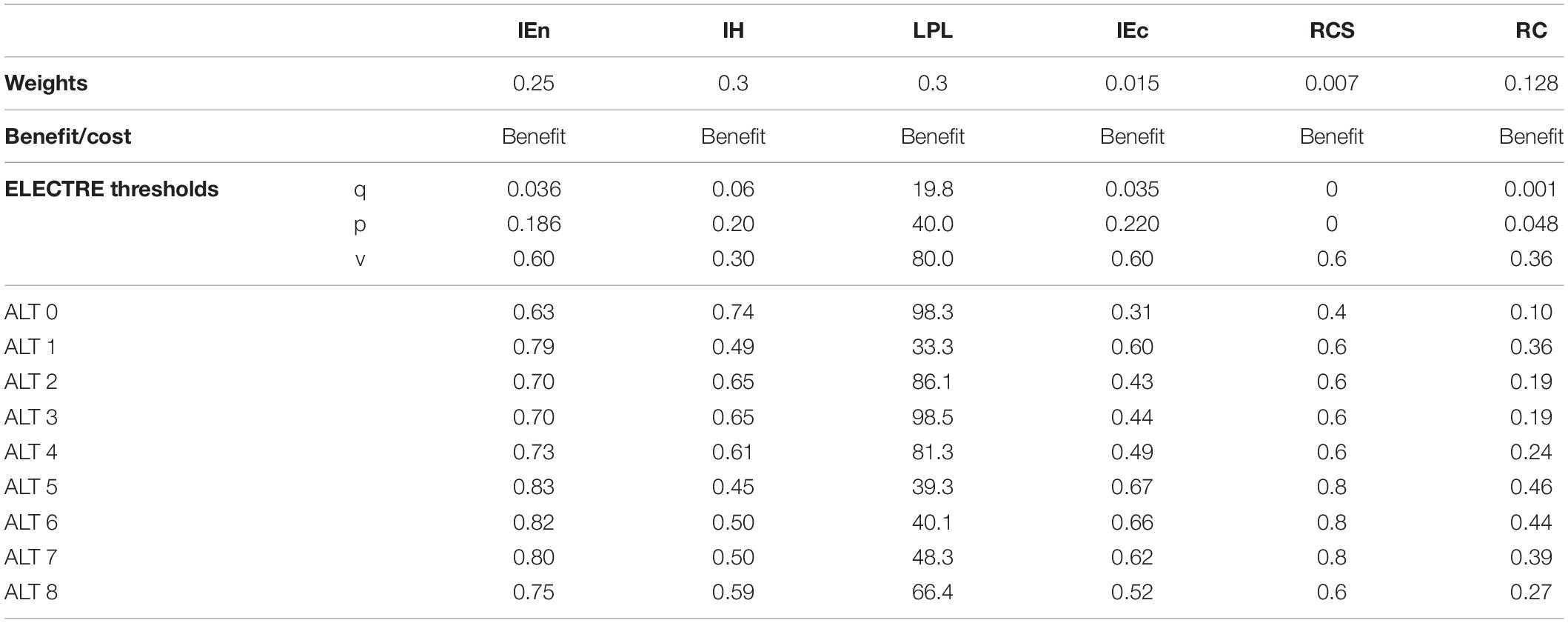
Table 3. Decision matrix of the Graines torrent case study, including the weights, the indicator type (benefit or cost) and the thresholds required by ELECTRE III (q = indifference, p = preference, v = veto).

The weights shown in Table 3 were defined based on a hierarchical allocation, according to the SHARE MCA method (see Supplementary Subsection 1.7) and based on the decision tree represented in Figure 2. The following weights were assigned to the four main criteria: 0.25 to Energy, 0.30 to both Environment and fishing and Landscape, 0.15 to Economy. These weights were agreed upon by all the involved actors, based on reasons that could be explained to external observers and policy-makers. The higher weight of Environment and fishing was due to the fact that this criterion represents two stakeholders’ interests (i.e., environmental heritage and fishing activities affected by the HP plant) and the related sets of laws. Similarly, the higher weight of Landscape was related to the protection needs of both landscape heritage and tourism activities in the affected area. Moreover, between Energy and Economy, a higher weight was assigned to the former, due to the importance of HP production as a renewable energy source contributing to regional, national, and European strategy for the reduction of GHG emissions.

As concerns the “leaves” of the decision tree, weights were allocated first to the two economic sub-criteria, i.e., 0.90 to Community income and 0.10 to HP producer income, because it was assumed that watercourses are public resources to be protected for the whole community. Afterward, the stakeholders defined the weights of the indicators associated with the sub-criterion Community income, i.e., 0.95 for RC and 0.05 for RCS. The significantly higher preference for RC aimed at highlighting the importance of economic incomes for local municipalities.

Therefore, the weights presented in Table 3 correspond to the leaves at the lowest level of the hierarchy (i.e., the indicators) and they were calculated by multiplying their weight in the group of leaves (equal to 1 if there is only one leaf) and the weight of the corresponding “branch” (or main criterion).

Table 3 also shows the thresholds defined for ELECTRE III. As explained in subsection “Application of the Different MCDM Methods to the Case Study,” these values were evaluated by the authors with the support of some experts and stakeholders. Information about the reasons leading to the definition of these thresholds is available in Supplementary Section 3, together with the other additional parameters required by AHP and SHARE MCA (i.e., pairwise comparisons and normalization functions, respectively). The coefficient υ for the VIKOR method, on the contrary, was set by the authors equal to 0.5, as explained in subsection “Application of the Different MCDM Methods to the Case Study.”

Comparison of the Rankings Obtained Through the Different MCDM Methods

The results obtained for the case study applying the seven MCDM methods are presented in Table 4. For SHARE MCA, SAW, WPM, and AHP, each alternative is associated with the corresponding final performance value (P_i), calculated according to the specific procedure, and rank (r_i). For TOPSIS, in addition to the ranks r_i, the distance of each alternative from the ideal solution ($D_i^{*}$) and from the negative-ideal solution ($D_i^{-}$), as well as its relative closeness to the ideal solution (RC_i), are also indicated. For these five methods, the ranking positions r_i are highlighted in bold type so that the results are more easily comparable. For VIKOR, the values S_i, R_i and Q_i of the three rankings generated by the method are shown, while in the row corresponding to r_i the ranks established based on the check of “acceptable advantage” (see Supplementary Subsection 4.5) are indicated. Moreover, the three alternatives identified as compromise solutions, i.e., ALT 3, ALT 4 and ALT 2, are highlighted in bold type. Finally, for ELECTRE III, the position of each alternative in the rankings generated by the ascending distillation (r_Ai) and by the descending distillation (r_Di) are presented, while the final pre-order of the alternatives is illustrated in Figure 3. More details about the intermediate results calculated for each method are available in Supplementary Section 4.

TABLE 4

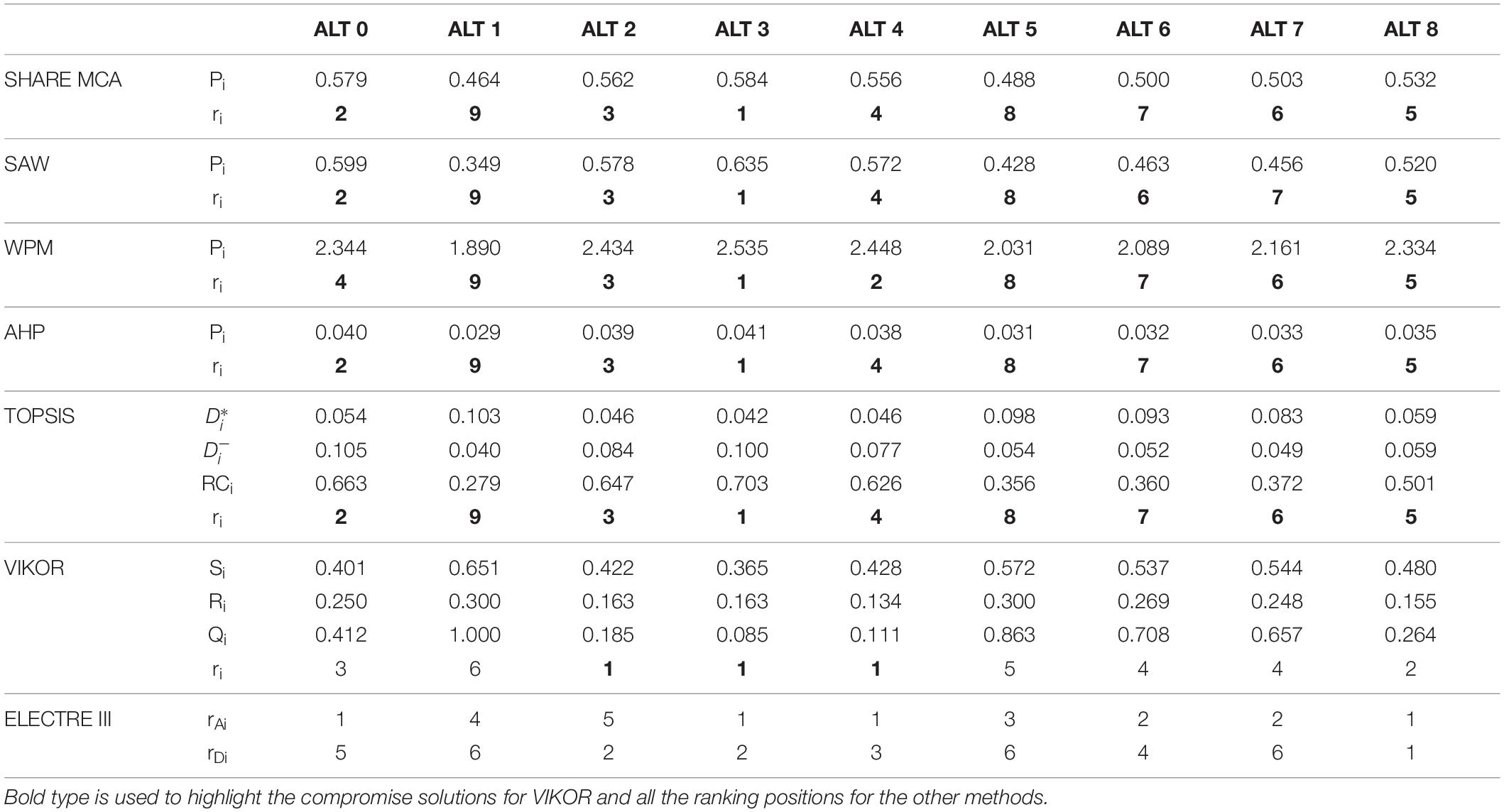
Table 4. Results of the Graines torrent case study according to the different MCDM methods, using the first scheme of weights (P_i = final performance value of alternative i; r_i = position in the ranking; $D_i^{*}$ = distance from the ideal solution, $D_i^{-}$ = distance from the negative-ideal solution, RC_i = relative closeness, calculated in TOPSIS; S_i, R_i, Q_i = values calculated in VIKOR; r_Ai = position in the ascending ranking, r_Di = position in the descending ranking, for ELECTRE III).

FIGURE 3

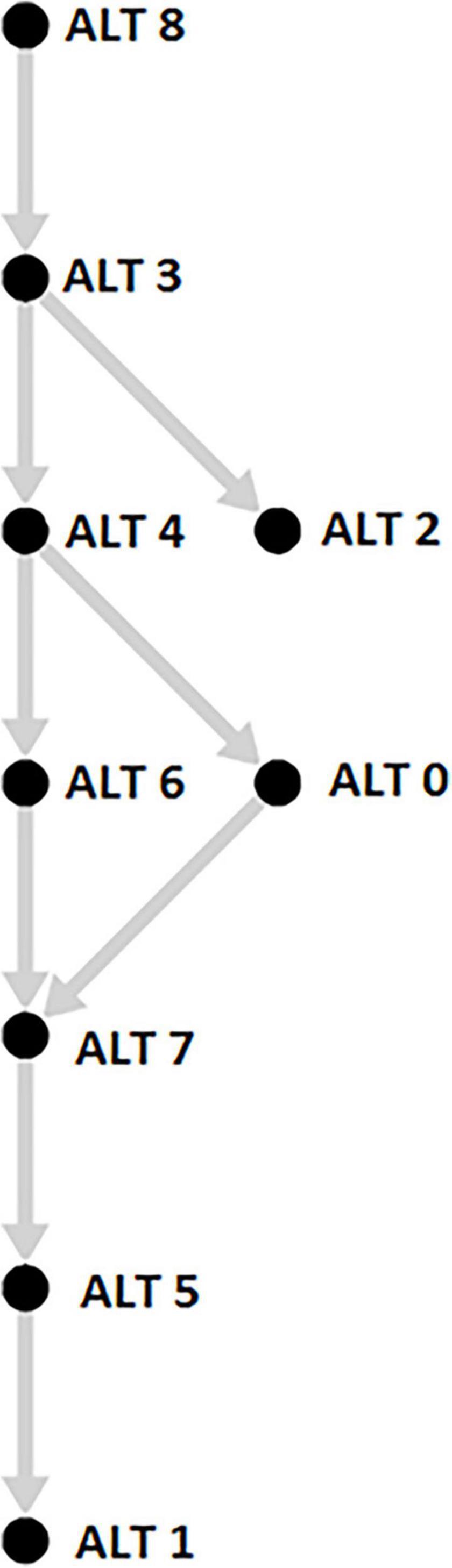
Figure 3. Final pre-order of the alternatives obtained with ELECTRE III with the first scheme of weights (generated by the SuperDecisions^® software; figure modified by the authors).

Similar rankings were obtained considering the first five methods (i.e., SHARE MCA, SAW, WPM, AHP, and TOPSIS), while VIKOR and ELECTRE III produced different types of results, not only in terms of ranking order but also of format (Table 4 and Figure 3). In particular, the results of the VIKOR method are three rankings (by Q, S and R) and a proposed set of compromise solutions. The final ranks r_i were established based on the check of the condition of “acceptable advantage”: for this reason, some alternatives are associated with the same rank (see Supplementary Subsection 4.5). In particular, for the case study, the best-ranked alternative by the measure Q (i.e., the one with the minimum value of Q) was ALT 3. However, this alternative could not be proposed as a compromise solution, because the condition of “advantage rate” [i.e., Q(ALT 4)−−Q(ALT 3) > DQ, where ALT 4 was the second-ranked alternative by Q and DQ = 0.125] was not satisfied. Therefore, a set of three compromise solutions was identified, i.e., ALT 3, ALT 4 and ALT 2 (for which the relation Q(ALTi)−Q(ALT 3) < 0.125 is still valid). As concerns the results of ELECTRE III, the final pre-order of the alternatives is not linear, but it is affected by some relations of incomparability (i.e., considering two alternatives A_1 and A_2, A_1 is incomparable to A_2 if A_1 does not outrank A_2 and A_2 does not outrank A_1 – see also Supplementary Subsection 1.6). Indeed, as highlighted by Figure 3, ALT 0 is incomparable to ALT 6, while ALT 2 is incomparable to all the other alternatives of the ranking, with the exception of ALT 8 and ALT 3. For these reasons, VIKOR and ELECTRE III were excluded from the subsequent statistical comparisons.

For the other five methods, with comparable results, Kendall’s tau and Spearman’s rho correlation tests were performed to analyze the correlation among the obtained rankings. The results of both statistical tests (Table 5) highlight a high correlation between the considered methods (τ≥0.778 and ρ≥0.917). Also looking at the graphic comparison between each of these five rankings with the aggregated order calculated through the Borda technique, the high similarity of all the rankings is evident (see Supplementary Figure 3).

TABLE 5

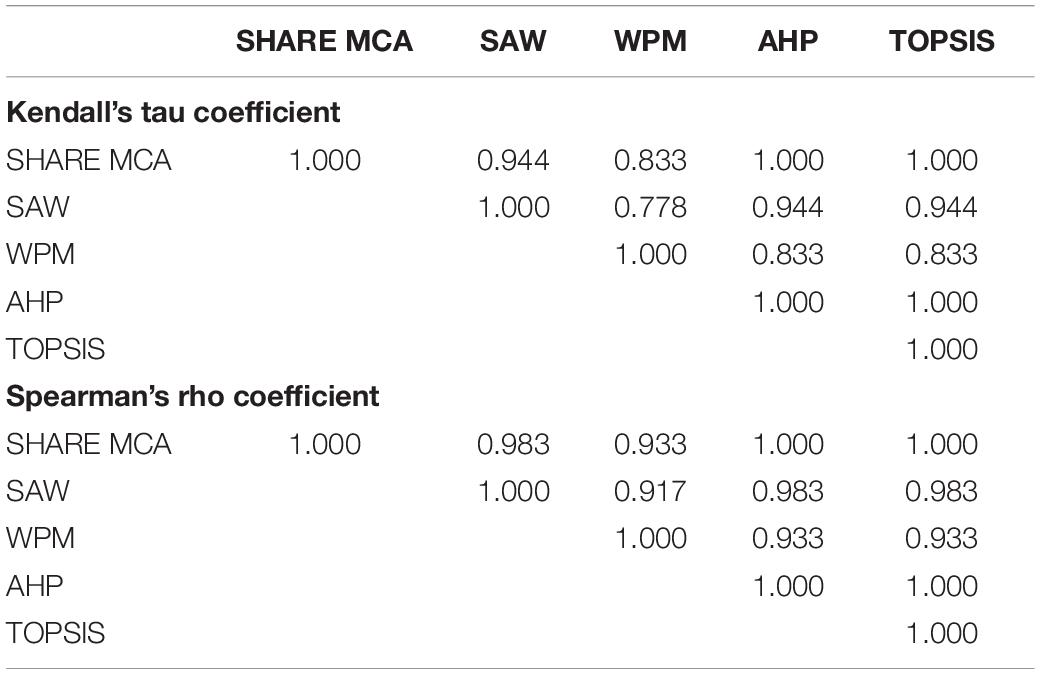
Table 5. Numerical results of Kendall’s tau and Spearman’s rho correlation tests between the compared methods (excluding VIKOR and ELECTRE III), with the first scheme of weights.

Furthermore, other two tests were performed to compare all the seven considered MCDM methods. First of all, since usually the upper part of the ranking is more interesting for the decision-makers (who generally select the final alternative among the best-ranked ones), the agreement between the top three ranked alternatives according to the different methods was checked. As shown in Table 4, the first three alternatives are the same (i.e., ALT 3, a “real-time” flow release alternative with higher values in summer months, ALT 0, the “reference alternative” quantified through a hydrological formulation, and ALT 2, a release scenario based on the MesoHABSIM application) for SHARE MCA, SAW, TOPSIS and AHP. ALT 3 is also the best-ranked alternative according to WPM, which classifies ALT 4 (a “real-time” scenario similar to ALT 3) in the second position, followed, again, by ALT 2. Moreover, ALT 2, ALT 3, and ALT 4 also represent the set of compromise solutions in VIKOR, while ELECTRE III ranks ALT 8 at the first place, followed by ALT 3 and by ALT 2 and ALT 4 (at the same rank because incomparable). Therefore, apart from ALT 8, there are no significant differences among the methods concerning the alternatives that result in the first three ranking positions.

The second test, on the contrary, evaluated the number of ranks matched, expressed as the percentage of the number of alternatives considered (where possible). Looking at Table 4, it can be noticed that SHARE MCA, TOPSIS and AHP returned the same final ranking (% of ranks matched = 100%), while the ranking produced by SAW only differs for ALT 6 and ALT 7, whose positions are switched compared to the previously mentioned methods (% of ranks matched = 77.8%). Also, the WPM final ranking is only slightly different from the other methods, with ALT 4 in the second rank (instead of ALT 0) and ALT 0 in the fourth rank (instead of ALT 4): therefore the % of ranks matched is 77.8% compared to SHARE MCA, TOPSIS and AHP, and 55.6% compared with SAW (since the ranks of ALT 6 and ALT 7 are switched in SAW). For VIKOR and ELECTRE III, again, the percentage of ranks matched compared with the rankings produced by the other methods could not be calculated, due to the different type of results. However, considering the ranking by Q calculated for VIKOR, the first three alternatives (ALT 3, ALT 4, and ALT 2, which are also the compromise solutions) are the same as WPM, but they are followed by ALT 8, which was ranked fifth according to the other methods. Moreover, ALT 0 is only in the fifth position of the ranking by Q, unlike SHARE MCA, SAW, TOPSIS, and AHP, which ranked ALT 0 second. On the contrary, the second part of the ranking is in line with the one obtained through the other methods, even if, considering the condition of “acceptable advantage,” ALT 7 and ALT 6 cannot be considered in two different positions. Finally, as illustrated in Figure 3, the final ranking obtained through ELECTRE III significantly differs, with ALT 8 in the first position and ALT 3 at the second place, followed by ALT 4 and ALT 2, which are incomparable (ALT 2 is also incomparable with the following alternatives). Besides, ALT 6 and ALT 0 (incomparable) precede ALT 7 in the ranking and ALT 5 (a “real-time” alternative characterized by relatively low releases) and ALT 1 (a fixed release scenario of 100 l/s) are the last alternatives, as for all the other considered methods.

Results of the Sensitivity Analysis

To investigate the robustness of the considered MCDM methods, a sensitivity analysis was performed by varying the weights of the indicators. A second scheme of weights was thus considered and the new results of each method were compared with the rankings obtained with the previous one. The other parameters of the considered methods (e.g., the thresholds of ELECTRE III, the normalization functions for SHARE MCA, etc.), on the contrary, were not modified.

The second scheme of weights was based on the assignment of equal importance to the four main criteria of the hierarchical structure, i.e., a weight of 0.25 was allocated to Energy, Environment and fishing, Landscape, and Economy. The weights assigned to the “leaves” of the decision tree, on the contrary, remained the same as described at the beginning of section “Results.” The final weights of the indicators (calculated by multiplying their weight in the group of leaves and the weight of the corresponding criterion), for this second scenario, are presented in Table 6.

TABLE 6

Table 6. Second scheme of weights assigned to the indicators for the sensitivity analysis.

Table 7 shows the new results obtained for the case study by applying the second scheme of weights, for all the seven MCDM methods. Again, the ranking positions r_i of the first five methods (i.e., SHARE MCA, SAW, WPM, AHP, and TOPSIS) and the compromise solutions of VIKOR are highlighted in bold type. For ELECTRE III, the final pre-order of the alternatives is illustrated in Figure 4.

TABLE 7

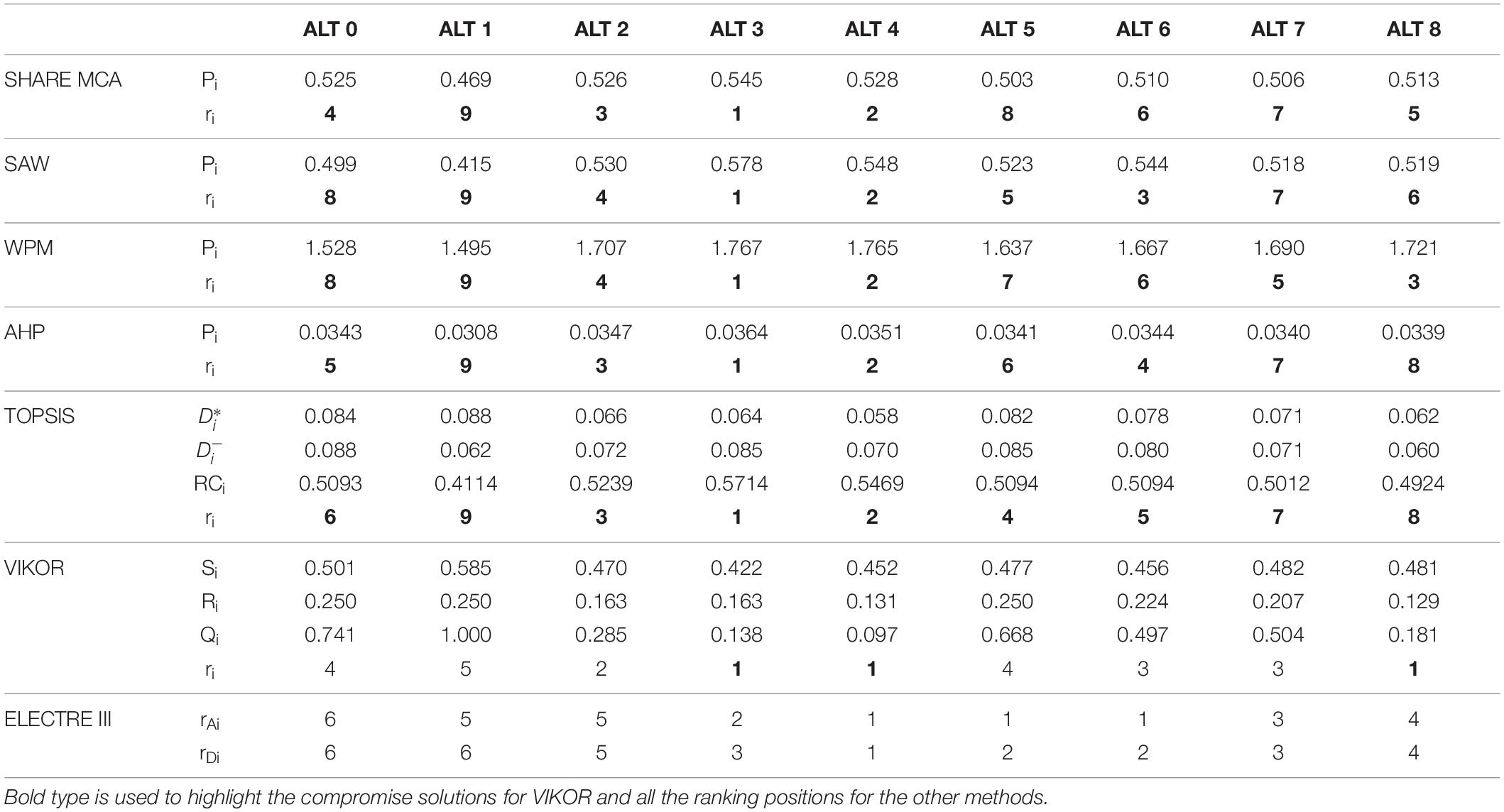
Table 7. Results of the Graines torrent case study for the seven MCDM methods, using the second scheme of weights (P_i = final performance value of alternative i; r_i = position in the ranking; D${}_{\text{i}}^{*}$ = distance from the ideal solution, D${}_{\text{i}}^{-}$ = distance from the negative-ideal solution, RC_i = relative closeness, calculated in TOPSIS; S_i, R_i, Q_i = values calculated in VIKOR; r_Ai = position in the ascending ranking, r_Di = position in the descending ranking, for ELECTRE III).

FIGURE 4

Figure 4. Final pre-order of the alternatives obtained with ELECTRE III with the second scheme of weights (generated by the SuperDecisions^® software; figure modified by the authors).

The results presented in Table 7 show that, using the second scheme of weights, the rankings generated by the considered MCDM methods are quite different, even if the first and the last ranked alternatives for SHARE MCA, SAW, WPM, AHP, and TOPSIS are always the same (i.e., ALT 3 and ALT 1, respectively—see also Supplementary Figure 5). This is evident also looking at the new results of Kendall’s tau and Spearman’s rho correlation tests applied to these five methods (presented in Supplementary Table 21), which are visibly lower than the values shown in Table 5 (with this new scheme of weights, 0.500≤τ≤0.889 and 0.633≤ρ≤0.950). The new graphic comparisons between each ranking and the aggregated Borda order are illustrated in Supplementary Figure 4.

Furthermore, comparing the rankings obtained considering the second scheme of weights with the previous ones (presented in Table 4), SHARE MCA and WPM methods seem the least affected by the selected set of weights. Considering the two rankings obtained for SHARE MCA, indeed, it can be noticed that the first and the third-ranked alternatives do not change and the only differences are due to the switch between ALT 0 and ALT 4 at the second and fourth ranks and between ALT 6 and ALT 7 at the sixth and seventh ranks. For WPM, on the contrary, the first and second-ranked alternatives (i.e., ALT 3 and ALT 4, respectively) remain the same, as well as the last one (ALT 9), while most of the other alternatives only shift one position between the two schemes of weights (e.g., ALT 2 moves from rank 3 to rank 4; only ALT 0 moves from rank 4 to rank 8). Based on these considerations, these two methods can be considered the most robust ones according to the results obtained in the case study.

SAW and TOPSIS, on the contrary, appear highly affected by the choice of the set of weights. Indeed, even if the first and the last ranked alternatives (i.e., ALT 3 and ALT 1, respectively) are the same in both the rankings obtained with the different schemes of weights, other alternatives’ ranks have a significant variation (e.g., ALT 0 moves from rank 2 to rank 8 in SAW and from rank 2 to rank 6 in TOPSIS). Slightly lower deviations characterize the AHP rankings.

As concerns the results of VIKOR, using the second scheme of weights the set of compromise solutions includes again three alternatives, i.e., ALT 3, ALT 4 (as for the first scheme of weights), and ALT 8 (which replaces ALT 2). Considering the ranking by Q, it can be noticed that no significant changes occur after the variation of the set of weights: most of the alternatives only shift one rank (e.g., at the top of the ranking, ALT 3 and ALT 4 are switched, as well as ALT 2 and ALT 8) or do not change their position (i.e., ALT 7, at the sixth position, and ALT 1, at the last place).

Finally, looking at the pre-order of the alternatives obtained with ELECTRE III using different schemes of weights (Figures 3, 4), it can be noticed that they are significantly different. The previous result was affected by some relations of incomparability, while the second scheme of weights generates a linear ranking, with only ALT 5 and ALT 6 resulting indifferent. Moreover, all the ranks change using different weights, including the first alternative (ALT 8), which moves from the first to the fifth position in the ranking, and the last alternative (ALT 0 instead of ALT 1). One of the major changes noticed after the variation of the weights is represented by the movement of ALT 5 from the second to last position to the second rank. This significant variation of the results after a relatively low modification of weights suggests a high sensitivity of ELECTRE III according to the considered case study.

Evaluation of the Different Methodological Approaches

The methodological approaches characterizing the seven MCDM techniques were compared based both on the results produced by the different methods and on the remarks made by the authors after testing the different techniques. Feedback collected from some stakeholders involved in the case study and a representative of the Regional Water Authority was also taken into account. The results of the comparative evaluation of the MCDM methodological approaches are summarized in Table 8 and discussed in subsection “Discussion About the Comparative Evaluation of the MCDM Methodological Approaches”. Moreover, the main strengths and weaknesses of each method are presented in Supplementary Table 23.

TABLE 8

Table 8. Synthetic evaluation of the methodological approach for the considered MCDM techniques (Additional parameters = need for additional parameters; Ease and transparency = ease of understanding and transparency; Input data = characteristics of the input data; Transformation = level of transformation of the original data; Visualization = visualization of the results; Consistency = consistency of the results; Discrimination = discrimination of the results; Feasibility and replicability = overall feasibility and replicability; Quant. = quantitative, Qual. = qualitative, r. = ranking, uncert. = uncertainty).

Discussion

Discussion About the Comparative Evaluation of the MCDM Methodological Approaches

The results of the evaluation shown in Table 8 reveal that the seven considered MCDM methods are characterized by different strengths and weaknesses. In this section, for each assessed feature, the evaluation of the different methodological approaches is further discussed by comparing their main characteristics.

The first feature, need for additional parameters, assesses the level of interaction with the user, i.e., the amount of information required to the decision-maker or involved stakeholders to obtain a final ranking of the alternatives. A high number of additional parameters usually increases the time necessary for the implementation of the method, also related to the need for explaining the required parameters to a non-technical user. It usually also increments subjectivity and potential errors, since this information is related to a choice carried out by the user (Dotoli et al., 2020). SAW, WPM and TOPSIS do not require additional parameters: only the scores and the weights of each indicator have to be collected. One additional parameter has to be defined for VIKOR, i.e., the coefficient υ, while a higher level of interaction with the users is required by the other three methods. A set of normalization functions, one for each indicator, has to be defined for SHARE MCA: in the case study considered in this paper, they were elaborated by the group of stakeholders involved in the decision-making process. Three thresholds, on the contrary, have to be established for each indicator in ELECTRE III. This assessment should be based on a careful analysis, which requires a clear understanding of the meaning of each threshold and deep knowledge of each indicator. Finally, AHP requires the highest level of interaction with the user, who is asked to perform several pairwise comparisons for each level of the hierarchical structure. As explained in Supplementary Subsection 1.3, for each pairwise comparison matrix of order n the number of judgments is n⋅(n−1)/2 (In this study the pairwise comparison process was simplified since the comparisons of alternatives with respect to each indicator were performed through “direct input,” as explained in subsection “Application of the Different MCDM Methods to the Case Study”).

The ease of understanding and the consequent level of transparency of the MCDM methods were evaluated by estimating the time needed by a generic user (including administrators and stakeholders without a technical background) to understand all the mathematical procedures. If any user can easily understand all the procedures, the results produced by a method will probably be widely accepted, due to a high level of transparency (Mahmoud and Garcia, 2000). Very complex methodological approaches, on the contrary, could be perceived as a “black box” and hardly achieve the trust of the public. Considering the MCDM methods used in this study, SAW is obviously the simplest one: indeed, it is well-known even to practitioners (Zanakis et al., 1998). WPM is also based on a simple formulation, but its mathematical concept is more “practitioner-unattractive” (Zanakis et al., 1998). SHARE MCA is based on the same principle of SAW; however, based on the experience acquired in Aosta Valley, it can be stated that the technique is not immediately accepted by non-technical stakeholders. This is probably due to the time necessary to understand the hierarchical structure of the problem, as well as the role of the normalization functions associated with each indicator. A similar evaluation can be made for AHP: the breakdown of the problem into a hierarchical structure facilitates the assignment of judgments by decision-makers, who can pairwise compare all the elements with the support of the fundamental scale of Saaty (Altunok et al., 2010). However, the calculation of the overall performance value for each alternative is usually performed with the help of a software package and this may decrease the level of confidence of a non-technical user. On the contrary, all the phases of TOPSIS and VIKOR can be performed in a simple spreadsheet and they are quite easy to be understood. However, more time may be required to explain to the user the new way in which they approach the problem, i.e., based on the concept of minimum distance from an ideal solution. ELECTRE III is characterized by the most complex methodological approach. The algorithm used is relatively difficult (Hodgett, 2016) since it requires the understanding of different concepts (e.g., outranking, strict and weak preference) and it is based on a large number of operations (e.g., calculation of the concordance and discordance matrices for each indicator), which require a lot of time to be explained and may not be understood by a non-technical user. The long procedure is usually computed with the help of a software tool, but the decision-maker may lack confidence in the final results if he does not widely understand how the input data are processed. Furthermore, difficulties are linked to the choice of realistic threshold values (Saracoglu, 2015).

Another considered feature concerned the characteristics of the input data, i.e., the possibility to use indicators characterized by quantitative and/or qualitative scores. Most of the MCDM methods used in this study require the input of quantitative scores. Only AHP and ELECTRE III can also handle qualitative scores. In AHP, the alternatives can be pairwise compared even with respect to a qualitative criterion/indicator: using the fundamental scale of Saaty, the decision-maker can measure how many times an alternative is more important than another one. The initial qualitative scores are thus transformed into numerical values in the corresponding pairwise comparison matrix. ELECTRE III, on the contrary, was specifically designed to deal with uncertainty, inaccuracy, and ill-determination of data, through a threshold approach. This method, indeed, is based on the use of “pseudo-criteria” and fuzzy binary outranking relations (Figueira et al., 2005). Therefore, it can handle ordinal or descriptive information, also with different dimensions, and it does not require the normalization of the decision matrix (Zanakis et al., 1998). Regarding the number of criteria and alternatives, AHP is affected by some restrictions: a high number of elements to be pairwise compared, indeed, can decrease the consistency of the judgments provided by the decision-maker. For example, Saaty suggested that the number of criteria or alternatives to be compared through AHP should be limited to nine (Lima Junior et al., 2014). ELECTRE III may also be considered more suitable for decision problems characterized by a limited number of criteria and alternatives, since it is frequently not able to generate a complete ranking of the alternatives (Caterino et al., 2009). For the other considered MCDM methods, there are no limitations.

Another feature assessed for the seven MCDM methods was the level of transformation of the original data and the risk to lose some initial information during their processing (when several transformation phases are required), thus affecting the final performance values. WPM received the best evaluation since the comparison of alternatives is performed through some ratios (one for each indicator). This structure of the method even does not require the normalization of the initial decision matrix (if all the indicators are of the same type, i.e., benefit or cost) (Caterino et al., 2009): hence, all the data are used in their original form. Similar remarks were made for ELECTRE III, which does not require normalization of data since it can also process ordinal and imprecise indicators (Zanakis et al., 1998). In the first phase of SHARE MCA, SAW, TOPSIS, and VIKOR, on the contrary, the decision matrix has to be normalized in order to transform the different types of indicators into comparable (non-dimensional) variables. This procedure partially alters the initial data, with a potential loss of information. Moreover, different methods of normalization can be used and this choice has also an effect on the final results (Jafaryeganeh et al., 2020). Similarly, in AHP, pairwise comparisons among the alternatives (with respect to each indicator), based on the fundamental scale of Saaty, transform the original data (Dotoli et al., 2020). In addition, even if the scores of alternatives for each indicator are introduced in the software through a direct input (i.e., keeping the initial decision matrix, as was done in this study), normalization is carried out by dividing the scores by their sum (Zanakis et al., 1998).

The visualization, or typology, of the results was also evaluated for the seven considered methods. As shown in Table 4, SHARE MCA, SAW, WPM, AHP, and TOPSIS generate a complete ranking of the alternatives. A performance value P(A_i) is also calculated for each alternative. VIKOR, on the contrary, produces three rankings (by Q, S, and R, with the corresponding performance values), from which one or more compromise solutions are proposed (Opricović and Tzeng, 2004). Moreover, in some cases, a complete ranking of the alternatives may not be generated (Zamani-Sabzi et al., 2016). The results of ELECTRE III (see Figure 3) are even more different since a performance value is not calculated for each alternative, but only an ordinal rank is assigned to them. This may reduce the level of transparency for the user. Moreover, the results can be affected by the presence of some relations of incomparability between the alternatives, which can generate an equivocal final ranking. In addition, in some cases, a complete ranking cannot be achieved (Hodgett, 2016).

To evaluate the consistency of the results, the outcomes of the sensitivity analysis were taken into account. As described in subsection “Results of the Sensitivity Analysis,” the sensitivity analysis was performed by applying a different scheme of weights and comparing the new results with the previous ones. SHARE MCA, WPM, and VIKOR were the least affected by the choice of weights and therefore they can be considered robust. A lower consistency was assessed for AHP and above all for SAW, TOPSIS, and ELECTRE III, whose rankings were affected by significant variations after the relatively small change of weights. In particular, for ELECTRE III, all the alternatives’ ranks changed, including the first and the last ones. For this reason, the consistency of these three methods was assessed as low. It has to be highlighted, however, that the sensitivity analysis performed in this study only took into account the weights. Other parameters, like the thresholds of ELECTRE III, the coefficient υ of VIKOR, or the normalization functions used in SHARE MCA, can affect the consistency of their results and should therefore be analyzed in a more in-depth study.

The discrimination of the results was aimed at evaluating, for each method, the difference between the alternatives within the produced ranking. It was assessed by calculating two percentage difference indexes, between the best and the worst-ranked alternatives (D_BW) and between the first and the second positions of the ranking (D_FS). The results are available in Supplementary Table 22). From this analysis, it was noticed that a high discrimination of the results is ensured by TOPSIS and SAW, while in SHARE MCA and AHP the performance values of the first and second-ranked alternatives are very close to each other. The highest discrimination, considering the ranking by Q, was noticed for VIKOR: in reality, this method already includes a similar check in the final phase of the procedure (i.e., the condition of “acceptable advantage”) to select the alternative(s) to be proposed as compromise solution(s). The indexes were not calculated for ELECTRE III, since this method does not provide a performance value for each alternative, but only an ordinal rank. However, the final ranking highlights the presence of alternatives that result indifferent after the procedures of descending and ascending distillation and ranks them in the same position (e.g., ALT 5 and ALT 6 in Figure 4).

Finally, based also on the previous evaluations, the last feature was assessed, i.e., the overall feasibility and replicability of the different MCDM methodologies. This feature aimed at evaluating not only the applicability and the effectiveness of each method in the considered case study, which was relatively simple, involving only one small HP plant, but also the possibility to adopt the procedure in more complex HP management decision-making processes, e.g., to identify the optimum management of a system of withdrawals located in an entire watershed. Therefore, not only the consistency and reliability of the results produced by the method is important, but also the transparency of the procedure and the possibility to directly involve different concerned stakeholders (even non-technical actors) in the decision-making process, without decreasing their level of trust, are essential. All these characteristics also influence the possibility to integrate a methodological approach in the regulatory and management tools.

Based on the remarks made by the authors and the stakeholders’ feedback, ELECTRE III was assessed as the least feasible among the considered MCDM methods, above all for complex decision-making problems. Despite its advantages (like a rigorous mathematical procedure based on the outranking concept and the possibility to deal with data affected by uncertainty and imprecision), indeed, the algorithm used is relatively complex and would require a lot of time to be understood by non-technical stakeholders or decision-makers. In addition, the final ranking, usually obtained by means of a software package, can be affected by some relations of incomparability between the alternatives, which are not associated with a performance value, but only with a rank position. In some cases, a complete ranking cannot even be achieved. All these aspects would reduce the level of trust of the involved stakeholders and decision-makers. Moreover, the results of the case study presented in this paper showed a low consistency of the method, since the results were significantly affected by the modification of weights.

Higher feasibility was assessed for AHP, even if the method requires a high level of interaction with the involved actors to perform the pairwise comparisons. This also implies a restriction on the number of alternatives and criteria that can be considered to ensure the consistency of the judgments: it could not be suitable, therefore, for highly complex decision problems. A positive characteristic of AHP is the breakdown of the problem into a hierarchical structure, which facilitates its understanding, but the calculation of the overall performance value of the alternatives is usually performed through a software tool, thus potentially reducing the level of confidence of non-technical stakeholders and decision-makers.

TOPSIS and above all SAW, on the contrary, can be easily explained even to non-technical actors and the mathematical procedures can be performed in a simple spreadsheet. This would probably increase the level of trust of stakeholders and decision-makers. However, the sensitivity analysis carried out in this study showed a relatively low consistency of the results, since the rankings were affected by significant changes after a relatively low variation of weights. Further analyses should be carried out in the future, considering also more complex HP management decision-making processes.

In contrast, the experience acquired in the real decision-making process carried out on the Graines torrent demonstrated the feasibility of SHARE MCA and its possibility to be officially integrated into regulatory tools. Even if the method was not immediately understood by the stakeholders and despite the need to define a normalization function for each indicator, indeed, the hierarchical structure (similar to the one used in AHP) allows decomposing, and thus simplifying, complex problems. Moreover, the calculation of the final performance values of the alternatives is based on the same additive principle of SAW, easy to explain and to be accepted also by non-technical actors. Furthermore, the sensitivity analysis performed in this paper proved the robustness of the method, even if the discrimination of the results is relatively low.

Finally, WPM and VIKOR also showed interesting characteristics, like the high consistency of the results and the relatively simple procedure, which can be performed in a simple spreadsheet. Nevertheless, (as stated by Zanakis et al., 1998 for WPM) their mathematical concepts may be more “practitioner-unattractive” compared, for example, to SAW and would therefore probably require more time to be explained and accepted by non-technical stakeholders and decision-makers. In addition, while the discrimination of the results provided by WPM is relatively low, VIKOR also checks the presence of an “acceptable advantage” between the first ranked alternative (by Q) and the following ones in order to define the set of compromise solutions. Further analyses should be carried out in future studies concerning more complex HP management problems.

Further Remarks on the Case Study and the Obtained Results

The aim of this study was not to identify a method that is better than the others across all possible conditions, but to investigate the applicability and effectiveness of different MCDM methods for a specific type of decision-making problems, i.e., the selection of a flow release scenario to be implemented downstream of HP plants.

The rankings of the alternatives generated by the seven considered methods (SHARE MCA, SAW, WPM, AHP, TOPSIS, VIKOR, and ELECTRE III), with the first set of weights, were generally highly correlated. Only VIKOR and ELECTRE III produced different results, not only in terms of ranking order but also of format. These observations are consistent with the conclusions of Zamani-Sabzi et al. (2016), who investigated and statistically compared the performances of 10 MCDM techniques (i.e., SAW, WPM, TOPSIS, four types of AHP, VIKOR, ELECTRE, and CP—compromise programming), concluding that SAW, TOPSIS, WPM, and AHP had a higher correlation, while the results of VIKOR and ELECTRE (and CP) were less consistent. This is probably due to the different, more elaborated, procedure used by these methods and the different types of ranking produced. Moreover, the sensitivity analysis performed in this study by adopting a second, slightly different, scheme of weights revealed a high consistency of some methods (i.e., SHARE MCA, WPM, and VIKOR), which can thus be considered robust.

These results, together with the comparative analysis of the different methodological approaches presented in subsection “Evaluation of the Different Methodological Approaches” and discussed in subsection “Discussion About the Comparative Evaluation of the MCDM Methodological Approaches,” can help the stakeholders involved in the decision-making process to be more aware of the intrinsic complexity of the different methods and the variability of the obtained rankings. This awareness should increase their sense of responsibility and degree of involvement.

Moreover, the similarity of the results obtained through the different MCDM methods could encourage the stakeholders in adopting, in future decision-making processes, also other techniques (in addition to the initially considered SHARE MCA method). Thus, the comparison of their results would increase the robustness of the final decision (i.e., the alternative considered as the optimal scenario according to different methods would more likely be the best one). This could also help the decision-maker, who would be more confident in adopting the optimal scenario and would more easily avoid conflicts among stakeholders.

Furthermore, the results showed that the alternatives ranked in the first positions always represented flow release scenarios variable during the year and above all “real-time” alternatives (i.e., varying on an hourly basis according to the watercourse discharge available upstream of the dam). For example, the first-classified alternative by all the methods (apart from ELECTRE III) was ALT 3, a “real-time” alternative based on a minimum flow of 70 l/s incremented by an additional release calculated as a percentage of the watercourse discharge, except for the summer months, characterized by a higher fixed release (see Table 2). ALT 4 (a “real-time” scenario representing a modified version of ALT 3) and ALT 2 (a release scenario characterized by fixed monthly values, ranging from 70 to 300 l/s, based on the MesoHABSIM application on the affected watercourse) were also ranked in the upper part of the ranking by all the methods (excluding ELECTRE III, with the second scheme of weights). On the contrary, ALT 1, a fixed release scenario of 100 l/s proposed by the HP company, was always ranked in last position (apart from the ranking produced by ELECTRE III considering the second scheme of weights, where it was classified second to last).

These results demonstrated that flow release scenarios foreseeing a fixed release for all the year are not sustainable, due to the high negative impacts on the watercourse ecology and landscape, which are even not counterbalanced by the high related economic income. On the contrary, “real-time” alternatives allow a more balanced distribution of negative and positive effects of the withdrawal, usually representing the best compromise among protection of river ecosystems, landscape safeguard, and HP production needs.

It has to be highlighted that the considered small HP plant was built recently and thus it could be equipped to implement real-time withdrawal. A continuous monitoring system, installed at the HP dam, provides the upstream flow data series (measured every 5 min and subsequently aggregated on an hourly basis) which, through a programmable logic controller, determine the opening or closing of the withdrawal devices. This system (which is frequently adopted in the regional context) allowed, during the decision-making process, the definition of such intermediate flow release scenarios (named “real-time” alternatives). These alternatives are more finely tuned with the natural flow regime than the scenarios that can be implemented downstream of older plants, characterized by fixed releases. They can, therefore, ensure a more natural variability of the flow, required by ecosystems to maintain their ecological functioning (Arthington et al., 2006).

This HP plant was considered in this study also because it is characterized by a simple withdrawal scheme (i.e., a single withdrawal point and a single release point), which allowed the use of a simple framework for the application of the different MCDM methods. The absence of other upstream water abstractions within the watershed also avoided the impact of additional hydrological alterations and supported the indicators’ reactiveness. Moreover, since the decision-making process was already concluded, flow rate series and the other data necessary for the implementation of the MCDM methods were available and a critical analysis about the procedure and the outcomes was possible.

By evaluating the methodological approaches of the considered MCDM techniques based on a set of features, in this paper some methods were identified as more feasible and replicable, also in more complex HP management decision-making processes. Indeed, the considered case study involved only one small HP plant, but the current management decisions, especially in mountain contexts already widely exploited for HP production, often concern systems of HP plants located in an entire watershed, where the upstream release scenario affects the downstream scenarios. Moreover, since the most suitable sites for large HP plants have already been exploited in the Alpine area, the focus is currently on the refurbishment or strengthening of the existing plants or on new small HP projects, located on the remaining unexploited rivers, with significant environmental effects (Ferrario and Castiglioni, 2017). Therefore, there is a risk of increasing pressure on still pristine river stretches, like headwaters, which have become increasingly rare (Alpine Convention–Platform Water Management in the Alps, 2011).

In this context, decision-making processes involving different concerned stakeholders are extremely important and the use of MCDM methods that ensure the reliability of the results, but also the transparency of the procedures, is necessary to increase the level of trust of all the involved actors. For these reasons, in this study, methods like ELECTRE III appeared hardly replicable for complex water management problems, due to the relatively complex algorithms used, which would be difficult to explain to (and be accepted by) non-technical stakeholders or decision-makers. On the contrary, methods characterized by relatively simple procedures are usually related to a higher level of perceived transparency and a higher trust for the obtained results. When providing reliable and consistent results, these methods can also be implemented in regulatory tools and actually applied for, even complex, HP management decision-making problems.

Conclusion

Multi-criteria decision-making (MCDM) is recognized as an important tool in addressing issues related to environmental management. Over the last decades, several MCDM methods have been adopted, in different countries, to solve conflicts over water resource use, including decision problems concerning hydropower planning and management. However, only few studies in this field have applied different MCDM techniques to the same case study to compare their results (e.g., Özelkan and Duckstein, 1996; Carriço et al., 2014; Ehteram et al., 2018). Nevertheless, assessing how the choice of different MCDM methods might affect the final decision (due to a potential different ranking of alternative options) is extremely important if MCDM is used in real decision-making processes that can lead to relevant actions. Such evaluation could also support the selection of the most appropriate approach to be used when dealing with HP management decisions.

Therefore, in this paper, SHARE MCA, SAW, WPM, AHP, TOPSIS, VIKOR, and ELECTRE III were applied to the same real case study of HP management, to select the optimal flow release scenario to be implemented downstream of a small run-of-the-river HP plant on the Graines torrent, in Aosta Valley. The same alternatives and indicators were considered in all the methods, as well as the indicators’ weights. A sensitivity analysis was also carried out by adopting a slightly different scheme of weights to assess the robustness of the methods. The results obtained with the first set of weights were generally highly correlated, while the sensitivity analysis showed a high consistency for some methods (i.e., SHARE MCA, WPM, and VIKOR), which can thus be considered robust.

The real decision-making process carried out on the Graines torrent proved the feasibility of SHARE MCA, which has led to an actual management decision endorsed by the Regional Government, and the possibility to officially integrate this method in regional regulatory tools. However, based on the results presented in this paper and according to the remarks made by the authors and the stakeholders’ feedback, other MCDM methods (like WPM and VIKOR) also showed interesting characteristics in terms of overall feasibility. Further thorough analyses should be carried out in the future to test their actual suitability also for more complex HP management decisions in the Alpine area.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

EV conceived the study, applied computational techniques, analyzed and synthesized study data, wrote the original draft, reviewed and edited the manuscript. AMM and CC conceived the study, provided supervision, validated the results, reviewed and edited the manuscript. ED, GN, and MP applied computational techniques and performed statistical analyses, analyzed and synthesized study data, and reviewed and edited the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was funded by Ph.D. student research grants and other resources for publishing from Politecnico di Torino and Regional Agency for the Protection of the Environment Valle d’Aosta.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We wish to acknowledge the representatives of the hydropower company Idroelettrica Brusson s.r.l. and of the Regional Water Authority (Regione Autonoma Valle d’Aosta—Gestione Demanio Idrico), as well as the other stakeholders involved in the decision-making process on the Graines torrent (i.e., Regional Fisheries Consortium—Consorzio Pesca; Regional Landscape Protection Service; Regional environmental assessment and air quality protection Service; Regional flora, fauna, hunting, and fishing Service), for their support in providing data and information related to the case study.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2021.635100/full#supplementary-material

References

Adhikary, P., Kundu, S., Roy, P. K., and Mazumdar, A. (2013). Optimum selection of hydraulic turbine manufacturer for SHP:MCDA or MCDM tools. World Appl. Sci. J. 28, 914–919. doi: 10.5829/idosi.wasj.2013.28.07.1373

CrossRef Full Text | Google Scholar

Alamanos, A., Mylopoulos, N., Loukas, A., and Gaitanaros, D. (2018). An integrated multicriteria analysis tool for evaluating water resource management strategies. Water 10:1795. doi: 10.3390/w10121795

CrossRef Full Text | Google Scholar

Alpine Convention (2009). Water and Water Management Issues: Report on the State of the Alps. Alpine Signals – Special Edition 2. Bolzano: Permanent Secretariat of the Alpine Convention.

Google Scholar

Alpine Convention–Platform Water Management in the Alps (2011). Common Guidelines for the use of Small Hydropower in the Alpine Region – Alpine Signals Focus 1. Longo: Permanent Secretariat of the Alpine Convention.

Google Scholar

Alpine Convention–Platform Water Management in the Alps (2018). Application of the Common Guidelines for the use of Small Hydropower in the Alpine Region. Innsbruck: Permanent Secretariat of the Alpine Convention.

Google Scholar

Altunok, T., Ozpeynirci, O., Kazançoǧlu, Y., and Yilmaz, R. (2010). Comparative analysis of multicriteria decision making methods for postgraduate student selection. Eurasian J. Educ. Res. 40, 1–15.

Google Scholar

Arthington, A. H., Bunn, S. E., Poff, N. L., and Naiman, R. J. (2006). The challenge of providing environmental flow rules to sustain river ecosystems. Ecol. Appl. 16, 1311–1318. doi: 10.1890/1051-0761(2006)016[1311:tcopef]2.0.co;2

CrossRef Full Text | Google Scholar

Athawale, V. M., and Chakraborty, S. (2012). Material selection using multi-criteria decision-making methods: a comparative study. Proc. Inst. Mech. Eng. Part L J. Mater. Design Appl. 226, 266–285. doi: 10.1177/1464420712448979

CrossRef Full Text | Google Scholar

Banihabib, M. E., Hashemi-Madani, F.-S., and Forghani, A. (2017). Comparison of compensatory and non-compensatory multi criteria decision making models in water resources strategic management. Water Resour. Manage. 31, 3745–3759. doi: 10.1007/s11269-017-1702-x

CrossRef Full Text | Google Scholar

Barton, D. N., Sundt, H., Bustos, A. A., Fjeldstad, H.-P., Hedger, R., Forseth, T., et al. (2020). Multi-criteria decision analysis in Bayesian networks - diagnosing ecosystem service trade-offs in a hydropower regulated river. Environ. Model. Softw. 124:104604. doi: 10.1016/j.envsoft.2019.104604

CrossRef Full Text | Google Scholar

Bratrich, C., Truffer, B., Jorde, K., Markard, J., Meier, W., Peter, A., et al. (2004). Green hydropower: a new assessment procedure for river management. River Res. Appl. 20, 865–882. doi: 10.1002/rra.788

CrossRef Full Text | Google Scholar

Bridgman, P. W. (1922). Dimensional Analysis. New Haven: Yale University Press.

Google Scholar

Brunke, M. (2002). Floodplains of a regulated southern alpine river (Brenno, Switzerland): ecological assessment and conservation options. Aquat. Conserv. 12, 583–599. doi: 10.1002/aqc.544

CrossRef Full Text | Google Scholar

Carriço, N. J. G., Gonçalves, F. V., Covas, D. I. C., Almeida, M., do, C., and Alegre, H. (2014). Multi-criteria analysis for the selection of the best energy efficient option in urban water systems. Procedia Eng. 70, 292–301. doi: 10.1016/j.proeng.2014.02.033

CrossRef Full Text | Google Scholar

Caterino, N., Iervolino, I., Manfredi, G., and Cosenza, E. (2009). Comparative analysis of multi-criteria decision-making methods for seismic structural retrofitting. Comput. Aided Civil Infrastruct. Eng. 24, 432–445. doi: 10.1111/j.1467-8667.2009.00599.x

CrossRef Full Text | Google Scholar

Ceballos, B., Lamata, M. T., and Pelta, D. A. (2016). A comparative analysis of multi-criteria decision-making methods. Prog. Artif. Intell. 5, 315–322. doi: 10.1007/s13748-016-0093-1

CrossRef Full Text | Google Scholar

Chien, F., Wang, C.-N., Nguyen, V. T., Nguyen, V. T., and Chau, K. Y. (2020). An evaluation model of quantitative and qualitative fuzzy multi-criteria decision-making approach for hydroelectric plant location selection. Energies 13:2783. doi: 10.3390/en13112783

CrossRef Full Text | Google Scholar

Creative Decision Foundation (2019). Super Decision Software for Decision Making. Available Online at: http://www.superdecisions.com/ (accessed August 21, 2020)

Google Scholar

de Borda, J.-C. (1781). Mémoire sur les élections au scrutin. Mémoires de l’Académie Royale des Sciences 1, 657–664.

Google Scholar

Dong, M., Li, S., and Zhang, H. (2015). Approaches to group decision making with incomplete information based on power geometric operators and triangular fuzzy AHP. Expert Syst. Appl. 42, 7846–7857. doi: 10.1016/j.eswa.2015.06.007

CrossRef Full Text | Google Scholar

Dotoli, M., Epicoco, N., and Falagario, M. (2020). Multi-Criteria decision making techniques for the management of public procurement tenders: a case study. Appl. Soft. Comput. 88:106064. doi: 10.1016/j.asoc.2020.106064

CrossRef Full Text | Google Scholar

Ehteram, M., Karami, H., and Farzin, S. (2018). Reservoir optimization for energy production using a new evolutionary algorithm based on multi-criteria decision-making models. Water Resour Manage 32, 2539–2560. doi: 10.1007/s11269-018-1945-1

CrossRef Full Text | Google Scholar

European Commission [EC] (2009). Directive 2009/28/EC of the European Parliament and of the Council of 23 April 2009 on the Promotion of the use of Energy from Renewable Sources and Amending and Subsequently Repealing Directives 2001/77/EC and 2003/30/EC. OJ L 140:16–62. Brussels: European Commission.

Google Scholar

Ferrario, V., and Castiglioni, B. (2017). Visibility/invisibility in the “making” of energy landscape. Strategies and policies in the hydropower development of the Piave river (Italian Eastern Alps). Energy Policy 108, 829–835. doi: 10.1016/j.enpol.2017.05.012

CrossRef Full Text | Google Scholar

Figueira, J., Greco, S., and Ehrgott, M. (2005). Multiple Criteria Decision Analysis: State of the Art Surveys. Boston: Springer Science & Business Media.

Google Scholar

Fishburn, P. C. (1967). Letter to the editor—additive utilities with incomplete product sets: application to priorities and assignments. Oper. Res. 15, 537–542. doi: 10.1287/opre.15.3.537

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuentes-Bargues, J. L., and Ferrer-Gisbert, P. S. (2015). Selecting a small run-of-river hydropower plant by the analytic hierarchy process (AHP): a case study of Miño-Sil river basin, Spain. Ecol. Eng. 85, 307–316. doi: 10.1016/j.ecoleng.2015.10.020

CrossRef Full Text | Google Scholar

Gingrich, S., Gaube, V., and Haberl, H. (2009). Energy in Climate Change – A CIPRA Background Report. Schaan: CIPRA International.

Google Scholar

Hajkowicz, S., and Collins, K. (2007). A review of multiple criteria analysis for water resource planning and management. Water Resour. Manage. 21, 1553–1566. doi: 10.1007/s11269-006-9112-5

CrossRef Full Text | Google Scholar

Hodgett, R. E. (2016). Comparison of multi-criteria decision-making methods for equipment selection. Int. J. Adv. Manuf. Technol. 85, 1145–1157. doi: 10.1007/s00170-015-7993-2

CrossRef Full Text | Google Scholar

Hwang, C.-L., and Yoon, K. (1981). Multiple Attribute Decision Making: Methods and Applications A State-of-the-Art Survey. New York, NY: Springer-Verlag Berlin Heidelberg.

Google Scholar

Jafaryeganeh, H., Ventura, M., and Guedes Soares, C. (2020). Effect of normalization techniques in multi-criteria decision making methods for the design of ship internal layout from a Pareto optimal set. Struct. Multidisc. Optim. 62, 1849–1863. doi: 10.1007/s00158-020-02581-9

CrossRef Full Text | Google Scholar

Ji, Y., Huang, G. H., and Sun, W. (2015). Risk assessment of hydropower stations through an integrated fuzzy entropy-weight multiple criteria decision making method: a case study of the Xiangxi River. Expert Syst. Appl. 42, 5380–5389. doi: 10.1016/j.eswa.2014.12.026

CrossRef Full Text | Google Scholar

Jiménez Capilla, J. A., Carrión, J. A., and Alameda-Hernandez, E. (2016). Optimal site selection for upper reservoirs in pump-back systems, using geographical information systems and multicriteria analysis. Renew. Energy 86, 429–440. doi: 10.1016/j.renene.2015.08.035

CrossRef Full Text | Google Scholar

Joubert, A., Stewart, T. J., and Eberhard, R. (2003). Evaluation of water supply augmentation and water demand management options for the city of cape town. J. Multicriteria Decis. Anal. 12, 17–25. doi: 10.1002/mcda.342

CrossRef Full Text | Google Scholar

Karjalainen, T. P., Marttunen, M., Sarkki, S., and Rytkönen, A.-M. (2013). Integrating ecosystem services into environmental impact assessment: an analytic–deliberative approach. Environ. Impact Assess. Rev. 40, 54–64. doi: 10.1016/j.eiar.2012.12.001

CrossRef Full Text | Google Scholar

Khanzadi, M., Nasirzadeh, F., Hassani, S. M. H., and Nejad Mohtashemi, N. (2016). An integrated fuzzy multi-criteria group decision making approach for project delivery system selection. Sci. Iran. 23, 802–814. doi: 10.24200/sci.2016.2160

CrossRef Full Text | Google Scholar

Köhler, B., Ruud, A., and Aas, Ø, and Barton, D. N. (2019). Decision making for sustainable natural resource management under political constraints–the case of revising hydropower licenses in Norwegian watercourses. Civil Eng. Environ. Syst. 36, 17–31. doi: 10.1080/10286608.2019.1615475

CrossRef Full Text | Google Scholar

Kokaraki, N., Hopfe, C. J., Robinson, E., and Nikolaidou, E. (2019). Testing the reliability of deterministic multi-criteria decision-making methods using building performance simulation. Renew. Sustain. Energy Rev. 112, 991–1007. doi: 10.1016/j.rser.2019.06.018

CrossRef Full Text | Google Scholar

Kumar, D., and Katoch, S. S. (2015). Sustainability assessment and ranking of run of the river (RoR) hydropower projects using analytical hierarchy process (AHP): a study from Western Himalayan region of India. J. Mt. Sci. 12, 1315–1333. doi: 10.1007/s11629-014-3156-4

CrossRef Full Text | Google Scholar

Lima Junior, F. R., Osiro, L., and Carpinetti, L. C. R. (2014). A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. Appl. Soft. Comput. 21, 194–209. doi: 10.1016/j.asoc.2014.03.014

CrossRef Full Text | Google Scholar

Mahmoud, M. R., and Garcia, L. A. (2000). Comparison of different multicriteria evaluation methods for the Red Bluff diversion dam. Environ. Model. Softw. 15, 471–478. doi: 10.1016/S1364-8152(00)00025-6

CrossRef Full Text | Google Scholar

Majumder, P., Majumder, M., Saha, A. K., and Nath, S. (2020). Selection of features for analysis of reliability of performance in hydropower plants: a multi-criteria decision making approach. Environ. Dev. Sustain. 22, 3239–3265. doi: 10.1007/s10668-019-00343-2

CrossRef Full Text | Google Scholar

Manikkuwahandi, T. D. S., Hornberger, G. M., and Baroud, H. (2019). Decision analysis for expansion of mahaweli multipurpose reservoir system in Sri Lanka. J. Water Resour. Plan. Manag. 145:05019013. doi: 10.1061/(ASCE)WR.1943-5452.0001094

PubMed Abstract | CrossRef Full Text | Google Scholar

Marttunen, M., and Suomalainen, M. (2005). Participatory and multiobjective development of watercourse regulation—creation of regulation alternatives from stakeholders’ preferences. J. Multicriteria Decis. Anal. 13, 29–49. doi: 10.1002/mcda.374

CrossRef Full Text | Google Scholar

Opricović, S. (1998). Multicriteria Optimization of Civil Engineering Systems. Ph.D Thesis, Belgrade: Faculty of Civil Engineering.

Google Scholar

Opricović, S., and Tzeng, G.-H. (2004). Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 156, 445–455. doi: 10.1016/S0377-2217(03)00020-1

CrossRef Full Text | Google Scholar

Opricović, S., and Tzeng, G.-H. (2008). A comparative analysis of the DEA-CCR model and the VIKOR method. Yugoslav J. Oper. Res. 18, 187–203. doi: 10.2298/YJOR0802187O

CrossRef Full Text | Google Scholar

Özelkan, E. C., and Duckstein, L. (1996). Analysing water resources alternatives and handling criteria by multi criterion decision techniques. J. Environ. Manag. 48, 69–96. doi: 10.1006/jema.1996.0066

CrossRef Full Text | Google Scholar

Parasiewicz, P. (2007). The MesoHABSIM model revisited. River Res. Appl. 23, 893–903. doi: 10.1002/rra.1045

CrossRef Full Text | Google Scholar

Pereira, V., Gomes Costa, H., Nepomuceno, L. D., and de, O. (2019). J-Electre-v2.0. Available online at: https://sourceforge.net/projects/j-electre/ (accessed September 14, 2020).

Google Scholar

Regione Autonoma Valle d’Aosta [RAVA] (2006). Piano di Tutela delle Acque (PTA) della Regione Autonoma Valle d’Aosta, Allegato G. Available online at: https://appweb.regione.vda.it/dbweb/pta/faqpta.nsf/Allegato_DMV.pdf?Openfileresource (accessed November 4, 2020).

Google Scholar

Roy, B. (1978). ELECTRE III: un algorithme de classement fondé sur une représentation floue des préférences en présence de critères multiples. Cahiers du CERO 20, 3–24.

Google Scholar

Saaty, T. L. (1980). The Analytic Hierarchy Process. New York, NY: McGraw-Hill.

Google Scholar

Šantl, S., and Steinman, F. (2015). Hydropower suitability analysis on a large scale level: inclusion of a calibration phase to support determination of model parameters. Water Resour. Manage. 29, 109–123. doi: 10.1007/s11269-014-0830-9

CrossRef Full Text | Google Scholar

Saracoglu, B. O. (2015). An experimental research study on the solution of a private small hydropower plant investments selection problem by ELECTRE III/IV, shannon’s entropy, and saaty’s subjective criteria weighting. Adv. Decis. Sci. 2015:548460. doi: 10.1155/2015/548460

CrossRef Full Text | Google Scholar

Scheurer, T., Weingartner, R., and Lanz, K. (2018). “Action needed to prevent future conflict over the use and management of water in the Alpine region in times of climate change and growing demand,” in Alpine Water – Common Good or Source of Conflicts? Proceedings of the ForumAlpinum 2018 and the 7th Water Conference, 4-6 June 2018, Breitenwang (Tyrol), eds L. Füreder, R. Weingartner, K. Heinrich, V. Braun, G. Köck, K. Lanz, et al. (Vienna: Austrian Academy of Sciences Press), 9–12.

Google Scholar

Schneider, F., Buser, T., and Graefe, O. (2014). Scales of justice in water governance: hydropower controversies in Switzerland. Water Policy 16, 137–154. doi: 10.2166/wp.2014.405

CrossRef Full Text | Google Scholar

SHARE project (2012). SHARE [Sustainable Hydropower in Alpine Rivers Ecosystems] project (Alpine Space Program 2007-2013). Available online at: http://www.alpine-space.org/2007-2013/projects/projects/index1d27.html?tx_txrunningprojects_pi1[uid]=22&tx_txrunningprojects_pi1[view]=singleView (accessed November 6, 2020)

Google Scholar

Singh, R. P., and Nachtnebel, H. P. (2016). Decision aid for hydropower project prioritisation in Nepal by applying Visual PROMETHEE. Int. J. Multicriteria Decis. Mak. 6, 316–342. doi: 10.1504/IJMCDM.2016.081389

CrossRef Full Text | Google Scholar

Soncini-Sessa, R., Canuti, D., Colorni, A., Villa, L., Vitali, B., Weber, E., et al. (2000). Use of multi-criteria analysis to resolve conflicts in the operation of a transnational multipurpose water system – The case of Lake Verbano (Italy-Switzerland). Water Int. 25, 334–346. doi: 10.1080/02508060008686841

CrossRef Full Text | Google Scholar

Stähly, S., Franca, M. J., Robinson, C. T., and Schleiss, A. J. (2019). Sediment replenishment combined with an artificial flood improves river habitats downstream of a dam. Sci. Rep. 9:5176. doi: 10.1038/s41598-019-41575-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Steele, K., Carmel, Y., Cross, J., and Wilcox, C. (2009). Uses and misuses of multicriteria decision analysis (MCDA) in environmental decision making. Risk Anal. 29, 26–33. doi: 10.1111/j.1539-6924.2008.01130.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevović, S., Milošević, H., Stevović, I., and Hadrovic, S. (2014). Sustainable management of water resources in Prokletije region. Industrija 42, 47–61. doi: 10.5937/industrija42-4699

CrossRef Full Text | Google Scholar

Supriyasilp, T., Pongput, K., and Boonyasirikul, T. (2009). Hydropower development priority using MCDM method. Energy Policy 37, 1866–1875. doi: 10.1016/j.enpol.2009.01.023

CrossRef Full Text | Google Scholar

Triantaphyllou, E., and Baig, K. (2005). The Impact of Aggregating Benefit and Cost Criteria in Four MCDA Methods. IEEE Trans. Eng. Manag. 52, 213–226. doi: 10.1109/TEM.2005.845221

CrossRef Full Text | Google Scholar

Truffer, B., Bratrich, C., Markard, J., Peter, A., Wüest, A., and Wehrli, B. (2003). Green Hydropower: the contribution of aquatic science research to the promotion of sustainable electricity. Aquat. Sci. 65, 99–110. doi: 10.1007/s00027-003-0643-z

CrossRef Full Text | Google Scholar

Tzimopoulos, C., Balioti, V., and Evangelides, C. (2013). “Fuzzy multi-criteria decision making method for dam selection,” in Proceedings of the 13th International Conference on Environmental Science and Technology (CEST), (Athens: CEST).

Google Scholar

Vassoney, E., Mammoliti Mochet, A., and Comoglio, C. (2017). Use of multicriteria analysis (MCA) for sustainable hydropower planning and management. J. Environ. Manag. 196, 48–55. doi: 10.1016/j.jenvman.2017.02.067

PubMed Abstract | CrossRef Full Text | Google Scholar

Vassoney, E., Mammoliti Mochet, A., and Comoglio, C. (2020). Multicriteria Analysis for the Assessment of Flow Release Scenarios from a Hydropower Plant in the Alpine Region. Water Resour. Manag. 34, 637–651. doi: 10.1007/s11269-019-02459-6

CrossRef Full Text | Google Scholar

Vassoney, E., Mammoliti Mochet, A., Rocco, R., Maddalena, R., Vezza, P., and Comoglio, C. (2019). Integrating meso-scale habitat modelling in the Multicriteria Analysis (MCA) process for the assessment of hydropower sustainability. Water 11:640. doi: 10.3390/w11040640

CrossRef Full Text | Google Scholar

Vezza, P., Parasiewicz, P., Spairani, M., and Comoglio, C. (2014). Habitat modeling in high-gradient streams: the mesoscale approach and application. Ecol. Appl. 24, 844–861. doi: 10.1890/11-2066.1

CrossRef Full Text | Google Scholar

Vezza, P., Zanin, A., and Parasiewicz, P. (2017). Manuale Tecnico-Operativo per la Modellazione e la Valutazione dell’integrità Dell’habitat Fluviale. ISPRA – Manuali e Linee Guida 154/2017. Roma: ISPRA.

Google Scholar

Vučijak, B., Kupusović, T., Midžić-Kurtagić, S., and Ćerić, A. (2013). Applicability of multicriteria decision aid to sustainable hydropower. Appl. Energy 101, 261–267. doi: 10.1016/j.apenergy.2012.05.024

CrossRef Full Text | Google Scholar

Wang, B., Nistor, I., Murty, T., and Wei, Y.-M. (2014). Efficiency assessment of hydroelectric power plants in Canada: a multi criteria decision making approach. Energy Econ. 46, 112–121. doi: 10.1016/j.eneco.2014.09.001

CrossRef Full Text | Google Scholar

Wibowo, S., Grandhi, S., and Tom, M. (2015). “A multicriteria analysis approach for evaluating the sustainability performance of hydropower projects under hesitant fuzzy environment,” in Proceedings of the 2015 7th IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and Conference on Robotics, Automation and Mechatronics (RAM), (Siem Reap: IEEE), 98–103. doi: 10.1109/ICCIS.2015.7274555

CrossRef Full Text | Google Scholar

Yang, Z., Yang, K., Wang, Y., Su, L., and Hu, H. (2020). Multi-objective short-term hydropower generation operation for cascade reservoirs and stochastic decision making under multiple uncertainties. J. Clean. Prod. 276:122995. doi: 10.1016/j.jclepro.2020.122995

CrossRef Full Text | Google Scholar

Zamani-Sabzi, H., King, J. P., Gard, C. C., and Abudu, S. (2016). Statistical and analytical comparison of multi-criteria decision-making techniques under fuzzy environment. Oper. Res. Perspect. 3, 92–117. doi: 10.1016/j.orp.2016.11.001

CrossRef Full Text | Google Scholar

Zanakis, S. H., Solomon, A., Wishart, N., and Dublish, S. (1998). Multi-attribute decision making: a simulation comparison of select methods. Eur. J. Oper. Res. 107, 507–529. doi: 10.1016/S0377-2217(97)00147-1

CrossRef Full Text | Google Scholar