Cell-Based Models in Plant Developmental Biology: Insights into Hybrid Approaches

Computer models are nowadays part of the biologist's toolbox for studying biological dynamics and processes. Tissue development and functioning results from extremely complicated dynamics, that usual analysis does not come very far in terms of understanding the processes underlying those dynamics. In this context, mathematical and numerical models can help to disentangle complex interactions and to analyze non-intuitive dynamics that drives tissue development and functioning. Since these are multi-scale processes, both in time and space, there is the need to develop an appropriate modeling approach. The most promising one is hybrid modeling, that is a synthesis of the differential equation based reaction-diffusion approach at molecular and chemical continuous scales, and the Individual-Based modeling approach for simulating the mechanical and behavioral interactions of the cell ensemble constituting the tissue. Such an approach has been often used in developmental biology, both for plants and animals. In this paper, a brief history of hybrid modeling approaches and tools will be reviewed, and a simple example of its application to a current problem in plant developmental biology (the appearance of vascular patterning during plant growth) will be illustrated, showing the intuitiveness and the strength of such an approach.

1. Introduction

During the first decade of the twenty-first century, biology has been profoundly transformed. The technological advances of this period contributed to produce a tremendous amount of biological data, which in turn has made computers fundamental tools in biology research.

Nowadays, researchers have means to investigate cell biophysical, biological and kinetic properties, providing large and very detailed amount of information to the scientific community. On the other hand, knowledge on how cell processes combine and give rise to tissue and organ properties is still meager, mainly because genetic analysis is time consuming when the number of interacting factors is large. As time passes, and data gathers, it is becoming extremely complicated to identify the networks underlying the regulation of cell activity, while considering all the parallel interactions that underlie cellular morphogenesis (Merks and Glazier, 2005).

Traditional research organizes results and develops new hypotheses about the behavior of gene networks using static schemes, an approach that is unfruitful in all but the simplest cases (Merks and Glazier, 2005). This suggests that reconstructing the dynamics of the genetic regulatory networks with wet research it is not sufficient. Furthermore, gene networks seem just one part of the story: insights on the role of mechanical and physical interactions are needed if one wants to truly elucidate emergent properties linked to tissues (Dupuy et al., 2008). During the development of multi-cellular organisms, cells are capable of interacting with each other through a range of biological and physical mechanisms. A description of these networks of interactions is essential for understanding how it is possible for tissues and organs to co-ordinate cellular activity (Dupuy et al., 2008).

Working at tissue-level many cellular dynamics have to be considered, such as cell growth, cell elongation and cell division: all these are still subjected to intense study and discussions scientific community. This is particularly felt with stem cells, whose ability to differentiate is intrinsically linked to specific biological functions in multi-cellular organisms. A widespread idea is to “interpret stem cells as non-hierarchical self-organizing dynamical systems” (De Matteis et al., 2013) and “stemness” not as an explicit cellular property: stem cells would be “dynamically selected and modified in response to cell-cell and cell-environment interactions on the basis of their potential and flexibility, rather than being specialized a priori” (De Matteis et al., 2013).

The difficulty of working with living tissues, together with the aforementioned multi-scale complexity, is a major limitation to describe such systems, and computer modeling appears particularly helpful to characterize the behavior of multi-cellular systems: working with theoretical models and numerical simulations has proven to be effective in disentangling the relationship between cellular processes and tissue-level arrangement (Jönsson and Krupinski, 2010).

2. Modeling in Plant Developmental Biology

The first pivotal moment in the history of mathematical modeling in developmental biology was the publication of D'Arcy Thompson “On growth and form” (Thompson, 1942), who spawned a geometrically-oriented approach to the problem. In plant biology, this path has been followed and extended by Lindenmayer with its L-system (Lindenmayer, 1975), a modeling framework for representing 1D linear and branching structures (e.g., cells, leaves, or shoots) in form of a sequence of elements. The “geometrical” approach has subsequently been adapted for describing 2D structures as a graph rotation system, and coded in vv-system (Smith, 2006) (for more information see Prusinkiewicz and Runions, 2012).

A second strong contribution to the formalization of developmental processes in biology came from the works of Hofmeister (1863), Sachs (1877), and Errera (1886): their mechanics theories on cells are the foundation of the modern approach to cell division, even if their use bring some discrepancy between models and observations (for a solution to this, see Besson and Dumais, 2011).

Another decisive contribution on theoretic developmental biology has been made by Turing, with his paper on biological pattern formation (Turing, 1952), whose concepts have been extensively used for showing that molecular-level interactions may lead to morphogenesis and differentiation. Turing used a system of partial differential equations (PDE) in his work, a mathematical tool widely used in biological modeling, for describing substance diffusion and reaction. This approach evolved to this day in plant science as a chemical/molecular-oriented one, mainly thanks the works of Meinhardt (1982).

Since the diffusion of these ideas, the contributions of mathematical modeling to developmental biology have grown substantially and contributed to many interesting results (for an in-depth review see Prusinkiewicz and Runions, 2012), but the issues with modeling multi-cellular systems have remained.

2.1. History of Cellular Based Models in Biology

During the last decade, more and more developmental plant biologists turned to mathematical models to explore their hypotheses, and specialized packages appeared for facilitating model construction. Following the realization that developmental processes depend on both geometrical and molecular dynamics, a synthesis of these two approaches has been performed, and some hybrid tools appeared on the scene. This hybrid approach has a deep conceptual meaning, since joining the geometrical and the molecular point of view means working simultaneously at different temporal and spatial scales (i.e., it is a multi-scale approach). A key point in this kind of approach is to establish a certain degree of simplification of cell processes, since using complex molecular models of the cell for simulating tissue-related dynamics (Krul et al., 2003) has been found very computationally demanding and too complex for gathering insights. It is possible to assimilate cells to well-mixed compartments and single cell functions can be represented in a very “simplified” way, still capturing the complexity of their spatial interactions. Considering a tissue as an ensemble of such “simplified” cells facilitates the search for the emergence of tissue organization due to the collective behaviors of the single cells; these behaviors are dependant on both cell internal processes and interactions with neighboring cells. Since chemical substances are signals regulating internal cell dynamics, reaction-diffusion processes, are key players in tissue modeling.

This approach is called cell-based modeling. As stated by Palm and Merks (2015): “The inputs to a cell-based model are the behavioral rules that cells follow. The output of a cell-based model is the tissue morphogenesis that follows indirectly from the collective behavior of the individual cells”

Spatially explicit, cell-based paradigms can be broadly classified according to the cells being part of a grid (in-lattice models) or not (off-lattice models).

A widespread in-lattice paradigm in animal developmental biology modeling is the Cellular Potts Model (CPM; Glazier and Graner, 1993), a modeling approach that considers single cells as agents trying to minimize their internal energy while growing, dividing, and interacting with chemical fields.

The CPM represent cells as a groups of neighboring pixels, distinguishing between boundary and non-boundary pixels in order to define interaction sites, and uses an energy-based approach for simulating growth, cell-cell interaction, and for maintaining cell shapes. Molecular details, i.e., substance production and diffusion, are handled by ODE and PDE (Ordinary and Partial Differential Equations) solvers coupled with geometric informations and with the growth process, that also permit to consider other continuous (eventually spatially-explicit) processes. The CPM approach has been successfully applied to a vast array of biological problems: here we will cite tissue patterning (Savill and Sherratt, 2003; Zeng et al., 2004), morphogenesis (Zajac et al., 2003), tumorigenesis (Turner and Sherratt, 2002), and vasculogenesis (Scianna and Preziosi, 2012).

While some models of plant systems have been produced within the CPM paradigm, it is considered unfit for simulating plant tissue dynamics. These are strongly influenced by the presence of a cell-wall, which is responsible for maintaining cell geometry, for preventing cell motility, and it is involved in substance (e.g., auxin) transport. The CPM lacks a proper way to simulate cell wall dynamics, and the paradigm chosen for cell geometry makes cell shape and motility (absent in almost all plant cells, due to the cell wall) difficult to control.

Merks et al. (2011) proposes an appropriate solution, starting from the CPM but using for geometry an off-grid modeling approach that describes cells as polygons delimited by cell walls, considered as separate entities and shared among adjacent cells. Walls are assimilated to mechanical springs, so that growth and mechanical interactions could be computed by means of a Markovian relaxation algorithm. Additional differential equations model diffusive transport across the two cell membranes and across the cell wall separating adjacent cells. As in the original CPM, sets of ordinary differential equations in each cell describe dynamics of biochemical networks and genetic regulatory networks.

Since the hybrid approach has proven itself fruitful, other variations have been developed, changing the way cell geometry and/or topology are defined, e.g., using L-system (Wabnik et al., 2013) or considering cells as polygonal (Dupuy et al., 2008) or Voronoi meshes (Mebatsion et al., 2006), as well as using different ways to describe cell walls and to render mechanical interactions, such as assimilating the structure to a spring (Shapiro et al., 2013) or a viscous fluid (Dupuy et al., 2008), and use appropriate physical models for simulating their behavior.

Since the diffusion of mathematical models as plant developmental biology tools, a few general purpose tools have been made, in order to allow non-programmers to enter the field.

The CPM has been integrated in the CompuCell3D software environment (Izaguirre et al., 2004—http://www.compucell3d.org), a python-based, extensible general-purpose framework used in biology for simulating in 2D and 3D a range of biological dynamics. Compucell3D has been used mainly for studies in human tumorigenesis (Boghaert et al., 2014; Swat et al., 2015) and animal tissue development (Dias et al., 2014), albeit other processes have been simulated (Popławski et al., 2008; Zhang et al., 2011; Giverso and Preziosi, 2014). It is not particularly suited for plant tissues, mainly because it is based on the CPM, although a model of root growth has been developed with this method (Grieneisen et al., 2007).

The plant-specific approach of Merks, based on the CPM, has been implemented in the VirtualLeaf modeling framework (Merks et al., 2011—https://biomodel.project.cwi.nl/software) for 2D tissue simulation. VirtualLeaf is written in C++, and comes with pre-programmed modules simulating many accepted results. It is possible to write new modules in order to test new hypotheses.

CellModeller (Dupuy et al., 2008—https://haselofflab.github.io/CellModeller/) is another stand-alone environment build with a modular approach and written in python, for modeling large-scale multi-cellular systems in 2D. As in other tools cell topologies are graph rotation system (i.e., composed of nodes and edges), and inter- and intra-cellular chemical interactions are formalized as PDEs and ODEs. Mechanical interactions and growth are simulated through physical laws regulating rearrangement of the cell nodes following strain/stress of the cell wall, itself rendered as a viscous fluid. This tool has been used for modeling microbial biofilms (Rudge et al., 2012), but his potential for modeling plant cells related dynamics has been often stated (Dupuy et al., 2008; Liu and Stewart, 2015).

Some other tools have been programmed as extension for pre-existing software environment, like CellZilla (Shapiro et al., 2013—http://www.cellzilla.info/) that extends the xlr8r (Shapiro et al., 2003) Mathematica package capabilities of solving chemical reactions as sets of ODE to 2D tissues. The topology of the cell is described as a set of nodes (vertexes), with the segments joining them (edges) being the cell wall. Using xlr8r, inter- and intra-cellular chemical interactions are formulated as differential equations; growth and mechanical interactions are modeled considering the walls subject to springs whose behavior is regulated by Hooke's law. CellZilla has been used for simulating auxin-driven development in the apical meristem of Arabidopsis thaliana L. (Nikolaev et al., 2013).

Finally, VPlants (https://team.inria.fr/virtualplants/) is a set of packages belonging the OpenAlea software environment that permit to analyze, model and simulate tissue dynamics (for detail on OpenAlea see Pradal et al., 2008). Its “Tissue” package permits to simulate tissues growth and division, starting from a single cell, or after reconstructing a digital tissue from a photograph. The cell is geometrically described as a polygon, and the user may choose different algorithms for growth; division is similarity coded on the basis of the user's needs. VPlants has been used for simulating, among other things, vascular development in A. thaliana (Muraro et al., 2014).

3. Example of Hybrid Model Approach

Vascular plants are characterized by a pervasive, specialized system of vessels, composed of two types of tissues: xylem, cells that transport water and mineral nutrient, and phloem cells that carry sugars and other organic molecules. The spatial position and differentiation of such vascular cells is established during early phases of tissue development. In the plant embryo, four cells buried inside the cell mass are activated as an undifferentiated tissue named procambium: they will grow and divide following specific procedures, increasing the number of cells and forming a cylinder of procambial tissue. As the embryo matures, two zones will start to act as “stock” of undifferentiated cells: one on top, called shoot apical meristem, and the other, called root apical meristem, on the lower part of the embryo. Adjacent to the two apical meristems, some procambial cells will further divide, generating precursors of vascular cells (Jouannet et al., 2015). Peculiar procambium arrangement patterns will emerge during this phase, that will be propagated by the two meristems as the plant grows in height.

These arrangement patterns vary among species (Beck et al., 1982) but also between the stem and the root of the same individual.

How these arrangements arise, how they are maintained, and what causes their diversity are open questions that have been puzzling plant scientists and modelers for a long time (Jeffrey, 1903; Sieburth and Deyholos, 2006; Muraro et al., 2014). From an experimental standpoint, studies in plant vascular morphogenesis have followed the reductionist route, as the key players shifted from structures (Esau, 1960) to cells, and from those to genes (Caño-Delgado et al., 2010) and proteins (Sieburth and Deyholos, 2006), with many regulatory elements discovered recently (Donner et al., 2009), most of them in the species A. thaliana. At the moment there is only an approximate knowledge of the underlying dynamics (Jouannet et al., 2015), derived mainly from studies on plant hormones like auxins (Scarpella et al., 2006), brassinosteroids (Vert and Chory, 2006), and cytokinines (Mähönen et al., 2006); most of these focus on single aspects, and there is the need for a clarification of the interaction of these aspects both spatially and temporally.

3.1. Existing Models and Limitations

Whilst mathematical models have proven to be a good tool in helping to understand the connections between cells and tissues (Jönsson and Krupinski, 2010), they do so focusing mainly on sub-cellular processes related to plant hormones, especially auxins (Prusinkiewicz and Runions, 2012). The first steps were laid by Sachs (1969), with the so-called 'canalization hypothesis', used by various molecular models exploring the vascularization processes (Mitchison, 1980; Feugier et al., 2005; Bayer et al., 2009).

The first to approach plant primary vascular structure specification and arrangement were Muraro et al. (2014), with a multicellular model that explores the hypothesis of a vascular patterning mechanism dependent on hormones interaction in a very specific context (the roots of A. thaliana in a steady-state condition). Starting from a set of experimentally determined factors (i.e., gene products and hormones), the authors build a model formalizing the interaction between these factors and propose a minimal regulatory network capable of maintaining a stable vascular pattern in Arabidopsis root without predefined positional information (Muraro et al., 2014). This model used VPlants from the OpenAlea environment to simulate the tissue geometry and auxin diffusion.

The theory of an auxin-dependant patterning in A. thaliana has been further explored with the model of De Rybel et al. (2014), which combined experimental evidence and modeling work to investigate the interactions between auxin and cytokinin and their involvement in early embryo development. The model, formulated using VirtualLeaf, shows how these hormones contribute to cell division and differentiation of vascular tissues providing positional cues for the establishment of a stable spatial pattern within a growing domain.

Another model, based on reaction-diffusion dynamics, has been proposed by Cartenì et al. (2014) for simulating the differentiation and the spatial patterning of procambium, phloem and xylem. This theoretical model was formulated as a set of activator–substrate systems (Meinhardt, 1982) describing the dynamics of nine diffusible morphogens whose interactions lead to the differentiation of vascular tissues and the emergence of their spatial patterns. This model, implemented in MATLAB (MathWorks Inc.—https://www.mathworks.com/products/matlab/) successfully recreated a broad range of vascular arrangements, working with a fixed domain and without considering individual cell dynamics.

In order to provide a procedural example of development of a hybrid model, we built a simple model of A. thaliana root and stem early vascular differentiation. The hybrid approach permits to take into account both the molecular and geometric perspectives (Figure 1), thus providing the chance to capture emergent properties linked to the interaction of these two phenomena The use of VirtualLeaf approximates spatial interactions among cells in a computationally convenient way (Merks and Glazier, 2005), even if it considers stochastic-based dynamics not necessarily linked with cells biological properties (Merks et al., 2011).

FIGURE 1

Figure 1. An individual agent is described by its geometric properties (Area, Shape and derived Center of mass) and cell type. Each type is characterized by a specific metabolism (ODE) with products whose concentration is dynamically linked with diffusion processes (PDE).

3.2. Model Description

As mentioned in the introduction, it is possible to work with tissue-related dynamics using a hybrid modeling approach (Vincenot et al., 2011), i.e., coupling an Individual-Based Model (IBM) with a continuous PDE/ODE mathematical model. Under this paradigm, the IBM will account for internal cell rules and cell-cell interactions, whilst a set of differential equations will regulate substance physics and continuous processes.

Vincenot et al. (2011) proposed a conceptual framework comprising a set of reference cases representing combination patterns of SD and IBM sub-models, which shall serve as building blocks for hybrid models. The model described here fits into case 2b of the framework, since cells are represented as IBM individuals and a SD sub-model is embedded in each cell to compute growth and substance dynamics. Single cells are then networked depending on the adjacency of their walls, forming thereby a tissue.

Starting from Cartenì et al. (2014), we built a hybrid, growing-domain model of cell growth and differentiation in the roots and stems of A. thaliana; this model considers simplified tissue dynamics, and the production of four diffusible, cross-reacting substances (S₀, S₁, S₂, and A_P) which are responsible for procambium differentiation and proliferation. In this particular case, the PDE mathematical formulation is a simplified version of the Reaction/Diffusion model presented in Cartenì et al. (2014).

The model is not meant to provide a one-to-one correspondence with specific gene products or plant hormones or insights into the molecular mechanisms of vascular differentiation. It was rather selected for the simplicity of formulation and for the fact that to date it is the only one that provides a general framework (although only theoretical) for the spontaneous emergence of different spatial arrangements of vascular bundles. For more detail on the models underlying assumptions, see Cartenì et al. (2014).

The model domain is a transversal section of growing A. thaliana tissue. Each one of the cells composing the tissue is a complex agent made by the cell itself and by a polygonal cell wall, shared with neighbor cells. The cell agent properties are the position, the type (Table 1), the area, and the concentration of all substances considered in the model.

TABLE 1

Table 1. Differentiation and substance production rules.

The model itself considers four substances:

• S₀, produced by the cell walls contacting the medium/outside. It represents the signal involved in the creation of a radial gradient that determines the establishment of pith, inner, and outer layers of cells.

• S₁ and S₂, produced respectively by the inner or the outer cells. These represent signal substrates regulating the production of the activator A_P.

• A_P, produced by the reaction between S₁ and S₂. It represents the procambium activator that triggers the differentiation of procambial cells.

All substances diffuse between cells but not outwards the tissue, and all four are considered homogeneous in the individual cell space.

In the model, cells grow at a constant rate (controlled by the parameter k_a, see Table 2), dividing if their size reach twice the original size. A theoretical substance (S₀), is then produced in the outermost layer of cells, contributing to the creation of an inside/outside gradient; and the other substances are produced according to cell type (Table 1). Each chemical species inside the cell diffuse through the tissue and react with each other according to the following equations:

$\begin{array}{cc}\frac{\partial S_0}{\partial t}={\sigma }_0-{\mu }_0{S}_0+D_{S_0}{\nabla }^2{S}_0& (1)\end{array}$

$\begin{array}{cc}\frac{\partial S_1}{\partial t}=\overline{{\sigma }_1}\left(1-\frac{S_1}{1+k_S{A}_P}\right)-{\rho }_S{A}_P^2{S}_1{S}_2+D_S{\nabla }^2{S}_1& (2)\end{array}$

$\begin{array}{cc}\frac{\partial S_2}{\partial t}=\overline{{\sigma }_2}\left(1-\frac{S_2}{1+k_S{A}_P}\right)-{\rho }_S{A}_P^2{S}_1{S}_2+D_S{\nabla }^2{S}_2& (3)\end{array}$

$\begin{array}{cc}\frac{\partial A_P}{\partial t}={\sigma }_{A_P}+{\rho }_{A_P}{A}_P^2{S}_1{S}_2-{\mu }_{A_P}{A}_P+D_{A_P}{\nabla }^2{A}_P& (4)\end{array}$

with:

$\begin{array}{cc}\overline{{\sigma }_1}=\{\begin{array}{ll}{\sigma }_S\hfill & \text{if cell is not type }0\text{ and is }\left(\text{type }1\text{ or type }2\right)\hfill \\ 0\hfill & \text{else}\hfill \end{array}& (5)\end{array}$

$\begin{array}{cc}\overline{{\sigma }_2}=\{\begin{array}{ll}{\sigma }_S\hfill & \text{if cell is not type }0\text{ and is }\left(\text{type }3\text{ or type }4\right)\hfill \\ 0\hfill & \text{else}\hfill \end{array}& (6)\end{array}$

TABLE 2

Table 2. List of parameters values.

Algorithmically, at the beginning of each simulation time step the concentration of the substances inside each cell is checked and, if any of the threshold values in Table 1 are met, the cell type attribute is updated; then the cell grows taking into account mechanical constraints due to cell-cell interactions, and the area and shape attributes are updated. After growth the cell size is checked for evaluating if to divide or not. The model then computes the reaction/diffusion module, based on its type (Table 1), and all substances first diffuse and then react among each other following the aforementioned system of Partial Differential Equations, taking into account geometry and topology. Then, the model enters the next time step.

In order to further explore the hybrid-model capabilities of VirtualLeaf, another simple assumption has been implemented for the description of cell growth and division. In this case cells still grow at a fixed rate, but the division threshold is modeled as inversely proportional to the S₀ concentration. Cell size increases with the distance from the outermost layer of cells.

Parameter definitions and values for both the variants of the model are the same; they are presented in Table 2.

3.3. Model Output and Discussion

A set of simulations was performed to test the capabilities of the model to reproduce the provascular patterns observed in A. thaliana plants (Figure 2).

FIGURE 2

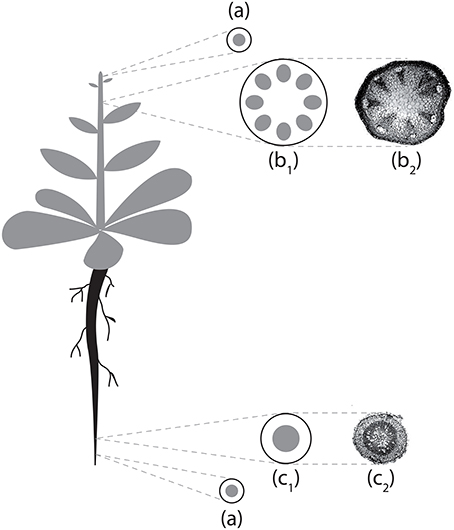
Figure 2. Schematization of Arabidopsis thaliana vascular structures in stem and primary root. (a) Stem/root tip; (b₁) stem section scheme; (b₂) stem section micrograph; (c₁) root section scheme; (c₂) root section micrograph. Micrographs reproduced with permission of Avsian-Kretchmer et al. (2002).

Figure 3 shows the output of two model simulations run for 1785 (Figure 3A) and 11505 (Figure 3B) time steps. All parameter values for the two simulations were the same.

FIGURE 3

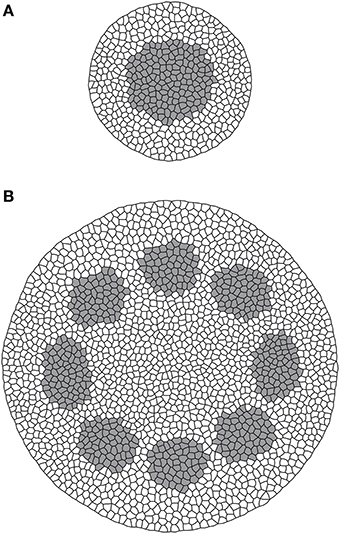
Figure 3. Model output for root (A) and stem (B) sections. Gray is procambium, white is non-procambial tissue.

From these results it is possible to observe how procambium arrangement is an emergent property dependent both on the reaction/diffusion dynamics that lead to the formation of Turing patterns (Turing, 1952) and on the tissue size, that influence the aforesaid dynamics and contribute to the differences between the stem (bigger domain) and the root (smaller domain) patterns. This model thus confirm, in a growing domain, the results presented by Cartenì et al. (2014). that the shift between a protostelic arrangement (Figure 3A) and a eustelic arrangement (Figure 3B) could be attributed only to the size of the domain in which the molecular dynamics occur. Moreover, both simulated sections show roughly the same cell number and the same total area of the reference photomicrographs (Figures 2c₁,b₂). However, in the real system, cells are heterogeneous in dimensions and the difference between the model and the real system can be reduced if a further assumption for growth and division dynamics is added to the model.

The output from the third model simulation (Figure 4) shows how a simple rule can affect the system state producing a difference in terms of size among the cell rows, linked to the concentration of S₀ inside the cells. Cells leaving meristematic zones often enlarge to hundreds of times their original size and the final size depends on the position they occupy in the radial arrangement. Cell expansion usually results from the combination of two processes: the increase in cell ploidy by endoreplication (DNA replication with no mitosis), and the complex process of cell expansion, which is driven by internal turgor pressure and restricted by the ability of cell walls to extend (Perrot-Rechenmann, 2010). These processes are under the control of several stimuli that can be spatially heterogeneous. In the presented simulation, this was achieved inserting the inverse of the concentration of a certain substance (S₀) as a term in the algorithm that triggers cell division. The condition may simulate the dynamics of a substance that inhibits cell growth, whose biological counterpart may be a sugar or a plant hormone (e.g., Evans et al., 1994).

FIGURE 4

Figure 4. Output from alternative growth model.

The proposed solution effectively reproduced the radial pattern of cell sizes observed in Arabidopsis stems (Figure 1). This result is an example of how a simple individual rule makes a complex collective behavior emerge and illustrate the potential of VirtualLeaf for exploring spatial-explicit tissue dynamics.

The spatial position of plant vascular cells is established during early phases of development, when some cells are activated as procambium, and it is maintained along the plant life-span. Procambium arrangement patterns vary among different species but also between the stem and the root of the same individual: how they arise, how they are maintained, and what causes their diversity are open questions. Modeling the dynamics of the system in a manner appropriate to answer these questions is considered a complex challenge, since the system analyzed is multi-scale and characterized by a vast number of processes. IBMs and PDEs are unsuitable for this task, mainly because taken separately, these approaches are not able to efficiently describe multi-scale systems: the former cannot account for continuous dynamics and the latter cannot work with discrete elements.

In our case, a purely IBM approach would not efficiently model the diffusion of substances among cells (a continuous process) while a PDE model would fail to represent the properties of the single cells, mainly because it considers the tissue as a whole characterized by average properties (for the meaning of whole in this context, see Vincenot et al., 2011). A hybrid modeling approach, instead, may be suitable because it permits to analyze multi-scale systems like tissues without oversimplifying them. Beside preventing conceptual approximations, this approach may became necessary in order to inspect properties emerging from the interaction of processes that cannot be modeled with the same paradigm, as those linking individual properties with diffusion dynamics. In order to test this hypothesis we built a model using a hybrid approach, i.e., individual-based rules for modeling networks and interactions, and differential equations to model growth and diffusion.

4. Conclusions

This paper presented a brief review of cellular-based modeling in plant developmental biology, pointing out its strength and showing available tools. The present state is that models addressing the dynamics of root and stem vascular differentiation are few, and almost all of them work with static-domains, albeit the modeling tools proposed are more than capable to handle growing domains.

The paper also presents an example on how to analyze tissue-related dynamics using a hybrid modeling approach. The presented modeling process showed that this approach represents an efficient way to simulate tissue-level dynamics, because it provides an intuitive manner to aggregate individual based dynamics with continuous processes like diffusion. A model built with this technique permits to observe emergent processes linked to the interaction of these discrete/continuous elements. A simple tissue growth model with a process-based condition of cell division shows how VirtualLeaf is capable to link spatial individual properties and process-based internal processes.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Avsian-Kretchmer, O., Cheng, J. C., Chen, L., Moctezuma, E., and Sung, Z. R. (2002). Indole acetic acid distribution coincides with vascular differentiation pattern during Arabidopsis leaf ontogeny. Plant Physiol. 130, 199–209. doi: 10.1104/pp.003228

PubMed Abstract | CrossRef Full Text | Google Scholar

Bayer, E. M., Smith, R. S., Mandel, T., Nakayama, N., Sauer, M., Prusinkiewicz, P., et al. (2009). Integration of transport-based models for phyllotaxis and midvein formation. Genes Dev. 23, 373–384. doi: 10.1101/gad.497009

PubMed Abstract | CrossRef Full Text | Google Scholar

Beck, C. B., Schmid, R., and Rothwell, G. W. (1982). Stelar morphology and the primary vascular system of seed plants. Bot. Rev. 48, 691–815. doi: 10.1007/BF02860874

CrossRef Full Text | Google Scholar

Besson, S., and Dumais, J. (2011). Universal rule for the symmetric division of plant cells. Proc. Natl. Acad. Sci. U.S.A. 108, 6294–6299. doi: 10.1073/pnas.1011866108

PubMed Abstract | CrossRef Full Text | Google Scholar

Boghaert, E., Radisky, D. C., and Nelson, C. M. (2014). Lattice-based model of ductal carcinoma in situ suggests rules for breast cancer progression to an invasive state. PLoS Comput. Biol. 10:e1003997. doi: 10.1371/journal.pcbi.1003997

PubMed Abstract | CrossRef Full Text | Google Scholar

Caño-Delgado, A., Lee, J.-Y., and Demura, T. (2010). Regulatory mechanisms for specification and patterning of plant vascular tissues. Annu. Rev. Cell Dev. Biol. 26, 605–637. doi: 10.1146/annurev-cellbio-100109-104107

PubMed Abstract | CrossRef Full Text | Google Scholar

Cartenì, F., Giannino, F., Schweingruber, F. H., and Mazzoleni, S. (2014). Modelling the development and arrangement of the primary vascular structure in plants. Ann. Bot. 114, 619–627. doi: 10.1093/aob/mcu074

PubMed Abstract | CrossRef Full Text | Google Scholar

De Matteis, G., Graudenzi, A., and Antoniotti, M. (2013). A review of spatial computational models for multi-cellular systems, with regard to intestinal crypts and colorectal cancer development. J. Math. Biol. 66, 1409–1462. doi: 10.1007/s00285-012-0539-4

PubMed Abstract | CrossRef Full Text | Google Scholar

De Rybel, B., Adibi, M., Breda, A. S., Wendrich, J. R., Smit, M. E., Novák, O., et al. (2014). Integration of growth and patterning during vascular tissue formation in Arabidopsis. Science 345, 1255215. doi: 10.1126/science.1255215

PubMed Abstract | CrossRef Full Text | Google Scholar

Dias, A. S., de Almeida, I., Belmonte, J. M., Glazier, J. A., and Stern, C. D. (2014). Somites without a clock. Science 343, 791–795. doi: 10.1126/science.1247575

PubMed Abstract | CrossRef Full Text | Google Scholar

Donner, T. J., Sherr, I., and Scarpella, E. (2009). Regulation of preprocambial cell state acquisition by auxin signaling in Arabidopsis leaves. Development 136, 3235–3246. doi: 10.1242/dev.037028

PubMed Abstract | CrossRef Full Text | Google Scholar

Dupuy, L., Mackenzie, J., Rudge, T., and Haseloff, J. (2008). A system for modelling cell–cell interactions during plant morphogenesis. Ann. Bot. 101, 1255–1265. doi: 10.1093/aob/mcm235

PubMed Abstract | CrossRef Full Text | Google Scholar

Errera, L. (1886). Sur une Condition Fondamentale d'équilibre des Cellules Vivantes. C. R. Hebd. Séances Acad. Sci. 103, 822–824.

Esau, K. (1960). Anatomy of seed plants. Soil Sci. 90, 149. doi: 10.1097/00010694-196008000-00031

CrossRef Full Text | Google Scholar

Evans, M. L., Ishikawa, H., and Estelle, M. A. (1994). Responses of Arabidopsis roots to auxin studied with high temporal resolution: comparison of wild type and auxin-response mutants. Planta 194, 215–222. doi: 10.1007/BF01101680

CrossRef Full Text | Google Scholar

Feugier, F. G., Mochizuki, A., and Iwasa, Y. (2005). Self-organization of the vascular system in plant leaves: inter-dependent dynamics of auxin flux and carrier proteins. J. Theor. Biol. 236, 366–375. doi: 10.1016/j.jtbi.2005.03.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Giverso, C., and Preziosi, L. (2014). “Using mathematical modelling as a virtual microscope to support biomedical research,” in Mathematical Models and Methods for Planet Earth, eds A. Celletti, U. Locatelli, T. Ruggieri, and E. Strickland (Zurich: Springer International Publishing), 59–71.

Google Scholar

Glazier, J. A., and Graner, F. (1993). Simulation of the differential adhesion driven rearrangement of biological cells. Phys. Rev. E 47, 2128. doi: 10.1103/physreve.47.2128

PubMed Abstract | CrossRef Full Text | Google Scholar

Grieneisen, V. A., Xu, J., Marée, A. F. M., Hogeweg, P., and Scheres, B. (2007). Auxin transport is sufficient to generate a maximum and gradient guiding root growth. Nature 449, 1008–1013. doi: 10.1038/nature06215

PubMed Abstract | CrossRef Full Text | Google Scholar

Hofmeister, W. (1863). Zusätze und berichtigungen zu den 1851 veröffentlichten untersuchungen der entwicklung höherer kryptogamen. Jahrb. Wiss. Bot. 3, 259–293.

Izaguirre, J. A., Chaturvedi, R., Huang, C., Cickovski, T., Coffland, J., Thomas, G., et al. (2004). Compucell, a multi-model framework for simulation of morphogenesis. Bioinformatics 20, 1129–1137. doi: 10.1093/bioinformatics/bth050

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeffrey, E. C. (1903). The structure and development of the stem in the Pteridophyta and Gymnosperms. Philos. Trans. R. Soc. B 195, 119–146. doi: 10.1098/rstb.1903.0004

CrossRef Full Text

Jönsson, H., and Krupinski, P. (2010). Modeling plant growth and pattern formation. Curr. Opin. Plant Biol. 13, 5–11. doi: 10.1016/j.pbi.2009.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Jouannet, V., Brackmann, K., and Greb, T. (2015). (pro) cambium formation and proliferation: two sides of the same coin? Curr. Opin. Plant Biol. 23, 54–60. doi: 10.1016/j.pbi.2014.10.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Krul, T., Kaandorp, J. A., and Blom, J. G. (2003). “Modelling developmental regulatory networks,” in Computational Science—ICCS 2003, eds P. M. A. Sloot, D. Abramson, A. V. Bogdanov, Y. E. Gorbachev, J. J. Dongarra, and A. Y. Zomaya (Berlin; Heidelberg: Springer-Verlag), 688–697.

Google Scholar

Lindenmayer, A. (1975). Developmental algorithms for multicellular organisms: a survey of l-systems. J. Theor. Biol. 54, 3–22. doi: 10.1016/S0022-5193(75)80051-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., and Stewart, C. N. (2015). Plant synthetic biology. Trends Plant Sci. 20, 309–317. doi: 10.1016/j.tplants.2015.02.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Mähönen, A. P., Bishopp, A., Higuchi, M., Nieminen, K. M., Kinoshita, K., Törmäkangas, K., et al. (2006). Cytokinin signaling and its inhibitor ahp6 regulate cell fate during vascular development. Science 311, 94–98. doi: 10.1126/science.1118875

PubMed Abstract | CrossRef Full Text | Google Scholar

Mebatsion, H. K., Verboven, P., Verlinden, B. E., Ho, Q. T., Nguyen, T. A., and Nicolaï, B. M. (2006). Microscale modelling of fruit tissue using voronoi tessellations. Comput. Electron. Agricul. 52, 36–48. doi: 10.1016/j.compag.2006.01.002

CrossRef Full Text | Google Scholar

Meinhardt, H. (1982). Models of Biological Pattern Formation. London: Academic Press.

Google Scholar

Merks, R. M. H., and Glazier, J. A. (2005). A cell-centered approach to developmental biology. Phys. A Stat. Mech. Appl. 352, 113–130. doi: 10.1016/j.physa.2004.12.028

CrossRef Full Text | Google Scholar

Merks, R. M. H., Guravage, M., Inzé, D., and Beemster, G. T. S. (2011). Virtualleaf: an open-source framework for cell-based modeling of plant tissue growth and development. Plant Physiol. 155, 656–666. doi: 10.1104/pp.110.167619

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchison, G. J. (1980). A model for vein formation in higher plants. Proc. R. Soc. Lond. B Biol. Sci. 207, 79–109. doi: 10.1098/rspb.1980.0015

CrossRef Full Text | Google Scholar

Muraro, D., Mellor, N., Pound, M. P., Lucas, M., Chopard, J., Byrne, H. M., et al. (2014). Integration of hormonal signaling networks and mobile micrornas is required for vascular patterning in Arabidopsis roots. Proc. Natl. Acad. Sci. U.S.A. 111, 857–862. doi: 10.1073/pnas.1221766111

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolaev, S. V., Zubairova, U. S., Penenko, A. V., Mjolsness, E. D., Shapiro, B. E., and Kolchanov, N. A. (2013). Model of structuring the stem cell niche in shoot apical meristem of Arabidopsis thaliana. Dokl. Biol. Sci. 452, 316–319. doi: 10.1134/S0012496613050104

PubMed Abstract | CrossRef Full Text | Google Scholar

Palm, M. M., and Merks, R. M. H. (2015). “Large-scale parameter studies of cell-based models of tissue morphogenesis using compucell3d or virtualleaf,” in Tissue Morphogenesis, ed C. M. Nelson (New York, NY: Springer), 301–322.

Google Scholar

Perrot-Rechenmann, C. (2010). Cellular responses to auxin: division versus expansion. Cold Spring Harbor Perspect. Biol. 2:a001446. doi: 10.1101/cshperspect.a001446

PubMed Abstract | CrossRef Full Text | Google Scholar

Popławski, N. J., Shirinifard, A., Swat, M., and Glazier, J. A. (2008). Simulation of single-species bacterial-biofilm growth using the glazier-graner-hogeweg model and the compucell3d modeling environment. Math. Biosci. Eng. MBE 5:355. doi: 10.3934/mbe.2008.5.355

PubMed Abstract | CrossRef Full Text | Google Scholar

Pradal, C., Dufour-Kowalski, S., Boudon, F., Fournier, C., and Godin, C. (2008). Openalea: a visual programming and component-based software platform for plant modelling. Funct. Plant Biol. 35, 751–760. doi: 10.1071/FP08084

CrossRef Full Text | Google Scholar

Prusinkiewicz, P., and Runions, A. (2012). Computational models of plant development and form. New Phytol. 193, 549–569. doi: 10.1111/j.1469-8137.2011.04009.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudge, T. J., Steiner, P. J., Phillips, A., and Haseloff, J. (2012). Computational modeling of synthetic microbial biofilms. ACS Syn. Biol. 1, 345–352. doi: 10.1021/sb300031n

PubMed Abstract | CrossRef Full Text | Google Scholar

Sachs, J. (1877). Über die Anordnung der Zellen in Jüngsten Pflanzentheilen. Würzburg: Stahel'schen.

Sachs, T. (1969). Polarity and the induction of organized vascular tissues. Ann. Bot. 33, 263–275.

Google Scholar

Savill, N. J., and Sherratt, J. A. (2003). Control of epidermal stem cell clusters by notch-mediated lateral induction. Dev. Biol. 258, 141–153. doi: 10.1016/S0012-1606(03)00107-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Scarpella, E., Marcos, D., Friml, J., and Berleth, T. (2006). Control of leaf vascular patterning by polar auxin transport. Genes Dev. 20, 1015–1027. doi: 10.1101/gad.1402406

PubMed Abstract | CrossRef Full Text | Google Scholar

Scianna, M., and Preziosi, L. (2012). Multiscale developments of the cellular potts model. Multiscale Model. Simul. 10, 342–382. doi: 10.1137/100812951

CrossRef Full Text | Google Scholar

Shapiro, B. E., Levchenko, A., Meyerowitz, E. M., Wold, B. J., and Mjolsness, E. D. (2003). Cellerator: extending a computer algebra system to include biochemical arrows for signal transduction simulations. Bioinformatics 19, 677–678. doi: 10.1093/bioinformatics/btg042

PubMed Abstract | CrossRef Full Text | Google Scholar

Shapiro, B. E., Meyerowitz, E. M., and Mjolsness, E. (2013). Using cellzilla for plant growth simulations at the cellular level. Front. Plant Sci. 4:408. doi: 10.3389/fpls.2013.00408

PubMed Abstract | CrossRef Full Text | Google Scholar

Sieburth, L. E., and Deyholos, M. K. (2006). Vascular development: the long and winding road. Curr. Opin. Plant Biol. 9, 48–54. doi: 10.1016/j.pbi.2005.11.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, C. (2006). On Vertex-vertex Systems and Their Use in Geometric and Biological Modelling. Ph.D. thesis, Calgary, Alta., Canada.

Swat, M. H., Thomas, G. L., Shirinifard, A., Clendenon, S. G., and Glazier, J. A. (2015). Emergent stratification in solid tumors selects for reduced cohesion of tumor cells: a multi-cell, virtual-tissue model of tumor evolution using compucell3d. PLoS ONE 10:e0127972. doi: 10.1371/journal.pone.0127972

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, D. W. (1942). On Growth and Form. Cambridge: Cambridge University Press.

Google Scholar

Turing, A. M. (1952). The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 237, 37–72. doi: 10.1098/rstb.1952.0012

CrossRef Full Text | Google Scholar

Turner, S., and Sherratt, J. A. (2002). Intercellular adhesion and cancer invasion: a discrete simulation using the extended potts model. J. Theor. Biol. 216, 85–100. doi: 10.1006/jtbi.2001.2522

PubMed Abstract | CrossRef Full Text | Google Scholar

Vert, G., and Chory, J. (2006). Downstream nuclear events in brassinosteroid signalling. Nature 441, 96–100. doi: 10.1038/nature04681

PubMed Abstract | CrossRef Full Text | Google Scholar

Vincenot, C. E., Giannino, F., Rietkerk, M., Moriya, K., and Mazzoleni, S. (2011). Theoretical considerations on the combined use of system dynamics and individual-based modeling in ecology. Ecol. Model. 222, 210–218. doi: 10.1016/j.ecolmodel.2010.09.029

CrossRef Full Text | Google Scholar

Wabnik, K., Robert, H. S., Smith, R. S., and Friml, J. (2013). Modeling framework for the establishment of the apical-basal embryonic axis in plants. Curr. Biol. 23, 2513–2518. doi: 10.1016/j.cub.2013.10.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Zajac, M., Jones, G. L., and Glazier, J. A. (2003). Simulating convergent extension by way of anisotropic differential adhesion. J. Theor. Biol. 222, 247–259. doi: 10.1016/S0022-5193(03)00033-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, W., Thomas, G. L., and Glazier, J. A. (2004). Non-turing stripes and spots: a novel mechanism for biological cell clustering. Phys. A Stat. Mech. Appl. 341, 482–494. doi: 10.1016/j.physa.2004.03.089

CrossRef Full Text | Google Scholar

Zhang, Y., Thomas, G. L., Swat, M., Shirinifard, A., and Glazier, J. A. (2011). Computer simulations of cell sorting due to differential adhesion. PLoS ONE 6:e24999. doi: 10.1371/journal.pone.0024999

PubMed Abstract | CrossRef Full Text | Google Scholar