A coordinated control strategy for active transient voltage support in DFIG-based wind farms

During the implementation of active voltage support in wind farms, coordinating the operation of multiple wind turbines presents significant challenges. The dynamic response of the entire wind farm becomes complex during grid faults, making it difficult to achieve coordinated voltage support across different wind turbines. To address this, a coordination control strategy for doubly fed wind farms is here proposed which is based on Q-learning informed by the sensitivity of voltage. First, a method for calculating the voltage sensitivity of DFIG-based wind farms is introduced, utilizing the arbitrary polynomial chaos approach. Additionally, the operational constraints of wind farms are defined based on the average short-circuit ratio of reactive power. The voltage support characteristics of multi-machine wind farms under grid fault conditions are then thoroughly explored. Subsequently, an improved Q-learning algorithm is developed, based on the sensitivity of voltage. This algorithm aids in optimizing the control commands, thus enhancing the effectiveness of the voltage support system. Finally, adopting this voltage sensitivity as the basis for the coordinated control commands and applying the improved Q-learning algorithm as the implementation mechanism, a coordinated control strategy for active voltage support in DFIG-based wind farms is proposed. Simulation results demonstrate that the proposed control strategy can provide effective active voltage support during grid faults.

1 Introduction

The ongoing transition of renewable energy from a supplementary to a primary power source is crucial for energy transformation (Global Wind Energy Council, 2022; Global Wind Energy Council, 2020). Currently, wind power has been extensively deployed on a large scale and substantial capacity. The large-scale integration of wind energy significantly alters the voltage dynamics of power systems, leading to frequent and extensive voltage fluctuations. During grid faults, abrupt voltage changes can precipitate large-scale disconnection incidents in wind farms, posing a significant threat to the safe and stable operation of the power grid (Chengmao et al., 2023; Mathis, 2023; Liu et al., 2020; Liu and Cheng, 2021).

To enhance the voltage of the point of common coupling (PCC) during faults, reactive power compensation devices (Kafshgari et al., 2019; Abulanwar et al., 2016; Bian et al., 2015), including capacitor reactors, on-load tap-changing transformers, and SVCs are employed. However, challenges persist, such as high construction and maintenance costs, insufficient dynamic reactive capacity during faults, and inadequate control strategies (Abulanwar et al., 2016). Consequently, active voltage support technology for wind farms has attracted considerable research (Hu et al., 2016; Ouyang et al., 2019).

Doubly fed induction generators (DFIGs), a pivotal model in the contemporary wind power generation industry, possess the capability to decouple active and reactive power outputs (Llrab et al., 2020; Liu and Cheng, 2021; Zhang et al., 2020). This characteristic makes DFIG-based wind turbines an important measure for improving the reactive power operational environment of wind farms (Ouyang et al., 2019; Yujun et al., 2018). A variable droop control scheme for reducing PCC voltage fluctuations is proposed in Li et al. (2018). While previous studies have optimized the reactive power injected into the grid by DFIG-based wind farms, the transient operational characteristics necessitate further exploration.

A two-stage voltage control method for wind farms with energy storage systems (ESSs) is proposed in Peng et al. (2024) to enhance the reactive power support capability of wind farms. However, due to the addition of ESSs, the construction cost of wind farms has increased, and the complexity of their transient characteristics will further increase. A wind farm power control strategy based on model predictive control was proposed by Zhao et al. (2017) and Zhang et al. (2023), which optimized the reactive power capacity of wind farms by adjusting the active power output. However, the coordinated control characteristics among multiple WTs have not been considered. Self-allocation strategies were introduced in Botong et al. (2023) for distributing reactive power output among multiple wind turbines (WTs) within a wind farm. Distributed voltage control architectures for wind farms were introduced by Ahmidi et al. (2012) to coordinate the reactive power output among multiple WTs. An optimization operation framework for WTs was proposed in Bhyri et al. (2024) to enhance the reactive power output capability of wind farms during fault crossing. However, the reactive power operating limitations of each WT were not considered in the these studies.

Additionally, a method was proposed in Dong et al. (2020) to enhance the resilience of turbines to voltage fluctuations by minimizing the imbalance in power generation among multiple WTs, while in Huang et al. (2020), voltage support was achieved by optimizing control parameters and compensating for delays in wind farm control systems. Coordinated sequence control based on multi-machine coordination and fault isolation has also been proposed to enhance the overall reactive support capability of wind farms (Zhang et al., 2019; Xiao and Heng, 2021). However, the above studies have not considered the various operational scenarios and constraints of wind farms, indicating that the applicability of their control systems requires further research (Tong et al., 2020; Cai et al., 2024; Zheng et al., 2020).

This paper proposes a novel coordinated control strategy for active transient voltage support in DFIG-based wind farms that aims to optimize the dynamic reactive power response characteristics of wind turbines and improve the voltage support capability of wind farms. The main contributions of this paper are as follows.

(1) A method for calculating the voltage sensitivity of DFIG-based wind farms utilizing arbitrary polynomial chaos (aPC) is presented which quantifies the impact of each WT on the voltage at the PCC.

(2) An operational constraint based on the short-circuit ratio is established, with the average value of reactive power taken into consideration, which could effectively prevent excess reactive power after fault clearance.

(3) An improved Q-learning based on voltage sensitivity (VS-Q) is innovated; based on this, a coordinated control strategy for active transient voltage support in DFIG-based wind farms is proposed to effectively improve the voltage level of wind-connected power systems during grid faults.

2 Voltage support characteristics and operational constraints of DFIG-based wind farms under grid faults

2.1 Reactive power support capacity of DFIG-based wind farms

When a wind farm implements voltage support, its available reactive power capacity is obtained by adding the reactive power output from the wind turbines. The total available reactive power capacity under current operating conditions, Q_ARC, and the sum of reactive power capacity increase due to reduced active power output, Q_IRC, can be expressed by Equation 1.

$\begin{array}{l}{Q}_{RPC}=\underset{Q_{ARC}}{\underbrace{{\displaystyle \sum _{g=1}^G}{Q}_{gref\_AR}+{\displaystyle \sum _{h=1}^H}{Q}_{href\_RL}}}+\underset{Q_{IRC}}{\underbrace{{\displaystyle \sum _{k=1}^K}{Q}_{kref\_SA}-Q_{loss}},}\\ G+H\le N,K\le N\end{array}(1)$

where $Q_{RPC}$ is the reactive power support capability of a wind farm, $Q_{gref\_AR}$ is the reference value for the reactive power output of the g^th WT under current operating conditions, $Q_{href\_RL}$ is the reactive power limit of the WT, $Q_{kref\_SA}$ is the reactive power added when the WT reduces its active power, and $Q_{loss}$ is the reactive power loss of the wind farm. G represents the number of WTs that have implemented the active voltage support but have not yet reached the reactive power output limit. Under the same operating condition, the number of WTs that have reached the reactive power limit is H. K denotes the number of WTs that reduce the active power to increase the reactive power output, and N is the total number of WTs in the wind farm.

The reactive power support capability of DFIG-based wind farms is determined by the reactive capacity of WTs. During the implementation of voltage support, the use of available reactive power capacity should be prioritized by a wind farm to prevent WTs from operating under extreme conditions.

2.2 Voltage sensitivity of a wind farm based on aPC

The key to achieving active voltage support for a wind farm is to adjust the reactive power output of each WT reasonably and accurately based on the impact of the WTs on the PCC voltage, which can achieve optimal control effects. The physical significance of voltage sensitivity can be defined as the influence exerted on the PCC voltage by the reactive power output of a WT within a wind farm. Therefore, the voltage sensitivity of wind farms can be utilized as a predetermined basis for determining the coordinated control parameters of the active voltage support. The aPC utilizes orthogonal polynomial expansion to assess the dependence of model outputs on parameters, enabling the calculation of voltage sensitivity. Thus, the weighted sum of multivariate orthogonal polynomial bases can be used to represent the degree to which the PCC voltage of a wind farm is affected by the reactive power output of the WTs. The voltage response variation at the PCC can be approximated by the following polynomial representation:

$\Upsilon \left(\mathbf{x},t;\mathit{\omega }\right)\approx {\displaystyle \sum _{j=0}^M}{c}_j\left(\mathbf{x},t\right){\mathit{\Psi }}_j\left(\mathit{\omega }\right),(2)$

where: $\mathit{\omega }$ is the input of the model, representing the reactive power generated by the wind farm comprising multiple WTs; $\Upsilon$ is the output of the model, representing the transient voltage response of the PCC; M is the number of polynomials, and its value depends on the number of wind turbines N and the polynomial order d; $c_j$ is a polynomial coefficient used to quantify the dependence of the model output $\Upsilon$ on the input parameter $\mathit{\omega }$ for each expected point in space $\mathbf{x}$ at time t. The simplified representation of the multivariate orthogonal polynomial basis of $\mathit{\omega }$ is $\mathit{\Psi }$, which can be further expressed by Equations 3, 4.

${\mathit{\Psi }}_k\left(\mathit{\omega }\right)={\displaystyle \prod _{j=1}^N}{H}_j^{\left({\alpha }_j^r\right)}\left({\omega }_j\right),{\displaystyle \sum _{j=1}^N}{\alpha }_j^r\le \mathrm{M},r=1,...,N,(3)$

$\left[\begin{array}{cccc}{\mu }_{0,j}& {\mu }_{1,j}& \cdots & {\mu }_{k,j}\\ {\mu }_{1,j}& {\mu }_{2,j}& \cdots & {\mu }_{k+1,j}\\ ⋮& ⋮& \ddots & ⋮\\ {\mu }_{k-1,j}& {\mu }_{k,j}& \cdots & {\mu }_{2k-1,j}\\ 0& 0& \cdots & 1\end{array}\right]\left[\begin{array}{l}{H}_{0,j}^{\left(k\right)}\\ H_{1,j}^{\left(k\right)}\\ \cdots \\ H_{k-1,j}^{\left(k\right)}\\ H_{k,j}^{\left(k\right)}\end{array}\right]=\left[\begin{array}{l}0\\ 0\\ \cdots \\ 0\\ 1\end{array}\right],(4)$

where $H_j$ is an orthogonal basis parameter, ${\alpha }_j^r$ is a multivariate index that contains the combination information of all possible products of a univariate polynomial, and the index α is an M × N matrix. ${\mu }_{i,j}$ is the i^th original statistical moment of the variable ${\omega }_i$.

The coefficient $c_j$ is further evaluated in Equation 2. The formula configuration focuses on the voltage change at PCC when the reactive power output of the WT changes, and satisfies the linear equation system shown by Equation 5.

${\mathbf{M}}_{\mathrm{\Psi }}\left(\mathit{\omega }\right){\mathbf{V}}_c\left(\mathbf{x},t\right)={\mathbf{V}}_{\Upsilon }\left(\mathbf{x},t;\mathit{\omega }\right),(5)$

where ${\mathbf{V}}_c$ is an M × 1 vector of coefficient $c_j$.The vector ${\mathbf{V}}_{\Upsilon }$ contains the model output for each configuration point. The M × N matrix ${\mathbf{M}}_{\mathrm{\Psi }}$ contains polynomials evaluated at the configuration points.

Based on aPC, the analysis of voltage sensitivity in multiple WTs allows the response variation of the PCC voltage to be expressed on a normalized polynomial basis. Its mean ${\mu }_{\mathrm{\Omega }}$ and variance ${\sigma }_{\mathrm{\Omega }}^2$ can be represented by Equation 6. The Sobol index for sensitivity analysis can be derived from Equations 7–9. The multi-parameter reactive voltage weighted global sensitivity index within the wind farm is expressed as Equation 10, reflecting the impact of reactive power output from multiple WTs on the PCC voltage.

${\mu }_{\mathrm{\Omega }}=c_0,{\sigma }_{\mathrm{\Omega }}^2={\displaystyle \sum _{j=1}^M}{c}_j^2,(6)$

$S_{i_1,...,i_s}=\frac{{\sum }_{j=1}^M{\chi }_j{c}_j^2}{{\sum }_{j=1}^M{c}_j^2},(7)$

$S_j^T={\displaystyle \sum _{\left(i_1,,,i_s\right);j\in \left(i_1,,,i_s\right)}}{S}_{i_1,,,i_s},(8)$

${\chi }_j=\left\{\begin{array}{l}1,\text{if\hspace{0.5em}}{\alpha }_j^k>0,\forall j\in \left(i_1,,,i_s\right)\\ 0,\text{if\hspace{0.5em}}{\alpha }_j^k=0,\forall j\in \left(i_1,,,i_s\right)\end{array}\right.,(9)$

$S_{{\omega }_j}^2={\displaystyle \sum _{k=0}^M}{c}_k^2{\displaystyle \sum _{i=0}^{{\alpha }_j^k-1}}{\left[b_i^{\left({\alpha }_j^k-1\right)}\right]}^2{P}_j^{\left(i\right)}\left({\omega }_j\right),(10)$

where $S_{i_1,...,i_s}$ is the Sobol index, which represents the contribution of variable ${\omega }_i$ to the total variance of the output space $\Upsilon$ , and $S_j^T$ summarizes all Sobol indices of variable ${\omega }_i$. Formula 10 reflects the impact of reactive power output of multiple WTs within the wind farm on PCC voltage and can be used as a measure of voltage sensitivity in wind farms.

2.3 Active support operation constraint of wind farms based on the average short-circuit ratio of reactive power

The reactive power output from wind farms may cause grid overvoltage after a fault is cleared. Therefore, it is essential to determine the maximum acceptable reactive power output of a wind farm under any grid disturbance. Constraints for voltage support and coordinated control can be defined based on the short-circuit ratio to prevent overvoltage issues in the power system with wind farms. The equivalent circuit of the power system with wind farms is shown in Figure 1.

Figure 1

Figure 1. Grid-connected equivalent circuit of the DFIG-farm.

Assuming that the DFIG operates at a constant power factor, the output power at the PCC can be expressed as Equation 11. The equivalent voltage at the PCC can be represented as Equation 12. After the grid fault cleared, the WTs gradually restore active output, at which point the output power at the PCC can be expressed as Equation 13, and the equivalent voltage of the PCC is represented as Equation 14.

$\left\{\begin{array}{l}{P}_{\text{wg}}={\displaystyle \sum _{i=1}^N}{P}_{\mathrm{c}i}-P_{\text{load}}\\ Q_{\text{wg}}=Q_{\text{rl}}=Q_{\mathrm{r}}-Q_{\text{load}},\end{array}\right.(11)$

$U_{\text{pcc}}=\sqrt{{\left(U_{\mathrm{e}}+\frac{Q_{\text{wg}}{X}_{\mathrm{e}}}{U_{\mathrm{e}}}\right)}^2+{\left(\frac{P_{\text{wg}}{X}_{\mathrm{e}}}{U_{\mathrm{e}}}\right)}^2,}(12)$

$\left\{\begin{array}{l}{P}_{\text{wg}}^{″}={\displaystyle \sum _{i=1}^N}{P}_{\mathrm{c}i}-P_{\text{load}}-{\displaystyle \sum _{i=1}^N}\Delta P_{\mathrm{c}i}+{\displaystyle \sum _{i=1}^N}\Delta P_{\mathrm{c}i}^{\prime }=P_{\text{wg}}-\Delta P_{\mathrm{w}}+\Delta P_{\mathrm{w}}^{\prime }\\ Q_{\text{wg}}^{″}=Q_{\mathrm{r}}^{″}-Q_{\text{load}}+{\displaystyle \sum _{i=1}^N}\Delta Q_{\mathrm{c}i}-{\displaystyle \sum _{i=1}^N}\Delta Q_{\mathrm{c}i}^{\prime }=Q_{\text{rl}}^{″}+\Delta Q_{\mathrm{w}}-\Delta Q_{\mathrm{w}}^{\prime }\end{array}\right.,(13)$

$U_{\text{pcc}}^{″}=\sqrt{{\left(U_{\mathrm{e}}^{″}+\frac{Q_{\text{rl}}^{″}{X}_{\mathrm{e}}}{U_{\mathrm{e}}^{″}}+\frac{\Delta Q_{\mathrm{w}}{X}_{\mathrm{e}}}{U_{\mathrm{e}}^{″}}-\frac{\Delta Q_{\mathrm{w}}^{\prime }{X}_{\mathrm{e}}}{U_{\mathrm{e}}^{″}}\right)}^2+{\left(\frac{P_{\text{wg}}{X}_{\mathrm{e}}}{U_{\mathrm{e}}^{″}}-\frac{\Delta P_{\mathrm{w}}{X}_{\mathrm{e}}}{U_{\mathrm{e}}^{″}}+\frac{\Delta P_{\mathrm{w}}^{\prime }{X}_{\mathrm{e}}}{U_{\mathrm{e}}^{″}}\right)}^2,}(14)$

where $P_{\text{wg}}$ and $Q_{\text{wg}}$ are the active and reactive power outputs of the wind farm, respectively. $Q_{\mathrm{r}}$ is the reactive power output by the reactive power compensation device, and Q_load is the reactive load at the PCC. $X_{\mathrm{e}}$ is the equivalent reactance of the connected system. $Q_{\mathrm{r}}^{″}$ is the output reactive power of the reactive power compensation device after the fault cleared. $\Delta P_{\mathrm{c}i}^{\prime }$ and $\Delta Q_{\mathrm{c}i}^{\prime }$ represent the changes in active and reactive power output of the i^th WT after the fault cleared, respectively. At this time, the active and reactive power recovery values of the wind farm are $\Delta P_{\mathrm{w}}^{\prime }$ and $\Delta Q_{\mathrm{w}}^{\prime }$, respectively. $U_{pcc}^{″}$ is the equivalent potential of the PCC after the fault cleared.

The steady-state operating voltage of the system is defined as 1p.u. If the constant component influence of the equivalent potential at the PCC is ignored and $X_{\mathrm{e}}=U_{\mathrm{e}}^2/S_{\text{cg}}$, the equivalent potential can be expressed as Equation 15.

$U_{\text{pcc}}^{″}=1+\frac{Q_{\text{rl}}^{″}}{S_{\text{cg}}}+\frac{{\sum }_{i=1}^N\Delta Q_{\mathrm{c}i}}{S_{\text{cg}}},(15)$

where $S_{\text{cg}}$ is the short-circuit capacity of the power system connected by the wind farm. To avoid overvoltage issues in the power system after fault clearance, the average reactive power output of all WTs in the wind farm at the moment of fault clearance is defined as Equation 16. Consequently, the operational constraint for voltage support coordination in the wind farm should satisfy Equation 17, which considers the reactive power characteristics of the wind farm. The proposed operational constraint enables a more precise evaluation of voltage support capability during the operation of multiple WTs, which can guide the allocation of reactive power output under grid faults. E_SCR

$Q_{\text{eve}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\Delta Q_{\mathrm{c}i,}(16)$

$E_{\text{SCR}}>\frac{N{S}_{\text{cg}}}{0.3S_{\text{cg}}-Q_{\text{rl}}^{″.}}(17)$

3 Coordinating the control of the overall structure

The issue of active voltage support in multiple WT DFIG-based wind farms can be described as coordinating the reactive power output of each WT based on their operational differences, aiming to maximize the wind farm’s reactive support capability. The voltage support problem under coordinated control in such wind farms exhibits Markov properties, which can be represented in the tuple Equation 18.

$\mathit{\chi }=\left[\mathit{S},\mathit{A},\mathit{T}\right],(18)$

where: $\mathit{S}$ is the state space of the power system connected by wind farms, represented as $\mathit{S}=\left[{\mathit{s}}_0,{\mathit{s}}_1,{\mathit{s}}_2,...,{\mathit{s}}_x\right]$; $\mathit{A}$ is the operation space of multiple WTs in the wind farm, which can be represented as $\mathit{A}=\left[{\mathit{A}}_0,{\mathit{A}}_1,{\mathit{A}}_2,...,{\mathit{A}}_x\right]$; $\mathit{T}$ is the probability of state transition.

Because of the Markov property, the voltage support issue in multiple WT DFIG-based wind farms can be solved through Q-learning for coordinated reactive power control under grid faults. The coordination control framework based on VS-Q is shown in Figure 2. Based on VS-Q, a coordinated control strategy for the transient voltage active support of DFIG-based wind farms is proposed, wherein the voltage sensitivity is utilized to characterize the impact of each WT on the PCC voltage and the reactive power output scheme of the wind farm is determined based on Q-learning to enhance the ability of wind farms to participate in power system voltage regulation.

Figure 2

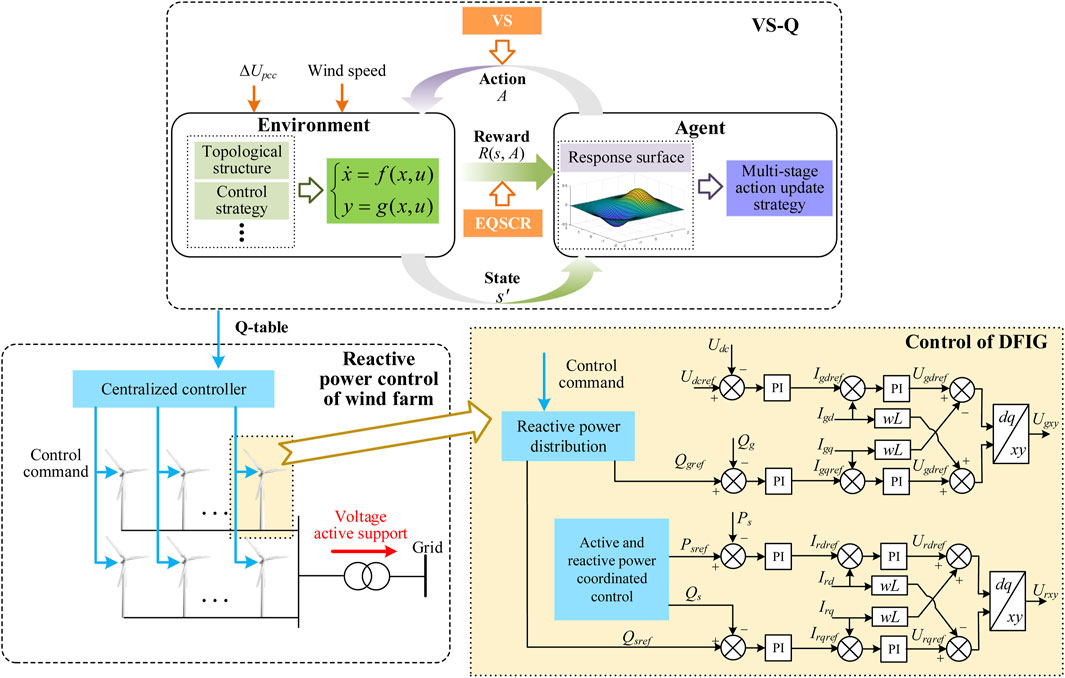
Figure 2. An overall coordinated control framework for transient voltage active support in DFIG-based wind farms based on VS-Q.

4 Coordination control strategy for voltage support in DFIG-based wind farms based on VS-Q

The coordination control of active voltage support in multiple WT DFIG-based wind farms exhibits Markov properties. Reinforcement learning can effectively derive decision-making strategies among multiple WTs. Therefore, an improved Q-learning method based on voltage sensitivity is proposed to achieve active voltage support for wind farms. The state set of VS-Q is represented as Equation 19, and the action set is represented as Equation 20. The reward function is crucial for an agent’s assessment of actions, fundamentally shaping its decision-making logic (Equation 21).

$\begin{array}{l}{\mathit{s}}_x=[{\mathit{P}}_{\mathrm{c}x},{\mathit{Q}}_{\mathrm{c}x},{\mathit{U}}_{\mathrm{c}x},{\mathit{U}}_{\text{PCC}x}|{\mathit{P}}_{\mathrm{c}x}=[P_{1x},P_{2x},...,P_{Nx}],\\ {\mathit{Q}}_{\mathrm{c}x}=[Q_{1x},Q_{2x},...,Q_{Nx}],{\mathit{U}}_{\mathrm{c}x}=[U_{1x},U_{2x},...,U_{Nx}]],\\ x=1,2,3....\end{array}(19)$

$\begin{array}{l}{\mathit{A}}_x=\left[a_1,a_2,...,a_N\right]\\ a_{1,2,...,N}\in \left[Q_{{\mathrm{c}}_0}^{\text{ref}},Q_{{\mathrm{c}}_{\text{AR}}}^{\text{ref}},Q_{{\mathrm{c}}_{\text{RL}}}^{\text{ref}},Q_{{\mathrm{c}}_{\text{SA}}}^{\text{ref}}\right],\end{array}(20)$

$R=\left\{\begin{array}{l}{\lambda }_{\text{pun}}{\displaystyle \sum _{i=1}^N}\frac{E_{\text{SCR}}-\frac{S_{\text{cg}}}{\Delta Q_{\mathrm{c}i}}}{E_{\text{SCR}}}{\mathit{s}}_x\notin {\mathit{S}}_{\text{con},}\\ \Delta U_{\text{PCC}}·{\lambda }_{\text{rew}}{\mathit{s}}_x\in {\mathit{S}}_{\text{con}}\end{array}\right.(21)$

where x is the environmental state number of the wind farm connected system and each state set constitutes the state space S of the environment. $Q_{\mathrm{c}\_0}^{\text{ref}}$ is the current action taken by the WT to maintain the existing reactive power output. $Q_{\mathrm{c}\_\text{AR}}^{\text{ref}}$ represents the reactive power output action taken by the WT. $Q_{\mathrm{c}\_\text{RL}}^{\text{ref}}$ is the action taken by the WT to output the reactive power limit. $Q_{\mathrm{c}\_\text{SA}}^{\text{ref}}$ is the action to reduce the active power and increase the reactive power for the WT. ${\lambda }_{\text{pun}}$ is the penalty coefficient, and ${\lambda }_{\text{rew}}$ is the reward coefficient. ${\mathit{S}}_{\text{con}}$ is the feasible state space, which is the set of system states that satisfy constraints.

To maximize voltage support at the PCC using a limited number of WTs, a multiple WT active voltage support coordination control based on VS-Q is proposed. This control utilizes a multi-stage action updating strategy for intelligent agents, allowing for the adjustment of individual output power and the coordination of reactive power among multiple machines. In the element selection phase of the strategy, the action transfer probabilities based on voltage sensitivity are represented as Equation 22. The element selection strategy is expressed as Equation 23, and the action updating strategy is represented as Equation 24. After the agent takes an action, the expected return of the system state can be expressed as Equation 25.

$P_{ai}=\left\{\begin{array}{l}\frac{S_{\omega 1}}{{\sum }_{k=1}^N{S}_{\omega k}}i=1\\ P_{ai-1}+\frac{S_{\omega i}}{{\sum }_{k=1}^N{S}_{\omega k}}i=2,...,N,\end{array}\right.(22)$

${\mathrm{\Pi }}_A=\left\{\begin{array}{l}{f}_c\left(a_1\right|\alpha \in \left.\left(0,1\right]\right)\\ f_c\left(a_i\left|\alpha \in \left[P_{ai-1},P_{ai}\right]\right.\right)\end{array}\right.i=2,...,N\alpha =rand\left(0,1\right],(23)$

$a_i=\left\{\begin{array}{l}{Q}_{\mathrm{c}\_l+1}^{\text{ref}}\beta \in (0,1-\gamma ],l=0,1,2\\ Q_{\mathrm{c}\_l}^{\text{ref}}\beta \in (\gamma ,1],l=3\end{array}\right.\beta =rand(0,1],(24)$

where $f_c$ is the action element selection function used to select elements that meet the requirements. $Q_{\mathrm{c}\_l}^{\text{ref}}$ is the current action value of the selected element by the intelligent agent. $\gamma$ is the action update factor used to achieve a balance between agent development and deep learning. $Q_{\mathrm{c}\_1}^{\text{ref}}$. $Q_{\mathrm{c}\_2}^{\text{ref}}$, and $Q_{\mathrm{c}\_3}^{\text{ref}}$ correspond to $Q_{\mathrm{c}\_\text{AR}}^{\text{ref}}$, $Q_{\mathrm{c}\_\text{RL}}^{\text{ref}}$, and $Q_{\mathrm{c}\_\text{SA}}^{\text{ref}}$ in the action set, respectively. The probability of the system transitioning from current state s to next state ${\mathit{s}}^{\prime }$ at the moment when the intelligent agent takes action A can be expressed as $T\left(\mathit{s},\mathit{A},{\mathit{s}}^{\prime }\right)$. At this point, the expected return of system state s can be expressed as:

$V\left(\mathit{s}\right)=R\left(\mathit{s}\right)+\underset{\mathit{A}}{\max }\zeta {\displaystyle \sum _{{\mathit{s}}^{\prime }}}T\left(\mathit{s},\mathit{A},{\mathit{s}}^{\prime }\right)V\left({\mathit{s}}^{\prime }\right),(25)$

where $\zeta$ is the discount factor that satisfies $\zeta \in \left[0,1\right]$, representing the impact of future rewards on current rewards. The goal of VS-Q is to find the optimal strategy (Equation 26). The update of the expected return for state transitions is represented as Equation 27. Finally, the optimal strategy is obtained in Equation 28.

${\mathrm{\Pi }}^{*}\left(\mathit{s}\right)=\arg \underset{\mathit{A}}{\max }{\displaystyle \sum _{{\mathit{s}}^{\prime }}}T\left(\mathit{s},\mathit{A},{\mathit{s}}^{\prime }\right)V^{*}\left({\mathit{s}}^{\prime }\right),(26)$

$V^{\mathrm{\Pi }}\left(\mathit{s}\right)=V^{\mathrm{\Pi }}\left(\mathit{s}\right)+\mu \left(R\left(\mathit{s}\right)+\zeta V^{\mathrm{\Pi }}\left({\mathit{s}}^{\prime }\right)-V^{\mathrm{\Pi }}\left(\mathit{s}\right)\right),(27)$

$Q\left(\mathit{s},\mathit{A}\right)\leftarrow Q\left(\mathit{s},\mathit{A}\right)+\mu \left[R\left(\mathit{s}\right)+\zeta \underset{\mathit{A}}{\max }Q\left({\mathit{s}}^{\prime },\mathit{A}\right)-Q\left(\mathit{s},\mathit{A}\right)\right].(28)$

Figure 3 shows the implementation process of voltage active support coordination control for a multiple WT DFIG-based wind farm based on voltage sensitivity and improved Q-learning.

Figure 3

Figure 3. Flowchart of the coordinated control strategy.

5 Simulation

This section calculates the voltage sensitivity of a multiple WT DFIG-based wind farm using MATLAB and develops a detailed electromagnetic transient model of the wind farm using PSCAD. The topology of the wind farm is shown in Figure 4. Each WT has a rated capacity of 2 MW, and the wind farm accounts for 42.7% of the total installed capacity of the system.

Figure 4

Figure 4. Simulation model.

First, set node 14 of the wind power grid connection system to experience a three-phase grounding fault at 12 s, lasting for 0.2 s. The statistical parameters of the aPC coefficient, namely the mean and standard deviation, are shown in Figure 5. Considering only the WT with the maximum operational difference, the results are shown in Figure 6. It can be seen that the output reactive power of the random group increases, and the voltage at the connection point shows an upward trend, indicating that the wind turbines significantly enhance the reactive power support of the grid connection system.

Figure 5

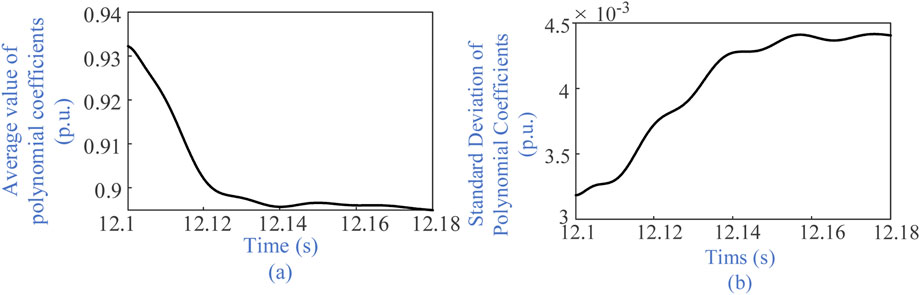
Figure 5. Statistical parameters of reactive power output from wind farms. (a) The average value of polynomial coefficients and (b) The standard deviation of polynomial coefficients.

Figure 6

Figure 6. Voltage response surface of the PCC under grid fault based on dual parameters.

The voltage sensitivity of the wind farm is illustrated in Figure 7. As shown, there are significant differences in voltage sensitivity among the WTs due to factors such as geographical environment, operating wind speed, and the topology structure of the wind farm.

Figure 7

Figure 7. Voltage sensitivity of DFIG-based wind farms based on aPC.

At node 14 of the wind power grid connection system, a three-phase ground fault occurred at 12 s, lasting 0.2 s. The voltage responses at the PCC under various controls (Fortmann et al., 2008; Kim et al., 2016) are shown in Figure 8, while the active and reactive power outputs of the wind farm are depicted in Figure 9. Figures 9–13 compares the active and reactive power output of different WTs in the wind farm under the proposed control and existing control (Fortmann et al., 2008; Kim et al., 2016). The proposed VS-Q enhances the reactive power output level of the wind farm, raising the average voltage at the grid connection point during the fault from 0.906 p. u. to 0.9357 p. u., and increasing the reactive power injected into the grid from 0.0106 p.u. to 1.5176 p. u.

Figure 8

Figure 8. Voltage response waveform of a DFIG-based wind farm (PCC voltage drops by 0.1 p. u.).

Figure 9

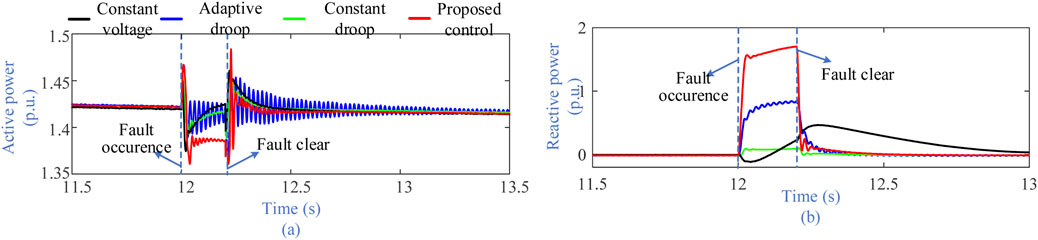
Figure 9. Output power waveform of a DFIG-based wind farm (PCC voltage drops by 0.1 p. u.). (a) active power of the WT and (b) is reactive power of the WT.

We introduce the increase rate of PCC voltage to characterize the control effect of different controls on the PCC voltage, specifically expressed as

$\rho =\frac{U_{\text{PCC}\_C}^{\text{eve}}-U_{\text{PCC}\_u}^{\text{eve}}}{U_{\text{PCC}\_u}^{\text{eve}}}\times 100\%,(29)$

where $U_{\text{PCC}\_u}^{\text{eve}}$ and $U_{\text{PCC}\_C}^{\text{eve}}$ are the PCC voltages under the constant voltage control and the other control effects, respectively. During the fault period, the increase rates of PCC voltage by the constant droop control, the adaptive droop control, and the proposed control were 0.33%, 1.51%, and 3.38%, respectively. The proposed control can adjust the reactive power output of WTs according to the actual operational state while avoiding the power oscillation caused by the adaptive droop control.

To further validate the proposed control, the output active and reactive power of WTs 3, 5, 8, and 12 during the fault period were extracted, with their power waveforms shown in Figures 10–13. The figures indicate that, compared to the other three controls, the proposed control can output more reactive power during grid faults and provide voltage support to the grid.

Figure 10

Figure 10. Waveform of WT 3. (a) active power of the WT and (b) is reactive power of the WT.

Figure 11

Figure 11. Waveform of WT 5. (a) active power of the WT and (b) is reactive power of the WT.

Figure 12

Figure 12. Waveform of WT 8. (a) active power of the WT and (b) is reactive power of the WT.

Figure 13

Figure 13. Waveform of WT 12. (a) active power of the WT and (b) is reactive power of the WT.

To further verify the control effect of the proposed control under different fault levels, a three-phase ground fault occurred at node 16, with a fault duration of 0.2 s. The voltage responses at the PCC under various control are shown in The voltage responses at the PCC under various control are shown in Figure 14, while the active and reactive power outputs under various controls (Proposed control; Fortmann et al., 2008; Kim et al., 2016) of the wind farm are depicted in Figure 15.

Figure 14

Figure 14. Voltage response waveform of a DFIG-based wind farm (PCC voltage drops by 0.45 p. u.).

Figure 15

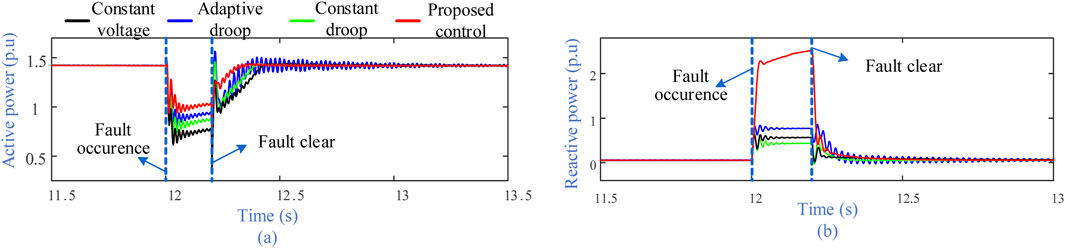
Figure 15. Output power waveform of a DFIG-based wind farm (PCC voltage drops by 0.45 p. u.). (a) active power of the WT and (b) is reactive power of the WT.

The calculation results show that the proposed control increases the average voltage of PCC during the fault from 0.454 to 0.4836 p. u. and increases the reactive power injected into the grid from 0.5442 to 2.2428 p. u. The increase rates of PCC voltage by the constant droop control, the adaptive droop control, and the proposed control were 1.41%, 3.47%, and 6.13%, respectively. The proposed control achieves active voltage support of the wind farm for the connected system.

6 Conclusion

This study has discussed the voltage support characteristics of multiple WT DFIG-based wind farms under grid faults. It proposes a method for calculating voltage sensitivity based on aPC and an active support operational constraint based on the average short-circuit ratio. Additionally, a coordination control for active voltage support based on VS-Q is proposed. Key conclusions include the following.

1. The aPC-based voltage sensitivity reflects the impact of each WT on the PCC voltage.

2. The active support constraint accounts for reactive power output and grid strength, preventing transient overvoltage after fault clearance.

3. VS-Q coordination control optimizes voltage support using sensitivity as a directive, enabling intelligent coordination of reactive power among turbines during grid faults, thereby enhancing transient voltage stability.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

SoY: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, writing–review and editing. LY: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. ZY: data curation, formal analysis, investigation, methodology, project administration, software, validation, and writing–review and editing. ZS: conceptualization, investigation, methodology, project administration, resources, software, and writing–review and editing. WX: conceptualization, data curation, investigation, methodology, software, validation, and writing–review and editing. LF: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, and writing–review and editing. SuY: data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by Science and Technology Project of State Grid Sichuan Electric Power Company (521996230009).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from State Grid Sichuan Electric Power Company. The funder had the following involvement in the study design, collection, analysis, interpretation of data, the decision to submit it for publication.

Generative AI statement

The authors declare that no generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2025.1566923/full#supplementary-material

References

Abulanwar, S., Hu, W., Chen, Z., and Iov, F. (2016). Adaptive voltage control strategy for variable-speed wind turbine connected to a weak network. IET Renew. Power Gener. 10, 238–249. doi:10.1049/iet-rpg.2015.0239

CrossRef Full Text | Google Scholar

Ahmidi, A., Guillaud, X., Besanger, Y., and Blanc, R. (2012). A multilevel approach for optimal participating of wind farms at reactive power balancing in transmission power system. IEEE Syst. J. 6 (02), 260–269. doi:10.1109/jsyst.2011.2163003

CrossRef Full Text | Google Scholar

Bhyri, A. K., Senroy, N., and Saha, T. K. (2024). Enhancing the grid support from dfig-based wind farms during voltage events. IEEE Trans. Power Syst. 39 (1), 733–744. doi:10.1109/tpwrs.2023.3239503

CrossRef Full Text | Google Scholar

Bian, X. Y., Geng, Y., Lo, K. L., Fu, Y., and Zhou, Q. B. (2015). Coordination of PSSs and SVC damping controller to improve probabilistic small-signal stability of power system with wind farm integration. IEEE Trans. Power Syst. 31, 2371–2382. doi:10.1109/tpwrs.2015.2458980

CrossRef Full Text | Google Scholar

Botong, L. I., Dingchuan, ZHENG, Bin, L. I., Jiao, X., Hong, Q., and Ji, L. (2023). Analysis of low voltage ride-through capability and optimal control strategy of doubly-fed wind farms under symmetrical fault. Prot. Control Mod. Power Syst. 8 (1), 36. doi:10.1186/s41601-023-00310-0

CrossRef Full Text | Google Scholar

Cai, Z., Huang, S., Wu, Q., Tai, N., Huang, W., Huang, S., et al. (2024). Nonlinear hybrid flatness control for suppressing overcurrent of DFIG during high voltage ride through. Electr. Power Syst. Res. 229 (Apr), 1.1–1.11. doi:10.1016/j.epsr.2024.110190

CrossRef Full Text | Google Scholar

Chengmao, D. U., Xiong, D. U., Tong, C., Li, Y., and Zhou, P. (2023). Stability analysis for DFIG-based wind farm grid-connected system under all wind speed conditions. IEEE Trans. Industry Appl. 59 (2 Pt.2), 2430–2445. doi:10.1109/TIA.2022.3218022

CrossRef Full Text | Google Scholar

Dong, Z., Li, Z., Du, L., Liu, Y., and Ding, Z. (2020). Coordination strategy of large-scale DFIG-based wind farm for voltage support with high converter capacity utilization. IEEE Trans. Sustain. Energy 12 (02), 1416–1425. doi:10.1109/tste.2020.3047273

CrossRef Full Text | Google Scholar

Fortmann, J., Wilch, Koch, F. and M., and Erlich, I. (2008). A novel centralised wind farm controller utilising voltage control capability of wind turbines. Fifth Power Syst. Comput. Conf.

Google Scholar

Global Wind Energy Council (2020). Global wind report 2019. Brussels, Belgium: Global Wind Energy Council. Available online at: https://gwec.net/global-wind-report-2019/ (Accessed on December 07, 2021).

Google Scholar

Global Wind Energy Council (2022). Brussels, Belgium, Global wind report. Available online at: https://gwec.net/global-wind-report-2022/ (Accessed on October 26, 2024).

Google Scholar

Hu, W., Abulanwar, S., Iov, F., and Chen, Z. (2016). Adaptive voltage control strategy for variable-speed wind turbine connected to a weak network. IET Renew. Power Gener. 10 (02), 238–249. doi:10.1049/iet-rpg.2015.0239

CrossRef Full Text | Google Scholar

Huang, S., Wu, Q., Guo, Y., and Rong, F. (2020). Hierarchical active power control of DFIG-based wind farm with distributed energy storage systems based on ADMM. IEEE Trans. Sustain. Energy 11 (02), 1528–1538. doi:10.1109/tste.2019.2929820

CrossRef Full Text | Google Scholar

Kafshgari, N. A., Ramezani, N., and Nouri, H. (2019). Effects of high frequency modeling and grounding system parameters on transient recovery voltage across vacuum circuit breakers for capacitor switching in wind power plants. Int. J. Electr. Power Energy Syst. 104, 159–168. doi:10.1016/j.ijepes.2018.06.046

CrossRef Full Text | Google Scholar

Kim, J., Seok, J., Muljadi, E., and Kang, Y. C. (2016). Adaptive Q-V scheme for the voltage control of a DFIG-based wind power plant. IEEE Trans. Power Electron. 31 (05), 3586–3599. doi:10.1109/tpel.2015.2464715

CrossRef Full Text | Google Scholar

Li, Y., Xu, Z., Zhang, J., and Meng, K. (2018). Variable droop voltage control for wind farm. IEEE Trans. Sustain. Energy 9 (1), 491–493. doi:10.1109/tste.2017.2726355

CrossRef Full Text | Google Scholar

Liu, J.-H., and Cheng, J.-S. (2021). Online voltage security enhancement using voltage sensitivity-based coherent reactive power control in multi-area wind power generation systems. IEEE Trans. Power Syst. 36, 2729–2732. doi:10.1109/tpwrs.2021.3053139

CrossRef Full Text | Google Scholar

Liu, Y., Lin, Z., Li, M., and Wu, Q. H. (2020). On the state-dependent switched energy functions of DFIG-based wind power generation systems. CSEE J. Power Energy Syst. 6, 318–328.

Google Scholar

Llrab, C., Oacv, B., Ercd, C., Jmg, D., and Ajsf, C. (2020). Generalized Predictive Control applied to the DFIG power control using state-space model and voltage constraints. Electr. Power Syst. Res. 182, 106227. doi:10.1016/j.epsr.2020.106227

CrossRef Full Text | Google Scholar

Mathis, WILLIAM (2023(). UK will speed up grid connections to boost clean power capacity. Environ. and Energy Rep., 121–122.

Google Scholar

Ouyang, J., Tang, T., Yao, J., and Li, M. (2019). Active voltage control for DFIG-based wind farm integrated power system by coordinating active and reactive powers under wind speed variations. IEEE Trans. Energy Convers. 34 (03), 1504–1511. doi:10.1109/tec.2019.2905673

CrossRef Full Text | Google Scholar

Peng, H., Huang, S., Wei, J., Wei, C., Wu, Q., Shen, F., et al. (2024). Two-stage decentralized optimal voltage control in wind farms with hybrid ESSs. IEEE Trans. Power Syst. 39 (5), 6552–6565. doi:10.1109/tpwrs.2024.3360451

CrossRef Full Text | Google Scholar

Tong, N., Lin, X., Li, Z., Fang, J., Zhuo, Y., Sui, Q., et al. (2020). Coordinated sequential control of individual generators for large-scale DFIG-based wind farms. IEEE Trans. Sustain. Energy 11 (03), 1679–1692. doi:10.1109/tste.2019.2936757

CrossRef Full Text | Google Scholar

Xiao, J. I. N., and Heng, NIAN (2021). Overvoltage suppression strategy for sending AC grid with high penetration of wind power in the LCC-HVDC system under commutation failure. IEEE Trans. Power Electron. 36 (9), 10265–10277. doi:10.1109/tpel.2021.3066641

CrossRef Full Text | Google Scholar

Yujun, L. I., Zhao, X. U., Zhang, J., and Meng, K. (2018). Variable droop voltage control for wind farm. IEEE Trans. Sustain. Energy 9 (1), 491–493. doi:10.1109/tste.2017.2726355

CrossRef Full Text | Google Scholar

Zhang, K., Geng, G., and Jiang, Q. (2020). Online tracking of reactive power reserve for wind farms. IEEE Trans. Sustain. Energy 11 (02), 1100–1102. doi:10.1109/tste.2019.2929673

CrossRef Full Text | Google Scholar

Zhang, Y., Kou, P., Zhang, Z., Li, H., Li, X., and Liang, D. (2023). Coordinated frequency and voltage optimal control of wind farm with nonlinear power constraints. IEEE Syst. J. 17 (3), 4934–4945. doi:10.1109/jsyst.2023.3273569

CrossRef Full Text | Google Scholar

Zhang, H., Gruson, F., Rodriguez, D. M. F., and Saudemont, C. (2019). Overvoltage limitation method of an offshore wind farm with DC series-parallel collection grid. IEEE Trans. Sustain. Energy 10 (1), 204–213. doi:10.1109/tste.2018.2829929

CrossRef Full Text | Google Scholar

Zhao, H., Wu, Q., Wang, J., Liu, Z., Shahidehpour, M., and Xue, Y. (2017). Combined active and reactive power control of wind farms based on model predictive control. IEEE Trans. Energy Convers. 32 (3), 1177–1187. doi:10.1109/tec.2017.2654271

CrossRef Full Text | Google Scholar

Zheng, Z., Wang, Y., Xiao, X., Huang, C., Xie, Q., et al. (2020). Response mechanism of DFIG to transient voltage disturbance under commutation failure of LCC-HVDC system. 35(6):2972–2979. doi:10.1109/TPWRD.2020.3005720

CrossRef Full Text | Google Scholar