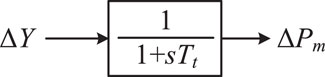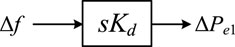System frequency response model and droop coefficient setting considering renewable energy participation in frequency regulation

The highly uncertain and uncontrollable power output of renewable energy sources (RES), when integrated into power systems at high penetration levels, reduces system inertia and introduces uncertain changes in system structure, parameters, and frequency response characteristics. This renders traditional frequency regulation analysis methods and frequency response models inapplicable, lacking a generalized model to describe renewable energy’s participation in frequency regulation. Thus, this paper proposes a method where RES utilize suitable means to reduce load, thereby contributing to frequency regulation. Furthermore, employing Virtual Synchronous Machine (VSM) technology, these renewable energy units emulate the inertia and droop characteristics of Synchronous Generators (SG), enabling their equivalent modeling alongside traditional generators within a single-machine aggregate model. An SFR (System Frequency Response) model integrating renewable energy’s frequency regulation has been established. This model enables the analysis of the relationships between the system’s equivalent droop coefficient and the frequency nadir, nadir time, and quasi-steady-state point. Furthermore, the required equivalent droop coefficients are proposed for various sending-end system capacities and operating conditions. Finally, the model’s validity and accuracy are confirmed through a modified WSCC 4-machine 10-bus system, offering theoretical underpinnings for stable system operation and optimized operational planning.

1 Introduction

Compared to traditional synchronous systems, the extensive integration of high-proportion electronic RES has substituted for some SG, resulting in a gradual reduction in system inertia and relatively weaker frequency regulation capability due to the decoupling characteristics of renewable energy power electronics and their maximum power tracking mode. In addition, the application of UHV large-capacity cross-regional DC transmission has blocked the cross-regional inertia support and power response under disturbances, seriously deteriorating the system frequency stability under large disturbances (Shi et al., 2018a; Ahmadi and Ghasemi, 2014; Wright et al., 2019; Lin et al., 2023). In interconnected power systems, frequency stability is an important indicator reflecting power quality, mainly representing the balance state of active power in power systems (Xue et al., 2024; Yin et al., 2024; Grebla et al., 2020; Mei et al., 2024). In traditional power systems, frequency control is primarily achieved by regulating the active power output of generator sets, enabling the system’s generation power to follow changes in system load power, thereby achieving active power balance across the entire system. This function is commonly referred to as LFC (Load Frequency Control) (Wu et al., 2023a). However, in power systems with a high penetration of renewable energy, the uncertainty of renewable energy output becomes a critical factor affecting the active power balance of the system (Wu et al., 2023b). Compared to traditional load disturbances, renewable energy output disturbances are more severe and highly unpredictable, posing challenges to the current load frequency control techniques, which lack suitable representation and handling of this uncertainty. The integration of high proportions of renewable energy inevitably has adverse effects on the quality and stability of frequency control (Zhixuan et al., 2024). Furthermore, renewable energy units exhibit significantly different frequency response characteristics from traditional energy units. Their replacement of traditional units leads to uncertain changes in system structure, parameters, and frequency response characteristics, further complicating frequency control (Rongpeng and Yang, 2024).

In response to the aforementioned issues regarding frequency response characteristics arising from the high integration of renewable energy, extensive research has been conducted by scholars both domestically and internationally. In Reference (Altaf et al., 2022), the study of the system’s frequency dynamic response through the ASF (Average System Frequency) is proposed. This model equates all generators in the system to a single-machine model while retaining the original turbine-governor systems of each unit. However, as the number of generators continues to increase, the proliferation of turbine-governor systems limits the applicability of this method. Building upon the ASF model, Reference (Quan and Pan, 2017) further simplifies the turbine-governor systems through equivalent aggregation, thereby approximating the entire power grid as a single-machine model with a centralized load model. The SFR model significantly reduces the order of the frequency response analysis model, enabling the calculation of analytical solutions for maximum frequency deviations and corresponding times under given disturbances. It is currently the most commonly used model for frequency response analysis. Reference (Xiaolin et al., 2021) established a two-stage distributionally robust unit commitment model for power systems with wind farms, based on the ASF model and its simplified SFR model, considering virtual inertia control and droop control of wind farms. Reference (Fan et al., 2020) employed the system SFR model to analyze the impact of key frequency control parameters, including inertia time constant, frequency regulation deadband, and governor droop, on system frequency response characteristics. Reference (Bo et al., 2020) developed an SFR model incorporating wind turbine integration, derived dynamic frequency quantification metrics, and constructed a unit commitment optimization model for wind-integrated systems considering dynamic frequency constraints. Reference (Malekpour et al., 2021) integrated wind power virtual inertia control into the traditional SFR model and analyzed its effect on system frequency response. Reference (Chang-gang et al., 2009) proposed a power system frequency dynamic analysis method based on the DC power flow method, which ignores the impact of reactive power-voltage variations on frequency dynamics and uses the DC power flow method to describe the system network flow equations, considering only generator motion equations and turbine-governor dynamics, with iterative integration methods to calculate post-disturbance system frequency dynamics. Reference (Banarkar et al., 2006) established equivalent models for SG, wind farms, and loads, using wind power fluctuations and frequency deviations as input and output variables, respectively, thereby simplifying a multi-machine system to a single-machine system. This enabled the establishment of a frequency-domain transfer function between system power fluctuations and frequency deviations, which was then used to analyze system frequency dynamics with the SFR model. Reference (Nguyen et al., 2015) quantitatively analyzed the impact of wind power integration on system equivalent inertia and damping constants. Through the modification of traditional SFR model parameters, it proposed an SFR model that considers wind power integration and derived the corresponding time-domain expression for maximum frequency deviation. Reference (Shi et al., 2018b) introduced an analytical method to aggregate a multi-machine SFR model into a single-machine model. Validation studies demonstrated that the proposed aggregated SFR model accurately represents the multi-machine SFR model.

This paper based on the mechanism of traditional thermal power unit inertia and primary frequency regulation (PFR) for system frequency adjustment, employs the SFR method to analyze the impact of various factors on system frequency dynamic characteristics after the participation of renewable energy units in frequency regulation. Considering the involvement of renewable energy units in frequency regulation, the SFR model is improved to derive expressions and correlations for the initial rate of frequency change, maximum frequency deviation, and steady-state frequency deviation. Through theoretical analysis, the mechanism of operating conditions influencing the frequency regulation capability of renewable energy units and system frequency dynamic behavior is revealed. The effectiveness of this improved SFR model is verified through simulations on the modified WCSS 4-machine 10-bus system.

2 Frequency response model

The frequency response characteristic of a power system refers to the variation in system frequency under unbalanced power conditions. This characteristic is influenced by factors such as the magnitude of the disturbing power, the inertia of prime movers, and the regulation characteristics of governors.

Under conditions that do not lead to power angle instability or voltage instability, the impact of reactive power and voltage variations can be neglected to focus on the primary relationship between frequency and active power, highlighting the main influencing factors. To reduce the computational burden and complexity of frequency dynamic analysis, this paper, based on the premise of a unified frequency across the entire grid, disregards spatial frequency variations and power angle stability issues. It aggregates the rotor motion equations of all generators in the system into an equivalent single-generator model with centralized loads, thereby deriving the system’s SFR.

2.1 SFR of prime mover and governor

The rotor motion equation of a synchronous generator describes the variation in rotor speed under unbalanced torque when fluctuations occur in the mechanical power output by the prime mover or the electromagnetic power output by the synchronous machine. It can be expressed as:

$\Delta P_m-\Delta P_e=2H_{sys}\frac{d\Delta f}{dt}(1)$

where ΔP_m is the mechanical power output of the prime mover; ΔP_e is the electromagnetic power output of the synchronous machine; Δf is the frequency variation (since the frequency f is directly proportional to the rotor angular velocity ω, for a more intuitive representation of the power-frequency relationship, the frequency deviation Δf will be used as a substitute for the angular velocity variation Δω; H_sys represents the equivalent inertia time constant of the generator set:

$H_{sys}=\frac{{\displaystyle \sum _{i=1}^n}{H}_i{S}_i}{{\displaystyle \sum _{i=1}^n}{S}_i}=\frac{{\displaystyle \sum _{i=1}^n}{H}_i{S}_i}{S_{B\left(SG\right)}}(2)$

where n represents the number of synchronous units in the system, S_i and H_i are their respective rated capacities and inertia time constants, while S_B(SG) denotes the total rated capacity of conventional SG. The system load’s response to frequency deviations is primarily encapsulated in the load damping constant D. When a frequency deviation occurs, the variation in load power is given by:

$\Delta P_L=D\Delta f(3)$

where ΔP_L represents the power variation of frequency-sensitive loads, and D is the load damping constant. Applying Laplace transforms to Equations 1 and 3 yields the equivalent model of the generator and load, as illustrated in Figure 1A. Figure 1B depicts the simplified version of this model.

Figure 1

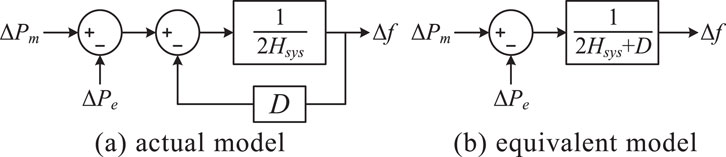
Figure 1. (A) actual model. (B) equivalent model. Equivalent model of load and traditional generator.

Traditional thermal power generation units employ steam turbines as their prime movers, and the mechanical power output of the prime mover can be controlled by adjusting the valve opening of the steam turbine. The process of loading and unloading the steam chamber and inlet pipe takes a certain amount of time. Therefore, the process of load-frequency control through regulating the steam flow passing through the steam turbine using control valves can be represented by an inertial element with a time constant T_t, as shown in Figure 2. The value of the time constant T_t typically ranges from 0.2 to 0.3 s.

Figure 2

Figure 2. Equivalent model of prime motor.

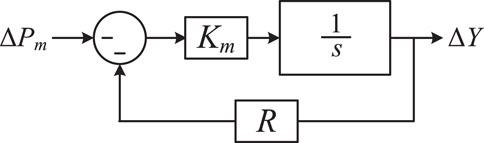
To distribute loads among multiple generator set reasonably, the governor system should be capable of reducing rotational speed when load power increases. This regulating characteristic can be achieved using an integral element with steady-state feedback, as illustrated in Figure 3.

Figure 3

Figure 3. Equivalent model of governor with droop control.

In the figure, R represents the equivalent droop coefficient of the generator set, which physically signifies the ratio between the frequency variation and the change in generator output power. By simplifying Figure 3 and combining it with Figure 2, we obtain the equivalent model of the prime mover and governor as shown in Figure 4, where T_s = 1/(K_mR) represents the inertia time constant of the governor.

Figure 4

Figure 4. Equivalent model of governor and prime motor.

2.2 Frequency regulation-capable SFR for RES

From Equations 1–3, it is evident that during active power disturbances in a power system containing synchronous machines, the system frequency undergoes an abrupt change. The generator sets, due to their rotational inertia, can provide energy proportional to the rate of frequency change, offering transient support to the system frequency. Larger inertia time constants of the generator set result in the release of more rotational kinetic energy. However, renewable energy systems such as wind and solar power generation are typically characterized by low inertia, and their output power is decoupled from the grid frequency, rendering them incapable of responding to frequency variations. With a high penetration of these renewable sources into the power system, the overall system inertia inevitably decreases, reducing the rotational inertia available to counter frequency changes and leading to degradation of frequency dynamic performance.

The VSM technology enables renewable energy interfaces, such as converters, to mimic the virtual inertia characteristics of synchronous machines by appending control loops. The basic working principle involves adjusting the output power of renewable energy units in response to frequency deviations during system disturbances, thereby equipping them with the capability to respond to frequency variations. Analogous to the rotational inertia effect of synchronous machines, the variation in output power of renewables through virtual inertia control in response to frequency changes is given by:

$\Delta P_{e1}=K_d\frac{d\Delta f}{dt}(4)$

where ΔP_e1 is variation in output power of renewable energy units under virtual inertia control, where k_d represents the virtual inertia coefficient. Applying the Laplace transform to Equation 4 yields the SFR of renewables equipped with virtual inertia characteristics, as depicted in Figure 5.

Figure 5

Figure 5. Frequency response model of RES under virtual inertia control.

To achieve a reasonable load distribution among multiple generator sets, traditional energy sources, under the influence of droop-equipped governors, exhibit a characteristic where output power increases with load increase. In contrast to rotational inertia, which provides transient support to the system frequency, the droop characteristic of generator sets reduces the steady-state error in system frequency after disturbances. The droop rate of generator sets can be expressed by Equation 5:

$R\left(\%\right)=\left(\frac{{\omega }_{NL}-{\omega }_{FL}}{{\omega }_0}\right)(5)$

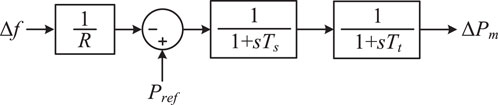
The magnitude of PFR capability in generator sets is intimately tied to their droop rates. When integrating low-inertia sources such as large wind farms or photovoltaic power stations into the grid, they are typically required to possess a certain level of PFR capability. By leveraging VSM technology to control the inverters of renewable energy interfaces, RES can exhibit a similar droop characteristic to traditional energy sources during frequency variations. In contrast to virtual inertia control, which can instantly respond to frequency changes, inverters executing droop control for frequency regulation require a certain time delay. Compared to the governor dynamics of traditional energy sources, the SFR of RES with droop characteristics is illustrated in Figure 6.

Figure 6

Figure 6. Frequency response model of RES under droop control.

Where K_R is the droop control coefficient of RES, also known as the PFR gain, is denoted as T_R, which represents the droop control time constant. ΔP_e2 signifies the variation in output power of renewable energy units under the influence of droop control.

2.3 SFR considering the integration RES

After renewable energy units acquire virtual inertia and droop characteristics similar to synchronous machines through VSM technology, these converter-based power sources can be aggregated with synchronous machines into a single-machine equivalent model. The SFR that considers the frequency regulation capability of renewables is depicted in Figure 7.

Figure 7

Figure 7. SFR model considering frequency control capability of renewable energy.

Where K_RES and K_m represent the proportions of actual output power contributed by renewable energy units and thermal power units, respectively, to the total system generation.

Without considering the virtual inertia provided by non-synchronous power sources, after replacing synchronous units with non-synchronous power sources of equal capacity, the system equivalent inertia time constant based on the total rated capacity of the system can be expressed by Equation 6:

$H_{SYS}^{\prime }=\frac{{\displaystyle \sum _{i=1}^{n-m}}{H}_i{S}_i}{{\displaystyle \sum _{i=1}^{n-m}}{S}_i+S_{B\left(NSG\right)}}=\frac{{\displaystyle \sum _{i=1}^n}{H}_i{S}_i-{\displaystyle \sum _{i=m+1}^n}{H}_i{S}_i}{{\displaystyle \sum _{i=1}^{n-m}}{S}_i}=H_{SYS}-\Delta H(6)$

where ΔH represents the equivalent inertia time constant of the synchronous units that have been replaced by non-synchronous power sources.

From an energy perspective, replacing synchronous units with non-synchronous power sources of equal capacity directly reduces the number of conventional synchronous units in operation. Consequently, the total rotational kinetic energy of the system decreases as the number of synchronous units diminishes, leading directly to a reduction in the system’s equivalent inertia level.

Under the premise of not considering the participation of asynchronous power sources in PFR, after replacing synchronous units with asynchronous power sources of equal capacity, the mechanical power gain coefficient of steam turbines, K_m can be expressed by Equation 7:

$K_{ms}^{\prime }=\frac{S_{B\left(s\right)}^{\prime }}{S_{B\left(SG\right)}^{\prime }+S_{B\left(NSG\right)}}=\frac{S_{B\left(s\right)}-\Delta S_{B\left(s\right)}}{S_{B\left(SG\right)}}=K_{ms}-\Delta K_{ms}(7)$

where ΔS_B(s) refers to the capacity of hydraulic turbines and steam turbines that have been replaced by non-synchronized power sources. ΔK_ms represents the variation in the mechanical power gain coefficient for hydraulic turbines and steam turbines.

Accordingly, the equivalent droop coefficient of the system, R′ can be expressed by Equation 8:

$\frac{1}{R^{\prime }}=\frac{1}{R_{sys}}-\frac{1}{R_s}\Delta K_{ms}=\frac{1}{R_{sys}}-\frac{1}{\Delta R}(8)$

where ΔR represents the variation in the equivalent droop coefficient of the system after it has been partially replaced by non-synchronous power sources.

In summary, since the total system capacity remains unchanged, replacing synchronous units with non-synchronous power sources of equal capacity directly alters the number of conventional synchronous units in operation. Consequently, the number of prime movers and governors of generating units decreases accordingly, leading to a gradual weakening of the frequency regulation capability of the governor system of generating units. Therefore, when synchronous units are replaced by non-synchronous power sources, the equivalent droop coefficient R′ of the system gradually increases, which is equivalent to reducing the system’s PFR capability.

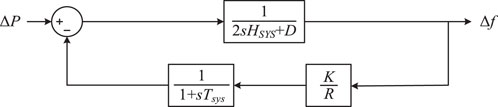
The SFR shown in Figure 7 can be further simplified, and by letting H_SYS = H_sys + K_d, the rotational inertia of conventional units and the virtual inertia of renewable energy units can be aggregated into the overall system inertia. Consequently, the SFR can be expressed as:

Where T_sys represents the equivalent response time constant of the system, and K denotes the participation factor of renewable energy in frequency regulation, as shown in Equation 9.

$K=1-k_{\text{SG}}+k_{\text{RE}}(9)$

where k_SG is the replaced portion of synchronous machines is denoted as the proportion of substitution, and k_RE represents the proportion of power electronic sources that provide both inertia and frequency regulation (if power electronic sources do not provide frequency regulation, then k_RE = 0). At this point, the equivalent inertia of the system is H_SYS, and the equivalent droop coefficient is K/R. For simplicity, this equivalent model is used in subsequent analysis to investigate the impact of PFR parameters on the system.

3 The relationship between frequency variation and model parameters

3.1 SFR considering the integration RES

Based on the SFR derived in the previous section from Figure 8, the transfer function from load disturbance to frequency variation can be expressed by Equation 10:

$\Delta f=\left[\frac{{\omega }_{\mathrm{n}}^2}{K\left(D+R^{-1}\right)}\right]\left[\frac{\left(1+T_{SYS}s\right)P_{\mathrm{d}}}{s\left(s^2+2\zeta {\omega }_{\mathrm{n}}+{\omega }_{\mathrm{n}}^2\right)}\right](10)$

Figure 8

Figure 8. Simplified SFR model considering frequency control capability of renewable energy.

Where ω_n and ζ represent the undamped natural frequency and damping ratio, respectively, and their expressions are shown in Equation 11:

$\left\{\begin{array}{l}{f}_n^2=\frac{DR+K}{2H_{SYS}R{T}_{SYS}}\\ \zeta =\left[\frac{2H_{SYS}R+\left(DR+K\right)T_{SYS}}{2\left(DR+K\right)}\right]f_{\mathrm{n}}\end{array}\right.(11)$

Assuming the magnitude of the disturbance is ΔP, applying the Laplace inverse transform to Equation 10 yields the expression of the system frequency response in the time domain, enabling the further derivation of evaluation parameters for the dynamic characteristics of system frequency, as shown in Equation 12.

$\left\{\begin{array}{l}\Delta f\left(t\right)=\frac{R\Delta P}{DR+K}\left[1+\alpha e^{-\zeta {\omega }_{\mathrm{n}}t}\sin \left({\omega }_{\mathrm{r}}t+\varphi \right)\right]\\ {\omega }_{\mathrm{r}}={\omega }_{\mathrm{n}}\sqrt{1-{\zeta }^2}\\ \alpha =\sqrt{\frac{1-2T_{SYS}\zeta {\omega }_{\mathrm{n}}+T_{SYS}^2{\omega }_{\mathrm{n}}^2}{1-{\zeta }^2}}\\ \varphi =\arctan \left(\frac{{\omega }_{\mathrm{r}}{T}_{SYS}}{1-\zeta f_{\mathrm{n}}{T}_{SYS}}\right)-\arctan \left(\frac{\sqrt{1-{\zeta }^2}}{-\zeta }\right)\end{array}\right.(12)$

At t = 0, the maximum rate of change of frequency (RoCoF) can be obtained. Based on the above analysis, it can be concluded that:

${\left.\frac{d\Delta f}{dt}\right|}_{t=0}=\frac{\Delta P}{2H_{SYS}+K}(13)$

At t = ∞, the quasi-steady-state frequency deviation of the system can be obtained.

$\Delta f_{\text{set}}=\Delta f\left(\infty \right)=\frac{\Delta P}{D+K/R}(14)$

Using typical parameters from the reference (Banarkar et al., 2006) as the model’s parameters, and under a power disturbance of 10% of the synchronous generator capacity, the system frequency response curves are compared after wind turbines replace SG at different proportions, as shown in Figure 9.

Figure 9

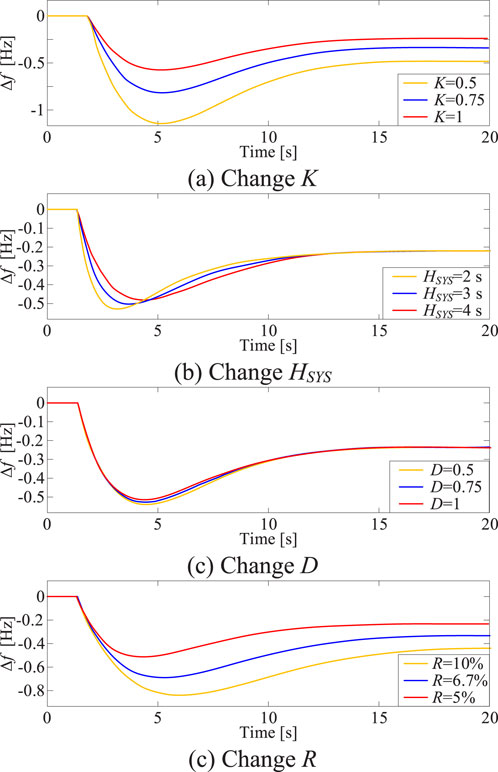
Figure 9. (A) Change K. (B) Change H_SY. (C) Change D. The characteristic of system frequency response.

From Figure 9A, it can be observed that as the proportion of wind power replacing SG increases (K decreases), the maximum frequency deviation, the maximum rate of change of frequency, and the quasi-steady-state frequency deviation all exhibit an increasing trend. Thus, all three evaluation indicators of system frequency response deteriorate, undoubtedly indicating that wind power integration has a negative impact on system frequency response characteristics, and this negative impact becomes more severe with an increasing proportion of wind power integration.

Figure 9B demonstrates that variations in H_SYS affect the magnitude of the system frequency rate of change post-disturbance. A smaller H_SYS results in a larger frequency rate of change throughout the PFR process, including an increased maximum value at the initial moment of the disturbance, consistent with the formula for calculating the maximum frequency rate of change given in Equation 13. Additionally, H_SYS significantly influences the system’s frequency nadir, with a smaller H_SYS leading to an earlier occurrence of the nadir and a larger maximum frequency deviation at this point.

According to Figure 9C, changes in D primarily impact the system maximum frequency deviation. A smaller D results in a larger maximum frequency deviation. While Equation 14 indicates that D also influences the quasi-steady-state frequency deviation, this effect is generally limited due to the typically small damping coefficients in power systems.

Finally, Figure 9D shows that variations in R affect the quasi-steady-state frequency deviation. A larger R delays the occurrence of the frequency nadir and leads to a larger maximum deviation at this point, as well as a larger quasi-steady-state frequency deviation.

3.2 The requirement of the droop coefficient

According to above section, the K and R significantly influence the Δf_set. Thus, the relationship between K, R, and Δf_set needs to be further establish to control the value of Δf_set under different conditions of K by adjusting R.

According to Equation 14, the R can be calculated by: Equation 12:

$R=\frac{K\Delta f_{\text{set}}}{\Delta P-\Delta f_{\text{set}}D}(15)$

It can be seen that the governing coefficient is directly proportional to K, while it is inversely prwxoportional to ΔP and D. Assuming a permissible quasi-steady-state frequency deviation of Δf_set = 0.2 Hz, the required droop coefficient R of the system is dependent on K, the integration of power electronic sources, and the active power disturbance ΔP. When the frequency regulation contribution of power electronic sources in the system decreases, an increase in the droop coefficient is necessary. Conversely, a larger active power disturbance requires a reduction in the equivalent droop coefficient to stabilize the system frequency.

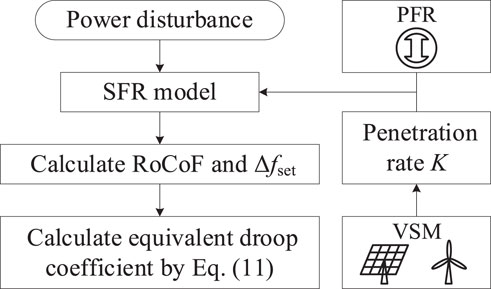
Finally, a flowchart is given by Figure 10 to obtain the equivalent droop coefficient R based on the proposed SFR in this paper.

Figure 10

Figure 10. Flowchart of the droop coefficient Setting.

4 Case studies

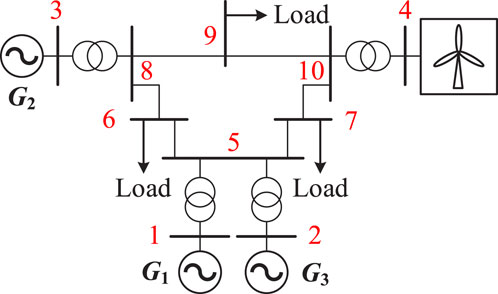
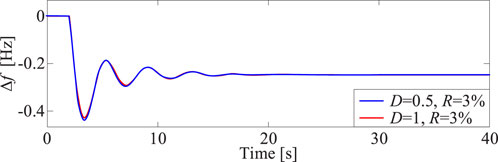
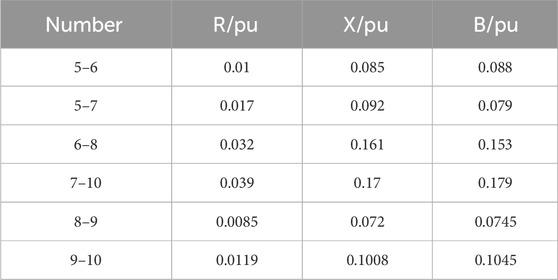
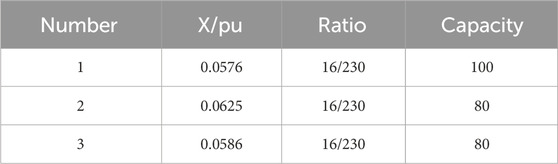
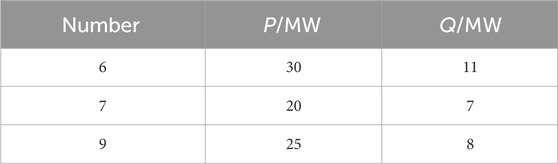
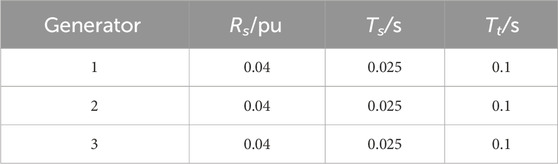
In this chapter, the test case employs the WSCC 4-machine 10-bus system, with a simulation model built on PSCAD to validate the effectiveness of the proposed SFR. The RES are modeled as common Direct-Drive Wind Turbines, as depicted in Figure 11. Generators 1, 2, 3, and Wind Turbines have a rated capacity of 20 MVA each. The system load is 75MW, and the system’s equivalent inertia constant is 4s. The system feeder line, transformer, load, and frequency regulation parameters are shown in Tables A1–A3. The system equivalent original droop coefficient R is set as 3%, with a renewable energy frequency regulation contribution ratio K = 1 and equivalent damping constant D is set as 1.

Figure 11

Figure 11. Modified WSCC 4-machine 10-bus system .

4.1 Performance of the proposed SFR

In order to verify the accuracy of the proposed SFR model, the active power disturbances of the load increase are respectively set as 8 MW, 12 MW, 16 MW (accounting for 10%, 15%, 20% of the system capacity separately) in PSCAD simulation model and SFR model. The frequency response curves and the errors between the PSCAD and SFR are respectively shown in Figure 12 and Table 1.

Figure 12

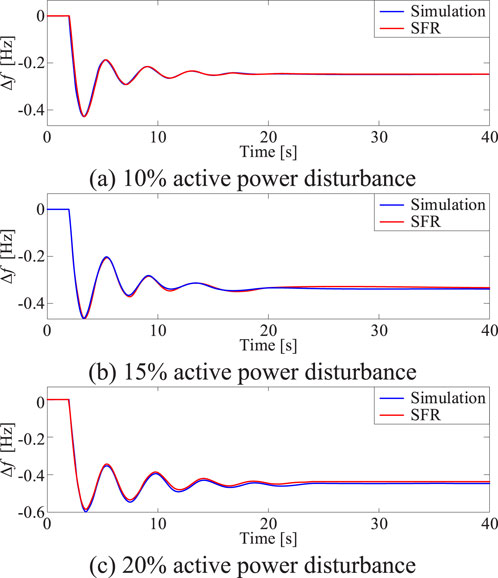
Figure 12. (A) 10% active power disturbance. (B) 15% active power disturbance. (C) 20% active power disturbance. Comparison results of system frequency response.

Table 1

Table 1. Error between the PSCAD model and SFR model.

From the above figure and table, it can be observed that the output of the SFR model closely matches the results of the time-domain simulation under various load increment scenarios. Even in the case of 20% load increment, which caused a frequency drop of 0.46Hz, the error in the minimum frequency value was only 2.377%. These simulation results convincingly demonstrate the effectiveness of the proposed SFR model.

4.2 Performance of the droop coefficient adjustment

When the system suffers a 20% active power disturbance (18 MW), to maintain the quasi-steady-state deviation Δf_set = 0.23 Hz, substituting parameters into Equation 15 yields a equivalent droop coefficient of 1.4%. As shown in Figure 13, which compares the frequency response curves before and after the adjustment, by appropriately modifying the droop coefficient, the quasi-steady-state deviation Δf_set can be maintained at 0.23 Hz even under larger active power disturbances.

Figure 13

Figure 13. Comparison results after changing R.

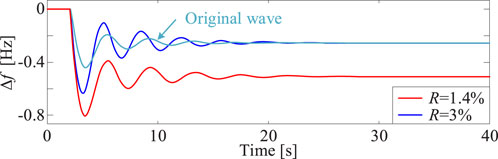
Under the scenario that the proportion of new energy sources participating in frequency regulation decreases, the overall frequency regulation capability of the system declines, leading to a shift in the demand for the droop coefficient. Keeping the power disturbance scenario in IV.A unchanged, the proportion of wind turbines participating in frequency regulation K is set to 0.5 and the simulation results are shown in Figure 14.

Figure 14

Figure 14. Comparison results after changing K.

Compared to the 10%-power-disturbance original waveform in IV.A, the decrease in K results in a deterioration of the system frequency stability, manifested by enlarged frequency fluctuations and an increase in Δf_set. To keep the Δf_set to its initial value of 0.23 Hz, substituting the relevant parameters into Equation 14, yields a required R of 1.4%. As shown in Figure 14, upon adjusting R using the proposed method, Δf_set is successfully reinstated to meet the original specification in IV.A, despite the reduction in K. However, due to the diminished participation of wind turbines in frequency regulation, the frequency fluctuation profile exhibits greater deviations compared to the original waveform.

To verify the impact of D on frequency regulation effectiveness, keeping the 10%-power-disturbance scenario outlined in Section 4.1 unchanged, the equivalent damping constant D is set to 0.5 and the simulation results are shown in Figure 15. According to Equation 15, the Δf_setD is much smaller than ΔP, so the impact of Δf_setD can be ignored, the droop regulation coefficient calculated by Equation 15 has not changed significantly. Thus, the droop coefficient doesn’t need to be adjusted with the change of D.

Figure 15

Figure 15. Comparison results after changing D.

5 Conclusion

This paper focuses on power systems with a high penetration of RES. A SFR is established to investigate the frequency response characteristics and the selection of droop coefficient post RES integration. The key contributions and innovations of this work are summarized as follows:

(1) For RES systems equipped with virtual inertia, an SFR model is established, which incorporates the participation of RES in frequency regulation. This SFR model is utilized to analyze the impact of various system equivalent parameters on frequency regulation. Through theoretical derivation, the relationship between the system’s governing coefficient, renewable energy penetration rate, and frequency disturbances is established, revealing the required droop coefficient under different frequency disturbance and RES penetration rate.

(2) The accuracy of the proposed SFR model is experimentally validated, confirming its ability to accurately reflect the changes in system parameters such as larger power disturbances or variations in the RES participation ratio in frequency regulation. This ensures that the calculated governing coefficient effectively responds to these changes, maintaining the frequency regulation results within the operational requirements of the power system.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YyS: Writing–original draft, Writing–review and editing. YZ: Writing–review and editing. SZ: Writing–review and editing. FL: Writing–review and editing. YuS: Writing–review and editing. YL: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadi, H., and Ghasemi, H. (2014). Security-constrained unit commitment with linearized system frequency limit constraints. IEEE Trans. POWER Syst. 29 (4), 1536–1545. doi:10.1109/tpwrs.2014.2297997

CrossRef Full Text | Google Scholar

Altaf, M. W., Arif, M. T., Saha, S., Islam, S. N., Haque, M. E., and Oo, A. M. T. (2022). Effective ROCOF-based islanding detection technique for different types of microgrid. IEEE Trans. INDUSTRY Appl. 58 (2), 1809–1821. doi:10.1109/tia.2022.3146094

CrossRef Full Text | Google Scholar

Banarkar, H., Luo, C., and Ooi, B. T. (2006). “Power system response to wind power fluctuations,” in 2005/2006 IEEE/PES transmission and distribution conference and exhibition. Dallas, TX, USA.

Google Scholar

Bo, W., Deyou, Y., and Guowei, C. (2020). Dynamic frequency constraint unit commitment in large-scale wind power grid connection. Power Syst. Technol. 44 (7), 2513–2519. doi:10.13335/j.1000-3673.pst.2019.2088

CrossRef Full Text | Google Scholar

Chang-gang, L., Yu-tian, L., and Heng-xu, Z. (2009). Power system frequency response analysis based on the Direct current load flow. Proc. CSEE 29 (34), 36–41.

Google Scholar

Fan, W., Haifeng, L., and Guoyi, X. (2020). Influence of key parameters of frequency control on frequency characteristics of power grid and sensitivity analysis. Power Syst. Prot. Control 48 (20), 1–8. doi:10.19783/j.cnki.pspc.191452

CrossRef Full Text | Google Scholar

Grebla, M., Yellajosula, J. R. A. K., and Høidalen, H. K. (2020). Adaptive frequency estimation method for ROCOF islanding detection relay. IEEE Trans. POWER Deliv. 35 (4), 1867–1875. doi:10.1109/tpwrd.2019.2956200

CrossRef Full Text | Google Scholar

Lin, J., Liu, B., and Xiao, H. (2023). Frequency characteristics of receiving end power grid for large-scale offshore wind power access. Guangdong Electr. Power 36 (3), 23–31.

Google Scholar

Malekpour, M., Kiyoumarsi, A., and Gholipour, M. (2021). 'Analytical system frequency response model with virtual synchronous wind turbines. IET Generation, Transm. Distribution 15 (6), 2618–2631. doi:10.1049/gtd2.12204

CrossRef Full Text | Google Scholar

Mei, Y., Gao, Y., and Li, C. (2024). Dynamic simulation study of the whole process of isolated network operation considering new energy connection. Guangdong Electr. Power 37 (1), 68–75.

Google Scholar

Nguyen, N., Almasabi, S., and Mitra, J. (2015). “Estimation of penetration limit of variable resources based on frequency deviation,” in 2015 north American power symposium (NAPS) (Charlotte, NC, USA), 1–6.

Google Scholar

Quan, R., and Pan, W. (2017). “A low-order system frequency response model for DFIG,” in Distributed wind power generation systems based on small signal analysis. Energies.

Google Scholar

Rongpeng, X., and Yang, W. (2024). Technical transformation of grid friendly power control system for doubly-fedInduction wind farm. GUANGDONGELECTRICPOWER 37 (6), 43–52.

Google Scholar

Shi, Q., Li, F., and Cui, H. (2018a). Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies. IEEE Trans. POWER Syst. 33 (6), 6355–6367. doi:10.1109/tpwrs.2018.2824823

CrossRef Full Text | Google Scholar

Shi, Q., Li, F., and Cui, H. (2018b). Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies. IEEE Trans. Power Syst. 33 (6), 6355–6367. doi:10.1109/tpwrs.2018.2824823

CrossRef Full Text | Google Scholar

Wright, P. S., Davis, P. N., Johnstone, K., Rietveld, G., and Roscoe, A. J. (2019). Field measurement of frequency and ROCOF in the presence of phase steps. IEEE Trans. Instrum. Meas. 68 (6), 1688–1695. doi:10.1109/tim.2018.2882907

CrossRef Full Text | Google Scholar

Wu, Z., Tian, E., and Chen, H. (2023a). Covert attack detection for LFC systems of electric vehicles: a dual time-varying coding method. IEEE/ASME Trans. Mechatronics 28 (2), 681–691. doi:10.1109/tmech.2022.3201875

CrossRef Full Text | Google Scholar

Wu, Z., Tian, E., and Chen, H. (2023b). Control methods of VSC converters for grid-following/forming operation under grid-side faults in PV energy storage systems. GUANGDONG Electr. POWER 36 (12), 47–56.

Google Scholar

Xiaolin, G., Ya, L., and Yang, F. (2021). Distributed robust unit commitment considering the whole process of inertia support and frequency regulations. Proc. CSEE 41 (12), 4043–4058. doi:10.13334/j.0258-8013.pcsee.200974

CrossRef Full Text | Google Scholar

Xue, Y., Chen, Y., Zheng, W., Tang, Y., Li, Z., Yang, C., et al. (2024). Sharing of primary frequency response using LCC-HVDC. IEEE Trans. POWER Deliv. 1 (1), 2457–2469. doi:10.1109/tpwrd.2024.3415052

CrossRef Full Text | Google Scholar

Yin, H., Qiu, W., Wu, Y., You, S., Tan, J., Hoke, A., et al. (2024). Field measurement and analysis of frequency and RoCoF for low-inertia power systems. IEEE Trans. INDUSTRIAL Electron. 71 (7), 7996–8006. doi:10.1109/tie.2023.3303622

CrossRef Full Text | Google Scholar

Zhixuan, L., Chen, Y., and Ying, X. (2024). Review of frequency stability analysis and control research of multi-area asynchronous interconnected systems. Power Syst. Technol. 1 (1), 1–25.

Google Scholar

Appendix

TABLE A1

TABLE A1. Feeders parameter.

TABLE A2

TABLE A2. Transformers parameter.

TABLE A3

TABLE A3. Loads parameter.

TABLE A4

TABLE A4. Speed control parameters of steam turbines.

Nomenclature

Abbreviations

RES Renewable Energy Sources

RoCoF Rate of Change of Frequency

SFR System Frequency Response

SG Synchronous Generators

VSM Virtual Synchronous Machine

Symbols

D Load damping constant

Δf Frequency variation

Δf_set Steady-state frequency deviation

H_i Respective inertia time constants

H_sys Generator’s equivalent inertia time constant

H_SYS Equivalent inertia time constant for SFR

k_d Virtual inertia coefficient

k_RE Proportion for RES

k_RE Proportion for SG

K_m Gain coefficient for SG

K_R Droop control coefficient for RES

K_RES Gain coefficient for RES

n The number of synchronous units

ΔP_e Electromagnetic power output

ΔP_e1 Power output variation for RES

ΔP_L Power variation of frequency-sensitive loads

ΔP_m Mechanical power output

R Equivalent droop coefficient

S_B(SG) total rated capacity of SG

S_i Respective rated capacities

T_s Inertia time constant for SG

T_sys Equivalent response time constant for SFR

T_t Time constant for SG

Δ_ω Angular velocity variation