Evaluating the impact of tilt angles and tracking mechanisms on photovoltaic modules in Ethiopia

This study investigated the influence of site location, tilt angle, and solar orientation on Ethiopia’s photovoltaic (PV) module performance. We determined optimal tilt angles for different time scales and locations across the country by analyzing global horizontal radiation data and employing various decomposition and transposition models. Results showed that optimal tilt angles increase with latitude, ranging from 0° to 47.9° monthly and from 14.1° to 21.5° annually. Seasonal optimal tilt angles were found to be 29.2°, 21.65°, 12.34°, and 8.8° for winter, autumn, spring, and summer, respectively. Additionally, the study compared the performance of PV modules with different tracking mechanisms. Dual/full-axis tracking yielded the highest energy gain (44.89%), while NS tracking resulted in a significant loss (28.46%). This research provides valuable insights for optimizing Ethiopia’s PV system design and installation, aiding in accurate energy assessment and forecasting.

1 Introduction

Solar energy, a sustainable and abundant resource, has emerged as a promising solution to global energy challenges. Photovoltaic (PV) modules and panels are pivotal devices for harnessing solar radiation and converting it into electricity (Lamoureux et al., 2015; Gao et al., 2016). Optimizing the installation of these panels is crucial to maximize energy output. Solar irradiance, ground reflectance, tilt angle, and orientation significantly influence PV system performance (Benghanem, 2011). While Ethiopia’s geographic location in the northern hemisphere necessitates southward-facing installations as illustrated in Figure 1, careful consideration of these factors is essential for achieving optimal energy yield and contributing to a sustainable energy future.

Figure 1

Figure 1. World map: northern and southern hemisphere (Goldberg and Gott, 2007).

The optimal tilt angle for PV modules/panels is a crucial factor in maximizing solar energy capture. This angle is influenced by factors such as latitude, location-specific solar radiation patterns, and the application of accurate modeling techniques (Yadav and Chandel, 2013). While latitude-based rules of thumb are commonly used, they often lack precision for diverse geographical regions (Ashetehe et al., 2022). Table 1 presents a compilation of optimal tilt angles for various global locations, offering a more comprehensive approach to solar panel installation.

Table 1

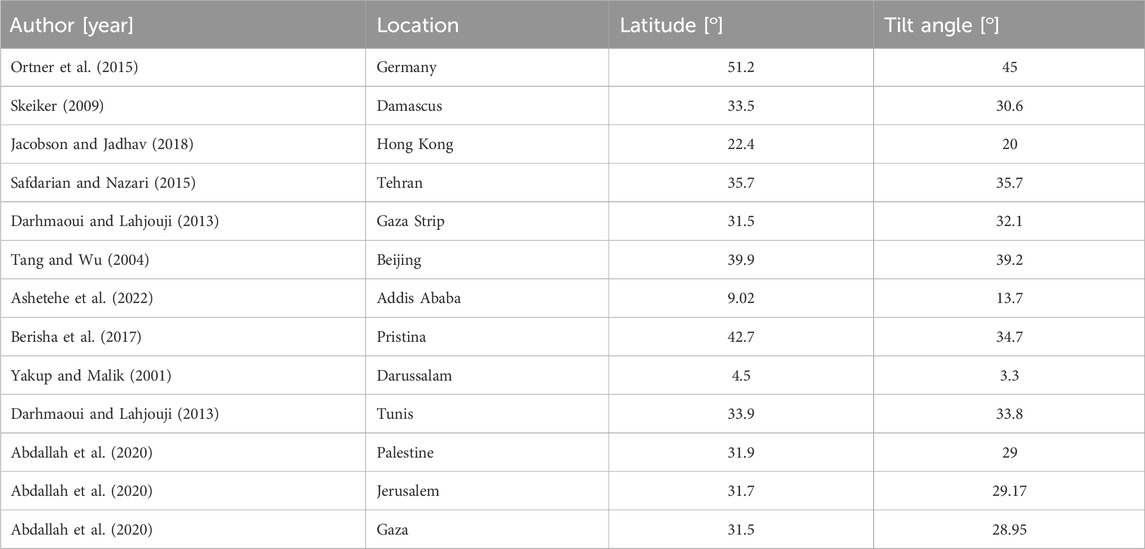
Table 1. Some of the previous works that were conducted to determine optimal tilt angles at different cities across the world.

Solar tracking systems, which adjust PV panel orientation to follow the sun’s path, significantly enhance solar energy capture compared to fixed-tilt systems (Zhu et al., 2020). These systems are essential for various PV applications, including rooftop and large-scale plants (Wang and Sueyoshi, 2017). Numerous studies have explored the performance benefits of different tracking systems. Table 2 presents a summary of tracking mechanisms implemented in different regions worldwide.

Table 2

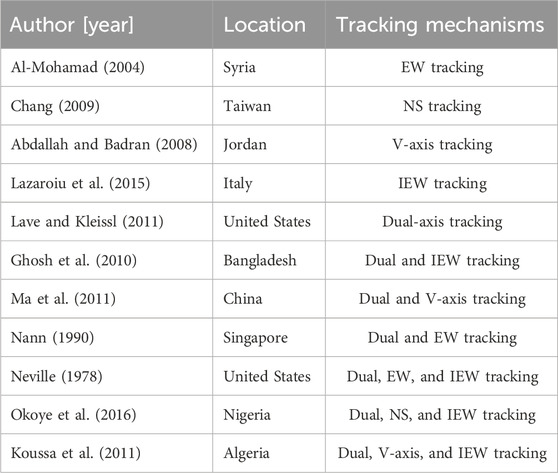
Table 2. Some of the previous works on optimizing solar radiation incidence on PV modules using different tracking mechanisms worldwide.

Here the study employed five solar tracking mechanisms: dual-axis, vertical-axis inclined surface, north-south, east-west, and inclined east-west axis tracking as illustrated in Figure 2. These configurations were implemented for 30 combination models (five decompositions and six transpositions) across the country. The solar angle parameters for each mechanism, as illustrated in Supplementary Figure S1 (Supplementary Material), are provided in Table 3.

Figure 2

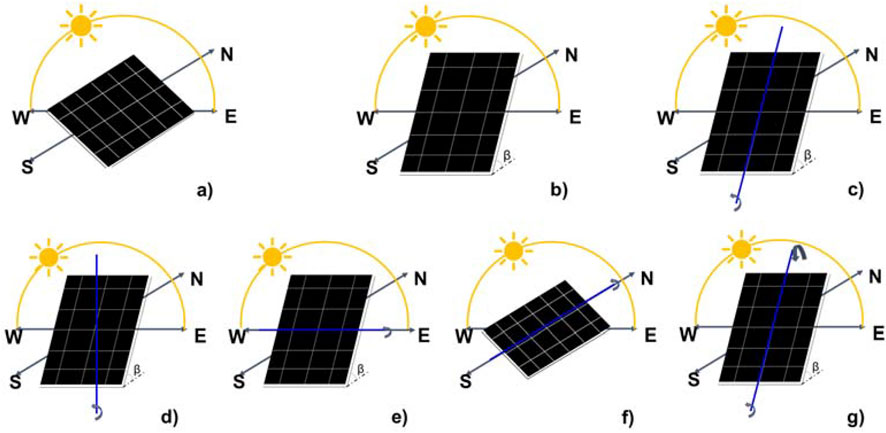
Figure 2. Illustrates various PV module tracking systems: (A) fixed horizontal, (B) fixed tilted south-facing, (C) inclined East-West, (D) vertical-axis, (E) North-South, (F) East-West, and (G) dual-axis (Zhu et al., 2020; Chang et al., 2009; Okoye et al., 2016).

Table 3

Table 3. Equations of solar angle parameters that are implemented for different tracking mechanisms (Zhu et al., 2020).

It is worth that, there is only 48.3% of the population had access to electricity in 2019, according to World Bank data, even if an enormous number of scholars were conducted worldwide (The World Bank, 2024). As a result, 92.8% of people live in cities and 36.3% in rural areas are electrified. Ethiopia, a country in East Africa with abundant solar resources, exhibits one of the lowest (hardly any) rates of solar energy production in the region as depicted in Figure 3 (Mekonnen et al., 2021). In addition, it is one of the least electrified countries and plans to construct new power plants; solar energy is one of the prior options for future sustainability for such a country. Consequently, we implemented different mechanisms to optimize the solar energy generated by the solar PV module/panel across the country.

Figure 3

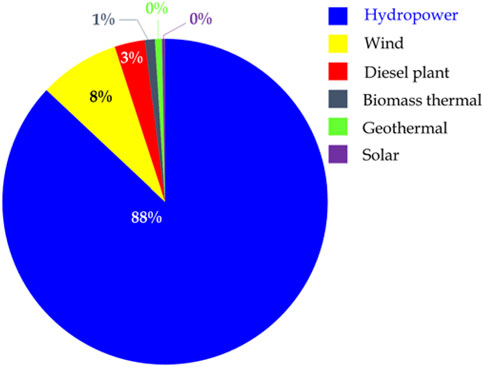
Figure 3. Power generation of Ethiopia (Mekonnen et al., 2021).

This study proposes a novel machine learning model for highly accurate global horizontal irradiance (GHI) prediction in Ethiopia (with, R² > 0.95, NSE > 0.94). An optimization framework determines optimal solar panel tilt angles, considering radiation distribution and tracking systems. The model incorporates panel characteristics for realistic energy potential and system performance estimates. This research emphasizes site-specific considerations for accurate solar energy system design and parameterization, supporting Ethiopia’s sustainable energy transition.

2 Study area, POA irradiance and PV cell/module

2.1 The study area

We utilized Python and ArcMap to process and analyze GHI data from the National Meteorological Institute (NMI) of Ethiopia. After preprocessing the data, we employed a stacked machine learning (ML) model to generate a (1° × 1°) GHI map of Ethiopia for 2022 as illustrated in Figure 4.

Figure 4

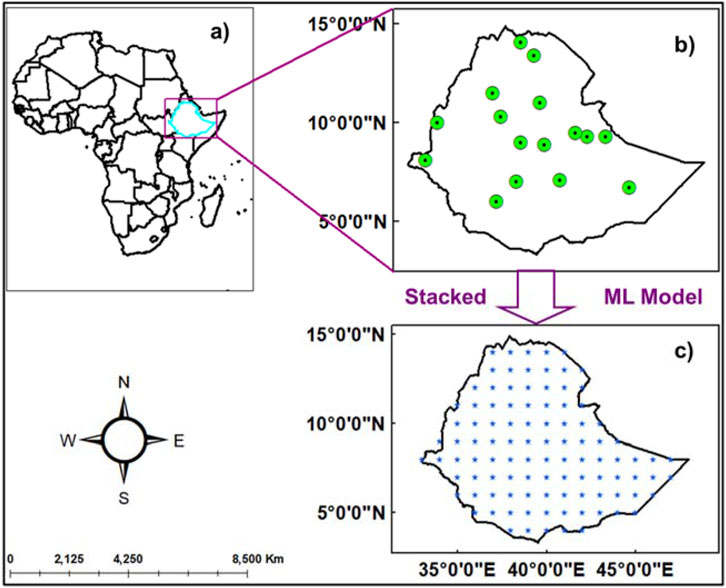
Figure 4. Study area and data source; map of Africa (A), map of Ethiopia, and stations that ground observational GHI [in W/m²] were accessed [green circle with a black dot at the center] (B), estimated 1° by 1° GHI map of Ethiopia using stacked (ensemble d) ML model (C).

2.2 POA irradiance and PV cell/module models

We employed five decomposition models Erbs et al. (1982), DISC (Maxwell, 1987), Boland et al. (2013), Louche et al. (1991), and Orgill and Hollands (1977) to derive DNI, DHI, and ground-reflected irradiance from GHI. Subsequently, we utilized three isotropic Liu and Jordan (1960), Badescu (2002), and Koronakis (1986) and three anisotropic [Reindl et al. (1990), Hay (1979), and Steven and Unsworth (1980)] models to estimate POA irradiance. Finally, we integrated the POA data into PVSystem.calcparams_cec () to determine PV module parameters (I_sc, V_oc, I_mp, V_mp, maximum power, efficiency) using a Canadian Solar module datasheet (see Supplementary Table S1) as depicted in Figure 5.

Figure 5

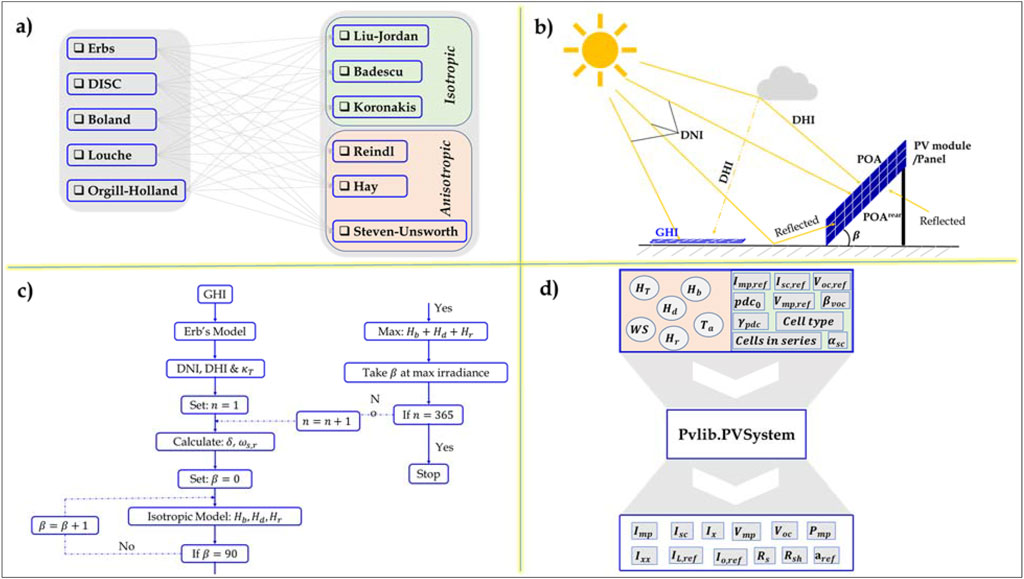
Figure 5. Depicts decomposition and transposition models (A), POA irradiance components (B), optimum tilt angle determination (C), and solar PV module electrical parameters (D).

3 Results and discussion

This research aimed to optimize PV integration into Ethiopia’s power infrastructure by determining ideal tilt angles and tracking mechanisms. Section 3.1 analyzed the optimal tilt angle’s monthly, seasonal, and annual variation with latitude. Section 3.2 assessed the spatial distribution of PV module performance for both horizontal and optimally tilted configurations. Finally, Section 3.3 evaluated the impact of different tracking mechanisms on PV module performance nationwide. The study considered four seasons: winter (Dec-Feb), spring (Mar-May), summer (Jun-Aug), and autumn (Sep-Nov).

3.1 Optimal tilt angle

3.1.1 Monthly optimal tilt angle

Figure 6 illustrates the monthly distribution of optimal PV module tilt angles across the country. A clear correlation emerges: higher latitudes necessitate larger tilt angles. The optimal tilt range spans from 0° in the summer months (June, July, August) to 47.9° in January. This suggests that maximizing solar gain during winter and autumn requires steeper PV module tilts. Conversely, shallower tilts are suitable for spring, while no tilt is needed in summer. Table 4 presents linear regression equations relating optimal tilt angle to latitude for the Erbs-Liu-Jordan model combination. Similar trends are observed in studies by Aksoy et al., Yunus et al., and Alhamer et al., confirming the latitude-dependent nature of optimal tilt angles for solar gain maximization (Aksoy Tırmıkçı and Yavuz, 2018; Yunus Khan et al., 2020; Alhamer et al., 2022).

Figure 6

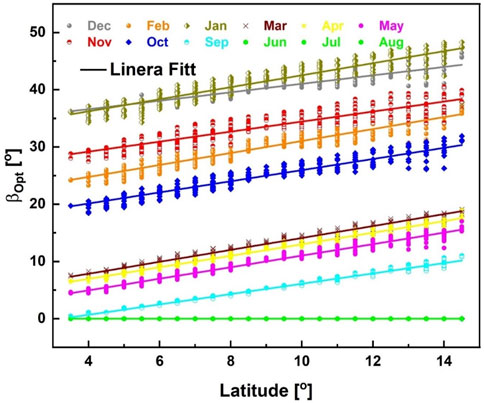
Figure 6. Monthly optimal tilt angle as a function of latitude (Erbs et al.-Liu-Jordan combination).

Table 4

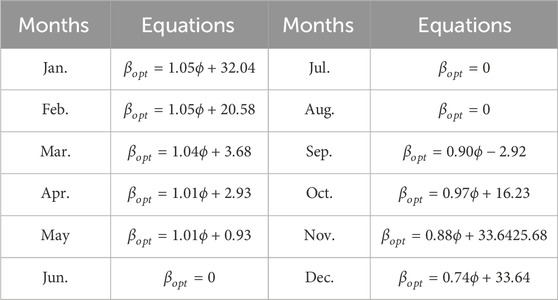
Table 4. Derived monthly optimal tilt angle models across the country (Erbs et al.-Liu-Jordan combination).

3.1.2 Seasonal optimal tilt angle

Figure 7 illustrates the seasonal variation of optimal tilt angles across the country, based on 30 Erbs-Liu-Jordan combination models. The average optimal tilt angle ranges from 24.80° to 33.60° in winter, 17.53°–25.77° in autumn, 8.67°–16.00° in spring, and 7.47°–10.13° in summer. This trend, where higher tilt angles are required in winter and lower angles in summer for maximum solar gain, aligns with the findings of Ashetehe et al. (2022). The linear relationships between latitude and optimal tilt angle for each season are detailed in Supplementary Table S2–S5.

Figure 7

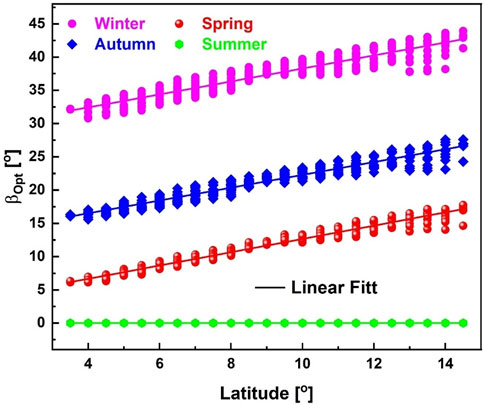
Figure 7. Seasonal distribution of optimal tilt angle across the country (Erbs et al.-Liu-Jordan combination model).

The analysis of 30 decomposition and transposition model combinations for optimal tilt angle estimation during autumn revealed significant variations in accuracy, with R² values ranging from 0.05 to 0.92. DISC-Reindl and Louche-Koronakis models demonstrated the highest and lowest correlations, respectively, emphasizing the importance of model selection. Anisotropic transposition models consistently yielded higher optimal tilt angles. Similar trends were observed for spring, with R² values ranging from 0.00 to 0.80. DISC-Koronakis, Orgill-Holland-Koronakis, Orgill-Holland-Liu-Jordan, Orgill-Holland-Hay, and Louche-Koronakis combinations exhibited the strongest correlations, while DISC and Erbs et al. with Liu-Jordan showed the weakest. In contrast, most models indicated a zero optimal tilt angle for summer, except for Boland-Liu-Jordan, Boland-Steven-Unsworth, DISC-Hay, Louche-Steven-Unsworth, and Orgill-Holland-Steven-Unsworth, which exhibited weaker correlations and non-zero tilt angles. This suggests the influence of the additional term in anisotropic models for diffused radiation coefficient. The winter season required substantial tilt angle adjustments, as evidenced by the higher slopes in the models compared to spring and summer. These findings underscore the importance of considering seasonal variations and model selection for accurate optimal tilt angle estimation and maximizing solar energy capture. Figure 8 illustrates the spatial distribution of seasonal optimal tilt angles across the nation.

Figure 8

Figure 8. Seasonal optimal tilt angle distribution map of Ethiopia.

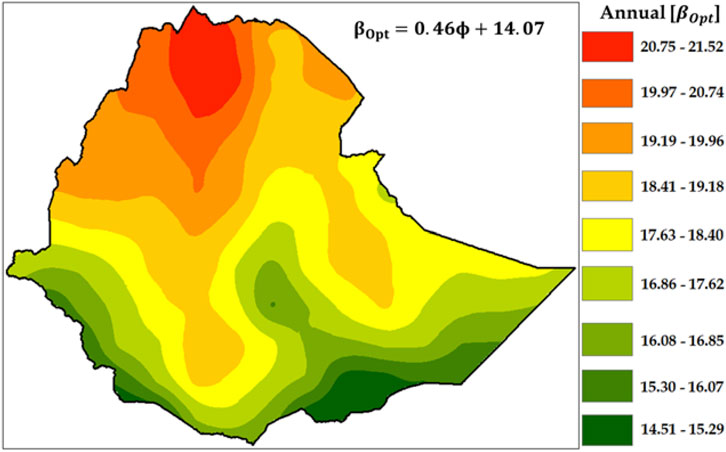
3.1.3 Annual optimal tilt angle

The annual optimal tilt angle in Ethiopia, varying from 14.10° to 21.53°, is consistently higher than the latitude by 7°–10° as depicted in Figure 9. This observation aligns with previous research and highlights the positive correlation between latitude and optimal tilt angle, where higher latitudes necessitate steeper panel inclinations for optimal solar energy harvesting (Duffie and Beckman, 1980). The linear model equation used to calculate the annual optimal tilt angle is also presented in Supplementary Table S6 and Supplementary Figure S2.

Figure 9

Figure 9. Annual optimal tilt angle distribution map of Ethiopia.

Overall, while frequent solar PV panel tilt adjustments can boost energy production, the labor costs often overshadow the gains. Studies indicate that less frequent adjustments, like quarterly or annually, can still yield substantial energy increases, ranging from 0% to 19.49% across various locations across the nation (Al Garni et al., 2019; Machidon and Istrate, 2023; Osmani et al., 2021). This approach balances energy maximization with cost minimization. The optimal adjustment frequency varies based on geographic location, panel tilt, and local solar irradiance patterns. However, for most installations, quarterly or annual adjustments are sufficient to achieve significant energy yields. Frequent adjustments, though beneficial, often have diminishing returns on investment. Thus, a tailored adjustment schedule can optimize energy production while minimizing operational expenses.

3.2 PV module performance

3.2.1 PV module mount at horizontal

Horizontally oriented PV modules in Ethiopia exhibit significant seasonal performance variations as illustrated in Table 5. Spring consistently yields the highest efficiency, ranging from 9.16% to 12.75%. Winter follows closely, with an efficiency range of 9.30%–12.34%. Autumn and summer exhibit lower performance, with efficiency ranges of 8.31%–11.93% and 6.88%–12.06%, respectively. A spatial analysis reveals that over 70% [i.e (area/total sum) $\times$ 100; for instance, the total sum of Ethiopia is $\sim$ 1.136$\times$ 10⁶ km (Gao et al., 2016)] of the country experiences high efficiency (10.97%–12.75%) during spring. In contrast, over 50% of the landmass faces reduced efficiency (6.88%–9.47%) in summer. Winter and autumn demonstrate intermediate performance, with 55% and 67% of the landmass, respectively, experiencing efficiency ranges of 10.83%–12.34% and 10.52%–12.29%. Understanding this spatial and seasonal distribution is crucial for optimizing solar energy harvesting and site selection in Ethiopia. By considering these factors, stakeholders can make informed decisions to maximize the potential of solar energy in the country. For further insight see Supplementary Figure S3.

Table 5

Table 5. PV module performance and landmass coverage in (%): horizontal mount.

3.2.2 PV module mount at optimal angle

PV modules mounted at optimal angles exhibited seasonal performance variations across the nation as illustrated in Table 6. Winter proved to be the most productive season, followed by spring, autumn, and summer. Efficiency ranged from 11.59% to 14.27% in winter, 9.59%–13.36% in spring, 8.81%–12.60% in autumn, and 6.88%–12.06% in summer. This optimal tilting yielded solar gains of 0%–19.49% compared to horizontal mounting, with no tilting required in summer. To further analyze performance, landmass coverage was assessed. Over 70% of the nation experienced 12.94%–14.27% efficiency in winter, while over 50% faced 6.88%–9.47% efficiency in summer. Spring and autumn showed intermediate performance with 11.54%–13.36% and 10.72%–12.60% efficiency over 69% and 58% of the landmass, respectively (see Supplementary Figure S4). Supplementary Figure S5 also shows the increased solar energy gain achieved by mounting PV modules at the optimal tilt angle compared to a horizontal mounting.

Table 6

Table 6. PV module performance and landmass coverage in (%): optimal tilt angle.

3.3 Tracking mechanisms

3.3.1 Vertical-axis tracking

Vertical-axis tracking significantly enhances solar energy capture, particularly during winter, as evidenced by the increased efficiency (15.11%–18.69%) compared to optimal tilt angle (11.00%–15.71%) and horizontal mounting (0%–30.68% gain). While autumn performance improves, summer benefits are minimal (0% gain). Notably, over 64% of the nation experiences high winter efficiency (16.91%–18.69%), contrasting with summer’s widespread low efficiency (6.88%–9.47%) across 50% of the landmass. Intermediate performance occurs in autumn (13.36%–15.71%) and spring (13.37%–15.63%) across 55% and 61% of the landmass, respectively (see Supplementary Figure S6). Table 7 details the seasonal performance of a vertical-axis tracking PV modules/panels. Supplementary Figure S7 also demonstrates the increased solar energy gain achieved by mounting PV modules using vertical axis tracking compared to the use of an optimal tilt angle or horizontal mounting.

Table 7

Table 7. PV module performance and landmass coverage in (%): vertical-axis tracking.

3.3.2 East-west (EW/IEW) tracking

Adjusting PV modules at an optimal tilt angle or implementing EW/IEW tracking significantly improved winter performance, with efficiencies ranging from 15.91% to 19.37%. This outperformed spring (13.37%–16.59%), autumn (12.83%–17.20%), and summer (9.82%–15.44%) seasons. EW/IEW tracking increased solar energy gain by 33.36%–63.00% compared to horizontal mounting, 33.36%–40.22% compared to optimal tilt, and 4.40%–33.36% compared to vertical-axis tracking. In winter, over 66% of the nation experienced 15.05%–16.99% efficiency, while summer saw a significant drop to 9.82%–12.63% over 50% of the landmass. Spring and autumn had intermediate performance, with 15.03%–17.20% (69% landmass) and 14.99%–16.59% (57% landmass) efficiency ranges, respectively (see Supplementary Figure S8). Table 8 provides a detailed breakdown of the seasonal performance of east-west axis tracking solar panels. Additionally, Supplementary Figure S9 illustrates the significant increase in solar energy yield achieved by employing an east-west tracking system for mounting solar panels compared to vertical axis tracking, optimal tilt angle positioning, or a horizontal mounting configuration.

Table 8

Table 8. PV module performance and landmass coverage in (%): EW/IEW tracking.

3.3.3 North-south (NS) tracking

NS tracking was found to be ineffective for low-latitude countries like Ethiopia, as confirmed by previous research Bahrami et al. (2016). PV modules with NS tracking exhibited the best performance in the spring season, with efficiency ranging from 6.42% to 10.70% as illustrated in Table 9. In contrast, winter, autumn, and summer seasons showed lower efficiency, with maximum losses of 63.00%, 40.22%, and 33.36%, respectively, compared to horizontal, optimal tilt, vertical axis, and IEW tracking (see Supplementary Figure S11). Over 56% of the nation experienced 6.42%–8.56% efficiency in spring, while winter, autumn, and summer seasons had lower coverage rates of 64%, 51%, and 56%, respectively (see Supplementary Figure S10).

Table 9

Table 9. PV module performance and landmass coverage in (%): NS tracking.

3.3.4 Dual-axis or full tracking (DAT)

Dual-axis tracking significantly enhanced solar energy generation, especially in winter, compared to other tracking mechanisms or fixed-tilt installations. Winter PV module efficiency ranged from 15.91% to 19.37%, surpassing spring (13.69%–16.99%), autumn (12.82%–17.27%), and summer (10.29%–15.82%) as illustrated in Table 10. The maximum solar energy gains relative to fixed-tilt, vertical-axis, IEW, and NS tracking were 62.99%, 40.26%, 37.71%, and 14.64% in winter, respectively (see Supplementary Figure S13). Notably, dual-axis and EW/IEW tracking yielded similar performance, particularly in winter and autumn, suggesting that EW/IEW tracking is a cost-effective alternative. Over 66% of the nation experienced high winter efficiency (17.65%–19.37%), while spring, autumn, and summer saw 70%, 57%, and 51% of the landmass with efficiency ranges of 15.35%–16.99%, 15.02%–17.27%, and 10.26%–13.04%, respectively (see Supplementary Figure S12).

Table 10

Table 10. PV module performance and landmass coverage in (%): Dual tracking.

3.3.5 Annual performance

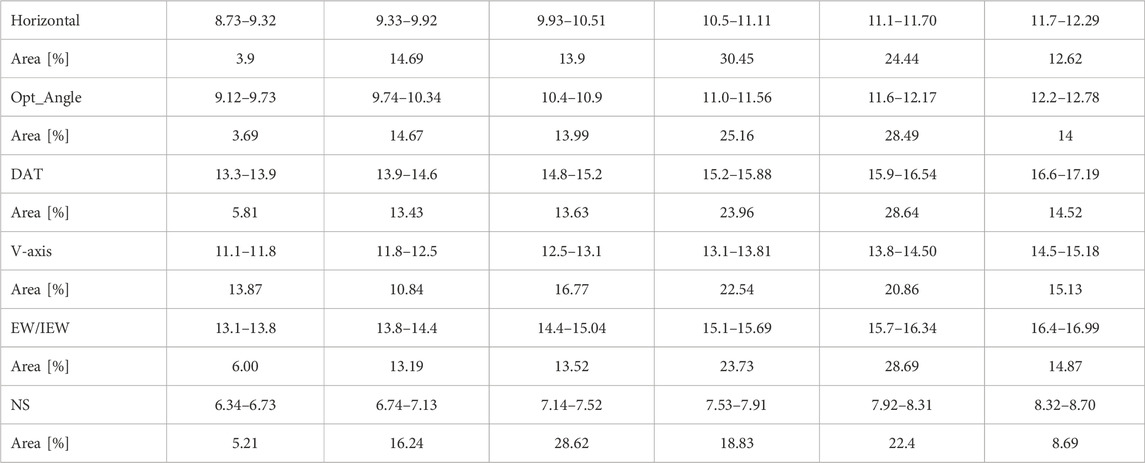
The annual performance efficiency of PV modules ranged from 8.73% to 17.19%, with dual/full tracking yielding the highest performance, followed closely by EW/IEW tracking as illustrated in Figure 10. Compared to horizontally mounted modules, dual/full tracking increased annual solar energy gain by up to 50.62%, while EW/IEW tracking increased it by up to 1.22% as presented in Figure 11. This suggests that implementing yearly optimal tilt angle for south-facing PV modules with EW/IEW tracking might be sufficient, potentially eliminating the need for specific IEW tilt angle calculations. Table 11 provides a detailed breakdown of the annual performance of PV module/panel at different scenarios.

Figure 10

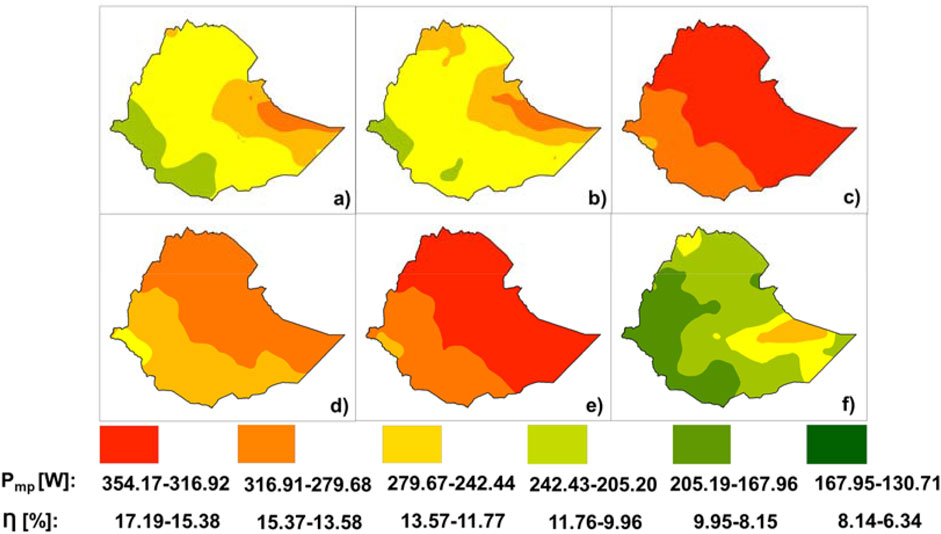
Figure 10. Illustrates the annual distribution of PV module efficiency (η) for various mounting configurations: horizontal (A), optimal tilt (B), dual/full tracking (C), vertical-axis tracking (D), EW/IEW tracking (E), and NS tracking (F).

Figure 11

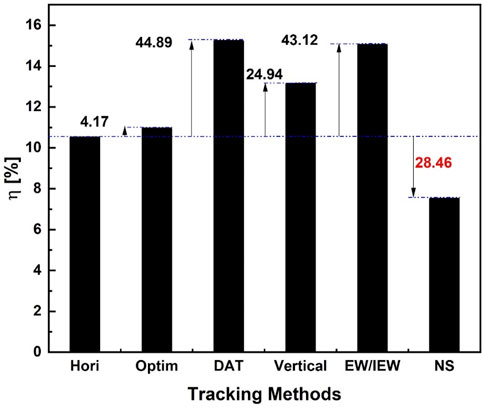
Figure 11. Annual solar energy gain for different implemented mechanisms relative to horizontally mounted solar PV module/panel.

Table 11

Table 11. PV module performance and landmass coverage in (%): Annual.

Solar tracking systems can significantly enhance solar energy harvesting, but their maintenance and operational costs pose significant challenges (Lorilla and Barroca, 2022; Sadat-Mohammadi et al., 2018). The moving parts of these systems are prone to wear and tear, particularly in harsh environments (Walker et al., 2020). Complex electrical components are also susceptible to failures and degradation. Access to skilled technicians and spare parts, especially in remote areas, can further increase maintenance costs and downtime. Therefore, a thorough evaluation of these factors is crucial to assess the overall cost-effectiveness of solar tracking systems in specific applications.

4 Conclusion

This research investigated the optimal tilt angles for photovoltaic (PV) modules across Ethiopia, considering various decomposition and transposition models. The study found that the optimal tilt angle increases with latitude for most months and seasons, except for the summer months (June, July, August). The annual optimal tilt angle was determined to be 7–10° greater than the latitude. Different tracking mechanisms were also evaluated, with dual-axis tracking showing the highest performance gain, followed by east-west/inclined east-west tracking. Vertical-axis tracking also yielded significant improvements, while north-south tracking resulted in a performance loss compared to horizontal mounting. This study provides valuable insights for PV system design and installation in Ethiopia. Future research will focus on refining solar energy prediction models by incorporating detailed environmental data and considering various PV module types.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AG: Writing–original draft, Writing–review and editing. AB: Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Financial support from the International Science Program (ISP, IPPS ETH: 03, 2021 – 2026) is gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1519725/full#supplementary-material

Abbreviations

$H_T$, Total irradiance on the tilted surface [W/m²]; $H_b$, Direct or beam irradiance [W/m²]; $H_d$, Diffused irradiance [W/m²]; $H_r$, Reflected irradiance [W/m²]; $T_a$, Ambient temperature [^oC]; $WS$, Wind speed [m/s]; $P_{dc0}$, DC-power reference condition [W]; ${\gamma }_{pdc}$, Temperature coefficients power [1/^oC]; ${\alpha }_{sc}$, Normalized temperature coefficient for I_sc [1/°C]; $I_{mp-ref}$, Current at maximum power point at reference conditions [A]; $I_{sc-ref}$, Short circuit current at reference conditions [A]; $I_{L-ref}$, Light-generated current at reference conditions [A]; $I_{o-ref}$, Diode saturation current at reference conditions [A]; $I_x$, Current at module V = 0.5*V_oc; $I_{xx}$, Current at module V = 0.5*(V_oc + V_mp); $I_{mp}$, Current at the maximum power point [A]; $I_{sc}$, Short circuit current [A]; $V_{mp-ref}$, Voltage at maximum power point at reference conditions [V]; $V_{oc-ref}$, Open circuit voltage at reference conditions [V]; $R_s$, Series resistance [Ω]; $R_{sh}$, Shunt resistance [Ω]; ${\beta }_{voc}$, Temperature coefficient for module open-circuit-voltage [V/^oC]; ${\alpha }_{mp}$, Normalized temperature coefficient for I_mp [1/°C].

References

Abdallah, R., Juaidi, A., Abdel-Fattah, S., and Manzano-Agugliaro, F. (2020). Estimating the optimum tilt angles for south-facing surfaces in Palestine. Energies 13 (3), 623. doi:10.3390/en13030623

CrossRef Full Text | Google Scholar

Abdallah, S., and Badran, O. O. (2008). Sun tracking system for productivity enhancement of solar still. Desalination 220, 669–676. doi:10.1016/j.desal.2007.02.047

CrossRef Full Text | Google Scholar

Aksoy Tırmıkçı, C., and Yavuz, C. (2018). Determining optimum tilt angles of solar surfaces in Sakarya, Turkey. Theor. Appl. Climatol. 133, 15–22. doi:10.1007/s00704-017-2174-x

CrossRef Full Text | Google Scholar

Al Garni, H. Z., Awasthi, A., and Wright, D. (2019). Optimal orientation angles for maximizing energy yield for solar PV in Saudi Arabia. Renew. energy 133, 538–550. doi:10.1016/j.renene.2018.10.048

CrossRef Full Text | Google Scholar

Alhamer, E., Grigsby, A., and Mulford, R. (2022). The influence of seasonal cloud cover, ambient temperature and seasonal variations in daylight hours on the optimal PV panel tilt angle in the United States. Energies 15 (20), 7516. doi:10.3390/en15207516

CrossRef Full Text | Google Scholar

Al-Mohamad, A. (2004). Efficiency improvements of photo-voltaic panels using a Sun tracking system. Appl. Energy 79, 345–354. doi:10.1016/j.apenergy.2003.12.004

CrossRef Full Text | Google Scholar

Ashetehe, A. A., Gessesse, B. B., and Shewarega, F. (2022). Development of optimal tilt angle models of a photovoltaic module for maximum power production: Ethiopia. Int. J. Photoenergy 2022 (1), 1–18. doi:10.1155/2022/8729570

CrossRef Full Text | Google Scholar

Badescu, V. (2002). A new kind of cloudy sky model to compute instantaneous values of diffuse and global solar irradiance. Theor. Appl. Climatol. 72 (1-2), 127–136. doi:10.1007/s007040200017

CrossRef Full Text | Google Scholar

Bahrami, A., Okoye, C. O., and Atikol, U. (2016). The effect of latitude on the performance of different solar trackers in Europe and Africa. Appl. energy 177, 896–906. doi:10.1016/j.apenergy.2016.05.103

CrossRef Full Text | Google Scholar

Benghanem, M. (2011). Optimization of tilt angle for solar panel: case study for Madinah, Saudi Arabia. Appl. Energy 88 (4), 1427–1433. doi:10.1016/j.apenergy.2010.10.001

CrossRef Full Text | Google Scholar

Berisha, X., Zeqiri, A., and Meha, D. (2017). Solar radiation—the estimation of the optimum tilt angles for southsouth-facing surfaces in pristina. Preprints 13. doi:10.20944/preprints201708.0010.v1

CrossRef Full Text | Google Scholar

Boland, J., Huang, J., and Ridley, B. (2013). Decomposing global solar radiation into its direct and diffuse components. Renew. Sustain. Energy Rev. 28, 749–756. doi:10.1016/j.rser.2013.08.023

CrossRef Full Text | Google Scholar

Chang, T. P. (2009). The gain of single-axis tracked panel according to extraterrestrial ra diation. Appl. Energy. 86 (7–8). doi:10.1016/j.apenergy.2008.08.002

CrossRef Full Text | Google Scholar

Darhmaoui, H., and Lahjouji, D. (2013). Latitude based model for tilt angle optimization for solar collectors in the Mediterranean region. Energy Procedia 42, 426–435. doi:10.1016/j.egypro.2013.11.043

CrossRef Full Text | Google Scholar

Duffie, J. A., and Beckman, W. A. (1980). Solar engineering of thermal processes. New York: Wiley.

Google Scholar

Erbs, D. G., Klein, S. A., and Duffie, J. A. (1982). Estimation of the diffuse radiation fraction for hourly, daily, and monthly-average global radiation. Sol. Energy 28, 293–302. doi:10.1016/0038-092x(82)90302-4

CrossRef Full Text | Google Scholar

Gao, K., Miao, J., Xiao, L., Deng, W., Kan, Y., Liang, T., et al. (2016). Multi-length-scale morphologies driven by mixed additives in porphyrin-based organic photovoltaics. Adv. Mater 28, 4727–4733. doi:10.1002/adma.201505645

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghosh, H. R., Bhowmik, N. C., and Hussain, M. (2010). Determining seasonal optimum tilt angles, solar radiations on variously oriented, single and double axis tracking surfaces at Dhaka. Renew. Energy 35, 1292–1297. doi:10.1016/j.renene.2009.11.041

CrossRef Full Text | Google Scholar

Goldberg, D. M., and Gott, J. R. (2007). Flexion and skewness in map projections of the earth. Cartogr. Int. J. Geogr. Inf. Geo- Vis. 42 (4), 297–318. doi:10.3138/carto.42.4.297

CrossRef Full Text | Google Scholar

Hay, J. E. (1979). Calculation of monthly mean solar radiation for horizontal and inclined surfaces. Sol. Energy 23 (4), 301–307. doi:10.1016/0038-092x(79)90123-3

CrossRef Full Text | Google Scholar

Jacobson, M. Z., and Jadhav, V. (2018). World estimates of PV optimal tilt angles and ratios of sunlight incident upon tilted and tracked PV panels relative to horizontal panels. Sol. Energy 169, 55–66. doi:10.1016/j.solener.2018.04.030

CrossRef Full Text | Google Scholar

Koronakis, P. S. (1986). On the choice of the angle of tilt for south facing solar collectors in the Athens basin area. Sol. Energy 36 (3), 217–225. doi:10.1016/0038-092x(86)90137-4

CrossRef Full Text | Google Scholar

Koussa, M., Cheknane, A., Hadji, S., Haddadi, M., and Noureddine, S. (2011). Measured and modelled improvement in solar energy yield from flat plate photovoltaic systems utilizing different tracking systems and under a range of environmental conditions. Appl. Energy 88 (5), 1756–1771. doi:10.1016/j.apenergy.2010.12.002

CrossRef Full Text | Google Scholar

Lamoureux, A., Lee, K., Shlian, M., Forrest, S. R., and Shtein, M. (2015). Dynamic kirigami structures for integrated solar tracking. Nat. Commun. 6, 8092. doi:10.1038/ncomms9092

PubMed Abstract | CrossRef Full Text | Google Scholar

Lave, M., and Kleissl, J. (2011). Optimum fixed orientations and benefits of tracking for capturing solar radiation in the continental United States. Renew. Energy 36, 1145–1152. doi:10.1016/j.renene.2010.07.032

CrossRef Full Text | Google Scholar

Lazaroiu, G. C., Longo, M., Roscia, M., and Pagano, M. (2015). Comparative analysis of fixed and sun tracking low power PV systems considering energy consumption. Energy Convers. Manage 92, 143–148. doi:10.1016/j.enconman.2014.12.046

CrossRef Full Text | Google Scholar

Liu, B. Y. H., and Jordan, R. C. (1960). The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy 4 (3), 1–19. doi:10.1016/0038-092x(60)90062-1

CrossRef Full Text | Google Scholar

Lorilla, F. M. A., and Barroca, R. (2022). Challenges and recent developments in solar tracking strategies for concentrated solar parabolic dish. Indones. J. Electr. Eng. Comput. Sci. 26 (3), 1368. doi:10.11591/ijeecs.v26.i3.pp1368-1378

CrossRef Full Text | Google Scholar

Louche, A., Notton, G., Poggi, P., and Simonnot, G. (1991). Correlations for direct normal and global horizontal irradiation on a French Mediterranean site. Sol. Energy 46 (4), 261–266. doi:10.1016/0038-092x(91)90072-5

CrossRef Full Text | Google Scholar

Ma, T., Li, G., and Tang, R. (2011). Optical performance of vertical axis three azimuth angles tracked solar panels. Appl. Energy 88, 1784–1791. doi:10.1016/j.apenergy.2010.12.018

CrossRef Full Text | Google Scholar

Machidon, D., and Istrate, M. (2023). Tilt angle adjustment for incident solar energy increase: a case study for Europe. Sustainability 15 (8), 7015. doi:10.3390/su15087015

CrossRef Full Text | Google Scholar

Maxwell, E. L. (1987). A quasi-physical model for converting hourly global horizontal to direct normal insolation (No. SERI/TR-215-3087). Golden, CO: Solar Energy Research Inst. (USA).

Google Scholar

Mekonnen, T., Bhandari, R., and Ramayya, V. (2021). Modeling, analysis and optimization of grid-integrated and islanded solar PV systems for the Ethiopian residential sector: considering an emerging utility tariff plan for 2021 and beyond. Energies 14 (11), 3360. doi:10.3390/en14113360

CrossRef Full Text | Google Scholar

Nann, S. (1990). Potentials for tracking photovoltaic systems and V-troughs in moderate climates. Sol. Energy 45, 385–393. doi:10.1016/0038-092x(90)90160-e

CrossRef Full Text | Google Scholar

Neville, R. (1978). Solar energy collector orientation and tracking mode. Sol. Energy 20, 7–11. doi:10.1016/0038-092x(78)90134-2

CrossRef Full Text | Google Scholar

Okoye, O. C., Taylan, O., and Baker, D. K. (2016). Solar energy potentials in strategically located cities in Nigeria: review, resource assessment, and PV system design. Renew. Sustain Energy Rev. 55, 550–566. doi:10.1016/j.rser.2015.10.154

CrossRef Full Text | Google Scholar

Orgill, J. F., and Hollands, K. G. T. (1977). Correlation equation for hourly diffuse radiation on a horizontal surface. Sol. Energy 19, 357–359. doi:10.1016/0038-092x(77)90006-8

CrossRef Full Text | Google Scholar

Ortner, M. H. A., Hiesl, A., and Haas, R. (2015). East to west—the optimal tilt angle and orientation of photovoltaic panels from an electricity system perspective. Appl. Energy 160, 94–107. doi:10.1016/j.apenergy.2015.08.097

CrossRef Full Text | Google Scholar

Osmani, K., Ramadan, M., Lemenand, T., Castanier, B., and Haddad, A. (2021). Optimization of PV array tilt angle for minimum levelized cost of energy. Comput. and Electr. Eng. 96, 107474. doi:10.1016/j.compeleceng.2021.107474

CrossRef Full Text | Google Scholar

Reindl, D. T., Beckman, W. A., and Duffie, J. A. (1990). Evaluation of hourly tilted surface radiation models. Sol. Energy 45 (1), 9–17. doi:10.1016/0038-092x(90)90061-g

CrossRef Full Text | Google Scholar

Sadat-Mohammadi, M., Nazari-Heris, M., Nafisi, H., and Abedi, M. (2018). “November. A comprehensive financial analysis for dual-axis sun tracking system in Iran photovoltaic panels,” in 2018 Smart Grid Conference (SGC), Iran, 28-29 November 2018 (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Safdarian, F., and Nazari, M. E. (2015). “Optimal tilt angle and orientation for solar collectors in Iran,” in Proceedings of the IEEE 10th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September (IEEE).

CrossRef Full Text | Google Scholar

Skeiker, K. (2009). Optimum tilt angle and orientation for solar collectors in Syria. Energy Convers. Manag. 50, 2439–2448. doi:10.1016/j.enconman.2009.05.031

CrossRef Full Text | Google Scholar

Steven, M. D., and Unsworth, M. H. (1980). The angular distribution and interception of diffuse solar radiation below overcast skies. Q. J. R. Meteorological Soc. 106 (447), 57–61. doi:10.1256/smsqj.44704

CrossRef Full Text | Google Scholar

Tang, R., and Wu, T. (2004). Optimal tilt-angles for solar collectors used in China. Appl. Energy 79, 239–248. doi:10.1016/j.apenergy.2004.01.003

CrossRef Full Text | Google Scholar

The World Bank (2024). The World Bank. Available at: https://data.worldbank.org.

Google Scholar

Walker, H., et al. (2020). Model of operation-and-maintenance costs for photovoltaic systems. Golden, CO (United States): National Renewable Energy Lab. NREL. No. NREL/TP-5C00-74840.

Google Scholar

Wang, D. D., and Sueyoshi, T. (2017). Assessment of large commercial rooftop photovoltaic system installations: evidence from California. Appl. Energy 188, 45–55. doi:10.1016/j.apenergy.2016.11.076

CrossRef Full Text | Google Scholar

Yadav, A. K., and Chandel, S. S. (2013). Tilt angle optimization to maximize incident solar radiation: a review. Renew. Sustain. energy Rev. 23, 503–513. doi:10.1016/j.rser.2013.02.027

CrossRef Full Text | Google Scholar

Yakup, M. A. B. H. M., and Malik, A. Q. (2001). Optimum tilt angle and orientation for solar collector in Brunei Darussalam. Renew. Energy 24, 223–234. doi:10.1016/s0960-1481(00)00168-3

CrossRef Full Text | Google Scholar

Yunus Khan, T. M., Soudagar, M. E. M., Kanchan, M., Afzal, A., Banapurmath, N. R., Akram, N., et al. (2020). Optimum location and influence of tilt angle on performance of solar PV panels. J. Therm. Analysis Calorim. 141, 511–532. doi:10.1007/s10973-019-09089-5

CrossRef Full Text | Google Scholar

Zhu, Y., Liu, J., and Yang, X. (2020). Design and performance analysis of a solar tracking system with a novel single-axis tracking structure to maximize energy collection. Appl. Energy 264, 114647. doi:10.1016/j.apenergy.2020.114647

CrossRef Full Text | Google Scholar