Flexible low carbon optimal dispatch of distribution networks considering the demand response of heat storage industrial loads

To cope with the uncertainty brought by the large-scale integration of renewable energy under the goal of carbon neutrality, it is necessary to tap and utilize flexible and adjustable resources from both the source and the load side at the same time. Hence, a flexible low-carbon optimal scheduling method for distribution networks is proposed in this paper, which takes into account the participation of heat storage industrial loads in demand response. Firstly, the model of the gas turbine equipped with a flexible carbon capture device is established, and the non-convex constraint introduced by the adjustable flue gas diversion ratio is convexified. Then the model of the fused magnesium load, a representative of heat storage industrial loads, is established for its participation in demand response. The segment linearization and convexification methods are performed on the conditional productivity constraints of the fused magnesium load. On this basis, a mixed-integer linear programming model for flexible and low-carbon optimal dispatch of the distribution network is developed by using the stochastic optimization theory and solved by commercial solvers. The proposed method is verified to be able to ensure the economic operation of the distribution network while reducing carbon emissions and promoting renewable energy consumption.

1 Introduction

As energy shortages and global warming issues have become increasingly severe, the major countries of the world have signed the Paris Agreement. Since the power industry is a major source of carbon emissions, these countries are vigorously promoting the deployment of renewable energy sources (RES) to relieve the pressure of decarbonization and achieve the anticipated emission reduction targets (Xu et al., 2023; Xu and Yi, 2023). However, the uncertainty, volatility, and anti-peak characteristics of the RES output pose a huge challenge to the stable operation of the system (Cheng et al., 2023; Tan et al., 2019). Since the distribution network is integrated with various types of distributed RES, how to ensure the continuity and reliability of power supply is a particularly evident challenge (Zhang et al., 2024; Zhang et al., 2023; Huang et al., 2020).

To address the challenges of integrating RES, gas turbines and demand response are becoming attractive measures (Zhang and Zhu, 2024; Condessa et al., 2023; de Chalendar et al., 2023). Gas turbines are an ideal choice as backup power sources for RES due to their high efficiency and relatively low carbon emissions. However, to achieve the emission reduction and the carbon neutrality targets, even gas turbines need further decarbonization. Gas turbines installed with flexible carbon capture technology (FCCGT) have high commercial maturity and do not require large-scale retrofits to the existing gas turbine, which is a promising technology to reduce carbon emissions (Fan et al., 2023). It is proposed in (Wilkes et al., 2021) that the quick-response capability of gas turbines is indispensable for providing system flexibility. When combined with post-combustion carbon capture technology, gas turbines offer critical support for the transition to a future low-carbon society. Integrating flexible combined-cycle gas turbines with carbon capture and storage technology is investigated and analyzed in (Chyong et al., 2023) for constructing low-carbon power systems. A laddered carbon trading-based operation model is proposed in (Gao et al., 2024) for an integrated electricity-gas system considering the complex combustion properties of hydrogen mixed gas turbine. In (Wang et al., 2022), the liquid storage carbon capture and power to gas technologies are applied to construct a coordinated heat and power operation model, which takes into account the carbon trading cost. Besides, due to the large thermal inertia of the heat storage industrial loads (HSIL), their operating power can be rapidly adjusted upward or downward with little impact on the production process, which play an important role in the demand-side management of the distribution network. Through demand response (DR) technology, HSIL can be flexibly dispatched within a certain range, which improves the matching degree of load demand and RES output and enhance the stability of the distribution system (Boldrini et al., 2024; Shao et al., 2021). Hence, exploiting the DR potential of HSIL helps balance the power supply and demand to enable the increase of RES integration, which indirectly contributes to carbon emission reduction (Wang J. et al., 2023). As one of the representative HSIL, magnesium load using an electric arc furnace (MLEAF) has a simple production process, but can provide significant regulation capability due to its thermal inertia. Therefore, modelling the DR participation of MLEAF with a low complexity has become a research focus in recent years. A novel adaptive Proportional-Integral-Derivative controller has been developed to regulate the melting current of MLEAF within desired parameters, resulting in significant energy savings (Wang W. et al., 2023). Based on a comprehensive analysis of the characteristics of electrical arc furnace, a refined model of MLEAF is developed in (Wang et al., 2024). Besides, a low-carbon dispatch method is proposed in (Zhao et al., 2024) to consider the demand regulation of MLEAF and the fluctuation of wind power generation, which achieves stable and reliable operation of the power system through the integration of thermal power plants and the introduction of battery energy storage systems.

However, there are still many challenges about how to effectively integrate FCCGT and the DR capacity of HSIL to relieve the distribution network dispatch pressure:

1) The uncertainty and anti-peak characteristics of RES output place higher requirements on the response speed and flexibility of the distribution network. If the RES output is low during load peaks, it will inevitably lead to an increase in FCCGT and carbon emissions, requiring the capture and processing of more CO₂. In this case, the power consumption of the carbon capture (CC) device of FCCGT increases accordingly, bringing extra load to the load peaks. This phenomenon is called “peak-on-peak,” which severely damages the power balance of the distribution network.

2) The large-scale utilization of flexible resources from both the supply and demand sides increases the complexity of the distribution network optimal dispatch model. Unreasonable modeling methods and solving algorithms not only fail to improve the economic efficiency of the dispatch plan but may even threaten the safety of distribution network operation and load power supply (Qi et al., 2023; Gabrielli et al., 2022). For example, the HSIL equipment’s working temperature has impacts on the production output and quality, so the changes in temperature need strict limits. If these impacts and limits are ignored in the DR model, the actual response willingness of HSIL may be much lower than expected, which brings greater pressure in turn to the distribution network operation (Wang et al., 2024; Yue et al., 2024).

To solve the problems above, a flexible low-carbon optimal dispatch model is proposed for the distribution network in this paper, which contains the models of FCCGT and a representative HSIL, i.e., MLEAF. The contributions of this model are listed below:

1) The model of FCCGT with storage tanks is constructed, where the non-linear constraints related to the adjustable flue gas diversion ratio is convexified by the McCormick envelope method.

2) The model for the DR participation of MLEAF is proposed, where 0-1 auxiliary variables are introduced to construct the piece-wise function-based production output constraints and the resulting bilinear terms are convexified.

3) Based on the models of FCCGT and MLEAF, a mixed-integer linear stochastic optimization model is established with typical forecast error scenarios of RES and load to realize the low-carbon dispatch of the distribution network, which can be solved by commercial solvers such as CPLEX.

The rest of the paper is organized as follows. In Section 2, the operation mechanism is analyzed and the linearized model is constructed for FCCGT. In Section 3, the DR model of MLEAF is established where the production output constraints are convexified. Then the flexible low-carbon optimal dispatch model of the distribution network is detailed with its objective function and constraints in Section 4. Numerical tests are performed on a modified IEEE 33-bus system and the results are discussed in Section 5. The conclusions are summarized in Section 6.

2 FCCGT operation mechanism and mathematical model

2.1 FCCGT structure and operation mode

Based on the combustion process, CC technologies can be classified into oxy-fuel combustion, pre-combustion capture, and post-combustion capture. Based on the operating modes, they can be divided into slipstream mode, storage mode, and integrated flexible operation mode.

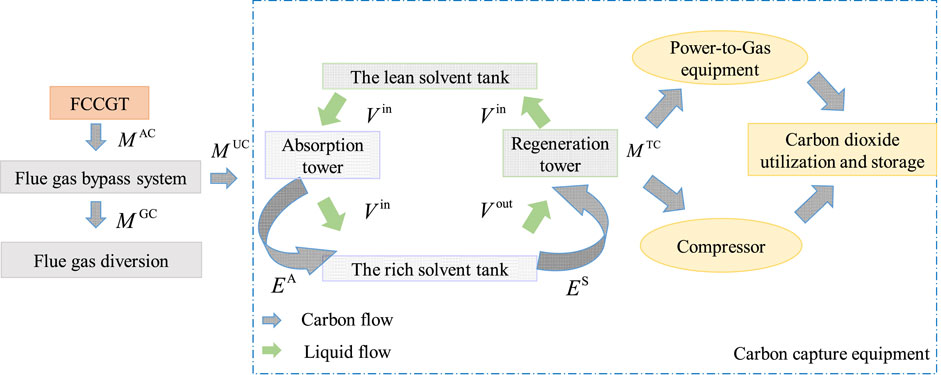
Considering the commercial and technological maturity, the post-combustion capture technology with integrated flexible operation mode is adopted by FCCGT, which is realized by installing a flue gas bypass system and a solvent storage tank on the gas turbine (Song et al., 2024). The operation process of FCCGT is shown in Figure 1.

Figure 1

Figure 1. Integrated flexible operation process of FCCGT.

FCCGT controls the flue gas bypass system to feed a certain proportion of the flue gas generated by the gas turbine into the absorption tower. In this tower, the flue gas reacts with an ethanolamine (MEA) solution to obtain a CO₂-rich solution, which is stored in the rich solution storage tank. The rich solution pump is then adjusted to control the rich solution fed to the regeneration tower, where the rich solution is heated with extracted steam to cause counter-reaction to separate CO₂ from the MEA. The separated CO₂ is partially used as feedstock of a power-to-gas facility to produce methane for the natural gas network, while the remaining CO₂ is compressed for storage. The regenerated lean MEA solution is pumped back into the lean solution storage tank and recirculated to the absorption tower for reuse. This integrated flexible operation allows FCCGT to efficiently capture and utilize the CO₂ generated by the gas turbine.

Compared to gas turbines equipped with traditional CC device, the unique features of FCCGT are:

1. Flexible and controllable flue gas diversion ratio: By adjusting the flue gas bypass system, the proportion of flue gas entering the CC device can be controlled, allowing a balance between operating costs and carbon emissions.

2. Flexible carbon capture based on solution storage tanks: The CC amount is decoupled with the CC power consumption, which leads to a wider range of net power output of FCCGT. Such CO₂ processing flexibility serves as a supplementary resource to promote the consumption of RES power and contribute to the power balance of the distribution network.

Due to these distinctive features, a targeted model needs to be established for FCCGT.

2.2 The mathematical model of FCCGT

According to Figure 1, the model reflecting the power output and real-time CC amount of FCCGT is expressed as follows:

$\left\{\begin{array}{l}{P}_t^{\text{FCC}}=P_{\mathrm{e},t}^{\text{FCC}}+\chi M_t^{\text{TC}}+P_t^{\mathrm{Y}}\\ M_t^{\text{TC}}=M_t^{\text{UC}}+E_t^{\mathrm{S}}-E_t^{\mathrm{A}}\\ M_t^{\text{UC}}={\theta }_{\max }^{\text{CC}}{\gamma }^{\text{FCC}}{\delta }_t{P}_t^{\text{FCC}}\\ M_t^{\text{AC}}={\gamma }^{\text{FCC}}{P}_t^{\text{FCC}}\\ M_t^{\text{GC}}=M_t^{\text{AC}}-M_t^{\text{UC}}\\ {\delta }_{\min }\le {\delta }_t\le {\delta }_{\max },P_{\min }^{\text{FCC}}\le P_t^{\text{FCC}}\le P_{\max }^{\text{FCC}}\\ 0\le M_t^{\text{TC}}\le \eta {\theta }_{\max }^{\text{CC}}{\gamma }^{\text{FCC}}{P}_{\max }^{\text{FCC}}\end{array}\right.(1)$

where t is the index of time. $P_t^{\text{FCC}}$ is the total power output of FCCGT. $P_{\mathrm{e},t}^{\text{FCC}}$ is the net power delivered to the distribution network by FCCGT. $P_t^{\mathrm{Y}}$ is the CC power consumption of the CC device. χ is the consumed power for capturing unit mass of CO₂ (MWh/t). $M_t^{\text{TC}}$ is the total mass of the captured CO₂, $M_t^{\text{UC}}$ is the mass of CO₂ entering the CC device after flue gas diversion (t). $E_t^{\mathrm{S}}$ is the mass of CO₂ supplied from the rich solution storage tank (t). $E_t^{\mathrm{A}}$ is the mass of CO₂ absorbed by the rich solution storage tank (t). ${\delta }_t$ is the flue gas diversion ratio. ${\theta }_{\max }^{\text{CC}}$ is the maximum CC level. $M_t^{\text{AC}}$ is the total mass of CO₂ produced by FCCGT (t). ${\gamma }^{\text{FCC}}$ is the CO₂ emission intensity of FCCGT (t/MWh). $M_t^{\text{GC}}$ is the mass of CO₂ emitted into the atmosphere from FCCGT after flue gas diversion (t). $P_{\max }^{\text{FCC}}$ and $P_{\min }^{\text{FCC}}$ are the upper and lower power limits of FCCGT.

According to (Equation 1), by controlling the inflow and outflow of the rich solution storage tank, the amount of CO₂ flowing into the absorption tower $M_t^{\text{UC}}$ can be different from that processed by regeneration tower $M_t^{\text{AC}}$ at the same time, which realizes the decoupling of CC amount and power consumption mentioned in the Introduction.

Since the CO₂ is stored in the solution in the state of MEA compound, the variables related to the mass of CO₂ in (Equation 1) should be converted the volume of MEA solution, which is then used to model the volumetric constraints of the solution storage tanks. The conversion between CO₂ mass and MEA volume is shown as:

$\left\{\begin{array}{l}{V}_t^{\text{in}}=\frac{E_t^{\mathrm{A}}{M}^{\text{MEA}}}{\psi S_t^{\text{MEA}}{\rho }_t^{\text{MEA}}{M}^{{\text{CO}}_2}}\\ V_t^{\text{out}}=\frac{E_t^{\mathrm{S}}{M}^{\text{MEA}}}{\psi S_t^{\text{MEA}}{\rho }_t^{\text{MEA}}{M}^{{\text{CO}}_2}}\end{array}\right.(2)$

where $V_t^{\text{in}}$ and $V_t^{\text{out}}$ are the MEA volume flowing into/out of the rich solution storage tank (m³). $M^{\text{MEA}}$ and $M^{{\text{CO}}_2}$ are the molar masses of MEA and CO₂ (g/mol). $\psi$ is the mass of CO₂ that can be absorbed by 1 mol of MEA (mol/mol). $S_t^{\text{MEA}}$ is the solution concentration. ${\rho }_t^{\text{MEA}}$ is the solution density (t/m³).

Then the volumetric constraints of the solution storage tanks can be modeled as follows:

$\left\{\begin{array}{l}{V}_t^{\mathrm{F}}=V_{t-1}^{\mathrm{F}}-V_t^{\text{out}}+V_t^{\text{in}}\\ V_t^{\mathrm{W}}=V_{t-1}^{\mathrm{W}}+V_t^{\text{out}}-V_t^{\text{in}}\\ V_0^{\mathrm{F}}=V_T^{\mathrm{F}}\\ 0\le V_t^{\mathrm{F}}\le V^{\mathrm{L}},0\le V_t^{\mathrm{W}}\le V^{\mathrm{L}}\end{array}\right.(3)$

where $V_t^{\text{FL}}$ and $V_t^{\text{WL}}$ are the MEA volumes in the rich and lean solution storage tanks at time t, respectively. $V_{t-1}^{\text{FL}}$ and $V_{t-1}^{\text{FL}}$ are the MEA volumes in the rich and lean solution storage tanks at time t-1, respectively. $V_0^{\text{FL}}$ and $V_T^{\text{FL}}$ are the MEA volumes in the rich solution storage tank at time 0 and T, respectively. T is the total time slots in a dispatching cycle. $V^{\mathrm{L}}$ is the volume of the solution storage tanks (m³).

Besides, the solution storage tanks should not flow in and out MEA simultaneously, and the inflow and outflow have upper limits, which are expressed as follows.

$\left\{\begin{array}{l}0\le E_t^{\mathrm{S}}\le \eta {\theta }_{\max }^{\text{CC}}{\gamma }^{\text{FCC}}{P}_{\max }^{\text{FCC}}{U}_t^{\mathrm{W}}\\ 0\le E_t^{\mathrm{A}}\le \eta {\theta }_{\max }^{\text{CC}}{\gamma }^{\text{FCC}}{P}_{\max }^{\text{FCC}}{U}_t^{\mathrm{F}}\\ 0\le E_t^{\mathrm{A}}\le M_t^{\text{TC}}\\ U_t^{\mathrm{W}}+U_t^{\mathrm{F}}=1\end{array}\right.(4)$

where $\eta$ is the maximum operational efficiency of the regenerator tower and the compressor. $U_t^{\mathrm{W}}$ and $U_t^{\mathrm{F}}$ are the 0-1 indicator variables reflecting the MEA volume changes in the lean and rich solution storage tanks, respectively.

2.3 The convexification of the FCCGT model

The bilinear term ${\delta }_t{P}_t^{\text{FCC}}$ in (Equation 1) leads to a non-convex FCCGT model. To convexify this bilinear term, McCormick envelopes are used and shown as below (Deng et al., 2021).

${\omega }_t={\delta }_t{P}_t^{\text{FCC}}(5)$

$\left\{\begin{array}{l}{\omega }_t\ge {\delta }_{\min }{P}_t^{\text{FCC}}+{\delta }_t{P}_{t,\min }^{\text{FCC}}-{\delta }_{\min }{P}_{t,\min }^{\text{FCC}}\\ {\omega }_t\ge {\delta }_{\max }{P}_t^{\text{FCC}}+{\delta }_t{P}_{t,\max }^{\text{FCC}}-{\delta }_{\max }{P}_{t,\max }^{\text{FCC}}\\ {\omega }_t\le {\delta }_{\max }{P}_t^{\text{FCC}}+{\delta }_t{P}_{t,\min }^{\text{FCC}}-{\delta }_{\max }{P}_{t,\min }^{\text{FCC}}\\ {\omega }_t\le {\delta }_t{P}_{t,\max }^{\text{FCC}}+{\delta }_{\min }{P}_t^{\text{FCC}}-{\delta }_{\min }{P}_{t,\max }^{\text{FCC}}\end{array}\right.(6)$

where ω_t is an auxiliary variable used to replace ${\delta }_t{P}_t^{\text{FCC}}$ in (Equation 1). Therefore, By combining the replaced (Equations 1, 6), the proposed FCCGT model is convexified.

3 The demand response model for MLEAF

MLEAF utilizes the heat generated by the alternating current arc to heat the dolomite ore to a molten state to obtain magnesium oxide crystals, so MLEAF is a representative high-energy-consuming HSIL. The MLEAF can control its load power by adjusting the electrodes with an electrode controller, which regulates the current within the furnace. Even if regulated with a small percentage of the rated power, MLEAF can effectively supplement the regulation capacity required by the distribution network, serving as a flexible DR resource. The specific model is described as follows.

3.1 The MLEAF model

Based on the production principles and operating modes of the MLEAF, its DR model for day-ahead optimal dispatch is constructed, which consists of the following constraints.

(1) Constraints of MLEAF regulatable capacity

$\left\{\begin{array}{l}{P}_{m,t}=P_m^{\text{base}}+P_{m,t}^{\mathrm{u}}-P_{m,t}^{\mathrm{d}}\\ s{u}_{m,t}+s{d}_{m,t}\le 1\\ 0\le P_{m,t}^{\mathrm{u}}\le s{u}_{m,t}{P}_{\max }^{\mathrm{u}}\\ 0\le P_{m,t}^{\mathrm{d}}\le s{d}_{m,t}{P}_{\max }^{\mathrm{d}}\end{array}\right.(7)$

where $P_{m,t}$ is the operating power of the MLEAF after regulation. $P_m^{\text{base}}$ is the rated power of the MLEAF. $P_{m,t}^{\mathrm{u}}$ and $P_{m,t}^{\mathrm{d}}$ are the power increment and decrement of the MLEAF. $s{u}_{m,t}$ and $s{d}_{m,t}$ are the 0-1 variables indicating the upward and downward regulation states of MLEAF, respectively. $P_{\max }^{\mathrm{u}}$ and $P_{\max }^{\mathrm{d}}$ are the maximum power increment and decrement of the MLEAF while ensuring safe operation.

(2) The constraints of regulation times of MLEAF

During a complete production cycle, the regulation times for each MLEAF should not exceed the predetermined upper limits to avoid adverse impact on the product purity. The relevant constraints are shown as follows:

$\left\{\begin{array}{l}{y}_{m,t}-z_{m,t}=s{u}_{m,t}-s{u}_{m,t-1}\\ y_{m,t}+z_{m,t}\le 1\\ \sum y_{m,t}+\sum z_{m,t}\le M\end{array}\right.(8)$

where $y_{m,t}$ and $z_{m,t}$ are the 0-1 variables indicating that MLEAF changes to the upward and downward regulation states, respectively. $M$ is the maximum regulation times of the MLEAF.

(3) The constraints of the MLEAF production output

To ensure that the MLEAF production output still meets requirements after participating in the DR project, the following constraints are constructed:

${\displaystyle \sum _{t=1}^T}\lambda \left(P_{m,t}\right)\cdot P_{m,t}\ge O_m(9)$

where $O_m$ is the target of MLEAF production output. $\lambda \left(P_{m,t}\right)$ is the piecewise linear function of the MLEAF yield to its power, which is shown as

$\lambda \left(P_{m,t}\right)=\left\{\begin{array}{l}{\lambda }_1,P_m^{\text{base}}-P_{\max }^{\mathrm{d}}\le P_{m,t}\le P_m^{\mathrm{r},\mathrm{d}}\\ {\lambda }_2,P_m^{\mathrm{r},\mathrm{d}}\le P_{m,t}\le P_m^{\mathrm{r},\mathrm{u}}\\ {\lambda }_3,P_m^{\mathrm{r},\mathrm{u}}\le P_{m,t}\le P_m^{\text{base}}+P_{\max }^{\mathrm{u}}\end{array}\right.(10)$

where λ₁、λ₂ and λ₃ are the MLEAF yield under the power decrease state, nominal state, and power increase state. $P_m^{\mathrm{r},\mathrm{d}}$ and $P_m^{\mathrm{r},\mathrm{u}}$ are the lower and upper limits of the rated state of MLEAF.

3.2 Linearization of MLEAF production output constraints

The MLEAF production output constraints given by Equations 9, 10 are conditional constraints, which cannot be solved by common commercial solvers directly. To address this problem, auxiliary variables are first used to perform piecewise linearization of (Equation 10):

$\left\{\begin{array}{l}{s}_{m,t}^{\mathrm{d}}+s_{m,t}^{\mathrm{r}}+s_{m,t}^{\mathrm{u}}=1\\ {\lambda }_{m,t}={\lambda }_1{s}_{m,t}^{\mathrm{d}}+{\lambda }_2{s}_{m,t}^{\mathrm{r}}+{\lambda }_3{s}_{m,t}^{\mathrm{u}}\\ P_{m,t}\le P_m^{\mathrm{r},\mathrm{d}}{s}_{m,t}^{\mathrm{d}}+P_m^{\mathrm{r},\mathrm{u}}{s}_{m,t}^{\mathrm{r}}+\left(P_m^{\text{base}}+P_{\max }^{\mathrm{u}}\right)s_{m,t}^{\mathrm{u}}\\ P_{m,t}\ge \left(P_m^{\text{base}}-P_{\max }^{\mathrm{d}}\right)s_{m,t}^{\mathrm{d}}+P_m^{\mathrm{r},\mathrm{d}}{s}_{m,t}^{\mathrm{r}}+P_m^{\mathrm{r},\mathrm{u}}{s}_{m,t}^{\mathrm{u}}\end{array}\right.(11)$

where λ_m,t is the output yield of the m-th MLEAF at time t. $s_{m,t}^{\mathrm{d}}$, $s_{m,t}^{\mathrm{r}}$ and $s_{m,t}^{\mathrm{u}}$ are 0–1 variables to indicate the three intervals of P_m,t divided in (Equations 10).

Based on (Equations 9, 11) can be rewritten as:

${\displaystyle \sum _t}{\lambda }_{m,t}{P}_{m,t}\ge O_m(12)$

Similarly with (Equation 1), the bilinear term in (Equation 12) can also be convexified using McCormick envelopes:

${\displaystyle \sum _t}{o}_{m,t}\ge O_m(13)$

where o_m,t is an auxiliary variable used to replace the bilinear term λ_m,tP_m,t in (Equation 12).

Although λ_m,t is discrete, it still has minimum and maximum values, which are λ₁ and λ₃, respectively. The minimum and maximum values P_m,t of are $P_m^{\text{base}}-P_{\max }^{\mathrm{d}}$ and $P_m^{\text{base}}-P_{\max }^{\mathrm{d}}$, respectively. Using the maximum and minimum values of λ_m,t and P_m,t, the linearized limits of o_m,t is constructed as:

$\left\{\begin{array}{l}{o}_{m,t}\ge {\lambda }_1{P}_{m,t}+{\lambda }_{m,t}\left(P_m^{\text{base}}-P_{\max }^{\mathrm{d}}\right)-{\lambda }_1\left(P_m^{\text{base}}-P_{\max }^{\mathrm{d}}\right)\\ o_{m,t}\ge {\lambda }_3{P}_{m,t}+{\lambda }_{m,t}\left(P_m^{\text{base}}+P_{\max }^{\mathrm{u}}\right)-{\lambda }_3\left(P_m^{\text{base}}+P_{\max }^{\mathrm{u}}\right)\\ o_{m,t}\le {\lambda }_3{P}_{m,t}+{\lambda }_{m,t}\left(P_m^{\text{base}}-P_{\max }^{\mathrm{d}}\right)-{\lambda }_3\left(P_m^{\text{base}}-P_{\max }^{\mathrm{d}}\right)\\ o_{m,t}\le {\lambda }_{m,t}\left(P_m^{\text{base}}+P_{\max }^{\mathrm{u}}\right)+{\lambda }_1{P}_{m,t}-{\lambda }_1\left(P_m^{\text{base}}+P_{\max }^{\mathrm{u}}\right)\end{array}\right.(14)$

Finally, the MLEAF production output constraints are composed of (Equations 11, 13, 14).

4 Flexible low-carbon optimal dispatch model of the distribution network

In the day-ahead optimal dispatch, the power curves of RES output and load is firstly forecasted. Then the historical forecast error data are used to construct forecast error scenarios. By combining the forecasted power curves with the forecast error scenarios, the day-ahead stochastic scenarios of RES output and load are obtained with their corresponding probabilities. On the basis of the scenarios, a flexible low-carbon stochastic optimal dispatch model is established for the distribution network by taking into account the CC amount and power consumption decoupling of FCCGT and the DR potential of MLEAF. The objective function and constraints of this dispatch model are detailed as below.

4.1 Typical scenario generation method

The scenario generation method in (Zhang et al., 2021) is adopted here, whose procedures are given below.

Step 1: Organize the historical forecast error data of RES and load power as a matrix.

Step 2: Compute the eigenvectors of the forecast error matrix. Based on the eigenvectors, the minimum volume enclosing ellipsoid of the historical error data points are determined.

Step 3: The circumscribed polyhedron of the ellipsoid is obtained by an expansion method. Then the coordinates of the vertices of the circumscribed polyhedron are the derived typical forecast error scenarios.

Step 4: Add each typical forecast error scenario to the base forecast power of RES and load to obtain their typical scenarios, which are used in the objective and constraints of the proposed Flexible low-carbon optimal dispatch model.

4.2 Objective function

The objective function of the proposed dispatch model is to minimize the total operation cost of the distribution network.

(1) The start-up and shut-down cost of the FCCGT

$C^{\text{FCC}}={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^{N_{\text{FCC}}}}\left[c_i^{\mathrm{u}}{I}_{i,t}\left(1-I_{i,t-1}\right)+c_i^{\mathrm{d}}{I}_{i,t-1}\left(1-I_{i,t}\right)\right](15)$

where i is the index of FCCGT. $N_{\text{FCC}}$ is the total number of FCCGTs. $c_i^{\mathrm{u}}$ and $c_i^{\mathrm{d}}$ are the start-up and shut-down costs of the i-th FCCGT. $I_{i,t}$ and $I_{i,t-1}$ are the 0-1 variables indicating the states of the i-th FCCGT at time t and time t−1, respectively.

(2) The operational cost of the FCCGT

$C^{\mathrm{R}}={\displaystyle \sum _{k=1}^{N_{\text{sce}}}}{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^{N_{\text{FCC}}}}{p}_k\left(c_{\text{fuel}}{P}_{t,k,i}^{\text{FCC}}+c_{\text{ccus}}\chi M_{t,k,i}^{\text{TC}}\right)(16)$

where k is the index of the typical scenarios. N_sce is the total number of typical scenarios. p_k is the weight coefficient of scenario k. $c_{\text{fuel}}$ is the unit fuel cost of the FCCGT electricity generation. $c_{\text{ccus}}$ is the unit operational cost of the CC device.

(3) The cost of purchasing power from the superior power grid

$C^{\text{Buy}}={\displaystyle \sum _{k=1}^{N_{\text{sce}}}}{\displaystyle \sum _{t=1}^T}{p}_k{c}_{\text{grid},t}{P}_{\mathrm{e},t,k}^{\text{buy}}(17)$

where $c_{\text{grid},t}$ is the price of the power purchased from the superior power grid. $P_{\mathrm{e},t,k}^{\text{buy}}$ is the quantity of purchased electricity.

(4) The subsidy cost for the DR incentive of MLEAF

$C^{\text{Mg}}={\displaystyle \sum _{k=1}^{N_{\text{sce}}}}{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{m=1}^{N_{\mathrm{M}}}}{p}_k\left(c_{\mathrm{m}1}{P}_{m,t,k}^{\mathrm{u}}+c_{\mathrm{m}2}{P}_{m,t,k}^{\mathrm{d}}\right)(18)$

where N_M is the total number of MLEAFs. c_m1 and c_m2 are the unit subsidies for increment and decrement responses of MLEAF, respectively.

(5) The carbon tax cost

This paper considers the implementation of a carbon tax policy in the distribution network and calculates the carbon tax cost associated with CO₂ emissions as follows:

$C^{\text{carb}}=c^{{\text{CO}}_2}{\displaystyle \sum _{k=1}^{N_{\text{sce}}}}{\displaystyle \sum _{t=1}^T}{p}_k\left({\displaystyle \sum _{i=1}^{N_{\text{FCC}}}}{M}_{t,k,i}^{\text{GC}}+{\lambda }_e{P}_{\mathrm{e},t,k}^{\text{buy}}\right)(19)$

where $c^{{\text{CO}}_2}$ is the carbon tax price. ${\lambda }_e$ is the average carbon emission factor corresponding to purchased electricity.

(6) The penalty cost for wind and solar power curtailment

$C^{\text{Curt}}=c^{\text{cur}}{\displaystyle \sum _{k=1}^{N_{\text{sce}}}}{\displaystyle \sum _{t=1}^T}{p}_k\left({\displaystyle \sum _{w=1}^{N_{\mathrm{w}}}}\Delta P_{w,t,k}^{\mathrm{W}}+{\displaystyle \sum _{v=1}^{N_{\mathrm{v}}}}\Delta P_{v,t,k}^{\text{PV}}\right)(20)$

where $c^{\text{cur}}$ is the penalty price of curtailed wind and solar electricity. N_w and N_v are the number of wind farms and photovoltaic power stations, respectively. $\Delta P_{w,t,k}^{\mathrm{W}}$ and $\Delta P_{v,t,k}^{\text{PV}}$ are the curtailed power of the w-th wind farm and the v-th photovoltaic power station, respectively.

(7) The load shedding cost

$C^{\text{LD}}=c^{\mathrm{L}}{\displaystyle \sum _{k=1}^{n_{\text{sce}}}}{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _b}{p}_k\Delta P_{b,t,k}^{\mathrm{L}}(21)$

where $c^{\mathrm{L}}$ is the penalty price of load shed. $\Delta P_{b,t,k}^{\mathrm{L}}$ is the load shed at bus b.

Based on (Equations 15–21), the total cost of the distribution network is calculated by Equation 22 as follows:

$\min C^{\text{FCC}}+C^{\mathrm{R}}+C^{\text{Buy}}+C^{\text{Mg}}+C^{\text{carb}}+C^{\text{Curt}}+C^{\text{LD}}(22)$

4.3 Constraints

(1) Constraints of FCCGT

The relevant constraints have been given by Equations 1–6.

(2) Constraints of MLEAF

The relevant constraints have been given by Equations 7–14.

(3) Power balance constraints

$P_{\mathrm{e},t,k}^{\text{buy}}+{\displaystyle \sum _w}\left(P_{w,t,k}^{\mathrm{W}}-\Delta P_{w,t,k}^{\mathrm{W}}\right)+{\displaystyle \sum _v}\left(P_{v,t,k}^{\text{PV}}-\Delta P_{v,t,k}^{\text{PV}}\right)={\displaystyle \sum _b}\left(P_{b,t,k}^{\text{Load}}-\Delta P_{b,t,k}^{\mathrm{L}}\right)+{\displaystyle \sum _m}{P}_{m,t,k}-{\displaystyle \sum _{i=1}^{N_{\text{FCC}}}}{P}_{\mathrm{e},t,k,i}^{\text{FCC}}(23)$

where $P_{w,t,k}^{\mathrm{W}}$ and $P_{v,t,k}^{\text{PV}}$ are the forecasted power of wind farm w and photovoltaic power station v. $P_{b,t,k}^{\text{Load}}$ is the forecasted load power at bus b.

(4) Transmission capacity constraints of power lines

$\begin{array}{l}\left|{\displaystyle \sum _b}{K}_{lb}\left[{\displaystyle \sum _b}{P}_{\mathrm{e},t,k}^{\text{buy}}+{\displaystyle \sum _{i\in b}}{P}_{\mathrm{e},t,k,i}^{\text{FCC}}+\right.\right.{\displaystyle \sum _{w\in b}}\left(P_{w,t,k}^{\mathrm{W}}-\Delta P_{w,t,k}^{\mathrm{W}}\right)+\\ {\displaystyle \sum _{v\in b}}\left(P_{v,t,k}^{\text{PV}}-\Delta P_{v,t,k}^{\text{PV}}\right)-\left.\left(P_{b,t,k}^{\text{Load}}-\Delta P_{b,t,k}^{\mathrm{L}}\right)-{\displaystyle \sum _{m\in b}}{P}_{m,t,k}\right|\le f_{l\max }\end{array}(24)$

where K_lb is the power flow distribution factor of bus b to line l (Cai et al., 2022). f_lmax is the maximum transmission power of line l.

(5) Wind and solar curtailment and load-shedding constraints

$\begin{array}{l}0\le \Delta P_{w,t,k}^{\mathrm{W}}\le P_{w,t,k}^{\mathrm{W}}\\ 0\le \Delta P_{v,t,k}^{\text{PV}}\le P_{v,t,k}^{\text{PV}}\\ 0\le \Delta P_{b,t,k}^{\text{Load}}\le P_{b,t,k}^{\mathrm{L}}\end{array}(25)$

(6) Power output and ramp constraints of FCCGT

$\left\{\begin{array}{l}{I}_{i,t}{P}_{\mathrm{e},i,\min }^{\text{FCC}}\le P_{\mathrm{e},t,k,i}^{\text{FCC}}\le I_{i,t}{P}_{\mathrm{e},i,\max }^{\text{FCC}}\\ -D{R}_i\le P_{\mathrm{e},t,i}^{\text{FCC}}-P_{\mathrm{e},t-1,i}^{\text{FCC}}\le U{R}_i\end{array}\right.(26)$

where UR_i and DR_i are the maximum upward and downward ramp rate of the i-th FCCGT.

(7) Minimum duration constraints of on and off states of FCCGT

$\left\{\begin{array}{l}\left(T_{i,t-1}^{\text{on}}-T_{i,\min }^{\text{on}}\right)\left(I_{i,t-1}-I_{i,t}\right)\ge 0\\ \left(T_{i,t-1}^{\text{off}}-T_{i,\min }^{\text{off}}\right)\left(I_{i,t}-I_{i,t-1}\right)\ge 0\end{array}\right.(27)$

where $T_i^{\text{on}}$ and $T_i^{\text{off}}$ are the minimum duration of on and off states of the i-th FCCGT. $I_{i,t}$ is a 0-1 variable which takes 1 for the on state and 0 for the off state. The constraints of the proposed flexible low-carbon dispatch model are finally composed of Equations 1–14 and Equations 23–27.

5 Numerical tests

5.1 Basic settings

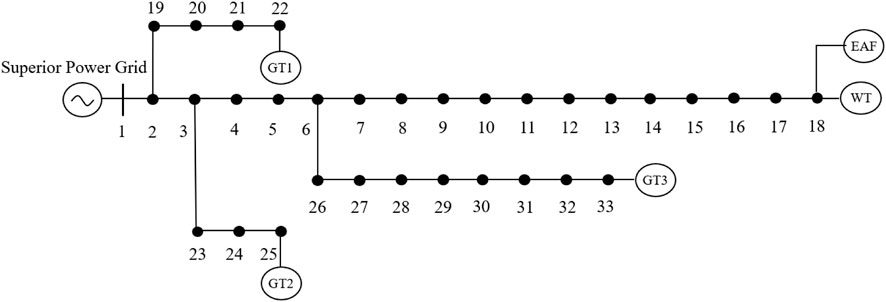
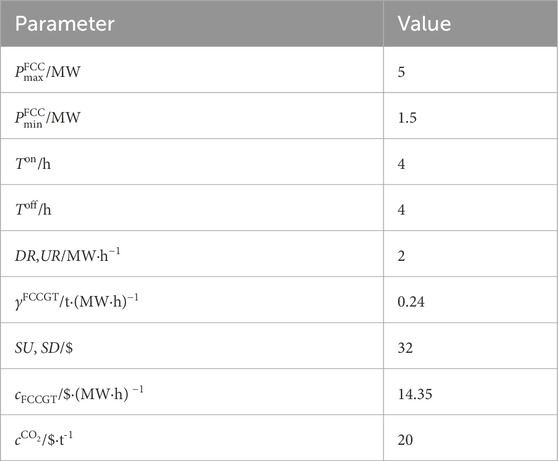
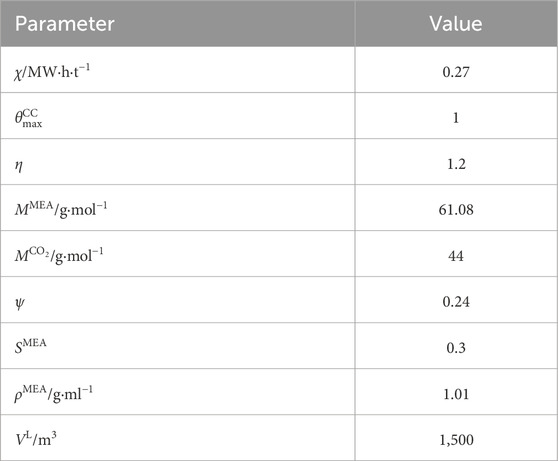
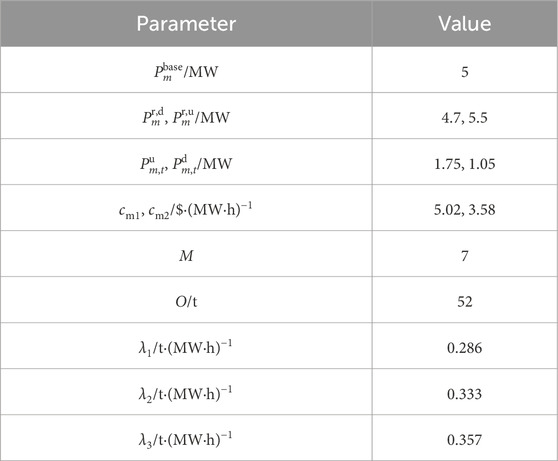
A modified IEEE 33-bus standard system is designed as the test distribution system, whose network structure is shown in Figure 2. This designed system includes three identical FCCGTs, i.e., GT1-GT3, which are connected to buses 22, 25, and 33, respectively. The technical parameters of GT1-GT3 are shown in Table 1. The three FCCGTs have the same type of CC devices, with the parameters listed in Table 2.

Figure 2

Figure 2. Test system based on a modified IEEE 33-bus standard system.

Table 1

Table 1. Parameters of FCCGT.

Table 2

Table 2. Parameters of CC device.

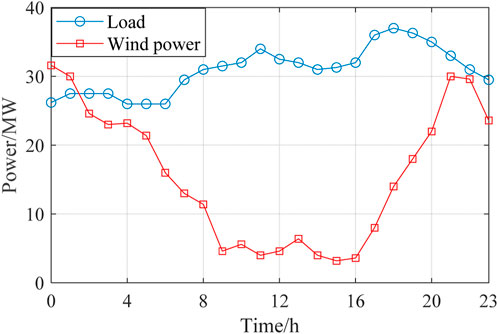
The wind farm is connected to Bus 18, with its forecasted power output shown in Figure 3. The penalty price for curtailing wind power is 100 $/MW·h. Apart from MLEAF, the forecasted power of all the other loads in the distribution network is also shown in Figure 3. The ratio of load at each bus to the total load is the same with that in the original IEEE 33-bus standard system, which can be found in (Yang et al., 2021) and not elaborated here.

Figure 3

Figure 3. The forecasted power of the wind farm and load.

The MLEAF is connected to Bus 18. When not participating in DR project, the MLEAF daily power curve is a horizontal line with its value equal to the rated power. The relevant parameters are shown in Table 3.

Table 3

Table 3. Parameters of MLEAF.

The electricity price for purchasing power from the superior power grid adopts time-of-use pricing, where the peak, flat and valley periods are divided according to the load curve shape shown in Figure 3. The corresponding prices for each period are shown in Table 4. The average carbon emission factor for purchased electricity is 0.65 t/MW h.

Table 4

Table 4. Time period division and electricity price.

Based on the parameters above, three different scenarios are designed for comparative analysis to verify that the incorporation of FCCGT and DR of MLEAF can improve the economic efficiency, low-carbon attribute and flexibility of the distribution network. These scenarios are as follows.

Scenario 1: GT1-GT3 are equipped with CC devices without solution storage tanks and with a fixed flue gas diversion ratio. The MLEAF does not participate in the DR project.

Scenario 2: GT1-GT3 are FCCGTs with adjustable flue gas diversion ratios. The MLEAF does not participate in the DR project.

Scenario 3: GT1-GT3 are FCCGTs with adjustable flue gas diversion ratios. The MLEAF takes part in the DR project. This scenario corresponds to the flexible low-carbon optimal dispatch model proposed in Section 4.

All three scenarios are modeled with the YALMIP toolbox and solved by the CPLEX solver on the MATLAB platform.

5.2 Comparison and analysis of dispatch results for the three scenarios

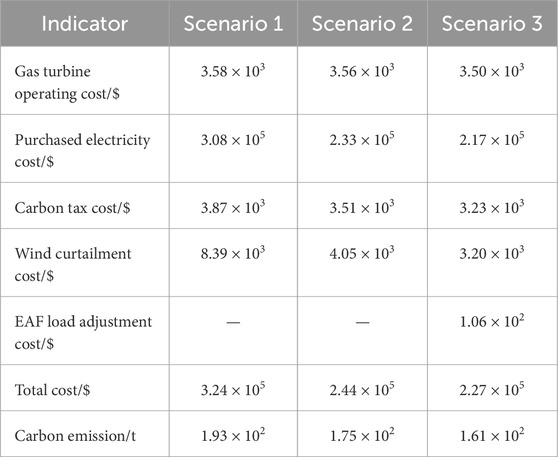
The dispatch costs are shown in Table 5.

Table 5

Table 5. Comparison of distribution network operating costs under different scenarios.

According to Table 5, it can be found that.

1) In Scenario 2, the carbon emission is reduced by 18 t compared to Scenario 1. The wind power curtailment penalty is decreased by 4,340 $. The total cost is decreased by 8,000 $. This indicates that the FCCGT has higher flexibility than gas turbines equipped with CC devices without solution storage tanks, which improves CC efficiency and promotes the utilization of renewable energy.

2) In Scenario 3, carbon emission is reduced by 14 t compared to Scenario 2. The total cost is decreased by 9.7 × 10⁴ $ and 1.7 × 10⁴ $ compared to Scenario 1 and Scenario 2, respectively. This indicates that, incorporating the DR of MLEAF into the distribution network dispatch can significantly improve the energy utilization efficiency, effectively reduce the peak loads and lower the carbon emission.

In summary, the effectiveness of the proposed flexible low-carbon optimal dispatch model is validated by comparing the total costs, carbon emissions and wind curtailment of the three scenarios.

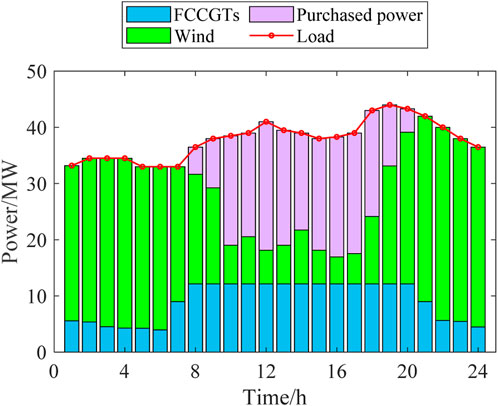
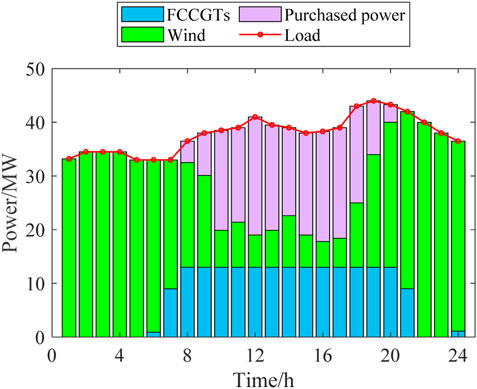
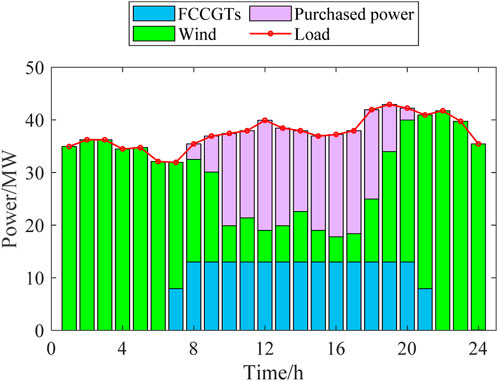
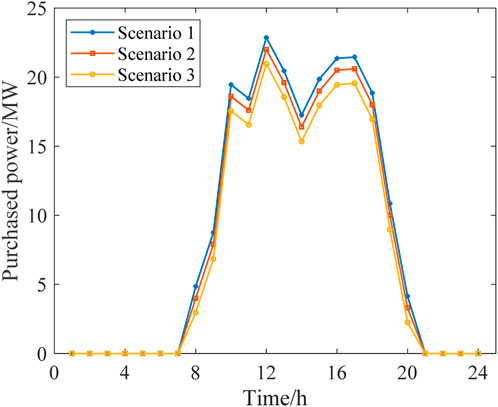
The dispatch schemes of the three scenarios are shown in Figures 4–6.

Figure 4

Figure 4. Dispatch scheme of scenario 1.

Figure 5

Figure 5. Dispatch scheme of scenario 2.

Figure 6

Figure 6. Dispatch scheme of scenario 3.

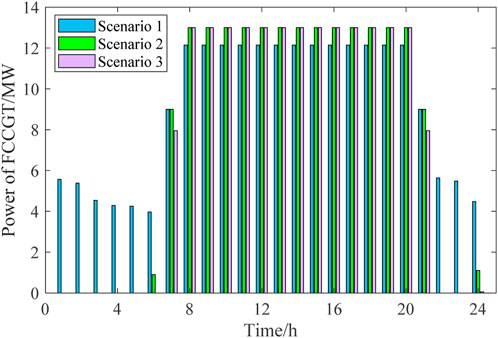
According to Figures 4–7, the outputs of all the power sources during the peak load periods are compared between the three scenarios. It can be found that the proposed model can optimize the output of FCCGTs and the wind farm, so the distribution network can effectively interact with the superior power grid to achieve the “peak shaving and valley filling” effect. More specifically, during peak periods, the external power purchase is decreased by utilizing MLEAF to reduce its own load. During off-peak periods, the consumption of wind power is increased through reasonable dispatching, which also reduces the external power purchase. Since the carbon emission factor of purchased electricity is higher than that of gas turbines and wind power, the proposed model results in a decrease in the total daily carbon emissions, which proves its low-carbon property.

Figure 7

Figure 7. Power purchased from the superior power grid of 3 scenarios.

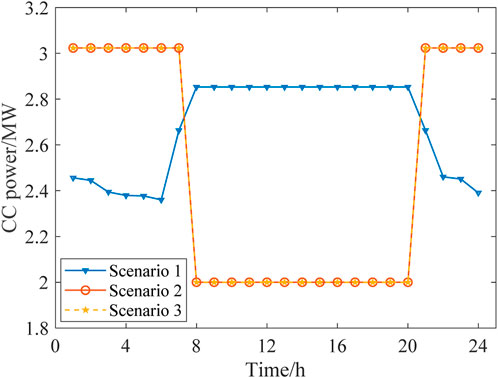
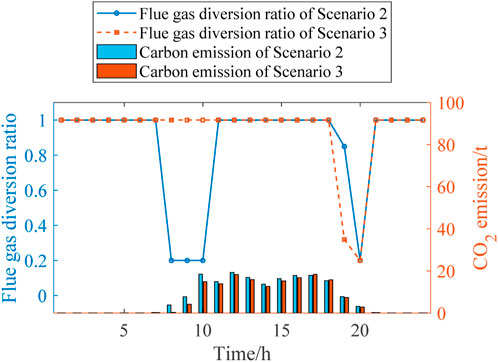
According to Figures 8, 9, the fixed gas diversion ratio in Scenario 1 results in a nearly constant high CC power during peak periods, which further leads to a shortage in the feed-in power of the FCCGTs and exacerbates the power generation deficit. In Scenarios 2 and 3, CO₂ that cannot be processed during peak periods is stored in the solution tanks and processed later in the off-peak periods. In this way, the CC power consumption during peak periods is reduced to zero, which allows FCCGTs to provide more feed-in power during peak periods and more CO₂ processing load during off-peak periods. Such flexibility promotes RES power consumption and achieves peak-shaving and valley-filling effects.

Figure 8

Figure 8. Power consumed by CC devices of 3 scenarios.

Figure 9

Figure 9. Feed-in power of FCCGTs of 3 scenarios.

According to Figure 10, during the peak period from 18:00 to 20:00, the gas diversion ratio in Scenario 3 is higher than that in Scenario 2. This is because the DR of the MLEAF alleviates the power output pressure of FCCGTs during peak periods. More specifically, MLEAF actively responds to the distribution network’s peak shaving instructions and reduces its load demand, so the required power output and the corresponding CO₂ generated by FCCGTs are both lowered. Therefore, FCCGTs can provide more CC power to process the smaller amount of carbon emission, which results in the higher flue gas diversion ratio in Scenario 3.

Figure 10

Figure 10. Flue gas diversion ratios and captured carbon of scenario 2 and scenario 3.

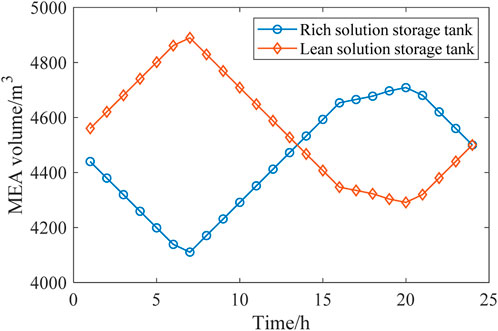
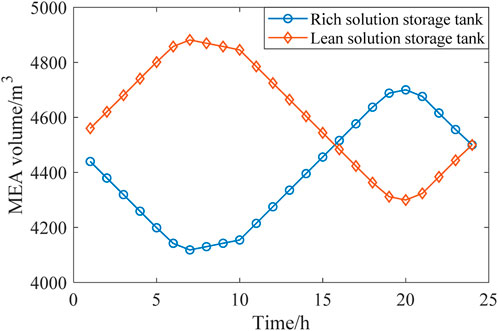
According to Figure 11, the solution volumes in the rich and lean solution tanks vary with time to react with the operation condition of the distribution network. During the peak periods, the MEA solution volume in the rich solution tank increases, which indicates that CC power is reduced in these periods and CO₂ is stored temporarily for later processing. During the valley periods, MEA flows out of the rich solution tank to release CO₂ and then flows into the lean solution tank, which indicates that the CC power increases to process the CO₂ temporarily stored in peak periods.

Figure 11

Figure 11. Stored MEA solution in the rich and lean solution tanks of scenario 2.

Through the coordinated operation of the rich and lean solution tanks, the CC amount and the CC power consumption are decoupled, contributing to the flexible low-carbon economic dispatch of the distribution network.

From the comparison of Figures 11, 12, it can be observed that compared to Scenario 2, Scenario 3 additionally considers the flexibility brought by the DR of MLEAF. Therefore, the CC devices can operate more efficiently across different load periods, which better balances the operating efficiency and energy consumption of the FCCGTs. With the flexibility from both the generation and load sides, the overall efficiency and stability of the distribution network is improved, which means lower operation costs and smaller environmental impact.

Figure 12

Figure 12. Stored MEA solution in the rich and lean solution tanks of scenario 3.

6 Conclusion

A novel flexible low-carbon optimal dispatch model is proposed in this paper for the distribution network, which coordinates FCCGTs and the DR of MLEAF to achieve balances between the operation efficiency, carbon emissions, RES power curtailment and load shedding amount. The correctness and advantages of the proposed model is verified by designed numerical tests. The specific conclusions are as follows:

1) By modelling the flexibility provided by the solution tanks and flue gas diversion system of FCCGTs, the carbon emission and processing is effectively controlled by the CC devices, which improves the utilization efficiency of fossil energy in the optimal dispatch of the distribution network.

2) The cooperation of the FCCGTs and the DR of MLEAF avoids the frequent start and stop of FCCGTs and alleviates the pressure peak regulation. Under this condition, the distribution network can operate in more stable and efficient mode, which realizes the environmental sustainability and economic benefits.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WW: Funding acquisition, Methodology, Software, Supervision, Writing–original draft, Writing–review and editing. HH: Conceptualization, Data curation, Software, Supervision, Writing–review and editing. XZ: Data curation, Project administration, Resources, Validation, Writing–review and editing. JT: Conceptualization, Formal Analysis, Validation, Writing–review and editing. SS: Conceptualization, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The financial aid received from Jiangsu Provincially Managed Industrial Projects (JC2024003) is gratefully acknowledged.

Conflict of interest

Authors WW, HH, and SS were employed by Nanjing Suyi Industrial Co., Ltd. Author XZ was employed by Nanjing Suyi Industrial Co., Ltd. Author JT was employed by Nanjing Huaqun Energy Group Co., Ltd.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boldrini, A., Koolen, D., Crijns-Graus, W., Worrell, E., and van den Broek, M. (2024). Flexibility options in a decarbonising iron and steel industry. Renew. Sustain. Energy Rev. 189, 113988. doi:10.1016/j.rser.2023.113988

CrossRef Full Text | Google Scholar

Cai, J., Hao, L., Xu, Q., and Zhang, K. (2022). Reliability assessment of renewable energy integrated power systems with an extendable Latin hypercube importance sampling method. Sustain Energy Techn 50, 101792. doi:10.1016/j.seta.2021.101792

CrossRef Full Text | Google Scholar

Cheng, L., Zang, H., Wei, Z., and Sun, G. (2023). Secure multi-party household load scheduling framework for real-time demand-side management. IEEE T Sustain Energ 14 (1), 602–612. doi:10.1109/tste.2022.3221081

CrossRef Full Text | Google Scholar

Chyong, C. K., Reiner, D. M., Ly, R., and Fajardy, M. (2023). Economic modelling of flexible carbon capture and storage in a decarbonised electricity system. Renew. Sust. Energ Rev. 188, 113864. doi:10.1016/j.rser.2023.113864

CrossRef Full Text | Google Scholar

Condessa, G. Á., Ismail, K. A. R., Hunt, J. D., Ponce Júnior, N., Velásquez, R. M. G., Borges, V. L., et al. (2023). Electricity generation potential from natural gas pressure reduction turbines in Brazil. Energ Effic. 16 (8), 97. doi:10.1007/s12053-023-10176-8

CrossRef Full Text | Google Scholar

de Chalendar, J. A., McMahon, C., Fuentes Valenzuela, L., Glynn, P. W., and Benson, S. M. (2023). Unlocking demand response in commercial buildings: empirical response of commercial buildings to daily cooling set point adjustments. Energ Build. 278, 112599. doi:10.1016/j.enbuild.2022.112599

CrossRef Full Text | Google Scholar

Deng, L., Sun, H., Li, B., Sun, Y., Yang, T., and Zhang, X. (2021). Optimal operation of integrated heat and electricity systems: a tightening McCormick approach. Engineering 7 (8), 1076–1086. doi:10.1016/j.eng.2021.06.006

CrossRef Full Text | Google Scholar

Fan, W., Ju, L., Tan, Z., Li, X., Zhang, A., Li, X., et al. (2023). Two-stage distributionally robust optimization model of integrated energy system group considering energy sharing and carbon transfer. Appl. Energ 331, 120426. doi:10.1016/j.apenergy.2022.120426

CrossRef Full Text | Google Scholar

Gabrielli, P., Campos, J., Becattini, V., Mazzotti, M., and Sansavini, G. (2022). Optimization and assessment of carbon capture, transport and storage supply chains for industrial sectors: the cost of resilience. Int. J. Greenh. Gas. Con 121, 103797. doi:10.1016/j.ijggc.2022.103797

CrossRef Full Text | Google Scholar

Gao, X., Wang, S., Sun, Y., and Zhai, J. (2024). Low-carbon operation of integrated electricity-gas system with hydrogen injection considering hydrogen mixed gas turbine and laddered carbon trading. Appl. Energ 374, 123902. doi:10.1016/j.apenergy.2024.123902

CrossRef Full Text | Google Scholar

Huang, Y., Chen, S., Chen, Z., Hu, W., and Huang, Q. (2020). Improved probabilistic load flow method based on D-vine copulas and Latin hypercube sampling in distribution network with multiple wind generators. IET Generation, Transm. and Distribution 14 (5), 893–899. doi:10.1049/iet-gtd.2019.1126

CrossRef Full Text | Google Scholar

Qi, X., Zhao, T., Liu, X., and Wang, P. (2023). Three-Stage stochastic unit commitment for microgrids toward frequency security via renewable energy deloading. IEEE T Smart Grid 14 (6), 4256–4267. doi:10.1109/tsg.2023.3263273

CrossRef Full Text | Google Scholar

Shao, C., Feng, C., Shahidehpour, M., Zhou, Q., Wang, X., and Wang, X. (2021). Optimal stochastic operation of integrated electric power and renewable energy with vehicle-based hydrogen energy system. IEEE T Power Syst. 36 (5), 4310–4321. doi:10.1109/tpwrs.2021.3058561

CrossRef Full Text | Google Scholar

Song, J., Zhang, Z., Mu, Y., Wang, X., Chen, H., Pan, Q., et al. (2024). Enhancing environmental sustainability via interval optimization for low-carbon economic dispatch in renewable energy power systems: leveraging the flexible cooperation of wind energy and carbon capture power plants. J. Clean. Prod., 442. doi:10.1016/j.jclepro.2024.140937

CrossRef Full Text | Google Scholar

Tan, W. S., Shaaban, M., and Ab Kadir, M. Z. A. (2019). Stochastic generation scheduling with variable renewable generation: methods, applications, and future trends. IET Generation, Transm. and Distribution 13 (9), 1467–1480. doi:10.1049/iet-gtd.2018.6331

CrossRef Full Text | Google Scholar

Wang, J., Wang, Q., and Sun, W. (2023a). Quantifying flexibility provisions of the ladle furnace refining process as cuttable loads in the iron and steel industry. Appl. Energ 342, 121178. doi:10.1016/j.apenergy.2023.121178

CrossRef Full Text | Google Scholar

Wang, W., Chai, T., Wang, H., and Wu, Z. (2023b). Signal-compensation-based adaptive PID control for fused magnesia smelting processes. IEEE T Ind. Electron 70 (9), 9441–9451. doi:10.1109/TIE.2022.3212392

CrossRef Full Text | Google Scholar

Wang, Y., Gao, S., Jia, W., Ding, T., Zhou, Z., and Wang, Z. (2022). Data-driven distributionally robust economic dispatch for park integrated energy systems with coordination of carbon capture and storage devices and combined heat and power plants. IET Renew. Power Gen. 16 (12), 2617–2629. doi:10.1049/rpg2.12436

CrossRef Full Text | Google Scholar

Wang, Y., Yang, Z., Zhao, X., Liu, H., Wang, D., and Liu, C. (2024). Fine-grained modeling and coordinated scheduling of source-load with energy-intensive electro-fused magnesium loads. IEEE Access 12, 47702–47712. doi:10.1109/access.2024.3381781

CrossRef Full Text | Google Scholar

Wilkes, M. D., Mukherjee, S., and Brown, S. (2021). Transient CO 2 capture for open-cycle gas turbines in future energy systems. Energy 216, 119258. doi:10.1016/j.energy.2020.119258

CrossRef Full Text | Google Scholar

Xu, D., Xiang, S., Bai, Z., Wei, J., and Gao, M. (2023). Optimal multi-energy portfolio towards zero carbon data center buildings in the presence of proactive demand response programs. Appl. Energ 350, 121806. doi:10.1016/j.apenergy.2023.121806

CrossRef Full Text | Google Scholar

Xu, J., and Yi, Y. (2023). Multi-microgrid low-carbon economy operation strategy considering both source and load uncertainty: a Nash bargaining approach. Energy (Oxford) 263, 125712. doi:10.1016/j.energy.2022.125712

CrossRef Full Text | Google Scholar

Yang, M., Li, J., Li, J., Yuan, X., and Xu, J. (2021). Reconfiguration strategy for DC distribution network fault recovery based on hybrid particle swarm optimization. Energies 14 (21), 7145. doi:10.3390/en14217145

CrossRef Full Text | Google Scholar

Yue, X., Liao, S., Xu, J., Ke, D., Wang, H., Yang, J., et al. (2024). Collaborative optimization of renewable energy power systems integrating electrolytic aluminum load regulation and thermal power deep peak shaving. Appl. Energ 373, 123869. doi:10.1016/j.apenergy.2024.123869

CrossRef Full Text | Google Scholar

Zhang, B., Hu, W., Ghias A, M. Y. M., Xu, X., and Chen, Z. (2023). Multi-agent deep reinforcement learning based distributed control architecture for interconnected multi-energy microgrid energy management and optimization. Energ Convers. Manage 277, 116647. doi:10.1016/j.enconman.2022.116647

CrossRef Full Text | Google Scholar

Zhang, S., Qiu, G., Liu, Y., Ding, L., and Shui, Y. (2024). Data-Driven distributionally robust optimization-based coordinated dispatching for cascaded hydro-PV-PSH combined system. Electronics-Switz. 13 (3), 667. doi:10.3390/electronics13030667

CrossRef Full Text | Google Scholar

Zhang, W., and Zhu, T. (2024). Flexible resource demand response scheduling strategy under 5G-V2X. Sustain. Energy, Grids Netw. 39, 101441. doi:10.1016/j.segan.2024.101441

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, Y., Shu, S., Zheng, F., and Huang, Z. (2021). A data-driven distributionally robust optimization model for multi-energy coupled system considering the temporal-spatial correlation and distribution uncertainty of renewable energy sources. Energy 216, 119171. doi:10.1016/j.energy.2020.119171

CrossRef Full Text | Google Scholar

Zhao, X., Wang, Y., Liu, C., Cai, G., Ge, W., Zhou, J., et al. (2024). Low carbon scheduling method of electric power system considering energy-intensive load regulation of electrofused magnesium and wind power fluctuation stabilization. Appl. Energ 357, 122573. doi:10.1016/j.apenergy.2023.122573

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

RES renewable energy sources

CC carbon capture

FCCGT gas turbines installed with flexible CC technology

HSIL heat storage industrial loads

DR demand response

MLEAF magnesium load using an electric arc furnace

Indices

t index of time

i index of FCCGT

w index of wind farms

v index of photovoltaic power stations

b index of load buses

l index of line

m index of MLEAF

Variables

${\mathit{P}}_{\mathit{t}}^{\mathbf{\text{FCC}}}$ total power output of FCCGT

${\mathit{P}}_{\mathbf{e},\mathit{t}}^{\mathbf{\text{FCC}}}$ FCCGT power delivered to distribution network

${\mathit{P}}_{\mathit{t}}^{\mathbf{Y}}$ power consumption of the CC device

${\mathit{M}}_{\mathit{t}}^{\mathbf{\text{TC}}}$ total mass of the captured CO₂

${\mathit{M}}_{\mathit{t}}^{\mathbf{\text{UC}}}$ mass of CO₂ supplied from/absorbed by the rich solution storage tank

${\mathit{\delta }}_{\mathit{t}}$ flue gas diversion ratio

${\mathit{M}}_{\mathit{t}}^{\mathbf{\text{AC}}}$ total mass of CO₂ produced by FCCGT

${\mathit{M}}_{\mathit{t}}^{\mathbf{\text{GC}}}$ mass of CO₂ emitted to the atmosphere by FCCGT

${\mathit{V}}_{\mathit{t}}^{\mathbf{\text{in}}}$, ${\mathit{V}}_{\mathit{t}}^{\mathbf{\text{out}}}$ MEA volume flowing into/out of the rich solution storage tank

${\mathit{S}}_{\mathit{t}}^{\mathbf{\text{MEA}}}$ solution concentration

${\mathit{\rho }}_{\mathit{t}}^{\mathbf{\text{MEA}}}$ solution density

${\mathit{V}}_{\mathit{t}}^{\mathbf{F}}{\mathit{V}}_{\mathit{t}}^{\mathbf{W}}$ MEA volumes in rich/lean solution storage tanks $U_t^{\mathrm{F}}$, $U_t^{\mathrm{W}}$ 0-1 variables indicating the MEA volume changes in the rich/lean solution storage tanks

${\mathit{P}}_{\mathit{m},\mathit{t}}$ operating power of the MLEAF after regulation

${\mathit{P}}_{\mathit{m},\mathit{t}}^{\mathbf{u}}$ power increment of the MLEAF

λ_m,t yield rate of the m-th MLEAF at time t

${\mathit{I}}_{\mathit{i},\mathit{t}}$ 0-1 variables indicating the states of FCCGT i

${\mathit{c}}_{\mathbf{g}\mathbf{r}\mathbf{i}\mathbf{d},\mathit{t}}$ price of power purchased from superior power grid

${\mathit{P}}_{\mathbf{e},\mathit{t},\mathit{k}}^{\mathbf{\text{buy}}}$ quantity of purchased electricity

$\mathbf{\Delta }{\mathit{P}}_{\mathit{w},\mathit{t},\mathit{k}}^{\mathbf{W}}$ curtailed power of wind farm w

$\mathbf{\Delta }{\mathit{P}}_{\mathit{v},\mathit{t},\mathit{k}}^{\mathbf{\text{PV}}}$ curtailed power of the photovoltaic station v

$\mathbf{\Delta }{\mathit{P}}_{\mathit{b},\mathit{t},\mathit{k}}^{\mathbf{L}}$ load shed at bus b

${\mathit{P}}_{\mathit{w},\mathit{t},\mathit{k}}^{\mathbf{W}}$ forecasted power of wind farm w

${\mathit{P}}_{\mathit{v},\mathit{t},\mathit{k}}^{\mathbf{\text{PV}}}$ forecasted power of photovoltaic station v

${\mathit{P}}_{\mathit{b},\mathit{t},\mathit{k}}^{\mathbf{\text{Load}}}$ forecasted load power at bus b

Parameters

$\mathit{\chi }$ consumed power for capturing unit mass of CO₂

${\mathit{\theta }}_{\mathbf{max}}^{\mathbf{\text{CC}}}$ maximum CC level

${\mathit{\gamma }}^{\mathbf{\text{FCC}}}$ CO2 emission intensity of FCCGT $P_{\max }^{\text{FCC}}$, $P_{\min }^{\text{FCC}}$ upper and lower power limits of FCCGT

${\mathit{M}}^{\mathbf{\text{MEA}}}$ molar masses of MEA

${\mathit{M}}^{{\mathbf{\text{CO}}}_{\mathbf{2}}}$ molar masses of CO₂

$\mathit{\psi }$ mass of CO₂ that can be absorbed by 1 mol of MEA

T total time slots in a dispatching cycle

${\mathit{V}}^{\mathbf{L}}$ volume of the solution storage tanks

${\mathit{P}}_{\mathit{m}}^{\mathbf{\text{base}}}$ rated power of MLEAF m

${\mathit{P}}_{\mathbf{max}}^{\mathbf{u}}$, ${\mathit{P}}_{\mathbf{max}}^{\mathbf{d}}$ maximum power increment/decrement of MLEAF

${\mathit{O}}_{\mathit{m}}$ target of MLEAF production output

λ₁, λ₂, λ₃ the MLEAF yield rates under the power decrease/nominal/increase state

$N_{\text{FCC}}$ total number of FCCGTs $c_i^{\mathrm{u}}$, $c_i^{\mathrm{d}}$ start-up/shut-down costs of FCCGT i

N_sce total number of scenarios

p_k weight coefficient of scenario k

${\mathit{c}}_{\mathbf{\text{fuel}}}$ unit fuel cost of the FCCGT electricity generation

${\mathit{c}}_{\mathbf{\text{ccus}}}$ unit operational cost of the CC device

N_M total number of MLEAFs

c_m1, c_m2 unit subsidy of increment/decrement response of MLEAF

${\mathit{c}}^{{\mathbf{\text{CO}}}_{\mathbf{2}}}$ carbon tax price

${\mathit{\lambda }}_{\mathit{e}}$ carbon emission factor of purchased electricity

${\mathit{c}}^{\mathbf{\text{cur}}}$ penalty price of curtailed wind and solar electricity

N_w the number of wind farms

N_v the number of photovoltaic power stations

${\mathit{c}}^{\mathbf{L}}$ penalty price of load shed

UR_i,DR_i upward/downward ramp rate of FCCGT i

${\mathit{T}}_{\mathit{i}}^{\mathbf{\text{on}}}$, ${\mathit{T}}_{\mathit{i}}^{\mathbf{\text{off}}}$ minimum duration of on/off states of FCCGT i