Optimal dispatch of an electricity-heat virtual power plant based on Benders decomposition

Recently, wind energy has been developed as an important technology to address the energy crisis. However, due to an unreasonable energy structure, wind power curtailment is becoming increasingly severe. Combined heat and power dispatch (CHPD) provided a solution for wind accommodation by utilizing the flexibility resources of district heating systems. Because of the imperfect dispatch methods and CHPD platforms, many wind power heating projects have not effectively linked the use of abandoned wind and heating. The virtual power plant (VPP) achieves the reasonable combination of controllable power sources, distributed energy, controllable loads, and energy storage systems within a certain area. Thus, we propose a VPP model based on combined dispatch of wind power and heat energy, which integrates wind turbines, thermal turbines, CHP units, etc., into a whole to join in the grid operation. Besides, to preserve the privacy of energy agents, Benders decomposition algorithm is adopted to solve the proposed model in this paper. The validity and efficiency of the proposed VPP model and Benders decomposition algorithm are verified via numerical cases.

1 Introduction

In recent years, wind energy has been developed as a key strategy to handle with the energy crisis. The total installed capacity of wind turbines is expected to reach 3,105.9 GW by 2030. However, due to an unreasonable energy structure and lack of flexibility, wind power curtailment is becoming increasingly severe. In Inner Mongolia in China, the total amount of wind curtailment reaches 5.06 billion, accounting for 8.9% of the total available output in 2021 (Zhao et al., 2023). Especially in winter, due to the large number of combined heat and power (CHP) units undertaking the heating task, the implementation of the “determining power by heat” operation mode seriously reduces the accommodation space of wind power (Li et al., 2016; Qu et al., 2020).

To address this crisis, some researchers have conducted research on the combined dispatch of wind power and heat energy (Li et al., 2024), such as demand response (Rigoni et al., 2021), energy storage deployment (Toubeau et al., 2021), flexibility reformation of thermal power units (Sun et al., 2020), etc. Rigoni et al. (2021) present a method that combines demand response aggregators with power operators for combined heat and power dispatch (CHPD). Meanwhile, many wind power heating demonstration projects are constantly emerging. However, due to the imperfect dispatch methods and CHPD platforms, many wind power heating projects have not effectively linked the use of abandoned wind and heating, resulting in only a small portion of wind power heating electricity coming from abandoned wind power, which deviates from the original intention of wind power heating projects.

In order to promote the efficient utilization and wind accommodation by wind power heating, many scholars generally consider wind power heating as a heat load side management resource. There are virtual power plant (VPP) projects that combine CHP units, wind turbines, and load side management within a certain region (Houwing et al., 2009). VPP refers to the reasonable combination of controllable power sources, distributed energy, controllable loads, and energy storage systems within a certain area, managed by a control center, and integrated into a whole to join in the grid operation Xia et al. (2016), Wang et al. (2022), Houwing et al. (2009) propose the formation of a VPP consisting of wind turbines and CHP units, achieving the objective of smoothing wind fluctuations and reducing operation costs. Xia et al. (2016) add an electric boiler to the VPP-CHPD operation model to achieve direct conversion of wind power to heating, reducing carbon emissions. However, due to the fact that the electric power system (EPS) and district heating system (DHS) belong to different energy agents, the traditional centralized dispatch cannot guarantee the privacy of each energy agents (Zhao et al., 2024). Therefore, VPP is difficult to apply in practice due to the demand for privacy preservation.

Many distributed optimal algorithms have been studied to ensure privacy preservation among energy agents. Each energy agent solves its own subproblem, only interacting boundary information to achieve the global optimal, implementing privacy preservation in a decoupled manner (Chen et al., 2020). As one of the most popular optimal algorithms in combined dispatch, the Benders decomposition algorithm has been widely applied in integrated energy system (Tan et al., 2023; Du et al., 2024). Tan et al. (2023) propose a coordinated optimization framework based on equivalent projection theory, which can be solved by Benders decomposition algorithm. Chen et al. (2020) propose a improved generalized Benders decomposition method to address the combined natural gas and power model without privacy leakage.

The main contributions of this paper are summarized as follows:

(1) To better accommodate wind energy, a VPP model based on combined dispatch of wind power and heat energy is proposed, which integrate wind turbines, thermal turbines, CHP units, etc. into a whole to join in the grid operation, reducing wind curtailment.

(2) Inspired by multi-agent characteristics, Benders decomposition algorithm is adopted to handle with the VPP model in this paper, in order to preserve the privacy of energy agents. The efficiency and accuracy of the algorithm are verified via numerical cases.

The remaining part of this paper is summarized as follows: The VPP model is formulated in Section 2. Section 3 focuses on the solution strategy based on Benders decomposition algorithms. Section 4 discusses the case studies. Section 5 summaries and concludes this paper.

2 Problem formulation

This section discusses the VPP model. Its goal is to maximize the profits of EPS and DHS, with the physical constraints related to two system.

2.1 Objective function

The objective of the virtual power plant model is to maximize the revenue of all units in EPS and DHS, i.e., to minimize their operation cost. And the objective function and constraints (Equations 1–5) are as follows:

$\min {\displaystyle \sum _{t\in T}}\left[{\displaystyle \sum _{i\in {\mathrm{\Omega }}^B}}{C}_i^B\left(f_{i,t}^B\right)+{\displaystyle \sum _{i\in {\mathrm{\Omega }}^{CHP}}}{C}_i^{CHP}\left(p_{i,t}^{CHP},h_{i,t}^{CHP}\right)+{\displaystyle \sum _{i\in {\mathrm{\Omega }}^W}}{C}_i^W\left(p_{i,t}^W\right)+{\displaystyle \sum _{i\in {\mathrm{\Omega }}^{TU}}}{C}_i^{TU}\left(p_{i,t}^{TU}\right)\right](1)$

where,

$\begin{array}{l}{C}_i^{CHP}\left(p_{i,t}^{CHP},h_{i,t}^{CHP}\right)={\alpha }_{i,2}^{CHP}{\left(p_{i,t}^{CHP}\right)}^2+{\alpha }_{i,1}^{CHP}{p}_{i,t}^{CHP}+{\alpha }_{i,0}^{CHP}\\ +{\beta }_{i,2}^{CHP}{\left(h_{i,t}^{CHP}\right)}^2+{\beta }_{i,1}^{CHP}{h}_{i,t}^{CHP}\\ +{\beta }_{i,0}^{CHP},\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^{CHP},\hspace{1em}t\in T\end{array}(2)$

$C_i^B\left(f_{i,t}^P\right)={\alpha }_i^B{f}_{i,t}^B,\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^B,\hspace{1em}t\in T(3)$

$C_i^W\left(p_{i,t}^W\right)={\alpha }_i^W\left|{\overline{p}}_i^W-p_{i,t}^W\right|,\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^W,\hspace{1em}t\in T(4)$

$C_i^{TU}\left(p_{i,t}^{TU}\right)={\alpha }_{i,2}^{TU}{\left(p_{i,t}^{TU}\right)}^2+{\alpha }_{i,1}^{TU}{p}_{i,t}^{TU}+{\alpha }_{i,0}^{TU},\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^{TU},\hspace{1em}t\in T(5)$

where, $\mathrm{\Omega }$ denotes the set of units. T is the set of time. $C$ denotes the unit operation cost. $f_{i,t}^B$ is the fuel consumption of heating boiler i during dispatch time t. $h_{i,t}^{CHP}$ is the heating power of CHP units during dispatch time t. $p_{i,t}^{CHP}$, $p_{i,t}^W$, $p_{i,t}^{TU}$ denote the electric power of CHP units, wind turbines and thermal units during dispatch time t respectively. ${\alpha }_{i,·}^{CHP}$, ${\beta }_{i,·}^{CHP}$, ${\alpha }_i^B$, ${\alpha }_i^W$, ${\alpha }_{i,·}^{TU}$ are the coefficient of cost function of units.

2.2 Constraints

The constraints in the VPP model include the constraints related to the DHS and the EPS, as follows i.e., (Equations 6–21) and (Equations 22–28):

2.2.1 District heating system

The heating source consists of CHP units and heating boilers. The heating output of heating sources must be controlled to a specific range due to the limitations of transmission capacity of pipelines and lines and feasible operation range (Xue et al., 2020).

${\underset{\_}{P}}_i^{CHP}\le P_{i,t}^{CHP}\le {\overline{P}}_i^{CHP},\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^{CHP},\hspace{1em}t\in T.(6)$

${\underset{\_}{H}}_i^{CHP}\le H_{i,t}^{CHP}\le {\overline{H}}_i^{CHP},\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^{CHP},\hspace{1em}t\in T.(7)$

${\underset{\_}{H}}_i^B\le H_{i,t}^B\le {\overline{H}}_i^B,\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^B,\hspace{1em}t\in T.(8)$

where, ${\overline{P}}_i^{CHP}$, ${\overline{H}}_i^{CHP}$, ${\overline{H}}_i^B$ are the maximum output of CHP units and heating boilers. ${\underset{\_}{P}}_i^{CHP}$, ${\underset{\_}{H}}_i^{CHP}$, ${\underset{\_}{H}}_i^B$ are the minimum output of them.

The output of heating source satisfies the specific heat capacity formula (Xue et al., 2020), as follows:

$H_{i,t}^B+H_{i,t}^{CHP}=c\cdot M_n\cdot \left({\tau }_{n,t}^S-{\tau }_{n,t}^R\right),\hspace{0.33em}\forall n\in {\mathrm{\Omega }}^{node},\hspace{1em}t\in T.(9)$

where, c is the specific heat capacity of water, $M_n$ is the total mass flow at node n, ${\tau }_{n,t}^S$ and ${\tau }_{n,t}^R$ are the node temperature in heating network during dispatch time t. The superscript S represents the supply network, and R represents the return network.

$H_{i,t}^B={\eta }_i{f}_{i,t}^B,\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^B,\hspace{1em}t\in T.(10)$

where, ${\eta }_i$ is the heating output efficiency of boilers in DHS.

To guarantee a certain level of heating quality, the node temperature connected to the heat sources must be maintained within a certain range:

${\underset{\_}{\tau }}_n^S\le {\tau }_{n,t}^S\le {\overline{\tau }}_n^S,\hspace{0.33em}\forall n\in {\mathrm{\Omega }}^{node},\hspace{1em}t\in T.(11)$

where, ${\underset{\_}{\tau }}_n^S$ and ${\overline{\tau }}_n^S$ are minimum and maximum node temperature in the supply network.

The mass flow rate of the supply and return pipeline at the same node should be consistent.

$M{S}_l^p=M{R}_l^p,\hspace{0.33em}t\in T.(12)$

The flow in the pipeline should be balanced, which means the inflow flow is equal to the outflow flow.

$\begin{array}{l}{\displaystyle \sum _{l\in {\mathrm{\Omega }}_n^{p+}}}M{S}_l^p-{\displaystyle \sum _{l\in {\mathrm{\Omega }}_n^{p-}}}M{S}_l^p={\displaystyle \sum _{i\in {\mathrm{\Omega }}_n^{CHP}}}M{S}_i^n-{\displaystyle \sum _{j\in {\mathrm{\Omega }}_n^D}}M{S}_j^n,\hspace{0.33em}t\in T,\\ {\displaystyle \sum _{l\in {\mathrm{\Omega }}_n^{p+}}}M{R}_l^p-{\displaystyle \sum _{l\in {\mathrm{\Omega }}_n^{p-}}}M{R}_l^p={\displaystyle \sum _{j\in {\mathrm{\Omega }}_n^D}}M{R}_j^n-{\displaystyle \sum _{i\in {\mathrm{\Omega }}_n^{CHP}}}M{R}_i^n,\hspace{0.33em}t\in T.\end{array}(13)$

$\underset{\_}{M}{S}_l^p\le M{S}_l^p\le \overline{M}{S}_l^p,\underset{\_}{M}{R}_l^p\le M{R}_l^p\le \overline{M}{R}_l^p(14)$

Moreover, the mixed temperature of node in DHS is presented as follows:

$\begin{array}{l}{\displaystyle \sum _{l\in {\mathrm{\Omega }}_n^{p-}}}\left({\tau }_{l,t}^{PS\_out}\cdot M{S}_l^p\right)={\tau }_{n,t}^S\cdot {\displaystyle \sum _{j\in {\mathrm{\Omega }}_n^{p+}}}M{S}_l^p,\hspace{0.33em}t\in T,\\ {\displaystyle \sum _{l\in {\mathrm{\Omega }}_n^{p-}}}\left({\tau }_{l,t}^{PR\_out}\cdot M{R}_l^p\right)={\tau }_{n,t}^R\cdot {\displaystyle \sum _{j\in {\mathrm{\Omega }}_n^{p+}}}M{R}_l^p,\hspace{0.33em}t\in T.\end{array}(15)$

where ${\tau }_{l,t}^{PS\_out}$ and ${\tau }_{l,t}^{\mathit{PR}\_out}$ are the outlet temperatures of pipelines in heating network, $M{S}_l^p$ and $M{R}_l^p$ are the mass flow of heating network. ${\mathrm{\Omega }}_n^{p+}$ and ${\mathrm{\Omega }}_n^{p-}$ are the set of inlet and outlet pipelines connected to node n. The first equation presents the supply network, and the second equation presents the return network. The inlet temperature of the mass flow in pipeline is consistent with the temperature of the nodes connected to it.

$\begin{array}{l}{\tau }_{l,t}^{PS\_in}={\tau }_{n,t}^S,\\ {\tau }_{l,t}^{\mathit{PR}\_in}={\tau }_{n,t}^R,\hspace{0.33em}\forall t\in T.\end{array}(16)$

where, ${\tau }_{l,t}^{PS\_in}$ and ${\tau }_{l,t}^{\mathit{PR}\_in}$ are the inlet temperatures in supply network and return network.

The heat loss and transfer delay of mass flow are involved in this paper, which can be computed as follow:

$\begin{array}{l}{\tau }_{l,t}^{PS\_out}={\tau }_t^0+\left({\tau }_{l,t}^{\prime PS\_out}-{\tau }_t^0\right)\times e^{-\frac{{\epsilon }_l\Delta t}{A_l\rho c}\left(\lceil {\phi }_l^S\rceil -0.5\right)},\hspace{0.33em}\forall l\in {\mathrm{\Omega }}^p,\\ {\tau }_{l,t}^{PR\_out}={\tau }_t^0+\left({\tau }_{l,t}^{\prime PR\_out}-{\tau }_t^0\right)\times e^{-\frac{{\epsilon }_l\Delta t}{A_l\rho c}\left(\lceil {\phi }_l^R\rceil -0.5\right)},\hspace{0.33em}\forall l\in {\mathrm{\Omega }}^p.\end{array}(17)$

$\begin{array}{l}{\tau }_{l,t}^{\prime PS\_out}=\left(1-\lceil {\phi }_l^S\rceil +{\phi }_l^S\right){\tau }_{l,t-\lceil {\phi }_l^S\rceil }^{PS\_in}+\left(\lceil {\phi }_l^S\rceil -{\phi }_l^S\right){\tau }_{l,t-\lceil {\phi }_l^S\rceil +1}^{PS\_in}\\ {\tau }_{l,t}^{\prime PR\_out}=\left(1-\lceil {\phi }_l^R\rceil +{\phi }_l^R\right){\tau }_{l,t-\lceil {\phi }_l^R\rceil }^{PR\_in}+\left(\lceil {\phi }_l^R\rceil -{\phi }_l^R\right){\tau }_{l,t-\lceil {\phi }_l^R\rceil +1}^{PR\_in}\end{array}(18)$

${\phi }_l^S=\frac{\rho A_l{L}_l}{M{S}_l^p},{\phi }_l^R=\frac{\rho A_l{L}_l}{M{S}_l^p},\hspace{0.33em}\forall l\in {\mathrm{\Omega }}^p(19)$

where, ${\mathrm{\Omega }}^p$ is the set of heating pipelines in DHS. ${\tau }_t^0$ is ambient temperature in DHS. ${\tau }_{l,t}^{\prime PS\_out}$ and ${\tau }_{l,t}^{\prime \mathit{PR}\_out}$ are intermediate variable. ${\phi }_l^S$ and ${\phi }_l^R$ are transfer time of heating pipelines in supply network and return network. $\rho$ is water density. ${\epsilon }_l$ is heat transfer factor. $\Delta t$ is the time interval. $L_l$ and $A_l$ are the length and cross area of pipelines.

The heating load $H_{i,t}^D$ can be represented by specific heat capacity formulation.

$H_{i,t}^D=c\cdot M_n\cdot \left({\tau }_{n,t}^S-{\tau }_{n,t}^R\right),\hspace{0.33em}\forall n\in {\mathrm{\Omega }}^{node},\hspace{0.33em}i\in {\mathrm{\Omega }}^{HL},\hspace{1em}t\in T.(20)$

where, ${\mathrm{\Omega }}^{HL}$ is the set of heating load. Similarly, the water temperature of return network must be limited a specific range (Xue et al., 2020).

${\underset{\_}{\tau }}_n^R\le {\tau }_{n,t}^R\le {\overline{\tau }}_n^R,\hspace{0.33em}\forall n\in {\mathrm{\Omega }}^{node},\hspace{1em}t\in T.(21)$

where ${\underset{\_}{\tau }}_n^R$ and ${\overline{\tau }}_n^R$ are the minimum and maximum node temperature in the return network.

2.2.2 Electric power system

The constraints related to EPS are presented as follows:

${\displaystyle \sum _{i\in {\mathrm{\Omega }}^{CHP}}}{P}_{i,t}^{CHP}+{\displaystyle \sum _{i\in {\mathrm{\Omega }}^{TU}}}{P}_{i,t}^{TU}+{\displaystyle \sum _{i\in {\mathrm{\Omega }}^W}}{P}_{i,t}^W={\displaystyle \sum _{d\in {\mathrm{\Omega }}^D}}{D}_{i,t}^L+{\displaystyle \sum _{d\in {\mathrm{\Omega }}^B}}{P}_{i,t}^B,\forall t\in T.(22)$

$\begin{array}{l}\hfill \left|\sum L{F}_{j,n}\cdot \left({\displaystyle \sum _{i\in {\mathrm{\Omega }}^{CHP}}}{P}_{i,t}^{CHP}+{\displaystyle \sum _{i\in {\mathrm{\Omega }}^{TU}}}{P}_{i,t}^{TU}+{\displaystyle \sum _{i\in {\mathrm{\Omega }}^W}}{P}_{i,t}^W-{\displaystyle \sum _{d\in {\mathrm{\Omega }}^D}}{D}_{i,t}^L-{\displaystyle \sum _{d\in {\mathrm{\Omega }}^B}}{P}_{i,t}^B\right)\right|\\ \hfill & \le F_j,\hspace{0.33em}\forall j\in {\mathrm{\Omega }}^{line},\hspace{1em}t\in T.\hfill \end{array}(23)$

${\underset{\_}{P}}_i^{TU}\le P_{i,t}^{TU}\le {\overline{P}}_i^{TU},\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^{TU},\hspace{1em}t\in T.(24)$

${\underset{\_}{P}}_i^W\le P_{i,t}^W\le {\overline{P}}_i^W,\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^W,\hspace{1em}t\in T.(25)$

$0\le s{u}_{i,t}^{TU}\le {\overline{R}}_i^{TU},0\le s{d}_{i,t}^{TU}\le {\underset{\_}{R}}_i^{TU},\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^G,\hspace{1em}t\in T.(26)$

$s{u}_{i,t}^{TU}\le {\overline{P}}_i^{TU}-P_{i,t}^{TU},s{d}_{i,t}^{TU}\le P_{i,t}^{TU}-{\underset{\_}{P}}_i^{TU},\hspace{0.33em}\forall i\in {\mathrm{\Omega }}^{TU},\hspace{1em}t\in T.(27)$

${\displaystyle \sum _{i\in {\mathrm{\Omega }}^{TU}}}s{u}_{i,t}^{TU}\ge SR{U}_t,{\displaystyle \sum _{\forall i\in {\mathrm{\Omega }}^{TU}}}s{d}_{i,t}^{TU}\ge SR{D}_t,\hspace{0.33em}\forall t\in T.(28)$

The energy balance constraint in EPS is presented in Equation 22. Equation 23 is the network capacity constraint. The unit output constraints of CHP units and wind turbines are showed in Equations 24, 25. Equations 26–28 are shows the ramping and spinning reserve constraints. $s{u}_{i,t}^{TU},s{d}_{i,t}^{TU}$ refer to the upward/downward ramping rate, $SR{U}_t,SR{D}_t$ refer to the spinning reserve, $L{F}_{j,n}$ refer to the shift factor.

3 Solving strategy

In this paper, the Benders decomposition method is proposed to solve the privacy information protection of the whole system. According to the variable type of the virtual power plant system, the original problem is decomposed into the main problem of the district heating system and the sub-problem of the electricity power system. There is no need for interactive privacy information between the electricity power system and the district heating system. Two systems only need to interact with the optimal output of the system and Benders cut constraints to solve the model.

3.1 Second-order control relaxion

In order to successfully apply Benders to solve the original problem, the model needs to be relaxed. This is because the change in flow rate introduces a bilinear term, which causes the subproblem of heat to be non-convex and cannot be solved.

To reduce the complexity of the model, the auxiliary variable ${\omega }_i$ is introduced to replace the product of M and T.

${\omega }_i=M_i{\tau }_i(29)$

Based on the above re-formulation, the above model can be transformed into the NCQCP model. However, constraint Equation 29 is still a nonlinear term, which needs to be dealt with. Therefore, the second-order control relaxation is introduced to relax the bilinear term, which could be solved efficiently by solvers such as the cplex.

Constraint Equation 29 is equivalent to the following Equation 30:

$\begin{array}{l}4{\epsilon }_i{\omega }_{1,i}={\left(M_i+{\epsilon }_i{\tau }_i\right)}^2\\ 4{\epsilon }_i{\omega }_{2,i}={\left(M_i-{\epsilon }_i{\tau }_i\right)}^2\\ {\omega }_i={\omega }_{1,i}-{\omega }_{2,i}\end{array}(30)$

where the parameters ${\epsilon }_i$ is to make the order of magnitude of the parameter close. The constraint is transformed into inequality constraint (Equations 31, 32):

$\begin{array}{l}4{\epsilon }_i{\omega }_{1,i}\ge {\left(M_i+{\epsilon }_i{\tau }_i\right)}^2\\ 4{\epsilon }_i{\omega }_{2,i}\ge {\left(M_i-{\epsilon }_i{\tau }_i\right)}^2\end{array}(31)$

$\begin{array}{l}4{\epsilon }_i{\omega }_{1,i}\le {\left(M_i+{\epsilon }_i{\tau }_i\right)}^2\\ 4{\epsilon }_i{\omega }_{2,i}\le {\left(M_i-{\epsilon }_i{\tau }_i\right)}^2\end{array}(32)$

Since constraint (Equation 32) is nonconvex, it is transformed into a second-order cone form (Equation 33).

$\begin{array}{l}{‖\begin{array}{l}{M}_i+{\epsilon }_i{\tau }_i\\ 1-{\epsilon }_i{\omega }_{1,i}\end{array}‖}_2\le 1+{\epsilon }_i{\omega }_{1,i}\\ {‖\begin{array}{l}{M}_i-{\epsilon }_i{\tau }_i\\ 1-{\epsilon }_i{\omega }_{2,i}\end{array}‖}_2\le 1+{\epsilon }_i{\omega }_{2,i}\end{array}(33)$

3.2 Decomposed model based on the benders decomposition

The Benders algorithm has certain requirements for the format. For the optimization problem of a specific format, it will divide the original problem into a main problem and two groups of sub-problems, namely, the feasibility subproblem and the optimal subproblem. Therefore, it is necessary to rewrite the original problem into a vector form that is easy to solve, which is expressed as follow Equation 34:

$\begin{array}{c}\underset{x_E,x_B,x_P}{\min }{C}_{OP}=C_E\left(x_E,x_B\right)+C_P\left(x_P\right)\\ \mathrm{s}.\mathrm{t}.A_E{x}_E+A_{BE}{x}_B=a_E\\ A_P{x}_P+A_{BP}{x}_B=a_P\\ B_E{x}_E+B_{BE}{x}_B\ge b_E\\ B_P{x}_P+B_{BP}{x}_B\ge b_P\\ D_E{x}_E\ge d_E\\ D_P{x}_P\ge d_P\end{array}(34)$

The main problem (Equation 35) is the optimization of the power system.

$\begin{array}{c}\underset{x_E,x_B}{\min }{C}_E=C_E\left(x_E,x_B\right)+\mu \\ \mathrm{s}.\mathrm{t}.A_E{x}_E+A_{BE}{x}_B=a_E\\ B_E{x}_E+B_{BE}{x}_B\ge b_E\\ D_E{x}_E\ge d_E\\ \mu \ge 0\end{array}(35)$

The solution to the main problem is brought into the subproblem. The $C_E$ refer to the objective functions of the main problem, $\mu$ is the bounds for the objective function of subproblem. If the subproblem is feasible, the optimal subproblem is obtained. The optimal subproblem (Equation 36) is the optimization of the district heating system.

$\begin{array}{c}\underset{x_P,x_B}{\min }{C}_P=C_P\left(x_P\right)\\ \mathrm{s}.\mathrm{t}.A_P{x}_P+A_{BP}{x}_B=a_P\\ B_P{x}_P+B_{BP}{x}_B\ge b_P\\ D_P{x}_P\ge d_P\\ x_B={\dot{x}}_B\end{array}(36)$

where $C_{MP}$ and $C_{SP}$ represent the objective functions of optimal subproblem. And the optimality cut is generated to update the $\mu$ in the main problem. which (Equations 37) is expressed as:

$C_P+{\lambda }_B^{\mathrm{T}}\left(x_B-{\dot{x}}_B\right)\le \mu (37)$

If the subproblem is infeasible with the fixed solution of the main problem, the feasibility subproblem is generated. The feasibility subproblem (Equation 38) is expressed as:

$\begin{array}{c}\underset{x_p,x_B,w}{\min }{C}_{FP}=w1+w2\\ \mathrm{s}.\mathrm{t}.A_P{x}_P+A_{BP}{x}_B=a_P\\ B_P{x}_P+B_{BP}{x}_B\ge b_P\\ D_P{x}_P\ge d_P\\ x_B={\dot{x}}_B+w1-w2\\ w1\ge 0,\hspace{0.33em}w2\ge 0\end{array}(38)$

where the $w1$ and $w2$ is the slack variables. And the feasibility cut (Equation 39) is expressed as follows:

$C_{FP}+{\lambda }_B^{\mathrm{T}}\left(x_B-{\dot{x}}_B\right)\le 0(39)$

3.3 Iteration procedure

The optimal solution needs to be obtained iteratively by the main problem and the subproblem. The summary of this Benders decomposition procedure is as follows:

Algorithm.The Benders Decomposition.

1. Initialize $N_{in}=0$, $U_b=+\infty$, $L_b=-\infty$

2. While $U_b-L_b<\delta$

3.  Solve the main problem and send the solution ${\dot{x}}_B^{N_{\text{out}}}$ to the subproblem

3.  IF SP is feasible

  THEN:

3.  The optimal subproblem is generated

3  Add the optimality cut to the main problem and solve the main problem

  ELSE:

3.  The feasibility subproblem is generated

3.  Add feasibility cut to the main problem and solve the main problem

4.  Update the value of the $U_b$, $L_b$, $N_{in}=N_{in+1}$

5. End While

The proposed solution strategy includes two problems, the primary problem (PP) is divided into the master problem (MP) and the subproblem (SP). To better and clearer illustrate the process of the consensus algorithm in this paper, we have added the descriptions of the pseudocode. The solution progress is expressed as follows:

First, the upper and lower bounds are initialized. And set the number of iterations $N_{in}$ is 0. Second, the first iteration is to solve the MP and send the initial value ${\dot{x}}_B^{N_{\text{out}}}$ to the SP. SP is solved and add the OC or FC to the SP. The next step is to solve the MP and update the value of the $U_b$, $L_b$, $N_{in}=N_{in+1}$.

If the convergence criterion $U_b-L_b<\delta$ is satisfied, the iteration procedure ends, otherwise the loop is continued until the criterion is satisfied. The detailed steps are shown in the Algorithm.

4 Case studies

4.1 Case setting

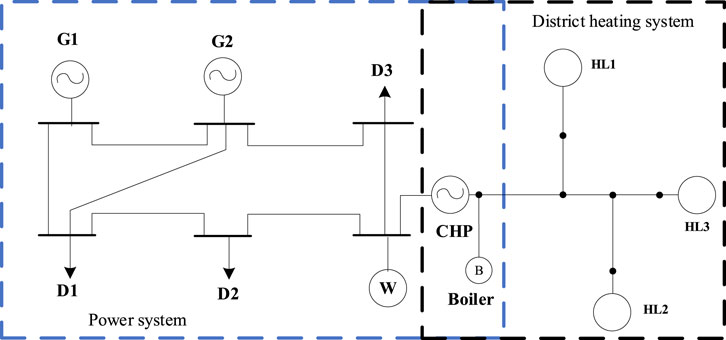
In this paper, a park-level power-heat virtual power plant considering mass flow is built to verify the validity of the model. Figure 1 shows the system of the P6H6, in which the two nodes are traditional power units, two nodes are wind farms, and one node is the CHP unit. The upper and lower temperature bounds of the mass flow rate in the supply pipeline are 110°C/80°C, and the temperature in the return pipeline is 70°C/40°C.

Figure 1

Figure 1. The configuration of the P6H6 system.

To prove the rationality and validity of the model, and solution method proposed in this paper, the following two schemes are set up and solved by the gurobi 9.5.0 software package. The results of different schemes are compared and analyzed:

Case 1. Chose the Quality regulation mode (refer to the constant flow and variable temperature).

Case 2. Chose the Quality–quantity regulation mode (refer to the variable flow and variable temperature).

4.2 Analysis of case results

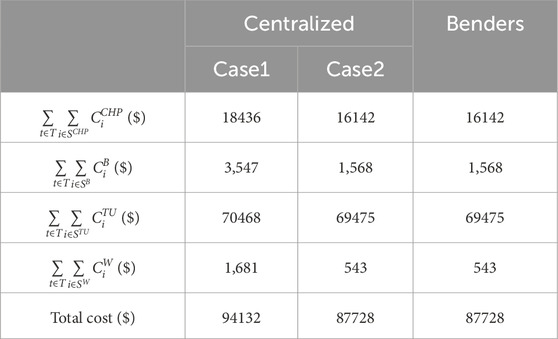
As shown in Table 1, the operating cost of the electricity-heat virtual power plant in Case 2 decreased by 6.8% the virtual power plant in Case 1. It can be seen that compared with the constant mass flow rate, the variable flow rate will have a wider adjustment range. Therefore, in Case 2, the cost of wind curtailment is further reduced. Moreover, the Benders algorithm is consistent with the results of the centralized algorithm. It further demonstrates the effectiveness of the Benders in this paper.

Table 1

Table 1. The cost of two modes in Case 1 and Case 2.

The dispatch results of the two cases are shown in Figure 2. The CHP units store more heat supply between 10:00–15:00, which can release more wind power at night, thus further improving the wind accommodation. The amount of heat stored during the day of Case 2 is 19% more than that of Case 1, and the wind power consumption is 4.1% more, which shows the superiority of variable flow and temperature mode. Through the combination of the two variables of mass flow rate and temperature, the adjustment range of CHP units becomes larger, CHP units bear more heat during the day, and the thermal power unit reduces the output. Obviously, in this mode, the output of wind power will be greater, thus reducing wind curtailment.

Figure 2

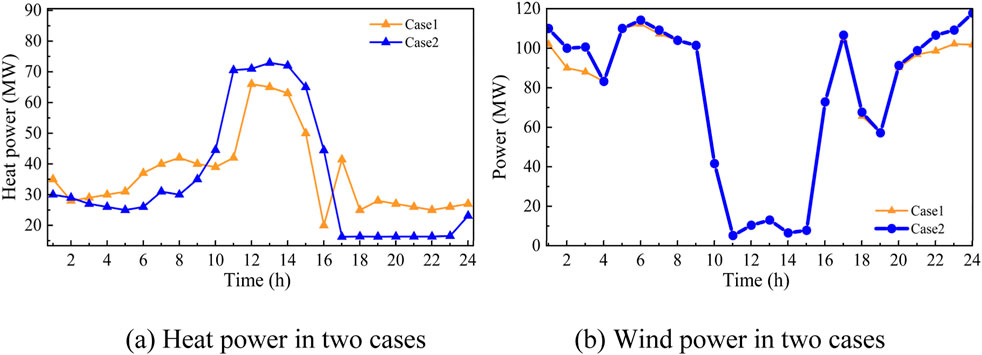
Figure 2. Comparison of power in two cases. (A) Heat power in two cases (B) Wind power in two cases.

Figure 3 compares the differences in temperature and mass flow rate at the source node under the two modes. From the difference between the two cases, it demonstrates the mode of variable flow rate and temperature in Case 1 has more advantages. This is because the change of mass flow rate in case 1 will make the change of temperature tend to be gentle. The supply temperature of Case 2 in Figure 3A is obviously lower than that of Case 1. Lower temperatures will bring less heat loss. The heat loss is reduced by 10.3% considering the flow rate in Figure 3B.

Figure 3

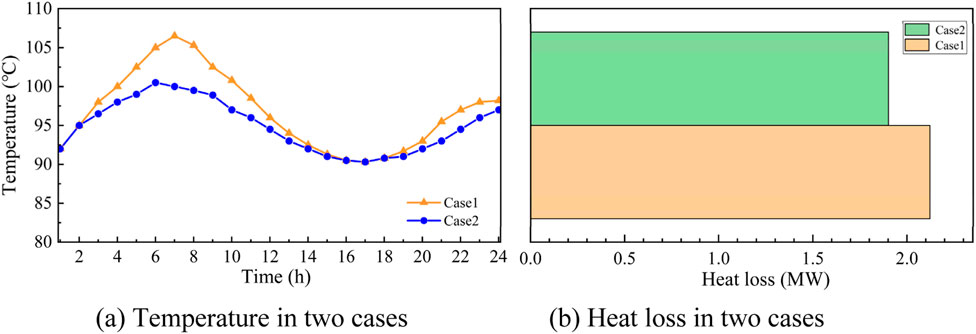
Figure 3. Comparison of temperature and heat loss in two cases. (A) Temperature in two cases (B) Heat loss in two cases.

5 Conclusion

This paper presented a VPP model considering the combined dispatch of wind power and heat energy with the variable mass flow rate mode, which reduces wind curtailment and heat loss. Besides, the Benders algorithm is adopted to solve the VPP model to protect the information privacy of energy agents. And the correctness of the model and the effectiveness of the algorithm are further verified in the case. In the future, we can consider extending the quality–quantity regulation mode to the secondary heating network, further analyze the architecture of the heating network, explore the mode suitable for each part, and achieve a better adjustment effect in the electricity-heat virtual power plant.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YW: Writing–original draft, Writing–review and editing. SY: Funding acquisition, Methodology, Supervision, Writing–review and editing. SZ: Resources, Software, Visualization, Writing–review and editing. LL: Conceptualization, Data curation, Supervision, Writing–review and editing. XY: Formal Analysis, Project administration, Supervision, Writing–original draft. JL: Investigation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Sichuan Science and Technology Program (2024YFHZ0138).

Conflict of interest

Authors YW, SY, SZ, LL, and XY were employed by Energy Planning and Research Institute of Southwest Electric Power Design Institute Co., Ltd. of China Power Engineering Consulting Group.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, B., Yin, R., Yin, G., Bu, L., and Sun, H. (2020). Decentralized optimal gas-power flow calculation via modified generalized Benders decomposition. in: 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 1366–1370. doi:10.1109/EI250167.2020.9346617

CrossRef Full Text | Google Scholar

Du, Y., Xue, Y., Wu, W., Shahidehpour, M., Shen, X., Wang, B., et al. (2024). Coordinated planning of integrated electric and heating system considering the optimal reconfiguration of district heating network. IEEE Trans. On Power Sys. 39, 794–808. doi:10.1109/TPWRS.2023.3242652

CrossRef Full Text | Google Scholar

Houwing, M., Papaefthymiou, G., Heijnen, P. W., and Iliü, M. D. (2009). Balancing wind power with virtual power plants of micro-CHPs. 2009 IEEE Bucharest Power Tech 2, 1–7. doi:10.1109/PTC.2009.5282056

CrossRef Full Text | Google Scholar

Li, H., Wu, Q., Yang, L., Zhang, H., and Jiang, S. (2024). Distributionally robust negative-emission optimal energy scheduling for off-grid integrated electricity-heat microgrid. IEEE Trans. On Sustainable Energy. 15, 803–818. doi:10.1109/TSTE.2023.3306360

CrossRef Full Text | Google Scholar

Li, Z., Wu, W., Shahidehpour, M., Wang, J., and Zhang, B. (2016). Combined heat and power dispatch considering pipeline energy storage of district heating network. IEEE Trans On Sustainable Energy. 7, 12–22. doi:10.1109/TSTE.2015.2467383

CrossRef Full Text | Google Scholar

Qu, M., Ding, T., Wei, W., Dong, Z., Shahidehpour, M., and Xia, S. (2020). An analytical method for generation unit aggregation in virtual power plants. IEEE Transac. On Smart Grid 11, 5466–5469. doi:10.1109/TSG.2020.3002104

CrossRef Full Text | Google Scholar

Rigoni, V., Flynn, D., and Keane, A. (2021). Coordinating demand response aggregation with LV network operational constraints. IEEE Trans. Power Syst. 36, 979–990. doi:10.1109/TPWRS.2020.3014144

CrossRef Full Text | Google Scholar

Sun, Y., Wang, L., Xu, C., Van, H. J., Maréchal, F., and Yang, Y. (2020). Enhancing the operational flexibility of thermal power plants by coupling high-temperature power-to-gas. Appl. Energy 263, 114608. doi:10.1016/j.apenergy.2020.114608

CrossRef Full Text | Google Scholar

Tan, Z., Yan, Z., Zhong, H., and Xia, Q. (2023). Non-iterative solution for coordinated optimal dispatch via equivalent projection-Part I: theory. IEEE Trans. Power Syst. 39, 890–898. doi:10.1109/tpwrs.2023.3258066

CrossRef Full Text | Google Scholar

Toubeau, J.-F., Bottieau, J., De, G. Z., Vallee, F., and Bruninx, K. (2021). Data-driven scheduling of energy storage in day-ahead energy and reserve markets with probabilistic guarantees on real-time delivery. IEEE Trans. Power Syst. 36, 2815–2828. doi:10.1109/TPWRS.2020.3046710

CrossRef Full Text | Google Scholar

Wang, K., Xue, Y., Guo, Q., Shahidepour, M., Zhou, Q., Wang, B., et al. (2022). A coordinated reconfiguration strategy for multi-stage resilience enhancement in integrated power distribution and heating networks. IEEE Trans. Smart Grid 14, 2709–2722. doi:10.1109/TSG.2022.3231590

CrossRef Full Text | Google Scholar

Xia, Y., Liu, J., Huang, Z., and Zhang, X. (2016). Carbon emission impact on the operation of virtual power plant with combined heat and power system. Front. Inf. Technol.Electron. Eng. 17, 479–488. doi:10.1631/FITEE.1500467

CrossRef Full Text | Google Scholar

Xue, Y., Li, L., Lin, C., Guo, Q., and Sun, H. (2020). Coordinated Dispatch of Integrated Electric and District Heating Systems Using Heterogeneous Decomposition. IEEE Trans. Sustain. Energy 11, 1495–1507. doi:10.1109/TSTE.2019.2929183

CrossRef Full Text | Google Scholar

Zhao, L., Xue, Y., Du, Y., Chang, X., Li, Z., Su, J., et al. (2024). Privacy-preserving combined heat and power dispatch based on information masking mechanism: a decentralized perspective. IEEE Trans. Smart Grid 15, 4550–4563. doi:10.1109/TSG.2024.3390128

CrossRef Full Text | Google Scholar

Zhao, L., Xue, Y., Sun, H., Du, Y., Chang, X., Su, J., et al. (2023). Benefit allocation for combined heat and power dispatch considering mutual trust. Appl. Energy 345, 121279. doi:10.1016/j.apenergy.2023.121279

CrossRef Full Text | Google Scholar