Coordinated optimization of control parameters for suppressing transient overvoltage in wind power DC transmission systems

With the increasing proportion of new energy in power systems, the instability issues of novel power systems become more prominent. This paper addresses the transient overvoltage problem in wind power DC transmission systems by proposing a method for transient overvoltage suppression based on doubly-fed wind turbines, high-voltage DC transmission systems, and SVC control parameter optimization. The electromagnetic transient model of the wind power DC transmission system is combined with intelligent optimization algorithms through joint invocation to achieve coordinated optimization of control parameters. Case studies validate the effectiveness of the proposed model and method. The results indicate that the improved genetic algorithm, SEGA, proposed in this paper, effectively suppresses overvoltage at the grid connection point of wind turbines. Furthermore, by simultaneously applying coordinated control strategies based on DFIG and SVC and optimizing parameters of HVDC, DFIG, and SVC, transient overvoltage phenomena can be effectively eliminated.

1 Introduction

With the launch of the United Nations-supported ‘Towards Zero Carbon’ initiative, reducing the consumption of fossil fuels and developing low-carbon and environmentally friendly new energy sources has become a key solution for existing energy and environmental issues (Qu et al., 2021). To promote the coordinated development of the environment and energy, and advance the reform of energy structure, the large-scale development of wind energy, photovoltaics, and other new energy sources, as well as the vigorous development of new energy generation technologies, have become the top priority for achieving the transformation of energy structure.

To meet the demand for large-scale integration of new energy sources and to enhance transmission capacity, ensuring the stable operation of power grids under extensive new energy generation (Johnson and Dessouky, 2021; Barnes et al., 2017), ultra-high voltage direct current (UHVDC) transmission projects have emerged as a crucial means due to their advantages such as high transmission capacity, low cost, minimal losses, and unrestricted transmission distances (Rahimi et al., 2011; Liu et al., 2014). This makes them instrumental in realizing large-scale wind power export and extensive deployment.

When large-scale wind power transmission systems experience phase-shifting failures or DC faults such as DC blocking, the reactive power balance between the converter station and the AC system is disrupted. This leads to a surplus of reactive power flowing into the sending-end grid, resulting in a transient voltage rise at the rectifier-side converter bus (Zheng et al., 2020). Furthermore, with the increased output of wind power and other new energy sources, the installed capacity of traditional thermal power units decreases, leading to a reduction in the strength of the AC system. This will further exacerbate the severity of transient overvoltage in the DC sending-end system.

Currently, there are studies focusing on the control strategies for transient overvoltage in high-voltage direct current (HVDC) transmission systems caused by DC faults leading to large-scale wind power integration. References (Ren et al., 2020; Ji et al., 2020) utilized DC flexible alternating current transmission system (FACTS) capabilities and coordinated wind farm capacitor switching to prevent large-scale new energy disconnection events, while optimizing the reactive power control characteristics of wind turbines to reduce overvoltage levels. Reference (Luo, 2019), based on the controllable power region of doubly fed induction generator (DFIG) wind farms and the short-term overload capacity of the sending-end converter station, proposed a coordinated control strategy for transient overvoltage mitigation considering DFIG, sending-end converter stations, and their reactive power compensation devices. Reference (Zhu, 2021) established a transient overvoltage control model based on rectifier-side and wind farm-based control parameters, with the objective of minimizing the overvoltage peak when high-voltage DC blocking faults occurred after wind turbines connected to the DC bus. Reference (Zhao et al., 2019) effectively suppressed transient overvoltage in the sending-end grid caused by phase-shifting failures resulting from DC-side three-phase ground faults, through phase-shifter capacity selection and parameter optimization of the DC system’s constant current control loop.

However, current research mainly focuses on emergency control at the grid level and system equipment regulation, often involving single reactive power compensation devices in control strategies. There is less emphasis on wind turbine fault ride-through capabilities combined with coordinated control of diverse equipment within the system, or providing only qualitative coordinated control strategies, with limited research on the hierarchical timing of equipment actions. Therefore, to meet the demand for safe and stable operation of large-scale wind power DC export systems, there is an urgent need to research transient overvoltage coordinated control strategies at the sending end of the grid, considering the diverse reactive power regulation capabilities of equipment and the dynamic characteristics of control systems.

This paper proposes a method for transient overvoltage suppression in wind power DC export systems by studying the impact of control parameters on transient overvoltage. The method considers the dynamic behavior and interaction effects of control systems involving doubly fed wind turbines, high-voltage DC transmission systems, and static VAR compensators (SVC). It establishes a coordinated optimization model for transient overvoltage suppression and utilizes an improved genetic algorithm for solving. By integrating the established electromagnetic transient model of wind power DC export systems with intelligent optimization algorithms through joint invocation, the method achieves coordinated optimization of control parameters, thereby suppressing overvoltage in the sending-end grid.

2 Mechanism of transient voltage rise in sending-end grid caused by DC faults

The main influencing factors of transient overvoltage at the DC sending end include: reactive power imbalance at converter stations, DC control parameters, control parameters of new energy sources, short-circuit ratio, etc. (Jiang et al., 2018; Wang et al., 2018) The surplus reactive power in the sending-end grid during fault conditions is the direct cause of transient overvoltage.

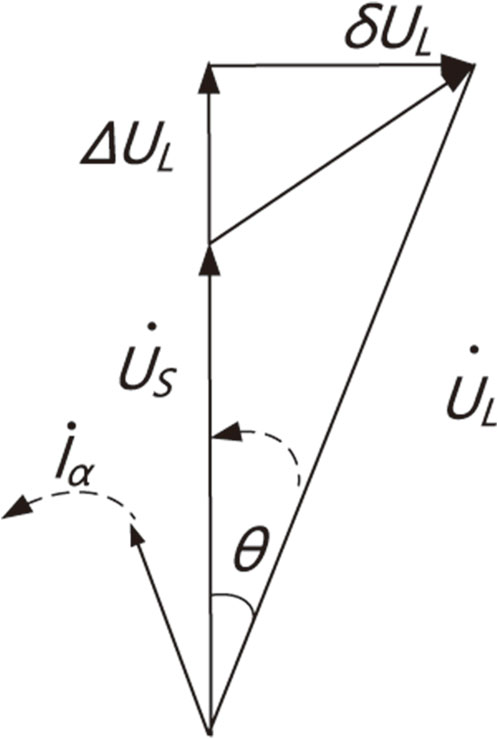
After a phase-shift failure occurs on the inverter side or a DC blocking fault occurs at the sending end, the DC transmission power decreases. The reactive power consumed by the converter station decreases, and the surplus reactive power provided by the reactive compensation device is sent back to the AC system, causing the bus voltage of the converter station to rise, resulting in transient overvoltage. The phasor diagram of the AC system at this time is shown in Figure 1.

Figure 1

Figure 1. The phasor diagram of AC line voltages during DC faults.

In the figure, $\delta U_L$ represents the horizontal component of the converter bus voltage, $\Delta U_L$ represents the vertical component, $U_S$ represents the equivalent potential of a generator, and $U_L$ represents the converter bus voltage.

Due to the active power emitted by the synchronous generator being related to $\delta U_L$, it can be seen from Figure 1 that $\delta U_L$ and $U_S$ have a 90° phase difference. This has a relatively minor impact on $U_L^{\prime }$ (the amplitude of the converter bus overvoltage), thus it can be neglected. Consequently, the final solution is obtained:

$U_L^{\prime }=\frac{U_L^2{U}_S-U_L{U}_S\sqrt{U_L^2-4\frac{\Delta Q_C{X}_S}{3}}}{\frac{2\Delta Q_C{X}_S}{3}}(1)$

In Equation 1, $X_S$ represents the equivalent reactance, and $\Delta Q_C$ represents the remaining reactive compensation capacity. It can be inferred that the transient overvoltage of the converter bus is associated with the equivalent potential of the generator, the equivalent reactance, and the remaining reactive compensation capacity.

The surplus reactive compensation capacity on the rectifier side, besides being returned to the converter bus, also surges into the AC system in large quantities. This results in significant reactive power impacts on the nearby DC-side wind farm, causing transient voltage rises at the sending end. The amplitude of the overvoltage is as shown in Equation 2.

$U_w^{\prime }=U_w+\Delta U_w=U_w+\frac{\left[\left(1+\Delta U{\left(X_w\right)}^2\right)-1\right]Q_w}{S_w}(2)$

In the equation, $\Delta U_w$ represents the transient voltage rise at the sending-end wind turbine generator terminal, $\Delta U\left(X_w\right)$ represents the functional relationship between the transient voltage rise at the sending-end wind turbine generator terminal and the equivalent reactance connecting the wind farm to the converter bus, $S_w$ represents the short-circuit capacity of the sending-end wind farm, and $Q_w$ represents the reactive power consumption of the wind turbine.

For wind power direct current (DC) transmission systems, the electrical distance between the wind farm at the sending end and the converter station is relatively short. In the event of a fault at the DC converter station, the surplus reactive power generated by the reactive compensation device is transmitted to the nearby wind farm, leading to overvoltage at the wind power grid connection point and potentially causing high-voltage interlocking tripping of wind turbine units. According to Equation 2, it can be observed that the amplitude of overvoltage at the wind turbine units near the sending end is similar to that at the converter bus, and both are related to the reactive power consumption of the turbines and the short-circuit capacity. The reactive power consumption of the turbines is mostly provided by fixed capacitor banks and dynamic reactive power compensation devices such as SVC. SVC has the characteristic of delayed reactive power compensation. Therefore, in situations of transient voltage increase in the wind power grid, capacitors and SVC may momentarily release more reactive power, thereby assisting in increasing voltage.

During a DC fault, the wind turbine units are in a fault ride-through state due to the voltage and power fluctuations of the converter bus. According to wind power grid connection standards, when the voltage sequence components at the grid connection point are between 1.1 p. u. and 1.3 p. u., the wind turbine units possess high voltage ride-through capability, absorbing dynamic reactive current from the system to provide voltage support. Its characteristic expression is as follows:

$I_q=K\left(U_w-1.1\right)I_{wN}(3)$

In Equation 3, $K$ is the dynamic reactive current proportional coefficient, and $I_{wN}$ is the rated current of the wind turbine unit.

Referring to the form of Equation 3, the dynamic reactive characteristics of the wind turbine units in the sending-end near area during high voltage ride-through can be expressed as:

$Q_{wf}=k_{wq}\left(U_L-1.1\right)U_L{S}_{wN}(4)$

In Equation 4, $k_{wq}$ is the dynamic reactive coefficient during the high voltage ride-through of the wind turbine, and $S_{wN}$ is the rated capacity of the turbine.

Assuming that the wind turbine units operate under unity power factor control, the active power of the wind turbine units remains consistent with the pre-fault level during a DC fault. Thus, the power characteristics of the wind turbine units in the sending-end near area during high voltage ride-through can be expressed as shown in Equation 5.

$S_{wf}=P_{wf}+j{Q}_{wf}=k_{wp}{P}_w+j{k}_{wq}\left(U_L-1.1\right)U_L{S}_{wN}(5)$

In the equation, $k_{wp}$ is the active coefficient during the high voltage ride-through of the wind turbine.

3 The impact of control parameters on transient overvoltage

The transient overvoltage in the DC sending-end system is not only influenced by the strength of the AC system and the operating conditions of the system, but also closely related to the dynamic response performance of the DC control system. By optimizing the configuration of control parameters, the dynamic response performance of the control system can be further improved, achieving the purpose of suppressing overvoltage (Ji, 2017).

3.1 The impact of wind power control parameters on transient overvoltage

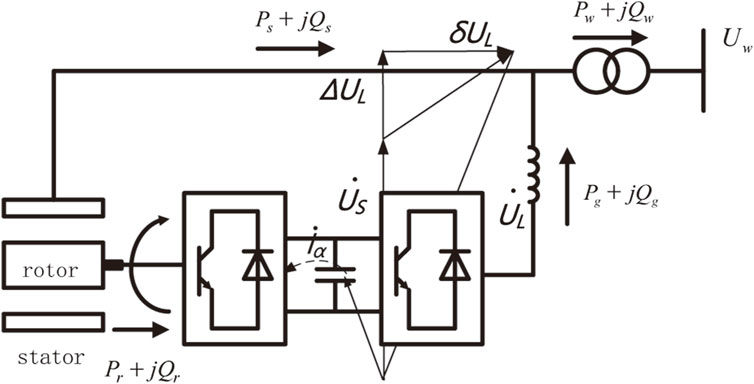
A doubly-fed induction generator (DFIG) mainly consists of blades, a gearbox, the doubly-fed induction generator itself, and a PWM converter. The power flow diagram of a DFIG under generator mode is shown in Figure 2.

Figure 2

Figure 2. The power flow diagram of DFIG.

The PWM converter includes the Grid Side Converter (GSC) and the Rotor Side Converter (RSC). The rotor windings are connected to the grid through a bidirectional frequency converter formed by the GSC and RSC. Therefore, by controlling the GSC and RSC, the rotor amplitude, phase, and frequency can be adjusted to regulate the active and reactive power output of the wind turbine. The main function of the GSC is to maintain the stability of the DC bus voltage, while the RSC can provide more reactive support. Hence, the mechanism by which the control parameters of the RSC affect transient overvoltage can be explored based on its control characteristics.

The Rotor Side Converter (RSC) adopts a dual-loop control based on stator voltage orientation vectors, including inner-loop current control and outer-loop power control, to achieve the decoupling of stator active and reactive power (Zhang et al., 2013). The dual-loop control diagram of the RSC is shown in Figure 3.

Figure 3

Figure 3. The dual-loop control diagram of RSC.

In the figure, $P_{s\_ref}$ and $Q_{s\_ref}$ are the reference values for stator-side active and reactive power respectively; $i_{qr\_ref}$ and $i_{dr\_ref}$ are the reference values for rotor current q-axis and d-axis components respectively; $i_{qr}$ and $i_{dr}$ are the measured values of rotor output current q-axis and d-axis components; $u_{qr}$ and $u_{dr}$ are the q-axis and d-axis components of rotor output voltage; $k_{p1}$ and $k_{i1}$ are the proportional and integral coefficients of the power outer-loop PI controller, $k_{p2}$ and $k_{i2}$ are the proportional and integral coefficients of the current inner-loop PI controller; $k_d$ is the cross-coupling term between the d-axis and q-axis.

By taking the first-order partial derivatives of the PI controller parameters in the power outer loop and current inner loop of the Rotor Side Converter (RSC), it can be derived that the stator output reactive power and rotor impedance are negatively correlated. Consequently, based on the correlation between rotor impedance and the parameters of the inner and outer loops, an approximation of the relationship between the total output reactive power of the wind turbine and the control parameters can be obtained. Specifically, reducing the proportional coefficients ($k_{p1}$, $k_{p2}$) or increasing the integral coefficients ($k_{i1}$, $k_{i2}$) of the inner and outer loops will increase $Q_{\mathrm{w}}$, whereas increasing the proportional coefficients ($k_{p1}$, $k_{p2}$) or decreasing the integral coefficients ($k_{i1}$, $k_{i2}$) will decrease $Q_{\mathrm{w}}$. The severity ranking of the impact of PI parameters on $Q_{\mathrm{w}}$ is as follows: $k_{p2}>k_{i2}>k_{i1}>k_{p1}$. Considering the numerous parameters involved in Doubly Fed Induction Generator (DFIG), to simplify the optimization model, priority is given for optimizing the proportional coefficient ($k_{p2}$) and integral coefficient ($k_{i2}$) of the current inner loop, thus achieving optimal control of wind turbine voltage response.

3.2 The impact of direct current system control parameters on transient overvoltage

The high-voltage direct current transmission control system includes constant current control (CCA), constant voltage control, and voltage dependent current limit control (VDCOL). Additionally, the inverter side also has constant extinction angle control to prevent phase-shifting failure caused by excessive overshoot of the controller resulting in an excessively small extinction angle. The CCA and VDCOL sections on the rectifier side are the main factors affecting the control performance of the DC system. The following explores the mechanism of how the control parameters of these two sections affect transient overvoltage.

(1) Rectifier-side constant current control (CCA)

The proportional coefficient and integral coefficient of the CCA control loop are important parameters that affect the transient overvoltage of the sending-end system. By adjusting these two parameters, the magnitude of overcurrent during phase-shifting failure can be quickly suppressed, thereby suppressing overvoltage. Additionally, it affects the subsequent recovery process, shortening the duration of overvoltage and reducing damage to the equipment. The expression for the triggering angle $\alpha$ of the rectifier-side converter station output by the CCA is as follows:

$\alpha ={\alpha }_0-K_{p1}\left(I_{\text{ord}}-I_{\text{dmeas}}\right)-K_{i1}\int \left(I_{\text{ord}}-I_{\text{dmeas}}\right)dt(6)$

In the equation, ${\alpha }_0$ represents the initial value of the triggering angle, $I_{\text{ord}}$ represents the reference value of the DC current, and $I_{\text{dmeas}}$ represents the measured value of the DC current.

The expression describing the relationship between the DC current and the triggering angle is as follows:

$I_d=\frac{1.35N_p{U}_L\left(\cos \alpha -\cos \beta \right)\pi }{12X_C}(7)$

In the equation, $I_{\mathrm{d}}$ represents the DC current, $\alpha$ represents the triggering angle, $N_p$ denotes the number of six-pulse converters per stage, $U_L$ signifies the rectifier-side converter bus voltage, $X_C$ stands for the commutation reactance, and $\beta$ denotes the converter lag angle.

From Equations 6, 7, it can be observed that the proportional coefficient and integral coefficient of the CCA control loop, as well as the DC current, are all negatively correlated. That is, as $K_{p1}$ and $K_{i1}$ increase, $\alpha$ decreases, leading to an increase in the DC current ($I_{\mathrm{d}}$). Consequently, the reactive power consumed by the converter station increases, while the exchange of reactive power between the rectifier station and the AC system decreases, thereby serving to suppress overvoltage.

(2) Rectifier-Side Voltage Dependent Current Limit Control (VDCOL)

When a DC fault leads to a decrease in the system’s DC voltage, VDCOL will activate to limit the DC current command, thereby reducing the reactive power consumption of the converter station and regulating the AC voltage.

The characteristic equation of the VDCOL control loop is:

$I=I_{ord}=\frac{I_{dh}-I_{dl}}{U_{dh}-U_{dl}}\left(U-U_{dl}\right)+I_{dl}(8)$

In the equation, $I_{dh}$ and $I_{dl}$ represent the maximum and minimum current commands of VDCOL, respectively, while $U_{dh}$ and $U_{dl}$ represent the dropout voltage and startup voltage of VDCOL, respectively.

From Equation 8, it can be observed that the DC current command value ($I_{ord}$) is dependent on the control parameters of VDCOL. Considering $I_{dh}$ as the rated DC current, taking partial derivatives with respect to $I_{dl}$, $U_{dh}$, and $U_{dl}$, the following relationships can be obtained: the DC current command value ($I_{ord}$) is positively correlated with the minimum current command ($I_{dl}$), while negatively correlated with $U_{dh}$ and $U_{dl}$. Therefore, reducing $I_{ord}$ can be achieved by increasing $I_{dl}$ and decreasing $U_{dh}$ and $U_{dl}$, thereby suppressing transient overvoltage. While $U_{dh}$, $U_{dl}$, and $I_{dl}$ have relatively minor effects on the magnitude of overvoltage and undervoltage, $I_{dl}$ significantly shortens the duration of overvoltage. Hence, it is preferable to prioritize optimizing the CCA control parameters $K_{p1}$ and $K_{i1}$, which have a higher impact on overvoltage, and the VDCOL control parameter $I_{dl}$ to reduce the reactive power sent back to the AC system at the sending end, achieving voltage response control (Ji, 2017).

3.3 The influence of SVC control parameters on transient overvoltage

The control modes of SVC mainly include fixed voltage control and fixed reactive power control. In order for SVC to perform reactive power adjustment promptly when overvoltage occurs in the system, achieve coordinated control with DFIG and the DC system, and suppress overvoltage, the fixed voltage control mode can be adopted. The expression for the reference value of reactive power provided by SVC is (Bao et al., 2021):

$Q_{SV{C}_{-}ref}=K_{p_{-}SVC}\left(V_{m_{-}ref}-V_m\right)+K_{i_{-}SVC}\frac{V_{m_{-}ref}-V_m}{s}(9)$

In Equation 9, $Q_{SV{C}_{-}ref}$ represents the reference value of reactive power provided by SVC, where $K_{p_{-}SVC}$ and $K_{i_{-}SVC}$ are the proportional and integral coefficients of the PI loop in the SVC control system, respectively, and $V_{m_{-}ref}$ is the reference value of the SVC branch terminal voltage.

From the above equation, it can be observed that the reactive power emitted by SVC is directly proportional to $K_{p_{-}SVC}$ and $K_{i_{-}SVC}$. When $K_{p_{-}SVC}$ and $K_{i_{-}SVC}$ are increased, SVC outputs more reactive power; conversely, when $K_{p_{-}SVC}$ and $K_{i_{-}SVC}$ are decreased, the reactive power transmitted by SVC also decreases. This is because the reactive power $Q_{SVC}$ emitted by SVC depends on the firing angle (${\alpha }_{SVC}$) of the internal thyristors and the variation of the branch terminal voltage, and ${\alpha }_{SVC}$ is determined by the control loop of SVC. Therefore, $K_{p_{-}SVC}$ and $K_{i_{-}SVC}$ can be considered as optimization targets for SVC control parameters in order to obtain the best response control performance.

3.4 Hierarchical time-sequence control strategy based on DFIG and SVC

Based on the analysis in Chapter 2, it is clear that the most critical solution to the overvoltage issue in the wind power DC transmission system after a DC fault is to leverage the system’s own reactive power regulation characteristics or utilize the fast response characteristics of reactive power compensation devices to absorb the excess reactive power from the sending-end grid. In order to quickly respond to fault conditions and effectively mitigate the low voltage caused by the delay effects of equipment after fault clearance, it is necessary to understand the action timing at each level.

Based on the dynamic reactive control response characteristics of DFIG and SVC, as indicated in reference (Ma et al., 2017), it is known that SVC is a circuit composed of TSC and TCR, while DFIG can be considered a circuit formed by GSC and RSC. The action delay of SVC is 20 ms, and the action delay of DFIG is 30 ms. Therefore, SVC acts before DFIG to participate in reactive response and determines the voltage ($U_w$) range at the wind turbine grid connection point after a DC fault, using $U_w\le 1.1p.u.$, $1.1p.u.<U_w<1.2p.u.$ and $U_w\ge 1.2p.u.$ as the voltage control action ranges. This establishes a hierarchical time-sequence control strategy based on DFIG and SVC. Taking DC blocking as an example, the control mode is as follows:

(1) When the system is operating normally or experiences a sudden voltage increase at the wind turbine grid connection point after a fault, but the voltage does not exceed 1.1 p. u. (i.e., $U_w\le 1.1p.u.$), neither DFIG nor SVC participates in reactive power regulation. In this case, it is sufficient to disconnect some filter banks of the rectifier station to restore the voltage.

(2) When the grid connection point voltage is in the range of $1.1p.u.<U_w<1.2p.u.$ after DC blocking, the SVC starts to operate after a 20 ms delay. At this point, the triggering signal for the TSC is set to $TS{C}_{\_on}=0$, locking the TSC branch, while a guiding communication signal is applied to the TCR branch, increasing the triggering angle $\mathit{\theta }$ to its maximum value ${\mathit{\theta }}_{\max }$, allowing the TCR to absorb reactive power, with DFIG not needing to participate in voltage response control.

(3) When a more severe DC fault occurs, such as bipolar blocking, causing the grid connection point voltage to exceed 1.2 p. u. (i.e., $U_w\ge 1.2p.u.$), the reactive power regulation capacity of the SVC is limited. Therefore, SVC alone is insufficient to meet the overvoltage suppression requirements. In this case, DFIG starts to operate after a 30 ms delay, coordinating the reactive power support strategy of the GSC and RSC to mitigate the impact of transient overvoltage, with both providing reactive power support together.

(4) When the grid connection point voltage is restored to $U_w\le 1.1p.u.$ and remains at this level for a period of time $\Delta \mathit{t}$ without rising again, the GSC and RSC return to normal operating mode, and the TSC branch is unlocked, allowing DFIG and SVC to exit reactive response and resume normal operation.

The flowchart of the hierarchical time-sequence control strategy based on DFIG and SVC is shown in Figure 4.

Figure 4

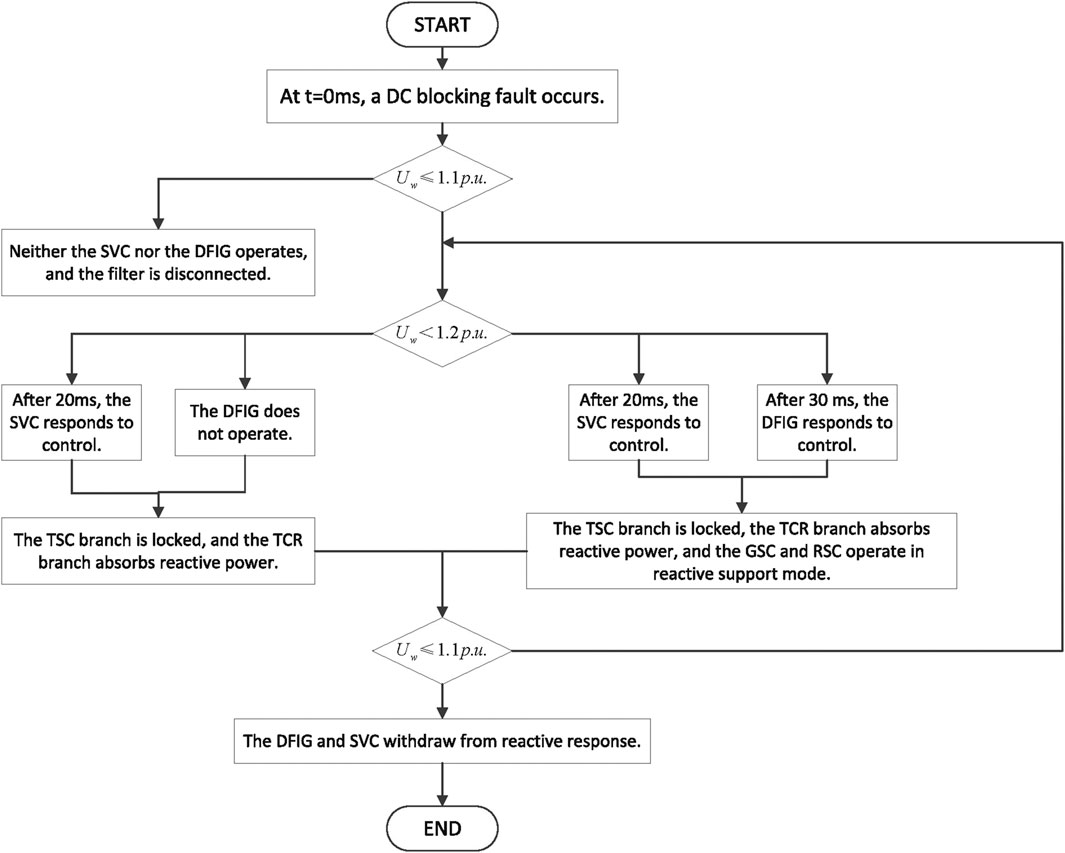
Figure 4. Flowchart of the hierarchical time-sequenced control strategy based on doubly-fed wind turbine and SVC.

4 The coordinated optimization model of transient overvoltage control parameters based on improved genetic algorithm

4.1 The coordinated optimization mathematical model for transient overvoltage control parameters suppression

4.1.1 Objective function

This paper aims to minimize the peak voltage at the grid-connected point of the wind turbine generator in the wind power DC transmission system. It establishes a coordinated optimization mathematical model for suppressing transient overvoltage control parameters. The model considers the proportional coefficient ($k_{p2}$) and integral coefficient ($k_{i2}$) of the current inner loop of the Doubly Fed Induction Generator (DFIG), the integral coefficient ($K_{p1}$) and proportional coefficient ($K_{i1}$) of the direct current Crowbar Circuit Amplifier (CCA) section, the minimum current command ($I_{dl}$) of the VDCOL section, and the proportional coefficient ($K_{p\_SVC}$) and integral coefficient ($K_{i\_SVC}$) of the PI loop of the SVC control system as optimization targets.

The expression of the objective function ($Z_{obj}$) is given by Equation 10.

$Z_{obj}\left(k_{p2},k_{i2},K_{p1},K_{i1},I_{dl},K_{p_{-}SVC},K_{i_{-}SVC}\right)=\min \left\{U_{w\max }\right\}(10)$

(2) Constraint conditions

The constraint conditions of the coordinated optimization mathematical model for suppressing transient overvoltage control parameters include power balance constraint, DFIG reactive power regulation range constraint, SVC reactive power capacity constraint, and inequality constraints on DFIG, HVDC, and SVC control parameters.

1) The power balance constraint

The input power at each node of the system and the node loads need to satisfy the power flow equations, which constitute the power balance constraint.

$\left\{\begin{array}{l}{P}_{gi}-P_{Li}=P_i\left(U,\theta \right)\\ Q_{gi}-Q_{Li}=Q_i\left(U,\theta \right)\end{array}\right.,i=1,2,\dots ,n(11)$

In Equation 11, $P_{gi}$ and $Q_{gi}$ represent the active and reactive power inputs at node $i$ in the system, respectively; $P_{Li}$ and $Q_{Li}$ represent the active and reactive power consumed by the load at node $i$ in the system, respectively; $P_i\left(U,\theta \right)$ and $Q_i\left(U,\theta \right)$ represent the power flow at node $i$; $U$ and $\theta$ denote the magnitude and phase angle of the node voltage.

2) DFIG reactive power regulation range constraint

The constraint condition for the reactive power regulation range of DFIG is:

$Q_{w\min }<\left|Q_w+\Delta Q_w\right|<Q_{w\max }(12)$

In Equation 12, $Q_w$ represents the power injected into the grid by the wind turbine before the fault; $\Delta Q_w$ represents the variation in reactive power output of the DFIG during the DC fault period; $Q_{w\min }$ and $Q_{w\max }$ denote the lower and upper limits of the DFIG reactive power regulation, respectively.

3) SVC reactive power capacity constraint

The reactive power capacity constraint of SVC is defined by the rated capacities of the TCR and TSC branches, and its reactive power regulation range should lie between the rated capacities of both branches, namely:

$Q_{TCR}^N\le Q_{SVC}+\Delta Q_{SVC}\le Q_{TSC}^N(13)$

In Equation 13, $Q_{SVC}$ represents the reactive power output of SVC before the fault, $\Delta Q_{SVC}$ denotes the change in reactive power of SVC during the DC fault period, $Q_{TSC}^N$ is the rated reactive power capacity of the TSC branch, and $Q_{TCR}^N$ is the rated reactive power capacity of the TCR branch.

4) Inequality constraints on control parameters for DFIG, HVDC, and SVC

The upper and lower limits of the PI loop parameters ($K_{p_{-}SVC}$ and $K_{i_{-}SVC}$) in the DFIG current inner loop control ($k_{p2}$ and $k_{i2}$), the direct current CCA loop control ($K_{p1}$ and $K_{i1}$), the VDCOL loop control ($I_{dl}$), and the SVC control system are constrained as follows:

$\left\{\begin{array}{l}{k}_{p2,\min }\le k_{p2}\le k_{p2,\max }\\ k_{i2,\min }\le k_{i2}\le k_{i2,\max }\\ K_{p1,\min }\le K_{p1}\le K_{p1,\max }\\ K_{i1,\min }\le K_{i1}\le K_{i1,\max }\\ I_{dl,\min }\le I_{dl}\le I_{dl,\max }\\ K_{p\_SVC,\min }\le K_{p\_SVC}\le K_{p\_SVC,\max }\end{array}\right.(14)$

In Equation 14, the subscripts “min” and “max” represent the lower and upper bounds of the parameters, respectively.

4.2 The solution of the coordinated optimization model of control parameters based on improved genetic algorithm

Genetic Algorithm (GA) is a stochastic global search optimization algorithm that simulates the process of natural selection and evolution in biological systems. The basic idea of GA is to select individuals with specific structural forms from the population for crossover and mutation, thereby generating a new population. The fitness of individuals is then evaluated, and individuals with strong fitness are retained for further reproduction, while those with poor fitness are eliminated. This process gradually converges towards the optimal solution.

To prevent the loss of the optimal individual in the current population during evolution and enhance the global convergence capability of traditional genetic algorithms, an elitism retention strategy is introduced. The basic idea of the elitism retention strategy is to construct an elite pool, where the fittest individuals are selected to fill it. Then, during each generation, the weakest individuals in the current population are eliminated during the selection and replenishment process, and new optimal individuals are reintroduced to fill the population.

To ensure that the transient overvoltage requirements are met at the direct current transmission end for bundled wind and thermal power delivery of new energy, this paper adopts an improved genetic algorithm with the introduction of an elitism retention strategy, called Strengthen Elitist Genetic Algorithm (SEGA) (Wang and Liu, 2019; Shao et al., 2010). During the evolution process of the population individuals, the elite individuals’ genes (i.e., the optimal individuals) are directly copied into the chromosomes of the next-generation population without undergoing crossover and mutation operations. This ensures the integrity of the elite individuals. The process aims to solve the coordinated optimization model for suppressing transient overvoltage. The workflow of controlling parameters optimization affecting transient overvoltage is as follows:

1) Setting up the electromagnetic transient simulation model involves specifying the voltage data to be tested and the control parameters to be optimized. The iteration accuracy ($\mathcal{E}$)is preset to obtain the objective function and primary constraints.

2) The decision variables of the coordinated optimization mathematical model for suppressing transient overvoltage control parameters are binary encoded to generate the initial population.

3) Each individual’s encoded parameters from the initial population are sequentially input into the electromagnetic transient simulation model to compute their fitness. After the simulation completes, the encoded individuals along with their fitness function values are recorded.

4) The SEGA algorithm is invoked to perform selection, crossover, and mutation operations on the individuals within the population, while preserving the genes of elite individuals by directly copying them into the next-generation population. The individual gene encodings are updated, and the parameters corresponding to the updated individual encodings are passed to the simulation model to compute fitness.

5) Calculate the average fitness value within the population to assess the similarity among individuals. Filter out highly similar individuals, update and record the fitness value, along with the encoding and corresponding parameters, of the best individual.

6) Check whether the iteration limit or desired accuracy has reached the termination condition. If it has, terminate the process; otherwise, return to step 4) for further optimization.

The coordinated optimization solving process based on the improved genetic algorithm SEGA is illustrated in Figure 5.

Figure 5

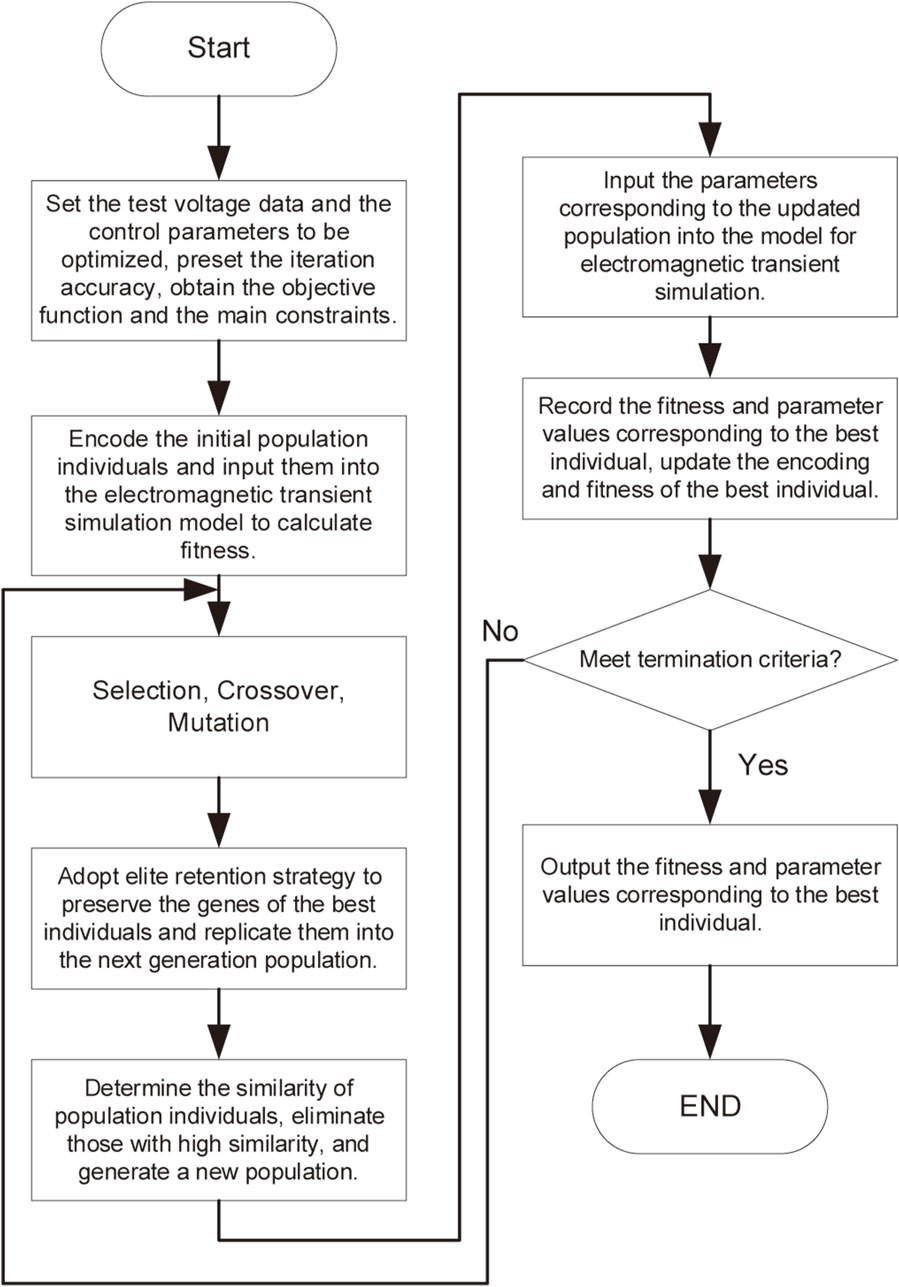
Figure 5. The flowchart of coordinated optimization solving process based on the improved genetic algorithm SEGA.

5 Case study analysis

5.1 PSCAD/EMTDC model of doubly-fed wind turbine connected to high-voltage DC transmission system

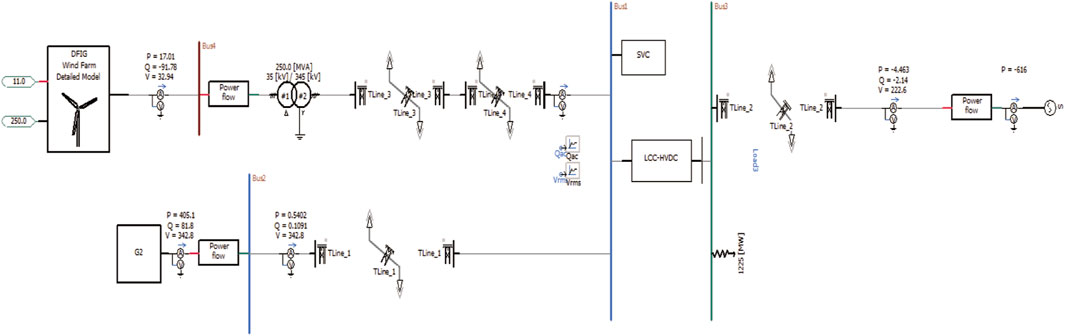
The paper adopts the model of a doubly-fed wind turbine connected to a high-voltage direct current (HVDC) transmission system as shown in Figure 6. In the model, direct current faults are configured to observe the variations in voltage, current, and power at the sending end of the grid.

Figure 6

Figure 6. The schematic diagram of the wind power DC transmission system.

After conducting operational tests on the established simulation model according to the bipolar full-voltage operation mode, and simulating the rectifier side voltage and current conditions of the high-voltage direct current transmission system as well as the export voltage and power of the DFIG equivalent wind farm, it demonstrates the correctness and effectiveness of the model established.

5.2 Simulation verification of the hierarchical time-sequenced control strategy based on DFIG and SVC

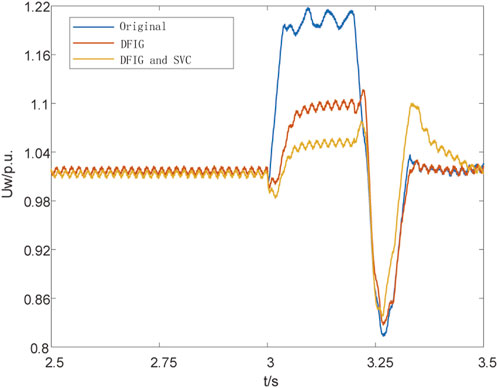
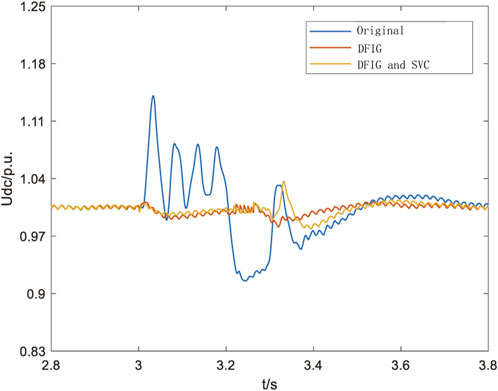
The SVC is connected to the rectifier station’s converter bus. A DC lockout fault is applied at 3 s, lasting for 0.2 s. The aim is to verify whether the overvoltage control strategy, after the addition of the SVC, can effectively suppress overvoltage above 1.2p.u. At this point, the DC system is set to bipolar lockout. The simulation observes the wind turbine connection point voltage, DC bus voltage, and the reactive power output of both the DFIG and SVC. The simulation results are shown in Figures 7, 8.

Figure 7

Figure 7. Wind turbine grid connection point voltage.

Figure 8

Figure 8. DC bus voltage.

From Figure 9, it can be seen that the reactive power output waveforms of the DFIG and SVC. At 20 ms, the SVC begins to respond and absorbs about 400Mvar of inductive reactive power. After 10 ms, by 30 ms, the DFIG’s reactive power regulation is activated, participating in the absorption of around 100 Mvar of surplus reactive power. Together, the two systems absorb approximately 500Mvar of reactive power, which is 165Mvar more than when the DFIG is solely involved in reactive power regulation. This effectively reduces the wind turbine connection point voltage from 1.22p.u. to 1.08p.u., a 3.3% improvement compared to relying solely on the reactive power support capability of the DFIG converter.

Figure 9

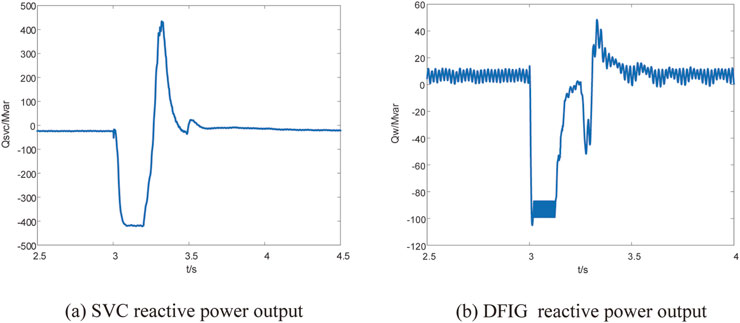
Figure 9. SVC and DFIG reactive power output waveform. (A) SVC reactive power output; (B) DFIG reactive power output.

After the fault is cleared, both the SVC and DFIG promptly withdraw from reactive power response, with the SVC returning to normal operation. This helps to mitigate the low voltage phenomenon after fault clearance to some extent. However, since the DFIG itself does not fully utilize its reactive power support capability, the improvement in the DC bus voltage is less noticeable compared to the control strategy that relies solely on the DFIG for reactive power regulation.

5.3 Transient overvoltage control strategy simulation analysis based on parameter optimization

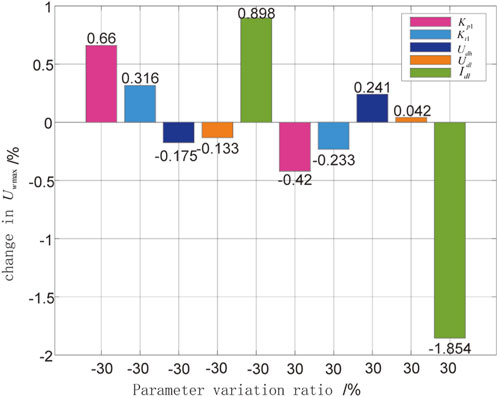
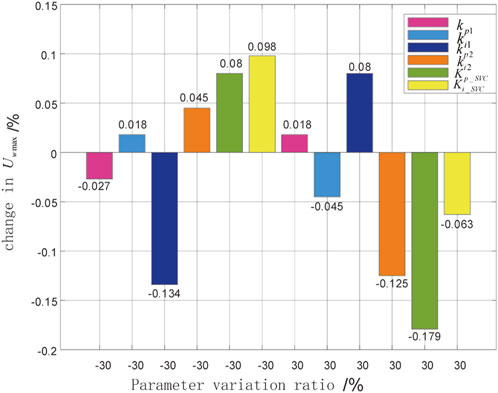
To verify the optimization performance of the coordinated transient overvoltage suppression optimization model in the wind power DC transmission system, it is necessary to analyze the sensitivity of transient overvoltage to the control parameters of HVDC, DFIG, and SVC respectively. By using the method of controlling variables, each parameter is adjusted up or down by 30% to obtain the percentage change of $U_{w\max }$ under different DFIG and SVC control parameters, as shown in Figures 10, 11.

Figure 10

Figure 10. Percentage change of $U_{w\max }$ under different HVDC control parameters.

Figure 11

Figure 11. Percentage change of $U_{w\max }$ under different DFIG and SVC control parameters.

From Figures 10, 11, it can be observed the varying degrees of influence of different control parameters on overvoltage. Therefore, during HVDC control, $K_{p1}$, $K_{i1}$, and $I_{dl}$ can be considered as the primary control parameters. While during DFIG and SVC control, $k_{p2}$, $k_{i2}$, $K_{p_{-}SVC}$, and $K_{i_{-}SVC}$ can be considered as the parameters for optimization, thus mitigating transient overvoltage.

Using the proposed transient overvoltage suppression coordinated optimization model based on improved genetic algorithm, the control parameters of DC, wind power, and SVC in the wind power DC transmission system are optimized. The parameter ranges are set as follows: $K_{p1}\in \left[1,2\right]$, $K_{i1}\in \left[0.01,0.025\right]$, $k_{p2}\in \left[0.1,3\right]$, $k_{i2}\in \left[0.01,0.05\right]$, $K_{p_{-}SVC}\in \left[0.1,1\right]$, $K_{i_{-}SVC}\in \left[0.001,0.01\right]$. A comparison analysis is conducted with the optimization results of the basic genetic algorithm (GA). In the rectification station of the wind power DC transmission system, a DC blocking fault is set, with a simulation duration of 3 s. The fault starts at 2 s and lasts for 0.2 s. The simulation iterations, or the number of iterations, are set to 50 times.

To better compare and analyze the effect of coordinated parameter optimization on overvoltage suppression, the simulation is divided into the following two scenarios:

Scenario 1: Only optimize HVDC control parameters.

Scenario 2: Coordinated optimization of HVDC, DFIG, and SVC control parameters.

(1) Only optimize HVDC control parameters

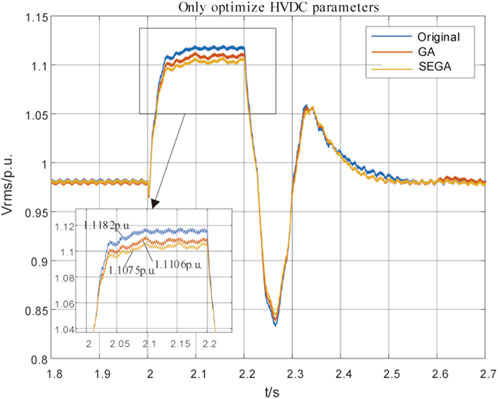
Using SEGA and traditional GA respectively, the control parameters of CCA and VDCOL on the rectification side of HVDC are optimized. The voltage of the wind turbine grid-connected bus under different optimization schemes is obtained, and the optimization results and simulation images are shown in Table 1 and Figure 12.

Table 1

Table 1. The optimization results solely for HVDC parameters.

Figure 12

Figure 12. The $U_{w\max }$ for different optimization schemes in Scenario 1

Compared with the initial state, applying optimization algorithms to optimize the parameters resulted in varying degrees of suppression in $U_{w\max }$. All control parameters increased, consistent with the trend of theoretical analysis. Among them, the voltage $U_{w\max }$ using the traditional GA algorithm decreased to 1.1106p.u., a reduction of 0.68%, while the voltage $U_{w\max }$ using the SEGA algorithm decreased to 1.1075p.u., a reduction of 0.96%. The latter achieves a 0.28% better overvoltage suppression effect compared to the former, demonstrating the superior global search capability of the SEGA algorithm. However, neither of the two optimization schemes was able to suppress the overvoltage to below 1.1p.u., indicating that further optimization of the control parameters for both the DFIG and SVC is required.

(2) Coordinated optimization of HVDC, DFIG, and SVC control parameters

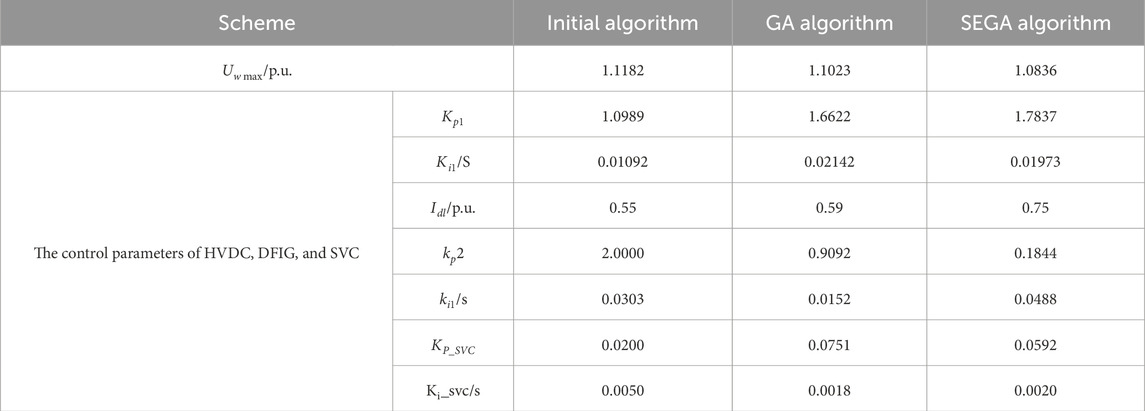
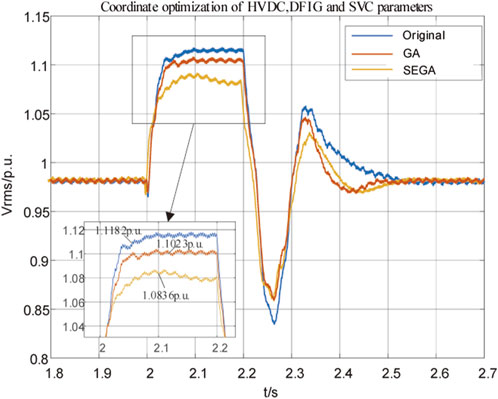
Using both SEGA and GA algorithms for coordinated optimization of HVDC, DFIG, and SVC control parameters, the parameter optimization results are shown in Table 2, and the grid-connected bus voltage of the wind turbine under different optimization schemes is shown in Figure 13.

Table 2

Table 2. The coordinated optimization results of HVDC, DFIG, and SVC parameters.

Figure 13

Figure 13. The $U_{w\max }$ for different optimization schemes in Scenario 2

Compared to the initial state, after employing the SEGA algorithm to coordinate and optimize the parameters of HVDC, DFIG, and SVC, $U_{w\max }$ decreased to 1.0836 p. u., a reduction of 3.2%, which is below 1.1 p. u. This successfully eliminated the transient overvoltage phenomenon. On the other hand, when using the traditional GA algorithm for parameter coordination and optimization, $U_{w\max }$ decreased to 1.1023 p. u., a reduction of 1.4% compared to optimizing only HVDC parameters. Although this reduction was higher in suppressing overvoltage, it still did not decrease below 1.1 p. u. This further validates the effectiveness and superiority of the coordinated optimization model for transient overvoltage suppression based on the improved genetic algorithm, SEGA.

5.4 Simulation verification of transient overvoltage control strategies under different operating conditions

The above simulation analyses were conducted under a single operating condition of the system. To validate the effectiveness of the transient overvoltage coordinated control strategy based on parameter optimization under multiple operating conditions, two operating scenarios were set: (1) Setting the monopole transmission power of the high-voltage DC transmission system to 1000 MW, with a total power output of 2000 MW in bipolar operation, wind power output of 400 MW, accounting for 20% of the total power output; (2) Setting the monopole transmission power of the high-voltage DC transmission system to 1000 MW, with a total power output of 2000 MW in bipolar operation, wind power output of 800MW, accounting for 40% of the total power output.

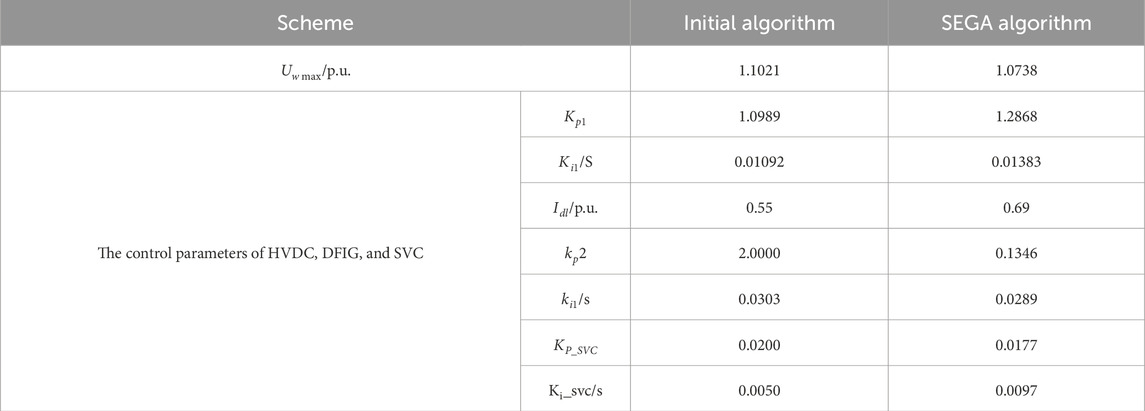
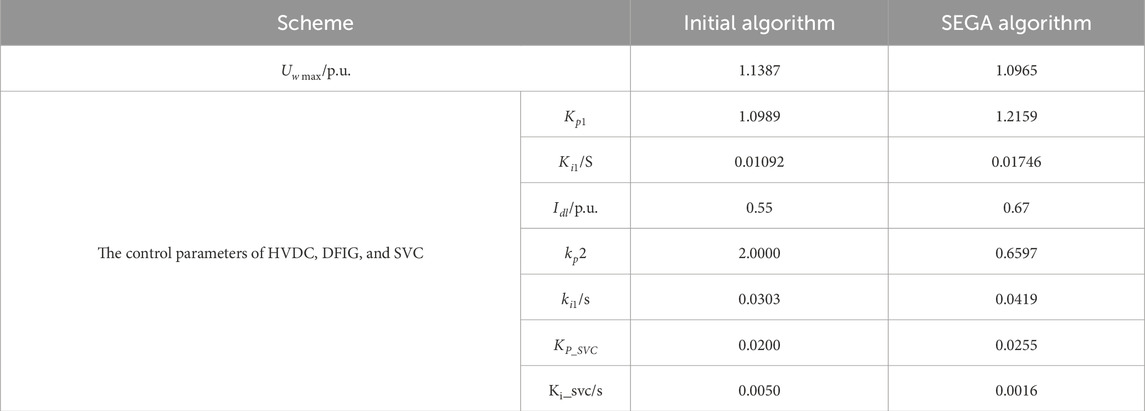
Using the SEGA algorithm to coordinate and optimize the control parameters of HVDC, DFIG, and SVC, the parameter optimization results are shown in Tables 3, 4. A comparative analysis is conducted on the peak voltage $U_{w\max }$ of the wind turbine grid connection point bus before applying the control strategy, with only DFIG and SVC coordinated control, and after simultaneous parameter optimization. The bus voltage of the wind turbine grid connection under different control strategies is illustrated in Figures 14, 15.

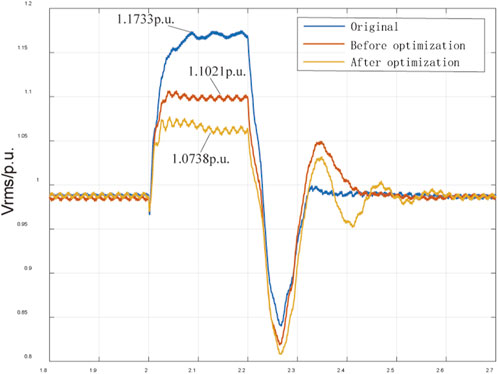
(1) Operating condition 1: Low wind power output

Table 3

Table 3. Parameter coordination optimization results under low wind power output.

Table 4

Table 4. Parameter coordination optimization results under high wind power output.

Figure 14

Figure 14. The $U_{w\max }$ under different control strategies at low wind power output.

Figure 15

Figure 15. The $U_{w\max }$ under different control strategies at high wind power output.

When the wind power output is low, the transient overvoltage reaches 1.1733 p. u. after a DC blocking fault occurs. After adopting a coordinated control strategy based on DFIG and SVC, the overvoltage decreases to 1.1021 p. u. Subsequently, after further optimization of the control parameters of HVDC, DFIG, and SVC, the overvoltage decreases to 1.0738 p. u., which is 2.4% lower than before parameter optimization. This indicates that optimizing the parameters can more effectively suppress overvoltage.

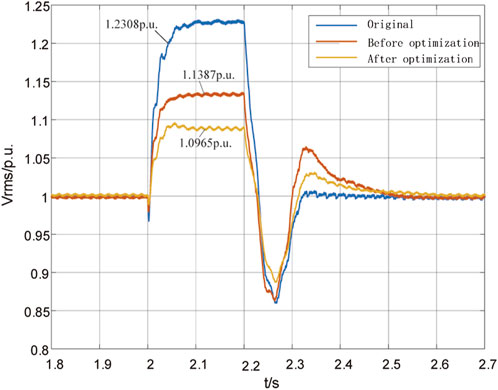
(2) Operating condition 2: High wind power output

Under high wind power output conditions, due to the increase in wind power DC output and the rise in the penetration rate of new energy sources, there is more excess reactive power after the DC blocking, leading to a higher severity of transient overvoltage compared to low wind power output, reaching 1.2306 p. u. By adopting coordinated control strategies with DFIG and SVC separately or by conducting parameter optimization based on these control strategies, the transient overvoltage is suppressed to 1.1387 p. u. and 1.0965 p. u. respectively, both higher than the operating conditions with low wind power output. However, after parameter optimization, the overvoltage is suppressed to below 1.1 p. u., confirming the effectiveness of transient overvoltage coordinated control strategies based on parameter optimization in eliminating transient overvoltage phenomena under various operating conditions.

6 Conclusion

To address the issue of transient overvoltage in wind power DC transmission systems, this paper establishes a coordinated optimization model for suppressing transient overvoltage, taking into account the control parameters of wind power, DC, and SVC. An improved genetic algorithm with an elite reservation strategy is employed to solve the model. Finally, simulations are conducted on both the CIGRE standard DC test model and the wind power DC transmission system for verification. The conclusions are as follows:

(1) Compared to optimizing only HVDC control parameters, coordinating the optimization of HVDC, DFIG, and SVC control parameters yields better results in suppressing overvoltage.

(2) SEGA (Self-Adaptive Elitist Genetic Algorithm) demonstrates better optimization results in coordinating control parameter optimization for wind power DC transmission systems compared to GA (Genetic Algorithm), effectively suppressing overvoltage at wind turbine grid connection points to a greater extent.

(3) The severity of transient overvoltage induced by DC blocking is higher at high wind power output compared to low wind power output operating conditions. Simultaneously optimizing the parameters of HVDC, DFIG, and SVC while applying coordinated control strategies based on DFIG and SVC can effectively eliminate transient overvoltage phenomena.

Future work will further explore improved methods for controlling transient overvoltage in wind power DC transmission systems.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JZ: Conceptualization, Writing–original draft. JD: Formal Analysis, Writing–review and editing. ML: Validation, Writing–review and editing. FW: Supervision, Writing–original draft. XS: Project administration, Writing–original draft. YL: Methodology, Writing–original draft. LS: Resources, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by Science and Technology Project of the State Grid (Project Number: 5200-202356128A-1-1-ZN).

Conflict of interest

Authors ML, FW, and XS were employed by State Grid Economic and Technological Research Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barnes, M., Van, H. D., Teeuwsen, S. P., and Callavik, M. (2017). HVDC systems in smart grids. Proc. IEEE 105 (11), 2082–2098. doi:10.1109/jproc.2017.2672879

CrossRef Full Text | Google Scholar

Bao, J., Xu, L., Ma, J., Chen, N., and Li, S. (2021). Reactive power voltage coordination control strategy of wind farms based on model predictive control. J. Yangzhou Univ. Nat. Sci. Ed. 24 (01), 49–56. doi:10.19411/j.1007-824x.2021.01.009

CrossRef Full Text | Google Scholar

Ji, H., Zhang, F., Kang, C., and Han, M. (2020). Voltage stability control strategy of wind-thermal-bundled power generation and DC transmission system. Electr. Power Constr. 41 (04), 126–132. doi:10.3969/j.issn.1000-7229.2020.04.015

CrossRef Full Text | Google Scholar

Ji, X. (2017). Optimization of HVDC control system for mitigating AC transient overvoltage. Power Syst. Technol. 41 (03), 721–728. doi:10.13335/j.1000-3673.pst.2017.0166

CrossRef Full Text | Google Scholar

Jiang, Q., Liu, T., Zeng, X., Ai, Q., Yin, Y., Liu, M., et al. (2018). Influence mechanism of comprehensive action of large-scale wind power and HVDC transmission system on sending system transient stability. Power Syst. Technol. 42 (07). doi:10.13335/j.1000-3673.pst.2018.0356

CrossRef Full Text | Google Scholar

Johnson, B. K., and Dessouky, S. S. (2021). High voltage direct current transmission. IEEE Power & Energy Mag. 19 (6), 5, 14. doi:10.1007/978-3-030-51661-1_2

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, Q., Dong, C., Zhang, L., and Wang, Z. (2014). Efficient and security transmission of wind, photovoltaic and thermal power of large-scale energy resource bases through UHVDC projects. Proc. CSEE, 34 (16), 2513–2522. doi:10.13334/j.0258-8013.pcsee.2014.16.001

CrossRef Full Text | Google Scholar

Luo, Y. (2019). The research of coordinated control strategy of large-scale wind power HVDC sending system under mono-polar block fault [D]. Chongqing: Chongqing University.

Google Scholar

Ma, X., Yang, H., Xu, F., and Zhao, H. (2017). “Shultz-gibson method based DC-link voltage suppression of DFIG-based wind turbines.” Automation Electr. Power Syst. 41 (24), 177–183. doi:10.7500/AEPS20170112005

CrossRef Full Text | Google Scholar

Qu, B., Liu, C., Li, D., and Guo, B. (2021). Research on the development strategy of electricity substitution under the target of ‘carbon neutrality. Power Demand Side Manag. 23 (02), 1–3+9. doi:10.3969/j.issn.1009-1831.2021.02.001

CrossRef Full Text | Google Scholar

Rahimi, E., Gole, A. M., Davies, J. B., Fernando, I. T., and Kent, K. L. (2011). Commutation failure analysis in multi-infeed HVDC systems. IEEE Trans. Power Deliv. 26 (1), 378–384. doi:10.1109/tpwrd.2010.2081692

CrossRef Full Text | Google Scholar

Ren, C., Ke, X., Fan, G., Liu, X., and Lu, H. (2020). Transient voltage stabilization and control optimization for Large⁃scale wind power UHV DC transmission system. High. Volt. Appar. 56 (05), 163–174. doi:10.13296/j.1001-1609.hva.2020.05.025

CrossRef Full Text | Google Scholar

Shao, K., Li, F., Jiang, B., Zhang, H., Tian, M., Li, W., et al. (2010). “Multipopulation genetic algorithm with adaptive genetic algorithm with adaptive search area[A],” in International cpnference on intelligent control and information processing, 619–623.

CrossRef Full Text | Google Scholar

Wang, C. F., and Liu, K. (2019). A randomly guided firefly algorithm based on elitist strategy and its applications. IEEE Access, 7, 130373, 130387. doi:10.1109/access.2019.2940582

CrossRef Full Text | Google Scholar

Wang, T., Bu, G., Dong, Y., Hou, J., Wang, Y., Mu, S., et al. (2018). Electromechanical transient model of VSC-HVDC considering dynamics of phase-locked loop. Power Syst. Technol. 42 (07). doi:10.13335/j.1000-3673.pst.2017.2930

CrossRef Full Text | Google Scholar

Zhao, X., Li, Y., Sun, G., Zhang, Y., and Zeng, L. (2019). Effect of commutation failure on the overvoltage on rectifier station in AC/DC hybrid power system with wind farms. High. Volt. Eng. 45 (11), 3666–3673. doi:10.13336/j.1003-6520.hve.20181205021

CrossRef Full Text | Google Scholar

Zhang, J., Xiao, X., Gao, B., Luo, C., and Chen, T. (2013). Mechanism and characteristic study on sub-synchronous control interaction of a DFIG-based wind-power generator. Trans. China Electrotech. Soc. 28 (12), 142–149+159.

Google Scholar

Zheng, Z., Wang, Y., Xiao, X., Huang, C., Wang, Y., and Xie, Q. (2020). Response mechanism of DFIG to transient voltage disturbance under commutation failure of LCC-HVDC system. IEEE Trans. Power Deliv. 35 (99), 2972–2979. doi:10.1109/tpwrd.2020.3005720

CrossRef Full Text | Google Scholar

Zhu, L. (2021). Transient Overvoltage Control Strategy in New Energy Sending-End Grid Based on HVDC Blocking Fault[D]. Beijing: North China Electric Power University.

Google Scholar