Lithium-ion battery SOH estimation method based on multi-feature and CNN-KAN

The promotion of electric vehicles brings notable environmental and economic advantages. Precisely estimating the state of health (SOH) of lithium-ion batteries is crucial for maintaining their efficiency and safety. This study introduces an SOH estimation approach for lithium-ion batteries that integrates multi-feature analysis with a convolutional neural network and kolmogorov-arnold network (CNN-KAN). Initially, we measure the charging time, current, and temperature during the constant voltage phase. These include charging duration, the integral of current over time, the chi-square value of current, and the integral of temperature over time, which are combined to create a comprehensive multi-feature set. The CNN’s robust feature extraction is employed to identify crucial features from raw data, while KAN adeptly models the complex nonlinear interactions between these features and SOH, enabling accurate SOH estimation for lithium batteries. Experiments were carried out at four different charging current rates. The findings indicate that despite significant nonlinear declines in the SOH of lithium batteries, this method consistently provides accurate SOH estimations. The root mean square error (RMSE) is below 1%, with an average coefficient of determination (R²) exceeding 98%. Compared to traditional methods, the proposed method demonstrates significant advantages in handling the nonlinear degradation trends in battery life prediction, enhancing the model’s generalization ability as well as its reliability in practical applications. It holds significant promise for future research in SOH estimation of lithium batteries.

1 Introduction

Driven by environmental issues and the ongoing depletion of fossil fuel reserves, the demand for electric vehicles is on the rise (Liu H. et al., 2024; Zhang et al., 2023a). Electric vehicles extensively utilize lithium batteries because of their substantial energy density and extended lifespan (Feng et al., 2020; Gao et al., 2022; Zhu et al., 2024). Nevertheless, the electrochemical reactions within lithium batteries during operation lead to aging, which gradually diminishes both their performance and state of health (SOH), ultimately reducing the vehicle’s lifespan (He et al., 2024). Given the close relationship between capacity decay and battery lifespan, SOH is commonly expressed as the ratio of current capacity to its original capacity (Tian et al., 2020). As a result, SOH has emerged as a crucial metric for assessing battery longevity (Chen et al., 2022; Yang et al., 2024). Moreover, the battery’s safety is intricately linked to its SOH. As the battery gradually ages, safety hazards such as spontaneous combustion and explosion also increase, seriously threatening the personal safety and property safety of users (Zhao et al., 2024). Hence, precise SOH estimation of lithium batteries is vital for ensuring the safety and prolonging the service life of power batteries, which is essential for enhancing the reliability of battery management systems (Wang et al., 2020; Yu et al., 2023).

In recent years, a variety of SOH estimation methods have been introduced, generally categorized into model-based (Amir et al., 2022; Liu et al., 2022; Rojas and Khan, 2022; Tran et al., 2021; Xiong et al., 2018; Xu et al., 2022; Yang et al., 2021a; Yang et al., 2021b; Ye et al., 2023; Zheng et al., 2021) and data-driven (Che et al., 2023; Cui and Joe, 2021; Feng et al., 2019; Jenu et al., 2022; Jiang et al., 2021; Li et al., 2022; Li et al., 2020; Ma et al., 2022; Xu et al., 2023; Zhang et al., 2019; Zhang et al., 2022; Zhang C et al., 2024; Zhang et al., 2023b; Zhang et al., 2020). The model-based method involves creating an equivalent model of a lithium-ion battery, which simulates its internal structure, materials, and the chemical reactions occurring within it. Model-based SOH estimation methods include empirical models, equivalent circuit models, and electrochemical models. Amir et al. (2022) proposed a dynamic equivalent circuit model. This model is founded on a 2-RC (Resistor-Capacitor) equivalent circuit, utilizing open circuit voltage (OCV) as a state function, while considering the battery’s degradation in various chemical environments. However, the applicability of the model is limited when the battery operating conditions change. Yang et al. (2021a) developed a voltage reconstruction model utilizing partial charging curves. This model reconstructs the complete terminal voltage curve by analyzing the relationship between the half-cell electrode equilibrium potential and the full-cell terminal voltage. Nevertheless, frequent adjustments and calibrations of parameters are required for different battery types and states. Xu et al. (2022) proposed a joint estimation method that combines an equivalent circuit model and a simplified electrochemical model. This method uses an equivalent circuit model to describe the dynamic behavior of the battery and identifies the model parameters online through the recursive least squares method. The simplified electrochemical model is used to describe the distribution of lithium content inside the battery and to link the irreversible loss of lithium with SOH, thereby achieving an accurate estimation of SOH.

Recently, the swift advancement of machine learning and artificial intelligence technologies has led data-driven methods for assessing the SOH to become increasingly prominent. Data-driven methods do not need to analyze the complex electrochemical reactions inside lithium batteries, and can directly establish estimation models based on extracted characteristics such as voltage, current, temperature, and charging time, making them more universal. Commonly used data-driven models in recent years include support vector machine (SVM) (Feng et al., 2019; Li et al., 2022), long short-term memory (LSTM) (Jiang et al., 2021; Zhang et al., 2019), gated recurrent unit (GRU) (Cui and Joe, 2021; Zhang et al., 2023b) and transformer (Xu et al., 2023).

These methods utilize a range of techniques, including Incremental Capacity Analysis (Jenu et al., 2022; Li et al., 2020; Zhang et al., 2022), Differential Thermal Voltammetry (DTV) (Che et al., 2023; Ma et al., 2022) and Differential Voltage Analysis (DVA) (Zhang et al., 2020). ICA transforms the traditional charge and discharge curve into an IC curve with more obvious characteristics. The characteristics contained in the IC curve can not only effectively reflect the degradation process of lithium batteries, but also describe the reaction mechanism of internal aging of lithium batteries. Li et al. (2020) extracted the peak position and peak height from IC curve, which was smoothed using a Gaussian filter, to indicate the extent of battery aging. Che et al. (2023) extracted features including peak position, height, and the area beneath the DTV curve. This method mainly extracts features under the constant current (CC) charging mode and does not take into account the performance in the constant voltage (CV) charging stage. In fact, charging data from CV stage is highly correlated with the battery’s SOH (Zhang C et al., 2024). Furthermore, during actual charging, the process rarely begins at full depletion of power, which imposes certain limitations on this method.

In traditional SOH estimation methods based on physical modeling and data-driven approaches, while certain progress has been made, these methods often show limitations in handling complex nonlinearity and time-varying characteristics. In recent years, with the rapid development of deep learning, more and more cutting-edge techniques have been introduced into SOH estimation, including attention mechanisms and hybrid neural network methods. Bao et al. (2022) proposed a hybrid network combining dilated convolutional neural networks and bidirectional gated recurrent units, effectively extracting local and global features from time series data. Bao et al. (2023) introduced a dimensional attention mechanism, enabling the model to automatically select features highly relevant to SOH degradation trends, significantly improving the generalization capability of the model. Liu et al. (2023) proposed a health status evaluation method that integrates aging features under dynamic operating conditions, and Wang et al. (2024) studied the coupling effect of state of charge and loading rate, offering new perspectives and methods for SOH estimation.

Considering the strengths and limitations of the above data-driven methods, this paper proposes a lithium-ion battery SOH estimation method based on a multi-feature CNN-KAN model and conducts an in-depth analysis of the relationship between battery charging data and SOH during CV stage. Even when the lithium battery SOH has a significant nonlinear downward trend, this method still has excellent SOH estimation accuracy. The key contributions of this study can be outlined as follows:

(1) Utilizing data from CV stage, both electrical and thermal characteristics were extracted to aid in estimating battery SOH. The electrical characteristics encompass the charging duration during CV stage, the time-integral of the current, and the current’s chi-square value. The Pearson correlation coefficient was applied to confirm the strong relationship between these electrical features and battery SOH. Following this, the electrical and thermal characteristics were integrated to create a multi-feature sequence, offering a comprehensive depiction of the battery’s dynamic behavior and thermal effects throughout the charging process. This methodology facilitates the deep learning model in constructing a more precise SOH estimation framework, drawing on multi-faceted battery aging data.

(2) A CNN-KAN deep learning model with excellent performance was established. This paper uses the outstanding performance of CNN in capturing local features and reducing noise to transform complex battery aging data into higher-level abstract features, thereby reducing noise and reducing the computational burden of subsequent models. KAN was used after CNN, which effectively captures the complex dependency between input features and SOH through a unique adaptive network and B-spline basis function, thereby augmenting the model’s generalization capability.

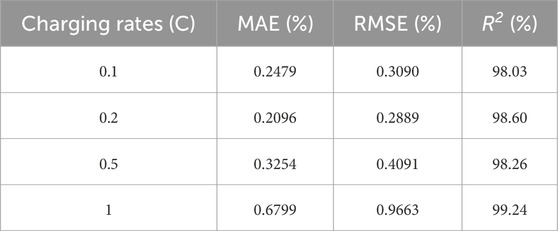
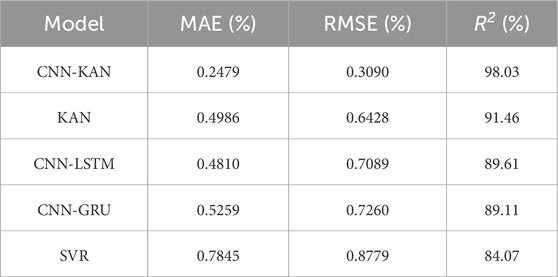
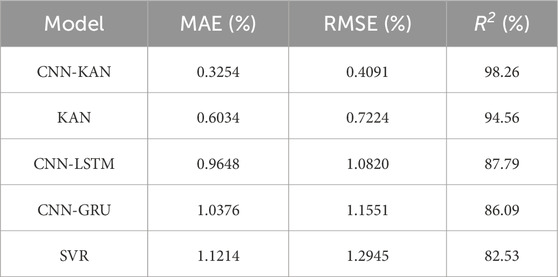
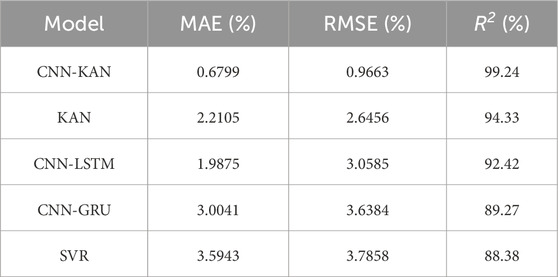
(3) Comprehensive SOH estimation verification and comparison with traditional models: The SOH estimation was performed following the methodology outlined in this paper, leveraging data from battery charge-discharge cycles across four distinct charging rates. Then it was compared with KAN, CNN-LSTM, CNN-GRU and SVR models. The experimental results demonstrate that when lithium batteries show significant nonlinear changes during aging, the algorithm proposed in this paper still performs extremely well. In the four data sets, compared with other models, the mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R²) are better than those of other models. The RMSE is 0.31%, 0.29%, 0.41% and 0.97%, and the R² is 98.03%, 98.60%, 98.26% and 99.24%, respectively.

To conclude, this paper extracts electrical features from lithium battery charging and discharging data, which exhibit a strong correlation with SOH, and integrates them with thermal features to construct a highly precise SOH estimation model. The efficacy of this approach is confirmed through experimental validation and comparative assessment.

The outline of the remaining chapters is structured as follows: Chapter 2 details the methods for extracting electrical and thermal features. Chapter 3 presents the proposed CNN-KAN model and discusses its benefits. Chapter 4 covers the process of acquiring battery aging data and describes experiments conducted using four different charging rate datasets based on the method introduced in this paper. The experimental outcomes indicate that the model offers distinct advantages. Finally, Chapter 5 provides a summary of this paper.

2 Feature extraction

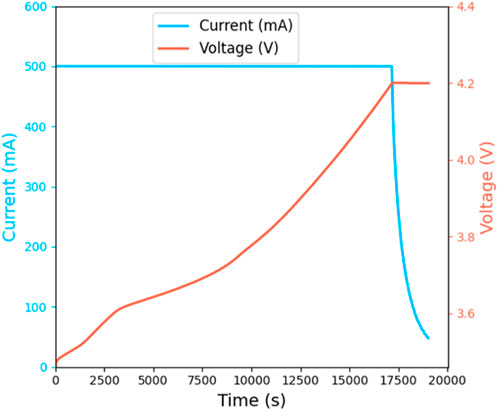
The CC-CV charging method is the primary approach used for charging lithium-ion batteries. Figure 1 illustrates the voltage curve over time during CC stage and the current curve over time during CV stage at a charging rate of 0.2C (500 mA). This study focuses on analyzing the data collected during CV stage. Key features such as the charging duration, the integral of current over time, and the chi-square value of current are extracted. The Pearson correlation coefficient is then applied to perform a correlation analysis on these features. Furthermore, thermal feature observed during CV stage are incorporated to offer a more in-depth analysis of battery behavior during charging. The data analyzed in this chapter was collected at a charging rate of 500 mA (0.2C).

Figure 1

Figure 1. CC-CV curve at a 0.2C charging rate.

2.1 Electrical features

2.1.1 Charging time

Figure 2A demonstrates that as the battery ages, the duration of the CV stage increases, with the red dashed line representing the cutoff current, which is set at 48 mA. This is due to the rise in internal impedance, which diminishes charging efficiency and subsequently prolongs the charging period. Based on this feature, the constant voltage charging time, $t_{\text{CV}}$, is identified as a key metric for evaluating battery’s aging process. The calculation formula is given in Equation 1:

$t_{\text{CV}}\left(c\right)=t_{\mathrm{e}}\left(c\right)-t_s\left(c\right)(1)$

where $t_{\mathrm{e}}\left(c\right)$ and $t_s\left(c\right)$ denote the end time of the entire charging stage and the start time of the CV charging stage, respectively, where c represents the number of charging cycles. Figure 2B shows the complete trend of charging time changing with the number of cycles at a 0.2C charging rate.

Figure 2

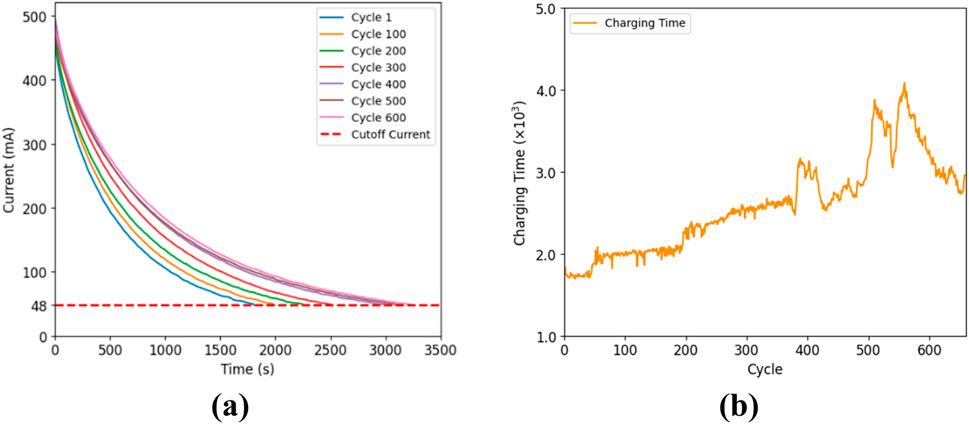
Figure 2. (A) Current-time curves under different cycle periods; (B) cycle number and charging time curve.

2.1.2 Integral of charging current

During the CV stage, current exhibits a dynamic decay, gradually diminishing until it reaches the cut-off threshold. The integral of current during this stage directly reflects the amount of energy stored, which is closely linked to the battery’s capacity. Figure 3A illustrates that as the battery ages, the integral of the current rises notably. Therefore, $S_{\mathrm{I}}$ is selected as the feature to characterize the battery degradation process, where $S_{\mathrm{I}}$ represents the integral of the current during the CV stage. The corresponding calculation formula is given in Equation 2:

$S_{\mathrm{I}}={{\displaystyle \int }}_{t_s}^{t_{\mathrm{e}}}{I}_c\left(t\right)\mathrm{d}t(2)$

where $I_c\left(t\right)$ denotes the current during the CV phase of cycle c. Figure 3B illustrates the trend of the current integral as a function of cycle number at a charging rate of 0.2C.

Figure 3

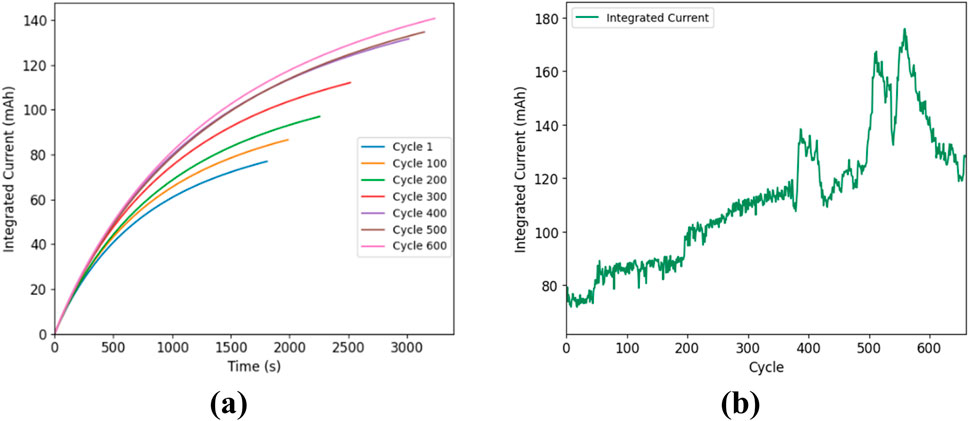
Figure 3. (A) The curve of current integral changing with time under various cycles; (B) The curve of cycle number and current integral.

2.1.3 Charging current chi-square

The chi-square statistic was proposed by Pearson in 1,900 as a statistical method for measuring the correlation or independence between variables. Since its proposal, the chi-square statistic has found applications across numerous fields, including image denoising and signal recognition. It is particularly effective in characterizing the dependence within observed data while also mitigating the impact of noise. The chi-square formula is given in Equation 3:

$S_{\overline{I}}={\displaystyle \sum _{c=1}^n}\frac{{\left(x_c-\overline{x_c}\right)}^2}{\overline{x_c}}(3)$

where $x_c$ represents the sampled voltage during the constant voltage charging stage in cycle c, n denotes the total number of battery charge and discharge cycles and $\overline{x_c}$ signifies the average current in the constant voltage charging stage for cycle c.

Due to frequent interference from various noise sources, the data collected at sampling points often fails to accurately reflect battery SOH. Therefore, this study calculated the chi-square value of the current data during the CV stage and filtered out noise through statistical analysis. The reason for choosing the chi-square value over other statistical measures lies in its ability to effectively capture deviations in the current data, particularly when identifying outliers or abnormalities. While other statistical measures could be considered, the chi-square value was chosen for its efficiency in detecting variations specific to the dataset used in this paper. As shown in Figure 4A, the internal materials gradually degrade, causing the battery to show more fluctuations and instabilities during the charging process. Figure 4B represents the change of the current chi-square value in each cycle, showing the statistical distribution difference of the battery during various cycle periods.

Figure 4

Figure 4. (A) The curve of the chi-square value of current changing with time; (B) The curve of cycle number and current chi-square value.

2.2 Correlation analysis

To further confirm the relationship between the electrical features extracted from CV stage and battery’s SOH, this study employs the Person correlation coefficient method for analysis of the aforementioned electrical features. The Pearson correlation coefficient is a statistical tool that measures the degree of linear correlation between two variables, denoted by r. The coefficient ranges from [−1,1], where r = 1 indicates a perfect positive correlation, r = −1 signifies a perfect negative correlation, and r = 0 denotes no linear correlation. The formula for calculating the Pearson correlation coefficient is given in Equation 4:

$r=\frac{\sum \left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{\sum {\left(x_i-\overline{x}\right)}^2\sum {\left(y_i-\overline{y}\right)}^2}}(4)$

where $x_i$ and $y_i$ are the sample values of the two variables, $\overline{x}$ and $\overline{y}$ denote their average values of two variables.

The Pearson correlation coefficient between electrical features extracted from CV stage and battery SOH were calculated. The results are shown in Table 1.

Table 1

Table 1. Pearson correlation coefficient between electrical features and battery SOH at a charging rate of 0.2C.

Figure 5 visualizes the correlation between the electrical features mentioned in Section 2.1 and the battery SOH. The three electrical features mentioned can significantly track the nonlinear trend of the battery aging process. After normalization, it can be seen that although the curves of the three features have roughly the same trend, the curves do not completely overlap, indicating that each feature has its own role in reflecting the information of the battery’s aging information. Considering that a single feature may not be fully and accurately describe health status and aging process of battery, this paper combines these three features to reduce the deviation caused by relying on a single feature and improve accuracy of the predictive model.

Figure 5

Figure 5. Normalized curve of battery SOH and electrical features.

2.3 Thermal feature

The temperature of a lithium battery is intricately connected to its SOH, primarily due to the significant impact of temperature on the physical and chemical transformations occurring within the battery. At elevated temperatures, a series of secondary reactions and degradation processes may take place within the battery, such as the oxidation of the cathode material and decomposition of the electrolyte (Hou et al., 2023; Zhang Z et al., 2024). These reactions expedite the battery’s aging process, causing a swift reduction in SOH. Conversely, at low temperatures, the electrolyte’s fluidity is greatly diminished, and ion transport becomes slow, resulting in a decrease in battery efficiency during charge and discharge, which accelerates the decay of SOH. This paper extracts the temperature integral value of the lithium battery during the CV stage as a thermal feature. The formula is shown in Equation 5:

$S_{\mathrm{T}}={{\displaystyle \int }}_{t_s}^{t_{\mathrm{e}}}{T}_c\left(t\right)\mathrm{d}t(5)$

where $T_c\left(t\right)$ is the temperature during the CV charging phase of cycle c.

$S_{\mathrm{T}}$ can represent the overall thermal accumulation effect of battery during the CV stage. Long-term thermal accumulation may lead to accelerated aging of battery materials and performance degradation. At the same time, $S_{\mathrm{T}}$ can smooth out short-term temperature fluctuations and noise by accumulating temperature data, and capture the overall temperature change trend of battery during the CV stage. Battery performance is affected by many factors, including electrochemical reactions, material properties, and operating conditions. As a thermal feature, facilitating the model’s accuracy in SOH estimation, and improving the model’s ability to generalize.

3 CNN-KAN model

3.1 CNN

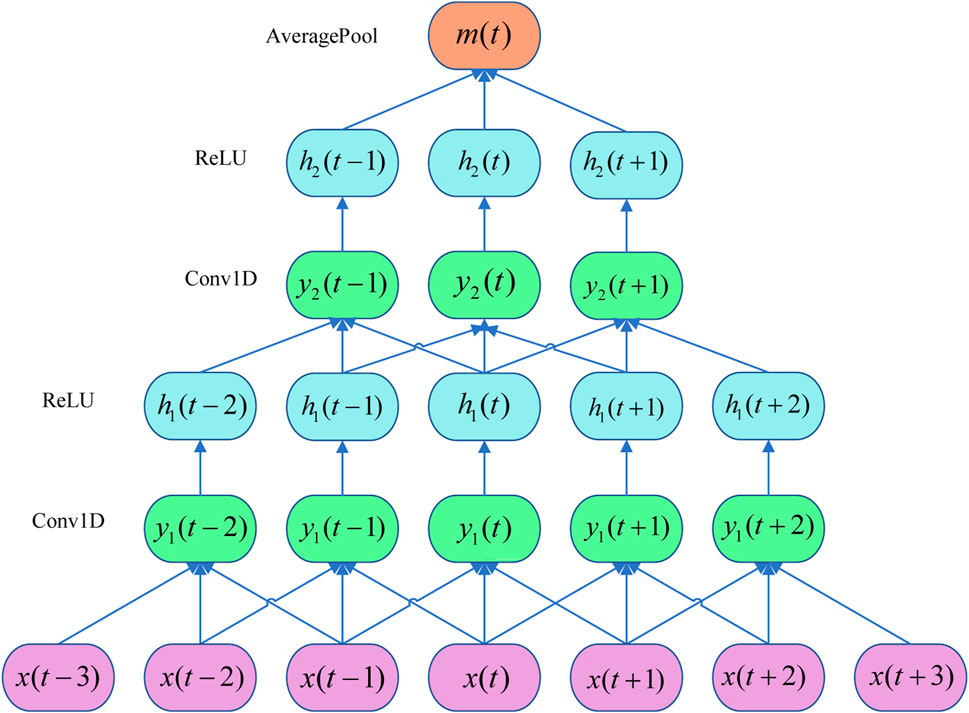
Convolutional Neural Network (CNN) were first introduced by Yann LeCun and others in the 1980s and are mainly used for computer vision tasks such as image classification and object detection. The fundamental concept of CNN involves utilizing convolution operations to extract local features of data and pooling operations to reduce the dimension of features, thereby reducing computational complexity while maintaining important features. Although CNN was originally designed to process two-dimensional image data, its principles can also be extended to time series data. One-dimensional convolutional neural network (1D CNN) is a convolutional neural network specifically designed to process one-dimensional data (Khan et al., 2024). It mainly extracts features from time series data by sliding convolution kernels along the time axis. Given the excellent performance of 1D CNN in time series tasks (Kim et al., 2023), this paper employs a two-layer 1D CNN to extract the electrical and thermal features of CV stage and capture temporal dependencies.

As depicted in Figure 6, the convolutional layer consists of two layers. The activation function is ReLU. Since time series usually contain complex nonlinear relationships, the ReLU activation function can introduce nonlinearity, so that the neural network can effectively learn and represent these complex nonlinear relationships, thereby enhancing prediction accuracy. Through utilizing multiple layers of convolution, the model builds and optimizes feature representation layer by layer, which can better capture and understand the details and global information of the input data. In addition, extracting features in stages can reduce the number of convolution kernels, minimizing the model’s parameters and reducing the risk of overfitting. The pooling layer uses average pooling which better retains the global information from the input data. The specific mathematical formulas are illustrated in Equations 6–10:

Figure 6

Figure 6. CNN structure.

3.1.1 Convolutional layer

$y_1\left(t\right)={\displaystyle \sum _{s=-\infty }^{\infty }}x\left(s\right)\cdot f_1\left(t-s\right)(6)$

where $y_1\left(t\right)$ represents the output from the first convolutional layer, $x\left(s\right)$ represents the one−dimensional input signal, $f_1\left(t-s\right)$ stands for the convolution kernel, $s$ indicates the index within the convolution kernel, and $t$ corresponds to time or space index.

$h_1\left(t\right)=\max \left(0,y_1\left(t\right)\right),(7)$

where $h_1\left(t\right)$ represents output from the first convolution layer following the application of the ReLU activation function.

$y_2\left(t\right)={\displaystyle \sum _{s=-\infty }^{\infty }}{h}_1\left(s\right)\cdot f_2\left(t-s\right)(8)$

where $y_2\left(t\right)$ represents output from the second layer of convolution, and $f_2{\left(t-s\right)}^{\leftarrow }$ represents the convolution kernel of the second layer.

$h_2\left(t\right)=\max \left(0,y_2\left(t\right)\right)(9)$

Where $h_2\left(t\right)$ represents the output from the second convolution layer following the ReLU activation function.

3.1.2 Pooling layer

$m\left(t\right)=\frac{1}{T}{\displaystyle \sum _{t=1}^T}{h}_2\left(t\right)(10)$

where $m$ represents output of the pooling layer and $T$ represents total number of time steps.

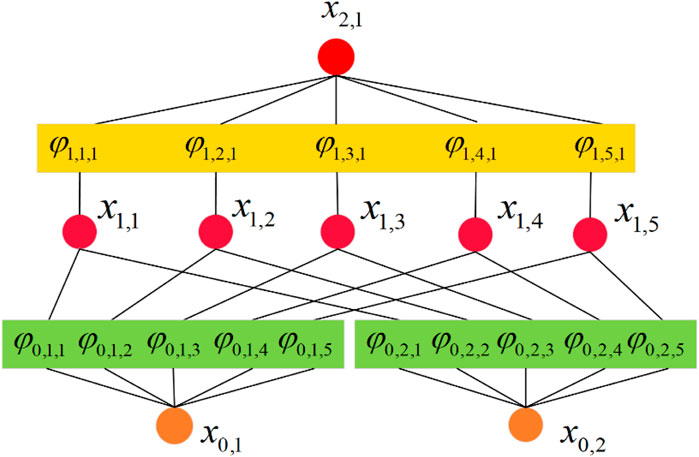
3.2 KAN

KAN is a network structure based on the Kolmogorov-Arnold representation theorem. The theorem states that any continuous multi-dimensional function $f\left(x_1,x_2,\dots ,x_n\right)$ can be represented as a nested combination of several functions of one variable. This provides a theoretical basis for the processing of high dimensional data (Liu Z. et al., 2024).The formula is provided in Equation 11:

$f\left(x_1,x_2,\dots ,x_n\right)={\displaystyle \sum _{q=1}^{2n+1}}{\mathrm{\Phi }}_q\left({\displaystyle \sum _{p=1}^n}{\phi }_{q,p}\left(x_p\right)\right)(11)$

where ${\mathrm{\Phi }}_q$ and ${\phi }_{q,p}\left(x_p\right)$ are continuous univariate functions, $q$ denotes the index for the outer summation, and $p$ denotes the index for the inner summation, $n$ is the dimensionality of the input.

This theory provides us with a powerful tool to deal with complex high-dimensional data problems. The data in the battery system is usually high-dimensional and SOH estimation involves multiple complex nonlinear relationships. KAN can reduce the complexity of high-dimensional data and achieve more effective modeling through its nonlinear activation and linear combination characteristics.

First, the input features $x_p$ are divided into adaptive grids. Each input feature is interpolated using B-spline functions over its corresponding grid interval.

The B-spline interpolation function is given in Equation 12:

$B_{i,k}\left(x\right)=\frac{x-t_i}{t_{i+k}-t_i}{B}_{i,k-1}\left(x\right)+\frac{t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}{B}_{i+1,k-1}\left(x\right)(12)$

where $t_i$ represents the position of the interpolation nodes, and k is the degree of the B-spline.

All the B-spline interpolation results are linearly combined to produce the final aggregated result ${\phi }_{q,p}\left(x_p\right)$. The formula is provided in Equation 13:

${\phi }_{q,p}\left(x_p\right)={\displaystyle \sum _{i=1}^N}{w}_i{B}_{i,k}\left(x_p\right)(13)$

where, $w_i$ are learnable weights and N is the number of interpolation nodes.

${\mathrm{\Phi }}_q$ is the global nonlinear transformation factor in the KAN model. It is used to aggregate the locally interpolated results ${\displaystyle {\sum }_{p=1}^n}{\phi }_{q,p}\left(x_p\right)$ for all input features $x_p$ and apply global nonlinear processing to them. The formula is provided in Equation 14:

${\mathrm{\Phi }}_q\left(y_q\right)=\sigma \left({\displaystyle \sum _{j=1}^m}{v}_{q,j}\cdot y_{q,j}+b_q\right)(14)$

where $y_q$ represents the sum of the locally interpolated results for all input features after interpolation, σ(⋅) is a nonlinear activation function, $v_{q,j}$ are learnable weights in the global nonlinear transformation layer, $b_q$ is the bias term, representing the offset, and $m$ is the number of nodes in the global function layer.

Figure 7 illustrates the KAN structure utilized in this study.

Figure 7

Figure 7. KAN model structure.

The main advantage of the KAN model lies in its use of learnable activation functions, which are parameterized through splines and placed on the edges, rather than relying on fixed activation functions at the nodes. Additionally, KAN eliminates the need for linear weight matrices found in traditional multi-layer perceptron (MLP), replacing them with univariate spline functions, making it more efficient in handling highly nonlinear and complex relationships. KAN is also better at mitigating the curse of dimensionality, particularly in tasks where compositional structures exist in the data, enabling more efficient feature extraction and approximation. Through adaptive grids and spline interpolation, KAN not only improves accuracy but also offers better interpretability and visualization capabilities.

CNN effectively captures the local features of the original feature sequence, reduces noise and alleviates the computational load on subsequent models. KAN follows CNN to capture complex dependencies between input features and SOH via its unique adaptive network and B-spline basis function, enhancing the model’s generalization capability.

4 Experiments and results analysis

4.1 Experimental data

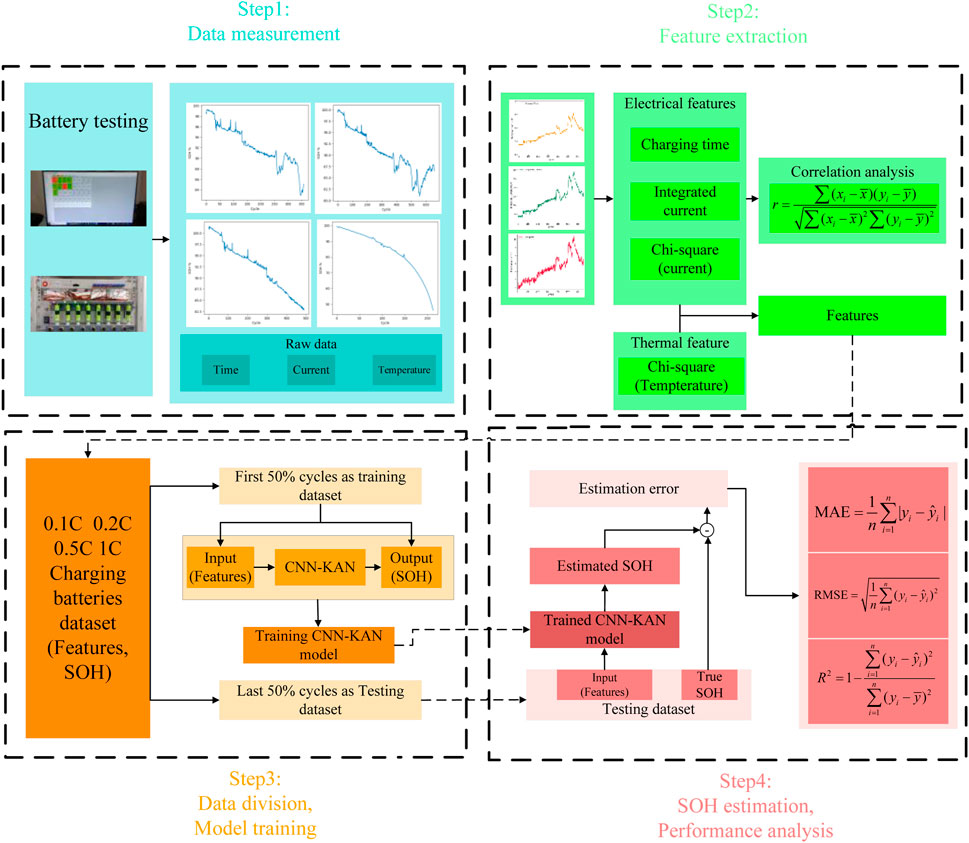
As shown in Figure 8, we conducted a charge-discharge cycle aging experiment on a group of cylindrical lithium-ion batteries with identical specifications on the Neware BTS 4,000 at room temperature, starting in August 2023. The experimental data was recorded using the upper computer in the testing system, including time, current, voltage, capacity, energy, temperature, et al. These data will be standardized to eliminate dimensional differences and accelerate model convergence. The rated capacity of these batteries is 2.5 Ah. The experimental procedure is as follows:

(1) Charging stage: CC-CV method was employed, with charging rates set at 0.1C (250 mA), 0.2C (500 mA), 0.5C (1,250 mA) and 1C (2,500 mA), respectively. When terminal voltage of batteries reached the upper limit of 4.2 V, the process transitioned to the CV stage, continuing until the current decreased to the predetermined cut-off value of 48 mA.

(2) Resting stage: After charging, the battery is given 5 min of rest time to stabilize its internal chemical state.

(3) Discharging stage: A CC discharge was performed at a rate of 0.5C until the terminal voltage dropped to the lower cut-off value.

Figure 8

Figure 8. Battery testing system.

In this study, the lithium battery SOH is defined as the ratio of its current maximum discharge capacity to its initial rated capacity when it leaves the factory, providing an accurate and intuitive indication of battery performance degradation. The formula is defined in Equation 15 (Wang et al., 2022):

$\text{SOH}=\frac{{\mathrm{Q}}_{\mathit{max}\text{capacity}}}{{\mathrm{Q}}_{\text{rated}\text{capacity}}}\times 100\%(15)$

where ${\mathrm{Q}}_{\mathit{max}\text{capacity}}$ represents the battery’s current maximum discharge capacity and $Q_{\text{rated}\text{capacity}}$ refers to its rated capacity upon leaving the factory.

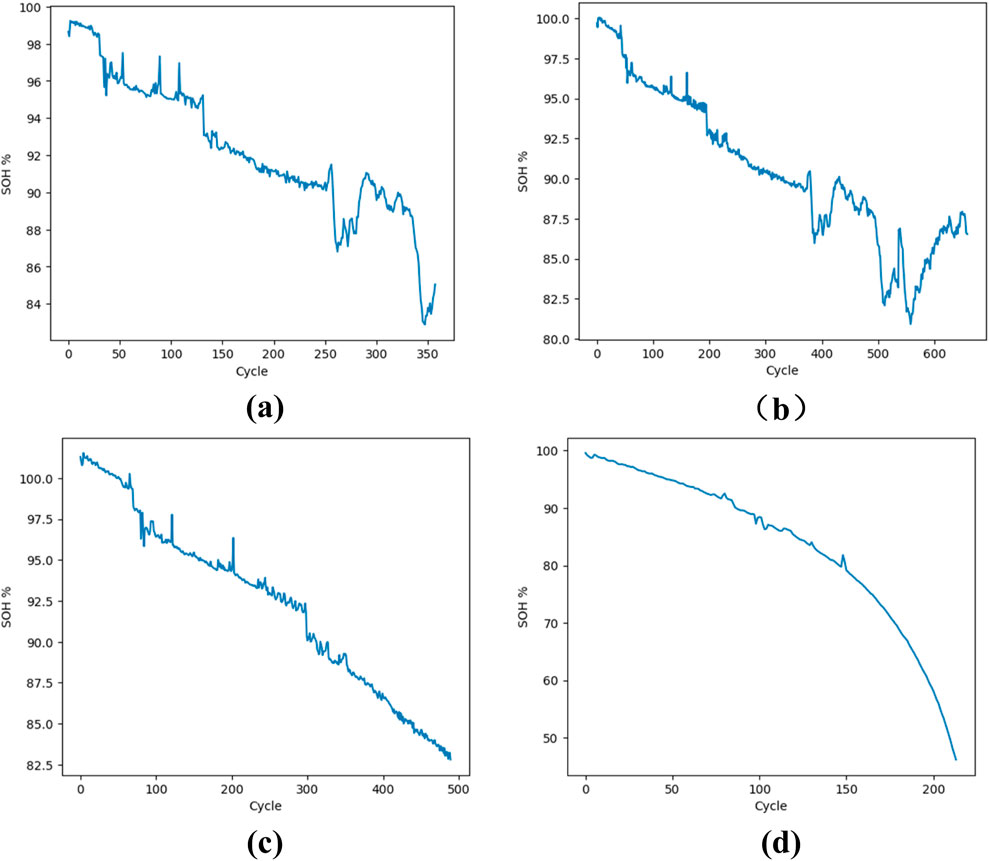
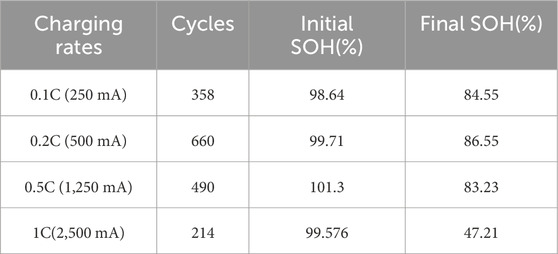
Figure 9A–D shows changes in four batteries SOH during multiple charge-discharge cycles at rates of 0.1C, 0.2C, 0.5C and 1C. The results show that battery SOH typically declines progressively with an increase in charge and discharge cycles. However, various factors, including temperature, charging rate, and aging mechanisms, significantly impact the battery, resulting in a complex and nonlinear SOH decay process. Battery capacity can exhibit different levels of regeneration across cycles. These influencing factors make the precise estimation of lithium battery SOH a challenging task. Table 2 shows the cycle aging parameters of the battery at four different charging rates.

Figure 9

Figure 9. (A) SOH at 0.1C; (B) SOH at 0.2C; (C) SOH at 0.5C; (D) SOH at 1C.

Table 2

Table 2. Battery aging parameters at four different rates.

4.2 Experimental results

The correlation coefficient between electrical features and battery SOH at four charging rates is calculated using the Person correlation coefficient method mentioned in Section 2.2. The results are presented in Table 3.

Table 3

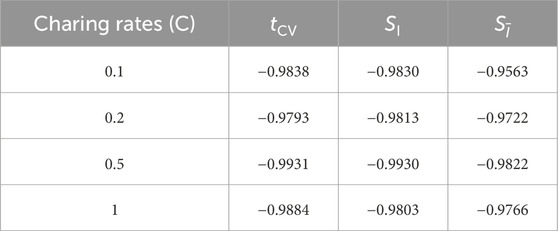
Table 3. Person correlation coefficient between electrical features and battery SOH at four different rates.

The table demonstrates that the Pearson correlation coefficients between the selected electrical parameters $t_{\text{CV}}$, $S_{\mathrm{I}}$ and $S_{\overline{I}}$ and the battery SOH across four different rates are nearly −1. This suggests a strong inverse relationship between these parameters and battery SOH, making them reliable indicators for monitoring battery aging trends.

As outlined in the second section of this paper, the electrical and thermal features attributes of lithium batteries during CV stage at various rates are extracted and paired with their corresponding SOH values to create a comprehensive dataset. To preserve dataset’s balance and ensure robust generalization in the model, the data is evenly split into training and test sets at a 1:1 ratio.

The training data is fed into the CNN-KAN model constructed in the third part of this paper. Taking 0.2C as an example, the number of filters of CNN in the model is 128, and each filter has a convolution kernel size of 3. The number of hidden layer neurons in the KAN part is 1,024 to process and interpret the features extracted by the convolution layer. To enhance the generalization ability of the model and prevent overfitting, L2 regularization with a coefficient of 1e-4 is applied after each convolution layer, and a dropout layer with a coefficient of 0.2 is added after the global average pooling layer. The optimization strategy for the model employs the Adam optimizer combined with an exponential decay learning rate scheduler, initializing the learning rate at 1e-4 with a decay rate of 0.9. This approach dynamically adjusts the learning rate, accelerates initial convergence, and allows for refinement with a lower learning rate in later stages. The model is trained for 100 epochs, with a batch size of 32, and the data is split with a training to validation set ratio of 8:2.

Figure 10 illustrates the experimental flowchart, which can be summarized as follows: First, battery tests are conducted at different charging rates to collect key data such as time, current, and temperature. Then, electrical and thermal features are extracted from the raw data to form a dataset. Next, the dataset is split into training and testing sets, which are used to train the CNN-KAN model. Finally, the model’s performance is evaluated by comparing the predicted SOH with the true SOH using error metrics like MAE, RMSE, and R².

Figure 10

Figure 10. Experiemental flowchart.

Figure 11 presents the results of the SOH estimation.

Figure 11

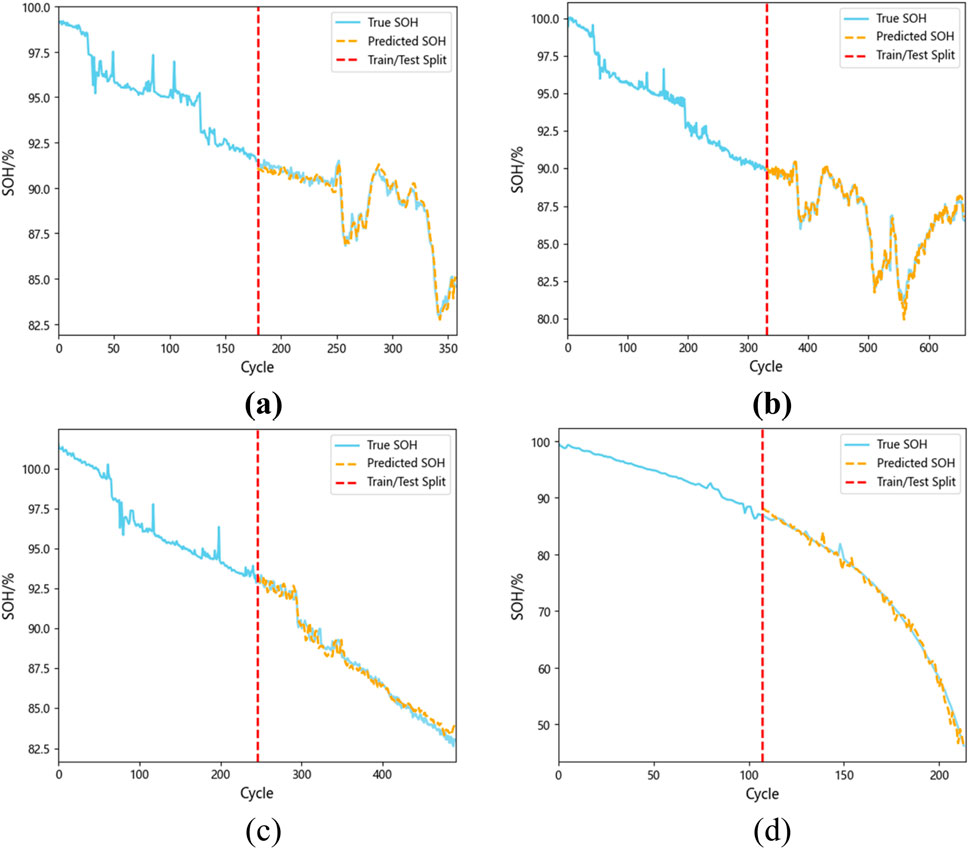
Figure 11. (A) SOH estimation results at 0.1C; (B) SOH estimation results at 0.2C; (C) SOH estimation results at 0.5C; (D) SOH estimation results at 1C.

To comprehensively evaluate accuracy of SOH estimation, this study utilized standard regression model performance evaluation indicators, including MAE, RMSE and R². These indicators provide an important quantitative basis for understanding model performance. The formulas used to calculate the above indicators are described by Equations 16–18:

$\text{MAE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left|y_i-{\widehat{y}}_i\right|(16)$

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(y_i-{\widehat{y}}_i\right)}^2}(17)$

$R^2=1-\frac{{\displaystyle \sum _{i=1}^n}{\left(y_i-{\widehat{y}}_i\right)}^2}{{\displaystyle \sum _{i=1}^n}{\left(y_i-\overline{y}\right)}^2}(18)$

where n represents the total number of charge and discharge cycles, $y_i$ represents actual SOH value, $\overline{y}$ is average of all actual SOH values and ${\widehat{y}}_i$ is estimated SOH value. In the case of MAE and RMSE, lower values correspond to higher model estimation accuracy. Regarding R², a value closer to 1 signifies a superior model fit. The outcomes of SOH estimation method presented in this study are displayed in Table 4.

Table 4

Table 4. Performance of CNN-KAN in estimating SOH at four charging rates.

At these four charging rates, the MAE of the estimation results remains below 0.7%, RMSE is under 1%, and the R² exceeds 98%. Specifically, at a 0.1C charging rate, due to the lower charging current leading to a longer charging time for each cycle, the data may be more susceptible to external interference and noise, resulting in more noticeable fluctuations. However, the R² still reaches 98.03% and the RMSE is 0.31%. Particularly at the 0.1C, 0.2C, and 0.5C charging rates, despite the true SOH value exhibiting significant nonlinear changes, the SOH can still be estimated accurately, demonstrating the model’s excellent fitting capability. These results clearly indicate that this approach can offer reliable and precise SOH estimates across various conditions.

4.3 Experimental comparisons

To verify the advantages of the CNN-KAN model, comparative experiments were conducted with KAN, CNN-LSTM, CNN-GRU and SVR models. We utilized the previously mentioned laboratory data across different charging rates, and the results of these comparisons are displayed in Figure 12A–D. Tables 5–8 provide a comparison of the MAE, RMSE and R² estimation results across diverse charging rates among the models.

Figure 12

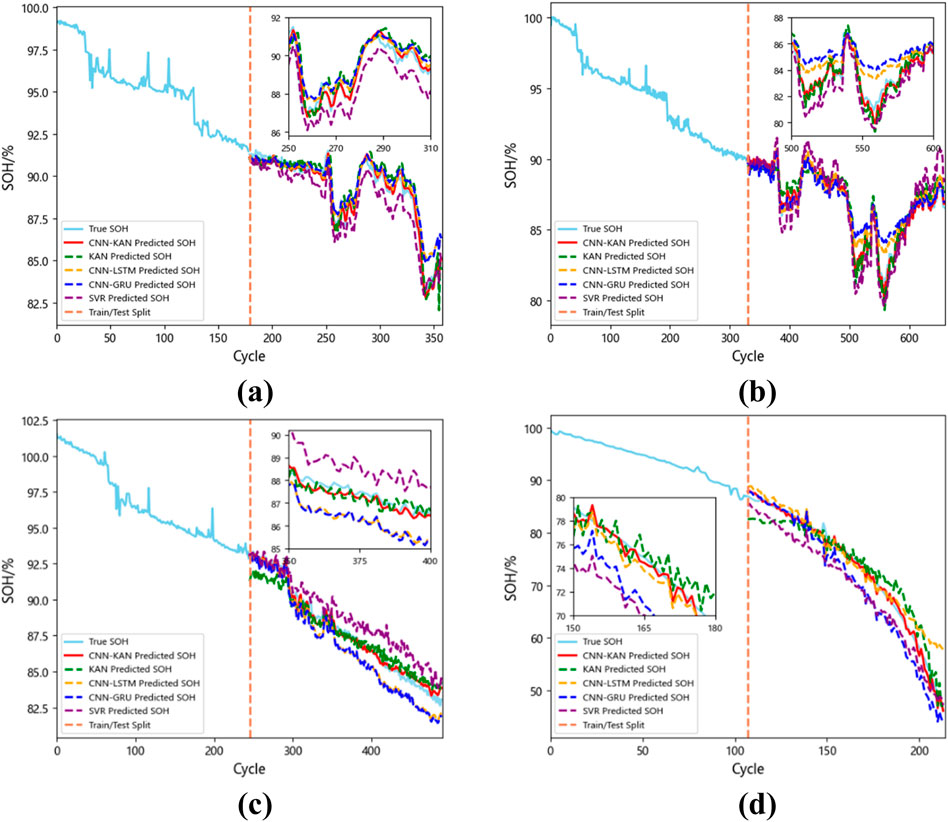
Figure 12. (A) Comparison of SOH estimation results at 0.1C; (B) Comparison of SOH estimation results at 0.2C; (C) Comparison of SOH estimation results at 0.5C; (D) Comparison of SOH estimation results at 1C.

Table 5

Table 5. Evaluation indicators at 0.1C.

Table 6

Table 6. Evaluation indicators at 0.2C.

Table 7

Table 7. Evaluation indicators at 0.5C.

Table 8

Table 8. Evaluation indicators at 1C.

The table shows that the introduced model surpasses the other four models. Leveraging the robust feature extraction capability of CNN, the CNN-KAN model presented in this paper achieves higher accuracy than the standalone KAN model, with RMSE reduced by at least 0.31% and R² increased by at least 3.7% across all four rates. Compared to traditional CNN-LSTM, CNN-GRU, and SVR models, the R² is improved by at least 6.82%.

LSTM and GRU capture long-term dependencies through their internal gating mechanisms, while SVR, as a regression algorithm based on statistical learning theory, can handle some nonlinearities using kernel functions. However, all three methods face limitations when dealing with highly nonlinear datasets. In contrast, KAN excels at handling complex nonlinear relationships by decomposing high-dimensional functions into combinations of univariate functions, making it more effective at capturing the nonlinear dependencies between input features and SOH.

The proposed CNN-KAN model can provide fast and accurate SOH estimation at different charging rates. These findings demonstrate that combining the electrical features of CV stage with the thermal feature, and processing their complex nonlinear relationship through an advanced neural network, is an effective method for monitoring battery health status.

5 Conclusion

This paper introduces a lithium-ion battery SOH estimation method built on multi-feature and CNN-KAN, which markedly improves the precision of SOH assessment.

This paper extracts the electrical and thermal features from the data of the CV stage of lithium batteries. The electrical features include the time, the integral of the current with respect to time and the chi-square value of the current. The features of lithium battery aging process are fully explored from the perspective of dynamic changes and long-term accumulation effects. The Person correlation coefficient method is employed to analyze and confirm that these features are highly correlated with battery SOH. Beyond the electrical features, the thermal feature of CV stage is as well combined to take into account the impact of the long-term accumulated thermal effect on the battery SOH. A mathematical model is then established that links these quantitative features with the battery SOH, ensuring precise SOH estimation based on the identified features for any charging cycle.

On this basis, this paper proposes a CNN-KAN model with excellent performance. This model leverages the strengths of CNN in efficiently extracting key features from raw data and KAN in effectively capturing complex nonlinear relationships in data through adaptive grids and B-spline basis functions. The model underwent thorough validation across four datasets with varying charging current rates. The findings reveal that despite the pronounced nonlinearity in the battery SOH decay process, MAE is 0.25%, 0.21%, 0.33% and 0.68%, RMSE is 0.31%, 0.29%, 0.41% and 0.97% and an average R² of 98.53%. At a charging rate of 1C, the upper R² is as high as 99.24%. Comparative experiments with KAN, CNN-LSTM, CNN-GRU, and SVR models further confirm the excellence of CNN-KAN.

This study presents a novel method for estimating the SOH of lithium-ion batteries by combining multiple features and a CNN-KAN model. The proposed method shows significant potential for real-world applications and future research. By analyzing electrical and thermal characteristics, the model offers a more comprehensive perspective on battery performance, making it particularly suitable for real-time monitoring of battery status in electric vehicles and renewable energy storage systems. This research lays the groundwork for exploring more advanced architectures or hybrid models to further enhance the accuracy of battery SOH prediction. Additionally, future studies could incorporate more environmental factors to further improve the model’s predictive capabilities. We believe this study will strongly support further exploration in the field of battery health diagnostics.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

ZZ: Writing–original draft, Writing–review and editing, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization. XiL: Data curation, Software, Validation, Visualization, Writing–review and editing. RZ: Data curation, Software, Visualization, Writing–review and editing. XuL: Writing–review and editing. SC: Writing–review and editing. ZS: Writing–review and editing. HJ: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the scientific research foundation for high-level personnel in Jinling Institute of Technology (jit-b-201811) and the Industry-University-Research Cooperation Project of Jiangsu Province (BY2021300).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amir, S., Gulzar, M., Tarar, M. O., Naqvi, I. H., Zaffar, N. A., and Pecht, M. G. (2022). Dynamic equivalent circuit model to estimate state-of-health of lithium-ion batteries. IEEE Access 10, 18279–18288. doi:10.1109/ACCESS.2022.3148528

CrossRef Full Text | Google Scholar

Bao, Z., Jiang, J., Zhu, C., and Gao, M. (2022). A new hybrid neural network method for state-of-health estimation of lithium-ion battery. Energies 15 (12), 4399. doi:10.3390/en15124399

CrossRef Full Text | Google Scholar

Bao, X., Chen, L., Lopes, A. M., Li, X., Xie, S., Li, P., et al. (2023). Hybrid deep neural network with dimension attention for state-of-health estimation of Lithium-ion Batteries. Energy 278, 127734. doi:10.1016/j.energy.2023.127734

CrossRef Full Text | Google Scholar

Che, Y., Vilsen, S. B., Meng, J., Sui, X., and Teodorescu, R. (2023). Battery health prognostic with sensor-free differential temperature voltammetry reconstruction and capacity estimation based on multi-domain adaptation. eTransportation 17, 100245. doi:10.1016/j.etran.2023.100245

CrossRef Full Text | Google Scholar

Chen, D., Zhang, W., Zhang, C., Sun, B., Cong, X., Wei, S., et al. (2022). A novel deep learning-based life prediction method for lithium-ion batteries with strong generalization capability under multiple cycle profiles. Appl. Energy 327, 120114. doi:10.1016/j.apenergy.2022.120114

CrossRef Full Text | Google Scholar

Cui, S., and Joe, I. (2021). A dynamic spatial-temporal attention-based GRU model with healthy features for state-of-health estimation of lithium-ion batteries. IEEE Access 9, 27374–27388. doi:10.1109/ACCESS.2021.3058018

CrossRef Full Text | Google Scholar

Feng, X., Weng, C., He, X., Han, X., Lu, L., Ren, D., et al. (2019). Online state-of-health estimation for Li-ion battery using partial charging segment based on support vector machine. IEEE Trans. Veh. Technol., 68(9), 8583–8592. doi:10.1109/TVT.2019.2927120

CrossRef Full Text | Google Scholar

Feng, F., Teng, S., Liu, K., Xie, J., Xie, Y., Liu, B., et al. (2020). Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 455, 227935. doi:10.1016/j.jpowsour.2020.227935

CrossRef Full Text | Google Scholar

Gao, X., Jia, Y., Zhang, W., Yuan, C., and Xu, J. (2022). Mechanics-driven anode material failure in battery safety and capacity deterioration issues: a review. Appl. Mech. Rev. 74 (6), 060801. doi:10.1115/1.4054566

CrossRef Full Text | Google Scholar

He, Y., Deng, Z., Chen, J., Li, W., Zhou, J., Xiang, F., et al. (2024). State-of-health estimation for fast-charging lithium-ion batteries based on a short charge curve using graph convolutional and long short-term memory networks. J. Energy Chem. 98, 1–11. doi:10.1016/j.jechem.2024.06.024

CrossRef Full Text | Google Scholar

Hou, W., Lu, Y., Ou, Y., Zhou, P., Yan, S., He, X., et al. (2023). Recent advances in electrolytes for high-voltage cathodes of lithium-ion batteries. Trans. Tianjin Univ. 29 (2), 120–135. doi:10.1007/s12209-023-00355-0

CrossRef Full Text | Google Scholar

Jenu, S., Hentunen, A., Haavisto, J., and Pihlatie, M. (2022). State of health estimation of cycle aged large format lithium-ion cells based on partial charging. J. Energy Storage 46, 103855. doi:10.1016/j.est.2021.103855

CrossRef Full Text | Google Scholar

Jiang, J., Zhao, S., and Zhang, C. (2021). State-of-Health estimate for the lithium-ion battery using chi-square and ELM-LSTM. World Electr. Veh. J. 12 (4), 228. doi:10.3390/wevj12040228

CrossRef Full Text | Google Scholar

Khan, M. K., Houran, M. A., Kauhaniemi, K., Zafar, M. H., Mansoor, M., and Rashid, S. (2024). Efficient state of charge estimation of lithium-ion batteries in electric vehicles using evolutionary intelligence-assisted GLA–CNN–Bi-LSTM deep learning model. Heliyon 10 (15), e35183. doi:10.1016/j.heliyon.2024.e35183

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J., Oh, S., Kim, H., and Choi, W. (2023). Tutorial on time series prediction using 1D-CNN and BiLSTM: a case example of peak electricity demand and system marginal price prediction. Eng. Appl. Artif. Intell. 126, 106817. doi:10.1016/j.engappai.2023.106817

CrossRef Full Text | Google Scholar

Li, X., Yuan, C., and Wang, Z. (2020). State of health estimation for Li-ion battery via partial incremental capacity analysis based on support vector regression. Energy 203, 117852. doi:10.1016/j.energy.2020.117852

CrossRef Full Text | Google Scholar

Li, R., Li, W., and Zhang, H. (2022). State of health and charge estimation based on adaptive boosting integrated with particle swarm optimization/support vector machine (AdaBoost-PSO-SVM) model for lithium-ion batteries. Int. J. Electrochem. Sci. 17 (2), 220212. doi:10.20964/2022.02.03

CrossRef Full Text | Google Scholar

Liu, W., Placke, T., and Chau, K. T. (2022). Overview of batteries and battery management for electric vehicles. Energy Rep. 8, 4058–4084. doi:10.1016/j.egyr.2022.03.016

CrossRef Full Text | Google Scholar

Liu, S., Nie, Y., Tang, A., Li, J., Yu, Q., and Wang, C. (2023). Online health prognosis for lithium-ion batteries under dynamic discharge conditions over wide temperature range. eTransportation 18, 100296. doi:10.1016/j.etran.2023.100296

CrossRef Full Text | Google Scholar

Liu, H., Deng, Z., Che, Y., Xu, L., Wang, B., Wang, Z., et al. (2024). Big field data-driven battery pack health estimation for electric vehicles: a deep-fusion transfer learning approach. Mech. Syst. Signal Process. 218, 111585. doi:10.1016/j.ymssp.2024.111585

CrossRef Full Text | Google Scholar

Liu Z., Z., Wang, Y., Vaidya, S., Ruehle, F., Halverson, J., Soljačić, M., et al. (2024) KAN: Kolmogorov-arnold networks. arXiv. Available at: http://arxiv.org/abs/2404.19756.

Google Scholar

Ma, B., Yang, S., Zhang, L., Wang, W., Chen, S., Yang, X., et al. (2022). Remaining useful life and state of health prediction for lithium batteries based on differential thermal voltammetry and a deep-learning model. J. Power. Sources 548, 232030. doi:10.1016/j.jpowsour.2022.232030

CrossRef Full Text | Google Scholar

Rojas, O. E., and Khan, M. A. (2022). A review on electrical and mechanical performance parameters in lithium-ion battery packs. J. Clean. Prod. 378, 134381. doi:10.1016/j.jclepro.2022.134381

CrossRef Full Text | Google Scholar

Tian, J., Xiong, R., and Shen, W. (2020). State-of-Health estimation based on differential temperature for lithium ion batteries. IEEE Trans. Power Electron. 35 (10), 10363–10373. doi:10.1109/TPEL.2020.2978493

CrossRef Full Text | Google Scholar

Tran, M.-K., Mathew, M., Janhunen, S., Panchal, S., Raahemifar, K., Fraser, R., et al. (2021). A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 43, 103252. doi:10.1016/j.est.2021.103252

CrossRef Full Text | Google Scholar

Wang, Y., Tian, J., Sun, Z., Wang, L., Xu, R., Li, M., et al. (2020). A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 131, 110015. doi:10.1016/j.rser.2020.110015

CrossRef Full Text | Google Scholar

Wang, S., Liu, K., Wang, Y., Stroe, D.-I., Fernandez, C., and Guerrero, J. M. (2022). Multidimensional lithium-ion battery status monitoring. 1st ed. Boca Raton, FL: CRC Press, 23. doi:10.1201/9781003333791

CrossRef Full Text | Google Scholar

Wang, C., Wang, R., Zhang, C., and Yu, Q. (2024). Coupling effect of state of charge and loading rate on internal short circuit of lithium-ion batteries induced by mechanical abuse. Appl. Energy 375, 124138. doi:10.1016/j.apenergy.2024.124138

CrossRef Full Text | Google Scholar

Xiong, R., Li, L., Li, Z., Yu, Q., and Mu, H. (2018). An electrochemical model based degradation state identification method of Lithium-ion battery for all-climate electric vehicles application. Appl. Energy 219, 264–275. doi:10.1016/j.apenergy.2018.03.053

CrossRef Full Text | Google Scholar

Xu, Z., Wang, J., Lund, P. D., and Zhang, Y. (2022). Co-estimating the state of charge and health of lithium batteries through combining a minimalist electrochemical model and an equivalent circuit model. Energy 240, 122815. doi:10.1016/j.energy.2021.122815

CrossRef Full Text | Google Scholar

Xu, R., Wang, Y., and Chen, Z. (2023). A hybrid approach to predict battery health combined with attention-based transformer and online correction. J. Energy Storage 65, 107365. doi:10.1016/j.est.2023.107365

CrossRef Full Text | Google Scholar

Yang, S., Zhang, C., Jiang, J., Zhang, W., Gao, Y., and Zhang, L. (2021a). A voltage reconstruction model based on partial charging curve for state-of-health estimation of lithium-ion batteries. J. Energy Storage 35, 102271. doi:10.1016/j.est.2021.102271

CrossRef Full Text | Google Scholar

Yang, S., Zhang, C., Jiang, J., Zhang, W., Zhang, L., and Wang, Y. (2021b). Review on state-of-health of lithium-ion batteries: characterizations, estimations and applications. J. Clean. Prod. 314, 128015. doi:10.1016/j.jclepro.2021.128015

CrossRef Full Text | Google Scholar

Yang, Y., Xu, Y., Nie, Y., Li, J., Liu, S., Zhao, L., et al. (2024). Deep transfer learning enables battery state of charge and state of health estimation. Energy 294, 130779. doi:10.1016/j.energy.2024.130779

CrossRef Full Text | Google Scholar

Ye, L., Peng, D., Xue, D., Chen, S., and Shi, A. (2023). Co-estimation of lithium-ion battery state-of-charge and state-of-health based on fractional-order model. J. Energy Storage 65, 107225. doi:10.1016/j.est.2023.107225

CrossRef Full Text | Google Scholar

Yu, Q., Nie, Y., Peng, S., Miao, Y., Zhai, C., Zhang, R., et al. (2023). Evaluation of the safety standards system of power batteries for electric vehicles in China. Appl. Energy 349, 121674. doi:10.1016/j.apenergy.2023.121674

CrossRef Full Text | Google Scholar

Zhang, C., Luo, L., Yang, Z., Du, B., Zhou, Z., Wu, J., et al. (2024). Flexible method for estimating the state of health of lithium-ion batteries using partial charging segments. Energy 295, 131009. doi:10.1016/j.energy.2024.131009

CrossRef Full Text | Google Scholar

Zhang, C., Zhu, Y., Dong, G., and Wei, J. (2019). Data-driven lithium-ion battery states estimation using neural networks and particle filtering. Int. J. Energy Res. 43 (14), er.4820–8241. doi:10.1002/er.4820

CrossRef Full Text | Google Scholar

Zhang, S., Guo, X., Dou, X., and Zhang, X. (2020). A rapid online calculation method for state of health of lithium-ion battery based on coulomb counting method and differential voltage analysis. J. Power Sources 479, 228740. doi:10.1016/j.jpowsour.2020.228740

CrossRef Full Text | Google Scholar

Zhang, C., Zhao, S., Yang, Z., and Chen, Y. (2022). A reliable data-driven state-of-health estimation model for lithium-ion batteries in electric vehicles. Front. Energy Res. 10, 1013800. doi:10.3389/fenrg.2022.1013800

CrossRef Full Text | Google Scholar

Zhang, C., Zhao, S., Yang, Z., and He, Y. (2023a). A multi-fault diagnosis method for lithium-ion battery pack using curvilinear Manhattan distance evaluation and voltage difference analysis. J. Energy Storage 67, 107575. doi:10.1016/j.est.2023.107575

CrossRef Full Text | Google Scholar

Zhang, C., Luo, L., Yang, Z., Zhao, S., He, Y., Wang, X., et al. (2023b). Battery SOH estimation method based on gradual decreasing current, double correlation analysis and GRU. Green Energy Intelligent Transp. 2 (5), 100108. doi:10.1016/j.geits.2023.100108

CrossRef Full Text | Google Scholar

Zhang, Z., Ji, C., Liu, Y., Wang, Y., Wang, B., and Liu, D. (2024). Effect of aging path on degradation characteristics of lithium-ion batteries in low-temperature environments. Batteries 10 (3), 107. doi:10.3390/batteries10030107

CrossRef Full Text | Google Scholar

Zhao, J., Feng, X., Pang, Q., Fowler, M., Lian, Y., Ouyang, M., et al. (2024). Battery safety: machine learning-based prognostics. Prog. Energy Combust. Sci. 102, 101142. doi:10.1016/j.pecs.2023.101142

CrossRef Full Text | Google Scholar

Zheng, Y., Cui, Y., Han, X., and Ouyang, M. (2021). A capacity prediction framework for lithium-ion batteries using fusion prediction of empirical model and data-driven method. Energy 237, 121556. doi:10.1016/j.energy.2021.121556

CrossRef Full Text | Google Scholar

Zhu, Y., Gu, X., Liu, K., Zhao, W., and Shang, Y. (2024). Rapid test and assessment of lithium-ion battery cycle life based on transfer learning. IEEE Trans. Transp. Electrification, 1. doi:10.1109/TTE.2024.3354107

CrossRef Full Text | Google Scholar