Impact of the power-controlled static synchronous machine on transient stability of power system

Compared with the grid-following (GFL)-converter-interfaced generations (CIG), the power-controlled static synchronous machine (PCSSM) can realize voltage and frequency control through the power tracking function, which has the potential to improve the transient stability of the power system. However, the evolution trend of transient stability of power systems with integrated power-controlled static synchronous machine is still unknown. This paper studies the transient stability characteristic of power systems after replacing synchronous generators (SGs) with the PCSSM. The PCSSM and GFL-CIG are integrated into the New England IEEE 39-bus test system, respectively. Firstly, we compare the transient stability of the PCSSM-integrated system with the GFL-CIG-integrated system by changing Converter-interfaced generation’s integration proportions and locations. Then, the impact of equivalent inertia coefficient J and damping coefficient D on the transient stability of the PCSSM-integrated system is analyzed. Finally, the advantages of PCSSM compared to GFL-CIG are compared and summarized.

1 Introduction

With the solid advancement of China’s carbon peaking and carbon neutralization scheme (Matevosyan et al., 2022), the installed capacity of new energy represented by wind power and photovoltaics is increasing yearly. According to the national power industry statistics released by the National Energy Administratio (Guo et al., 2022), by the end of 2022, the total installed capacity of photovoltaic-based solar power generation and wind power generation has reached 29.6% of the total installed capacity in China. New energy sources with power electronic converters are becoming the main sources for building new energy power systems in China (Huang et al., 2021; Liu et al., 2020). Meanwhile, the proportion of converter-interfaced generations (CIGs) increases rapidly, which makes the stability of new power systems challenging (Wang et al., 2022).

According to CIGs’ control strategy, they can be divided into grid-following (GFL)-CIGs and grid-forming (GFM)-CIGs (Li et al., 2022), and their external characteristics are current source and voltage source, respectively.

The synchronization of the GFL-CIG tracks the phase of the point of common coupling (PCC) through a phase-locked loop (PLL). Compared with synchronous machines, the advantages of CIGs are sensitive response and flexible control (Taul et al., 2019). The conventional GFL-CIG lacks inertia and damping characteristics. As a result, the integration of GFL-CIG will weaken the inertia and damping characteristics of the integrated power systems (Mansour et al., 2021). PCSSM is improved based on conventional GFL-CIG by adding the synchronous machine emulated loop (SMEL) (Zhang et al., 2022), which can accurately emulate the characteristics of the synchronous machine, making PCSSM equipped with the ability of voltage support and frequency support.

Sufficient research results are on hand for the transient stability study of SGs (Grigsby, 2007), but they cannot be directly applied to the PCSSM due to their different dynamics. Xue et al. (2023) put forward an analytical analysis method for the transient stability of the GFL-CIG-integrated system and analyzed the impact of the injection current of the GFL-CIG on the transient stability of the GFL-CIG-integrated system. Shuai et al. (2018) studied the transient stability of the virtual synchronous generator (VSG) using Lyapunov’s direct method and analyzed the effect of the reactive power control loop on transient stability. Wu and Wang (2020) evaluated the impact of the active power of (GFM)-CIG on the transient stability of a GFM-CIG-integrated power system. Huang et al. (2019) analyzed the transient stabilization mechanism of the sag-controlled CIG based on the equal area method. The above references all adopt the transient stability analysis model to explore the mechanism of transient stability of small-scale CIG-integrated systems. However, for the CIG-integrated muti-machine system, it is difficult to establish an analytical model to analyze its transient stability due to the high-order nonlinearity of multi-machine systems. Some scholars have also applied the artificial intelligence method to transient stability analysis (Zhang et al., 2021), but it needs a long time to be repeated to train the model to achieve its accuracy. The time-domain simulation method can obtain accuracy without the necessity to train the model, and it can accurately and intuitively portray the transient stability characteristics of power systems containing a high percentage of power electronic converters (Hatziargyriou et al., 2020). Hence, this paper adopts electromagnetic transient simulation to qualitatively study the transient stability when one or more PCSSMs are integrated into a multi-machine system.

Li et al. (2020) replaced the SGs with CIGs in a 4-machine system with equal capacity, analyzing how the proportion of CIGs, synchronization mechanism, and grid-connected location affect the transient stability of the AC system based on the time-domain simulation. Guan et al. (2016) analyzed the dynamics of the synchronous generator emulation control strategy, which adopts the frequency-power control, and clarified how controller parameters in the CIG influence the dynamics of the CIG and characteristics of CIG’s interaction with the single machine infinite bus system based on the time-domain simulation. However, the existing theoretical models and simulation analysis on the synchronous machine-emulated CIGs mainly adopt VSG control, droop control, and other control strategies that emulate the characteristics of the SG. It has rarely been reported how PCSSM with SMEL impacts the transient stability of the CIG-integrated system. Besides, it is necessary to clarify the comparison of the transient stability between the PCSSM-integrated system and convential GFL-CIG-integrated system. Hence further investigation is needed.

To fill the gap, this paper analyzes the impact of the PSSM with embedded SMEL on transient stability of power systems for the first time. Integrate the GFL-CIG and PCSSM into the New England IEEE 39-bus test system, respectively. Compare the transient stability of the PCSSM-integrated system with the GFL-CIG-integrated system by changing their integration proportions and locations. Set different coefficients, J, and damping coefficients, D, of the SMEL to illustrate their impact on the transient stability of the power system with integrated PCSSM.

The rest of the paper is organized as follows. The control strategy of PCSSM is described in Section 2. Section 3 Compares the differences in transient stability between a single-PCSSM-integrated system and a single-GFL-CIG-integrated system. Section 4 compares transient stability differences between multi-PCSSM-integrated and multi-GFL-CIG-integrated systems. Section 5 analyzes the impact of the equivalent inertia coefficient and damping coefficient in the PCSSM on the transient stability of the PCSSM-integrated system. Section 6 discusses and concludes the findings of the paper.

2 Control strategy of PCSSM

2.1 The strategy of steady-state operation control in PCSSM

The topology structure and control block diagram of the PCSSM are shown in Supplementary Figure S1. The control strategies of the rectifier side and the inverter side are similar, so we describe the PCSSM based on the single-ended model.

The PCSSM in Supplementary Fig.1 is connected with the point of common connection (PCC) through the transformer and then incorporated into the power system through the line impedance. U_s and i_s represent the voltage and current of the PCC, respectively, and their amplitudes are expressed as I_s and U_s. U_sdq denote the voltage in the dq frame, and m_dq are the voltage modulation value of the PCSSM in the dq frame. I_sdq are the current of the PCC in the dq frame. I_dq^* are the current reference. P_s and Q_s denote the instantaneous active and reactive power of the PCSSM, respectively. P^* and Q^* are their references. θ_pll is the phase angle of u_s generated by the PLL. The DC side of the PCSSM can be equipped with energy storage. The function of the SMEL inside the CIG is to regenerate the internal potential and power angle required for power command calculation when voltage and frequency fluctuate in the system. Therefore, the PCSSM can be equipped with voltage and frequency support capabilities.

Equation 1 obtains the voltage amplitude of PCC, and the output active power P_s and reactive power Q_s of the PCSSM can be calculated according to the instantaneous power theory (Cheng et al., 2020), as shown in Equation 2.

$U_s=\sqrt{{u_{sd}}^2+{u_{sq}}^2}(1)$

$\begin{array}{l}{P}_s=\frac{3}{2}{u}_{sd}{i}_{sd}\\ Q_s=-\frac{3}{2}{u}_{sd}{i}_{sq}\end{array}(2)$

SMEL is used to emulate the operation characteristics of the SG, which comprises a voltage support loop and a frequency support loop. The output of the voltage support loop is used to emulate the transient potential E′_qset of the SG (ignoring the salient pole effect of the SG). The expression is shown as Equation 3.

$E_{qset}^{\prime }=E_{qref}^{\prime }+T_v\left(s\right)\left(U_{\text{ref}}-U_{\mathrm{s}}\right)(3)$

In the formula, E′_qset represents the actual value of the transient potential emulating the operation of the SG, which participates in calculating the outer loop power reference of the PCSSM. U_ref and E′_qref are the references for SG terminal voltage and transient potential, respectively. T_v(s) is the transfer function in the complex frequency domain, which emulates the excitation circuit of SG. We choose the first-order inertia link. The transfer function selection can affect the PCSSM’s steady-state control accuracy and dynamic response performance.

The frequency regulation and rotor balance movement parts in the frequency support loop are shown in Equations 4, 5, respectively.

$P_m=P_{ref}+G_f\left(s\right)\left({\omega }_{ref}-{\omega }_{pll}\right)(4)$

In the formula, P_mref is the reference of the mechanical power, and P_m is the active power used to emulate the operation of the prime motor. ω_ref and ω_pll denote the rated angular frequency and the actual frequency of the PCC tracked by the PLL, respectively, and G_f(s) is the transfer function in the complex frequency domain of the frequency regulator.

${\theta }_{set}={\theta }_{ref}+\frac{1}{s}\cdot \frac{1}{Js+D}\left(P_m-P_s\right)(5)$

In the formula, θ_set is the reference of the power angle emulating the operation of the SG. J and D are the equivalent inertia coefficient and damping coefficient in the process of rotor movement, respectively. Then, according to the E′_qset and θ_set of the above SMEL, the outer loop power command value P_ref and Q_ref can be obtained, as shown in Equations 6, 7, respectively.

$P_{ref}=\frac{E_{qset}^{\prime }{U}_s}{x_d}\sin {\theta }_{set}(6)$

$Q_{ref}=\frac{U_s\left(E_{qset}^{\prime }\cos {\theta }_{set}-U_s\right)}{x_d}(7)$

where x_d is the internal reactance emulating the operation of the SG. With the SMEL, PCSSM can realize voltage support and frequency support.

2.2 The strategy of steady-state operation control in PCSSM

Next, the strategy of fault-current limitation in PCSSM under the fault state is analyzed.

In Supplementary Figure S2, i_dqref are the current references of the PCSSM in the dq frame when PCSSM does not enter the fault-current limitation mode, i_dqfau are the current references in the dq frame as PCSSM enters the fault-current limitation mode, i_dq^* are the final current references of the PCSSM according to the judgment of the bus voltage amplitude U_s. E^′_qfau and θ_fau are the emulated SG’s transient potential and the power angle in the fault-current limitation mode. X^′_d is the transient reactance of the emulated SG. The relationship between the vectors under the fault-current limitation mode is shown in Supplementary Figure S3.

When a short circuit fault occurs on the AC side, the PCSSM detects that the AC bus PCC voltage U_s drops below the set threshold, the switching state will be changed from 0 to 1, as shown in Supplementary Figure S2, which means the working mode will turn to the fault-current limitation mode. At this time, the power command will be simultaneously switched to the fault mode. Under the fault-current limitation mode, the references of the current in the dq frame should satisfy Equation 8. E^′_qfau and θ_fau are obtained from Equation 9.

$\left\{\begin{array}{l}\left|{I_d}^{*}\right|=\left|I_{dfau}\right|=I_{\text{set}}\\ \left|{I_q}^{*}\right|=\left|I_{qfau}\right|=\sqrt{I_{\max }^2-I_{\text{set}}^2}\end{array}\right.(8)$

Where I_dq* are the references of the current in the dq frame, I_set is the default value of the current in the d-axis, and I_max is the magnitude of the current in the fault-current limitation mode. I_dqfau are the currents in the dq frame during fault mode.

$\begin{array}{l}{U}_{sd}=x_d^{\prime }{I}_{qfau}\\ U_{sq}=\sqrt{U_s^2-U_{sd}^2}\\ E_{qfau}^{\prime }=U_{sq}+x_d^{\prime }{I}_{dfau}\\ {\theta }_{fau}=\arctan \left(\frac{U_{sq}}{U_{sd}}\right)\end{array}(9)$

Where x′_d is used to emulate the transient reactance of the SG, and U_sq and U_sd are the components of the AC bus voltage U_s under the d and q axis coordinates. The command values of active and reactive power of the outer loop power under fault-current limitation mode can be obtained by Equations 8, 9, respectively.

$P_{fau}=\frac{E_{qfau}^{\prime }{U}_{\mathrm{s}}}{x_d^{\prime }}\sin {\theta }_{fau}(10)$

$Q_{fau}=\frac{U_s\left(E_{qfau}^{\prime }\cos {\theta }_{fau}-U_{\mathrm{s}}\right)}{x_d^{\prime }}(11)$

3 Comparison of differences in transient stability between a single-PCSSM-integrated system and a single-GFL-CIG-integrated system

Supplementary Figure S4 shows the original New England IEEE 39-bus system. SG contains a prime motor, governor, excitation, and power system stabilizer. The parameters of SG, PCSSM, line, and load can be seen in (Zhang et al., 2022; Xue et al., 2023). In Supplementary Figure S4, N represents the node, and the critical-clearing time (CCT) in this paper is measured at 32s by setting the three-phase short-circuit fault at the specified node in Table 1. In addition, the phase angle difference between the internal potential of each SG and the internal potential of the SG31 is uniformly used as the relative power angle θ of each SG, such as the relative power angle of the 30th SG is expressed as θ₁₀.

Table 1

Table 1. CCT of selected nodes in Original 10 SGs system and single GFL-CIG-integrated system.

Adopt the New England IEEE 39-bus system as a test system (as shown in Supplementary Figure S4). The PCSSM emulates the dynamic characteristics of the SG through the internal SMEL and owns the ability of voltage support and frequency support. Realize CIG integration with the New England IEEE 39-bus system by replacing the SG with CIG in the New England IEEE 39-bus system. To more visually and exactly compare differences in transient stability between a single-PCSSM-integrated system and a single GFL-CIG-integrated system, the active and reactive power output of the CIG on the AC side is equal to the active and reactive power output of the SG before the CIG’s integration.

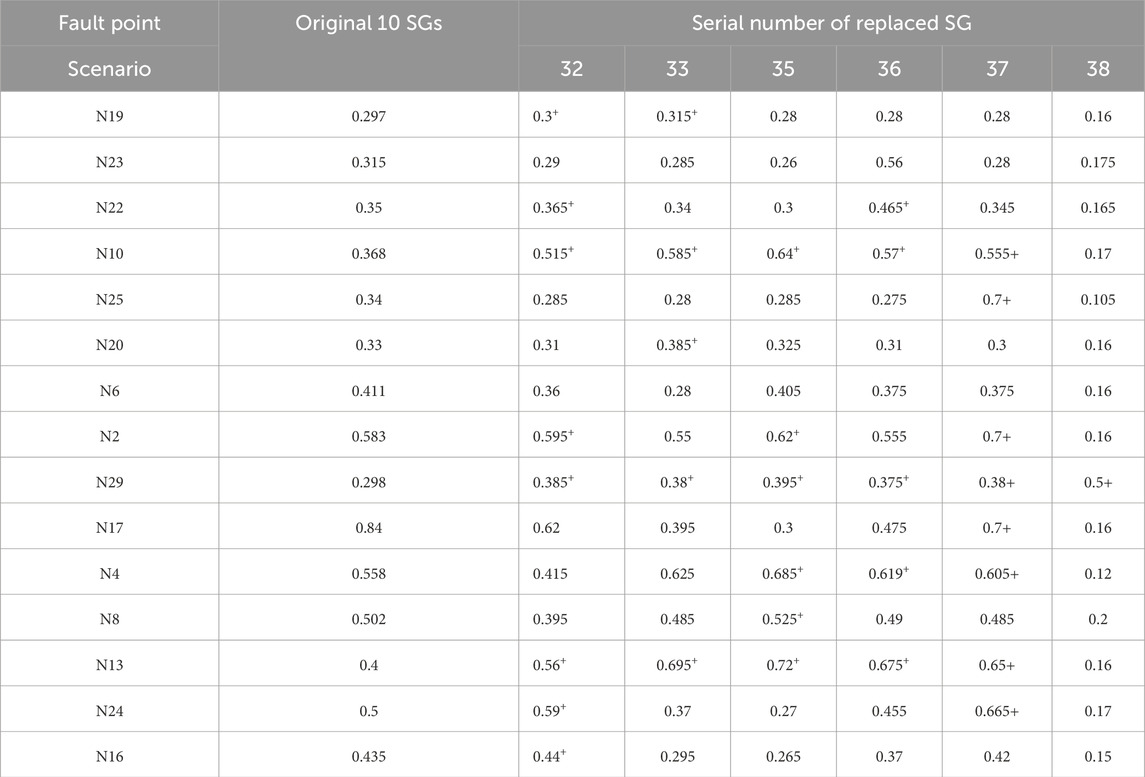
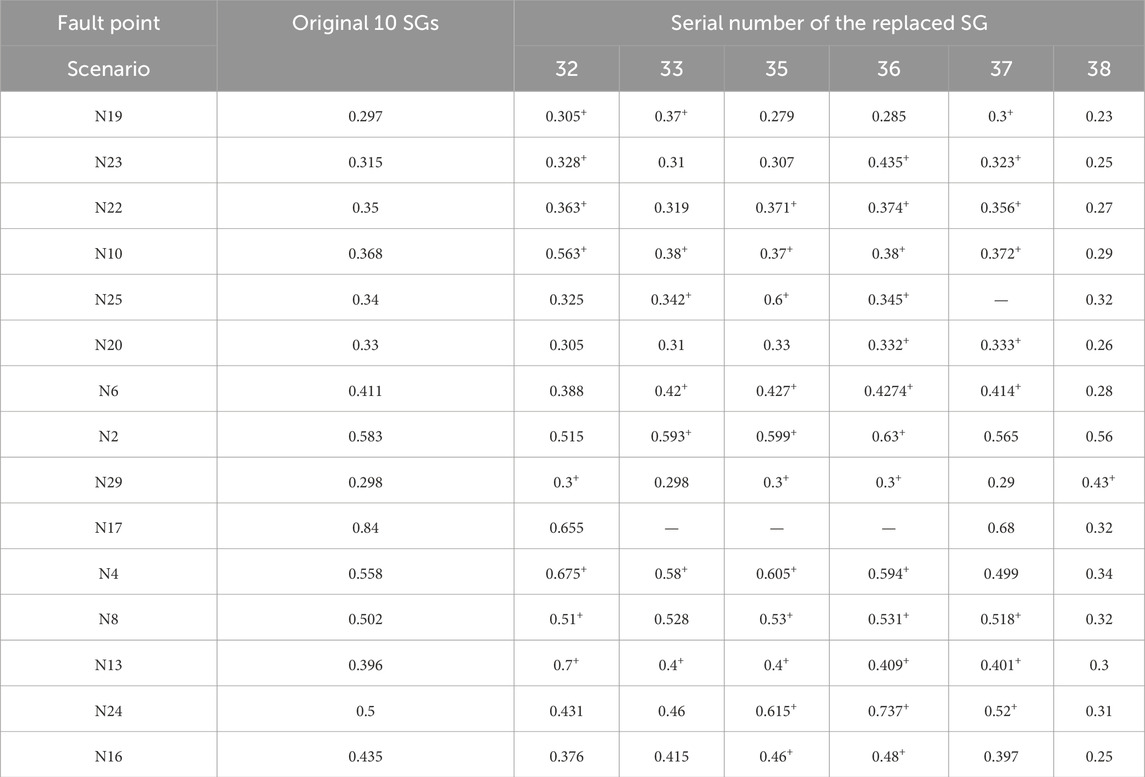
First, only one GFL-CIG or PCSSM is integrated into the New England IEEE 39-bus system. Replace SG32, SG33, SG35, SG36, and SG37,SG38 with CIG (referring in particular to GFL-CIG or PCSSM), respectively, among which the SG33, SG35, and SG36 positions are concentrated, while 32 and 37 positions are far away and relatively dispersed. The three-phase short-circuit fault is applied at each power outlet and nodes 4, 8, 13, 16, and 17, and the CCT of each point is solved based on the electromagnetic transient simulation model in PSCAD/EMTDC, as shown in Tables 1, 2. If the CCT exceeds 1s, it is represented as “/”. The CCT of the node enhanced by CIG is marked with “+” in the upper right corner.

(1) The unit of the CCT is “s”, if the CCT exceeds 1s, it is represented as “/”.

(2) The CCT of the node enhanced by CIG is marked with “+” in the upper right corner.

Table 2

Table 2. CCT of selected nodes in Original 10 SGs system and single-PCSSM-integrated system.

“+” represents a longer delay of CCT, which means the enhancement of transient stability between the generators after the CIG’s integration. Compare differences in transient stability between a single-PCSSM-integrated system and a single-GFL-CIG-integrated system, the “+” area of the single-PCSSM-integrated system is significantly more than the single-GFL-CIG-integrated system, which reveals transient stability of a single-PCSSM-integrated system is more robust than that of a single-GFL-CIG-integrated system. Besides, it can be found that the “+” area is mainly concentrated in the integration area of the GFL-CIG or PCSSM. This proves that the integration of PCSSM primarily affects the transient stability of the integration area and can not improve the transient stability of the whole system. In the New England IEEE 39-bus system, the transient stability of the region can be enhanced by integrating the PCSSM, e.g., before PCSSM’s integration, the CCT of N19 is 0.297s. After the PCSSM replaces the SG33, the CCT of N19 is extended to 0.37s, representing that the transient stability of N19 has been boosted.

The short-circuit ratio (SCR) can be used to measure the magnitude of the grid strength (Zheng, 2022). SCR is defined as the ratio of the short-circuit capacity S_N of the AC bus to the rated DC power P_dN of the CIG. SCR can be expressed as Equation 12:

$SCR=\frac{S_{\text{sc}}}{P_{\mathrm{d}N}}=\frac{1}{\left|Z\right|}(12)$

Z is the equivalent impedance from the AC system to the AC bus.The reference impedance Z_acb of the AC system can be calculated by U_N²/P_dN, U_N is the reference voltage of AC system. Therefore, SCR can also be expressed as Equation 13:

$SCR=\frac{1}{\left|Z\right|/Z_{\text{acb}}}=\frac{1}{\left|Z_{pu}\right|}(13)$

The SCR is inversely related to the nominal value of the equivalent impedance |Z_pu|.

Based on Equation 13, We calculated the SCR for each of the six CIG’s integration position in Table1 and Table 2. Which is shown in Table 3.

Table 3

Table 3. SCR for each of the six CIG’s integration position.

Since the SCR can be used to characterize the magnitude of the grid strength, in Table 3, we can find that N25 has the highest grid strength among the six nodes and N29 has the lowest grid strength among the six nodes. Among six conditions, when the GFL-CIG replaces the SG37, i.e., the GFL-CIG is integrated with N25, the CCT of most nodes in the integrated system extends more compared to integrating the GFL-CIG with the other five nodes respectively, which indicates that integrating the GFL-CIG into the node with higher grid strength can improve the transient stability of the AC system more obviously. While when the GFL-CIG is integrated with the N29 with lower grid strength, the transient stability of the integrated system decreases significantly compared to integrating the GFL-CIG with the other five nodes respectively. Therefore, when the GFL-CIG is integrated with the node with higher grid strength, there is an improvement in the transient stability of the integrated system, but when the GFL-CIG is integrated with the node with comparatively lower grid strength, there may be a negative impact on the transient stability of the integrated system. For PCSSM-integrated system, when the PCSSM is integrated with N25, which has a higher grid strength, is not much different from PCSSM’s integration with other nodes. However, when the PCSSM is integrated with N29, which has a comparatively lower grid strength, the transient stability of the integrated system is decreased, but the decline is less than the GFL-CIG’s integration.

4 Comparison of the transient stability of the multi-PCSSM-integrated system with that of the multi-GFL-CIG-integrated system

After verifying that the transient stability of the single-PCSSM-integrated system is better than the single-GFL-CIG-integrated system, we gradually increase the integration number of the PCSSM and the GFL-CIG to analyze whether the PCSSM still has the advantage over GFL-CIG in improving the transient stability of the system as the integration number of CIG increases.

(1) The unit of the CCT is “s”, if the CCT exceeds 1s, it is represented as “/”.

(2) The CCT of the node enhanced by CIG is marked with “+” in the upper right corner.

4.1 Transient stability of the power system when adjacent SGs are replaced by PCSSMs or GFL-CIGs

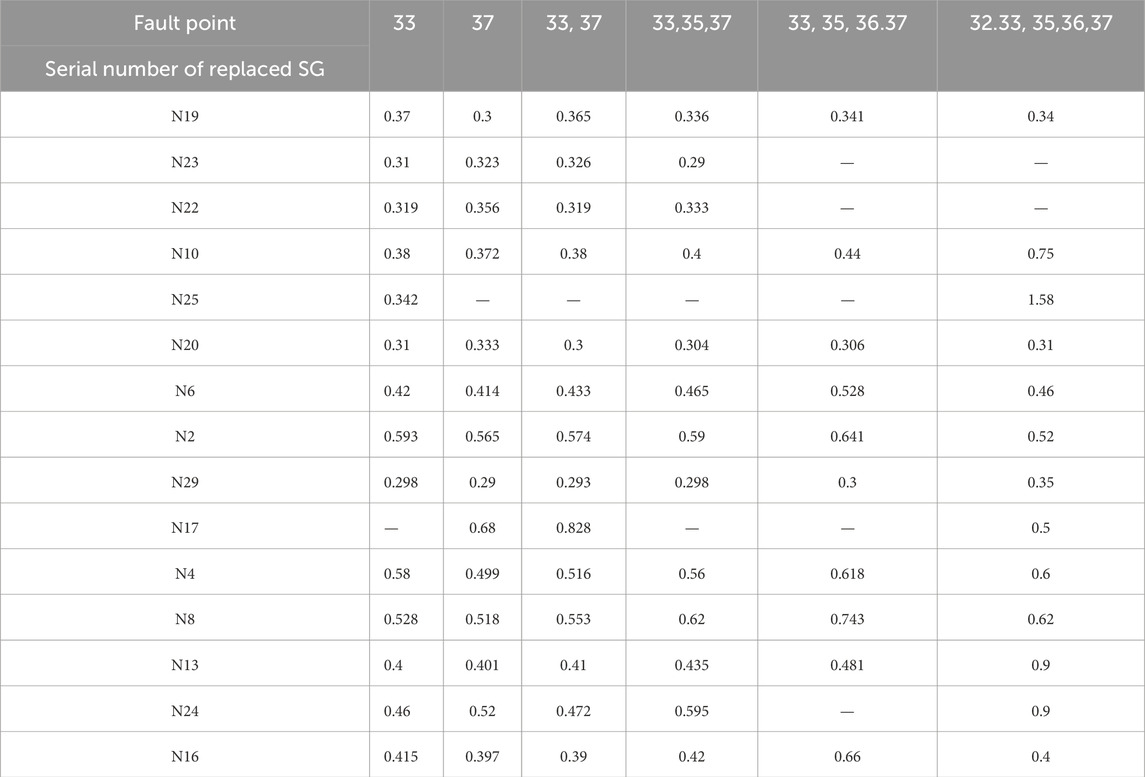
During the integration of CIGs, we find that if GFL-CIGs are integrated into adjacent locations, the CCT of some nodes in the multi-GFL-CIG-integrated system will significantly reduce. Take N24 as an example. When GFL-CIGs replace SG33, SG35, and SG36 simultaneously, the CCT of N24 is reduced to 0.022s. However, if the above SGs are replaced by PCSSM, the CCT at this point is extended to be greater than 1s. Table 4 shows the CCT of the power system in the scene where the replaced SGs containing adjacent SG35 and SG36 in the New England IEEE 39-bus system.

Table 4

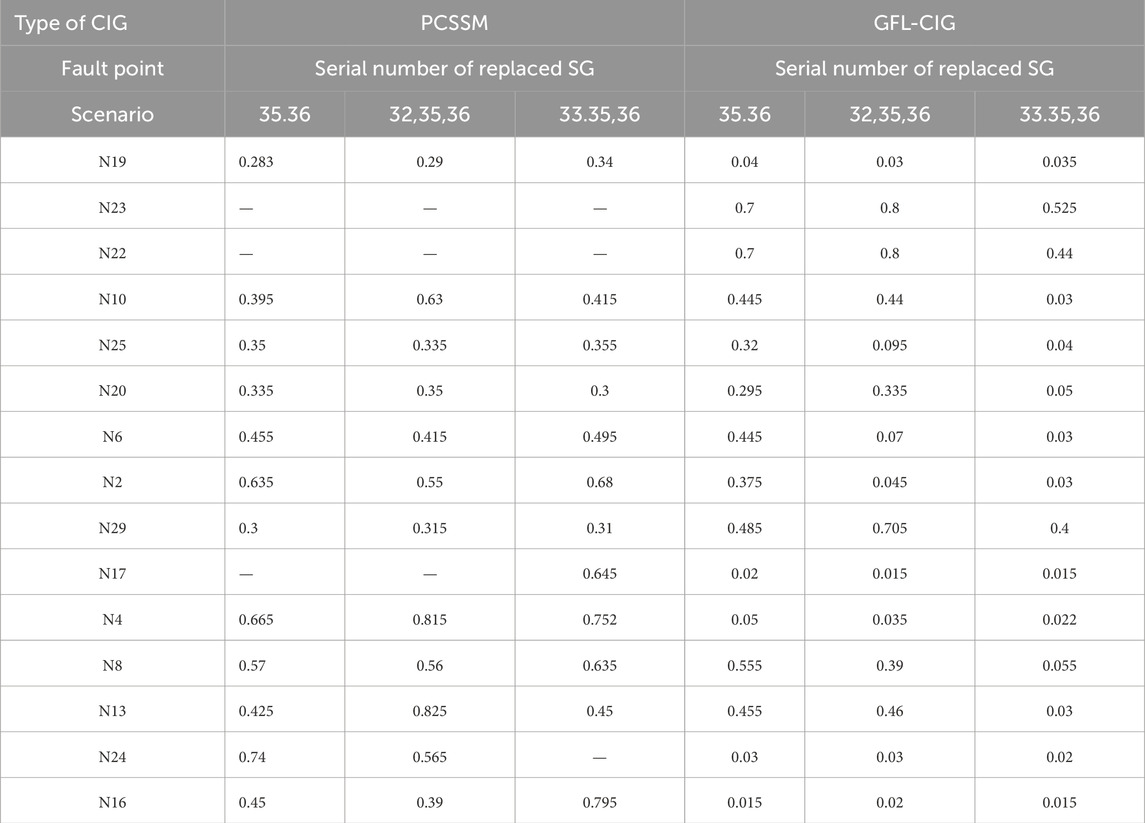
Table 4. CCT of selected nodes in multi-PCSSM-integrated system and Multi-GFL-CIG-integrated system.

When PCSSMs and GFL-CIGs replace SG 33, SG35, and SG36 into the system respectively, a three-phase short-circuit fault of 0.022s is set at N24 adjacent to the three PCSSMs, and the active power, reactive power, voltage, and internal frequency of PLL in PCSSMs or GFL-CIGs curves of the exit bus at the integration’s position of each PCSSM or GFL-CIG are obtained as shown in Supplementary Figure S5. It can be seen that the advantage of PCSSM over GFL-CIG in improving the transient stabilization capability of the system is mainly reflected in the voltage support and frequency support of PCSSM to the system.

When a three-phase short-circuit fault occurs at N24 in PCSSMs-integrated system, as the PCSSM is equipped with a voltage support loop, the three PCSSMs in the system will increase the reactive power, as is shown in Supplementary Figure S5D–F, which can reduce the degree of the system voltage drop, as shown in Supplementary Figure S5A–C. In the PCSSMs-integrated system and GFL-CIGs-integrated system, the PCSSMs or GFL-CIG connected to N35 and N36 cannot send out active power due to the occurrence of the three-phase short-circuit fault Supplementary Figure S6D–E, resulting in the rise of its bus frequency as shown in Supplementary Figure S6A, B, while the PCSSM connected to N33, can reduce its active output to inhibit the rise of the frequency due to its internal frequency support loop, as shown in Supplementary Figure S6C after sensing the rise of the bus frequency at N33 as shown in Supplementary Figure S6F.

Taking another fault as an example, observe the fault response characteristics of the multi-PCSSM-integrated and multi-GFL-CIG-integrated systems to compare their differences in transient stability. Replace the SG33, SG35, and SG36 with the GFL-CIG and apply 0.01s and 0.025s three-phase short-circuit faults to N4, respectively.

To analyze the impact of GFL-CIGs’ integration on the transient stability of the system, this paper choose SG32 to be typical of SGs and GFL-CIG35 to be typical of the integrated GFL-CIGs. As is seen from Supplementary Figure S7, when we set 0.01s three-phase short-circuit fault at N4 at 32s, the active power of the SG32 and GFL-CIG35 will drop quickly during the fault in the Supplementary Figure S7E, multi-GFL-CIG-integrated system can keep stable when the system suffering from 0.01s three-phase short-circuit fault at N4, there is no power angle destabilization between SGs in Supplementary Figure S7E, and PLL of the GFL-CIG35 does not appear to be out of lock as the actual current and voltage in the dq frame of the GFL-CIG35 can still follow their current references in Supplementary Figure S7A, B. The voltage drop of the bus at the exit of the GFL-CIG35 is almost the same with that of SG32, as shown in Supplementary Figure S7F. The excitation system of the SG32 functions and generates reactive power during voltage drops, but the GFL-CIG35 can not act for voltage drop and its reactive power of GFL-CIG35 fluctuates greatly in Supplementary Figure S7D. If the three-phase short-circuit fault duration is extended to 0.02s, it will be found that the SG34, which is close to the fault point, begins to appear power angle dissipation and instability, which is shown in Supplementary Figure S8C, and the PLL of the GFL-CIG35 is out of the lock as the actual current and voltage in the dq frame far exceeds their current reference, as shown in Supplementary Figure S8A, B. The fault response characteristics of the system are poor in Supplementary Figure S8D–F. It indicates that the transient stability of the system deteriorates significantly after the SG33, SG35, and SG36 are replaced by the GFL-CIG.

Replace SG33, SG35, and SG36 with PCSSMs, and apply 0.025s three-phase short-circuit fault to get the fault response characteristic of the multi-PCSSM-integrated system as shown in Supplementary Figure S9. Different from the GFL-CIG, PCSSM can generate reactive power to overcome during voltage drops in Supplementary Figure S9D, which therefore improves transient stability of the system. Thus, when suffering from the same fault, in the multi-PCSSM-integrated system, the actual current and voltage in the dq frame of PCSSM35 can still follow their references as shown in Supplementary Figure S9A, B. The system can also maintain good operating characteristics in Supplementary Figure S9B–F, and there will be no power angle destabilization between SGs, as shown in Supplementary Figure S9C. It indicates that when replaced SGs contain SG35 and SG36, which are electrically close, the PCSSM can effectively reduce the risk of PLL unlocking, which is prone to appear in the multi-GFL-CIG-integrated system.

4.2 The influence of PCSSM’s integration proportion on the transient stability of the multi-PCSSM-integrated system

Table 5 shows the CCT of selected nodes in different scenarios where the number of integrated PCSSM increases from one to 5 in the New England IEEE 39-bus system.

(1) The unit of the CCT is “s”, if the CCT exceeds 1s, it is represented as “/”.

(2) The CCT of the node enhanced by CIG is marked with “+” in the upper right corner.

Table 5

Table 5. CCT of selected nodes in the multi-PCSSM-integrated system.

As is seen from Table 5, in most cases, with the increasing proportion of PCSSMs, the CCT of the system is gradually prolonged. It presents that the transient stability of the power system is enhanced when the proportion of PCSSM’s integration increases. Next, analyze the few situations where the transient stability of the power system is aggravated when the integration proportion of PCSSM increases. On condition that the system has replaced the SG33 and SG37 with PCSSM, continuing to replace the SG35 with PCSSM, it is found that the CCT of N23 decreases from 0.326s to 0.29 s after SG35 is replaced. This is because the transient stability of N23 in the SG35-replaced system is the least desirable compared with that in other one-SG-replaced systems (as shown in Table 2), where only a single SG is replaced with a PCSSM. Similarly, when the system replaces the SG33, SG35, SG36, and SG37 with the PCSSM, it is found that the CCT of N16 decreases from 0.66s to 0.4s after replacement. This is because the transient stability of N16 is the weakest in the SG32-replaced system compared with that in other one-SG-replaced systems.

Suppose the influence of the position of CIG integration is excluded. In that case, the integration proportion of PCSSM is positively correlated with the system’s transient stability, i.e., the higher the integration proportion of PCSSM, the stronger the system’s transient stability.

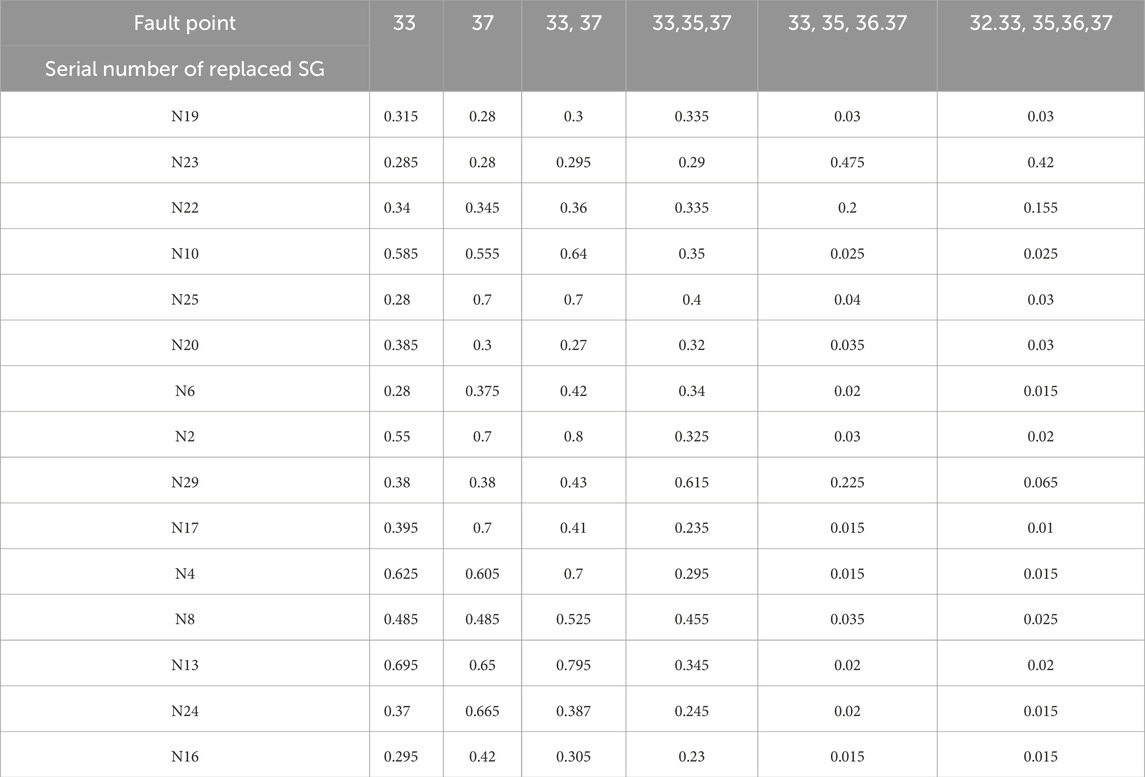
Similarly, Table 6 shows the CCT of selected nodes in different scenarios where the number of integrated GFL-CIG increases from one to 5 in the New England IEEE 39-bus system.

(1) The unit of the CCT is “s”, if the CCT exceeds 1s, it is represented as “/”.

(2) The CCT of the node enhanced by CIG is marked with “+” in the upper right corner.

Table 6

Table 6. CCT of selected nodes in the multi-GFL-CIG-integrated system.

Different from the PCSSM, when the number of integrated GFL-CIG increases from one to 5 in the New England IEEE 39-bus system, the transient stability of the integrated system will be weakened. This is because the GFL-CIG relies heavily on phase-locked loop operation, which externally behaves as a current source, and when the number of integrated GFL-CIG increases, the grid strength will decrease, thus the transient stability of the integrated system will be weakened.

5 Coefficient J and damping coefficient D in the PCSSM on transient stability of the PCSSM-integrated system

The equivalent inertia coefficient J in the SG is a physical quantity related to the size of its rotor. J usually increases (Laaksonen, 2023) with the increase of rated power. After determining the influence factors, such as the rotor size and rated power of the SG, the equivalent inertia coefficient J of the SG and the damping coefficient D remain unchanged. The synchronous machine emulation in PCSSM is realized by digital emulation, the equivalent inertia coefficient J and damping coefficient D in Equation 5 are adjustable parameters. Taking the PCSSM-integrated system, which replaced SG37 with the PCSSM, as an example (as shown in Supplementary Figure S10), the impact of the equivalent inertia coefficient J and the damping coefficient D in the SMEL on the transient stability of PCSSM-integrated system is simulated and analyzed.

Since one of the functions of PLL is to detect the frequency of PCC, the angular frequency of PLL in PCSSM can measure the influence of J value variation on the transient stability of the PCSSM-integrated system. 0.322s three-phase short-circuit fault occurs at N23 (the SG36 bus outlet), and the fixed damping coefficient D is a constant value of 40. Change the equivalent inertia coefficient J, and set J as 0.5, 5, and 10 to obtain the PLL’s angular frequency changes, as shown in Supplementary Figure S11A. When the system is subjected to the same disturbance, J increases from 0.5 to 5, the PLL frequency fluctuation increases slightly, and the frequency of the PCC can finally return to the rated value. At this time, the transient stability of the power system can be maintained. When J increases to 10, the PLL’s angular frequency will oscillate continuously, and its fluctuation is more obvious. It indicates that when the J increases, the transient stability of the PCSSM-integrated system decreases, and the system is more susceptible to external disturbance.

Keep J = 10 and set D as 40, 45, and 50, respectively. The internal PLL’s angular frequency changes of the PCSSM are shown in Supplementary Figure S11B. As seen in Supplementary Figure S11, PLL’s angular frequency oscillation disappears when D is 45, and PLL frequency can be smoothly restored to the rated value. When D is further increased to 50, PLL’s angular frequency fluctuation decreases and tends to be stable after a while. This indicates that with the increase of damping coefficient D, PLL’s angular frequency fluctuation can be effectively reduced, which is conducive to maintaining the transient stability of the PCSSM-integrated system. Next, the influence of the change of J and D parameters on the fault response characteristics of the system is analyzed.

Supplementary Figure S12 shows the PCSSM-integrated system’s dynamic response characteristics when 0.322s three-phase short-circuit fault occurs at N23. Supplementary Figure S12A–C correspond to different values of equivalent inertia coefficient J and damping coefficient D in PCSSM. When 0.322s three-phase short-circuit fault occurs at point N23, the bus voltage will drop sharply, and the active power at the exit of SG36 will drop rapidly to 0. The SG36 will absorb more reactive power to compensate for the voltage drop, as shown in Supplementary Figure S12A, B. After the fault is cleared, the PCSSM can restore the normal operating state in Supplementary Figure S12A, B. Keep D unchanged and let J increase from 5 to 10, Or keep J unchanged and D decrease from 41 to 40. At this time, set the same 0.322s three-phase short-circuit fault at point N23, the PCSSM-integrated system turns unstable as is shown in Supplementary Figure S12C, power angles of SGs sustain oscillation, and the power as well as voltage at the exit of the SG 36 will also be significantly oscillated and unstable, which will spread to other SGs near the fault point, resulting in the oscillation instability between the SGs, as shown in Supplementary Figure S12C.

6 Conclusion

This paper studies the impact of PCSSM on the transient stability of power systems. The advantages of the PCSSM over GFL-CIG in transient stability are compared. The conclusions are summarized as follows.

(1) Both the GFL-CIG and the PCSSM can effectively improve the integrated system’s transient stability when only one CIG is integrated into some specified nodes of the New England IEEE 39-bus system. In contrast, the ability to improve the system transient stability of PSSM is better than that of the GFL-CIG.

(2) When GFL-CIGs are integrated into adjacent locations, PLL in GFL-CIG is extremely prone to lose synchronization, and power systems with multi-GFL-CIG will be oscillatory and unstable after the fault is cleared. The above situation will not occur in the PCSSM-integrated system. In engineering applications, when the adjacent position needs to be configured with new energy sources, PCSSM may have more vital adaptability in this scenario.

(3) Excluding the impact of PCSSM’s integration position, when PCSSMs are integrated into the muti-machine system like the New England IEEE 39-bus system, the integration proportion of PCSSM is positively correlated with the transient stability of the system, i.e., the greater the integration proportion of PCSSM, the stronger the transient stability of the integration system.

(4) When only one PCSSM is integrated into the New England IEEE 39-bus system, the Equivalent inertia coefficient J decreases, and the damping coefficient D of the PCSSM increases, the transient stability of the integration system will be stronger.

The conclusions drawn in this paper can provide a reference for further theoretical research on the transient stability of large-scale power grids with high penetration of CIGs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LQ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. ZZ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. XY: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. XZ: Writing–original draft, Writing–review and editing, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1470006/full#supplementary-material

References

Cheng, H., Shuai, Z., Shen, C., Liu, X., Li, Z., and Shen, Z. J. (2020). Transient angle stability of paralleled synchronous and virtual synchronous generators in islanded microgrids. IEEE Trans. Power Electron. 35 (8), 8751–8765. doi:10.1109/tpel.2020.2965152

CrossRef Full Text | Google Scholar

Grigsby, L. L. (2007). Power system stability and control. Boca Raton, FL: CRC Press.

Google Scholar

Guan, M., Zhang, H., Lou, P., **a, X., Yao, J., and Gu, G. (2016). Analysis of VSC-HVDC station characteristic in synchronous machine emulation. Power Syst. Technol. 40 (06), 1743–1750. doi:10.13335/j.1000-3673.pst.2016.06.020

CrossRef Full Text | Google Scholar

Guo, X., Zhu, D., Zou, X., Yang, Y., Kang, Y., Tang, W., et al. (2022). Analysis and enhancement of active power transfer capability for DFIG-based WTs in very weak grid. IEEE J. Emerg. Sel. Top. Power Electron. 10, 3895–3906. doi:10.1109/jestpe.2021.3089235

CrossRef Full Text | Google Scholar

Hatziargyriou, N., Milanovic, J., Rahmann, C., Ajjarapu, V., Canizares, C., Erlich, I., et al. (2020). Definition and classification of power system stability–revisited and extended. IEEE Trans. Power Syst. 36 (4), 3271–3281. doi:10.1109/tpwrs.2020.3041774

CrossRef Full Text | Google Scholar

Huang, L., Xin, H., Wang, Z., Zhang, L., Wu, K., and Hu, J. (2019). Transient stability analysis and control design of droop-controlled voltage source converters considering current limitation. IEEE Trans. Smart Grid 10, 578–591. doi:10.1109/tsg.2017.2749259

CrossRef Full Text | Google Scholar

Huang, S., Yao, J., Pei, J., Chen, S., Luo, Y., and Chen, Z. (2021). Transient synchronization stability improvement control strategy for grid-connected VSC under symmetrical grid fault. IEEE Trans. Power Electron. 37 (5), 4957–4961. doi:10.1109/tpel.2021.3131361

CrossRef Full Text | Google Scholar

Laaksonen, H. (2023). Improvement of power system frequency stability with universal grid-forming battery energy storages. IEEE Access 11, 10826–10841. doi:10.1109/access.2023.3241229

CrossRef Full Text | Google Scholar

Li, X., Xu, Z., and Zhang, Z. (2020). Electromagnetic transient simulation study on transient stability of AC power grid with non-synchronous machine sources. Electr. Power Autom. Equip. 40 (09), 57–68. doi:10.16081/j.epae.202009020

CrossRef Full Text | Google Scholar

Li, Y., Gu, Y., and Green, T. C. (2022). Revisiting grid-forming and grid-following inverters: a duality theory. IEEE Trans. Power Syst. 37 (6), 4541–4554. doi:10.1109/tpwrs.2022.3151851

CrossRef Full Text | Google Scholar

Liu, Y., Yao, J., Pei, J., Zhao, Y., Sun, P., Zeng, D., et al. (2020). Transient stability enhancement control strategy based on improved PLL for grid connected VSC during severe grid fault. IEEE Trans. Energy Convers. 36 (1), 218–229. doi:10.1109/tec.2020.3011203

CrossRef Full Text | Google Scholar

Mansour, M. Z., Me, S. P., Hadavi, S., Badrzadeh, B., Karimi, A., and Bahrani, B. (2021). Nonlinear transient stability analysis of phased-locked loop-based grid-following voltage-source converters using Lyapunov’s direct method. IEEE J. Emerg. Sel. Top. Power Electron. 10 (3), 2699–2709. doi:10.1109/JESTPE.2021.3057639

CrossRef Full Text | Google Scholar

Matevosyan, J., MacDowell, J., Badrzadeh, B., Cheng, C., Dutta, S., Rao, S. D., et al. (2022). “Grid-forming technology in energy systems integration,” in ESIG high share of inverter-based generation task force: report.

Google Scholar

Shuai, Z., Shen, C., Liu, X., Li, Z., and Shen, Z. J. (2018). Transient angle stability of virtual synchronous generators using Lyapunov’s direct method. IEEE Trans. Smart Grid 10 (4), 4648–4661. doi:10.1109/tsg.2018.2866122

CrossRef Full Text | Google Scholar

Taul, M. G., Wang, X., Davari, P., and Blaabjerg, F. (2019). An overview of assessment methods for synchronization stability of grid-connected converters under severe symmetrical grid faults. IEEE Trans. Power Electron. 34 (10), 9655–9670. doi:10.1109/tpel.2019.2892142

CrossRef Full Text | Google Scholar

Wang, T., Ji, T., Jiao, D., Li, Y., and Wang, Z. (2022). Transient synchronization stability analysis of PLL-based VSC using Lyapunov’s direct method. Int. J. Electr. Power and Energy Syst. 141, 108135. doi:10.1016/j.ijepes.2022.108135

CrossRef Full Text | Google Scholar

Wu, H., and Wang, X. (2020). A mode-adaptive power-angle control method for transient stability enhancement of virtual synchronous generators. IEEE J. Emerg. Sel. Top. power Electron. 8 (2), 1034–1049. doi:10.1109/jestpe.2020.2976791

CrossRef Full Text | Google Scholar

Xue, Y., Zhang, Z., Zhang, N., Hua, W., Wang, G., and Xu, Z. (2023). Transient stability analysis and enhancement control strategies for interconnected AC systems with VSC-Based generations. Int. J. Electr. Power and Energy Syst. 149, 109017. doi:10.1016/j.ijepes.2023.109017

CrossRef Full Text | Google Scholar

Zhang, Y., Zhao, Q., Tan, B., and Yang, J. (2021). A power system transient stability assessment method based on active learning. J. Eng. 2021 (11), 715–723. doi:10.1049/tje2.12068

CrossRef Full Text | Google Scholar

Zhang, Z., Xue, Y., and Xu, Z. (2022). Versatile static synchronous machine and its reference machine following control strategy. IET Renew. Power Gener. 16 (15), 3184–3196. doi:10.1049/rpg2.12567

CrossRef Full Text | Google Scholar

Zheng, X. U. (2022). Reasonable definition and calculation method of power grid strength under the back ground of new type power systems. High. Volt. Eng. 48 (10), 3805–3819.

Google Scholar