- Electric Power Research Institute, State Grid Gansu Electric Power Co., Ltd., Lanzhou, China
The exponential proliferation of renewable energy has resulted in a significant mismatch between power supply and demand, especially during extreme events. This incongruity presents challenges in efficiently harnessing renewable energy and enhancing the resilience of the power grid. To address this issue, this paper proposes shared energy storage (SES) planning based on the adaptive alternating direction method of multipliers (AADMM). The objective is to fully leverage SES, enhance the local consumption level of renewable energy, ensure power grid resilience, and reduce operational costs. First, to ensure the effective utilization of SES while minimizing initial investment and construction costs, a planning model for SES is formulated. Secondly, to maximize the benefits for multiple prosumers within the renewable energy and SES station, a profit maximization model for multiple prosumers is established. Lastly, to guarantee the privacy security of SES and multi-prosumers while optimizing computational efficiency, a distributed computing model for SES based on AADMM is developed. The results of the example show that the proposed model can not only reduce the cost of 47.96 CNY, but also increase the power self-sufficiency rate by 21.86%. In addition, compared with the traditional distributed optimization, the number of iterations of AADMM is increased by 47.05%, and the computational efficiency is increased by 54.67%. In addition, market prices have a great impact on energy trading, and the impact of market pricing on the operation of the park is not considered in our current research. In this case, our future research aims to consider how to price reasonably between prosumers and between prosumers and SES, so as to realize the stable participation of each subject in the energy market.
1 Introduction
With the continuous advancement of the “dual-carbon” goals, China’s photovoltaic (PV) has experienced rapid development, with large-scale integration into the user-side becoming a future trend (He et al., 2021; Li R. et al., 2024). However, the intermittent and fluctuating characteristics of PV output poses challenges to the stable operation of traditional power grids (Peterssen et al., 2024). Generally, two-part electricity pricing is adopted in PV and energy storage integrated industrial parks. The two-part electricity price can guide prosumers to use electricity during the trough period, so as to smooth the load curve of the power system, reduce the peak load of the system, and improve the stability and power supply capacity of the power system. Energy storage can utilize the peak-valley price difference to store energy, alleviate the impact of PV output fluctuations, and promote the local consumption of PV (Yan et al., 2023). Therefore, the two-part tariff has significant advantages in reducing power supply costs and promoting the rational application of resources.
Existing energy storage business modes are primarily divided into distributed energy storage and shared energy storage (SES) (Abdalla et al., 2023). However, the high initial investment costs and longer payback periods of distributed energy storage impose significant economic pressure on both producers and consumers. Additionally, existing distributed energy storage systems often operate in a “self-storage, self-use” mode, leading to substantial idle energy storage resources on the user-side and revealing significant issues of investment inefficiency, thus failing to achieve maximum utilization efficiency of energy storage systems (Li and Okur, 2023; Wald et al., 2023; Ji et al., 2024). In contrast, SES can complement the load demands of multiple prosumers, enhancing the efficiency of energy storage utilization and fostering a cooperative and mutually beneficial relationship between SES and prosumers (Zhu et al., 2023; Aghdam et al., 2023; Alfaverh et al., 2023). Moreover, SES can distribute the initial investment and construction costs among multiple prosumers, thereby reducing the initial investment risks for each participant. Therefore, promoting energy sharing between SES and prosumers has become the core strategy to enhance the energy efficiency and economic viability of energy parks (Ruan et al., 2024; Xie et al., 2024).
PV and energy storage integrated stations typically comprise multiple prosumers. Existing studies on SES often focus on the centralized optimization of SES and prosumers. For instance, in (Tercan et al., 2022), authors targeted communities by optimizing the capacity of distributed SES on the user-side based on energy sharing, with the objective functions of minimizing investment payback periods and line losses. In (Li L. et al., 2024), industrial parks with different electricity consumption characteristics were analyzed. It investigates energy interaction mechanisms between decentralized SES and multiple industrial users, with the optimization configuration of distributed SES aiming to maximize the overall net profit of multiple users. Additionally, a centralized optimization and scheduling model for multiple parks through electric-thermal mutual aid was proposed in (Liu Z. et al., 2023), effectively improving the overall energy utilization efficiency and operational economics by coupling different energy sources.
In the SES model, information security issues involving various prosumers pose a significant challenge. A widely adopted approach to address such challenges is the alternating direction method of multipliers (ADMM). Each prosumer can use ADMM to independently solve their respective objective utility functions. The Lagrange multipliers are updated based on the constraints, achieving interactive power balance among multiple prosumers, and SES within the PV storage park. For instance, in (Maneesha and Swarup, 2021), the ADMM algorithm was employed to solve a proposed model for the operation of multiple microgrids and obtain global interactive power quantities. Authors in (Sun et al., 2024) introduced an optimized model for combined transmission and distribution units, considering the state of charge constraints for energy storage. This model was decomposed into transmission unit combination models and distribution network economic dispatch models based on distributed optimization theory, with ADMM used for iterative solving. While these studies utilizing ADMM address privacy concerns between participants, they do not fully guarantee the solution efficiency of distributed optimization (Chen et al., 2017). In the process of solving the traditional ADMM, due to the different initial values of the penalty factor, the number of iterations is too numerous and the iteration time is too lengthy. In order to solve the above problems, some literatures propose an adaptive ADMM method to improve the solution efficiency, and the adaptive ADMM improves the distributed convergence speed by changing the penalty factor of each iteration. For example, Zhao et al. (2024) proposes a novel ADMM with adaptive penalty parameter to hedge against wind fluctuation, which further ensures improves the sensitivity of the penalty parameter. Cui et al. (2020) adopts the ADMM with adaptive penalty parameters to solve the energy cooperation between prosumers and community energy storage to improve the convergence performance. The adaptive ADMM (AADMM) promotes the convergence of variables by dynamically adjusting the penalty parameter during the iteration process, thus effectively reducing the dependence of ADMM on the initial value and avoiding the problem of slow convergence caused by improper penalty factor.
To address these issues, this paper proposes a research approach for photovoltaic and energy storage integrated park with SES planning based on the adaptive alternating direction method of multipliers (AADMM). Firstly, an SES capacity planning model is established to ensure the economic feasibility of SES configuration. Secondly, to maximize the benefits for multiple prosumers, an economic model for multiple prosumers is developed based on two-part electricity pricing. Subsequently, AADMM is applied to perform distributed optimization on the established SES capacity planning model and the economic benefit model for multiple prosumers. Finally, simulation verification is conducted in a photovoltaic storage park containing multiple prosumers.
2 Planning of SES under multiple PV stations
Independently configuring energy storage for each prosumer entails challenges such as high configuration costs, low energy storage utilization efficiency, and a reduced on-site consumption rate of new energy sources (Zhang et al., 2024). In contrast, when multiple prosumers with diverse load demands collaborate with SES, they can enhance the on-site consumption level of renewable energy, thereby reducing the operational costs of the PV station integrated park microgrid. Figure 1 illustrates the operational framework of SES in the PV integrated park studied in this paper.
The PV storage park includes N prosumers, each of which is equipped with a separate PV system, and the prosumers and SES are connected to the grid. On the premise that the PV system of the prosumer can meet its own load demand, the excess PV output can be sold to the power grid to increase its own income or stored in the SES for subsequent use; when the prosumer’s PV system cannot meet its own load demand, energy can be purchased from SES or power grid (Zhang et al., 2018). SES is charged during the period when the PV output of prosumers is more and the load demand is less. Discharge in the period of low PV output, high load demand and high electricity price. Therefore, the cost of purchasing electricity from the power grid by the prosumers due to their insufficient PV power generation is reduced. At the same time, the distributed intelligent controller is embedded in the equipment of the energy system, so that the prosumers and SES can control their own energy supply and demand, perform local two-way communication and realize distributed optimization calculation.
2.1 Planning model of SES
In the context of a two-part electricity pricing mechanism, this paper establishes a SES planning model for multiple PV stations with the objective of minimizing overall costs. The approach involves three main steps: initially constructing an optimization configuration model for SES, developing a model aimed at maximizing the benefits of prosumers, and finally, formulating a collaborative SES planning model for PV stations under cooperative conditions.
The configuration of SES entails rational planning to maximize its efficiency and benefits. The objective function Fes for optimizing the configuration include transaction cost with the grid C1, initial installation cost C2, and operational cost C3. The specific calculation formula is as follows:
Regarding transaction costs with the grid, a two-part electricity pricing mechanism is adopted. This mechanism includes both an energy charge based on actual electricity consumption and a demand power charge based on the user’s maximum monthly demand power. SES engages in arbitrage by charging during periods of low electricity prices and discharging during periods of high prices. By shifting load demands, the user’s demand is reduced, consequently lowering costs for the consumer and enhancing the benefits of SES. Therefore, the transaction cost C1 between SES and the grid can be expressed as follows:
where
The initial installation cost of SES, denoted as C2, primarily comprises capacity and power costs (Wang YX. et al., 2024; Wang D. et al., 2024). These two components constitute the main expenses for the initial installation of the SES system and can be expressed as follows:
where
As for operation and maintenance cost of SES, it is closely associated with the charging and discharging power of the system. Variations in SES charging and discharging power directly impact the frequency and complexity of maintenance. Therefore, the operational cost of SES C3 can be expressed as follows:
where
In the process of planning SES, to ensure the stable operation of the PV station, certain inherent constraints must be satisfied (Ma et al., 2022; Jiao et al., 2021). These constraints include the following:
Equation 5 represent the charging and discharging power constraints of the SES, where
2.2 SES planning for multiple PV prosumers sharing
For prosumer n, its operational cost, denoted as Fpv, encompass the transaction costs of buying and selling electricity within time period h. Utilizing the two-part pricing mechanism, the operational cost can be calculated as follows:
where
In order to ensure that the prosumers can stably participate in the operation of the optical storage park, the following constraints need to be met (Zhang et al., 2022; Liu J. et al., 2023).
where Equation 7 represent the non-negativity constraints on the power bought and sold by prosumer n within time period h. Equation 7 ensures that prosumer n cannot purchase and sell electricity at the same time. Equation 7 represents the power balance constraint, where
In order to reduce the operational cost of PV prosumers and optimize SES configuration, collaboration between prosumers and SES is essential. A planning model for minimizing the costs of PV prosumers needs to be established. Here,
where Equation 8 ensures that the energy sharing plan between prosumers and SES is consistent, that is, the energy transmitted to SES by prosumers at the same time h is the same as the energy obtained by SES from prosumers. Similarly, Equation 9 ensures that the prosumer’s payment to SES is consistent with the payment obtained by SES from the prosumer at time h.
Firstly, according to Equations 1–5 and Equations 6–9, we can know the respective cost functions of SES and prosumers when they do not cooperate. Then, according to the payment mechanism of prosumers and SES shown in Equation 9, the overall objective function of SES and prosumers when they cooperate is as follows:
SES needs to meet the following constraints when cooperating with prosumers:
Furthermore, Equation 9 ensures that
3 Distributed optimization model based on AADMM
Assuming
ADMM is a distributed algorithm used for solving large-scale convex optimization problems in statistics, machine learning, and related fields. It offers the advantage of privacy preservation during distributed optimization scheduling. Each prosumer and SES individually solves their respective objective utility functions, achieving interactive energy balance among multiple prosumers and SES within the PV stations. Therefore, to solve the problem via ADMM, the augmented Lagrangian of the SES planning model according to Equation 10 is formulated:
where let
Based on the principles of ADMM, the iterative optimization of Equation 12 is carried out (Chen et al., 2024; Zhang et al., 2021). The specific iteration equation is as follows:
where
According to the definition of ADMM, by giving dual residual
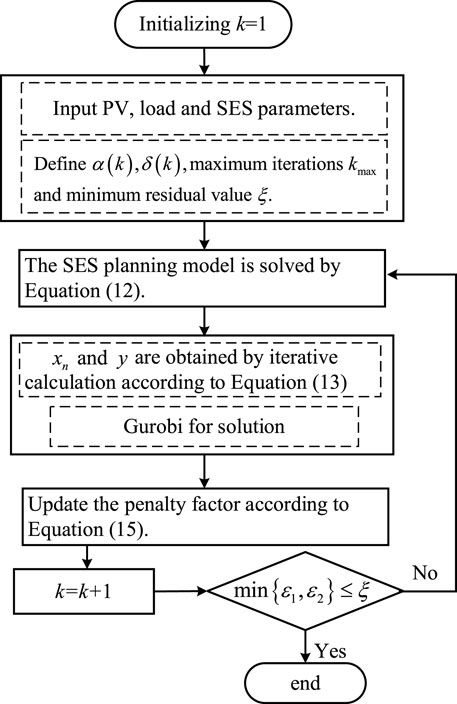
In summary, the distributed solution steps for the SES planning under multiple PV prosumers sharing model based on ADMM are as follows:
Step 1: Initialization: Set the maximum number of iterations
Step 2: Iterative Solution: Utilize Equation 12 to solve the SES planning model for PV prosumers. Employ Equation 13 to iteratively calculate the energy transferred from prosumers to SES, denoted as
Step 3: Convergence Check: Use Equation 14 for convergence testing. If the convergence criterion is met, terminate the computation and output the results. Otherwise, set k = k+1, proceed to step 2 for the next round of iterative optimization, and continue until convergence.
Step 4: Output Results:
In general, the ADMM algorithm is highly sensitive to the choice of penalty parameters, manifested as follows: when the penalty parameter is small, the convergence of Lagrange multipliers is slow, and when it is large, the convergence speed of decision variables is fast. This sensitivity can lead to issues such as excessive iteration counts and prolonged iteration times due to the different initial values chosen for the penalty parameter during the solution process. Therefore, this paper proposes an adaptive adjustment of the penalty parameter size to regulate the convergence speed of Lagrange multipliers and decision variables, aiming to reduce the number of iterations and convergence time in distributed computing. In summary, the adaptive update scheme based on adaptive AADMM is as follows:
where k represents the iteration count, while
In summary, the flow chart of distributed optimization model based on AADMM for SES planning for multiple PV prosumers sharing is shown in Figure 2.
4 Simulation and discussion
4.1 System description and parameter settings
This paper introduces data from five prosumers within a time range of 7:00–19:00, covering a period of 12 h. The load demand curve for prosumers is depicted in Figure 3A, while Figure 3B illustrates the PV output power (Liu et al., 2017). The electricity purchase price from the grid follows a two-part pricing system, where valley periods are 0:00 - 8:00 with electricity price 0.37CNY/kWh, flat periods are 12:00 - 17:00/21:00 - 24:00 with electricity 0.82CNY/kWh, and peak periods are 8:00 12:00/17:00 - 21:00 with electricity price 1.36CNY/kWh. The demand power charge is 38 CNY per month, and the on-grid power is 0.3CNY/kWh. The unit capacity cost of SES is 0.650 CNY/kWh, the unit power cost of SES is 0.245 CNY/kW, SES unit power operational cost is 0.1 CNY/kW, with charging and discharging efficiencies of 0.94 and 1.05, and an energy rate coefficient of 0.3. When using the AADMM algorithm for solution, the algorithm’s iteration precision is set to 0.0001, the penalty parameter is
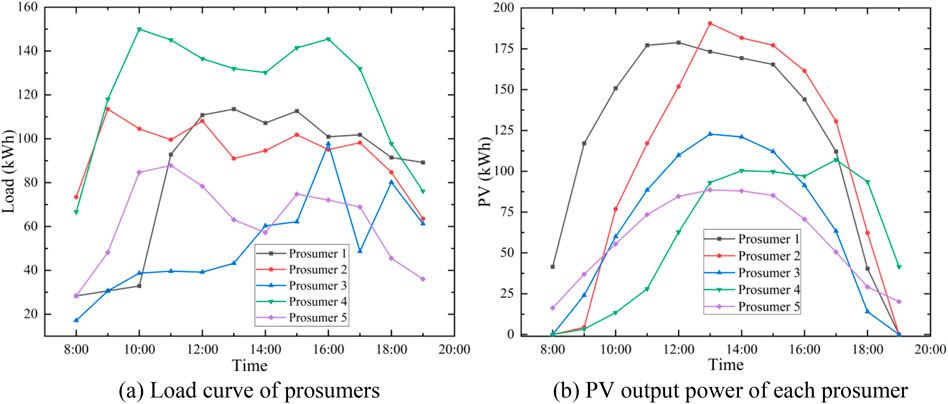
Figure 3. Load and PV characteristics of prosumers. (A) Load curve of prosumers. (B) PV output power of each prosumer.
4.2 Simulation results
When prosumers do not engage in energy cooperation with SES, the net load curve of prosumer is depicted in Figure 4A. When the PV output power of prosumers satisfies the load demand, the excess PV output is sold to the grid. However, when the PV output power is insufficient to meet the load demand, electricity needs to be purchased from the superior grid to fulfill the demand. In this scenario, the utilization efficiency of PV is low, and it fails to achieve maximum energy efficiency and local consumption of PV power, which is easy to cause the power grid reverse heavy overload.
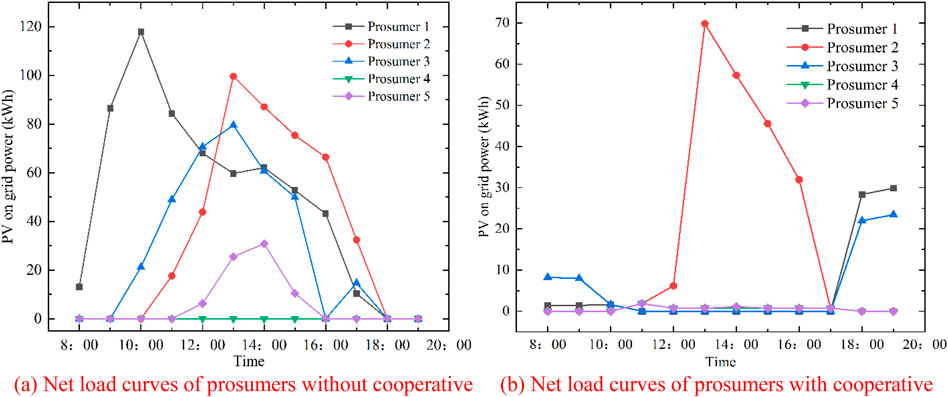
Figure 4. Net load curves of prosumers with and without cooperative. (A) Net load curves of prosumers without cooperative. (B) Net load curves of prosumers with cooperative.
In the energy cooperation mode, SES stores the surplus energy from prosumers’ high PV output, sells excess PV output to the grid after reaching maximum SES capacity, and shares energy with prosumers during periods of low PV output. The on-grid power of PV under energy cooperation between prosumers and SES is illustrated in Figure 4B. Through collaborative energy sharing, the PV grid power for prosumers significantly decreases. For instance, at 13:00-15:00, prosumer 2 has high PV output and low load demand, leading to the surplus PV output being sold to the grid. Overall, energy cooperation redistributes excess PV output to SES, achieving on-site consumption of PV power, and ensuring the resilience operation of the distribution network.
Table 1 presents a comparison of the economic cost for SES and prosumers under non-cooperative and cooperative modes. It is observed that SES, through peak-valley price arbitrage and on-site consumption of PV power, reduces the costs of the PV prosumers and increases the self-sufficiency. The self-sufficiency rate of prosumers increases from 71.05% to 92.91%, and the comprehensive electricity cost decreases from 1090.78 CNY to 1042.82 CNY. This implies that more PV power is locally consumed by prosumers, reducing reliance on traditional power plants, achieving “self-production and self-consumption,” improving energy utilization efficiency, and reducing the overall operational cost, ultimately maximizing energy efficiency. Figure 5 shows the power balance curve of prosumer 1 with or without cooperation. As shown in Figure 5, when there is no cooperation, user 1 can only trade with the power grid, which increases the dependence on the power grid and cannot carry out peak-valley arbitrage. When user 1 cooperates with SES, the user can transfer the excess power to SES.
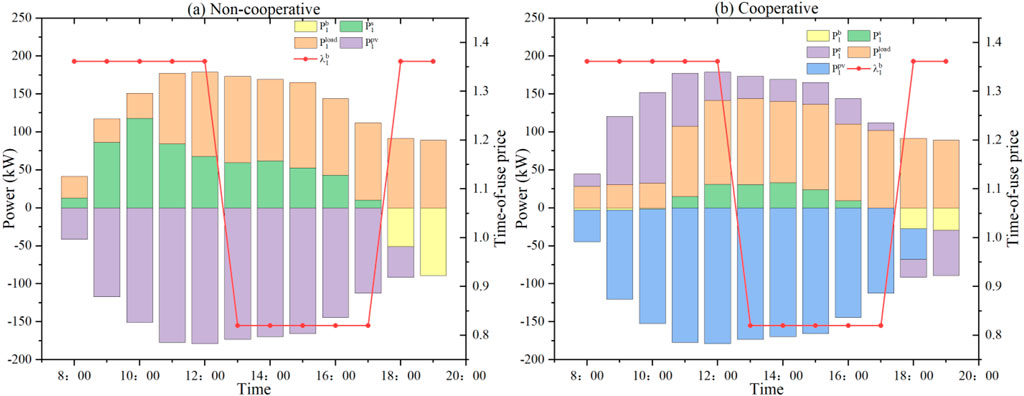
Figure 5. Power balance curve of user 1 with or without cooperation. (A) Non-corrperative. (B) Corrperative.
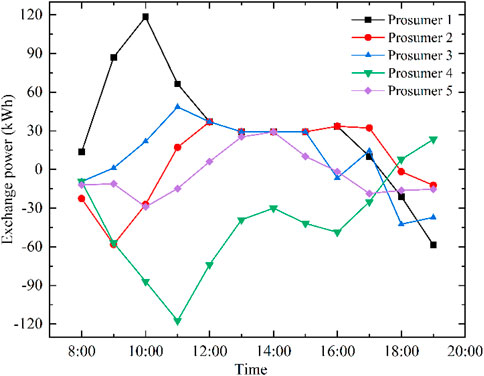
In the energy cooperation mode, the optimal energy-sharing curve among prosumers is illustrated in Figure 6. Prosumer 4, with low PV output and high load demand, absorbs energy to meet the demand. Other prosumers store surplus energy in SES during periods of high PV production for subsequent self-load demands. The SES planning model for the PV station optimizes SES operational scheduling strategies, taking SES state of charge as an optimization parameter to maximize economic benefits. Based on the provided data, the optimal SES capacity configuration is determined to be 333.50 kWh. Taking prosumer 2 as an example, the power optimization results are shown in Figure 7A. When its own PV output cannot meet the load demand, prosumer 2 needs to purchase electricity from the grid or SES. On the contrary, when its own PV output remains after meeting the load demand, prosumer 2 sells the remaining electricity to the grid or transmits it to SES for use by other prosumers. The SES charging and discharging power, along with the state of charge curve, are depicted in Figure 7B. The SES state of charge pattern corresponds to the time-of-use pricing periods, with discharging occurring during peak pricing hours (8:00 -9:00 and 18:00 -19:00) and coinciding with peak pricing periods. Charging occurs during standard pricing hours (13:00 -17:00) and aligns with non-peak pricing periods. The state of charge curve follows the “low charge, high discharge” characteristic typical of SES.
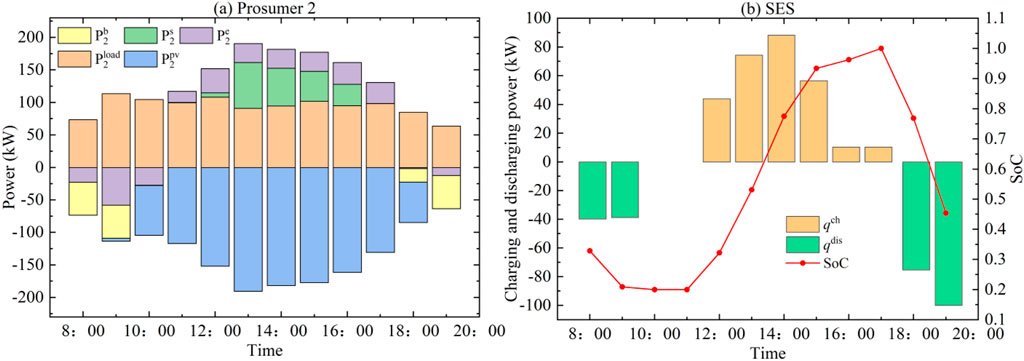
Figure 7. Optimization results of prosumer 2 and charging/discharing of SES under sharing. (A) Prosumer 2. (B) SES.
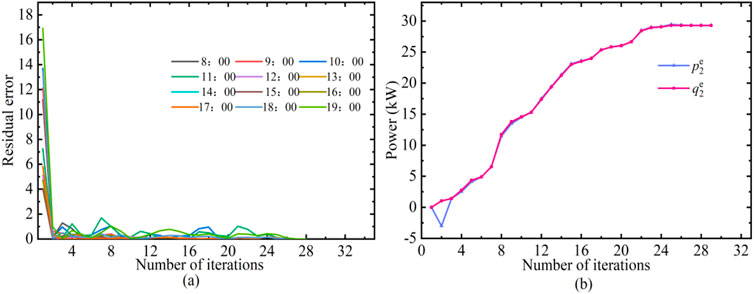
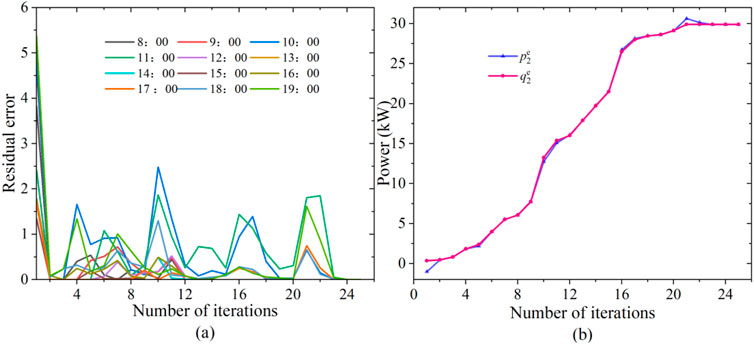
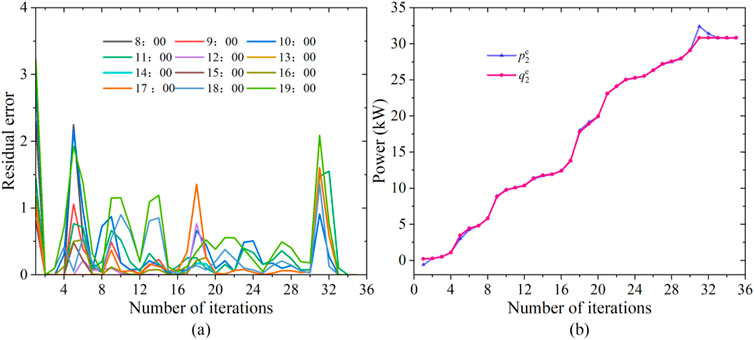
This paper presents AADMM to iteratively solve the SES planning for multiple PV prosumers sharing. A comparison between ADMM and AADMM algorithms is presented in Table 2. The following conclusions can be drawn from Table 2. Firstly, different penalty parameter selections require varying iteration counts and time to achieve the same algorithmic accuracy. Hence, the initial choice of the penalty parameter can impact the algorithm’s iteration count and time. Secondly, for the proposed model in this paper, smaller initial penalty factors result in better convergence performance. The adaptive penalty parameter proposed in AADMM significantly reduces both the iteration count and iteration time compared to the fixed penalty parameter. Furthermore, the algorithm’s improvement varies with different parameter initializations. For both ADMM and AADMM, a value of 0.3 is a preferable parameter choice. The adaptive penalty parameter in AADMM accelerates the algorithm’s convergence process during the iterative stage. For instance, with a value of 0.3, the algorithm converges after 28 iterations. The convergence curves for residual errors at different time steps are illustrated in Figure 8A. At the same time, as shown in Figure 8B, taking prosumer 2 at 15: 00 as an example, as the number of iterations increases, the power transmitted by the prosumer 2 to the SES and the power received by the SES from prosumer 2 gradually tend to be consistent, reaching a global optimum. In addition, in order to show the influence of different penalty factor initial values on AADMM, this paper shows the iterative effect at α = 0.3, 0.5. As shown in Figures 9, 10, regardless of the initial value of the penalty factor, AADMM can self-adjust and ultimately achieve global optimization. This corresponds to Figure 8 and Table 2.
5 Conclusion
In order to investigate the impact of SES on prosumers, enhance prosumer self-sufficiency, reduce the operational cost, and simultaneously ensure privacy protection and expedite optimization calculations, this paper proposes a research methodology for PV prosumers with SES sharing based on AADMM. Simulation results indicate that: 1) The SES planning for multiple PV prosumers sharing model proposed in this paper can significantly reduce the cost of the optical storage park and increase the electricity self-sufficiency rate of the prosumers in the park. Compared with the optical storage park without SES, the cost is reduced by 47.96 CNY, and the electricity self-sufficiency rate is increased by 21.86%. 2) SES planning can make full use of energy storage resources, so that the prosumers in the optical storage park can reduce the cost of purchasing electricity from the grid and improve the self-sufficiency rate of electricity. 3) The distributed optimization algorithm of AADMM is used to solve the SES planning for multiple PV prosumers sharing model. Compared with ADMM, the number of iterations and computational efficiency are increased by 47.05% and 54.67% on average. This method improves the convergence speed of the algorithm while ensuring the stability of the algorithm, and can effectively protect the privacy of each prosumer and SES.
In order to increase the electricity self-sufficiency rate of prosumers and reduce the operating cost of the optical storage park, this paper proposes the SES planning for multiple PV prosumers sharing model based AADMM. However, P2P trading can be carried out between prosumers to achieve energy sharing in the park and promote the local consumption of PV. Therefore, the P2P trading between prosumers will be the research direction of the coordinated operation of prosumers in the park in the future. In addition, market prices have a great impact on energy trading, and the impact of market pricing on the operation of the park is not considered in our current research. In this case, our future research aims to consider how to price reasonably between prosumers and between prosumers and SES, so as to realize the stable participation of each subject in the energy market.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
LZ: Conceptualization, Investigation, Writing–original draft. JZ: Conceptualization, Investigation, Validation, Supervision, Writing–review and editing. QL: Investigation, Supervision, Writing–review and editing. ZZ: Investigation, Supervision, Writing–review and editing. PG: Investigation, Supervision, Writing–review and editing. RZ: Conceptualization, Investigation, Supervision, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by State Grid Gansu Electric Power Company Science and Technology Project on Coordinated and Optimized Configuration Method of New Energy and Energy Storage for Large-scale Wind and Photovoltaic Power Transmission System Oriented to System Resilience Improvement (No. 52272223000U).
Conflict of interest
Authors LZ, JZ, QL, ZZ, PG, and RZ were employed by State Grid Gansu Electric Power Co., Ltd.
The authors declare that this study received funding from State Grid Gansu Electric Power Company. The funder had the following involvement in the study: the funders provided the necessary data in the paper, including PV and load data, and supervised the writing of the article.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdalla, A. A., El Moursi, M. S., El-Fouly, T. H. M., and Hosani, K. H. A. (2023). A novel adaptive power smoothing approach for PV power plant with hybrid energy storage system. IEEE Trans. Sustain. Energy 14 (3), 1457–1473. doi:10.1109/tste.2023.3236634
Aghdam, F. H., Mudiyanselage, M. W., Mohammadi-Ivatloo, B., and Marzband, M. (2023). Optimal scheduling of multi-energy type virtual energy storage system in reconfigurable distribution networks for congestion management. Appl. Energy 333, 120569. doi:10.1016/j.apenergy.2022.120569
Alfaverh, F., Denai, M., and Sun, Y. (2023). A dynamic peer-to-peer electricity market model for a community microgrid with price-based demand response. IEEE Trans. Smart Grid 14 (5), 3976–3991. doi:10.1109/tsg.2023.3246083
Chen, J., Zheng, J., Wu, P., Zhang, L., and Wu, Q. (2017). Dynamic particle swarm optimizer with escaping prey for solving constrained non-convex and piecewise optimization problems. Expert Syst. Appl. 86, 208–223. doi:10.1016/j.eswa.2017.05.047
Chen, P., Ye, Y., Wang, H., Bu, S., Tang, Y., and Strbac, G. (2024). Holistic coordination of transactive energy and carbon emission right trading for heterogenous networked multi-energy microgrids: a fully distributed adaptive consensus ADMM approach. Sustain. Energy Technol. Assessments 64, 103729. doi:10.1016/j.seta.2024.103729
Cui, S., Wang, Y. W., Shi, Y., and Xiao, J. W. (2020). Community energy cooperation with the presence of cheating behaviors. IEEE Trans. Smart Grid 12 (1), 561–573. doi:10.1109/tsg.2020.3022792
He, W., King, M., Luo, X., Dooner, M., and Wang, J. (2021). Technologies and economics of electric energy storages in power systems: review and perspective. Adv. Appl. Energy 4, 100060. doi:10.1016/j.adapen.2021.100060
Ji, Z., Li, W., and Niu, D. (2024). Optimal investment decision of agrivoltaic coupling energy storage project based on distributed linguistic trust and hybrid evaluation method. Appl. Energy 353, 122139. doi:10.1016/j.apenergy.2023.122139
Jiao, P. H., Chen, J. J., Cai, X., Wang, L., Zhao, Y., Zhang, X., et al. (2021). Joint active and reactive for allocation of renewable energy and energy storage under uncertain coupling. Appl. Energy 302, 117582. doi:10.1016/j.apenergy.2021.117582
Li, L., Peng, K., Yang, X., and Liu, K. (2024b). Coordinated design of multi-stakeholder community energy systems and shared energy storage under uncertain supply and demand: a game theoretical approach. Sustain. Cities Soc. 100, 105028. doi:10.1016/j.scs.2023.105028
Li, N., and Okur, Ö. (2023). Economic analysis of energy communities: investment options and cost allocation. Appl. Energy 336, 120706. doi:10.1016/j.apenergy.2023.120706
Li, R., Hu, Y., Wang, X., Zhang, B., and Chen, H. (2024a). Estimating the impacts of a new power system on electricity prices under dual carbon targets. J. Clean. Prod. 438, 140583. doi:10.1016/j.jclepro.2024.140583
Liu, J., Chen, J., Yan, G., Chen, W., and Xu, B. (2023b). Clustering and dynamic recognition based auto-reservoir neural network: a wait-and-see approach for short-term park power load forecasting. Iscience 26 (8), 107456. doi:10.1016/j.isci.2023.107456
Liu, N., Yu, X., Wang, C., and Wang, J. (2017). Energy sharing management for microgrids with PV prosumers: a Stackelberg game approach. IEEE Trans. Industrial Inf. 13 (3), 1088–1098. doi:10.1109/tii.2017.2654302
Liu, Z., Chen, Y., Yang, X., and Yan, J. (2023a). Power to heat: opportunity of flexibility services provided by building energy systems. Adv. Appl. Energy 11, 100149. doi:10.1016/j.adapen.2023.100149
Ma, M., Huang, H., Song, X., Peña-Mora, F., Zhang, Z., and Chen, J. (2022). Optimal sizing and operations of shared energy storage systems in distribution networks: a bi-level programming approach. Appl. Energy 307, 118170. doi:10.1016/j.apenergy.2021.118170
Maneesha, A., and Swarup, K. S. (2021). A survey on applications of alternating direction method of multipliers in smart power grids. Renew. Sustain. Energy Rev. 152, 111687. doi:10.1016/j.rser.2021.111687
Peterssen, F., Schlemminger, M., Lohr, C., Niepelt, R., Hanke-Rauschenbach, R., and Brendel, R. (2024). Impact of forecasting on energy system optimization. Adv. Appl. Energy 15, 100181. doi:10.1016/j.adapen.2024.100181
Ruan, G., Qiu, D., Sivaranjani, S., Awad, A. S., and Strbac, G. (2024). Data-driven energy management of virtual power plants: a review. Adv. Appl. Energy 14, 100170. doi:10.1016/j.adapen.2024.100170
Sun, B., Jing, R., Zeng, Y., Wei, W., Jin, X., and Huang, B. (2024). Three-side coordinated dispatching method for intelligent distribution network considering dynamic capacity division of shared energy storage system. J. Energy Storage 81, 110406. doi:10.1016/j.est.2023.110406
Tercan, S. M., Demirci, A., Gokalp, E., and Cali, U. (2022). Maximizing self-consumption rates and power quality towards two-stage evaluation for solar energy and shared energy storage empowered microgrids. J. Energy Storage 51, 104561. doi:10.1016/j.est.2022.104561
Wald, D., Johnson, K., King, J., Comden, J., Bay, C. J., Chintala, R., et al. (2023). Shifting demand: reduction in necessary storage capacity through tracking of renewable energy generation. Adv. Appl. Energy 10, 100131. doi:10.1016/j.adapen.2023.100131
Wang, D., Zhang, C., Li, J., Zhu, L., Zhou, B., Zhou, Q., et al. (2024b). A novel interval power flow method based on hybrid box-ellipsoid uncertain sets. IEEE Trans. Power Syst. 39, 6111–6114. doi:10.1109/tpwrs.2024.3391921
Wang, Y. X., Chen, J. J., Zhao, Y. L., and Xu, B. (2024a). Incorporate robust optimization and demand defense for optimal planning of shared rental energy storage in multi-user industrial park. Energy 301, 131721. doi:10.1016/j.energy.2024.131721
Wu, Y., Wang, C., and Wang, Y. (2024). Cooperative game optimization scheduling of multi-region integrated energy system based on ADMM algorithm. Energy 302, 131728. doi:10.1016/j.energy.2024.131728
Xie, H., Ahmad, T., Zhang, D., Goh, H. H., and Wu, T. (2024). Community-based virtual power plants’ technology and circular economy models in the energy sector: a Techno-economy study. Renew. Sustain. Energy Rev. 192, 114189. doi:10.1016/j.rser.2023.114189
Yan, G. J., Chen, J. J., Liu, J. Y., Chen, W., and Xu, B. (2023). Random clustering and dynamic recognition-based operation strategy for energy storage system in industrial park. J. Energy Storage 73, 109192. doi:10.1016/j.est.2023.109192
Zhang, C., Liu, Q., Zhou, B., Chung, C. Y., Li, J., Zhu, L., et al. (2022). A central limit theorem-based method for DC and AC power flow analysis under interval uncertainty of renewable power generation. IEEE Trans. Sustain. Energy 14 (1), 563–575. doi:10.1109/tste.2022.3220567
Zhang, Q., Dehghanpour, K., and Wang, Z. (2018). Distributed CVR in unbalanced distribution systems with PV penetration. IEEE Trans. Smart Grid 10 (5), 5308–5319. doi:10.1109/tsg.2018.2880419
Zhang, Q., Guo, Y., Wang, Z., and Bu, F. (2021). Distributed optimal conservation voltage reduction in integrated primary-secondary distribution systems. IEEE Trans. Smart Grid 12 (5), 3889–3900. doi:10.1109/tsg.2021.3088010
Zhang, Y. Q., Chen, J. J., Wang, Y. X., and Feng, L. (2024). Enhancing resilience of agricultural microgrid through electricity–heat–water based multi-energy hub considering irradiation intensity uncertainty. Renew. Energy 220, 119739. doi:10.1016/j.renene.2023.119739
Zhao, B., Qian, T., Li, W., Xin, Y., Zhao, W., Lin, Z., et al. (2024). Fast distributed co-optimization of electricity and natural gas systems hedging against wind fluctuation and uncertainty. Energy 298, 131420. doi:10.1016/j.energy.2024.131420
Keywords: renewable energy, shared energy storage, planning, distributed optimization, resilience
Citation: Zhao L, Zhang J, Lv Q, Zhang Z, Gao P and Zhang R (2024) AADMM based shared energy storage planning for resilience improvement of renewable energy stations. Front. Energy Res. 12:1467627. doi: 10.3389/fenrg.2024.1467627
Received: 20 July 2024; Accepted: 16 August 2024;
Published: 10 September 2024.
Edited by:
Zhenjia Lin, Hong Kong Polytechnic University, Hong Kong SAR, ChinaReviewed by:
Qianzhi Zhang, Cornell University, United StatesLirong Deng, Shanghai University of Electric Power, China
Jiehui Zheng, South China University of Technology, China
Copyright © 2024 Zhao, Zhang, Lv, Zhang, Gao and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Long Zhao, MTUxNzE1MzUyQHFxLmNvbQ==
 Long Zhao
Long Zhao Jinping Zhang
Jinping Zhang Qingquan Lv
Qingquan Lv