The inlet valve closing (IVC) timing plays a crucial role in engine combustion, which impacts engine performance and emissions. This study attempts to measure the potential to use n-butanol (Bu) and its blends with the neat diesel in a common rail direct injection (CRDI) engine. The computational fluid dynamics (CFD) simulation is carried out to estimate the performance, combustion, and exhaust emission characteristics of n-butanol–diesel blends (0%–30% by volume) for variable valve timings. An experimental study is carried out using standard valve timing and blends to validate the CFD model (ESE AVL FIRE). After validation, the CFD model is employed to study the effect of variable valve timings for different n-butanol–diesel blends. Extended coherent flame model-3 zone (ECFM-3Z) is implemented to conduct combustion analysis, and the kappa–zeta–f (k–ζ–f) model is employed for turbulence modeling. The inlet valve closing (IVC) time is varied (advanced and retarded) from standard conditions, and optimized valve timing is obtained. Advancing IVC time leads to lower cylinder pressure during compression due to reduced trapped air mass. The brake thermal efficiency (BTE) is increased by 4.5%, 6%, and 8% for Bu10, Bu20, and Bu30, respectively, compared to Bu0. Based on BTE, optimum injection timings are obtained at 12° before the top dead center (BTDC) for Bu0 and 15° BTDC for Bu10, Bu20, and Bu30. Nitrogen oxide (NO_x) emissions increase due to complete combustion. Due to IVC timing, further carbon monoxide and soot formation decreased with blends and had an insignificant effect.

Highlights

• The impact of different IVC timings on the performance of CRDI engines fueled with butanol–diesel blends has been studied.

• A computational model is developed by the chemical kinetics mechanism.

• Peak in-cylinder pressure is increased for all early inlet valve closing timings for all n-butanol–diesel blends.

• An increase in ignition delay is associated with later inlet valve closing timings.

1 Introduction

The current landscape of global energy is experiencing unprecedented changes manifested by the pressing need to solve several related problems simultaneously (Wu and Hobbs, 2002). The most pressing is the depletion in the supply of new fossil fuel reserves, which threatens the current energy systems, such as conventional diesel and gasoline engines (Lamani et al., 2017a; Kalair et al., 2021). At the same time, awareness of environmental pollution and the consequences of air pollution to public health are now leading to increasingly stringent emission regulations throughout most regions in the world (Lamani et al., 2020; Wolde-Rufael and Weldemeskel, 2020). Considering all these factors, along with the broader impacts of climate change, a transformation in how energy is generated and used is required.

2 Literature survey

Faced with such challenges, researchers are working harder to find alternative fuels that can replace traditional ones without compromising energy needs and the environment. Diesel engines, known for their high thermal efficiency and durability, are central to this endeavor (Lamani et al., 2017b; Bidir et al., 2021). Particularly, they remain a major environmental issue for nitrogen oxide (NOx) and particulate matter (PM) emissions (Wasilewski et al., 2024). An alternative to address these emissions is to dilute diesel by adding alternative fuels like alcohols (Surisetty et al., 2011; Bedar et al., 2017; Erdiwansyah et al., 2019). Butanol is among the alcohols being studied and is considered a promising candidate owing to certain physicochemical properties, such as higher energy content, higher miscibility with diesel, and lower hygroscopicity relative to ethanol (Lamani et al., 2016; Yusuf et al., 2020; Truong et al., 2021; Vadivelu et al., 2023). There have been several studies on biofuel production through butanol synthesis, and several of them focus on comparing the potentialities and limitations of various biotechnological and chemical ways of this process. The articles summarize the sustainability of lignocellulosic butanol and the properties of butanol–diesel blends, their impact on combustion parameters, and the ability of butanol to be applied as a blending component for diesel fuels in commercial engines (Veza et al., 2023; Žvar Baškovič et al., 2023).

The intake valve closing (IVC) timing is a very important parameter in engine operation, which affects the volumetric efficiency, the combustion issue, and the engine performance and emissions (Demir et al., 2022). Optimizing the air–fuel mixture, improving the efficiency of the combustion process, and consequently minimizing emissions are some of the operational characteristics resulting from the adjustment of the IVC timing (Lou and Zhu, 2020).

Investigation of the influence of early inlet valve closure (EVIC) timing on exhaust emissions, specific fuel consumptions, and exhaust gas temperature of a turbocharged CRDI engine at low load and fixed level of NOx was carried out by Zammit et al. (2015). A reduction in soot emissions was observed, whereas carbon monoxide (CO) and hydrocarbon (HC) were increased. Jia et al. (2013) studied the effect of late intake valve closing (LIVC) on the combustion and emission characteristics of a diesel engine using a multidimensional model. LIVC leads to a significant delay in ignition timing by decreasing the effective compression ratio across the entire operating range, and hence, LIVC is an effective method for the reduction of nitrogen oxide (NOx) emissions. In addition, soot reduction with LIVC was observed in the low-to-medium load range. Benajes et al. (2009) studied the effect of the early inlet valve closing (EIVC) angle. They witnessed the reduction of in-cylinder pressure and density. They observed that in EIVC, the effective compression ratio was reduced, which resulted in lower total intake mass flow rate. EIVC reduces flame temperatures due to the lower initial temperature before the start of injection. Thus, it caused a reduction in NOx emissions; however, it increased soot and CO emissions because of lower flame temperature and oxygen mass concentration during the late diffusion-controlled combustion, which slows down both CO and soot oxidation processes.

Ojeda (2010) explored the effects of LIVC and observed that a lower effective compression ratio and in-cylinder temperature increased ignition delay. LIVC, EGR, supercharging, and high-pressure fuel injection simultaneously reduce NOx and smoke for light duty. Sjöblom (2014) investigated the effect of variable inlet valve timing in association with low-temperature combustion (LTC) and witnessed higher thermal efficiency and lesser exhaust emissions. Jia and Jia (2009) carried out three-dimensional computational fluid dynamics (CFD) to investigate the effect of LIVC on the combustion and emission characteristics of a diesel engine with premixed charge compression ignition (PCCI) combustion. LIVC is employed to control the optimum ignition timing to decrease nitrogen oxide (NOx) and soot emissions by the effective compression ratio and increasing premixing, but it results in more HC and CO emissions. With higher intake pressure, late IVC can reduce NOx, soot, HC, and CO emissions simultaneously.

A numerical study on the effect of intake valve timing on the performance of natural gas–diesel dual-fuel engines and multi-objective optimization was conducted by Jung et al. (2017). They witnessed the reduction in emissions with consistent thermal efficiency and concluded that when the natural gas energy proportion (NGP) increased, the brake power decreased, and nitrogen oxide (NOx) emissions decreased because of low combustion efficiency and a lower temperature in the cylinder. Han et al. (2010) studied the effect of LIVC and EGR in a single-cylinder diesel engine in the low-load condition. They observed a suitable combination of EGR with late intake valve closing was effective in reducing nitrogen oxide emissions.

The aim of the study reported in this article is to examine the benefits of early inlet valve closure timings for different injection timings. However, the influence of different operational variables on the use of butanol–diesel blends has not been previously studied with respect to a common rail direct-injection diesel engine. Further investigation of the effect of biobutanol–diesel blends on CRDI engines with CFD simulations is scant. CFD simulations offer the prospect of achieving a deeper insight into comprehending in-cylinder combustion. In this study, we explore the details of variations in the engine emissions and combustion characteristics for various n-butanol–diesel blends and different inlet valve closing injection timings. Variable valve timing (VVT) is a technique that is employed in CFD simulations.

3 Experimental setup, models, and methodology

3.1 Research methodology

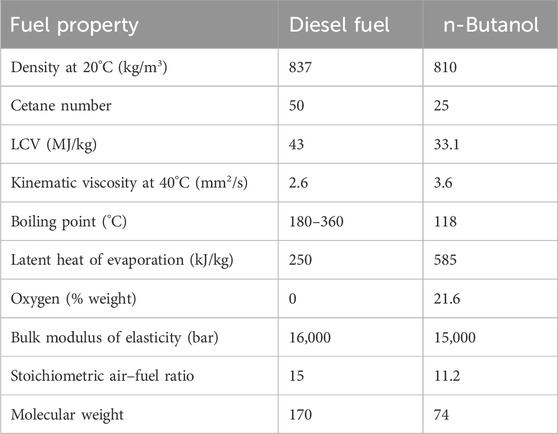
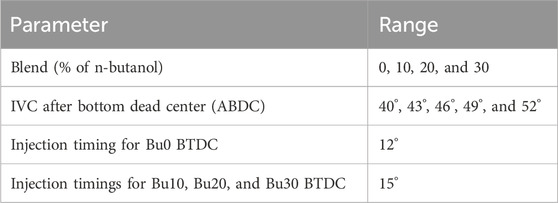
The aim of the present work is to numerically analyze the effects of different IVC timings on the performance and emission characteristics of a common rail diesel engine fed by various butanol–diesel blends. The analysis is conducted using a validated computational model, which simulates engine performance under varying IVC timings and butanol–diesel blend ratios. In the present investigation, n-butanol–diesel blends are considered for numerical and experimental studies. n-butanol is blended with neat diesel to obtain different blends varying from 0% to 30% by volume. Bu0, Bu10, Bu20, and Bu30 represent 0%, 10%, 20%, and 30% n-butanol in neat diesel, respectively. The basic physical properties of n-butanol and neat diesel used in this investigation are compared in Table 1 (Rakopoulos et al., 2010), and the range of simulation parameters is listed in Table 2.

Table 1

Table 1. Properties of diesel and n-butanol.

Table 2

Table 2. Range of simulation parameters.

3.2 Experimental setup

The schematic diagram and representation of the experimental facility are shown in Figure 1. A twin-cylinder CRDI engine with an open electronic control unit (ECU) developed by NIRA Control AB was used to study the engine performance, emission, and combustion characteristics.

Figure 1

Figure 1. Schematic representation of the experimental setup and IVC timing.

The specifications of the engine are listed in Table 3. The fuel from the tank is supplied to the accumulator (common rail) using a high-pressure fuel pump at a constant injection pressure of 100 MPa. Common rail pressure is maintained by the pressure control valve (PCV), and the required fuel supplied to the injector is controlled by a solenoid valve. The operating parameters of the engine are controlled by the open ECU. Pressure versus crank angle data are measured using a piezoelectric-based pressure transducer. The signal of cylinder pressure is acquired at every 1° crank angle for 100 cycles, and the average value of 100 cycles is considered for combustion analysis. The pressure signal is fed into the NI USB-6210 DAQ and then to a data acquisition card linked to the computer. Furthermore, engine tail pipe emissions are measured using an exhaust gas analyzer (AVL 444) with a diesel probe. Soot emissions are measured using an opacity meter (AVL 415SE).

Table 3

Table 3. Specifications of the engine.

3.3 CFD code and meshing of geometry

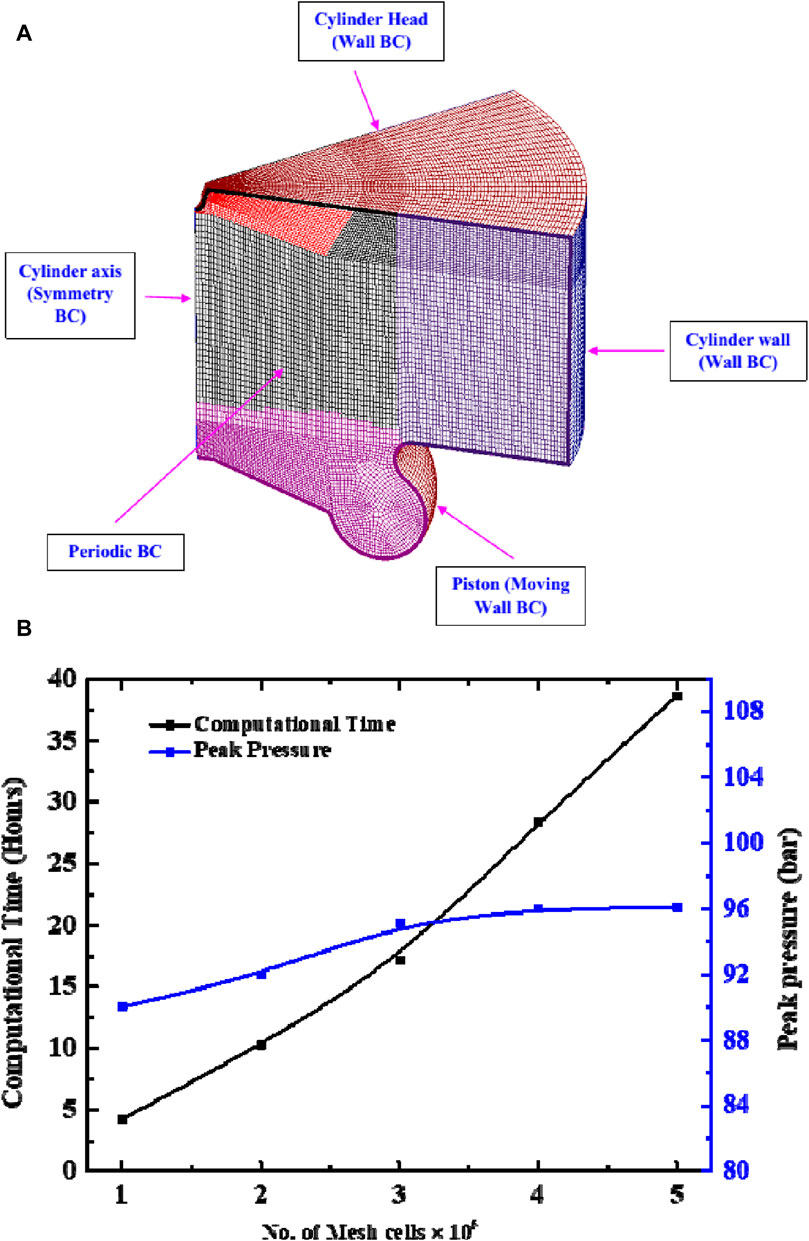
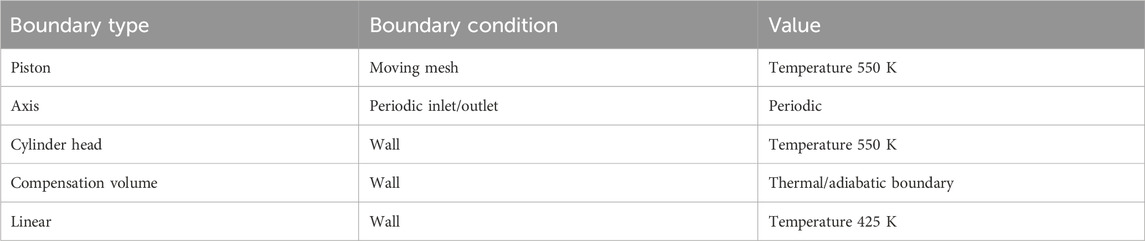
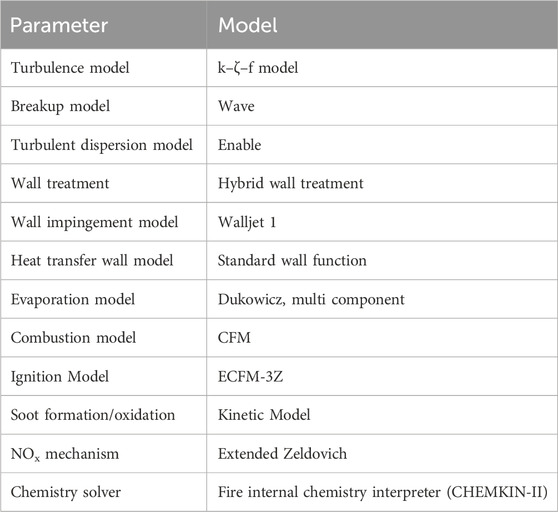
The AVL ESE CFD tool is used for engine geometric modeling, computational meshing, and simulation for the present study. The injector with seven holes is located centrally on the top of the piston; hence, a 51.43° sector is chosen for the simulation. The three-dimensional computational domain of piston geometry is shown in Figure 2A. To reduce the computational time, a high-pressure cycle is considered. Simulation is started and ended at the inlet valve close and exhaust valve open positions, respectively. A grid independence test has been carried out to obtain the optimum grid size, as shown in Figure 2B. Results have been checked for peak pressure and computational time for various grid sizes. It has been observed that considered parameters are invariant with change in the total number of grids at/after 3×10⁵. The models and boundary conditions used in the simulation are listed in Tables 4, 5, respectively.

Figure 2

Figure 2. (A) Three-dimensional computational domain. (B) Grid independence study of peak pressure.

Table 4

Table 4. Boundary conditions employed for the simulation.

Table 5

Table 5. Models employed for the simulation.

3.3.1 Governing equations

The average mass densities of the transport equation are computed into three zones. The chemical species of fuel (O₂, N₂, NO, CO₂, CO, H₂, H₂O, O, H, N, OH, and soot) are elucidated into three zones. This technique is used in the present research by employing the three-zone ECFM model. Therefore, when “burned gases” are mentioned, they include the real burned gases in the mixed zone (zone M_b in Figure 3) plus a part of the unmixed fuel (zone F_b in Figure 3) and air (zone Ab in Figure 3). The fuel is allocated in two slices, the fuel existing in the fresh gases and the fuel in the burned gases. Fuel transport equations for unburned and burned fuel mass fractions, unmixed species, mixing time, oxygen mass fraction, nitrogen monoxide model, soot mass fraction (Equations 1–10) and eddy viscosity, turbulent time scale (Equations 12–Equations 16) are as follows (Colin and Benkenida, 2019):

$\frac{\partial \left(\overline{\rho }{\stackrel{\sim }{Y}}_{Fu}^u\right)}{\partial t}+\frac{\partial \left(\overline{\rho }{\stackrel{\sim }{\mathrm{u}}}_{\mathrm{i}}\overline{\rho }{\stackrel{\sim }{Y}}_{Fu}^u\right)}{\partial x_i}=\frac{\partial }{\partial x_i}\left(\left(\frac{\mu }{S_c}+\frac{{\mu }_t}{{S_c}_t}\right)\frac{\partial {\stackrel{\sim }{Y}}_{Fu}^u}{\partial x_i}\right)+\overline{\rho }{\stackrel{\sim }{\dot{S}}}_{Fu}^u+{\overline{\dot{\omega }}}_{Fu}^u-{\overline{\dot{\omega }}}_{Fu}^{u\to b}.(1)$

Figure 3

Figure 3. Extended coherent flame model.

The equations for the unmixed species, i.e., fuel and air are as follows:

$\frac{\partial \left(\overline{\rho }{\stackrel{\sim }{Y}}_{Fu}^F\right)}{\partial t}+\frac{\partial \left(\overline{\rho }{\stackrel{\sim }{\mathrm{u}}}_{\mathrm{i}}{\stackrel{\sim }{Y}}_{Fu}^F\right)}{\partial x_i}-\frac{\partial }{\partial x_i}\left(\left(\frac{\mu }{S_c}+\frac{{\mu }_t}{{S_c}_t}\right)\frac{\partial {\stackrel{\sim }{Y}}_{Fu}^F}{\partial x_i}\right)=\overline{\rho }{\stackrel{\sim }{\dot{S}}}_{Fu}^F+\overline{\rho }{\stackrel{\sim }{\dot{E}}}_{Fu}^{F\to M},(2)$

$\frac{\partial \left(\overline{\rho }{\stackrel{\sim }{Y}}_{O_2}^A\right)}{\partial t}+\frac{\partial \left(\overline{\rho }{\stackrel{\sim }{\mathrm{u}}}_{\mathrm{i}}{\stackrel{\sim }{Y}}_{O_2}^A\right)}{\partial x_i}-\frac{\partial }{\partial x_i}\left(\left(\frac{\mu }{S_c}+\frac{{\mu }_t}{{S_c}_t}\right)\frac{\partial {\stackrel{\sim }{Y}}_{O_2}^A}{\partial x_i}\right)=\overline{\rho }{\stackrel{\sim }{\dot{E}}}_{O_2}^{A\to M},(3)$

${\overline{\dot{E}}}_{Fu}^{F\to M}=-\frac{1}{{\tau }_m}{\stackrel{\sim }{Y}}_{Fu}^F\left(1-{\stackrel{\sim }{Y}}_{Fu}^F\frac{\overline{\rho }{M}^M}{{\overline{\rho }}^u\left|{}_u{M}_{Fu}\right.}\right),(4)$

${\overline{\dot{E}}}_{O_2}^{A\to M}=-\frac{1}{{\tau }_m}{\stackrel{\sim }{Y}}_{O_2}^A\left(1-\frac{{\stackrel{\sim }{Y}}_{O_2}^A}{{\stackrel{\sim }{Y}}_{O_2}^{\infty }}\frac{\overline{\rho }{M}^M}{{\overline{\rho }}^u\left|{}_u{M}_{air+EGR}\right.}\right),(5)$

where τ_m is the mixing time, which is defined as

${\tau }_m^{-1}=\frac{\epsilon }{k}.(6)$

The oxygen mass fraction in unmixed air is computed as follows:

${\stackrel{\sim }{Y}}_{O_2}^{\infty }=\frac{{\stackrel{\sim }{Y}}_{{TO}_2}}{{1-\stackrel{\sim }{Y}}_{TFu}}.(7)$

The transport equation model for nitrogen monoxide is given by

$\frac{\partial \left(\overline{\rho }{\stackrel{\sim }{Y}}_{NO}\right)}{\partial t}+\frac{\partial \left({\overline{\mathrm{u}}}_{\mathrm{i}}\overline{\rho }{\stackrel{\sim }{Y}}_{\text{NO}}\right)}{\partial x_i}=\frac{\partial }{\partial x_i}\left(\overline{\rho }{D}_{\mathrm{t}}\frac{\partial {\stackrel{\sim }{Y}}_{\text{NO}}}{\partial x_i}\right)+{\overline{S}}_{\text{NO}},(8)$

${\overline{S}}_{\text{NO}}=M_{\text{NO}}\left(\frac{d{c}_{\text{NO}\text{thermal}}}{dt}+\frac{d{c}_{\text{NO}\text{prompt}}}{dt}\right),(9)$

where $\overline{\rho },{\stackrel{\sim }{Y}}_{NO},{\stackrel{\sim }{u}}_i,x_i,$ and $D_t$ are Reynolds averaged fuel density, the mean mass fraction of NO_x, density-weighted average velocity, Cartesian coordinates, and the diffusion coefficient, respectively.

The terms M_NO, $\frac{d{c}_{\text{NO}\text{thermal}}}{dt}$, and $\frac{d{c}_{\text{NO}\text{prompt}}}{dt}$ in Equation 9 are the molar mass NO_X, rate of formation of thermal NO_X, and rate of formation of prompt NO_X, respectively.

The transport equation model for the formation of the soot mass fraction ${\varphi }_s$ is given by

$\frac{\partial }{\partial t}\left(\overline{\rho }{\stackrel{\sim }{\varphi }}_s\right)+\frac{\partial }{\partial x_j}\left(\overline{\rho }{\overline{u}}_j{\overline{\varphi }}_s\right)=\frac{\partial }{\partial x_j}\left(\frac{{\mu }_{eff}}{{\sigma }_s}\frac{\partial {\overline{\varphi }}_s}{\partial x_j}\right)+S_{{\phi }_s}.(10)$

The soot formation rate is defined as (Kuo, 1986; Heywood, 1998)

$S_{{\phi }_s}=S_n+S_g+S_{O_2},(11)$

where $S_n$ represents the soot nucleation, $S_g$ represents the soot growth, and $S_{O_2}$ represents the soot oxidation.

3.3.2 Turbulent flow and heat transfer

Since most of the IC engine-related fluid flow problems are turbulent, it is of utmost importance to precisely model the phenomenon of turbulence for accurate simulation of real flows. This is essential as turbulence not only determines the particulars of fluid flow but also strongly influences the chemical and physical methods that take place during mixture formation and combustion. AVL FIRE offers the recently developed k–ξ–f turbulence model, which is validated for IC engine-related flow, heat transfer, and combustion processes (Basara, 2006).

3.3.3 k–ζ–f model

The k–ζ–f model is employed to treat turbulent flow inside the cylinder. To improve numerical stability, the ${\overline{\mathrm{v}}}^2-f$ model needs to be solved for the velocity scale ratio $\zeta ={\overline{\mathrm{v}}}^2/k$ instead of velocity scale ${\overline{\mathrm{v}}}^2$.

The eddy viscosity is defined as

${\nu }_t=C_{\mu }\zeta \frac{k^2}{\epsilon },(12)$

where k, ε, and ξ are obtained by solving the following set of model equations:

$\rho \frac{Dk}{Dt}=\rho \left({\mathrm{P}}_k-\epsilon \right)+\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right],(13)$

$\rho \frac{D\epsilon }{Dt}=\rho \frac{C_{\epsilon 1}^{*}{P}_k-C_{{\epsilon }_2}\epsilon }{T}+\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_{\epsilon }}{{\sigma }_k}\right)\frac{\partial \epsilon }{\partial x_j}\right],(14)$

$\rho \frac{D\zeta }{Dt}=\rho f-\rho \frac{\zeta }{k}{P}_k+\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\zeta }}\right)\frac{\partial \zeta }{\partial x_j}\right].(15)$

To obtain f, the following equation is adopted:

$f-L^2\frac{{\partial }^{2}f}{\partial x_j\partial x_j}=\left(C_1+C_2\frac{P_k}{\zeta }\right)\frac{\left(\frac{2}{3}-\zeta \right)}{T}.(16)$

Turbulent time scale T and length scale L are given by

$T=\max \left(\min \left(\frac{k}{\epsilon },\frac{a}{\sqrt{6}{C}_{\mu }^{\nu }\left|S\right|\zeta }\right),C_T{\left(\frac{v^3}{\epsilon }\right)}^{1/2}\right),$

$L=C_L\max \left(\min \left(\frac{k^{3/2}}{\epsilon }\right),C_{\eta }\frac{{\nu }^{3/4}}{{\epsilon }^{1/4}}\right).$

Additional modifications to the ε equation include dampening the constant C_ε1 close to the wall, thus resulting in $C_{\epsilon 1}^{*}=C_{\epsilon 1}\left(1+0.045\sqrt{1/\zeta }\right).$

For flows in the IC engine, the k–ξ–f model not only leads to more accurate results in comparison to the much simpler two-equation eddy viscosity models of the k–ξ–f type but also exhibits a high degree of numerical robustness.

3.3.4 Fuel spray and wall film

The spray model universally adopted in AVL FIRE for simulations of IC-engine spray and mixture formation is based on the Lagrangian discrete droplet method (DDM). While the standard Eulerian conservation equations describe the continuous gaseous phase, the dispersed phase transportation is calculated by tracking the trajectories of droplet parcels. A parcel consists of a number of droplets that are assumed to have the same physical properties and behave similarly when they move, break up, hit a wall, or evaporate.

The standard wave model (Naber and Reitz, 1987; Reitz, 1988) is used for the atomization modeling. In this model, the wavelength and other physical and dynamic parameters of the injected fuel and the domain fluid determine the growth of an initial perturbation on a liquid surface. The use of the standard wave model with blob injection (initial droplets have the diameter of the nozzle orifice) for simulation results in lower vaporization of fuel near the nozzle as the droplets are still large in the beginning and, therefore, hardly get evaporated. Wall interaction of liquid droplets plays a major role in diesel engines, especially for small-bore diesel engines, where the distance between the injector and the bowl is very small. If the large quantity of the fuel is not evaporated or atomized, then it will hit the wall, which influences the combustion and emission characteristics, as incomplete combustion in the vicinity of the wall will result in high HC emission emissions and soot particles. The behavior of a droplet at the wall interaction depends on several parameters like droplet velocity, diameter, droplet properties, wall surface roughness, and wall temperature. At very low inlet velocities, the droplet sticks to the wall or the wall film, whereas for higher inlet velocities, a vapor or gas boundary layer is trapped underneath the droplet, which causes the liquid to rebound. During rebound, parts of the kinetic energy are dissipated, and the outgoing normal velocity is usually lower than the incoming normal velocity, and any further increase of the velocity leads either to the spread or the splash regime. In the spread regime, the complete liquid has hardly any normal velocity and is spread along the wall. In the splash regime, part of the liquid remains near the surface, while the rest is reflected and brakes up into secondary droplets (Tatschl, 2009).

3.3.5 Evaporation model

The Dukowicz model, which assumes a uniform droplet temperature profile, is applied for treating the heat-up and evaporation of the droplets. In addition, the rate of change of droplet temperature is determined by heat balance, and it states that the heat convection from the gas to the droplet either heats the droplet or supplies heat for vaporization. The heat and mass transfer processes are described by a model originally derived by Dukowicz (Dukowicz, 1979). Essentially, it is based on the following assumptions: spherical symmetry, quasi-steady gas-film around the droplet, uniform droplet temperature along the drop diameter, uniform physical properties of the surrounding fluid, and liquid–vapor thermal equilibrium on the droplet surface. In the evaporation model of Dukowicz, it is considered that the droplet is evaporating in a non-condensable gas. Therefore, it uses a two-component system in the gas-phase composed of the vapor and the non-condensable gas, even though each component may consist of a mixture of different species.

3.3.6 Combustion model

The ECFM-3Z model is a modified version of ECFM, which is based on the flame surface density approach. ECFM features take care of premixed flame, knock, and pollution formation. With ECFM features, ECFM-3Z takes care of the diffusion flame and the mixing process. In this model, each computational cell is divided into three mixing zones. The three zones are the pure fuel zone, air plus EGR zone, and mixed zone. Various multi-component capacities exist in the three-zone extended coherent flame model (Colin and Benkenida, 2019). The schematic representation is shown in Figure 3.

4 Results and discussion

In this section, the results of the numerical (CFD) studies on the CRDI engine’s performance are presented. Results are obtained for n-butanol–diesel blends for various IVC timings.

4.1 Validation

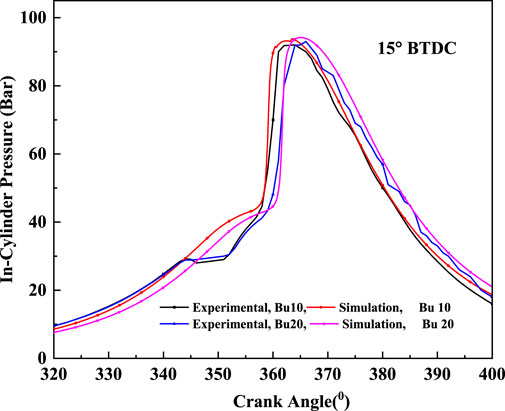
In the present investigation, the simulation is validated for pressure versus crank angle from the experimental results obtained from the author’s laboratory for conditions listed in Table 2 for standard IVC timing. Comparison between experimental and simulation results for Bu10 and Bu20 at optimum IT are portrayed in Figure 4. For all cases, CFD results show good agreement with experimental data.

Figure 4

Figure 4. Validation with experimental results.

4.1.1 Effect of inlet valve closing timing on the engine’s brake thermal efficiency

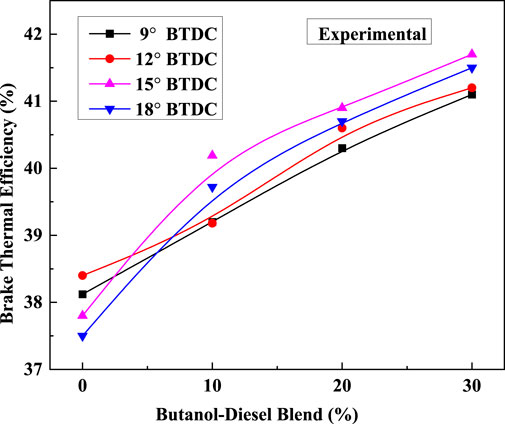
Experimental results on the effect of injection timing and n-butanol–diesel blends on brake thermal efficiency (BTE) are presented in Figure 5. The ratio of the actual measurement of thermochemical energy liberated from the fuel and conversion of thermochemical energy in the form of BP to the fuel energy during the rotation of the crankshaft to evaluate the performance of the heat engine operated with diesel fuel or different blends is technically called the BTE. The results show that there is a significant increase in BTE for all butanol–diesel blends compared to Bu0. The enhancement of diffusive combustion is obtained from oxygen-enriched blends, and hence, the total combustion duration is shortened. The increase in BTE with butanol blends is also ascribed to its higher burning velocity of 45 cm/s compared to 33 cm/s for diesel (Sarathy et al., 2009; Sayin, 2010). BTE is increased by ∼4.5%, 6%, and 8% for Bu10, Bu20, and Bu30, respectively, compared to Bu0. Based on BTE, the optimum injection timings are obtained at 12° BTDC for Bu0 and 15° BTDC (common injection timing) for Bu10, Bu20, and Bu30.

Figure 5

Figure 5. Variation in brake thermal efficiency of various fuel blends.

4.2 Effect of inlet valve closing timing on the in-cylinder pressure

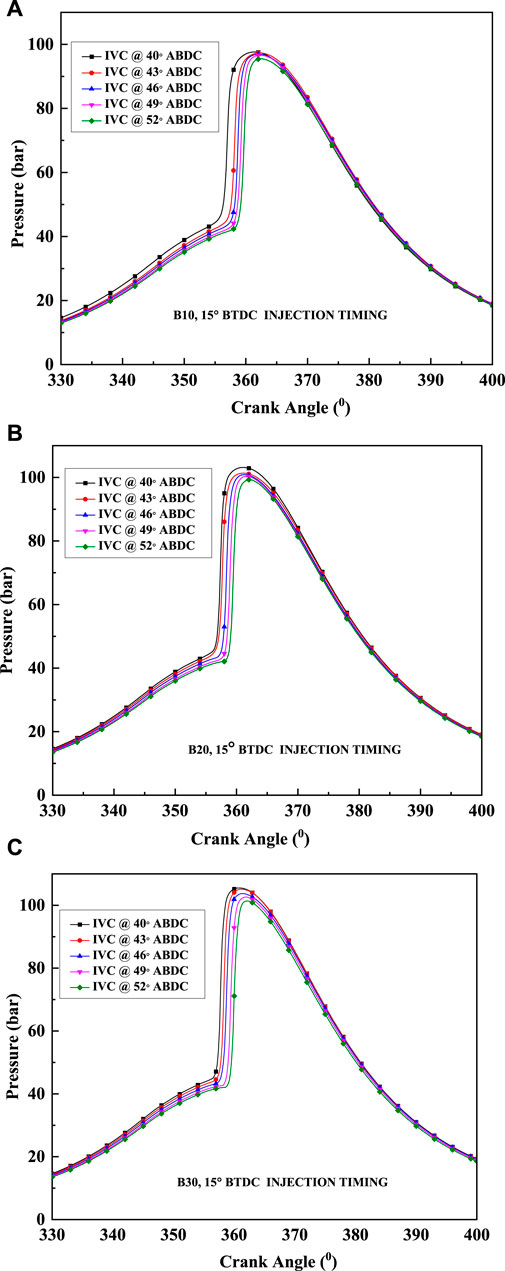
The amount of pressure increase in the cylinder is an essential combustion factor in predicting the actual combustion that takes place during the crank angle rotations from BDC to TDC. Figures 6A–C show the numerical results of in-cylinder pressure versus crank angle for various biobutanol–diesel blends (10, 20, and 30%) at different IVC timings. For all EIVC timings, the peak pressure in the engine cylinder can be reached due to the increased volumetric efficiency. On delaying the IVC timing, the maximum in-cylinder pressure decreased significantly due to the engine’s lower volumetric efficiency. For LIVC timings, combustion is delayed, whereas it is started early for all EIVC timings. Due to the decrease in the effective compression ratio, the start of combustion is delayed. A similar trend is observed for all biobutanol–diesel blends.

Figure 6

Figure 6. In-cylinder pressure versus crank angle for (A) B10, (B) B20, (C) B30.

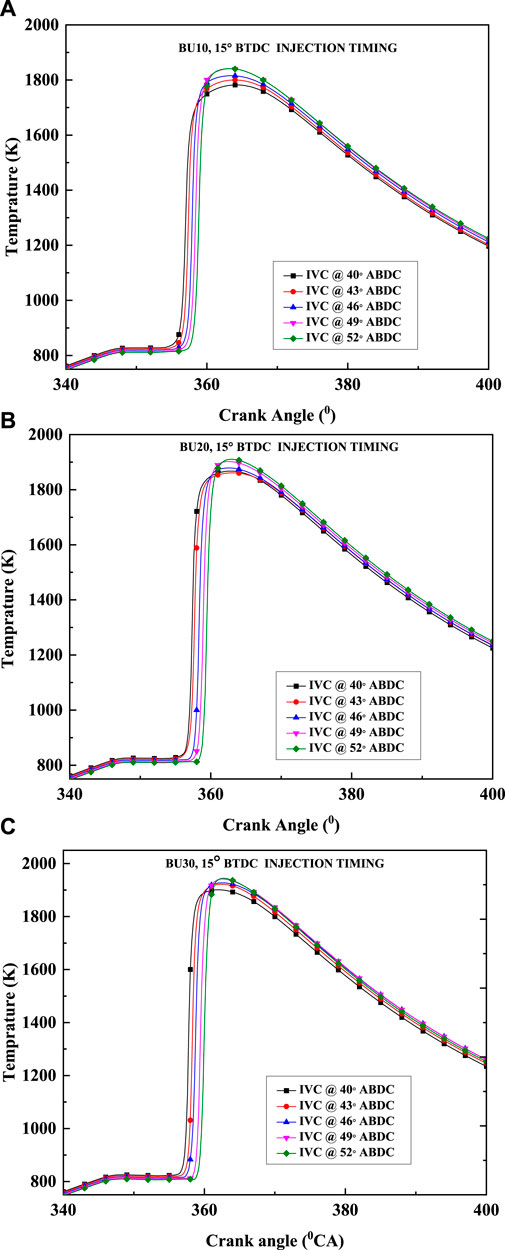
4.3 Effect of inlet valve closing timing on the in-cylinder temperature

Figures 7A–C show the in-cylinder temperature versus crank angle for various biobutanol–diesel blends (10, 20, and 30%) at different IVC timings. It is observed that the start of combustion is similar to in-cylinder pressure, as shown in Figure 6, whereas the peak in-cylinder temperature is increased for all LIVC timings. Higher in-cylinder temperature is attributed to the relatively rich fuel mixture of biobutanol–diesel blends. Furthermore, for 30% biobutanol–diesel blends, the peak in-cylinder temperature is marginally increased compared to other blends due to successive increases in oxygen concentration. This is due to the amount of energy brought into the cylinder by the fuel and the efficient combustion process.

Figure 7

Figure 7. In-cylinder temperature versus crank angle for (A) B10, (B) B20, (C) B30.

4.4 Effect of inlet valve closing timing on emissions

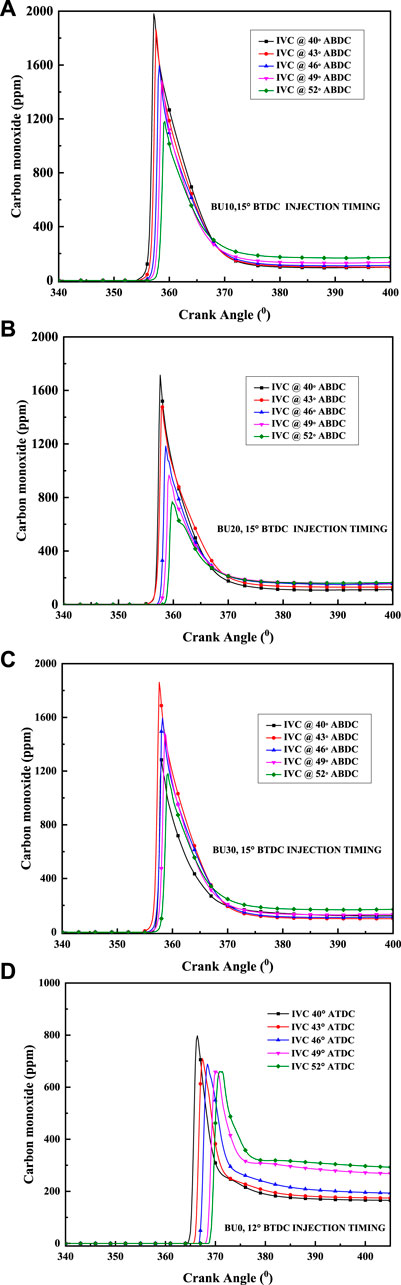
4.4.1 CO emission

This section provides the effect of varying inlet valve timing on emission characteristics. Figures 8A–C show the numerical results of in-cylinder carbon monoxide formation versus crank angle for various biobutanol–diesel blends (10, 20, and 30%) at different IVC timings, respectively. Figure 8D depicts the CO emissions at 12° BTDC, in which the maximum thermal efficiency is observed for pure diesel engine operation. Carbon monoxide emissions are colorless and odorless, and carbon monoxide is emitted due to incomplete combustion, which occurs due to the lack of oxygen supply at the end of the combustion. The 30% biobutanol blends at 15° BTDC show a lower amount of CO emissions in comparison to other valve timing and fuel blends. CO is formed because of incomplete combustion occurring due to a lack of free oxygen during combustion. Since butanol blends are oxygenated, they promote CO oxidation, thereby enhancing the complete combustion process. For higher biobutanol–diesel blends and IVC timings, CO emissions are reduced compared to those of lower blends.

Figure 8

Figure 8. CO emissions versus crank angle for (A) B10, (B) B20, (C) B30, (D) B0.

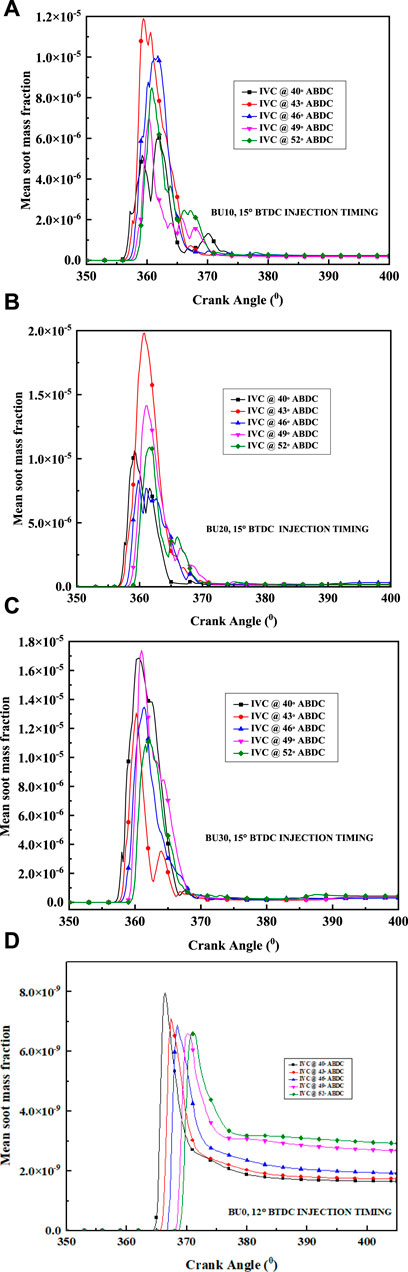
4.4.2 Soot emission

Figures 9A–C show the numerical results of in-cylinder soot formation versus crank angle for various biobutanol–diesel blends (10, 20, and 30%) at different IVC timings. Figure 9D represents the soot emissions for pure diesel engine operation at 12° BTDC. The particulate matter (PM) is composed of soot and is accountable for the smoke (Ulusoy, 2020). Smoke occurs in engines mainly due to poor/partial combustion caused by factors such as increased viscosity, higher C/H fraction, incomplete vaporization, and excessive fuel entering the combustion chamber, especially in the premixed combustion phase. Smoke opacity formation occurs under air deficit conditions, which locally exist in the engine cylinder and increase as the air/fuel ratio decreases. Soot is formed by poor oxygen thermal cracking of long-chain molecules (Pan et al., 2021). For all IVC timings and biobutanol–diesel blends, the effect on soot emission is insignificant.

Figure 9

Figure 9. Soot emissions versus crank angle for (A) B10, (B) B20, (C) B30, (D) B0.

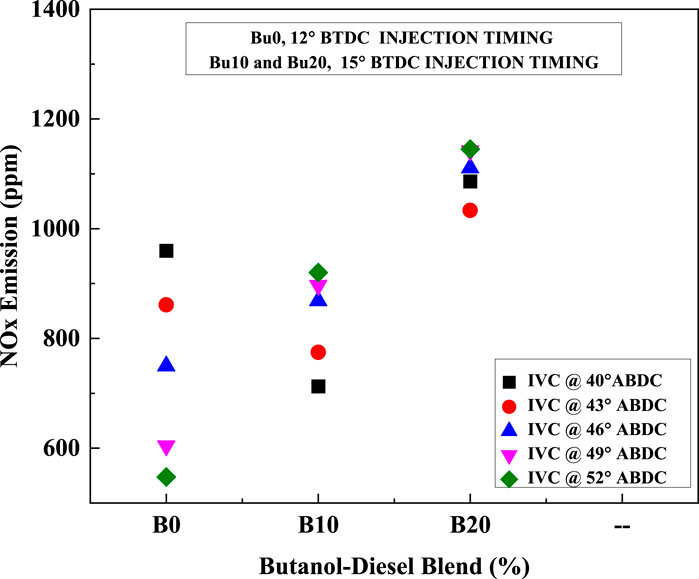
4.4.3 NO_x emission

Figure 10 shows the numerical result of in-cylinder NO_x formation versus crank angle for various bio-butanol–diesel blends (0, 10, and 20, by volume) at different IVC timings. NOx formation relies on several factors, such as cylinder chamber temperatures, mixing time, oxygen availability, and adiabatic temperature of the flame. At higher cylinder temperatures, N₂ and O₂ react and form NOx formations. Higher in-cylinder pressures and temperatures from early valve closing can increase NOx emissions due to higher combustion temperatures. The main reason for NO_x formation in the cylinder is the temperature effect. With the addition of bio-butanol–diesel blend, the oxygen concentration increases due to complete combustion. It is observed that when complete combustion occurs, a high release rate occurs, which increases the temperature (i.e. NO_x emissions) at all IVC.

Figure 10

Figure 10. NO_x emissions versus crank angle.

5 Conclusion

In the present study, numerical investigations were carried out to determine the effects of n-butanol–diesel blend ratios and IVC timing on the combustion and exhaust emission characteristics of CRDI engines. Based on the obtained results, the following conclusions are drawn:

• A significant increase in brake thermal efficiency is observed in the case of biobutanol–diesel blends compared to neat diesel. The enhancement of diffusive combustion is caused by oxygen-enriched blends, and hence, the total combustion duration is shortened. The increase in BTE with butanol blends is also ascribed to its higher burning velocity of 45 cm/s compared to 33 cm/s for diesel. BTE is increased by ∼4.5%, 6%, and 8% for Bu10, Bu20, and Bu30, respectively, compared to Bu0. Based on BTE, the optimum injection timings are obtained at 12° BTDC for Bu0 and 15° BTDC for Bu10, Bu20, and Bu30.

• Peak in-cylinder pressure is increased for all early inlet valve closing timings for all n-butanol–-diesel blends. The highest peak pressure is observed for the Bu30 case. For late inlet valve closing timings, the ignition delay is increased.

• Peak in-cylinder temperature is higher for all LIVC timings. For LIVC timings, combustion is delayed, whereas it is started early for all EIVC timings. Due to the decrease in the effective compression ratio, the start of combustion is delayed. A similar trend is observed for all biobutanol–diesel blends.

• Increasing the butanol content in the blends results in enhanced oxidation, which leads to a reduction in soot and CO due to a higher oxygen/carbon ratio. Smoke opacity formation occurs under air deficit conditions, which locally exist in the engine cylinder and increase as the air/fuel ratio decreases. Soot is formed by poor oxygen thermal cracking of long-chain molecules. For all IVC timings and biobutanol–diesel blends, the effect on soot emissions is insignificant.

• Increasing the butanol content in the blends leads to higher NO_x emissions due to complete combustion. The formation of NO_x in the cylinder is the temperature effect. With the addition of the bio-butanol–diesel blend, the oxygen concentration increases, promoting complete combustion. It is observed that when complete combustion occurs, a high release rate occurs, which increases the temperature (i.e., NO_x emission) at all IVC.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

VL: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. KS: formal analysis, investigation, methodology, supervision, visualization, writing–review and editing, conceptualization, and writing–original draft. DR: formal analysis and writing–review and editing. AY: data curation, formal analysis, investigation, methodology, software, visualization, and writing–review and editing. GK: conceptualization, data curation, formal analysis, investigation, methodology, resources, supervision, visualization, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The support provided by AVL-AST, Graz, Austria, for the usage of AVL-FIRE software is gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Basara, B. (2006). Eddy viscosity transport model based on elliptic relaxation approach. AIAA J. 44, 1686–1690. doi:10.2514/1.20739

CrossRef Full Text | Google Scholar

Bedar, P., Chitragar, P. R., Shivaprasad, K. V., and Kumar, G. N. (2017). Performance and emission analysis of a single cylinder CI engine using Simarouba glauca biodiesel. , 1519– 1527. doi:10.1007/978-81-322-2743-4_145

CrossRef Full Text | Google Scholar

Benajes, J., Molina, S., Martín, J., and Novella, R. (2009). Effect of advancing the closing angle of the intake valves on diffusion-controlled combustion in a HD diesel engine. Appl. Therm. Eng. 29, 1947–1954. doi:10.1016/j.applthermaleng.2008.09.014

CrossRef Full Text | Google Scholar

Bidir, M. G., Millerjothi, N. K., Adaramola, M. S., and Hagos, F. Y. (2021). The role of nanoparticles on biofuel production and as an additive in ternary blend fuelled diesel engine: a review. Energy Rep. 7, 3614–3627. doi:10.1016/j.egyr.2021.05.084

CrossRef Full Text | Google Scholar

Colin, O., and Benkenida, A. (2019). The 3-zones extended coherent flame model (Ecfm3z) for computing premixed/diffusion combustion HAL id: hal-02017326 the 3-zones extended coherent flame model (ECFM3Z) for computing premixed/diffusion combustion. Oil Gas. Sci. Technol. - Rev. IFP 59, 593–609. doi:10.2516/ogst:2004043

CrossRef Full Text | Google Scholar

Demir, U., Coskun, G., Soyhan, H. S., Turkcan, A., Alptekin, E., and Canakci, M. (2022). Effects of variable valve timing on the air flow parameters in an electromechanical valve mechanism – a cfd study. Fuel 308, 121956. doi:10.1016/j.fuel.2021.121956

CrossRef Full Text | Google Scholar

Dukowicz, J. K. (1979). Quasi-steady droplet phase change in the presence of convection. doi:10.2172/6012968

CrossRef Full Text | Google Scholar

Erdiwansyah, , Mamat, R., Sani, M. S. M., Sudhakar, K., Kadarohman, A., and Sardjono, R. E. (2019). An overview of Higher alcohol and biodiesel as alternative fuels in engines. Energy Rep. 5, 467–479. doi:10.1016/j.egyr.2019.04.009

CrossRef Full Text | Google Scholar

Han, J., Lee, J., Kim, H., and Lee, K. (2010). A study on the effect of valve timing on the combustion and emission characteristics for a 4-cylinder PCCI diesel engine. World Acad. Sci. Eng. Technol. 46, 861–867.

Google Scholar

Heywood, J. B. (1998). Internal combustion engine fundamentals. New York.

Google Scholar

Jia, M., Li, Y., Xie, M., and Wang, T. (2013). Numerical evaluation of the potential of late intake valve closing strategy for diesel PCCI (premixed charge compression ignition) engine in a wide speed and load range. Energy 51, 203–215. doi:10.1016/j.energy.2012.12.041

CrossRef Full Text | Google Scholar

Jia, Z. P. M., and Jia, M. (2009). Full engine cycle CFD investigation of effects of variable intake valve closing on diesel PCCI combustion and emissions. Energy Fuels 23, 5855–5864. doi:10.1021/ef900688v

CrossRef Full Text | Google Scholar

Jung, J., Song, S., and Hur, K. B. (2017). Numerical study on the effects of intake valve timing on performance of a natural gas-diesel dual-fuel engine and multi-objective Pareto optimization. Appl. Therm. Eng. 121, 604–616. doi:10.1016/j.applthermaleng.2017.03.036

CrossRef Full Text | Google Scholar

Kalair, A., Abas, N., Saleem, M. S., Kalair, A. R., and Khan, N. (2021). Role of energy storage systems in energy transition from fossil fuels to renewables. Energy Storage 3, 1–27. doi:10.1002/est2.135

CrossRef Full Text | Google Scholar

Kuo, K. K. (1986). Principles of combustion.

Google Scholar

Lamani, V. T., Yadav, A. K, and Kumar, G. N. (2016). “CFD simulation of a common rail diesel engine with biobutanol-diesel blends for various injection timings,” in Biofuels and bioenergy (BICE2016). Editor C. Springer (Springer), 143–160. doi:10.1007/978-3-319-47257-7_14

CrossRef Full Text | Google Scholar

Lamani, V. T., Yadav, A. K., and Gottekere, K. N. (2017a). Performance, emission, and combustion characteristics of twin-cylinder common rail diesel engine fuelled with butanol-diesel blends. Environ. Sci. Pollut. Res. 24, 23351–23362. doi:10.1007/s11356-017-9956-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Lamani, V. T., Yadav, A. K., and Gottekere, K. N. (2020). Effect of exhaust gas recirculation rate on performance, emission and combustion characteristics of a common-rail diesel engine fuelled with n-butanol–diesel blends. Biofuels 11, 389–398. doi:10.1080/17597269.2017.1369631

CrossRef Full Text | Google Scholar

Lamani, V. T., Yadav, A. K., and Narayanappa, K. G. (2017b). Influence of low-temperature combustion and dimethyl ether-diesel blends on performance, combustion, and emission characteristics of common rail diesel engine: a CFD study. Environ. Sci. Pollut. Res. 24, 15500–15509. doi:10.1007/s11356-017-9113-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Lou, Z., and Zhu, G. (2020). Review of advancement in variable valve actuation of internal combustion engines. Appl. Sci. 10, 1216. doi:10.3390/app10041216

CrossRef Full Text | Google Scholar

Naber, J. D., and Reitz, R. D. (1987). “Modeling engine spray/wall impingement,” in SAE technical paper. doi:10.4271/880107

CrossRef Full Text | Google Scholar

Ojeda, W. (2010). Impact of variable valve timing on low temperature combustion. Dir. Engine-Efficiency Emiss. Res.

Google Scholar

Pan, M., Wang, Y., Wei, J., Huang, H., and Zhou, X. (2021). Impact of carbon chain length of alcohols on the physicochemical properties and reactivity of exhaust soot. Sci. Total Environ. 799, 149434. doi:10.1016/j.scitotenv.2021.149434

PubMed Abstract | CrossRef Full Text | Google Scholar

Rakopoulos, D. C., Rakopoulos, C. D., Giakoumis, E. G., Dimaratos, A. M., and Kyritsis, D. C. (2010). Effects of butanol-diesel fuel blends on the performance and emissions of a high-speed di diesel engine. Energy Convers. Manag. 51, 1989–1997. doi:10.1016/j.enconman.2010.02.032

CrossRef Full Text | Google Scholar

Reitz, R. (1988). Modeling atomization processes in high-pressure vaporizing sprays. At. Spray. Technol. 3, 309–337.

Google Scholar

Sarathy, S. M., Thomson, M. J., Togbé, C., Dagaut, P., Halter, F., and Mounaim-Rousselle, C. (2009). An experimental and kinetic modeling study of n-butanol combustion. Combust. Flame 156, 852–864. doi:10.1016/j.combustflame.2008.11.019

CrossRef Full Text | Google Scholar

Sayin, C. (2010). Engine performance and exhaust gas emissions of methanol and ethanol-diesel blends. Fuel 89, 3410–3415. doi:10.1016/j.fuel.2010.02.017

CrossRef Full Text | Google Scholar

Sjöblom, J. (2014). in Sustainable automotive technologies (Cham: Springer). doi:10.1007/978-3-319-17999-5_6

CrossRef Full Text | Google Scholar

Surisetty, V. R., Dalai, A. K., and Kozinski, J. (2011). Alcohols as alternative fuels: an overview. Appl. Catal. A Gen. 404, 1–11. doi:10.1016/j.apcata.2011.07.021

CrossRef Full Text | Google Scholar

Tatschl, R. (2009). 3D-CFD simulation of mixture formation, combustion and heat transfer processes with AVL FIRE. NAFEMS Int. J. CFD Case Stud. 8, 51–63. doi:10.59972/r5w8vet6

CrossRef Full Text | Google Scholar

Truong, T. T., Nguyen, X. P., Pham, V. V., Le, V. V., Le, A. T., and Bui, V. T. (2021). Effect of alcohol additives on diesel engine performance: a review. Energy Sources, Part A recover. Util. Environ. Eff. 00, 1–25. doi:10.1080/15567036.2021.2011490

CrossRef Full Text | Google Scholar

Ulusoy, Y. (2020). Investigation of particulate matter by FTIR, TEM and elemental analyses in a diesel engine operating on diesel and waste cooking oil-biodiesel. Environ. Sci. Pollut. Res. 27, 500–509. doi:10.1007/s11356-019-06741-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Vadivelu, T., Ramanujam, L., Ravi, R., Vijayalakshmi, S. K., and Ezhilchandran, M. (2023). An exploratory study of direct injection (DI) diesel engine performance using CNSL—ethanol biodiesel blends with hydrogen. Energies 16, 415. doi:10.3390/en16010415

CrossRef Full Text | Google Scholar

Veza, I., Irianto, T., Hoang, A., Yusuf, A. A., Herawan, S. G., Soudagar, M. E. M., et al. (2023). Effects of Acetone-Butanol-Ethanol (ABE) addition on HCCI-DI engine performance, combustion and emission. Fuel 333, 126377. doi:10.1016/j.fuel.2022.126377

CrossRef Full Text | Google Scholar

Wasilewski, J., Krzaczek, P., Szyszlak-Bargłowicz, J., Zając, G., Koniuszy, A., Hawrot-Paw, M., et al. (2024). Evaluation of nitrogen oxide (NO) and particulate matter (PM) emissions from waste biodiesel combustion. Energies 17 (2), 328–26. doi:10.3390/en17020328

CrossRef Full Text | Google Scholar

Wolde-Rufael, Y., and Weldemeskel, E. M. (2020). Environmental policy stringency, renewable energy consumption and CO2 emissions: panel cointegration analysis for BRIICTS countries. Int. J. Green Energy 17, 568–582. doi:10.1080/15435075.2020.1779073

CrossRef Full Text | Google Scholar

Wu, J., and Hobbs, R. (2002). Key issues and research priorities in landscape ecology: an idiosyncratic synthesis. Landsc. Ecol. 17, 355–365. doi:10.1023/A:1020561630963

CrossRef Full Text | Google Scholar

Yusuf, A. A., Inambao, F. L., and Farooq, A. A. (2020). Impact of n-butanol-gasoline-hydrogen blends on combustion reactivity, performance and tailpipe emissions using TGDI engine parameters variation. Sustain. Energy Technol. Assessments 40, 100773. doi:10.1016/j.seta.2020.100773

CrossRef Full Text | Google Scholar

Zammit, J. P., McGhee, M. J., Shayler, P. J., Law, T., and Pegg, I. (2015). The effects of early inlet valve closing and cylinder disablement onfuel economy and emissions of a direct injection diesel engine. Energy 79, 100–110. doi:10.1016/j.energy.2014.10.065

CrossRef Full Text | Google Scholar

Žvar Baškovič, U., Katrašnik, T., Faussone, G. C., Grilc, M., and Seljak, T. (2023). Ultra-low emission power generation utilizing chemically stabilized waste plastics pyrolysis oil in RCCI combustion concept. J. Environ. Manage. 344, 118711. doi:10.1016/j.jenvman.2023.118711

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature