- 1School of Software, Changsha Social Work College, Changsha, China
- 2School of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha, China
- 3College of Electrical and Information Engineering, Hunan University, Changsha, China
As the electric power market reform deepens, the strategic role of load aggregators in demand-side response becomes increasingly important. The inherent variability of distributed renewable energy generation and user demand response often leads to a mismatch between the purchased electricity and the market bid volume, resulting in punitive costs for companies. To address this issue, this study treats demand-side controllable loads as dispatchable resources and proposes a tiered pricing strategy to adjust power distribution. By establishing a Stackelberg leader-follower game model, the study promotes a mutually beneficial relationship between load aggregators and controllable load users. Through case studies, this paper examines the operational profits of load aggregators and the power adjustment behaviors of controllable load users under tiered and fixed compensation pricing schemes. The results indicate that tiered compensation pricing significantly reduces punitive costs and enhances user participation in demand response.
1 Introduction
In recent years, the deepening of electricity market reforms has increasingly highlighted the strategic role of load aggregators in demand-side response. Time-of-use pricing mechanisms, as a crucial tool for electricity demand-side management, more closely align electricity prices with supply costs through differentiated pricing. This effectively guides users to adjust their electricity consumption at different times, ensuring the safety and stability of the power system (Zhang et al., 2021; Liu et al., 2023). With the increasing complexity and interdependence of power systems, especially concerning False Data Injection Attacks (FDIA) and Voltage Stability Assessment (VSA), the vulnerability and resilience of power systems have become key research focuses (Yang and Wang, 2024). To address these challenges, various innovative methods have been proposed. For instance, Ding and Liu (2017) introduced an AC false data injection attack method based on robust tensor principal component analysis, which generates false data without requiring system parameters, overcoming the limitations of traditional bad data detection methods. Additionally, Yang et al. (2023) proposed a domain-adaptive voltage stability assessment method that quickly adapts to topological changes, reducing retraining needs and improving assessment accuracy. These research findings provide significant theoretical and practical support for further refining pricing mechanisms.
As key intermediaries in the electricity market, load aggregators are responsible for integrating and scheduling various demand-side resources. By providing aggregated load curves and related information, load aggregators can participate in competitive bidding for demand response and sign various trading contracts (Lv et al., 2023). Moreover, considering the potential threat of false data injection attacks to the power system, load aggregators need the capability to counter such attacks to ensure data authenticity and system stability (Yang et al., 2024).
Different countries exhibit significant differences in power adjustment and balancing mechanisms. For example, the UK and Nordic countries tend to adopt decentralized market models, adjusting and settling deviation power through intraday balancing markets (Khodadadi et al., 2020). In contrast, the US and Australia prefer centralized market models, where bids and quantities are submitted on trading platforms within a specified time and matched based on price and time priority (Çelebi and Flynn, 2020). Currently, China is transitioning from a long-term trading market to a combined long-term and spot trading market. Provinces are experimenting with decentralized or centralized market models in the spot market based on local conditions (Liangyuan et al., 2022). For instance, regions like Western Inner Mongolia and Fujian conduct decentralized spot markets based on long-term physical contracts (Zhu et al., 2023). In this model, generators and consumers independently determine power consumption curves in the day-ahead stage and adjust imbalances through day-ahead and balancing trades (Watanabe et al., 2018). The essence of this model lies in the scheduling arrangements based on bilateral contracts, with system dispatch departments ensuring contract fulfillment and power balance dispatch (Reddy et al., 2015). However, most regions in China still conduct spot market transactions through monthly settlement of long-term trades, leading to significant imbalance penalty costs for load aggregators (Jiang et al., 2019; Lu et al., 2022). Therefore, considering the uncertainties in load demand and distributed power output, it is crucial for load aggregators to maximize their benefits by setting reasonable compensation prices to incentivize controllable loads to participate in demand response transactions.
Designing reasonable, flexible, and effective demand-side pricing mechanisms is critical for motivating user participation in demand response and improving resource utilization efficiency (Xu et al., 2021; Jiang et al., 2023). In terms of organizing electricity market transactions, demand-side users can be classified into single market type transactions and multi-type market transactions. In single market type transaction scenarios, drawing from research experiences in the stock trading field, Chen et al. (2019) proposed a trading algorithm that combines auction and continuous bidding. Additionally, a fixed-ratio total deviation settlement method was designed for non-full transactions, and a phased user-side deviation evaluation mechanism was introduced (Wang L. et al., 2023). To address the economic rationality issues of traditional deviation balancing mechanisms, a pre-bid-based monthly deviation balancing mechanism was proposed to minimize deviation adjustment costs, encouraging low-cost units to replace high-cost units for power generation (Fu et al., 2022). In the context of coupled multi-type market transactions, the design methods of electricity price difference contracts were discussed, including setting contract prices, effective directions, benchmark prices, and design parameters for decomposing contract quantities (Nobis et al., 2020). Additionally, considering the practical situation of China’s electricity trading and dispatch management system, a day-ahead market clearing model compatible with long-term physical contracts was proposed to bridge the gap between long-term physical contract delivery and grid operation constraints (Liu et al., 2020). The reinforcement learning methods for studying electricity spot market pricing mechanisms examined the impact of different pricing mechanisms on the organization of long-term trades (Wang Y. et al., 2023). Finally, Gong et al. (2021) proposed a government-authorized price difference contract settlement mechanism, considering fairness and hedging functions as a differentiated and predetermined approach.
Based on the above analysis, this paper aims to explore the optimization of interests between load aggregators and proxy power users. The innovations are in several aspects: First, considering the deviation penalties of long-term trading contracts, positive and negative balance penalty prices are introduced to evaluate the penalty costs arising from the discrepancy between bid volumes and actual electricity consumption. Second, utilizing demand-side storage, distributed photovoltaics, and controllable loads as dispatchable resources, a multi-option compensation contract for power regulation of controllable load/storage devices based on the cost functions of controllable load users or storage users is proposed. Furthermore, a Stackelberg game model is established to explore the application of tiered pricing strategies in demand response, aiming to reduce power trading deviation costs while enhancing user participation and economic benefits. Lastly, a reverse induction method based on genetic algorithms is employed to solve the proposed model, and the effectiveness of the model and method is verified through case simulations.
Main Contributions of This Paper:
1. Proposing a multi-option controllable load power regulation compensation contract based on hierarchical pricing, effectively reducing deviation costs in electricity transactions and providing flexible pricing options to meet different user needs.
2. Constructing a Stackelberg leader-follower game model to optimize compensation pricing strategies, achieving an economic benefit balance between load aggregators and users.
3. Using genetic algorithms to verify the effectiveness of the proposed model and strategies, providing theoretical support and empirical evidence for the formulation of demand response strategies in the electricity market.
2 Problem description
The operational model of load aggregators in the electricity market involves the integration of load resources, market bidding, and trading processes. By aggregating distributed renewable energy generation and user demand, load aggregators can more accurately predict and adjust loads, thereby reducing penalty costs associated with deviations. Additionally, by integrating different types of load resources, such as residential users, commercial users, and storage systems, load aggregators can enhance system flexibility and responsiveness, ensuring grid stability and efficiency. However, penalty costs related to power deviations increase operational pressure on load aggregators, necessitating effective demand response strategies and compensation mechanisms to mitigate these costs.
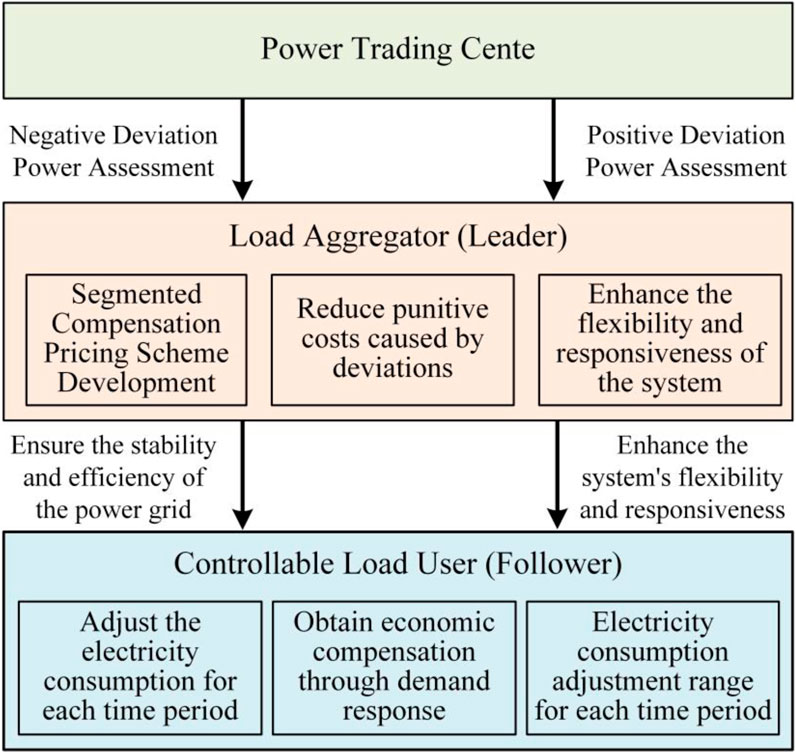
To address these issues, this paper proposes a bi-level game approach based on a Stackelberg game model. In the game, the load aggregator, acting as the leader, first formulates a reasonable power procurement strategy and tiered compensation pricing scheme to maximize operational revenue and incentivize user participation in demand response. The controllable load users, as followers, adjust their electricity consumption behavior according to the compensation strategy provided by the load aggregator, obtaining economic compensation by reducing electricity consumption during peak periods or increasing consumption during off-peak periods. Through this bi-level game model, load aggregators can significantly reduce deviation penalties and related costs while enhancing user participation in demand response, achieving mutually beneficial economic outcomes. The process flow of the problem description is illustrated in Figure 1.
2.1 Design of load aggregator operating mechanism
As renewable energy and energy storage systems continue to develop, traditional grid users are gradually transitioning from passive recipients to active participants in power balancing. Load aggregators play a crucial role by integrating the loads of numerous residential, commercial, and energy storage users. This not only enhances the overall flexibility and responsiveness of the system but also significantly reduces costs associated with power deviations. Load aggregators are essential in the electricity market, facilitating the effective utilization of distributed generation and demand response resources.
In medium-to long-term trading in the electricity market, load aggregators develop purchasing and flexible pricing strategies based on forecasts of end-user demand, expected production from distributed generation, and market fluctuation costs. The trading center assesses load aggregators to ensure the accuracy of their load responses and power assessments. In turn, load aggregators formulate their purchasing strategies and pricing schemes based on this information (Yang et al., 2022). This process requires load aggregators to possess precise forecasting capabilities and the flexibility to adjust strategies in a continuously evolving market environment.
Due to the volatility of distributed generation and the uncertainty of load demand, load aggregators may face discrepancies when assessing power deviations and actual consumption. The trading center imposes deviation assessment fees based on the positive and negative imbalance of deviation power, compelling load aggregators to make accurate forecasts and manage loads effectively. By utilizing a segmented compensation pricing mechanism, load aggregators incentivize users to modify their consumption behaviors, reducing usage during peak periods while increasing consumption during off-peak periods, thereby achieving overall system balance.
As illustrated in Figure 1, load aggregators serve a critical role in connecting the demand side with the power supply side. The demand side consists of a large number of dispersed and controllable load devices, such as air conditioners, electric vehicles, and water heaters. Load aggregators secure control over these controllable loads by signing contracts with end users of these devices (Bruninx et al., 2020). While ensuring that user comfort is not compromised, load aggregators optimize the operation and control of these devices to adjust power deviations during peak and off-peak periods, thereby minimizing the punitive costs associated with deviations. Load aggregators not only enhance system flexibility and responsiveness through the integration of load resources but also encourage users to adjust their consumption behaviors through effective pricing strategies. The specific power assessment formula established by load aggregators is as follows:
The trading center establishes the baseline electricity purchase quantity
In the formula
2.2 Design of segmented compensation mechanism for controllable load power adjustment
To implement effective power adjustments for controllable loads, load aggregators have designed a segmented compensation mechanism that includes both power reduction compensation contracts and power increase compensation contracts. These contracts provide varying levels of financial incentives based on the time sensitivity and cost differences of load adjustments, encouraging users to reduce consumption during peak electricity demand periods and increase usage during off-peak periods.
Through power reduction contracts, users are compensated for decreasing their electricity consumption during high-demand intervals, which helps alleviate the burden on the grid and reduce reliance on expensive emergency power sources. In contrast, power increase contracts incentivize users to take advantage of lower electricity prices during off-peak periods, thereby optimizing the energy distribution within the grid.
To ensure the effectiveness of this compensation mechanism, a multi-option segmented compensation design has been introduced, allowing different types of loads to select the most suitable compensation plan based on their specific circumstances (Bouakkaz et al., 2020). This flexible compensation strategy not only considers the economic costs associated with load adjustment for users but also reflects their contributions to grid stability, thus motivating various users to actively participate in demand response activities within the electricity market.
2.2.1 Compensation contract for controllable load power reduction
Demand aggregators create tiered power reduction compensation contracts for users participating in load shedding, offering
Due to the varying costs of load power reduction for controllable load users across different time periods, implementing a uniform power reduction compensation price may hinder user engagement in demand response initiatives. Following the methodology proposed in the literature (Wang et al., 2021), the power reduction compensation price
In the formula:
2.2.2 Controllable load incremental power compensation contract
When demand aggregators experience a negative deviation in electricity volume, the economic compensation
In the formula:
3 Dynamic compensation pricing model for controllable load power adjustment based on leader-follower game decision-making
Implementing controllable load management strategies within power systems presents a complex optimization challenge involving dynamic interactions between load aggregators and multiple controllable load users. These interactions are governed by supply interruption compensation contracts established between the load aggregator and users, where the operating costs of the load aggregator are directly influenced by the power adjustments of controllable load users. Users are required to adjust their electricity consumption behavior in accordance with the demand response directives issued by the load aggregator to achieve cost efficiency while ensuring the stability of the power supply system.
To address this issue, this paper constructs an interactive model among the load aggregator and multiple controllable load users, which can be framed as a
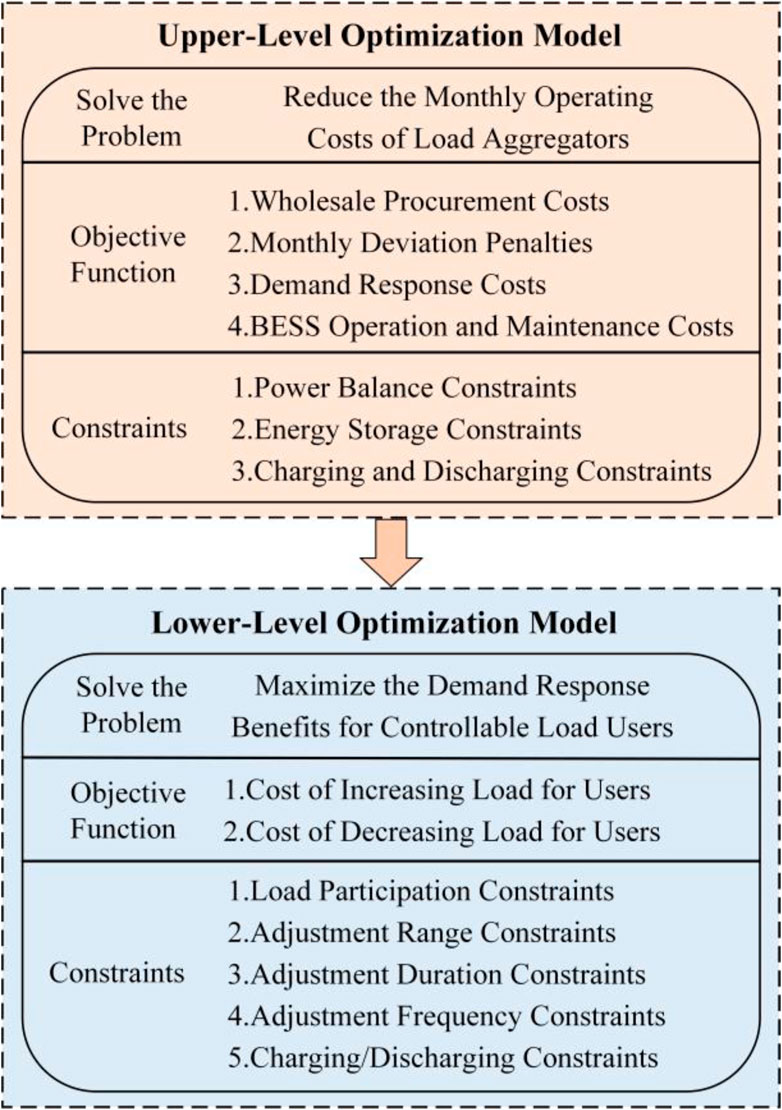
The upper-level optimization model is managed by the load aggregator, aiming to minimize its monthly operating costs. These costs encompass wholesale electricity procurement expenses, penalties associated with monthly deviation in consumption, demand response costs for controllable loads, and operational maintenance costs for Battery Energy Storage Systems (BESS). To achieve this, the load aggregator must establish capacity increase or decrease compensation contracts and make charging and discharging decisions for the BESS. During the upper-level optimization process, constraints regarding power balance, storage operational limits, and charging/discharging regulations must be satisfied.
Conversely, the lower-level optimization model is handled by the controllable load users, who seek to maximize their demand response benefits. Users gain economic compensation by adjusting their loads to either reduce or increase electricity consumption. The lower-level optimization process must adhere to constraints related to participation in demand response, adjustments in controllable load power range, duration of power adjustments, frequency of power adjustments, and energy storage charging/discharging limitations.
To accurately simulate and predict system behavior under this game structure, the load aggregator can employ a Monte Carlo sampling method to generate typical daily scenarios based on monthly trading data, thereby estimating monthly deviation in consumption. This statistical simulation technique not only effectively captures the volatility of the electricity market but also provides decision support aimed at optimizing operational costs and maximizing user benefits.
By designing a segmented compensation pricing model, the load aggregator can incentivize users to participate in demand response programs, leading to effective control of monthly consumption deviations and significant reductions in penalty costs. This strategic pricing mechanism optimizes the operational costs of the load aggregator while fostering active user engagement through economic incentives, collectively promoting the stability and sustainable development of the electricity market.
Figure 2 illustrates the structure of the Stackelberg game model proposed in this paper, which simulates the interactive decision-making processes between load aggregators and controllable load users.
3.1 Upper-level optimization model
The upper-level optimization problem of the model aims to effectively reduce the monthly operating costs of the load aggregator by incorporating capacity increase or decrease power compensation contracts, along with the charging and discharging power of the Battery Energy Storage System (BESS), as key decision variables.
3.1.1 Upper-level optimization objective function
The monthly operational costs of demand aggregators consist of four components: the cost of purchasing electricity from the wholesale market, denoted as
In the model,
3.1.2 Upper-level optimization constraints
(1) Power Balance Constraints
In the formula:
(2) Constraints on Energy Storage Operation
In the equation:
(3) Energy Storage Charging and Discharging Constraints
Equations 21, 22 represent the charging and discharging conversion constraints of the energy storage system; Equation 23 specifies that at any given moment, the Battery Energy Storage System (BESS) can only be in one of three states: charging, discharging, or idle.
3.2 Lower-level optimization model
3.2.1 Lower-level optimization objective function
The lower-level optimization problem in the model aims to maximize the demand response benefits for controllable load users (see Equations 24–31). By adjusting the power increases and decreases across different time periods, the model seeks to enhance system flexibility and efficiency under varying demand and market conditions, while also maintaining system stability and economic viability.
As delineated in reference (Ma et al., 2023), the costs associated with increasing.
In the equation,
3.2.2 Lower-level optimization constraints
(1) Controllable Load Participation Constraints
If participation in demand response increases the user’s own benefits, users will voluntarily enter into power adjustment contracts with the load aggregator. Conversely, if participation does not yield additional benefits, users will choose not to participate. This means that the compensation received for power adjustments must not be less than the additional losses incurred by these adjustments. This condition can be expressed as:
(2) Controllable Load Power Adjustment Range Constraints
In the equation:
(3) Controllable Load Power Adjustment Duration Constraints
In the equation,
(4) Constraints on the Frequency of Power Adjustments for Controllable Loads
To prevent excessive and prolonged power adjustments for users with controllable loads, constraints have been imposed on the frequency of such adjustments during the scheduling period, as delineated in Equations 36, 37.
In the equation,
(5) Energy Storage Charging and Discharging Constraints
Equation 38 indicates that user
4 Model solution method
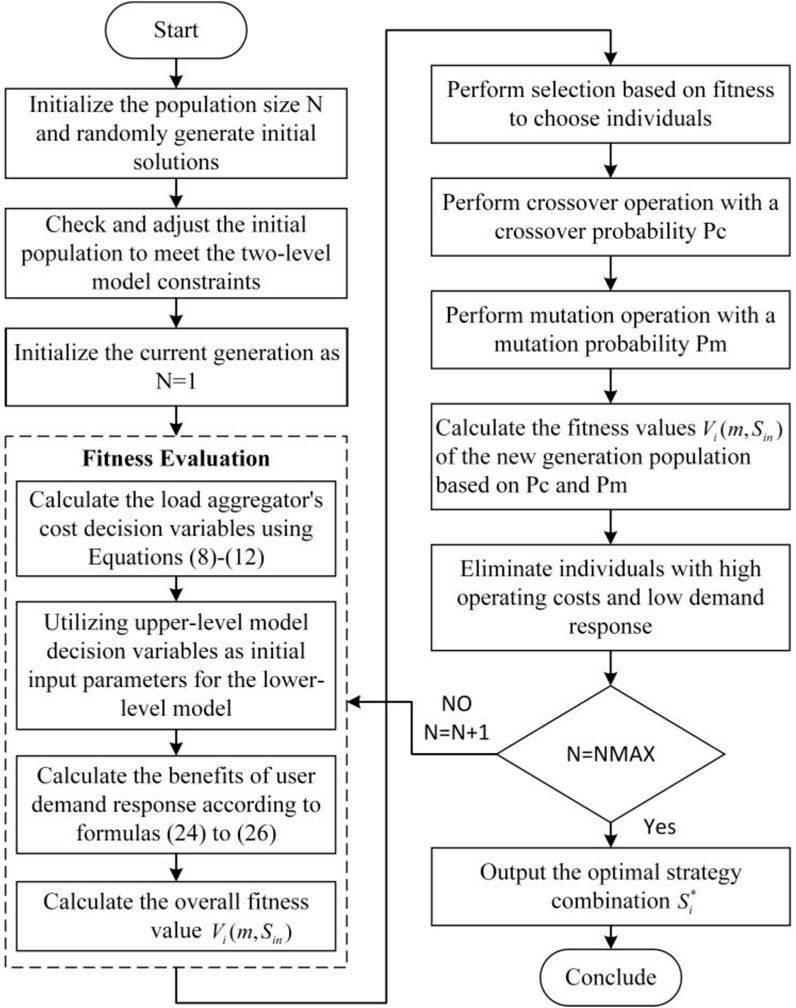
In this study, we employ the Stackelberg game theory to model and address the interaction and decision-making processes between load aggregators and controllable load users. The Stackelberg game model is particularly suitable for such leader-follower scenarios, allowing for detailed analysis and prediction of the strategic interactions between the load aggregator (as the leader) and controllable load users (as the followers) in the electricity market. To account for the nonlinearity and complexity of the problem, we integrate nonlinear programming techniques with genetic algorithms for optimization.
The genetic algorithm generates new populations through operations such as selection, crossover, and mutation, increasing population diversity to prevent premature convergence while continually optimizing strategies throughout the iterative process.
In the model, the load aggregator acts as the leader and is represented by the variable
During the strategy selection process, the load aggregator selects the optimal strategy
To provide a clearer representation of the model solution process, we have designed a flowchart for the two-level optimization model, as shown in Figure 3. This diagram illustrates the steps from parameter initialization, initial population generation, fitness calculations, to strategy updates and optimization during the iterative process. Given the nonlinearity of the problem, the model utilizes genetic algorithms to solve the Stackelberg leader-follower game model.
The genetic algorithm generates new populations through operations such as selection, crossover, and mutation. First, the roulette wheel selection method is employed to choose high-fitness individuals (with a crossover probability denoted as
In the initial population generation and adjustment phase, the load aggregator selects strategies from the strategy space
If the new fitness results indicate an improvement in strategies, the selection, crossover, and mutation operations continue, calculating the fitness values
5 Analysis of case studies
5.1 Case study parameters
This study focuses on the participation of a load aggregator representing a mixed-use residential and commercial community in the electricity market. The community comprises six mixed-use buildings equipped with photovoltaic panels and houses a total of 200 households. The data used in this study is sourced from the actual load data of the Source-Load Aggregation Interaction Response Platform of Hunan Power Company in August 2023. This data is used to validate the model’s effectiveness and practicality.
To comprehensively derive the power usage patterns of the entire community, we conducted a Monte Carlo simulation based on the electricity consumption data of these 200 households, generating scenarios for power deviation coefficients. These coefficients follow a Gaussian distribution with a mean of 0 and a standard deviation of 1.9651. The range for evaluating power deviations in all simulated scenarios is set to ±2%.
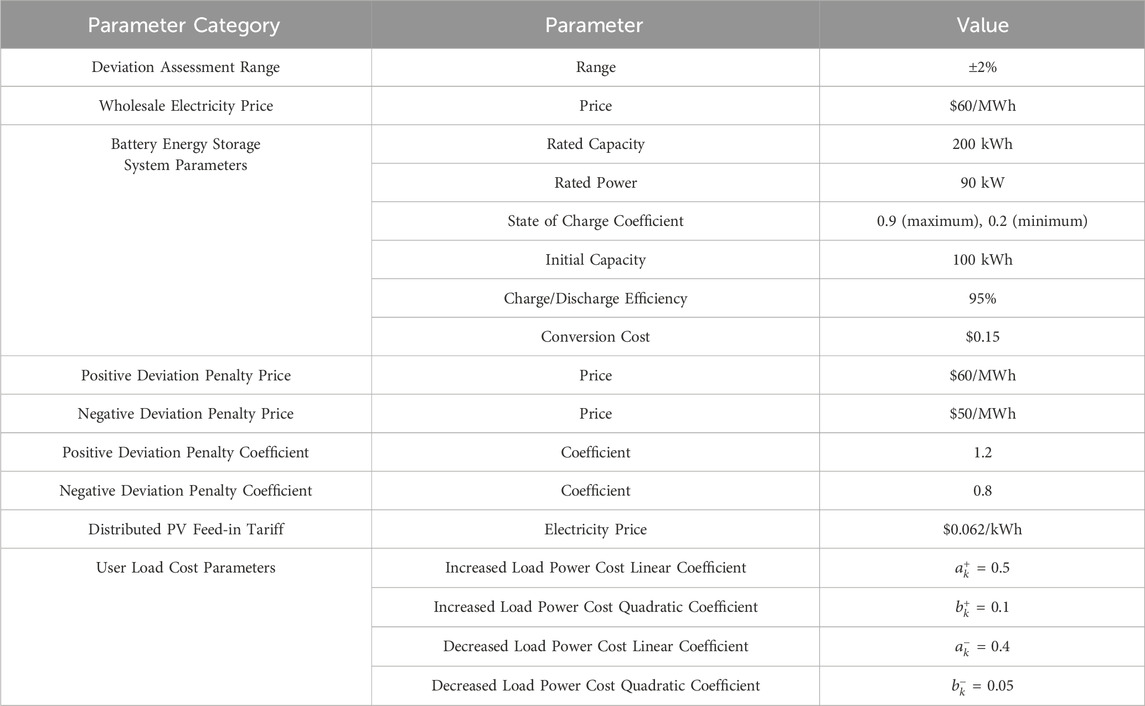
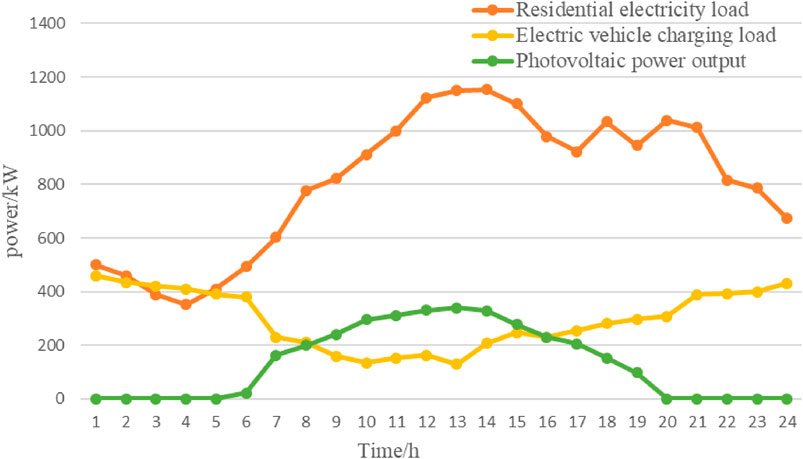
In the case analysis, we assume a wholesale electricity price of $60 per megawatt-hour, utilizing the actual load data from the community in August. The parameters involved in the model are listed in Table 1, “Price Range for Peak Shaving Services” and Table 2, “Key Parameters for Load Aggregator Pricing Strategies” These tables display the electricity demand of 100 households on a typical day in August. Figure 4 illustrates the load curve for the entire community on a typical day in August, based on the simulation predictions.
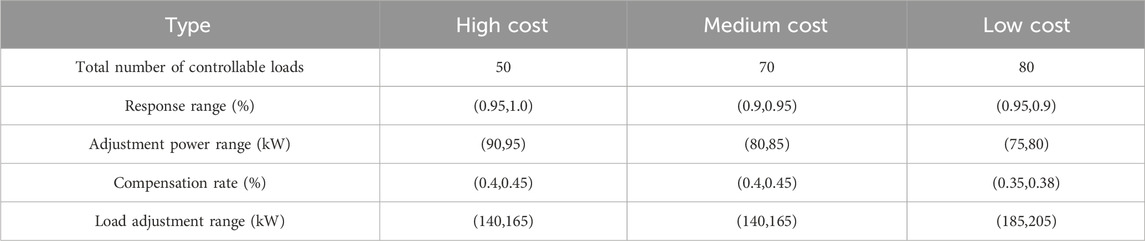
To clearly present the calculation results, we assume that the aggregated controllable loads are divided into three types of users: high-cost, medium-cost, and low-cost. The maximum frequency of power adjustments for each type of controllable load is limited to four times within the entire scheduling period. The parameters for the battery energy storage system are set as follows: rated capacity of 200 kWh, rated power of 90 kW, maximum and minimum state of charge coefficients of 0.9 and 0.2, respectively, initial capacity of 100 kWh, charge and discharge efficiency of 95%, and both discharge-to-charge and charge-to-discharge conversion costs of $0.15. The parameters for different types of controllable loads are shown in Table 3.
5.2 Monthly market deviation assessment results under different scenarios
This section compares and analyzes the effectiveness of demand response programs by setting three different operational scenarios. The specific scenarios are described as follows:
1. Scenario 1: Traditional Mode: In this scenario, all loads are traditional, and no demand response programs are implemented. Consequently, deviations in electricity consumption are not effectively managed, leading to higher deviation assessment costs and the highest total cost.
2. Scenario 2: Fixed Compensation Price Mode: In this scenario, the load aggregator employs a fixed compensation price strategy to incentivize controllable loads to mitigate deviations in electricity consumption. This strategy induces a moderate level of user response, partially covering the deviation, resulting in lower overall costs compared to Scenario 1.
3. Scenario 3: Tiered Compensation Contract Mode: This scenario uses a tiered compensation contract to more actively incentivize controllable loads to balance electricity consumption deviations. Due to the highest level of user participation, deviation assessment costs are significantly reduced. Although the duration and frequency of power adjustments for controllable loads are constrained, this scenario achieves the lowest total cost and the most effective deviation mitigation among all scenarios.
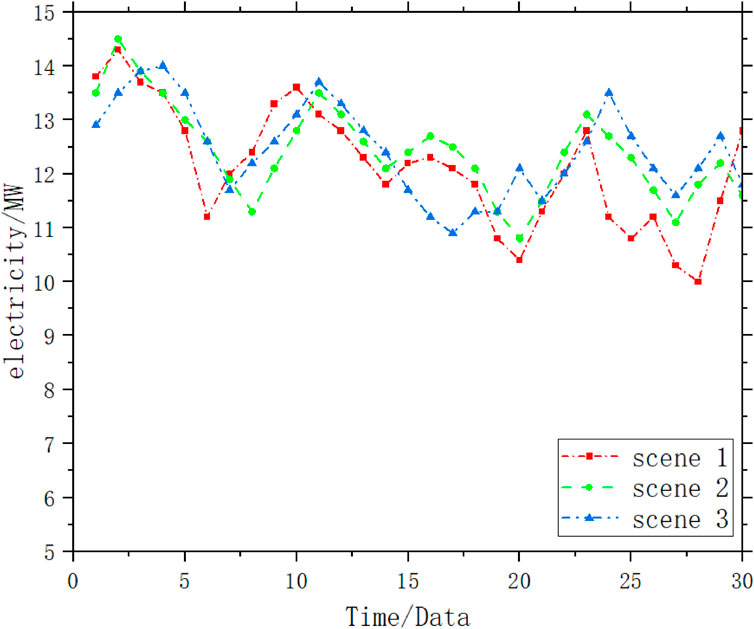
Figure 5 illustrates the monthly electricity consumption variations under different scenarios, visually depicting the impact of each scenario on electricity management. Additionally, to gain deeper insights into the effectiveness of different scenarios, we analyzed the outlier data points and found that the tiered compensation strategy excels in managing fluctuating loads, significantly reducing overall deviation costs. This demonstrates that flexible compensation strategies not only motivate active user participation but also enhance system stability.
Table 4 compares the cost situations of load aggregators under different scenarios (see Table 4). From the table, it is evident that Scenario 3, employing a dynamic compensation strategy, performs best in reducing deviation energy and lowering overall costs.
5.3 Revenue analysis under different deviation penalty prices
To explore the impact of different deviation penalty prices on the economic behavior of electricity market participants, this section sets multiple deviation penalty coefficients to assess their effect on the monthly operating costs of load aggregators and the demand response benefits for controllable load users. Additionally, it analyzes how the compensation prices for power adjustments can be modified under these varying penalty prices to optimize market behavior and enhance overall system efficiency.
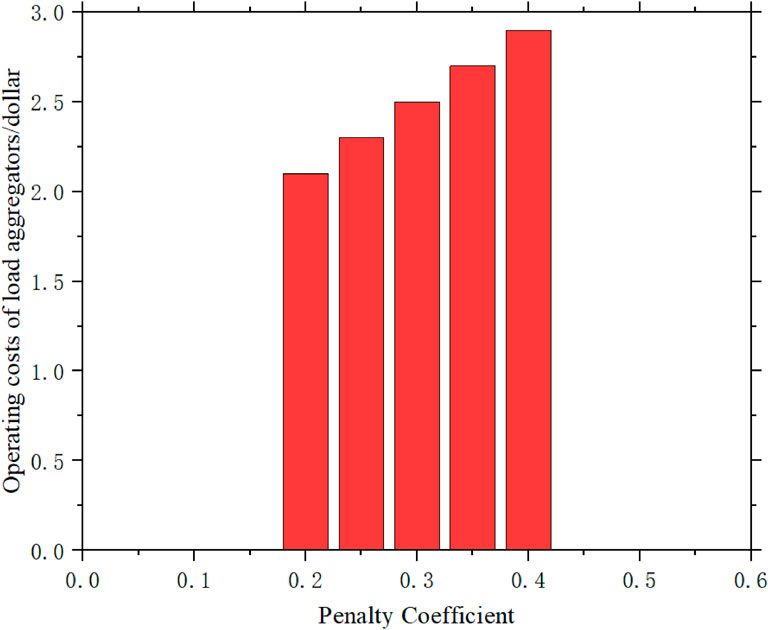
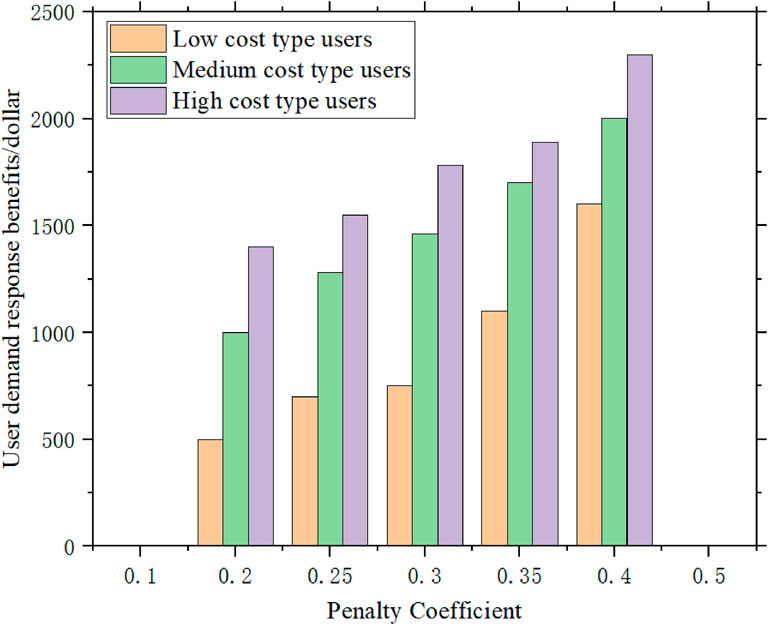
Figure 6 shows the trend of increasing monthly operating costs for load aggregators as the deviation penalty coefficients rise. Moreover, as illustrated in Figure 7, user compensation benefits also increase with higher penalty coefficients, reflecting the market’s sensitivity to deviations and its response to strategic adjustments.
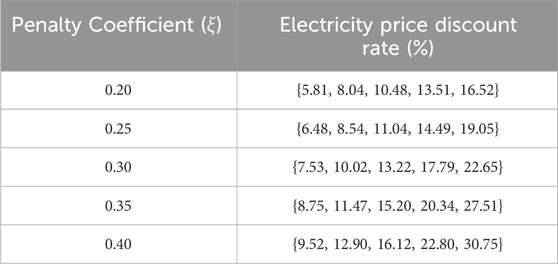
Tables 5, 6 detail the compensation prices for power reduction and power increase under different deviation penalty coefficients, respectively. The data indicate that as the penalty coefficients increase, both the compensation rate and the price discount rate for electricity show an upward trend. This strategy aims to incentivize users to adjust their electricity consumption behavior, thereby reducing the overall operating costs of the market and enhancing system stability.
As the deviation penalty coefficients increase, the monthly operating costs for load aggregators rise, compelling them to enhance the management of controllable loads and optimize their strategies. This economic pressure motivates load aggregators to actively seek efficient demand response solutions to minimize electricity procurement costs and deviation penalties.
By increasing the compensation prices for controllable loads, users are incentivized to flexibly adjust their electricity usage patterns. This not only helps aggregators control costs but also improves the load regulation capability and stability of the entire power system. Additionally, as compensation prices are adjusted, the participation and benefits of controllable load users increase accordingly.
This dynamic further promotes the application and development of demand-side response technologies, contributing to the dual enhancement of economic and environmental benefits in the electricity market.
6 Conclusion
This paper proposes a segmented multi-option controllable load power adjustment compensation contract based on a game theory framework, aiming to optimize demand response strategies in the long-term market environment prior to the spot market. This approach treats demand-side controllable loads as dispatchable resources. By establishing segmented compensation contracts between load aggregators and users, the method gains control over the operation of controllable load equipment, optimizing their operation to reduce the discrepancy between bid volumes and actual power consumption.
1. Economic Win-Win Objective: To achieve an economic win-win situation for both load aggregators and controllable load users, this study constructs a 1-K type Stackelberg leader-follower game model. This model thoroughly considers the economic benefits of both load aggregators and controllable load users, reducing the operating costs of the load aggregators while enabling controllable load users to gain economic benefits through power adjustments.
2. Design of Segmented Compensation Price Contracts: The segmented compensation price contracts designed in this study are valuable for motivating users to participate in demand response. This not only helps load aggregators formulate more effective demand response pricing strategies but also enhances user participation in demand response by inducing controllable load users to demonstrate demand elasticity, thereby effectively reducing the penalty costs for load aggregators.
3. Monte Carlo Simulation and Optimization: Using the Monte Carlo method, the compensation prices for incentivizing controllable load user power adjustments were optimized based on deviation scenarios generated in typical daily scenarios of monthly transactions. Extending this model to shorter time scales, such as the intraday balancing market, could further smooth out deviations arising from day-ahead market transactions. However, due to the current maturity level of China’s electricity market, along with market mechanisms and technological and economic constraints, this study has not delved deeper into the spot market analysis.
This research provides an innovative perspective to optimize demand response strategies in the electricity market and offers practical strategic recommendations for electricity market designers to enhance overall market efficiency and reliability. Future research can explore broader market conditions and additional model application scenarios to further validate and expand the findings of this study. Case studies indicate that segmented compensation pricing strategies significantly reduce the penalty costs for load aggregators by 25% and increase user participation by 30%. These results demonstrate the effectiveness and potential economic benefits of segmented compensation pricing strategies in demand response.
4. Future Work: In our future work, we will consider integrating artificial intelligence and machine learning technologies to optimize demand response strategies. Additionally, we will study the economic viability and implementation effects of segmented compensation strategies under different policy environments, providing decision support for policymakers.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.
Author contributions
HY: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. ZZ: Data curation, Funding acquisition, Software, Writing–original draft. RL: Conceptualization, Funding acquisition, Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. WZ: Conceptualization, Methodology, Project administration, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the National Natural Science Foundation of China (7217010719 and 72171026); supported by Hunan Provincial Natural Science Foundation of China (2022JJ60103 and 2024JJ8025); funded by the Innovation Fund for Industry-University-Research Cooperation of Chinese Universities - Next-Generation Information Technology Innovation Project (2021ITA10023); and supported by the Hunan Province Science Popularization Special Project (2022ZK4045).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bouakkaz, A., Mena, A., Haddad, S., and Ferrari, M. (2020). Efficient energy scheduling considering cost reduction and energy saving in hybrid energy system with energy storage. J. energy storage 33, 101887. doi:10.1016/J.EST.2020.101887
Bruninx, K., Pandžić, H., Cadre, H., and Delarue, E. (2020). On the interaction between aggregators, electricity markets and residential demand response providers. IEEE Trans. Power Syst. 35, 840–853. doi:10.1109/TPWRS.2019.2943670
Çelebi, O., and Flynn, J. (2020). Priority design in centralized matching markets. ERN Mark. Struct. Top. doi:10.2139/ssrn.3382580
Chen, K., Lin, J., and Song, Y. (2019). Trading strategy optimization for a prosumer in continuous double auction-based peer-to-peer market: a prediction-integration model. Appl. Energy 242, 1121–1133. doi:10.1016/J.APENERGY.2019.03.094
Ding, Y., and Liu, J. (2017). “Real-time false data injection attack detection in energy internet using online robust principal component analysis,” in 2017 IEEE conference on energy internet and energy system integration (EI2), 1–6. doi:10.1109/EI2.2017.8245663
Fu, T., Li, K., and Xie, T. (2022). Research on optimal model of generation dispatching for medium and long-term electricity contracts based on CPLEX algorithm. IEEE 6th Inf. Technol. Mechatronics Eng. Conf. (ITOEC) 6, 304–308. doi:10.1109/ITOEC53115.2022.9734662
Gong, J., Cheng, J., Qiao, S., Wang, K., Lai, X., Xu, C., et al. (2021). Decomposition method of government authorized contracts considering unbalanced funds. 2021. IEEE 6th Int. Conf. Comput. Commun. Automation (ICCCA), 908–913. doi:10.1109/iccca52192.2021.9666362
Jiang, W., Lin, X., Yang, Z., Tang, J., Zhang, K., Zhou, M., et al. (2023). An efficient user demand response framework based on load sensing in smart grid, Front. Energy Res., 11. doi:10.3389/fenrg.2023.1141374
Jiang, Y., Hou, J., Lin, Z., Wen, F., Li, J., He, C., et al. (2019). Optimal bidding strategy for a power producer under monthly pre-listing balancing mechanism in actual sequential energy dual-market in China. IEEE Access 7, 70986–70998. doi:10.1109/ACCESS.2019.2919347
Khodadadi, A., Herre, L., Shinde, P., Eriksson, R., Söder, L., and Amelin, M. (2020). Nordic balancing markets: overview of market rules. 17th Int. Conf. Eur. Energy Mark. (EEM), 1–6. doi:10.1109/EEM49802.2020.9221992
Liangyuan, W., Shuyuan, L., Xiaomin, L., and Linyan, W. (2022). “Research on coordination between medium-long-term electricity trade and spot market trade,” in 2022 4th international conference on smart power and internet energy systems (SPIES), 2165–2170. doi:10.1109/SPIES55999.2022.10082397
Liu, S., Xu, J., Xing, C., Liu, Y., Tian, E., Cui, J., et al. (2023). Study on dynamic pricing strategy for industrial power users considering demand response differences in master–slave game. Sustainability 15, 12265. doi:10.3390/su151612265
Liu, S., Yang, Z., Xia, Q., Lin, W., Shi, L., and Zeng, D. (2020). Power trading region considering long-term contract for interconnected power networks. Appl. Energy 261, 114411. doi:10.1016/j.apenergy.2019.114411
Lu, T., Zhang, W., Wang, Y., Xie, H., and Ding, X. (2022). Medium- and long-term trading strategies for large electricity retailers in China’s electricity market. Energies 15, 3342. doi:10.3390/en15093342
Lv, H., He, Y., Hu, L., Chen, S., Ma, R., and Ma, N. (2023). “A multi-market collaborative trading model for load aggregator,” in 2023 IEEE/IAS industrial and commercial power system asia (I&CPS asia), 1235–1240. doi:10.1109/ICPSAsia58343.2023.10294764
Ma, L., Sun, C., Gao, S., Ma, Y., Ge, X., and Wang, F. (2023). A correction method for customer baseline load estimation considering demand response rebound effect based on equivalent electricity price model. 2023. IEEE IAS Glob. Conf. Renew. Energy Hydrogen Technol. (GlobConHT), 1–6. doi:10.1109/GlobConHT56829.2023.10087836
Nobis, M., Wyrwoll, L., Moser, A., and Raths, S. (2020). “Impact of market-coupling on electricity price modeling in fundamental unit-commitment approaches,” in 2020 6th IEEE international energy conference (ENERGYCon), 740–743. doi:10.1109/ENERGYCon48941.2020.9236434
Reddy, S., Bijwe, P., and Abhyankar, A. (2015). Real-time economic dispatch considering renewable power generation variability and uncertainty over scheduling period. IEEE Syst. J. 9, 1440–1451. doi:10.1109/JSYST.2014.2325967
Wang, L., Chen, J., Peng, K., Zhao, Y., and Zhang, X. (2021). Reward fairness-based optimal distributed real-time pricing to enable supply-demand matching. Neurocomputing 427, 1–12. doi:10.1016/j.neucom.2020.11.034
Wang, L., Xu, Q., Li, L., Bo, X., Wang, P., and Jiang, T. (2023a). “Pricing method for deviations in the electricity market taking into account load factor levels,” in 2023 IEEE international conference on image processing and computer applications (ICIPCA), 1241–1245. doi:10.1109/ICIPCA59209.2023.10257957
Wang, Y., Swaminathan, V., Granger, N., Perez, C., and Michler, C. (2023b). Deep reinforcement learning for power trading. ArXiv, abs/2301, 08360. doi:10.48550/arXiv.2301.08360
Watanabe, F., Kawaguchi, T., Ishizaki, T., Takenaka, H., Nakajima, T., and Imura, J. (2018). Machine learning approach to day-ahead scheduling for multiperiod energy markets under renewable energy generation uncertainty. IEEE Conference on Decision and Control CDC, 4020–4025. doi:10.1109/CDC.2018.8619775
Xu, B., Wang, J., Guo, M., Lu, J., Li, G., and Han, L. (2021). A hybrid demand response mechanism based on real-time incentive and real-time pricing. Energy 231, 120940. doi:10.1016/J.ENERGY.2021.120940
Yang, G., Du, S., Duan, Q., and Su, J. (2022). Deep reinforcement learning-based trading strategy for load aggregators on price-responsive demand. Comput. Intell. Neurosci. 2022, 1–14. doi:10.1155/2022/6884956
Yang, H., and Wang, Z. (2024). A false data injection attack approach without knowledge of system parameters considering measurement noise. IEEE Internet Things J. 11 (1), 1452–1464. doi:10.1109/JIOT.2023.3288983
Yang, H., Wang, Z., and Qiu, R. C. (2023). Data domain adaptation for voltage stability evaluation considering topology changes. IEEE Trans. Power Syst. 38 (3), 2834–2844. doi:10.1109/TPWRS.2022.3185629
Yang, H., Zhang, W., Chung, C. Y., Wang, Z., Qiu, W., and Liang, Z. (2024). “AC false data injection attack based on robust tensor principle component analysis,” in IEEE transactions on industrial informatics. doi:10.1109/TII.2024.3390389
Zhang, R., Jiang, T., Li, G., Li, X., and Chen, H. (2021). Stochastic optimal energy management and pricing for load serving entity with aggregated TCLs of smart buildings: a Stackelberg game approach. IEEE Trans. Industrial Inf. 17, 1821–1830. doi:10.1109/TII.2020.2993112
Keywords: load aggregators, controllable load management, tiered compensation strategies, stackelberg game theory, demand-side response
Citation: Yang H, Zhang Z, Liang R and Zhao W (2024) Research on time-of-use compensation pricing strategies for load aggregators based on user demand response. Front. Energy Res. 12:1442194. doi: 10.3389/fenrg.2024.1442194
Received: 14 June 2024; Accepted: 26 August 2024;
Published: 10 September 2024.
Edited by:
Yingjun Wu, Hohai University, ChinaReviewed by:
Haoasn Yang, Hong Kong Polytechnic University, Hong Kong SAR, ChinaWenlong Liao, Swiss Federal Institute of Technology Lausanne, Switzerland
Copyright © 2024 Yang, Zhang, Liang and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hongzhao Yang, Mzg3NjI4NjRAcXEuY29t
 Hongzhao Yang
Hongzhao Yang Zhan Zhang1
Zhan Zhang1