Cluster dynamics study on nano damage of RPV steels under proton irradiation at 290°C

Irradiation-induced defects such as dislocation loops, cavities or solute clusters and chemical composition segregation of reactor pressure vessel (RPV) steel are the root causes of irradiation embrittlement. Combining two nucleation mechanisms, namely, the uniform nucleation and non-uniform nucleation of solute clusters (such as Cu-rich phase), a cluster kinetic simulation was established based on the reaction rate theory, and the co-evolution of matrix damage and Cu-rich phase in low-copper RPV steel was simulated under irradiation. And the average size and number density of defective clusters and solute clusters were established with irradiation dose. Compared with the average size and number density of dislocation loops observed by transmission electron microscopy (TEM) of proton irradiated RPV steel at 290°C, the verification results show that the cluster dynamics model considering both the nucleation mechanism of interstitial dislocation loops and vacancy clusters can well simulate the irradiation damage behavior of materials.

Introduction

Nuclear power is an important part of China’s modern energy system to achieve cleanliness, efficiency, safety, and sustainability. The reactor pressure vessel (RPV) is a primary safety component of a pressurized water reactor (PWR) nuclear power plant, which loads the core and supports all components inside the reactor. It serves as a safety boundary for primary coolant pressure and radioactive material shielding. RPV is the only non replaceable component. Neutron irradiation can reduce the toughness of RPV materials and increase the risk of brittle failure. The lifespan of nuclear power plants is determined by the operation life of RPV.

The neutron irradiation damage problem of RPV steel is a key issue for the long-term and safe operation of nuclear power plants. Neutron irradiation of RPV steel involves two principal effects. Firstly, nuclear transmutation reaction, and the deexcitation process may also trigger γ, β radiation. Secondly, The collision of neutrons with lattice atoms could form primary collision atoms (PKA), which triggers a cascade of collision processes, including displacement damage and ionization damage. Displacement damage is the most important role, which induce excess interstitial atoms and vacancies. The migration, aggregation, and annihilation of interstitial atoms and vacancies, as well as their interactions with solute atoms and existing defects such as defects of line, surface, and body, or irradiation products such as H and He, ultimately form nanoscale point defect clusters (such as dislocation loops and voids), complexes of point defects and solute yards, solute atom clusters (such as Cu rich clusters or Ni-Mn-Si rich clusters), or interface weakening element segregation (such as P). These nano-structure features hinder dislocation movement or weaken the interface, which cause hardening and embrittlement of RPV materials. Under high dose irradiation conditions, the embrittlement process of RPV steel may be accelerated beyond expectations, ultimately leading to a reduction in the safety window of RPV operation parameters, endangering its structural integrity and restricting its long-term economic and safe operation (Qingmao Wan, 2013; Wang et al., 2020; Ke and Spencer, 2022).

The performance data of RPV materials under high dose irradiation is scarce or scattered in various countries. So it is not possible to reliably extrapolate the prediction model of RPV performance in regulations to new service conditions (Wan et al., 2010). Conducting high dose irradiation testing and evaluating RPV materials directly in experimental or commercial reactors is costly, time-consuming, difficult to control parameters. And neutron irradiation materials and specimens are radioactive and must be operated in hot rooms. Therefore, only a few key parameters can be selectively implemented, so it difficult to conduct comprehensive and systematic neutron irradiation experimental research. Ion irradiation of RPV materials causes displacement damage, ionization damage, and minimal doping. When selecting the appropriate ion energy for irradiation, the collision between the incident ion and the lattice atoms generates cascade collisions induced by PKA, resulting in displacement damage, which plays a major role. Because of the similar mass between protons and neutrons, proton irradiation is commonly used to simulate neutron irradiation to study radiation damage issues.

The experimental method of high flux proton irradiation is used to simulate the irradiation process of materials in nuclear reactors. Combined with theoretical analysis, the performance and related laws of nuclear power materials can be studied (Chitra and and Kotliar, 2000; Huibin et al., 2017; Cui et al., 2020). However, there are also drawbacks such as time consumption and harsh environment for experiment. In contrast, computer simulation methods (He et al., 2012; Mathew et al., 2018; Shimodaira et al., 2018) can not only save a lot of manpower and material resources, reduce development costs, but also provide “experimental data” under extreme conditions (ultra-high radiation, ultra-high pressure, and ultra-high temperature), so as to overcome experimental difficulties. They can also obtain microscopic details of material changes under irradiation conditions and obtain information that cannot be obtained in macroscopic experiments. It has very important theoretical significance for the prediction and evaluation of high dose radiation damage in RPV steel.

The cluster dynamics model based on mean field approximation has high computational efficiency and can quickly describe defect reaction events that occur at different time scales within the same framework. It simulates the diffusion reaction process of defects (clusters) to study the changes of single or small defects with time, space, and size (Wan et al., 2011; Wan Q. M et al., 2012; Yoshiie et al., 2015). It can achieve the same spatial resolution as transmission electron microscopy (TEM). Therefore, cluster dynamics can simulate the kinetic evolution process of defects under reactor irradiation dose across time scales (ps to year) and spatial scales (nm to m).

This study focuses on low copper RPV steel as the research object, establishes a model based on the average rate field theory, and develops a cluster dynamics program for radiation damage. It simulates the micro evolution process of various defects such as migration, aggregation, and nucleation during the radiation damage process, studies the generation and evolution of dislocation loops, voids, and solute clusters, the results of which were compared and verified by the experimental results. The study will provide reference for the prediction and evaluation radiation embrittlement of RPV.

2 Cluster dynamics model and method

2.1 Assumption

Radiation generates displacement cascades and isolated point defects between cascades, which include endogenous vacancy clusters, endogenous interstitial clusters, and endogenous isolated point defects. Most vacancy and interstitial atoms recombine and annihilate. The ratio of endogenous vacancy clusters and interstitial atomic clusters in displacement cascades to the total number of surviving point defects will decay with increasing irradiation dose. The three-dimensional cavity changes include (1) endogenous vacancy clusters of displacement cascades; (2) Two vacancies aggregate to form nuclei; (3) Vacancy clusters capture Cu atoms and transform into Cu rich clusters. The variation of two-dimensional planar interstitial clusters (or dislocation loops) includes (1) endogenous interstitial clusters of displacement cascades; (2) Two interstitial atoms aggregate to form nuclei; (3) Interstitial clusters capture Cu atoms and transform into Cu rich clusters. Three dimensional Cu rich clusters can also nucleate through the aggregation of two Cu atoms, which belongs to uniform nucleation, namely, homogeneous nucleation. Vacancy clusters or interstitial clusters capture Cu atoms and transform into Cu rich clusters, which belongs to heterogeneous nucleation.

2.2 Basic equations

2.2.1 Changes in monomer concentration

Isolated vacancies, interstitial atoms, and Cu atoms can be collectively referred to as monomers. During the irradiation process, the concentrations of vacancies, interstitial atoms, and Cu atoms will evolve over time, and their evolution equations can be expressed as Eqs 1–3:

$\begin{array}{l}d{C}_{\mathrm{i}}/dt=P\left(1-{\epsilon }_{\mathrm{r}}\right)\left(1-k{\epsilon }_{\text{ic},\text{dc}}\right)-Z_{\mathrm{i},\mathrm{v}}\left(D_{\mathrm{i}}+D_{\mathrm{v}}\right)C_{\mathrm{i}}{C}_{\mathrm{v}}-Z_{\mathrm{i},\mathrm{i}}{D}_{\mathrm{i}}{C}_{\mathrm{i}}{C}_{\mathrm{i}}\\ -Z_{\mathrm{i},\mathrm{d}}{D}_{\mathrm{i}}{C}_{\mathrm{i}}\rho -Z_{\mathrm{i},\text{ic}}{D}_{\mathrm{i}}{C}_{\mathrm{i}}{S}_{\text{ic}}-Z_{\mathrm{i},\text{vc}}{D}_{\mathrm{i}}{C}_{\mathrm{i}}{S}_{\text{vc}}\end{array}(1)$

$\begin{array}{l}d{C}_v/dt=P\left(1-{\epsilon }_{\mathrm{r}}\right)\left(1-k{\epsilon }_{\text{vc},\text{dc}}\right)-Z_{\mathrm{v},\mathrm{i}}\left(D_{\mathrm{i}}+D_{\mathrm{v}}\right)C_{\mathrm{i}}{C}_{\mathrm{v}}-Z_{\mathrm{v},\mathrm{v}}{D}_{\mathrm{v}}{C}_{\mathrm{v}}{C}_{\mathrm{v}}\\ -Z_{\mathrm{v},\mathrm{d}}{D}_{\mathrm{v}}{C}_{\mathrm{v}}\rho -Z_{\mathrm{v},\text{ic}}{D}_{\mathrm{v}}{C}_{\mathrm{v}}{S}_{\text{ic}}-Z_{\mathrm{v},\text{vc}}{D}_{\mathrm{v}}\left(C_{\mathrm{v}}-C_{\mathrm{v},\text{emit}}\right)S_{\text{vc}}\end{array}(2)$

$\begin{array}{l}d{C}_{Cu}/dt=-{{Z_{Cu}}_{,}}_{Cu}{D}_{Cu}{C}_{Cu}-{{Z_{Cu}}_{,}}_{vc}{D}_{Cu}{S}_{vc}\\ -{{Z_{Cu}}_{,}}_{ic}{D}_{Cu}{S}_{ic}-{{Z_{Cu}}_{,}}_{crp}{D}_{Cu}\left(C_{Cu}-C_{Cu,emit}\right)S_{crp}\end{array}(3)$

In the formula: $C_{\mathrm{i}}$, $C_{\mathrm{v}}$ and $C_{Cu}$ represents the concentrations of interstitial atoms, vacancies, and Cu atoms, respectively; $C_{\mathrm{v},\text{emit}}$ and $C_{Cu,emit}$ represents the concentration of vacancies on the surface of voids and the concentration of Cu atoms at the interface of Cu rich phases, respectively; $P$ is the damage rate, i.e., the injection rate, in units of dpa/s; The recombination probability ${\epsilon }_{\mathrm{r}}$ of Frenkel point defects during the displacement cascade cooling process and ${1-\epsilon }_{\mathrm{r}}$ is represented by the damage efficiency. ${\epsilon }_{\text{ic},\text{dc}}$ is the percentage of interstitial atoms in the endogenous interstitial clusters of the displacement cascades; While ${\epsilon }_{\text{vc},\text{dc}}$ is the percentage of vacancies in the endogenous vacancy clusters of the displacement cascades; $Z$ is the combination constants or capture reaction constants, the lower corners of $\mathrm{i}$, $\mathrm{v}$, $\text{Cu}$, $\text{ic}$, $\text{vc}$, $\text{CRP}$ and$\rho$ respectively represent interstitial atoms, vacancies, Cu atoms, dislocation loops, voids, Cu rich phases, and dislocation lines density in the matrix; And ${\mathrm{D}}_{\mathrm{i}}$, ${\mathrm{D}}_v$ and$D_{Cu}$ is the diffusion coefficients of interstitial atoms, vacancies and Cu atoms, respectively; And $S_{ic}$, $S_{vc}$ and $S_{crp}$ represents the sink strength of dislocation loops, voids and Cu rich phase for absorption point defects, respectively.

2.2.2 Concentration evolution of clusters

Dislocation loops, vacancies, and Cu rich phases can be collectively referred to as clusters. During the irradiation process, the concentration and size of dislocation loops, vacancies, and Cu rich phases will evolve over time, and their evolution equation can be expressed as Eqs 4–6:

$d{C}_{\text{loop}}/dt=\frac{1}{2}{Z}_{\text{ii}}{D}_i{C}_i{C}_i+C_{ic,dc}-Z_{Cu,ic}{D}_{Cu}{C}_{Cu}{S}_{ic}(4)$

$d{C}_{void}/dt=\frac{1}{2}{Z}_{vv}{D}_v{C}_v{C}_v+C_{vc,dc}-Z_{Cu,vc}{D}_{Cu}{S}_{vc}(5)$

$d{C}_{crp}/dt=\frac{1}{2}{Z}_{Cu,Cu}{D}_{Cu}{C}_{Cu}{C}_{Cu}+Z_{Cu,ic}{D}_{Cu}{C}_{Cu}{S}_{ic}+Z_{Cu,vc}{D}_{Cu}{C}_{Cu}{S}_{vc}(6)$

In the formula: $C_{\text{loop}}$、 $C_{void}$ and$C_{crp}$ represents the concentration of dislocation loops, voids, and Cu rich phases, respectively; $C_{ic,dc}$ and $C_{vc,dc}$ represents the concentrations of endogenous interstitial clusters and endogenous vacancy clusters in the displacement cascades, respectively.

2.2.3 Cluster size evolution

During the irradiation process, the size of dislocation loops, voids, and Cu rich phases will evolve over time, and their evolution equation can be expressed as Eqs 7–9:

$\begin{array}{l}d{N}_{loop}/dt=\left({{Z_i}_{,}}_{ic}{D}_i{C}_i-{Z_{v,}}_{ic}{D}_v{C}_v\right)S_{ic}/C_{loop}\\ +N_{ic,dc}{C}_{ic,dc}/C_{loop}-{Z_{Cu,}}_{ic}{D}_{Cu}{C}_{Cu}{S}_{ic}/C_{loop}\end{array}(7)$

$\begin{array}{l}d{N}_{void}/dt=\left[{Z_{v,}}_{vc}{D}_v\left(C_v-C_{v,emit}\right)-{{Z_i}_{,}}_{vc}{D}_i{C}_i\right]S_{vc}/C_{void}\\ +N_{vc,dc}{C}_{vc,dc}/C_{void}-{Z_{Cu,}}_{vc}{D}_{Cu}{C}_{Cu}{S}_{vc}/C_{void}\\ +4\pi R_{void}\left[{Z_{v,}}_{vc}{D}_v\left(C_v-C_{v,emit}\right)-{{Z_i}_{,}}_{vc}{D}_i{C}_i\right]\end{array}(8)$

$\begin{array}{l}d{N}_{crp}/dt=\left[{Z_{Cu,}}_{crp}{D}_{Cu}\left(C_{Cu}-C_{Cu,emit}\right)\right]S_{crp}/C_{crp}\\ +{Z_{Cu,}}_{vc}{D}_{Cu}{C}_{Cu}{S}_{vc}/C_{crp}+{Z_{Cu,}}_{ic}{D}_{Cu}{C}_{Cu}{S}_{ic}/C_{crp}\\ +4\pi R_{crp}\left[{Z_{Cu,}}_{crp}{D}_{Cu}\left(C_{Cu}-C_{Cu,emit}\right)\right]\end{array}(9)$

In the formula, $N_{loop}$, $N_{void}$ and$N_{crp}$ represents the number of monomers contained in each dislocation loop, void, and Cu rich phase, respectively; And $N_{ic,dc}$ and $N_{vc,dc}$ is the number of interstitial atoms contained in each endogenous interstitial atomic cluster and the number of vacancies contained in the endogenous vacancy cluster of displace cascades, respectively; And $R_{loop}$, $R_{void}$ and$R_{crp}$ is the radii of each dislocation loop, void, and Cu rich phase, in units of the number of monomers.

The radius of dislocation loops, vacancies, and Cu rich phases can be expressed as Eqs 10–12:

$R_{loop}={\left(\frac{N_{loop}}{\pi }\right)}^{\frac{1}{2}}(10)$

$R_{void}={\left(\frac{3N_{void}}{4\pi }\right)}^{\frac{1}{3}}(11)$

$R_{crp}={\left(\frac{3N_{crp}}{4\pi }\right)}^{\frac{1}{3}}(12)$

2.2.4 Cluster hardening

The increase in yield strength caused by irradiation-induced dislocation loops, voids, and Cu rich phases can be expressed as Eq. 13:

$\Delta \sigma =\alpha MGb\left\{\begin{array}{l}\sqrt{\rho }-\sqrt{{\rho }_0},\text{for\hspace{0.17em}dislocation\hspace{0.17em}line}\\ \sqrt{2RN},\text{for\hspace{0.17em}disloation\hspace{0.17em}loops},\text{voids\hspace{0.17em}or\hspace{0.17em}Cu}-\text{rich\hspace{0.17em}phase}\end{array}\right.(13)$

In the formula: $\alpha$ is the strengthening factor, with a value of 0.1 for dislocation lines; For dislocation loops, the value is 0.267; For voids, the value is 0.05; For the rich Cu phase, the value is 0.15. And $\rho$ are ${\rho }_0$ the dislocation line density after irradiation and the initial dislocation line surface density, respectively.

Based on the research results of Garner and Wolfer, the following equation for the evolution of dislocation lines can be proposed (Eq. 14):

$d\rho /dt=B{\rho }^{\frac{1}{2}}-A{\rho }^{\frac{3}{2}}(14)$

The superposition method of various cluster hardening contributions adopts the sum of squares square root method. It can be expressed as Eq. 15.

${\sigma }_{tot}=\sqrt{\sum {\sigma }_i^2}(15)$

2.3 Main parameters

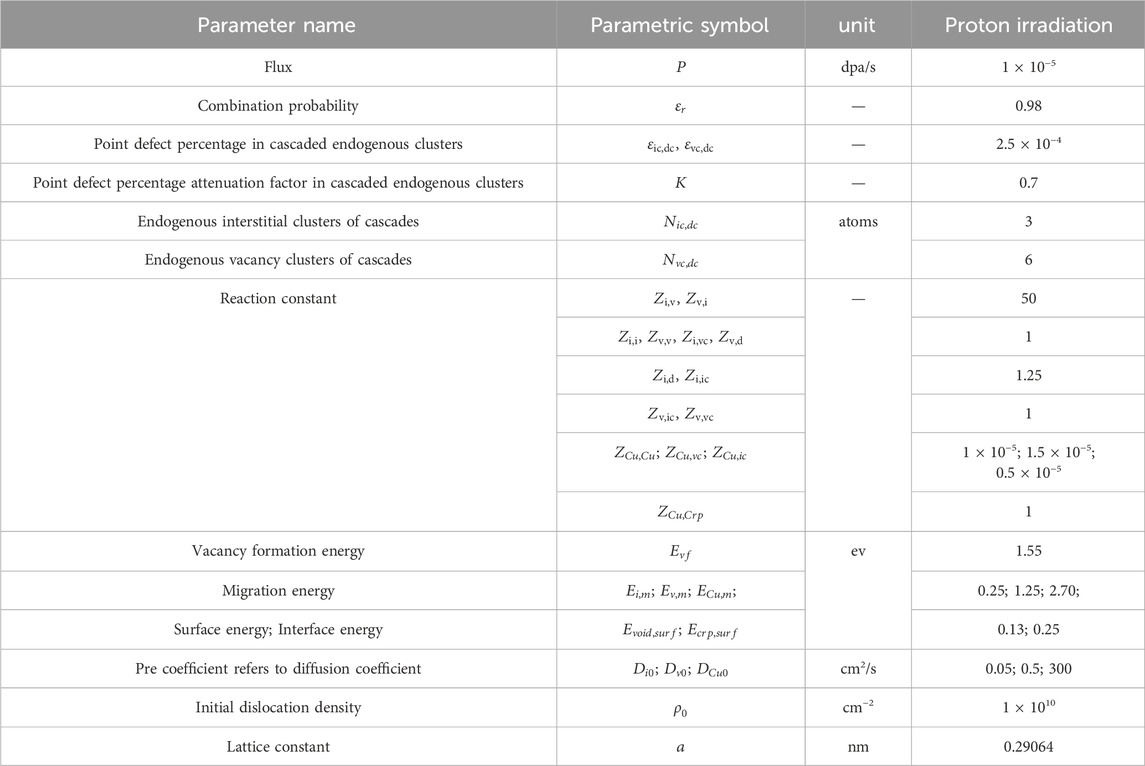
When solving the partial differential equation of the average rate field, it is important to choose material parameters as accurately as possible, which is beneficial for obtaining reliable prediction results. Table 1 lists the main input parameters for proton irradiated RPV steel at 290°C. Most of the parameters come from literature data (Gan et al., 1999; Kwon et al., 2003; Dubinko et al., 2009; Qingmao Wan, 2013).

Table 1

Table 1. Main input parameters of proton-irradiated RPV steel at 290°C.

2.4 Algorithm for multi-dimensional pathological differential equations

This model belongs to multidimensional ill conditioned rigid differential equations. If we consider the size distribution of various clusters, the number of equations will reach approximately 10⁹. This study does not currently consider the size distribution of clusters and only calculates the average size of clusters. The algorithm used is the Runge Kutta method, and a simulation program for nano-structure damage has been developed.

3 Calculation results

3.1 Cluster evolution

Figure 1 shows the dynamic simulation results of A508-3 steel under proton irradiation at 290°C, including a 3 × 5 array diagram. The first line shows the interstitial defects and the hardening components of dislocation loops with the variation of irradiation dose. While the second line shows the vacancy type defects and the hardening components of voids with the variation of irradiation dose. The third line shows the Cu atomic related cluster and the hardening component of Cu rich phases with the variation of irradiation dose. The columns a-e represents monomer concentration, number of monomers contained in the cluster, cluster concentration, cluster size, and cluster hardening component, respectively.

Figure 1

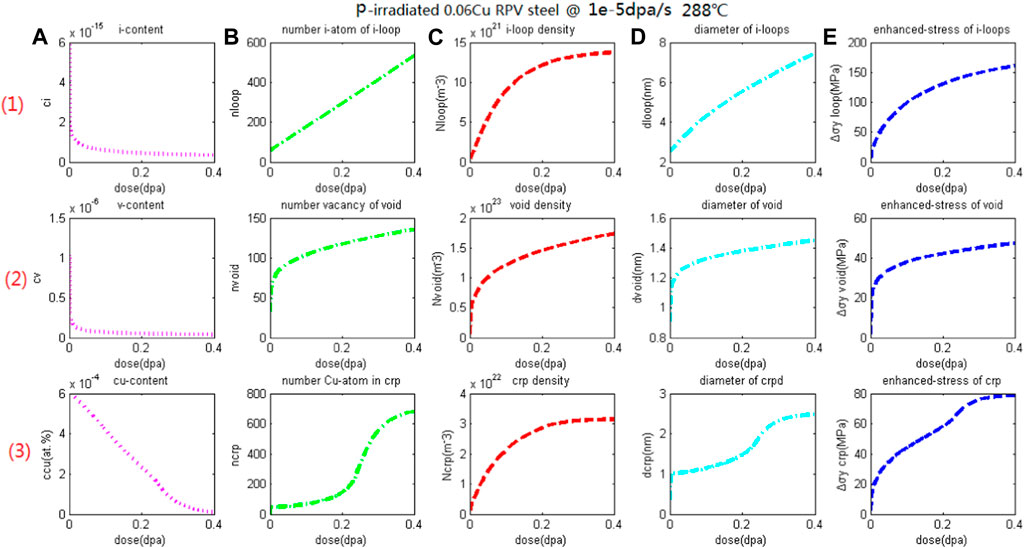
Figure 1. Dynamic simulation results of A508-3 steel irradiation at 290°C, the variation of clusters, i.e., (1) interstitial dislocation loops, (2) microvoids, and (3) Cu-rich phases with irradiation flux, including (A) monomer concentration; (B) the number of monomers in the cluster, (C) the concentration of the cluster; (D) cluster diameter; (E) The amount of hardening caused by clusters.

Within the irradiation dose range of 0.01–0.4 dpa, (a) the concentration range of interstitial atoms is 3.4 × 10⁻¹⁶−1.3 × 10⁻¹⁵, which gradually decreases with increasing irradiation dose and tends towards equilibrium concentration, with an order of magnitude of 10⁻¹⁶; (b) The number of interstitial atoms contained in every dislocation loop is approximately 100–500; (c) The density range of dislocation loops is 1.3 × 10²¹–1.3 × 10²² m⁻³, which gradually increases with the increase of irradiation dose, fast firstly and then slow, with an order of magnitude of 10²² m⁻³; (d) The diameter is about 2–8 nm, and the diameter shows an increasing trend with increasing dose, and the growth rate shares the same “fast followed by slow” type; (e) The hardening component of dislocation loops shows a similar increasing trend with the irradiation dose, first fast and then slow, increasing from less than 50–160 MPa up to 0.4 dpa.

Within the irradiation dose range of 0.01 to 0.4 dpa, (a) the vacancy concentration range is 4 × 10⁻⁸–1.6 × 10⁻⁷, which gradually decreases with increasing irradiation dose and tends towards equilibrium concentration, with an order of magnitude of 10⁻⁸; (b) The number of vacancies contained in a void is approximately 50–150; (c) The density range of voids is 6.0 × 10²¹–1.3 × 10²³ m⁻³, which gradually increases with the increase of irradiation dose, fast firstly and then slow, with an order of 10²³m⁻³; (d) The diameter is about 1–1.5 nm, and the diameter shows an increasing trend with increasing dose, and the growth rate shares the same “fast followed by slow” type; (e) The hardening component of voids shows a similar increasing trend with the irradiation dose, first fast and then slow, increasing from less than 25–50 MPa up to 0.4 dpa.

Within the irradiation dose range of 0.01 to 0.4 dpa, (a) the concentration range of Cu atoms is 9.6 × 10⁻⁶–5.9 × 10⁻⁴, which decreases continuously with increasing irradiation dose; (b) The number of Cu atoms in the Cu-rich phase is approximately 100–800; (c) The density range of Cu rich phases is 4.0 × 10²⁰–3.1 × 10²² m⁻³, which gradually increases with the increase of irradiation dose, fast firstly and then slow, with an order of magnitude of 10²² m⁻³; (d) The diameter is about 1–2.5 nm, and the diameter shows an increasing trend with increasing dose, and the growth rate shares the same “fast followed by slow” type; (d) The hardening component of the Cu-rich phases shows a similar increasing trend with the irradiation dose, first fast and then slow, increasing from less than 20–80 MPa up to 0.4 dpa, which is close to the saturation hardening amount of Cu rich phase. The supersaturated solid solution Cu atoms basically precipitate.

3.2 Relationship between cluster hardening component and total hardening amount

Figure 2 shows the variation of various hardening amounts of A508-3 steel under proton irradiation at 290°C with the irradiation dose. Below 0.05 dpa, the hardening components of dislocation loops, voids, and Cu rich phases are comparable for the contribution of the total hardening amount; After 0.05 dpa, the hardening components of dislocation loops, Cu rich phases, voids, and dislocation line networks are ranked in descending order, with hardening component of dislocation loops dominating the total hardening amount. This indicates that the evolution of dislocation loops is the dominant factor for the irradiation embrittlement of A508-3 steel under high dose proton irradiation conditions at 290°C.

Figure 2

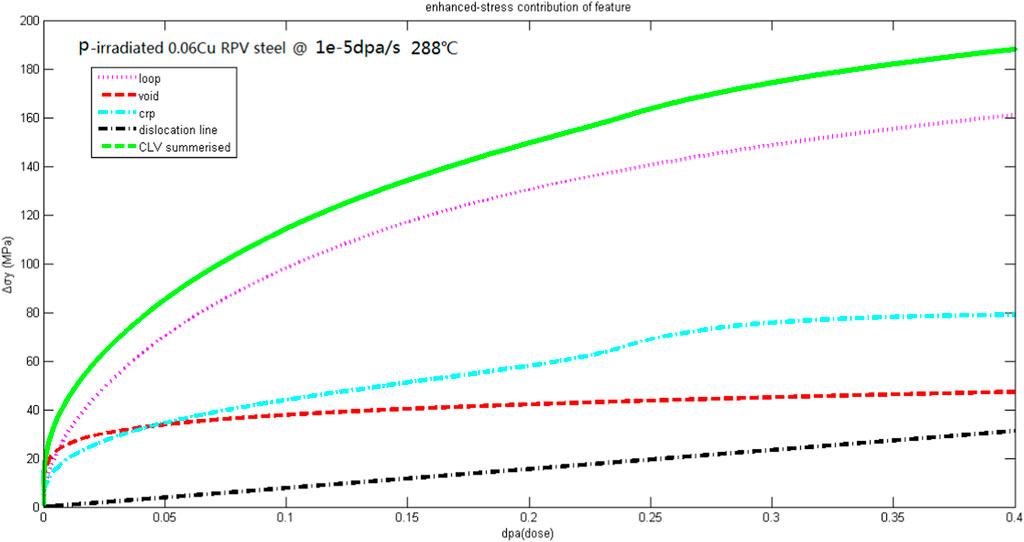
Figure 2. Dynamic simulation results of A508-3 steel irradiated by protons at 290°C, the contribution of clusters, i.e., (1) interstitial dislocation loops, (2) microvoids, (3) Cu-rich phases, and (4) dislocation lines, to irradiation hardening.

4 Experimental verification

The high-temperature proton irradiation test utilizes the 320 kV high charge ion experimental research platform of the National Laboratory of Heavy Ion Accelerator at Lanzhou Institute of Modern Physics. Using an incident beam perpendicular to the surface of the sample, with a scanning area of approximately 1.5 cm² × 1.5 cm², the total current intensity of the proton beam reaching the sample stage is approximately 25 μ A. The vacuum degree is better than 1 × 10⁻⁴ Pa, and the temperature control accuracy is ±5°C. Under the proton irradiation at 290°C, the proton beam density is approximately 6.8 × 10¹³ ion/cm²-s, equivalent to 11 μ A/cm². This irradiation was conducted to 5.57 ion/cm² × 10¹⁷ ion/cm², equivalent to 0.163 dpa. The measured size and number density values were obtained by quantifying the dislocation loops of proton irradiated Chinese A508-3 RPV steel using TEM (Wan Q et al., 2012; Lei et al., 2014). The comparison between the experimental measured values of dislocation loops and the simulated values of cluster dynamics is shown in Table 2. The verification results show that for the dislocation loops in RPV steel irradiated with 290°C proton, the calculated values of cluster dynamics are on the same order of magnitude as the TEM measured values in proton irradiation experiments, with a size deviation of 50%, a number density of 10%, and a hardening deviation of 20%. This indicates that cluster dynamics can effectively simulate the proton irradiation of RPV steel at 290°C.

Table 2

Table 2. Experimental measurements and simulated values of cluster dynamics of dislocation loops in proton-irradiated Chinese A508-3 RPV steel at 290°C.

5 Conclusion

Considered both the homogeneous nucleation mechanisms and the heterogeneous nucleation mechanisms of solute clusters, the study developed a simulation program based on cluster dynamics model for the nano-structure evolution of RPV steel during irradiation. The average size and number density evolution of interstitial dislocation loops, voids, and solute clusters generated by proton irradiation at 290°C were calculated, which were compared and verified with TEM measurements of specific proton irradiation experiment for Chinese A508-3 RPV steels at 0.163 dpa. The research results indicate that the simulation results are roughly consistent with the experimental results. Subsequent research can consider developing more universal cluster dynamics simulation methods with much more defects, conducting parameter sensitivity analysis and comprehensive experimental data validation.

Data availability statement

The datasets presented in this article are not readily available due to some procedural restrictions. Requests to access the datasets should be directed to d2FucWlhbmdtYW9AcXEuY29t.

Author contributions

QW: Conceptualization, Data curation, Writing–original draft, Writing–review and editing. GS: Formal Analysis, Writing–original draft, Writing–review and editing, Conceptualization. JT: Methodology, Supervision, Writing–review and editing. JP: Validation, Writing–review and editing. LC: Software, Writing–review and editing, Writing–original draft. DW: Supervision, Writing–review and editing. HL: Project administration, Writing–review and editing. HD: Investigation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by the Zhejiang Provincial Natural Science Foundation of China under Grant No. LGG20E010005, No. LY21E010001, Dean’s Fund of nuclear industry college under Grant No. YZJJ-2023-05.

Conflict of interest

Author GS was employed by China United Gas Turbine Technology Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chitra, G., and Kotliar, R. (2000). Dynamical mean-field theory and electronic structure calculations. Phys. Rev. B 62 (19), 12715–12723. doi:10.1103/physrevb.62.12715

CrossRef Full Text | Google Scholar

Cui, S., Mamivand, M., and Morgan, D. (2020). Simulation of Cu precipitation in Fe-Cu dilute alloys with cluster mobility. Mater. Des. 191, 108574. doi:10.1016/j.matdes.2020.108574

CrossRef Full Text | Google Scholar

Dubinko, V. I., Kotrechko, S. A., and Klepikov, V. F. (2009). Irradiation hardening of reactor pressure vessel steels due to the dislocation loop evolution. Radiat. Eff. Defects Solids 164 (10), 647–655. doi:10.1080/10420150903115743

CrossRef Full Text | Google Scholar

Gan, J., Was, G. S., and Stoller, R. E. (1999). Modeling of microstructure evolution in austenitic stainless steels irradiated under light water reactor condition. J. Nucl. Mater 299 (1), 53–67. doi:10.1016/s0022-3115(01)00673-0

CrossRef Full Text | Google Scholar

He, X., Guo, L., Wu, S., Yang, P., and Wen, Y. (2012). Multiscale modeling and experiment validation of microstructure evolution induced by Ar+ irradiation in Hastlloy C276. Atomic Energy Sci. Technol. 46 (2), 130–132. doi:10.7538/yzk.2012.46.02.0129

CrossRef Full Text | Google Scholar

Huibin, Ke, Peter, W., Edmondson, P. D., Almirall, N., Barnard, L., Robert Odette, G., et al. (2017). Thermodynamic and kinetic modeling of Mn-Ni-Si precipitates in low-Cu reactor pressure vessel steels. Acta Mater 138, 10–26. doi:10.1016/j.actamat.2017.07.021

CrossRef Full Text | Google Scholar

Ke, J. H., and Spencer, B. W. (2022). Mn-Ni-Si precipitates coupled with radiation-induced segregation in low-Cu reactor pressure vessel steels. J. Nucl. Mater. 569, 153–163. doi:10.1016/j.jnucmat.2022.153910

CrossRef Full Text | Google Scholar

Kwon, J., Kwon, S. C., and Hong, J. H. (2003). Prediction of radiation hardening in reactor pressure vessel steel based on a theoretical model. Ann. Nucl. Energy 30 (15), 1549–1559. doi:10.1016/s0306-4549(03)00102-6

CrossRef Full Text | Google Scholar

Lei, J., Ding, H., Shu, G. G, and Wan, Q. M. (2014). Study on the mechanical properties evolution of A508-3 steel under proton irradiation. Nucl. Instrum. Methods Phys. Res. Sect. B 338, 13–18. doi:10.1016/j.nimb.2014.07.030

CrossRef Full Text | Google Scholar

Mathew, J., Parfitt, D., Wilford, K., Riddle, N., Alamaniotis, M., Chroneos, A., et al. (2018). Reactor pressure vessel embrittlement: Insights from neural network modelling. J. Nucl. Mater 502, 311–322. doi:10.1016/j.jnucmat.2018.02.027

CrossRef Full Text | Google Scholar

Qingmao Wan (2013). “Microstructure evolution law and brittlement Prediction model of reactor pressure vessel steels under the irradiation condition,”. [dissertation] (Wuhan: Wuhan University), 1–209.

Google Scholar

Shimodaira, M., Toyama, T., Yoshida, K., Inoue, K., Ebisawa, N., Tomura, K., et al. (2018). Contribution of irradiation-induced defects to hardening of a low copper reactor pressure vessel steel. Acta Mater 155, 402–409. doi:10.1016/j.actamat.2018.06.015

CrossRef Full Text | Google Scholar

Wan, Q., Shu, G., Ding, H., and Wang, R. (2010). Anyalysis on life extension of PWR-RPV in USA and key isssues on life extension of RPV in China. Press. Vessel 27 (6), 105–109. doi:10.3969/j.issn.1001-4837.2010.06.010

CrossRef Full Text | Google Scholar

Wan, Q., Shu, G., Wang, R., Ding, H., Xiao, P., Qi, Z., et al. (2012b). Study on the microstructure evolution of A508-3 Steel under proton irradiaiton. Acta metall. Sin 48 (8), 929–934. doi:10.3724/sp.j.1037.2012.00060

CrossRef Full Text | Google Scholar

Wan, Q. M., Shu, G. G., Wang, R. S., Ding, H., Peng, X., Zhang, Q., et al. (2012a). Characterization of proton irradiation-induced defect in the 508-3 steel by slowpositron beam. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 287 (0), 48–152. doi:10.1016/j.nimb.2012.04.013

CrossRef Full Text | Google Scholar

Wan, Q. M., Wang, R. S., Shu, G. G., Ding, H., Huang, P., Feng, L., et al. (2011). Analysis method of Charpy V-notch impact data before and after electron beam welding reconstitution. Nucl. Eng. Des 241, 459–463. doi:10.1016/j.nucengdes.2010.11.005

CrossRef Full Text | Google Scholar

Wang, X., Yao, W., Ying, L., and Dong, Y. (2020). Numerical simulation of irradiation induced precipitates in low copper RPV steels based on cluster dynamics. Nucl. Power Eng. 41 (S1), 188–193. doi:10.13832/j.jnpe.2020.S1.0188

CrossRef Full Text | Google Scholar

Yoshiie, T., Sato, K., Xu, Q., and Naga, Y. (2015). Reaction kinetic analysis of reactor surveillance data. Nucl. Instrum. Methods Phys. Res. B 352, 125–129. doi:10.1016/j.nimb.2015.01.028

CrossRef Full Text | Google Scholar