
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Energy Res. , 09 August 2024
Sec. Wind Energy
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1435455
 Belachew Desalegn1,2*
Belachew Desalegn1,2* Bimrew Tamrat1,3*
Bimrew Tamrat1,3*Recent research generally reports that the intermittent characteristics of sustainable energy sources pose great challenges to the efficiency and cost competitiveness of sustainable energy harvesting technologies. Hence, modern sustainable energy systems need to implement a stringent power management strategy to achieve the maximum possible green electricity production while reducing costs. Due to the above-mentioned characteristics of sustainable energy sources, power management systems have become increasingly sophisticated nowadays. For addressing the analysis, scheduling, and control problems of future sustainable power systems, conventional model-based methods are completely inefficient as they fail to handle irregular electric power disturbances in renewable energy generations. Consequently, with the advent of smart grids in recent years, power system operators have come to rely on smart metering and advanced sensing devices for collecting more extensive data. This, in turn, facilitates the application of advanced machine learning algorithms, which can ultimately cause the generation of useful information by learning from massive data without assumptions and simplifications in handling the most irregular operating behaviors of the power systems. This paper aims to explore various application objectives of some machine learning algorithms that primarily apply to wind energy conversion systems (WECSs). In addition, an enhanced proportional integral (PI) (2DoF) algorithm is particularly introduced and implemented in a doubly fed induction generator (DFIG)-based WECS to enhance the reliability of power production. The main contribution of this article is to leverage the superior qualities of the PI (2DoF) algorithm for enhanced performance, stability, and robustness of the WECS under uncertainties. Finally, the effectiveness of the study is demonstrated by developing a virtual reality in a MATLAB-Simulink environment.
Because of the large fluctuations and uncertainties in generating renewable energy, the associated power systems have become increasingly sophisticated nowadays. For addressing the analysis, scheduling, and control issues of future renewable power systems, it is difficult to use conventional model-based methods. With the advent of smart grids in recent years, power system operators have come to rely on smart metering and advanced sensing devices for collecting more extensive data. This facilitates the application of advanced machine learning algorithms, which can ultimately cause the generation of useful information by learning from massive data without assumptions and simplifications in handling the complexity of the nonlinear operating behavior of power systems (Desalegn et al., 2023a; Singh and Rizwan, 2021). Briefly, an illustration that involves the study’s problem statements and methodical flows for addressing the problems is given in Figure 1. In the subsequent paragraphs of this section, based on recently published studies, this paper thoroughly summarizes various application objectives of machine learning algorithms in renewable power systems that primarily include the wind energy conversion system (WECS).
First, advanced machine/deep learning algorithms can be applied for the optimization and control of power and energy systems (Figure 2). In this regard, multiple studies utilizing various techniques were introduced. For instance, Wei et al. (2022) proposed a method based on a “multi-objective optimization for enhancing the operation of an electricity–hydrogen integrated system.” In this study, an “enhanced multitasking multi-objective optimization algorithm” was developed using the “implicit information of different optimization tasks.” Finally, comparative-based tests by this study demonstrated that the implemented method can perform a superior convergence compared to conventional methods. Wang D. et al. (2022) introduced further optimization techniques for realizing an ideal “dispatch of a multi-energy complementary power generation system.” Enhanced “cuckoo search, hybrid firefly, and particle swarm optimization techniques” were used for the “short-term and mid–long-term scheduling,” respectively. Comparative-based tests finally demonstrated the effectiveness of the techniques used in achieving “joint scheduling of the multi-energy complementary power generation system.” A “reactive power dispatch method,” which relies on the “Gaussian bare-bones bat algorithm,” was introduced by Qu et al. (2022) to enhance the safety and stability of the power system. This study evaluated the performance of the proposed method by conducting simulation tests on “IEEE 14-bus, 57-bus, and 118-bus systems,” and the robustness and effectiveness of the proposed reactive power dispatch method were finally demonstrated by the comparison results.
As part of achieving optimization and control objectives, Wang Q. et al. (2022) used a PID control strategy for a boost converter, which is applied in renewable power generations, relying on a “genetic algorithm and back-propagation neural network.” The employed method combined the global optimization capability of the genetic method and the adaptive features of a neural network for achieving the desired optimization and control objectives. In addition, the effectiveness of the proposed method was validated through comparative tests. On the other hand, a deep reinforcement learning-based algorithm was proposed by Li et al. (2022a) for the power management of an interconnected energy conversion system. In order to determine the control decisions, this work implemented a “swarm intelligence-based deep deterministic policy gradient algorithm.” The effectiveness of the study method was demonstrated by carrying out comparative evaluations on a four-area (two areas in West China and two areas in England) load frequency model. Moreover, a data model-driven “rescheduling method of a large-scale power grid” that implements “deep reinforcement learning” was implemented by Li et al. (2022b) to enhance both rotor angle and transient voltage stabilities. A Markov decision process was initially modeled by considering the transient stability constraint. In solving the Markov decision process, an enhanced distributed distributional deep deterministic policy gradient method was used. The effectiveness of the proposed method was finally demonstrated by conducting comparative tests on the New England 39-bus system and an actual power grid.
Second, advanced machine learning algorithms can be used in power systems and electrical equipment for parameter identification, state estimation, and fault detection (Figure 2). Under this category, numerous studies proposed different machine learning algorithms and also demonstrated the effectiveness of the methods on different models of power systems and electrical equipment. Some of these works are discussed briefly. A “fast low-frequency oscillation identification method” was introduced by Zhang et al. (2022) to improve power system operation. First, the “low-frequency oscillation and attenuation factor” were divided into 12 and 4 segments, respectively, and then the oscillation identification task was adapted using a “two bi-directional long short-term memory neural network.” The effectiveness of this study was validated to confirm the outperforming capability of the proposed method against other benchmark methods through comparative results. Peng et al. (2022) proposed a method of impedance identification for maximum power point tracking (MPPT)-controlled photovoltaic converters based on a model-agnostic meta-learning algorithm. According to this study, using data collected under different weather conditions, the employed method was observed to tune its initial model. After finishing the learning process, the adaptive model would adapt to new conditions using only few samples. The effectiveness and superiority of the proposed model were finally demonstrated through comparative results. Furthermore, Wang Y. et al. (2022) proposed a “clustering method for the wind turbines in a wind farm” through ensemble modeling. In order to identify the clustering indicators and simplify the wind farm model, “blending and extreme gradient boosting” algorithms were combined, and “density-based spatial clustering of applications with a noise” algorithm was utilized to realize clustering and fuse the clustering results. The effectiveness of the proposed study model was finally verified by conducting simulation tests.
Third, enhanced machine learning algorithms can be considered for advanced application in power plants in the case of forecasting sustainable energy generation (Figure 2). Similarly, a large number of studies have recently introduced various algorithms for application in forecasting the generation of sustainable energy, including wind and solar power. A few of these studies are summarized here. A smoothing method for wind energy fluctuation considering the short-term forecasting results was designed by Zheng and Jin (2022). In obtaining the forecasting results of wind power, the method based on the “multi-dimensional nonlinear exponential smoothing prediction” algorithm was first used, and then frequency conversion entropy was utilized. Finally, the reliability and feasibility of the employed method were verified through simulation results. On the other hand, Shan et al. (2022) proposed the recurrent neural network-based solar irradiance forecasting method using historical climate and irradiance data. By considering different input factors, comparative evaluations were conducted on an open-access dataset, and the advantages of the implemented algorithm over other benchmark algorithms were conclusively demonstrated by comparison results.
Advanced algorithms that include model predictive, fuzzy logic inference systems, neural networks, and different machine and deep learning models were broadly introduced in recent works for enhancing wind power systems by tackling some specific issues. First, as stated by Xiong et al. (2022) and Chaka et al. (2024), for instance, advanced machine/deep learning algorithms that utilize long short-term memory (LSTM) and convolutional neural networks (CNNs) can be applied to improve the accuracy of wind forecasting, which is crucial for the effective management of wind power systems. These algorithms can help provide more genuine forecasts, capacitating better scheduling and planning of wind power generation by analyzing historical weather data, sensor inputs, and other pertinent parameters. Second, the application of advanced machine/deep learning algorithms that use support vector machines (SVMs) and recurrent neural networks (RNNs) can be observed in the detection and diagnosis of faults in wind power system devices according to problem statements provided by Dhibi et al. (2022) and Liang et al. (2020). According to these statements, the proposed algorithms can have the following objectives: deviation identifications, potential failure predictions, enabling prompt maintenance or repairs, downtime minimization, and system performance optimization by analyzing real-time data from sensors and comparing them to conventional operating patterns. Third, enhanced algorithms that implement adaptive fuzzy PI and model predictive control (MPC) can optimize various control strategies applied in WECSs (Aissaoui et al., 2013; Huang et al., 2019). In the control of power systems and electrical equipment, as shown in Figure 3, these algorithms can dynamically tune control parameters for maximizing power output, enhancing system stability, and responding to grid requirements by regularly analyzing real-time sensor data, weather conditions, and power grid dynamics.
Fourth, the implementation of advanced machine learning algorithms based on support vector regression (SVR) and random forest (RF) can be seen in terms of the effective prediction of the power output and wind power system load demand (Ighravwe and Mashao, 2020; Qureshi et al., 2023). They can provide correct forecasts of power production and consumption, allowing reliable grid integration and energy management by analyzing historical data, weather conditions, and remaining pertinent factors. Fifth, control optimization of individual wind power plants within a wind farm can also be achieved through the application of advanced algorithms that rely on MPC (Liao et al., 2023), fuzzy logic control (FLC) (Rekioua et al., 2023), and reinforcement learning (RL) (Huang et al., 2023). These algorithms can regulate power system settings in real time for power production maximization, system fatigue reduction, and overall improvement of system efficiency by considering factors including wind speed, turbine wellbeing, wake effects, and grid conditions. Sixth, machine learning models that realize the applications of a genetic algorithm (GA) and particle swarm optimization (PSO) can help in estimating the optimal layout and positioning of wind power plants within a wind farm (Liu et al., 2021; Song et al., 2023). They can optimize the arrangement of power plants for increasing power production, minimizing wake losses, and reducing interference among plants by inspecting factors that include wind conditions, terrain, and wake effects.
Moreover, machine/deep learning algorithms can inspect large volumes of data collected from wind power systems for extracting useful insights, identifying patterns, and supporting decision-making processes (Brahmane and Deshmukh, 2023; Javaid et al., 2023; Elyasichamazkoti and Khajehpoor, 2021). This can incorporate the inspection of historical performance, identification of trends, optimization of maintenance schedules, and facilitation of sophisticated decision-making for the power system operators. Figure 4 shows the application of an advanced machine learning approach in enhancing wind farm optimization and control objectives. It is essential to underscore that the choice of algorithm relies on the specific dataset, control strategy, optimization objectives, features, and other factors. The capability of machine learning algorithms can vary depending on factors, including the sophistication of the system dynamics, control constraints, and existing computational tools. Hence, it is important to test with various algorithms and fine-tune them depending on specific optimization and control problems to attain the expected results. In general, despite challenges related to data availability and quality, complex system dynamics, regulatory and compliance issues, system adaptation and robustness, integration with existing infrastructure, etc. (Lipu et al., 2021; Ahmed et al., 2020; Abkar et al., 2023), the investigation of real-world case studies demonstrates the practical applications and capabilities of machine learning algorithms in the optimization of wind farm power production, monitoring and fault detection of wind turbine conditions, forecasting wind power, enhancing wind turbine control strategies, and optimization of the wind farm layout (Göcmen et al., 2020). Evaluations of performance metrics and findings from case studies also offer valuable insights into the effectiveness and innovative features of these algorithms.
By considering the above summaries that are made on the applications of machine/deep learning-based algorithms in wind power systems, Section 1.2 specifically proposes a novel proportional integral (PI) algorithm for application in smoothing electric power production with a WECS that is based on a doubly fed induction generator (DFIG).
This paper introduces an improved machine learning algorithm based on the PI (2DoF) algorithm for application in the optimization and control of a DFIG-based wind power system. In addition to utilizing control gain values, the PI control (2DoF) algorithm uses set-point control optimization for adjusting the WECS parameters, which can result in enhanced power production compared to the regular PI control algorithm (Desalegn et al., 2022a). This proposed algorithm develops a novel controller model that works based on “two degrees of freedom” to adjust control loop parameters, and this controller is often identified to be a PI (2DoF) model. Unlike the conventional controller model that mostly works well only for the normal operating condition of the power system, the employed model of controller or PI (2DoF) is distinguished by its efficiency of rapidly rejecting the power signal disturbances without causing a significant generation of overshoots in the tracking of control set points, and this is what makes it a better candidate for enhancing the overall efficiency of wind energy conversion (Huba et al., 2021; Karanam and Shaw, 2022; Abdel-hamed et al., 2023). The PI controller (2DoF) is also an excellent choice for alleviating the impact of power harmonic distortion that could result from the changes between the generated signal statistics of input and control parameters (Das et al., 2023; Bingi et al., 2019; Guras et al., 2022). Consequently, the stated novel feature of the proposed controller model can lead to a desirable improvement in the overall performance of the system.
As the PI controller (2DoF) involves a supplementary degree of freedom, it enables the autonomous control of the proportional and integral objectives. This allows great adaptability in adjusting the controller and boosting its operational capability compared to a traditional PI controller. This study aims to deploy optimization techniques by estimating the optimal control parameters for the PI controller (2DoF). This enables calibrating the controller to increase power output, enhance stability, and improve tracking performance. This paper focuses on introducing robust control strategies that can manage unpredictable operating patterns and disturbances usually created in a DFIG-based WECS. The proposed PI control (2DoF) algorithm is required to offer enhanced robustness and flexibility to fluctuating conditions of wind and system dynamics. In general, this review signifies a broad evaluation of the performance of a wind power system that relies on a DFIG utilizing a PI controller (2DoF). This involves evaluating performance metrics such as effective power transfer, power quality, and tracking precision.
This work endeavors to convey multidimensional contributions that generally portend theoretical and practical aspects. These contributions include inspiring future researchers to work on continuous improvements of existing algorithms through further advanced research studies and developments, enabling discoveries of the newest algorithms for applications in wind farm systems, and helping the development of the most reliable model platforms for evaluating the performances of machine/deep learning algorisms in real-world emulations. The main contribution of this work is endeavoring to leverage the superior features of the PI (2DoF) algorithm, which are shown in Figure 5, in the optimization and control of a DFIG-relying wind power system more efficaciously, resulting in enhanced capability, stability, and robustness under the occurrences of uncertainties.
Furthermore, this review presents a comparative evaluation and quantification of the performances of the PI (2DoF) algorithm-based controller model against that of the “traditional (conventional) PI” model under the consideration of both normal- (linear) and low-voltage (nonlinear) operating modes of a 2-MW power rating DFIG-based system. In order to further demonstrate the study’s effectiveness, the overall system model is developed in a MATLAB-Simulink software environment by enacting an “indirect field-oriented control (IFOC) strategy” on the rotor side converter (RSC) of the power system. In addition, this discusses the simulation findings against “the recommended practice and requirements” introduced by IEEE for “modern power system harmonic distortion control.”
The remainder of the paper is organized as follows: Section 2 demonstrates the method for the application of an enhanced PI (2DoF) algorithm in a DFIG-based WECS. This section also presents control configurations and mathematical models for the mechanical and electrical systems and the proposed controller model are illustrated. Section 3 constitutes MATLAB-Simulink environment-based simulations of the DFIG system and controller models, which use different parameters and a wind speed of 10 m/s. Section 4 displays the simulation results and discusses the results against power system requirements and expected standards, and the overall efficiency of the proposed controller model is also quantified compared with that of the conventional counterpart. Finally, Section 5 presents the conclusion and future research opportunities.
A DFIG-based WECS that is assumed to be connected to a power grid system and comprising a three-bladed turbine, gearbox system, electric generator, power electronic device, and step-up transformer is considered in this work. The overall structure of this proposed system is shown in Figure 6. Furthermore, the turbine system is tied to the generator via the gearbox for adapting the slow speed of the turbine shaft to the machine speed. The generator stator is directly connected to the grid, whereas the rotor is coupled to it via the power converter. Two stages of the control system could be established: 1) the rotor-side converter (RSC) allows a regulation of the active and reactive power generations of the stator such that the active power reference is transferred from the MPPT strategy and 2) the grid-side converter (GSC) ensures control of the DC voltage link and the rotor reactive power. The RSC control alone is implemented by this study.
The RSC control method is considered for developing an electrical control system that can robustly and smartly respond to irregular variations in electrical control parameters, including the rotor direct and quadrature (alternating) currents. This can thereby allow an indirect implementation of the rotor speed. Unlike the control methods widely considered in numerous published works for enhancing the operations of various wind power systems by adjusting mechanical control parameters, the RSC control method is the most compelling and effective in addressing crucial control challenges that include alternating current harmonic distortions and direct current switching transients, which could affect the proper functioning and safety of the most core subsystem of the WECS (Benbouhenni et al., 2024a; Benbouhenni et al., 2024b). Moreover, using this method can result in a better enhancement of power production reliability by enabling safe operations of the electrical components of a system and ensuring overall system automation. Accordingly, “IFOC” accompanied with a “PI controller (2DoF)” is provided to smooth the DFIG system operation mode that relies on variable wind speed. More details are presented in Sections 2.1–2.3.
For the maximum extraction of wind energy with the turbine system, a control algorithm implemented on the set-point parameters is necessary, and this algorithm may help facilitate the development of the device with enhanced performance (Desalegn et al., 2022b). Mathematically, optimal wind power production can be estimated according to the relation provided in Eq. 1:
In the most recent studies, two types of control strategies were primarily stated for the enhancement of wind power production: the first is an MPPT strategy without the mechanical speed regulation of the system, whereas the second is an MPPT strategy that is based on mechanical speed regulation.
The MPPT strategy without mechanical speed regulation is considered in this study as realizing a correct estimation of wind speed would be much harder with the mechanical speed control-based MPPT strategy due to the following reasons (Ihedrane et al., 2019; Zamzoum et al., 2018; Boubzizi et al., 2018; Okedu, 2017):
⁃ The wind speed-measuring device (an anemometer) would usually be installed at a location behind the rotor of the turbine, which would result in an incorrect estimation of wind-speed data.
⁃ A significant variation in the wind-speed measurements could result from the heights at which the measuring device (anemometer) is set up, especially when the range (diameter) of the swept area of the blades is large. For example, the range (diameter) of the swept area of the blades is normally taken to be 70 m for a wind turbine with a rotor radius of 1.5 m. Consequently, an anemometer application might use the wind-speed data measured over a very limited area, which is evidently insufficient to represent the measurement of the mean wind speed blowing over the broader surface surrounding the blades.
In general, as the inefficiency of the MPPT strategy that implements mechanical speed control would not lead to an accurate measurement of wind-speed data, this could ultimately cause a suboptimal production of wind power. The inefficiency of the mechanical speed control-based MPPT strategy stems from its use of an anemometer as an unavoidable requirement. Given that wind speed is typically characterized as frequently fluctuating over a larger area, it is hard to obtain an accurate estimation of the mean wind speed using an anemometer as the device is naturally limited to measuring wind speed in a very limited area. Consequently, a large number of wind turbine systems now rely on the application of a novel MPPT strategy that does not require the use of anemometers for wind-speed data estimations, and the wind-speed data are assumed to change constantly, as shown by the control structure in Figure 7. Furthermore, Eq. 2 defines the new MPPT strategy without needing to rely on mechanical speed regulation:
With the omission of the “mechanical torque”
The “reference value” for the system’s “electromagnetic torque” may be obtained by relying on the computation using the mathematical expressions given in Eqs 4–6:
Moreover, aerodynamic torque
By making substitutions and rearrangements serially, the rotor’s (reference) electromagnetic torque
On the other hand, the aerodynamic torque (reference) may be defined as a function of its coefficient
Accordingly, the (reference) electromagnetic torque should be redefined using Eqs 4, 7 in order to derive an expression given in Eq. 8:
The control principle of FOC involves orienting the field along one of its axes in order to make the operating modes of the induction machine resemble those of an independently excited DC machine.
Accordingly, the stator field (
Based on the “Park transformation” specifically applied to the wind power system relying on the DFIG, an expression for the “voltage at the terminals of phase “
such that
Electrical machines with medium- and high-power scales are often used in wind power generation, and in these cases, the stator winding resistance
Under the assumption that the “electrical grid voltages and the stator flux” are constant, the stator voltage components are represented as shown in Eq. 12:
Furthermore, under a similar choice where the “stator field” is oriented along the “d-axis,” the stator’s current components (direct and quadrature) can be represented according to mathematical models, which are given in Eq. 13:
On the other hand, the mathematical expression for the system rotor electromagnetic torque
Using the expressions for
With
In order to develop the mathematical expressions for the rotor voltage components as functions of the rotor current components, the rotor field flux components (
Finally, using the expressions for the rotor field flux components
Among the mathematical illustrations given in Figure 5,
⁃ The rotor voltage components
⁃ For a given (proposed) model of a controller, the rotor
⁃ The reactive-power reference value should be set to zero, which results in achieving a unity power factor on the stator side, and consequently, an enhanced power quality would ultimately be delivered to the grid. In addition, the ideal value of the power factor should be maintained by the active power reference.
Figure 10 shows the proposed control setup with the study parameters based on the implementation of an “IFOC” strategy for maximum electrical power point tracking (MEPPT). A power control method that uses a “two-level pulse width modulation (2L PWM)” and that involves an application of a machine learning algorithm-based controller model was illustrated to implement the IFOC strategy for MEPPT under linear (normal) and nonlinear (low voltage) operating scenarios of a

Table 1. Proposed optimal values for the control gains and set-point weights of PI (2DoF) based on the model-based tuning method.
Moreover, the principle of control optimization using the “PI controller (2DoF)” for the
A model simulation of the proposed DFIG-based wind energy harvesting system is built by applying “MATLAB-Simulink” platform-based different built-in blocks of the system’s components in order to achieve the effectiveness of the previously outlined power control objectives. A wind speed of
Furthermore, the “PI controller (2DoF)” model simulation (in controlling rotor current components and electromagnetic torque) and MPPT model simulation (for transforming rotor speed, rotor current components, and electromagnetic-torque based on IFOC strategy) are incorporated in the control system model simulation. The “electrical system model” simulation, “control system model” simulation, “mechanical system model” simulation, “aerodynamic system model” simulation, “wind speed model” simulation, and other components, including the two-level-based PWM generator and powergui and involving input specifications, are integrated to form the overall system model simulation, as shown in Figure 12. Model simulation for wind speed estimation (Figure 13) and the PI controller (2DoF) (Figure 14) are specifically illustrated. The PWM block is designed to regulate the rotor current (direct and quadrature) components’ signal amplitudes in order to protect the electrical components (particularly the generator) of the system from possible damage as a result of overcurrent. The “powergui block” is used for the discretization of the system’s electrical component so that the simulation is run at fixed time steps, and with this study, a “discrete phasor” method is set to be used.
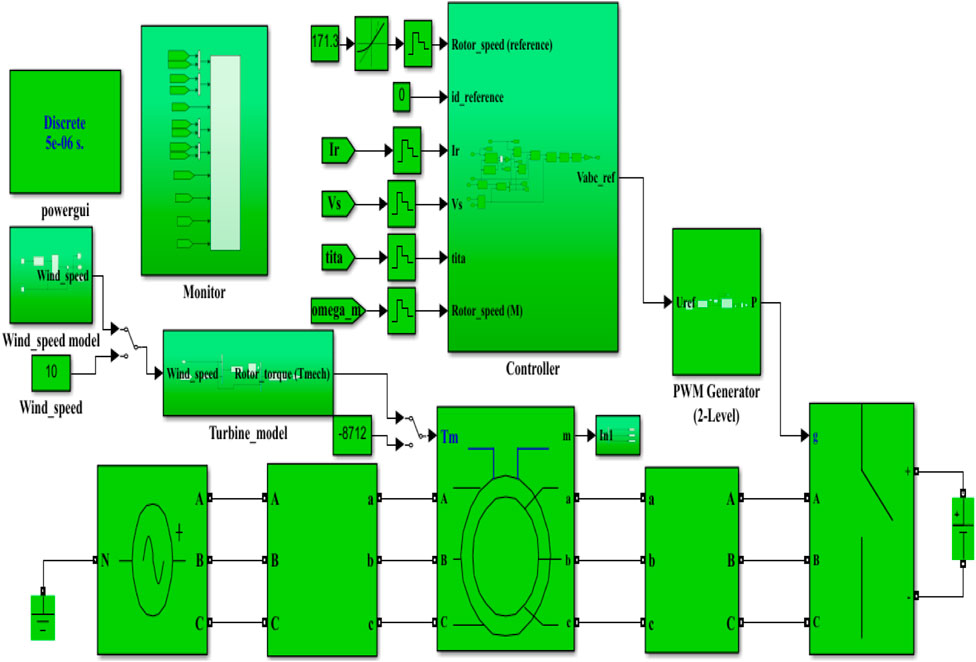
Figure 12. Overall simulated model of the proposed system in the MATLAB-Simulink platform (Desalegn et al., 2023b).
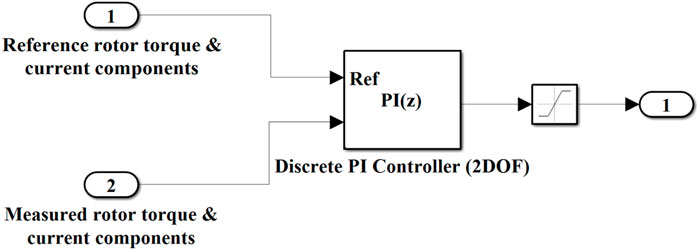
Figure 14. Simulated model of the PI controller (2DoF) for the control of the rotor current components and torque (Desalegn et al., 2022a).
In this study, the impact of the rotor current components on the power reliability under both linear/normal and nonlinear (low-voltage) operating modes of the “2-MW DFIG WECS” is investigated using the “IFOC-based PI controller (2DoF).” A random simulation of wind speed was performed at 10 m/s, as shown in Figure 15, such that it was used to numerically estimate electromagnetic torque [reference] (
The simulation visualization shown in Figure 16 represents the operating characteristics of the proposed DFIG technology-based wind power system under the assumption that the system would behave according to the normal specification of the voltage that was rated to be 690 V. In addition, the visualization shown in Figure 17 reveals the capability of this same proposed system in the nonlinear scenario such that the rated stator voltage would instantaneously decrease by 90% as per the assumption of this study, forcing the system to operate under a low-voltage scale of 69 V. As shown in Figures 16, 17, the two operating scenarios of the system result in significantly different qualities of power production performances as the generated signal distortions of the control parameters are observed to be lower under a normal-voltage operating scenario (Figure 16) and highly notable under a low-voltage operating scenario (Figure 17). High total harmonic distortion, particularly due to the alternating current signal, may cause the system to produce power with significantly compromised quality; hence, modern power systems are required to operate within the acceptable limits of harmonic distortions.
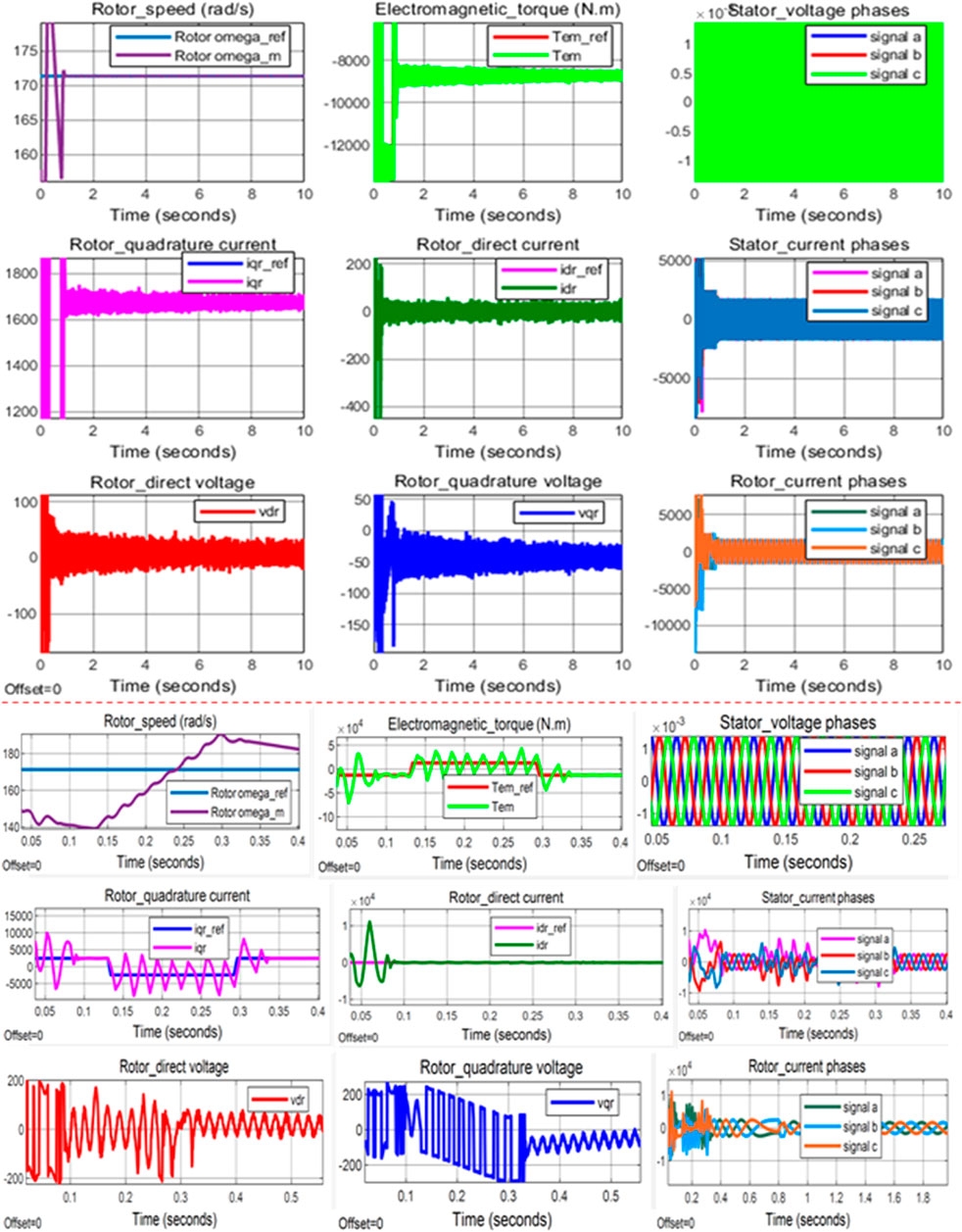
Figure 16. Control parameter simulation results under the normal-voltage operating scenario of the system (Desalegn et al., 2022a).
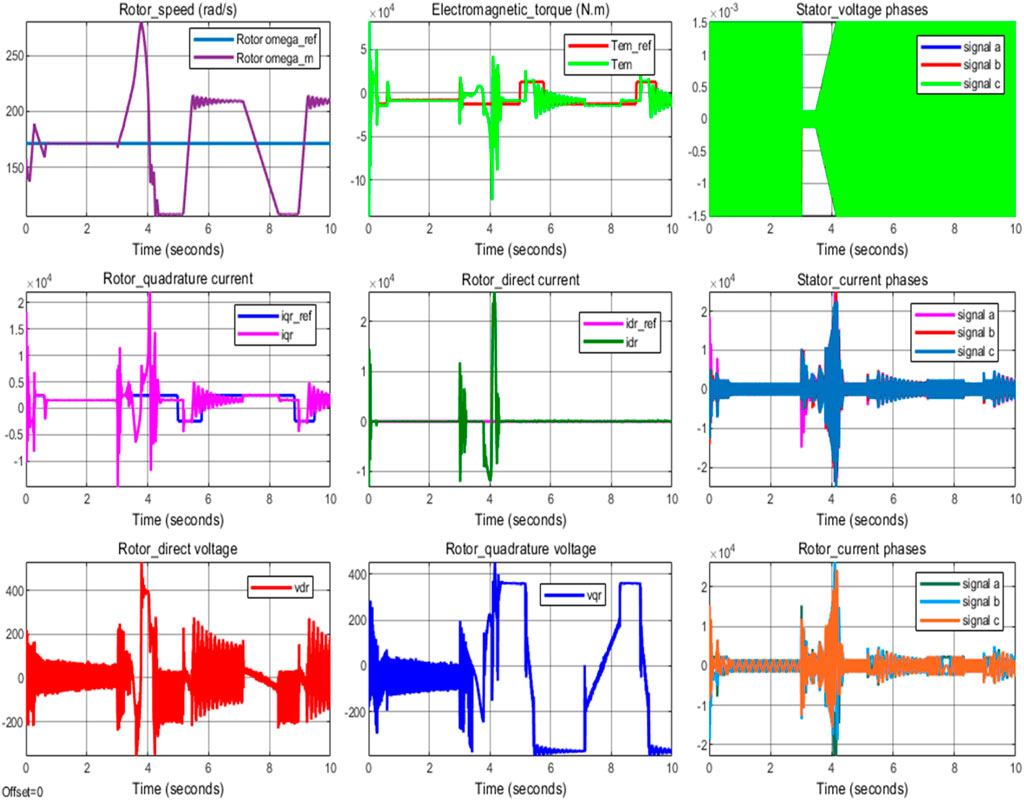
Figure 17. Control parameter simulation results under the low-voltage operating scenario of the system (Desalegn et al., 2022a).
In addition, the evaluations of the signal statistics that are generated to represent the control parameters in Tables 2, 3 show that the qualities of the system’s operating performances for the two operating scenarios are comparatively and objectively quantified. Accordingly, the performances of the proposed PI (2DoF) model under both linear/normal and nonlinear/low-voltage operating scenarios can be comparatively demonstrated relying on the statistics given in Tables 2, 3.
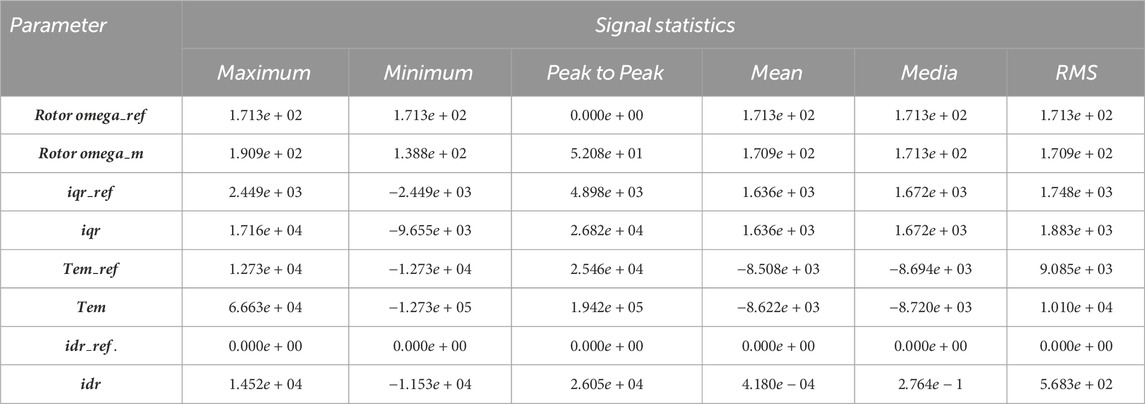
Table 2. Generated signal statistics of the control parameters under the normal-voltage operating scenario.
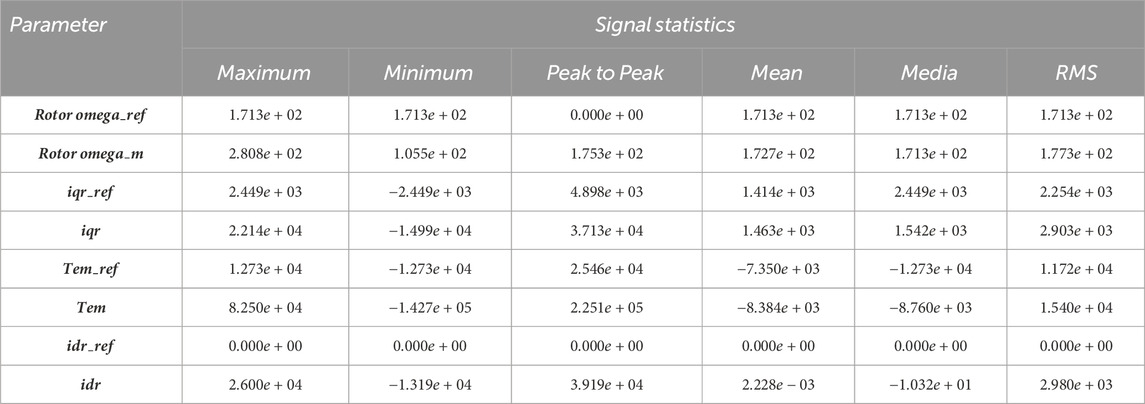
Table 3. Generated signal statistics of the control parameters under the low-voltage operating scenario.
By utilizing the “signal statistics” given in “Tables 2, 3,” one of the ways to quantify the PI (2DoF) performances is computationally determining the values of the “total harmonic distortion factor” of the system’s quadrature/alternating current signals. The “total harmonic distortion factor” is dimensionally expressed in percentage (%) after subtracting the “root mean square (RMS)” values of the “reference quadrature-current” signals from those of the measured quadrature current signals and then dividing the substation results by the RMS values of the reference current signals, as mathematically defined in Eq. 20. The estimated results of the harmonic distortion factor of the quadrature current signals can eventually be utilized in order to determine whether the PI controller (2DoF) performances improve or degrade the quality of power production under the above-mentioned operating scenarios of the system’s stator voltage. The estimated values of the harmonic distortion factor generally indicate the levels of peaks in the signals of the rotor quadrature current and identify the DFIG system’s capacity to produce a certain amount of current. The level of the harmonic-distortion factor of the output quadrature-current signal has been recommended to be within
Furthermore, the distortion factor of the rotor quadrature current (
By utilizing Eq. 16, the amount of electrical power transfer under both scenarios can also be obtained and comparatively discussed against the baseline rating
The control capability of the “PI controller (2DoF)” can also be comparatively demonstrated against that of the conventional PI controller model as follows (Figures 18, 19; Table 4). Under the normal-voltage operating scenario, both controller models allow an approximately similar scale of electric power transfer,

Table 4. Overall comparison of the PI (2DoF) vs PI performances considering the main control results.
Further comparison between the control performances of the two controller models can also be demonstrated under the low-voltage operating scenario, where the amount of electric power transfer is estimated at
Once again, a document introduced by a prestigious institution in the Distribution Committee of the IEEE Power and Energy Society (2014) indicated recommendations for modern power system requirements and expected standards that involve setting a maximum limit for the total harmonic distortion level of the alternating current and mitigating a switching transient that could result from a sudden reverse of the flow direction of the direct current in power systems’ electrical components. This document states that the maximum limit of the harmonic distortion factor equaling 25% is acceptable only if the switching transient is not encountered in the power systems’ electrical components. Furthermore, a harmonic distortion factor that is lower than the maximum limit (25%) is desirable only if the switching transient can be proven to be mitigated. When a harmonic distortion factor that is larger than the maximum limit results from an alternating current’s signal, a given power system tends to produce electric power with an undesirable quality. When a flow direction of direct current is found to be reversed under a sudden voltage disturbance in a given power system, it may cause the generation of a high amount of heat in an electrical component of the power system, which could ultimately cause a total electric power outage by damaging the system electrical component.
In general, the above-mentioned requirements and expected standards apply to any modern power system operating in two possible modes: linear (normal) voltage operating mode and nonlinear (low voltage) operating mode, according to the assumptions set forth by this work. Hence, in this work, the results of the harmonic distortion factor of the rotor alternating (quadrature) current and the switching transient of the direct current with the proposed and conventional algorithms can be comparatively validated accordingly. The summarized results of the total harmonic distortion factor of the rotor quadrature current and the mean signal of the direct current (Table 4) show that the PI (2DoF) algorithm closely performs according to the recommended requirements and expected standards for modern power systems, while the conventional PI algorithm performs against the recommended requirements and expected standards, particularly during the nonlinear operating mode of the DFIG system.
• This study developed an enhanced PI (2DoF) algorithm-based controller model in a DFIG-based WECS for enhancing the reliability of wind energy conversion by regulating total harmonic distortions and ensuring an optimal electric power transfer along with mitigating switching transients. The linear and nonlinear operational characteristics of a system have been separately examined by implementing control on the rotor alternating current in keeping the harmonic distortions at reasonable factors, and a similar control strategy has also been applied on the rotor direct current in mitigating the switching transients such that the effective power transfer is deemed optimal. Subsequently, the performances of the simulated PI controller (2DoF) model have been evaluated and validated based on the harmonic distortion and switching transient requirements that were recommended for the operation of modern power systems. In addition, the performances of this controller model have been comparatively tested against those of the conventional PI model. Ultimately, the simulation results have shown that the PI (2DoF) controller performs well compared with the conventional PI.
• By utilizing noble features of the PI (2DoF) algorithm, the results of this work are mainly associated with enhancing control for minimizing the total harmonic distortion by regulating the proposed power system’s alternating current and mitigating switching transients by regulating the direct current of the system, thereby maximizing the effective electric power transfer. The results have indicated that the utilized algorithm has enhanced wind power production potential by sublimating the operating modes of the DFIG-based wind power system. However, these results may only signify that further applications and investigations of machine learning algorithms are needed in future work for revolutionizing wind farm industries.
• On the other hand, this study indicates that the low-voltage operating behavior of the DFIG system is the most relevant research problem, and consequently, the low-voltage operating scenario-based results of the system need to be further improved in future research. To this end, more robust controller models are required to be implemented for significantly minimizing the distortion factor of the rotor quadrature current, thus achieving a reliable electric power transfer. In this regard, the most recent literature reviews suggest the implementation of hybrid controller models by claiming that two different controller models can significantly enhance power reliability when used jointly rather than independently. This is because the operations of sustainable energy conversion technologies, including the DFIG-based WECS, largely rely on highly nonlinear parameters, and as each individual controller model has its own advantages and limitations in managing different control parameters, integrating different controller models would allow us to harness their respective control advantages while alleviating their various limitations. For instance, the sliding mode controller model is robust at ensuring maximum power transfer, but it introduces a chattering problem to a power system, while the fuzzy logic controller model is intelligent in predicting a phenomenon with a higher degree of nonlinearity. Thus, the hybridization of these two controller models may optimize the complexity of the power system operation.
• Moreover, future research opportunities involve smart grid integration, machine learning applications, and advanced control algorithms. These require exploring opportunities for integrating wind power systems into smart grid systems, qualifying sophisticated grid management and wind power distribution, examining machine learning techniques to optimize the power systems’ adaptive capabilities and performance, and investigating and introducing the newest control algorithms to further enhance the efficiency and reliability of the power systems.
BD: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. BT: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abad, G., Lopez, J., Rodrıguez, M., Marroyo, L., and Iwanski, G. (2011). Doubly fed induction modeling and control. 633 Available at: https://www.wiley.com/en-ca/Doubly+Fed+Induction+Machine%3A+Modeling+and+Control+for+Wind+Energy+Generation+-p-9780470768655 (Accessed September 16, 2022).
Abdel-hamed, A. M., Abdelaziz, A. Y., and El-Shahat, A. (2023). Design of a 2DOF-PID control scheme for frequency/power regulation in a two-area power system using dragonfly algorithm with integral-based weighted goal objective. Energies 16 (1), 486. doi:10.3390/EN16010486
Abkar, M., Zehtabiyan-Rezaie, N., and Iosifidis, A. (2023). Reinforcement learning for wind-farm flow control: current state and future actions. Theor. Appl. Mech. Lett. 13 (6), 100475. doi:10.1016/J.TAML.2023.100475
Ahmed, S. D., Al-Ismail, F. S. M., Shafiullah, M., Al-Sulaiman, F. A., and El-Amin, I. M. (2020). Grid integration challenges of wind energy: a review. IEEE Access 8, 10857–10878. doi:10.1109/ACCESS.2020.2964896
Aissaoui, A. G., Tahour, A., Essounbouli, N., Nollet, F., Abid, M., and Chergui, M. I. (2013). A Fuzzy-PI control to extract an optimal power from wind turbine. Energy Convers. Manag. 65, 688–696. doi:10.1016/J.ENCONMAN.2011.11.034
Benbouhenni, H., Bizon, N., Mosaad, M. I., Colak, I., Djilali, A. B., and Gasmi, H. (2024a). Enhancement of the power quality of DFIG-based dual-rotor wind turbine systems using fractional order fuzzy controller. Expert Syst. Appl. 238 (Mar), 121695. doi:10.1016/J.ESWA.2023.121695
Benbouhenni, H., Yessef, M., Colak, I., Bizon, N., Kotb, H., AboRas, K. M., et al. (2024b). Dynamic performance of rotor-side nonlinear control technique for doubly-fed multi-rotor wind energy based on improved super-twisting algorithms under variable wind speed. Sci. Rep. 14 (1), 5664. doi:10.1038/s41598-024-55271-7
Bingi, K., Ibrahim, R., Karsiti, M. N., Hassan, S. M., and Harindran, V. R. (2019). Real-time control of pressure plant using 2DOF fractional-order PID controller. Arab. J. Sci. Eng. 44 (3), 2091–2102. doi:10.1007/s13369-018-3317-9
Boubzizi, S., Abid, H., El hajjaji, A., and Chaabane, M. (2018). Comparative study of three types of controllers for DFIG in wind energy conversion system. Prot. Control Mod. Power Syst. 3 (1), 21–12. doi:10.1186/s41601-018-0096-y
Brahmane, A. V., and Deshmukh, S. R. (2023). “Artificial intelligence-based energy management system for renewable energy sources,” in 2023 4th International Conference on Electronics and Sustainable Communication Systems, ICESC 2023 - Proceedings, Coimbatore, India, 06-08 July 2023, 727–731. doi:10.1109/ICESC57686.2023.10193623
Chaka, M. D., Semie, A. G., Mekonnen, Y. S., Geffe, C. A., Kebede, H., Mersha, Y., et al. (2024). Improving wind speed forecasting at Adama wind farm II in Ethiopia through deep learning algorithms. Case Stud. Chem. Environ. Eng. 9, 100594. doi:10.1016/J.CSCEE.2023.100594
Das, D., Chakraborty, S., and Naskar, A. K. (2023). Controller design on a new 2DOF PID structure for different processes having integrating nature for both the step and ramp type of signals. Int. J. Syst. Sci. 54, 1423–1450. doi:10.1080/00207721.2023.2177903
Desalegn, B., Gebeyehu, D., and Tamirat, B. (2022b). Wind energy conversion technologies and engineering approaches to enhancing wind power generation: a review. Heliyon 8, e11263. doi:10.1016/j.heliyon.2022.e11263
Desalegn, B., Gebeyehu, D., and Tamrat, B. (2022a). Evaluating the performances of PI controller (2DOF) under linear and nonlinear operations of DFIG-based WECS: a simulation study. Heliyon 8 (12), e11912. doi:10.1016/J.HELIYON.2022.E11912
Desalegn, B., Gebeyehu, D., and Tamrat, B. (2023b). Smoothing electric power production with DFIG-based wind energy conversion technology by employing hybrid controller model. Energy Rep. 10, 38–60. doi:10.1016/j.egyr.2023.06.004
Desalegn, B., Gebeyehu, D., Tamrat, B., and Tadiwose, T. (2023a). Wind energy-harvesting technologies and recent research progresses in wind farm control models. Front. Energy Res. 11, 81. doi:10.3389/fenrg.2023.1124203
Dhibi, K., Mansouri, M., Bouzrara, K., Nounou, H., and Nounou, M. (2022). Reduced neural network based ensemble approach for fault detection and diagnosis of wind energy converter systems. Renew. Energy 194, 778–787. doi:10.1016/J.RENENE.2022.05.082
Distribution Committee of the IEEE Power and Energy Society (2014). IEEE recommended practice and requirements for harmonic control in electric power systems sponsored by the transmission and distribution committee IEEE power and energy society. IEEE.
Elyasichamazkoti, F., and Khajehpoor, A. (2021). Application of machine learning for wind energy from design to energy-Water nexus: a Survey. Energy Nexus 2, 100011. doi:10.1016/J.NEXUS.2021.100011
Göcmen, T., Kölle, K., Andersen, S. J., Eguinoa, I., Duc, T., Campagnolo, F., et al. (2020). Launch of the FarmConners wind farm control benchmark for code comparison. J. Phys. Conf. Ser. 1618 (2), 022040. doi:10.1088/1742-6596/1618/2/022040
Gohar, R., and Servati, F. (2014). Modeling a DFIG-based wind turbine focusing on DFIG and aerodynamic models. Eur. Online J. Nat. Soc. Sci. 3 (3), 744–757. Available at: https://european-science.com/eojnss/article/view/982.
Guras, R., Strambersky, R., and Mahdal, M. (2022). The PID and 2DOF control of the integral system - influence of the 2DOF parameters and practical implementation. Meas. Control (United Kingdom) 55 (1–2), 94–101. doi:10.1177/00202940221076961
Huang, S., Wu, Q., Guo, Y., and Rong, F. (2019). Optimal active power control based on MPC for DFIG-based wind farm equipped with distributed energy storage systems. Int. J. Electr. Power & Energy Syst. 113, 154–163. doi:10.1016/J.IJEPES.2019.05.024
Huang, Y., Lin, S., and Zhao, X. (2023). Multi-agent reinforcement learning control of a hydrostatic wind turbine-based farm. IEEE Trans. Sustain Energy 14 (4), 2406–2416. doi:10.1109/TSTE.2023.3270761
Huba, M., Chamraz, S., Bistak, P., and Vrancic, D. (2021). Making the PI and PID controller tuning inspired by ziegler and nichols precise and reliable. Sensors (Basel) 21 (18), 6157. doi:10.3390/S21186157
Ighravwe, D. E., and Mashao, D. (2020). Analysis of support vector regression kernels for energy storage efficiency prediction. Energy Rep. 6, 634–639. doi:10.1016/J.EGYR.2020.11.171
Ihedrane, Y., el Bekkali, C., Bossoufi, B., and Bouderbala, M. (2019). “Control of power of a DFIG generator with MPPT technique for wind turbines variable speed,” in Green energy and technology. Editor H. Machrafi (United Arab Emirates (UAE): Bentham Science Publishers), 105–129. doi:10.1007/978-981-13-1945-7_5/COVER/
Javaid, U., Usman, R. M., and Javaid, A. (2023). “Investigating the energy production through sustainable sources by incorporating multifarious machine learning methodologies,” in 3rd IEEE International Conference on Artificial Intelligence, ICAI 2023, Islamabad, Pakistan, 22-23 February 2023, 233–237. doi:10.1109/ICAI58407.2023.10136677
Karanam, A. N., and Shaw, B. (2022). A new two-degree of freedom combined PID controller for automatic generation control of a wind integrated interconnected power system. Prot. Control Mod. Power Syst. 7 (1), 20–16. doi:10.1186/s41601-022-00241-2
Kerrouche, K., Mezouar, A., and Belgacem, K. (2013). Decoupled control of doubly fed induction generator by vector control for wind energy conversion system. Energy Procedia 42, 239–248. doi:10.1016/J.EGYPRO.2013.11.024
Li, J., Yang, S., Yu, T., and Zhang, X. (2022b). Data-driven optimal PEMFC temperature control via curriculum guidance strategy-based large-scale deep reinforcement learning. IET Renew. Power Gener. 16 (7), 1283–1298. doi:10.1049/RPG2.12240
Li, J., Yao, J., Yu, T., and Zhang, X. (2022a). Distributed deep reinforcement learning for integrated generation-control and power-dispatch of interconnected power grid with various renewable units. IET Renew. Power Gener. 16 (7), 1316–1335. doi:10.1049/RPG2.12310
Liang, J., Zhang, K., Al-Durra, A., and Zhou, D. (2020). A novel fault diagnostic method in power converters for wind power generation system. Appl. Energy 266, 114851. doi:10.1016/J.APENERGY.2020.114851
Liao, W., Wu, Q., Cui, H., Huang, S., Gong, Y., and Zhou, B. (2023). Model predictive control based coordinated voltage control for offshore radial DC-connected wind farms. J. Mod. Power Syst. Clean Energy 11 (1), 280–289. doi:10.35833/MPCE.2020.000685
Lipu, M. S. H., Miah, M. S., Hannan, M. A., Hussain, A., Sarker, M. R., Ayob, A., et al. (2021). Artificial intelligence based hybrid forecasting approaches for wind power generation: progress, challenges and prospects. IEEE Access 9, 102460–102489. doi:10.1109/ACCESS.2021.3097102
Liu, Z., Fan, S., Wang, Y., and Peng, J. (2021). Genetic-algorithm-based layout optimization of an offshore wind farm under real seabed terrain encountering an engineering cost model. Energy Convers. Manag. 245, 114610. doi:10.1016/J.ENCONMAN.2021.114610
Okedu, K. E. (2017). Benefits and weak points of various control strategies in enhancing variable speed wind turbine transient performance. Renew. Energy Focus 19–20, 104–116. doi:10.1016/J.REF.2017.06.001
Peng, Y., Wang, Y., Liu, Y., Gao, K., Yin, T., and Yu, H. (2022). Few-shot learning based multi-weather-condition impedance identification for MPPT-controlled PV converters. IET Renew. Power Gener. 16 (7), 1345–1353. doi:10.1049/RPG2.12430
Qu, Z., Dong, Y., Mugemanyi, S., Yu, T., Bo, X., Li, H., et al. (2022). Dynamic exploitation Gaussian bare-bones bat algorithm for optimal reactive power dispatch to improve the safety and stability of power system. IET Renew. Power Gener. 16 (7), 1401–1424. doi:10.1049/RPG2.12428
Qureshi, S., Shaikh, F., Kumar, L., Ali, F., Awais, M., and Gürel, A. E. (2023). Short-term forecasting of wind power generation using artificial intelligence. Environ. Challenges 11, 100722. doi:10.1016/J.ENVC.2023.100722
Rekioua, D., Mokrani, Z., Kakouche, K., Rekioua, T., Oubelaid, A., Logerais, P. O., et al. (2023). Optimization and intelligent power management control for an autonomous hybrid wind turbine photovoltaic diesel generator with batteries. Sci. Rep. 13 (1), 21830–21831. doi:10.1038/s41598-023-49067-4
Shan, S., Xie, X., Fan, T., Xiao, Y., Ding, Z., Zhang, K., et al. (2022). A deep-learning based solar irradiance forecast using missing data. IET Renew. Power Gener. 16 (7), 1462–1473. doi:10.1049/RPG2.12408
Singh, U., and Rizwan, M. (2021). A systematic review on selected applications and approaches of wind energy forecasting and integration. J. Institution Eng. (India) Ser. B 102 (5), 1061–1078. doi:10.1007/s40031-021-00618-1
Song, J., Kim, T., and You, D. (2023). Particle swarm optimization of a wind farm layout with active control of turbine yaws. Renew. Energy 206, 738–747. doi:10.1016/J.RENENE.2023.02.058
Wang, D., Peng, D., Huang, D., Ren, L., Yang, M., and Zhao, H. (2022a). Research on short-term and mid-long term optimal dispatch of multi-energy complementary power generation system. IET Renew. Power Gener. 16 (7), 1354–1367. doi:10.1049/RPG2.12366
Wang, Q., Xi, H., Deng, F., Cheng, M., and Buja, G. (2022b). Design and analysis of genetic algorithm and BP neural network based PID control for boost converter applied in renewable power generations. IET Renew. Power Gener. 16 (7), 1336–1344. doi:10.1049/RPG2.12320
Wang, Y., Li, Y. G., Xie, H., Wu, B. Y., and Yang, Y. N. (2022c). Cluster division in wind farm through ensemble modelling. IET Renew. Power Gener. 16 (7), 1299–1315. doi:10.1049/RPG2.12276
Wei, X., Sun, Y., Zhou, B., Zhang, X., Wang, G., and Qiu, J. (2022). Carbon emission flow oriented multitasking multi-objective optimization of electricity-hydrogen integrated energy system. IET Renew. Power Gener. 16 (7), 1474–1489. doi:10.1049/RPG2.12402
Xiong, B., Lou, L., Meng, X., Wang, X., Ma, H., and Wang, Z. (2022). Short-term wind power forecasting based on attention mechanism and deep learning. Electr. Power Syst. Res. 206, 107776. doi:10.1016/J.EPSR.2022.107776
Zamzoum, O., El Mourabit, Y., Errouha, M., Derouich, A., and El Ghzizal, A. (2018). Power control of variable speed wind turbine based on doubly fed induction generator using indirect field-oriented control with fuzzy logic controllers for performance optimization. Energy Sci. Eng. 6 (5), 408–423. doi:10.1002/ESE3.215
Zhang, C., Xu, Z., Zhang, K., Wu, Y., Liu, Q., Wei, J., et al. (2022). Long short-term memory-based robust and qualitative modal feature identification of non-stationary low-frequency oscillation signals in power systems. IET Renew. Power Gener. 16 (7), 1368–1379. doi:10.1049/RPG2.12352
Zheng, X., and Jin, T. (2022). A reliable method of wind power fluctuation smoothing strategy based on multidimensional non-linear exponential smoothing short-term forecasting. IET Renew. Power Gener. 16 (16), 3573–3586. doi:10.1049/RPG2.12395
Keywords: wind power system, doubly fed induction generator-based wind energy conversion system, optimization and control, advanced algorithms, proportional integral (2DoF)
Citation: Desalegn B and Tamrat B (2024) Overview of the PI (2DoF) algorithm in wind power system optimization and control. Front. Energy Res. 12:1435455. doi: 10.3389/fenrg.2024.1435455
Received: 20 May 2024; Accepted: 18 July 2024;
Published: 09 August 2024.
Edited by:
Galih Bangga, DNV GL, United KingdomReviewed by:
Omveer Singh, Gautam Buddha University, IndiaCopyright © 2024 Desalegn and Tamrat. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Belachew Desalegn, YmVsYWNoZXdkZXNhbGVnbjc2QGdtYWlsLmNvbQ==; Bimrew Tamrat, YmV0c2Vsb3RiaW1AZ21haWwuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.