
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 11 July 2024
Sec. Sustainable Energy Systems
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1420393
This article is part of the Research Topic Optimal Scheduling of Demand Response Resources In Energy Markets For High Trading Revenue and Low Carbon Emissions View all 34 articles
Shared energy storage offers substantial savings on construction costs and improves energy efficiency for users, yet its business model as an independent economic entity remains unclear. An optimal scheduling method for cooperative operation of shared energy storage among multiple user types is proposed in this paper, which relied on asymmetric Nash bargaining to define operational schedules and pricing strategies effectively. Initially, a cost-benefit model for shared energy storage operators, along with power generation users, demand-side consumers, and microgrid prosumers is developed. Then, a cooperative game framework is established using asymmetric Nash bargaining principles which decomposes the problem into two parts: minimizing social total cost through cooperative operation scheduling and determining service fee pricing for equitable benefit distribution. For benefit distribution, the bargaining power of users is adjusted based on their alliance contribution, ensuring revenue distribution is aligned with individual contributions and improving fairness in pricing. Subsequently, the adaptive penalty factor alternating direction multiplier method (ADMM) algorithm is employed for distributed equilibrium solving, enhancing the convergence speed and safeguarding user privacy. Finally, the economics and feasibility of the proposed cooperation framework for shared energy storage are validated through a numerical example.
In the context of rapid economic development, global electricity demand continues to rise. However, environmental pollution becomes severe due to the increasing use of fossil fuels. Promoting the transition towards a cleaner energy structure with a high proportion of renewable energy has become a global consensus (Rehmani et al., 2018). Nevertheless, the stochasticity and volatility of renewable energy still presents challenges for efficient utilization and flexible scheduling in power grids and energy systems (Shivashankar et al., 2016). Integrating energy storage systems into smart grids can be a potent means to enhance the operational characteristics and stability of power systems by providing buffering capabilities. In recent years, due to its adaptable control over charging and discharging, energy storage has been extensively applied in various scenarios including mitigating fluctuations in new energy output, regulating grid frequency, optimizing transmission flow, as well as peak valley spread arbitrage for user-side (Li and Wang, 2021).
In traditional energy storage applications, individual investments are typically made to construct energy storage systems and optimize operation strategies for profitability (Ding et al., 2021; Tsioumas et al., 2021; Shi et al., 2022). However, this approach often leads to redundant capacity with low utilization rates. Fluctuations in renewable energy sources and loads can result in idle periods, leading to resource wastage. With the advent of Internet of Things technology and the concept of “sharing economy,” a “peer-to-peer” (P2P) trading model has emerged. This model allows individuals with unused distributed energy storage capacity or surplus stored energy to sell it to others for their use (Tushar et al., 2020), decoupling ownership rights from energy usage rights. This significantly improves upon the limitations of traditional profit models and utilization rates associated with energy storage (Xia et al., 2022). The economic advantages of P2P models over user-grid transactions (P2G) are confirmed by (Yaldiz et al., 2021), while discussing optimal configurations for photovoltaic generation and energy storage among different prosumers. The operational and configuration disparities among energy storage systems with varying ownership structures in P2P markets are studied by (Rodrigues et al., 2020), where user-owned structure exhibit the highest net present value. Energy interaction through distributed storage enables users to achieve significant cost reductions. However, distributed energy storage sharing still requires individuals to possess a certain proportion of stored energy, and users still face the substantial investment and construction costs associated with energy storage.
Operators of “shared energy storage (SES)” have emerged as independent economic agents that invest in and manage large-scale energy storage stations (Liu et al., 2017). These operators are obliged to design market mechanisms that properly facilitate transactions with users. Through these mechanisms, users can lease energy storage to fulfill their specific needs such as peak shaving, frequency regulation, and optimizing demand curves without incurring the costs associated with constructing energy storage facilities. SES efficiently addresses challenges like high costs and low utilization rates through expenses sharing and economies of scale. The installation and operation costs, allocation of energy storage capacity, and profitability between SES and distributed energy storage systems are compared in literature (Lombardi and Schwabe, 2017; Walker and Kwon, 2021), clearly illustrating the economic advantages and development prospects of SES.
At present, the methods of energy storage sharing can be broadly categorized into capacity sharing and energy sharing. The capacity-based allocation scheme involves dividing the total energy storage capacity into blocks and assigning them to users. In the mechanism proposed in (Jo and Park, 2020), users initially have an equal share of energy storage capacity, which they can dynamically adjust through additional capacity trading among users. In reference (Zhao et al., 2019), energy storage aggregators possess physical energy storage and distribute it as virtual capacity to users, determining the allocated capacity for each user through a two-stage algorithm. However, a simple division of capacity alone cannot facilitate energy interaction between users or optimize social benefits. On the other hand, employing an energy-sharing scheduling strategy allows for better utilization of complementarity in energy distribution among users over flexible time scales, thereby enhancing both energy efficiency and integration of renewable sources. In (Zhang et al., 2022), the equilibrium of a peer-to-peer market between SES operators acting as energy suppliers and residential users is investigated, where the pricing of energy is determined by the supply-demand relationship in the market. Furthermore, prosumers interactions with SES to achieve minimal overall societal cost are explored in (He et al., 2022), while considering ideal profit realization ratio for equitable benefit distribution purposes. Nevertheless, most existing literature primarily focus on establishing mechanisms for energy transactions with prosumer-type users.
SES has multiple application scenarios. The rapid growth of distributed energy has transformed many consumers into prosumers (Parag and Sovacool, 2016), necessitating an urgent improvement in renewable energy consumption. Emerging energy entities like virtual power plants and integrated energy systems actively participate in grid optimization (Yu et al., 2019), while demand response facilitates user-side active involvement in source-grid interaction (Hui et al., 2020). These diverse energy interaction demand scenarios offer significant application prospects for SES. SES provides multiple profit-making opportunities that conventional storage cannot combine concurrently, including peak-valley price arbitrage (Li et al., 2021), participation in ancillary services (Ma et al., 2022), assist market bidding (Zhang et al., 2023), as well as optimizing the output of wind farm groups (Song et al., 2023). SES is applied by (He et al., 2023) to frequency regulation in microgrid clusters while ensuring frequency safety and increasing economic benefits from storage. SES is utilized to lower operating costs and reduce carbon emissions on integrated energy systems in (Hu et al., 2024). However, existing literature only focuses on a single scenario for using SES without exploring its full commercial potential extensively. Therefore, developing fair and sustainable scheduling methods along with benefit distribution mechanisms becomes crucial when dealing with multi-user application scenarios to ensure stable operation of SES.
Game theory provides a valuable framework for resolving conflicting interests among multiple stakeholders (Tushar et al., 2018). Control strategies for SES can be categorized into non-cooperative games and cooperative games, depending on the presence of position conflicts or cooperation between entities. In non-cooperative games, users and SES operators are assumed to have contradictory interests, with each party making decisions solely based on their own benefit. Equilibrium is attained when members cannot increase their individual utility by altering their own strategies alone. Consumers involved in SES capacity allocation as a generalized non-cooperative game are modeled in (Xiao et al., 2022), using the alternating direction multiplier method (ADMM) and heavy ball method to optimize both capacity and energy distribution. In reference (Li et al., 2023), under the stackelberg game framework, SES sells energy to users at specific prices while users adjust their electricity consumption strategies accordingly. The double-layer model is transformed into a mixed integer linear programming model through the mathematical programming with equilibrium constraints and linearizing techniques.
Reaching global efficiency with individual optimal equilibrium is challenging in non-cooperative games. Therefore, operators and users can adopt a cooperative game control strategy by signing agreements with the common interest goal of maximizing social welfare. Cooperative games necessitate fair and reasonable mechanisms to redistribute the cooperative surplus before and after the cooperation, determining the final benefits for each participant. Common methods of profit distribution include the nucleolus method (Yang et al., 2021), Shapley value method (Xie et al., 2022), Nash bargaining (Wang et al., 2024), etc. Constraint generation technology is introduced by (Chen et al., 2023) to enhance the nucleolus method and obtain a cost allocation approach for collaborative alliances of energy storage users (Chen et al., 2023). An improved Shapley algorithm is employed under blockchain technology to allocate SES operating costs among different nodes (Yu et al., 2023). However, when there are numerous agents involved, the Shapley method encounters dimension explosion issues while solving the nucleolus method becomes more complex. The Nash bargaining method effectively achieves global optimality with low computational complexity, making it a commonly used approach for addressing benefit allocation problems. Nash bargaining is utilized to resolve payment issues in electricity-gas energy-sharing between micro-energy grids and energy storage and initial distribution results are adjusted based on investment return periods of energy storage (Wang et al., 2023). The scheduling of SES in local integrated energy systems is explored, using Nash bargaining to allocate benefits (Chen et al., 2022). Nevertheless, the above literature exclusively employs the general Nash bargaining, which ensures that all members have equal profit increase ratios, neglecting individual members’ distinct contributions to overall energy interaction. Some asymmetric Nash bargaining models are characterized by single factor, which is still not being comprehensive enough.
For multi-agent games, protecting individual privacy while solving optimization problems has become particularly important. The ADMM algorithm has received attention because it allows the decomposition of variables for distributed problem-solving, enabling each agent to solve independently and couple to the global optimum. The ADMM algorithm is used for decentralized solving of peer-to-peer transaction frameworks of interconnected microgrids in (Wei et al., 2021). In (Xia et al., 2023), ADMM is employed to solve the inter-microgrid market while preserving privacy, based on the model of the objective uncertainty and risk preference inside microgrids. However, the convergence of the ADMM is quite sensitive to the choice of penalty factors. Selecting appropriate penalty factors can significantly accelerate the convergence speed.
Based on the existing literature, this study investigates an optimization strategy for cooperative operation of SES based on asymmetric Nash bargaining, aiming to enhance various benefits and improve the economic efficiency of energy storage operators. Firstly, the user types are further refined, including three categories: power generation users, demand-side consumers, and microgrid prosumers. Subsequently, a cooperative game model based on asymmetric Nash bargaining is developed and decomposed into two sub-problems: cooperative operation scheduling and benefit allocation. Pricing negotiations for SES services are conducted based on criteria such as marginal contribution, inter-energy interaction contribution, and peak-time energy contribution as measures of bargaining power, ensuring that each user’s interests are enhanced after cooperation while promoting alliance stability and fairness. The adaptive penalty factor ADMM algorithm is applied to achieve decentralized solutions while enhancing privacy protection. This improved ADMM algorithm reduces sensitivity to penalty factor parameter selection and accelerates convergence speed.
The schematic diagram of the cooperative energy storage sharing framework is illustrated in Figure 1. SES operators possess a specific scale of physical energy storage and maintain data centers capable of processing user data to optimize charge and discharge control. For users, all services typically provided by self-built energy storage systems are available through SES projects. It reduces the burden of substantial investments in individual energy storage solutions. The set of users in this article is denoted as
To further enhance overall energy efficiency, SES operators and users can establish cooperation agreements to promote energy interaction and complementation among users. This collaboration can be divided into two stages. In the first stage, all parties optimize the operational scheduling plan of SES with the common objective of maximizing social welfare. Instead of selling excess energy to the grid at a low price, energy is stored in SES, allowing other users to reduce the high costs of purchasing electricity. Distributed optimization methods enable users to securely transmit only their optimal dispatch power requirements for SES to the operator’s data center for computation. In the second stage, a fair distribution is determined for the cooperative surplus, providing incentives to individuals who significantly contribute in energy sharing strategies. Fair profit distribution ensures that the interests of each participant in the SES project are enhanced, guaranteeing the stability of the cooperation. The optimization prioritizes day-ahead scheduling, with a single operation horizon is defined as 1 day and denoted as
SES operators invest in, construct, and maintain physical storage facilities. The costs account for daily investment and construction expenses, as well as maintenance costs due to storage degradation from charging and discharging, while the revenues are derived from service fees charged to users. The total cost of the SES can be expressed as follows:
where
The corresponding constraints is formulated below:
where
There is often a discrepancy between the planned output and the actual predicted output of the renewable energy power plant. Insufficient actual output would result in penalties, whereas excessive actual output would lead to wastage of resources. Therefore, by employing SES, power plants can optimize tracking generation plans and minimize deviation costs. User group
where
User
where
Demand-side consumers such as large industries are subject to a two-part tariff consisting of an electricity charge and a basic charge. The electricity charge is based on the actual consumption of electricity at different time period, while the basic charge is often declared monthly based on peak demand. In this context, consumers can participate in SES projects, using energy storage to optimize their load curve and reduce basic charges and electricity charges through peak-to-valley price differences and energy exchange. This article models consumers with three types of demand response (DR) capabilities: transferable, reducible, and interruptible loads. The set of consumer-type users is denoted as
where
The constraints for user
where
In addition, the relevant constraint about power conservation is as follows:
where
Prosumers can sell their excess power to the main grid. However, the selling price offered by the grid is relatively low and does not fully cover all associated costs. Prosumers can engage in energy arbitrage through SES and effectively increase clean energy utilization, thus reducing the expenditure associated with procuring electricity from the grid and conventional fuel-based energy sources. The set of prosumers can be denoted as
where
The constraints of the diesel engine for user
where
Furthermore, the other constraints of prosumers can be expressed as follows:
where
Considering the overall power and capital flow balance, there are also the following system constraints:
In a cooperative operational mode, users engage in negotiations and interactions with the SES operator regarding the precise quantity of energy required and service fees. If participating in the cooperative mode can effectively reduce their own electricity costs, an interactive agreement is reached. This problem can be modeled as a cooperative game based on Nash bargaining theory. General Nash bargaining assumes equal contributions from all participants due to symmetric axioms; however, during actual negotiation processes, individuals who make greater contributions should have stronger bargaining power to obtain higher profits. Therefore, we adopt asymmetric Nash bargaining as the foundation for this cooperative game model which can be represented as follows:
where
Due to the problem (23) representing a complex, non-convex, and nonlinear problem that is difficult to solve directly, it is necessary to perform an equivalent transformation. The original problem can be converted into two sequential subproblems (Wang et al., 2024): a first-stage problem of cooperative operation scheduling for minimum social cost, and a second-stage problem of benefit distribution.
SP1: problem of cooperative operation scheduling for minimum social cost
Due to
The problem (24) can be reformulated as a dedicated operational scheduling problem without payment decisions:
By solving SP1, the charging and discharging strategy for SES, as well as the energy scheduling strategy for each user, can be determined. Subsequently, in order to establish appropriate pricing for each user, the solution process continues with SP2.
SP2: problem of benefit distribution
The SP2 aims to allocate the surplus of cooperation, wherein only the pricing of service fees is variable, and the negotiation process determines the pricing of energy storage services for each user.
To ensure that individuals who contribute more receive greater benefits, this paper adopts an asymmetric Nash bargaining framework, wherein the bargaining power factor measuring contribution are quantitatively calculated through the marginal contribution factor, energy interaction contribution factor, and peak-time energy contribution factor.
Marginal contribution (MC) factor (Mi et al., 2022):
The contribution to overall benefits is assessed by quantifying the rate of marginal change in an individual’s costs before and after engaging in cooperation, which is calculated as follows.
Since this value may exceed 1, to balance the magnitude of various indicators, normalization is performed to obtain the marginal contribution factors
Energy interaction contribution (EC) factor:
Increasing energy interactions with SES is believed to enhance energy use efficiency within the alliance and effectively reduce overall electricity costs. Both providing and using stored energy are considered contributory actions. The formulas for calculating the energy interaction contribution factor
Peak-time energy contribution (PC) factor:
Users who provide energy to SES to maintain its charge state during peak electricity price periods contribute more significantly. This contribution factor solely measures user behavior to incentivize users to charge the storage. The energy storage factor
where
Based on the above contribution indicators, the total bargaining power of the SES and users can be obtained:
where
Obtaining all energy usage information from different stakeholders is unsafe and impractical. To address this, a distributed algorithm that only acquires limited energy interaction variables is employed. ADMM can efficiently compute convex optimization problems with separable variable equality constraints. Therefore, an improved ADMM algorithm with adaptive penalty factors is implemented to sequentially solve SP1 and SP2.
For the energy operation optimization SP1, there exists a global nonlinear coupling constraint (21), which disrupts the decomposability of the main problem. Therefore, introduce
The augmented Lagrangian function for the problem (26) can be expressed as:
where
The ADMM algorithm is used to decompose the separable variable problem, alternately iterating between the SES operator and each user in every iteration, and coupling through the update of Lagrangian multipliers, to achieve a distributed solution to the algorithm. The steps of alternate iteration are as follows:
Given the SES charging and discharging strategy, user
Given the shared energy demand of each user, the SES operator optimizes the operation strategies:
Update the auxiliary variables
Update the Lagrange multiplier
The penalty factor in the ADMM algorithm plays a crucial role in both the convergence and convergence speed of the algorithm. An appropriate penalty factor can significantly enhance the efficiency of convergence. Therefore, this paper employs an adaptive penalty factor ADMM based on the original algorithm. Initially, the primal and dual residuals are calculated:
where
After each iteration, the penalty factor is updated according to the following rule:
where
The condition of iterative convergence is:
where
For the solution of SP2, concerning benefit distribution, we also introduce
where
The iterative solving steps of SP2 are analogous to those of SP1, and are not reiterated.
The numerical example considers a cooperation system comprising one SES operator, two power generation side users, one demand-side consumer user, and two microgrid prosumer users. Generation side users 1 and 2 are a wind farm and a photovoltaic station, respectively, with a generation deviation penalty of 0.45 ¥/kW. User 3 is an industrial user following a two-part electricity tariff, with a demand price of 40 ¥/kW per month and an electricity price based on the TOU prices of Jiangsu Province, China, with peak hours (8:00–12:00, 17:00–21:00) set at 1.0697 ¥/kWh, off-peak hours (0:00–8:00) at 0.3139 ¥/kWh, and normal hours (12:00–17:00, 21:00–24:00) at 0.6418 ¥/kWh. Additionally, the DR load proportions represent 10% of the total load. The compensation costs for three types of load response are 0.2, 0.5, and 0.4 ¥/kWh, respectively. The maximum reduction ratio for reducible load is 80%, with a daily total interruption limit of 4 h and 2 interruptions per day. Prosumer users 4 and 5 both possess loads and distributed renewable energy, with user 4 also equipped with a diesel generator. Relevant parameters of the diesel generator are as indicated in Table 1, and pollutant emission are shown in Table 2. Prosumer users purchase electricity at the TOU prices, and sell electricity at a fixed price of 0.25 ¥/kWh. Figure 2 illustrates the output curves for generation side users, in accordance with their dispatch plans and the load along with renewable energy generation curves for other users on a typical day. The energy exchange cap with the SES is set at 1,000 kW. The specifics of the SES are detailed in Table 3.
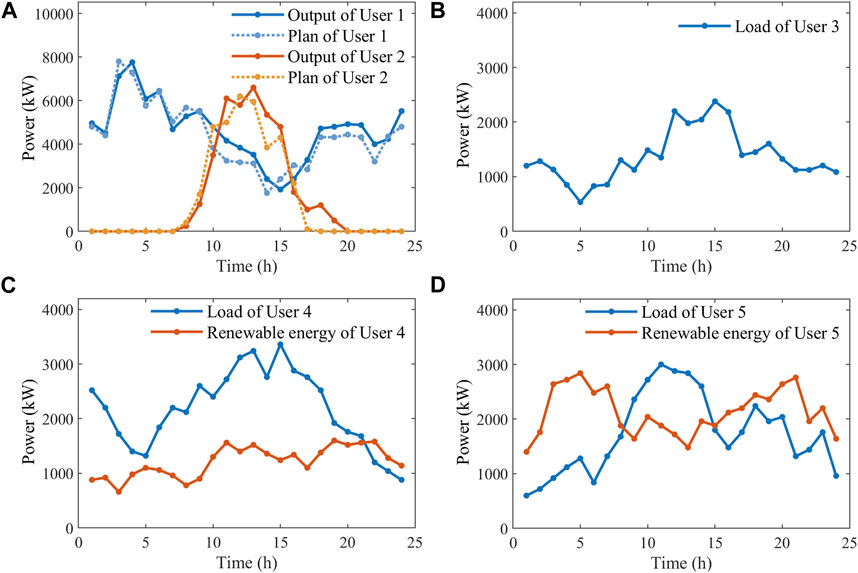
Figure 2. Renewable energy output and scheduling/load curves for users on a typical day. (A): User 1 and User 2; (B): User 3; (C): User 4; (D) User 5.
Figure 3 displays the energy interaction scheduling results between the SES and all users, where positive interaction values indicate users charging the storage, and negative values mean the SES is discharging to the users. During the period from 00:00 to 8:00 with the low TOU price, a majority of users engage in charging activities, leading to an increase in its SOC. From 8:00 to 18:00, certain users experience high energy demand surpassing supply capacity, resulting in continuous discharge from the SES. Subsequently, from 18:00 to 24:00, user demand decreases and there is a slight increase in the SOC for the SES. Overall scheduling maintains consistent levels at both ends for normal operation during subsequent cycles. Specific observation of user behavior reveals that, in this case, generation-side users 1 and 2 primarily supply power to the storage, especially during 8:00–18:00, where they serve as the main energy providers. Conversely, demand-side user 3 solely consumes electricity as it lacks renewable energy sources. Prosumer-type users 4 and 5 are observed to engage in both charging and discharging behaviors. User 5, having abundant renewable energy resources, contributes more energy, charging the SES during the periods of 0:00–8:00 and 15:00–24:00 to help accumulate energy in the SES. By aggregating surplus energy into SES, users ensure sufficient power supply during high-priced peak consumption periods while fully leveraging temporal and spatial complementarity among various users’ energies to reduce overall alliance electricity costs.
Table 4 shows the original deviation penalty power for users 1 and 2, as well as the combined deviation penalty power values for shared and self-built energy storage. It is evident that participation in both shared and self-built energy storage results in a reduction of the deviation penalties. Self-built energy storage achieves better plan tracking effects. For a possible reason that, during certain periods, the cost of deviation penalties is less than the energy costs of other users, leading SES to reallocate energy to these other users. Nonetheless, SES still meets most of the demand smoothing needs for source-side users, with users 1 and 2 seeing a reduction in penalty costs by 2365.6 ¥ and 1056.5 ¥, respectively. User 3′s operation result with SES is illustrated in Figure 4. As a consumer user, it is noticeable that this user predominantly relies on electricity from the SES. By discharging stored energy, it effectively mitigates peak loads and significantly reduces peak electricity demand by 1588.3 kW, resulting in substantial savings of 2117.7 ¥ per day in basic charges. Additionally, during periods of low electricity prices from 4:00–5:00, this user strategically opts to procure electricity from the grid and store it in the SES for peak-valley price arbitrage. Although this behaviour temporarily incurs additional costs for the user, it ultimately yields greater alliance benefits after benefit distribution. The result of user 4 is depicted in Figure 5. Despite having distributed energy resources, user 4 opt to utilize energy from the SES during high-demand periods between 9:00–21:00. Using SES instead of self-built systems reduces diesel generator output significantly from 4945.3 kW to 1260 kW, cutting diesel generation costs by 1922.5 ¥ and environmental pollution control expenses by 1077.8 ¥. The scheduling result of user 5 is shown in Figure 6. While selling electricity to the grid yields direct income, it does so at a lower unit price; however, providing energy through energy storage offers greater overall benefits. Consequently, this user prioritizes charging the energy storage during periods of abundant renewable energy and sells any remaining electricity to the grid. The comparison of grid transaction volumes for consumers and prosumers participating in SES and self-built energy storage is illustrated in Figure 7. It is clear that, in the early stages of SES scheduling, the electricity purchased from the grid by users is similar to that during periods using self-built storage, though the electricity sold decreases. When there is sufficient energy stored, it is noticeable that the electricity purchases from the grid significantly decrease for all users, with energy being maximally circulated within the alliance. User 3, 4, and 5 respectively saved 14484.7 ¥, 4751 ¥, and 771.1 ¥ in grid electricity purchasing costs.
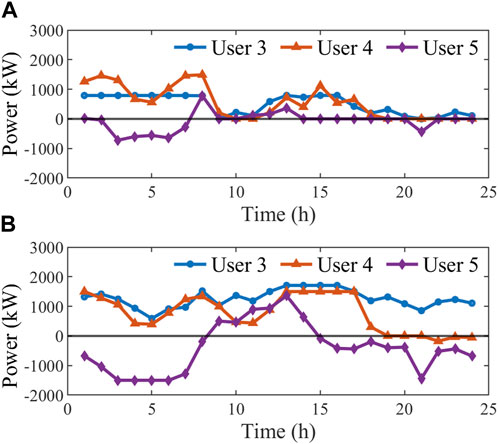
Figure 7. Grid transaction power for consumers and prosumers with SES and self-built energy storage. (A) With SES; (B) With self-built energy storage.
After negotiations, the total costs for each entity when participating in SES compared to self-built energy storage are presented in Table 5. A positive value for the SES service fee indicates payment to the SES, while a negative value represents receiving subsidies for energy supply from SES. It is evident that all parties’ benefits have increased after engaging in SES compared to the non-cooperative state. The total social cost has decreased by 41.3%, from 48,130.8 ¥ to 19,873.4 ¥, achieving mutual complementarity and benefit within cooperative alliances. Regarding pricing for SES service fees, users 1, 2, and 5 who contribute energy to the entire alliance can also receive subsidies for their energy supply and thus attain higher profits. From the table, it can be seen that after the profit distribution, all individuals have received positive profits from participating in SES. User 5 has the highest profit, reaching 7930.1 ¥, benefiting from compensation for providing a large amount of renewable energy to the alliance. Participating in shared storage cooperation can effectively improve the economic benefits for all parties involved. The above results confirm the economic viability of SES.
The computed results of bargaining factors for each party in asymmetric Nash bargaining are presented in Table 6. It is apparent that user 5 makes the most significant contribution to the overall alliance due to its highest marginal benefit post-cooperation and high levels of energy interaction, including significant energy contributions during peak periods. User 4 has the smallest bargaining factor, attributed to its less energy interaction and absence of energy provision during peak periods. Comparing the asymmetric Nash bargaining employed in this study with the general Nash bargaining, as depicted in Figure 8. Under general Nash bargaining, each party can attain equal profits. Although this distribution method reduces income disparity among parties, it overlooks variations in their contributions to the alliance, thus lacking fairness. In the asymmetric Nash bargaining proposed in this paper, are distributed according to the calculated contribution factors. For instance, Microgrid User 5 contributes a substantial amount of renewable energy during operation scheduling, resulting in a high Nash bargaining factor of 0.399. However, under general Nash bargaining principles alone, it would only receive an average profit of 3312.2 ¥; whereas under asymmetric Nash bargaining principles it can achieve significant profits of up to 7930.1 ¥ with an increase of 4617.9 ¥. Asymmetric Nash bargaining enables higher economic returns for parties making greater contributions to the alliance thereby promoting equity and sustainability.
The algorithm employed in this study achieves global optimality through distributed iteration among different entities, with each user only required to transmit the exchange power
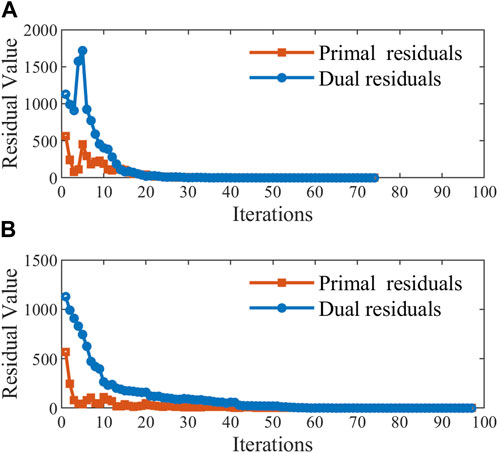
Figure 10. Comparison of convergence of the residuals in SP1 between improved/standard ADMM. (A) Improved ADMM; (B) Standard ADMM.
This paper introduces a new cooperative game framework for SES, exploiting the complementation of energy among power suppliers, consumers, and prosumers. By using shared storage as a nexus for energy interaction, it optimizes societal energy utilization, reduces the energy costs for users, and eliminates the high capital expenses of building individual storage systems. Through an asymmetric Nash bargaining approach based on each entity’s contribution to the alliance, the framework ensures a fair distribution of cooperative surpluses and establishes pricing strategies for storage, promoting equitable negotiation of interests. Moreover, the adaptive penalty factor ADMM algorithm is employed for distributed solving of operational scheduling and pricing decisions related to SES, reducing communication burdens while safeguarding user privacy. The enhanced algorithm exhibits faster convergence compared to standard ADMM methods, minimizing the impact of penalty factors on convergence. This paper focuses on day-ahead scheduling optimization but does not account for uncertainties from the volatility of renewable energy and load outputs, nor the physical constraints of the network structure. Future research could address these gaps by incorporating measures for uncertainty and analyzing the impact on line power flows within the shared framework.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
MX: Data curation, Methodology, Software, Writing–original draft, Writing–review and editing. YY: Data curation, Methodology, Writing–original draft, Writing–review and editing. QX: Formal Analysis, Supervision, Writing–review and editing. LF: Data curation, Writing–original draft. RT: Validation, Writing–review and editing. HJ: Validation, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Key Research and Development Program of China (2022YFB2703500).
Author RT was employed by the State Grid Jiangsu Electric Power Co., Ltd., Yangzhou Power Supply Company
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Chen, C. M., Li, Y., Qiu, W. Q., Liu, C., Zhang, Q., Li, Z. Y., et al. (2022). Cooperative-game-based day-ahead scheduling of local integrated energy systems with shared energy storage. Ieee Trans. Sustain. Energy 13 (4), 1994–2011. doi:10.1109/tste.2022.3176613
Chen, C. M., Liu, C., Ma, L. Y., Chen, T. W., Wei, Y. Q., Qiu, W. Q., et al. (2023). Cooperative-game-based joint planning and cost allocation for multiple park-level integrated energy systems with shared energy storage. J. Energy Storage 73, 108861. doi:10.1016/j.est.2023.108861
Ding, Y. X., Xu, Q. S., Xia, Y. X., Zhao, J., Yuan, X. D., and Yin, J. P. (2021). Optimal dispatching strategy for user-side integrated energy system considering multiservice of energy storage. Int. J. Electr. Power and Energy Syst. 129, 106810. doi:10.1016/j.ijepes.2021.106810
He, X., Xiao, J. W., Cui, S. C., Liu, X. K., and Wang, Y. W. (2022). A new cooperation framework with a fair clearing scheme for energy storage sharing. IEEE Trans. Industrial Inf. 18 (9), 5893–5904. doi:10.1109/tii.2021.3137823
He, X. T., Ge, S. Y., Liu, H., Xu, Z. Y., Mi, Y., and Wang, C. S. (2023). Frequency regulation of multi-microgrid with shared energy storage based on deep reinforcement learning. Electr. Power Syst. Res. 214, 108962. doi:10.1016/j.epsr.2022.108962
Hu, J. J., Wang, Y. D., and Dong, L. (2024). Low carbon-oriented planning of shared energy storage station for multiple integrated energy systems considering energy-carbon flow and carbon emission reduction. Energy 290, 130139. doi:10.1016/j.energy.2023.130139
Hui, H. X., Ding, Y., Shi, Q. X., Li, F. X., Song, Y. H., and Yan, J. Y. (2020). 5G network-based Internet of Things for demand response in smart grid: a survey on application potential. Appl. Energy 257, 113972. doi:10.1016/j.apenergy.2019.113972
Jo, J., and Park, J. (2020). Demand-side management with shared energy storage system in smart grid. IEEE Trans. Smart Grid 11 (5), 4466–4476. doi:10.1109/tsg.2020.2980318
Li, B. Y., Yang, Q. M., and Kamwa, I. (2023). A novel stackelberg-game-based energy storage sharing scheme under demand charge. IEEE/CAA J. Automatica Sinica 10 (2), 462–473. doi:10.1109/jas.2023.123216
Li, S. L., Zhu, J. Z., and Dong, H. J. (2021). A novel energy sharing mechanism for smart microgrid. IEEE Trans. Smart Grid 12 (6), 5475–5478. doi:10.1109/tsg.2021.3094329
Li, X. J., and Wang, S. X. (2021). Energy management and operational control methods for grid battery energy storage systems. CSEE J. Power Energy Syst. 7 (5), 1026–1040. doi:10.17775/cseejpes.2019.00160
Liu, J. K., Zhang, N., Kang, C. Q., Kirschen, D., and Xia, Q. (2017). Cloud energy storage for residential and small commercial consumers: a business case study. Appl. Energy 188, 226–236. doi:10.1016/j.apenergy.2016.11.120
Lombardi, P., and Schwabe, F. (2017). Sharing economy as a new business model for energy storage systems. Appl. Energy 188, 485–496. doi:10.1016/j.apenergy.2016.12.016
Ma, Y. X., Hu, Z. C., and Song, Y. H. (2022). Hour-ahead optimization strategy for shared energy storage of renewable energy power stations to provide frequency regulation service. IEEE Trans. Sustain. Energy 13 (4), 2331–2342. doi:10.1109/tste.2022.3194718
Mi, Y., Cai, P. C., Fu, Y., Wang, P., and Lin, S. F. (2022). Energy cooperation for wind farm and hydrogen refueling stations: a RO-based and nash-harsanyi bargaining solution. Ieee Trans. Industry Appl. 58 (5), 6768–6779. doi:10.1109/tia.2022.3188233
Parag, Y., and Sovacool, B. K. (2016). Electricity market design for the prosumer era. Nat. Energy 1, 16032. doi:10.1038/nenergy.2016.32
Rehmani, M. H., Reisslein, M., Rachedi, A., Erol-Kantarci, M., and Radenkovic, M. (2018). Integrating renewable energy resources into the smart grid: recent developments in information and communication technologies. IEEE Trans. Industrial Inf. 14 (7), 2814–2825. doi:10.1109/tii.2018.2819169
Rodrigues, D. L., Ye, X. M., Xia, X. H., and Zhu, B. (2020). Battery energy storage sizing optimisation for different ownership structures in a peer-to-peer energy sharing community. Appl. Energy 262, 114498. doi:10.1016/j.apenergy.2020.114498
Shi, Z. D., Wang, W. S., Huang, Y. H., Li, P., and Dong, L. (2022). Simultaneous optimization of renewable energy and energy storage capacity with the hierarchical control. CSEE J. Power Energy Syst. 8 (1), 95–104. doi:10.17775/cseejpes.2019.01470
Shivashankar, S., Mekhilef, S., Mokhlis, H., and Karimi, M. (2016). Mitigating methods of power fluctuation of photovoltaic (PV) sources - a review. Renew. Sustain. Energy Rev. 59, 1170–1184. doi:10.1016/j.rser.2016.01.059
Song, X. L., Zhang, H. Q., Fan, L. R., Zhang, Z., and Peña-Mora, F. (2023). Planning shared energy storage systems for the spatio-temporal coordination of multi-site renewable energy sources on the power generation side. Energy 282, 128976. doi:10.1016/j.energy.2023.128976
Tsioumas, E., Jabbour, N., Koseoglou, M., Papagiannis, D., and Mademlis, C. (2021). Enhanced sizing methodology for the renewable energy sources and the battery storage system in a nearly zero energy building. IEEE Trans. Power Electron. 36 (9), 10142–10156. doi:10.1109/tpel.2021.3058395
Tushar, W., Saha, T. K., Yuen, C., Smith, D., and Poor, H. V. (2020). Peer-to-Peer trading in electricity networks: an overview. IEEE Trans. Smart Grid 11 (4), 3185–3200. doi:10.1109/tsg.2020.2969657
Tushar, W., Yuen, C., Mohsenian-Rad, H., Saha, T., Poor, H. V., and Wood, K. L. (2018). Transforming energy networks via peer-to-peer energy trading:the potential of game-theoretic approaches. IEEE Signal Process. Mag. 35 (4), 90–111. doi:10.1109/msp.2018.2818327
Walker, A., and Kwon, S. (2021). Analysis on impact of shared energy storage in residential community: individual versus shared energy storage. Appl. Energy 282, 116172. doi:10.1016/j.apenergy.2020.116172
Wang, L. L., Xian, R. C., Jiao, P. H., Liu, X. H., Xing, Y. W., and Wang, W. (2024a). Cooperative operation of industrial/commercial/residential integrated energy system with hydrogen energy based on Nash bargaining theory. Energy 288, 129868. doi:10.1016/j.energy.2023.129868
Wang, Z., Hou, H., Zhao, B., Zhang, L. Q., Shi, Y., and Xie, C. J. (2024b). Risk-averse stochastic capacity planning and P2P trading collaborative optimization for multi-energy microgrids considering carbon emission limitations: an asymmetric Nash bargaining approach. Appl. Energy 357, 122505. doi:10.1016/j.apenergy.2023.122505
Wang, Z. C., Chen, L. J., Li, X. Z., and Mei, S. W. (2023). A Nash bargaining model for energy sharing between micro-energy grids and energy storage. Energy 283, 129065. doi:10.1016/j.energy.2023.129065
Wei, C., Shen, Z. Z., Xiao, D. L., Wang, L. C., Bai, X. Q., and Chen, H. Y. (2021). An optimal scheduling strategy for peer-to-peer trading in interconnected microgrids based on RO and Nash bargaining. Appl. Energy 295, 117024. doi:10.1016/j.apenergy.2021.117024
Xia, Y. X., Xu, Q. S., Chen, L., and Du, P. W. (2022). The flexible roles of distributed energy storages in peer-to-peer transactive energy market: a state-of-the-art review. Appl. Energy 327, 120085. doi:10.1016/j.apenergy.2022.120085
Xia, Y. X., Xu, Q. S., Huang, Y., Liu, Y. H., and Li, F. X. (2023). Preserving privacy in nested peer-to-peer energy trading in networked microgrids considering incomplete rationality. IEEE Trans. Smart Grid 14 (1), 606–622. doi:10.1109/tsg.2022.3189499
Xiao, J. W., Yang, Y. B., Cui, S. C., and Liu, X. K. (2022). A new energy storage sharing framework with regard to both storage capacity and power capacity. Appl. Energy 307, 118171. doi:10.1016/j.apenergy.2021.118171
Xie, Y. Z., Yao, Y., Wang, Y. W., Cha, W. Q., Zhou, S., Wu, Y., et al. (2022). A cooperative game-based sizing and configuration of community-shared energy storage. Energies 15 (22), 8626. doi:10.3390/en15228626
Yaldiz, A., Gökçek, T., Sengör, I., and Erdinç, O. (2021). Optimal sizing and economic analysis of Photovoltaic distributed generation with Battery Energy Storage System considering peer-to-peer energy trading. Sustain. Energy Grids Netw. 28, 100540. doi:10.1016/j.segan.2021.100540
Yang, Y., Hu, G. Q., and Spanos, C. J. (2021). Optimal sharing and fair cost allocation of community energy storage. IEEE Trans. Smart Grid 12 (5), 4185–4194. doi:10.1109/tsg.2021.3083882
Yu, J., Liu, J. C., Wen, Y. J., and Yu, X. (2023). Economic optimal coordinated dispatch of power for community users considering shared energy storage and demand response under blockchain. Sustainability 15 (8), 6620. doi:10.3390/su15086620
Yu, S. Y., Fang, F., Liu, Y. J., and Liu, J. Z. (2019). Uncertainties of virtual power plant: problems and countermeasures. Appl. Energy 239, 454–470. doi:10.1016/j.apenergy.2019.01.224
Zhang, T. H., Qiu, W. Q., Zhang, Z., Lin, Z. Z., Ding, Y., Wang, Y. T., et al. (2023). Optimal bidding strategy and profit allocation method for shared energy storage-assisted VPP in joint energy and regulation markets. Appl. Energy 329, 120158. doi:10.1016/j.apenergy.2022.120158
Zhang, W. Y., Zheng, B. S., Wei, W., Chen, L. J., and Mei, S. W. (2022). Peer-to-peer transactive mechanism for residential shared energy storage. Energy 246, 123204. doi:10.1016/j.energy.2022.123204
Keywords: shared energy storage, multi-type users, cooperative game, asymmetric nash bargaining, adaptive ADMM
Citation: Xu M, Yang Y, Xu Q, Fang L, Tang R and Ji H (2024) Asymmetric Nash bargaining for cooperative operation of shared energy storage with multi-type users engagement. Front. Energy Res. 12:1420393. doi: 10.3389/fenrg.2024.1420393
Received: 20 April 2024; Accepted: 14 June 2024;
Published: 11 July 2024.
Edited by:
Bin Zhou, Hunan University, ChinaReviewed by:
Zhiyi Li, Zhejiang University, ChinaCopyright © 2024 Xu, Yang, Xu, Fang, Tang and Ji. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qingshan Xu, eHVxaW5nc2hhbkBzZXUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.