A hierarchical game framework for peer-to-peer energy trading in distribution networks considering the participation of prosumers

The advent of the peer-to-peer energy trading has dramatically altered the conventional dynamics of distribution networks. Prosumers, managing independently and engaging in peer-to-peer (P2P) energy exchanges, introduce critical challenges for the economical and secure operations of these networks. This research presents a hierarchical framework designed to manage P2P energy interactions between prosumers and to facilitate flexible operation within the distribution network at the substation level. The upper layer of the model aims to stabilize market prices within the distribution framework, while the lower layer establishes a P2P energy trading platform that upholds fairness and safeguards the privacy of the prosumer participants. A fixed-point mapping approach is utilized to assess the interactions between market stabilization efforts and prosumer bidding strategies within this framework. Through simulations, we illustrate the logical soundness and effectiveness of our proposed model and approach. The findings indicate that the proposed model and the energy trading framework could substantially improve the overall welfare of all stakeholders involved.

1 Introduction

Recent advancements in demand-side distributed power and communication control technology have transformed traditional consumers in the substation area into prosumers capable of generating electricity (Sheng et al., 2023). These prosumers can independently manage their in-ternal flexible resources, facilitating a transition from the current oligopoly market to a more open and adaptable market (Khorasany et al., 2021). A study cited in the literature (Bo et al., 2023) suggests that individuals with distributed power sources should engage in direct transactions to enhance local consumption capabilities by leveraging the spatial-temporal coupling and complementary attributes of various energy sources. Prosumers typically prefer power trading to be conducted independently, proactively, and with privacy protection (Nezamabadi and Vahidinasab, 2021). However, the conventional market model faces challenges in accommodating the trading methods of prosumers, as its centralized dispatching system struggles to optimize market activities while considering individual behaviors (Xie et al., 2022a; Xie S. et al., 2021). Therefore, there is an urgent need to explore energy trading models tailored for prosumer transactions that integrate collaborative optimization technology.

Research has demonstrated that the concept of an distribution network (DN) is an effective approach for managing and dispatching the internal resources of a distribution network (Xie et al., 2020). To optimize the existing distribution network and prosumer cluster, a two-layer optimization model is commonly used. In (Penkovskii et al., 2020; Xiangsheng et al., 2024), the Stackelberg game (i.e., master-slave game) is employed to establish an interactive optimization model between system operators and prosumer clusters. The objective is to achieve win-win benefits and coordinated development for all participants. However, this model may cause congestion in the distribution network, resulting in higher clearing prices and lower energy utilization. To address these issues, the introduction of an energy sharing mechanism can help smooth out uncertainty, reduce peak demand, and effectively promote the consumption of distributed resources. As an alternative, market operators have gradually implemented energy sharing in the electricity market (Xie et al., 2022b). This enables the surplus electricity generated from distributed energy resources (DER) to be utilized for trading (Li et al., 2023). However, there are still challenges to consider when designing a trading mechanism. One challenge is how to coordinate the participation of a large number of prosumers while also considering the scalability of the algorithm. Another challenge is how to establish a fair-trading mechanism that allows prosumers to participate based on their own preferences, while also ensuring the privacy of personal information.

The increasing number of prosumers in contemporary power systems has resulted in a considerable amount of research on power energy sharing technology from various perspective. In (Zhang et al., 2020; Wang et al., 2023), researchers have examined different approaches to ensure fair income distribution in alliances formed by photovoltaic participants and operators. One approach involves applying the Shapley value method (Wang et al., 2023), while another approach combines the kernel method and the Shapley value method to distribute profits among alliance participants (Zhang et al., 2020). Research conducted in (Han et al., 2023; Zou et al., 2023) utilizes Nash negotiation theory to distribute profits among alliance members while ensuring individual privacy. Nevertheless, both the kernel method and Shapley value method face the obstacle known as the “curse of dimensionality” when the number of alliance participants increases (Wu et al., 2020). Additionally, these methods are complex to solve and fail to consider the diverse contributions of each participant.

The current research has utilized the distributed optimization strategy based on the Lagrangian relaxation method and the alternating direction multiplier method (ADMM) to coordinate the optimization of market trading strategies (KRANING et al., 2014). In (Wang et al., 2020), the authors employ the Lagrangian relaxation method and the sub-gradient method to achieve product development through electric energy transactions between consumers, with the Lagrange multiplier serving as a price signal. To preserve the cost function information, an iterative algorithm based on subgradients is proposed in (Gregoratti and Matamoros, 2015), using concepts from economics such as the “supply and demand model” and “market” to explain the algorithm’s iteration process. Studies in (Yan et al., 2023) introduce an interactive iteration mechanism for the relaxed Lagrangian function and demonstrate its convergence to the centralized optimum. These studies indicate that the P2P trading mechanism can enhance the operating economy of prosumers. However, the above research solely focuses on the single-layer bidding mechanism from the participants’ perspective, which presents challenges in effectively integrating the P2P trading mechanism with the safe and economic dispatch of the distribution network.

The research often overlooks the decision-making challenges in multi-layer and multi-agent collaboration in peer-to-peer energy trading. This paper introduces a hierarchical game framework for energy trading among prosumers in distribution networks. The aim is to improve energy exchange efficiency and promote fairness. A novel distributed coordination mechanism is proposed to ensure fair trading while protecting prosumer privacy, using Lagrangian relaxation and the subgradient method. The model shows that this mechanism can achieve global economic optimization through decentralized means. Additionally, a hierarchical game model is established for interactive energy trading, ensuring mutual benefits and proving the existence of a game equilibrium solution. Simulation experiments validate the effectiveness of the proposed model in promoting resource consumption and maximizing participant interests.

2 A P2P energy sharing framework between DSO and prosumers

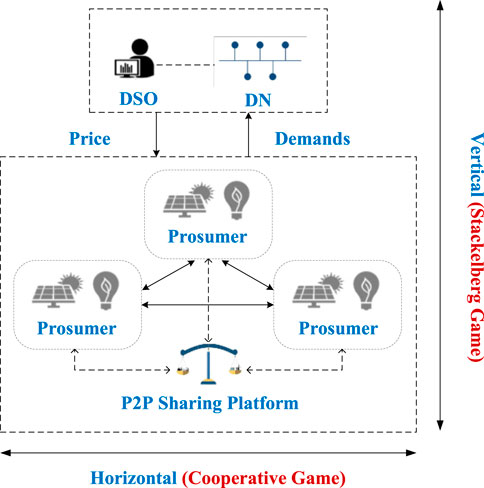
Existing studies often assume that the electricity prices set by the upper-level DSO are fixed, and the lower-level participants make decisions based on these fixed prices (Cai et al., 2023). However, this assumption fails to consider the crucial interplay between supply and demand, which restricts the practical implementation of strategies for both parties engaged in market transactions. In order to overcome this limitation, this paper introduces a hierarchical distributed collaboration architecture based on P2P energy sharing, as illustrated in Figure 1. The proposed framework divides the intricate energy market transaction model into two dimensions: 1) the vertical tra, which encompasses the Stackelberg game between the active distribution network (leader) and the prosumer cluster (follower), and 2) the horizontal dimension, which entails a cooperative game of prosumer P2P energy sharing at the lower-level.

Figure 1

Figure 1. The P2P energy sharing framework.

The proposed P2P sharing aims to coordinate and optimize energy scheduling and trading strategies. In the lower-layer prosumer model, each prosumer engages in transaction negotiations based on the energy sharing mechanism, leveraging the complementary advantages of energy between prosumers and consumers to enable cooperative operation. Once the P2P transaction is negotiated and resolved, the prosumer will provide feedback on the optimized bidding power to the upper layer, ensuring that its own constraints are met, and engage in multi-subject bidding. The DSO will utilize the prosumer’s bidding information and the load forecast value of each node of the distribution network to clear the market. This two-dimensional game structure more effectively illustrates the market’s tiered coordination relationship.

3 A Hierarchical model for coordinating operators and prosumers

3.1 Upper layer: DSO model

A second order cone program (SOCP) model is proposed for the distribution network operation:

$\mathbf{\text{DN}}-\mathbf{\text{OP}}:\min \left\{F_{\text{DN}}\left(\cdot \right)|\mathrm{s}.\mathrm{t}.\text{ CnsPDN\hspace{0.05em}}\right\}$

where $F_{\text{DN}}$ is defined as:

$F_{\text{DN}}\left(p_{k,t}^{\mathrm{G}}\right)={\displaystyle \sum _{t\in T}}{\displaystyle \sum _{k\in N_g}}{a}_k{\left(p_{k,t}^{\mathrm{G}}\right)}^2+b_k{p}_{k,t}^{\mathrm{G}}+c_k(1)$

and the constraint sets “$\mathbf{\text{CnsPDN}}$” are as follows:

$p_{n,t}^{\mathrm{G}}-p_{n,t}^{\mathrm{D}}={\displaystyle \sum _{k\in \mathrm{\Pi }\left(n\right)}}{p}_{nk,t}^l-\left(p_{mn,t}^l-{\stackrel{\sim }{I}}_{mn,t}{R}_{mn}\right),\forall mn\in L(2)$

$q_{n,t}^{\mathrm{G}}-{\overline{q}}_{n,t}^{\mathrm{D}}={\displaystyle \sum _{k\in \mathrm{\Pi }\left(n\right)}}{q}_{nk,t}^l-\left(q_{mn,t}^l-{\stackrel{\sim }{I}}_{mn,t}{X}_{mn}\right),\forall mn\in L(3)$

${\stackrel{\sim }{U}}_{n,t}={\stackrel{\sim }{U}}_{m,t}-2\left(p_{mn,t}{R}_{mn}+q_{mn,t}{X}_{mn}\right)+{\stackrel{\sim }{I}}_{mn,t}{\left(Z_{mn}\right)}^2(4)$

${‖2p_{mn,t}^{l}2q_{mn,t}^l{\stackrel{\sim }{I}}_{mn,t}-{\stackrel{\sim }{U}}_{m,t}‖}_2^T\le {\stackrel{\sim }{I}}_{mn,t}+{\stackrel{\sim }{U}}_{m,t},\forall mn(5)$

$0\le {\stackrel{\sim }{I}}_{mn,t}\le {\overline{I}}^2,\forall mn\in L,{{\displaystyle \underset{¯}{U}}}^2\le {\stackrel{\sim }{U}}_{n,t}\le {\overline{U}}^2,\forall n\in N(6)$

$0\le p_{mn,t}^l\le {\overline{p}}^l,0\le q_{mn,t}^l\le {\overline{q}}^l,\forall mn\in l\in L(7)$

${\underset{\_}{p}}_n^{\mathrm{G}}\le p_{n,t}^{\mathrm{G}}\le {\overline{p}}_n^{\mathrm{G}},{\underset{\_}{q}}_n^{\mathrm{G}}\le q_{n,t}^{\mathrm{G}}\le {\overline{q}}_n^{\mathrm{G}},\forall n\in N(8)$

$p_{n,t}^{\mathrm{D}}={\overline{p}}_{n,t}^{\mathrm{D}},\forall n\in \left\{N/{\mathcal{E}}_N\right\}(9)$

$p_{n,t}^{\mathrm{D}}={\overline{p}}_{n,t}^{\mathrm{D}}+p_{n,t}^d,\forall n\in {\mathcal{E}}_N(10)$

where $p_{n,t}^{\mathrm{G}}$ ($q_{n,t}^{\mathrm{G}}$) is the active (reactive) power generation at bus n; $p_{mn,t}^l$ ($q_{mn,t}^l$) is the active (reactive) power injection at bus n; ${\stackrel{\sim }{U}}_{n,t}$, ${\stackrel{\sim }{I}}_{n,t}$ is the quare magnitude of current (voltage); $N$ and $L$ are the bus and line sets, where $N=\left\{1,\cdots ,\left|N\right|\right\}$; $\mathrm{\Pi }\left(n\right)$ denotes the set of child buses of bus n; ${\mathcal{E}}_N$ is the set of prosumers, and ${\mathcal{E}}_N=\left\{1,\cdots ,\left|N_p\right|\right\}$; $T$ is time period set; $a_k$, $b_k$, $c_k$ are the cost coefficients; $R_{mn}$, $X_{mn}$, and $Z_{mn}^l$ are the resistance, reactance, and impedance, respectively; ${\overline{p}}_{n,t}^D$ (${\overline{q}}_{n,t}^D$) is the active (reactive) power load; ${\overline{p}}_n^{\mathrm{G}}$, ${\underset{\_}{p}}_n^{\mathrm{G}}$, ${\overline{q}}_n^{\mathrm{G}}$, ${\underset{\_}{q}}_n^{\mathrm{G}}$ are the power limitations of generators; $\overline{U}$, ${\displaystyle \underset{¯}{U}}$ are the boundaries of voltage magnitude; $\overline{I}$ is upper bound of line current; ${\overline{p}}^l$ (${\overline{q}}^l$) is the upper bound of active (reactive) power flow. Eqs 2, 3 represent the node power flow balance constraints, while Eqs 4, 5 depict the relationship constraints between node voltage and branch power flow and current. Eq. 6 outlines the constraints on line current and node voltage amplitude. Eq. 7 enforces the line power limit constraint, while Eq. 8 represents the generator active and reactive output constraints. Eqs 9, 10 define the active load for general nodes and prosumer nodes, respectively.

3.2 Lower layer: prosumer model

This subsection discusses the presence of prosumers connected to the active distribution network, where a number of DGs including renewable ones has been installed at certain buses. In order to enable peer-to-peer transactions among prosumers, constraints on transmission capacity are taken into account. Prosumers are given the opportunity to submit bids to the DSO to purchase electricity and counterbalance any imbalances caused by the introduction of new energy generation through flexible adjustments in their load. The lower layer model for prosumer is presented as follows:

$\min \left\{F_{\text{user}}\left(\cdot \right)|\mathrm{s}.\mathrm{t}.\mathbf{CnsUser}\right\}$

The objective function $F_{\text{user}}$ is defined in Eqs 11, 12:

$F_{\text{user}}={\displaystyle \sum _{t\in T}}{\displaystyle \sum _{i\in {\mathcal{E}}_N}}\left(-U_{i,t}+{\lambda }_{i,t}^{\text{LMP}}{p}_{i,t}^d\right)(11)$

$U_{i,t}=-{\beta }_i^1{\left(d_{i,t}\right)}^2+{\beta }_i^2{d}_{i,t}(12)$

where $U_{i,t}$ is the utility function of prosumer $i\in {\mathcal{E}}_N$; ${\beta }_i^1$, ${\beta }_i^2$ are the coefficients of quadratic term and primary term, both positive numbers.and the constraint sets “$\mathbf{\text{CnsUser}}$” are as follows:

$w_{i,t}+{\displaystyle \sum _{j\ne i,j\in {\mathcal{E}}_N}}{p}_{ij,t}^{\mathrm{P}2\mathrm{P}}+p_{i,t}^d=d_{i,t}+d_{i,t}^f,\forall i\in {\mathcal{E}}_N(13)$

${\underset{\_}{d}}_i\le d_{i,t}\le {\overline{d}}_i,\forall i\in {\mathcal{E}}_N(14)$

$-{\overline{p}}_i^{\mathrm{P}2\mathrm{P}}\le p_{ij,t}^{\mathrm{P}2\mathrm{P}}\le {\overline{p}}_i^{\mathrm{P}2\mathrm{P}},\forall i\ne j,i\in {\mathcal{E}}_N(15)$

$p_{ij,t}^{\mathrm{P}2\mathrm{P}}+p_{ji,t}^{\mathrm{P}2\mathrm{P}}=0,\forall i\ne j,i\in {\mathcal{E}}_N(16)$

$0\le p_{i,t}^d\le {\overline{p}}_i^d(17)$

Where $p_{i,t}^d$ is the bidding power of prosumer $i$; $d_{i,t}$ is the elastic load of prosumer $i$; $p_{ij,t}^{\mathrm{P}2\mathrm{P}}$ is the sharing power value between prosumer $i$ and $j$, which $p_{ij,t}^{\mathrm{P}2\mathrm{P}}>0$ represents purchasing power from prosumer $j$ and $p_{ij,t}^{\mathrm{P}2\mathrm{P}}<0$ represents selling power to prosumer $j$; ${\lambda }_{i,t}^{\text{LMP}}$ is the distribution market clearing price; $w_{i,t}$ is the forecast value of renewable energy output of prosumer $i$; $d_{i,t}^f$ is the fixed load of prosumer $i$; ${\overline{d}}_i$, ${\underset{\_}{d}}_i$ are the power limitations of $d_{i,t}$; ${\overline{p}}_i^{\mathrm{P}2\mathrm{P}}$ is the maximum value of energy sharing; ${\overline{p}}_i^d$ is upper bound of $p_{i,t}^d$; Eq. 13 represents the power balance constraints for prosumers. Eq. 14 enforces elastic load constraint, while Eq. 15 represents the upper and lower limits of $p_{ij,t}^{\mathrm{P}2\mathrm{P}}$. Eq. 16 shows energy sharing balance among prosumers. Eq. 17 represents power limit constraints for bidding power.

The optimization problem described is centralized and focused on prosumers. Upon analyzing its structure, it becomes apparent that all constraints, with the exception of the common constraint Eq. 16, are independent of each other across different prosumers. Introducing a Lagrangian multiplier to Eq. 16 allows for decomposition of the problem through a local Lagrangian function, yielding Eq. 18 as follows:

$L\left(\mathrm{\lambda }\right)={\displaystyle \sum _{t\in T}}{\displaystyle \sum _{i\in {\mathcal{E}}_N}}-U_{i,t}+{\lambda }_{i,t}^{\text{LMP}}{p}_{i,t}^d+{\lambda }_{i,t}\left(p_{ij,t}^{\mathrm{P}2\mathrm{P}}+p_{ji,t}^{\mathrm{P}2\mathrm{P}}\right)(18)$

This decomposition results in the relaxation of the prosumer problem, allowing it to be decoupled into individual prosumer subproblems. As a result, the objective function for each prosumer is:

$F_{\text{user},i}={\displaystyle \sum _{t\in T}}\left(-U_{i,t}+{\lambda }_{i,t}^{\text{LMP}}{p}_{i,t}^d\right)+{\displaystyle \sum _{t\in T}}{\displaystyle \sum _{j\ne i,j\in {\mathcal{E}}_N}}{\lambda }_{j,t}{p}_{ij,t}^{\mathrm{P}2\mathrm{P}}(19)$

Due to the economic importance of Lagrange multipliers, the second term in the objective function is understood as the cost shared among prosumers. Additionally, a coordination mechanism should be designed to attain centralized optimal outcomes by adjusting the objective function (19). This coordination mechanism will function through an iterative process. In the ($k+1$)-th iteration, the objective function of the prosumer $i$ is modified as:

$\begin{array}{l}{F}_{\text{user},i}={\displaystyle \sum _{t\in T}}\left(-U_{i,t}+{\lambda }_{i,t}^{\text{LMP}}{p}_{i,t}^d\right)+{\displaystyle \sum _{t\in T}}{\displaystyle \sum _{j\ne i,j\in {\mathcal{E}}_N}}{\lambda }_{j,t}^k{p}_{ij,t}^{\mathrm{P}2\mathrm{P}}\\ +{\displaystyle \sum _{t\in T}}{\displaystyle \sum _{j\ne i,j\in {\mathcal{E}}_N}}\frac{\rho }{2}{\left(p_{ij,t}^{\mathrm{P}2\mathrm{P}}+p_{ji,t}^{\mathrm{P}2\mathrm{P},k}\right)}^2\end{array}(20)$

where $k$ is the index of iteration. $\rho$ is the penalty parameter, and the quadratic term can be understood as the penalty cost caused by the imbalance of energy sharing. In order to achieve the feasibility of the original problem, the subgradient method is used to update the Lagrange multiplier:

${\lambda }_{i,t}^{k+1}={\lambda }_{i,t}^k+\rho \left(p_{ij,t}^{\mathrm{P}2\mathrm{P},k+1}+p_{ji,t}^{\mathrm{P}2\mathrm{P},k+1}\right)(21)$

This paper analyzes the above distributed coordination model from an economic perspective, ${\lambda }_{i,t}^k$ is equivalent to the sharing price of the $k$-th prosumer $i$ participating in P2P transactions. Other prosumers who want to trade with prosumer $i$ must execute at this price. When the demand of prosumer $i$ exceeds the available supply from other prosumers, that is $p_{ij,t}^{\mathrm{P}2\mathrm{P},k+1}+p_{ji,t}^{\mathrm{P}2\mathrm{P},k+1}>0$, the sharing platform updates the sharing price according to Eq. 21, resulting in an increase in the price of prosumer $i$.

4 Qualitative analysis based on P2P energy sharing mechanism

4.1 Horizontal dimension: analysis of distributed P2P coordination mechanism

Two concerns arise regarding the P2P coordination mechanism outlined in the lower-level prosumer model: 1) Is there a guarantee of convergence for this proposed mechanism? 2) Upon convergence, does the equilibrium closely approximate or equal the optimal solution?

Proposition 1. The distributed P2P coordination mechanism proposed can converge to centralized optimization.

Proof. Add a constant term ${\lambda }_{j,t}^k{p}_{ji,t}^{\mathrm{P}2\mathrm{P},k}$ to Eq. 20, which will not affect the optimal solution of the original problem. The objective function is modified to Eq. 22 as follows:

$\begin{array}{c}{F}_{\text{user},i}={\displaystyle \sum _{t\in T}}\left(-U_{i,t}+{\lambda }_{i,t}^{\text{LMP}}{p}_{i,t}^d\right)+{\displaystyle \sum _{t\in T}}{\displaystyle \sum _{j\ne i,j\in {\mathcal{E}}_N}}{\lambda }_{j,t}^k\left(p_{ij,t}^{\mathrm{P}2\mathrm{P}}+p_{ji,t}^{\mathrm{P}2\mathrm{P},k}\right)\\ +{\displaystyle \sum _{t\in T}}{\displaystyle \sum _{j\ne i,j\in {\mathcal{E}}_N}}\frac{\rho }{2}{\left(p_{ij,t}^{\mathrm{P}2\mathrm{P}}+p_{ji,t}^{\mathrm{P}2\mathrm{P},k}\right)}^2\end{array}(22)$

The proposed mechanism has evolved into the classic ADMM framework. It has been demonstrated that in the context of convex optimization problems, distributed ADMM can converge to centralized optimization (Yan et al., 2023).

4.2 Vertical dimension: master-slave game equilibrium analysis

Upon completion of the P2P energy sharing transaction, prosumers have the opportunity to engage in the distribution market to enhance their profits. The DSO determines the clearing price based on the bidding power of prosumers. Additionally, market pricing strategies can impact the bidding power of prosumers. The Stackelberg game is a useful tool to illustrate this hierarchical decision-making framework.

$\mathbf{\text{UL}}:{\mathit{\lambda }}^{\text{LMP}}=\mathit{argmin}\left\{F_{\text{DN}}\left(\cdot \right)\left|\mathrm{s}.\mathrm{t}.\right.\mathbf{\text{CnsPDN}}\right\}$

$\mathbf{\text{LL}}:p^d=\mathit{argmin}\left\{F_{\text{user}}\left(\cdot \right)\left|\mathrm{s}.\mathrm{t}.\right.\mathbf{\text{CnsUser\hspace{0.05em}}}\right\}$

Where ${\mathit{\lambda }}^{\text{LMP}}\triangleq \left\{{\lambda }_{j,t}^{\text{LMP}}\right\}$, $p^d\triangleq \left\{p_{i,t}^d\right\}$, this article uses local marginal price (LMP) as the clearing price in the distribution market (Xie Shiwei et al., 2021), corresponding to the dual variable in Eq. 2. Assuming (${\mathit{\lambda }}^{\text{LMP},*},p^{d,*}$) is the equilibrium solution of the game.

When the game model reaches Nash equilibrium, neither player can unilaterally change their strategy to achieve greater benefits. Before solving for the Stackelberg equilibrium solution, it is essential to prove its existence and uniqueness by utilizing the following theorem.

Theorem 1. For the proposed Stackelberg game model with a single leader and multiple followers, there is a unique Stackelberg equilibrium if the following conditions are satisfied (Yu and Hong, 2016):

eq \o\ac(○,1) The strategy set of leader and followers are nonempty, compact and convex set.

eq \o\ac(○,2) When the leader’s strategy is given, all followers have a unique optimal solution.

eq \o\ac(○,3) When the follower’s strategy is given, the leader has a unique optimal solution.

Proof. From the above three conditions to prove.

1) Due to the strategy sets of the optimal power flow model and the energy management model for prosumers in the distribution network are both nonempty, compact and convex action sets in Euclidean space, the condition eq \o\ac(○,1) of Theorem 1 is satisfied.

2) For the energy management model of low level prosumer cluster, by substituting its power balance constraint into the objective function, it is obtained by 23:

$\begin{array}{l}{F}_{\text{user}}={\displaystyle \sum _{t\in T}}{\displaystyle \sum _{i\in {\mathcal{E}}_N}}({\beta }_i^1{\left(w_{i,t}+{\displaystyle \sum _{j\ne i,j\in {\mathcal{E}}_N}}{p}_{ij,t}^{\mathrm{P}2\mathrm{P}}+p_{i,t}^d-d_{i,t}^f\right)}^2\\ \left.-{\beta }_i^2\left(w_{i,t}+{\displaystyle \sum _{j\ne i,j\in {\mathcal{E}}_N}}{p}_{ij,t}^{\mathrm{P}2\mathrm{P}}+p_{i,t}^d-d_{i,t}^f\right)+{\lambda }_{i,t}^{\text{LMP}}{p}_{i,t}^d\right)\end{array}(23)$

The first derivative of $F_{\text{user}}$ with respect $p_{i,t}^d$ is

$\frac{\partial F_{\text{user}}}{\partial p_{i,t}^d}=2{\beta }_i^1\left(D_{i,t}+p_{i,t}^d\right)-{\beta }_i^2+{\lambda }_{i,t}^{\text{LMP}}(24)$

where $D_{i,t}=w_{i,t}+{\displaystyle {\sum }_{j\ne i,j\in {\mathcal{E}}_N}}{p}_{ij,t}^{\mathrm{P}2\mathrm{P}}-d_{i,t}^f$ is a constant term.

The second derivative of $F_{\text{user}}$ is given by Eq. 25:

$\frac{{\partial }^2{F}_{\text{user}}}{\partial p_{i,t}^d\partial p_{j,t}^d}=\left\{\begin{array}{l}2{\beta }_i^{1}i=j,\forall t\\ 0i\ne j,\forall t\end{array}\right.(25)$

he Hessian matrix is strictly positive definite and has a minimum value, indicating the existence of an optimal solution for the prosumer model under the leader strategy. This satisfies the condition eq \o\ac(○,2) in Theorem 1.

3) For the optimal power flow model of the upper level distribution network, a unique pricing strategy can be derived based on the bidding power of the lower level prosumer cluster, considering the physical meaning of local marginal price and literature findings. This strategy meets the condition eq \o\ac(○,3) in Theorem 1.

5 Solving algorithm

5.1 P2P distributed coordination algorithm

In order to ensure the reliable and efficient operation of prosumer clusters, it is essential to coordinate resources among prosumers and facilitate optimal peer-to-peer energy trading. Prosumers are often hesitant to disclose their private information due to privacy concerns and information imbalances, while sharing platforms must efficiently manage resources for a large number of prosumers, a time-consuming task. To address these challenges, this article introduces a novel distributed coordination mechanism for facilitating energy trading and determining transaction prices among prosumers. Algorithm 1 offers a comprehensive overview of this coordination mechanism, with publicly available data from prosumers limited to sharing power values and transaction prices.

Algorithm 1.P2P distributed coordination mechanism.

1. Set iteration index $k=0$, convergence error tolerance $\delta >0$, penalty parameter $\rho >0$.

2. Prosumers initialize the trading price ${\lambda }_{j,t}^0=0,j\in {\mathcal{E}}_N$, and desired traded energy $p_{ij,t}^{\mathrm{P}2\mathrm{P},0}$.

3. while || ${\lambda }_{i,t}^{k+1}-{\lambda }_{i,t}^k$ || $\ge \delta$ do

4.  for all prosumers do

5.   $p_{ij,t}^{\mathrm{P}2\mathrm{P},k+1}$ = argmin (20)

     s.t. (13)–(17)

6.   Update ${\lambda }_{j,t}^{k+1}$ as (21)

7.  end

8.  $k=k+1$

9.  Calculate || ${\lambda }_{i,t}^{k+1}-{\lambda }_{i,t}^k$ ||

10. end

5.2 Fixed point algorithm

Two traditional methods are commonly used for solving two-layer models. One method involves the stationary point approach, where the lower-level model is replaced with equivalent KKT conditions. However, a large number of Big-M constraints and binary variables lead to non-convexity and nonlinearity of the model, which not only increases the computational burden of large scale cases but also makes it difficult to ensure the uniqueness of the equilibrium solution (Kazempour et al., 2013). Another approach is the utilization of fixed point algorithms where prosumers keep utility functions private and iteratively interact by exchanging price and quantity offers, as demonstrated in Algorithm 2, although proving theoretical convergence can be challenging (Wang et al., 2018). The subsequent section will delve into the discussion on the algorithm’s convergence.

Algorithm 2.Fixed point algorithm.

1. Set the iteration $r=0$, convergence error tolerance $\epsilon >0$.

2. Prosumers initialize the bidding power $p_{i,t}^{d,0}$.

3. for $r$ = $1:N^{\mathrm{M}}$ do

4.  Solving the following Problem to get ${\mathit{\lambda }}^{\text{LMP}}$:

5.   ${\mathit{\lambda }}^{\text{LMP}}$ = argmin (1)

     s.t. (2)–(10)

6.  Call Algorithm 1 with ${\mathit{\lambda }}^{\text{LMP}}$

  and obtain $p_{i,t}^{d,r}$.

7.   if || $p_{i,t}^{d,r+1}-p_{i,t}^{d,r}$ || $\le \epsilon$ then

    break

8. end for

5.3 Algorithm convergence analysis

The research demonstrates that the proposed P2P distributed coordination algorithm can effectively achieve optimal results similar to a centralized system. In the context of a two-layer model involving prosumer clusters in the distribution market, the intricate mathematical nature of the market equilibrium problem poses challenges for ensuring the convergence of Algorithm 2. This section offers a simplified geometric explanation to explore the conditions under which Algorithm 2 can successfully converge. Let Make denote the power market clearing problem and represent the prosumer cluster problem, both of which are convex optimization problems. The fixed point provided can be utilized to determine the equilibrium point of the Stackelberg game, as given in Eq. 26.

$\left[{\mathit{\lambda }}^{\text{LMP}}\right]=\mathrm{\Gamma }\left(p^d\right)\&\left[p^d\right]=\mathrm{\Theta }\left({\mathit{\lambda }}^{\text{LMP}}\right)(26)$

setting $\frac{\partial F_{\text{user}}}{\partial p_{i,t}^d}=0$, (24) can be derived as follows:

${\lambda }_{i,t}^{\text{LMP}}=-2{\beta }_i^1\left(D_{i,t}+p_{i,t}^d\right)+{\beta }_i^2,\forall i(27)$

let demand response curve $\left[{\mathit{\lambda }}^{\text{LMP}}\right]={\mathrm{\Theta }}^{-1}\left(p^d\right)$ defined in Eq. 27. The iterative process of the fixed point algorithm can be described by the “cobweb” model shown in Figure 2, where the equilibrium point corresponds to the intersection of the supply and demand curves. The fixed point can only converge when the slope of the demand response curve exceeds the price response curve.

Figure 2

Figure 2. The geometric explanation behind the fixed point. (A) convergence (B) divergence.

Based on this, provide the convergence conditions for the fixed point algorithm of the model in this article, as given in Eq. 28:

$\left|\left.\frac{\partial \mathrm{\Gamma }\left(p_{i,t}^d\right)}{\partial p_{i,t}^d}\right|\right.<\left|\left.\frac{\mathrm{d}{\mathrm{\Theta }}^{-1}\left(p_{i,t}^d\right)}{\mathrm{d}{p}_{i,t}^d}\right|\right.=2{\beta }_i^1\le 2ma{x}_{\forall i}\left({\beta }_i^1\right)(28)$

Evidently, ${\beta }_i^1$ value will affect the convergence performance of the proposed model.

6 Case study

6.1 Case description

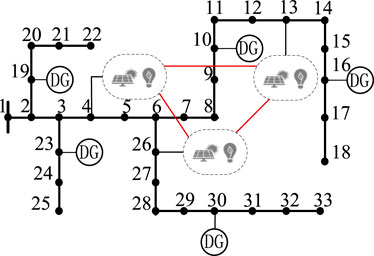
The simulation test adopts an improved IEEE 33-bus system, based on the Matlab platform, programmed and solved using the YALMIP toolbox and Gurobi solver. For the improved testing system, as shown in Figure 3, nodes 10, 16, 19, 23, and 30 are connected to five distributed power sources respectively; 4, 13, and 26 nodes are connected to three prosumers, among which prosumer 1 and prosumer 3 are equipped with photovoltaic units, and prosumer 2 is equipped with wind turbines; The voltage level of active distribution network is 12.66 kV, the allowable deviation of node voltage is set to ±5%. The parameters of the distribution system are shown in Supplementary Table SA1. The parameters of prosumers are shown in Table 1, and the renewable energy output and load curve of prosumers are shown in Supplementary Appendix SB.

Figure 3

Figure 3. The structure of an improved 33 node power distribution system.

Table 1

Table 1. Parameters of prosumers.

The upper limit of energy sharing power between prosumer 1 and 2 is 150 kW, the upper limit of energy sharing power between prosumer 2 and 3 is 200 kW, and the upper limit of energy sharing power between prosumer 1 and 3 is 180 kW. Convergence error tolerance $\epsilon ={10}^{-3}$, $\delta ={10}^{-2}$. all prosumers have an initial transaction price and expected sharing power is zero in P2P transactions, penalty parameter $\rho =10$. Fixed point iteration for initial bidding power $p^{d,0}=0$, maximum number of iterations $N^{\mathrm{M}}$ = 20.

6.2 Analysis of algorithm results

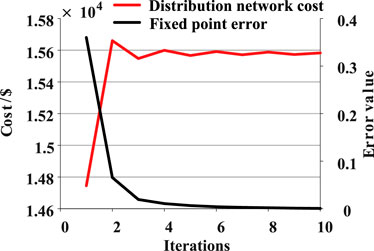
Figure 4 displays the iteration curve of the outer level fixed point algorithm, illustrating that as the number of iterations increases, the convergence speed decreases. By the 10th iteration, the iteration error has approached 0, reaching the termination iteration standard. The operating cost of the DN ultimately converges to $15582.9, which shows the closed-loop negotiation process effectively. The curve confirms the existence and uniqueness of the game equilibrium solution, as well as the convergence of the fixed point algorithm.

Figure 4

Figure 4. The convergence results related to distribution network.

Figure 5 illustrates the convergence of the P2P energy sharing mechanism among prosumers in the final fixed point iteration, displaying the convergence outcomes of the objective functions for each prosumer. The graph indicates that the algorithm reaches convergence after 36 iterations with high accuracy. Based on Figure 4, it is evident that the operational costs of the DN and the prosumers remain unchanged. The iteration results demonstrate that the P2P energy sharing coordination mechanism proposed in this study successfully achieves energy supply-demand equilibrium and efficiently identifies the global optimal solution.

Figure 5

Figure 5. The convergence results related to prosumers.

6.3 Analysis of simulation results

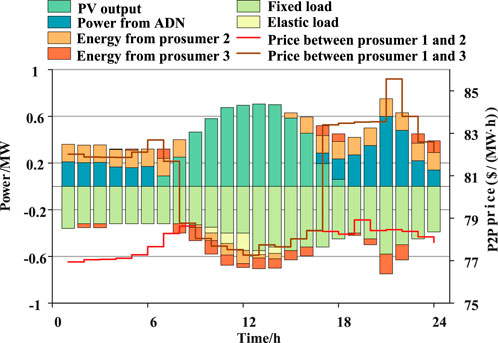
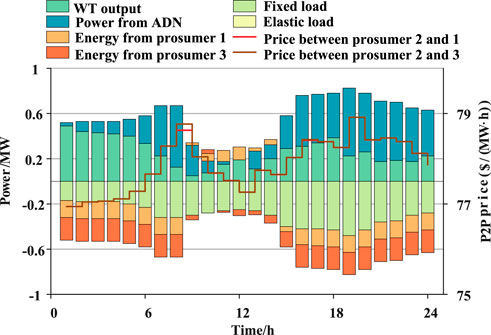
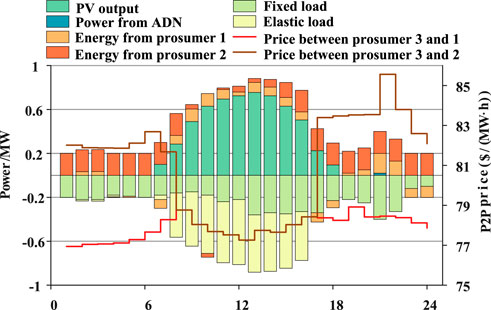
Figures 6–8 illustrate the power dispatching strategy and P2P transaction prices of prosumers 1–3. The symmetrical characteristics in these figures demonstrate a balance between power generation and consumption among the prosumers, highlighting the effectiveness of the P2P trading mechanism proposed in this study. Prosumers 1 and 3, which have a high proportion of PV, choose to sell electricity to other prosumers during the 7:00–18:00 photovoltaic output period. Additionally, during the periods of 1:00–7:00 and 18:00–24:00, the transaction prices for prosumers 1 and 3 are higher, making it more cost-effective for prosumer 1 to engage in trade with prosumer 2 when power supply is low. In some cases, prosumer 1 may even profit by purchasing electricity from prosumer 2 and selling it to prosumer 3. Prosumer 2 relies on wind power as its renewable energy source, with higher output at night and lower output during the day. The complementary energy profiles between prosumer 2 and prosumers 1 and 3 lead to frequent P2P trading interactions.

Figure 6

Figure 6. Prosumer 1 power scheduling strategy and P2P transaction price.

Figure 7

Figure 7. Prosumer 2 power scheduling strategy and P2P transaction price.

Figure 8

Figure 8. Prosumer 3 power scheduling strategy and P2P transaction price.

It is evident that the primary purchasers of electricity from the DN are prosumer 1 and 2, because the local marginal price at the distribution node where prosumer 3 is located is higher. Prosumer 3 derives greater utility from energy use, hence prioritizing energy trading with other prosumers to increase elastic loads and reducing costs. Prosumer 1 and 2 can also leverage the P2P mechanism for their benefit. Moreover, the P2P mechanism partially eases the power supply burden on the DN by altering the local power flow within the distribution network, while considering both the collective and individual advantages of prosumers.

Table 2 presents a comparison of scheduling costs for prosumers in various scenarios. In the absence of P2P energy transactions, prosumers solely rely on interactions with the power grid, which increases the cost by 9.8% compared to the P2P transactions proposed in this study. It verifies the effectiveness of P2P energy sharing mechanism considered in this paper. Furthermore, when compared to Case 2 and Case 3, the approach outlined in this article can achieve similar outcomes to centralized optimization. The distinction is that centralized management aims to minimize the total cost of prosumer clusters as a whole, without considering the cost allocation of shared power. Prosumer 3 consistently engages in energy trading with prosumer 1 and 2, causing prosumer 1 and 2 to purchase more electricity from the grid, which may be perceived as economically unfair. In contrast, the decentralized cooperation method employed in this mechanism ensures the protection of prosumers’ information privacy.

Table 2

Table 2. Comparison of prosumer scheduling costs under different cases.

Case 1. prosumers do not consider P2P transactions.

Case 2. prosumers adopt centralized optimization to solve the lower level model.

Case 3. prosumers adopts the P2P energy sharing mechanism proposed in this article to solve the lower level model.

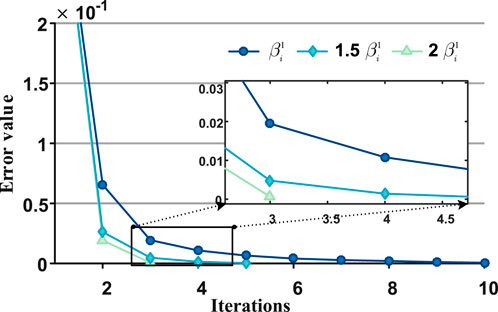
6.4 Convergence analysis of fixed point algorithm with different ${\beta }_i^1$

In the previous section, the convergence condition of the fixed point iteration is analyzed, that is, the value of the utility function will affect the convergence performance of the fixed point algorithm. Figure 9 shows the convergence performance of different through fixed point algorithm, provide the convergence process of fixed point iteration for three scenarios of parameter ${\beta }_i^1$, 1.5 ${\beta }_i^1$ and 2 ${\beta }_i^1$ respectively. It is with the increase of the ${\beta }_i^1$ value that the fixed point algorithm can achieve faster convergence, and the validity of the fixed point convergence condition of the previous analysis is verified.

Figure 9

Figure 9. Fixed point iterative convergence performance of different ${\beta }_i^1$.

7 Conclusion

This paper introduces a novel two-layer P2P energy sharing framework aimed at addressing the challenges arising from the growing integration of prosumers in active distribution networks. The framework is structured with the distribution system operator at the helm, followed by prosumer clusters engaging in P2P energy sharing. The lower level of the framework breaks down the centralized model of prosumer clusters using the Lagrange relaxation principle and subgradient method, presenting a distributed P2P energy sharing coordination mechanism with a sound economic interpretation that enables each prosumer to make independent decisions. The use of a fixed point algorithm as a distributed technology to resolve the Stackelberg game is discussed, along with an algorithm convergence analysis for the model. The key findings of the study are summarized as follows:

(1) The P2P energy sharing and coordination mechanism presented in this study aims to optimize prosumers’ benefits from transactions and enhance the efficient use of renewable energy. The use of algorithms theoretically allows for achieving a globally optimal solution and making rational allocation decisions regarding energy sharing transaction costs.

(2) The hierarchical coordination management strategy based on Stackelberg game effectively achieves a win-win outcome between DSOs and prosumers. It determines the optimal pricing strategy for the active distribution network and the energy demand of prosumers. The strategy is validated through theory and simulation, confirming the existence and uniqueness of the game equilibrium solution. Additionally, it addresses the theoretical limitations in the convergence of fixed-point algorithms.

(3) This article explores the implementation of a clearing mechanism for P2P energy sharing, enabling prosumers to engage in energy transactions in a decentralized and secure manner to foster cooperation. By comparing it with traditional peer-to-grid energy trading, the study demonstrates the operational advantages for both DSOs and prosumers through the P2P energy sharing mechanism, ultimately enhancing the balance between supply and demand among prosumers. The hierarchical collaborative optimization scheduling model proposed in this paper effectively coordinates the interconnected operations of prosumers while aligning with the operational objectives of the DN.

Due to the difficulty in verifying the convergence of fixed point iterative algorithm from a theoretical perspective. Resting on the price demand curve, this article innovatively proposes a criterion for the existence of market equilibrium, the obtained game equilibrium solution can be regarded as a reasonable planning scheme that conforms to engineering reality.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZS: Writing–original draft, Conceptualization. ZL: Conceptualization, Funding acquisition, Writing–review and editing, Writing–original draft. BJ: Data curation, Investigation, Methodology, Software, Writing–review and editing. HL: Methodology, Visualization, Writing–review and editing. FY: Resources, Software, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project supported by “Research on Fast Inertia Response and Flexible Interaction Technology for Distribution Networks integrated with Large-scale Charging Facilities (5400-202155459A-0-0-00)”.

Conflict of interest

Authors ZS, ZL, HL, and FY were employed by State Grid Energy Internet Research Institute Co., Ltd. Author BJ was employed by Xinjiang Information Industry Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1420039/full#supplementary-material

References

Bo, R., Bai, L., Conejo, A. J., Wu, J., Jiang, T., Ding, F., et al. (2023). Special section on local and distributed electricity markets. IEEE Trans. Smart Grid 14 (2), 1347–1352. doi:10.1109/tsg.2022.3228852

CrossRef Full Text | Google Scholar

Cai, P., Yang, Mi, Xing, H., Li, H., and Wang, P. (2023). Hierarchical coordinated energy management strategy for electricity-hydrogen integrated charging stations based on IGDT and hybrid game. Electr. Power Syst. Res. 223, 109527. doi:10.1016/j.epsr.2023.109527

CrossRef Full Text | Google Scholar

Gregoratti, D., and Matamoros, J. (2015). Distributed energy trading: the multiple-microgrid case. IEEE Trans. Industrial Electron. 62 (4), 2551–2559. doi:10.1109/tie.2014.2352592

CrossRef Full Text | Google Scholar

Han, J., Liu, N., and Catalão, J. P. S. (2023). Optimization of distribution network and mobile network with interactive balance of flexibility and power. IEEE Trans. Power Syst. 38 (3), 2512–2524. doi:10.1109/tpwrs.2022.3180792

CrossRef Full Text | Google Scholar

Kazempour, S. J., Conejo, A. J., and Ruiz, C. (2013). Generation investment equilibria with strategic producers—Part I: formulation. IEEE Trans. Power Syst. 28 (3), 2613–2622. doi:10.1109/tpwrs.2012.2235467

CrossRef Full Text | Google Scholar

Khorasany, M., Paudel, A., Razzaghi, R., and Siano, P. (2021). A new method for peer matching and negotiation of prosumers in peer-to-peer energy markets. IEEE Trans. Smart Grid 12 (3), 2472–2483. doi:10.1109/tsg.2020.3048397

CrossRef Full Text | Google Scholar

Kraning, M., Chu, E., Lavaei, J., and Boyd, S. (2014). Dynamic network energy management via proximal message passing. Found. Trends Optim. 1 (2), 70–122. doi:10.1561/9781601987150

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., Wang, L., and Yang, N. (2023). Distributed tri-layer risk-averse stochastic game approach for energy trading among multi-energy microgrids. Appl. Energy 331, 120282. doi:10.1016/j.apenergy.2022.120282

CrossRef Full Text | Google Scholar

Nezamabadi, H., and Vahidinasab, V. (2021). Arbitrage strategy of renewable-based microgrids via peer-to-peer energy-trading. IEEE Trans. Sustain. Energy 12 (2), 1372–1382. doi:10.1109/tste.2020.3045216

CrossRef Full Text | Google Scholar

Penkovskii, A., Stennikov, V., and Kravets, A. (2020). Bi-level modeling of district heating systems with prosumers. Energy Rep. 6, 89–95. doi:10.1016/j.egyr.2019.11.046

CrossRef Full Text | Google Scholar

Sheng, H., Wang, C., Dong, X., Meng, K., and Dong, Z. (2023). Incorporating P2P trading into DSO's decision-making: a DSO-prosumers cooperated scheduling framework for transactive distribution system. IEEE Trans. Power Syst. 38 (3), 2362–2375. doi:10.1109/tpwrs.2022.3187191

CrossRef Full Text | Google Scholar

Wang, C., Wei, W., Wang, J., Wu, L., and Liang, Y. (2018). Equilibrium of interdependent gas and electricity markets with marginal price based bilateral energy trading. IEEE Trans. Power Syst. 33 (5), 4854–4867. doi:10.1109/tpwrs.2018.2796179

CrossRef Full Text | Google Scholar

Wang, Y., Chen, J., Zhao, M., Li, B., Shi, H., and You, H. (2023). Maximum energy penetration rate of PV in distribution network under security constraints based on game theory. IEEE Trans. Power Syst. 38 (4), 3427–3439. doi:10.1109/TPWRS.2022.3207512

CrossRef Full Text | Google Scholar

Wang, Y., Huang, Z., Shahidehpour, M., Lai, L. L., and Zhu, Q. (2020). Reconfigurable distribution network for managing transactive energy in a multi-microgrid system. IEEE Trans. Smart Grid 11 (2), 1286–1295. doi:10.1109/tsg.2019.2935565

CrossRef Full Text | Google Scholar

Wu, X., Li, H., Wang, X., and Zhao, W. (2020). Cooperative operation for wind turbines and hydrogen fueling stations with on-site hydrogen production. IEEE Trans. Sustain. Energy 11 (4), 2775–2789. doi:10.1109/tste.2020.2975609

CrossRef Full Text | Google Scholar

Xiangsheng, X., Jianxiao, W., Rui, L., David, J. H., and Kang, C. (2024). Large-scale aggregation of prosumers toward strategic bidding in joint energy and regulation markets. Appl. Energy 271, 115159. doi:10.1016/j.apenergy.2020.115159

CrossRef Full Text | Google Scholar

Xie, S., Hu, Z., and Wang, J. (2021b). Dynamic flow equilibrium of urban power and transportation networks considering the coupling in time and space. Proc. CSEE 41 (24), 8408–8424. doi:10.13334/j.0258-8013.pcsee.210830

CrossRef Full Text | Google Scholar

Xie, S., Hu, Z., Wang, J., and Chen, Y. (2020). The optimal planning of smart multi-energy systems incorporating transportation, natural gas and active distribution networks. Appl. Energy 269, 115006. doi:10.1016/j.apenergy.2020.115006

CrossRef Full Text | Google Scholar

Xie, S., Wu, Q., Hatziargyriou, N. D., Zhang, M., Zhang, Y., and Xu, Y. (2022a). Collaborative pricing in a power-transportation coupled network: a variational inequality approach. IEEE Trans. Power Syst. 38 (1), 783–795. doi:10.1109/tpwrs.2022.3162861

CrossRef Full Text | Google Scholar

Xie, S., Wu, Q., Hatziargyriou, N. D., Zhang, M., Zhang, Y., and Xu, Y. (2022b). Collaborative pricing in a power-transportation coupled network: a variational inequality approach. IEEE Trans. Power Syst. 38 (1), 783–795. doi:10.1109/tpwrs.2022.3162861

CrossRef Full Text | Google Scholar

Xie, S., Xu, Y., and Zheng, X. (2021a). On dynamic network equilibrium of a coupled power and transportation network. IEEE Trans. Smart Grid 13 (2), 1398–1411. doi:10.1109/tsg.2021.3130384

CrossRef Full Text | Google Scholar

Yan, D., Ma, C., and Chen, Y. (2023). Distributed coordination of charging stations considering aggregate EV power flexibility. IEEE Trans. Sustain. Energy 14 (1), 356–370. doi:10.1109/tste.2022.3213173

CrossRef Full Text | Google Scholar

Yu, M., and Hong, S. H. (2016). A real-time demand-response algorithm for smart grids: a Stackelberg game approach. IEEE Trans. Smart Grid 7 (2), 879–888. doi:10.1109/TSG.2015.2413813

CrossRef Full Text | Google Scholar

Zhan, X., Yang, J., Wang, X., Shen, Y., and Qian, X. (2022). Robust pricing strategy of power retailer considering linkage of real-time market. Power Syst. Technol. 46 (06), 2141–2153.

Google Scholar

Zhang, R., Jiang, T., Li, F., Chen, H., and Li, X. (2020). Coordinated bidding strategy of wind farms and power-to-gas Facilities using a cooperative game approach. IEEE Trans. Sustain. Energy 11 (4), 2545–2555. doi:10.1109/tste.2020.2965521

CrossRef Full Text | Google Scholar

Zou, Y., Xu, Y., Feng, X., and Nguyen, H. D. (2023). Peer-to-Peer transactive energy trading of a reconfigurable multi-energy network. IEEE Trans. Smart Grid 14 (3), 2236–2249. doi:10.1109/tsg.2022.3223378

CrossRef Full Text | Google Scholar