Enhanced bi-level optimal scheduling strategy for distribution network with multi-microgrids considering source-load uncertainties

With the increasing integrations of renewable energy resources into distribution networks (DNs) and microgrids (MGs), the imperative for an effective market scheduling mechanism becomes paramount to enhance the operational safety, reliability, and economic efficiency of distribution grids. Taking advantage of bi-level programming theory, this study meticulously formulates a comprehensive optimization scheduling model for the multi-MGs distribution network. The upper-level optimization objective is to minimize both the operational losses and total costs of the DN. Concurrently, the lower-level optimization pursues the maximization of daily operational revenue for MGs. Recognizing the pervasive impact of the inherent uncertainty associated with renewable energy sources on system safety and reliability, a cutting-edge scenario-based stochastic planning framework is introduced. The methodology integrates a heuristic matrix matching approach to effectively handle the intricate challenges posed by uncertainties from wind and photovoltaic generations. Moreover, in addressing the proposed nonlinear models, a sophisticated method is employed, utilizing the second-order cone relaxation and linearization methods. These methods meticulously transform the upper and lower-level models into second-order cone planning and mixed-integer linear programming issues, respectively. Finally, the proposed methodologies are rigorously scrutinized and validated with intricate case studies, providing a nuanced understanding of their efficacy. The empirical results underscore the theoretical feasibility and superiority of the proposed scheduling scheme. Notably, the operational performance of the DN as well as the economic viability of multiple MGs can also be significantly improved.

1 Introduction

Aiming at the targets of carbon emission peak and carbon neutrality, the large-scale integrations of new energy generations is one of the important means to promote the leapfrog development of energy structure transformation (National Energy Administration, 2021). Microgrids (MGs) can effectively integrate load clusters and distributed resources, such as photovoltaics (PV), micro-gas turbine (MT), fuel cell (FC), wind turbine (WT), energy storage systems, etc., which are considered as an effective form of renewable energy management and will play an important role in future power distribution systems (Chen Q. et al., 2023; Chen X. et al., 2023). However, with the continuous expansion of the installed scale of renewable power generators, the proportion of renewable energy generation and power electronic devices within microgrids increases rapidly, leading to the prominent issues of reduced inertia, frequency deviation, and power angle instability (Chang et al., 2022; Elshenawy et al., 2022). As a result, advanced intelligent scheduling and cooperative control methods are urgently needed to improve the operational reliability and economy of MGs, so as to better cope with emergencies, failures or bad weather and meet the needs of the end users as well as the power grid (Bidgoli and Ahmadian, 2022; Wang X. et al., 2023).

Microgrids, as systems integrating generation, distribution, storage, and consumption, involve a plethora of uncertain information during their planning and operation stages. These uncertainties can generally be categorized into two aspects including uncertainties from renewable generators and load, as well as uncertainties related to energy storage and demand response (Prathapaneni and Detroja, 2019). To ensure the efficient and stable operation of MGs under uncertainties, Nikmehr et al. (Nikmehr et al., 2017) introduced an optimal scheduling approach for MGs, emphasizing a microgrid-centric perspective. Their method comprehensively addresses uncertainties in demand response and wind power forecasting, offering a fresh angle to enhance the economic viability and stability of MGs. Dixit et al. (Dixit et al., 2023) concentrated on the energy management of MGs, with a thorough consideration of integrating demand response and renewable energy, aiming at enhancing the energy utilization efficiency of MGs through optimal scheduling techniques. Shakti et al. (Singh et al., 2016) incorporated renewable energy sources and energy storage systems into the MGs, achieved cooperative operation among various components within the MGs by coordinated scheduling strategy, leading to an enhancement in overall performance of the system. Wang et al. (Wang et al., 2018) achieved economically and reliably operated MGs through prudent scheduling, taking demand response into account. Lee et al. (Lee and Tuegeh, 2020) significantly enhanced the robustness and stability of MGs by optimizing scheduling strategies, carefully considering the uncertainties associated with renewable energy and load fluctuations. Shi et al. (Shi et al., 2021) utilized the central limit theorem to describe the uncertainties from wind and PV power output. Based on this, they established a multi-objective scheduling model based on weakly robust optimization, with the aims of minimizing MG’s operating costs and pollutant emissions. Gao et al. (Gao et al., 2018) proposed a two-stage adaptive robust optimization scheduling method for MGs, in which the K-means clustering method was proposed to preprocess historical data and obtain the probability distribution of wind power output. Qiu and Xuan et al. (Xuan et al., 2017; Qiu et al., 2018) utilized confidence level modeling to quantify the conservatism of wind power output representation. They quantitatively analyzed the impact of wind power output uncertainty on MG’s scheduling and constructed a multi-objective optimization model with environmental and risk costs as objectives.

The above-mentioned studies have provided profound insights into the optimization scheduling of microgrids and distribution networks (DNs), offering valuable references for future research in this area. However, with the widespread adoption of renewable energy sources, microgrids of various types now incorporate a diverse mix of distributed energy resources. This evolution has thrust the multi-microgrid-distribution system into the limelight as a research focal point, offering prospects for heightened flexibility and reliability within the DNs. In this complex landscape, MGs’ owners are compelled not only to coordinate among adjacent MGs but also to collaborate closely with distribution system operators. That is, MGs not only vie with each other for resources and market share but also grapple with potential conflicts of interest in relation to the distribution system. Consequently, the optimization techniques tailored for individual MG can not be directly employed to address the systemic optimization challenges inherent in coordinating the operation of multi-MGs and the DNs.

In response to the aforementioned challenges, recently, two-layer optimal scheduling models were proposed to achieve the optimal operation of MGs and power systems. Scholars worldwide have conducted extensive investigations on the conceptual modeling (Wang K. et al., 2023; Jani and Jadid, 2023; Lei et al., 2023; Luo et al., 2023), nonlinear solution algorithms (Chen C. et al., 2023; Mi et al., 2023; Wu et al., 2023), and feasibility verification (Li and Wang, 2023; Li et al., 2024) of these two-layer optimal scheduling approaches. For example, Lei et al. (Lei et al., 2023) developed a trading strategy for MGs within an intelligent DN, taking into account the influence of carbon quotas. A bi-level optimization method is employed to construct a trading model for the distribution-side power market, with genetic algorithms and sequential quadratic planning algorithms used to determine the optimal clearing strategy for microgrids and the optimal scheduling scheme for distribution system operators, respectively. Jani et al. (Jani and Jadid, 2023) introduced a bi-level optimization approach for day-ahead and real-time transactive energy markets in multi-MGs, aiming to optimize the energy management schedules and minimize operating costs, demonstrating significant cost reductions through cooperative strategies and battery energy storage integration. Wu et al. (Wu et al., 2023) proposed a cooperative energy trading model for multi-MGs in DNs, integrating peer-to-peer trading under network constraints. It employs a two-stage approach utilizing CVaR-based risk quantification and Nash Bargaining theory for cooperative welfare maximization and market clearing, respectively, showcasing improved cost reduction and voltage security through its suggested energy trading model. Li et al. (Li et al., 2024) proposed an iterative bi-level scheduling approach combining multi-step reconfiguration and objective reduction to address challenges posed by distributed renewable energy inDNs, resulting in significant reductions in network losses, voltage deviations, and improvements in peak shaving and valley filling. Nevertheless, current optimization efforts concerning multi-microgrid and distribution network primarily concentrate on fundamental optimization issues related to system operation. Further exploration is warranted to elucidate the impact of source-load uncertainty on operational performance. Scenario-based stochastic optimization and robust optimization techniques have demonstrated certain advantages in handling uncertainties (Li et al., 2019; Zhang and Xu, 2019; Wang Y. et al., 2023). But the intrinsic correlations between different uncertainties remains inadequately explored within the multi-layer optimization operation scheduling problems.

Therefore, taking into account the uncertainty associated with PV/wind power output, power load, and electricity price, this paper proposes a two-layer optimal scheduling scheme to facilitate the operational decision-making for both multi-microgrids and the distribution system incorporating an electrolytic hydrogen production unit. The specific work and contributions can be summarized as follows. (1) The proposed model can not only minimize the operational losses and total costs within DNs but also maximize daily operational revenue for MGs. Moreover, the potential conflicts of interest of different MGs are considered. (2) To effectively address uncertainties, a scenario matrix based on the heuristic moment matching method is presented, enabling accurate characterization of random moments and correlations among historical scenarios. Additionally, to efficiently address the nonlinear nature of the two-layer models, the second-order cone relaxation and linearization methods are utilized to transform it into second-order cone programming and mixed integer linear programming problems, subsequently solved using commercial solvers. (3) Ultimately, through simulation case studies, the proposed scheme’s outstanding performance in enhancing the economic, environmental, and operational stability of the system is validated.

2 System architecture and mathematical modeling

2.1 System architecture

Built upon the two-layer optimization theory, this paper delves into addressing the intricate challenges of integrating multi-MGs within distribution networks. In this framework, the upper level is denoted as the leader optimization problem, while the lower level constitutes the follower optimization problem. Each level encompasses distinct objective functions, constraints, and decision variables (Zhang and Xu, 2019; Li et al., 2024). Specifically, the upper-level optimization aims to minimize operational losses and the total cost of the regional distribution system, whereas the lower-level optimization seeks to maximize the daily operational profit of the MGs. To contend with uncertainties, a scenario stochastic programming framework and heuristic moment matching method are employed. Additionally, the second-order cone relaxation and the linearization methods are utilized to linearize both the upper and lower-level models. The structure of the proposed optimization framework is illustrated in Figure 1, with the detailed construction process of the distributed two-layer model depicted in Figure 2.

Figure 1

Figure 1. Optimization scheduling framework of distribution network with multi-MGs.

Figure 2

Figure 2. Flowchart of the bi-level scheduling framework of distribution network with multi-MGs.

2.2 Upper-level optimization model

2.2.1 Objective function

The objectives of upper optimization model are to minimize the system operating losses and the total costs of DN.

1) The operation losses of distribution system primarily include electrical energy conversion losses in resistors, inductors, capacitors, and other components, as well as the losses in transmission lines, transformers, and other equipment. Reducing the operating loss of distribution system is a crucial objective for enhancing power utilization efficiency and lowering energy costs. The calculation model for operation losses can be formulated as follows.

$G_1\left(t\right)=\min {\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{\left(i,j\right)\in L}}\frac{P_{ij}^2\left(t\right)+Q_{ij}^2\left(t\right)}{U_{ij,N}^2}{R}_{ij}(1)$

where, G₁(t) is the operating losses of the distribution system; T the total running time; L the branch circuit. P_ij(t) and Q_ij(t) are respectively the active power and reactive power of branch ij (line from node i to node j) at the scheduling time t. U_ij is the rated voltage of branch ij; R_ij the resistance of branch ij.

2) In addition to the operation losses, another optimization objective function is also established to minimize the operation costs of distribution network, so as to reduce the power costs and provide more economical and reliable power services to the end users. The operating costs of distribution network mainly include: $C_t^{DM}$ (the net cost of selling/purchasing electricity from the DN to day-before wholesale market during the scheduling time t) and $C_t^{MG\mathrm{i}}$ (the cost of power exchanged between the DN operator and the ith MG).

$C_t^{DM}={\rho }_t^{DM}\times P_t^{DM-DSO}(2)$

$C_t^{MGi}={\rho }_t^{RM}{\displaystyle \sum _{i=1}^N}\left(P_t^{MGi-DSO}\right)(3)$

where ${\rho }_t^{DM}$ and ${\rho }_t^{RM}$ are the electricity prices of wholesale market/retail market at time t (¥/MWh) respectively; $P_t^{DM-DSO}$ is the exchanged electricity (MW) between the distribution network and the wholesale market at time t, and $P_t^{MGi-DSO}$ is the exchanged electricity (MW) between the distribution network and the i microgrid at time t. N indicates the total number of microgrids.

Therefore, the objective function of minimizing the cost of the distribution system is:

$G_2\left(t\right)=\mathit{Min}\left[{\displaystyle \sum _{t=1}^{24}}\left(C_t^{DM}+C_t^{MGi}\right)\right](4)$

3) Considering the operating losses and total costs of the distribution system comprehensively, the upper-level optimization objective function model can be expressed as:

$F_{\text{upper}}\left(t\right)=\min \left[{\omega }_1{G}_1\left(t\right)+{\omega }_2{G}_2\left(t\right)\right](5)$

where F_upper is the upper objective function; ω₁ and ω₂ are the weight coefficients utilized for balancing the two goals. Through extensive consultations, along with rich literature references, it is concluded that the operating losses and total costs are both important, especially for DN with multi-MGs (Li and Wang, 2023; Wu et al., 2023; Li et al., 2024). Consequently, in this paper, ω₁ and ω₂ are determined as 0.5 through user settings.

2.2.2 Constraint functions

2.2.2.1 Node voltage constraints

In power systems, the voltage level of each node needs to be kept within a reasonable range to ensure the stability and reliability of the system. Namely,

$U_{i,\min }\le U_i\left(t\right)\le U_{i,\max }(6)$

where U_i,min and U_i,max are the upper and lower limits of the node voltage.

2.2.2.2 Power flow constraints

Power flow constraints prevent device overload and improve the safety and reliability of distribution system. The power constraint and voltage constraint equations are shown as (7) and (8), respectively.

$\left\{\begin{array}{l}{\displaystyle \sum _{i\in u\left(j\right)}}\left[P_{ij}\left(t\right)-\frac{P_{ij}^2\left(t\right)+Q_{ij}^2\left(t\right)}{U_{ij}^2\left(t\right)}{R}_{ij}\right]+P_j^{\text{PCC}}\left(t\right)={\displaystyle \sum _{h\in v\left(j\right)}}{P}_{jh}\left(t\right)+P_j^{\text{Load}}\left(t\right)\\ {\displaystyle \sum _{i\in u\left(j\right)}}\left[Q_{ij}\left(t\right)-\frac{P_{ij}^2\left(t\right)+Q_{ij}^2\left(t\right)}{U_{ij}^2\left(t\right)}{X}_{ij}\right]+Q_j^{\text{PCC}}\left(t\right)={\displaystyle \sum _{h\in v\left(j\right)}}{Q}_{jh}\left(t\right)+Q_j^{\text{Load}}\left(t\right)\end{array}\right.(7)$

$U_j^2\left(t\right)=U_i^2\left(t\right)+\frac{P_{ij}^2\left(t\right)+Q_{ij}^2\left(t\right)}{U_{ij}^2\left(t\right)}\left(R_{ij}^2+X_{ij}^2\right)-2\left[P_{ij}\left(t\right)R_{ij}+Q_{ij}\left(t\right)X_{ij}\right](8)$

where u(j) and v(j) are the branch first node sets, respectively with node j as the end node and node j as the first node; X_ij is the reactance value of the branch ij; P_jh(t) and Q_jh(t) are the active and reactive power of branch jh at time t, respectively; $P_j^{Load}\left(t\right)$ and $Q_j^{Load}\left(t\right)$ are the active and reactive powers of the load node at time t, respectively; $P_j^{PCC}\left(t\right)$ and $Q_j^{PCC}\left(t\right)$ are the active and reactive powers at the PCC junction point of distributed generation equipment. U_i(t) and U_j(t) are the voltage of nodes i and j at time t.

2.2.2.3 Power trading constraints in wholesale market

This constraint serves to restrict the maximum capacity of power system to either sell or buy power, thereby ensuring that transactions occur within a controlled range to uphold system stability and security.

$P_t^{DM-DSO}\le P_{\max }^{DM-DSO}(9)$

where $P_{\max }^{DM-DSO}$ is the maximum transaction power (MW) between the distribution system operator and the wholesale market.

2.2.2.4 Microgrid power trading constraints

$P_{\min }^{MG-DSO}\le P_t^{MGi-DSO}\le P_{\max }^{MG-DSO}(10)$

where $P_{\min }^{MG-DSO}$ and $P_{\max }^{MG-DSO}$ represent the minimum and maximum allowable exchange powers (MW) between the distribution system and the MGs.

2.3 Low-level microgrid optimization model

2.3.1 Objective function

Considering day ahead as the scheduling time scale, an optimization model is formulated aiming to optimize the economy and environmental sustainability of MGs. In the model, several economic objectives such as the costs associated with starting and stopping electrolytic hydrogen production equipment, fuel cell equipment, electricity buying and selling, penalties for wind and solar abandonment, and equipment maintenance costs are considered. Moreover, environmental objectives like the costs associated with carbon, nitrogen, and sulfur oxide emissions are also taken into account. Combining the requirements of both economy and environmental protection, the lower-level optimization objective function is defined as maximizing the daily operating income, as calculated with:

$F_{lower}=\max \left(f_1-f_2-f_3-f_4-f_5-f_6\right)(11)$

and,

$\left\{\begin{array}{l}{f}_1={\displaystyle \sum _{t=1}^T}\left(cou{t}_t{P}_{out,t}-ci{n}_t{P}_{in,t}\right)\\ f_2={\displaystyle \sum _{t=1}^T}\left(\alpha \Delta P_{pv,t}+\beta \Delta P_{wt,t}\right)\\ f_3={\displaystyle \sum _{i=1}^N}\left[K_{OMi}\times P_i\left(t\right)\right]\\ f_4={\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^3}{\gamma }_j\cdot E{P}_{ij}\cdot P_i\left(t\right)\\ f_5={\displaystyle \sum _k^K}{\displaystyle \sum _{t=1}^T}\left(C^{M,boot}{A}_{on,k,t}^M+C^{M,shut}{A}_{off,k,t}^M\right)\\ f_6={\displaystyle \sum _j^J}{\displaystyle \sum _{t=1}^T}\left(C^{N,boot}{A}_{on,j,t}^N+C^{N,shut}{A}_{off,j,t}^N\right)\end{array}\right.(12)$

where f₁ is the income from electricity sales of MGs and superior power grid; f₂ the cost of wind and light abandonment; f₃ the operation and maintenance costs of MGs; f₄ the environmental cost; f₅ the start-up and shutdown costs of electrolytic cell in hydrogen production system; f₆ the fuel cell start-stop cost. cin_t and cout_t are the unit prices of the electricity purchased and saled at moment t. P_in,t and P_out,t are the electricity power purchased and saled at moment t. α and β are the penalty coefficients from the abandonment of PV and wind power. ΔP_pv,t and ΔP_wt,t are the abandonment power from PV and wind farms. K_OMi is the unit power maintenance factor of the ith MG’s supply; P_i(t) the output power of the ith MG at time t; γ_j the conversion coefficient of the jth pollutant; EP_ij the emission of pollutant j in the ith MG. C^M,boot and C^M,shut are the start-up and shut-down costs of the M^th electrolytic cell. $A_{on,k,t}^M$ and $A_{off,k,t}^M$ donate the start-up and shut-down action of the M^th electrolytic cell. C^N,boot and C^N,shut are the start-up and shutdown costs of the N^th hydrogen fuel cell. $A_{on,l,t}^M$ and $A_{off,l,t}^M$ represent the start and shutdown action of the N^th hydrogen fuel cell.

2.3.2 Constraint functions

2.3.2.1 Power balance constraints

$P_{mg,t}+P_{pv,t}+P_{wt,t}+P_{in,t}+P_{dis,t}+{\displaystyle \sum _k^K}{P}_{k,t}^M={\displaystyle \sum _j^J}{P}_{j,t}^N+P_{ch,t}+P_{out,t}+P_{load,t}(13)$

where P_dis,t is the discharge power of the battery at time t; P_ch,t the charging power of the battery at time t. P_mg,t, P_pv,t and P_wt,t are the absorbed power of turbine units, photovoltaic and wind power at time t, respectively. P_load,t the electricity load at time t; $P_{k,t}^N$ the working power of M electrolytic cell at time t; $P_{l,t}^N$ the working power of the N fuel cell at time t. P_in,t and P_out,t are the powers of MGs received from and output to distribution network.

2.3.2.2 Power exchange constraints:

$0\le \left|P_{grid}\left(t\right)\right|\le P_{i,\max }^{\text{PCC}}\left(t\right)(14)$

where P_grid(t) is the power exchanged between the MGs and power grid at time t; $P_{i,\max }^{PCC}\left(t\right)$ the maximum power interaction of the PCC node.

2.3.2.3 Start and stop model constraints of multiple types of electrolyzers and fuel cells

$\left\{\begin{array}{l}{\displaystyle \sum _{t=1}^T}{A}_{on,k,t}^M\le A_{on}^{M,\max }\\ A_{on,k,t-{\alpha }^M}^M-A_{off,k,t}^M=U_{k,t}^M-U_{k,t-1}^M\\ A_{on,k,t}^M\le 1-U_{k,t-1}^M\\ A_{off,k,t}^M\le U_{k,t-1}^M\\ {\displaystyle \sum _{t=1}^T}{A}_{off,k,t}^M\le A_{off}^{M,\max }\end{array}\right.(15)$

2.3.2.4 Start and stop frequency constraints of multiple types of electrolyzers and fuel cells

$\left\{\begin{array}{l}{\displaystyle \sum _{t=1}^T}{A}_{on,j,t}^N\le A_{on}^{N,\max }\\ A_{on,j,t-{\alpha }^M}^N-A_{off,j,t}^N=U_{j,t}^N-U_{j,t-1}^N\\ A_{on,j,t}^N\le 1-U_{j,t-1}^N\\ A_{off,j,t}^N\le U_{j,t-1}^N\\ {\displaystyle \sum _{t=1}^T}{A}_{off,j,t}^N\le A_{off}^{N,\max }\end{array}\right.(16)$

where $A_{on}^{M,\max }$, $A_{off}^{M,\max }$ and $A_{on}^{N,\max }$, $A_{off}^{N,\max }$ are the upper limits of startup and shutdown times of the electrolytic cell and hydrogen fuel cell within a day, respectively.

2.3.2.5 Operating power limits of multiple types of electrolyzers and fuel cells

$\left\{\begin{array}{l}{P}_{k,t}^M\ge \left(U_{k,t}^M{P}^{M,\min }+{\displaystyle \sum _{\tau =0}^{{\alpha }^M-1}}{A}_{on,k,t-\tau }^M{P}^{M,boot}\right)\\ P_{k,t}^M\le \left(U_{k,t}^M{P}^{M,\max }+{\displaystyle \sum _{\tau =0}^{{\alpha }^M-1}}{A}_{on,k,t-\tau }^M{P}^{M,boot}\right)\\ \left|P_{k,t}^M-P_{k,t-1}^M\right|\le \left(U_{k,t}^M\Delta P^{M,\max }+\left(1-U_{k,t}^M\right)P^{M,\max }\right)\end{array}\right.(17)$

2.3.2.6 Ramping rate constraints of multiple types of electrolyzers and fuel cells

$\left\{\begin{array}{l}{P}_{j,t}^N\ge \left(U_{j,t}^N{P}^{N,\min }+{\displaystyle \sum _{\tau =0}^{{\alpha }^N-1}}{A}_{on,j,t-\tau }^N{P}^{N,boot}\right)\\ P_{j,t}^N\le \left(U_{j,t}^N{P}^{N,\max }+{\displaystyle \sum _{\tau =0}^{{\alpha }^N-1}}{A}_{on,j,t-\tau }^N{P}^{N,boot}\right)\\ \left|P_{j,t}^N-P_{j,t-1}^N\right|\le \left(U_{j,t}^N\Delta P^{N,\max }+\left(1-U_{j,t}^N\right)P^{N,\max }\right)\end{array}\right.(18)$

where P^M,min and P^M,max are the upper and lower limits of the working powers in the M^th electrolytic cell when it is turned on. P^M,boot is the electrolytic cell load; ΔP^M,max the maximum climbing power per time unit of the M^th electrolytic cell in working state; α^M the start-up delay; $U_{k,t}^M$ the switching state of the electrolyzer. P^N,max and P^N,min are the upper and lower limits of the operating power of the hydrogen fuel cell in the startup state. P^N,boot is the hydrogen power consumed during startup; ΔP^N,max the maximum climbing power per time unit under startup state; α^N the fuel cell startup delay; $U_{l,t}^N$ the switching state of the fuel cell.

3 Uncertainties modeling and optimization model solving algorithm

3.1 Uncertainties modeling

To address the uncertainties in the input data such as wind and PV output power, load demand and electricity price, in this paper, a scenario-based stochastic programming method is employed, in which a heuristic moment matching method is utilized to construct the scenario matrix that approximates the stochastic properties of historical scenarios by reducing the number of scenarios. While the inclusion of additional scenarios may enhance the fidelity of the model approximation, it also leads to a significant increase in computational complexity. To capture random moments and correlations effectively, the heuristic moment matching method employs cubic transformation and matrix manipulation, wherein the first four random moments including expectation, standard deviation, skewness, and kurtosis are selected to preserve the stochastic nature of the scenarios (Ehsan et al., 2019).

For a sample scenario matrix that includes M PV outputs, wind power outputs, load demands and electricity price scenarios, firstly, the correlation matrix (R) of hourly PV output, wind power output, load demand and electricity price and the target time (M_i,k) are calculated. Then, the relevant standardized value ($M_{i,2}^{NT}$) can be calculated as follows.

$\left\{\begin{array}{l}{M}_{i,1}^{NT}=0,M_{i,2}^{NT}=1\\ M_{i,3}^{NT}=\frac{M_{i,3}^T}{{\left(\sqrt{M_{i,2}^T}\right)}^3},M_{i,4}^{NT}=\frac{M_{i,4}^T}{{\left(M_{i,2}^T\right)}^4}\end{array}\right.(19)$

where i = 1, 2, 3, four represents the four considered uncertain parameters, and k = 1, 2, 3, four represents the first four random moments.

Furthermore, N_m scenarios are randomly generated from N_w uncertainties, and the normal distribution N (0, 1) is considered to determine the matrix X_Nm×Nw. Use the matrix transformation shown as (20) to satisfy the correlation matrix R by converting X_Nm×Nw to the matrix Y_Nm×Nw.

$\left\{\begin{array}{l}\mathit{\gamma }=\mathit{L}\times \mathit{X}={\displaystyle \sum _{j=1}^i}{\mathit{L}}_{ij}\times {\mathit{X}}_i\\ \mathit{R}=\mathit{L}{\mathit{L}}^T\end{array}\right.(20)$

where L is the lower triangular matrix of the correlation matrix determined by Cholesky decomposition.

The standard normal random variable Y_Nm×Nw is converted to a non-normal random variable Z_Nm×Nw using the cubic transformation to satisfy the standardized target moment of the historical scenario.

$Z_i={\alpha }_i+{\beta }_i{\gamma }_i+{\kappa }_i{\gamma }_i^2+{\lambda }_i{\gamma }_i^3(21)$

Since, the constants α_i, β_i, κ_i and λ_i can be calculated.

Then, the correlation error (ε_c) and the time error (ε_m) are calculated. And the proposed algorithm tends to converge when the calculated error is less than the predefined threshold (5%).

${\epsilon }_c={\displaystyle \sum _{i=1}^{N_m}}\sqrt{\frac{2}{N_{\omega }\left(N_{\omega }-1\right)}{\displaystyle \sum _{i=1}^{N_f}}{\displaystyle \sum _{i=1}^{N_f}}\left(R_{il}^G-R_{il}^{NT}\right)}(22)$

${\epsilon }_m={\displaystyle \sum _{i=1}^{N_m}}\left(\left|M_{il}^G-M_{il}^{NT}\right|+{\displaystyle \sum _{k=2}^4}\left|M_{ik}^G-M_{ik}^{NT}\right|/M_{ik}^{NT}\right)(23)$

Finally, the scenario matrix Ω that includes PV output, wind power output, load demand and electricity price can be calculated with (24).

${\mathit{\Omega }}^M=\sqrt{M_{i,2}^T}\times {\mathit{Z}}_i+M_{i,3}^{NT}(24)$

3.2 Solving algorithm for optimization models

The constraints within the upper-level optimization model encompass nonlinear component, such as power flow constraints, rendering the upper-level scheduling a high-order non-convex problem. Traditional methods often struggle to attain the global optimal solution due to this complexity. To address these challenges, in this paper, the second-order cone relaxation technique is employed to linearize the power flow equations and other related constraints and inequalities within the distribution network containing multiple microgrids, thereby transforming them into linear second-order cone programming equations for solution (Guo et al., 2013). Simultaneously, the lower-level optimization model entails the determination of output ranges and optimization operation problems, in which the nonlinear components are addressed through piecewise linearization. Subsequently, the lower-level optimization problem is reformulated as a mixed-integer linear programming problem to be solved (Zhao et al., 2014).

Once the upper-layer and lower-layer models are transformed into second-order cone programming and mixed integer linear programming problems, respectively, the proposed two-layer optimal scheduling model can be efficiently solved using the commercial solver CPLEX. The PCC power calculated by the upper-layer optimization model serves as the scheduling instruction for the purchase/sale of power by the lower-layer MGs allowing the lower-layer MGs’ optimization model to conduct optimization calculations under specified PCC power conditions. If a solution is found, the optimization process is completed, and the final scheduling result is generated. However, if no solution is obtained, the optimization results will be fed back to the upper-level model, which adjusts the upper and lower limits of PCC power and recalculates until a convergent optimal feasible solution is achieved. The solution flow of the adopted two-layer optimization model is illustrated in Figure 3.

Figure 3

Figure 3. Solution flowchart for bi-level optimization scheduling models.

In Figure 3, the specific implementation process of the mixed integer linear programming algorithm mainly includes four aspects. 1) Define optimization problems and objective functions, 2) define the decision variables; 3) define the constraints and add them to this optimization problem; 4) solve the optimal value using MATLAB software. The CPLEX solver employs the branch and bound method as its fundamental framework for solving mixed integer linear programming problems. Within this framework, the solver initially branches integer variables to construct a search tree. Subsequently, it utilizes a linear programming solver to address the linear relaxation problem for each node in the search tree. Finally, the search process is optimized through pruning strategies, heuristic methods, and other advanced technologies to efficiently locate the optimal solution or ascertain the infeasibility of the problem. Upon completion of the solution process by the CPLEX solver, the initial scheduling strategy is derived. This includes determining the exchange power be-tween the microgrid and the main grid for each time period, specifying the output of wind turbines and photovoltaics, and regulating the charging and discharging power of the energy storage system.

4 Case studies

4.1 Structure and parameters of case studies

To validate the effectiveness of the proposed scheduling strategy, enhancements are made to the standard IEEE33 node example, with a comprehensive analysis conducted on the distribution system featuring multiple MGs. The basic structure of this system is established as Figure 4. The upgraded IEEE33-node system comprises 3 MGs, namely, MG1, MG2, and MG3, with the distributed power sources connected to nodes 7, 22, 24, and 27, and the MGs linked to nodes 11, 18, and 31. The MGs configuration encompass various components such as PVs, WTs, MT, hydrogen storage systems (HES), FCs, and battery energy storage (BES). The parameters of the distributed power supplies in the DN are detailed in Table 1, while the MGs’ parameters are provided in Table 2. It should be noted that in this paper, a satellite time synchronization-based dual-mode switching strategy for MGs is used (Bi et al., 2022).

Figure 4

Figure 4. Structure of the IEEE33 node test network.

Table 1

Table 1. Output parameters of each unit in DN.

Table 2

Table 2. Output parameters of each unit in DN.

Based on the time-of-use electricity prices and the on-grid electricity prices of renewable energy in China, the electricity purchase and sales prices for each period are presented in Table 3. Additionally, Table 4 outlines the pollutant emission factors of various micropower sources along with their corresponding conversion costs. Utilizing a scheduling period of 24 h, the PV and wind output prediction curves within the MGs, as well as the load demand curves between the DN and each MG, are normalized, as depicted in Figure 5. To conduct testing on the network, Figure 4 was utilized, and MATLAB software was employed for solving and verification purposes.

Table 3

Table 3. Electricity purchase and sale prices in each period.

Table 4

Table 4. Pollutant emission factors.

Figure 5

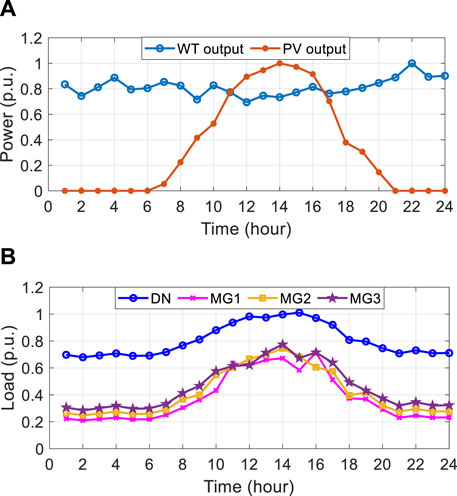
Figure 5. Typical daily output and load curves. (A) is “Forecast curves of the output power from WTs and PVs.” (B) is “Load demand curves of DN and MGs.”

4.2 Optimization scheduling result analysis

Utilizing the output and load curves depicted in Figure 5 as input, the proposed dual-layer optimal scheduling model is solved following the process outlined in Figure 3. Subsequently, the optimal scheduling results for the distribution network nodes and internal component of the 3 MGs are obtained, as illustrated in Figure 6.

Figure 6

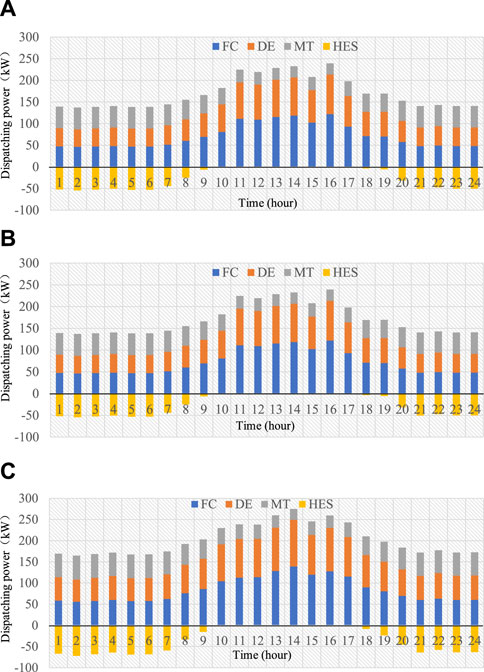
Figure 6. (A) is Microgrid 1 scheduling optimization results, (B) is Microgrid 2 scheduling optimization results and (C) is Microgrid 3 scheduling optimization results.

Based on the data analysis, owing to the consideration of environmental protection and economic objectives, the load of the MGs is primarily fulfilled by controlled FCs and renewable energy sources. The load demands of the 3 MGs steadily increase over time. During low-load valley price periods from 00:00 to 06:00 and from 21:00 to 24:00, the HESs absorb electrical energy from the MGs to produce hydrogen, resulting in a total scheduling power of 610.38 kW. Conversely, during peak hours, the FCs discharge power to the system while the HESs stop working. This enables the MGs to achieve output power balance and fully capitalize on the time difference in electricity prices to minimize the respective operating costs.

Furthermore, overall, the MGs export surplus power to distribution system, thereby alleviating the grid’s burden during periods of high load, and contributing to the smooth operation of the distribution network. Meanwhile, due to the low maintenance costs and minimal pollution emissions, FCs exhibit the lowest operating and environmental protection costs. For instance, the unit nitride emissions amount to only 0.152% of those from gas turbines, while the unit sulfur dioxide emissions are just 36.76% of MTs. Thus, as depicted in Figure 6, during MGs’ operation, taking MG 1 as an example, the fuel cell power generation (1846.72 kW) is pretty after wind power (1931.44 kW), accounting for 39.8% of the total power generation.

Figure 7 shows the power exchange curves (PCC power) between the 3 MGs and the DN. It can be seen that when the loads of MGs are low relative to the power generations, the PCC power is positive, and the MGs output power to DN. On the contrary, when the load demands are relatively large, the MGs purchase power from DN through the PCC, mainly in the 11:00-18:00 period. The PCC power output can reduce the output of other power supplies, and which can coordinate the power flow balance of the network and maximize the use of renewable energy. Taking MG 1 as an example, the total positive power is 966.45 kW with PCC positive power time accounting for 83.33%, the negative total power is 237.18 kW with the PCC negative power time accounting for only 16.67%.

Figure 7

Figure 7. Exchange power between the DN and MGs.

Upon solving the two-layer optimal scheduling model, the specific numerical optimization results for the DN are acquired, depicted as Figure 8. Additionally, the network’s operating loss and voltage offset are also investigated, as given in Figure 9. In scenario 1, multiple MGs are integrated into the DN, whereas in scenario 2, these MGs remain unintegrated.

Figure 8

Figure 8. Power losses in DN under different scenarios.

Figure 9

Figure 9. Voltage offsets in DN under different scenarios.

As depicted in Figure 8, the line losses of the distribution system exhibit a positive correlation with the load demands, with the daily optimization operation of the DN primarily catering to the load demand through the output of each power supplies. In scenario 1, the maximum power loss is reduced from 72.5 kW in scenario 2–68.1 kW. This represents a reduction of 10.2% in the sum of power losses and a 6.8% decrease in the total sum of power losses.

As seen from Figure 9, in scenario 1, the maximum voltage offset is 0.132 p. u, compared to 0.103 p. u in scenario 2. This reduction to 0.103 p. u results in approximately a 25.6% decrease in the sum of node voltage offsets compared to scenario 2. During the peak period of MGs’ load, the DN must supply electricity to the MGs, leading to significant network losses and voltage fluctuations. Conversely, during the low-load period, the MGs deliver electricity to the DN, thereby reducing the output of DN units and subsequently minimizing network losses and voltage fluctuations. In comparison with the optimal operation results, it is evident that although the integration of multiple MGs may slightly increase the overall operational costs of DN (13,356 yuan for scenario 1 and 11,390 yuan for scenario 2), it significantly reduces the operation losses and voltage fluctuations of the DN system.

For sensitivity analysis, during the 01:00-06:00 period, the exchange power between the microgrid and the PCC of DN remains relatively stable. However, as depicted in Figures 7–9, an increase in electricity prices and PV output leads to a corresponding rise in exchange power of the 3 MGs. Notably, during 11:00-14:00 period, the predicted PV output exhibits a continuous increase, resulting in a 2–4 kW rise in power loss within DN under both scenarios. Additionally, a voltage deviation for 0.016-0.018 p. u. is observed. This phenomenon is attributed to the fluctuation of renewable energy, coinciding with peak electricity prices. Consequently, the exchange power between MGs and the DN experiences varying degrees of decrease, with MG two showing the most significant reduction from 9.46 kW to −95.32 kW. Similarly, during the peak electricity price period from 18:00 to 21:00, the exchange power between the MGs and the DN decreases. However, during this timeframe, the predicted PV output de-creases as well, resulting in a reduction in power loss and voltage offset within the DN under both two scenarios.

5 Conclusion

This paper presents a bi-level optimal scheduling model for a multi-MGs and DN system. By introducing a scenario-based stochastic framework and the heuristic moment matching method, the multi-source uncertainties are effectively addressed. An improved IEEE33 node test system is established, and the effectiveness of the proposed approaches is verified through case studies. Specific conclusions are as follows.

(1) Despite that the integration of multiple MGs into the DN leads to an increase in the overall operation costs, it significantly reduces the operation losses (by approximately 6.8%) and voltage fluctuations (by about 25.6%). This helps achieve an effective balance between the operational economy, environmental protection, and stability of DN.

(2) Through the optimal scheduling scheme, the MGs’ load can primarily be met by controlled FCs and renewable energy, enabling smart utilization of electricity prices and consequent reduction in respective operating costs.

(3) During the periods with low MGs’ load demands, the MGs can function as a power source and sell electricity to the DN. Conversely, during periods of high load, the MGs act as consumers and purchase power from the DN through the PCC. This process ensures power flow balance within the network while maximizing the utilization of renewable energy sources.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GL: Conceptualization, Funding acquisition, Methodology, Validation, Writing–original draft. XL: Conceptualization, Methodology, Supervision, Validation, Writing–review and editing. LK: Formal Analysis, Software, Visualization, Writing–review and editing. WX: Funding acquisition, Software, Writing–review and editing. SY: Formal Analysis, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Science and Technology Project of State Grid Shandong Electric Power Company (520610230004).

Conflict of interest

Authors GL, XL, LK, WX, and SY were employed by State Grid Shandong Electric Power Company.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bi, Y., Xu, B., Zhao, Y., Cai, F., and Lu, M. (2022). Seamless transfer control strategy between grid-connected and islanding operation for synchronous fixed-frequency microgrid. Power Syst. Technol. 46, 923–932. doi:10.13335/j.1000-3673.pst.2021.1245

CrossRef Full Text | Google Scholar

Bidgoli, M. A., and Ahmadian, A. (2022). Multi-stage optimal scheduling of multi-microgrids using deep-learning artificial neural network and cooperative game approach. Energy 239, 122036. doi:10.1016/j.energy.2021.122036

CrossRef Full Text | Google Scholar

Chang, J., Du, Y., Chen, X., Lim, E., Wen, H., Li, X., et al. (2022). Frequency regulation in adaptive virtual inertia and power reserve control with high PV penetration by probabilistic forecasting. Front. Energy Res. 10, 929113. doi:10.3389/fenrg.2022.929113

CrossRef Full Text | Google Scholar

Chen, C., Miao, S., Yao, F., Wang, Y., Wang, J., and Wei, Y. (2023c). Hierarchical cooperative dispatching strategy of multi-microgrid and distribution networks based on multi-agent algorithm. Power Syst. Autom. 47, 57–65. doi:10.7500/AEPS20221115002

CrossRef Full Text | Google Scholar

Chen, Q., Wang, W., and Wang, H. (2023a). Coordinated optimization of active distribution network with multiple microgrids considering demand response and mixed game. Power Syst. Autom. 47, 99–109. doi:10.7500/AEPS20220920003

CrossRef Full Text | Google Scholar

Chen, X., Zhang, Y., Huang, Z., and Xie, S. (2023b). Bi-level robust economic dispatch of distribution network and multiple microgrids considering locational marginal price. Power Autom. Equip. 43, 51–58. doi:10.16081/j.epae.202301004

CrossRef Full Text | Google Scholar

Dixit, S., Singh, P., Ogale, J., Bansal, P., and Sawle, Y. (2023). Energy management in microgrids with renewable energy sources and demand response. Comput. Electr. Eng. 110, 108848. doi:10.1016/j.compeleceng.2023.108848

CrossRef Full Text | Google Scholar

Ehsan, A., Cheng, M., and Yang, Q. (2019). Scenario-based planning of active distribution systems under uncertainties of renewable generation and electricity demand. CSEE J. Power Energy Syst. 5, 56–62. doi:10.17775/cseejpes.2018.00460

CrossRef Full Text | Google Scholar

Elshenawy, M., Fahmy, A., Elsamahy, A., El Zoghby, H. M., and Kandil, S. A. (2022). Improving frequency response for AC interconnected microgrids containing renewable energy resources. Front. Energy Res. 10, 1035097. doi:10.3389/fenrg.2022.1035097

CrossRef Full Text | Google Scholar

Gao, H. C., Choi, J. H., Yun, S. Y., Lee, H. J., and Ahn, S. J. (2018). Optimal scheduling and real-time control schemes of battery energy storage system for microgrids considering contract demand and forecast uncertainty. Energies 11, 1371. doi:10.3390/en11061371

CrossRef Full Text | Google Scholar

Guo, L., Liu, W., Cai, J., Hong, B., and Wang, C. (2013). Robust optimal scheduling of multi-microgrid and bidding strategy of VCG mechanism considering renewable energy-load uncertainty. Energy Convers. Manag. 74, 433–445. doi:10.13335/j.1000-3673.pst.2022.0843

CrossRef Full Text | Google Scholar

Jani, A., and Jadid, S. (2023). Two-stage energy scheduling framework for multi-microgrid system in market environment. Appl. Energy 336, 120683. doi:10.1016/j.apenergy.2023.120683

CrossRef Full Text | Google Scholar

Lee, C., and Tuegeh, M. (2020). Optimal optimisation-based microgrid scheduling considering impacts of unexpected forecast errors due to the uncertainty of renewable generation and loads fluctuation. IET Renew. Power Gener. 14, 321–331. doi:10.1049/iet-rpg.2019.0635

CrossRef Full Text | Google Scholar

Lei, W., Sun, W., Zhao, Y., and Mingfei, B. (2023). Research on market trading strategy of multi-microgrid intelligent power distribution system based on Bi-level optimization. Front. Energy Res. 10, 1032051. doi:10.3389/fenrg.2022.1032051

CrossRef Full Text | Google Scholar

Li, J., Chen, J. J., Wang, Y. X., and Chen, W. (2024). Combining multi-step reconfiguration with many-objective reduction as iterative bi-level scheduling for stochastic distribution network. Energy 290, 130198. doi:10.1016/j.energy.2023.130198

CrossRef Full Text | Google Scholar

Li, X., and Wang, M. (2023). Robust optimization scheduling and VCG mechanism bidding strategy for multiple microgrids considering source load uncertainty. Grid Technol. 47, 2330–2345.

Google Scholar

Li, Y., Wang, P., Gooi, H., Ye, J., and Wu, L. (2019). Multi-objective optimal dispatch of microgrid under uncertainties via interval optimization. IEEE Trans. Smart Grid 10, 2046–2058. doi:10.1109/tsg.2017.2787790

CrossRef Full Text | Google Scholar

Luo, J., Han, B., Xu, J., Li, Z., Lin, D., and Li, G. (2023). Homology Identification and Equivalent Modelling of Multi-microgrid Based on Relaxed Variation Coefficients. Power Syst. Autom. 47, 67–74. doi:10.7500/AEPS20230222001

CrossRef Full Text | Google Scholar

Mi, Y., Chen, Y., Chen, B., Han, Y., and Yuan, M. (2023). Shared Energy Storage Multi-Objective Allocation Strategy Considering Integrated Energy Microgrid Access to Active Distribution Network. Journal of Shanghai Jiao Tong University. doi:10.16183/j.cnki.jsjtu

CrossRef Full Text | Google Scholar

National Energy Administration (2021). The 14th five year plan for the development of renewable energy. Beijing China: National Development and Reform Commission.

Google Scholar

Nikmehr, N., Najafi-Ravadanegh, S., and Khodaei, A. (2017). Probabilistic optimal scheduling of networked microgrids considering time-based demand response programs under uncertainty. Appl. Energy 198, 267–279. doi:10.1016/j.apenergy.2017.04.071

CrossRef Full Text | Google Scholar

Prathapaneni, D. R., and Detroja, K. P. (2019). An integrated framework for optimal planning and operation schedule of microgrid under uncertainty. Sustain. Energy, Grids Netw. 19, 100232. doi:10.1016/j.segan.2019.100232

CrossRef Full Text | Google Scholar

Qiu, H. F., Zhao, B., Gu, W., and Bo, R. (2018). Bi-level two-stage robust optimal scheduling for AC/DC hybrid multi-microgrids. IEEE Trans. Smart Grid 9, 5455–5466. doi:10.1109/tsg.2018.2806973

CrossRef Full Text | Google Scholar

Shi, G. Y., He, Y., Zhang, J., Zhang, Y., and Liu, Y. (2021). Research on weak robust multi-objective optimal dispatching of microgrid. Electr. Power Sci. Eng. 37, 9–17. doi:10.3969/j.ISSN.1672-0792.2021.05.002

CrossRef Full Text | Google Scholar

Singh, S., Singh, M., and Kaushik, S. (2016). Optimal power scheduling of renewable energy systems in microgrids using distributed energy storage system. IET Renew. Power Gener. 10, 1328–1339. doi:10.1049/iet-rpg.2015.0552

CrossRef Full Text | Google Scholar

Wang, K., Zhao, W., Zhang, W., Yu, J., and Li, R. (2023b). Optimal allocation of microgrid under the background of carbonpeaking and neutralization. Power Demand Side Manag. 25, 86–92. doi:10.3969/j.issn.1009-1831.2023.04.014

CrossRef Full Text | Google Scholar

Wang, X., Chen, S., Zhou, Y., Wang, J., and Cui, Y. (2018). Optimal dispatch of microgrid with combined heat and power system considering environmental cost. Energies 11, 2493. doi:10.3390/en11102493

CrossRef Full Text | Google Scholar

Wang, X., Gao, C., Liu, Y., Liang, D., and Hou, S. (2023a). Multi-stage dynamic programming method for hydrogen-electric coupled microgrid considering multiple uncertainties. Power Autom. Equip. 43, 77–83+150. doi:10.16081/j.epae.202212015

CrossRef Full Text | Google Scholar

Wang, Y., Li, Y., Cao, Y., Shahidehpour, M., Jiang, L., Long, Y., et al. (2023c). Optimal operation strategy for multi-energy microgrid participating in auxiliary service. IEEE Trans. Smart Grid 14, 3523–3534. doi:10.1109/tsg.2023.3250482

CrossRef Full Text | Google Scholar

Wu, J., Zhao, P., Li, L., Shi, F., and Li, B. (2023). Multi-microgrids distributed peer-to-peer energy trading in distribution system considering uncertainty risk. Int. J. Electr. Power and Energy Syst. 152, 109234. doi:10.1016/j.ijepes.2023.109234

CrossRef Full Text | Google Scholar

Xuan, P. Z., Zhu, J. Z., and Xie, P. (2017). Multi-objective optimization method of robust dispatch conservativeness of power system with wind power. South. Power Syst. Technol. 11, 4600–4608. doi:10.13648/j.cnki.issn1674-0629.2017.02

CrossRef Full Text | Google Scholar

Zhang, W., and Xu, Y. (2019). Distributed optimal control for multiple microgrids in a distribution network. IEEE Trans. Smart Grid 10, 3765–3779. doi:10.1109/tsg.2018.2834921

CrossRef Full Text | Google Scholar

Zhao, Y., An, Y., and Ai, Q. (2014). Research on size and location of distributed generation with vulnerable node identification in the active distribution network. IET Generation Transm. Distribution 8, 1801–1809. doi:10.1049/iet-gtd.2013.0887

CrossRef Full Text | Google Scholar