Reinforcement learning and game theory based cyber-physical security framework for the humans interacting over societal control systems

A lot of infrastructure upgrade and algorithms have been developed for the information technology driven smart grids over the past twenty years, especially with increasing interest in their system design and real-world implementation. Meanwhile, the study of detecting and preventing intruders in ubiquitous smart grids environment is spurred significantly by the possibility of access points on various communication equipment. As a result, there are no comprehensive security protocols in place preventing from a malicious attacker’s accessing to smart grids components, which would enable the interaction of attackers and system operators through the power grid control system. Recently, dynamics of time-extended interactions are believed to be predicted and solved by reinforcement learning technology. As a descriptive advantage of the approach compared with other methods, it provides the opportunities of simultaneously modeling several human continuous interactions features for decision-making process, rather than specifying an individual agent’s decision dynamics and requiring others to follow specific kinematic and dynamic limitations. In this way, a machine-mediated human-human interaction’s result is determined by how control and physical systems are designed. Technically, it is possible to design dedicated human-in-the-loop societal control systems that are attack-resistant by using simulations that predict such results with preventive assessment and acceptable accuracy. It is important to have a reliable model of both the control and physical systems, as well as of human decision-making, to make reliable assumptions. This study presents such a method to develop these tools, which includes a model that simulates the attacks of a cyber-physical intruder on the system and the operator’s defense, demonstrating the overall performance benefit of such framework designs.

1 Introduction

Power systems are among the most highly complex and delicate systems of engineering around the globe. Power systems have become increasingly complex in recent years since modern equipment, including distributed generators (DGs), storage devices, and monitoring equipment, has been incorporated into them. Cyber-Physical Systems (CPS) are advanced engineered systems that include computing, communicating, and controlling functions (Zhang et al., 2022). A Cyber-Physical Power System consists of a power system combined with monitoring equipment, creating the Cyber-Physical Power System (CPPS). There are separate laws for information, communication, and power in a CPPS. Information technology boosts the economy and improves the reliability of power systems (Ponce-Jara et al., 2017). Providing accurate and trustworthy information improves the performance of electric utilities (Kirschen and Bouffard, 2008). A greater degree of precision in fault detection and isolation allows the CPPS to work more reliably (Butt et al., 2021).

Over the last years, many other works are studied on the security of CPSs (Wu et al., 2021; Liu et al., 2019), including some human-in-the-loop considerations with dynamic interaction over the societal control system. However, the comprehensive modeling of the CPS security features with power system monitoring physical information linked to human interaction decision-making process is still under study. In Wu et al. (2021), several operational objectives of the CPS are described in light of a range of security concerns. Chang et al. (2021) presents a mathematical model for analyzing and detecting different threats on a CPS. Liu et al. (2020) proposes a hierarchical structure for CPS security and develops a cross-layer method for preventing attacks. Zhang et al. (2021) focuses on robust denial-of-service control. Liu et al. (2019) examines cascading failures resulting from malicious intrusions and proposes defenses for CPS security. Rajasekaran et al. (2023) and Ghiasi et al. (2023) have both drawn significant attention to the issue of smart grid security. Rajasekaran et al. (2023) analyzes a variety of security methods to increase the viability of smart grids in the event of an attack. Similarly, Ghiasi et al. (2023) analyzes a variety of cyber-attacks against the smart grid and proposes measures to improve the system’s security. In spite of the fact that these studies all contribute to smart grid and cyber security, only a small number take into account attacker-defender interactions. Typically, attackers aim to cause harm to systems by selecting an attack method, whereas defenders aim to minimize damages. CPS attackers and defenders are interconnected, so studying interactions between them is crucial. As well, it was presumed that defenders and attackers in Liu et al. (2020) and Zhang et al. (2021) acted in an optimal and strategic manner as rational players. Stress, insufficient data, and limitations like time restrictions and complex situations can limit people’s rationality in security risks or insufficient data situations (De Neys, 2023). Decision nodes can be represented by a game-theoretic framework using two essential elements. First, utility functions or reward functions measure the related advantages of various decisions based on the individual’s aims expressed through a decision node. Secondly, solution concepts determine how humans make decisions. Human behavior can be precisely represented by a solution concept when it is chosen as a model. A mathematical model representing the human’s mental approximations is an integral component of the solution concept when the human’s decisions cannot be exhaustively explored.

The simplified model of the electric grid is retained in this study, however, a number of significant improvements are made. To begin with, the SCADA operator’s certainty is eliminated during an attack, forcing them to work efficiently regardless of whether they are under attack or not. Secondly, it is more helpful to use these predictions to design physical and control systems rather than just predicting the outcome of an attack. Thirdly, design extensions require numerical evaluations of a greater number of case studies, and computational algorithms are being developed to speed up simulations. Therefore, the designer develops solution concepts and reward functions that accurately resemble the decision making methods of cyber-physical attackers as well as SCADA operators. A SNFG contains game theoretic models within the decision nodes to illustrate how the physical state evolves and what data human and automation nodes can access. By using this model, various system designs outcomes can be predicted by designers. This allows him to enhance his own “designer’s reward function.” It is similar to mechanism design’s economic theory (Gao, 2022), in which an external policymaker designs an equilibrium game for a particular purpose. In contrast to mechanism design, this study assumes no equilibrium behavior, and it is therefore possible to employ the standard control methods mentioned earlier (Wolpert and Bono, 2013; Camerer et al., 2019). Additionally, this study contributes to research in the field of network security and game theory (Ezhei and Ladani, 2017). Assuming that the human operator detects attackers from SCADA state, the model is related to intrusion detection systems (Paul et al.; Wang et al., 2021). The human operator is also modelled in this study as a means of mitigating damage following the detection of an attack. In this way, the model makes a contribution to intrusion response research (Kiennert et al., 2018).

Following is a summary of the remainder of the study. A simplified electrical distribution circuit and the SCADA that controls it are described in Section 2. The third part discusses the reinforcement learning (RL) and game theory solution concept. The simulation outcomes are described in Section 4 and how they were used to evaluate design options. The conclusion is presented in Section 5.

2 Simplified electrical grid model

The study retains the simplified electric grid model from prior work to model adversarial interactions between defenders and attackers (Frost et al., 2022). Figure 1 shows a schematic of a radial distribution circuit consisting of three nodes. $V_1$ is controlled by the SCADA by the tap changer at Node 1 of the substation, as shown in Figure 1. There is a large aggregate of reactive $q_2$ and real $p_2$ loads at node 2, although their fluctuation is limited. There are real $p_3$ and reactive $q_3$ outputs at node three, which represent a DG. Figure 1 shows $V_i$, $q_i$, and $p_i$ as voltage, reactive and real power injections into the node $i$. In the circuit segment $i$, the real power flow, reactive power flow, resistance, and reactance are represented as $P_i$, $Q_i$, $r_i$, and $x_i$. LinDistFlow is used in this simple setting (Salkuti, 2021) with representation as Eqs (1) and (2).

$P_2=-p_3,Q_2=-q_3,P_1=P_2+p_2,Q_1=Q_2+q_2(1)$

$V_2=V_1-\left(r_1{P}_1+x_1{Q}_1\right),V_3=V_2-\left(r_2{P}_2+x_2{Q}_2\right)(2)$

$x_i$ is set to 0.03 and $r_i$ is set to 0.03 after normalizing all terms by $V_0$. Simulation steps representing 1 min are used to model the attacker-defender game. As a means of simulating consumer real load fluctuations, p_2 is determined by a uniform distribution within [$p_{2,\mathit{min}},p_{2,\mathit{max}}$], where $q_2=0.5p_2$. There is a constant amount of real power injection $p_3$ in node three. The design parameters for the game are $p_{2,\mathit{max}}$ and $p_3$, which are constant for each game instance, and the parameters are changed in order to test the effect of these parameters on the result of attacker-defender games. Each scenario sets $p_{2,\mathit{min}}$ 0.05 less than $p_{2,\mathit{max}}$.

Figure 1

Figure 1. The simplified power distribution network feeder line.

The suggested simplified game involves the SCADA operator (defender) maintaining voltages $V_2$ and $V_3$ between acceptable operational limits (explained further here). Operators typically have two control options: ULTC for adjusting voltage $V_1$, or the DG’s reactive power output $q_3$. A compromising system was identified, and the attacker controls $q_3$, whereas the defender controls $V_1$. The decision node of the defender is affected by variations of $V_1$, whereas the decision node of the attacker is affected by variations of $q_3$. In the following study of cyber attacking issues, both the action power and reactive power information might be manipulated by the malicious attacker via injecting false data samples of itemized apparent power or changing the monitoring itemized power factor information, indirectly impacting the original active power and reactive power-relevant physical information (Regula et al., 2016).

It is possible for the attacker to manipulate $q_3$, change $Q_i$, and result in a significant deviation from 1.0 p.u for the customer node’ voltage $V_2$. This could result in a loss of revenue if the equipment of the customer is damaged or if the computers or computer-related controllers are disrupted (Nelson and Lankutis, 2016). The reward function models the goals of the attacker as the following Eq (3):

$R_A=\mathrm{\Theta }\left(V_2-\left(1+ϵ\right)\right)+\mathrm{\Theta }\left(\left(1-ϵ\right)-V_2\right)(3)$

In which, $ϵ$ shows the half width of the allowable limits of normalized voltage. As a step function, $ϵ\sim 0.05$. $\mathrm{\Theta }\left(.\right)$ represents the voltage deviation threshold that must be crossed by the attacker to cause damage to the distribution system.

The defender, however, maintains $V_2$ and $V_3$ close to 1.0 p.u. In addition, the defender is capable of responding to small voltage deviations without benefiting the attackers. The reward function expresses the goals of the defender.

$R_D=-{\left(\frac{V_2-1}{ϵ}\right)}^2-{\left(\frac{V_3-1}{ϵ}\right)}^2(4)$

3 The basics

A basic building block of the suggested game theoretical model is presented below. RL and game theory are the building blocks. These pieces are explained below in a very limited manner, using semi-formal language for ease of comprehension, and with sufficient detail to enable comprehension of the essential information needed to comprehend the remainder of this parts.

3.1 Game theory

In game theory, strategic agents interact with each other. As they make their own decisions, strategic agents consider what other agents might do and how it might affect the game. Based on exact calculations, this theory predicts what will happen when these interactions take place.

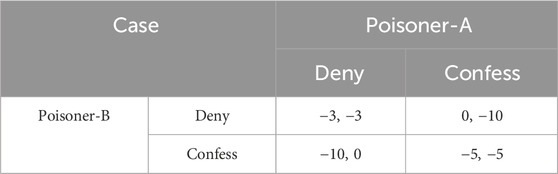
A player is an entity that can influence a game by its moves (or actions, or decisions). Essentially, a player’s tactic is the way in which he or she determines what actions to take. It is possible to determine how a game unfolds using a solution approach, which is a well-known rule. In the same manner as a system dynamics equilibrium, a Nash equilibrium describes a situation in which different players are not motivated to depart from the action they have planned. Thus, Nash equilibrium consists of players choosing the most effective actions to counteract those of their opponents. The Prisoner’s Dilemma is a common game in which Nash equilibrium is visible. The game involves two prisoners, named A and B, who cannot speak to each other because they are placed in different rooms. Each of them receives the information: Prisoner A is freed when confessing the crime, but Prisoner B has to spend 10 years in prison for denying the crime. The same applies to Prisoner B’s release when he confesses, while Prisoner A will spend 10 years in prison for denying the crime. A 3-year sentence will be imposed on each of them if they refuse to confess. A 5-year prison sentence awaits them both for confessing. The game can be represented as a matrix in Table 1, in which players’ payoffs are inversely proportional to their prison sentences. The “Confess, Confess” option, even though it results in a poor payoff, is the sole Nash equilibrium because nobody is willing to alter their decision after reaching it. Several Nash equilibriums might exist for a given game, and Nash equilibrium differs from game to game.

Table 1

Table 1. Prisoner’s dilemma.

Quantal response equilibrium is another equilibrium concept in which rather than responding to other players in the optimal way, players are more likely to play actions with higher expected payoffs when they select a probability distribution over their action space.

Equilibrium cannot be predicted by every solution concept. Accordingly, for instance, level-k thinking identifies various levels of reasoning to the player in the context of a non-equilibrium game theory model of strategic interaction (Hough and Juvina, 2022). The model provides a minimum level of reasoning as level-0, representing non-strategic thinking, which basically implies the players with this reasoning ignore other players’ actions when setting their strategies. When faced with level-0 opponents, a level-1 player will take the most effective action. In a similar way, a level-k player will respond most effectively if he believes others have been reasoning at level-(k-1). Hence, iterated optimal responses are assumed in the model (Jin, 2021). The solution concept’s findings are corroborated with varied successes by experiments reported in Jiang et al. (2019).

A simple level-k reasoning scheme is illustrated by taking two people walking in a university corridor along a collision route, Diana and Ritchie. When Ritchie chooses to keep moving regardless of Diana’s potential actions, he is regarded as a non-strategic thinker at level-0. Diana can be modeled as a level-1 player if she accepts that Ritchie is a level-0 thinker and thus steps right. An example such as this illustrates the challenge of making level-k predictions despite research findings: players may be misinformed about other players. Moreover, level-0 algorithms affect various levels’ behavior patterns, regardless of whether players accurately predict the level of their opponents. Because of this, level-0 has been called the anchoring level. It is true that these “problems” exist, but in the context of modeling humans, they might in fact be seen as advantages. As explained earlier, in the case of CPHS involving several humans, adequate predictions require models that cannot necessarily predict the best behavior. It is also possible to view level-k thinking as representing intelligent agents’ interactions without any interaction history, because their presumptions on the strategies of the other agents cannot be completely accurate. As a result, human reactions that are not the best can be observed that provide the most effective responses to what they believe concerning the surrounding environment around them.

3.2 Reinforcement learning

In reinforcement learning (RL) models, rewards and punishments are used to represent learning. For the purpose of clarifying the explanation, and in order to better understand the RL algorithm applied to the CPHS model structure presented here, it is necessary to define the essential elements of RL and explain some terms that are common to most RL techniques. Agents in RL could alter the environments in which they operate by taking actions. In RL, the goal is to find the best set of action sequences for one agent for reaching a particular goal by interacting with the environment, as indicated by the state of that environment. It may be necessary to make a mobile robot (agent) move left, right, forward, and backward (actions), depending upon whether it is going to move left, right, forward, or backward (goal) in a 10 by 10 grid-world with obstacles. Here, the state is the grid position where the robot resides.

As the agent (or its designer) learns for achieving a specific goal, RL describes its preferences using a reward function. When the robot reaches the goal state of point B, the reward is 0, else a constant negative value. A policy consists of a probabilistic map between states and actions. When an agent is operating, the RL algorithm is responsible for finding a policy maximizing a cumulative discounted reward. The cumulative reward can be expressed in the following Eq (5):

$C={\displaystyle \sum _{t=0}^{\infty }}{\gamma }^t{r}_t(5)$

In which, $\gamma$ shows the discount factor. $r$ shows the reward of each step $t$. It has been proposed that different RL methods can be used to find action sequences that will maximize (1). In accordance with the policy used, each of the techniques estimates a value function, which is essentially a measure of the benefits of a certain state. The value function is expressed in the following Eq (6):

$V^{\pi }\left(s\right)=E_{\pi }\left\{{\displaystyle \sum _{k=0}^{\infty }}{\gamma }^t{r}_{t+k}\left|s_t=s\right.\right\}(6)$

In which, $\pi$ shows the used policy. $s$ shows state. The RL method is characterized by estimating the same function, which represents a specific action’s $\left(a\right)$ value at a particular state. The function has the following definition Eq (7):

$Q^{\pi }\left(s,a\right)=E_{\pi }\left\{{\displaystyle \sum _{k=0}^{\infty }}{\gamma }^t{r}_{t+k}\left|s_t=s,\right.a_t=s\right\}(7)$

RL aims at maximizing (optimizing) the value function by selecting the optimal policy ${\pi }^{*}$. This optimum value function can be represented by ${V^{\pi }}^{*}$, and it has greater or equal state values than all other value functions resulting from policies other compared to the optimum one. A representation of this is ${V^{\pi }}^{*}\left(s\right)\ge V^{\pi }\left(s\right),\forall \pi ,\forall s$. The optimum action value function is expressed as ${Q^{\pi }}^{*}\left(s,a\right)\ge Q^{\pi }\left(s,a\right),\forall \pi ,\forall \left(s,a\right)$. Having found the optimum action value function, the policy should:

${\pi }^{*}\left(s\right)=\mathit{arg}\underset{a}{\max }{Q^{\pi }}^{*}\left(s,a\right)(8)$

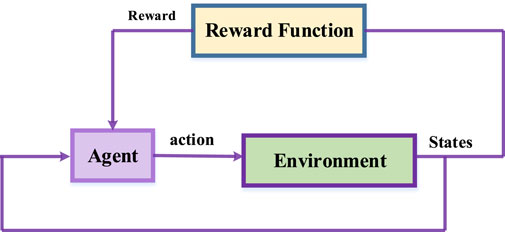
Based on the answer of the question “how to find the optimal value function,” RL algorithm type is determined. Sometimes, training is used to find the optimum policy. The training procedure for RL is illustrated in Figure 2. As shown, the agents observe the state and perform actions accordingly. As a result, the environment changes and new states are created. A reward signal has been generated when the reward function evaluates the new states. This signal is used by the agent for updating the policy as it is being trained, and the new action is taken in the next cycle. The paper introduces a fundamental RL algorithm, Q-learning, and later presents two other RL techniques used in the game-theoretic model structure.

Figure 2

Figure 2. RL procedure.

3.2.1 Q-learning

Q-learning plays an important part in RL (Banik et al., 2021). By utilizing the update rule, Q-learning realizes incremental estimations of the optimum action-value function in the following Eq (9):

$Q_{k+1}\left(s_t,a_t\right)=Q_k\left(s_t,a_t\right)+\alpha \left(r_t+\gamma \underset{a}{\max }{Q}_k\left(s_{t+1},a_t\right)-Q_k\left(s_t,a_t\right)\right)(9)$

In which, $\alpha$ shows the step size. $\gamma$ shows the forgetting factor. While training, Q-learning does not consider the policy employed by the agent for exploring the environment, requiring the agent to move from one state to another. Off-policy techniques refer to RL algorithms in which exploration and value function updates (or policy updates) exist independently. As long as all state-action pairs $\left(s,a\right)$ are observed in training, and as the number of observations approaches infinity, then the learned action value function Q will converge to the optimum action-value function $Q^{*}$ at a probability of 1. A variant of stochastic approximation conditions denoted with ${\displaystyle \sum _{k=1}^{\infty }}\alpha k=\infty ,{\displaystyle \sum _{k=1}^{\infty }}{\alpha }_k^2\le \infty$, guarantees convergence of the step size parameter. When the step size parameter is fixed, convergence occurs in the mean when $0\le \alpha \le 1$. In general, when there is no model for the environment, constantly observing the state-action pairs becomes critical for algorithms designed to reach convergence to the optimum solution (Arulkumaran et al., 2017). Future rewards are valued based on the discount factor $\gamma$. A zero $\gamma$ agent, for example, maximizes solely the immediate rewards. A value of 1 indicates that the agent is becoming more farsighted.

Algorithm 1.NFQ algorithm.

1) Set k equal to zero

2) Initialize the NN

3) While k < N do

4)  Produce experience set $\mathrm{G}=\{\left(\text{inpu}{\mathrm{t}}^{\mathrm{i}},\text{targe}{\mathrm{t}}^{\mathrm{i}}\right)$, $\left.i=1,2,\dots ,\#E\right\}$ in which

5)   $inpu{t}^i=s^i,a^i,$ in which $s^i$ defines the state, and also $a^i$ defines the action of $i^{th}$ experience

6)   $targe{t}^i=r^i+\gamma {\min }_{\mathrm{a}}{Q}_k\left({s^{\prime }}^i,a\right)$, in which $r^i$ defines the transition cost and $\gamma {\min }_{\mathrm{a}}{Q}_k\left({s^{\prime }}^i,a\right)$

    defines the weight expected maximum path reward for the next state ${s^{\prime }}^i$

7) Compute the batch error as ${\displaystyle \sum _{i=1}^n}{\left(Q^k\left(s_i,a_i\right)-targe{t}^i\right)}^2$, in which $n$ is referred to the experience set volume

8) Train the network in order to minimize the error of patch, applying resilient back-propagation and retrieved $Q_{k+1}$

9) $k=k+1$

10)  End while

3.2.2 Neural fitted Q-learning

Many RL approaches estimate Q values rather than maintaining a table of Q values. In large state spaces, the method can be particularly helpful. Due to their universal approximation property, neural networks (NN) offer the best tools for storing Q-values compactly. As opposed to the traditional Q-learning approach described earlier, a state-action value is not kept in a table, but rather calculated using a function derived from the NN framework: The approximate Q-value is calculated from the NN output by feeding a state-action pair as input to it. In order to train the NN, first define an error function representing the difference between the present and desired Q-values, and later minimize the function by backpropagation. In spite of the fact that the NN can be useful for determining the Q-values, failure is possible, either entirely or by involving impractical convergence times, as a result of global representation (Fisher et al., 2020): in the training procedure, NN weights update as every state-action pair is introduced, as well as affecting other pairs’ Q-values. Other training gains may be nullified as a result. In contrast, the global representation increases the generalization power of NNs because it assigns the same Q-value to similar state-action pairs, thereby removing the necessity of training NNs for all feasible pairs. It is consequently necessary to devise a strategy for exploiting and eliminating the property.

Fisher et al. (2020) proposes neural fitted Q-learning that combines the generalization power of NNs with its potential downside effects that store old experiences in the form of 3-tuples $\left(s,a,s\right),$ where s shows the initial state, $a$ shows the action performed, and $s$ shows the state attained, and reuse them after an update occurs when new information is added. In Algorithm 1, the NFQ approach has been presented for a set of experiences denoted by E. To implement NFQ learning, greedy search, accessible Q-values, and random exploration should be combined rather than just collecting experiences at random.

3.2.3 Jaakkola RL

When training by RL, an agent utilizes data from the environment. The “state” of the environment is usually referred to as the data. The Markov property refers to a state containing all related data regarding how the agent and environment have interacted in the past and in the present (Szepesvári, 2022). Markov Decision Processes (MDPs) are learning tasks that involve interactions with Markov-property environments. In particular, by expressing the probability of moving from state “s” to state “$s^{\prime }$” and receiving a reward “r”, for an action “a” as $P\left(s^{\prime },r|s,a\right)$, when the probability is dependent on “s” and “a” independently of previous actions and states. MDPs are assumed to be the basis of most RL techniques with guarantees of convergence. Though the fundamental dynamics in the study are MDPs, just a few states can be observed by the agents in the aerospace and automotive applications. As a result, in the agent’s perspective, the tasks consist of Partially Observable Markov Decision Processes (POMDP). A RL algorithm such as the Jaakkola algorithm (Jaakkola et al., 1994) was designed especially for models of POMDP systems, thus making it an appropriate approach for the study’s learning tasks. As well as the Q-function, Jaakkola algorithm likewise uses the value function, V. In every state-action pair, Q values equal 0 at the start. Furthermore, a uniform probability distribution is used for every state. As a result, for every iteration $\left(s,a,s^{\prime }\right)$, Q and V values change as follows as the following Eq (10):

$\begin{array}{c}{\beta }_t\left(s,a\right)=\left(1-\frac{{\chi }_t\left(s,a\right)}{K_t\left(s,a\right)}\right){\gamma }_t{\beta }_{t-1}\left(s,a\right)+\frac{{\chi }_t\left(s,a\right)}{K_t\left(s,a\right)}\\ {\beta }_t\left(s\right)=\left(1-\frac{{\chi }_t\left(s\right)}{K_t\left(s\right)}\right){\gamma }_t{\beta }_{t-1}\left(s\right)+\frac{{\chi }_t\left(s\right)}{K_t\left(s\right)}\\ \begin{array}{c}{Q}_t\left(s,a\right)=\left(1-\frac{{\chi }_t\left(s,a\right)}{K_t\left(s,a\right)}\right)Q_{t-1}\left(s,a\right)+{\beta }_t\left(s,a\right)\left(R_t-R\right)\\ V_t\left(s\right)=\left(1-\frac{{\chi }_t\left(s\right)}{K_t\left(s\right)}\right)V_{t-1}\left(s\right)+{\beta }_t\left(s\right)\left(R_t-R\right)\end{array}\end{array}(10)$

In which, $s$ shows the state. $a$ shows the action. t shows the time step. In addition, ${\chi }_t\left(s,a\right)\left({\chi }_t\left(s\right)\right)$ equals one when the certain state-action pair (state) has been observed, else, 0. $K_t\left(m,a\right)\left(K_t\left(s\right)\right)$ shows the number of times the state-action pair (state) has been observed. $R_t$ shows the reward in time step t. R shows average reward. ${\gamma }_t$ shows the discount factor. When Q and V functions are calculated, Jaakkola algorithm would update its trained policy $\pi \left(a|s\right)$ with the update rule in the following Eq (11).

$\pi \left(a|s\right)=\left(1-ϵ\right)\pi \left(a|s\right)+ϵ{\pi }^1\left(a|s\right)(11)$

In which, $ϵ$ shows the update rate. ${\pi }^1\left(a|s\right)$, the policy that the trained policy has been altered towards, shows a greedy-policy according to the computed $Q\left(s,a\right)$. Therefore, ${\pi }^1\left(a|s\right)=1$ when the action “a” would have the maximum Q-value in a certain state “s”. If the condition is met, the average reward will increase with the policy update (Jaakkola et al., 1994) in the following Eq (12).

$\underset{a}{\max }\left[Q\right.\left(s,a\right)\left.-V\left(s\right)\right]>0(12)$

As long as condition (8) is not true, the average reward would increase until the local optimum is reached.

There are 2 hyper-parameters in the Jaakkola algorithm: the update rate and the discount factor. It is important to choose as a number between 0 and 1 at the beginning and to schedule it so that it would converge to one at the boundary in order to ensure that convergence is guaranteed. In contrast, must meet.

4 Simulation outcomes

In the following simulation and discussions, we assume a simplified power distribution network that support distributed generation installment with possible false data injection and cyber-attack changing variables that are described by a zero-sum attacker-defender game. As a result of space restrictions and interest in modeling different attacking issues, just level-1 defenders versus level-0 attackers were considered by using similar analogy and setup of Kiennert et al. (2018) in the cyber physical system of power distribution network. Frost et al. (2022) used the level-0 attacker policy. It is assumed that this level-0 attacker has knowledge regarding interacted smart grids systems and has an advanced attack method despite being level-0.

4.1 Level-0 attacker

The level-0 attacker moves 1 step time to higher $q_3$ when $V_2<1$ and lower $q_3$ when $V_2>1$. It is a bit random choosing $V_2$ for the drift direction, but this is just the behavior of a level-0 attacker. The movement in $q_3$ results in a movement in $Q_1$ and, if the defender does not compensate, a movement in $V_2$. A level-1 defender which is unable to detect an attacker compensates by setting $V_1$ oppositely as $V_2$ for keeping the average of $V_2$ and $V_3$ near 1.0. Continuing this slow movement, the level-0 attacker forces the unaware level-1 defender for ratcheting $V_1$ close to $v_{\mathit{min}}$ or $v_{\mathit{max}}$. As a result of understanding the power flow formula and the physical status via observing the fully transparent voltage and current information, the level-0 attacker shows the time of “strike,” i.e., an abrupt alteration of $q_3$ against movement pushes $V_2$ beyond $\left[1-\epsilon ,1+\epsilon \right]$. The level-0 attacker policy is described in the following way:

In which, ${\theta }_A$ shows a threshold parameter triggering the strike. During the study, ${\theta }_A=0.07>ϵ$ is employed for indicating the timing of attacker strikes that accumulate rewards.

4.2 Level-1 defender—level-0 attacker dynamics

A simulation and modeling procedure are demonstrated in 2 scenarios. According to the 1st scenario, a level-1 defender would optimize his policy versus a level-0 attacker 50 percent of the time, i.e., $p=0.5$ in the node “A exist” in Figure 3. According to the 2nd scenario, the level-1 defender would optimize his policy versus a “normal” system, i.e., $p=0$ in “A exist.” The repeated SNFG in the figure is composed of 3 independent SNFGs that are “glued” to each other within the semi Bayes nodes. Both level-1 defenders do not differ significantly in the 1st half of the simulations, i.e., $p=0$. A level-0 attacker having $p=1$ would be presented during time step 50. Accordingly, level-1 defenders with $p=0$ are vulnerable to “drift-and-strike” attacks. A level-1 defender having a policy with $p=0.5$, on the other hand, maintains somewhat stable $V_1$ even following 50 time steps. There are times when $V_3$ does not meet desired limits, but less than previously, and $V_2$ never does.

Figure 3

Figure 3. The repeated semi net-form game (SNFG) applied for modeling attackers and defenders/operators in a CPS.

4.3 Policy dependence on within defender training

The following section presents some initial research into the tradeoffs involved in attacker-defender game design. Despite the fact that policy optimization and policy assessment in reinforcement learning are closely connected, they are two separate methods. A constant set of parameters is used in training, including attacker presence probability p and the game parameters $p_{2,\mathit{max}}$ and $p_{3,\mathit{max}}$. The policy evolves through a number of training runs until it reaches a constant reward at each time step. It is then possible to evaluate the converged policy versus the conditions trained for, as well as for conditions other than those for which it was trained.

There are seven possible values of $p$, distributed logarithmically between 0.01 to 1.0. If individual learnt policies in different reinforcement learning algorithm are optimized versus level-0 attackers at probability $p$, a set of 7 level-1 defenders can be generated. After that, the defenders will be simulated 7 times, versus the similar level-0 attacker with a similar range of p similar to the training process. Here, $p_{2,\mathit{max}}=1.4$ and $p_{3,\mathit{max}}=1$. Measurement of level-1 defender efficiency at each time step is calculated in simulation, in other words, ${\displaystyle \sum _{i=1}^N}{R}_D^i/N_p$, and normalized by the $p$ in the simulation. Figure 4 shows the outcomes.

Figure 4

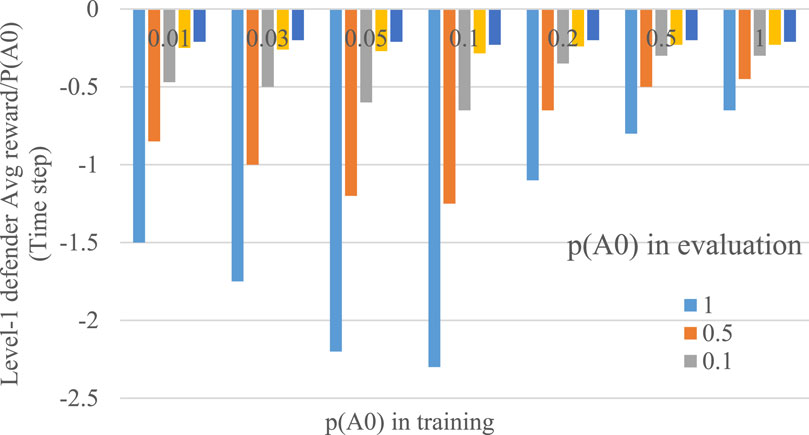
Figure 4. Level-1 defender reward at each time step of level-0 attacker presence in simulation $\left({\displaystyle \sum _{i=1}^N}{R}_D^i/N_p\right)$ versus the probability of attacker which are in training.

When a sufficient number of Monte Carlo examples is possible, and p is small in the policy optimization process (that is, training), the majority of system states $S$ rarely or never are observed, especially those involving an attacker. Policy optimization outcomes are unreliable since RL algorithms fail to estimate Q values accurately either for Q-learning or Jaakkola learning algorithm. As a result, the state-action policy mapping is replaced with the level-0 defender policy. The level-1 defenders trained with $p<0.1$ continue to function ineffectively. The level-1 defender efficiency improves as a result of sufficient states being observed sufficiently in $p\ge 0.2$. The rest of the study uses $p=0.2$ as the level-1 defender training threshold.

4.4 Design procedure and social welfare (SW)

When $V_2$ or $V_3$ are significantly deviated from 1.0 p.u., it can result in damage to devices or decreased efficiency as a result of malfunctioning computers or computer-related industrial controllers (Regula et al., 2016). A distributed generation attack at each single node can increase the probability of these voltage deviations. Additionally, the generator feeds energy into the grid, resulting in a benefit to society. Larger generators (higher $p_{3,\mathit{max}}$) contribute a greater amount of power and are generally beneficial to society. Large generators, though, may cause large voltage deviations and substantial financial damage if they are damaged.

In order to assess energy costs versus productivity loss, dollars are used as a measurement. Electricity’s SW is reasonably predicted since its value, despite being unpredictable both in time and place, is estimated with a fairly precise average value. A flat-rate customer cost approximates electric energy’s value. With highly regulated markets, energy prices are prone to distortion, and they may not accurately reflect the true power cost. Although cost provides an accurate estimate of monetary value in the model, market distortions due to cyber attacking might need to be adjusted for each case. This study involves virtually installing a generator at one single node of a distribution network and estimating its energy value in $C_E=\$80/MW-hr$. According to Nelson and Lankutis (2016), users with greater sensitivity dominate the price, which is likewise affected by grid position and time - these customers’ locations and their usage patterns determine the price. $C_{PQ}=\$300$/sensitive consumer/per power quality event is an estimate of the average price of a power quality event.

4.4.1 Level-1 defender efficiency versus ${\mathrm{p}}_{2,\max },{\mathrm{p}}_{3,\max }$

By refreshing the attacker-defender game in Figure 3, it shows an iterated SNFG whose output node “A exist” would fix the likelihood of the attacker being present for the remainder of the N steps in the Q-learning process, making the outcomes of all episode simulations independent from one another. The average reward of the level-1 defender for being subjected to attack 100% of the time $\left(p=1\right)$ and 0% of the time $\left(p=0\right)$, is determinable for all intermediate values of $p$. This is the basis for the following discussion. Based on Figure 4, level-1 defenders trained versus level-0 attackers (with $p=0.2$) for an array of ${\mathit{p}}_{2,\mathit{max}},{\mathit{p}}_{3,\mathit{max}}$) restrictions. Following that, the level-1 defenders are simulated using $p=1$ and $p=0$ for calculating their average reward. Figure 5 shows the outcomes of $\left(p_{2,\mathit{max}},p_{3,\mathit{max}}\right)$ restrictions with $p=0.01$. There are 2 critical thresholds where the average reward of the level-1 defenders drops sharply, that is, at $p_{3,\mathit{max}}>1.5$ and at $p_{2,\mathit{max}}>1.9$. Subsequent analysis focuses on the area $p_{3,\mathit{max}}<1.5$ prior to the sharp decline in the average reward.

Figure 5

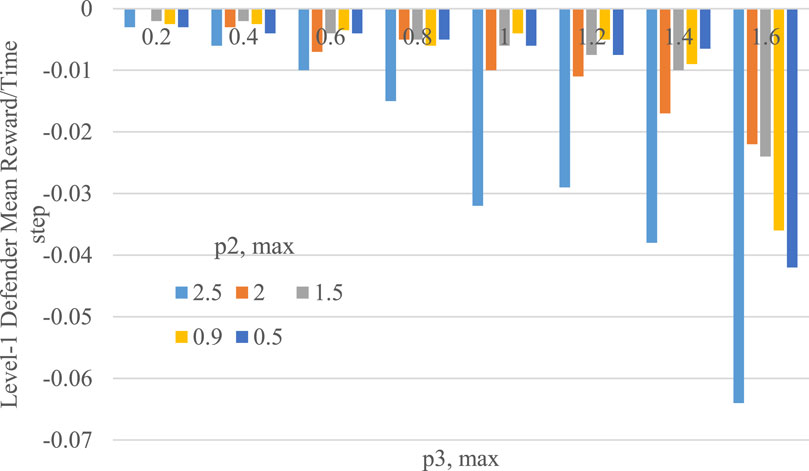
Figure 5. The level-1 defender’s mean reward entire simulation time steps as a function of $p_{3,\mathit{max}}$ for a 1% likelihood of an attack on one single node. Each curve defines a different amount of $p_{2,\mathit{max}}$ amongst [0.2∼2.5].

4.4.2 Level-1 defender ${\mathrm{p}}_{3,\max }$ sensitivity

A SW surface plot can be generated from the power quality and energy price estimations in Figure 5. Nonetheless, the variety of variables can result in a multidimensional set of graphic plots that would make interpreting the outcomes challenging. As a result, reducing the dimensionality and generating results with a stronger sense of imagination would be the goal. In general, level-1 defenders’ rewards decrease linearly using $p_{3,\mathit{max}}$ with $p_{3,\mathit{max}}<1.5$. This is the slope of the curve that represents the level-1 defenders’ average reward versus $p_{3,\mathit{max}}$, and Figure 6 shows these sensitivities against $p_{2,\mathit{max}}$.

Figure 6

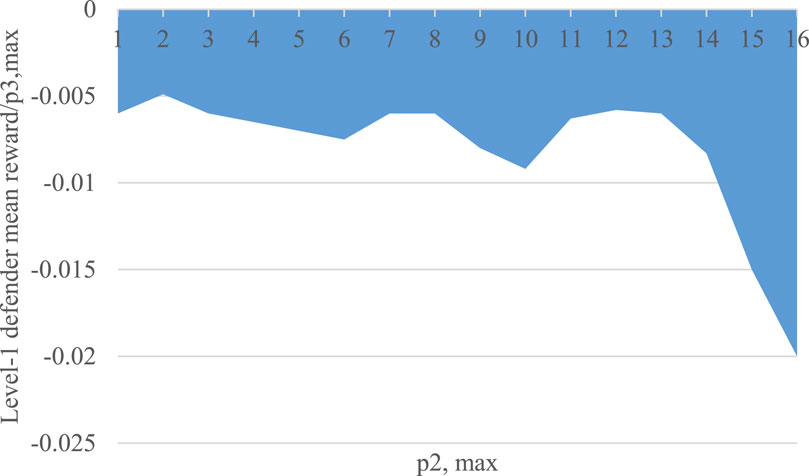
Figure 6. The slope of the datum in Figure 5 with $p_{3,\mathit{max}}\le 1.5$.

A more detailed analysis of Figure 6 requires relating defenders’ average rewards to power quality events, and later converting those costs into SW costs with $C_{PQ}$. The reward $R_D$ of a defender is expressed by Eq. 4 by adding 2 smooth functions (from $V_2$ and $V_3$). Each individual contribution equals one if $V_2$ or $V_3$ equals $1+ϵ$ or $1-ϵ$. In spite of the fact that the deviations do not seem serious, it can be deemed a power quality event, and the SW price can be estimated with $R_D{C}_{PQ}$. As voltage deviations increase (decrease), $R_D$ rises (falls), and correspondingly, SW costs rise (fall) as deviations increase (decrease). The slope of $\sim 0.006$/(MW of $p_{3,\mathit{max}}$) in Figure 6 indicates a SW price of $108/(MW of $p_{3,\mathit{max}}$)/hr with a $C_{PQ}=\$300$/sensitive consumer/per power quality event based on Regula et al. (2016) and social welfare increasement of protection of power system operation, with 1 min simulation time steps, and with 1 sensitive consumer on the distribution network. The social welfare monetary value of the energy of $80/MW-hr exceeds the SW price resulting from reduced power quality under $C_{PG}$. Figure 7 shows the break-even power quality price against $p_{2,\mathit{max}}$. Positive SW is contributed by points of $C_{PQ}$ and $p_{2,\mathit{max}}$ to the left of the curve, while negative welfare is contributed by those to the right.

Figure 7

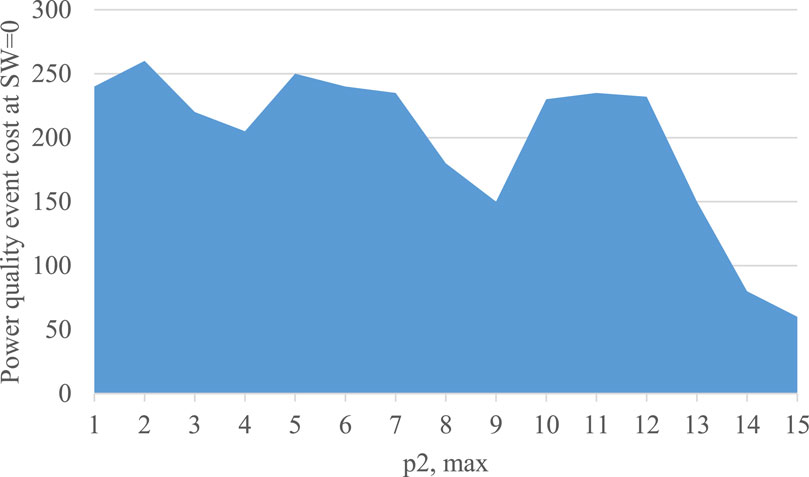
Figure 7. The price of a power quality event yielding a 0 SW contribution at one single node versus $p_{2,\mathit{max}}$.

5 Conclusion

This paper proposes a new game-theoretic framework of human-human cyber-attack interaction with reinforcement learning technology, which aims to prevent intruders from maliciously interacting with SCADA operators. Using the proposed model and method, an adversarial interaction’s result is estimated, and their social welfare gains is estimated accordingly. As a summary, there are numerous interesting features of modeled interactions that can be found in the studied framework. Firstly, there is an asymmetric interaction since the SCADA operator cannot be confident whether the attacker is available, and rather employs an easy statistical analysis of memory as a means of determining the presence of the attacker. Secondly, a considerable amount of automation mediated the interaction, and the outcomes of the suggested scheme or relevant schemes are used to design this automation in a way that maximizes the social welfare increasement caused by the reasonable protection of the smart grid environment. In the future work, it is possible to extend and improve the schemes presented here in a variety of manners. There are several benefits to expanding the scheme to include larger, more accurate grid models, including transmission grids and feeder-level distribution network, in which meshed systems have a greater complicated impact. In contrast to the setting up of this paper, complex power grid model will support several points for cyber intruders to conduct attacks, and defenders have more sophisticated reward functions and memories by using more advanced reinforcement learning solution methods.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YC: Conceptualization, Data curation, Investigation, Software, Writing–original draft, Writing–review and editing. CT: Data curation, Formal Analysis, Methodology, Software, Validation, Writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arulkumaran, K., Deisenroth, M. P., Brundage, M., and Bharath, A. A. (2017). Deep reinforcement learning: a brief survey. IEEE Signal Process. Mag. 34 (6), 26–38. doi:10.1109/msp.2017.2743240

CrossRef Full Text | Google Scholar

Banik, S., Loeffler, T. D., Batra, R., Singh, H., Cherukara, M. J., and Sankaranarayanan, S. K. (2021). Learning with delayed rewards—a case study on inverse defect design in 2D materials. ACS Appl. Mater. Interfaces 13 (30), 36455–36464. doi:10.1021/acsami.1c07545

PubMed Abstract | CrossRef Full Text | Google Scholar

Butt, O. M., Zulqarnain, M., and Butt, T. M. (2021). Recent advancement in smart grid technology: future prospects in the electrical power network. Ain Shams Eng. J. 12 (1), 687–695. doi:10.1016/j.asej.2020.05.004

CrossRef Full Text | Google Scholar

Camerer, C. F., Nave, G., and Smith, A. (2019). Dynamic unstructured bargaining with private information: theory, experiment, and outcome prediction via machine learning. Manag. Sci. 65 (4), 1867–1890. doi:10.1287/mnsc.2017.2965

CrossRef Full Text | Google Scholar

Chang, Q., Ma, X., Chen, M., Gao, X., and Dehghani, M. (2021). A deep learning based secured energy management framework within a smart island. Sustain. Cities Soc. 70, 102938. doi:10.1016/j.scs.2021.102938

CrossRef Full Text | Google Scholar

De Neys, W. (2023). Advancing theorizing about fast-and-slow thinking. Behav. Brain Sci. 46, e111. doi:10.1017/s0140525x2200142x

CrossRef Full Text | Google Scholar

Ezhei, M., and Ladani, B. T. (2017). Information sharing vs. privacy: a game theoretic analysis. Expert Syst. Appl. 88, 327–337. doi:10.1016/j.eswa.2017.06.042

CrossRef Full Text | Google Scholar

Fisher, A., Mago, V., and Latimer, E. (2020). Simulating the evolution of homeless populations in Canada using modified deep q-learning (mdql) and modified neural fitted q-iteration (mnfq) algorithms. IEEE Access 8, 92954–92968. doi:10.1109/access.2020.2994519

CrossRef Full Text | Google Scholar

Frost, J., Watkins, O., Weiner, E., Abbeel, P., Darrell, T., Plummer, B., et al. (2022). Explaining reinforcement learning policies through counterfactual trajectories. arXiv Prepr. arXiv:2201.12462.

Google Scholar

Gao, Y. (2022). A reflection on postwar neoclassical economics: the shift from general equilibrium theory to the new microeconomic theories. Mod. China 48 (1), 29–52. doi:10.1177/00977004211054844

CrossRef Full Text | Google Scholar

Ghiasi, M., Wang, Z., Niknam, T., Dehghani, M., and Ansari, H. R. (2023) “Cyber-physical security in smart power systems from a resilience perspective: concepts and possible solutions,” in Cyber-physical security in smart power systems from a resilience perspective: concepts and possible solutions, 9. Cham: Springer International Publishing, 67–89. doi:10.1007/978-3-031-20360-2_3

CrossRef Full Text | Google Scholar

Hough, A., and Juvina, I. (2022). Understanding and modeling coordination in the minimum effort game. InProceedings Annu. Meet. Cognitive Sci. Soc. 44 (44).

Google Scholar

Jaakkola, T., Singh, S., and Jordan, M. (1994). Reinforcement learning algorithm for partially observable Markov decision problems. Adv. neural Inf. Process. Syst. 7.

Google Scholar

Jiang, K., You, D., Merrill, R., and Li, Z. (2019). Implementation of a multi-agent environmental regulation strategy under Chinese fiscal decentralization: an evolutionary game theoretical approach. J. Clean. Prod. 214, 902–915. doi:10.1016/j.jclepro.2018.12.252

CrossRef Full Text | Google Scholar

Jin, Y. (2021). Does level-k behavior imply level-k thinking? Exp. Econ. 24 (1), 330–353. doi:10.1007/s10683-020-09656-w

CrossRef Full Text | Google Scholar

Kiennert, C., Ismail, Z., Debar, H., and Leneutre, J. (2018). A survey on game-theoretic approaches for intrusion detection and response optimization. ACM Comput. Surv. (CSUR) 51 (5), 1–31. doi:10.1145/3232848

CrossRef Full Text | Google Scholar

Kirschen, D., and Bouffard, F. (2008). Keeping the lights on and the information flowing. IEEE Power Energy Mag. 7 (1), 50–60. doi:10.1109/mpe.2008.930656

CrossRef Full Text | Google Scholar

Liu, J., Zhang, W., Ma, T., Tang, Z., Xie, Y., Gui, W., et al. (2020). Toward security monitoring of industrial cyber-physical systems via hierarchically distributed intrusion detection. Expert Syst. Appl. 158, 113578. doi:10.1016/j.eswa.2020.113578

CrossRef Full Text | Google Scholar

Liu, W., Chen, Y., Wang, L., Liu, N., Xu, H., and Liu, Z. (2019). An integrated planning approach for distributed generation interconnection in cyber physical active distribution systems. IEEE Trans. Smart Grid 11 (1), 541–554. doi:10.1109/tsg.2019.2925254

CrossRef Full Text | Google Scholar

Nelson, J. P., and Lankutis, J. D. (2016). Putting a price on power interruptions: how utilities and customers can share interruption costs. IEEE Ind. Appl. Mag. 22 (4), 30–40. doi:10.1109/mias.2015.2459107

CrossRef Full Text | Google Scholar

Paul, S., Makkar, T., and Chandrasekaran, K. “Extended game theoretic dirichlet based collaborative intrusion detection systems. InComputational intelligence, cyber security and computational models,” in Proceedings of ICC3 2015 2016. Singapore: Springer, 335–348.

Google Scholar

Ponce-Jara, M. A., Ruiz, E., Gil, R., Sancristóbal, E., Pérez-Molina, C., and Castro, M. (2017). Smart Grid: assessment of the past and present in developed and developing countries. Energy strategy Rev. 18, 38–52. doi:10.1016/j.esr.2017.09.011

CrossRef Full Text | Google Scholar

Rajasekaran, A. S., Azees, M., and Al-Turjman, F. (2023). A comprehensive survey on security issues in vehicle-to-grid networks. J. Control Decis. 10 (2), 150–159. doi:10.1080/23307706.2021.2021113

CrossRef Full Text | Google Scholar

Regula, M., Otcenasova, A., Roch, M., Bodnar, R., and Repak, M. (2016). “SCADA system with power quality monitoring in Smart Grid model,” in 2016 IEEE 16th international conference on environment and electrical engineering (EEEIC) (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Salkuti, S. R. (2021). Optimal location and sizing of shunt capacitors with distributed generation in distribution systems. ECTI Trans. Electr. Eng. Electron. Commun. 19 (1), 34–42. doi:10.37936/ecti-eec.2021191.222295

CrossRef Full Text | Google Scholar

Szepesvári, C. (2022). Algorithms for reinforcement learning. Springer Nature.

Google Scholar

Wang, Z., Li, C., Jin, X., Ding, H., Cui, G., and Yu, L. (2021). Evolutionary dynamics of the interdependent security games on complex network. Appl. Math. Comput. 399, 126051. doi:10.1016/j.amc.2021.126051

CrossRef Full Text | Google Scholar

Wolpert, D., and Bono, J. (2013). Distribution-valued solution concepts. Available at SSRN 1622463 April 2, 2013).

Google Scholar

Wu, C., Yao, W., Pan, W., Sun, G., Liu, J., and Wu, L. (2021). Secure control for cyber-physical systems under malicious attacks. IEEE Trans. Control Netw. Syst. 9 (2), 775–788. doi:10.1109/tcns.2021.3094782

CrossRef Full Text | Google Scholar

Zhang, C. L., Yang, G. H., and Lu, A. Y. (2021). Resilient observer-based control for cyber-physical systems under denial-of-service attacks. Inf. Sci. 545, 102–117. doi:10.1016/j.ins.2020.07.070

CrossRef Full Text | Google Scholar

Zhang, K., Shi, Y., Karnouskos, S., Sauter, T., Fang, H., and Colombo, A. W. (2022). Advancements in industrial cyber-physical systems: an overview and perspectives. IEEE Trans. Industrial Inf. 19, 716–729. doi:10.1109/tii.2022.3199481

CrossRef Full Text | Google Scholar