CPS-based power tracking control for distributed energy storage aggregator in demand-side management

The deployment of distributed energy storage on the demand side has significantly enhanced the flexibility of power systems. However, effectively controlling these large-scale and geographically dispersed energy storage devices remains a major challenge in demand-side management. In this paper, we propose a CPS-based framework for controlling a distributed energy storage aggregator (DESA) in demand-side management. Within this framework, a distributed power tracking control algorithm is designed to ensure both power tracking and state-of-charge (SoC) balancing among the energy storage units (ESUs) within the DESA. The proposed algorithm utilizes a distributed observation-based approach that relies solely on local communication. It is demonstrated that the algorithm achieves power tracking convergence within a fixed time, while asymptotically achieving SoC balancing when assuming a connected communication network among the storage units. To validate the theoretical analysis and demonstrate the effectiveness of the proposed control strategy, an example scenario comprising six ESUs is presented.

1 Introduction

The rapid growth of renewable energy generation (REG) has yielded significant benefits in terms of reducing carbon emissions and promoting sustainable energy development (Bull, 2001). However, REG presents greater volatility and intermittency compared to traditional power generation sources like thermal and gas-fired power, which poses significant challenges to the safe, stable, and economically efficient operation of power systems.

In the traditional power system, real-time power balance between power generation and consumption is primarily achieved through adjustments in the output of generating units, such as primary and secondary frequency control of thermal power units (Dörfler et al., 2015). These generating units need to reserve spare capacity as a regulating capability. As the proportion of REG continues to rise, the required reserve capacity for the power system also increases rapidly, leading to elevated operating costs. Additionally, the decreasing proportion of traditional generating units further reduces the system’s reserve capacity. Therefore, it is crucial to explore new sources of flexibility and resilience in the power system, such as energy storage (Jafari et al., 2022), demand response (Pinson et al., 2014), and advanced grid management technologies (Wei et al., 2023).

Energy storage plays a pivotal role in the power system by absorbing excess energy during periods of surplus supply and releasing stored energy to meet peak power demand (Wang et al., 2023). With the declining manufacturing and operating costs of energy storage, it is becoming an increasingly important resource for regulating future power systems. Consequently, energy storage has garnered significant attention in recent years (Li and Wang, 2019; Sun et al., 2019).

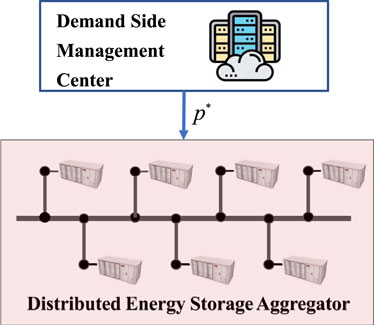
While centralized energy storage power stations are effective for grid regulation (Wang et al., 2022), their construction is often limited by safety and space constraints. To overcome these limitations, a distributed energy storage aggregator (DESA) can be formed by connecting multiple small-capacity energy storage units (ESUs) deployed in a decentralized manner on the demand side, facilitated by a communication network. Through the design of a distributed cooperation mechanism for the DESA, it can function as a unified entity, participating in the regulation of the power system (Lin et al., 2022). DESA can play a crucial role in participating in various power markets as a unified entity, encompassing the frequency regulation, energy, capacity, energy storage, and peak shaving markets (Xu et al., 2018; Lamp and Samano, 2022). DESA participates as a unified entity in various electricity markets or demand response programs, generating a total power profile through market bidding and clearing processes. The total power profile is, in fact, the desired power trajectory of DESA. To achieve maximum profits in these markets, DESA coordinates the charging and discharging of its ESUs, ensuring that the total power of DESA tracks the desired power trajectory. This coordination is a key technology for DESA’s effective participation in various power markets.

Given the large scale of DESA, a distributed control architecture is commonly employed (Kang et al., 2022; Zhao et al., 2022). Each ESU within DESA is equipped with communication and measurement devices, enabling the exchange of state information with neighboring nodes. By leveraging local measurements and exchanged information, each ESU can adjust its charging and discharging power, ultimately achieving the total desired trajectory. This approach facilitates effective coordination and control of ESUs, enabling DESA to participate in various grid regulation markets and maximize its profits.

The coordinated tracking process of the total desired trajectory also serves as the allocation process for regulation tasks among ESUs within DESA. The fundamental allocation criterion is to balance the SoC (Han et al., 2021) among ESUs. Balancing the SoC offers several benefits. Firstly, it improves the overall energy efficiency of the system by ensuring optimal utilization of each unit. Secondly, it reduces the risk of premature failure or degradation of individual units, thereby extending the lifespan of the entire storage system. Thirdly, it enhances the stability and reliability of the power grid by ensuring sufficient energy storage capacity to respond to sudden changes in demand or supply.

ESUs within DESA can exhibit variations in their operating characteristics, even if they have the same specifications, due to manufacturing process deviations and differences in operating conditions. These variations can directly impact the maintenance of SoC balancing among individual units. Consequently, the development of effective control strategies to ensure SoC balancing in DESA has become a crucial research topic in the field of energy storage systems.

In centralized energy storage stations, a centralized control method is commonly employed, requiring a central control center to monitor and manage the entire system (Wang et al., 2022). However, implementing a centralized algorithm in typical DESAs with a large number of ESUs and wide geographical dispersion incurs high communication costs and practical implementation challenges (Cao et al., 2008). On the other hand, the decentralized control method, which relies solely on local measurement information, eliminates the need for a central controller or communication between units. However, it suffers from drawbacks such as slow convergence speed and low accuracy (Zeng et al., 2022).

In contrast, distributed control (Guan et al., 2010; Liu et al., 2023) has emerged as a promising alternative for the management of DESAs, overcoming the weaknesses of both centralized and decentralized control methods. It is considered an important option for future distributed resource management in power grids (Hu et al., 2020; 2017). With the advancements in information technology and the advantages offered by distributed control methods in DESA management, distributed cooperative control has gained significant attention (Guo et al., 2017). However, some existing methods still rely on a small amount of global information, such as the average desired power and the average state information of the ESUs. For instance, a distributed SoC balancing algorithm based on an event-triggered mechanism is proposed in (Xing et al., 2019a) using these global information factors. Nevertheless, obtaining such global information for every ESU can be challenging.

To overcome the reliance on global information, a distributed observation algorithm is proposed in (Cai, 2020) to estimate the average desired power and average state of the ESUs. The observation values obtained through this algorithm gradually approach the true average power and state. A distributed robust economic dispatch strategy is developed in (Huang et al., 2022) to achieve the energy management of IESs in the presence of misbehaving units. In (Li et al., 2019), an event-triggered-based distributed algorithm with distributed execution, asynchronous communication, and independent calculation is proposed to solve the issues of cooperative energy management for multienergy systems formed by many energy bodies. A distributed SoC balance control approach is proposed in (Xing et al., 2019b), which is developed with event-triggered signal transmissions. However, achieving asymptotic convergence may not always be feasible in practical applications due to time constraints and the need for fast response times. Although designing event-triggered control method can significantly reduce communication between agents, it also fails to improve convergence speed. Therefore, it is necessary to develop control strategies that can ensure convergence within a finite time period. Two types of estimators are proposed in (Meng et al., 2021) to address the problem of distributed SoC balance control. One achieves asymptotic estimation and the other achieves finite time estimation. In (Ding et al., 2019), a distributed finite-time secondary control scheme is proposed for DESAs subject to denial-of-service attacks. These finite time method offer a faster convergence rate compared to the asymptotic method. However, it is important to note that the convergence rate of the finite-time method is not universally constant. It depends on the initial conditions of the DESA and certain designed control parameters. This variability in convergence rate can limit the applicability of the finite-time method in certain situations, where the system’s parameters may not be easily adjustable or predictable.

Motivated by the preceding discussion, this paper is dedicated to addressing the challenges of power tracking and SoC balancing in DESA through the implementation of a distributed control approach based on the CPS framework. To overcome the practical limitations of asymptotic convergence and finite-time convergence methods, as well as to alleviate the impact of the initial conditions on convergence time in DESA, we propose a distributed control method based on distributed observation with fixed-time convergence properties. This method achieves convergence within a fixed time, independent of the initial state, and solely reliant on the designed control parameters. By establishing a precise upper limit on the time required for DESA to achieve power tracking, it effectively mitigates the risks associated with convergence time uncertainty and is better suited for real-time control and rapid response requirements. By utilizing fixed time stability theory, we provide conditions for achieving fixed time power tracking and establish a relationship between convergence time and the control parameters. It is demonstrated that the power tracking convergence can achieve within a fixed time, while the SoC balancing is achieved asymptotically, if the communication network among the storage units is connected. Finally, an example consisting of six ESUs is presented to demonstrate the correctness of the theoretical analysis and the rapid convergence of the proposed control strategy. The main contributions of this paper can be summarized in two aspects.

1. Different from the asymptotic observers (Cai, 2020) and the finite time observers (Meng et al., 2021), two new fixed time observers based on distributed observation are proposed in this paper to achieve power tracking fixed time convergence. The convergence time is independent of the initial conditions of the DESA, which solely depends on the control strategy parameters.

2. The method proposed in this paper enables rapid tracking of total power within a fixed timeframe while ensuring asymptotic convergence for SoC balancing. This feature allows DESA to efficiently perform tasks assigned by the Load-Side Management Center, particularly in power tracking. The asymptotic convergence of SoC does not impede its practical usability. Thus, the power control strategy holds significant promise for enhancing load management effectiveness.

The structure of this paper is as follows: Section 2 provides the model and control objectives of the DESA. Section 3 presents a distributed observer-based control for DESA with fixed time convergence, including the design of fixed-time observers and a distributed control scheme. Finally, a simulation example is provided in Section 4 to verify the effectiveness and rapid convergence of the proposed method.

Notations: Let ${\lambda }_{\min }(A)$ and ${\lambda }_{\max }(A)$ represent the minimum and maximum eigenvalues of matrix $A$, respectively. The symbols $\mathbf{R}$, ${\mathbf{R}}_{+}$, ${\mathbf{R}}^N$, ${\mathbf{R}}^{N\times N}$ represent the sets of real numbers, non-negative real numbers, $N$-dimensional real number vectors, and $N\times N$ real number matrices, respectively. For $x\in \mathbf{R}$, the function ${\text{sig}}^{\varphi }(x)={\left|x\right|}^{\varphi }\text{sign}(x)$ is defined, φ is a constant, where $\text{sign}(\cdot )$ is defined as:

$\text{sign}\left(x\right)=\left\{\begin{array}{cc}-1,\hfill & \text{if\hspace{0.17em}}x<0,\hfill \\ 0,\hfill & \text{if\hspace{0.17em}}x=0,\hfill \\ 1,\hfill & \text{if\hspace{0.17em}}x>0.\hfill \end{array}\right.$

for a vector $\mathbf{x}={(x_1,x_2,\dots ,x_n)}^T$, the $p$-norm is given by:

${‖\mathbf{x}‖}_p={\left({\left|x_1\right|}^p+{\left|x_2\right|}^p+\cdots +{\left|x_n\right|}^p\right)}^{\frac{1}{p}},$

where $p$ is a positive real number. The infinity norm of $\mathbf{x}$ is defined as the maximum absolute value of its elements:

$\Vert \mathbf{x}{\Vert }_{\infty }=\underset{1\le i\le n}{\max }|x_i|.$

additionally, $x^p={(x_1^p,x_2^p,\dots ,x_n^p)}^T$, and ${\mathbf{1}}_N$ represents an $N$-dimensional column vector with all elements equal to 1.

2 Problem definition and modeling

2.1 CPS-based framework

This paper focuses on a DESA that comprises $N$ ESUs. In the context of demand-side management, the DESA functions as a unified entity that interacts with the power grid, as shown in Figure 1. The demand-side management center periodically sends control commands, denoted as $p^{*}$, to the DESA, typically at intervals of 1 h or 15 min. A fundamental challenge is to effectively coordinate the output of each ESU within the DESA to achieve the desired tracking of the total output power with respect to the reference command $p^{*}$.

Figure 1

Figure 1. The DESA in demand management.

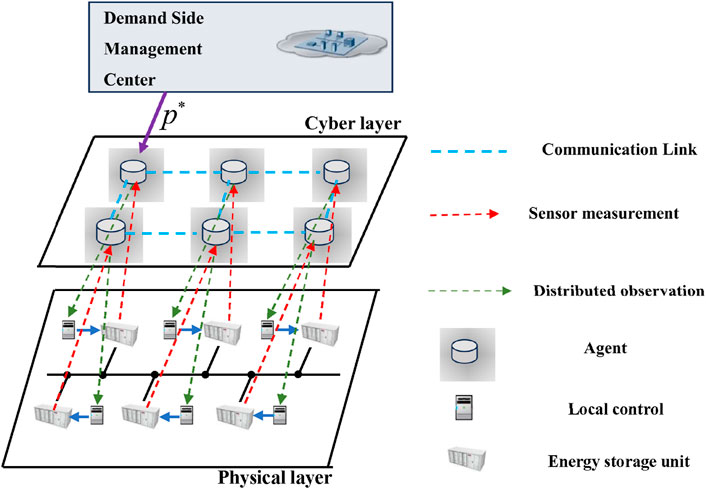
To address this challenge, we propose a distributed control framework for DESA based on the CPS architecture, illustrated in Figure 2. At the physical layer, the DESA consists of $N$ ESUs, each equipped with its own local controller. Meanwhile, at the cyber layer, $N$ agents represent the corresponding ESUs in the physical layer. These agents possess local communication and computation abilities within the cyber layer, enabling them to access operation data from neighboring agents and facilitate data interactions. This allows for the transfer of distributed observation signals to the ESUs’ local controllers, ultimately enabling control to be achieved.

Figure 2

Figure 2. CPS architecture.

Within the cyber layer, the proposed framework integrates a distributed observer. By implementing distributed observation, the proposed framework enables the achievement of shared control command $p^{*}$. Furthermore, this distributed observation mechanism facilitates accurate estimation of the overall SoC for the entire DESA.

At the physical layer, the local controllers leverage the information provided by the distributed observer to effectively regulate the corresponding ESUs. This ensures that each unit operates in accordance with the desired control objectives. Through the collaborative efforts of the cyber and physical layers, the proposed framework establishes a seamless coordination between the distributed observer, local controllers, and ESUs.

In our approach, we employ a graph to describe the communication network involving the interactions among agents. The nodes in the graph represent agents, and the edges denote the communication links in the cyber layer. Let $G=(\mathcal{N},\mathcal{E})$ be a graph, where $\mathcal{N}=\{\mathrm{1,2},\dots ,N\}$ and $\mathcal{E}\subseteq \mathcal{N}\times \mathcal{N}$ represent the sets of nodes and edges, respectively. The set ${\mathcal{N}}_i=\{j|(i,j)\in \mathcal{E}\}$ denotes the neighbor set of node $i$. The adjacency matrix associated with $G$ is denoted as $A=[a_{ij}]\in {\mathbf{R}}^{N\times N}$, where $i,j\in \mathcal{N}$. Specifically, $a_{ij}=a_{ji}=1$ if $(i,j)\in \mathcal{E}$; otherwise, $a_{ij}=a_{ji}=0$. The Laplacian matrix of $G$ is defined as $L=[L_{ij}]\in {\mathbf{R}}^{N\times N}$, where $i,j\in \mathcal{N}$. Specifically, $L_{ij}=-a_{ij}$ when $i\ne j$, and $L_{ii}={\sum }_{j=1,j\ne i}^N{a}_{ij}$. A graph $G$ is said to be connected if there exists a path of adjacent nodes between any two nodes. For more comprehensive information, please refer to (Ren and Beard, 2008). We assume that there exists at least one ESU capable of obtaining the desired power information $p^{*}$. For an ESU $i$, we define $b_i\in \{\mathrm{0,1}\}$, where $b_i$ takes the value of 1 if the ESU $i$ receives the desired power information $p^{*}$, and 0 otherwise.

2.2 Mathematical preliminaries

Connected graphs possess the following important property, which will be utilized in the subsequent analysis.

Lemma 1. (Liu et al., 2013) Let $G$ be a graph with Laplacian matrix $L\in {\mathbf{R}}^{N\times N}$, and let $B\in {\mathbf{R}}^{N\times N}$ be a diagonal matrix with non-negative diagonal entries and at least one positive diagonal entry. Then, the matrix $L+B$ is positive definite if $G$ is connected.

Lemma 2. Consider the nonlinear system

$\dot{g}\left(t\right)=f\left(g\left(t\right)\right),g\left(0\right)=g_0,$

where $g={[g_1,\dots ,g_N]}^T\in {\mathrm{R}}^N$, $f:{\mathrm{R}}^N\to {\mathrm{R}}^N$ is a continuous function on ${\mathrm{R}}^N$, and $f(0)=0$. Let $V:{\mathrm{R}}^N\to \mathrm{R}$ be a continuous positive definite function satisfying the inequality

$\dot{V}\left(g\right)\le -a{V}^b\left(g\right)-c{V}^d\left(g\right),$

where $a,c>0$, $b>1$, and $0<d<1$. Then, the origin of the nonlinear system is globally fixed-time stable, i.e., $g(t)=0$ for $t<T$, where the convergence time $T$ is bounded as follows

$T\le T_{\max }≔\frac{1}{a\left(b-1\right)}+\frac{1}{c\left(d-1\right)}.$

The subsequent three lemmas will also be used in the subsequent proofs.

Lemma 3. (Zuo et al., 2019) For any vector $x\in {\mathrm{R}}^{\ell }$, if $p>q>0$ are scalar constants, then the following inequality holds:

$\Vert x{\Vert }_p\le \Vert x{\Vert }_r\le {\ell }^{\frac{1}{r}-\frac{1}{p}}\Vert x{\Vert }_p.$

Lemma 4. (Zuo et al., 2019) For any non-negative numbers ${\xi }_1,{\xi }_2,\dots ,{\xi }_N$, the following inequalities hold:

${\displaystyle \sum _{i=1}^N}{\xi }_i^{\varpi }\ge {\left({\displaystyle \sum _{i=1}^N}{\xi }_i\right)}^{\varpi },0<\varpi <1,$

and

${\displaystyle \sum _{i=1}^N}{\xi }_i^{\varpi }\ge N^{1-\varpi }{\left({\displaystyle \sum _{i=1}^N}{\xi }_i\right)}^{\varpi },1<\varpi <\infty .$

Lemma 5. (Trefethen and Bau, 2022) Let A be a positive definite $n\times n$ matrix. Then there exists a unique lower triangular matrix $Q$ of size $n\times n$ such that $A=Q{Q}^T$, where the diagonal elements of $Q$ are all positive.

2.3 Mathematical model

ESU $i$ has a state of charge denoted by $So{C}_i(t)\in [\mathrm{0,1}]$ at time $t$, representing the ratio of its charge capacity to its maximum charge capacity. The evolution of $So{C}_i(t)$ over time can be characterized by the Coulomb counting method:

${SoC}_i\left(t\right)={SoC}_i\left(0\right)-\frac{1}{C_i}{\int }_0^t{I}_i\left(s\right)ds,i\in \mathcal{N},(1)$

where ${SoC}_i(0)$ represents the initial SoC of ESU $i$, $I_i(t)\in \mathbf{R}$ represents the current flowing through unit $i$ at time $t$, and $C_i\in {\mathbf{R}}^{+}$ represents the charge capacity of unit $i$. Differentiating both sides of Eq. 1 with respect to time $t$, we obtain:

${\dot{SoC}}_i\left(t\right)=-\frac{1}{C_i}{I}_i\left(t\right),i\in \mathcal{N}.(2)$

The output voltage of the ESU $i$ is denoted by $V_i(t)\in \mathbf{R}$ is assumed to be constant throughout the scheduling period, i.e., $V_i(t)=V_i$, where $V_i$ represents the constant output voltage of ESU $i$. This assumption is commonly adopted in many literature sources (Tan et al., 2012). Therefore, the charging or discharging power of the ESU $i$ is

$P_i\left(t\right)=V_i{I}_i\left(t\right),(3)$

where $P_i(t)\in \mathbf{R}$ denote the output power of the $i$th ESU. A negative value of $P_i(t)$ indicates that a charging state, while a positive value indicates a discharging state. Then, the evolution of SoC of $i$th ESU can be expressed as a function of the output power:

${\dot{SoC}}_i\left(t\right)=-\frac{1}{C_i{V}_i}{P}_i\left(t\right),i\in \mathcal{N}.(4)$

each ESU has its own maximum charging and discharging power, denoted as

$P_i^{\min }\le P_i\left(t\right)\le P_i^{\max },$

where $P_i^{\min }<0$ and $P_i^{\max }>0$ are the maximum discharging power and charging power of ESU $i$, respectively. Then, the maximum charging and discharging power of the DESA can be given as:

$P^{\min }={\displaystyle \sum _{i=1}^N}{P}_i^{\min },\text{and}{P}^{\max }={\displaystyle \sum _{i=1}^N}{P}_i^{\max }.$

then, the total output power of the DESA is

$P\left(t\right)={\displaystyle \sum _{i=1}^N}{P}_i\left(t\right),$

which should bounded by

$P^{\min }\le P\left(t\right)\le P^{\max }.$

The primary focus of this paper is to develop a distributed controller for individual ESUs in the DESA. The controller is designed with two main objectives: precise tracking of the reference power setpoint $(p^{*})$ and effective management of SoC to achieve balance among the ESUs. The control objectives of DESA are as follows:

1. The total charging/discharging power of DESA tracks the total desired power, that is

$\underset{t\to \infty }{\lim }\Vert {\displaystyle \sum _{i=1}^N}{P}_i\left(t\right)-p^{*}\Vert =0,i\in \mathcal{N}.$

2. All battery units achieve SoC balancing, that is

$\underset{t\to \infty }{\lim }\Vert {SoC}_i\left(t\right)-{SoC}_j\left(t\right)\Vert =0,i,j\in \mathcal{N}.$

3 Fixed-time observer-based power tracking control

In this section, a distributed control method based on a fixed-time observer is proposed to achieve both SoC balancing and accurate power tracking in the context of the DESA. This control method is applicable for both charging and discharging modes, ensuring the performance in both scenarios.

3.1 Discharging mode

For the discharging mode, the distributed control is formulated as follows:

$P_i\left(t\right)=\frac{C_i{V}_{i}So{C}_i\left(t\right)}{N{\tilde{\beta }}_i\left(t\right)}{\tilde{P}}_i^{*}\left(t\right),(5)$

$\left\{\begin{array}{c}{\dot{\stackrel{̃}{P}}}_i^{*}\left(t\right)=-\alpha {\xi }_i^{2-\frac{p}{q}}-\beta {\xi }_i^{\frac{p}{q}},\hfill \\ {\xi }_i\left(t\right)={\displaystyle \sum _{j\in {\mathcal{N}}_i}}{a}_{ij}\left({\tilde{P}}_i^{*}\left(t\right)-{\tilde{P}}_j^{*}\left(t\right)\right)+b_i\left({\tilde{P}}_i^{*}\left(t\right)-p^{*}\right),\hfill \end{array}\right.(6)$

$\left\{\begin{array}{c}{\tilde{\beta }}_i\left(t\right)={\displaystyle \sum _{j\in {\mathcal{N}}_i}}{a}_{ij}\left({\varsigma }_i\left(t\right)-{\varsigma }_j\left(t\right)\right)+C_i{V}_{i}So{C}_i\left(t\right),\hfill \\ {\dot{\varsigma }}_i\left(t\right)=-\mu sign\left({\displaystyle \sum _{j\in {\mathcal{N}}_i}}{a}_{ij}\left({\tilde{\beta }}_i\left(t\right)-{\tilde{\beta }}_j\left(t\right)\right)\right)-\sigma si{g}^{\varphi }\left({\displaystyle \sum _{j\in {\mathcal{N}}_i}}{a}_{ij}\left({\tilde{\beta }}_i\left(t\right)-{\tilde{\beta }}_j\left(t\right)\right)\right),\hfill \end{array}\right.(7)$

where ${\tilde{P}}_i^{*}(t)$ denotes the estimation of $P_i(t)$, ${\tilde{\beta }}_i(t)$ denotes the estimation of ${\beta }_i(t)$, ${\beta }_i(t)$ is the product of $C_i$, $V_i$, and $So{C}_i(t)$ for ESU $i$, ${\xi }_i(t)$ and ${\varsigma }_i(t)$ are the internal states. $\varphi >1$, $\gamma ,\alpha$, $\beta$, $\mu$, and $\sigma$ are positive constants, and $p$ and $q$ are positive odd integers with $p<q$.

Remark 1. Observer Eq. 6 is specifically designed to observe the reference command $p^{*}$. On the other hand, Observer Eq. 7 is utilized to estimate the overall SoC. With the observed states, we develop a local controller Eq. 5 to dynamically update $P_i(t)$ in real-time. This control method is designed to make use of local information as well as information from neighboring nodes.

Theorem 1. Suppose that $G$ is a connected graph and at least one ESU is capable of receiving the tracking reference $p^{*}$. The distributed observer Eq. 6, with any initial ${\tilde{P}}_i^{*}\left(0\right)<P^{\mathit{max}}$, $i\in \mathcal{N}$, can accurately estimate ${\tilde{P}}_i^{*}\left(t\right)=p^{*}$, for $t\in [T_1,+\infty )$ in the discharging mode, where the upper bound of T₁ satisfies Eq. 8

$T_1\le T_{1,\max }=\frac{2q\beta N^{\frac{q-p}{2q}}{\left(2{\lambda }_{\min }\left(L+B\right)\right)}^{\frac{p}{2q}-\frac{3}{2}}+2q\alpha {\left(2{\lambda }_{\min }\left(L+B\right)\right)}^{-\frac{1}{2}-\frac{p}{2q}}}{\alpha \beta \left(q-p\right)}.(8)$

Proof. Let $e_{1,i}(t)={\tilde{P}}_i^{*}(t)-p^{*},i\in \mathcal{N}$, then we can get

$\begin{array}{c}{\dot{e}}_{1,i}=-\alpha {\left({\displaystyle \sum _{j\in N}}{a}_{ij}\left({\tilde{P}}_i^{*}\left(t\right)-{\tilde{P}}_j^{*}\left(t\right)\right)+b_i\left({\tilde{P}}_i^{*}\left(t\right)-p^{*}\right)\right)}^{2-\frac{p}{q}}\hfill \\ -\beta {\left({\displaystyle \sum _{j\in N}}{a}_{ij}\left({\tilde{P}}_i^{*}\left(t\right)-{\tilde{P}}_j^{*}\left(t\right)\right)+b_i\left({\tilde{P}}_i^{*}\left(t\right)-p^{*}\right)\right)}^{\frac{p}{q}}\hfill \\ =-\alpha {\left({\displaystyle \sum _{j\in N}}{l}_{ij}{e}_{1,j}+b_i{e}_{1,i}\right)}^{2-\frac{p}{q}}-\beta {\left({\displaystyle \sum _{j\in N}}{l}_{ij}{e}_{1,j}+b_i{e}_{1,i}\right)}^{\frac{p}{q}}\hfill \end{array}$

let $e_1={(e_{\mathrm{1,1}},e_{\mathrm{1,2}},\dots ,e_{1,N})}^T$, then

${\dot{e}}_1=-\alpha {\left(\left(L+B\right)e_1\right)}^{2-\frac{p}{q}}-\beta {\left(\left(L+B\right)e_1\right)}^{\frac{p}{q}}.(9)$

note that $L+B$ is a positive matrix, hence we can construct the following Lyapunov candidate function

$V_1=\frac{1}{2}{\left(e_1\right)}^T\left(L+B\right)e_1.$

differentiating $V_1(t)$ along the trajectories of Eq. 9, one has

${\dot{V}}_1=-\alpha {\left(\left(L+B\right)e_1\right)}^T{\left(\left(L+B\right)e_1\right)}^{2-\frac{p}{q}}-\beta {\left(\left(L+B\right)e_1\right)}^T{\left(\left(L+B\right)e_1\right)}^{\frac{p}{q}}.$

note that $p$ and $q$ are all positive odd integers with $p<q$, then

${\dot{V}}_1\le -\alpha {\left({‖\left(L+B\right)e_1‖}_{3-\frac{p}{q}}\right)}^{3-\frac{p}{q}}-\beta {\left({‖\left(L+B\right)e_1‖}_{1+\frac{p}{q}}\right)}^{1+\frac{p}{q}}.(10)$

note that $L+B$ is a positive definite matrix, then from Lemma 5, there exists a unique lower triangular matrix $Q$, such that

$L+B=Q{Q}^T.$

then, one has

${‖\left(L+B\right)e_1‖}_2^2={\left(e_1\right)}^{T}Q{Q}^{T}Q{Q}^T{e}_1\ge 2{\lambda }_{\min }\left(L+B\right)V_1$

from Lemma 3, one has

${‖\left(L+B\right)e_1‖}_{1+\frac{p}{q}}\ge {‖\left(L+B\right)e_1‖}_2\ge \sqrt{2{\lambda }_{\min }\left(L+B\right)V_1},$

which implies

${\left({‖\left(L+B\right)e_1‖}_{1+\frac{p}{q}}\right)}^{1+\frac{p}{q}}\ge {\left(2{\lambda }_{\min }\left(L+B\right)V_1\right)}^{\frac{1}{2}+\frac{p}{2q}}.(11)$

also from Lemma 3, one has

$\Vert \left(L+B\right)e_1{\Vert }_2\le N^{\frac{1}{2}-\frac{1}{3-p/q}}\Vert \left(L+B\right)e_1{\Vert }_{3-p/q},$

which implies

$\begin{array}{ll}\hfill & {‖\left(L+B\right)e_1‖}_{3-\frac{p}{q}}\ge N^{-\left(\frac{1}{2}-\frac{1}{3-p/q}\right)}{‖\left(L+B\right)e_1‖}_2\hfill \\ \hfill & \ge N^{-\left(\frac{1}{2}-\frac{1}{3-p/q}\right)}\sqrt{2{\lambda }_{\min }\left(L+B\right)V_1}.\hfill \end{array}$

then, one has

${\left({‖\left(L+B\right)e_1‖}_{3-\frac{p}{q}}\right)}^{3-\frac{p}{q}}\ge N^{\frac{p-q}{2q}}{\left(2{\lambda }_{\min }\left(L+B\right)V_1\right)}^{\frac{3}{2}-\frac{p}{2q}}.(12)$

substituting Eqs 11, 12 into Eq. 10 yields:

${\dot{V}}_1\le -\alpha N^{\frac{p-q}{2q}}{\left(2{\lambda }_{\min }\left(L+B\right)\right)}^{\frac{3}{2}-\frac{p}{2q}}{V_1}^{\frac{3}{2}-\frac{p}{2q}}-\beta {\left(2{\lambda }_{\min }\left(L+B\right)\right)}^{\frac{1}{2}+\frac{p}{2q}}{V_1}^{\frac{1}{2}+\frac{p}{2q}}.$

it is easy to check that the conditions of Lemma 2 is satisfied, and the corresponding parameters are

$a=\alpha N^{\frac{p-q}{2q}}{\left(2{\lambda }_{\min }\left(L+B\right)\right)}^{\frac{3}{2}-\frac{p}{2q}}>0,$

$b=\frac{3}{2}-\frac{p}{2q}>1,$

$c=\beta {\left(2{\lambda }_{\min }\left(L+B\right)\right)}^{\frac{1}{2}+\frac{p}{2q}}>0,$

$d=\frac{1}{2}+\frac{p}{2q}\in \left(\mathrm{0,1}\right),$

and

$T_{1,\max }=\frac{2q\beta N^{\frac{q-p}{2q}}{\left(2{\lambda }_{\min }\left(L+B\right)\right)}^{\frac{p}{2q}-\frac{3}{2}}+2q\alpha {\left(2{\lambda }_{\min }\left(L+B\right)\right)}^{-\frac{1}{2}-\frac{p}{2q}}}{\alpha \beta \left(q-p\right)}.$

hence, the proof of Theorem 1 is completed.

Theorem 2. Suppose that $G$ is a connected graph. For the distributed observer Eq. 7 with ${\varsigma }_i(0)=0$, if

$\mu \ge \frac{\sqrt{N}}{{\lambda }_2\left(L\right)}{P}^{\max }+\epsilon ,$

$‖{\tilde{\beta }}_i\left(t\right)-\frac{1}{N}{\sum }_{j=1}^N{C}_i{V}_{i}So{C}_i\left(t\right)‖$ can convergence to zero with a fixed time $T_{2,max}$, that is

${\tilde{\beta }}_i\left(t\right)=\frac{1}{N}{\displaystyle \sum _{j=1}^N}{C}_i{V}_{i}So{C}_i\left(t\right),t\in \left[T_2,+\infty \right),$

where the upper bound of T₂ satisfies Eq. 13

$T_{2,\max }:=\frac{2N^{\varphi }}{\sigma {\left(\sqrt{2{\lambda }_{\min }\left(L^2\right)}\right)}^{\varphi +1}\left(\varphi -1\right)}+\frac{\sqrt{2}}{\epsilon \sqrt{{\lambda }_{\min }\left(L^2\right)}}.(13)$

Proof. Let

${\beta }_i\left(t\right)=C_i{V}_{i}So{C}_i\left(t\right),$

and

$e_{2,i}={\tilde{\beta }}_i\left(t\right)-\frac{1}{N}{\displaystyle \sum _{j=1}^N}{\beta }_j\left(t\right),\text{for}i\in \mathcal{N}.$

from Eq. 4, one has ${\dot{\beta }}_i(t)=P_i(t)$, and

${\dot{e}}_{2,i}={\displaystyle \sum _{j\in {\mathcal{N}}_i}}{a}_{ij}\left({\dot{\varsigma }}_i\left(t\right)-{\dot{\varsigma }}_j\left(t\right)\right)+{\dot{\beta }}_i\left(t\right)-\frac{1}{N}{\displaystyle \sum _{j=1}^N}{\dot{\beta }}_j\left(t\right).$

let

$\varsigma \left(t\right)=\left({\varsigma }_1\left(t\right),{\varsigma }_2\left(t\right),\dots ,{\varsigma }_N\left(t\right)\right),$

$\beta \left(t\right)=\left({\beta }_1\left(t\right),{\beta }_2\left(t\right),\dots ,{\beta }_N\left(t\right)\right),$

$\tilde{\beta }\left(t\right)=\left({\tilde{\beta }}_1\left(t\right),{\tilde{\beta }}_2\left(t\right),\dots ,{\tilde{\beta }}_N\left(t\right)\right),$

and

$e_2\left(t\right)=\left(e_{\mathrm{2,1}}\left(t\right),e_{\mathrm{2,2}}\left(t\right),\dots ,e_{2,N}\left(t\right)\right).$

moreover, $G$ is a connected undirected graph. It follows from (George et al., 2017), one has

$L\cdot L^{+}=\left(I_N-\frac{1}{N}{\mathbf{1}}_N{\mathbf{1}}_N^T\right),$

where $L^{+}$ is the generalized inverse of $L$. Then, one has

${\dot{e}}_2\left(t\right)=L\dot{\varsigma }\left(t\right)+L\cdot L^{+}\dot{\beta }\left(t\right).$

$L{e}_2\left(t\right)=L\tilde{\beta }\left(t\right)-\frac{1}{N}L{1}_N{1}_N^T\beta \left(t\right)=L\tilde{\beta }\left(t\right),$

since $L{1}_N=0$.

We can construct the following Lyapunov candidate function

$V_2=\frac{1}{2}{\left(e_2\left(t\right)\right)}^T\left(e_2\left(t\right)\right).$

differentiating $V_2(t)$ along the trajectories of Eqs 2, 7, one has

$\begin{array}{ll}\hfill {\dot{V}}_2& ={\left(e_2\left(t\right)\right)}^T\left(L\dot{\varsigma }\left(t\right)+L\cdot L^{+}\dot{\beta }\left(t\right)\right)\hfill \\ \hfill & =-\mu {‖L\tilde{\beta }\left(t\right)‖}_1-\sigma {\left(L\tilde{\beta }\left(t\right)\right)}^{T}si{g}^{\varphi }\left(L\tilde{\beta }\left(t\right)\right)\hfill \\ \hfill & +{\left(L\tilde{\beta }\left(t\right)\right)}^T{L}^{+}\dot{\beta }\left(t\right).\hfill \end{array}$

From Lemma 4, one has

$\begin{array}{ll}\hfill \sigma {\left(L\tilde{\beta }\left(t\right)\right)}^{T}si{g}^{\varphi }\left(L\tilde{\beta }\left(t\right)\right)& =\sigma {\displaystyle \sum _{j=1}^N}{\left|{\left[L\tilde{\beta }\left(t\right)\right]}_i\right|}^{\varphi +1}\hfill \\ \hfill & \ge \sigma N^{-\varphi }{\left({\displaystyle \sum _{j=1}^N}\left|{\left[L\tilde{\beta }\left(t\right)\right]}_i\right|\right)}^{\varphi +1}\hfill \\ \hfill & =\sigma N^{-\varphi }{\left({‖L\tilde{\beta }\left(t\right)‖}_1\right)}^{\varphi +1},\hfill \end{array}$

where ${\left[L\tilde{\beta }\left(t\right)\right]}_i$ is the $i$-th element of the vector $L\tilde{\beta }(t)$. It follows from (George et al., 2017), one has

$\begin{array}{ll}\hfill {\left(L\tilde{\beta }\left(t\right)\right)}^T{L}^{+}\dot{\beta }\left(t\right)& \le {\sigma }_{\max }\left(L^{+}\right)\sqrt{N}{‖L\tilde{\beta }\left(t\right)‖}_1{‖\dot{\beta }\left(t\right)‖}_{\infty }\hfill \\ \hfill & \le \frac{\sqrt{N}}{{\lambda }_2\left(L\right)}{‖L\tilde{\beta }\left(t\right)‖}_1{‖\dot{\beta }\left(t\right)‖}_{\infty },\hfill \end{array}$

where ${\sigma }_{\max }(\cdot )$ denotes the maximum singular value and ${\sigma }_{\max }(L^{+})=\frac{1}{{\lambda }_2\left(L\right)}$. Then, one has

$\begin{array}{c}{\dot{V}}_2\le -\mu {‖L\tilde{\beta }\left(t\right)‖}_1-\sigma N^{-\varphi }{‖L\tilde{\beta }\left(t\right)‖}_1^{\varphi +1}+\frac{\sqrt{N}}{{\lambda }_2\left(L\right)}{‖L\tilde{\beta }\left(t\right)‖}_1{‖\dot{\beta }\left(t\right)‖}_{\infty }\hfill \\ \le -\left(\mu -\frac{\sqrt{N}}{{\lambda }_2\left(L\right)}{‖\dot{\beta }\left(t\right)‖}_{\infty }\right){‖L\tilde{\beta }\left(t\right)‖}_1-\sigma N^{-\varphi }{‖L\tilde{\beta }\left(t\right)‖}_1^{\varphi +1}.\hfill \end{array}$

for

$\mu \ge \frac{\sqrt{N}}{{\lambda }_2\left(L\right)}{P}^{\max }+\epsilon ,$

$\begin{array}{c}{\dot{V}}_2\le -\epsilon {‖L\tilde{\beta }\left(t\right)‖}_1-\sigma N^{-\varphi }{‖L\tilde{\beta }\left(t\right)‖}_1^{\varphi +1}\hfill \\ \le -\epsilon {‖L{e}^2‖}_2-\sigma N^{-\varphi }{‖L{e}^2‖}_2^{\varphi +1}\hfill \\ \le -\sigma N^{-\varphi }{\left(\sqrt{2{\lambda }_{\min }\left(L^2\right)}\right)}^{\varphi +1}{V}_2^{\frac{\varphi +1}{2}}-\epsilon \sqrt{2{\lambda }_{\min }\left(L^2\right)}{V}_2^{\frac{1}{2}}.\hfill \end{array}$

it is easy to check that the conditions of Lemma 2 is satisfied, and the corresponding parameters are

$a=\sigma N^{-\varphi }{\left(\sqrt{2{\lambda }_{\min }\left(L^2\right)}\right)}^{\varphi +1},$

$b=\frac{\varphi +1}{2}>1,$

$c=\epsilon \sqrt{2{\lambda }_{\min }\left(L^2\right)},$

$d=\frac{1}{2},$

and

$T_{2,\max }:=\frac{2N^{\varphi }}{\sigma {\left(\sqrt{2{\lambda }_{\min }\left(L^2\right)}\right)}^{\varphi +1}\left(\varphi -1\right)}+\frac{\sqrt{2}}{\epsilon \sqrt{{\lambda }_{\min }\left(L^2\right)}}.$

hence, the proof is completed.

Theorem 3. Suppose that $G$ is a connected graph and at least one ESU is capable of receiving the tracking reference $p^{*}$. Under the distributed control Eqs 5–7 with

$\mu \ge \frac{\sqrt{N}}{{\lambda }_2\left(L\right)}{P}^{\max }+\epsilon ,$

can achieve asymptotic SoC balancing, and power tracking in a fixed time, i.e.,

$\underset{t\to \infty }{\lim }‖S\mathrm{o}{C}_i\left(t\right)-So{C}_j\left(t\right)‖=0,$

and

$‖{\displaystyle \sum _{i=1}^N}{P}_i\left(t\right)-p^{*}‖=0,t\ge \max \left\{T_{1,\max },T_{2,\max }\right\}.$

Proof. According to Theorem 1, 2, when $t\in \left[T_{\max },+\infty \right)$, $P_i^{*}\left(t\right)=p^{*}$, and ${\beta }_i\left(t\right)=\frac{1}{N}{\sum }_{j=1}^N{C}_i{V}_{i}So{C}_i\left(t\right)$. Then, similar to (Xing et al., 2019b), both SoC balancing and power tracking are achieved by controller Eq. 7. Hence, the proof of Theorem 3 is completed.

3.2 Charging mode

For the charging mode, the distributed control is formulated as follows:

$P_i\left(t\right)=\frac{C_i{V}_i\left(1-So{C}_i\left(t\right)\right)}{N{\tilde{\beta }}_i\left(t\right)}{\tilde{P}}_i^{*}\left(t\right),(14)$

$\left\{\begin{array}{c}{\dot{\stackrel{̃}{P}}}_i^{*}\left(t\right)=-\alpha {\xi }_i^{2-\frac{p}{q}}-\beta {\xi }_i^{\frac{p}{q}},\hfill \\ {\xi }_i\left(t\right)={\displaystyle \sum _{j\in N}}{a}_{ij}\left({\tilde{P}}_i^{*}\left(t\right)-{\tilde{P}}_j^{*}\left(t\right)\right)+b_i\left({\tilde{P}}_i^{*}\left(t\right)-p^{*}\right),\hfill \end{array}\right.(15)$

$\left\{\begin{array}{c}{\tilde{\beta }}_i\left(t\right)={\displaystyle \sum _{j\in {\mathcal{N}}_i}}{a}_{ij}\left({\varsigma }_i\left(t\right)-{\varsigma }_j\left(t\right)\right)+C_i{V}_i\left(1-So{C}_i\right)\left(t\right),\hfill \\ {\dot{\varsigma }}_i\left(t\right)=-\mu sign\left({\displaystyle \sum _{j\in {\mathcal{N}}_i}}{a}_{ij}\left({\tilde{\beta }}_i\left(t\right)-{\tilde{\beta }}_j\left(t\right)\right)\right)-\sigma si{g}^{\varphi }\left({\displaystyle \sum _{j\in {\mathcal{N}}_i}}{a}_{ij}\left({\tilde{\beta }}_i\left(t\right)-{\tilde{\beta }}_j\left(t\right)\right)\right).\hfill \end{array}\right.(16)$

Similar to the discharge mode, we can draw similar theorem for the charging mode.

Theorem 4. Suppose that $G$ is a connected graph and at least one ESU is capable of receiving the tracking reference $p^{*}$. Under the distributed control Eqs 5–7 with

$\mu \ge \frac{\sqrt{N}}{{\lambda }_2\left(L\right)}{P}^{\max }+\epsilon ,$

can achieve asymptotic SoC balancing, and power tracking in a fixed time, i.e.,

$\underset{t\to \infty }{\lim }‖S\mathrm{o}{C}_i\left(t\right)-So{C}_j\left(t\right)‖=0,$

and

$‖{\displaystyle \sum _{i=1}^N}{P}_i\left(t\right)-p^{*}‖=0,t\ge \max \left\{T_{1,\max },T_{2,\max }\right\}.$

Remark 2. Different from the asymptotic observer proposed in (Cai, 2020) and finite-time observer proposed in (Meng et al., 2021), two new fixed-time observers are proposed in this paper to ensure both power tracking and SoC balancing. It is worth noting that the convergence time of the asymptotic observer is infinite, and the convergence time of the finite-time observer depends on the initial state of the DESA, while the convergence time of the proposed observers Eqs 5–7, 14–16 is independent of the initial conditions, which only depends on the control parameters. As a result, the proposed fixed-time observers offer a deterministic convergence time irrespective of the initial conditions, allowing for faster and more precise power tracking through adjustment of the control parameters.

Remark 3. It is worth noting that the method proposed in this paper enables fast tracking of the total desired power within a fixed time, while ensuring asymptotic convergence for the balancing of the SoC. This convergence characteristic allows the DESA to efficiently fulfill tasks assigned by the Load-Side Management Center, particularly in terms of total power tracking. The asymptotic convergence of SoC does not impede its practical usability. Therefore, the power control strategy presented in this paper exhibits considerable potential for effective load management applications. Further research can focus on refining this strategy to achieve both fixed-time convergence for power tracking and asymptotic convergence for SoC balancing, thereby enhancing its applicability and performance.

4 Numerical experiment

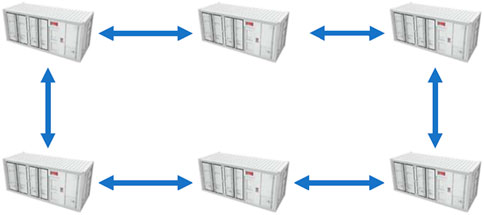
In this section, we present simulation results to show the effectiveness and superiority of the obtained results with some existing works. Suppose that DESA consists of 6 SoC of ESUs, and the communication topology is shown in Figure 3. Obviously, the communication between ESUs is bidirectional, and assume that only ESU 1 can receive the desired power information.

Figure 3

Figure 3. The communication network among 6 battery units.

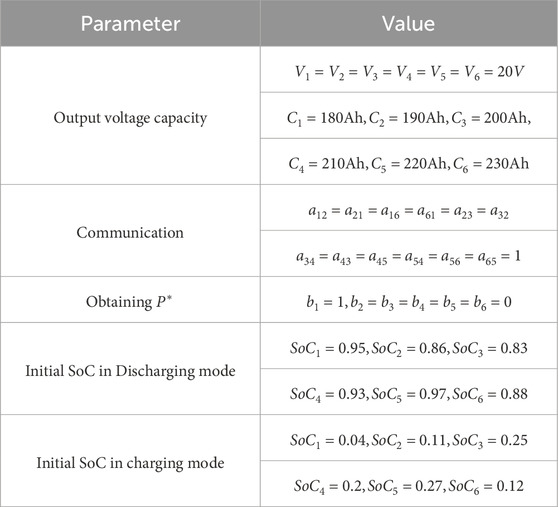
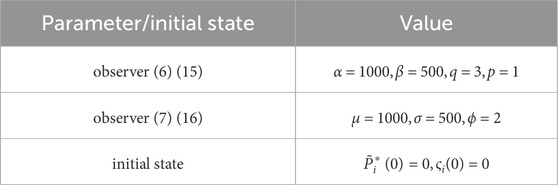
Three cases are presented to demonstrate the effectiveness and advancement of the proposed algorithm. The DESA parameters for the three cases are listed in Table 1, and the control parameters selected based on Theorems 1–4 are listed in Table 2. In simulation Cases 1 and 2, we will compare with the finite-time method proposed in reference Meng et al. (2021).

Table 1

Table 1. The parameters of the DESA.

Table 2

Table 2. The control parameters.

Case I (Charging mode): In this case, the desired power of the DESA is given as follows:

$p^{*}\left(t\right)=4200\sin \left(t\right)-4200.$

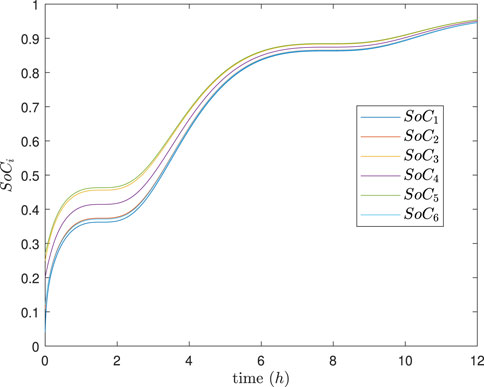
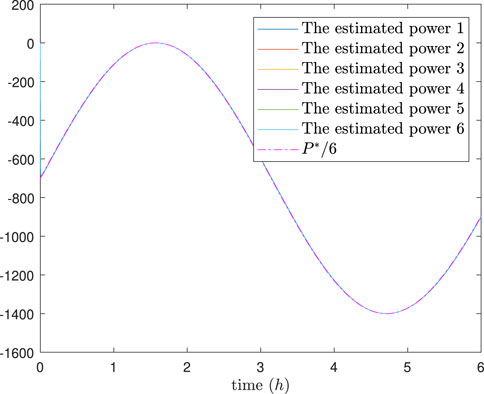
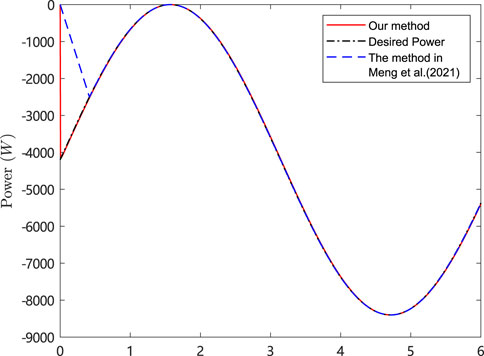
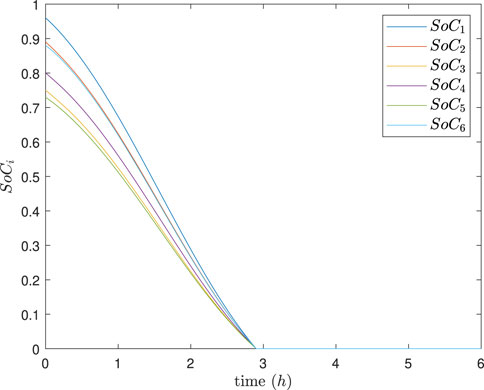
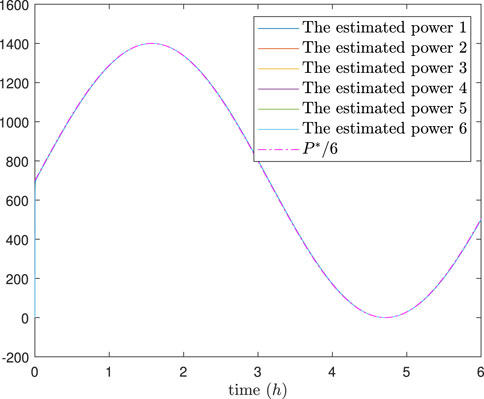
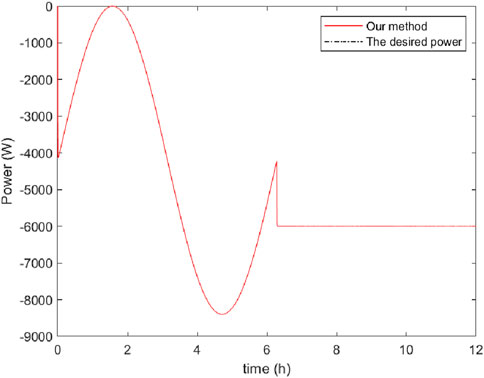
The simulation results are depicted in Figures 4–8. In Figures 4, 5, it can be observed that SoC balancing among the ESUs is achieved under two methods; Figures 6, 7 show that the power of ESU in the DESA is also tacked under two methods. From Figure 6, it is evident that the method proposed in Meng et al. (2021) can achieve power tracking of each ESU at $t=0.42s$, while from Figure 7, our proposed method can achieve power tracking in an instant. It should be highlighted that our proposed method exhibits rapid tracking of the desired power compared with the method in Meng et al. (2021), which is depicted in Figure 8.

Figure 4

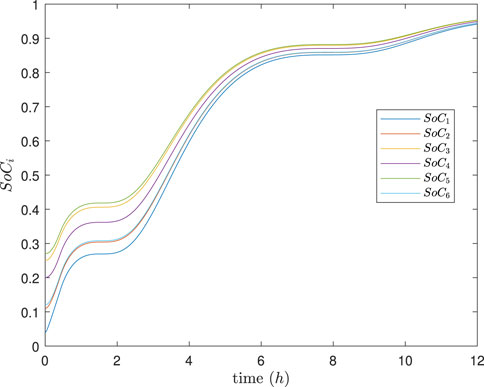
Figure 4. SoC of each ESU under the method in Meng et al. (2021).

Figure 5

Figure 5. SoC of each ESU under our method.

Figure 6

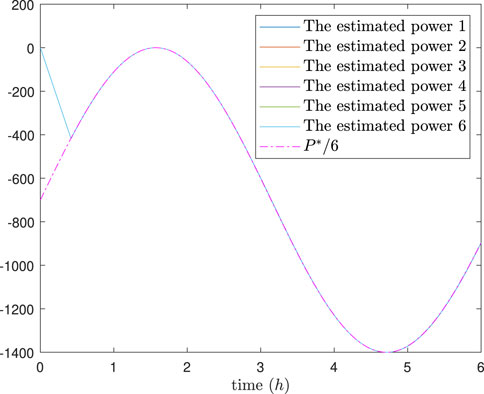
Figure 6. The estimated power of each ESU under the method in Meng et al. (2021).

Figure 7

Figure 7. The estimated power of each ESU under our method.

Figure 8

Figure 8. The comparison of the total output power of DESA.

Case II (Disharging mode): In this case, the desired power of the DESA is given as follows:

$p^{*}\left(t\right)=4200\sin \left(t\right)+4200.$

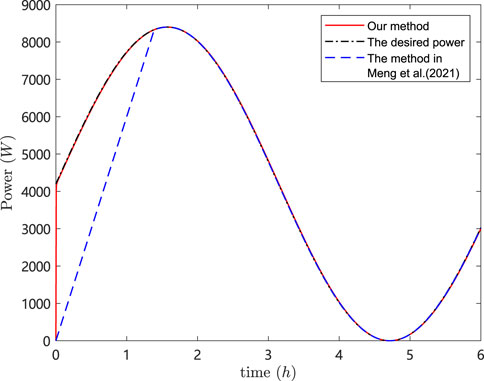
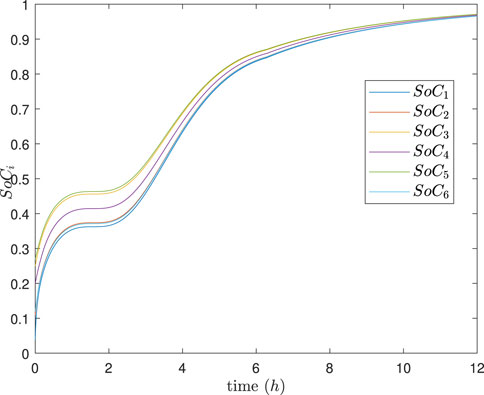
The simulation results are depicted in Figures 9–13. In Figures 9, 10, it can be observed that SoC balancing among the ESUs is achieved under two methods, but our method can achieve SoC balancing more quickly; Figures 11–13 show that the power of each ESU and the total power of the DESA is also tacked under two methods. From Figures 6–13, it is evident that the method proposed in Meng et al. (2021) can achieve power tracking of each ESU at $t=1.38s$, while from Figure 7, our proposed method can achieve power tracking in an instant. It should be highlighted that our proposed method exhibits rapid tracking of the desired power compared with the method in Meng et al. (2021) since the convergence speed of the proposed method surpasses that of the finite-time method proposed in Meng et al. (2021).

Figure 9

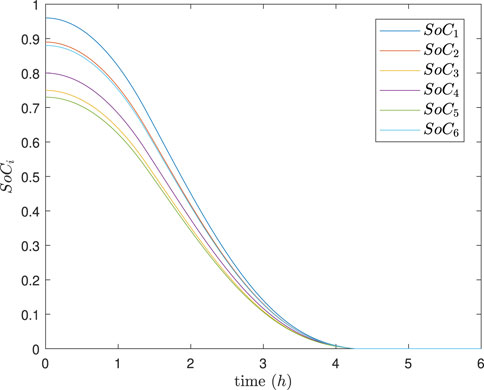
Figure 9. SoC of each ESU under the method in Meng et al. (2021).

Figure 10

Figure 10. SoC of each ESU under our method.

Figure 11

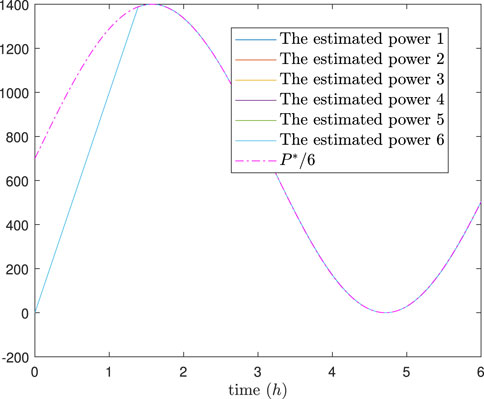
Figure 11. The estimated power of each ESU under the method in Meng et al. (2021).

Figure 12

Figure 12. The estimated power of each ESU under our method.

Figure 13

Figure 13. The comparison of the total output power of DESA.

Case III (Charging mode with varying desired power): In this case, to show the DESA demonstrates efficient adaptation to variations in the desired power of the DESA, which is given as follows:

$p^{*}\left(t\right)=\left\{\begin{array}{c}4200\sin \left(t\right)-4200,t\le 2\pi ,\hfill \\ -6000,t>2\pi .\hfill \end{array}\right.$

The simulation results are depicted in Figures 14, 15, which show that SoC balancing among the ESUs the total power of the DESA is also tacked and the total power of the DESA is also tacked under our method. In addition, even in the event of a change in the desired total power at $t=2\pi$h without compromising the SoC balance. This demonstrates the robustness of the proposed approach in maintaining the desired energy distribution among the ESUs. This robustness is crucial for maintaining the stability and longevity of the energy storage units, as well as for optimizing the overall performance of the energy storage system within the DESA framework.

Figure 14

Figure 14. SoC of each ESU under our method in case III.

Figure 15

Figure 15. The total output power of DESA under our method in case III.

5 Conclusion

In this paper, we investigate the SoC balancing and power tracking control of DESA with multiple heterogeneous ESUs. We have developed two fixed-time distributed observer models that are instrumental in estimating the aggregate desired power output and the average state of the battery units. Compared to existing asymptotic observers and finite-time observers, these observers significantly enhance the convergence speed. Subsequently, we conduct a thorough theoretical analysis to substantiate the efficacy of the control strategy, which is predicated on the aforementioned fixed-time distributed observers. This strategy is further validated through an array of simulation examples that demonstrate its practical applicability. We would extend these results to distributed control of DESA with time delays or communication constraints in future work.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XJ: Conceptualization, Methodology, Project administration, Writing–review and editing. TP: Conceptualization, Formal Analysis, Writing–review and editing. HL: Conceptualization, Project administration, Writing–original draft. YZ: Formal Analysis, Methodology, Software, Writing–review and editing. HZ: Investigation, Software, Validation, Writing–review and editing. WG: Data curation, Investigation, Writing–original draft. YC: Methodology, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the China Southern Power Grid Company Limited under the Grant No. 036000KK52222009 (GDKJXM20222125).

Acknowledgments

This article is grateful to China Southern Power Grid Power Grid Project for funding.

Conflict of interest

The authors declare that this study received funding from China Southern Power Grid Company Limited. The funder had the following involvement in the study: part of the study design, data collection and analysis, decision to publish, and preparation of the manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bull, S. R. (2001). Renewable energy today and tomorrow. Proc. IEEE 89, 1216–1226. doi:10.1109/5.940290

CrossRef Full Text | Google Scholar

Cai, H. (2020). Power tracking and state-of-energy balancing of an energy storage system by distributed control. IEEE Access 8, 170261–170270. doi:10.1109/ACCESS.2020.3024714

CrossRef Full Text | Google Scholar

Cao, J., Schofield, N., and Emadi, A. (2008). “Battery balancing methods: a comprehensive review,” in 2008 IEEE vehicle power and propulsion conference (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Ding, L., Han, Q.-L., Ning, B., and Yue, D. (2019). Distributed resilient finite-time secondary control for heterogeneous battery energy storage systems under denial-of-service attacks. IEEE Trans. Industrial Inf. 16, 4909–4919. doi:10.1109/tii.2019.2955739

CrossRef Full Text | Google Scholar

Dörfler, F., Simpson-Porco, J. W., and Bullo, F. (2015). Breaking the hierarchy: distributed control and economic optimality in microgrids. IEEE Trans. Control Netw. Syst. 3, 241–253. doi:10.1109/tcns.2015.2459391

CrossRef Full Text | Google Scholar

George, J., Freeman, R. A., and Lynch, K. M. (2017). “Robust dynamic average consensus algorithm for signals with bounded derivatives,” in 2017 American control conference (ACC), 352–357. doi:10.23919/ACC.2017.7962978

CrossRef Full Text | Google Scholar

Guan, Z.-H., Liu, Z.-W., Feng, G., and Wang, Y.-W. (2010). Synchronization of complex dynamical networks with time-varying delays via impulsive distributed control. IEEE Trans. Circuits Syst. I Regul. Pap. 57, 2182–2195. doi:10.1109/tcsi.2009.2037848

CrossRef Full Text | Google Scholar

Guo, F., Wen, C., and Song, Y.-D. (2017). Distributed control and optimization technologies in smart grid systems. Boca Raton, FL, United States: CRC Press.

Google Scholar

Han, H., Zhu, Y., Shi, G., Su, M., and Sun, Y. (2021). A local-distributed and global-decentralized soc balancing method for hybrid series-parallel energy storage system. IEEE Syst. J. 16, 2289–2299. doi:10.1109/jsyst.2021.3068167

CrossRef Full Text | Google Scholar

Hu, X., Liu, Z.-W., Wen, G., Yu, X., and Liu, C. (2020). Voltage control for distribution networks via coordinated regulation of active and reactive power of dgs. IEEE Trans. Smart Grid 11, 4017–4031. doi:10.1109/tsg.2020.2989828

CrossRef Full Text | Google Scholar

Hu, X., Zhou, H., Liu, Z.-W., Yu, X., and Li, C. (2017). Hierarchical distributed scheme for demand estimation and power reallocation in a future power grid. IEEE Trans. Industrial Inf. 13, 2279–2290. doi:10.1109/tii.2017.2670065

CrossRef Full Text | Google Scholar

Huang, B., Li, Y., Zhan, F., Sun, Q., and Zhang, H. (2022). A distributed robust economic dispatch strategy for integrated energy system considering cyber-attacks. IEEE Trans. Industrial Inf. 18, 880–890. doi:10.1109/TII.2021.3077509

CrossRef Full Text | Google Scholar

Jafari, M., Botterud, A., and Sakti, A. (2022). Decarbonizing power systems: a critical review of the role of energy storage. Renew. Sustain. Energy Rev. 158, 112077. doi:10.1016/j.rser.2022.112077

CrossRef Full Text | Google Scholar

Kang, W., Chen, M., Guan, Y., Tang, L., Vasquez, Q, J. C., Guerrero, J. M., et al. (2022). Distributed event-triggered optimal control method for heterogeneous energy storage systems in smart grid. IEEE Trans. Sustain. Energy 13, 1944–1956. doi:10.1109/tste.2022.3176741

CrossRef Full Text | Google Scholar

Lamp, S., and Samano, M. (2022). Large-scale battery storage, short-term market outcomes, and arbitrage. Energy Econ. 107, 105786. doi:10.1016/j.eneco.2021.105786

CrossRef Full Text | Google Scholar

Li, X., and Wang, S. (2019). Energy management and operational control methods for grid battery energy storage systems. CSEE J. Power Energy Syst. 7, 1026–1040. doi:10.17775/CSEEJPES.2019.00160

CrossRef Full Text | Google Scholar

Li, Y., Zhang, H., Liang, X., and Huang, B. (2019). Event-triggered-based distributed cooperative energy management for multienergy systems. IEEE Trans. Industrial Inf. 15, 2008–2022. doi:10.1109/TII.2018.2862436

CrossRef Full Text | Google Scholar

Lin, Y., Li, X., Zhai, B., Yang, Q., Zhou, J., Chen, X., et al. (2022). A two-layer frequency control method for large-scale distributed energy storage clusters. Int. J. Electr. Power & Energy Syst. 143, 108465. doi:10.1016/j.ijepes.2022.108465

CrossRef Full Text | Google Scholar

Liu, X.-K., Wang, Y.-W., Liu, Z.-W., and Huang, Y. (2023). On the stability of distributed secondary control for dc microgrids with grid-forming and grid-feeding converters. Automatica 155, 111164. doi:10.1016/j.automatica.2023.111164

CrossRef Full Text | Google Scholar

Liu, Z. W., Guan, Z. H., and Zhou, H. (2013). Impulsive consensus for leader-following multiagent systems with fixed and switching topology. Math. Problems Eng. 2013, 1–10. Article ID 378246. doi:10.1155/2013/762861

CrossRef Full Text | Google Scholar

Meng, T., Lin, Z., and Shamash, Y. A. (2021). Distributed cooperative control of battery energy storage systems in dc microgrids. IEEE/CAA J. Automatica Sinica 8, 606–616. doi:10.1109/jas.2021.1003874

CrossRef Full Text | Google Scholar

Pinson, P., Madsen, H., and O׳Malley, M. (2014). Benefits and challenges of electrical demand response: a critical review. Renew. Sustain. Energy Rev. 39, 686–699. doi:10.1016/j.rser.2014.07.098

CrossRef Full Text | Google Scholar

Ren, W., and Beard, R. W. (2008). Distributed consensus in multi-vehicle cooperative control. Springer London.

Google Scholar

Sun, Y., Zhao, Z., Yang, M., Jia, D., Pei, W., and Xu, B. (2019). Overview of energy storage in renewable energy power fluctuation mitigation. CSEE J. Power Energy Syst. 6, 160–173. doi:10.17775/CSEEJPES.2019.01950

CrossRef Full Text | Google Scholar

Tan, N. M. L., Abe, T., and Akagi, H. (2012). Design and performance of a bidirectional isolated dc–dc converter for a battery energy storage system. IEEE Trans. Power Electron. 27, 1237–1248. doi:10.1109/TPEL.2011.2108317

CrossRef Full Text | Google Scholar

Trefethen, L. N., and Bau, D. (2022). Numerical linear algebra, 181. Philadelphia, PA, United States: SIAM.

Google Scholar

Wang, S., Li, F., Zhang, G., and Yin, C. (2023). Analysis of energy storage demand for peak shaving and frequency regulation of power systems with high penetration of renewable energy. Energy 267, 126586. doi:10.1016/j.energy.2022.126586

CrossRef Full Text | Google Scholar

Wang, W., Huo, Q., Zhang, N., Yin, J., Ni, J., Zhu, J., et al. (2022). Flexible energy storage power station with dual functions of power flow regulation and energy storage based on energy-sharing concept. Energy Rep. 8, 8177–8185. doi:10.1016/j.egyr.2022.06.035

CrossRef Full Text | Google Scholar

Wei, G., Chi, M., Liu, Z.-W., Ge, M., Li, C., and Liu, X. (2023). Deep reinforcement learning for real-time energy management in smart home. IEEE Syst. J. 17, 2489–2499. doi:10.1109/JSYST.2023.3247592

CrossRef Full Text | Google Scholar

Xing, L., Mishra, Y., Tian, Y.-C., Ledwich, G., Zhou, C., Du, W., et al. (2019a). Distributed state-of-charge balance control with event-triggered signal transmissions for multiple energy storage systems in smart grid. IEEE Trans. Syst. Man, Cybern. Syst. 49, 1601–1611. doi:10.1109/tsmc.2019.2916152

CrossRef Full Text | Google Scholar

Xing, L., Mishra, Y., Tian, Y.-C., Ledwich, G., Zhou, C., Du, W., et al. (2019b). Distributed state-of-charge balance control with event-triggered signal transmissions for multiple energy storage systems in smart grid. IEEE Trans. Syst. Man, Cybern. Syst. 49, 1601–1611. doi:10.1109/tsmc.2019.2916152

CrossRef Full Text | Google Scholar

Xu, B., Shi, Y., Kirschen, D. S., and Zhang, B. (2018). Optimal battery participation in frequency regulation markets. IEEE Trans. Power Syst. 33, 6715–6725. doi:10.1109/tpwrs.2018.2846774

CrossRef Full Text | Google Scholar

Zeng, Y., Zhang, Q., Liu, Y., Zhuang, X., and Guo, H. (2022). Hierarchical cooperative control strategy for battery storage system in islanded dc microgrid. IEEE Trans. Power Syst. 37, 4028–4039. doi:10.1109/TPWRS.2021.3131591

CrossRef Full Text | Google Scholar

Zhao, T., Parisio, A., and Milanović, J. V. (2022). Distributed control of battery energy storage systems in distribution networks for voltage regulation at transmission–distribution network interconnection points. Control Eng. Pract. 119, 104988. doi:10.1016/j.conengprac.2021.104988

CrossRef Full Text | Google Scholar

Zuo, Z., Han, Q., and Ning, B. (2019). Fixed-time cooperative control of multi-agent systems. Cham, Switzerland: Springer International Publishing.

Google Scholar

Nomenclature