Innovative machine learning for drilling fluid density prediction: a novel central force search-adaptive XGBoost in HPHT environments

Oil and gas industries are facing a special dilemma when it comes to high-pressure, high-temperature (HPHT) drilling as the accurate forecasting of the drilling fluid density (DFD) is a vital factor for safe and efficient operations. Complicated relationships and inconsistencies in HPHT situations are rarely mapped by current forecasting models, while their buggy performance and safety risks during drilling can be underestimated. In this research, we propose a novel machine learning (ML) approach to enhance the accuracy of DFD anticipation under HPHT conditions: central force search-adaptive extreme gradient boosting (CFS-XGB). This paper uses a dataset that has drilling variables together with the DFD for HPHT situations to examine the accuracy of the CFS-XGB model. Excluding the abnormalities of data or mistakes, the reliability of the original data is maintained by applying min–max normalization. After that, finding the important features with the help of the boosted principal component analysis (BPCA) approach to the normalized data will ensure a major improvement in the CFS-XGB methodology’s prediction efficacy. This research is experimented in the Python platform, and the performance of the proposed CFS-XGB method is analyzed in terms of MSE, R2, and AAPRE metrics. The suggested approach performs better than the current methods in forecasting the drilling fluid concentration in HPHT settings, according to the experimental data. This development in predictive modeling helps increase the productivity and safety of drilling operations, which will eventually help the oil and gas sector manage the challenges posed by HPHT drilling settings.

1 Introduction

Drilling fluid is created and maintained in surface pits or tanks and is a mixture of water, chemicals, bentonite, and weighting additives that circulate throughout the borehole during drilling operations. Apart from cleaning the wellbore by removing bit cuttings on the outside, circulation of drilling fluid also keeps the bottom of the wellbore hydrostatically pressured to cool and lubricate the drill bit string while drilling proceeds, preventing the formation fluids from entering the wellbore (Davoodi et al., 2023). In reservoir zones, which can occur several kilometers below the surface, a vertical borehole is required to safely generate hydrocarbons, for which rotating rigs equipped with subsystems to facilitate safe drilling processes are used. Bit nozzles pull up drilling fluid for recirculation and maintenance; this fluid is then filtered by the solid’s control systems and pushed back into tanks (Gul, 2021). Because of safety measures and well control difficulties that affect workers’ lives along with the high expense of the operations, drilling operations are regarded as the most crucial among the oil and gas operations. Controlling of the activities will be aided by several sensors monitoring the drilling processes alongside downhole sensors on the surface (Abdelaal et al., 2023a). When drilling narrow window zones, where the difference between the hole and formation fracture pressures is not large, equivalent circulation density (ECD), one of the characteristics, should be taken into particular consideration (Bashir et al., 2021). Drilling HPHT oil wells is a relatively new frontier in hydrocarbon deposit discovery and development. According to Highoose Limited, there is yet a higher risk of breakdown in HPHT wells because of the intense pressure of the surroundings (Okonkwo and Joel, 2023).

Drilling and filling of wells are not carried out in the energy field as they were performed over a century ago because oil is not found in the exact same favorable areas. It is also presumed that the industry’s perspective has changed during the past 10 years (Agwu et al., 2020). A downward or wider bore design has been influenced by drilling fluid hydraulics. For engineers to effectively design a good profile and increase the drilling efficiency while lowering hazards and cutting non-productive time (NPT), a reliable model with optimum drilling fluid hydraulic systems is consequently essential (Alsaihati et al., 2020). Geothermal power stations are a dependable energy source with low environmental impact, yet the cost of the drilling procedure accounts for approximately 25% of the total investment. Drilling involves rotary, circulation, and hoisting systems (Mengich et al., 2022). Viscose mixes known as drilling fluids or muds are used in drilling circulation systems for cooling and lubricating the drill bit as well as to transport rock cuttings to the surface (Pedrosa et al., 2021). Hydrocarbon extraction in the petroleum sector involves a difficult process called oil and gas well drilling. These issues are caused by the uncontrolled movement of drilling fluid through the rock during drilling. For the purposes of reinforcing the drilled formations, moving cuttings more easily, maintaining a steady pressure in the borehole, and chemically regulating the borehole, drilling fluid is utilized (Krishna et al., 2020). Due to the rise in temperature and pressure inside the formation owing to continuous drilling, the rheology of a drilling fluid changes. This inability of the rheology to be accurately represented by surface conditions itself has an effect on the accuracy of drilling hydraulics computation. The research aim is enhancing the prediction of DFD in the HPHT environment by developing CFS-XGB.

1.1 Contribution

The principal undertaking for this study is to employ ML techniques to create the notion of DFD prediction in an HPHT context.

✓ Used dataset that has drilling variables together with the DFD for HPHT situations to examine the accuracy.

✓ The introduction of the central force search-adaptive extreme gradient boosting model has greatly improved the predictive accuracy for DFD in HPHT conditions.

✓ Min–max normalization will add no anomalies or inconsistencies to the data, thus assuring reliability. This preprocessing step is very critical to maintain data integrity and increase the CFS-XGB model’s efficiency.

✓ Boosted principal component analysis can extract only relevant features from the normalized data. This refines the input variables and considerably raises the accuracy of prediction for the CFS-XGB model.

The CFS-XGB model is applicable to the remaining studies’ following categories: Section 2 examines the related works. Section 3 presents our suggested methodology. Section 4 presents the results of the study. Section 5 presents the subject of debate, while Section 6 presents the conclusions of the study.

2 Related works

The prediction of the density of drilling fluids using different machine learning and artificial intelligence models was evaluated by Syah et al. (2021) for establishing the best model that can be applied in the field. The least-square support vector machine-genetics algorithms (LSVM-GA), the radial basis function method (RBF), and the particle swarm optimization-adaptive neuro-fuzzy inferences system (PSO-ANFIS) were some of the models created at the programming stage. Al-Rubaii et al. (2023) designed the “equivalent circulation density and mud weight” specialized models, specifically ECDeffc.m and MWeffc.m, to perform the optimization of drilling performance and analysis of various real-time drilling parameters. Such models not only contribute to the aversion of problems such as blowouts and mistakes related to trapped pipes but also offer very accurate estimations of drilling conditions that are capable of detecting problems in real-time. The particle swarm optimization–least-squares support vector machine (PSO-LSSVM) technique was the most accurate, with the maximum accuracy and the lowest variation factor. Gamal et al. (2021) tested whether machine learning algorithms could provide an exact ECD with only data from the drilling. Some of these techniques were an artificial neural network (ANN) and adaptable network-based fuzzy inference system (ANFIS). The research utilized the actual motion of the drilling variables “of the horizontal drilling segment, including penetration rate, rotation acceleration, torque and standpipe volume.” Samnejad et al. (2020) suggested a new model in which the mechanical properties of drilling fluids in pre-API conditions were explained with a combination of physics, API data gathered at a site, and from laboratory testing, along with machine learning algorithms.

Abdelaal et al., 2023b developed an ML architecture that can be used to predict the rheological properties of the drilling fluids during the drilling process. The structure forecasts the viscometer values by frequent mud readings, and then it uses pre-existing algorithms to estimate additional mud characteristics with the use of mud density (MD) and mud flow viscometer (MFV). Ghamdi et al. (2021) sought to enhance ROP by incorporating MPD with AI analysis. Kandil et al. (2023) used machine learning methods such as an “artificial neural network (ANN), passive-aggressive regressor and K-nearest neighbours” based on the Levenberg–Marquardt back-propagation algorithm in predicting ECD. All these models were based on a few key operational variables that have been obtained during drilling operations using downhole sensors. Al-Rubaii (2024) developed a borehole clean index, HCI, to improve drill hole cleaning as a way of improving well drillability. These were the properties of the holes and drilling fluids, together with the majority of the drilling parameters affecting it. In understanding how drill hole cleaning works, both the engineering parameters and chemistry involved have to be considered.

Alkinani et al. (2020) proposed a new method of ECD prediction prior to drilling that utilized artificial neural networks. After the ECD had been predicted, it can then be kept within the allowable window through manipulation of the critical drilling parameters affecting ECD. The results of the research have indicated that the developed network had very small error tolerance in ECD prediction globally before drilling. Gautam et al. (2021) suggested a simple principle of momentum transfer of liquids to estimate the viscosity of the drilling fluids at HPHT conditions. The model was relatively straightforward yet able to reproduce the rheology of many drilling fluids at least on a predictive basis. Quitian-Ardila et al. (2024) developed a constitutive equation for modeling rheological data at an HPHT condition and carried out the rheological characterization of the “water-based drilling fluid, WBDF” with xanthan gum. The fluid showed shear-thinning behavior. Temperature had a stronger effect compared to pressure; however, their correlation was extremely strong. Tariq et al. (2024) suggested an ML technique for the forecast of the fluid linear swell pattern of shale wafers based on sodium bentonite. The shale wafers were exposed to various WBDFs, which were reconstituted in the presence of a few inorganic salts such as potassium chloride, KCl; sodium chloride, NaCl; and magnesium chloride, MgCl₂, which are the three types of chloride.

3 Methodology

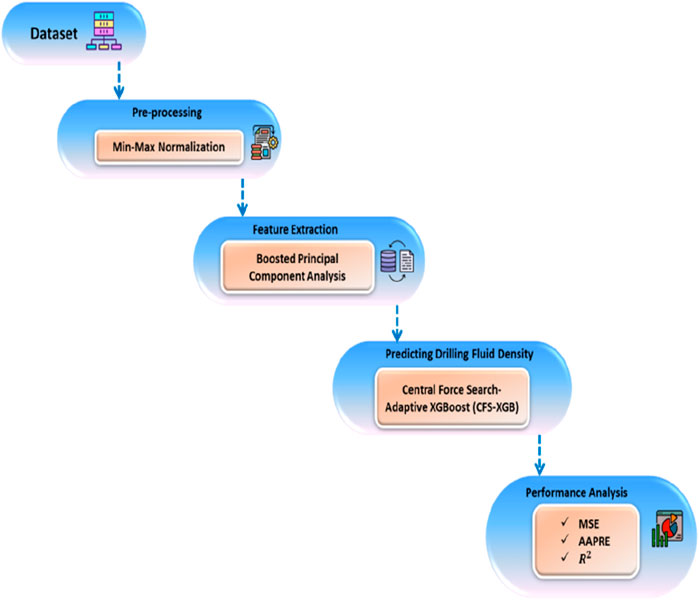
Initially, the data were gathered, normalized using min–max normalization, and then analyzed using boosted PCA to identify significant characteristics and create a flexible prediction model. It includes DFD prediction in HPHT situations using a new CFS-XGB technique. Figure 1 depicts the proposed overview.

Figure 1

Figure 1. Overview of the proposed workflow (source: author).

3.1 Dataset gathering

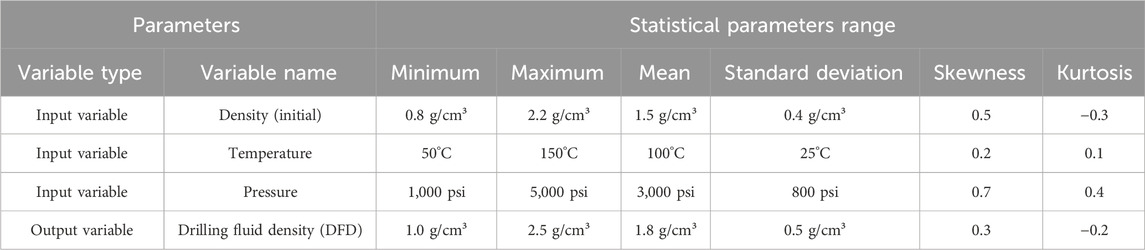
The current research gathered more than 880 datasets with varying fluid kinds, beginning densities (densities at standard pressure and temperature), temperature, and pressure (Alizadeh et al., 2021). The dataset is divided into two major groups for the proper creation of the model. In building the model, approximately 80% of real data points were used in the training phase, and the remaining, 20%, were test data used to test the performance. Table 1 summarizes key statistical parameters of input and output variables that are used in the drilling fluid density forecasting model. It contains the minimum, maximum, mean, standard deviation, skewness, and kurtosis with regard to initial density, temperature, pressure, and the resulting DFD. The initial density ranges from 0.8 to 2.2 g/cm³, with a mean of 1.5 g/cm³. Temperature ranges from 50°C to 150°C, with a mean of 100°C. Pressure ranges from 1,000 psi to 5,000 psi, with a mean of 3,000 psi. DFD varies from 1.0 to 2.5 g/cm³, with a mean of 1.8 g/cm³.

Table 1

Table 1. Variability of input influencing the variable and output.

3.2 Data preprocessing

Min–max normalization data convert the density data of the drilling fluid into a constant range, such as [0,1], by converting the value of each feature in relation to the minimum and maximum values in the dataset. This way, all the features will equally contribute to the prediction model in ensuring that the improvement in the rate of convergence will be the same in both normal and HPHT wells. By using min–max normalization (Equations 1, 2), the original data, x, is transformed linearly into the specified interval ${NEW}_{\mathit{max}}-{NEW}_{\mathit{min}}$.

$w_J={NEW}_{\mathit{min}}+\left({NEW}_{\mathit{max}}-{NEW}_{\mathit{min}}\right)\times \left(\frac{w_j-w_{\mathit{min}}}{w_{\mathit{max}}-w_{\mathit{min}}}\right).(1)$

$w_{\mathit{max}}=\begin{array}{c}\max w_j,w_{\mathit{min}}\\ 1\le j\le M\end{array}\begin{array}{c}=\min w_j,w_{\max }\\ 1\le j\le M\end{array}.(2)$

Using this approach, the data get properly scaled from $w_{\mathit{max}},w_{\mathit{min}}$ to ${NEW}_{\mathit{max}}-{NEW}_{\mathit{min}}$. The advantages of this approach are that all interactions among data elements are perfectly maintained. This approach never corrupts the data. Min–max normalization has simple rules along with an adjustable range. It works better than other approaches.

3.3 Feature extraction using boosted principal component analysis (BPCA)

Boosted principal component analysis is a relatively new technique to enhance the DFD prediction accuracy in capturing the high-pressure, high-temperature drilling environment. BPCA improves traditional PCA by adding a boosting mechanism to the model that can better handle variance in the data and select principal components more robustly, thus leading to better feature representation for predictive modeling. For the purpose of feature extraction, a boosted principal component analysis was used. This technique can be referred to as multi-linear principal component analysis (MPCA). The orthonormal projection of the input from feature information to MPCA was focused similarly to that of PCA, and the predicted feature was a tensor of the same order as the feature samples with reduced dimensions. The groupings of unified characteristics were denoted as follows in Equation 3:

$w=\left\{w_1,w_2,\dots ,w_n\right\}.(3)$

In this case, $w_1\in Q^{t_1*\dots .*t_L}$ represents the $N^{th}$ L-mode input-feature key-points with size $t_1\ast \dots .\ast t_L$. In order to transfer the primary featured scaled space $Q^{t_1*\dots .*t_L}$ into the scalar space $Q^{e{v}_1*e{v}_2*\dots e{v}_l}\left(e{v}_l<=t_L\right)$, the MPCA describes the multi-linear modification of the features. The multi-linear feature transformation projects out nonlinear high-dimensional features of this type and produces the best low-dimensional linear feature set. The following modification of multi-linear features was identified as per Equation 4:

$V^l\in Q^{t_l*\dots .*e{v}_l},l=1,\dots ,L.(4)$

Then, the definition of this variable $x_1\in Q^{e{v}_1*\dots *e{v}_L}$ is given as per Equation 5 follows:

$x_1=w_1\ast V^{{\left(1\right)}^S}\ast V^{{\left(2\right)}^S}\ast \dots \ast L{V}^{{\left(L\right)}^S}\in Q^{e{v}_1*e{v}_2*\dots e{v}_l,n=1,\dots ,N}.(5)$

The goal of MPCA is to control the L-projection matrices to make use of the entire tensor scatter, represented by $\phi \left(x\right)$. This is done as per Equations 6, 7.

$V^l\in Q^{t_l*e{v}_l},l=1,\dots ,N.(6)$

$\phi \left(x\right)=\sum _{n=1}^N{\left|x_1\right|}^2.(7)$

This time, eigenvectors $\left(e{v}_l\right)$ that correspond to the biggest eigenvalues of the $e{v}_l$ matrix were the initial-projection matrices as show in Equation 8.

${\phi }^{\left(n\right)}=\sum _{n=1}^N{W}_1\left(l\right)..W_{1\left(n\right)}^{S}l=1,\dots L.(8)$

According to the following ratio in Equation 9, dimensionality $\left(e{v}_l\right)$ might be constant for every $l$.

$Q^{\left(n\right)}=\frac{\sum _{i_{l=1}}^{e{v}_l}{{{\gamma }_i}_l}^{\left(l\right)}}{\sum _{i_{l=1}}^{t_l}{{{\gamma }_i}_l}^{\left(l\right)}}\ge 0.96.(9)$

In the above equation, the l-model total-scatter matrix’s ${i_l}^{th}$ eigenvalues are represented by the variable ${{{\gamma }_i}_l}^{\left(l\right)}$. The ideal linear collection of features converted improves the classification accuracy, and this improved method yields the most accurate results.

3.4 Predicting DFD

CFS-XGB represents a novel machine learning methodology that would improve the accuracy for drilling fluid density prediction under HPHT conditions. It combines the central force with extreme gradient boosting to provide an optimized feature selection method for model performance in complex drilling environments.

3.4.1 Central force search optimization (CFS)

CFS optimization is a fine-tuned optimization technique for predictive models to improve their accuracy in the prediction of DFD under high-pressure, high-temperature (HPHT) conditions. This approach is deeply entrenched in the idea of simulating a central force field that guides the search process toward optimal solutions. CFS, concerning its application in DFD forecasting, fine-tunes model parameters for best performance and feature selection for better predictive accuracy. CFS is used to find an $M_c$-dimensional goal function $e\left(\overrightarrow{w}\right)$ specified on a decision set of potential solutions.

$\mathrm{\Omega }\left.:\{w\right|\left|\left.{\overrightarrow{w}}_j^{\mathit{min}}\le w_j\le w_j^{\mathit{max}},1\le j\le M_c\right\}\right.,w_j\mathfrak{\in }\mathfrak{R};\text{\hspace{0.17em}here\hspace{0.5em}}w=\left(w_1,w_2,\dots \dots ..,w_{M_c}\right).\Omega \text{\hspace{0.17em}\hspace{0.17em}is\hspace{0.17em}enclosed\hspace{0.17em}by\hspace{0.17em}the\hspace{0.17em}}{2M}_c\text{\hspace{0.17em}planes}{O}_{jl}\left.:\{w\right|\left|\left.w=\left(w_1,\dots ..,w_{j-1},W_{jl},w_{j+1},\dots ..,w_{M_c}\right)\right\}\right..\text{\hspace{0.17em}Whereas\hspace{0.17em}}{W}_{jl}=\left\{\begin{array}{c}{w}_j^{\mathit{min}},l=1\\ w_j^{\mathit{max}},l=2\end{array}\right\}\left(\text{notice\hspace{0.17em}that\hspace{0.17em}}j=1,\dots \dots .,M_c;l=1,2\text{\hspace{0.17em}throughout}\right)$.

It is sampled by CFS by flying “probes” across it over several “time” increments (iterations). The exact position of every probe, represented by the vector, is used to incrementally calculate a measure for $e\left(\overrightarrow{w}\right)$ capability.

At step $i-1$, “probe p” is located at ${\overrightarrow{Q}}_{i-1}^o={\sum }_{j=1}^{M_c}{w}_j^{o,i-1}{\widehat{f}}_j$,

where $0\le i\le M_s$ is the iteration index, ${\widehat{f}}_j$ is the unit matrix along the $j^{th}$ vector axis, and $M_s$ is the overall number of steps (notice that step 0 is the first). The probe number is $1\le i\le M_o$, and the overall number of probes is $M_o$. Probe $o$ departs at step from the position ${\overrightarrow{Q}}_{i-1}^o$.

$i-1$ to ${\overrightarrow{Q}}_{i-1}^o={\sum }_{j=1}^{M_c}{w}_j^{o,i}{\widehat{f}}_j$ at step $i$ due to the (constant) acceleration ${\overrightarrow{b}}_{i-1}^o={\sum }_{j=1}^{M_c}{b}_j^{o,i-1}{\widehat{f}}_j$ produced at step $i-1$ by the CFO “masses” discovered by the probe distributions.

The trajectory and acceleration of the probe, respectively, are determined using the following two stochastic “equations of motion” to determine the probe’s motion in “CFO space” as show in Equations 10, 11:

${\overrightarrow{Q}}_i^o={\overrightarrow{Q}}_{i-1}^o+{\overrightarrow{b}}_{i-1}^o.(10)$

${\overrightarrow{b}}_{i-1}^o={\displaystyle \sum _{\begin{array}{c}m=1\\ m\ne o\end{array}}^{M_o}}V\left(N_{i-1}^m-N_{i-1}^o\right).\left(N_{i-1}^m-N_{i-1}^o\right)\times \frac{{\left(\overrightarrow{Q}\right.}_{i-1}^m-{\overrightarrow{Q}}_{i-1}^o)}{‖{\overrightarrow{Q}}_{i-1}^m-{\overrightarrow{Q}}_{i-1}^o‖}.(11)$

The objective function’s fitness at probe $o$’s position at time step $i-1$ is represented by $N_{i-1}^o=e\left(w_1^{o,i-1},w_2^{o,i-1},\dots \dots ,w_{M_c}^{o,i-1}\right)$. At that particular step (iteration), every other probe has a fitness value associated with it: $N_{i-1}^m,m=1,\dots ..,o-1,o+1,\dots ..,M_o$. “$V\left(.\right)$ is the unit step function,” which is derived as $V\left(y\right)=\left\{\begin{array}{c}1,y\ge 0\\ 0otherwise\end{array}\right\}$. It should be noted that for ${\overrightarrow{Q}}_{i-1}^m={\overrightarrow{Q}}_{i-1}^o,$, $m\ne o$ r, as probe $m$ has then fused with probe $o$ and it is unable to apply any gravitational force to $o$. Since $N_{i-1}^m=N_{i-1}^o$, the acceleration equation in this instance is uncertain, and it is set to 0.

3.4.2 Extreme gradient boosting method (XGBoost)

The XGBoost method has been used to develop an effective model with fast computing times. The accurate prediction of the drilling fluid density is very critical for wellbore stability and optimization of drilling performance, especially in a high-pressure, high-temperature drilling environment. The high-end gradient boosting method—XGBoost—utilizes this strength and ability to deal with the complex nonlinear relationship in drilling data to boost the prediction accuracy of DFD. The equation models use a blending approach for predicting decision tree losses, which optimizes future forecasts. Still, another part of the model creation process reports the importance of the influence of each feature on the final prediction of the efficiency score of the building. This feature value indicates the general predictive power of each attribute toward learning outcomes. XGBoost produces decision trees concurrently, which makes parallelization easier. The algorithm has the important property of distributed computing, which allows it to process large and complex models efficiently. The examination of extensive and varied datasets defines it as out-of-core computing. This analytical technique is used to control resource use in an efficient manner. Every iteration should involve the introduction of a new model to reduce errors.

Equation 12 is the objective of the XGBoost function at step t:

$K\left(s\right)=\sum _{j=1}K(y_{ou{t}_i},y_{ou{t}_j^{\left(s-1\right)}}+e_s\left(w_j\right)+h\left(g_s\right).(12)$

By using data from the training dataset, the variable ${\mathrm{y}}_{\text{ou}{\mathrm{t}}_{\mathrm{i}}}$ denotes a known real value. It is possible to represent the combined component as $\mathrm{e}\left(\mathrm{w}+\text{dw}\right)$, where $x=yOut{1}_j^{\left(s-1\right)}$. Using the Taylor approximation is essential. The function $f\left(w\right)$ can be approximated in the simplest linear form as show in Equation 13 follows:

$e\left(w\right)=e\left(a\right)+e(a\left(w-a\right){dw=f}_s\left(w_j\right).(13)$

This evaluation is being done in relation to the loss equation $K$, which is represented by $e\left(w\right)$. The variables dx and a represent the new learning that must be incorporated into step $s$ and the projected output $\left(s-1\right)$ from the prior method, respectively (Equations 14, 15).

$e\left(w\right)=e\left(a\right)+e\left(a\right)\left(w-a\right)+0.5e^{\prime }\left(a\right){\left(x-a\right)}^2.(14)$

$K\left(s\right)=\sum _{j=1}\left[K\left(y_{ou{t}_i},y_{ou{t}_j^{\left(s-1\right)}}\right)+g_j{e}_s\left(w_j\right)+0.5l_j{e}_s^2\left(w_j\right)\right]+h\left(e_s\right).(15)$

Following the removal of the constant components, the removed objectives that require reduction at step $s$ also exist as show in Equation 16.

$K1\left(s\right)=\sum _{j=1}\left[g_j{e}_s\left(w_j\right)+0.5l_j{e}_s^2\left(w_j\right)\right]+h\left(e_s\right).(16)$

3.4.3 Central force search-adaptive XGBoost (CFS-XGB)

CFS-XGB is a novel methodology applied for the estimation of key variable DFD in HPHT settings for drilling operations. In the approach presented herein, central force search will be used with the effective machine learning method of XGBoost. The central force search models simulate the motion of celestial objects borne out of the idea of gravitational force to produce the most accurate results within a multifunctional environment. With the help of CFS, the program efficiently searches through the search space and, therefore, easily identifies optimum model parameters for precise density prediction. A revised version of the very famous and efficient gradient boosting algorithm, called XGBoost, is integrated within the CFS framework. Due to the reciprocal advantages between central force search and XGBoost, this CFS-XGB could competently search through the vast solution space by enhancing the prediction accuracy and optimizing model parameters. CFS-XGB provides iterative improvements that deliver an improved performance and accurate density forecasts in varied drilling circumstances. The advantages associated with the CFS-XGB in this DFD forecasting exercise are many. First, it is efficient for drilling since real-time density estimation will enable supporting of decision-making throughout the operation. Second, its flexibility to change drilling circumstances ensures that it yields reliable performance in different conditions and, hence, improves the general safety and reliability of the operation. Details of the central force search adaptive XGBoost methodology are shown in pseudocode 1.

4 Result

The performance was evaluated by comparing the proposed method with existing methods. The performance was estimated in various metrics such as MSE, AAPRE, and R². The existing papers include ABR-DT (adaptive boosting regression with decision tree) (Hashemizadeh et al., 2021), SVM (support vector machine) (Hashemizadeh et al., 2021), PSO-ANN (particle swarm optimization with artificial neural network) (Ahmadi et al., 2018), FIS (fuzzy inference system) (Ahmadi et al., 2018), DT (decision tree) (Hashemizadeh et al., 2021), and GA-FIS (genetic algorithm with fuzzy inference system) (Ahmadi et al., 2018).

The Python 3.11.8 version was implemented with the help of a Windows 11 laptop, which was equipped with Intel i7 11th Gen CPU and a 64 GB RAM, which had been used for testing.

Figure 2A plots a temperature histogram in the range of minimum 50°C to maximum 150°C, with the mean temperature equal to 100°C. This will depict the distribution of a set of temperatures and the frequency of their occurrence within various ranges of temperature. Figure 2B plots a histogram of pressure from minimum 1,000 psi to maximum 5,000 psi, with a mean pressure of 3,000 psi. This will graph the distribution of the values of pressure so that one can see how often pressures of different magnitudes are represented in the dataset.

Figure 2

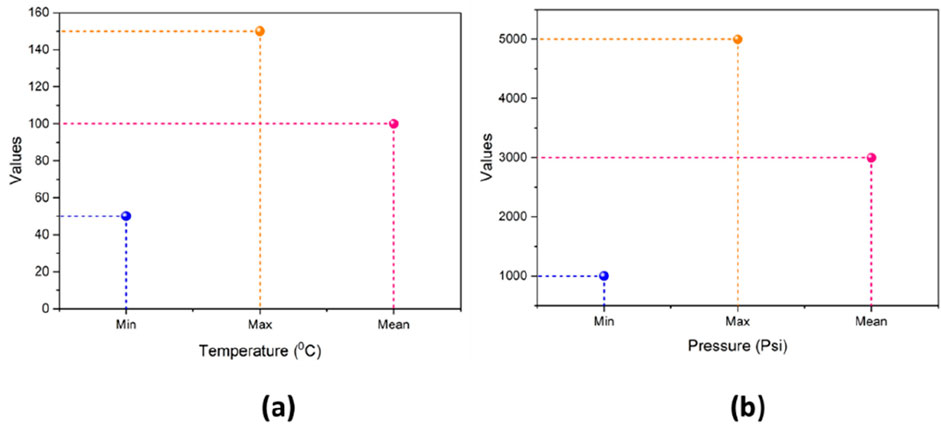
Figure 2. Histograms showing the distribution of (A) temperature ($\mathbf{50}°\mathit{C}\mathit{t}\mathit{o}\mathbf{150}°\mathit{C},\mathit{m}\mathit{e}\mathit{a}\mathit{n}=\mathbf{100}°\mathit{C}$) and (B) pressure ($\mathbf{1000}\mathit{p}\mathit{s}\mathit{i}\mathit{t}\mathit{o}\mathbf{5000}\mathit{p}\mathit{s}\mathit{i},\mathit{m}\mathit{e}\mathit{a}\mathit{n}=\mathbf{3000}\mathit{p}\mathit{s}\mathit{i}$) in the dataset.

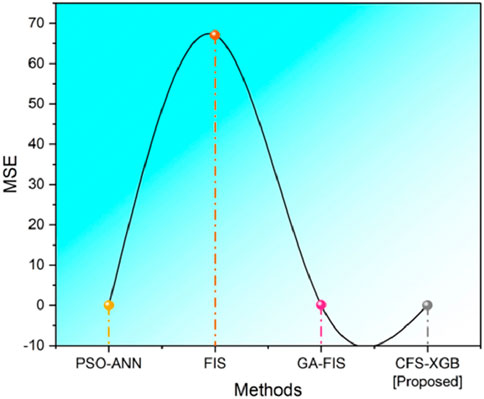
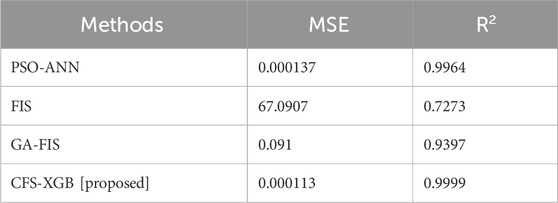
The mean squared error is an often-used statistic to evaluate the performance of the regression model. The error is the distinction between the actual and anticipated numbers, and its simple formula is the average of the squares of the errors. The disparity between the predicted and actual densities of the drilling fluids across the dataset, for example, would be measured by MSE when computing DFD. Figure 3 shows the MSE values of our suggested approach versus the MSE values of current approaches. PSO-ANN, FIS, and GA-FIS have MSE values of 0.0001374, 67.0907, and 0.091, respectively. The recommended CSF-XGB approach yields an MSE value of 0.0001134. It demonstrates that our suggested approach outperforms the existing methods.

Figure 3

Figure 3. Result of MSE (source: author).

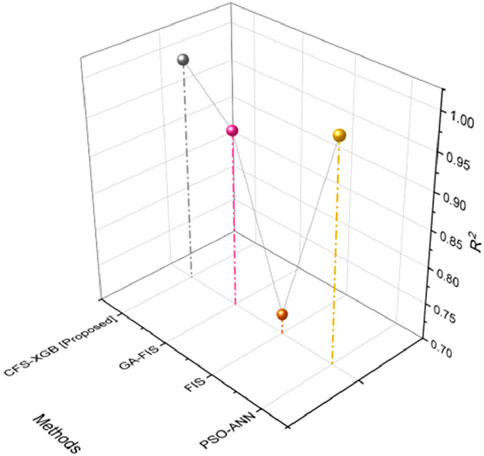
The percentage of the variance in the dependent variable that can be predicted from the independent variable is represented by the statistical measure known as R². R² would show the rate at which the selected framework predicts the variability in DFD in the context of DFD prediction. The R² value of our recommended and proposed strategy is displayed in Figure 4. The R² values of PSO-ANN, FIS, and GA-FIS are 0.9964, 0.7273, and 0.9397, respectively. The R² value obtained with the suggested CSF-XGB method is 0.9999. It proves that our proposed method works better than the existing approaches. Table 2 displays the MSE and R² results.

Figure 4

Figure 4. Result of R² (source: author).

Table 2

Table 2. Result of MSE and R².

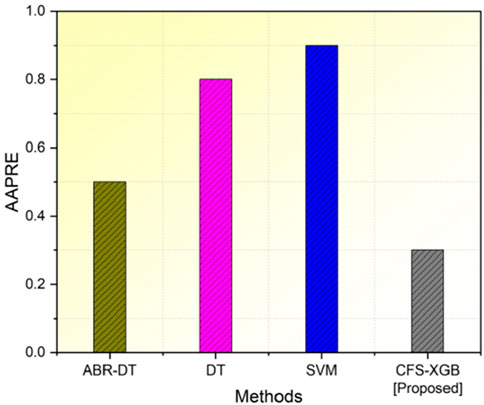
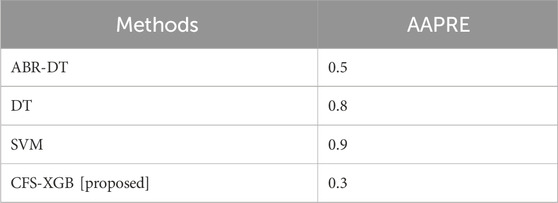
The average absolute percent relative error (AAPRE) measures the average of the absolute percentage errors relative to the true values and gives a sense of the accuracy of the predictions in percentage terms. AAPRE provides information on the average percentage difference between the projected and actual densities in the context of DFD prediction. Figure 5; Table 3 shows the AAPRE value for our suggested approach in addition to the AAPRE values of the existing approaches. AAPRE values for ABR-DT, DT, and SVM are 0.5, 0.8, and 0.9, respectively. The AAPRE value obtained using the suggested CSF-XGB method is 0.3. It proves that our proposed method works better than the existing approaches.

Figure 5

Figure 5. Result of AAPRE (source: author).

Table 3

Table 3. Result of AAPRE.

Sensitivity analysis was done to find out if the inputs affected the result (DFD, for example). Then, the quantitative effects of the parameters were determined using a relevance factor as follows:

$s=\frac{\sum _{j=1}^m\left(Y_{l,i}-\overline{Y_l}\right)\left(X_j-\overline{X}\right)}{\sqrt{\sum _{j-1}^m{\left(Y_{l,i}-\overline{Y_l}\right)}^2{\sum }_{j=1}^m{\left(X_j-\overline{X}\right)}^2}},(17)$

where $m$ is the total number of data points, $X_j$ is the output, $Y_l$ is the mean of input $l$, and $X$ is the mean output. $Y_{l,i}$ stands for input $j$ of variable $l$. The relevance factor is a scale that ranges from $-1to+1$; a greater effect on the related parameter is indicated by a larger relevance factor. A negative influence suggests that an improved parameter would cause the goal to decrease, whereas a positive influence suggests that boosting a specific input will enhance the target parameters. The temperature and initial density were two of the characteristics with a direct effect on the results. Furthermore, an inverse relationship between DFD and the pressure was discovered, meaning that increase in pressure results in a decrease in DFD. Table 4 presents the sensitivity analysis findings. As shown with a relevance factor of −0.04, pressure was determined to have the biggest negative effects.

Table 4

Table 4. Result of sensitivity analysis.

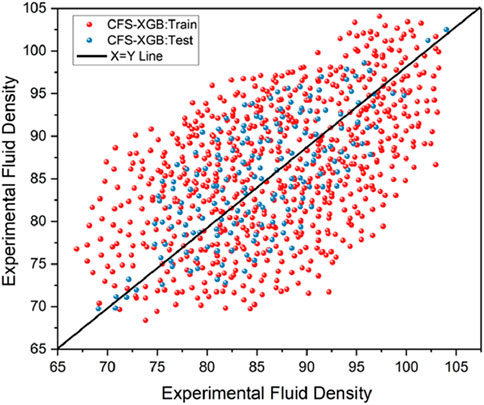
To depict the performance of generated models, graphical error analyses were used with statistical parameter assessments. Cross-plots show the predicted and experimental values. A more compact area around the unit slope line (X = Y) indicates an improved model. Figure 6 shows cross-plots for the proposed models. The suggested CFS-XGB model performs well, as evidenced by the fact that the bulk of points are positioned around the unit slope line. During the training phase, 80% of the real data points were used to develop the model, with the remaining 20% serving as test data for assessing performance.

Figure 6

Figure 6. Cross-plots of CFS-XGB fluid density (source: author).

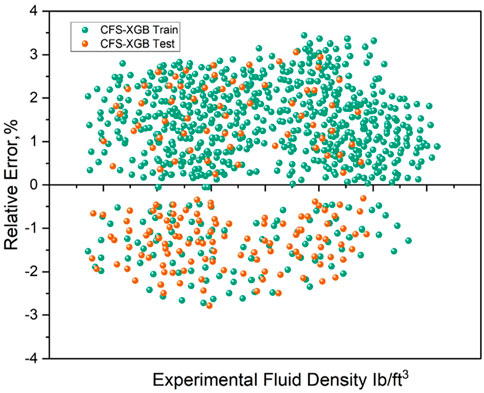
For the most precise model, CFS-XGB, Figure 6 displays the cross-plots in addition to the error distribution plot. It plots a relative error value with respect to the fluid density test results. In the case of an accurate model, the points lie around the zero error line in such a plot. Figure 7 shows that the CFS-XGB method could predict with very high accuracy, as can be noticed from the proximity of the points to the zero-error line.

Figure 7

Figure 7. Error distribution plot for the CFS-XGB method (source: author).

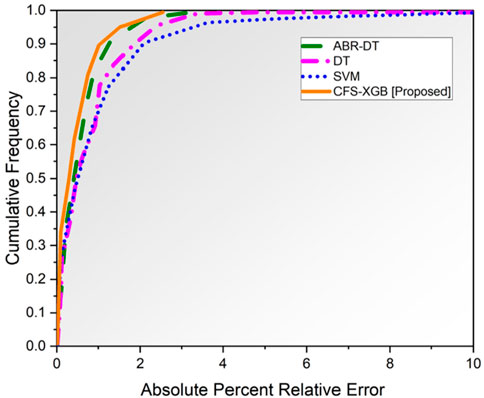
Figure 8 displays cumulative frequency error graphs for comparing model performance. The supplied chart demonstrates that the CFS-XGB model is more effective than the DT, SVM, and ABR-DT models.

Figure 8

Figure 8. Result of the cumulative frequency error (source: author).

5 Discussion

The traditional methods to predict the drilling fluid density (DFD) for the HPHT environment, such as DT, ABR-DT, SVM, PSO-ANN, FIS, and GA-FIS, have their limitations. Although DT (Hashemizadeh et al., 2021) models are interpretable, they can inherently be weak in attaining the power to model the complex, nonlinear relationships in HPHT settings, which could, in turn, lead to overfitting due to noise pollution. ABR-DT (Hashemizadeh et al., 2021) improved the predictive power of models or weak learners by reducing the variance. However, it might be prone to overfitting due to high-dimensional data and might require much parameter tuning. While SVMs (Hashemizadeh et al., 2021) can be useful to deal with small to medium data, they become expensive, less efficient, and are not suitable for large data with high dimensions that are often associated with HPHT drilling. Both PSO-ANN and GA-FIS (Ahmadi et al., 2018) were integrated optimization techniques with neural networks and fuzzy systems, respectively, to enhance the predictive accuracy, though they might be computational consumers, and hence would need high computational resources and more time to have converged. In addition, these models may not be robust and generalized under different drilling conditions. FIS (Ahmadi et al., 2018) was capable of handling uncertainty and imprecise data, but it may be less capable in a highly dynamic or complex HPHT environment where the ability to define precise membership functions and rules becomes too difficult. Furthermore, PSO-ANN and GA-FIS models are less interpretable in nature, and hence, not much actionable insight could be drawn from the predictions, which is very important in HPHT scenarios because decisions are to be made in real-time. The problem is overcome by introducing the CFS-XGB model, which outperforms traditional methods in forecasting DFD, leading to better productivity and safety in HPHT drilling operations. This advancement can help the oil and gas industry better manage the complexities and risks associated with HPHT environments.

6 Conclusion

DFD regulation is essential in HPHT drilling environments. To provide safe and effective drilling operations while limiting formation damage, this entails maintaining the proper fluid weight to offset harsh downhole conditions. This paper proposes a new machine learning methodology of central force search-based adaptive XGBoosting for improving DFD detection in HPHT drilling environments. The data gathered are preprocessed using min–max normalization. The key features are identified using BPCA, which may improve the effectiveness of the prediction. The Python platform is used to simulate our proposed method. It reveals better results with reduced MSE along with increased R-square and reduced RMSE metrics. Compared to existing methods, this technique outperforms the state-of-the-art models for the density forecasting of drilling fluid in HPHT scenarios. Under HPHT scenarios, the CFS-XGB method faces an issue with high-dimensional data management and may require further fine-tuning for execution in real-time applications. Future developments are oriented toward advanced optimization methods, enhancing its scalability, integration, and robustness.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

GS: conceptualization, data curation, investigation, methodology, resources, validation, visualization, writing–original draft, and writing–review and editing. RM: formal analysis, investigation, methodology, resources, software, supervision, validation, writing–original draft, and writing–review and editing. RC: conceptualization, funding acquisition, investigation, methodology, supervision, validation, visualization, writing–original draft, and writing–review and editing. KL: data curation, investigation, methodology, resources, software, validation, visualization, writing–original draft, and writing–review and editing. VK: data curation, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. SR: data curation, investigation, methodology, resources, validation, visualization, writing–original draft, and writing–review and editing. ME: methodology, resources, supervision, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This article was co-funded by the European Union under the REFRESH—Research Excellence For Region Sustainability and High-tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Program Just Transition.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelaal, A., Elkatatny, S., Gamal, H., and Ziadat, W. (2023a). “Drilling data based approach for equivalent circulation density prediction while drilling,,” in Paper presented at the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GA, June, 2023. doi:10.56952/ARMA-2023-0722

CrossRef Full Text | Google Scholar

Abdelaal, A., Ibrahim, A. F., and Elkatatny, S. (2023b). Data-driven framework for real-time rheological properties prediction of flat rheology synthetic oil-based drilling fluids. ACS omega 8 (16), 14371–14386. doi:10.1021/acsomega.2c06656

PubMed Abstract | CrossRef Full Text | Google Scholar

Agwu, O. E., Akpabio, J. U., and Dosunmu, A. (2020). Artificial neural network model for predicting the density of oil-based muds in high-temperature, high-pressure wells. J. Petroleum Explor. Prod. Technol. 10, 1081–1095. doi:10.1007/s13202-019-00802-6

CrossRef Full Text | Google Scholar

Ahmadi, M. A., Shadizadeh, S. R., Shah, K., and Bahadori, A. (2018). An accurate model to predict drilling fluid density at wellbore conditions. Egypt. J. Petroleum 27 (1), 1–10. doi:10.1016/j.ejpe.2016.12.002

CrossRef Full Text | Google Scholar

Alizadeh, S. M., Alruyemi, I., Daneshfar, R., Mohammadi-Khanaposhtani, M., and Naseri, M. (2021). An insight into the estimation of drilling fluid density at HPHT condition using PSO-ICA-and GA-LSSVM strategies. Sci. Rep. 11 (1), 7033. doi:10.1038/s41598-021-86264-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Alkinani, H. H., Al-Hameedi, A. T. T., Dunn-Norman, S., and Lian, D. (2020). Application of artificial neural networks in the drilling processes: can equivalent circulation density be estimated prior to drilling? Egypt. J. Petroleum 29 (2), 121–126. doi:10.1016/j.ejpe.2019.12.003

CrossRef Full Text | Google Scholar

Al-Rubaii, M., Al-Shargabi, M., Aldahlawi, B., Al-Shehri, D., and Minaev, K. M. (2023). A developed robust model and artificial intelligence techniques to predict drilling fluid density and equivalent circulation density in real-time. Sensors 23 (14), 6594. doi:10.3390/s23146594

PubMed Abstract | CrossRef Full Text | Google Scholar

Al-Rubaii, M. M. (2024). “A new automated carrying capacity index model optimizes hole cleaning efficiency and rate of penetration by applying machine learning technique,” in International petroleum technology conference. doi:10.2523/IPTC-23896-MS

CrossRef Full Text | Google Scholar

Alsaihati, A., Elkatatny, S., and Abdulraheem, A. (2020). Real-time prediction of equivalent circulation density for horizontal wells using intelligent machines. ACS omega 6 (1), 934–942. doi:10.1021/acsomega.0c05570

PubMed Abstract | CrossRef Full Text | Google Scholar

Bashir, M. N., Naseer, M. N., Quazi, M. M., Wakeel, M. S., Ali, I., Soudagar, M. E. M., et al. (2021). Systematic review of drilling problems and their solutions in petroleum engineering. Pet. Eng. 5. doi:10.33150/JITDETS-5.2.1

CrossRef Full Text | Google Scholar

Davoodi, S., Mehrad, M., Wood, D. A., Ghorbani, H., and Rukavishnikov, V. S. (2023). Hybridized machine learning for prompt prediction of rheology and filtration properties of water-based drilling fluids. Eng. Appl. Artif. Intell. 123, 106459. doi:10.1016/j.engappai.2023.106459

CrossRef Full Text | Google Scholar

Gamal, H., Abdelaal, A., and Elkatatny, S. (2021). Machine learning models for equivalent circulating density prediction from drilling data. ACS omega 6 (41), 27430–27442. doi:10.1021/acsomega.1c04363

PubMed Abstract | CrossRef Full Text | Google Scholar

Gautam, S., Guria, C., and Gope, L. (2021). Prediction of high-pressure/high-temperature rheological properties of drilling fluids from the viscosity data measured on a coaxial cylinder viscometer. SPE J. 26 (05), 2527–2548. doi:10.2118/206714-PA

CrossRef Full Text | Google Scholar

Ghamdi, A., Saihati, A., Abdelrahman, M., Omar, M., and Abdulraheem, A. (2021). “Improving rate of penetration in high-pressure high-temperature gas wells by utilization of managed pressure drilling and artificial intelligence,” in SPE/IADC Middle East drilling technology conference and exhibition. doi:10.2118/202159-MS

CrossRef Full Text | Google Scholar

Gul, S. (2021). Machine learning applications in drilling fluid engineering: a review. Int. Conf. Offshore Mech. Arct. Eng. 85208, V010T11A007. doi:10.1115/OMAE2021-63094

CrossRef Full Text | Google Scholar

Hashemizadeh, A., Maaref, A., Shateri, M., Larestani, A., and Hemmati-Sarapardeh, A. (2021). Experimental measurement and modeling of water-based drilling mud density using adaptive boosting decision tree, support vector machine, and K-nearest neighbors: a case study from the South Pars gas field. J. Petroleum Sci. Eng. 207, 109132. doi:10.1016/j.petrol.2021.109132

CrossRef Full Text | Google Scholar

Kandil, A., Khaled, S., and Elfakharany, T. (2023). Prediction of the equivalent circulation density using machine learning algorithms based on real-time data. AIMS Energy 11 (3), 425–453. doi:10.3934/energy.2023023

CrossRef Full Text | Google Scholar

Krishna, S., Ridha, S., Vasant, P., Ilyas, S. U., and Sophian, A. (2020). Conventional and intelligent models for detection and prediction of fluid loss events during drilling operations: a comprehensive review. J. Petroleum Sci. Eng. 195, 107818. doi:10.1016/j.petrol.2020.107818

CrossRef Full Text | Google Scholar

Mengich, H., Kabugu, M., and Ondiaka, M. N. (2022). Prediction of rheological properties of recirculating water-based drilling mud in geothermal exploration using artificial neural networks with tensor Flow. Eur. J. Energy Res. 2 (4), 49–56. doi:10.24018/ejenergy.2022.2.4.77

CrossRef Full Text | Google Scholar

Okonkwo, S. I. F., and Joel, O. F. (2023). Modelling the effects of temperature and pressure on equivalent circulating density (ECD) during drilling operations using artificial neural networks. J. Eng. Res. Rep. 25 (9), 70–82. doi:10.9734/jerr/2023/v25i9982

CrossRef Full Text | Google Scholar

Pedrosa, C., Saasen, A., and Ytrehus, J. D. (2021). Fundamentals and physical principles for drilled cuttings transport—cuttings bed sedimentation and erosion. Energies 14 (3), 545. doi:10.3390/en14030545

CrossRef Full Text | Google Scholar

Quitian-Ardila, L. H., Andrade, D. E., and Franco, A. T. (2024). A proposal for a constitutive equation fitting methodology for the rheological behavior of drilling fluids at different temperatures and high-pressure conditions. Geoenergy Sci. Eng. 233, 212570. doi:10.1016/j.geoen.2023.212570

CrossRef Full Text | Google Scholar

Samnejad, M., Gharib Shirangi, M., and Ettehadi, R. (2020). “A digital twin of drilling fluids rheology for real-time rig operations,” in Paper presented at the Offshore Technology Conference, Houston, TX, May, 2020. doi:10.4043/30738-MS

CrossRef Full Text | Google Scholar

Syah, R., Ahmadian, N., Elveny, M., Alizadeh, S. M., Hosseini, M., and Khan, A. (2021). Implementation of artificial intelligence and support vector machine learning to estimate the drilling fluid density in high-pressure high-temperature wells. Energy Rep. 7, 4106–4113. doi:10.1016/j.egyr.2021.06.092

CrossRef Full Text | Google Scholar

Tariq, Z., Murtaza, M., Alrasheed, S. A., Kamal, M. S., Yan, B., and Mahmoud, M. (2024). An experimental study and machine learning modeling of shale swelling in extended reach wells when exposed to diverse water-based drilling fluids. Energy and Fuels 38, 4151–4166. doi:10.1021/acs.energyfuels.3c05129

CrossRef Full Text | Google Scholar