An optimization dispatching strategy for integrated electricity and natural gas systems with fast charging stations

With the increasing number of electric vehicles (EVs), a large amount of charging load will affect the safety and economic operation of the distribution network (DN). In this paper, an optimization dispatching strategy for integrated electricity and natural gas systems (IEGS) with fast charging stations (FCSs) is proposed to address the impact of fast charging loads. Firstly, the FCS load model is established based on the simulation of vehicle traveling and vehicle charging. Secondly, a natural gas supply model is established, which includes constraints such as the adjustment range, direction, and total number of supply flow adjustments. Then, an optimization dispatching strategy for IEGS based on energy storage and gas storage is proposed. Finally, the effectiveness of the proposed strategy is verified. The simulation results show that when the proposed strategy is applied, the voltage of FCS node will be stabilized within a good range. And the energy purchase cost will be reduced by more than 50%. The proposed method improves the carrying capacity of DN for FCSs.

1 Introduction

With the development of energy system, modern energy system infrastructure has evolved into the coupled system with electricity and natural gas, which typically includes multiple large-scale and geographically diverse energy regions. The similarity in the consumption of electricity and natural gas leads to that the key task of the coupled system is the coordinating optimization (Qi et al., 2019). Due to the increasing penetration of gas turbines, the power system and natural gas system are becoming increasingly bidirectional coupled (Conejo et al., 2020). In order to address the challenges of optimization dispatching of natural gas and power integrated systems, scholars have conducted research on the optimization dispatching model of integrated electricity and natural gas systems.

Scholars have recognized the significant regulatory potential that arises from the synergy between power and natural gas systems. However, the modeling and solving techniques for constrained optimization problem needed to be improved (Zhou et al., 2023). To address this, various researchers have proposed different models and methods.

1.1 Optimization models and energy flow

Zhang et al. (2021) proposed a two-layer quadratic curve optimal energy flow model. The optimal flow model of conical AC power was established in the upper level model. And the power generation cost of natural gas generator units was calculated based on the marginal price of natural gas. Jia et al. (2020) proposed a probabilistic energy flow convex optimization method for the integrated energy system. The piecewise linear approximation method was used to linearize the nonlinear objective function. Thereby the probabilistic energy flow calculation model was transformed into a linear programming model. The gas turbines were applied to improve power generation and consumption balance in short-term dispatching to achieve closer coordination between power system and natural gas system (Mirzaei et al., 2020). Zeng et al. (2019) proposed an integrated electricity and natural gas systems (IEGS) model that takes into account electricity to natural gas facilities and gas storage facilities. In addition, sequential Monte Carlo (SMC) method was used to evaluate the reliability of IEGS. Nasiri et al. (2023) proposed a two-layer dispatching model based on the multiple energy service providers (MESP). MESP minimizes the cost of purchasing electricity and natural gas by operating energy storage systems and demand response plans (DRPs). A Lagrangian relaxation multi-step strategy was proposed to realized collaborative optimization of IEGS (Faridpak et al., 2020).

1.2 Performance evaluation and resilience

Qi et al. (2017) proposed a flexible model to evaluate the performance of (IEGS) in extreme weather conditions, namely the energy assistance between the power system and the natural gas network. Shao et al. (2017) proposed a comprehensive planning algorithm for IEGS to enhance the resilience of the power system under extreme conditions. And a variable uncertainty set has been developed to describe the interaction between power system expansion status and extreme events. Correa-Posada and Sánchez-Martın (2014) proposed an optimal power flow calculation model, which considers the N-1 criteria for IEGS. And a fault analysis method for natural gas systems was established to realized rapid fault analysis based on the linear sensitivity factor method. Meng et al. (2019) proposed a sequential energy flow analysis method for IEGS based on multiple balance nodes. Ni et al. (2016) proposed a multi energy optimal power flow solution method for IEGS. Based on the concept of energy hubs, the coupling relationship between different energy systems was considered.

1.3 Innovative methods

Qin et al. (2019) proposed a hybrid multi-objective optimization and game theory approach (HMOGTA) to realized optimized operation of an integrated energy system consisting of an electric and natural gas (E&G) utility network, multiple distributed energy stations (DESs), and multiple energy users (EU). Unified models and data-driven methods: However, due to the different characteristics of control mechanisms, network topology, and dynamic processes between power system and gas system, it is difficult to realized the collaborative optimization of IEGS. In order to solve this problem, a unified transient energy flow model was proposed based on the singular perturbation theory and dynamic model of IEGS (Huang et al., 2022). Wang et al. (2021) proposed a data-driven opportunity constrained method for calculating the optimal power flow of IEGS. Tabebordbar et al. (2023) proposed an optimization framework to control the optimal scale of cogeneration and P2G technology in IEGS. Gao et al. (2023) designed a rolling scheduling framework for IEGS. Based on the framework a partial differential equation mathematical model was proposed. The dynamics of natural gas pipelines and the operational characteristics of P2G facilities can be expressed accurately to maintain the authenticity of IEGS in the rolling scheduling process. Wang et al. (2020) proposed a two-stage low-carbon operational planning model based on bilateral trading mechanism and active demand side management (DSM), aiming to reduce carbon emissions. The carbon emission flow (CEF) model is used to track emissions and calculate carbon intensity, considering energy storage systems.

1.4 IEGS with FCSs

Wu et al. (2022) proposed a novel carbon-oriented expansion planning model of IEGS with FCSs to determine the optimal alternatives, locations, and sizes for ecofriendly candidate assets, including roof-top PV panels and fuel cell (FC) units in each FCS, as well as renewable energy units and carbon capture and storage (CCS) systems in IEGS. Salvatti et al. (2024) an optimized power management strategy for FCS with integrated battery energy storage systems (BESS) was proposed. The proposed strategy aimed to monitor the variation in AC voltage at the point of common coupling (PCC) and the state of charge (SOC) of the BESS, with the objective of establishing a deterministic formulation to find the optimal instantaneous BESS power level. Shi et al. (2022) proposed a novel sensitivity analysis-based FCS planning approach, which considers the voltage sensitivity of each sub-network in the distribution network and charging service availability for EV drivers in the transportation network.

The above literature mainly studies the issue of FCS integration into IEGS from a planning perspective. But the operation guidance for IEGS is not provided. Li et al. (2021) proposed a bi-level optimal scheduling model for community integrated energy system (CIES) with an charging station in multi-stakeholder scenarios, where an integrated demand response program comprising a dynamic pricing mechanism was designed. Weng et al. (2020) proposed a joint planning model of active distribution network and transportation network including electricity, gas, heat, and traffic loads. Zhang et al. (2024) proposed a two-stage robust operation method of electricity-gas-heat integrated MEMGs considering heterogeneous uncertainties was proposed to coordinate multiple energy carriers. Jiang et al. (2023) has conducted research on the coordinated scheduling of IEGS from the perspective of carbon emissions. And the committed carbon emission operation region (CCEOR) was proposed. Zheng et al. (2021) peoposed a data-driven integrated electricity-gas system stochastic co-optimisation model to co-optimise these two energy systems for day-ahead market clearance. For the public transport in IEGS, Zhu et al. (2023) proposed coordination planning of IEGS and charging station considering carbon emission reduction in this article that responds effectively to emerging concerns with energy and transportation integration inefficiencies and is less environmentally friendly.

1.5 Contributions

Although the above research has conducted a systematic study on IEGS, it has ignored the load characteristics of DN. More and more electric vehicles (EVs) will be connected to distribution network (DN), especially the connection of fast charging stations (FCSs), which will have a negative impact on the operation of DN. In response to the shortcomings of the above research, the main contributions of this paper are as follows:

(1) Based on DTALite simulation, the travel status of vehicles is simulated. The process of EV travel and charging is simulated through hourly and timely rolling to achieve multi time scale charging load modeling. The charging price follows the principle of hourly rolling based on TOU. The changes of travel path will be simulated due to charging. And the charging load model is established.

(2) An optimization dispatching strategy considering energy storage and gas storage is proposed for IEGS. A natural gas supply model is established, which includes constraints such as the adjustment amplitude, direction, and total number of supply flow adjustments. Simulation results showed that the proposed strategy can improve the reliability and economy of IEGS. The negative impact of FCSs on the operation of DN is reduced.

2 System model

2.1 EVs model

In this paper, the model of EVs can be divided into three parts for modeling, namely the initial power model, the travel power model, and the charging power model.

(1) The initial power model

The initial power model represents the remaining battery capacity of EVs when the EVs departs. The initial power model is shown in Equation 1.

$S_{\text{EV}}=S_{\text{EV}}^{\text{ini}}(1)$

where $S_{\text{EV}}^{\text{ini}}$ is the initial battery remaining power of EV; $S_{\text{EV}}$ is the battery remaining power of EV.

(2) The travel power model

$S_{\text{EV}}^{\prime }=S_{\text{EV}}^{\text{ini}}-L_{\text{road}}{\delta }_{\text{EV}}(2)$

In Equation 2, $S_{EV}^{\prime }$ is the battery remaining power of EV after completing the trip; $L_{road}$ is the travel mileage; ${\delta }_{EV}$ is the unit mileage power consumption of EVs.

(3) The charging power model

$S_{\text{EV}}^{″}=S_{\text{EV}}^{\prime }+p_{\text{pile}}\Delta t(3)$

In Equation 3, $S_{\text{EV}}^{″}$ is the battery remaining power of EV after completing charging; $p_{\text{pile}}$ is the charging power of the charging pile; $\Delta t$ is the charging time of EV.

2.2 Fast charging station load model

In this paper, EVs will choose nearby fast charging stations for charging. Therefore, the charging load is related to the number of vehicles going to FCS for charging. The charging load model is shown in Equations 4–5.

$P_{\text{FCS}}={\displaystyle \sum _{i_{\text{FCS}}=1}^{n_{\text{FCS}}}}{\mu }_{i_{\text{FCS}}}{p}_{\text{pile}}(4)$

${\mu }_{i_{\text{FCS}}}=\left\{\begin{array}{cc}1& \text{Charging pile used}\\ 0& \text{Charging station used}\end{array}\right.(5)$

where $P_{\text{FCS}}$ is the charging load of FCS; ${\mu }_{i_{\text{FCS}}}$ is a binary variable representing the occupancy of charging pile; $i_{\text{FCS}}$ is the ID of the fast charging pile; $n_{\text{FCS}}$ is the number of charging piles within FCS.

2.3 Natural gas supply system model

The Weymouth equation is an equation used to calculate the flow characteristics of fluids in pipelines under flow pressure and temperature conditions. This equation considers the influence of fluid compressibility on flow measurement, especially under high pressure and high flow conditions. The Weymouth equation can help engineers predict and calculate fluid flow in pipelines more accurately. In natural gas supply systems, the Weymouth equation is usually used to describe the pipeline retention state of the natural gas network which is described in Equation 6.

$\left|G_{mn,\text{ave},t}\right|G_{mn,\text{ave},t}=C_{mn}^2\left({\pi }_{m,t}^2-{\pi }_{n,t}^2\right)(6)$

where $G_{mn,\text{ave},t}$ is the average flow of natural gas in pipeline $mn$ at time $t$; ${\pi }_{m,t}$ and ${\pi }_{n,t}$ are the gas pressures at node $m$ and node $n$ of the natural gas pipeline respectively; $C_{mn}$ is the Weymouth constant, which is related to physical properties such as pipeline temperature, pipeline length, pipeline diameter, and pipeline friction.

The flow balance constraints of the natural gas network are as follows:

${\displaystyle \sum _{n\in {\mathfrak{R}}_P\left(n\right)}}\left(G_{mn,t}^e-G_{mn,t}^h\right)+{\displaystyle \sum _{s\in {\mathfrak{R}}_s\left(n\right)}}\left(G_{s,t}^{out}-G_{s,t}^{in}\right)+{\displaystyle \sum _{c\in {\mathfrak{R}}_C\left(n\right)}}{G}_{c,t}^C={\displaystyle \sum _{l\in {\mathfrak{R}}_{GL}\left(n\right)}}{G}_{l,t}^L+{\displaystyle \sum _{g\in {\mathfrak{R}}_g\left(n\right)}}{G}_{g,t}^{GT}(7)$

In Equation 7, ${\mathfrak{R}}_P\left(n\right)$ is the set of natural gas pipelines connected to node $n$; ${\mathfrak{R}}_s\left(n\right)$ is the set of natural gas storge connected to node $n$; ${\mathfrak{R}}_C\left(n\right)$ is the set of natural valve stations connected to node $n$; ${\mathfrak{R}}_{GL}\left(n\right)$ is the set of natural gas load connected to node $n$; ${\mathfrak{R}}_g\left(n\right)$ is the set of gas turbine connected to node $n$; $G_{mn,t}^e$ and $G_{mn,t}^h$ are the gas flow at the end and beginning of the natural gas pipeline $mn$ at time $t$ respectively; $G_{s,t}^{out}$ and $G_{s,t}^{in}$ are the release and intake volume of the natural gas storage at time $t$; $G_{c,t}^C$ is the natural gas flow of the natural valve station at time $t$; $G_{l,t}^L$ is the gas flow of the natural gas load connected to node $n$ at time t; $G_{g,t}^{GT}$ is the gas flow of the gas turbine connected to the node $n$ at time $t$.

Meanwhile, a linear storage model is applied to describe the dynamic characteristics of natural gas pipelines.

$R_{mn,t}=L_{mn}{\pi }_{mn,\text{ave},t}(8)$

$R_{mn,t}=R_{mn,t-1}+G_{mn,t}^h-G_{mn,t}^e(9)$

${\pi }_{mn,\text{ave},t}=\frac{{\pi }_{m,t}+{\pi }_{n,t}}{2}(10)$

$G_{mn,\text{ave},t}=\frac{G_{mn,t}^e+G_{mn,t}^h}{2}(11)$

where $R_{mn,t}$ is the natural gas reserve of the pipeline $mn$ at time $t$; ${\pi }_{mn,\text{ave},t}$ is the average pressure of natural gas pipeline $mn$; $L_{mn}$ is the length of the pipeline.

The pressure constraints at natural gas pipeline nodes, pipeline operation constraints, and gas supply constraints at natural gas valve stations are defined in Equations 12–14:

${\pi }_{t,\min }\le {\pi }_t\le {\pi }_{t,\max }(12)$

$R_{mn,t,\min }\le R_{mn,t}\le R_{mn,t,\max }(13)$

$G_{c,t,\min }^C\le G_{c,t}^C\le G_{c,t,\max }^C(14)$

where ${\pi }_{t,\max }$ and ${\pi }_{t,\min }$ are the upper and lower limits of the node gas pressure respectively; $R_{mn,t,\max }$ and $R_{mn,t,\min }$ are the upper and lower limits of the pipeline retention respectively; $G_{c,t,\max }^C$ and $G_{c,t,\min }^C$ are the upper and lower limits of natural valve station gas supply volume.

2.4 Natural gas storage device model

The constraints of natural gas storage devices are defined in Equations 15–20:

$R_{s,t}=R_{s,t-1}-w_{s,t}^{out}\frac{G_{s,t}^{out}}{{\eta }_{s,out}}+w_{s,t}^{in}{G}_{s,t}^{in}{\eta }_{s,in}(15)$

$G_{s,t.\min }^{out}\le G_{s,t}^{out}\le G_{s,t,\max }^{out}(16)$

$G_{s,t.\min }^{in}\le G_{s,t}^{in}\le G_{s,t,\max }^{in}(17)$

$w_{s,t}^{out}=\left\{\begin{array}{cc}0& \text{Not releasing gas}\\ 1& \text{Releasing gas}\end{array}\right.(18)$

$w_{s,t}^{in}=\left\{\begin{array}{cc}0& \text{Not inflating gas}\\ 1& \text{ Inflating gas}\end{array}\right.(19)$

$0\le w_{s,t}^{in}+w_{s,t}^{out}\le 1(20)$

where $R_{s,t}$ is the storage capacity of the natural gas storage device at time $t$; ${\eta }_{s,in}$ and ${\eta }_{s,out}$ are the inflation efficiency and release efficiency of the gas storage device respectively; $w_{s,t}^{out}$ and $w_{s,t}^{in}$ are binary variables that represent the inflation and deflation status of the gas storage device; $G_{s,t,\max }^{out}$ and $G_{s,t.\min }^{out}$ are the maximum and minimum release capacities of the gas storage device respectively; $G_{s,t,\max }^{in}$ and $G_{s,t.\min }^{in}$ are the maximum and minimum inflation capacities of the gas storage device respectively.

3 Optimal dispatching strategy

3.1 Objection function

In this paper, a collaborative optimization dispatching strategy is proposed for IEGS with FCSs to realize safe and economical operation of the system.

Objection function:

The objection function is divided into two parts: the operating costs of the power system and the natural gas network. And the specific expression is as follows:

$\min {\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{c=1}^{N_c}}{\lambda }_{c,t}{G}_{c,t}^C+{\displaystyle \sum _{t=1}^T}{\lambda }_{P,t}{P}_t^{Grid}(21)$

In Equation 21, ${\lambda }_{c,t}$ is the gas supply price of the natural valve station at time t; ${\lambda }_{P,t}$ is the TOU of DN; $P_t^{Grid}$ is the purchase electricity of DN; $T$ is the number of time periods.

3.2 Constraints

Distribution network constraints are defined in Equations 22–27.

$U_{\min }^2\le V_{i,t}\le U_{\max }^2(22)$

$0\le l_{ij,t}\le l_{ij,\max }(23)$

$P_{ij,t}+{\displaystyle \sum _{i_G=1}^{N_{\mathrm{G}}}}{\kappa }_j{P}_{t,i_G}=r_{ij}{l}_{ij,t}+p_{j,t}+{\displaystyle \sum _{j:j\to k}}{P}_{jk,t}+{\displaystyle \sum _{i_{\text{FCS}}=1}^{N_{\text{FCS}}}}{\upsilon }_j{P}_{t,i_{\text{FCS}}}(24)$

$Q_{ij,t}=x_{ij}{l}_{ij,t}+q_{j,t}+{\displaystyle \sum _{j:j\to k}}{Q}_{jk,t}(25)$

$V_{i,t}+l_{ij,t}\left(r_{ij}^2+x_{ij}^2\right)=2\left(r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t}\right)+V_{j,t}(26)$

${‖\begin{array}{c}2P_{ij,t}\\ 2Q_{ij,t}\\ V_{i,t}-l_{ij,t}\end{array}‖}_2\le V_{i,t}+l_{ij,t}(27)$

where $\mathfrak{R}$ is the set of DN nodes; $P_{ij,t}$ is the active power of branch $ij$; $Q_{ij,t}$ is the reactive power of branch $ij$; $V_{i,t}$ is the square of the voltage amplitude; $l_{ij,t}$ is the square of the current amplitude; $U_{\min }$ and $U_{\max }$ are the minimum and maximum values of node voltage amplitude respectively; $r_{ij}$ is the resistance value of branch $ij$; $x_{ij}$ is the reactance value of branch $ij$; $i_G$ is the ID of gas turbine; $N_G$ is the number of gas turbine; $P_{t,i_G}$ is the active power output of gas turbine; ${\kappa }_j$ is a binary variable that indicates whether the gas turbine is installed at node $j$; $p_{j,t}$ is the active load of node $j$; $q_{j,t}$ is the reactive load of node $j$; ${\upsilon }_j$ is a binary variable that indicates whether FCS is installed at node $j$.

Natural gas network constraints:

The gas supply system model is defined in this paper. The constraint conditions for the natural gas network are (3)–(8).

At the same time, the adjustment constraints for natural gas valve stations include natural gas supply flow constraints, supply volume adjustment constraints, supply volume adjustment frequency constraints, and supply flow limit constraints. The adjustment constraints for natural gas valve stations are defined in Equations 28–34.

$\left(w_t^{+}+w_t^{-}\right)\Delta G_{c,t}^C\le \left|G_{c,t}^C-G_{c,t-1}^C\right|\le \left(w_t^{+}+w_t^{-}\right)\Delta G_{c,t}^C(28)$

$0\le w_t^{+}+w_{t+1}^{-}\le 1(29)$

$0\le w_t^{-}+w_{t+1}^{+}\le 1(30)$

$0\le w_t^{+}+w_{t+1}^{+}\le 1(31)$

$0\le w_t^{-}+w_{t+1}^{-}\le 1(32)$

$0\le w_t^{+}+w_t^{-}\le 1(33)$

$0\le {\displaystyle \sum _t^T}{w}_t^{+}+w_t^{-}\le N_{\max }^C(34)$

where $\Delta G_{c,t}^C$ is the amount of natural gas valve station climbing and landslide; $w_t^{+}$ is a binary variable, when $w_t^{+}=1$, the natural gas valve station will increase the gas supply; when $w_t^{+}=0$, the natural gas valve station will not increase the gas supply; $w_t^{-}$ is a binary variable, when $w_t^{-}=1$, the natural gas valve station will reduce the gas supply; when $w_t^{-}=0$, the natural gas valve station will not reduce the gas supply; $N_{\max }^C$ is the maximum number of times a natural gas valve station can adjust its gas supply.

4 Algorithm design

4.1 Charging load calculation method

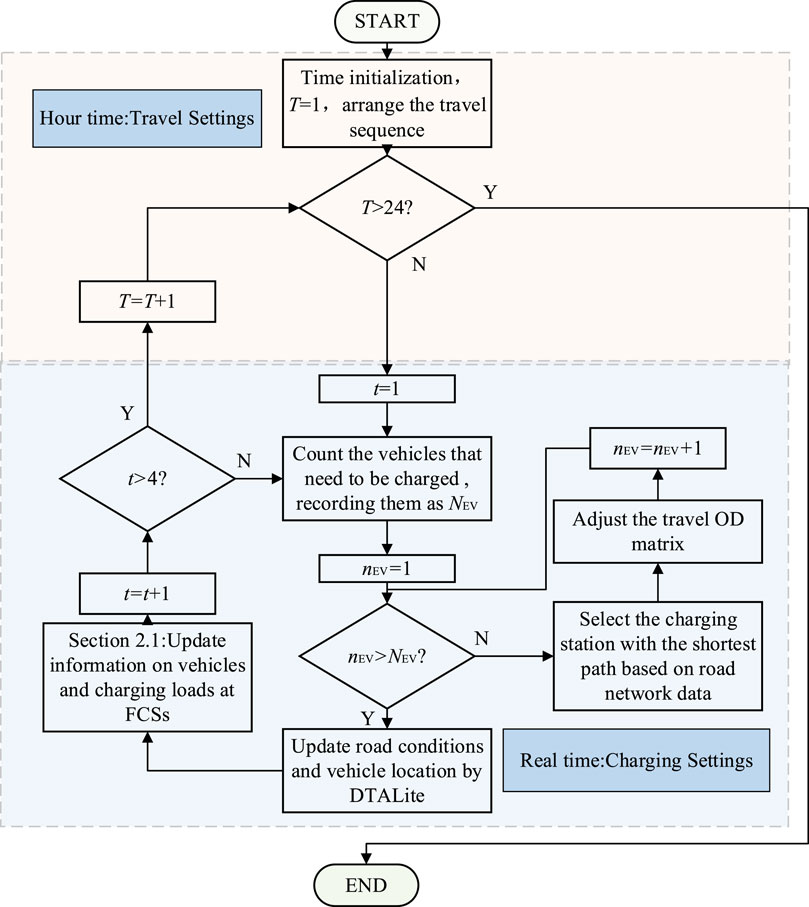
In terms of charging load simulation calculation, based on simulating vehicle travel, it is assumed that EVs will go to the nearest charging station to complete charging. Therefore, the simulation process of vehicle travel and vehicle charging is shown in the Figure 1. And DTALite is applied for simulation of vehicle travel.

Figure 1

Figure 1. Charging load calculation process.

4.2 Optimization dispatching strategy calculation method

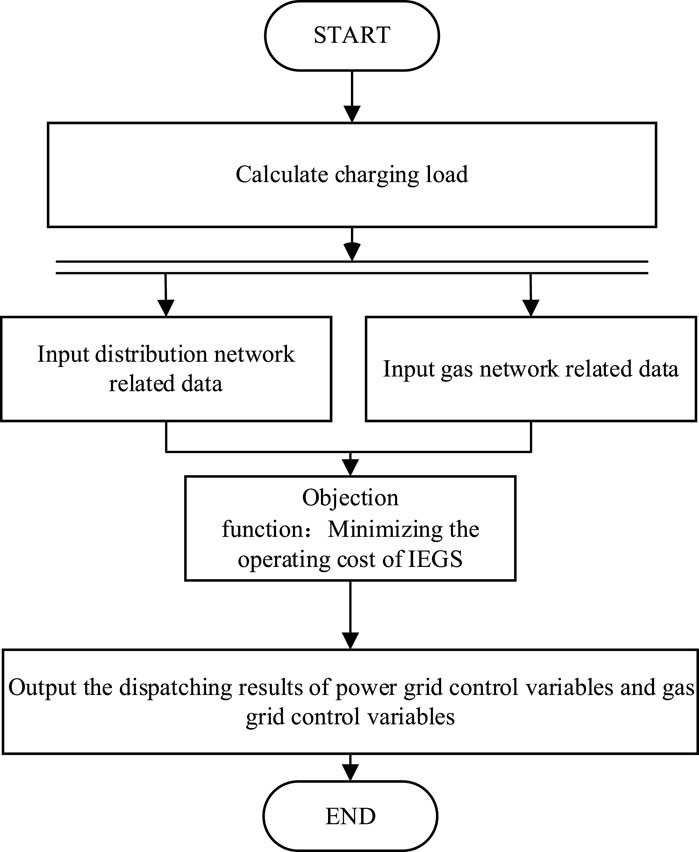
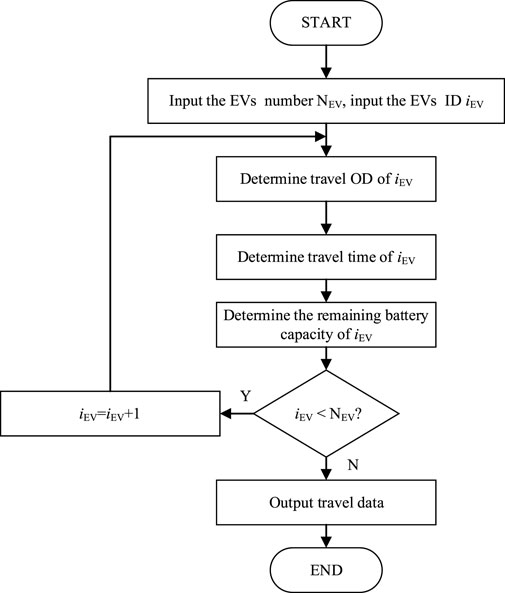
In terms of optimizing the calculation method of dispatching strategy, the calculation process is shown in Figure 2. In Figure 2, the calculation process is divided into hour time part and real time part. In hour time part, the vehicles travel plan for each hour within a day will be counted. In real time part, the travel of vehicles will be simulated. And the FCSs selection of EVs will be simulated every 15 min. And the process of generating travel data is shown in Figure 3.

Figure 2

Figure 2. Optimizing dispatch strategy solving process.

Figure 3

Figure 3. The process of generating travel data.

The steps of the algorithm are as follows:

Step 1: Calculate the charging load based on the proposed charging load calculation method. The charging plan for EVs will not be changed. And EVs will go to the fixed FCSs for charging.

Step 2: (1) Input distribution network related data: load data, distribution network topology data.

(2) Input gas network related data: gas load data, gas network topology data.

Step 3: Optimize calculations: The optimization objective is to minimize the operation cost of IEGS. The constraints include DN operation constraints, GN operation constraints, FCSs constraints, and gas turbine constraints.

Objection function: (21)

Constraints: (6)–(11), (22)–(34)

Step 4: Output the dispatching results of IEGS. The dispatching results of IEGS include the operating status of DN and the operation costs of IEGS.

5 Case study

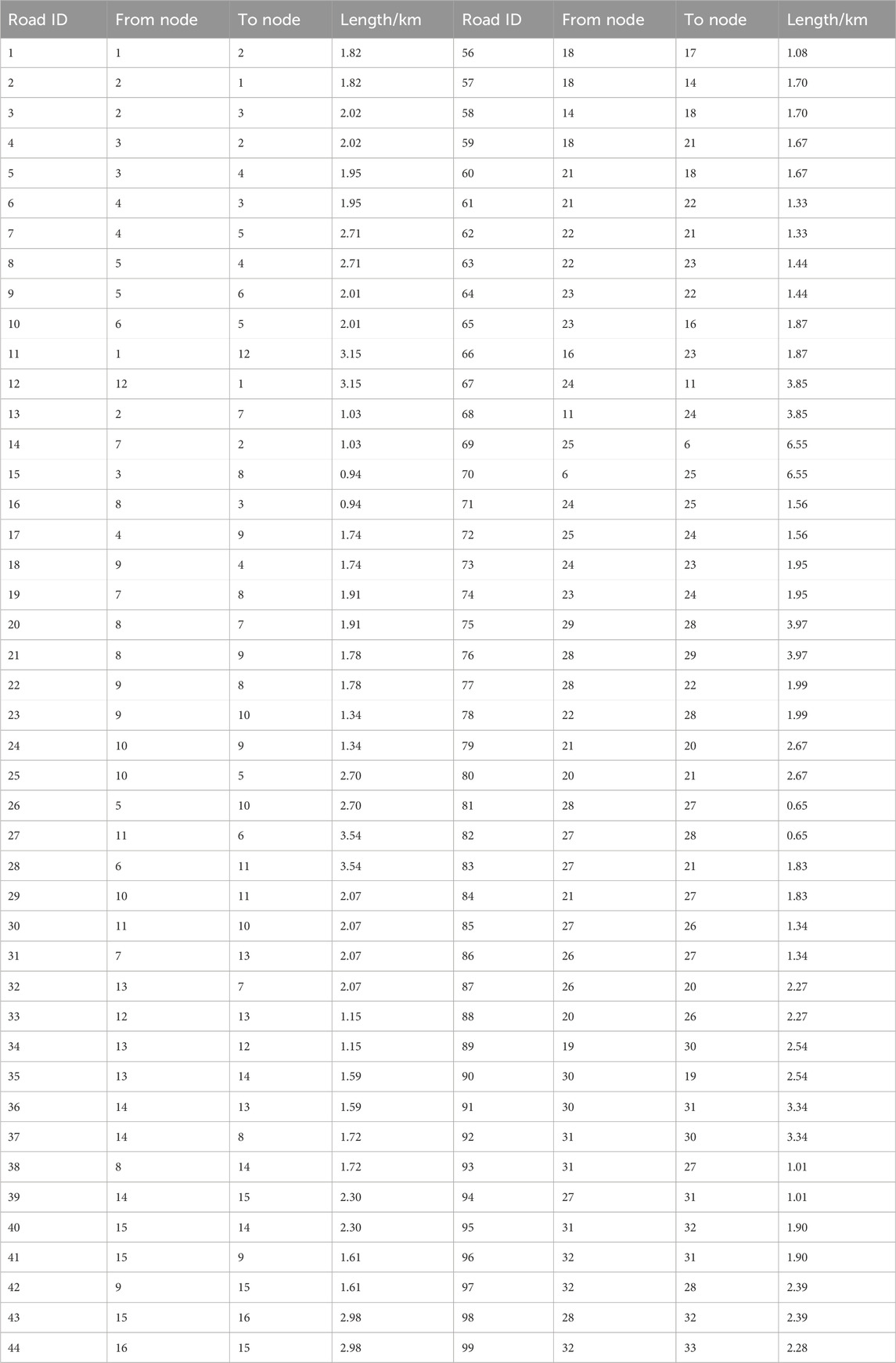
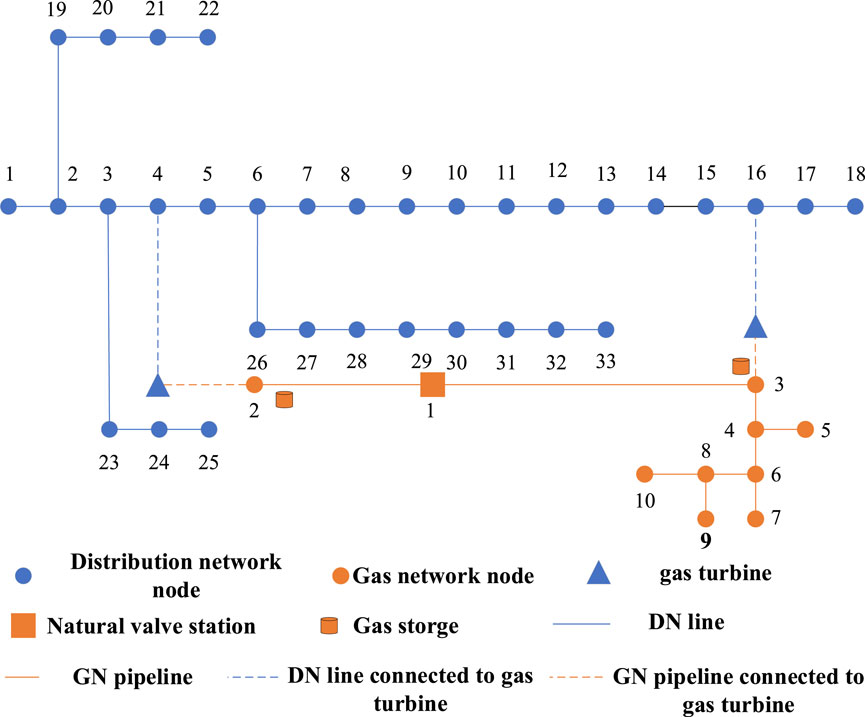
In terms of the setting of IEGS, we select the IEEE 33 node system as the DN part. Gas turbines are equipped at nodes 4 and 16 to realize coupling with the natural gas network. At the same time, a road network size of about 10*10 km² is selected. The roads are all two-way roads. The road network data is shown in Table 1. There are 5 FCSs in the road network, which are located in three different DNs. Among them, two FCSs are located in DN of IEGS. The data settings for IEGS are shown in Figures 4, 5 and Table 2. In this paper, the travel data is generated based in NHTS. The SOC of EVs follows a uniform distribution between 10% and 90%. When the SOC of EVs is below 20%, EVs will go to the FCSs for charging. The proportion of travel distribution is shown in Table 3. In this paper, all the simulations are conducted in the MATLAB 2020a, Gurobi and DTALite in a 64-bit Windows environment with YALMIP toolbox, on a PC with Core i5-8265u CPU @1.60 GHz and 8 GB RAM.

Table 1

Table 1. Road network data.

Figure 4

Figure 4. IEGS architecture.

Figure 5

Figure 5. Road network structure.

Table 2

Table 2. FCS setting.

Table 3

Table 3. The proportion of travel distribution.

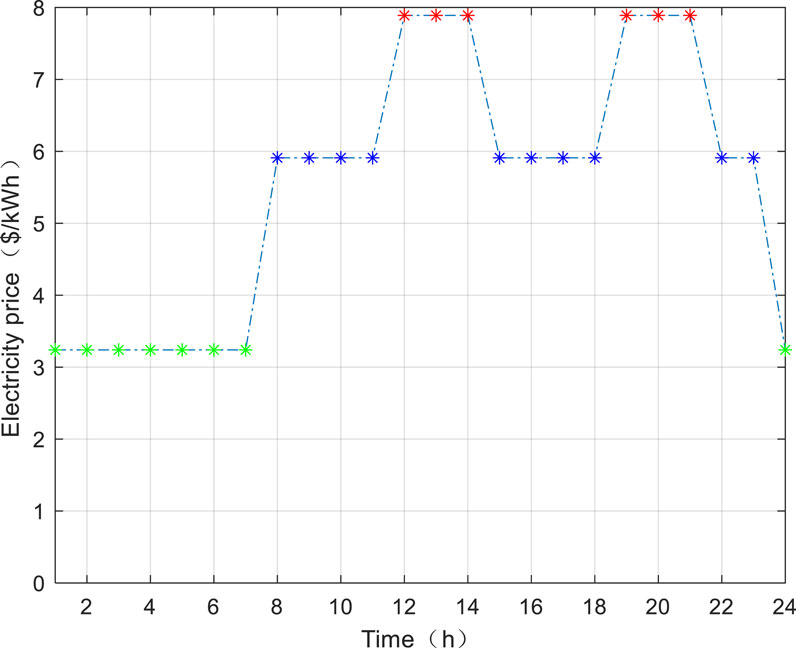
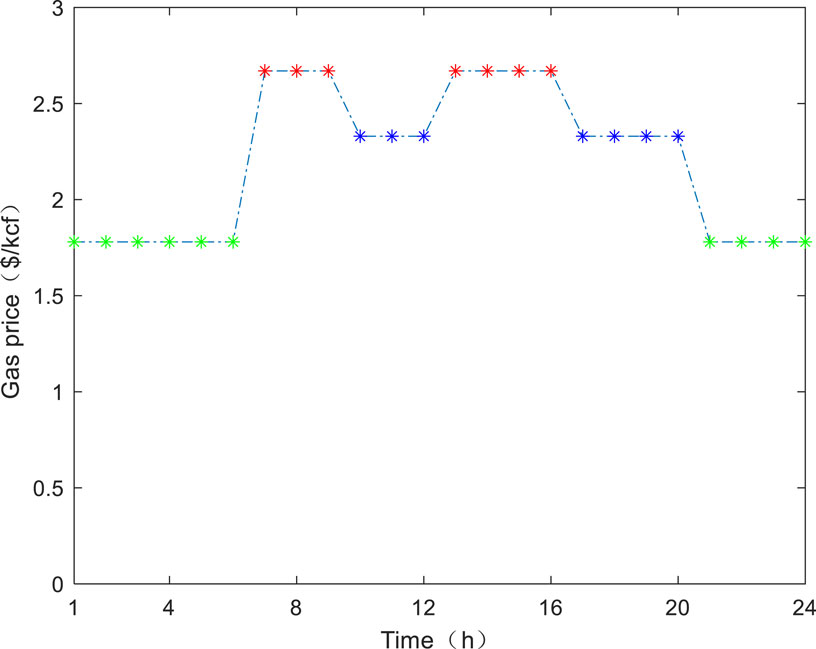
In the calculation process, TOU is applied for DN and the gas network. The distribution of TOU is shown in the Figures 6, 7. The distribution of charging load is shown in the Figure 8.

Figure 6

Figure 6. TOU of distribution network.

Figure 7

Figure 7. TOU of gas network.

Figure 8

Figure 8. Charging load curve.

The parameters of gas storge is shown in Table 4.

Table 4

Table 4. The parameters of gas storage.

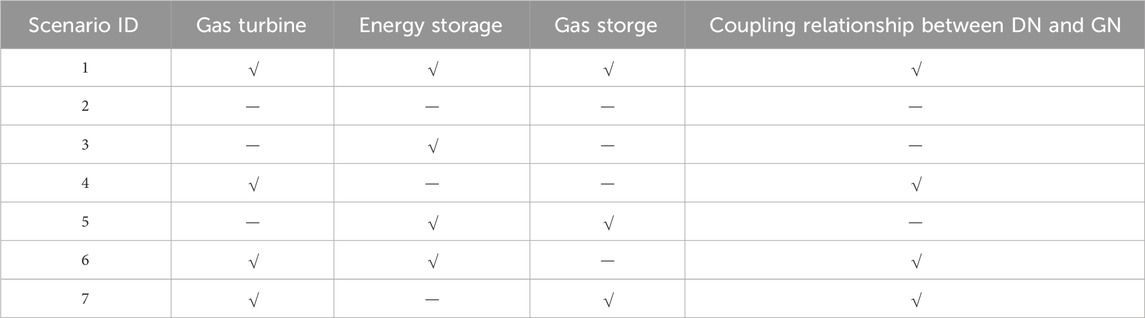
At the same time, in order to verify the effectiveness of the dispatching strategy for IEGS, 7 scenarios are set for analysis, which are shown in Table 5.

Table 5

Table 5. The scenario setting.

For scenario 1, DN and GN are coupled. The energy storage and the gas storage are installed. For scenario 2, DN and GN are not coupled. The energy storage and the gas storage are not installed. For scenario 3, DN and GN are not coupled. The energy storage is installed. The gas storage is not installed. For scenario 4, DN and GN are coupled. The energy storage and the gas storage are not installed. For scenario 5, DN and GN are not coupled. The energy storage and the gas storage are not installed. For scenario 6, DN and GN are coupled. The energy storage is installed. The gas storage is not installed. For scenario 7, DN and GN are coupled. The energy storage is not installed. The gas storage is installed.

5.1 Comparative analysis of DN voltage

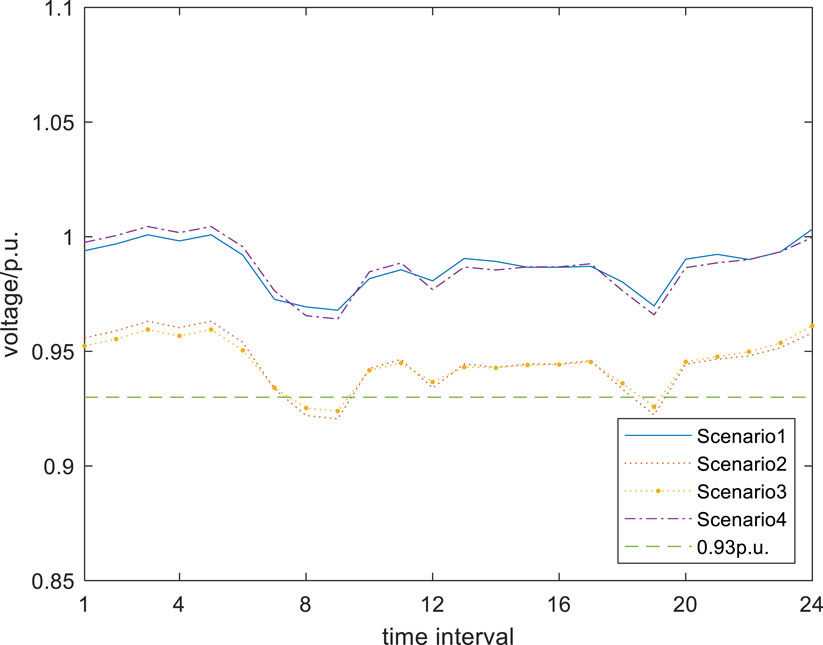
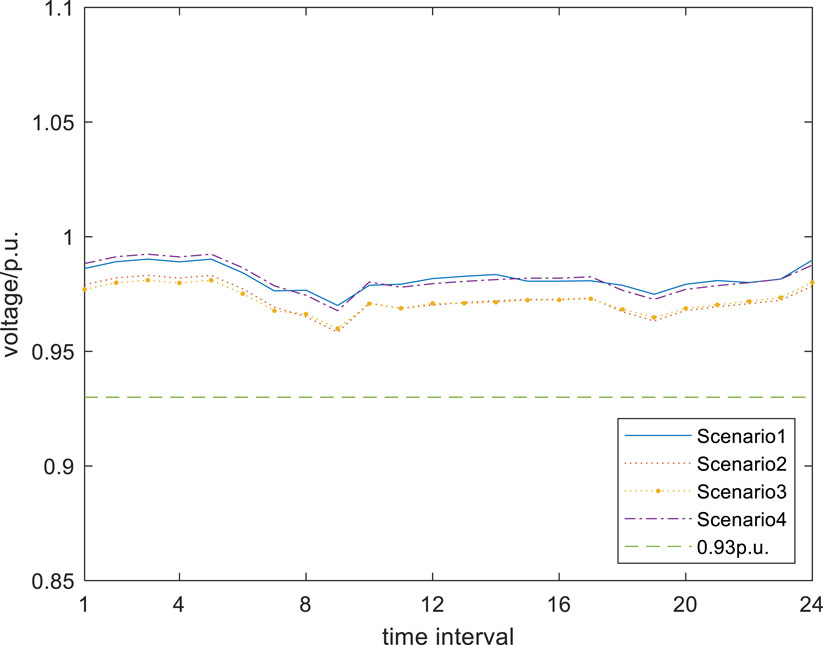
The voltage distribution of FCSs nodes is shown in Figures 9, 10.

Figure 9

Figure 9. FCS 1 node voltage.

Figure 10

Figure 10. FCS 4 node voltage.

For FCS 1 node, when DN is coupled with the gas network and equipped with energy and gas storage devices, the voltage of FCS 1 node does not exceed the limit. At the same time, when DN is coupled with the gas grid without energy storage and gas storage devices, the voltage of FCS 1 node also does not exceed the limit. When the distribution network is not coupled with the gas network, according to scenario 2 and scenario 3, it can be seen that even with energy storage installed, it is difficult to meet the safe and stable operation requirements of DN. And the voltage exceeds the lower limit. From scenarios 3 and 4, it can be seen that equipping energy storage devices in DN can to some extent alleviate the problem of voltage exceeding the lower limit caused by charging loads, but this problem has not been solved.

For FCS 2 node, the voltage does not exceed the lower limit. The voltage distribution in scenario 1 and scenario 4 is better than that in scenario 2 and scenario 3. When DN is coupled with the gas network, it can improve the operation of DN. With the support of gas turbines, the operation pressure of DN is alleviated.

From the voltage distribution, it can be seen that equipping a certain capacity of ES within DN cannot solve the voltage limit problem caused by charging loads. When the gas turbines are applied to realize system coupling between DN and GN, the voltage will be maintained within a good range. Therefore, the coupled operation of DN and the GN can better support the stable operation of DN.

5.2 Energy purchase cost analysis

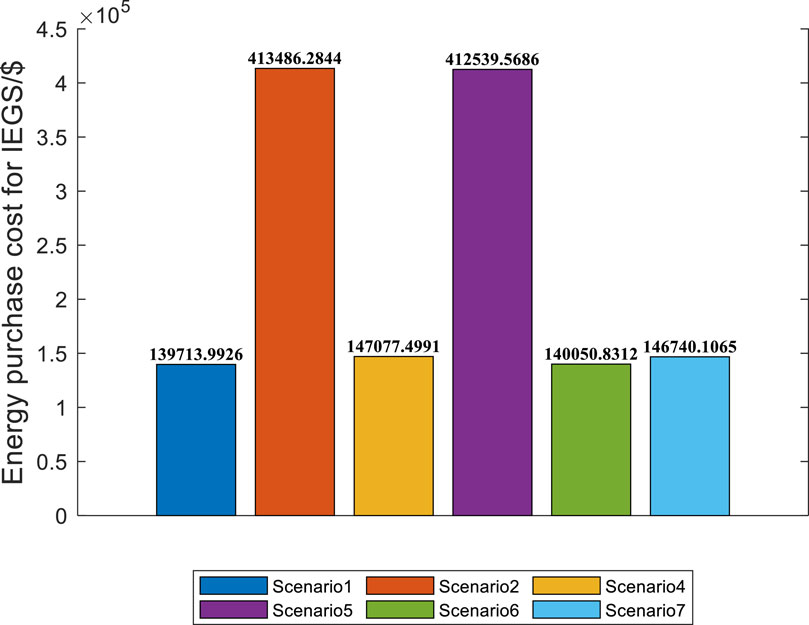
The comparison of electricity purchase costs for DN is shown in Figure 11. The comparison of gas purchase costs for gas networks is shown in Figure 12. The comparison of energy purchase costs for IEGS is shown in Figure 13.

Figure 11

Figure 11. Electricity purchase cost for distribution network.

Figure 12

Figure 12. Gas purchase cost for gas network.

Figure 13

Figure 13. Energy purchase cost for IEGS.

In Figure 11, when DN and gas network are coupled through gas turbines, the gas network can provide energy to DN to reducing the amount of electricity purchased of DN. The purchase of electricity has been reduced. When DN and gas network operate independently, DN lacks energy support from gas network, so more electricity needs to be purchased to meet the load demand. The purchase of electricity has been increased.

For Figure 12, the gas network does not need to provide energy support to DN in scenario 2 and scenario 5. It only needs to meet the gas load demand of the gas network, so the cost of purchasing gas is relatively low. When the energy coupling between the gas network and the distribution network is realized through gas turbines, the gas network can support the energy to DN, so the gas purchase cost of the gas network will be increased.

For Figure 13, due to the independent operation of the distribution network and gas network in scenario 2 and scenario 5, there is a lack of energy support between the two systems. The gas network cannot provide energy support to DN based on TOU, which increases the overall operating cost of IEGS.

When the gas turbines are applied to realize system coupling between DN and GN, the electricity purchase cost of DN will be reduced significantly. But the natural gas purchase cost of DN will be increased significantly. For the energy purchase cost of IEGS, when the stable state of the systems is ignored, the energy purchase cost of IEGS will be decrease significantly owing to the support to DN from GN.

5.3 Analysis of active power loss for DN

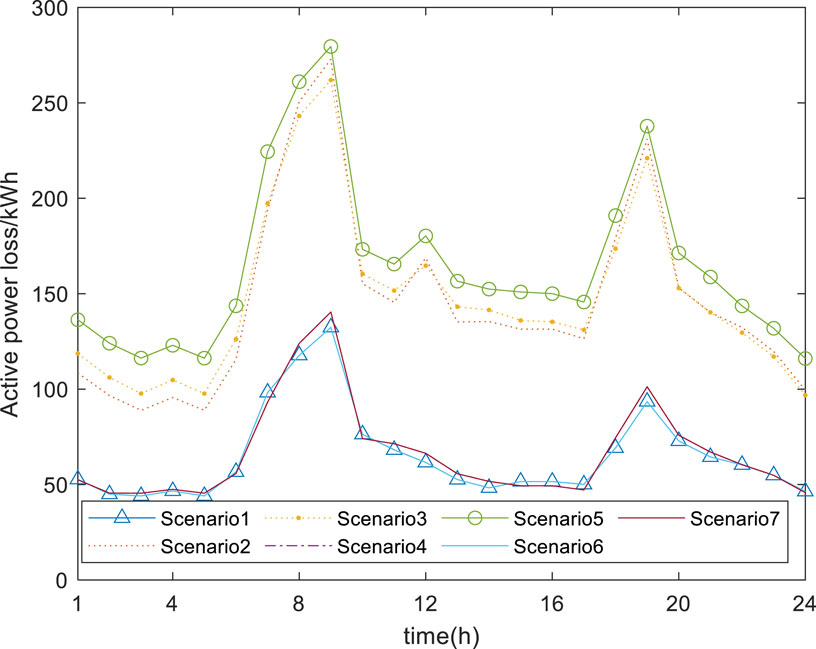
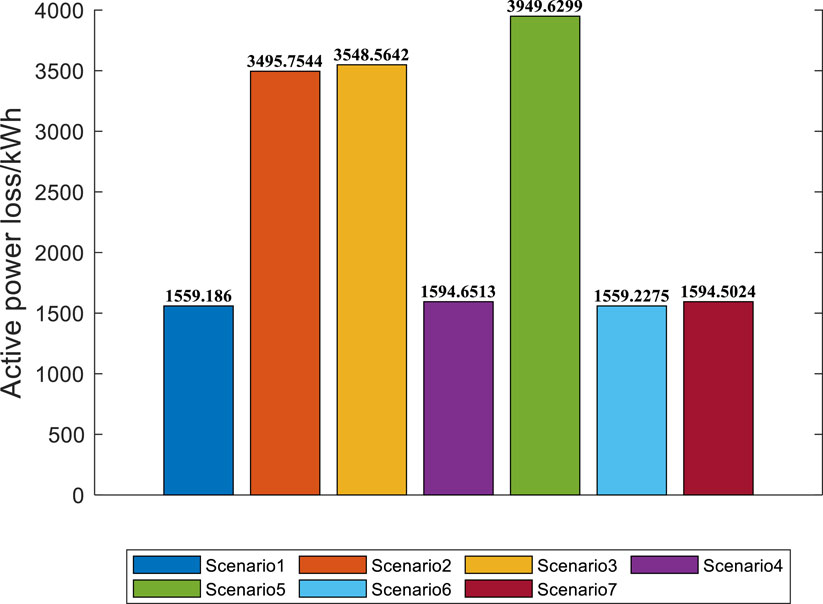
The comparative distribution of time-sharing active power loss and total active power loss for DN is shown in Figures 14, 15.

Figure 14

Figure 14. Timeshare active power loss.

Figure 15

Figure 15. Total active power loss.

In Figure 14, the active power loss of DN coupling with the gas network is much smaller than the active power loss of the independent operation of DN. In Figure 15, the total active power loss of DN coupling with the gas network is much smaller than the active power loss of the independent operation of DN. At the same time, when energy storage and gas storage equipment are equipped in the integrated energy system of electricity and gas coupling, it reduces the active power loss of the distribution network to a certain extent.

6 Conclusion

In this paper, an optimized scheduling strategy is proposed for IEGS connected to FCSs. Firstly, a dynamic charging load modeling method is proposed. The travel and charging process of the EVs is simulated. The precision of charging load modeling is improved. Secondly, the energy support and mutual assistance between DN and gas network are realized. And the economic operation of IEGS is realized based on energy storage and gas storage devices.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LG: Writing–review and editing, Writing–original draft, Software, Resources, Project administration. YS: Writing–review and editing, Writing–original draft, Software, Methodology, Formal Analysis. HL: Writing–review and editing, Writing–original draft, Formal Analysis. KZ: Writing–review and editing, Writing–original draft. YY: Writing–review and editing, Writing–original draft. MQ: Writing–review and editing, Writing–original draft. ZT: Writing–review and editing, Visualization.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors LG, HL, KZ, and YY were employed by Guangdong Power Grid Energy Investment Co., Ltd. Authors YS, MQ, and ZT were employed by Dongfang Electronics Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Conejo, A. J., Chen, S., and Constante, G. E. (2020). Operations and long-term expansion planning of natural-gas and power systems: a market perspective. Proc. IEEE 108 (9), 1541–1557. doi:10.1109/jproc.2020.3005284

CrossRef Full Text | Google Scholar

Correa-Posada, C. M., and Sánchez-Martın, P. (2014). Security-constrained optimal power and natural-gas flow. IEEE Trans. Power Syst. 29 (4), 1780–1787. doi:10.1109/tpwrs.2014.2299714

CrossRef Full Text | Google Scholar

Faridpak, B., Farrokhifar, M., Murzakhanov, I., and Safari, A. (2020). A series multi-step approach for operation Co-optimization of integrated power and natural gas systems. Energy 204, 117897. doi:10.1016/j.energy.2020.117897

CrossRef Full Text | Google Scholar

Gao, H., Li, Z., Wang, C., Chen, S., Fan, M., and Sun, H. (2023). Rolling dispatch framework of integrated electricity-gas system considering power-to-gas facilities and natural gas network dynamics: modelling and case studies. Int. J. Electr. Power and Energy Syst. 152, 109259. doi:10.1016/j.ijepes.2023.109259

CrossRef Full Text | Google Scholar

Huang, B., Wang, L., Wang, R., Han, R., and Sun, Q. (2022). A unified model for transient flow analysis of the integrated electric power and natural gas system with multiple time scales. Int. J. Electr. Power and Energy Syst. 142, 108133. doi:10.1016/j.ijepes.2022.108133

CrossRef Full Text | Google Scholar

Jia, W., Ding, T., Huang, C., Wang, Z., Zhou, Q., and Shahidehpour, M. (2020). Convex optimization of integrated power-gas energy flow model with applications to probabilistic energy flow. IEEE Trans. Power Syst. 36 (2), 1432–1441. doi:10.1109/tpwrs.2020.3018869

CrossRef Full Text | Google Scholar

Jiang, Y., Ren, Z., and Li, W. (2023). Committed carbon emission operation region for integrated energy systems: concepts and analyses. IEEE Trans. Sustain. Energy 15, 1194–1209. doi:10.1109/tste.2023.3330857

CrossRef Full Text | Google Scholar

Li, Y., Han, M., Yang, Z., and Li, G. (2021). Coordinating flexible demand response and renewable uncertainties for scheduling of community integrated energy systems with an electric vehicle charging station: a bi-level approach. IEEE Trans. Sustain. Energy 12 (4), 2321–2331. doi:10.1109/tste.2021.3090463

CrossRef Full Text | Google Scholar

Meng, Q. W., Guan, Q. S., Jia, N., Zhang, L. X., and Wang, Y. S. (2019). An improved sequential energy flow analysis method based on multiple balance nodes in gas-electricity interconnection systems. IEEE Access 7, 95487–95495. doi:10.1109/access.2019.2929875

CrossRef Full Text | Google Scholar

Mirzaei, M. A., Nazari-Heris, M., Mohammadi-Ivatloo, B., Zare, K., Marzband, M., and Anvari-Moghaddam, A. (2020). A novel hybrid framework for co-optimization of power and natural gas networks integrated with emerging technologies. IEEE Syst. J. 14 (3), 3598–3608. doi:10.1109/jsyst.2020.2975090

CrossRef Full Text | Google Scholar

Nasiri, N., Saatloo, A. M., Mirzaei, M. A., Ravadanegh, S. N., Zare, K., Mohammadi-ivatloo, B., et al. (2023). A robust bi-level optimization framework for participation of multi-energy service providers in integrated power and natural gas markets. Appl. Energy 340, 121047. doi:10.1016/j.apenergy.2023.121047

CrossRef Full Text | Google Scholar

Ni, L., Feng, C., Wen, F., and Salam, A. (2016). Optimal power flow of multiple energy carriers with multiple kinds of energy storage. IEEE Power Energy Soc. General Meet. (PESGM) 39, 1–5. doi:10.1109/pesgm.2016.7741940

CrossRef Full Text | Google Scholar

Qi, F., Shahidehpour, M., Wen, F., Li, Z., He, Y., and Yan, M. (2019). Decentralized privacy-preserving operation of multi-area integrated electricity and natural gas systems with renewable energy resources. IEEE Trans. Sustain. Energy 11 (3), 1785–1796. doi:10.1109/tste.2019.2940624

CrossRef Full Text | Google Scholar

Qi, S., Wang, X., Wang, Y., Tian, S., and Wang, R. (2017). “Integrated probabilistic energy flow analysis in natural gas and electricity coupled systems considering the randomness of wind power,”in 2017 IEEE Conference on Energy Internet and Energy System Integration (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Qin, Y., Wu, L., Zheng, J., Li, M., Jing, Z., Wu, Q. H., et al. (2019). Optimal operation of integrated energy systems subject to coupled demand constraints of electricity and natural gas. CSEE J. Power Energy Syst. 6 (2), 444–457. doi:10.17775/CSEEJPES.2018.00640

CrossRef Full Text | Google Scholar

Salvatti, G. A., da Rosa, J. M., Carati, E. G., Mezaroba, M., and Rech, C. (2024). Deterministic power management strategy for fast charging station with integrated energy storage system. Sustain. Energy, Grids Netw. 37, 101251. doi:10.1016/j.segan.2023.101251

CrossRef Full Text | Google Scholar

Shao, C., Shahidehpour, M., Wang, X., Wang, X., and Wang, B. (2017). Integrated planning of electricity and natural gas transportation systems for enhancing the power grid resilience. IEEE Trans. Power Syst. 32 (6), 4418–4429. doi:10.1109/tpwrs.2017.2672728

CrossRef Full Text | Google Scholar

Shi, X., Xu, Y., Guo, Q., Sheng, Y., Sun, H., Chen, F., et al. (2022). Novel planning approach for fast-charging station in integrated system. CSEE J. Power Energy Syst. 9 (5), 1832–1844.

Google Scholar

Tabebordbar, A., Rastegar, M., and Ebrahimi, M. (2023). Reliability-oriented optimal sizing of power-to-gas and combined heat and power technologies in integrated electricity and natural gas transmission systems. Sustain. Cities Soc. 95, 104593. doi:10.1016/j.scs.2023.104593

CrossRef Full Text | Google Scholar

Wang, J., Wang, C., Liang, Y., Bi, T., Shafie-khah, M., and Catalão, J. P. (2021). Data-driven chance-constrained optimal gas-power flow calculation: a Bayesian nonparametric approach. IEEE Trans. Power Syst. 36 (5), 4683–4698. doi:10.1109/tpwrs.2021.3065465

CrossRef Full Text | Google Scholar

Wang, Y., Qiu, J., Tao, Y., Zhang, X., and Wang, G. (2020). Low-carbon oriented optimal energy dispatch in coupled natural gas and electricity systems. Appl. Energy 280, 115948. doi:10.1016/j.apenergy.2020.115948

CrossRef Full Text | Google Scholar

Weng, C., Hu, Z., Xie, S., Chen, Z., Liu, S., and Du, Y. (2020). Coupled planning of suburban integrated energy system with electric-biogas-traffic considering fast charging station equalization. IEEE Access 8, 226008–226025. doi:10.1109/access.2020.3044459

CrossRef Full Text | Google Scholar

Wu, T., Wei, X., Zhang, X., Wang, G., Qiu, J., and Xia, S. (2022). Carbon-oriented expansion planning of integrated electricity-natural gas systems with EV fast-charging stations. IEEE Trans. Transp. electrification 8 (2), 2797–2809. doi:10.1109/tte.2022.3151811

CrossRef Full Text | Google Scholar

Zeng, Z., Ding, T., Xu, Y., Yang, Y., and Dong, Z. (2019). Reliability evaluation for integrated power-gas systems with power-to-gas and gas storages. IEEE Trans. Power Syst. 35 (1), 571–583. doi:10.1109/tpwrs.2019.2935771

CrossRef Full Text | Google Scholar

Zhang, R., Chen, Y., Li, Z., Jiang, T., and Li, X. (2024). Two-stage robust operation of electricity-gas-heat integrated multi-energy microgrids considering heterogeneous uncertainties. Appl. Energy 371, 123690. doi:10.1016/j.apenergy.2024.123690

CrossRef Full Text | Google Scholar

Zhang, R., Jiang, T., Li, F., Li, G., Li, X., and Chen, H. (2021). Conic optimal energy flow of integrated electricity and natural gas systems. J. Mod. Power Syst. Clean Energy 9 (4), 963–967. doi:10.35833/mpce.2020.000244

CrossRef Full Text | Google Scholar

Zheng, X., Xu, Y., Li, Z., and Chen, H. (2021). Co-optimisation and settlement of power-gas coupled system in day-ahead market under multiple uncertainties. IET Renew. Power Gener. 15 (8), 1632–1647. doi:10.1049/rpg2.12073

CrossRef Full Text | Google Scholar

Zhou, B., Ai, X., Fang, J., Li, K., Yao, W., Chen, Z., et al. (2023). Function-space optimization to coordinate multi-energy storage across the integrated electricity and natural gas system. Int. J. Electr. Power and Energy Syst. 151, 109181. doi:10.1016/j.ijepes.2023.109181

CrossRef Full Text | Google Scholar

Zhu, J., He, C., Cheung, K., Luo, F., Liu, Y., Guo, T., et al. (2023). Coordination planning of integrated energy system and electric vehicle charging station considering carbon emission reduction. IEEE Trans. Industry Appl. 59, 7555–7569. doi:10.1109/tia.2023.3298330

CrossRef Full Text | Google Scholar