
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Energy Res. , 06 May 2024
Sec. Energy Storage
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1391692
This article is part of the Research Topic Optimization and Data-driven Approaches for Energy Storage-based Demand Response to Achieve Power System Flexibility View all 25 articles
The temporal variation of wind power is primarily influenced by wind speed, exhibiting high levels of randomness and fluctuation. The accuracy of short-term wind power forecasts is greatly affected by the quality of Numerical Weather Prediction (NWP) data. However, the prediction error of NWP is common, and posing challenges to the precision of wind power prediction. To address this issue, the paper proposes a NWP wind speed error correction model based on Residual Network-Gated Recurrent Unit (ResNet-GRU). The model corrects the forecasted wind speeds at different heights to provide reliable data foundation for subsequent predictions. Furthermore, in order to overcome the difficulty of selecting network parameters for the combined prediction model, we integrate the Kepler Optimization Algorithm (KOA) intelligent algorithm to achieve optimal parameter selection for the model. We propose a Convolutional Neural Network-Long and Short-Term Memory Network (CNN-LSTM) based on Attention Mechanism for short-term wind power prediction. Finally, the proposed methods are validated using data from a wind farm in northwest China, demonstrating their effectiveness in improving prediction accuracy and their practical value in engineering applications.
In the context of “dual carbon” goals, accelerating the transformation of the energy structure towards a low-carbon, clean, and renewable energy system, with a focus on new energy sources, is an important initiative to achieve the dual carbon targets (REN et al., 2022). Currently, China’s wind power industry is experiencing rapid development, with a continuously thriving market and increasing wind power grid integration (Hui et al., 2021). However, the current power system scheduling and operation mechanisms in China are not sound, and there is insufficient peak-shifting capacity to meet the requirements of large-scale wind power grid integration, leading to significant curtailment of wind power in some regions. To effectively address wind curtailment and improve the scheduling and operation capabilities of the power system, precise wind power output forecasting is essential. The accuracy of wind power forecasting directly affects the scheduling optimization of the power grid (Yusheng et al., 2015; Weisheng et al., 2021).
Currently, wind power forecasting techniques can be broadly classified into two categories based on modeling mechanisms: physical methods and statistical learning methods (Ahmed and Khalid, 2019; Wang et al., 2021). Physical methods utilize fluid dynamics and thermodynamics models to solve for wind speed, wind direction, and other information based on the topography and terrain of the wind farm. The wind power output is then calculated using the wind power curve. Due to limitations in spatiotemporal resolution, physical methods are generally more suitable for medium to long-term forecasting. On the other hand, statistical learning methods analyze historical data from wind farms to establish nonlinear mappings between wind power characteristics and forecast results. With the rapid development of artificial intelligence in recent years, many researchers have introduced deep learning algorithms to address the aforementioned issues (Anbo et al., 2022). Deep learning methods, such as LSTM (Zhu et al., 2017), backpropagation (Liu et al., 2020), Dropout (Niu et al., 2018), Attention Mechanism (AM) (Zhou et al., 2021), and others, have been widely applied in forecasting tasks, benefiting from the increased availability and complexity of collected data.
In short-term wind power forecasting, utilizing NWP for wind power prediction is more realistic and practical (DU, 2019). However, the quality of NWP data significantly impacts the accuracy of the forecasts, and it has been observed that there are inherent errors between NWP data and actual measurements. To mitigate these inherent errors, numerous researchers have focused on correcting NWP wind speed. In reference (Ding et al., 2019), a variational mode decomposition technique was used to decompose NWP wind speed, followed by correction using the GRU. Reference (Hu et al., 2021) considered the spatial correlation of wind speed and employed Gaussian Process Regression (GPR) to improve the correlation between forecasted and actual wind speeds. Reference (Song et al., 2018) analyzed NWP data from multiple locations and established a wind speed correction model using temporal convolutional neural networks, which enhanced the accuracy of wind speed correction. However, most of the mentioned correction methods rely on a single neural network, and the exploration of the relationship between NWP data and actual measurements is not fully comprehensive. Additionally, these models are prone to issues such as gradient explosion during the training process.
Due to the limited predictive capability of a single model, it often results in low robustness and weak applicability. Therefore, the combination prediction model has gradually demonstrated its advantages. However, although the combination model integrates the advantages of individual models, it can also increase the complexity of the model. The complex network structure of the combination model leads to increased uncertainty and difficulty in selecting prediction model parameters. Hence, many scholars have made improvements by combining a series of optimization algorithms. In reference (Li et al., 2022), the Isolation Forest Algorithm (IAO) was used to detect abnormal data, and the improved Eagle Optimization Algorithm (EOA) was employed to optimize the parameters of the LSTM model, thereby establishing the IAO-LSTM model for wind power prediction. In reference (Guangzheng et al., 2022a), the Improved Grey Wolf Optimization (IGWO) algorithm was utilized to determine the number of hidden layer nodes and the learning rate of the model’s weight, proposing a LightGBM-GRU point prediction model that achieved better predictive performance compared to other algorithms. However, the aforementioned optimization algorithms have complex structures, slow convergence speeds, and are prone to getting trapped in local optimal solutions. Therefore, it is necessary to select more suitable intelligent algorithms, especially for cases with multiple hyperparameters to be optimized.
To address the aforementioned limitations, this paper proposes a NWP wind speed error correction model based on a combination of ResNet and GRU models. It corrects the multi-height forecasted wind speeds of NWP prediction points to accurately reflect the wind speed at hub height, which characterizes the wind farm power output more precisely. Finally, by combining the corrected NWP wind speeds with real-time wind farm power output data, a KOA-CNN-LSTM-Attention combination prediction model is constructed, which incorporates the KOA intelligent optimization algorithm. Experimental results demonstrate that the proposed method significantly improves the prediction accuracy compared to existing methods, providing new insights for enhancing the accuracy of short-term wind power prediction.
NWP is a method of predicting future weather conditions by solving fluid mechanics and thermodynamics equations that describe the process of weather evolution based on certain boundary and initial conditions (Guangzheng et al., 2024). However, the spatial and temporal resolution of NWP data, geographic location, terrain, and other factors may result in deviations between NWP data and the measured data at wind farm sites. Short-term wind power prediction models are established based on NWP data and measured operational data at wind farms, but errors in NWP wind speed can greatly affect the accuracy of short-term wind power predictions (Miao et al., 2022).
The distribution and error curves of NWP wind speed and measured wind speed are compared in Figure 1, which shows that both NWP wind speed and actual wind speed follow a two-parameter Weibull distribution mainly in the wind speed range of 3–15 m/s. However, compared with measured wind speed, NWP wind speed has fewer subdivisions in the main wind speed range, indicating that measured wind speed fluctuates more frequently in this wind speed range, while the overall fluctuation of predicted wind speed is lower. The error between NWP wind speed and measured wind speed can be divided into longitudinal error and lateral error. The longitudinal error mainly manifests as amplitude differences between NWP wind speed and measured wind speed, as shown in Figure 1C. The lateral error mainly manifests as phase delay between NWP wind speed and measured wind speed, as shown in Figure 1D. Moreover, the error between NWP forecasted wind speed and measured wind speed at wind farms varies dynamically in different seasons, including different directions and step sizes of delays, differences in amplitude, and varying degrees of missed and false forecasting information for wind energy fluctuations.
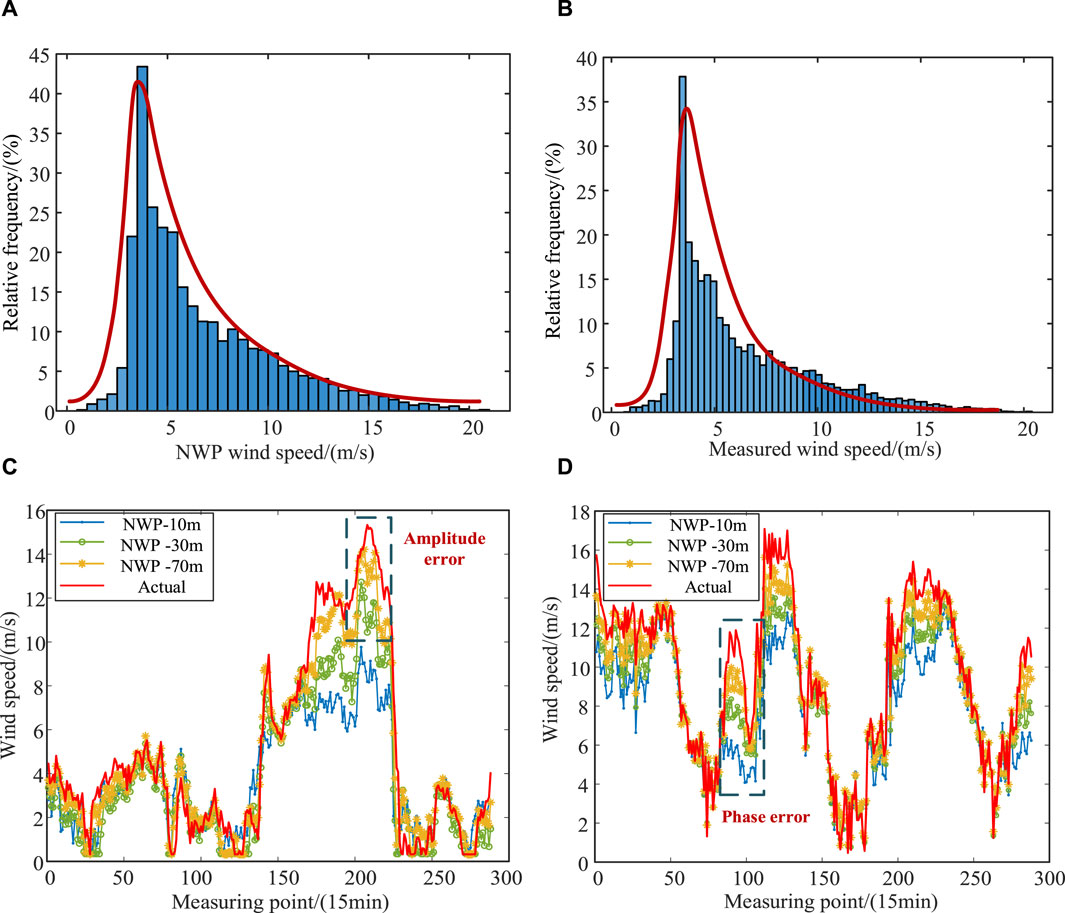
Figure 1. Error analysis of wind speed. (A,B) are the wind speed distribution map. (A): NWP wind speed distribution, (B): Measured wind velocity distribution. (C,D) are the analysis of wind speed error. (C): Error analysis of NWP Wind Speed and Measured Wind Speed (winter), (D): Error analysis of NWP Wind Speed and Measured Wind Speed (summer).
Due to the significant fluctuations in measured wind speeds, this study aims to leverage the ResNet module’s powerful feature extraction capabilities to uncover the periodicity and temporal relationships within the historical wind speed sequences. The ResNet module, known for its deep residual structure, effectively addresses the issues of gradient vanishing and explosion in deep neural networks, thereby enhancing feature extraction capabilities (Yldz et al., 2021). Moreover, the ResNet module mitigates information loss and facilitates smooth information flow through the use of shortcut connections. To capture the volatility of wind speed, the GRU model is employed as the learning model. The GRU model, equipped with gate mechanisms, effectively addresses the long-term dependency problem while avoiding the issues of gradient vanishing and explosion present in traditional Recurrent Neural Network (RNN) models (Yu et al., 2023). Consequently, the GRU model demonstrates excellent performance in time-series data modeling tasks. Therefore, this study proposes the ResNet-GRU wind speed correction model, which not only effectively learns and utilizes the relationship between NWP model and measured data but also predicts more accurate wind speeds. Additionally, both the ResNet module and GRU model have been optimized classic models, requiring fewer computational resources and less time compared to other complex models during training and prediction, thus demonstrating characteristics of computational efficiency. The schematic diagram of the proposed model is presented in Figure 2.
In this study, the fully connected layer following the time-series modeling layer is utilized for wind speed correction. The known actual wind speed data and the output of the numerical model are employed as supervisory signals to optimize the model parameters by minimizing the error between the predicted and actual values. The Mean Squared Error (MSE) is adopted as the loss function for this purpose. The formula for MSE is as follows:
where,
The CNN-LSTM hybrid model is designed to handle time-series matrices composed of relatively independent feature sequences. It effectively utilizes CNN to extract spatially local correlated features from the data, while LSTM compensates for CNN’s limitation in capturing long-term dependencies within sequential data (Guangzheng et al., 2021). Since the features used for wind power prediction (such as wind speed, wind direction, temperature, precipitation, and air pressure) are relatively independent time-series features, it becomes challenging to describe the inherent relationships between these features over time. Using either CNN or LSTM alone fails to simultaneously extract the inter-sequence correlations and long-term patterns in feature time-series. Traditional CNN-LSTM networks simply concatenate the CNN and LSTM components, which may disrupt the temporal correlations between sequences. Therefore, improvements upon the traditional CNN-LSTM model are necessary to overcome these drawbacks. This paper proposes an enhanced neural network algorithm that combines the Attention mechanism with CNN-LSTM. The key advantage of this algorithm lies in the inclusion of an Attention layer between the CNN network and LSTM layer. By computing the relevance scores between the input sequence’s hidden layer vectors and the output, different attention weights are assigned to meteorological factors, highlighting the critical influencing features. Consequently, this approach addresses the challenge of preserving crucial information when dealing with long input sequences.
CNN input is wind power historical power data and multi-impact characteristic data. The data is divided into d days, n data per day, and m meteorological factors per data, to form an n×m×d matrix as the input structure of CNN model. The output expression of CNN convolution layer is shown in Eq. 2:
where:
The CNN pooling layer uses 2 × 2 filters and a sliding window of step 1 to sample, reduce the data feature size, reduce network parameters, and then input the data to the LSTM layer via the fully connected layer. First, the input vector calculates the intermediate state of meteorological data through the hidden layer of LSTM, and the attention mechanism uses the function
where:
Secondly, the attention weight
where:
Due to the numerous hyperparameters involved in the training process of the CNN-LSTM-Attention hybrid model, such as learning rate, kernel size, and number of LSTM units, it is a challenging task to select and adjust these hyperparameters appropriately. The selection of these parameters directly impacts the quality of the prediction results in practical applications, thus necessitating the integration of optimization algorithms for parameter selection. The Kepler optimization algorithm (KOA) is a heuristic optimization algorithm based on Kepler’s law in the natural world. This algorithm simulates the motion of planets in the Solar System and utilizes iterative search to find the optimal solution (Abdel-Basset et al., 2023) In KOA, each planet and its position represent a candidate solution, and the optimization process is achieved by randomly updating based on the best solution found so far (the Sun), enabling more efficient exploration and utilization of the search space. Its advantages lie in its fast convergence speed, high search accuracy, and strong interpretability. The mathematical expression of this algorithm is as follows:
where:
where r is a number that is generated randomly on the basis of the normal distribution, while
Where: r4 is randomly generated numerical values at interval [0, 1],
In this paper, KOA algorithm is used to optimize the learning rate, convolution kernel size, number of neurons and other parameters in the CNN-LSTM-Attention model, taking the minimum Mean Absolute Percentage Error (MAPE) as the objective function. The formula is as follows:
where:
This paper conducts a case study using data from a wind farm in northwest China. The installed capacity of the wind farm is 200 MW, and the experimental data and information includes the output power of the wind farm and various meteorological factors throughout 2018–2019. Specifically, data from January 25th to 31st, 2019 was selected for validating the prediction results. The data is divided into observed data and NWP data, both with a resolution of 15 min. The observed data contains measured values of wind turbine active power and hub-height wind speed, while the NWP data contains wind speed forecast values at four heights: 10 m, 30 m, 50 m, and 70 m. The NWP data is updated once a day at 00:00, so the wind power day-ahead forecast results are also updated on a rolling basis at 00:00 each day.
In this section, the proposed ResNet-GRU network is employed to correct the NWP wind speed data of the wind farm. To validate the applicability of the proposed correction model, meteorological and wind power data from the winter and summer seasons of 2019 are selected for wind speed correction result verification. During each correction, 80% of the data from the preceding time period is used to train the correction model, while the remaining 20% is used to validate the effectiveness of the wind speed correction. The comparison graph of forecasted wind speed before and after correction against the measured wind speed is shown in Figure 3.
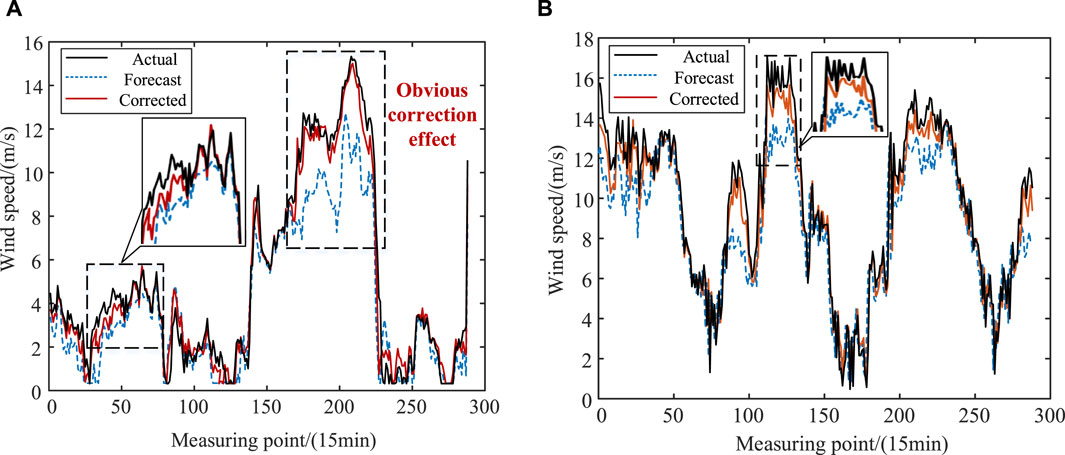
Figure 3. Comparison of NWP wind speed correction results in different seasons. (A): Comparison of NWP wind speed correction results (winter), (B): Comparison of NWP wind speed correction results (summer).
From the curve fitting results shown in the above figure, the following observations can be made:
1) The NWP wind speed forecasts for this wind farm exhibit relatively small errors during the summer season, while the forecast errors are relatively larger during the winter season.
2) The NWP wind speed curve appears relatively smooth, whereas the measured wind speed curve exhibits more pronounced fluctuations and may experience sudden changes. These changes manifest as local peaks or valleys, which are of short duration and difficult for NWP to accurately predict, resulting in missed forecasts. This is evident in the highlighted section of the graph.
3) During periods of significant wind speed fluctuations, the NWP wind speed forecasts for this wind farm tend to underestimate the measured wind speed to a considerable extent. To address this issue, the error correction model developed in this study learns from the differences between NWP and measured wind speeds in historical samples and effectively corrects the errors between NWP and measured wind speeds during the application phase.
This study employs the Keras framework in Python to construct a short-term wind power prediction model based on the CNN-LSTM architecture. The model’s initialization parameters, including the learning rate of the model’s network weights, the size of the convolution kernel, and the number of neurons, are determined by the KOA algorithm, while the sigmoid function is selected as the model’s activation function. The original training data range for the model comprises winter season data from 2018–2019, with a test set consisting of 7 days after the cutoff range of this training set. To validate the predictive performance of the proposed algorithm, the LSTM(Guangzheng et al., 2022b), CNN-LSTM (ZHAO et al., 2019), CNN-LSTM-Attention (Guangzheng et al., 2021), and KOA-CNN-LSTM-Attention methods are applied to predict the wind power output of the wind farm, with corresponding results presented in Table 1. Deterministic prediction error can be manifested as horizontal and vertical errors. In this paper, we selected vertical error evaluation indicators including Mean Absolute Error (MAE), MAPE, Root Mean Square Error (RMSE), and horizontal error evaluation indicators such as correlation coefficient as the performance evaluation indicators for prediction. A comparison of the forecast curves and error metrics across different methods is shown in Figure 4.

Figure 4. Comparison of prediction results of different algorithms. (A): Comparison of prediction curves of different algorithms; (B, C) is the comparison of results with or without KOA optimization algorithm error, (B): the prediction error when the model does not use KOA optimization algorithm, (C): the prediction error after the model uses KOA optimization algorithm.
The KOA-CNN-LSTM-Attention algorithm proposed in this paper has the best overall prediction performance. Compared with the sub-optimal CNN-LSTM-Attention algorithm, the error indicators MAE, RMSE and MAPE are reduced by 6.235%, 6.281% and 7.620%, respectively. It shows the superiority of KOA algorithm. Combined with KOA algorithm, the parameters of the model are better selected on the basis of single CNN-LSTM algorithm, so the prediction accuracy is further improved.
Improving the accuracy of NWP is crucial for enhancing the precision of short-term wind power forecasting. However, current NWP forecast data exhibits significant discrepancies compared to the measured wind speeds, thereby limiting the accuracy of short-term wind power prediction. In light of this issue, this study proposes the following approaches:
1) An error correction model based on ResNet-GRU is established to effectively rectify the discrepancies between NWP and measured wind speeds during the application stage. By learning from historical samples, this model captures the differences between NWP and actual measurements.
2) A short-term wind power prediction model based on KOA-CNN-LSTM-Attention is developed to optimize key parameters such as learning rate, convolution kernel size, and number of neurons in complex models. This optimization significantly enhances the predictive performance of the model.
Furthermore, the measured wind power and wind speed data exhibit greater randomness and volatility compared to NWP forecast data. This indicates that smooth NWP data faces challenges in accurately tracking and predicting wind energy fluctuations at high spatiotemporal resolutions, leading to increases in both missed detection rates and false alarm rates. Therefore, our future research will focus on exploring how to utilize real-time wind farm and anemometer data with higher update frequencies to perform rolling corrections on NWP data, thereby achieving more accurate wind power forecasts.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
SW: Writing–original draft. HL: Writing–review and editing. GY: Writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Author SW was employed by Power Dispatching Control Center of State Grid Shaanxi Electric Power Co., Ltd. Author HL was employed by Electric Power Research Institute of State Grid Hubei Electric Power Co., Ltd.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abdel-Basset, M., Mohamed, R., Azeem, S. A. A., Jameel, M., and Abouhawwash, M. (2023). Kepler optimization algorithm: a new metaheuristic algorithm inspired by Kepler's laws of planetary motion. Knowledge-based Syst. 268, 110454. doi:10.1016/j.knosys.2023.110454
Ahmed, A., and Khalid, M. (2019). A review on the selected applications of forecasting models in renewable power systems. Renew. Sustain. Energy Rev. 100, 9–21. doi:10.1016/j.rser.2018.09.046
Anbo, MENG, Chen, S., Zuhong, O. U., Ding, W., Zhou, H., Fan, J., et al. (2022). A hybrid deep learning architecture for wind power prediction based on bi-attention mechanism and crisscross optimization. Energy 238, 121795. PB. doi:10.1016/j.energy.2021.121795
Ding, M., Zhou, H., Xie, H., Wu, M., Nakanishi, Y., and Yokoyama, R. (2019). A gated recurrent unit neural networks based wind speed error correction model for short-term wind power forecasting. Neurocomputing 365, 54–61. Nov.6. doi:10.1016/j.neucom.2019.07.058
Du, P. W. (2019). Ensemble machine learning-based wind forecasting to combine NWP output with data from weather station. IEEE Trans. Sustain. energy 10 (4), 2133–2141. doi:10.1109/tste.2018.2880615
Guangzheng, Yu, Lingxu, S., Qi, D., Cui, G., Wang, S., Xin, D., et al. (2024). Ultra-short-term wind power forecasting techniques: comparative analysis and future trends. Front. Energy Res. 11, 2296–598X. doi:10.3389/fenrg.2023.1345004
Guangzheng, Y. U., Liu, L. U., Tang, B., Wang, S., Yang, X., and Chen, R. (2021). Improved hybrid neural network ultra-short-term PV power prediction method based on cloud map feature extraction. Proceeding CSEE 41 (20), 6989–7003. doi:10.13334/j.0258-8013.pcsee.201929
Guangzheng, Y. U., Liu, L. U., Tang, B., Wang, S., and Dong, Q. (2022a). Research on ultra-short-term piecewise prediction method for offshore wind power considering transformational weather. Proc. CSEE 42 (13), 4859–4871. doi:10.13334/j.0258-8013.pcsee.211771
Guangzheng, Y. U., Liu, C., Tang, Bo, Chen, R., Lu, L., Cui, C., et al. (2022b). Short-term wind power prediction for regional wind farms based on spatial-temporal characteristic distribution. Renew. Energy 199, 599–612. doi:10.1016/j.renene.2022.08.142
Hu, S., Xiang, Y., Shen, X. D., Liu, J. Y., Liu, J. C., and Li, J. H. (2021). Wind power prediction model considering spatial correlation between meteorological factors and wind speed. Automation Electr. Power Syst. 45 (7), 9. doi:10.7500/AEPS20200218012
Hui, L. I., Dong, L. I. U., and Yao, D. (2021). Research and judgment on the development of China's power system facing the goal of carbon peaking and carbon neutrality. Proc. CSEE 41 (18), 6245–6259. doi:10.13334/j.0258-8013.pcsee.210050
Li, Z., Luo, X. R., Liu, M. J., Cao, X., Du, S., and Sun, H. (2022). Short-term prediction of the power of a new wind turbine based on IAO-LSTM. Energy Rep. 8, 9 025–029 037. doi:10.1016/j.egyr.2022.07.030
Liu, H., Yang, R., and Duan, Z. (2020). Wind speed forecasting using a new multi-factor fusion and multi-resolution ensemble model with real-time decomposition and adaptive error correction. Energy Convers. Manag. 217, 112995. doi:10.1016/j.enconman.2020.112995
Miao, C., Wang, X., Li, H., Han, L., and Wen, C. (2022). Wind power day-ahead forecast based on wind speed error correction of Numerical Weather forecast. Power Grid Technol. 46 (09), 3455–3464. (in Chinese). doi:10.13335/J.1000-3673.pst.2022.0834
Niu, Z., Zeyuan, Y., Bo, L., and Wenhu, T. (2018). Short-term wind power prediction model based on depth-gated cyclic unit neural Network. Electr. Power Autom. Equip. 38 (5), 7. doi:10.16081/j.issn.1006-6047.2018.05.005
Ren, D., Xiao, J., Hou, J., Du, E., Jin, C., and Liu, Y. (2022). Research on the construction and evolution of new electric power system under double carbon target. Power Grid Technol. 222 (10), 3831–3839. doi:10.13335/j.1000-3673.pst.2022.0387
Song, J., Peng, Y., Cai, H., Xia, Y., and Wang, X. (2018). Research on short-term wind power prediction considering multi-location NWP and atypical characteristics. Power Grid Technol. 42 (10), 3234–3242. doi:10.13335/j.1000-3673.pst.2018.0492
Wang, Y., Zou, R., Liu, F., Zhang, L., and Liu, Q. (2021). A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 304 (1), 117766. doi:10.1016/j.apenergy.2021.117766
Wang, W., Wang, Z., Dong, C., Liang, Z., Feng, S., and Wang, B. (2021). Status and error analysis of short-term forecasting Technology of wind power in China. Automation Electr. Power Syst. 45 (1), 17–27. doi:10.7500/AEPS20200324003
Yldz, C., Akgz, H., Korkmaz, D., and Budak, U. (2021). An improved residual-based convolutional neural network for very short-term wind power forecasting. Energy Convers. Manag. 28 (1), 113731. doi:10.1016/j.enconman.2020.113731
Yu, G. Z., Lu, L., Tang, B., Wang, S. Y., and Chung, C. Y. (2023). Ultra-short-term wind power subsection forecasting method based on extreme weather. IEEE Trans. Power Syst. 38 (6), 5045–5056. doi:10.1109/TPWRS.2022.3224557
Yusheng, X., Yu, C., Zhao, J., Kang, X., Qiuwei, G., and Ya, Y. (2015). A review on short-term and ultra-short-term wind power prediction. Automation Electr. Power Syst. 39 (6), 141–151. doi:10.7500/AEPS20141218003
Zhao, X., Haikun, W. E. I., Wang, H., Zhu, T., and Zhang, K. (2019). 3D-CNN-based feature extraction of ground-based cloud images for direct normal irradiance prediction. Sol. Energy 181, 510–518. doi:10.1016/j.solener.2019.01.096
Zhou, Y., Yu, G., Liu, J., Ziheng, S., and Pei, K. (2021). Offshore wind power prediction based on improved long-term cyclic convolutional neural networks. Automation Electr. Power Syst. 45 (03), 183–191. doi:10.7500/AEPS20191212003
Keywords: short-term wind power prediction, ResNet-GRU, wind speed correction, CNN-LSTM-attention, kepler optimization algorithm(KOA)
Citation: Wang S, Liu H and Yu G (2024) Short-term wind power combination forecasting method based on wind speed correction of numerical weather prediction. Front. Energy Res. 12:1391692. doi: 10.3389/fenrg.2024.1391692
Received: 26 February 2024; Accepted: 09 April 2024;
Published: 06 May 2024.
Edited by:
Yitong Shang, Hong Kong University of Science and Technology, ChinaReviewed by:
Yikui Liu, Stevens Institute of Technology, United StatesCopyright © 2024 Wang, Liu and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guangzheng Yu, cG93ZXJ5Z3pAc2hpZXAuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.