- School of Automation, Guangdong University of Technology, Guangzhou, Guangdong, China
To simultaneously solve the problems of the state-of-charge (SOC) equalization and accurate current distribution among distributed energy storage units (DESUs) with different capacities in isolated DC microgrids, a multi-storage DC microgrid energy equalization strategy based on the hierarchical cooperative control is proposed. In the primary control layer, the link between the droop coefficient and SOC is established through a logarithmic function, and the droop coefficient is adaptively adjusted according to the SOC value in order to achieve fast SOC equalization. In the secondary control layer, by designing a coordinated state factor, only one PI controller is required to eliminate the influence of the line impedance on the accurate distribution of the output current and the DC bus voltage drop. In the communication layer, local nodes only need to communicate with neighboring nodes without the need for a central controller, and the dynamic consistency algorithm is used to obtain the average value information about the energy storage system (ESS). Finally, the feasibility and effectiveness of the proposed control strategy are verified by experimental analysis on the DC microgrid hardware-in-the-loop experimental platform.
1 Introduction
With the continuous development of science, technology, and industrial technology, the global energy crisis is becoming more and more serious, and the shortage of traditional fuels and the environmental pollution problems caused by them are also increasing. At the same time, the continuous improvement and gradual maturity of renewable energy technologies such as solar power and wind power provide a new way to solve the energy crisis (Lin et al., 2018; Hoang and Lee, 2020; Huang et al., 2022). Therefore, many countries are focusing on distributed power generation using renewable energy as the energy source. Compared with the traditional large-scale centralized generation and distribution modes, distributed generation technology has the advantages of real-time control, low investment, flexible installation location, a short construction period, high energy utilization, and low environmental pollution (Morstyn et al., 2018). However, for DC microgrids operating on isolated islands, distributed power sources, due to their randomness, volatility, and uncontrollability, can greatly reduce power quality, thereby affecting the stable operation of the microgrid (Yang et al., 2021; YNan et al., 2021). Therefore, it is necessary to configure distributed energy storage systems (DESSs) to suppress energy fluctuations (Hosseinipour and Hojabri, 2018).
In DESSs, each DESU is often connected to the bus bar in parallel. Since the initial SOC or capacity of each DESU may not be consistent, the SOC of each DESU may be inconsistent during charging and discharging, resulting in some DESUs exiting the system early due to overcharging or over discharging, leading to asymmetric operation of the microgrid (Bi et al., 2019; Hoang and Lee, 2021). Therefore, it is necessary to coordinate and control the DESU’s output current and SOC, ensuring that each DESU’s output current is accurately distributed according to the capacity ratio and the SOC is balanced (Yang et al., 2022).
Droop control is widely used in energy distribution in DC microgrids for its advantages such as high reliability and plug-and-play. Zhou et al. (2020) introduced an optimal control method for multi-battery energy storage systems in islanded DC microgrids, leveraging the PI consensus algorithm to enhance robustness against time delays. However, this and other studies (Li et al., 2022) failed to address the crucial issue of SOC balancing in their control loops, potentially causing overcharging or over-discharging of energy storage units. To address SOC balancing, research has explored linking the droop coefficient and SOC. Lu et al. (2014) and Lu et al. (2015) constructed a link by a power function to dynamically adjust the droop coefficient to achieve fast SOC equalization. However, the SOC equalization accuracy is low, and the bus voltage drop introduced by the droop coefficient has not been effectively compensated. To eliminate the bus voltage drop, Li et al. (2014) and Shahbazi et al. (2016) not only modified the virtual impedance but also dynamically adjusted the output voltage reference of the DESU based on changes in SOC to achieve SOC equalization and bus voltage stabilization. Zhi et al. (2020) designed the droop coefficient to be proportional to SOC during charging and inversely proportional to SOC during discharging, thus achieving both SOC equalization and power equalization and improving the stability of the DC bus voltage by enhancing the inertia of the DC microgrid. Xu et al. (2020) achieved SOC equalization by setting the droop coefficient to be inversely and positively proportional to the nth power of SOC during charging and discharging, respectively. In addition, the given reference voltage is changed by the multi-intelligent body technique, which compensates for the bus voltage variation caused by the droop coefficient. However, the aforementioned studies did not consider the effect of line impedance on SOC equalization and power distribution.
To simultaneously stabilize the bus voltage and eliminate the influence of line impedance on SOC equalization and current distribution, an autonomous voltage regulation scheme was proposed by Yang et al. (2018), which compensates for the voltage drop caused by line impedance by setting virtual resistors to achieve stable voltage. However, the value of the virtual resistance is equal to the line impedance, so the line impedance information must be known, and the line impedance is affected by factors such as environmental changes, which leads to unequal line impedance and makes impedance information difficult to obtain accurately, further reducing the effectiveness of the control method. Liu et al. (2018) measured line resistance information by injecting pulse perturbations and detecting changes in the output voltage and current, which are used to compensate for droop coefficients and restore DC bus voltage. However, in practical operation, it is difficult to eliminate interference caused by various environmental factors, so the accuracy of this method is not high enough. To completely eliminate the influence of line impedance on SOC equalization and accurate current distribution, Chen et al. (2018) proposed a two-level layered voltage control scheme, which uses a consistency algorithm to estimate the average DC bus voltage, eliminates the influence of line impedance, and achieves SOC equalization and voltage stabilization. Shafiee et al. (2014) proposed a distributed hierarchical control framework, which adjusts the droop coefficient in real-time based on changes in SOC in the primary control layer. A voltage regulator based on the consistency algorithm is introduced in the secondary control layer to eliminate the bus deviation, and again, the power equalization distribution is achieved by a power controller. Hoang and Lee (2019) proposed a virtual power rating method based on SOC, which achieved accurate current distribution. However, the aforementioned literature did not consider the situation where the capacity of DESUs is different.
To achieve SOC equalization and accurate current distribution among different capacity DESUs simultaneously, Lin and Wang Zhi Xin (2020), Zeng et al. (2022a), and Mi et al. (2023) constructed the connection between the droop coefficient and SOC by setting the convergence function and dynamically adjusting the droop coefficient to quickly achieve SOC equalization between DESUs of different capacities. Lin and Wang Zhi Xin (2020) and Zeng et al. (2022a) designed a virtual voltage drop equalizer and a voltage compensator, which, respectively, eliminate the impact of line impedance on output current accuracy and compensate for bus voltage drop. Mi et al. (2023), on the other hand, achieved the aforementioned objectives by introducing virtual power rating compensation and voltage compensation. However, the aforementioned methods all use two PI controllers to form a secondary control to achieve energy equalization, and the parallel connection of both PI controllers affects the same variables, which makes the design of control parameters more difficult. As a result, recent research has focused on developing more simplified and efficient control strategies to address these limitations. Zhang et al. (2022) proposed a distributed cooperative control strategy that employs a single controller, simplifying system complexity. Chen et al. (2020) demonstrated that each supercapacitor or battery utilizes only neighboring information exchange rather than global communication, enjoying equal priority in participating in the voltage or SOC regulation. (Wu et al., 2018) introduced an SOC balancing strategy in AC microgrids that does not require communication or a central controller, thus enhancing system scalability. Jiang et al. (2023) proposed a double-ascent algorithm to optimize current distribution coefficients online, reducing current losses. Both Zeng et al. (2022b) and Lin et al. (2022) introduced exponential functions, where the ratio of each energy storage unit’s SOC to the average SOC of all units is used as the input to the droop coefficient. Morstyn et al. (2016) achieved SOC balancing by comparing the SOC of a unit with its neighboring units. However, the SOC balancing speed of these control strategies remains relatively slow.
The expansion strategies of DC microgrids can be classified as centralized, decentralized, and distributed. However, centralized control suffers from a single point of failure, requires a high bandwidth communication network, and is difficult to expand (Nasirian et al., 2015; Hoang and Lee, 2020), while decentralized control leads to problems such as poor voltage regulation and inaccurate load distribution. Distributed control, on the other hand, is more suitable for microgrids with its high reliability, simple communication network, and easier scalability (Anand et al., 2013). Among them, distributed control based on a consistency algorithm becomes the most attractive control scheme, which eliminates the need for a central controller and obtains global average information by simply exchanging information with neighboring nodes.
Based on the aforementioned analysis, a DESS composed of multiple DESUs mainly faces the following challenges in SOC equalization and accurate current distribution:
1. Most of the current studies on accurate output current distribution and bus voltage recovery use two or more PI controllers for regulation. However, since the controlled quantities are linked to each other, changing any of the control parameters arbitrarily will have an impact on the overall effect, increasing the difficulty of parameter design.
2. Currently, research on SOC equalization and fast current sharing mostly only considers the influence of line impedance in DESS with parallel DESUs of the same capacity, ignoring the impact of differences in the capacity of each DESU during continuous charging and discharging. As a result, the practicality of the method is reduced.
To solve the aforementioned problems, a multi-storage islanded DC microgrid energy balancing strategy based on the hierarchical cooperative control is proposed in this paper, and the advantages of the proposed control strategy are as follows:
1. In the primary control layer, this paper introduces a multi-storage islanded DC microgrid energy balancing strategy grounded in hierarchical cooperative control, aimed at addressing the SOC equalization issue in DESS composed of DESUs with varying capacities. This strategy innovatively leverages the properties of logarithmic functions to devise a novel adaptive droop coefficient adjustment scheme. Within this adaptive framework, a faster SOC equalization rate is achieved by harnessing the characteristics of the logarithmic function, along with the integration of a purposefully designed acceleration factor and adjustment coefficients.
2. In the secondary control layer, the coordinated state factor ξ is introduced, aimed at reducing the complexity of parameter design. By employing a single PI controller, it can simultaneously achieve precise current distribution and bus voltage recovery, thereby enhancing the accuracy of SOC equalization. This design not only effectively decreases the number of PI controllers in the secondary control layer, simplifying the control structure, but also addresses the issues of bus voltage dips and inaccurate output current distribution arising from improper droop coefficients in the primary control. Consequently, a controller is added to the secondary control to facilitate bus voltage compensation and precise current allocation, ultimately enhancing system stability, optimizing energy management efficiency, and ensuring exceptional performance of the DC microgrid across various operating scenarios.
The rest of this paper is organized as follows: Section 2 of this paper introduces the structure of a DC microgrid containing multiple DESUs and analyzes the shortcomings of traditional droop control. In Section 3, a hierarchical cooperative control-based energy balance strategy is introduced in detail, which achieves SOC equalization and precise current distribution through the cooperation of primary and secondary layers and the communication layer. In Section 4, a detailed exploration of the parameter selection for the adjustment scheme of the droop coefficients in the primary control layer is presented. In Section 5, the stability of the proposed control strategy is analyzed using the example of a DC microgrid consisting of two ESUs of equal capacity. Then, the effectiveness and feasibility of the proposed strategy are confirmed in Section 6 through experimental verification under three operating conditions. Finally, Section 7 summarizes the whole paper and draws conclusions.
2 DC microgrid structure and control analysis
2.1 DC microgrid structure
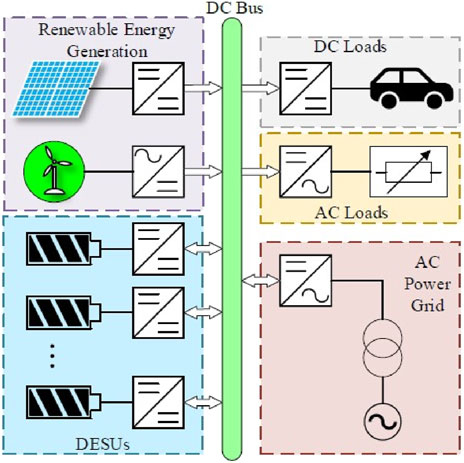
The DC microgrid is mainly composed of new energy generation units such as photovoltaic and wind power, multiple DESUs, AC and DC loads, and grid-connected interfaces, and its structure is shown in Figure 1. The AC grid is connected to the DC bus through the interface converter, which is in a networked state, or it is not connected to the grid, in an islanded state.
2.2 Conventional droop control
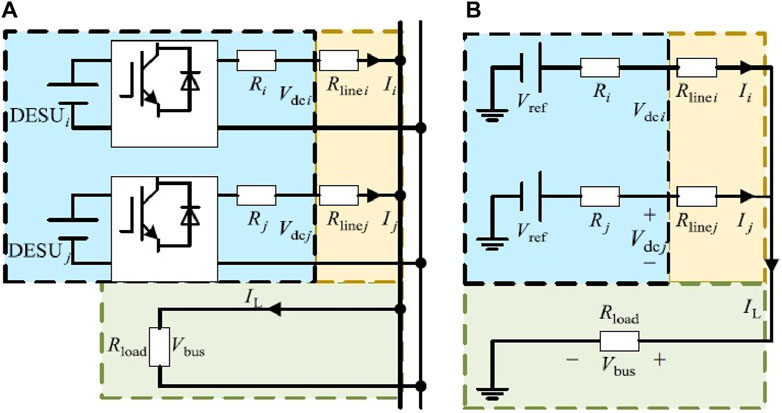
Droop control is commonly used for SOC equalization control. However, due to the influence of line impedance, the traditional droop control cannot achieve accurate current distribution and bus voltage recovery. Figure 2 shows the equivalent model of DESS with two DESUs connected in parallel under conventional droop control.
From the equivalent circuit diagram shown in Figure 2B, the expression of the output voltage of the ith ESU can be obtained as
where Vdci is the output voltage of the ith DESU; Vref is the reference value of the bus voltage; and Ri and Ii are the droop coefficient and output current of the ith DESU, respectively.
The output current of each DESU satisfies
where Vbus is the output bus voltage, Rlinei is the line impedance of the ith DESU, and Rload is the load resistance.
The expression of the bus voltage is
From Eq. 3, it can be seen that the relationship between the output current of each DESU is
To prevent overcharging or over discharging of DESUs, which may lead to premature withdrawal of DESUs from the system, SOC equalization control is required for a DESS consisting of multiple DESUs.
Using the Coulomb counting method to estimate the SOC value of DESUs (Yuji et al., 2021), we obtain
where SOCi, SOCi0, and Cratei are the current SOC value, initial SOC value, and rated capacity of the ith DESU, respectively.
The derivation of Eq. 5 can be obtained as follows:
From Eq. 6, it can be seen that when the SOC of each DESU is equal, in order to maintain a continuous balance of SOC, the output current ratio of each DESU should be equal to the capacity ratio. Substituting Eq. 4 into Eq. 6 yields
For the traditional droop control, Ri = Rj, Rlinei ≠ Rlinej. Considering that the line impedance is difficult to measure and can change due to environmental factors, it can be seen from Eqs 2, 7 that the traditional droop control is difficult to meet the accurate distribution of the output current of each DESU, and it is difficult to meet the SOC equalization condition, regardless of whether the capacity of each DESU is the same.
3 Hierarchical control strategy
The overall block diagram of the proposed hierarchical control strategy is shown in Figure 3, where DESUi denotes the ith DESU; ILi and Vi are the inductor current and virtual voltage drop of the ith DESU, respectively; and SOCavg is the average value of the SOC of DESS obtained by the consistency algorithm.
3.1 Primary control layer
The multi-storage islanded DC microgrid energy balancing strategy based on the hierarchical cooperative control is proposed in this paper. It utilizes the properties of logarithmic functions to design a new adaptive droop coefficient adjustment scheme. To achieve fast SOC equalization, it can be seen from Eq. 6 that during the discharge process, for DESUs with larger SOC, the slope of the SOC decrease should be larger so that they have a larger output current, which requires a smaller droop coefficient. On the other hand, for DESUs with smaller SOC, the vice versa is also true. Therefore, this article proposes an adaptive droop coefficient adjustment scheme, as shown in Eq. 8. In the established adaptive droop factor adjustment scheme, SOC can be made to have a faster equalization speed by using the properties of the logarithmic function and the designed acceleration factor and adjustment coefficients.
where Roi is the initial value of the droop coefficient of the ith DESU, n is the equalization acceleration factor, and m is the regulation factor.
3.2 Secondary control layer
In order to eliminate the influence of line impedance, achieve accurate current distribution and bus voltage output with a given reference voltage value, and reduce the number of PI controllers in the secondary control layer, this paper designs a coordinated state factor ξ in the secondary control layer. With only one PI controller, the accurate distribution of the output current of DESUs and the recovery of the bus voltage can be achieved without knowing the line impedance. By further enhancing the SOC equalization accuracy, the control structure is simplified.
The expression for the coordination state factor ξi is
where the expression of λi is
where k is the adjustment factor, and in order to avoid λi from taking zero, the value of k should be taken as a larger number, which is taken as 40 in this paper.
The PI controller GPI3(s) can be used to obtain the voltage compensation amount ΔuVi:
where ξavg is the average value of the coordination state factor obtained by the consistency algorithm for ξi.
In Eq. 11, it can be seen that λi will converge after the regulation of the PI controller, and then, from Eq. 10, the virtual pressure drop Vi of each DESU will converge as
From Eq. 8, it can be seen that the droop coefficient of each DESU will converge to the initial droop coefficient when the SOC of each DESU is equalized, so when the SOC is equalized, the following equation is satisfied:
From Eq. 13, it can be seen that, depending on the secondary control layer, the output current of each DESU can be precisely distributed in proportion to its capacity. Substituting Eq. 13 into Eq. 7, we obtain SOCi’ = SOCj’. Therefore, when the SOC equalization is finished, the SOC among each DESU can always be kept consistent, which again verifies the effectiveness of the proposed control strategy.
In addition, when the virtual voltage drops of each DESU are equal, Vbus = Vref can be obtained from Eqs 9–11, which means that the bus voltage is satisfied to be equal to the given reference voltage.
In summary, for the DESS composed of DESUs with different capacities, the influence of line impedance is eliminated through the introduction of ξi and the adjustment of the PI controller. At the same time, the output current is accurately distributed according to the rated capacity ratio of the DESU and the output of the bus voltage at a given reference voltage. Superimposing the voltage compensation amount of Eq. 11 on the droop control output voltage reference value Vrefi, we obtain
3.3 Communication layer
Dynamic consistency algorithms can be used to eliminate dependence on global communication, enable information sharing between distributed units, and reduce communication costs (Meng et al., 2014; Ma et al., 2022).
In this paper, a dynamic consistency algorithm is utilized to obtain the mean value information. According to the proposed improved droop control strategy, each node needs to obtain the average value of SOC and ξ, and the consistency algorithm is rewritten in the form as shown in Eq. 15.
where p and q are the number of nodes in the network and Zp is the local measurement data of node p; Xp(g) and Xp (g+1) are the estimates of node p on the average value of the data across the network at the g and g+1 iterations, respectively; Dpq(g) and Dpq (g+1) are the cumulative amount of the difference between node p’s and node q’s estimates at the g and g+1 iterations, respectively; Dpq (0) = [0, 0, 0]; Np is the set of nodes connected to node p; and hpq is the connection weight.
3.4 Layered control flow
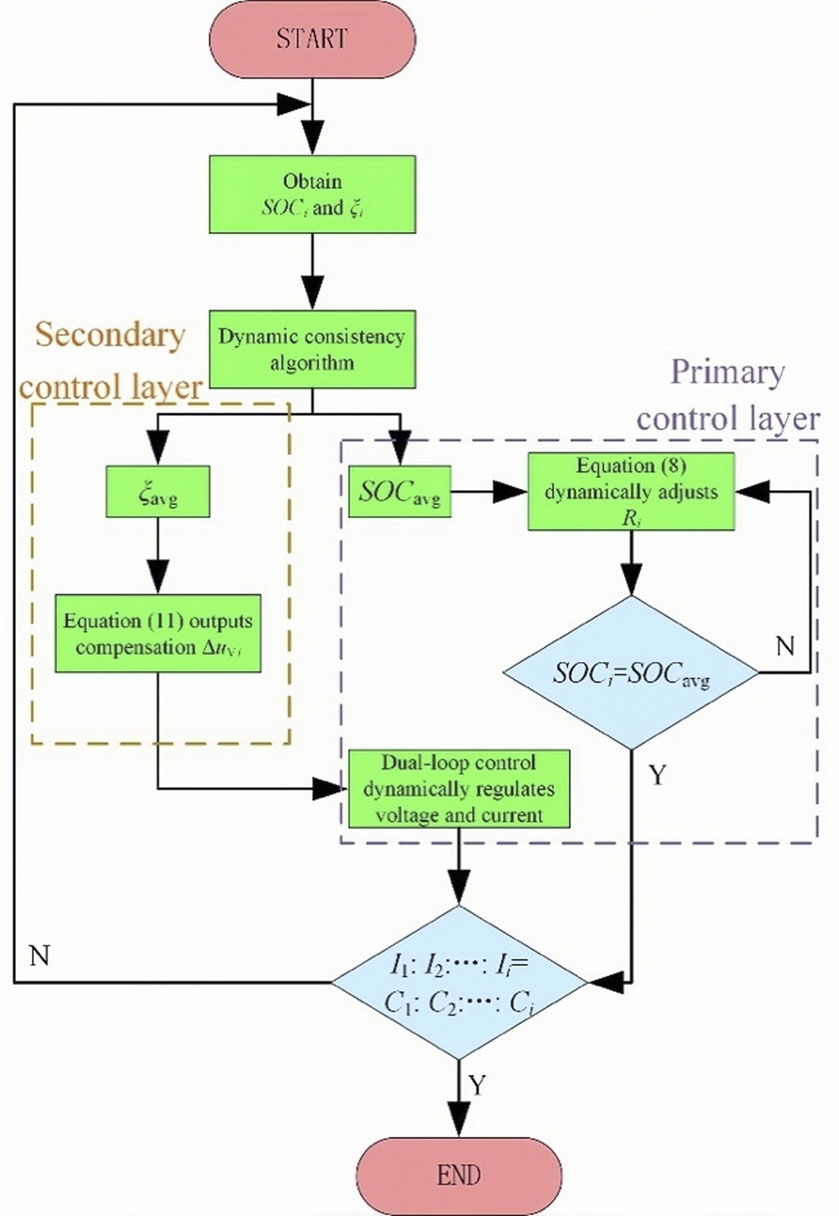
Figure 4 presents the hierarchical control flowchart of the control strategy proposed in this paper. The specific steps are as follows:
1) Each energy storage unit collects information on its local SOC and coordination state factor ξ, exchanges information with adjacent energy storage units through a consensus algorithm, and obtains the system’s average information SOCavg and ξavg through multiple iterations within the local energy storage unit.
2) At the primary control layer, each energy storage unit dynamically adjusts the droop coefficient using the collected average SOC (SOCavg) of the energy storage system and local information, according to Eq. 8, to achieve rapid SOC balancing.
3) If the SOC values of the individual energy storage units are not equal to the average SOC value of the energy storage system, the process returns to step 2 to dynamically adjust the droop coefficient size using Eq. 8. Otherwise, it proceeds to the next step.
4) At the secondary control layer, the local energy storage unit combines its local information with the average coordination state factor ξavg of the energy storage system to obtain a voltage compensation value ΔuVi through the PI controller using Eq. 11.
5) The output voltage compensation value ΔuVi from the secondary control layer is incorporated into the double-loop control of the primary control layer to dynamically adjust the output voltage and current magnitudes of the energy storage unit.
6) After dynamically adjusting the voltage and current at the primary control layer or satisfying the condition of SOCi = SOCavg, a judgment is made on whether the output current magnitudes of the energy storage units satisfy the ratio I1: I2:…: Ii = C1: C2:…: Ci. If the aforementioned equation is not satisfied, the output current of the energy storage units is adjusted from the beginning of the control loop. If the equation is satisfied, the control process ends.
4 Parameter analysis
To enhance the SOC equalization effect and ensure the stability of the ESS, it is necessary to make rational selections for the parameters in Eq. 8, primarily focusing on the choice of the initial droop coefficient Roi, the equalization acceleration factor n, and the adjustment coefficient m. For an ESS consisting of ith ESUs, the relationship between SOCavg and SOCi satisfies the following condition:
Therefore, the ESS consisting of four ESUs is analyzed by taking the variation range of SOCavg/SOCi from 1/4 to 5 with SOCavg/SOCi as the independent variable.
For the equilibrium acceleration factor n, fixing the initial value of the droop coefficient Roi = 4 and adjustment factor m = 14, the curve of variation in the droop factor for increasing n from 100 to 600 with each increase of 100 is obtained as shown in Figure 5A.
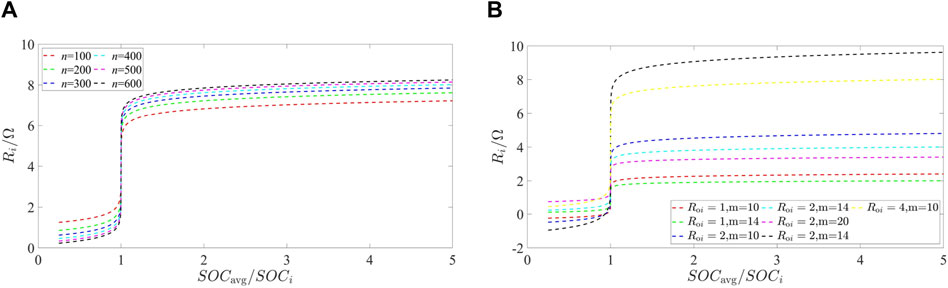
Figure 5. Variation curves of Ri for different n, Roi, and m: (A) Ri for different n and (B) Ri for different Roi and m.
In order to achieve fast SOC equalization, it is required that the SOC descent rate of the ESU with larger SOCi is fast, and the SOC descent rate of the ESU with smaller SOCi is slow. For the ESU with larger SOCi, its output current should be larger to obtain a larger descent rate. In addition, a large output current means a small droop coefficient of the ESU, so from Figure 5A, it can be seen that for the ESU with larger SOCi, where 1/4<SOCavg/SOCi<1, it is best to take a larger value of n in order to keep it in the state of lower Ri for a long period of time. In addition, for the storage unit with smaller SOCi, where 1<SOCavg/SOCi, the droop coefficient should be kept. Ri is always in the high droop coefficient state, and a larger n is needed to obtain a larger droop coefficient.
In summary, the larger the value of n, the better the droop coefficient; however, from Figure 5A, it can be found that when n take a value greater than 400, its droop coefficient change range increase is particularly small, so choosing n = 400 can be better.
Because the initial value of the droop coefficient Roi and the adjustment coefficient m both directly affect the upper and lower limits of the range of variation in the droop coefficient, so n = 400 can be fixed, and the graph of the variation in the droop coefficient of the seven combinations of Roi and m can be obtained, as shown in Figure 5B.
As can be seen from Figure 5B, no matter what value of Roi is taken, when m is taken as 10, for the case of larger SOCi, a negative droop coefficient occurs, and therefore, the value of m should be larger. In addition, when fixing Roi = 2 and m takes 20, for the case of larger SOC, the droop coefficient is the largest among the drawn curves, which does not meet the requirement of the small droop coefficient, and the fluctuation range of its droop coefficient is also very limited, which cannot satisfy the requirement of a fast SOC equilibrium, so m takes 14 as the most appropriate. When fixing m = 14, a large initial droop coefficient is required in order for the droop coefficient to have a sufficient range of variation, where n = 1 does not fulfill the requirement. However, when Roi takes a large value, the droop coefficient Ri produces a large jump in the SOC near equilibrium (near SOCavg/SOCi = 1); when Roi = 4, Ri will repeatedly jump across in 1.3, 4, and 6.3 in large steps, and since the output current size will be dynamically adjusted in the secondary control layer according to the size of the droop coefficient of the ESU, it will inevitably result in large current fluctuations before and after the equalization of the SOC, thus affecting the stabilization of the bus voltage. In summary, Roi taking the range of 2–3 is the most appropriate.
5 Stability analysis
In this section, to analyze the stability of the control strategy proposed in this paper, a DC microgrid consisting of two equally capacity ESUs is taken as an example.
The equivalent model for stability analysis is shown in Figure 6, where the SOC is equivalent to an inertial link (Li et al., 2017) and its transfer function can be expressed as
The output current is connected to a low-pass filter with a transfer function of
where ωc is the cutoff frequency of the low-pass filter.
The DC voltage closed-loop transfer function can be simplified as (Gu et al., 2014)
where τ is the time constant under the action of the switch. Since the bandwidth of the droop control loop is designed to be much smaller than the switching frequency, the value of τ is very small, and its delay effect can be ignored.
As can be seen from Figure 6 and Eqs 17–19, the relationships are as follows:
The output current of the first converter is
Among them,
Without considering the communication delay among ESUs, the output voltage of the first converter can be obtained by combining Eqs 20–22.
By applying small-signal analysis to linearize the variables in Eq. 23, the small-signal model expression can be derived as follows:
Figure 7 illustrates the root locus of the parameters Rv and ωc. As can be observed from Figures 7A, B, the droop coefficient Rv and the cutoff frequency ωc play a dominant role in system stability. It is advisable not to set the droop coefficient too high; instead, it should be selected based on the stability analysis results, along with a balance between the current sharing accuracy and bus voltage deviation. The selection of the cutoff frequency ωc should take into account the trade-off between overshoot and adjustment time, and its value is primarily influenced by the sampling frequency and system hardware parameters.
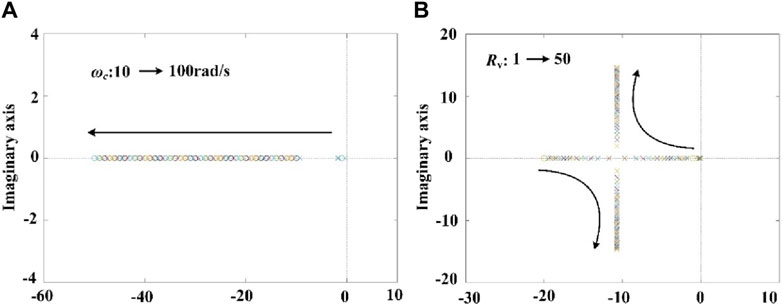
Figure 7. Root locus of the characteristic equation in a closed-loop system: (A) Rv = 1, ωc increase and (B) ωc = 20 rad/s, Rv increase.
6 Experimental verification
To verify the effectiveness and feasibility of the proposed control strategy, a hardware-in-the-loop experimental platform based on RT-LAB is built in this paper, as shown in Figure 8. The DC microgrid system, shown in Figure 2, is constructed using the upper mechanism, which mainly consists of four DESUs and one load resistor. The aforementioned model is added to the real-time simulator OP5600, the proposed control strategy is deployed in the DSP controller, and the experimental waveforms are transferred to the oscilloscope through the I/O port. In order to further prove the advantages of the proposed control strategy in terms of speed, stability, and the reliable operation under different operating conditions, three different operating conditions are constructed and analyzed in this paper.
The capacity ratio of the four DESUs in the DESS is 2:2:3:3; the initial SOC values are 0.90, 0.87, 0.85, and 0.83 in order; the initial droop coefficients are 2, 2, 4/3, and 4/3, respectively; and the line impedances of the transmission lines of each DESU are 0.40Ω, 0.50Ω, 0.60Ω, and 0.70Ω, respectively, with bus voltage reference values Vref = 400 V and load resistance Rload = 20Ω.
6.1 Case 1: normal discharge of DESS
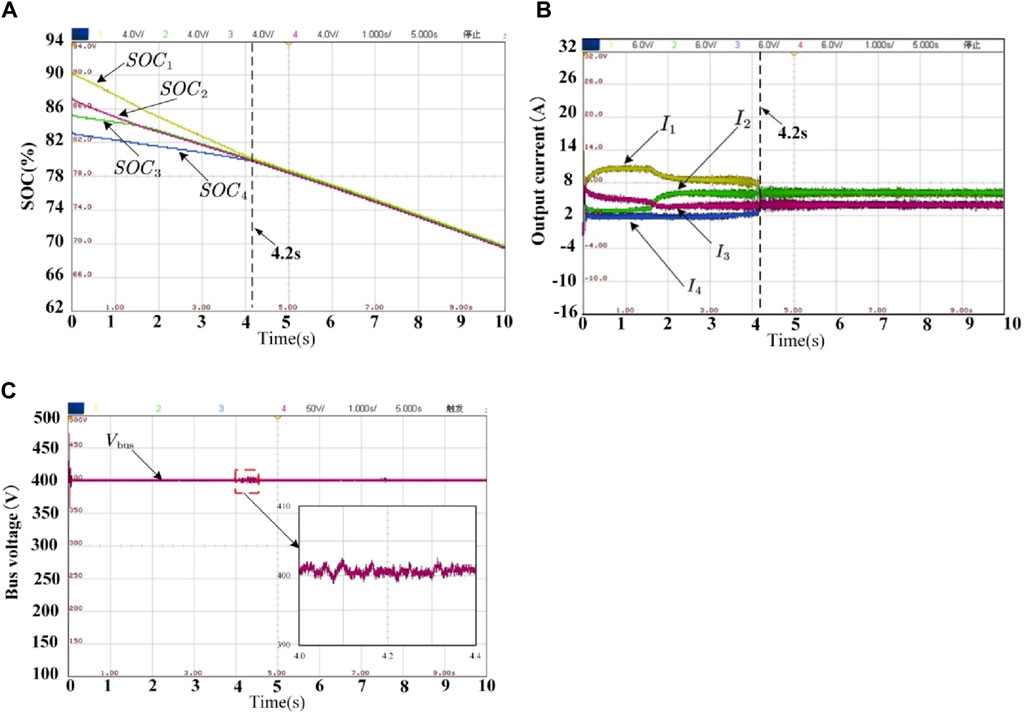
To verify the rapidity and reliability of the proposed control strategy, an equalization process of SOC during the normal discharge of the DESS was constructed, and the experimental results of the proposed control strategy (Figure 9) were compared with those of Lin and Wang Zhi Xin (2020) (Figure 10).
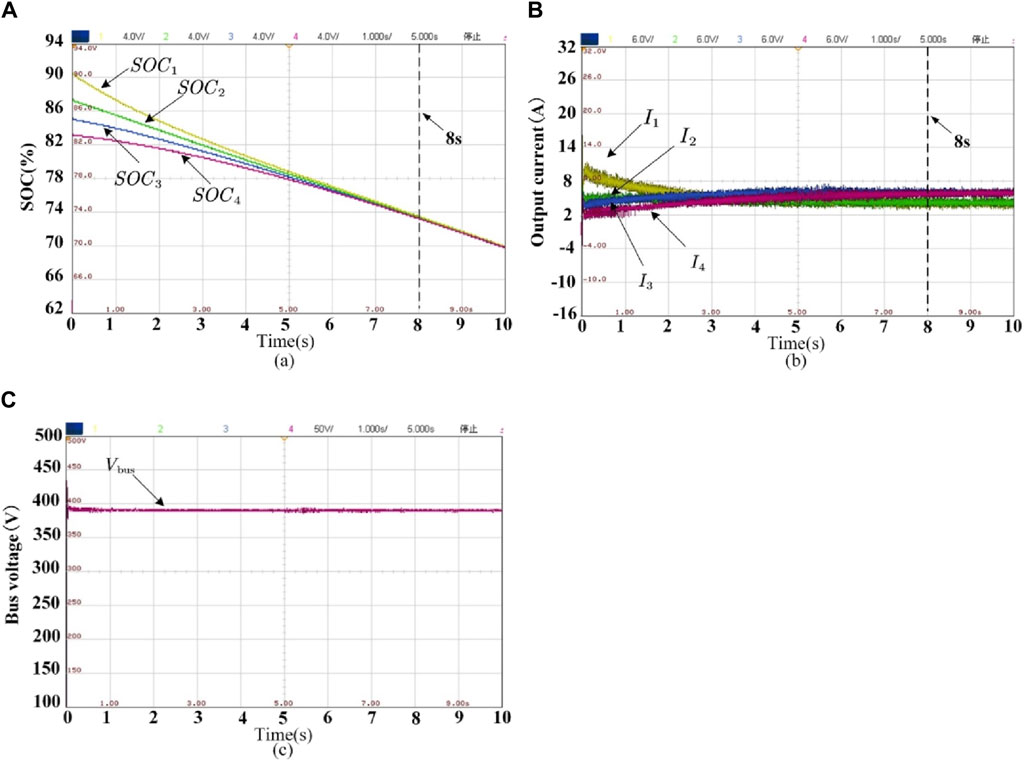
Figure 10. Experimental results of Lin and Wang Zhi Xin (2020): (A) SOC value; (B) output current; (C) bus voltage.
From the comparison of Figure 9A and Figure 10A, it can be seen that the proposed control strategy achieved SOC equalization in only 4.2 s, while Lin and Wang Zhi Xin (2020) took approximately 8 s to achieve SOC equalization. In addition, from Figure 9B and Figure 10B, it can be seen that the proposed control strategy achieved the accurate current distribution at 4.2 s. The output currents I1–I4 are 4A, 4A, 6A, and 6A, respectively, which satisfy the ratio of 2:2:3:3. The output currents I1–I4 of Lin and Wang Zhi Xin (2020) at 8 s are 3.9A, 3.9A, 5.85A, and 5.85A, respectively, which also meet the requirements of 2:2:3:3. However, comparing Figure 9C and Figure 10C, it can be found that the proposed control strategy achieves the recovery of the bus voltage, which is basically stabilized at the reference voltage of 400 V, while the bus voltage of Lin and Wang Zhi Xin (2020) is always stabilized at 390 V or less, and the recovery of the bus voltage is not achieved. From the aforementioned analysis, it can be seen that both the control strategy proposed in this paper and in Lin and Wang Zhi Xin (2020) achieve SOC equalization and accurate current distribution at the same time, but the speed of SOC equalization and accurate current distribution of the control strategy proposed in this paper is significantly better than that of Lin and Wang Zhi Xin (2020), and the time is reduced by more than half, and the rapidity is strongly confirmed. In addition, the control strategy proposed in this paper can achieve bus voltage restoration and ensure power quality, which is lacking in Lin and Wang Zhi Xin (2020).
6.2 Case 2: line impedance changes
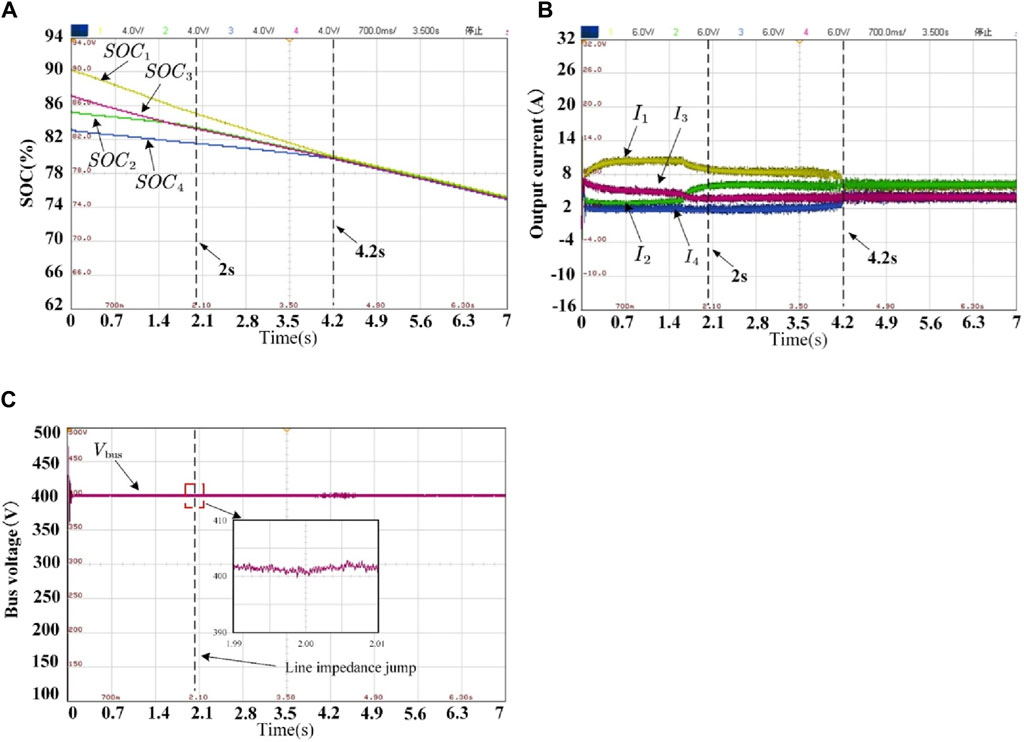
Due to the influence of environmental factors on the impedance of the transmission line in practical work and to verify that the proposed control strategy can achieve SOC balance, the precise distribution of output current, and bus voltage recovery when the line impedance changes, the impedance of the third DESU jumped from 0.60 Ω to 0.30 Ω after 2 s of the experiment. The experimental results are shown in Figure 11.
The comparison of the results from Figure 11A and Figure 9A shows that when the line impedance jumps, the SOC equalization effect of the DESS is still fast and reaches equalization at 4.2 s. The results are the same as those in the normal operating condition and are not greatly affected. From Figure 11B, it can be seen that the proposed control strategy can still achieve accurate current distribution in the face of sudden changes in line impedance, and the output current of each DESU is proportional to the SOC value when it is not equalized and achieves both SOC equalization and accurate current distribution at 4.2 s. The output currents I1–I4 are 4A, 4A, 6A, and 6A, respectively, satisfying the ratio of 2:2:3:3. From Figure 11C, it can be seen that before and after the line impedance jump, the bus voltage of the DESS does not undergo a significant jump and remains stable at an approximate reference voltage of 400 V.
6.3 Case 3: DESU exits randomly
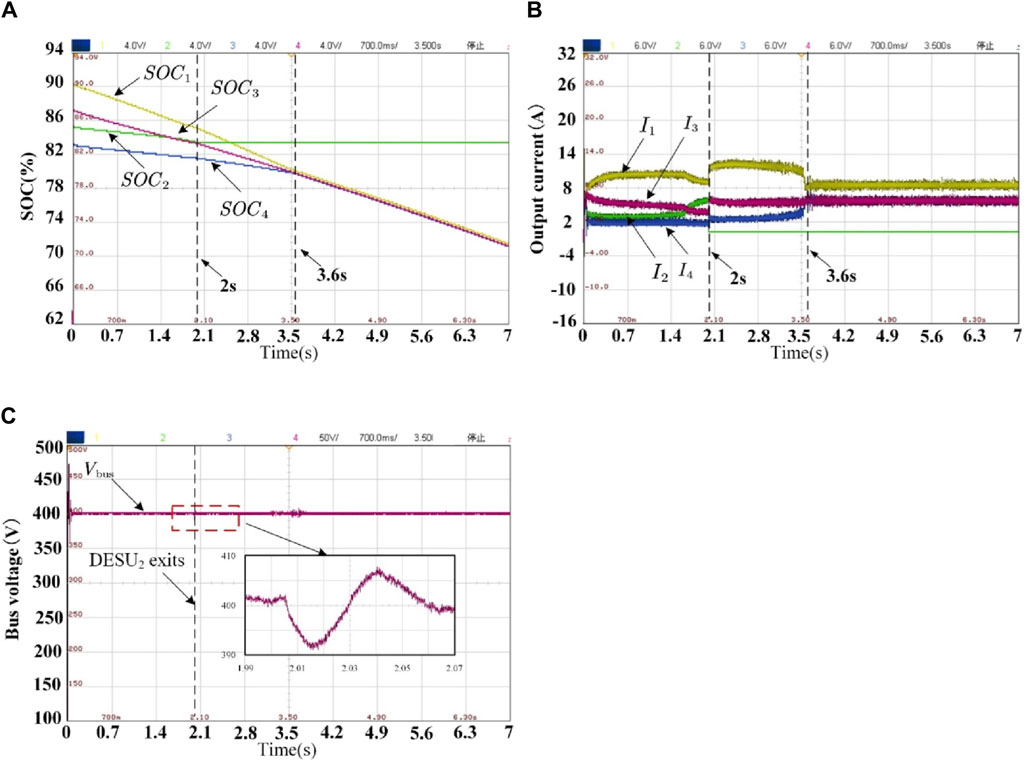
To simulate the situation that any DESU withdraws from operation due to a fault during operation, the second DESU withdraws from operation when the experiment is carried out for 2 s. The experimental results are shown in Figure 12.
From Figures 12A, B, it can be seen that the current of the load will be shared by the remaining three DESUs when the second DESU drops out, so the output current of each DESU increases. With the synergy of the primary and secondary control layers, the remaining three DESUs dynamically adjust the output current, and the SOC is quickly equalized, and the SOC equalization and precise current distribution of each DESU are realized at the same time in 3.6 s. The output currents I1, I3, and I4 are 5A, 7.5A, and 7.5A, respectively, satisfying the ratio of 2:3:3 and meeting the capacity ratio of 2:3:3, which are the remaining three DESUs. From Figure 12C, it can be seen that the bus voltage overshoot of the DESS is 2.25%, and the maximum voltage increase is 2% after the second DESU drops out at 2 s, but the bus voltage returns to the reference voltage level after only 0.06 s. The reliability of the system is guaranteed. The experimental results show that although one DESU is dropped due to fault, the remaining DESUs can quickly adjust the output current of each DESU under the coordination of the primary and secondary control layers, which ensures the rapid equalization of SOC and the rapid recovery of bus voltage.
7 Conclusion
For DESS composed of DESUs with different capacities, this paper proposes a multi-storage islanded DC microgrid energy balancing strategy based on the hierarchical cooperative control and draws the following conclusions:
1. In the primary control layer, an adaptive droop coefficient adjustment scheme is proposed so that the DESU with large SOC has a smaller droop coefficient, while the DESU with small SOC has a larger droop coefficient. The SOC of the former will drop at a faster rate, while the latter is slower, finally achieving fast SOC equalization.
2. In the secondary control layer, the coordinated state factor ξ is designed to eliminate the influence of the line impedance of the system, and after the regulation of the PI controller, the precise distribution of the output current of the DESU and the bus voltage recovery are realized at the same time.
3. By using the consistency algorithm to obtain the average information on the DESS, the communication bridge between the primary and secondary layers is established, which greatly reduces the communication pressure of the system.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
CX: conceptualization, investigation, methodology, writing–original draft, validation, and visualization. MW: conceptualization, investigation, methodology, validation, visualization, and writing–original draft. DL: data curation, methodology, supervision and formal analysis. LY: conceptualization, funding acquisition, project administration, resources, supervision, writing–review and editing, writing–original draft, and methodology.
Funding
The authors declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Anand, S., Fernandes, B. G., and Guerrero, J. (2013). Distributed control to ensure proportional load sharing and improve voltage regulation in lowvoltage dc microgrids. IEEE Trans. Power Electron. 28 (4), 1900–1913. doi:10.1109/tpel.2012.2215055
Bi, K., Sun, L., An, Q., and Duan, J. (2019). Active soc balancing control strategy for modular multilevel super capacitor energy storage system. IEEE Trans. Power Electron. 34 (5), 4981–4992. doi:10.1109/tpel.2018.2865553
Chen, X., Shi, M., Sun, H., Li, Y., and He, H. (2018). Distributed cooperative control and stability analysis of multiple dc electric springs in a DC microgrid. IEEE Trans. Industrial Electron. 65 (7), 5611–5622. doi:10.1109/tie.2017.2779414
Chen, X., Shi, M., Zhou, J., Chen, Y., Zuo, W., Wen, J., et al. (2020). Distributed cooperative control of multiple hybrid energy storage systems in a DC microgrid using consensus protocol. IEEE Trans. Ind. Electron. 67 (3), 1968–1979. doi:10.1109/tie.2019.2898606
Gu, Y., Xiang, X., Li, W., and He, X. (2014). Mode-adaptive decentralized control for renewable DC microgrid with enhanced reliability and flexibility. IEEE Trans. Power Electron. 29 (9), 5072–5080. doi:10.1109/tpel.2013.2294204
Hoang, K. D., and Lee, H. H. (2019). Accurate power sharing with balanced battery state of charge in distributed dc microgrid. IEEE Trans. Industrial Electron. 66 (3), 1883–1893. doi:10.1109/tie.2018.2838107
Hoang, K. D., and Lee, H. H. (2020a). “State of charge balancing of distributed batteries with different capacities in dc microgrid,” in IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, October 18-21, 2020, 3703–3707. doi:10.1109/iecon43393.2020.9254915
Hoang, K. D., and Lee, H. H. (2021). State of charge balancing for distributed batteries in dc microgrids without communication networks. J. Power Electron 12 (4), 405–415. doi:10.1007/s43236-020-00188-3
Hoang, K. D. L. H., and Lee, H. H. (2020b). State of charge balancing for distributed battery units based on adaptive virtual power rating in a DC microgrid. J. Electr. Eng. Technol. 15, 2121–2131. doi:10.1007/s42835-020-00482-x
Hosseinipour, A., and Hojabri, H. (2018). Virtual inertia control of pv systems for dynamic performance and damping enhancement of DC microgrids with constant power loads. IET Renew. Power Gener. 12 (4), 430–438. doi:10.1049/iet-rpg.2017.0468
Huang, B., Zheng, S., Wang, R., Wang, H., Xiao, J., and Wang, P. (2022). Distributed optimal control of dc microgrid considering balance of charge state. IEEE Trans. Energy Convers. 37 (3), 1–2174. doi:10.1109/tec.2022.3169462
Jiang, Y., Yang, Y., Tan, S. C., and Hui, S. Y. R. (2023). Dual-ascent hierarchical control-based distribution power loss reduction of parallel-connected distributed energy storage systems in DC microgrids. IEEE J. Emerg. Sel. Top. Ind. Electron 4 (1), 137–146. doi:10.1109/jestie.2022.3189577
Li, C., Dragicevic, T., Diaz, N. L., Vasquez, J. C., and Guerrero, J. M. (2014). “Voltage scheduling droop control for state-of-charge balance of distributed energy storage in DC microgrids,” in 2014 IEEE International Energy Conference (ENERGYCON), Dubrovnik, Croatia, 13-16 May 2014, 1310–1314. doi:10.1109/energycon.2014.6850592
Li, P., Zhang, C., Yuan, R., Kan, Z., and Chen, Y. (2017). Load current sharing method of distributed energy storage systems by improved SOC drooping control. Proc. CSEE 37 (13), 3746–3754. doi:10.13334/j.0258-8013.pcsee.161527
Li, Q., Li, R., Pu, Y., Li, S., Sun, C., and Chen, W. (2022). Coordinated control of electric-hydrogen hybrid energy storage for multi-microgrid with fuel cell/electrolyzer/PV/battery. J. Energy Storage 42, 103110. doi:10.1016/j.est.2021.103110
Lin, G., Liu, J., Zhou, Y., Li, Y., Rehtanz, C., Wang, S., et al. (2022). An inertia-emulation-based cooperative control strategy and parameters design for multi-parallel energy storage system in islanded DC microgrids. IET Generation, Transm. Distribution 16 (21), 4370–4385. doi:10.1049/gtd2.12605
Lin, J. W., and Wang Zhi Xin, Z. Y. (2020). Energy control strategy of distributed energy storage system considering different capacities in isolated DC microgrid. Electr. Power Autom. Equip. 40 (10), 139–146.
Lin, P., Wang, P., Xiao, J., Wang, J., Jin, C., and Tang, Y. (2018). An integral droop for transient power allocation and output impedance shaping of hybrid energy storage system in DC microgrid. IEEE Trans. Power Electron. 33 (7), 6262–6277. doi:10.1109/tpel.2017.2741262
Liu, C., Zhao, J., Wang, S., Lu, W., and Qu, K. (2018). Active identification method for line resistance in dc microgrid based on single pulse injection. IEEE Trans. Power Electron. 33 (7), 5561–5564. doi:10.1109/tpel.2017.2784565
Lu, X., Sun, K., Guerrero, J. M., Vasquez, J. C., and Huang, L. (2014). State-of-charge balance using adaptive droop control for distributed energy storage systems in DC microgrid applications. IEEE Trans. Industrial Electron. 61 (6), 2804–2815. doi:10.1109/tie.2013.2279374
Lu, X., Sun, K., Guerrero, J. M., Vasquez, J. C., and Huang, L. (2015). Double-quadrant state-of-charge-based droop control method for distributed energy storage systems in autonomous DC microgrids. IEEE Trans. Smart Grid 6 (1), 147–157. doi:10.1109/tsg.2014.2352342
Ma, D., Liu, M., Zhang, H., Wang, R., and Xie, X. (2022). Accurate power sharing and voltage regulation for AC microgrids: an event-triggered coordinated control approach. IEEE Trans. Cybern. 52 (12), 13001–13011. doi:10.1109/tcyb.2021.3095959
Meng, L., Dragicevic, T., Guerrero, J. M., and Vasquez, J. C. (2014). “Dynamic consensus algorithm based distributed global efficiency optimization of a droop controlled DC microgrid,” in 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13-16 May 2014, 1276–1283. doi:10.1109/energycon.2014.6850587
Mi, Y., Guo, J., Fu, Y., Wang, C., and Wang, P. (2023). Accurate power allocation of multienergy storage island DC microgrid based on virtual power rating. IEEE Trans. Power Electron. 38 (1), 261–270. doi:10.1109/tpel.2022.3201373
Morstyn, T., Hredzak, B., and Agelidis, V. G. (2016). Cooperative multi-agent control of heterogeneous storage devices distributed in a DC microgrid. IEEE Trans. Power Syst. 31 (4), 2974–2986. doi:10.1109/tpwrs.2015.2469725
Morstyn, T., Savkin, A. V., Hredzak, B., and Agelidis, V. G. (2018). Multi-agent sliding mode control for state of charge balancing between battery energy storage systems distributed in a DC microgrid. IEEE Trans. Smart Grid 9 (5), 4735–4743. doi:10.1109/tsg.2017.2668767
Nasirian, V., Moayedi, S., Davoudi, A., and Lewis, F. L. (2015). Distributed cooperative control of DC microgrids. IEEE Trans. Power Electron. 30 (4), 2288–2303. doi:10.1109/tpel.2014.2324579
Shafiee, Q., Dragiˇcevi c, T., Vasquez, J. C., and Guerrero, J. M. (2014). Hierarchical control for multiple DC-microgrids clusters. IEEE Trans. Energy Convers. 29 (4), 922–933. doi:10.1109/ssd.2014.6808857
Shahbazi, M., Kazemtabrizi, B., and Dent, C. (2016). “Coordinated control of dc voltage magnitudes and state of charges in a cluster of dc microgrids,” in 2016 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGTEurope), Ljubljana, Slovenia, 9-12 October 2016, 1–5. doi:10.1109/isgteurope.2016.7856272
Wu, Q., Guan, R., Sun, X., Wang, Y., and Li, X. (2018). SoC balancing strategy for multiple energy storage units with different capacities in islanded microgrids based on droop control. IEEE J. Emerg. Sel. Top. Power Electron. 6 (4), 1932–1941. doi:10.1109/jestpe.2018.2789481
Xu, D., Xu, A., Yang, C., and Shi, P. (2020). A novel double-quadrant soc consistent adaptive droop control in DC microgrids. IEEE Trans. Circuits Syst. II Express Briefs 67 (10), 2034–2038. doi:10.1109/tcsii.2019.2945009
Yang, M., Jiahang, G., Si, Y., Pengcheng, C., Liang, J., Wang, Y., et al. (2021). A power sharing strategy for islanded dc microgrid with unmatched line impedance and local load. Electr. Power Syst. Res. 192, 106983. doi:10.1016/j.epsr.2020.106983
Yang, M., Jin, D., Junfei, C., Shuai, S., Xin, C., Liu, R., et al. (2022). State of charge balancing strategy for energy storage system in islanded DC microgrid based on microtuning virtual resistance. Electr. Power Syst. Res. 209, 107921. doi:10.1016/j.epsr.2022.107921
Yang, Q., Jiang, L., Zhao, H., and Zeng, H. (2018). Autonomous voltage regulation and current sharing in islanded multi-inverter dc microgrid. IEEE Trans. Smart Grid 9 (6), 6429–6437. doi:10.1109/tsg.2017.2712658
Ynan, Q., Wei, F., Wei, W., Xiaodong, L., and Sucheng, L. (2021). Soc balancing method for energy storage systems in dc microgrids using simplified droop control. J. Power Electron 21, 1200–1212. doi:10.1007/s43236-021-00260-6
Yuji, Z., Qinjin, Z., Yancheng, L., Xuzhou, Z., Long, C., Niu, M., et al. (2021). State-of-charge dynamic balancing strategy for distributed energy storage system in dc shipboard microgrid. Int. J. Electr. Power Energy Syst. 133, 107094. doi:10.1016/j.ijepes.2021.107094
Zeng, Y., Zhang, Q., Liu, Y., Zhuang, X., and Guo, H. (2022a). Hierarchical cooperative control strategy for battery storage system in islanded dc microgrid. IEEE Trans. Power Syst. 37 (5), 4028–4039. doi:10.1109/tpwrs.2021.3131591
Zeng, Y., Zhang, Q., Liu, Y., Zhuang, X., and Guo, H. (2022b). Hierarchical cooperative control strategy for battery storage system in islanded DC microgrid. IEEE Trans. Power Syst. 37 (5), 4028–4039. doi:10.1109/tpwrs.2021.3131591
Zhang, Q., Zeng, Y., Liu, Y., Zhuang, X., Zhang, H., Hu, W., et al. (2022). An improved distributed cooperative control strategy for multiple energy storages parallel in islanded dc microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 10 (1), 455–468. doi:10.1109/jestpe.2021.3072701
Zhi, N., Ding, K., Du, L., and Zhang, H. (2020). An soc-based virtual dc machine control for distributed storage systems in dc microgrids. IEEE Trans. Energy Convers. 35 (3), 1411–1420. doi:10.1109/tec.2020.2975033
Keywords: DC microgrid, distributed energy storage system, state of charge, current distribution, voltage compensation
Citation: Xie C, Wei M, Luo D and Yang L (2024) Energy balancing strategy for the multi-storage islanded DC microgrid based on hierarchical cooperative control. Front. Energy Res. 12:1390621. doi: 10.3389/fenrg.2024.1390621
Received: 23 February 2024; Accepted: 29 May 2024;
Published: 24 June 2024.
Edited by:
Jiawei Wang, Technical University of Denmark, DenmarkReviewed by:
Dazhong Ma, Northeastern University, ChinaYun Yang, Nanyang Technological University, Singapore
Copyright © 2024 Xie, Wei, Luo and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ling Yang, eWFuZ2xpbmdfMTk5MkAxNjMuY29t
 Chen Xie
Chen Xie Ling Yang
Ling Yang