Development and calibration of a bio-geo-reactive transport model for UHS

The increased share of renewable energy sources will lead to large fluctuations in energy availability and increases energy storage’s significance. Large-scale hydrogen storage in the subsurface may become a vital element of a future sustainable energy system because stored hydrogen becomes an energy carrier available on demand. Large hydrogen amounts can be stored in porous formations such as former gas fields or gas storages, while caverns can contribute with high deliverability. However, the storage of hydrogen induces unique processes in fluid-fluid and rock-fluid interactions (for example, bio- and geochemical reactions), which may affect the efficiency of the storage. In the present study, a mathematical model describing the two-phase multicomponent flow in porous media, including bio- and geochemical reactions, is developed to predict these hydrogen-related processes. The proposed model extends an existing model in the open source simulator DuMu^x describing the bio-reactive transport process considering methanation and sulfate-reduction by geochemical reactions. Significant attention is placed on the reduction from pyrite-to-pyrrhotite coming with the generation of harmful hydrogen sulfide. This reaction is calibrated by developing a kinetic model in DuMu^x that mimics the observations of reactor experiments from literature. The developed and calibrated model is afterwards used for simulation runs on field scale to assess the impact on Underground Hydrogen Storage (UHS) operations. The developed kinetic model describes the reduction from pyrite-to-pyrrhotite in agreement with the observations in the literature, whereby particular focus was placed on the hydrogen sulfide production rate. The consecutive implementation of the transport model in DuMu^x on field scale, including the bio- and geochemical reactions, shows the potential permanent hydrogen losses caused by reactions and temporary ones induced by gas-gas mixing with the initial and cushion gas.

1 Introduction

Within the last decade, an increasing shift from fossil fuels to renewable energy sources is evident with respect to the global climate movement. Typically the supply from renewable energy sources such as wind and solar are subject to fluctuations seasonally but also daily. A similar behavior is also observable for the energy demand, although the oscillation often differs significantly, leading to an increasing importance of energy buffers in a sustainable energy system for the future. Here, converting excess electrical energy into other energy carriers such as hydrogen, methane, and ammonia, which can be subsequently consumed when demanded, is regarded as a suitable solution. This concept is called Power-to-X, whereby the X relates to the form of energy or usage (e.g., power-to-heat, power-to-gas, and power-to-liquid) (Götz et al., 2016). Recently, hydrogen has been a promising candidate within the field of power-to-gas due to its versatile usage as an energy carrier and resource for various industries (e.g., steel industry). In 2019, Hebling et al. (2019) prognosticated a hydrogen demand within a range of 800 TWh to 2250 TWh for Europe by 2050, while more recent predictions are higher with an overall hydrogen demand of more than 4000 TWh for the entire EU by 2050 (Groß et al., 2022). This high demand requires sufficient storage capacities to ensure the supply of hydrogen. Here, the storage in the porous subsurface, such as depleted gas fields, offers a good potential due to its large capacity and global availability in direct comparison to caverns. Contrary caverns leached into salt formations allow for higher deliverabilities and faster changes in production and injection cycles, ensuring short-term energy fluctuations (Tek, 1996). Due to the limited capacity and local salt availability restrictions, both storage types behave symbiotically and do not replace each other (Cihlar et al., 2021). In this study, the storage within the porous formation is focused; nonetheless, some observations and conclusions are applicable to both storage types.

1.1 Relevant processes during UHS

During the storage of hydrogen in the subsurface, a chemical component that has never been present or only in low concentrations in the formation may induce new processes and phenomena. In the following, the influence of hydrogen on the storage operation is categorized for hydrodynamic, microbial, and geochemical processes. A more extensive overview of relevant processes during UHS can be found in Reitenbach et al. (2015), Dopffel et al. (2021), and Heinemann et al. (2021).

1.2 Hydrodynamics

When focusing on the hydrodynamics inside the pores of the storage formation, typically, a two-phase saturated system composing several chemical species is considered. Here, two types of displacement have to be reviewed: 1) immiscible displacement for the phases and 2) miscible displacement for the components within the gas. Both are highly influenced by the thermodynamic properties of the phase components. Due to the low atom mass of hydrogen, thermodynamic properties such as density and viscosity are significantly lower than other relevant stored gaseous components (e.g., ${\mu }_{\mathrm{C}{\mathrm{H}}_{\mathrm{4}}}/{\mu }_{{\mathrm{H}}_{\mathrm{2}}}\approx 1.5$, ${\varrho }_{\mathrm{C}{\mathrm{H}}_{\mathrm{4}}}/{\varrho }_{{\mathrm{H}}_{\mathrm{2}}}\approx 9.4$ at T = 50°C and p = 100 bar). Focusing on the displacement of the aqueous phase by the gaseous phase, the displacement becomes more instable with increasing hydrogen concentrations due to increasing mobility ratios of the displaced and displacing fluid. Merely, this instability manifests itself in viscous fingering (Saffman-Taylor instability (Saffman and Taylor, 1958)), but also gravity segregation due to large density differences is expected (Paterson, 1983). In particular, this instable displacement is critical during the development of UHS in aquifers, while for depleted gas fields and existing gas storages, this effect is often assumed to be less significant (Feldmann et al., 2016). For these types of storage, the gas-gas mixing with the initial and remaining gas cushion becomes more relevant. The already mentioned phenomena can also be present within the miscible displacement while the mixing is additionally influenced by the processes of molecular diffusion and mechanical dispersion. Molecular diffusion can be defined as the flux resulting from the tendency to balance concentration differences due to the Brownian motion of molecules (Fick, 1855). Generally, this process is assumed to be slower than the advective flux, but the higher the concentration gradient, the faster the diffusive flux and, consequently, the mixing behavior (Fick, 1855). Unlike molecular diffusion, mechanical dispersion originates from the complexity of a porous medium, resulting in different lengths of flow paths and varying flow velocities at the microscopic level (Bear, 1979). This process encompasses various phenomena occurring at the pore scale and depends on the scale (Dentz et al., 2023). Generally, mixing caused by mechanical dispersion is accelerated in the presence of strong inhomogeneities and high flow velocities (Bear, 1979). Overall, the stronger the gas-gas mixing, the higher is the affinity of hydrogen to mix with the cushion gas, leading to a temporal loss. To ensure the efficient operation of UHS, the proper selection of operation rates and well placement is required to mitigate the mentioned phenomena. As an example, the placement of the well perforation at the reservoir crest can minimize the influences of gravitational segregation.

1.3 Microbiology

It is generally accepted that the surface offers ideal conditions for organisms to survive, which is why one might assume that the subsurface represents the complete opposite. However, even under these harsh conditions of high temperatures, pressures, and salinities, organisms have evolved and adapted to thrive in such environments, enabling them to reproduce and preserve their species (Lipman, 1931; Ghiorse and Wilson, 1988). Reproduction is achieved by cell division, which results from the metabolism that requires substrates (electron and carbon source). The fact that hydrogenotrophic microorganisms could impact the operation of UHS was indicated during the storage of hydrogen-containing town gas in the 1980s in Lobodice, Czech Republic. A significant shift in the gas composition from hydrogen and carbon dioxide to methane was detected, which was later accounted for by the presence of methanogenic microorganisms (Šmigáň et al., 1990; Buzek et al., 1994). Consequently, since then, more attention has been placed on the characterization of the microbial system during UHS. In particular critical are the methanogenic archaea (Eq. 1), the sulfate-reducing bacteria (Eq. 2), and the homoacetogenic bacteria/archaea (Eq. 3) (Heinemann et al., 2021; Ahn et al., 2023).

$\mathrm{4}{\mathrm{H}}_{\mathrm{2}}+\mathrm{C}{\mathrm{O}}_{\mathrm{2}}\to \mathrm{C}{\mathrm{H}}_{\mathrm{4}}+\mathrm{2}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}(1)$

$\mathrm{5}{\mathrm{H}}_{\mathrm{2}}+\mathrm{S}{\mathrm{O}}_{\mathrm{4}}^{\mathrm{2}-}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{S}+\mathrm{4}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}(2)$

$\mathrm{4}{\mathrm{H}}_{\mathrm{2}}+\mathrm{2}\mathrm{C}{\mathrm{O}}_{\mathrm{2}}\to \mathrm{C}{\mathrm{H}}_{\mathrm{3}}\mathrm{C}\mathrm{O}\mathrm{O}\mathrm{H}+\mathrm{2}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}(3)$

Although all species lead to a loss of hydrogen with simultaneous contamination of the stored fluid, the sulfate-reducing bacteria produce hydrogen sulfide, which is highly corrosive and toxic. Therefore, a particular risk from this type of microorganism is expected. Nevertheless, not only changes in the fluid composition are expected, but petrophysical properties can also be affected by the presence of microorganisms. Microorganisms attached to the surface can result in bio-clogging, where the pore and throat size are significantly reduced, yielding lower porosity and permeability (Eddaoui et al., 2021). Generally, the risk increases with higher water saturations as the microbes live in the aqueous phase. On the contrary, the risk of bio-clogging can be assumed to be lower for depleted gas fields and existing storages where the water saturations are typically close to the connate saturation.

The presence of the different species differs significantly among geological formations, and the growth depends on the present reservoir conditions (Thaysen et al., 2021). Therefore, the microbial consortium has to be evaluated independently for every formation to assess the impact of microbiology on the operation of UHS.

1.4 Geochemistry

Typically, natural gas fields are several tens of millions of years old, allowing the complete system to reach thermodynamic and chemical equilibrium. However, these equilibria are disrupted by the injection of new chemical components such as hydrogen. Among other things, these new chemical components may induce reactions with the rock minerals (Heinemann et al., 2021). These types of reactions, where dissolved components in the fluids interact with the minerals of the rock, are referred to as geochemical reactions (Bethke, 1996). Thereby, geochemical reactions often follow a path of mineral dissolution, where one or more minerals dissolve in the liquid phase, followed by either remaining dissolved or precipitating out of solution (Bethke, 2021). While dissolution typically enhances petrophysical properties, precipitation can lead to pore clogging or even cause geomechanical issues. Furthermore, the reaction products can contaminate the stored fluids, making the occurrence of the reaction unfavorable.

In the context of UHS, the occurrence of geochemical reactions can significantly impact the operation regarding economics and safety. Therefore, in the last decades, the amount of research activities targeting these reactions has grown. Here, one of the most prominent geochemical reactions related to hydrogen is the pyrite-to-pyrrhotite reduction, where hydrogen sulfide is produced, coming with corrosive and harmful characteristics. Pyrite (FeS₂) can be frequently found in low concentrations up to a few percent in many sandstones (Pettijohn et al., 1972), and the reaction may become relevant for many storage formations. As products of the reaction, pyrrhotite and hydrogen sulfide are generated. The hydrogen sulfide generation may impact, on the one hand, the reproduction of harmful gas, which requires additional processing steps, leading to significant cost increases in operation. On the other hand, the integrity of the well may be endangered due to its corrosive effect on wellbore materials. First concerns of this reaction occurring during UHS arose when storing hydrogen-containing town gas in Beyne, France (Bourgeois et al., 1979). However, the observed hydrogen sulfide concentration of 20 mg⋅ Sm⁻³ did not necessarily conclude the presence of the reaction and could also be explained by sulfate-reducing bacteria (Bourgeois et al., 1979). Later on, the reaction was investigated experimentally in Truche et al. (2010) focusing on nuclear waste disposals. During the exposure of pure pyrite, an abundant amount of the pyrite was reduced to pyrrhotite with the simultaneous generation of hydrogen sulfide within 2 weeks. However, the investigated experimental conditions of temperature ranges 90°C–180°C and pressures from 80 bar to 140 bar (10% H₂), respectively (Truche et al., 2010). In particular, the investigated temperatures exceed typical UGS conditions. Gaucher et al. (2009) observed an inhibiting effect of carbonates on the generation of hydrogen sulfide. In a consecutive study, Truche et al. (2013) observed reactions even at lower temperatures and higher rates at alkaline conditions, concluding that acidic reservoirs could be better UHS candidates.

Apart from the pyrite-to-pyrrhotite reduction, the oxidation of hydrogen by hematite (Fe₂O₃) has been observed in laboratory experiments (Ostertag-Henning, 2023). Sandstone samples containing hematite were exposed for over 1 month at a pressure of 120 bar and a temperature of 120°C. Although hydrogen oxidation was not significant, remarkable changes in the mineral composition could be observed (Ostertag-Henning, 2023). Besides the reduction/oxidation of iron-bearing minerals, further reactions were implied. Simulation studies of geochemical reactions with PHREEQC (Charlton and Parkhurst, 2011) indicated that K-feldspar, kaolinite, and dolomite could precipitate, while quartz, illite, and calcite could dissolve (Hemme and van Berk, 2018). Bo et al. (2021) performed a similar simulation study and strengthened the assumption of calcite dissolution related to the introduction of hydrogen. The simulated calcite dissolution was also observed experimentally during the exposure of rock samples to a hydrogen atmosphere in autoclave experiments (Pudlo et al., 2016). Focusing on the sealing capacity of the storage, beneficial effects of hydrogen have been stated. Within the simulation study of Hemme and van Berk (2018), albitization of clay-rich rocks has been observed, typically yielding a reduction of porosity and thereby improving the sealing capacity.

Nevertheless, there are also experimental studies where no reactions were observed (Bardelli et al., 2014; Hassanpouryouzband et al., 2022), so that the presence of geochemical reactions caused by the injection of hydrogen into the subsurface is still controversial (Heinemann et al., 2021).

1.5 Numerical simulation of the reactive transport process during UHS

Numerical reservoir simulation is a powerful tool to model and predict the transport processes in porous rocks. In recent years, various simulations for UHS have been conducted. Regarding the field scale, most simulations focused on pure transport affected by different thermodynamic properties and hysteresis of relative permeability curves (Bo et al., 2023; Lysyy et al., 2023), which have been observed in the laboratory. Additionally, simulation studies have been applied to evaluate operational designs, such as different types of cushion gas and well configurations (Chai et al., 2023; Harati et al., 2023). However, these studies have often neglected hydrogen reactions, which are significant for particular storages. Here, the consideration of the reactive transport is necessary (Carrera et al., 2022). In 2018, Hagemann (2018) developed a mathematical model with subsequent numerical implementation in the open source simulator DuMu^x to predict the bioreactive transport process during hydrogen storage in the porous subsurface. This study’s focus was modeling potential biochemical reactions caused by microorganisms being present in the pores of the rock. Simplified growth models were implemented in some commercial simulators (Elgendy et al., 2023; Khoshnevis et al., 2023; Wang et al., 2023). Focusing on the implementation of Hagemann (2018), the work was primarily based on literature observations and lacked in calibration with actual laboratory investigations. Other reactions, such as geochemical reactions, which could impact UHS efficiency, were not considered, and the analysis of gas-gas mixing between injected and initial gases was performed, but it relied on simplified thermodynamic properties (e.g., ideal gas law).

To address these limitations, the existing simulation model in DuMu^x is extended by the prominent geochemical reaction of pyrite-to-pyrrhotite reduction to predict the impact on UHS. Subsequently, this reaction is calibrated by laboratory investigations from the literature by reproducing their results. Additionally, more applicable thermodynamic correlations are used (e.g., real gas law) to improve its description at typical UGS conditions. In the last step, a recently published UHS scenario was simulated with the calibrated model to identify potential impacts on the operation of UHS on the field scale.

2 Mathematical model for bio-geo-reactive transport in porous media

To model the unique processes during UHS, the transport equation for two phases (gas and water) with multiple components is considered. The continuity equation can be expressed component-wise as follows:

$\begin{array}{ll}\hfill & \frac{\partial \left(\varphi {\sum }_{\alpha =g,w}{\varrho }_{\alpha }{c}_{\alpha }^{\kappa }{S}_{\alpha }\right)}{\partial t}+\nabla \cdot {\displaystyle \sum _{\alpha =g,w}}\left({\varrho }_{\alpha }{c}_{\alpha }^{\kappa }\frac{K{k}_{r\alpha }}{{\mu }_{\alpha }}\right.\hfill \\ \hfill & ·\nabla \left.\left({\rho }_{\alpha }g-p_{\alpha }\right)-{\varrho }_{\alpha }{D}_{\text{diff,}\alpha }^{\kappa }\nabla c_{\alpha }^{\kappa }\right)=q^{\kappa }\hfill \end{array}(4)$

where ϕ is the porosity, ϱ denotes the molar density in mol · m⁻³, c is the mole fraction, S is the saturation of the phase α, K is the absolute permeability in m², k_r is the relative permeability, μ is the phase’s dynamic viscosity in Pa · s, ρ is the phase’s density in kg · m⁻³, g is the gravitational acceleration in m · s⁻², D_diff is the effective diffusion coefficient in m · ² s⁻¹, and q is the source term in mol m⁻³ · s⁻¹. The subscript α indicates the phases water (w) and gas (g), and the superscript κ represents the fluid components.

The porosity in the storage term is time-dependent as the pore space is dynamic over time due to reactions with the solid phase. Since the solid phase is assumed to be immobile, the material balance for the solid phase can be expressed as follows:

${\varrho }^{{\kappa }_s}\frac{\partial {\varphi }_s^{{\kappa }_s}}{\partial t}=q^{{\kappa }_s}(5)$

where ${\varrho }^{{\kappa }_s}$ denotes the molar density of the solid component κ_s in mol · m⁻³, ${\varphi }_s^{{\kappa }_s}$ is the volume fraction of the solid component, and q corresponds to the source term in mol · m⁻³ · s⁻¹.

As additional equations, the sum of saturations, concentrations, and volume fractions have to be unity, respectively.

${\displaystyle \sum _{\alpha }}{S}_{\alpha }=1(6)$

${\displaystyle \sum _{\kappa }}{c}_{\alpha }^{\kappa }=1\text{for:\hspace{0.17em}}\alpha =g,w(7)$

$\varphi +{\varphi }_s^{\text{inert}}+{\displaystyle \sum _{{\kappa }_s}}{\varphi }_s^{{\kappa }_s}=1\text{or}\varphi ={\varphi }_0-{\displaystyle \sum _{{\kappa }_s}}{\varphi }_s^{{\kappa }_s}(8)$

where ${\varphi }_s^{\text{inert}}$ corresponds to the volume fraction of the inert mineral, and ϕ₀ corresponds to the maximum porosity $({\varphi }_0=1-{\varphi }_s^{\text{inert}})$.

The source term permits the introduction of artificial sources and sinks in the domain. In the first place, this term is used to implement the bio- and geochemical reactions, but also the operation by a well is considered within this term. Consequently, it can be expressed by the following equations:

For fluid components κ:

$q^{\kappa }=q_{\text{bio}}^{\kappa }+q_{\text{geo}}^{\kappa }+q_{\text{well}}^{\kappa }(9)$

For solid components κ_s:

$q^{{\kappa }_s}=q_{\text{geo}}^{{\kappa }_s}(10)$

where $q_{\text{bio}}^{\kappa }$ is the biochemical source in mol · s⁻¹ · m⁻³, $q_{\text{geo}}^{\kappa }$ is the geochemical source in mol · s⁻¹ · m⁻³, and $q_{\text{well}}^{\kappa }$ is the source/sink due to the operation of the well in mol · s⁻¹ · m⁻³.

2.1 Biochemical reactions

To consider the presence and activity of microorganisms, the interdependent growth and conversion are modeled. In general, the mathematical model of the biochemical reactions relies on the work of Hagemann (2018). The dynamic size of the microorganisms’ population is governed by the continuous growth and decay of individuals. While the growth is expressed by a double Monod model (Monod, 1949), the continuous decay of individuals depends on the number of microbes present.

$\begin{array}{ll}\hfill \frac{\partial \left(n\cdot S_w\varphi \right)}{\partial t}& =\left(\underset{{\psi }^{\text{growth}}}{\underbrace{{\psi }_{\text{max}}^{\text{growth}}\cdot \left(\frac{c_w^{S1}}{{\alpha }^{S1}+c_w^{S1}}\right)\left(\frac{c_w^{S2}}{{\alpha }^{S2}+c_w^{S2}}\right)}}-\underset{{\psi }^{\text{decay}}}{\underbrace{b\cdot n}}\right)\hfill \\ \hfill & \cdot n\cdot S_w\cdot \varphi \hfill \end{array}(11)$

where n is the number of microbes in m⁻³, ψ^growth is the growth rate in s⁻¹, ${\psi }_{\text{max}}^{\text{growth}}$ is the maximum growth rate in s⁻¹, $c_w^S$ is the mole fraction in the aqueous phase of substrate S (e.g., H₂, CO₂), and α^S is the half-velocity constant, ψ^decay is the decay rate in s⁻¹, and b is the decay factor in m³ · s⁻¹.

The conversion of substrates to products is controlled by the growth rate of the microbes which is considered in the source term:

$q_{\text{bio}}^{\kappa }=\varphi {\gamma }_{\text{bio}}^{\kappa }\frac{{\psi }^{\text{growth}}}{Y}n{S}_w(12)$

where ${\gamma }_{\text{bio}}^{\kappa }$ is the stoichiometric coefficient of the reaction and Y is the yield factor in mol⁻¹.

This mathematical model can be implemented independently for every microbial species, while the only interaction of the species is the competition for substrates (substrate-limited model).

2.2 Geochemical reactions

Interactions between the fluid and solid phases can have various impacts on the storage process. Changes in fluid composition and alterations in petrophysical properties are the main concerns regarding UHS. To consider geochemical reactions, the changes in the phase composition are considered in the source term. Geochemical reactions are typically modeled with 1) kinetic or 2) equilibrium models. In the present study, kinetic models are the focus, although the implementation allows an interface for equilibrium models in analogy to the kinetic models. A general formulation for kinetic models can be expressed as follows (Lasaga et al., 1994):

$q_{\text{geo}}^{\kappa }={\gamma }_{\text{geo}}^{\kappa }\left(A_s^{r_s}k{\left(1-\frac{Q_m}{K_m}\right)}^{\theta }\right){\varphi }_s^{r_s}(13)$

where γ_geo is the stoichiometric coefficient of component κ, $A_s^{r_s}$ is the reactive specific surface area of the reactive mineral r_s in m² · m⁻³, k is the rate constant in mol · s⁻¹ · m⁻², Q_m and K_m are mass coefficients, θ is a tuning parameter, and ${\varphi }_s^{r_s}$ is the solid reactant’s volume fraction.

The dissolution and precipitation of minerals result in changes in porosity and permeability. The variation in porosity is accounted for in Eq. 8. To represent alterations in permeability, the Kozeny-Carman model (Kozeny, 1927; Carman, 1939) is utilized:

$K\left(\varphi \right)=K_0{\left(\frac{1-{\varphi }_0}{1-\varphi }\right)}^2{\left(\frac{\varphi }{{\varphi }_0}\right)}^3(14)$

where K₀ and ϕ₀ are the reference permeability and porosity, respectively. In general, small changes in porosity already lead to a significant change in permeability.

3 Realization of bio-geo-reactive transport model in the open source simulator DuMu^x

While commercial simulators profit with good numerical optimization and ease by a defined interface, open source simulators are typically distributed as source code that is only limited user-friendly due to its structure and restricted interface with the user. However, they have an adaptability to specific needs, leading to high popularity in research. As a consequence, the developed mathematical model is implemented in the open source simulator DuMu^x. DuMu^x is in development by the University of Stuttgart (Institute of Modeling Hydraulic and Environmental Systems) since 2007 (Flemisch et al., 2011; Koch et al., 2020). It is based on DUNE (Bastian et al., 2021) and is provided as an additional module to simulate fluid flow in porous media, including chemical reactions. Regarding the simulation of UHS operations, the open source simulator DuMu^x already showed its good potential to cover the transport process. The comparison with SLB Eclipse (E300), a representative of commercial reservoir simulators, showed congruent results for the pure transport (Hogeweg et al., 2022) and pressure development during operations. Additionally, first implementations of biochemical reactions related to hydrogen were modeled in DuMu^x (Hagemann et al., 2018; Eddaoui et al., 2021). To date, the implementation of the particular biochemical model is unique and it has already shown excellent results during the application for an accompanying simulation for a pilot test (Strobel et al., 2019).

3.1 Implementation of bio-geo-reactive transport model, fluid model, solid system, and reactions

Focusing on the transport in porous media coupled with reactions, the default two-phase n-component model in DuMu^x was extended by bio- and geochemical reactions. For this purpose, new fluid and solid systems incorporating the relevant chemical components were introduced. The fluid model encompasses two phases, gas and water, each comprising nine components: water (H₂O), methane (CH₄), hydrogen (H₂), carbon dioxide (CO₂), ethane (C₂H₆), a pseudo component (C₃₊), nitrogen (N₂), sulfate $(\mathrm{S}{\mathrm{O}}_{\mathrm{4}}^{\mathrm{2}-})$, and hydrogen sulfide (H₂S). Phase equilibria are determined by a combination of Raoult’s law and Henry’s law (Henry, 1803), accounting for vaporization and dissolution between the phases. To calculate the density of the gas phase, the commonly used Peng-Robinson Equation of State (EoS) (Peng and Robinson, 1976) is employed. The effects of temperature and pressure on the fluid mixture’s viscosity are modeled using two correlations. Firstly, the full extended form of Stiel and Thodos (1961) is used to determine low-pressure viscosity. Additionally, the Lohrenz et al. (1964) correlation is employed to compute corrected high-pressure viscosity. For considering the process of gas-gas mixing by molecular diffusion, the fluid system contains the recently developed correlation for UHS (Hogeweg et al., 2023b). Concerning the solid system, three solid components are taken into account: pyrite (FeS₂), pyrrhotite (FeS), and an inert component, quartz (SiO₂). The implementation of the solid phase draws partially from the work conducted by Hommel (2016). In this study, it is assumed that the rock is incompressible, and alterations in the volume fractions of the reactive minerals and porosity are solely a result of geochemical reactions. In the context of the methanation and sulfate-reduction processes, microorganisms are integrated into the solid system as pseudo components, denoted as MG (for methanogens) and SR (for sulfate-reducing bacteria), respectively. The chemical reactions were realized as additional classes providing source-modifying reaction methods.

4 Calibration of geochemical reaction based on laboratory observations

Various geochemical reactions are suspected to occur during the injection of hydrogen in the subsurface (Heinemann et al., 2021). However, a significant part of these reactions has only a minor impact on the operation and/or is irrelevant to the time horizon of interest. One of the most controversial reactions is the pyrite-to-pyrrhotite reduction coming with the generation of harmful hydrogen sulfide. A simplified reaction stoichiometry assuming that the reaction is only occurring in one direction can be expressed as follows:

${\text{FeS}}_2+{\text{H}}_2\to \text{FeS}+{\text{H}}_2\text{S}(15)$

Laboratory experiments in the early 2010s (Truche et al., 2010) addressed this reaction and observed a significant amount of generated hydrogen sulfide. To predict the pyrite-to-pyrrhotite-reduction on larger scales and thereby assess the potential risk, these experiments are reproduced in DuMu^x on a lab scale to be applied on the field scale afterward.

4.1 Description of laboratory procedure and observations

To observe the reaction, Truche et al. (2010) exposed pure pyrite to an argon-hydrogen (10% H₂) atmosphere at pressures of 80 bar–180 bar and temperatures of 90°C–180°C . In the first step, ultrafine pyrite was exposed to this atmosphere, and quantitative analyses proved the presence of the reaction. For buffering, minor parts of calcite were added to the pyrite powder. To quantify the amount of hydrogen sulfide produced and subsequently build a model, experiments on crushed pyrite powder were performed.

The experimental workflow was composed of the following steps: 1) Placing solid and liquid material in the high-pressure reactors, 2) flushing with argon to remove dissolved oxygen, and 3) increase the pressure by injecting the argon hydrogen gas to the defined experimental condition (Truche et al., 2010). During the exposure with a time of up to 14 days, liquid samples were taken from the reactor periodically. With a focus on modeling the reaction quantitatively, Truche et al. (2010) selected eight out of eleven performed experiments with sized pyrite particles and reproduced the experiments within PHREEQC (Charlton and Parkhurst, 2011). The corresponding experimental matrix is depicted in Table 1. For the selection of experiments, the amount of hydrogen sulfide released was determined, and afterward, a correlation in dependency of pressure, temperature, and time was developed depending on the parameters of temperature, pressure, pH, and time of exposure. The experimental data and the trend of the developed correlation are depicted in Figure 1. Generally, the highest reaction rates are observed at the beginning of the experiment with a truncating behavior in the later phase. Further, higher partial pressures and temperatures lead to a promoting behavior for the reaction rate. Truche et al. (2010) supposed that the reaction follows a dissolution-precipitation reaction where the pyrite dissolves into the liquid phase, reacts, and afterward partially precipitates as pyrrhotite. Regarding the sharp reduction of the H₂S generation, potential reasons such as approaching the equilibrium conditions or diffusive effects on the micro scale were concluded. Nevertheless, it seemed that the reaction is controlled by many factors such as temperature, partial pressure of hydrogen, specific surface area, pH, and also present hydrogen sulfide content (Truche et al., 2010). Based on the laboratory experiments, Truche et al. 2010 developed a simplified model describing the hydrogen sulfide generation. However, this model was developed in 0D simulations and may not be suitable for implementation in a transport model. For the purpose of field scale simulations, hydrogen may only be present locally and time-delayed. With this correlation, the reaction would even take place when the partial pressure of hydrogen was zero (= no hydrogen present). To allow the implementation for more complex systems, the results of Truche et al. (2010) are used to develop a new kinetic model in this study.

Table 1

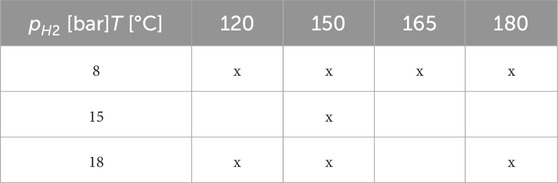
Table 1. Experimental matrix design for the characterization of pyrite-to-pyrrhotite reduction with crushed pyrite powder (Truche et al., 2010).

Figure 1

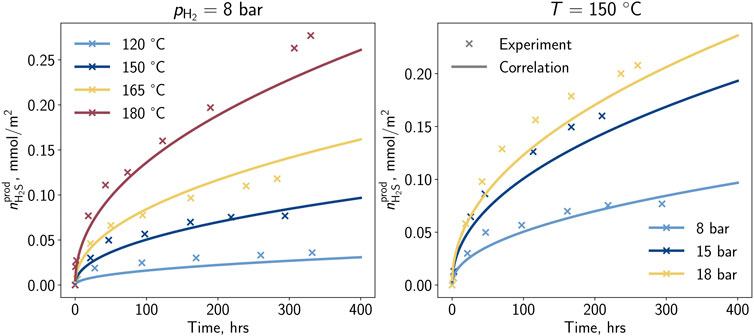
Figure 1. Hydrogen sulfide per surface area generated by the pyrite-to-pyrrhotite reduction determined in the laboratory and the proposed correlation (Truche et al., 2010)—Impact of (A) temperature and (B) partial pressure of H₂.

4.2 Implementation of laboratory experiments in DuMu^x

To develop the new kinetic model, the reactor experiments with pure pyrite samples of Truche et al. (2010) were reproduced within DuMu^x, including the development of a new mathematical model describing the kinetics of the reaction. A simple 1D simulation with only one grid cell containing the volume of the reactor (300 mL/450 mL) was defined and the initialization was according to the experimental procedure. The water saturation ranged from 55% to 71%. The initial volume fraction of pyrite grains (A_spec = 780 m² kg⁻¹) was defined as 5%. The temperature (120°C, 150°C, 165°C, and 180°C) and partial pressure (8 bar, 15 bar, and 18 bar) was initialized based on the experiments. Noteworthy, all laboratory experiments were conducted with a gas composition of 10% H₂ and 90% Ar, merely the absolute pressure was changed to achieve the variance in partial pressure of hydrogen. During the simulation, all spatial boundaries were defined as Neumann no-flow boundaries. This led to an implementation where no flow can occur and the PDE system from Eqs 4, 5 could be reduced to the following system of ODEs. For fluid components κ = H₂O, Ar, H₂, H₂S:

$\frac{d\left(\varphi {\sum }_{\alpha =g,w}{\varrho }_{\alpha }{c}_{\alpha }^{\kappa }{S}_{\alpha }\right)}{dt}=q_{\text{geo}}^{\kappa }(16)$

For solid components κ_s = FeS₂, FeS:

${\varrho }^{{\kappa }_s}\frac{d{\varphi }_s^{{\kappa }_s}}{dt}=q_{\text{geo}}^{{\kappa }_s}(17)$

Here, only changes in the fluid composition are caused by the geochemical reaction represented by the source term.

4.3 Development of kinetic reaction model describing pyrite-to-pyrrhotite reduction

After implementing the experimental conditions in DuMu^x, a mathematical model was developed and matched with the laboratory observations. The limited amount of experiments did not allow to build a typical kinetic rate relationship including mass action coefficients. Hence, an empirical rate model mimicking the experimental results was developed, which, nevertheless, originated from the general formulation (cf. Eq. 13):

$q_{\text{geo}}^{\kappa }={\gamma }_{\text{geo}}^{\kappa }\left(A_s^{\mathrm{F}\mathrm{e}{\mathrm{S}}_{\mathrm{2}}}k\underset{\delta }{\underbrace{{\left(1-\frac{Q_m}{K_m}\right)}^{\theta }}}\right){\varphi }_s^{\mathrm{F}\mathrm{e}{\mathrm{S}}_{\mathrm{2}}}(18)$

where $A_s^{\mathrm{F}\mathrm{e}{\mathrm{S}}_{\mathrm{2}}}$ is the specific surface area of the mineral pyrite in m² · m⁻³, k is the rate constant in mol · m⁻² · s⁻¹, δ is representing the dimensionless mass action term of the general formulation, and ${\varphi }_s^{\mathrm{F}\mathrm{e}{\mathrm{S}}_{\mathrm{2}}}$ corresponds to the volume fraction of pyrite.

With respect to the simplified form of the pyrite-to-pyrrhotite reduction (Eq. 15), the stoichiometric coefficients γ_geo can be expressed as follows:

${\gamma }_{\text{geo}}\left(\begin{array}{c}\hfill {\text{H}}_2\hfill \\ \hfill {\text{H}}_2\text{S}\hfill \\ \hfill {\text{FeS}}_2\hfill \\ \hfill \text{FeS}\hfill \\ \hfill \dots \hfill \end{array}\right)=\left(\begin{array}{c}\hfill -1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \end{array}\right)(19)$

For non-participating components such as H₂O and Ar the coefficient is zero.

In the experimental work of Truche et al. (2010), a progressive reduction of the reaction rate was observed. As mentioned earlier, Truche et al. (2010) concluded that beyond other influencing parameters, the hydrogen and hydrogen sulfide concentrations are crucial parameters controlling the overall reaction. For this purpose, the mass action term is represented by the coefficient δ which depends on the mentioned concentrations in the liquid phase ($c_w^{{\mathrm{H}}_{\mathrm{2}}}$ and $c_w^{{\mathrm{H}}_{\mathrm{2}}\mathrm{S}}$). Furthermore, the rate constant k depends on the thermodynamic parameters of temperature and pressure. For the experiments, it is assumed that the surface is completely exposed for the reaction, while in the subsurface, the pyrite is incorporated in other minerals of the rock matrix. To achieve circumstances mirroring reality, introducing a dimensionless scaling factor C_scaling is commonly applied to reduce the exposed reactive surface and simultaneously the reaction rate. Established values are in the range of 10⁻³ to 10⁻¹ (Bourg et al., 2015). Overall, this yields the following kinetic reaction rate:

$q_{\text{geo}}={\gamma }_{\text{geo}}k\left(p,T\right)\delta \left(c_w^{{\mathrm{H}}_2},c_w^{{\mathrm{H}}_{2}S}\right)A_s^{\mathrm{F}\mathrm{e}{\mathrm{S}}_{\mathrm{2}}}{\varphi }_s^{\mathrm{F}\mathrm{e}{\mathrm{S}}_{\mathrm{2}}}{C}_{\text{scaling}}(20)$

Due to the limited number of data points, the correlation was built based on basic functions such as linear for pressure and exponential function for temperature. For the kinetic rate constant, a best match is achieved as follows:

$k\left(p,T\right)=4.23\cdot 10^{-18}p\cdot {1.01015}^{4.8T-1050}(21)$

where the pressure is in Pa and the temperature is in K.

For the mass term, a rational term was used. For the denominator (here: hydrogen sulfide concentration) a case distinction for values tending against zero is required:

$\delta \left(c_w^{{\mathrm{H}}_2},c_w^{{\mathrm{H}}_{2}S}\right)=\frac{{c_w^{{\mathrm{H}}_2}}^2}{c_w^{{\mathrm{H}}_{2}S}}\text{with:\hspace{0.17em}}{c}_w^{{\mathrm{H}}_{2}S}=\left\{\begin{array}{cc}10^{-8},\hfill & \text{\hspace{0.17em}for\hspace{0.17em}}{c}_w^{{\mathrm{H}}_{2}S}\le 10^{-8}\hfill \\ c_w^{{\mathrm{H}}_{2}S},\hfill & \text{\hspace{0.17em}for\hspace{0.17em}}{c}_w^{{\mathrm{H}}_{2}S}>10^{-8}\hfill \end{array}\right.(22)$

The result of the developed correlation is depicted in Figure 2. For temperatures below 165°C a good match is achieved, while for 180°C a deviation from the experimental observations is remarkable. During the development of the correlation, particular focus was placed on lower temperatures, which led to higher deviations for higher temperatures. A proper match is visible for the low and medium-pressure experiments, and for the high-pressure case, only a small deviation in the advanced experiment is observable. Besides the measurements at reference partial pressures and temperatures, two additional measurements were selected by Truche et al. (2010) for developing the correlation. In the present study, these additional experiments were used to validate the new model (cf. Figure 3).

Figure 2

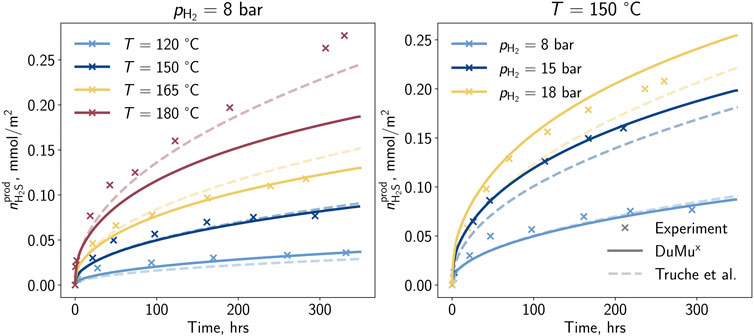
Figure 2. Hydrogen sulfide per surface area generated by the pyrite-to-pyrrhotite reduction determined in the laboratory (Truche et al., 2010), with the correlation of Truche et al. (2010), and the model developed in this study.

Figure 3

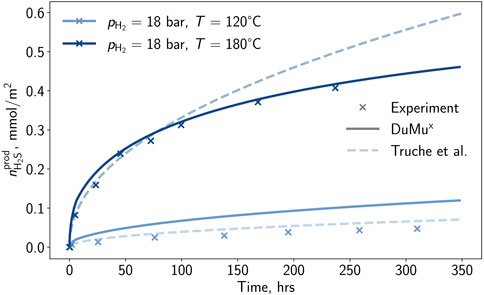
Figure 3. Hydrogen sulfide per surface area generated by the pyrite-to-pyrrhotite reduction determined in the laboratory (Truche et al., 2010), with the correlation of Truche et al. (2010), and the model developed in this study at conditions outside of the reference conditions.

In summary, the recently developed correlation (cf. Eq. 20) demonstrates the capability to reproduce the experimental findings of Truche et al. (2010) within an acceptable accuracy. It provides a satisfactory match for measurements beyond the reference conditions. Compared to the correlation developed by Truche et al. (2010), the recent correlation exhibits similar quality, with improved behavior regarding pressure dependency, and can be implemented in time- and spatial-dependent simulations. However, it is crucial to note that the modeling of the kinetic rate relies on eight experiments conducted at high temperatures, primarily for potential nuclear waste disposal scenarios. The exact impact of hydrogen concentration and absolute pressure is still uncertain due to the experiments maintaining a static hydrogen concentration of 10%. It is recommended to conduct independent analyses involving additional experimental investigations with varying hydrogen concentrations and absolute pressures, followed by modeling to enhance the developed correlation describing the reaction.

5 Application of simulation model on field scale

To investigate the developed bio-geochemical simulation model on field scale, a recently developed benchmark study for UHS scenarios (Hogeweg et al., 2022) was extended. Here, the focus was on incorporating geochemical reactions and comparing their impact on the UHS operation.

5.1 Simulation scenario description

While the original benchmark scenario primarily addressed variations in injection fluid composition (low and high hydrogen content), this study extends the investigation to explore the effects of both geochemical and biochemical reactions on UHS operations. Four cases were defined to achieve this, each varying in the presence of reactions (see Figure 4).

Figure 4

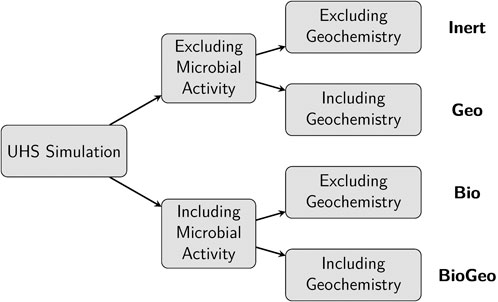
Figure 4. Simulation cases varying in microbial activity and hydrogen content in the injection stream.

5.2 Field characteristics/static model

A corner point grid based on a semi-artificial geological structure was used for the spatial discretization of the simulation. Overall, it consists of 44652 (61 × 61 × 12) grid cells with a dimension of 50 m × 50 m (x- and y-direction) and a varying thickness. The petrophysical properties were distributed heterogeneously, and the permeability was additionally defined as anisotropic. The average porosity is 15%, and the mean horizontal permeability is 143 mD (k_v ∼ 3mD), which can be observed in some sandstone formations in Northern Germany (permeability distribution based on a modified poro-perm-correlation).

5.3 Initialization

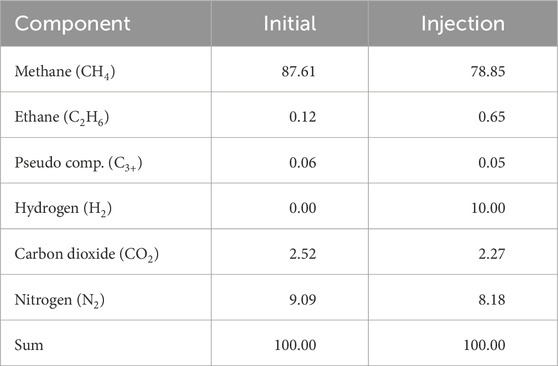
The system was initialized with a pressure of p_GWC = 81.6 bar at the gas-water-contact at a depth of 1210 m. A transition zone was established by the capillary pressure (Brooks and Corey (1964) parameter λ = 2.0, p_e = 0.1 bar) separating the gas and water zone. The initial gas composition in the gas zone was defined as natural gas (see Table 2) (Gecko Instruments GmbH, 2023). With respect to the vaporization of water in the gaseous phase, there is a minor concentration of H₂O in the gas phase. The liquid phase additionally contained sulfate $(c_w^{\mathrm{S}{\mathrm{O}}_{\mathrm{4}}^{\mathrm{2}-}}=0.03375\text{\%})$ and, depending on the case, microorganisms (methanogenic archaea and sulfate-reducing bacteria). The initial mineral concentration of pyrite was defined homogeneously as 1% (total volume fraction), whereby it typically varies from not detectable up to a few percentages for sandstones (Pettijohn et al., 1972; Ardakani et al., 2016). Regarding the reactivity of the pyrite, 1% were assumed to be reactive (C_scaling = 0.01), which is in the range of values from the literature (Bourg et al., 2015). The isothermal temperature was set to 80°C, different from the initial benchmark study (60°C), as geochemical reactions are not expected at lower temperatures.

Table 2

Table 2. Relevant fluid compositions in molar percent.

5.4 Operation schedule

In the present study, the schedule comprises two sections: 1) Conversion from natural gas storage into UHS and 2) Regular storage operation. In both sections, the injection/production occurs along a single well located in the center of the structure. The injected gas compositions remain constant (see Table 2). With respect to the step-wise development of UHS, a low hydrogen concentration of 10% may be interesting in first field projects (e.g., Underground Sun Storage (RAG Austria, 2017), and HySTORAGE (Strobel et al., 2023). The first section, the conversion, is characterized by a bottom-hole-pressure controlled injection, which is incrementally increased from 90 bar to 102 bar (step size: 4 bar) to increase the reservoir pressure and raise the hydrogen content in the storage. Four injection periods consisting of 60 days with 1 month of idle time in between are simulated. After the conversion, regular storage cycles are conducted. The regular operation consists of alternating injection and production with a constant rate of q = 6 ⋅ 10⁵ Sm³ ⋅ d⁻¹. The injection duration is identical to the withdrawal (90 days) to equalize the cumulative volumes. Like the conversion cycles, the regular storage cycles are separated by idle times.

5.5 Results and discussion

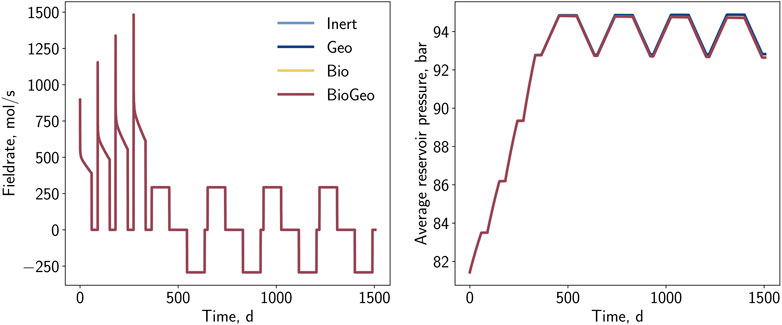
In general, four simulation cases were conducted, varying in the presence of bio- and geochemical reactions. Figure 5 illustrates relevant field parameters of the simulations. In the initial injection periods, pressure-controlled injection is notably evident, characterized by varying rates and progressively decreasing behavior. After the conversion, the regular operation with constant rates becomes visible. All cases exhibit identical behavior in this phase, and no differences are observed regarding the operation rate. During the conversion, a step-wise increase in pressure from 81.6 bar to 93 bar is observed and attributed to the injection of the natural gas-hydrogen blend to establish an initial hydrogen cushion within the storage. The subsequent storage cycles feature alternating pressure with an amplitude of approximately 2 bar. While the pressure trend is nearly identical for all cases during the conversion period, initial differences emerge during the storage operation. A progressive pressure drop over time is observed for cases considering biochemical reactions, while geochemical reactions appear to have a negligible impact on the average reservoir pressure. The pressure drop caused by biochemical reactions arises from the consumption of 5 and 6 mol of substrate, and the discharge of 3 and 5 mol of products, respectively.

Figure 5

Figure 5. Field rate and average reservoir pressure in dependency of time for all four cases.

During UHS, the composition of the gas produced is essential. Significant variations and contaminations by specific components, such as hydrogen sulfide, are unfavorable. Figure 6 displays the corresponding mole fractions of relevant gases (H₂, CO₂, and H₂S) during the four production periods. The impact of the general mixing but also the impact of potential bio- and geochemical reactions is observable. Generally, it is reasonable that the share of hydrogen in the production stream is close to the injection concentration at the beginning of each cycle. This fraction decreases with time as the gas is recovered from more distant regions, which is more likely to be mixed with the initial gas. Overall, this mixing can be counted as a loss of hydrogen and is, therefore, mainly responsible for the efficiency of UHS. Contrary to chemical reactions, this hydrogen loss can be partially compensated during the final depletion of the storage and can be assumed to be temporary. Regarding cases considering chemical reactions, the drop in the hydrogen fraction in the withdrawal stream is more significant, indicating additional losses. For the particular growth conditions, the influence of methanation and sulfate-reduction seems to be stronger than the pyrite-to-pyrrhotite-reduction. Further conclusions can be obtained from evaluating additional major relevant components such as carbon dioxide (cf. Figure 6B). In cases where carbon dioxide acts as a substrate for methanation, the carbon dioxide concentration monotonously decreases within each cycle. For the remaining cases, the concentration drops initially but recovers thereafter. This behavior can be an indicator to detect the presence of microorganisms consuming carbon dioxide, while the hydrogen fraction could be interpreted as ambiguous, as the reduction could also be caused by the mixing with the initial gas. The products of the reactions are also visible in the production stream. Due to the initial absence of hydrogen sulfide, it can be clearly distinguished from the injected and cushion gas. Here, it is visible that with increasing cycles, the hydrogen sulfide content in the gas stream increases. Remarkably, for cases including the geochemical reactions, the hydrogen sulfide concentration at the beginning of each cycle does not correspond to the injection concentration; moreover, it seems that pyrite and hydrogen are progressively converted during the idle state of the well. This can be explained by the fact that the reaction is far from equilibrium at higher hydrogen fractions in combination with low or absent hydrogen sulfide, which leads to an acceleration of the reaction. Conversely, the presence of sulfate-reducing bacteria decreases the reaction rate of the pyrite-to-pyrrhotite reduction over time.

Figure 6

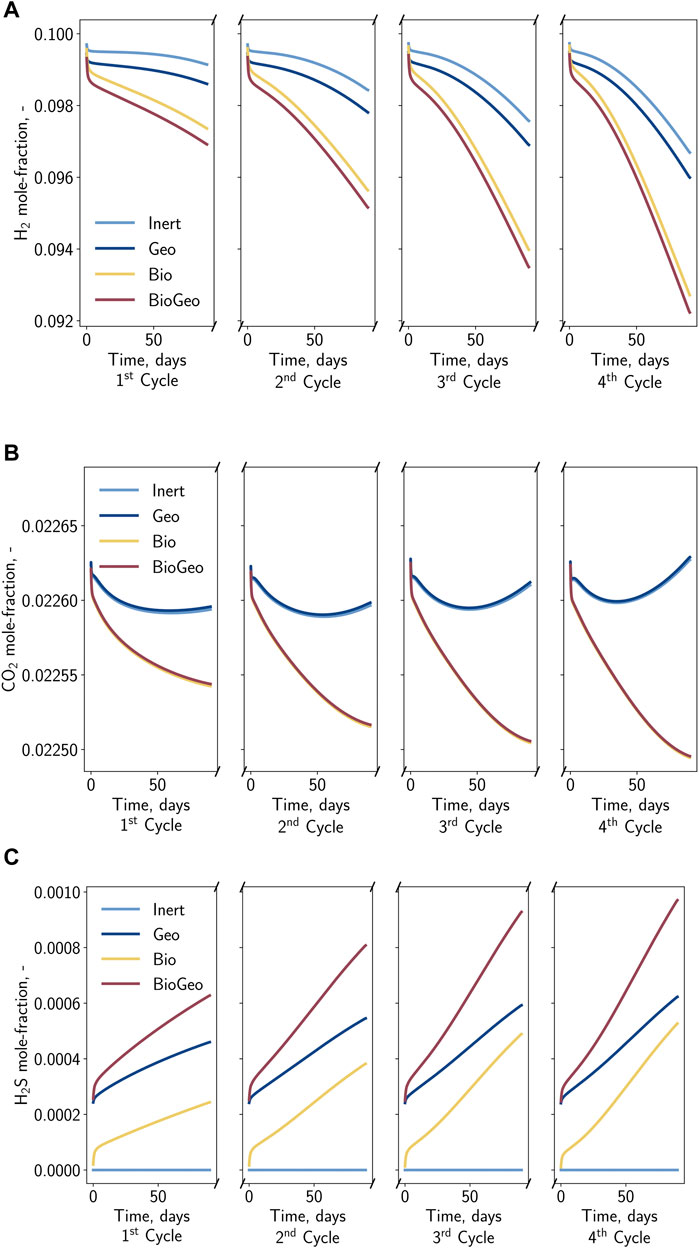
Figure 6. Gas composition in the gas stream during the four withdrawal periods. (A) Hydrogen mole fraction, (B) Carbon dioxide mole fraction, (C) Hydrogen sulfide mole fraction.

The observations from the gas composition during withdrawal can also be seen when looking at the spatial distribution of hydrogen, pyrite, and microbial density of the two species. Focusing on the hydrogen fraction (cf. Figure 7), the highest hydrogen content remains close to the wellbore and decreases with growing distance until reaching the initial cushion gas. The geochemical reaction mainly occurs around the wellbore, indicated by a ratio of the actual to initial pyrite smaller than unity. Here, the cyclic displacement of hydrogen sulfide leads to a repeated reaction rate acceleration. More distanced regions are consequently more saturated with hydrogen sulfide due to the displacement and the generation by sulfate-reducing bacteria. This leads to conditions close to the equilibrium of the geochemical reaction. The accumulation of hydrogen sulfide similar to a halo around the wellbore is observable in Figure 8.

Figure 7

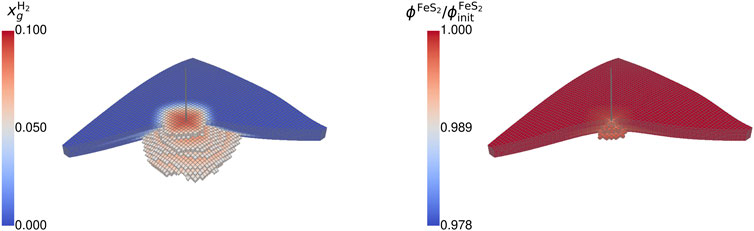
Figure 7. Spatial distribution of (A) hydrogen mole fraction (gaseous phase) and (B) the ratio of current to initial pyrite volume fraction at the end of the fourth storage cycle for case BioGeo (threshold: 50% and 80%).

Figure 8

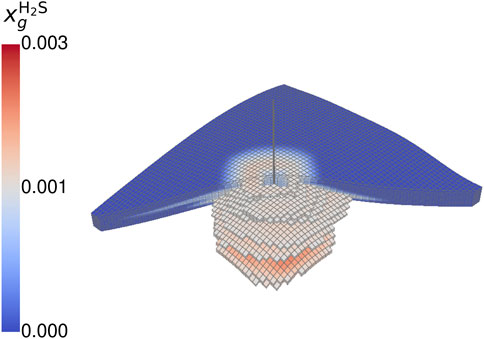
Figure 8. Spatial distribution of hydrogen sulfide mole fraction at the end of the fourth storage cycle for case BioGeo (threshold: 50%).

The observations from the spatial analysis are also visible in the geochemical conversion rate, as depicted in Figure 9. The step-wise increase in the reaction rate is discernible, caused by the growing hydrogen cushion. Nevertheless, the equilibrium of the reaction is progressively achieved, indicated by a drop in the reaction rate. With the overall increasing hydrogen sulfide content, the reaction decelerates globally, and it becomes less dominant with increasing storage cycles. It is visible that the geochemical reaction occurs slower for cases where sulfate-reducing bacteria are active, as they contribute to a higher overall hydrogen sulfide concentration, easing the reaction.

Figure 9

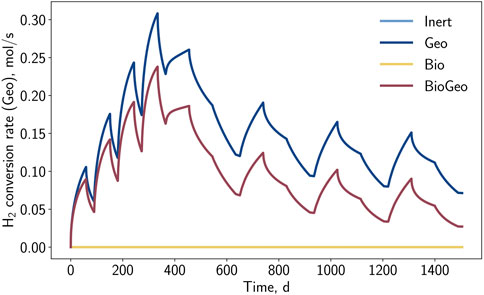
Figure 9. Hydrogen conversion rate by geochemical reaction (pyrite-to-pyrrhotite-reduction) in the entire storage formation versus time.

Focusing on the activity of microorganisms (cf. Figure 10), it is expected that the microorganism populations follow the spatial distribution of hydrogen, and their population density achieves the highest number around the wellbore, as a continuous substrate supply is ensured. This expectation is true for methanogenic archaea, as the injection stream provides the substrates continuously, and it achieves the maximum expected microbial density of n_max = 9265n_init. Conversely, as sulfate is only considered to be present initially and not generated by an additional source, one of the sulfate-reducing bacteria’s substrates becomes progressively limiting. This limitation is visible in the near-wellbore area, where the density of sulfate-reducing bacteria is low after some time. In the wellbore cells, the concentration is at its maximum, as it is drying out (S_w → 0), and the habitat of the microorganisms vanishes.

Figure 10

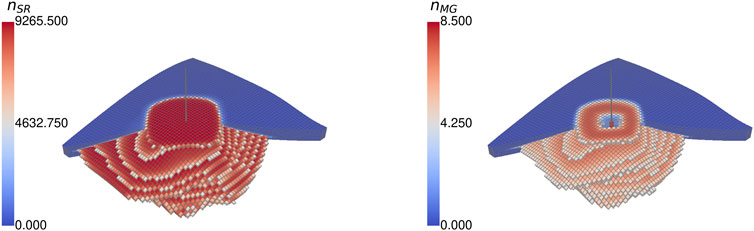
Figure 10. Spatial distribution of (dimensionless) microbial density of (A) sulfate-reducing organisms and (B) methanogenic microbes at the end of the fourth storage cycle of Case BioGeo (threshold: 50%).

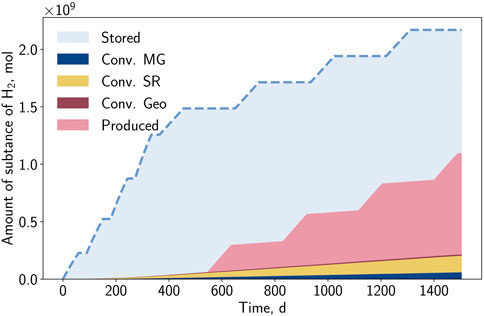
During the operation, the injected hydrogen will partially be reproduced, converted, and also remain in storage. Figure 11 displays this distribution for the case BioGeo, where all reactions are considered. The storage operation is clearly visible together with the step-wise behavior in hydrogen injected and produced. As the presence of the reactions is independent of the operation rates, the reactions occur continuously, leading to a progressive hydrogen loss. Due to the high amounts of hydrogen introduced during the conversion phase and the consecutive injection and withdrawal rates being balanced, it is expected that after four storage cycles, a large portion of the total injected hydrogen (≈49.4%) remains in the formation. Another 40.7% of the injected hydrogen is recovered during the four production periods. The remaining part (≈9.9%) is a permanent loss of hydrogen caused by bio- and geochemical reactions.

Figure 11

Figure 11. Distribution of hydrogen in the system versus time for case BioGeo.

The share of consumed hydrogen for each chemical reaction is depicted in Figure 12. With the selected reaction kinetics, the dominance of sulfate-reduction (6.6%) over methanation (2.7%) and pyrite-to-pyrrhotite-reduction (0.6%) can be identified. Nevertheless, it is expected that the shares of sulfate-reduction and pyrite-to-pyrrhotite-reduction will decrease due to substrate limitation and reaching overall equilibrium, respectively.

Figure 12

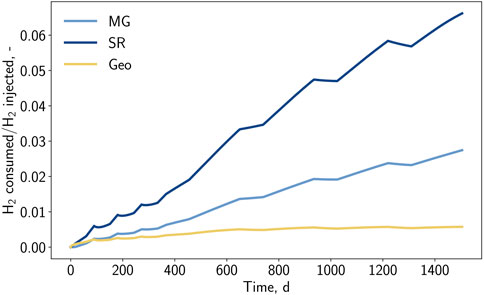
Figure 12. Fraction of consumed hydrogen by bio and geochemical reactions over the injected hydrogen amount versus time for case BioGeo.

6 Conclusion and outlook

The storage of hydrogen in the porous subsurface has some significant differences compared to the conventional storage of natural gas. Besides hydrodynamic phenomena such as viscous fingering and density override, the gas-gas mixing of injected and initial gas due to molecular diffusion and mechanical dispersion becomes crucial and significantly impacts the storage efficiency. Additionally, permanent hydrogen losses by bio- and geochemical reactions are expected. Hydrogenotrophic microorganisms potentially consume significant parts of the stored hydrogen and simultaneously lead to contamination of the stored gas. Similar outcomes can result from geochemical reactions producing harmful products like hydrogen sulfide. However, until today, only a few experiments have been conducted to investigate these reactions on field scale, and the prediction of the processes was only covered partially by numerical simulations.

Addressing these unique processes, an existing mathematical model describing the bio-reactive transport process (Hagemann, 2018) was extended by the potential geochemical reaction of pyrite-to-pyrrhotite. The developed model was implemented in the open source simulator DuMu^x and calibrated based on laboratory investigations from literature. The geochemical modeling comprised the development of a kinetic reaction model on a laboratory scale in DuMu^x. It allows the reproduction of the hydrogen sulfide generation during the reactor experiments of Truche et al. (2010) where pyrite was exposed to a hydrogen atmosphere at high temperatures and pressure. After the calibration, the developed bio-geo transport model was implemented for a benchmark scenario on a semi-artificial geological structure. Simulations of a simplified UHS operation, including conversion and consecutive storage cycles, revealed permanent hydrogen losses due to reactions and temporary losses induced by gas-gas mixing with the initial and cushion gas. For this specific scenario and the defined reaction parameters, approximately 10% of the injected hydrogen was converted by reactions, and an increasing share of cushion gas was detected in the withdrawal stream, indicating gas-gas mixing. Indicators for specific reactions were identified based on the composition of the production gas, allowing for insights into potential risks.

Although the model calibration primarily relies on laboratory observations, and while this already offers a necessary scientific foundation, the transfer from laboratory to field scale remains a critical step. Real field tests are necessary to further develop and validate the model in a realistic subsurface environment.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://data.goettingen-research-online.de/dataset.xhtml?persistentId=doi:10.25625/GNHQ93.

Author contributions

SH: Writing–original draft, Writing–review and editing, Investigation, Methodology, Software, Visualization. BH: Supervision, Writing–review and editing, Conceptualization, Funding acquisition, Project administration. VB: Methodology, Writing–original draft. LG: Supervision, Writing–review and editing, Project administration, Funding acquisition.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project has received funding from the Fuel Cells and Hydrogen 2 Joint Undertaking (now Clean Hydrogen Partnership) under grant agreement No. 101006632. This Joint Undertaking receives support from the European Union’s Horizon 2020 research and innovation programme, Hydrogen Europe and Hydrogen Europe Research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahn, A.-C., Hidalgo-Ulloa, A., Pereva, Y., Lomans, B., and Sousa, D. Z. (2023). Review of the window of viability of the different microbial metabolisms relevant for subsurface H2 storage applications. H2020 HyUSPRe Proj. Rep. D3.1.

Google Scholar

Ardakani, O. H., Chappaz, A., Sanei, H., and Mayer, B. (2016). Effect of thermal maturity on remobilization of molybdenum in black shales. Earth Planet. Sci. Lett. 449, 311–320. doi:10.1016/j.epsl.2016.06.004

CrossRef Full Text | Google Scholar

Bardelli, F., Mondelli, C., Didier, M., Vitillo, J. G., Cavicchia, D. R., Robinet, J.-C., et al. (2014). Hydrogen uptake and diffusion in Callovo-Oxfordian clay rock for nuclear waste disposal technology. Appl. Geochem. 49, 168–177. doi:10.1016/j.apgeochem.2014.06.019

CrossRef Full Text | Google Scholar

Bastian, P., Blatt, M., Dedner, A., Dreier, N.-A., Engwer, C., Fritze, R., et al. (2021). The Dune framework: basic concepts and recent developments. Comput. Math. Appl. 81, 75–112. doi:10.1016/j.camwa.2020.06.007

CrossRef Full Text | Google Scholar

Bear, J. (1979). McGraw-hill series in water resources and environmental engineering. London; New York: McGraw-Hill International Book Co.Hydraulics of groundwater

Google Scholar

Bethke, C. (1996). Geochemical reaction modeling: concepts and applications. New York: Oxford University Press.

Google Scholar

Bethke, C. M. (2021). Geochemical and biogeochemical reaction modeling. Cambridge University Press, 3. doi:10.1017/9781108807005

CrossRef Full Text | Google Scholar

Bo, Z., Boon, M., Hajibeygi, H., and Hurter, S. (2023). Impact of experimentally measured relative permeability hysteresis on reservoir-scale performance of underground hydrogen storage (UHS). Int. J. Hydrogen Energy 48, 13527–13542. doi:10.1016/j.ijhydene.2022.12.270

CrossRef Full Text | Google Scholar

Bo, Z., Zeng, L., Chen, Y., and Xie, Q. (2021). Geochemical reactions-induced hydrogen loss during underground hydrogen storage in sandstone reservoirs. Int. J. Hydrogen Energy 46, 19998–20009. doi:10.1016/j.ijhydene.2021.03.116

CrossRef Full Text | Google Scholar

Bourg, I. C., Beckingham, L. E., and DePaolo, D. J. (2015). The nanoscale basis of CO₂ trapping for geologic storage. Environ. Sci. Technol. 49, 10265–10284. doi:10.1021/acs.est.5b03003

PubMed Abstract | CrossRef Full Text | Google Scholar

Bourgeois, J. P., Aupaix, N., Bloise, R., and Millet, J. L. (1979). Proposition d’explication de la formation d’hydrogène sulfuré dans les stockages souterrains de gaz naturel par réduction des sulfures minéraux de la roche magasin. Rev. l’Institut Français Pétrole 34, 371–386. doi:10.2516/ogst:1979013

CrossRef Full Text | Google Scholar

Brooks, R. H., and Corey, A. T. (1964). Hydraulic properties of porous media and their relation to drainage design. Trans. ASAE 7, 0026–0028. doi:10.13031/2013.40684

CrossRef Full Text | Google Scholar

Buzek, F., Onderka, V., Vančura, P., and Wolf, I. (1994). Carbon isotope study of methane production in a town gas storage reservoir. Fuel 73, 747–752. doi:10.1016/0016-2361(94)90019-1

CrossRef Full Text | Google Scholar

Carman, P. C. (1939). Permeability of saturated sands, soils and clays. J. Agric. Sci. 29, 262–273. doi:10.1017/S0021859600051789

CrossRef Full Text | Google Scholar

Carrera, J., Saaltink, M. W., Soler-Sagarra, J., Wang, J., and Valhondo, C. (2022). Reactive transport: a review of basic concepts with emphasis on biochemical processes. Energies 15, 925. doi:10.3390/en15030925

CrossRef Full Text | Google Scholar

Chai, M., Chen, Z., Nourozieh, H., and Yang, M. (2023). Numerical simulation of large-scale seasonal hydrogen storage in an anticline aquifer: a case study capturing hydrogen interactions and cushion gas injection. Appl. Energy 334, 120655. doi:10.1016/j.apenergy.2023.120655

CrossRef Full Text | Google Scholar

Charlton, S. R., and Parkhurst, D. L. (2011). Modules based on the geochemical model PHREEQC for use in scripting and programming languages. Comput. Geosciences 37, 1653–1663. doi:10.1016/j.cageo.2011.02.005

CrossRef Full Text | Google Scholar

Cihlar, J., Mavins, D., and van der Leun, K. (2021). Picturing the value of underground gas storage to the European hydrogen system. Tech. Rep. Gas Infrastructure Europe.

Google Scholar

Dentz, M., Hidalgo, J. J., and Lester, D. (2023). Mixing in porous media: concepts and approaches across scales. Transp. Porous Media 146, 5–53. doi:10.1007/s11242-022-01852-x

CrossRef Full Text | Google Scholar

Dopffel, N., Jansen, S., and Gerritse, J. (2021). Microbial side effects of underground hydrogen storage – knowledge gaps, risks and opportunities for successful implementation. Int. J. Hydrogen Energy 46, 8594–8606. doi:10.1016/j.ijhydene.2020.12.058

CrossRef Full Text | Google Scholar

Eddaoui, N., Panfilov, M., Ganzer, L., and Hagemann, B. (2021). Impact of pore clogging by bacteria on underground hydrogen storage. Transp. Porous Media 139, 89–108. doi:10.1007/s11242-021-01647-6

CrossRef Full Text | Google Scholar

Elgendy, A. M., Pizzolato, A., Maniglio, M., Geloni, C., Panfili, P., and Topini, C. (2023). Reactive transport modelling of H2 storage in depleted gas fields: an approach to implement biogeochemical reactions in a compositional reservoir simulator. Austria: SPE: Vienna. doi:10.2118/214434-MS

CrossRef Full Text | Google Scholar

Feldmann, F., Hagemann, B., Ganzer, L., and Panfilov, M. B. (2016). Numerical simulation of hydrodynamic and gas mixing processes in underground hydrogen storages. Environ. Earth Sci. 75, 1165. doi:10.1007/s12665-016-5948-z

CrossRef Full Text | Google Scholar

Fick, A. (1855). Ueber diffusion. Ann. Phys. Chem. 170, 59–86. doi:10.1002/andp.18551700105

CrossRef Full Text | Google Scholar

Flemisch, B., Darcis, M., Erbertseder, K., Faigle, B., Lauser, A., Mosthaf, K., et al. (2011). DuMux: DUNE for multi-{phase,component,scale,physics,…} flow and transport in porous media. Adv. Water Resour. 34, 1102–1112. doi:10.1016/j.advwatres.2011.03.007

CrossRef Full Text | Google Scholar

Gaucher, E., Tournassat, C., Pearson, F., Blanc, P., Crouzet, C., Lerouge, C., et al. (2009). A robust model for pore-water chemistry of clayrock. Geochimica Cosmochimica Acta 73, 6470–6487. doi:10.1016/j.gca.2009.07.021

CrossRef Full Text | Google Scholar

Gecko Instruments GmbH (2023). Die erdgaszusammensetzungen in deutschland. Available at: https://www.gecko-instruments.de/pages/produkte/precisive/erdgas-zusammensetzung.php. (Accessed 2023-April-26)

Google Scholar

Ghiorse, W. C., and Wilson, J. T. (1988). Microbial ecology of the terrestrial subsurface. Adv. Appl. Microbiol. (Elsevier) 33, 107–172. doi:10.1016/S0065-2164(08)70206-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Götz, M., Lefebvre, J., Mörs, F., McDaniel Koch, A., Graf, F., Bajohr, S., et al. (2016). Renewable Power-to-Gas: a technological and economic review. Renew. Energy 85, 1371–1390. doi:10.1016/j.renene.2015.07.066

CrossRef Full Text | Google Scholar

Groß, T., Dunkel, P., Franzmann, D., Heinrichs, H., Linßen, J., and Stolten, D. (2022). H2 supply from renewable energy sources, H2 demand centers and H2 transport infrastructure. H2020 HyUSPRe Project Report D1.2.

Google Scholar

Hagemann, B. (2018). Numerical and analytical Modeling of gas Mixing and bio-reactive transport during Underground hydrogen storage, vol. Band 50 of schriftenreihe des energie-forschungszentrums niedersachsen. 1. edition edn. Göttingen: Cuvillier Verlag.

Google Scholar

Hagemann, B., Ganzer, L., and Panfilov, M. (2018). “Field scale modeling of bio-reactions during underground hydrogen storage,” in Ecmor XVI - 16th European conference on the mathematics of oil recovery (Barcelona, Spain: EAGE Publications BVNetherlands). Proceedings. doi:10.3997/2214-4609.201802116

CrossRef Full Text | Google Scholar

Harati, S., Rezaei Gomari, S., Gasanzade, F., Bauer, S., Pak, T., and Orr, C. (2023). Underground hydrogen storage to balance seasonal variations in energy demand: impact of well configuration on storage performance in deep saline aquifers. Int. J. Hydrogen Energy 48, 26894–26910. doi:10.1016/j.ijhydene.2023.03.363

CrossRef Full Text | Google Scholar

Hassanpouryouzband, A., Adie, K., Cowen, T., Thaysen, E. M., Heinemann, N., Butler, I. B., et al. (2022). Geological hydrogen storage: geochemical reactivity of hydrogen with sandstone reservoirs. ACS Energy Lett. 7, 2203–2210. doi:10.1021/acsenergylett.2c01024

PubMed Abstract | CrossRef Full Text | Google Scholar

Hebling, C., Ragwitz, M., Fleiter, T., Groos, U., Härle, D., Held, A., et al. (2019). “Eine Wasserstoff-Roadmap für Deutschland,” in Position paper, Fraunhofer-Institut für System-und Innovationsforschung ISI (Freiburg, Karlsruhe & Freiburg: Karlsruhe Fraunhofer-Institut für Solare Energiesysteme ISE).

Google Scholar

Heinemann, N., Alcalde, J., Miocic, J. M., Hangx, S. J. T., Kallmeyer, J., Ostertag-Henning, C., et al. (2021). Enabling large-scale hydrogen storage in porous media – the scientific challenges. Energy & Environ. Sci. 14, 853–864. doi:10.1039/D0EE03536J

CrossRef Full Text | Google Scholar

Hemme, C., and van Berk, W. (2018). Hydrogeochemical modeling to identify potential risks of underground hydrogen storage in depleted gas fields. Appl. Sci. 8, 2282. doi:10.3390/app8112282

CrossRef Full Text | Google Scholar

Henry, W. (1803). Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures. Philosophical Trans. R. Soc. Lond. 93, 29–274. doi:10.1098/rstl.1803.0004

CrossRef Full Text | Google Scholar

Hogeweg, S., and Hagemann, B. (2023). GitLab repository - dumux-hyuspre. Available at: https://gitlab.tu-clausthal.de/asho13/dumux-hyuspre/(Accessed December 18, 2023).

Google Scholar

Hogeweg, S., Hagemann, B., and Ganzer, L. (2023a). Data for: HyUSPRe - work Package 6 - validated open-source reservoir modelling software that can simulate coupled flow. Geochem. Microbiol. Process. a porous Reserv. under operational hydrogen storage Cond. doi:10.25625/GNHQ93

CrossRef Full Text | Google Scholar

Hogeweg, S., Michelsen, J., Hagemann, B., and Ganzer, L. (2023b). Empirical and numerical modelling of gas–gas diffusion for binary hydrogen–methane systems at underground gas storage conditions. Transp. Porous Media 151, 213–232. doi:10.1007/s11242-023-02039-8

CrossRef Full Text | Google Scholar

Hogeweg, S., Strobel, G., and Hagemann, B. (2022). Benchmark study for the simulation of underground hydrogen storage operations. Comput. Geosci. 26, 1367–1378. doi:10.1007/s10596-022-10163-5

CrossRef Full Text | Google Scholar

Hommel, J. (2016). Modelling biogeochemical and mass transport processes in the subsurface: investigation of microbially induced calcite precipitation. doi:10.18419/OPUS-8770

CrossRef Full Text | Google Scholar

Khoshnevis, N., Hogeweg, S., Goncalves Machado, C., and Hagemann, B. (2023). “Numerical modeling of bio-reactive transport during underground hydrogen storage – a benchmark study,” in The fourth EAGE global energy transition conference and exhibition (Paris, France: European Association of Geoscientists & Engineers), 1–5. doi:10.3997/2214-4609.202321087

CrossRef Full Text | Google Scholar

Koch, T., Gläser, D., Weishaupt, K., Ackermann, S., Beck, M., Becker, B., et al. (2020). DuMux 3 – an open-source simulator for solving flow and transport problems in porous media with a focus on model coupling. Comput. Math. Appl. 81, 423–443. doi:10.1016/j.camwa.2020.02.012

CrossRef Full Text | Google Scholar

Kozeny, J. (1927). Über kapillare Leitung des Wassers im Boden: (Aufstieg, Versickerung u. Anwendung auf die Bewässerung). Hölder-Pichler-Tempsky, A.-G. [Abt.] Akad. D. Wiss.

Google Scholar

Lasaga, A. C., Soler, J. M., Ganor, J., Burch, T. E., and Nagy, K. L. (1994). Chemical weathering rate laws and global geochemical cycles. Geochimica Cosmochimica Acta 58, 2361–2386. doi:10.1016/0016-7037(94)90016-7

CrossRef Full Text | Google Scholar

Lipman, C. B. (1931). Living microörganisms in ancient rocks. J. Bacteriol. 22, 183–198. doi:10.1128/jb.22.3.183-198.1931

PubMed Abstract | CrossRef Full Text | Google Scholar

Lohrenz, J., Bray, B. G., and Clark, C. R. (1964). Calculating viscosities of reservoir fluids from their compositions. J. Petroleum Technol. 16, 1171–1176. doi:10.2118/915-PA

CrossRef Full Text | Google Scholar

Lysyy, M., Fernø, M. A., and Ersland, G. (2023). Effect of relative permeability hysteresis on reservoir simulation of underground hydrogen storage in an offshore aquifer. J. Energy Storage 64, 107229. doi:10.1016/j.est.2023.107229

CrossRef Full Text | Google Scholar

Monod, J. (1949). The growth of bacterial cultures. Annu. Rev. Microbiol. 3, 371–394. doi:10.1146/annurev.mi.03.100149.002103

CrossRef Full Text | Google Scholar

Ostertag-Henning, C. (2023). “Geochemical reactions of iron oxides with hydrogen in the porespace of sandstones: processes, kinetics & limitations of the extent of reaction,” in Development of a micromodel design Algorithm for heterogeneous reservoir rocks (edinburgh).

Google Scholar

Paterson, L. (1983). The implications of fingering in underground hydrogen storage. Int. J. Hydrogen Energy 8, 53–59. doi:10.1016/0360-3199(83)90035-6

CrossRef Full Text | Google Scholar

Peng, D.-Y., and Robinson, D. B. (1976). A new two-constant equation of state. Industrial Eng. Chem. Fundam. 15, 59–64. doi:10.1021/i160057a011

CrossRef Full Text | Google Scholar

Pettijohn, F. J., Potter, P. E., and Siever, R. (1972). Mineral and chemical composition. New York, NY: Springer US, 25–67. doi:10.1007/978-1-4615-9974-6_2

CrossRef Full Text | Google Scholar

Pudlo, D., Henkel, S., and Gaupp, R. (2016). Verbundvorhaben H2STORE, Teilprojekt 3: Sedimentologisch-fazielle und mineralogisch-geochemische Untersuchungen an Reservoir-und Deckgesteinen: Abschlussbericht zum Verbundvorhaben H2STORE Teilprojekt 3: Berichtszeitraum: 01.08.2012-31.12.2015. Tech. rep., Friedrich-Schiller-Universität Jena, Inst. für Geowiss. Lehrstuhl für Allg. Hist. Geol. doi:10.2314/GBV:873830806

CrossRef Full Text | Google Scholar

RAG Austria, A. G. (2017). AXIOM angewandte Prozesstechnik GesmbH, Verbund AG, Montanuniversität Leoben, Universität für Bodenkultur Wien, and Energieinstitut an der Johannes Kepler Universität Linz (31.11.2017). Underground Sun Storage: Publizierbarer Endbericht. Tech. Rep. RAG Austria Ag. Wien.

Google Scholar

Reitenbach, V., Ganzer, L., Albrecht, D., and Hagemann, B. (2015). Influence of added hydrogen on underground gas storage: a review of key issues. Environ. Earth Sci. 73, 6927–6937. doi:10.1007/s12665-015-4176-2

CrossRef Full Text | Google Scholar

Saffman, P. G., and Taylor, G. I. (1958). The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 245, 312–329. doi:10.1098/rspa.1958.0085

CrossRef Full Text | Google Scholar

Šmigáň, P., Greksák, J., Kozánková, J., Buzek, F., Onderka, V., and Wolf, I. (1990). Methanogenic bacteria as a key factor involved in changes of town gas stored in an underground reservoir. FEMS Microbiol. Lett. 73, 221–224. doi:10.1016/0378-1097(90)90733-7

CrossRef Full Text | Google Scholar

Stiel, L. I., and Thodos, G. (1961). The viscosity of nonpolar gases at normal pressures. AIChE J. 7, 611–615. doi:10.1002/aic.690070416

CrossRef Full Text | Google Scholar

Strobel, G., Hagemann, B., and Ganzer, L. (2019). History matching of bio-reactive transport in an Underground hydrogen storage field case. doi:10.3997/2214-4609.201900258

CrossRef Full Text | Google Scholar

Strobel, G., Kosack, C., Bombach, P., Fischer, A., Hagemann, B., and Hogeweg, S. (2023). HySTORAGE: preliminary investigations of possible hydrogen losses with focus on a planned hydrogen storage field test in Bierwang. Celle, Germany: DGMK/ÖGEW Frühjahrstagung 2023.

Google Scholar

Tek, M. (1996). Natural gas Underground storage: inventory and deliverability. PennWell Books. (PennWell Pub.).

Google Scholar

Thaysen, E. M., McMahon, S., Strobel, G. J., Butler, I. B., Ngwenya, B. T., Heinemann, N., et al. (2021). Estimating microbial growth and hydrogen consumption in hydrogen storage in porous media. Renew. Sustain. Energy Rev. 151, 111481. doi:10.1016/j.rser.2021.111481

CrossRef Full Text | Google Scholar

Truche, L., Berger, G., Destrigneville, C., Guillaume, D., and Giffaut, E. (2010). Kinetics of pyrite to pyrrhotite reduction by hydrogen in calcite buffered solutions between 90 and 180°C: implications for nuclear waste disposal. Geochimica Cosmochimica Acta 74, 2894–2914. doi:10.1016/j.gca.2010.02.027

CrossRef Full Text | Google Scholar

Truche, L., Jodin-Caumon, M.-C., Lerouge, C., Berger, G., Mosser-Ruck, R., Giffaut, E., et al. (2013). Sulphide mineral reactions in clay-rich rock induced by high hydrogen pressure. Application to disturbed or natural settings up to 250 °C and 30 bar. Chem. Geol. 351, 217–228. doi:10.1016/j.chemgeo.2013.05.025

CrossRef Full Text | Google Scholar

Wang, G., Pickup, G., Sorbie, K., De Rezende, J., Zarei, F., and Mackay, E. (2023). Bioreaction coupled flow simulations: impacts of methanogenesis on seasonal underground hydrogen storage. Int. J. Hydrogen Energy 55, 921–931. doi:10.1016/j.ijhydene.2023.11.035

CrossRef Full Text | Google Scholar