Estimation of abnormal states in shunt capacitor banks using transient disturbance feature extraction

Shunt capacitor banks are essential for reactive power compensation, ensuring voltage stability, and reducing system losses. These banks consist of multiple units with components in series and parallel. A few component failures do not immediately affect the safe operation of the capacitor bank, but component breakdown can lead to voltage redistribution. Under combined factors such as system overvoltage and equipment aging, and others can trigger an avalanche effect causing capacitor breakdown, resulting in significant safety accident risks. Practical operation experience shows that partial component breakdown generates many transient disturbance signals. Quantitative analysis of these signals can detect capacitor bank anomalies early. This paper proposes the quantitative extraction of transient disturbance characteristics using the Prony algorithm and estimates the phase and number of capacitors that break down to judge capacitor anomalies. The simulation part verifies the theoretical analysis and detection algorithm’s correctness through numerical simulations and PSCAD (Power Systems Computer Aided Design) electromagnetic transient simulations. The numerical simulations consider different signal lengths, noise levels, attenuation coefficients, and oscillation frequencies. In the PSCAD simulation environment, verification models are built under varying sampling frequencies, numbers of breakdown components, signal lengths, and signal-to-noise ratios. These simulation results verify the accuracy of the detection algorithm under different conditions.

1 Introduction

Capacitor banks are an important means of reactive power compensation to ensure the safety and operational efficiency of power grid operations. Capacitor banks have a variety of long-term adverse factors, such as frequent casting and cutting operations, overvoltage, harmonics, and manufacturing process defects. Shunt capacitor bank insulation faults are frequent, with component breakdown being the most common internal fault (Santoso, 2007). In recent years, several capacitor bank explosions have been induced by internal insulation failure, seriously affecting the stability of the power grid and personnel and equipment safety.

Capacitors are usually equipped with internal component protection and external unbalance protection to ensure the safe operations of shunt capacitor banks (Institute of Electrical and Electronics Engineers. Std 1036-2010, 2010). Most capacitor units are equipped with internal fuse protections to isolate faulty components. Thus, when a few components within the capacitor break down, the remaining normal components can continue to operate (Beere, 1987). The capacitor fault characteristics will not reach the unbalance protection action conditions and will not cause the protection to trip. The overvoltage increases the fault section of the intact components, making breakdown failure more probable. Therein, most shunt capacitor banks easily develop into significant faults from internal weak faults (Xiaoyu et al., 2015). Bringing security risks to shunt capacitor bank operations. When the overvoltage develops to a certain degree, internal faults expand in the capacitor and protection action, ultimately causing the shunt capacitor bank to fail and shut down. If the protection fails to act in time, several component breakdowns will cause the capacitor to exhibit short-circuit faults, leading to capacitor explosions and other accidents. Therefore, timely and sensitive monitoring and localization of capacitor bank component breakdown is vital for ensuring the safety of capacitor banks.

For capacitors equipped with online monitoring devices, traditional state characteristic parameters such as capacitance and dielectric loss factor can be measured directly or indirectly calculated to achieve early detection and diagnosis of component breakdown faults in capacitors (Li and Li, 2017). Capacitance is the primary and most intuitive state characteristic parameter of capacitors, as component breakdown faults cause capacitance changes. Dielectric loss is the energy lost under the action of electric fields, and the dielectric loss factor reflects the overall insulation status of capacitor equipment. Monitoring and analyzing these two state parameters can detect component breakdown faults in capacitors and assess their severity. Moghaddam (Moghaddam, 2017) designed an insulation online monitoring and fault diagnosis system based on virtual instrument technology and LabVIEW software. This system used the capacitance change rate and dielectric loss as feature inputs to establish a fuzzy fault diagnosis model. However, the accuracy of the model membership functions should be improved. Directly measuring these state parameters requires specific monitoring equipment (such as a dielectric loss measurement device), has very high precision requirements, and is usually only applicable to single capacitors, indicating its economic inefficiency.

With the widespread application of power quality analyzers, fault recorders, and other waveform monitoring devices, important data foundations have been provided to diagnose and analyze capacitor group breakdown faults based on power disturbances (Silverstein and Follum, 2020). Previous studies have mainly explored online monitoring and fault analyses for parallel capacitor groups based on voltage/current monitoring data. However, these have primarily utilized steady-state quantities to define new characteristics for analyses and calculations, thus obtaining information on component breakdown faults in parallel capacitor groups.

For instance, Jie et al. (2022) evaluated and calculated steady-phase and amplitude changes in the unbalanced currents of capacitor groups before and after faults. This method can quickly determine the branches of faulty capacitor units and calculate the number of faulty capacitor units. Additionally, Shilong et al. (2020) proposed a scheme based on an unbalanced neutral current to enhance the online monitoring capability of internal faults in parallel capacitor groups. Jouybari-Moghaddam et al. (2017) used the compensation current of the neutral point to define differences in the steady-state phase quantities of unbalanced neutral point currents before and after faults to determine the faulty phase. They applied the positive or negative coefficients of the compensation current to judge the faulty arm. Pavan and Das (2020) defined the negative sequence compensation current for locating the faulty phase and faulty arm, allowing for isolating the occurrence of breakdown faults in both arms with the same or different faulty phases. Goodarzi and Allahbakhshi (2022) utilized discrete Fourier transforms to extract the neutral point voltage and current steady-state phasors. They located the faulted phase by detecting the unbalanced neutral point current changes before and after the fault.

Actual analyses revealed that although the breakdown of capacitor units changes the steady-state voltage and current, these changes are relatively small and easily affected by factors such as system voltage fluctuations. This poses significant limitations for precise diagnosis. In contrast, the transient components of breakdown fault disturbances offer salient features, easy disturbance separation, and rich information content. As a result, exploring parallel capacitor group fault diagnosis methods based on the transient feature analysis of breakdown fault disturbances has vital engineering significance (Wischkaemper et al., 2016).

This paper analyzes the physical process of component breakdown and fault transient characteristics of shunt capacitor banks in detail. We analyze the waveform characteristics of fault transient processes on the key monitoring points of shunt capacitor banks, derive and analyze the quantitative relationship between the key parameters of the transient signals on the R-C circuit, and introduce the transient power perturbation feature extraction-based shunt capacitor bank anomaly estimation method based on the signal characteristic parameter extraction algorithm (e.g., Prony’s algorithm). Finally, numerical analyses and electromagnetic transient simulations verify the proposed method to estimate capacitance. The capacitor state detection based on analyzing the capacitance change is of important theoretical value and engineering significance for improving capacitor state perceptions.

2 Transient characterization of capacitor bank structures and component breakdown

2.1 Shunt capacitor bank structure and operational characteristics

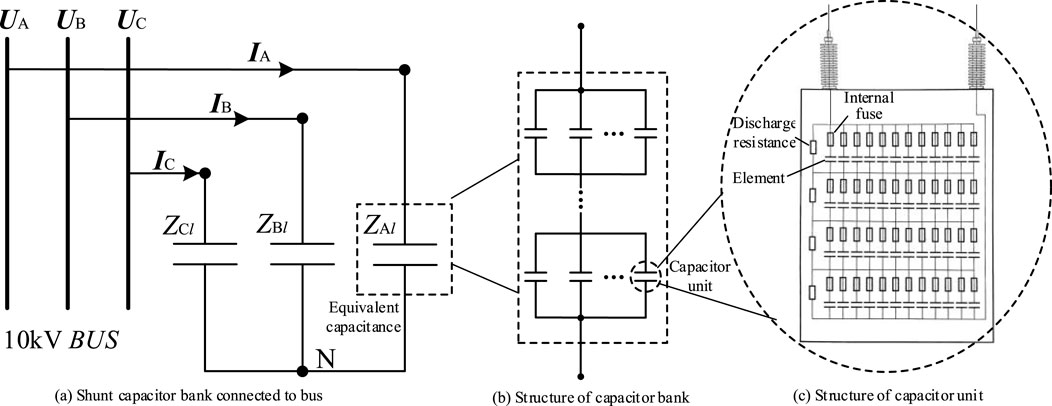
In Figure 1, the existing capacitor bank for reactive power compensation and filtering is connected directly in parallel to the 10 kV bus. Each phase of the capacitor bank consists of several capacitor units in series and parallel. The number of series and parallel units is determined primarily by the capacity of a single capacitor unit to withstand the voltage level decisions. The capacitor unit structure is shown in Figure 1, where each capacitor unit consists of several elements in series and parallel. Each capacitor element is series-connected to the internal fuse. When a single capacitor element breakdown occurs, the internal fuse quickly isolates the fault, and the capacitor unit returns to normal operations. When many components break down, the capacitor withstand voltage is no longer uniformly distributed, making it easy to induce avalanche with capacitor breakdown, resulting in a significant safety accident.

Figure 1

Figure 1. Diagram showing the shunt capacitor bank element structure.

2.2 Transient characterization of a capacitive element in breakdown

The capacitive element adopts an internal fuse structure, and its fault process includes two stages: capacitive element breakdown and fuse melting. The energy in the system is redistributed when in a breakdown state, equivalent to the fault capacitive element in series being directly shorted, resulting in a transient signal. When the capacitive element allows more current to flow, the fuse rapidly melts (about 1 ms) (Xu et al., 2022), and the faulty element is isolated. The same series section of the capacitor progresses in the charging state. Analyzing the component breakdown fault process shows the internal fuse impedance and capacitor unit lead impedance are much smaller than the system impedance. Thus, the calculation is ignored.

The current production technology of capacitors and components is generally used to highlight the folded edge of aluminum foil structures to achieve the series-parallel connection. Therefore, the components of the lead pieces for the resistance and inductance can be disregarded. Figure 2 shows the simplified circuit for the decoupling equivalent three-phase shunt capacitor bank component breakdown fault. The $U_A$, $U_B$, and $U_C$ are the three-phase symmetrical power supply terminal voltage, $R_1$ and $L_1$ are the system positive-sequence equivalent resistance and equivalent inductance, $i_A$, $i_B$, and $i_C$ are the port three-phase currents, and $C_A$, $C_B$, and $C_C$ are the three-phase capacitance values.

Figure 2

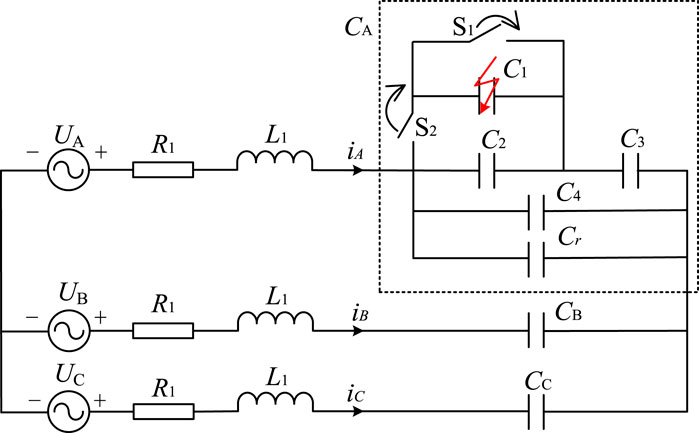
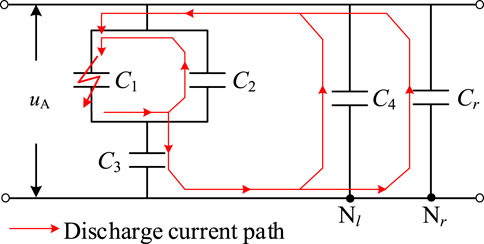
Figure 2. Simplified circuit of three-phase capacitor bank element breakdown fault after decoupling.

Three assumptions are made to simplify the analysis. 1) The system is in a steady state when a component fails. 2) The number of series segments in the double-star capacitor bank is 1. 3) The internal fuse can effectively fuse and isolate the faulty component, preventing the occurrence of arcing. It is assumed that a capacitor unit in the left arm of phase A of the double-star capacitor bank experiences component breakdown at time $t_1$, and the fuse blows at time $t_2$. These two actions are equivalent to a switch closing and a switch opening. In Figure 2, $C_1$ is the capacitance of the breakdown capacitor, $C_2$ is the equivalent capacitance of the remaining components in the same faulty series segment as the breakdown component, $C_3$ is the equivalent capacitance of the non-faulty series segments within the capacitor unit, $C_4$ is the equivalent capacitance of the remaining capacitor units in the left arm in parallel with the faulty capacitor unit, and $C_{\mathrm{r}}$ is the equivalent capacitance of the right arm.

Assuming the port voltage for the A-phase shunt capacitor bank is $u_A$, the voltage on $C_3$ before fault is $u_{C3}=\frac{n-1}{n}{u}_A$ ($n$ is the number of series segments in the capacitor unit). The $t_1$ moment $S_1$ is closed, making the component $C_1$ break down. The faulty series segments ($C_1$ + $C_2$) are shorted, and the intact component $C_2$ connected in parallel with $C_1$ is discharged to the point of breakdown. At this time, the voltage on $C_3$ abruptly changes to $u_{C3}^{\prime }=u_A$, increasing the amplitude of the total voltage of non-faulty segments. As $i_{C3}=C_3\frac{d{u}_{C3}}{dt}$, the amplitude of the current in the branch where the faulty capacitor unit is located increases. According to Kirchhoff’s current law (KCL), the other capacitor units connected in parallel with the faulty capacitor unit and non-faulty phase-parallel capacitor bank will also discharge to the breakdown element.

The above analysis derives the internal discharge current circuit diagram for the component breakdown moment of the fault phase shunt capacitor bank, as shown in Figure 3. The breakdown occurs in the positive half of the voltage. The discharge current is reversed if the breakdown occurs in the voltage’s negative half. The breakdown component in the branch circuit discharge current is used to blow the fuse current. The component is usually near the peak voltage breakdown when the frequency current is just over zero. Further, the actual capacitor unit of the external circuit in the presence of inductance delays the frequency current injection into the fault branch circuit (Yan et al., 2016). Moreover, the interval between the component breakdown $t_1$ and the moment of faulty branch being removed $t_2$ is extremely short (less than 1 ms) (Technical Committee for Standardization of, 2011). Therefore, the faulty branch discharge current does not contain the industrial frequency component. The fault branch discharge current is expressed, as shown in Equation 1 (Jiabi, 2021).

$i_{\text{fuse}}\left(t\right)=I_{\text{fu}}{e}^{-{\delta }_{\text{fu}}\left(t-t_1\right)}\cos \left({\omega }_{\text{fu}}t+{\phi }_{\text{fu}}\right),t_1\le t<t_2(1)$

where $I_{\text{fu}}$, ${\omega }_{\text{fu}}$, ${\delta }_{\text{fu}}$, and ${\phi }_{\text{fu}}$ are the amplitude, angular frequency, attenuation coefficient, and initial phase angle of the transient discharge current caused by element breakdown, respectively. Figure 4 shows the voltage and current waveforms of a typical capacitive element breakdown. The component breaks down at the peak of the positive half-cycle in the voltage waveform of phase A. The diagram shows that the faulty phase voltage waveform undergoes a sudden change toward zero at the moment of component breakdown. In contrast, the direction of the change in the current waveform has the opposite polarity. After the fuse blows, the oscillation magnitude of the transient current is greater than the transient voltage, giving a larger ratio of the transient component amplitude to the fundamental frequency amplitude. The duration of this transient process depends on the magnitude of the decay factor and indirectly depends on the line impedance parameters. The transient current typically tends to zero within 1–2 cycles.

Figure 3

Figure 3. Discharge current circuit inside the capacitor bank in case of component breakdown.

Figure 4

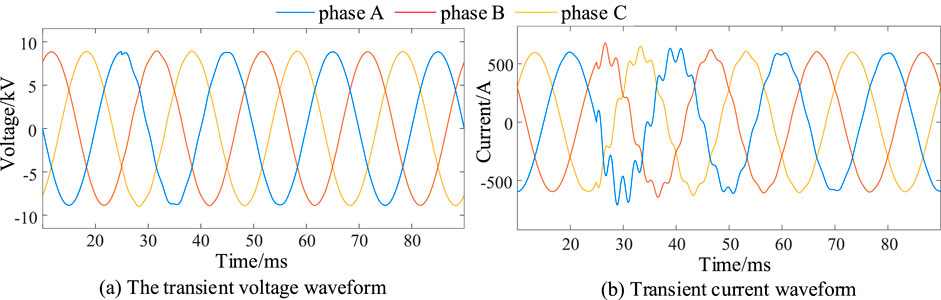
Figure 4. The voltage and current transient disturbance waveforms caused by capacitor element breakdown.

3 Capacitance estimation algorithm based on attenuated transient signal calculations

3.1 Calculation of capacitance parameters based on attenuated oscillatory transient signals

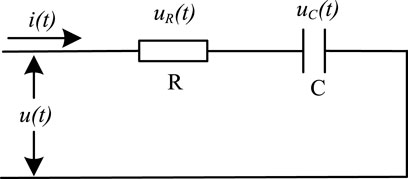
The transient characterization of double-star shunt capacitor bank component breakdown faults in Section 2 suggests that the transient voltage and current components at the port of the shunt capacitor bank caused by component breakdown faults are high-frequency attenuation signals. Neglecting the resistance and inductance inside the shunt capacitor bank simplifies the R-C circuit model. The resistance value $R$ is small, and the capacitance $C$ is large, with a simplified circuit shown in Figure 5. In the diagram, $u\left(t\right)$, $u_R\left(t\right)$, and $u_{\mathrm{C}}\left(t\right)$ represent the port voltage, the voltage across the resistor $R$, and the voltage across the capacitor $C$, respectively.

Figure 5

Figure 5. Simplified R-C circuit of the shunt capacitor bank.

Assuming $i\left(t\right)$ is the instantaneous value of the port current signal of the shunt capacitor bank, it can be expressed as:

$i\left(t\right)=I_{mag}\cdot \cos \left(\omega t+{\phi }_i\right)\cdot e^{-\tau t}(2)$

in the Equation 2, $I_{mag}$, $\omega$, ${\phi }_i$, and $\tau$ represent the amplitude, angular frequency, phase angle, and attenuation coefficient of the port current, respectively.

According to the voltage and current differential equations $i\left(t\right)=C\frac{d{u}_C\left(t\right)}{dt}$ of the capacitive element, $u_{\mathrm{C}}\left(t\right)$ and $u\left(t\right)$ are given by Equation 3 (Wen-hai et al., 2014):

$\left\{\begin{array}{l}{u}_R\left(t\right)=i\left(t\right)\cdot R=I_{mag}\cdot R\cdot \cos \left(\omega t+{\phi }_i\right)\cdot e^{-\tau t}\\ u_C\left(t\right)=\frac{1}{C}\cdot \int i\left(t\right)dt=\frac{1}{C}\cdot I_{mag}\cdot \int \cos \left(\omega t+{\phi }_i\right)\cdot e^{-\tau t}dt\\ =\frac{I_{mag}}{C\left({\tau }^2+{\omega }^2\right)}\cdot e^{-\tau t}\cdot \left[-\tau \cdot \cos \left(\omega t+{\phi }_i\right)+\omega \cdot \sin \left(\omega t+{\phi }_i\right)\right]\\ u\left(t\right)=u_R\left(t\right)+u_{\mathrm{C}}\left(t\right)\end{array}\right.(3)$

The combined simplification is shown in Equations 4, 5.

$\left\{\begin{array}{l}{u}_C\left(t\right)=\frac{I_{mag}}{C\cdot \sqrt{{\tau }^2+{\omega }^2}}\cdot \cos \left(\omega t+{\phi }_i+{\theta }_C\right)\cdot e^{-\tau t}\\ u\left(t\right)=\frac{I_{mag}\cdot \sqrt{{\left[R\cdot C\cdot \left({\tau }^2+{\omega }^2\right)-\tau \right]}^2+{\omega }^2}}{C\cdot \left({\tau }^2+{\omega }^2\right)}\cdot \cos \left(\omega t+{\phi }_i+{\theta }^{\prime }\right)\cdot e^{-\tau t}\end{array}\right.(4)$

$\left\{\begin{array}{l}{\theta }_C={\tan }^{-1}\left(-\frac{\tau }{\omega }\right)-\frac{\pi }{2}\\ {\theta }^{\prime }={\tan }^{-1}\left(\frac{R\cdot C\cdot \left({\tau }^2+{\omega }^2\right)-\tau }{\omega }\right)-\frac{\pi }{2}\end{array}\right.(5)$

Therefore, further derivations of the circuit parameters $R$ and $C$ held deduce the relationship for the attenuation oscillation signal parameters as:

$\left\{\begin{array}{l}C=-\frac{\omega \cdot I_{mag}}{U_{mag}\cdot \sin \left({\phi }_u-{\phi }_i\right)\cdot \left({\tau }^2+{\omega }^2\right)}\\ R=\frac{\omega \cdot U_{mag}\cdot \cos \left({\phi }_u-{\phi }_i\right)-\tau \cdot U_{mag}\cdot \sin \left({\phi }_u-{\phi }_i\right)}{\omega \cdot I_{mag}}\end{array}\right.(6)$

Both the $R$ and $C$ parameter calculations are affected by the signal amplitude and attenuation coefficient. When the attenuation coefficient is $\tau =0$, Equation 6 degenerates to the calculation of the circuit parameters under a steady-state sinusoidal signal.

3.2 Algorithm for quantitative transient signal extraction

The transient signal characteristics generated manifest primarily as attenuation and high-frequency attenuation signals when the capacitive element breaks down. The industrial frequency steady-state and noise signals are shown in Equation 7 (Bollen et al., 2005). The $A_i$, $f_i$, ${\delta }_i$, and ${\phi }_i$ are the amplitude, frequency, attenuation coefficient, and initial phase of the $i$ th frequency component, respectively, and $\xi \left(t\right)$ is Gaussian noise. It is sufficient to make $t=s\Delta t$ to represent the discrete sampled signal. An effective signal analysis tool is required to separate the fault transient characteristic parameters from the mixed signals and compute them to meet the computational needs of the fault diagnosis and analysis.

$y\left(t\right)={\displaystyle \sum _{i=1}^p}{A}_i\cdot e^{-{\delta }_{i}t}\cos \left(2\pi f_{i}t+{\phi }_i\right)+\xi \left(t\right)(7)$

Existing common methods for power signal feature extraction include the fast Fourier transform (FFT), wavelet analysis, singular value decomposition (SVD), TLS-ESPRIT algorithm,and Prony algorithm. The FFT is a frequency-domain analysis of the signal that calculates the amplitude and phase of the signal components at different frequencies. However, it cannot estimate the attenuation coefficient of the signal. The results of the wavelet analysis are easily affected by matches between the basis function and the analyzed signal. The SVD reconstructs the characteristic signal and noise separation. However, the separate SVD calculations cannot provide the specific value of the signal characteristic quantity. The TLS-ESPRIT algorithm is applied primarily to frequency estimation. The Prony algorithm can effectively estimate the frequency, decay coefficients, and phase information of signals, demonstrating strong adaptability in analyzing signals containing multiple frequency components and decay. In scenarios with significant noise interference, the Prony algorithm performs well in signal reconstruction and noise suppression, effectively extracting signal characteristics. Relative to some other complex signal processing algorithms, the Prony algorithm holds an advantage in computational efficiency, swiftly and accurately obtaining the signal’s characteristic parameters.

Taking all the above factors into consideration, utilizing the Prony algorithm for calculating transient signal characteristic parameters is reasonable, as it can accurately extract signal frequency, decay coefficients, and other parameters, while possessing high computational efficiency and applicability (Hauer et al., 1990). The principle of this method is briefly described below.

Prony’s algorithm uses a combination of $P$ exponential terms to achieve an approximate fit to the original data. This approach fits equally spaced sampled data with a linear combination of exponential terms. From this, information such as the amplitude, phase, damping factor, and signal frequency can be analyzed. As early as 1795, Prony proposed a linear combination of complex exponential functions to describe the mathematical model of equally spaced sampling data, often referred to as the Prony model, which gives an approximate solution for linearization. The method quantitatively writes the transient signal of the capacitor casting or breakdown in mathematical expressions. The capacitance estimation can be realized by extracting the transient perturbation signal based on Prony’s approach. The steps are as follows:

The original signal of Equation 7 is sampled at equal intervals. The Prony mathematical model is described as:

$\widehat{y}\left(n\right)={\displaystyle \sum _{i=1}^p}{b}_i{z}_i^n,n=0,1,...,L-1(8)$

where $p$ is the model order, $L$ is the number of sampling points, $L\ge 2n$, and $b_i$ and ${\mathrm{z}}_i$ are complex numbers of:

$\left\{\begin{array}{l}{b}_i=A_i{e}^{\mathrm{j}{\phi }_i}\\ z_i=e^{\left({\delta }_i+\mathrm{j}2\pi f_i\right)\Delta t}\end{array}\right.(9)$

The fitted values $b_i$ and ${\mathrm{z}}_i$ in Equation 9 contain the fault information consisting of the amplitude, phase, frequency, and attenuation coefficient of the original signal. The error $\epsilon \left(n\right)$ is the difference between the original signal and the fitted signal as:

$\epsilon \left(n\right)=y\left(n\right)-\widehat{y}\left(n\right)(10)$

The key to computing the signal parameters for the Prony model is to find the chi-solution of the linear constant coefficient difference equation corresponding to Equation 8 when ${\displaystyle \sum _{n=0}^{N-1}}{\left[\epsilon \left(n\right)\right]}^2$ takes a minimum value. Considering $b_i$ as the coefficient vector of the equation and ${\mathrm{z}}_i$ as the solution, the characteristic polynomial of ${\mathrm{z}}_i$ is:

$G\left(z\right)={\displaystyle \prod _{k=1}^p}\left(z-z_k\right)={\delta }_0{z}^p+a_1{z}^{p-1}+\cdots +{\delta }_{p-1}z+{\delta }_p(11)$

The recursive difference equation of Equation 8 can be constructed as:

$\widehat{y}\left(n\right)+{\displaystyle \sum _{i=1}^p}{\delta }_i\widehat{y}\left(n-i\right)=0,p\le n\le N-1(12)$

The equation for $y\left(n\right)$ is obtained by relating the difference expression of Equation 12 to the error expression in Equation 10, as shown in Equation 13.

$y\left(n\right)+{\displaystyle \sum _{i=1}^p}{\delta }_{i}y\left(n-i\right)-{\displaystyle \sum _{i=1}^p}{\delta }_i\epsilon \left(n-i\right)=0(13)$

The minimum value of ${\displaystyle \sum _{n=0}^{N-1}}{\left[\epsilon \left(n\right)\right]}^2$ can be found using the method of least squares, and the parameter ${\delta }_i$ at $\frac{\partial {\epsilon }_p}{\partial {\delta }_i}=0$ is required. The obtained solution set ${\left({\delta }_1,{\delta }_2,\cdots ,{\delta }_p\right)}^{\mathrm{T}}$ is substituted into the characteristic Equation 11 to obtain the characteristic root $z_k\left(k=1,2,...,p\right)$. The characteristic root is then substituted into Equation 8 to obtain the linear equation about $b_i$ and its solution vector, as shown in Equation 14.

$\mathit{Z}\mathit{b}=\widehat{\mathit{y}}\Rightarrow \mathit{b}={\left({\mathit{Z}}^{\mathrm{T}}\mathit{Z}\right)}^{-1}{\mathit{Z}}^{\mathrm{T}}\widehat{\mathit{y}}(14)$

where $\mathit{Z}=\left[\begin{array}{cccc}1& 1& 1& 1\\ z_1& z_2& \cdots & z_p\\ ⋮& ⋮& \ddots & ⋮\\ z_1^{L-1}& z_2^{L-1}& \cdots & z_p^{L-1}\end{array}\right]$ and $\mathit{b}={\left[b_1,b_2,\cdots ,b_p\right]}^{\mathrm{T}}$. The vector $\mathit{b}$ is then substituted back into the polynomial $G\left(z_k\right)=0$, from which the characteristic parameters of each frequency component of the signal can be calculated as shown in Equation 15.

$\left\{\begin{array}{l}{A}_i=\left|b_i\right|\\ f_i=\frac{\text{angle}\left(z_i\right)}{2\pi \Delta t}\\ {\delta }_i=\frac{\ln \left|z_i\right|}{\Delta t}\\ {\phi }_i=\text{angle}\left(b_i\right)\end{array}\right.(15)$

The model order $p$ and noise level in practical applications impact the calculation results of the Prony algorithm. A larger $p$ and lower noise level give more accurate calculation results. However, a greater $p$ will increase the algorithm’s computational requirements and redundancy terms. The component thermal breakdown fault perturbation signal contains an intermediate frequency steady-state component and a high-frequency attenuation component. Therefore, the electrical breakdown fault signal contains a steady-state component at power frequency and two high-frequency attenuation components. Therein, the value $p=3$ is taken theoretically. In practice, this value needs to be increased appropriately to improve the calculation accuracy.

4 Simulation verification

4.1 Numerical simulation verification

The attenuated oscillating signal flowing under the R-C circuit is generated by direct simulations based on MATLAB to verify the correctness of the algorithm. The circuit parameters are $R=10\mathrm{\Omega }$ and $C=300\mu F$ with a signal sampling frequency of 10 kHz. The signal $S$ consists of 2 components: an industrial frequency component and a high-frequency component at several hundred Hz.

$\begin{array}{l}S=S_1+S_2\\ =A_1\cos \left(2\pi f_{1}t+{\phi }_1\right)+A_2{e}^{-\tau t}\cos \left(2\pi f_{2}t+{\phi }_2\right)\end{array}(16)$

where $S_1$ represents the steady-state industrial frequency, $S_2$ represents the high-frequency attenuation component, $A_1$, $A_2$, $f_1$ , $f_2$, ${\phi }_1$, and ${\phi }_2$ are the amplitudes, frequencies, and phases of the two signals, respectively, and $\tau$ is the attenuation coefficient of the high-frequency transient signals. The $A_1$ and $A_2$ are in units of A, $f_1$ and $f_2$ are in units of Hz, and ${\phi }_1$ and ${\phi }_2$ are in units of degrees.

According to experience, the current parameter is set as:

$\left\{\begin{array}{l}{S}_1:A_1=996,f_1=50,{\phi }_1=30\\ S_2:A_2=149,{\tau }_2=55,f_2=945,{\phi }_2=153\end{array}\right.(17)$

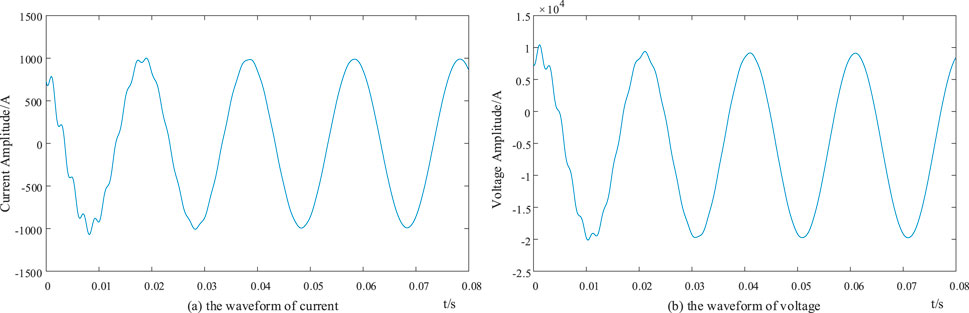
The corresponding voltage and current waveforms are deduced based on the differential equation of the R-C circuit, as shown in Figure 6.

Figure 6

Figure 6. Current (A) and voltage (B) waveforms of the R-C circuit based on numerical simulations.

The capacitance and resistance parameters are calculated using the traditional FFT and based on the proposed electric power perturbation feature. The electric power perturbation feature approach utilizes the Prony algorithm to extract characteristic parameters from the attenuated oscillating signal. Some values of the parameters in Equation 17 are modified appropriately, and the effects of the signal length, noise signal, signal attenuation coefficient, and signal oscillation frequency on the two calculation methods are considered. The error is calculated as:

$error\left(\%\right)=\left|\frac{\text{calculated}\text{value}-\text{accuracy}\text{value}}{\text{accuracy}\text{value}}\right|\times 100\%(18)$

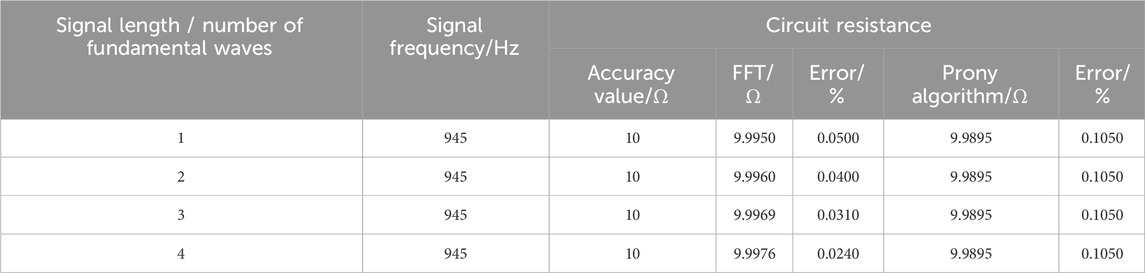
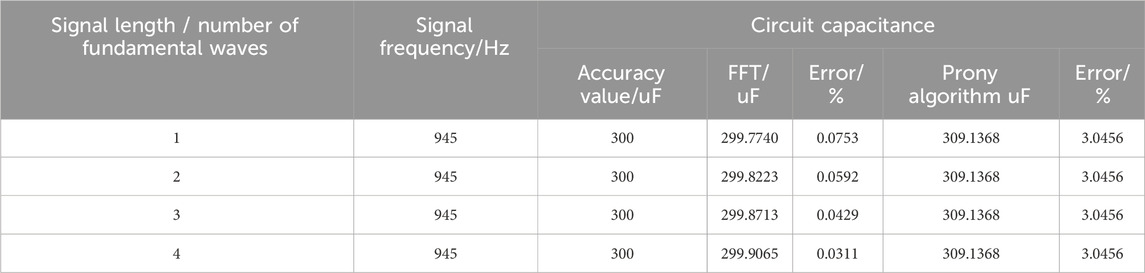
4.1.1 Impact of signal length on circuit parameter calculations

The circuit parameters are calculated using the attenuated oscillating signal $S_2$ in the mixed signal from Equation 16. The effects of different signal lengths on the calculation results are considered. The circuit resistance and capacitance calculation results are shown in Tables 1, 2, respectively. The calculation errors for the resistance and capacitance based on the FFT are smaller, but these errors are influenced by the signal length. This is because the signal tends to be more sinusoidal in the steady state as the signal length increases. Therefore, the calculations based on the FFT are more accurate, but the Prony algorithm is less affected by changes in the signal length.

Table 1

Table 1. Effect of signal length on the resistance calculations.

Table 2

Table 2. Effect of signal length on capacitance calculations.

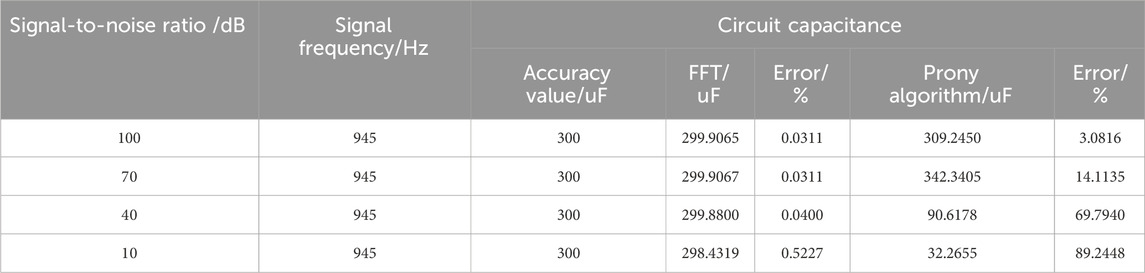
4.1.2 Effect of noise on the circuit parameter calculations

The same attenuation oscillatory signal $S_2$ is used to consider the impact of noise on the circuit parameter calculations. Tables 3, 4 show that the resistance and capacitance calculation errors based on the FFT transform are smaller and less affected by noise changes, while the Prony algorithm is significantly affected by noise, and its error increases for smaller signal-to-noise ratios. This is because the FFT transformation is relatively stable and produces smaller errors when calculating resistance and capacitance, with a relatively small impact from noise. In contrast, the Prony algorithm demands a higher level of signal accuracy, and once disturbed by noise, it significantly affects the extraction of signal frequency components, leading to increased calculation errors. Particularly, as the signal-to-noise ratio decreases, the influence of noise on the Prony algorithm becomes more pronounced, resulting in a significant increase in errors.

Table 3

Table 3. Effect of noise on the resistance calculations.

Table 4

Table 4. Effect of noise on the capacitance calculations.

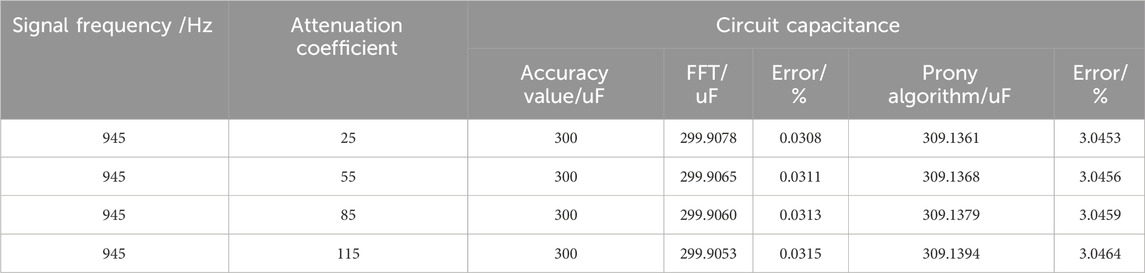
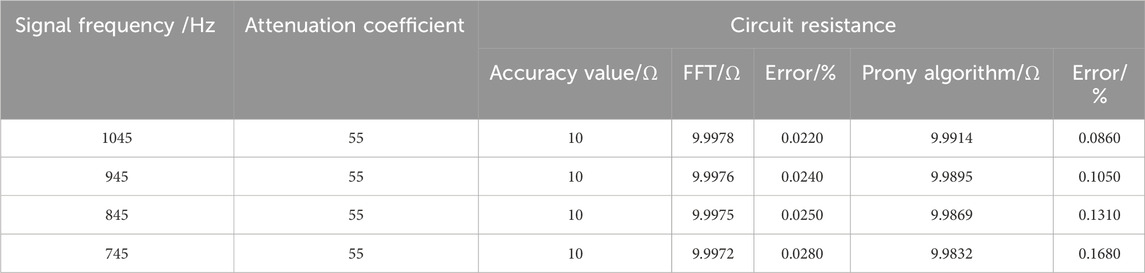
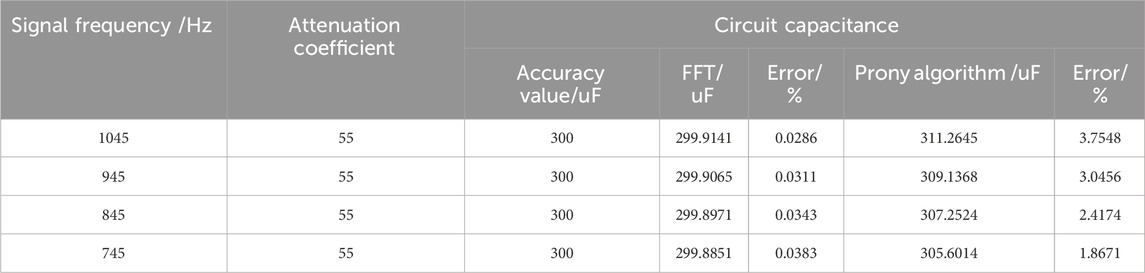
4.1.3 Signal attenuation coefficient effect on parameter calculations

The impacts of the attenuation coefficient on the circuit parameter calculations are shown in Tables 5, 6. The attenuation coefficient of the FFT-based resistance and capacitance calculations has a small impact. A smaller attenuation coefficient gives less computational error. When the signal attenuation coefficient is small, the signal tends to be a steady-state sinusoid; therefore, the FFT-based calculations are more accurate. The Prony algorithm is affected by the attenuation coefficient because large attenuations shorten the available signal duration and increase the errors.

Table 5

Table 5. Effect of attenuation coefficient on the resistance calculations.

Table 6

Table 6. Effect of attenuation coefficient on the capacitance calculations.

4.1.4 Effect of signal oscillation frequency on the parameter calculations

The impacts of the oscillation frequency on the circuit parameter calculations are shown in Tables 7, 8. The signal oscillation frequency does not significantly affect the FFT-based capacitance calculation but impacts the Prony algorithm-based capacitance calculations. This is because in the FFT algorithm, frequency components are averaged onto different frequency points, while the Prony algorithm can more accurately determine the frequency components of the signal. Therefore, in the case of complex or difficult-to-distinguish signal frequencies, the capacitance calculation using the Prony algorithm will be more significantly affected.

Table 7

Table 7. Effect of oscillation frequency on the resistance calculations.

Table 8

Table 8. Effect of oscillation frequency on the capacitance calculations.

A comprehensive analysis of the impact of the signal length, signal-to-noise ratio, attenuation coefficient, and oscillation frequency on the two calculation methods found the following. 1) The FFT-based loop resistance and capacitance calculations are affected by the signal length as longer signals gradually tend to be steady-state sinusoids. The noise greatly impacted the calculations, but the attenuation coefficient and oscillation frequency had no significant impact. 2) The Prony algorithm is significantly affected by noise, mainly in the parameter extraction algorithm. The impact of the attenuation coefficient and oscillation frequency are smaller, and the signal length has no impact.

4.2 PSCAD/EMTDC simulation verification

4.2.1 Introduction to the simulation and analysis model and parameters

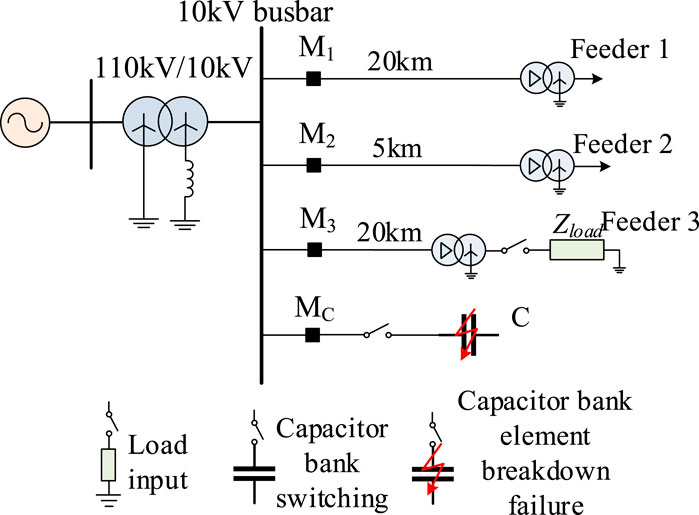
A PSCAD was built based on the actual 10 kV capacitor bank as a simulation analysis model to verify the correctness of the quantitative extraction based on transient signals, as shown in Figure 7. The total simulation time was 5 s, the capacitor element breakdown time was 3.93 s, and the fuse time was 3.931 s (because it is shorter, so the component breakdown of the short-circuit state is negligible). The arc-canceling coil grounds the center point of the system. The capacitor bank is a single-star connection with an internal fuse structure and neutral point ungrounded operational mode.

Figure 7

Figure 7. Simulation model for the 10 kV capacitor breakdown.

The capacitor bank parameters are set as shown in Table 9. The $C_{\text{be}}$ is the rated capacitance of the single-phase capacitor bank, $C_{\text{ue}}$ is the rated capacitance of the capacitor unit, $M$ and $N$ are the number of parallel and series segments of the capacitor bank unit, and $m$ and $n$ are the number of parallel and series components inside the capacitor unit.

Table 9

Table 9. Simulation parameters for the single star shunt capacitor bank.

4.2.2 Impact of the four influencing factors on the two calculation methods

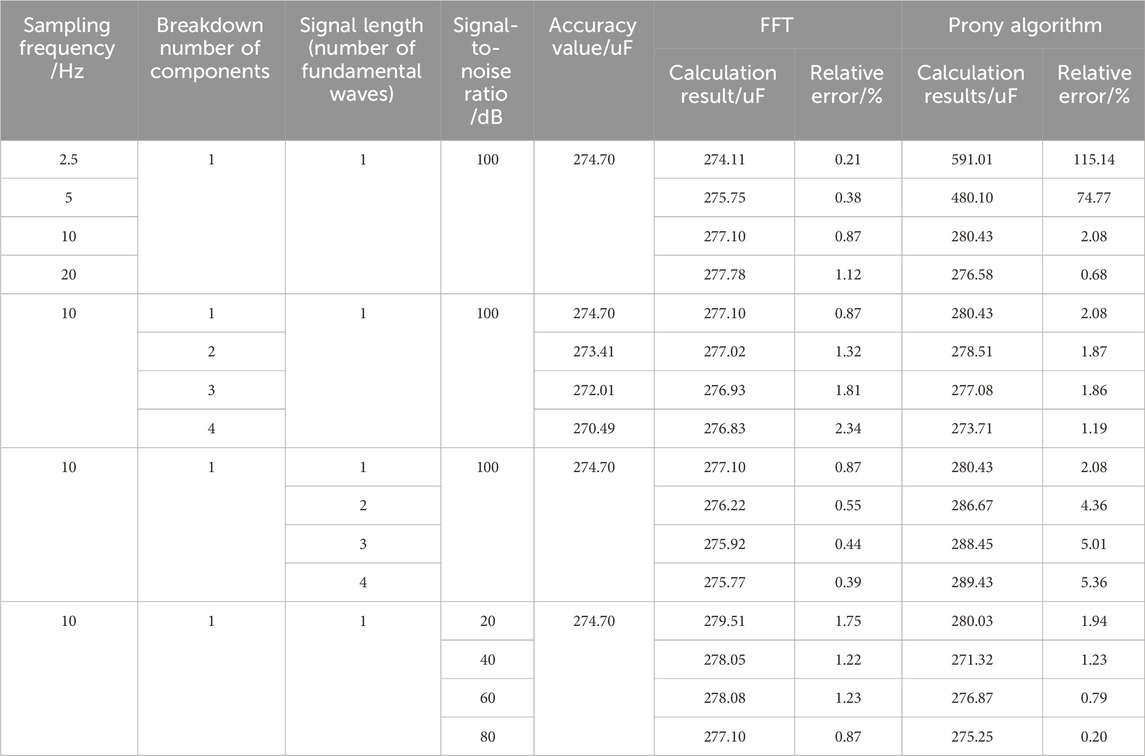
The capacitance parameters are calculated using the traditional FFT and the proposed electric power perturbation feature method. The proposed method utilizes the Prony algorithm to extract the characteristic parameters of the attenuated oscillating signal. Some of the parameter values from Figure 5 are modified appropriately, and the effects of the sampling frequency, number of breakdown elements, signal length, and signal-to-noise ratio on the two calculation methods are considered. The error calculations are shown in Equation 18.

The following conclusions are made from Table 10. 1) The sampling frequency and signal length significantly affect the FFT-based capacitance calculations. As the sampling frequency decreases or the signal length increases, the signal gradually tends toward a steady-state sinusoid. The noise has a noticeable impact on the calculation results. 2) The Prony algorithm is also significantly affected by the sampling frequency and signal length, but the results are opposite to the traditional FFT. As the sampling frequency increases or the signal length decreases, the power disturbance characteristics are more obvious, and the noise has greater effects on the signal feature parameter extraction.

Table 10

Table 10. Comparison of the two signal analysis methods under various fault situations.

In addition, with an increased number of component breakdowns, the results of both algorithms change, which can be quantitatively analyzed to determine the specific number of component breakdowns.

5 Conclusion

This study focuses on the diagnosis of faults in parallel capacitor banks, using the Prony algorithm for quantitative feature extraction of transient disturbance signals, and based on the quantitative relationship between transient signals and capacitance to achieve the judgment of capacitor abnormalities. Experimental results show that high-frequency transient disturbance signals generated during capacitor switching or breakdown contain critical information about the capacitor’s condition, manifested as decay oscillations ranging from hundreds of Hz to kHz. Through multiple sets of numerical simulations and validation using PSCAD electromagnetic transient simulations, the accuracy and effectiveness of the method have been proven, providing new analytical tools and theoretical basis for the condition monitoring and health management of parallel capacitor banks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LZ: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. MM: Conceptualization, Formal Analysis, Validation, Visualization, Writing–original draft, Writing–review and editing. WX: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Software, Validation, Writing–original draft, Writing–review and editing. YZ: Formal Analysis, Visualization, Writing–original draft, Writing–review and editing. BH: Investigation, Writing–original draft, Writing–review and editing. WwZ: Data curation, Investigation, Writing–original draft, Writing–review and editing. WhZ: Data curation, Investigation, Resources, Software, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We thank the College of Electrical Engineering, Sichuan University for providing access and support to the computer resources required to carry on this work. We thank the Guilin Power Capacitor Co., Ltd. for providing us with the testing platform.

Conflict of interest

Authors LZ, YZ, BH, and WZ were employed by Heyuan Power Supply Bureau of Guangdong Electric Power Grid Co., Ltd.

Author MM was employed by Electric Power Research Institute of Guangdong Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

This research was supported by China Southern Power Grid Company Technology Project Limited (Project Number: 031600KK52220003). The funder was involved in the following aspects of the study: study design, data collection, and provision of technical resources.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beere, P. (1987). Internal fuses – a superior method for protecting high-voltage power capacitors. Vector Electr Eng. 6, 8–9.

Google Scholar

Bollen, M. H. J., Styvaktakis, E., and Gu, I. Y. H. (2005). Categorization and analysis of power system transients. IEEE Trans. Power Deliv. 20, 2298–2306. doi:10.1109/TPWRD.2004.843386

CrossRef Full Text | Google Scholar

Goodarzi, A., and Allahbakhshi, M. (2022). Online condition monitoring algorithm for element failure detection and fault location in double wye shunt capacitor banks. Int. J. Electr. Power Energy Syst. 137, 107864. doi:10.1016/j.ijepes.2021.107864

CrossRef Full Text | Google Scholar

Hauer, J. F., Demeure, C. J., and Scharf, L. L. (1990). Initial results in Prony analysis of power system response signals. IEEE Trans. Power Syst. 5, 80–89. doi:10.1109/59.49090

CrossRef Full Text | Google Scholar

Institute of Electrical and Electronics Engineers. Std 1036-2010 (2010). IEEE guide for the application of shunt power capacitors. IEEE Publications.

Google Scholar

Jiabi, L. (2021). Research on technologies of shunt capacitor operation condition monitoring based on disturbance data analysis. Shandong: Shandong University. [dissertation/master’s thesis].

Google Scholar

Jie, W., Zhengwei, C., Rongsen, L., and Shilong, L. (2022). “Fault detection approach for shunt capacitor banks based on unbalanced current,” in 6th IEEE conference on energy internet and energy system integration, EI2. doi:10.1109/EI256261.2022.10116168

CrossRef Full Text | Google Scholar

Jouybari-Moghaddam, H., Sidhu, T. S., Dadash Zadeh, M. R. D., and Parikh, P. P. (2017). Enhanced fault-location scheme for double wye shunt capacitor banks. IEEE Trans. Power Deliv. 32, 1872–1880. doi:10.1109/TPWRD.2016.2583381

CrossRef Full Text | Google Scholar

Li, S., and Li, J. (2017). Condition monitoring and diagnosis of power equipment: review and prospective. High. Volt. 2, 82–91. doi:10.1049/hve.2017.0026

CrossRef Full Text | Google Scholar

Moghaddam, H. J. (2017) Fault location in high voltage shunt capacitor banks, E82. Canada: University of Western Ontario.

Google Scholar

Pavan, P. S., and Das, S. (2020). Novel method for location of internal faults in ungrounded double wye shunt capacitor banks. IEEE Trans. Power Deliv. 36, 899–908. doi:10.1109/TPWRD.2020.2996268

CrossRef Full Text | Google Scholar

Santoso, S. (2007). On determining the relative location of switched capacitor banks. IEEE Trans. Power Deliv. 22, 1108–1116. doi:10.1109/TPWRD.2007.893195

CrossRef Full Text | Google Scholar

Shilong, L., Yufei, T., Mingzhong, L., Jie, W., and Xiangxi, D. (2020). A novel online monitoring method for double-y type shunt capacitor bank. New York: Institute of Electrical and Electronics Engineers Inc., 296–300. doi:10.1109/AEEES48850.2020.9121385

CrossRef Full Text | Google Scholar

Silverstein, A., and Follum, J. (2020). High-resolution, time-synchronized grid monitoring devices. PNNL-29770. North American: synchrophasor initiative technical report.

Google Scholar

Technical committee for standardization of power capacitors in the power industry parallel capacitor device technology and application (2011). Beijing: China Electric Power Press.

Wen-hai, Z., Xian-Yong, X., Jing-Gang, Y., Yong, L., Ming-You, Y., and Qian, X. (2014). Circuit parameter calculation based on characteristic parameters and pseudo-impedance of damped oscillation signal. Acta Phys. Sin., 63. doi:10.7498/aps.63.098403

CrossRef Full Text | Google Scholar

Wischkaemper, J. A., Benner, C. L., Russell, B. D., and Manivannan, K. (2016). Application of waveform analytics for improved situational awareness of electric distribution feeders. IEEE Trans. Smart Grid 6 (6), 2041–2049. doi:10.1109/TSG.2015.2406757

CrossRef Full Text | Google Scholar

Xiaoyu, C., Jianyong, Z., and Jun, M. E. I. (2015). Power capacitor banks failure warning method based online intelligence LC oscillation frequency variation and its implementation. Power Syst. Prot. Control. 1674-3415(2015)05-0144-06.

Google Scholar

Xu, W., Huang, Z., Xie, X., and Li, C. (2022). Synchronized waveforms – a frontier of data-based power system and apparatus monitoring, protection, and control. IEEE Trans. Power Deliv. 37, 3–17. doi:10.1109/TPWRD.2021.3072889

CrossRef Full Text | Google Scholar

Yan, F., He, H., Wang, Z., Yin, T., and Cheng, Z. (2016). Internal fuse performance of high voltage capacitor unit. Gaodianya Jishu High. Volt. Eng. 42, 1790–1796.

Google Scholar