Analyzing grid connected shaded photovoltaic systems with steady state stability and crow search MPPT control

The field of research in maximum power point tracking (MPPT) methods is making significant progress with a wide range of techniques, from simple yet inefficient approaches to more complex but effective ones. Therefore, it is important to suggest a simple and effective strategy to control the global maximum power point (GMPP) of a photovoltaic (PV) system especially under partial shading conditions (PSC). This paper proposes a novel metaheuristic MPPT called the Crow Search Algorithm (CSA) to ameliorate the tracking performance of a grid connected shaded PV system. The CSA is a nature inspired method based on the intelligent behaviors of crows in its search process for hidden food sources. This novel method succeeds to mitigate the adverse impacts of partial shading on the performance of PV systems by accurately tracking the GMPP. Based on the small-signal dynamic model, the stability of the proposed system is analyzed. Simulation results for three different levels of partial shading, including zero, weak, and severe shading, demonstrate the better performance of the suggested CSA compared to fuzzy logic controller (FLC) and Inc-Cond techniques. In fact, the comparison is carried out in terms of simplicity of implementation, high efficiency, and low power loss, decreasing considerably the convergence time.

1 Introduction

Renewable energy sources have a vital importance in electric power generation due to shortage and environmental impacts of conventional fuels. Several studies expect that more than 45% of the global energy supply will be generated by solar energy. However, the performance of photovoltaic (PV) system is strongly dependent on weather and climate change. Besides, a major interest has been given to the study of possible optimal autonomous exploitation of the PV source regardless the climatic conditions. In this framework, optimization algorithms are an appropriate tool for solving complex problems in the field of renewable energy systems. But the developed Maximum Power Point Tracking (MPPT) algorithms are frequently very reliant on the accuracy of the mathematical model in relation to the generator and on the weather, particularly if partial shading occurs. Partial shading results in power inefficiency and keeps a photovoltaic system from performing at its best. Authors in (Eltamaly et al., 2018) have classified MPPT methods into conventional, soft computing, and hybrid methods.

Conventional techniques like Incremental Conductance (IC), Extremum Seeking Control (ESC), Hill Climbing (HC), perturb and Observe (P&O), Fractional Short Circuit (FSC), Fractional Open Circuit (FOC) and others are effective when used in consistent temperature and irradiation conditions (Ahmed and Salam, 2015).

However, they fail to track the Maximum Power Point (MPP) under Partial Shading Conditions (PSC) caused by the non-uniform irradiation of the PV arrays. The problem becomes complex in shaded conditions since the PV array exhibits several local maxima (LMs) (Maki and Valkealahti, 2012). The current MPPT efficiency is reduced when there are multiple peaks because they can’t distinguish the global maximum (GM) between the LMs.

In order to overcome the limitations of conventional techniques, soft computing techniques have been developed in literature. These methods comprise the metaheuristic and the artificial intelligence techniques. The application of intelligent algorithms is prevalent whether for system modeling, identification, or control. They may be considered as alternative solutions due to their flexibility to changes in system conditions, and their resilience to disturbances and modeling errors.

Authors in (Kermadi et al., 2020a) have developed a detailed review of shaded PV system MPPT algorithms. Concerning Artificial Intelligence (AI) based MPPT, an enhanced MPPT technique was proposed by Yilmaz et al. in (Yilmaz et al., 2019) to improve accuracy in PV systems under fluctuating atmospheric conditions. while Salah and Ouali (Salah and Ouali, 2011) compared a FLC and an artificial neural network (ANN) based techniques in maximum power point tracker for PV systems and confirmed through simulations result the superior performance and efficiency of FLC over ANN in tracking capabilities. Compared with conventional techniques these AI methods offer better performances and boost the PV energy production’s efficiency as presented in (BOUNECHBA et al., 2014).

In spite of their advantages, these methods heavily rely on the specific attributes of the photovoltaic (PV) system and necessitate prior knowledge of the model specifications. According to Karatepe and Hiyama (Karatepe and Hiyama, 2009), both FLC and ANN exhibit limitations in effectively tracing the Global Maximum Power Point (GMPP) under PSCs.

Within this framework, numerous researchers have delved into the challenge of MPPT challenge using metaheuristic optimization techniques. High efficiency and a fair computational cost are guaranteed by these "smart” procedures during the resolution process (Wang et al., 2020). Kermadi et al. proposed several of the most effective metaheuristic optimization techniques in the literature in (Kermadi et al., 2020a) as: Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Artifcial Bee Colony (ABC), Bat Algorithm (BA), Grey Wolf Optimization, Cuckoo Search (CS), (GWO), Firefly Algorithm (FA), Flower Pollination Algorithm (FPA), and Dragonfy Optimization Algorithm (DFO), Firefly Algorithm (FA) and Whale Optimization Algorithm (WOA). These methods are able to decrease the deficiencies of AI-based and traditional MPPT techniques.

Shaiek et al. in (Miyatake et al., 2011) suggested A GA based MPPT technique for shaded PV systems and simulation results proved that the suggested method outperforms conventional methods in following the GMPP under PSCs. Miyatake et al. (Ishaque and Salam, 2012) introduced PSO for experimental MPPT studies, and many researchers suggested improvements in standard PSO technique including Deterministic PSO (DPSO) in (Chowdhury and Saha, 2010), Adaptive Perceptive PSO (APPSO) in (Ram and Rajasekar, 2017) and Leader PSO (LPSO) in (Ahmed and Salam, 2014). These modified PSO methods offer better performances, but they are extremely sophisticated including an important number of variables.

Combining simulation and experimental data, authors (Sundareswaran et al., 2014) verified the Cuckoo Search algorithm’s (CS) ability to track GMPP under rapid changes of irradiance and temperature. In (Mohanty et al., 2015) an evolutionary ABC technique has been developed for a Photovoltaic Generator (PVG) under PSC while Mohanty et al. (Kaced et al., 2017) confirmed experimentally the efficacious application of GWO method for resistive and inductive loads under shade conditions.

Authors in (Wu and Yu, 2018) employed the BA method to address shading issues. Their work highlighted the performance of this technique to attain the GMPP as confirmed with validation in experiments as well as simulation. Authors in (Mirza et al., 2019), on the other hand, introduced an enhanced version of the Bat Algorithm (IBAT) for MPPT. This improvement involved the incorporation of an adaptive weight parameter, thereby enhancing the algorithm’s capacity for global search. The modified algorithm ensured rapid and accurate GMPP tracking surpasses numerous other MPPT techniques. In (Balaji and Fathima, 2022), It has been observed by Mirza et al. that the majority of soft computing techniques in literature only address the basic Partial Shading (PS) problem, with little attention paid to the Dynamic partial Shading (DPS) problem. In order to address the PS and DPS concerns, they therefore proposed solutions for these bio-inspired soft computing-based methodologies by proposing ACOA, DFO, and GRNNFFOA MPPT techniques.

Despite the impressive advantages of the aforementioned meta-heuristic methods, the majority of them have limitations such as software complexity and numerous tuning variables. To address these problems, researchers proposed combining two approaches into a hybrid method that retains the merits of each (Lian et al., 2014). In (Sundareswaran et al., 2015) Lian et al. combined both P§O and PSO algorithms in order to reduce the convergence time of the particles search space.

In the same vein, authors in (Mohamed et al., 2019), based on the advantages of P&O, ameliorated the GA response and proposed a hybrid GA-P&O technique under PSC. Mohamed et al. (Askarzadeh, 2016a) implemented PSO-GSA technique for tracking the GMPP and compared it to GWO, Moth-Flame Optimization (MFO) and Salp Swarm Algorithm (SSA) methods. Simulation results demonstrated the stability, success rate, and tracking efficiency of the suggested hybrid technique. Moreover, despite their excellent performances, the modified and the hybrid methods are more complex and increase the complexity of the system.

Among the methods mentioned earlier, a new population based metaheuristic algorithm called Crow Search Algorithm (CSA) has been developed by Askarzadeh (Hinojosa et al., 2018) to solve global optimization problem. This technique is derived from the food stealing behavior of crows (Houam et al., 2021).

Its promising results in global optimization issues have encouraged its application in solving real-nonlinear and multimodal optimization problems in various engineering fields.

Moreover, Moghaddam et al. has suggested CSA in (Moghaddam et al., 2019) for designing a stand-alone hybrid PV/wind/battery system. Houam et al. [29] have developed an efficient metaheuristic technique to control MPP of a partially shaded standalone PV systems using CSA and they exclusively analyze the stability of the PV generator. Motivated by the aforementioned limitations, the present paper proposes the development and the stability analysis of a two-stage grid connected shaded PV system. Tracking the GMPP of a shaded PV generator is optimized by an intelligent approach based on CSA and compared with both a conventional and an AI method.

The paper is structured as follows: section 2 presents the detailed mathematical model of the studied structure. Considering the dynamics of the PV generation, a small-signal model of a two-stage grid connected PV system was built in section 3. The small-signal stability analysis method was used to analyze the influence of the PV generation. The effect of partial shading on PV characteristics and the theories of the Inc-Cond, the FLC and the suggested CSA based MPPT algorithms are introduced in Section 4 and 5, respectively. The simulation studies are performed and discussed in Sections 6. Final conclusions are presented in Section 7.

2 System modeling

In this study, a two stage connected converter system, as shown in Figure 1, is used. As the front stage to shift the PV output voltage to a high level for the grid-connected inverter. The power system consists of a shaded PV generator, a boost converter and a three-phase inverter.

FIGURE 1

FIGURE 1. System configuration of a two-stage grid connected PV.

2.1 PV generator

The photovoltaic system under study consists of two PV arrays connected in series, with one of them being shaded. When subjected to uniform climatic conditions, the entire system generates a power output of 2000W. Figure 2 provides the P-V (power-voltage) and I-V (current-voltage) characteristics of the system and the used parameters of the studied PV system are shown in Table 1.

FIGURE 2

FIGURE 2. I-V and P-V characteristics of the PV system under nominal conditions.

TABLE 1

TABLE 1. Parameters of the solar module.

The accurate model of a PV cell is very complicated, and some parameters are difficult to measure directly. Thus, it is not convenient for research and application. By simplifying calculation equations, a practical engineering model was used in this paper.

The current cell is described by:

$\mathrm{I}={\mathrm{I}}_{\text{sc}}\left[1-{\mathrm{C}}_1\left({\mathrm{e}}^{\frac{\mathrm{U}}{{\mathrm{C}}_2{\mathrm{U}}_{\text{oc}}}}-1\right)\right](1)$

The expressions of C1 and C2are given by:

${\mathrm{C}}_1=\left(1-\frac{{\mathrm{I}}_{\mathrm{m}}}{{\mathrm{I}}_{\text{sc}}}\right){\exp }^{\frac{\mathrm{U}}{{\mathrm{C}}_2{\mathrm{U}}_{\text{oc}}}}(2)$

${\mathrm{C}}_2=\frac{\frac{{\mathrm{U}}_{\mathrm{m}}}{{\mathrm{U}}_{\text{oc}}}}{\mathrm{Ln}\left(1-\frac{{\mathrm{I}}_{\mathrm{m}}}{{\mathrm{I}}_{\text{sc}}}\right)}(3)$

Where Isc is the short-circuit current, Uoc is the open-circuit voltage, Im and Um are the current and the voltage at the maximum power, respectively.

The voltage and the current of PV array are written as:

$\left\{\begin{array}{l}{\mathrm{U}}_{\text{pv}}={\mathrm{N}}_{\mathrm{s}}\mathrm{U}\\ {\mathrm{I}}_{\text{pv}}={\mathrm{N}}_{\mathrm{p}}\mathrm{I}\end{array}\right.(4)$

Then the PV current is deduced as:

${\mathrm{I}}_{\text{pv}}={\mathrm{N}}_{\mathrm{p}}{\mathrm{I}}_{\text{sc}}\left[1-{\mathrm{C}}_1\left({\mathrm{e}}^{\frac{\mathrm{U}}{{\mathrm{N}}_{\mathrm{s}}{\mathrm{C}}_2{\mathrm{U}}_{\text{oc}}}}-1\right)\right](5)$

2.2 DC/DC converter

A boost converter controlled by a MPPT control system ensures the connection between the GPV and the DC bus. Its configuration is given in Figure 3.

FIGURE 3

FIGURE 3. Boost configuration.

The output voltages and current of the boost converter during steady state are expressed as follows:

$\left\{\begin{array}{l}{\mathrm{U}}_{\text{dc}}=\frac{{\mathrm{U}}_{\text{pv}}}{1-\mathrm{D}}\\ {\mathrm{I}}_{\text{dc}}=\left(1-\mathrm{D}\right).{\mathrm{I}}_{\text{pv}}\end{array}\right.(6)$

The DC Bus capacitor voltage is given by:

${\mathrm{C}}_{\text{dc}}\frac{\mathrm{d}{\mathrm{U}}_{\text{dc}}}{\text{dt}}={\mathrm{I}}_{\mathrm{c}}(7)$

where Ic is the capacitor current.

2.3 Gride side modeling

Assuming that the loss of both the boost converter and the inverter can be ignored. Then, the output power of a PV array is equal to the sum of the power of a DC capacitor and the output power of an inverter and in order to mitigate the harmonics injected into the grid, a filter comprising an inductance Lf is employed. The dynamic model of the grid is then given by:

$\left\{\begin{array}{l}{\mathrm{V}}_{{\mathrm{g}}_{\mathrm{d}}}={\mathrm{V}}_{{\mathrm{i}}_{\mathrm{d}}}+{\mathrm{L}}_{\mathrm{f}}\frac{\mathrm{d}{\mathrm{i}}_{{\mathrm{g}}_{\mathrm{d}}}}{\text{dt}}+\mathrm{\omega }{\mathrm{L}}_{\mathrm{f}}{\mathrm{i}}_{{\mathrm{g}}_{\mathrm{q}}}\\ {\mathrm{V}}_{{\mathrm{g}}_{\mathrm{q}}}={\mathrm{V}}_{{\mathrm{i}}_{\mathrm{q}}}+{\mathrm{L}}_{\mathrm{f}}\frac{\mathrm{d}{\mathrm{i}}_{{\mathrm{g}}_{\mathrm{q}}}}{\text{dt}}-\mathrm{\omega }{\mathrm{L}}_{\mathrm{f}}{\mathrm{i}}_{{\mathrm{g}}_{\mathrm{d}}}\\ {\mathrm{U}}_{\text{dc}}.\mathrm{C}\frac{\mathrm{d}{\mathrm{U}}_{\text{dc}}}{\text{dt}}={\mathrm{I}}_{\mathrm{C}}{\mathrm{U}}_{\text{dc}}+\frac{3}{2}{\mathrm{V}}_{{\mathrm{g}}_{\mathrm{d}}}{\mathrm{i}}_{{\mathrm{g}}_{\mathrm{d}}}\end{array}\right.(8)$

Where ${\mathrm{i}}_{\text{gd}}$ and ${\mathrm{i}}_{\text{gq}}$ represent the d-q grid current components and ${\mathrm{V}}_{\text{gd}}$ and ${\mathrm{V}}_{\text{gq}}$ are the d-q inverter voltage components.

The inverter’s main objective is to regulate the voltage of the DC bus and manage the power exchanges with the grid. Additionally, controlling this converter allows for the establishment of currents at the frequency of the grid. The value of igq was set to zero. The voltage and current control equations were provided as Eq. 9.

$\left\{\begin{array}{l}{{\mathrm{i}}_{\text{gd}}}^{*}={\mathrm{K}}_{\mathrm{p}1}\left({\mathrm{U}}_{\text{dc}}^{*}-{\mathrm{U}}_{\text{dc}}\right)+{\mathrm{K}}_{\mathrm{I}1}\int \left({\mathrm{U}}_{\text{dc}}^{*}-{\mathrm{U}}_{\text{dc}}\right)\text{dt}\\ {\mathrm{i}}_{\text{gq}}^{*}=0\\ {\mathrm{v}}_{\text{id}}^{*}={\mathrm{K}}_{\mathrm{p}2}\left({\mathrm{i}}_{\text{gd}}^{*}-{\mathrm{i}}_{\text{gd}}\right)+{\mathrm{K}}_{\mathrm{I}2}\int \left({\mathrm{i}}_{\text{gd}}^{*}-{\mathrm{i}}_{\text{gd}}\right)\text{dt}-\mathrm{\omega }{\mathrm{L}}_{\mathrm{f}}{\mathrm{i}}_{\text{gq}}+{\mathrm{v}}_{\text{gd}}\\ {\mathrm{v}}_{\text{iq}}^{*}={\mathrm{K}}_{\mathrm{p}2}\left({\mathrm{i}}_{\text{gq}}^{*}-{\mathrm{i}}_{\text{gq}}\right)+{\mathrm{K}}_{\mathrm{I}2}\int \left({\mathrm{i}}_{\text{gq}}^{*}-{\mathrm{i}}_{\text{gq}}\right)\text{dt}-\mathrm{\omega }{\mathrm{L}}_{\mathrm{f}}{\mathrm{i}}_{\text{gd}}+{\mathrm{v}}_{\text{gq}}\end{array}\right.(9)$

Figure 4 displays the configurations of voltage and current controllers.

FIGURE 4

FIGURE 4. Grid side controllers’ configuration.

3 Small signal stability analysis model of a two-stage PV grid-connected converter system

This part examines the stability of the PV power system under consideration. The entire small-signal model of the system is required for studying system stability. In fact, investigations of tiny signal stability are often based on a linearized system around an operational point. The dynamic system’s differential equations are linearized, and the system eigenvalues are calculated using the characteristic equation.

The state variables of the controllers are introduced R_dc, R_id and R_iq where:

$\left\{\begin{array}{l}\frac{\mathrm{d}{\mathrm{R}}_{\text{dc}}}{\text{dt}}={\mathrm{U}}_{\text{dc}}^{*}-{\mathrm{U}}_{\text{dc}}\\ \frac{\mathrm{d}{\mathrm{R}}_{\text{id}}}{\text{dt}}={\mathrm{i}}_{\text{gd}}^{*}-{\mathrm{i}}_{\text{gd}}\\ \frac{\mathrm{d}{\mathrm{R}}_{\text{iq}}}{\text{dt}}={\mathrm{i}}_{\text{gq}}^{*}-{\mathrm{i}}_{\text{gq}}\end{array}\right.(10)$

Linearizing (1)–(10) around steady-state values, the overall system’s differential equations are provided by:

$\frac{\mathrm{d}\Delta \mathrm{x}}{\text{dt}}=\mathrm{A}\Delta \mathrm{x}+\mathrm{B}\Delta \mathrm{u}(11)$

Where:

$\mathrm{X}={\left[{\mathrm{U}}_{\text{dc}}{\mathrm{R}}_{\mathrm{v}}{\mathrm{R}}_{\text{id}}{\mathrm{R}}_{\text{iq}}{\mathrm{i}}_{\text{gd}}{\mathrm{i}}_{\text{gq}}\right]}^{\mathrm{T}}(12)$

$\mathrm{U}=\left[{\mathrm{v}}_{\text{gd}}{\mathrm{v}}_{\text{gq}}\right](13)$

The eigenvalues of matrix A are defined as: .

${\mathrm{\delta }}_{\mathrm{i}}={\mathrm{\sigma }}_{\mathrm{i}}\pm \mathrm{i}{\mathrm{\omega }}_{\mathrm{i}}(14)$

The oscillation frequency, Hz, and the damping ratio are given by:

$\left\{\begin{array}{l}\mathrm{f}=\frac{{\mathrm{\omega }}_{\mathrm{i}}}{2\mathrm{\pi }}\\ \mathrm{\xi }=\frac{-{\mathrm{\sigma }}_{\mathrm{i}}}{\sqrt{{{\mathrm{\sigma }}_{\mathrm{i}}}^2+{{\mathrm{\omega }}_{\mathrm{i}}}^2}}\end{array}\right.(15)$

The derivation of the A and B matrices will be discussed in the following paragraph.

3.1 Derivation for A and B matrices

$\left\{\begin{array}{l}\frac{\text{dUdc}}{\text{dt}}=\frac{{\mathrm{N}}_{\mathrm{p}}{\mathrm{I}}_{\text{sc}}\left[1-{\mathrm{C}}_1\left({\mathrm{e}}^{\frac{\mathrm{U}}{{\mathrm{N}}_{\mathrm{s}}{\mathrm{C}}_2{\mathrm{U}}_{\text{oc}}}}-1\right)\right]}{{\mathrm{C}}_{\text{dc}}}-\frac{3{\mathrm{v}}_{\text{gd}}}{2{\mathrm{C}}_{\text{dc}}{\mathrm{U}}_{\text{dc}}}{\mathrm{i}}_{\text{gd}}\\ \frac{\mathrm{d}{\mathrm{R}}_{\mathrm{v}}}{\text{dt}}={\mathrm{K}}_{\mathrm{p}1}\left({\mathrm{U}}_{\text{dc}}^{*}-{\mathrm{U}}_{\text{dc}}\right)+{\mathrm{K}}_{\mathrm{i}1}{\mathrm{R}}_{\text{id}}-{\mathrm{i}}_{\text{gd}}\\ {\mathrm{L}}_{\mathrm{f}}\frac{\mathrm{d}{\mathrm{i}}_{\text{gd}}}{\text{dt}}={\mathrm{v}}_{\text{id}}+{\mathrm{k}}_{\mathrm{p}2}\left[{\mathrm{K}}_{\mathrm{p}1}\left({\mathrm{U}}_{\text{dc}}^{*}-{\mathrm{U}}_{\text{dc}}\right)+{\mathrm{K}}_{\mathrm{i}1}{\mathrm{R}}_{\text{dc}}-{\mathrm{i}}_{\text{gd}}\right]+{\mathrm{K}}_{\mathrm{i}2}{\mathrm{R}}_{\text{id}}-{\mathrm{v}}_{\text{id}}^{*}\\ {\mathrm{L}}_{\mathrm{f}}\frac{\mathrm{d}{\mathrm{i}}_{\text{gq}}}{\text{dt}}={\mathrm{v}}_{\text{iq}}+{\mathrm{K}}_{\mathrm{p}2}\left(0-{\mathrm{i}}_{\text{gq}}\right)+{\mathrm{K}}_{\mathrm{i}2}{\mathrm{R}}_{\text{iq}}-{\mathrm{v}}_{\text{iq}}^{*}\end{array}\right.(16)$

Linearizing (10) and (16) around steady-state values, (17) is given by:

$\left\{\begin{array}{l}\frac{\mathrm{d}\Delta {\mathrm{U}}_{\text{dc}}}{\text{dt}}=\frac{3{\mathrm{v}}_{\text{gd}}{\mathrm{i}}_{\text{gd}}}{2{\mathrm{C}}_{\text{dc}}{{\mathrm{U}}_{\text{dc}}}^2}\Delta \text{Udc}-\frac{{\mathrm{N}}_{\mathrm{p}}{\mathrm{I}}_{\text{sc}}\left[1-{\mathrm{C}}_1\left({\mathrm{e}}^{\frac{\mathrm{U}}{{\mathrm{N}}_{\mathrm{s}}{\mathrm{C}}_2{\mathrm{U}}_{\text{oc}}}}-1\right)\right]}{{\mathrm{C}}_{\text{dc}}{\mathrm{U}}_{\text{dc}}}\Delta \text{Udc}-\frac{3{\mathrm{v}}_{\text{gd}}}{2{\mathrm{C}}_{\text{dc}}{\mathrm{U}}_{\text{dc}}}\Delta {\mathrm{i}}_{\text{gd}}\\ \frac{\mathrm{d}\Delta {\mathrm{R}}_{\text{dc}}}{\text{dt}}=-\Delta {\mathrm{U}}_{\text{dc}}\\ \frac{\mathrm{d}\Delta {\mathrm{R}}_{\text{id}}}{\text{dt}}=-{\mathrm{K}}_{\mathrm{p}1}\Delta {\mathrm{U}}_{\text{dc}}+{\mathrm{K}}_{\mathrm{i}1}\Delta {\mathrm{R}}_{\text{dc}}-\Delta {\mathrm{i}}_{\text{gd}}\\ \frac{\mathrm{d}\Delta {\mathrm{R}}_{\text{iq}}}{\text{dt}}=-\Delta {\mathrm{i}}_{\text{gq}}\\ \frac{\mathrm{d}\Delta {\mathrm{i}}_{\text{gd}}}{\text{dt}}=-\frac{{\mathrm{K}}_{\mathrm{p}1}{\mathrm{K}}_{\mathrm{p}2}}{{\mathrm{L}}_{\mathrm{f}}}\Delta {\mathrm{U}}_{\text{dc}}+\frac{{\mathrm{K}}_{\mathrm{i}1}{\mathrm{K}}_{\mathrm{p}2}}{{\mathrm{L}}_{\mathrm{f}}}\Delta {\mathrm{R}}_{\text{dc}}-\frac{{\mathrm{K}}_{\mathrm{p}2}}{{\mathrm{L}}_{\mathrm{f}}}\Delta {\mathrm{i}}_{\text{gd}}+\frac{{\mathrm{K}}_{\mathrm{i}2}}{{\mathrm{L}}_{\mathrm{f}}}\Delta {\mathrm{R}}_{\text{id}}\\ \frac{\mathrm{d}\Delta {\mathrm{i}}_{\text{gq}}}{\text{dt}}=-\frac{{\mathrm{K}}_{\mathrm{p}2}}{{\mathrm{L}}_{\mathrm{f}}}\Delta {\mathrm{i}}_{\text{gq}}+\frac{{\mathrm{K}}_{\mathrm{i}2}}{{\mathrm{L}}_{\mathrm{f}}}\Delta {\mathrm{R}}_{\text{iq}}\end{array}\right.(17)$

Thus, the state matrix A and the output matrix B are as follows:

$A=\left[\begin{array}{cccccc}\frac{3{\mathrm{v}}_{\text{gd}}{\mathrm{i}}_{\text{gd}}}{2{\mathrm{C}}_{\text{dc}}{{\mathrm{U}}_{\text{dc}}}^2}-\frac{{\mathrm{N}}_{\mathrm{p}}{\mathrm{I}}_{\text{sc}}\left[1-{\mathrm{C}}_1\left({\mathrm{e}}^{\frac{\mathrm{U}}{{\mathrm{N}}_{\mathrm{s}}{\mathrm{C}}_2{\mathrm{U}}_{\text{oc}}}}-1\right)\right]}{{\mathrm{C}}_{\text{dc}}{\mathrm{U}}_{\text{dc}}}& 0& 0& 0& -\frac{3{\mathrm{v}}_{\text{gd}}}{2{\mathrm{C}}_{\text{dc}}{\mathrm{U}}_{\text{dc}}}& 0\\ -1& 0& 0& 0& 0& 0\\ -{\mathrm{K}}_{\mathrm{p}1}& {\mathrm{K}}_{\mathrm{i}1}& 0& 0& -1& 0\\ 0& 0& 0& 0& 0& -1\\ \frac{{\mathrm{K}}_{\mathrm{p}1}{\mathrm{K}}_{\mathrm{p}2}}{{\mathrm{L}}_{\mathrm{f}}}& \frac{{\mathrm{K}}_{\mathrm{i}1}{\mathrm{K}}_{\mathrm{p}2}}{{\mathrm{L}}_{\mathrm{f}}}& \frac{{\mathrm{K}}_{\mathrm{i}2}}{{\mathrm{L}}_{\mathrm{f}}}& 0& -\frac{{\mathrm{K}}_{\mathrm{p}2}}{{\mathrm{L}}_{\mathrm{f}}}& 0\\ 0& 0& 0& \frac{{\mathrm{K}}_{\mathrm{i}2}}{{\mathrm{L}}_{\mathrm{f}}}& 0& -\frac{{\mathrm{K}}_{\mathrm{p}2}}{{\mathrm{L}}_{\mathrm{f}}}\end{array}\right](18)$

$B=\left[\begin{array}{cccccc}\frac{-3{\mathrm{i}}_{\text{gd}}}{2{\mathrm{C}}_{\text{dc}}{\mathrm{U}}_{\text{dc}}}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right](19)$

Table 2 shows the parameters of the explored system. The eigenvalues of the state matrix A are computed as shown in Table 3 Five eigenvalues were obtained with negative real part. According to Lyapunov, this system is small signal marginally stable.

TABLE 2

TABLE 2. Studied system parameters.

TABLE 3

TABLE 3. State matrix eigenvalues.

4 Effect of partial shading on PV characteristics

The issue of shading arises when different lighting conditions expose the system. It is important to note that the systems electrical performance depends on both the cell specifications and the conditions of irradiation. Shaded modules, acting as a load utilize a portion of the generated power, that influences the behavior of the system leading potentially to hot spot problems.

Hot spotting represent a performance concern, in PV modules where certain solar cells become significantly heated due to mismatches resulting in reduced output power. This phenomenon occurs when dividual cells or groups of them operate at aberrant temperatures and activate at bias, squandering the power that was intended to provide the stimulus. Additionally, these hot areas cause PV panels to age and can sustain irreversible damage. To mitigate spotting effects bypass diodes are commonly employed in parallel, with PV modules. The purpose is to raise the total short circuit current and open circuit voltage by limiting the reverse voltage across spotted or shaded solar cells.

Two irradiations are simulated for the system under study: G1 and G2. The I-V and P-V characteristics, which consist of two extremums, are displayed in Figure 5. It is observed that the second generator’s illumination has an impact on the system’s overall appearance, especially on the second extremum, which may represent a Local Maximum (LM) or a Global Maximum (GM).

FIGURE 5

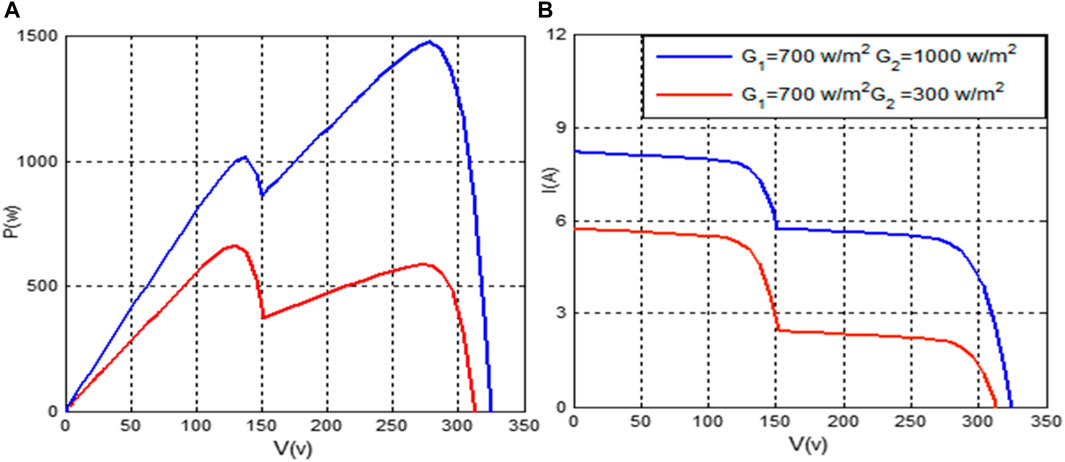
FIGURE 5. Characteristics of the studied Shaded PV generator (A) I-V Characteristic (B) P-V Characteristic.

5 Implementation of MPPT methods for optimization problem

5.1 Inc-Cond technique

The Inc-Cond technique is the commonly employed MPPT method. It adjust continuously the output voltage of the generator by comparing the instantaneous conductance $\frac{{\mathrm{I}}_{\text{pv}}}{{\mathrm{V}}_{\text{pv}}}$ to its negative local variation $\frac{\Delta {\mathrm{I}}_{\text{pv}}}{\Delta {\mathrm{V}}_{\text{pv}}}$ in order to regulate the operating point on the I-V characteristic to the MPP corresponding voltage.

5.2 Fuzzy MPPT controller

Given that the fuzzy logic approach is acknowledged as a model-free technique, dealing with imprecise inputs and handling non-linearity, the FLC based MPPT strategy is developed to improve the PV response.

The inputs and variables of the suggested controller are: $\mathrm{E}$ and $\Delta \mathrm{E}$, given by Eqs 3, 4, where P_pv (n) and V_pv (n) represent the output power and voltage of the PV generator at the sampling instant n.

$\mathrm{E}\left(\mathrm{n}\right)=\frac{{\mathrm{P}}_{\text{pv}}\left(\mathrm{n}\right)-{\mathrm{P}}_{\text{pv}}\left(\mathrm{n}-1\right)}{{\mathrm{V}}_{\text{pv}}\left(\mathrm{n}\right)-{\mathrm{V}}_{\text{pv}}\left(\mathrm{n}-1\right)}(20)$

$\Delta \mathrm{E}\left(\mathrm{n}\right)=\mathrm{E}\left(\mathrm{n}\right)-\mathrm{E}\left(\mathrm{n}-1\right)(21)$

The fuzzification step, requires seven fuzzy levels called NB (negative big), NM (negative medium), NS (negative small), ZE (zero), PS (positive small), PM (positive medium) and PB (positive big).

The memberships functions of the input and output variables are given in Figure 6.

FIGURE 6

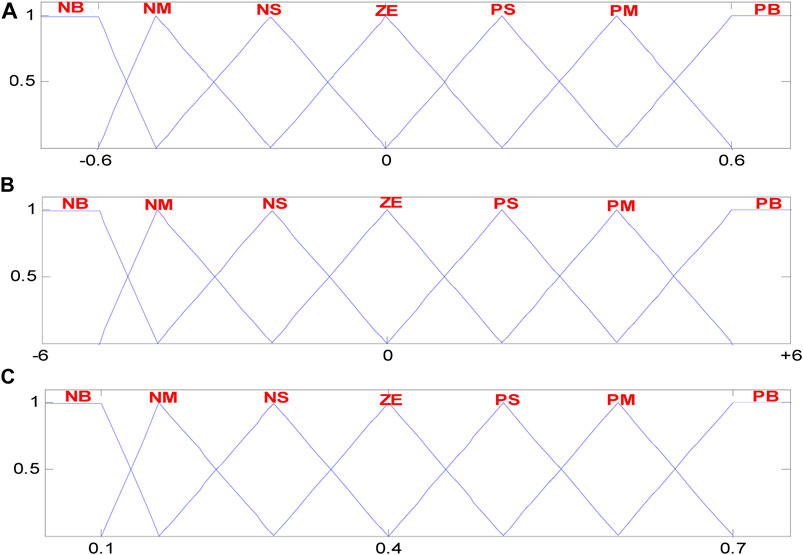
FIGURE 6. Membership functions (A) input variable E(n) (B) input variable Δ E(n) (C) output variable α.

Table 4 presents the 49 fuzzy rules used in the FLC inference approach.

TABLE 4

TABLE 4. The fuzzy controller’s forty-nine rules.

5.3 Crow search algorithm

Crows are considered as highly intelligent birds, which are able to evoke faces and inform each other when an inauspicious one approaches. They exhibit remarkable abilities to sophisticated communication techniques and long-term memories, allowing them to recall their food’s hiding place. Moreover, crows tracks other crows or birds to discover the location of their hidden food in order to steal it. Conversely, when a crow becomes aware of being tracked, it resorts to changing its position to deceive others and maintain the secrecy of its own hidden food.

This paper introduces a newly developed population-based metaheuristic algorithm called CSA based on the intelligent behaviors mentioned earlier.

The following is a summary of the CSA’s tenets:

• Crows live in flocks and memorize the locations of their hiding spots.

• Crows stalk people to smuggle food from them.

• Crows conceal their food by moving in unpredictable ways.

Step 1: Setting up changeable parameters and decision variables

Decision variables are defined for the optimization problem, and the values of the CSA’s adjustable parameters (N, fl, itermax, and AP) are found where:

N: size of flock.

the greatest number of iterations, or itermax.

fl stands for flight length.

Step2: Initialization of crows’ position and memory

In a one-dimensional environment including N crows randomly positioned, each decision variables, is characterized by a position ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{k}}$ and a memory ${\mathrm{m}}_{\mathrm{i}}^{\mathrm{k}}$ for a specified iteration k.

${\mathrm{x}}_{\mathrm{i}}=\left[{\mathrm{x}}_1............{\mathrm{x}}_{\mathrm{N}}\right](22)$

${\mathrm{m}}_{\mathrm{i}}=\left[{\mathrm{m}}_1............{\mathrm{m}}_{\mathrm{N}}\right](23)$

Every crow’s memory is initialized with the presumption that they have concealed their food at their original locations.

Step3: evaluation of fitness function position and memory

The quality of the initial position is evaluated through a fitness function.

Step4: Generation of new position

In order to generate a new position and assuming that at at iteration k crow i tries to follow crow j to identify its hidden location of food. At this moment, depending on the value of the AP parameter, the position of crows are updated as follow:

State1: $\mathrm{r}\ge \text{AP}$

Where r is a random number varying between [0 1].

This situation signifies that crow j is unconscious that crow i is following it hence the position of crow i at an iteration (k+1) is updated according to the following equation:

${\mathrm{x}}_{\mathrm{i}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{i}}^{\mathrm{k}}+\mathrm{r}\times \text{fl}\times \left({\mathrm{m}}_{\mathrm{j}}^{\mathrm{k}}-{\mathrm{x}}_{\mathrm{i}}^{\mathrm{k}}\right)(24)$

State2: $\mathrm{r}<\text{AP}$

During this state, crow j is conscious that crow i is following it so it tries to trick it by moving randomly in the research space referring to the given equation:.

${\mathrm{x}}_{\mathrm{i}}^{\mathrm{k}+1}=\mathrm{a}:\text{random\hspace{0.5em}location}$

The schematic of the update states and the effect of fl on the search capability are described in Figure 7.

Step 5: Assessment of the fitness function for newly created positions

FIGURE 7

FIGURE 7. Intelligent movement for the crows (A) fl < 1 (B) fl > 1.

After updating the position of each crow, the objective function of each new position is evaluated.

Step 6: update memory

The fitness values for each vector, both past and present, are used to update the memory. as follows:

${\mathrm{m}}_{\mathrm{i}}^{\mathrm{k}+1}=\left\{\begin{array}{l}{\mathrm{x}}_{\mathrm{i}}^{\mathrm{k}+1}\text{\hspace{1em}if\hspace{0.5em}fitness}\left({\mathrm{x}}_{\mathrm{i}}^{\mathrm{k}+1}\right)>\text{fitness}\left({\mathrm{x}}_{\mathrm{i}}^{\mathrm{k}}\right)\\ {\mathrm{m}}_{\mathrm{i}}^{\mathrm{k}}\text{\hspace{1em}otherwise}\end{array}\right.(25)$

The four initial values of the vectors positions and memory are applied successively.

They are given by:

${{\mathrm{V}}_{\text{pv}}}_{\mathrm{i}}^0=\left[{\mathrm{V}}_1^0{\mathrm{V}}_2^0{\mathrm{V}}_3^0{\mathrm{V}}_4^0\right]=\left[0.20.40.60.8\right]\times 2{\mathrm{V}}_{\text{oc}}(26)$

${\mathrm{m}}_{\mathrm{i}}^0=\left[{\mathrm{m}}_1^0{\mathrm{m}}_2^0{\mathrm{m}}_3^0{\mathrm{m}}_4^0\right]=\left[0.20.40.60.8\right]\times 2{\mathrm{V}}_{\text{oc}}(27)$

The evaluation of the quality of initial positions is computed by using the expression of the fitness function below:

${{\mathrm{P}}_{\text{pv}}}_{\mathrm{i}}^{\mathrm{k}}={\mathrm{V}}_{\text{pvi}}^{\mathrm{k}}\times {\mathrm{I}}_{\text{pv}}(28)$

The boost converter’s duty cycle and output voltage are correlated in the following way:

${\mathrm{\alpha }}_{\mathrm{i}}^{\mathrm{k}}=1-\frac{{\mathrm{V}}_{\text{pvi}}^{\mathrm{k}}}{2{\mathrm{V}}_{\text{oc}}}(29)$

To update the positions and the memory of the four crows the expressions below are used:

${\mathrm{V}}_{\text{pvi}}^{\left(\mathrm{k}+1\right)}=\left\{\begin{array}{l}{\mathrm{V}}_{\text{pvi}}^{\mathrm{k}}+\mathrm{r}\times \text{fl}\times \left({\mathrm{m}}_{\mathrm{j}}^{\mathrm{k}}-{\mathrm{V}}_{\text{pvi}}^{\mathrm{k}}\right)\text{\hspace{1em}if\hspace{0.17em}}\mathrm{r}\ge \text{AP}\\ \mathrm{a}\text{\hspace{1em}if\hspace{0.17em}}\mathrm{r}<\text{AP}\end{array}\right.(30)$

In reality, the CSA needs to be reinitialized to find the new MPP in such circumstances of abrupt changes in the operating point brought on by variations in solar insolation. If this procedure is not followed, the global maximum and the local one cannot be updated automatically. The suggested criterion to reinitialize the MPPT technique is realized using variations in output voltage and output power as explained by Eqs (31), (32) respectively.

$\left|\left.{\mathrm{V}}_{\text{pvi}}^{\mathrm{k}+1}-{\mathrm{V}}_{\text{pvi}}^{\mathrm{k}}\right|\right.<\Delta \mathrm{V}(31)$

$\left|\left.\frac{{\mathrm{P}}_{\text{pv}}^{\mathrm{k}+1}-{\mathrm{P}}_{\text{pv}}^{\mathrm{k}}}{{\mathrm{P}}_{\text{pv}}^{\mathrm{k}}}\right|\right.>\Delta \mathrm{P}(32)$

Figure 8 shows the different CSA implementation processes for global optimization problem-based MPPT.

FIGURE 8

FIGURE 8. Flowchart of the proposed CSA technique.

6 Results and discussion

In order to demonstrate the effectiveness of the suggested CSA technique in mitigating the negative impacts of PSC on the MPPT controller’s performance in grid connected PV system, simulation studies using MATLAB/SIMULINK environment have been carried out. These studies encompassed three distinct partial shading scenarios. The tuned parameters of the proposed methods are displayed in Table 5. Three simulation scenarios were selected to assess the efficiency of the CSA-based MPPT technique in comparison with the Inc-Cond and FLC-based MPPT techniques, as depicted in Figure 9.

• First scenario: Under this specific scenario, both PVG1 and PVG2 experience identical uniform irradiation levels of 1000W/m².

• Second scenario: In this particular situation, partial shading is introduced to PVG2.: The PVG1 is exposed to 1000w/m² while the second PVG is subjected to 600 w/m².

• Third scenario: This case involves evaluating the proposed CSA-based MPPT technique under suddenly variation of the illumination.

TABLE 5

TABLE 5. Tuning parameters of the proposed MPPT methods.

FIGURE 9

FIGURE 9. Illumination cases (A). First case, (B) second case (C) Third case.

The P-V characteristics of the PVG under various circumstances are displayed in Figure 10.

FIGURE 10

FIGURE 10. P-V characteristics of the PVG under different cases.

7 Discussion and analysis

Based on the acquired simulation results which are shown in Figures 11–13 an accurate comparison study between the three proposed algorithms is explained in Table 6. The bold value provided in Table 6 represent the extracted power and the mismatch power loss of the studied CSA method. The performance indices considered include the extracted Pv power and the mismatch power loss (MML) which is given by:

$\text{MML}=\frac{\text{Maximum}\text{Extracted}\text{Power}}{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{\mathrm{P}}_{\max }\left(\mathrm{i}\right)}\times 100(33)$

FIGURE 11

FIGURE 11. Simulated System responses under case (1). (A) Inc-Cond (B) FLC (C) CSA.

FIGURE 12

FIGURE 12. Simulated System responses under case (2) (A) Inc-Cond (B) FLC (C) CSA.

FIGURE 13

FIGURE 13. Simulated System responses under case (3) (A) Inc-Cond (B) FLC (C) CSA.

TABLE 6

TABLE 6. statistical results of the used MPPT methods in the critical case 3 of PSC.

Case (1): In this case, PVG1 and PVG2 are subjected to the same uniform irradiation (1000W/m²). The P–V characteristic exhibits a singular GMPP peak at 2000W as presented in Figure 10. CSA method achieved after 0.31Sec the GMPP at 2000 W, without any steady state oscillations, while FLC and Inc-Cond methods reached 1950W and 1980W respectively after 0.68 s and.0.65 s with small steady state oscillations. It is noted that the response of CSA technique presents also less oscillations in the transient phase compared to that generated by other methods. Comparing to Inc–Cond and FLC methods, the CSA technique is more accurate, in fact the rate of oscillation and fluctuation noted in the response is reduced.

Case (2): the PVG1 is exposed to 1000w/m2 while the second PVG is subjected to 600 w/m2. This case yielded two peaks on the P–V curve as presented in Figure 10: the first one is a LMPP at 966w and the second one is a GMPP at 1256w. Figure 12 shows that CSA method converged to the GMPP of 1256 W after 0.49 s while both FLC and Inc_Cond stuck around the LMPP, they stopped at the first peak encountered. The FLC converged to 960w after 0.4s while the conventional Inc Cond reached 950W after 0.2s. Therefore, only the first local or global maximum—that is considered as the maximum power point for the shaded system—is achieved by these techniques, and they are unable to reach the global maximum if it is situated at the second level.

Case (3): In this case, there are two sequences in the variation’s illumination scenario shown in Figure 9C. While the value of G2 varies from 600W/m2 to 400W/m2 at t = 1s, value of G1 is kept constant at 1000w/m2. Two GMPP are present in the PV characteristics. The first one is on the right side with 1256w and the second one is in the left side with 966w. The CSA technique succeeds in reaching the GMPP in every sequence and its response varies from 1256w to 966w.

It is clear from the above discussion that both Inc-Cond and FLC remain fixed around the LMPP, which is always powered lower than the GMPP. This significantly lowers the power provided by the PV system and contributes to the hot spot that forms on the shaded PV modules.

8 Conclusion

This present paper introduces the Crow Search Algorithm (CSA), a meta-heuristic optimization technique designed to address the adverse impacts of partial shading on the accurate pursuing the optimal maximum power point in a two stage grid connected PV system. A small-signal model of the studied system was considered to analyze the stability using Lyaponov function. The digital simulation results illustrated the exceptional capability of CSA technique in effectively tracking the GMPP across three different partial shading scenarios. Despite the dynamic shifts in climatic conditions, the recommended CSA technique demonstrated remarkable effectiveness in tracking the GMPP even in intricate shading scenarios. The CSA technique reduces the total power loss and extracts the maximum power from the studied PVG. The obtained results of the latter MPPT method are compared also with the FLC and Inc-Cond methods and they recorded better performance in terms of mismatch power loss with an average of 78.26%, for the three scenarios of simulation, whereas 56.77% and 57.15% were recorded for FLC and Inc-Cond techniques. Ultimately, a qualitative assessment utilizing statistical analysis validated the superior performance of the CSA technique.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary materials, further inquiries can be directed to the corresponding authors.

Author contributions

MB: Conceptualization, Formal Analysis, Investigation, Methodology, Resources, Software, Writing–original draft, Writing–review and editing. AA: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–original draft, Writing–review and editing. AS: Formal Analysis, Investigation, Methodology, Resources, Software, Validation, Writing–original draft, Writing–review and editing, Writing–review and editing. IH: Formal Analysis, Funding acquisition, Investigation, Methodology, Resources, Validation, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Norwegian University of Science and Technology.

Acknowledgments

The authors would like to acknowledge the support of the Norwegian University of Science and Technology for paying the Article Processing Charges (APC) of this publication. The authors would like to thank Prince Sultan University, Riyadh, Saudi Arabia for their support. Special acknowledgment to Automated Systems and Soft Computing Lab (ASSCL), Prince Sultan University, Riyadh, Saudi Arabia. In addition, the authors wish to acknowledge the editor and anonymous reviewers for their insightful comments, which have improved the quality of this publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, J., and Salam, Z. (2014). A maximum power point tracking (MPPT) for PV system using cuckoo search with partial shading capability. Appl. Energy 119, 118–130. doi:10.1016/j.apenergy.2013.12.062

CrossRef Full Text | Google Scholar

Ahmed, J., and Salam, Z. (2015). A critical evaluation on maximum power point tracking methods for partial shading in PV systems. Renew. Sustain Energy Rev. 47, 933–953. doi:10.1016/j.rser.2015.03.080

CrossRef Full Text | Google Scholar

Askarzadeh, A. (2016a). A novel metaheuristic method for solving constrained engineering optimization problems: crow searchalgorithm. Comput. Struct. 169, 1–12. doi:10.1016/j.compstruc.2016.03.001

CrossRef Full Text | Google Scholar

Balaji, V., and Fathima, A. P. (2022). Hybrid algorithm for MPPT tracking using a single current sensor for partially shaded PV systems. Sustain. Energy Technol. Assessments 53, 102415. doi:10.1016/j.seta.2022.102415

CrossRef Full Text | Google Scholar

Bounechba, H., Bouzid, A., Nabti, K., and Benalla, H. (2014). Comparison of perturb and observe and fuzzy logic in maximum power point tracker for PV systems. Energy Procedia 50, 677–684. doi:10.1016/j.egypro.2014.06.083

CrossRef Full Text | Google Scholar

Chowdhury, S. R., and Saha, H. (2010). Maximum power point tracking of partially shaded solar photovoltaic arrays. Sol. Energy Mater Sol. Cells 94 (9), 1441–1447. doi:10.1016/j.solmat.2010.04.011

CrossRef Full Text | Google Scholar

Eltamaly, A. M., Farh, H. M., and Othman, M. F. (2018). A novel evaluation index for the photovoltaic maximum power point tracker techniques. Sol. Energy 174, 940–956. doi:10.1016/j.solener.2018.09.060

CrossRef Full Text | Google Scholar

Hinojosa, S., Oliva, D., Cuevas, E., Pajares, G., Avalos, O., and Gálvez, J. (2018). Improving multi-criterion optimization with chaos: a novel multi-objective chaotic crow search algorithm. Neural Comput. 29 (8), 319–335. doi:10.1007/s00521-017-3251-x

CrossRef Full Text | Google Scholar

Houam, Y., Terki, A., and Bouarroudj, N. (2021). An efficient metaheuristic technique to control the maximum power point of a partially shaded photovoltaic system using crow search algorithm (CSA). J. Electr. Eng. Technol. 16, 381–402. doi:10.1007/s42835-020-00590-8

CrossRef Full Text | Google Scholar

Ishaque, K., and Salam, Z. (2012). A deterministic particle swarm optimization maximum power point tracker for photovoltaic system under partial shading condition. IEEE Trans. Ind. Electron 60 (8), 1–3206. doi:10.1109/tie.2012.2200223

CrossRef Full Text | Google Scholar

Kaced, K., Larbes, C., Ramzan, N., Bounabi, M., and Dahmane, Z. e. (2017). Bat algorithm based maximum power point tracking for photovoltaic system under partial shading conditions. Sol. Energy 158, 490–503. doi:10.1016/j.solener.2017.09.063

CrossRef Full Text | Google Scholar

Karatepe, E., and Hiyama, T. (2009). Artificial neural network-polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions. IET Renew. Power Gener. 3 (2), 239–253. doi:10.1049/iet-rpg:20080065

CrossRef Full Text | Google Scholar

Kermadi, M., Salam, Z., Eltamaly, A. M., Ahmed, J., Mekhilef, S., Larbes, C., et al. (2020a). Recent developments of MPPT techniques for PV systems under partial shading conditions: a critical review and performance evaluation. IET Renew. Power Gener. 14 (17), 3401–3417. doi:10.1049/iet-rpg.2020.0454

CrossRef Full Text | Google Scholar

Lian, K., Jhang, J., and Tian, I. (2014). A maximum power point tracking method based on perturb-and-observe combined with particleswarm optimization. IEEE J. Photovolt. 4 (2), 626–633. doi:10.1109/jphotov.2013.2297513

CrossRef Full Text | Google Scholar

Maki, A., and Valkealahti, S. (2012). Power losses in long string and parallel-connected short strings of series-connected silicon-based photovoltaic modules due to partial shading conditions. IEEE Trans. Energy Convers. 27, 173–183. doi:10.1109/tec.2011.2175928

CrossRef Full Text | Google Scholar

Mirza, A. F., Ling, Q., Javed, M. Y., and Mansoor, M. (2019). Novel MPPT techniques for photovoltaic systems under uniform irradiance and Partial shading. Sol. Energy 184, 628–648. doi:10.1016/j.solener.2019.04.034

CrossRef Full Text | Google Scholar

Miyatake, M., Veerachary, M., Toriumi, F., Fujii, N., and Ko, H. (2011). Maximum power point tracking of multiple photovoltaic arrays: a PSO approach. IEEE Trans. Aerosp. Electron Syst. 47 (1), 367–380. doi:10.1109/taes.2011.5705681

CrossRef Full Text | Google Scholar

Moghaddam, S., Bigdeli, M., Moradlou, M., and Siano, P. (2019). Designing of standalone hybrid PV/wind/battery system using improved crow search algorithm considering reliability index. Int. J. Energy Environ. Eng. 10 (4), 429–449. doi:10.1007/s40095-019-00319-y

CrossRef Full Text | Google Scholar

Mohamed, M. A., Diab, A. A. Z., and Rezk, H. (2019). Partial shading mitigation of PV systems via different meta-heuristic techniques. RenewEnergy 130, 1159–1175. doi:10.1016/j.renene.2018.08.077

CrossRef Full Text | Google Scholar

Mohanty, S., Subudhi, B., and Ray, P. K. (2015). A new MPPT design using grey wolf optimization technique for photovoltaic system under partial.

Google Scholar

Ram, J. P., and Rajasekar, N. (2017). A new robust, mutated and fast tracking LPSO method for solar PV maximum power point tracking under partial shaded conditions. 201:45–59. doi:10.1016/j.apenergy.2017.05.102

CrossRef Full Text | Google Scholar

Salah, C. B., and Ouali, M. (2011). Comparison of fuzzy logic and neural network in maximum power point tracker for PV systems. Electr. Power Syst. Res. 81 (1), 43–50. doi:10.1016/j.epsr.2010.07.005

CrossRef Full Text | Google Scholar

Sundareswaran, K., Sankar, P., Nayak, P. S. R., Simon, S. P., and Palani, S. (2014). Enhanced energy output from a PV system under partial shaded conditions through artificial bee Colony. IEEE Trans. Sustain Energy 6 (1), 198–209. doi:10.1109/tste.2014.2363521

CrossRef Full Text | Google Scholar

Sundareswaran, K., Vigneshkumar, V., and Palani, S. (2015). Development of a hybrid genetic algorithm/perturb and observe algorithm for maximum power point tracking in photovoltaic systems under non-uniform insolation. IET Renew. Power Gen. 9 (7), 757–765. doi:10.1049/iet-rpg.2014.0333

CrossRef Full Text | Google Scholar

Wang, Z., Luo, Q., and Zhou, Y. (2020). Hybrid metaheuristic algorithm using butterfly and flower pollination base on mutualism mechanism for global optimization problems. Eng. Comput. 37, 3665–3698. doi:10.1007/s00366-020-01025-8

CrossRef Full Text | Google Scholar

Wu, Z., and Yu, D. (2018). Application of improved bat algorithm for solar PV maximum power point tracking under partially shaded condition. Appl. Soft Comput. 62, 101–109. doi:10.1016/j.asoc.2017.10.039

CrossRef Full Text | Google Scholar

Yilmaz, U., Turksoy, O., and Teke, A. (2019). Improved MPPT method to increase accuracy and speed in photovoltaic systems under variable atmospheric conditions. Int. J. Electr. Power Energy Syst. 113, 634–651. doi:10.1016/j.ijepes.2019.05.074

CrossRef Full Text | Google Scholar