- 1Xuzhou Power Supply Company of State Grid Jiangsu Electric Power Supply Co Ltd., Xuzhou, Jiangsu, China
- 2Electrical Engineering School, Southeast University, Nanjing, Jiangsu, China
The “load-following” characteristic of the power system makes the electricity consumption behavior on the load side crucial for the low-carbon operation of the distribution network. To address this, this paper proposes an improved dynamic carbon emission factor for the distribution network, taking into account the spatiotemporal characteristics of carbon emission intensity and the integration capacity of photovoltaics (PV). Based on this, a calculation method for the carbon emissions of the distribution network load is provided. Subsequently, for commercial and industrial user scenarios, demand response models are separately constructed for commercial and industrial loads based on different driving mechanisms. Using time-of-use electricity prices as decision variables, optimization scheduling of the distribution network is carried out with the objectives of minimizing scheduling costs and carbon emissions. At the same time, a case study is conducted in an improved IEEE-33 node distribution network. The results indicate that, under the guidance of the improved dynamic carbon emission factor, load transfer can be achieved through fluctuating electricity prices, effectively reducing the scheduling costs of the distribution network, decreasing carbon emissions, and enhancing the PV integration capacity of the distribution network in different user scenarios. Finally, it is hoped that in the future, this optimization method can be widely applied, and further research can explore coordinated strategies among generation, network, load, and storage to advance the development of the power industry.
1 Introduction
Since the proposal of the Dual Carbon Goals by the 75th United Nations General Assembly in September 2020, various industries have been continuously moving towards the direction of green and low-carbon initiatives. As a crucial infrastructure supporting modern society, the power system plays a key role in achieving low-carbon emission objectives. The distribution network, being the end of the power system and connected to end-users, has a direct and far-reaching impact on carbon emission levels through its scheduling methods and topological structure (Kang et al., 2009). Therefore, it is an urgent task to develop rational optimization and scheduling plans, considering the carbon emission characteristics of different loads in the distribution network, to reduce carbon emissions while ensuring the economic operation of the distribution network.
In recent years, research on carbon emissions in power systems has shifted from generation to the load side. Although carbon emissions primarily originate from the generation side, distributed generation units on the distribution network side have almost zero carbon emissions. However, due to the diversity and uncertainty of distribution network loads, changes in load flow will occur, and carbon flow is dependent on the existence of load flow. The introduction of different loads will change the carbon emission intensity of the distribution network. Therefore, considering the carbon emission flow theory (Zhou et al., 2012), research on the low-carbon optimization operation of distribution networks under different scenarios is conducted. The distribution characteristics of carbon emission flow in distribution systems developed by (Zhou and Kang, 2019) and establishes a carbon emission flow calculation model for energy storage components, proposing an optimization method for the operation of distribution systems towards low-carbon goals. The responsibility of carbon emissions shifts from the generation side to the load side and considers low-carbon optimization scheduling (Ge et al., 2023) based on carbon emission flow theory and demand response using carbon prices as a pricing signal, providing new insights for reducing system carbon emissions. (Zhang et al., 2023) addresses the issue of a singular low-carbon means on the load side in low-carbon scheduling and proposes a two-layer low-carbon economic scheduling model for power systems considering multiple carbon reduction methods coupled with the carbon potential of sources and loads. All of these studies introduce the theory of carbon emission flow into the power system, guiding electricity use for different types of users based on their electricity consumption characteristics but without optimizing considerations for load response characteristics and flexibility.
From the perspective of demand response, the optimization scheduling of flexible loads has gradually become a research focus for reducing carbon emissions. Considering the carbon emission characteristics of thermal power units and cement factories (Han et al., 2023), which proposed environmentally economic scheduling of typical industrial loads with positive demand response. Literature (Li et al., 2022a; Ibrahim et al., 2023) introduces a new mechanism for reducing carbon emissions in power systems by guiding users to respond actively, taking into account the users’ own carbon reduction intentions or the price factors in the carbon market as incentive signals. A distributed resource low-carbon scheduling strategy for distribution networks based on the carbon potential of nodes, considering both the economic and low-carbon aspects of power grid operations proposed in (Xue et al., 2019; Song et al., 2023a). The above studies on demand response in power systems do not take into account the impact of abandoned wind and solar power on the carbon emissions of distribution networks, as well as the differences in carbon emissions due to electricity consumption at different times.
In summary, based on the carbon emission flow theory, this paper proposes an improved dynamic carbon emission factor calculation method considering temporal and spatial characteristics and the integration capacity of new energy sources. For different user scenarios, demand response models for commercial and industrial loads with the objectives of minimizing scheduling costs and carbon emissions are separately established. Finally, a case study is conducted on an IEEE-33 node distribution network, validating that the proposed model can effectively shift high-carbon emission periods to low-carbon emission periods in different scenarios while enhancing the photovoltaic integration capacity of the distribution network.
2 Calculation method for carbon emissions in distribution networks
2.1 Improved dynamic carbon emission coefficient for distribution networks
The traditional quantification of carbon emission levels in distribution networks mainly relies on the nodal carbon potential of the system. For a specific node, it is described as the ratio of the carbon flow into that node to its active power. Physically, it represents the carbon emission per unit of electricity consumed at the node, corresponding to the carbon emission density of the generator at that node and the weighted average of the carbon flow densities of adjacent nodes concerning the injected power from generators and adjacent nodes. The unit is kgCO2/kW·h (Zhou et al., 2012) Eq. 1.
In the equation, ej represents the carbon potential of Node j, Pj represents Injected power at node j, PG,j represents the injected power from generator units connected to node j, ρj represents the carbon flow density at node j, ρG,j represents the carbon potential of generatorn units connected to node j.
The traditional calculation for dynamic carbon emission factor in distribution networks is as follow Eq. 2 (Zhou and Kang, 2019):
In the equation, CDis,t represents the dynamic carbon emission factor of the urban distribution network at time t, Pj,t represents the active load magnitude of node t at time t, ej,t represents the carbon potential magnitude of node t at time t, calculated based on the carbon emission flow theory, N represents the set of nodes within the distribution network.
The traditional dynamic carbon emission factor for distribution networks reflects the carbon emissions per unit of electricity consumption at time t. However, the improved dynamic carbon emission factor takes into account the equivalent carbon emissions generated by adding new energy sources. During these times, all electricity consumption in the distribution network comes from photovoltaic output, resulting in a dynamic carbon emission factor of zero for the distribution network. In such cases, users, when considering changes in their electricity consumption based on the dynamic carbon emission factor, cannot perceive the curtailed solar power at the moment when the carbon emission factor is zero. The closer its value is to zero, the higher the level of new energy consumption. Therefore, the equivalent reduction in carbon emissions is also different in article (Ge et al., 2022). The improved expression for the calculation of the dynamic carbon emission factor is as follows:
In the equation,
2.2 Calculation of carbon emissions in distribution networks
Based on the carbon potential matrix E formed by the carbon potential at each node in the distribution network and the active power flow matrix at load nodes, the carbon emissions at the load nodes can be determined, clearly defining the carbon emission responsibilities of different nodes.
The active power flow matrix at a specific node can be defined as a diagonal matrix, as shown below:
Since there are no losses in the active power transmission between nodes, the off-diagonal elements are 0, the calculation for the diagonal elements is as follows Eq. 5 (Chen et al., 2023):
In the equation,k+ represents the set of branches connected to node j that are adjacent and have generating units with power output, when a specific node is not adjacent to any generating units, that is
Combining (Eqs. 3, 4), the calculation method for the node carbon potential matrix is as follows for (Chen et al., 2023) Eq. 6:
In the equation, E represents the node carbon potential matrix, PB represents the matrix of branch flow distribution,
In distribution networks with a high proportion of photovoltaics, the carbon potential at a node is affected by both photovoltaic power sources and energy storage elements in discharge mode. If the distribution network lacks generating units and energy storage components, then in such a scenario, the carbon potential at all nodes equals the carbon potential of the main network. However, if the distribution network includes generating units and energy storage components, given the main network’s carbon potential, distribution network load, and generating unit outputs, it becomes possible to calculate the distribution of branch power flows and branch carbon flow density. Subsequently, node carbon potentials can be determined based on the carbon flow density of the branches.
If the dynamic carbon emission factor matrix
3 Demand response load model in distribution network
3.1 Incentive-based demand response
Traditional incentive-based demand response (Xu and Guo, 2023) mainly involves users adjusting or reducing electricity consumption during peak demand periods to receive discounts or compensation. This paper proposes an incentive-based demand response load considering the dynamic carbon emission factor. In this approach, agreements are pre-signed between the power supplier and the consumer. The dispatch center issues instructions the day before the demand response, and based on the dynamic carbon emission factor, the load is transferred from high carbon periods to low carbon periods. The load remains unchanged during neutral carbon periods. According to the agreement, users receive compensation after load transfer. The expression for compensation is as follows for Eq. 8 (Ge et al., 2022):
In the equation,
3.2 Price-based demand response
Price-based demand response in (Li et al., 2023) involves changing the original electricity consumption behavior based on changes in electricity prices. It mainly includes two methods: time-of-use pricing demand response and tiered pricing demand response. This paper primarily adopts time-of-use pricing demand response, aiming to improve the economic and low-carbon performance of the distribution network by responding to variations in electricity prices.
For electricity consumption periods under different carbon emission intensities, users will adjust their electricity consumption structure (Kaile et al., 2020). The electricity price level will not only affect the load of that period, but also affect the load of other periods, which is a multi period demand response. Based on the relationship between electricity quantity and price demand balance, and the multi-period electricity quantity-price elasticity matrix, users’ response behavior can be comprehensively characterized. The ratio of electricity quantity to price change rate can be described as the electricity quantity-price elasticity matrix, representing the sensitivity of electricity consumption in each period to prices. The expression is as follows for Eq. 9 (Zhou et al., 2016):
In the equation,
The expression for the electricity quantity-price elasticity matrix M under time-of-use pricing is Eq. 10 (Zhou et al., 2016):
In the equation,
The expressions for the self-elasticity coefficient and cross-elasticity coefficients for the high-carbon period are as follows for Eqs 11, 12 (Zhou et al., 2016):
In the equation,
The expression for electricity consumption in the high-carbon, normal-carbon, and low-carbon periods after multi-period demand response is as follows Eq. 13 (Ge et al., 2022):
In the equation, E1 represents electricity consumption in multiple periods after demand response, E0 represents electricity consumption in the periods before demand response, E0,h、E0,m、E0,l represent electricity consumption in the high-carbon, normal-carbon, and low-carbon periods before price-based demand response, P0,h、P0,m、P0,l represent the fixed electricity prices in the high-carbon, normal-carbon, and low-carbon periods before price-based demand response, respectively.
With a daily cycle and a 1-h sampling interval, assuming the set of dynamic carbon emission factors for all time periods on a given day is
The peak and off-peak membership degrees for the maximum point on the dynamic carbon emission factor curve are 1 and 0, respectively, while for the minimum point, they are 0 and 1, Assuming a membership degree threshold of
4 Low-Carbon scheduling optimization model for distribution NetworksFeature selection
For commercial loads, the inherent industry constraints and limited ability to shift electricity usage to off-peak hours make time-of-use pricing less effective for load transfer, thus they are more appropriately classified as reducible loads in paper (Qiang et al., 2023). Therefore, this paper considers them as loads that can be reduced. In practical operation, instructions can be issued to these types of load users to reduce a portion of their load in response to their own situation, which can refers to (Lixia and Yun, 2023). They will receive corresponding compensation. On the other hand, industrial loads can shift some of their load within a certain time range without affecting overall production plans and lifestyle needs, achieving load peak shaving and valley filling during the scheduling period without compromising production plans and lifestyle needs.
4.1 Low-carbon scheduling optimization model for commercial loads in distribution networks
4.1.1 The objective function
In the formula Eq.15,
4.1.2 Constraints
a) Load reduction constraint
In the formula,
b) The constraint on photovoltaic (PV) output
In the formula,
4.2 Optimization model for low-carbon scheduling of industrial loads in distribution networks
4.2.1 The objective function
The demand response of industrial loads in an industrial park is primarily considered with electricity price as a guide (He at al., 2023). By incentivizing industrial users through benefits, a portion of high carbon-emission periods is shifted to low carbon-emission periods. The specific objective function is as follows:
Where
4.2.2 Decision variables
In the optimization scheduling model, the electricity prices during periods of different carbon emission intensities
4.2.3 Constraints
a) Constraints on Photovoltaic Output
The article does not consider the issue of distributed photovoltaic power flow backfeeding according to (Zhou and Kang, 2019). Therefore, when the photovoltaic output exceeds the distribution network load, a portion of the photovoltaic power will be curtailed, resulting in curtailed solar energy.
The value of
b) Constraints related to load transfer
Where
c) Constraints related to electricity price fluctuations
In the formula,
d) Power balance constraint
Where
4.3 The solution process for low-carbon scheduling of industrial and commercial loads
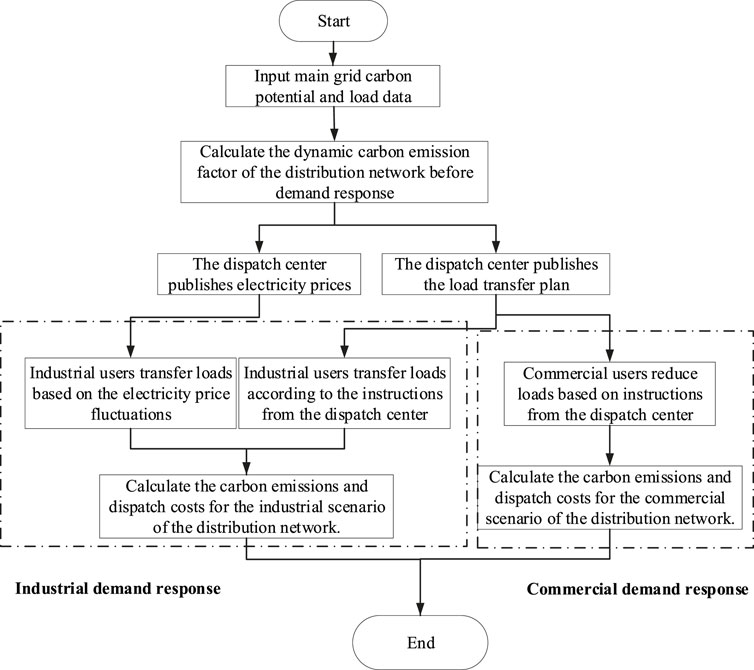
As shown in Figure 1, for different user scenarios, first determine the load power of industrial and commercial loads. For industrial loads, there are two main scheduling methods. One is to arrange production based on the high and low electricity prices, and the other is to respond to transferable load scheduling instructions and report to the dispatch center the load arrangement after demand response. Unlike industrial loads, commercial loads cannot transfer loads and are not affected by electricity prices. The dispatch center mainly issues instructions to reduce loads, and the load reduction is completed in the specified time period. The dispatch center provides compensation according to the agreement, ultimately reducing the dispatch cost and carbon emissions of the distribution network (Song et al., 2023b; Shi et al., 2024).
5 Case study
5.1 Basic data
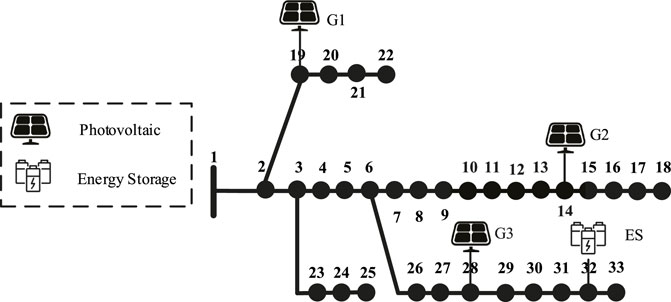
For the modified IEEE 33-node system in the commercial load scenario, the locations of various photovoltaic (PV) units and energy storage are shown in Figure 2. In this study, three distributed PV units with a capacity of 400 kW each are installed at nodes 14, 19, and 28. Additionally, an energy storage system with a capacity of 400 kW/400 kWh is added at node 32.
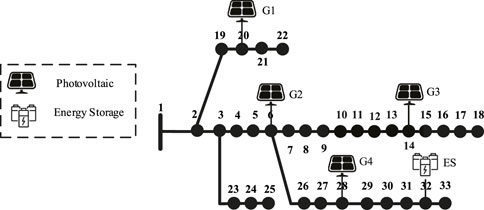
Schematic diagram of the modified IEEE 33-node system for the industrial load scenario as shown in Figure 3. Distributed photovoltaic units with capacities of 1,000 kW are installed at nodes 6, 15, 20, and 28. Additionally, an energy storage device with a capacity of 1000 kW/1,000 kWh is added at node 32.
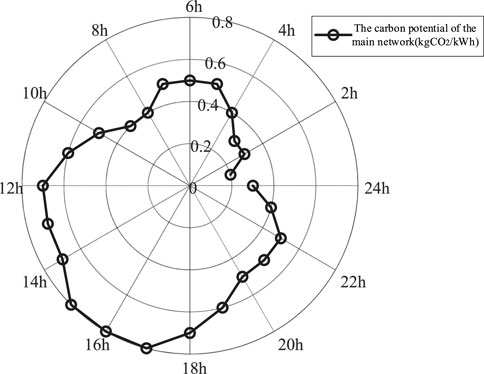
The carbon potential of the main network has been predetermined, as referenced in [4], and its temporal distribution is illustrated in Figure 4.
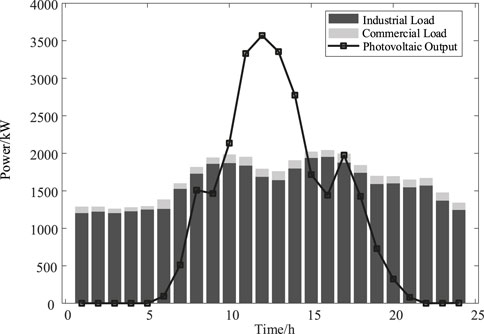
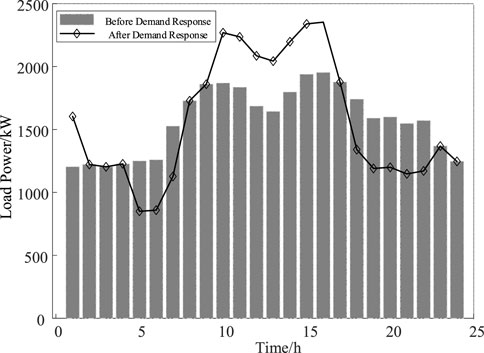
Distributed photovoltaic power generation is mainly influenced by the intensity of sunlight and is also affected by the temperature and humidity of the photovoltaic power generation equipment (Wu et al., 2019; Li et al., 2022b). In this paper, we mainly consider standalone photovoltaic power generation systems and do not consider the issue of power flow feedback. And energy storage and photovoltaic only provide output and do not participate in actual scheduling operations. The photovoltaic output is based on the power generated by a typical day during the summer solstice in a certain area of Jiangsu Province, sampled at 1-h intervals. The load data and photovoltaic output are shown in Figure 5.
On the summer solstice day, the load exhibits a classic double-peak pattern. The commercial load output accounts for approximately 10% of the industrial load output. The photovoltaic (PV) output starts at 6 a.m., peaks around noon at 12 p.m., and concludes by 10 p.m. in the evening.
5.2 Analysis of optimization scheduling results for commercial load
The time period for reducing commercial loads is mainly concentrated from 12:00 to 19:00, while the load output remains unchanged in other time periods, as shown in Figure 6.
Combined with Cplex solution, the results of traditional commercial load optimization scheduling are shown in Table 1. After traditional commercial load demand response on the summer solstice, it decreased by 4.71%, the scheduling cost decreased by 5.2%, carbon emissions decreased by 10.37%, and the compensation cost was 131.17 yuan.
On the other hand, we also compared and analyzed the scheduling results using traditional carbon emission factors and improved carbon emission factors, as shown in Table 2. Due to the fact that scheduling costs do not involve carbon emission factors, whether traditional or improved carbon emission factors are used, scheduling costs remain unchanged; The improvement of the carbon emission factor takes into account the equivalent reduction in carbon emissions from photovoltaic waste, resulting in a decrease of 475.81 kg in carbon emissions compared to before the improvement.

Table 2. Comparison of carbon emission factor scheduling results before and after commercial load improvement.
5.3 Analysis of industrial load optimization and scheduling results
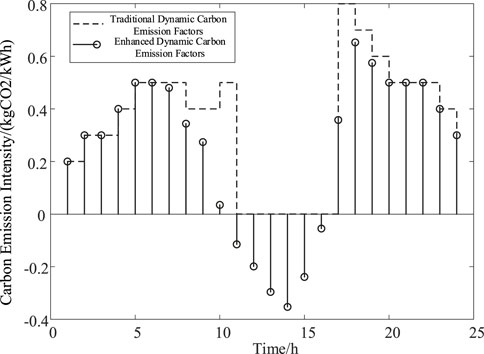
Combining the distribution network and photovoltaic output data, the dynamic carbon emission factors of the distribution network before and after the improvement can be obtained, as shown in Figure 7. The positive half of the dynamic carbon emission factor on the Y-axis represents the overall carbon emission level of the distribution network, with values closer to zero indicating lower carbon emissions at that time. From 11 to 16 o’clock, when the photovoltaic output in the distribution network is high, the traditional carbon emission factor is zero, indicating the occurrence of curtailed photovoltaic power. However, it cannot reflect the difference in curtailed photovoltaic power at different times. The improved dynamic carbon emission factor shows negative values during curtailed periods, with higher absolute values indicating higher curtailed amounts, and values closer to zero indicating higher levels of renewable energy integration.
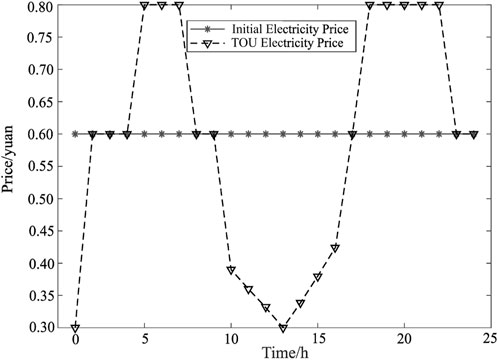
The paper divides the 24 h of a day into three electricity consumption periods: high carbon, medium carbon, and low carbon, based on the magnitude of carbon emissions. Each period consists of 8 h. The decision variable in this study is the time-of-use electricity price. The electricity price influences the amount of electricity consumed during different periods. Additionally, considering the variation in curtailed solar power during periods with negative carbon emission factors, the time-of-use electricity prices also differ accordingly. The time-of-use electricity prices after demand response are illustrated in Figure 8.
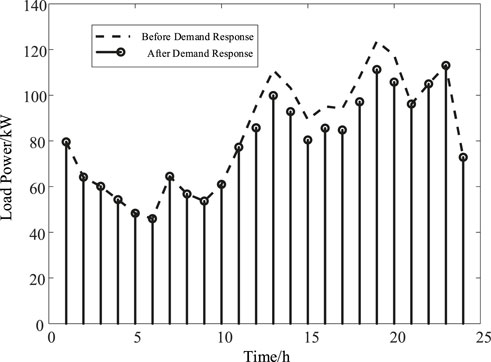
After demand response of industrial load, the distribution grid load is shifted from periods with higher carbon emission factors to those with lower carbon emission factors, as shown in Figure 9. The optimization results of demand response for industrial load are presented in Table 3. Compared to the situation before demand response, the carbon emissions have decreased by 1976.70 kg, and the curtailed solar energy rate has reduced by 4.73%. Additionally, the reduction in carbon emissions before and after demand response based on traditional carbon emission factors is 1250.38 kg. Considering the improved carbon emission factors after demand response, there is an increase of 36.7%. On the other hand, similar to the commercial load scenario, we also compared and analyzed the demand response scheduling results using traditional and improved carbon emission factors, as shown in Table 4. The scheduling cost remained unchanged, and the carbon emissions decreased by 1448.05 kg.

Table 4. Comparison of carbon emission factor scheduling results before and after industrial load improvement.
In addition, to verify the flexibility and transferability of the model, in a 96 node system, as long as the output of distributed power sources and energy storage is given, Still, like 33 nodes, demand response is achieved by adjusting electricity prices for different periods of carbon emission intensity, thereby optimizing the objective function of the entire distribution network (Yang et al., 2023). On the other hand, in the scenario examples involved in this article, due to the relatively simple 10 kV voltage level network, which does not involve many substations and distributed power sources, there is no need for a lot of nodes. Only 33 nodes are needed to simulate the distribution network in the real world and perform basic operation scheduling operations.
6 Conclusion
This paper proposes a low-carbon economic optimization scheduling model for the distribution network, considering an improved dynamic carbon emission factor to shift carbon emissions from the “source” side to the “load” side. Initially, based on the improved dynamic carbon emission factor, the method for calculating the carbon emissions of the distribution network is determined. Subsequently, for both commercial and industrial user scenarios, demand response models are established based on electricity prices and compensation fees, considering system scheduling and constraints. The distribution network is then optimized for scheduling from both economic and low-carbon perspectives. The proposed method is analyzed and validated through an improved IEEE 33-node system.
The results indicate that in the commercial user scenario, issuing load reduction commands during specified time periods from the dispatch center can effectively reduce the system’s scheduling costs and carbon emissions. In the industrial user scenario, incentives based on electricity prices and compensation fees guide users to shift loads from periods with higher carbon emissions to those with lower emissions. Additionally, during periods of high photovoltaic output, adjusting load consumption based on the amount of curtailed energy has increased the photovoltaic integration rate in the distribution network, reducing both carbon emissions and scheduling costs. It is hoped that in the future, this optimization method can be widely applied, and further research can explore coordinated strategies among generation, network, load, and storage to advance the development of the power industry (Pang et al., 2015).
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
XR: Funding acquisition, Supervision, Writing–original draft. HG: Project administration, Writing–review and editing. XZ: Investigation, Writing–review and editing. JG: Data curation, Software, Writing–review and editing. LH: Methodology, Supervision, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Science and Technology Project of State Grid Jiangsu Electric Power Company (“Assessment and Visualization of Low-carbon Technologies for Carbon Neutrality-oriented Distribution Network Framework,” Grant number: J2022118). The authors declare that this study received funding from Xuzhou Power Supply Company of State Grid Jiangsu Electric Power Supply Co Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Conflict of interest
Authors XR, HG, and XZ were employed by Xuzhou Power Supply Company of State Grid Jiangsu Electric Power Supply Co Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chen, H., Mao, W., and Zhang, R. (2021). Low carbon optimization scheduling of power system source load coordination based on carbon emission flow theory. Power Syst. Prot. Control 49 (10), 1–11. doi:10.19783/j.cnki.pspc.200932
Chen, J., Wang, C., and Liu, C. (2023). Dynamic low-carbon dispatch method for power system based on improved carbon emission flow theory. China Electr. Power 56 (03), 162–172.
Ge, J., Liu, Z., and Wang, C. B. (2023). Research on low-carbon optimization operation method of distribution system based on carbon emission flow. Power Grid Technol. 1-10. doi:10.13335/j.1000-3673.pst.2023.0602
Ge, Y., Niu, C., Li, D., and Wang, C. (2022). “Low-carbon economic dispatch of distribution network with carbon capture power plant considering carbon trading,” in 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China, July, 2022, 637–642. doi:10.1109/ICPSAsia55496.2022.9949729
Han, G., Xiong, Li, and Xu, J. (2023). Environmental and economic scheduling of typical industrial load emission characteristics considering demand response. Automation Electr. Power Syst. 47 (08), 109–119.
He, X., Liu, J., and Gao, H. (2023). Robust planning model for solar-energy storage distribution in industrial parks considering photovoltaic uncertainty and low-carbon demand response. Smart Power 51 (02), 69–76.
Ibrahim, S., Laura, M., and Alparslan, M. Z. (2023). Voltage constraint-oriented management of low carbon technologies in a large-scale distribution network. J. Clean. Prod. 2023, 408.
Kaile, Z., Lexin, C., Lulu, W., Xinhui, Lu, and Tao, D. (2020). A coordinated charging scheduling method for electric vehicles considering different charging demands. Energy 2020, 213. doi:10.1016/j.energy.2020.118882
Kang, C., Chen, Q. X., and Xia, Q. (2009). “Research prospects of low-carbon power technology,” 33(02):1–7.
Li, Y., Zhang, N., and Du, E. (2022a). Research on low-carbon demand response mechanism and benefit analysis of power system based on carbon emission flow. Chin. J. Electr. Eng. 42 (08), 2830–2842. doi:10.13334/j.0258-8013.pcsee.220308
Li, Z., Guo, P., and Ma, N. (2022b). Reactive power optimization for distribution system with DG by particle swarm optimization algorithm integrating dual strategies. South. Power Syst. Technol. 16 (6), 14–22+81.
Li, Z., Peng, X., Xu, Y., Zhong, F., Ouyang, S., and Xuan, K. (2023). A stackelberg game-based model of distribution network-distributed energy storage systems considering demand response. Mathematics 12 (1), 34. doi:10.3390/math12010034
Lixia, C., and Yun, Z. (2023). Low carbon economic scheduling of residential distribution network based on multi-dimensional network integration. Energy Rep. 9 (S7), 438–448. doi:10.1016/j.egyr.2023.04.192
Pang, S., Zhang, C., and Zhang, Di (2015). Optimization charging strategy for electric vehicles in residential communities based on adaptive mutation particle swarm optimization algorithm. Electr. Appl. 34 (20), 85–89.
Qiang, L., Yan, J., and Changyu, D. (2023). Low-carbon optimization of distribution networks under the consideration of new energy integration. J. Phys. Conf. Ser. (1), 2659.
Shao, Z., Zhao, Q., and Zhao, Y. (2021). Independent microgrid power supply coordination and configuration optimization. Power Grid Technol. 45 (10), 3935–3946. doi:10.13335/j.1000-3673.pst.2020.2028
Shi, C., Zhu, Y., and Liu, Y. (2024). Low-carbon economic scheduling of wind power-inclusive power systems based on world model deep reinforcement learning. Grid Technol. 1-15. doi:10.13335/j.1000-3673.pst.2023.1899
Song, Z., Hua, F., and Chen, X. (2023a). Distributed resource low-carbon scheduling strategy for distribution networks based on node carbon potential. High. Volt. Technol. 49 (06), 2320–2332. doi:10.13336/j.1003-6520.hve.20230216
Song, Z., Hua, F., and Chen, X. (2023b). Low carbon scheduling strategy for distributed resources in distribution networks based on node carbon potential. High. Volt. Technol. 49 (06), 2320–2332. doi:10.13336/j.1003-6520.hve.20230216
Wu, G., Wu, WANG, and Zhang, Y. (2019). Time decoupled dynamic extended reactive power optimization in incremental distribution network with photovoltaic-energy storage hybrid system. Power Syst. Prot. Control 47 (9), 173–179.
Xiyun, Y., Lingzhuochao, M., Xintao, G., Ma, W., Fan, L., and Yang, Y. (2023). Low-carbon economic scheduling strategy for active distribution network considering carbon emissions trading and source-load side uncertainty. Electr. Power Syst. Res. 2023, 223. doi:10.2139/ssrn.4370986
Xu, G., and Guo, Z. (2023). Resilience enhancement of distribution networks based on demand response under extreme scenarios. IET Renew. Power Gener. 18 (1), 48–59. doi:10.1049/rpg2.12895
Xue, K., Chu, Y., and Zi, L. (2019). Low carbon economic optimization scheduling of integrated energy systems considering flexible loads. Renew. Energy 37 (08), 1206–1213. doi:10.13941/j.cnki.21-1469/tk.2019.08.016
Yang, Mi, Zhou, J., and Lu, C. (2023). Multi-objective two-layer planning of distribution networks based on improved generative adversarial network and carbon footprint. Chin. J. Electr. Eng. 1-15.
Zhang, H., Wang, R., and Liu, Y. (2023). Double layer low-carbon economic dispatch of power systems considering the coupling of source load carbon potential. Power Constr. 44 (12), 28–42.
Zhou, T., and Kang, C. (2019). Research on low-carbon optimization operation method of distribution system based on carbon emission flow. Glob. Energy Internet 2 (03), 241–247. doi:10.19705/j.cnki.issn2096-5125.2019.03.005
Zhou, T., Kang, C., and Xu, Q. (2012). Theoretical exploration of carbon emission flow analysis in power systems. Automation Electr. Power Syst. 36 (07), 38–43+85.
Keywords: carbon emission flux theory, improved dynamic carbon emission factor, distribution network, demand response load, low carbon scheduling
Citation: Ren X, Gao H, Zhang X, Gu J and Hong L (2024) Multivariate low-carbon scheduling of distribution network based on improved dynamic carbon emission factor. Front. Energy Res. 12:1380260. doi: 10.3389/fenrg.2024.1380260
Received: 01 February 2024; Accepted: 04 March 2024;
Published: 04 April 2024.
Edited by:
Yuanxing Xia, Hohai University, ChinaReviewed by:
Yongli Ji, Nanjing Institute of Technology (NJIT), ChinaJicheng Fang, State Grid Nanjing Power Supply Company, China
Copyright © 2024 Ren, Gao, Zhang, Gu and Hong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jie Gu, MTc0Mzc4OTQ4OEBxcS5jb20=
 Xiaofeng Ren1
Xiaofeng Ren1 Jie Gu
Jie Gu